The 2020 European Seismic Hazard Model: overview and results

The 2020 update of the European Seismic Hazard Model (ESHM20) is the most recent and up-to-date assessment of seismic hazard for the Euro-Mediterranean region. The new model, publicly released in May 2022, incorporates refined and cross-border harmonized earthquake catalogues, homogeneous tectonic zonation, updated active fault datasets and geological information, complex subduction sources, updated area source models, a smoothed seismicity model with an adaptive kernel optimized within each tectonic region, and a novel ground motion characteristic model. ESHM20 supersedes the 2013 European Seismic Hazard Model (ESHM13; Woessner et al., 2015) and provides full sets of hazard outputs such as hazard curves, maps, and uniform hazard spectra for the Euro-Mediterranean region. The model provides two informative hazard maps that will serve as a reference for the forthcoming revision of the European Seismic Design Code (CEN EC8) and provides input to the first earthquake risk model for Europe (Crowley et al., 2021). ESHM20 will continue to evolve and act as a key resource for supporting earthquake preparedness and resilience throughout the Euro-Mediterranean region under the umbrella of the European Facilities for Seismic Hazard and Risk consortium (EFEHR Consortium).

1 Introduction

The 2020 update of the European Seismic Hazard Model (ESHM20; Danciu et al., 2021a) is the third generation of pan-European probabilistic seismic hazard models (Jimenez et al., 2003; Woessner et al., 2015). ESHM20 serves as the reference hazard model in the Euro-Mediterranean region, with the goal of supporting earthquake mitigation and resilience planning (Bisch, 2018; Crowley et al., 2021; Santarsiero, 2018). Overall, ESHM20 is developed within the seismotectonic probabilistic framework (Danciu and Giardini, 2015), incorporating seismicity, tectonic and geological datasets, and information. Within this probabilistic framework, several assumptions are made; e.g. earthquake occurrence in time and space is modelled as a memory-less process requiring declustering of the earthquake catalogue to remove the dependent earthquakes; tectonic regionalization to separate regions with different geodynamical settings; seismogenic sources and active faults as proxies for future seismicity; a novel backbone ground motion model; and open access to its datasets, components, and results. The exceedance probabilities of various ground motion intensity types and levels are then computed for the entire Euro-Mediterranean region using a regional hazard model that combines multiple seismogenic sources and a backbone ground motion model to account for epistemic uncertainty. The main characteristics of ESHM20 can be summarized as follows:

• It is a community-driven model, with earth science scientists, hazard and risk experts, engineers, and practitioners participating in the development phase. A core team was responsible for conducting research, coordinating the development, and collaborating closely with regional experts on a variety of tasks, from gaining access to raw data to the design and implementation of the model. Community feedback and recommendations were carefully considered via multiple channels, such as one-on-one meetings between core team members and regional experts, regional workshops, technical webinars, and conferences.

• It includes updated, unified, and cross-border harmonized input datasets, i.e. earthquake catalogues both historical (Rovida et al., 2022; Rovida and Antonucci, 2021) and instrumental (Grünthal and Wahlström, 2012; Lammers et al., 2023), tectonic info, geological faults, and subduction zones (Basili et al., 2022, 2023). There is an extension of the model to cover the Canary Islands and Azores archipelago.

• Seismogenic source models are revisited and updated, including a harmonized uniform area source model and a hybrid source model that combines active faults and background smoothed seismicity. Inherent epistemic uncertainties in the earthquake rates are handled via multiple values of the parameters of a Gutenberg–Richter (GR) model, specifically a_GR, b_GR, and upper-bound magnitude M_max. We also used alternative models of the magnitude frequency distributions, e.g. double truncated GR distribution and a tapered Pareto distribution (Kagan and Jackson, 2000), to characterize the seismic productivity of the area sources.

• It uses the Engineering Strong Motion (ESM) database, the largest database of ground motion recordings in the Euro-Mediterranean region, curated and uniformly processed as described by Lanzano et al. (2019);

• It offers a novel ground motion model (GMM) logic tree based on the concept of a regionalized backbone approach (Kotha et al., 2020, 2022; Weatherill et al., 2020, 2024; Weatherill and Cotton, 2020). This novel approach capitalizes upon the large ESM database, and it follows the concepts initially proposed by Douglas (2018). A new ground motion predictive model for ground shaking from shallow crustal seismicity was developed and calibrated to reflect region-to-region differences in source and attenuation scaling and their epistemic uncertainties across Europe (Kotha et al., 2020, 2022; Weatherill et al., 2020). Notably, such features of the ground motion models have not been captured explicitly in earlier GMM logic trees (e.g. Delavaud et al., 2012; Danciu et al., 2018a; Pagani et al., 2020). This approach was further adapted to regions of limited data such as the stable cratonic region of northeastern Europe (Weatherill and Cotton, 2020) and the subduction and deep seismicity sources by capitalizing on recent developments in regionalized ground motion modelling worldwide.

• Statistical testing and sanity checks were routinely integrated as part of the model-building process. We used statistical tests of earthquake rate forecasts to select the declustering technique and determine the magnitude–time completeness intervals, while sanity checks were also conducted to assess the consistency of the earthquake rate forecast of individual source models and the final ensemble model. Sensitivity analyses, as well as comparisons with national hazard models, were conducted as part of the model-building development.

• The main logic tree combines both the earthquake rate forecast and backbone ground motion model, and it was designed for the large-scale computation of the ground-shaking hazard depicted by peak ground acceleration (PGA) and a pseudo-acceleration response spectrum (SA) at 15 spectral ordinates from 0.05 to 5 s. The horizontal component is described by the 50th percentile of the response spectra of two horizontal components projected onto all non-redundant azimuths, i.e. “RotD50” (Kotha et al., 2020).

• Complex computational models and pathways were implemented in the OpenQuake hazard engine (version 3.14, https://github.com/gem/oq-engine, last access: August 2024; Pagani et al., 2014) which was continuously enhanced throughout the model development cycle. The computational input files are released publicly under an open Creative Commons license (see https://creativecommons.org/, last access: May 2024), which allows users to reproduce the results and adapt the model for different needs and applications. All input datasets and the results are publicly available at http://www.hazard.efehr.org (last access: August 2024; Danciu et al., 2017, 2021a) and at the project's repository (https://gitlab.seismo.ethz.ch/efehr, last access: August 2024). Additional links and repositories are listed in the “Code and data availability” section of this paper.

Furthermore, during the model development we established a close collaboration with a working group from the Technical Committee of the European Committee for Standardization (TC250/CEN). This working group is responsible for updating the seismic action specifications within the Eurocode standards (SC8). During its final development cycle between 2020 and 2021, experts from Albania, Bulgaria, Croatia, France, Finland, Greece, Germany, Italy, Iceland, Portugal, Romania, Slovenia, Sweden, Switzerland, Türkiye, and Norway evaluated and tested the ESHM20 components and outcomes. Although no final agreement had been reached at the time this paper was submitted for publication, the convener suggested to SC8 that the two ground-shaking hazard maps derived from ESHM20 will be included in the next generation of EN1998-1-1 Annex G (Labbé and Paolucci, 2022). These maps will serve as an informative reference of ground-shaking values across the Euro-Mediterranean region as part of the next update of the European seismic design code (CEN EN1998-1-1) in the region.

ESHM20 underwent a release cycle that included a community preview version, a beta version, and a final version that was made available in December 2021 and publicly released in May 2022. The collaboration between the model core team, community members, and communication experts was essential to this release, with the goal of making outreach products to efficiently communicate earthquake-related hazards and risk models and results. The approach used to make the hazard and risk model accessible and easily understandable to the general public drew upon communication concepts derived from mass media, including communication principles, key messages, specific products, and target audiences. Two surveys were conducted to ensure that these outreach products met the needs of end users, with a focus on the interactive hazard and risk web viewer and specialized posters illustrating the European earthquake hazard and risk maps (Dallo et al., 2024). The outreach materials are available in various languages.

In this contribution, we provide an overview of the background, scientific and collaborative framework, computational aspects, and key results of ESHM20. Many aspects of the updated hazard model are presented and discussed in the model's technical report (Danciu et al., 2021a) and the lessons learned in Danciu et al. (2022), while the remaining components are part of this special issue. Accompanying papers describe the historical catalogue (Rovida et al., 2022), the ground motion models (Weatherill et at., 2024), and overall model implementation and documentation (EFEHR Technical Report; Danciu et al., 2021a). A description of the active fault database and subduction systems is described by Basili et al. (2022, 2023). We begin by illustrating and discussing the key differences between ESHM20 and its precursor ESHM13 (Giardini et al., 2014) in Sect. 2. In Sect. 3, we describe key input datasets underpinning ESHM20. Subsequently, in Sect. 4 we describe details of the spatio-temporal earthquake rate forecasts and the methodologies adopted. Section 5 provides a concise overview of ground motion models, while Sect. 6 explores the primary logic tree and computational aspects in more detail. The latter section delves into the main findings of ESHM20, including the contributions to hazard from different seismogenic source models, as well as the associated range of uncertainties. Finally, Sect. 7 summarizes the main outcomes and offers an outlook for future research directions. Overall, this paper aims to describe the key features of the model, its results, and their accessibility. Readers are encouraged to access ESHM20's input datasets, documentation, and computational files on the publicly accessible repository listed in the “Code and data availability” section of this paper.

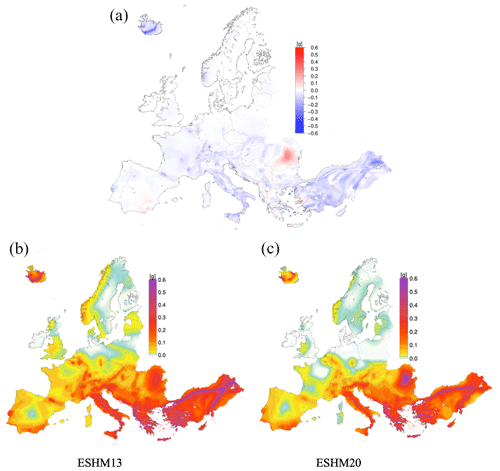
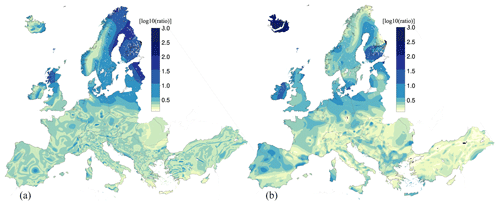
Figure 1 The top panel (a) highlights regions where the mean peak ground acceleration (PGA) values for ESHM20 increased (shown in red) or decreased (shown in blue) as compared to ESHM13. The bottom panels (b) and (c) show the spatial distribution of the mean PGA for a return period of 4745 years for ESHM13 (b) and ESHM20 (c). The maps are both estimated for a generic rock site class with a shear wave velocity V_s30 ∼ 800 m s⁻¹.

2 ESHM20 (Danciu et al., 2021a) vs. ESHM13 (Woessner et al., 2015): what is different?

Regional seismic hazard models are evolving models that progress over time, with the most recent models based on updated input datasets and the most recent scientific outcomes. This is obvious when comparing, for instance, the ground motion datasets underlying some of the ground motion models used in ESHM13 (Delavaud et al., 2012; Woessner et al., 2015), with an average of about 500 strong motion records used, and more recent GMMs. Nowadays, the significantly larger datasets make empirical ground motion models more robust (Kotha et al., 2020, 2022; Kuehn et al., 2019; Lanzano et al., 2019, 2020; Manea et al., 2022) and support the development of regional adjustments and modelling of epistemic uncertainties (Douglas, 2018; Kowsari et al., 2023; Lavrentiadis et al., 2023; Weatherill and Cotton, 2020). Similarly, the updates to the earthquake catalogues and revisiting the seismogenic source models must be accounted for as a potential source of differences between the two models. The spatial distributions of the peak ground acceleration (PGA) for a return period of 475 years of both ESHM13 and ESHM20 have similar spatial patterns, and the difference map given in Fig. 1 illustrates how the PGA_ESHM20 and PGA_ESHM13 mean values differ at each location. Overall, when compared with ESHM13 the PGA values of ESHM20 for a return period of 475 years have been decreased in various regions. There are certain regions in Albania, Greece, southern Portugal, southern Spain, and western Türkiye that exhibit lower values when compared with ESHM13. Such differences are the result of various factors including updated input datasets, updated seismogenic source models, updated subduction sources, updated slip rates and maximum magnitude of the active fault, and a different source model logic tree (Danciu et al., 2021a, 2022).

Indeed, all these changes resulted in an updated earthquake rate forecast. Comparison earthquake rate forecast maps between the two versions of the European hazard models are given in the Supplement.

Moreover, the changes to the ground motion models are significant due to the way in which epistemic uncertainties were handled, with a paradigm shift from multiple ground motion models (Delavaud et al., 2012) to the regional backbone approach (Douglas, 2018; Weatherill et al., 2020). Weatherill et al. (2020) compare the ground motion of the two regional hazard models for the active shallow crust and find that the ESHM20 models compute lower values for very short spectral periods (PGA and peak surface acceleration (PSA) 0.1 s) than those used in ESHM13; differences also occur at greater distances, where the general trend for ESHM20 is towards faster attenuation. Furthermore, the ground motion regionalization used in ESHM20 can be considered a partially non-ergodic model (Weatheril et al., 2024). Consequently, the core and body of the ESHM20 regional backbone logic tree predict smaller motions than the ESHM13 ground motion logic tree. It is worth noting that the ground motion models of ESHM13 are based on datasets of ground motion recordings from outside of Europe. These recordings may have a different attenuation rate, reflect unique source characteristics, or exhibit site conditions not found in the ESM database (Lanzano et al., 2019). In contrast, the increased number of strong motion records from the Apennine region in Italy shifts the centre of the strong motion dataset toward conditions that are predominantly more rapidly attenuating than the rest of Europe. Comparison plots between the ground motion models used in ESHM20 and ESHM13 are also given in the Supplement. Additional factors may also contribute to these differences in weighting schemes applied to the two models, as well as the model implementation in OpenQuake (Pagani et al., 2014). In ESHM13, the weighting scheme is return-period-dependent and applied in post-processing, whereas in ESHM20 the weights are applied to each branch. A sampling technique of the entire logic tree was then used to obtain the results of ESHM20. To conclude, the transition from ESHM13 to ESHM20 represents the continuous effort in regional seismic hazard advancement, and ESHM20, with its updated datasets, methodological enhancements, and comprehensive model integration, now stands as the reference model for the region, superseding ESHM13.

3 Main input datasets

ESHM20 is based on the integration of multidisciplinary datasets and expert information. The main datasets include the unified earthquake catalogue, both historical (Rovida et al., 2022; Rovida and Antonucci, 2021) and instrumental (Lammers et al., 2023) earthquake catalogues, shallow active faults and subduction systems (Basili et al., 2022), and ground motion recordings (Lanzano et al., 2019). All datasets were meticulously collected, uniformly processed, and harmonized across the pan-Euro-Mediterranean region. However, due to the heterogeneous seismogenic characteristics across the Euro-Mediterranean region, the compiled datasets exhibited variations in completeness, both spatially and temporally. This inherent variability in the quality of data presented significant modelling challenges for both seismogenic source and ground motion characterization, ultimately influencing ESHM20's overall uncertainties and outcomes. A tectonic regionalization of the Euro-Mediterranean region was developed using the information and data from the ESHM13 and NEAMTHM18 models (Basili et al., 2021). The regionalization consists of 11 tectonic domains, namely active volcanoes, back-arc and orogenic collapse, continental rift, oceanic rift, contractional wedge, accretionary wedge, conservative boundary, transform zones proper, shield, stable continental region, and stable oceanic region. This regionalization is the basis for the tectonic layer (i.e. hereinafter TECTO), which is later used for organizing the spatial consistency of the seismogenic sources.

The European Fault-Source Model 2020 (EFSM20; Basili et al., 2022) is a compilation of the existing regional active fault databases. EFSM20 includes 1248 crustal faults spanning a total length of 95 100 km and 4 subduction systems, namely the Gibraltar, Calabrian, Hellenic, and Cyprus arcs. The fault model covers a region with a buffer of 300 km around all European countries (except for Overseas Countries and Territories) and a maximum depth of 300 km for the subducting slabs. All parameters (i.e. fault trace, geometry, depth, length, width, strike, dip, rake, and slip rate values) needed to develop a seismogenic source model were estimated for crustal faults and subduction systems (Basili et al., 2023).

The Unified Earthquake Catalogue consists of two parts: the European PreInstrumental Earthquake Catalogue EPICA v.1.1 (Rovida et al., 2022; Rovida and Antonucci, 2021), with seismicity that occurred between the years 1000 and 1899 CE, and the so-called instrumental earthquake catalogue (with seismicity that took place after 1900 CE) based on the updated European-Mediterranean Earthquake Catalogue (EMEC) (Lammers et al., 2023). EPICA v1.1 includes earthquake data from 1000 to 1899 CE and builds upon the latest knowledge gathered in the European Archive of Historical Earthquake Data (AHEAD; Albini et al., 2013; Locati et al., 2014; Rovida and Locati, 2015). It contains 5703 earthquakes with maximum observed intensity above 5.0 or M_w larger than 4.0. It is based on 160 macroseismic data point (MDP) sources and 39 regional catalogues selected from AHEAD. These datasets were considerably updated with respect to those used for compiling the historical catalogue for ESHM2013 (Stucchi et al., 2013). A systematic analysis of these data resulted in the selection of the most representative description of each earthquake, independently from national constraints. For 3297 earthquakes, parameters are newly assessed from MDPs using harmonized procedures based on the attenuation of macroseismic intensity from macroseismic data points (MDPs), with the goal of ensuring consistency of earthquake parameters across countries. These parameters are then combined and integrated with parameters harmonized from recent regional catalogues. The instrumental earthquake catalogue spans from 1900 to 2014 CE and updates the earlier EMEC, constructed and adapted for use in ESHM13 by Grünthal et al. (2013). EMEC compiles earthquake data from various local, national, and international earthquake bulletins, along with special studies for particular regions or earthquake sequences. The data are then harmonized by applying region-specific hierarchies that identify the preferred earthquake source from those compiled for each event. Using region-specific and magnitude-scale conversion relations, earthquake magnitudes are rendered into a common reference magnitude scale, equivalent to moment magnitude (M_w). During the compilation process, the European catalogue was aligned with existing harmonized national catalogues where possible, which along with special studies were prioritized over local and national bulletins. The updated EMEC extends the most recent period of coverage that previously ended in 2006 (Grünthal and Wahlstöm, 2012; Grünthal et al., 2013) and incorporates recent national catalogues such as the Catalogo Parametrico di Terremoti Italiani (CPTI) and the 2017 French Seismic Catalogue (F-CAT; Manchuel et al., 2018), among others. The instrumental earthquake catalogue now contains over 55 700 shallow and deep earthquakes with M_w greater than 3.5 (Lammers et al., 2023). The unified earthquake catalogue was further analysed to identify and remove the foreshocks and aftershocks as a prerequisite of the Poisson assumption for the earthquake recurrence rates. The unified earthquake catalogue was declustered using the default declustering method (Grünthal, 1985), the same as in ESHM13. We then performed comparisons amongst various declustering techniques, including the time–space window method (Gardner and Knopoff, 1974; Uhrhammer, 1986), cluster method (Reasenberg, 1985), and the spatial–time-correlation metric-based declustering (Zaliapin et al., 2008).

At a glance, the cluster method retained the highest number of events post-declustering, surpassing both Zaliapin's approach and the standard time–space window technique (Grünthal, 1985) used in ESHM13. Additional spatial analyses, i.e. comparison of events per 50 km by 50 km grid cells, as well as statistical tests, suggested that the cluster method (Reasenberg, 1985) is an alternative to the reference declustering method (Grünthal, 1985). Various statistical tests (i.e. Kolmogorov–Smirnov (KS), Student's t test, and w test; Mizrahi et al., 2021; Nandan et al., 2021) were used to evaluate the declustering technique by comparing the rate forecasts derived from learning (up to December 2006) and target (January 2007 to December 2014, M_w > 4.5) catalogues. The target catalogue was declustered with the same technique, and the activity rates were estimated at the regional level. None of the declustering methods significantly outperformed the reference (i.e. Grünthal, 1985) method. However, the cluster method (Reasenberg 1985) emerged as a potential alternative due to its robust testing performance and identification of more mainshocks. Initially, two alternative declustering methods were part of the logic tree of the seismogenic sources of the pre-release model. However, due to an overall increase in computational complexity, we decided to simplify the model. After conducting several sensitivity analyses, the alternative cluster-based declustering method (Reasenberg 1985) was not implemented. In addition, there were open discussions within the scientific community about the implications and challenges associated with declustering. Numerous studies (Beauval et al., 2006, 2013; Marzocchi et al., 2020; Marzocchi and Taroni, 2014; Meletti et al., 2021; Mizrahi et al., 2021; Sesetyan et al., 2018; Taroni and Akinci, 2021) have explored the effects of declustering and implications for seismic hazard modelling. These studies suggest that the use of declustering could lead to reduced seismicity rates, potentially resulting in underestimated hazard estimates, especially in regions characterized by seismic swarms and prolonged aftershock sequences. However, we acknowledge the ongoing need for further research to explore this topic in greater depth, as well as time to reach a community consensus; nonetheless our approach closely adheres to current practices in the field (Gerstenberger et al., 2020). Likewise, the assessment of the catalogue completeness is arguably as crucial, if not more so, than the choice of the declustering algorithm. The key parameter in this case is the magnitude of completeness (M_c), defined as the lowest value of magnitude at which all events are detected in space and time. M_c is variable in space and time, and – in general terms – it decreases with time given the increase in the density of seismic stations. To effectively accomplish this in ESHM20, a new algorithm that combines the temporal course of earthquake frequency (TCEF) approach (Nasir et al., 2013) with the maximum curvature method (Wiemer and Wyss, 2000; Woessner and Wiemer, 2005) was proposed. This innovative method involved an iterative process beginning with the declustering of the earthquake catalogue, followed by dividing it into various magnitude intervals and generating cumulative earthquake time series for each interval. The time series were used to visualize and detect the change points in the catalogue's completeness. Next, statistical tests were used to validate the findings. Finally, the results of this procedure were the M_c values and completeness time intervals for the completeness super zones (CSZs) of ESHM20. Details are given in Sect. 2.2 of the ESHM20 Technical Report (Danciu et al., 2021a).

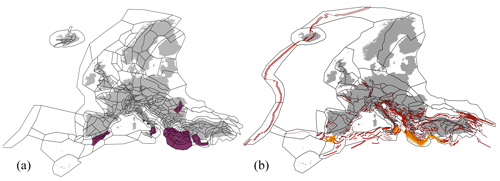
Figure 2 Schematic illustration of ESHM20's seismogenic source models: (a) shallow crust area sources (outlined in black), volcanic area sources (filled black polygons), and deep seismicity and subduction in-slab (purple polygons); (b) shallow crust active faults (red lines), subduction interface (orange polylines). Tectonic zonation is highlighted as black polygons.

4 Seismogenic source models: spatio-temporal earthquake rate forecast

The ESHM20 seismogenic source characterization builds upon the ESHM13 legacy, and it comprises four distinct source models to capture the spatial and temporal variability in earthquake occurrence across the pan-European region.

• Unified area source model. This model updates the ESHM13 area source model by incorporating new area sources of the recent national seismic hazard models and considering the feedback and opinions of the local experts. More specifically, the model incorporates contributions from the recent earthquake hazard models from Italy (Meletti et al., 2021; Visini et al., 2022), Germany (Grünthal et al., 2018), Spain (Benito Oterino et al., 2012; Rivas-Medina et al., 2018), the United Kingdom (Mosca et al., 2022), Slovenia (Šket Motnikar et al., 2022), Switzerland (Wiemer et al., 2016), Türkiye (Sesetyan et al., 2018), Iceland (Halldórsson et al., 2022), France (Baize et al., 2013), Bulgaria (Solakov et al., 2014), Finland (Fülöp et al., 2023), the Balkan region (Mihaljević et al., 2017), and Romania (Vacareanu et al., 2016). Further, cross-border harmonization (i.e. removing the overlapping area sources at national borders) is applied to all sources, following Danciu et al. (2018b) and Pagani et al. (2020). This source model includes regions of homogenous seismicity classified as shallow crustal, volcanic, subduction in-slab, and deep seismicity (e.g. Vrancea region, Romania). They define regions with a known history or potential for seismic activity but not necessarily all associated with specific faults (see Fig. 2a).

• Hybrid model of active faults and background smoothed seismicity. The model integrates active faults with background seismicity in regions where the active faults are identified; otherwise, a grid-based smoothed seismicity is used. An adaptive kernel was regionally calibrated and used for smoothing the seismicity. In Fig. 2b, the active faults (red lines) are primarily observed along the tectonic boundary that extends through the Mediterranean region. This would likely include countries like Greece, Türkiye, and Italy and regions along the coastlines of the Adriatic, Aegean, and Ionian seas. The European Fault-Source Model 2020 (EFSM20; Basili et al., 2023) is the update of active faults across the Euro-Mediterranean region, following the European Database of Seismogenic Faults (EDSF) (Basili et al., 2013) which was used for ESHM13. The dataset covers the Mid-Atlantic Ridge, the Caucasus, northern Africa, and Iceland, with 1248 crustal faults spanning 95 100 km and 4 subduction systems. The model includes a 300 km buffer around all European countries (excluding Overseas Countries and Territories) and a maximum subducting slab depth of 300 km. The shallow faults are defined as composite faults (Haller and Basili, 2011; Basili et al., 2013), are not segmented, and can accommodate earthquake ruptures of any size up to the maximum magnitude (M_max) at any location along their length and width. This definition inherently includes multi-segmented ruptures within individual fault systems such as the 2023 Türkiye–Syria M_w 7.8 rupture, which is represented in our model as a single event within its respective fault system. However, ruptures that jump from one fault system to another are not considered in the current implementation.

• Subduction sources. These sources represent the subduction interface and in-slab seismicity of the Hellenic, Cyprian, Calabrian, and Gibraltar arcs.

• Non-subducting deep seismicity sources. This model accounts for nested seismicity with depth in Vrancea, Romania, and the cluster of deep seismicity in the southern Iberian Peninsula.

Earthquake activity rates for individual seismogenic sources are estimated under the assumption that regional seismicity follows a memoryless Poisson process. This process is characterized by a stationary mean rate of occurrence defined by a Gutenberg–Richter (GR) model and its main parameters (a_GR and b_GR). The activity rate parameters are estimated for large-scale tectonic domains (TECTO zonation layer) and the zonation-based area source model (ASM) using the declustered unified earthquake catalogue and the magnitude–time completeness intervals. The TECTO zonation layer as shown in Fig. 2b is used to organize the spatial distribution of the source models within the model, delineating the areas with similar characteristics inferred from geological, geophysical, and seismological data. Each polygon within the TECTO layer represents a combination of multiple area sources and provides a basis for estimating more stable GR parameters given the larger number of earthquakes within each TECTO zone. The seismic productivity of the active shallow faults is calculated by converting long-term geological or geodetic slip rates into activity rates under the assumption of moment conservation (Anderson and Luco, 1983; Bungum, 2007; Danciu et al., 2018b). In this approach, the seismic moment rate is analytically converted into the number of earthquake ruptures per magnitude bin per year, and then this number is uniformly distributed over the entire fault area. Therefore, we do not apply any statistical fitting procedure. For each fault, three slip rates (converted to a_GR), three M_max values, a single regional b_GR value (from TECTO), and the average fault area are considered. The M_max values of each fault source are obtained from empirical magnitude and fault geometry scaling relationships (Leonard, 2010, 2014) and take into account the full range of uncertainties of the fault geometries and the scaling relations. The three M_max values of each fault correspond to represent the 2nd, median, and the 98th quantiles of the M_max distribution.

Similarly, the empirical equations of Allen and Hayes (2017) were used to estimate the M_max for subduction interface sources; the activity parameters were obtained from a rather complex logic tree with more than 2800 end-branches. For area sources, the M_max is updated following the strategy of ESHM13. The lower value of the M_max is calculated using the highest-magnitude value observed for that tectonic regime, including the average standard error in that magnitude in the entire earthquake catalogue. The second and third values of M_max add 0.3 and 0.6 magnitude increments to the lower-bound magnitude value, respectively. Finally, two types of magnitude–frequency distributions (MFDs) are used to characterize the earthquake recurrence models for the area sources: a double truncated GR and a tapered Pareto distribution (TPD; Kagan and Jackson, 2000).

Statistical testing and sanity checks are critical components of the model-building process, particularly when reaching scientific consensus is difficult (Meletti et al., 2021). We performed statistical analyses to assess earthquake rate forecasts within the seismogenic source model at each development stage. Sanity checks were routinely conducted by comparing the forecasted total number of earthquakes across different magnitude bins (M_w ∼ 4.5 to 8.5) against the observed number of events within various tectonic domains. These sanity checks helped us to identify and address discrepancies in the forecasts and reconcile them when possible. Additionally, retrospective testing was conducted by estimating the information gain, which quantifies the differences in performance between earthquake rate models using only the observed M_w ≥ 6 earthquakes from the unified earthquake catalogue. Again, the information was used to assess the performance of each individual source model, as well as of the ensemble earthquake rate forecast.

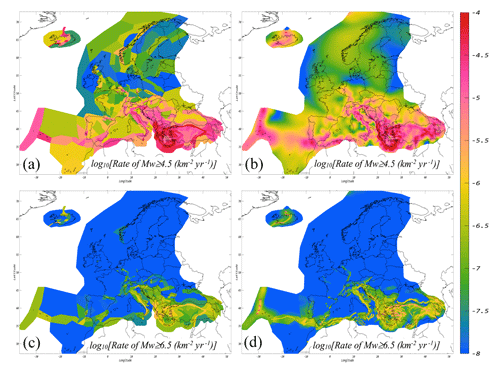
Figure 3 Spatial distribution of annual recurrence rates in log units as forecasted by ESHM20's seismogenic source models. Panel (a) displays the annual rates for events with M_w > 4.5 forecasted by the shallow area sources, while panel (b) shows those from the hybrid model incorporating active shallow crust faults and background smoothed seismicity. Similarly, panel (c) presents the annual rates for events with M_w > 6.5 from shallow area sources and panel (d) from the hybrid model with active shallow faults and background smoothed seismicity. All rates are normalized per unit of area.

Figure 3 illustrates the spatial distribution of the forecasted annual rates of the two main source models. Figure 3a displays the rates for events with M_w ≥ 4.5 from shallow area sources, while Fig. 3b shows those from the hybrid model incorporating active shallow faults and background smoothed seismicity. Similarly, Fig. 3c presents the rates for events with M_w ≥ 6.5 from shallow area sources and Fig. 3d from the hybrid model with active shallow faults and background smoothed seismicity. It is worth noticing that the earthquake rate forecasts across the two primary source models of the ESHM20 model exhibit remarkably consistent trends, though the spatial variability in the earthquake rates is still evident. For instance, in the case of M_w ≥ 4.5, the spatial variability in the earthquake rates is more clearly driven by the shapes of specific area sources, as opposed to the more diffused pattern observed in the smoothed seismicity. Similarly, for magnitudes greater than M_w ≥ 6.5, the consistency of the spatial pattern of the forecasted earthquake rates is even more evident. This is a direct consequence of a deliberate modelling decision to use active faults as spatial proxies in the delineation of area sources, as seen in Fig. 3c and d. However, the forecasted earthquake rates tend to be higher for active faults in comparison to those of area sources. ASM forecasts a net yearly rate of M_w ≥ 4.5 of about 91.60 and 1.26 for events with M_w ≥ 6.5. On the other hand, hybrid rate forecasts (active faults and smoothed seismicity) forecast a net yearly rate of about 82.40 for M_w ≥ 4.5 and 2.03 for M_w ≥ 6.5.

5 Ground motion characteristic models: synopses

The ground motion model (GMM) used in ESHM20 incorporates regional features of the seismic source, path and site conditions, and aleatory (random) and epistemic (model-to-model) uncertainties. Epistemic uncertainty is typically captured using multiple ground motion models selected from the literature and applied as alternative branches in a logic tree (Delavaud et al., 2012; Danciu et al., 2018b; Lanzano et al., 2020). However, the widely used multiple model approach has some limitations, such as the tendency for selected models to share common underlying data, leading to similar predictions for well-represented scenarios (e.g. magnitude range 4.5 to 5.5 and source-to-site distances from 30 to 100 km), inconsistent parameterizations between models, and cases where epistemic uncertainty may be underestimated owing to a lack of suitable models in the literature. To address these issues, in ESHM20 we adopt a scaled-backbone approach that develops on ideas first suggested by Douglas (2018). For shallow crustal seismicity a suitable backbone GMM is developed from the large dataset of ground motion observations in the ESM database (Lanzano et al., 2019). With these data, region-specific adjustments are constrained within the regression and their corresponding distributions applied in the hazard calculation to capture epistemic uncertainty. These adjustments account for region-to-region variability in the model and allow for a more complex representation of the underlying uncertainty. The use of region-specific adjustments also enables the transition from an ergodic to a non-ergodic model, where systematic effects in specific regions are identified and extracted from the aleatory variability. This process helps reduce aleatory uncertainty and allows new data to refine the model calibration over time. The ESHM20 backbone model for active shallow crust is built upon the regional ground motion model of Kotha et al. (2020, 2022), with the development of the ESHM20 GMM logic tree proposed by Weatherill et al. (2020) and the final details of the implementation given in Weatherill et al. (2024).

The purely data-driven approach for the development and calibration of the “regionalized, scaled-backbone logic tree” cannot be applied as is to all regions of Europe as data are limited or absent in some cases. For example, in the tectonically stable “cratonic” region of northeastern Europe the seismological properties of the crust differ significantly from those of southern and western Europe, warranting a different approach to ground motion characterization and its epistemic uncertainty. Weatherill and Cotton (2020) propose a GMM logic tree for application in northeastern Europe. They do so by first analysing different geophysical datasets for Europe to demonstrate the close analogy between the stable “shield” region of the Baltic Sea and its surrounding countries and the tectonically stable crust of the central and eastern United States (CEUS). Then, leveraging the suite of GMMs recently developed for the CEUS as part of the Next Generation Attenuation East (NGA East) project (Goulet et al., 2021), they fit a modified form from Kotha et al. (2020) to the distribution of expected ground motions predicted by the different NGA East GMMs. The model-to-model variability, σ_μ, is used to quantify the scaling factors to be applied to this new backbone to represent the epistemic uncertainty in the expected ground motions for this low-seismicity region.

The regionalized backbone GMM concept was further expanded to encompass deeper seismic activity, specifically in regions such as Vrancea, Romania, as well as subduction systems including the Hellenic, Cypriot, Calabrian, and Gibraltar arcs. Given the limited availability of ground motion data pertaining to earthquakes occurring in subduction zones, the development of a new GMM for subduction and deep seismicity was not straightforward. The so-called “BC Hydro” model of Abrahamson et al. (2016) has been identified as a suitable backbone GMM for the subduction regions. This GMM fulfils the necessary criteria of the project and exhibits a consistently good fit to observed data in the ESM database across various spectral periods in each of the three subduction regions. Moreover, it was determined that the Abrahamson et al. (2016) ground motion model (GMM) for subduction in-slab events is also applicable to the Vrancea deep non-subduction zone. Using the ground motion data for these regions included in the ESM database for small- to moderate-magnitude earthquakes, we adjust the anelastic attenuation term to align it with the seismological properties of the eastern Mediterranean; however, the narrow magnitude range of recordings prevent us from recalibrating the source scaling GMM selected. Additionally, the BC Hydro GMM includes a fore-arc and back-arc scaling term with faster attenuation for back-arc sites, and a trend also presents itself in the ground motion data from the Hellenic arc and Vrancea deep seismic zones. While the fore-arc and back-arc scaling coefficients were not themselves revised owing to the limited dataset in the back-arc regions, further modifications were made to the BC Hydro model to allow a smoother transition from the fore-arc to the back-arc regime, thus preventing sudden drops in hazard across the fore-arc and back-arc margin. Scaling factors to capture epistemic uncertainty in the source stress parameter and anelastic attenuation coefficients for the subduction and deep seismicity GMM were calibrated from the analysis of region-to-region variability equal across different subduction zones worldwide, following observations from the NGA-Subduction project. The complete description of the development of the scaled-backbone GMM logic tree for subduction and deep seismicity is found in Weatherill et al. (2024).

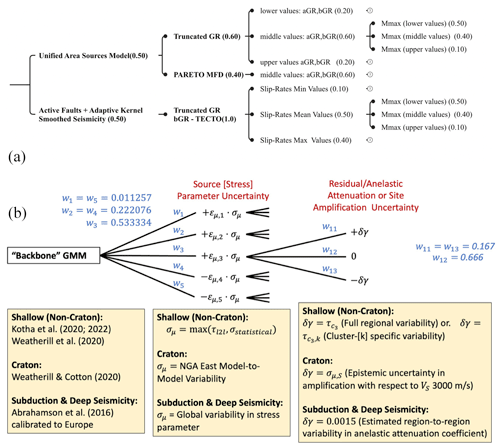
Figure 4 Schematic overview of the main logic tree for shallow crust regions as defined for the ESHM20 computational model. Panel (a) illustrates the asymmetric branching structure of the seismogenic source models. Panel (b) presents the branching levels of the ground motion models, highlighting both the default and cluster-specific scaled-backbone models as implemented by Weatherill et al. (2024).

6 ESHM20: main logic tree and computational aspects

The epistemic uncertainties in ESHM20 are handled in a logic tree framework, reflecting the current state of practice in seismic hazard assessment. Given the size of the computational region and the complexity of the two sub-components of the logic tree, we aimed at a balanced logic tree structure where the epistemic uncertainty of both the individual source models and the ground motion models is adequately represented. In ESHM13, due to combined factors such as the complexity of the input models, large-scale geographical grid, size and volume of the hazard results, and software and hardware constraints, a collapsed earthquake rate for each of the three seismogenic sources was used. This was combined with the multiple ground motion prediction equations (GMPEs) in a post-processing step to estimate the weighted mean and the weighted quantiles of ESHM13. A consequence of this decision is that the quantile range of the results is very narrow in many parts of the model. Hence, in ESHM20, we aimed to capture the body, centre, and range of the expected ground motion. The main logic tree combines the two main components, i.e. the seismogenic sources and the ground motion models as illustrated in Fig. 4. The former, given in Fig. 4a, consists of four branching levels, corresponding to a source-type branching level and three more branching levels depicting the epistemic uncertainty of the type of magnitude frequency distribution, activity parameters (Gutenberg–Richter parameters, i.e. a_GRs, b_GRs), and upper magnitudes (M_max). A key aspect was related to the use of correlated or non-correlated uncertainties of the activity rate parameters. The implementation of uncorrelated uncertainties is suitable for site-specific hazard analyses, while they pose computational challenges at the regional level. For instance, having a source model with three fully correlated branches for a_GR, three for b_GR, and three for M_max would result in nine logic tree branches in total. However, the upper and lower branches would represent extreme cases, leading to exceptionally high or low activity rates. On the other hand, uncorrelated uncertainties would require permuting all combinations of a_GR, b_GR, and M_max for all sources, resulting in an exponentially large number of realizations (i.e. 9 end-branches and 400 area sources will result in 9⁴⁰⁰ uncorrelated end-branches) that makes it impracticable for large-scale regional models like the Euro-Mediterranean region. Sensitivity analyses were conducted, and for the model implementation we considered the correlated end-branches for the seismogenic source model (Papadopoulos and Danciu, 2022). The epistemic uncertainty of the ground motion is extensively described by Weatherill and Cotton (2020) and Weatherill et al. (2020), and its development involved several iterations. Initial tests of the complete seismic hazard model were followed by minor modifications to the GMM logic trees (see Fig. 4b) for shallow seismicity in ESHM20. The original logic tree structure was preserved, with adjustments made to improve the representation of epistemic uncertainty. Specifically, the number of branches for source region uncertainty was increased to five, while the three-branch representation for attenuation region uncertainty was retained. This approach was also applied to the logic tree case for the cratonic sources. A higher numbers of branches were considered but were found to be computationally prohibitive (Weatherill et al., 2024). Practical decisions were made to streamline computational time and make the best use of hardware resources. These decisions include using a single branch for smoothed seismicity and the subduction interface and a reduced number of grid points, particularly offshore. Other optimizations included using point ruptures, weighted depths for sources, and the dominant style of faulting. For a comprehensive representation of epistemic uncertainty, we used the random sampling technique in OpenQuake to sample 10 000 logic tree end-branches. Moreover, it is worth noting that for the implementation and computation of the 2020 European Seismic Risk Model (ESRM20; Crowley et al., 2021), a collapsed earthquake rate model was adopted to mitigate the potential impact of biased correlations within epistemic uncertainty for stochastic catalogue generation. Additionally, differences exist in the utilization of ground motion models for risk assessment, and the consideration of regional-scale site response modelling, as detailed in Crowley et al. (2021). The configuration file for ESHM20 and ESRM20 calculations in OpenQuake and the main input files (Danciu et al., 2021c) are publicly available (see the “Code and data availability” section). Noteworthy, OpenQuake features open-source libraries and supports standardized, backward-compatible file formats. Some of the main results and products derived from the ESHM20 computational model are presented and discussed in the next section.

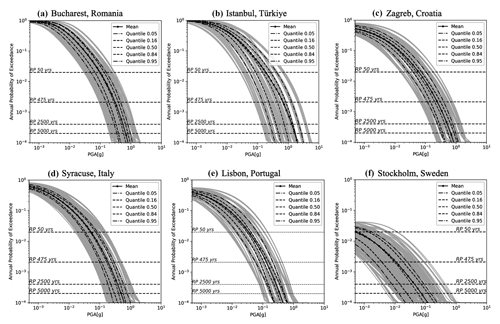
Figure 5 Full distribution of hazard curves for 10 000 samples of the ESHM20 main logic tree. Mean and five quantiles (5th, 16th, 50th, 84th, 95th) are given for Bucharest (Romania), Istanbul (Türkiye), Zagreb (Croatia), Syracuse (Italy), Lisbon (Portugal), and Stockholm (Sweden). These results are applicable to generic rock soil conditions with a shear wave velocity (V_s30) of 800 m s⁻¹.

6.1 ESHM20: main results

The ESHM20 results provide time-independent earthquake ground-shaking exceedance probabilities described as hazard curves, uniform hazard spectra, and hazard maps. Mean, median (50th percentile), and four key quantiles (5th, 16th, 84th, and 95th) are provided for various intensity measure types: PGA and spectral acceleration (SA) over a range of fundamental periods (0.05 to 5 s) with 5 % damping. The hazard maps and the uniform hazard spectra (UHS) are reported for five annual probabilities of exceedance (APEs), i.e. 0.02, 0.0021, 0.001, 0.000404, and 0.0002, which correspond to the five return periods of 50, 475, 975, 2475, and 5000 years, respectively. The ESHM20 results are valid for RotD50 of the horizontal components (Boore et al., 2006; Boore, 2010) as provided by the selected ground motion models and estimated for a uniform rock site condition of V_s30 ∼ 800 m s⁻¹. Hazard curves are calculated up to extremely low annual probabilities (e.g. 10⁻⁴, which corresponds to return periods of about 10 000 years). However, a degree of caution is required when interpreting curves or derived results at these low probability levels, where the aleatory uncertainties of the ground motion (Bommer and Abrahamson, 2006) and the robustness of the earthquake rates must be carefully analysed, similar to site-specific hazard modelling (Bommer et al., 2013; Renault et al., 2010). Therefore, hazard maps are limited to a maximum APE of $\mathrm{1}/\mathrm{5000}$ or an equivalent return period of 5000 years to address these challenges. Figure 5 illustrates the hazard curves, mean, and five quantiles (5th, 16th, 50th, 84th, and 95th) for Bucharest (Romania), Istanbul (Türkiye), Zagreb (Croatia), Syracuse (Italy), Lisbon (Portugal), and Stockholm (Sweden).

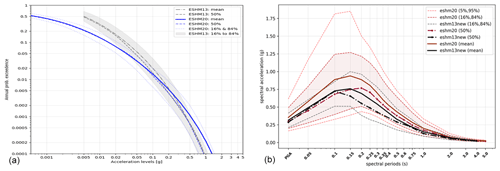
Figure 6 Comparative plots of ESHM20 and ESHM13 for L'Aquila (42.3; 13.382), Italy. Panel (a) illustrates the hazard curves for PGA distributions of ESHM20 and ESHM13. Panel (b) displays a comparison of the mean; median; and the 5th, 16th, 84th, and 95th quantiles of uniform hazard spectra (UHS) for both models for an APE of $\mathrm{1}/\mathrm{475}$. The shaded area highlights the 16th–84th interval. These results are applicable to generic rock soil conditions with a shear wave velocity (V_s30) of 800 m s⁻¹.

The quantiles were obtained from a distribution of hazard curves (in grey lines in Fig. 6) corresponding to 10 000 end-branch samples of the main logic tree given in Fig. 4. The body and range of hazard curves depict the combined uncertainties of both the seismogenic sources and ground motion at each location. Bucharest and Syracuse exhibit a similar range of hazard estimates and a narrow quantile range. Notably, at these locations, the configuration of the logic tree is different, combining more than a single seismotectonic environment, i.e. active shallow and non-subduction deep seismicity of Vrancea for Bucharest and for Syracuse, a complex combination of active shallow, subduction interface, in-slab of the Calabrian arc, and volcanic seismicity. Similarly, Istanbul is subjected to shallow active seismicity, in particular to the very seismically active faults of the north Anatolian fault system. Zagreb is primarily exposed to the shallow seismicity, while Lisbon is affected by shallow seismicity both on- and offshore, including the southern offshore source responsible for the 1755 earthquake. The range of seismic hazard curves depicting the end-branch realizations is wide for Stockholm when compared with the other locations. This wide distribution depicts the complexity of the ground motion characteristic models considered for this craton region, i.e. the scalable regional backbone logic tree (Goulet et al., 2021; Weatherill and Cotton, 2020), as well as the contribution from the area source and the smoothed seismicity branches. Furthermore, the hazard curves at different locations have different decay within the range of the APE of interest from $\mathrm{1}/\mathrm{50}$ to $\mathrm{1}/\mathrm{5000}$.

The decay of the hazard curves indicates changes in hazard estimates: a fast decay results in high hazard values, whereas a slow decay indicates a low hazard value at a given APE. In comparison with other locations, Istanbul and Bucharest exhibit high seismic hazard values across all APEs as indicated by the faster decay of the hazard curves, while the decay of the hazard curves for Stockholm is the slowest, resulting in the lowest hazard PGA values.

We conducted thorough investigations into the correlation between hazard curve decay and input source parameters, examining how the decay rate changes across varying return periods and geographical locations. One notable finding from our analysis is the lack of a clear correlation between the hazard curve decay exponent and seismic parameters such as b_GR or M_max. Surprisingly, our tests indicate that ground motion aleatory variability does not play a significant role in influencing the hazard curve decay factor. Instead, in high-seismicity areas, the hazard exponent tends to increase, particularly for very long return periods exceeding 5000 years, while in regions of low to moderate seismicity, this increase is less pronounced. Furthermore, we observed localized decreases in the hazard curve decay near active faults, especially in moderately active zones where fault activity dominates long-return-period hazard estimates. These insights, summarized by Bard et al. (2022) and Danciu et al. (2022), suggest that the dynamics governing hazard curve decay are more complex than previously assumed, prompting ongoing investigations at the time of this publication (Bard et al., 2024).

Figure 6 provides a comparison between ESHM20 and ESHM13 for hazard curves (Fig. 6a) and for UHS (Fig. 6b) for L'Aquila, Italy. The hazard curves cross each other at an APE of about 0.1, with the ESHM13 hazard curves being higher than the those of ESHM20 for lower acceleration levels and then ESHM20 hazard curves exceeding those of ESHM13. The range between the two quantiles (16th and 84th) is also consistent. Next, the UHS comparison indicates that median spectral acceleration values are consistent with the previous model, ESHM13, for spectral periods less than 0.1 s. However, for longer spectral periods, ESHM20 provides higher values. The mean and quantile values (5th, 16th, 84th, 95th) at an APE of $\mathrm{1}/\mathrm{475}$ from ESHM20 are higher than those from ESHM13; in contrast, the range between the 16th and 84th quantiles for L'Aquila of ESHM13 is notably narrower than those in ESHM20. This difference is important because it reflects the methodological differences in the two regional hazard models. ESHM20's broader uncertainty range indicates potentially a more robust distribution around the mean and median values, a result of the balanced logic tree of both seismogenic source and ground motion models. In contrast, ESHM13 only considers mean recurrence parameters and few GMPEs, which may result in underestimating the uncertainty range. This is evident in Fig. 6, where the mean and medians are depicted together with the distribution of hazard curves for each of the 10 000 samples of the logic tree. It is important to reiterate that the ESHM13 quantiles are sensitive to the model implementation, which did not explore the full logic tree of the source model and ground motion due to computational constraints. The observations for L'Aquila are not representative of the entire model, as at each site across the Euro-Mediterranean region, the hazard estimates are driven by different components of the model. Hence, to explore additional materials and comparison plots, including hazard curves and UHS for 420 cities, we encourage the readers to visit the dedicated repository listed in the “Code and data availability” section. A table depicting the ground-shaking estimates of ESHM20 and ESHM13 at the location of capital cities in the Euro-Mediterranean region is provided in the Supplement. Last but not least, all results of these two hazard models are available online at http://www.hazard.efehr.org.

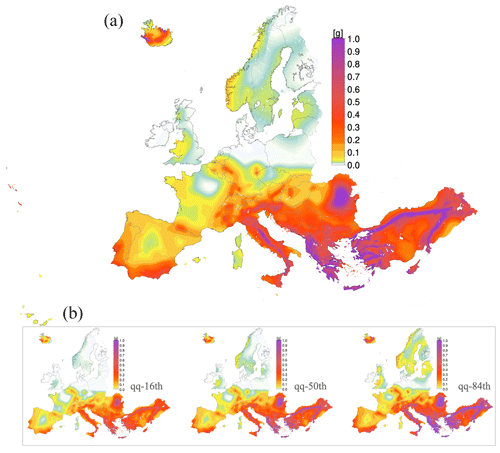
Figure 7 (a) Spatial distribution of the mean values of spectral acceleration at 0.2 s for ESHM20 with an APE of $\mathrm{1}/\mathrm{475}$; the 16th, 50th, and 84th quantiles are shown in (b). All values are estimated on a generic rock soil conditions of V_s30 ∼ 800 m s⁻¹.

Next, in Fig. 7 we illustrate the spatial distribution of the spectral acceleration at the fundamental period of vibration of 0.2 s, i.e. SA (0.2 s) mean values for APE of $\mathrm{1}/\mathrm{475}$. This hazard map incorporates both the uncertainties of the seismogenic sources and the spatially variable backbone ground motion model and uncertainty that is depicted by percentile estimates (5th, 95th), which are also shown in Fig. 5. The distribution of equiprobable probabilistic ground motion levels is consistent with and resembles the patterns observed in regions with a history of documented seismic activity or located near active faults. High-ground-shaking regions are observed along the Mediterranean belt, extending through Greece, Italy, and parts of the Balkans. These regions are tectonically active due to the complex interactions between the African, Eurasian, and Anatolian tectonic plates. Similarly, in the Iberian Peninsula, southern Spain and Portugal show a moderate to high level of ground-shaking hazard. This is consistent with the historical and geological data, as these regions have experienced significant earthquakes in the past, such as the 1755 Lisbon earthquake. Low-ground-shaking levels are visible in the northern, northwest, and central parts of Europe, including the UK, northern France, Germany, and Scandinavia. These regions exhibit low seismotectonic activity and historically experienced less frequent and severe seismic events. For the first time, the model includes the Canary Islands. The inclusion of the Azores Islands is also worth noticing, as this archipelago is another seismically active region. This is due to the complex tectonic junction of three major plates (i.e. northern American, Eurasian, and African plates), resulting in elevated levels of seismic hazard. Likewise, the ground-shaking values for Iceland fall within the moderate to high range, incorporating both shallow seismicity from tectonic origin and volcanic activity. This reflects the intricate nature of the Mid-Atlantic Ridge, as well as the relatively frequent volcanic activity. The hazard maps for the 16th, 50th, and 84th quantiles of SA at 0.2 s are also illustrated in Fig. 7. Additional hazard maps and comparison plots for ESHM20 and ESHM13 are available in the Supplement, as well as online at http://www.hazard.efehr.org. Last but not least, at the time of this submission, the disaggregation matrices of different ground motion levels corresponding to the APE of $\mathrm{1}/\mathrm{475}$ and $\mathrm{1}/\mathrm{2475}$ are scheduled to be uploaded to the online repository. The disaggregation of seismic hazard will provide insights into the predominant scenarios (magnitude and distance) at the selected APE for all computational grid points of the Euro-Mediterranean region.

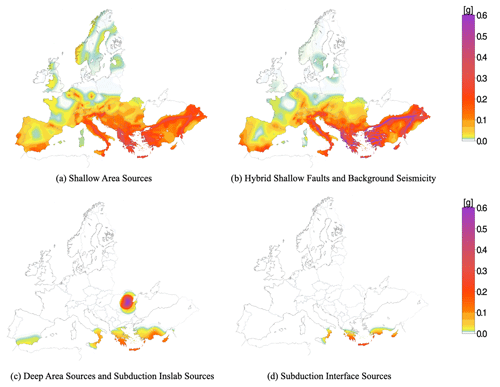
Figure 8 Ground-shaking hazard maps for PGA [g] mean for the main components of ESHM20 seismic source characterization: (a) shallow area sources, (b) hybrid model combining the active faults and the smoothed seismicity, (c) deep seismicity and subduction intraslab, and (d) subduction interface models for an APE of $\mathrm{1}/\mathrm{475}$. These results are applicable to generic rock soil conditions with a V_s30 of 800 m s⁻¹.

6.2 ESHM20: hazard contribution per seismogenic source model

Hazard maps for each component of the seismogenic source model, i.e. the area source model and the hybrid source model combining the active faults plus background smoothed seismicity, subduction in-slab plus deep seismicity, and subduction interface, are given in Fig. 8. These hazard maps depict the mean PGA values for APE of $\mathrm{1}/\mathrm{475}$ for a reference rock condition of V_s30 ∼ 800 m s⁻¹. The calculation is done with the corresponding logic tree of each source model (i.e. for the shallow crust, the upper or lower part of the logic tree described in the upper panel of Fig. 4) and the full backbone ground motion models. The area sources, illustrated in Fig. 8a, provide a narrower range of PGA values than the result computed with the hybrid model. The delineation of the area source geometries is visible in the ground-shaking map, in particular in regions of low to moderate seismicity (i.e. Spain, France, Germany, UK, and northern Europe). Moreover, as expected, the hybrid model shows peaks of ground motion along the main seismically active faults incorporated in the model. The hybrid source model, given in Fig. 8b, provides the largest PGA values in regions with faults of high seismicity such us the north and east Anatolian fault systems, Türkiye, Gulf of Corinth, Greece, and the central Apennines in Italy. The contribution of background seismicity in the proximity of faults results in similar patterns with the area source in regions like the Balkans, southern Spain, Portugal, and France. There is a consistent hazard pattern due to smoothed seismicity and area sources in southern Europe, particularly in Italy, Greece, and Türkiye. Obvious differences between these two models are also visible in northern Europe, i.e. Norway, Sweden, and Finland. This is a clear indication that in central and northern Europe, the area sources are controlling the seismic hazard. The contribution of deep seismicity to the overall hazard, as seen in Fig. 8c, is typically lower than that of the other source models. However, the Vrancea source is an exception, exhibiting remarkably high hazard estimates with PGA values that are strongly azimuth-dependent relative to the orientation of the Carpathian Mountains. As indicated in Fig. 7d, the subduction interface model is particularly important in regions prone to subduction zone earthquakes in southern Europe. This model shows a wide range of PGA values depending on the specific characteristics of the subduction interface. Its contribution can be significant in terms of potential ground-shaking levels due to the large magnitudes associated with subduction zone sources. It is important to note that the subduction sources of the Hellenic, Cyprian, Calabrian, and Gibraltar arcs, along with the deep seismicity sources, complement the two source models proposed for the shallow crust: the area sources and the hybrid fault and background smoothed seismicity model.

If we consider lower APEs, i.e. $\mathrm{1}/\mathrm{2500}$ or $\mathrm{1}/\mathrm{5000}$, the relative contributions of each component of the source models to the overall hazard are expected to change. The recurrence rates and higher magnitudes, which play a more important role in controlling the hazard at these low return periods, will likely identify the contribution of active faults and the subduction interface due to the increased contribution of M_max. In general, the components of the source model make a balanced contribution to the overall hazard, as shown by the distribution of the hazard curves illustrated in Fig. 5. This is the outcome of the first seismogenic source model in Europe which accounts both for the spatial and temporal variability in each component and for the epistemic uncertainties of the individual seismogenic sources.

Figure 9 Spatial distribution of quantile ratios: 84th to 16th (a) and 95th to 5th (b) for ESHM20. The log10(ratio) depicts PGA for a return period of 475 years and a reference rock condition of V_s30 ∼ 800 m s⁻¹.

6.3 ESHM20: epistemic uncertainty range

We use the quantile ratios, i.e. log10(95th/5th) and log10(84th/16th), to map the spatial variability across the Euro-Mediterranean region. Figure 9 illustrates the spatial distribution of these two ratios for PGA at an APE of $\mathrm{1}/\mathrm{475}$. The spatial pattern appears to be similar between the two quantile ratios, and as expected the 95th to 5th quantile ratio is generally higher than the 84th to 16th quantile ratio. Relatively high values, i.e. a factor greater than 3, are shown in northern Europe, the Baltic area, and specific regions in northern Scotland. These high ratio values are mainly due to very low values of the 5th and 16th quantiles as seen in the hazard curves for Stockholm in Fig. 5. Note that the ratio values are in log10 scale; thus the very low values of 0.1 will correspond to a very narrow range of about 1.25 between the quantiles (mainly log10(84th/16th)), which might suggest a very strong correlation of the logic tree branches, resulting in overlapping end-branches. However, in the majority of regions the log10(84th/16th) value is lower than 1.0, resulting in a range of up to 10 between the 16th and 84th PGA values. This range increases in northern Europe, where the log10(84th/16th) ratio values are greater than 1.5, resulting in a very high range between these two quantiles for the estimated PGA. Similarly, the spatial pattern of log10(95th/5th) depicts very high values in northern Europe, suggesting a very large variability in the ground motion hazard estimates in the region. This observation is consistent with what was found in ESHM13, albeit the range of ratio values is slightly lower mainly due to a different logic tree configuration and model implementation (Danciu et al., 2022). However, the quantile ratios exhibit values that are in line with other regional seismic hazard models (Şeşetyan et al., 2018) or site-specific seismic hazard models (Douglas et al., 2014).

6.4 ESHM20: transfer to engineering community

The engagement of the scientific and engineering communities has been a priority in the development cycle of ESHM20 since the early stages of the project. The engineering requirements were specified by the CEN SC8 working group, which is coordinating the definition of the seismic action of the next version of the European seismic design code (Bisch, 2018). Their requirements were aligned with the new definition of the standard response spectra, particularly with regard to its anchoring points. Specifically, the current scaling practice based on a single parameter (PGA) is being replaced by a new anchoring system with two parameters: Sα, which is the spectrum value on a plateau that covers a certain spectral period range (i.e. 0.05 s and 0.4 s), and Sβ, which is the spectrum value at 1 s spectral period (Labbé and Paolucci, 2022). The pseudo-acceleration response spectrum continues to be the basis of the new design spectrum definition in EC-8. The ESHM20 core team has interacted with the SC8 working group for knowledge transfer, providing access to all inputs, datasets, models, and results. Several bilateral meetings and four plenary meetings took place in the last phase of the model development cycle from 2020 to 2021. Moreover, ESHM20 was evaluated with different comparison and testing activities for several countries in Europe: France, Greece, Italy, Norway, Portugal, Romania, Slovenia, and Switzerland. Iervolino et al. (2023) have analysed two Italian seismic hazard models (MPS04: Stucchi et al., 2011; MPS19: Meletti et al., 2021) and ESHM20 against ground motion recordings. The strong motion data were gathered from 143 seismic stations of the Italian seismic network, and the analysis was conducted for several intensity measure types, i.e. PGA, SA at 0.3 s, and SA at 1 s, as well as four return periods. A hypothesis test was set up to account for the number of exceedances observed at each station, and if a value falls within the non-rejection band, the test is considered successful. In total, 36 hypothesis tests were performed, each representing the combination of all models and parameters. The results suggested that all three models (i.e. MPS04, MPS19, and ESHM20) perform adequately considering a 5 % significance level. Another important finding of the study was that the all-hazard models tend to overpredict exceedances at a 50-year return period.

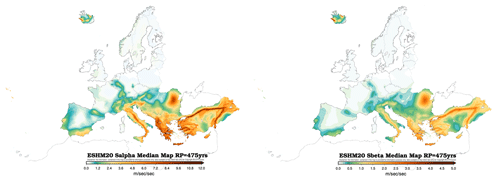
Figure 10 Informative hazard maps for median Sα475 (left) and Sβ475 (right) values for 475-year return period and class type A of EC8 with a V_s30 of 800 m s⁻¹ (Labbé and Paolucci, 2022).

The two informative hazard maps, namely Sα475 and Sβ475, as derived from ESHM20 for a 475-year return period, for soil type A (V_s30 ∼ 800 m s⁻¹) as requested by the CEN EC8 are shown in Fig. 10. To calculate the Sα475, it is first necessary to identify the T_peak, which corresponds to the largest value of the median UHS for a 475-year return period; then the Sα475 is estimated as an average of spectral values between the period range of 0.5 T_peak to 1.5 T_peak. The use of median values was a decision taken by the CEN/TC 250/SC 8 and summarized in Labbé and Paolucci (2022). Additionally, the second-generation Eurocode 8 draft (FprEN 1998–1-1, 2024) states that while these median values are used for these specific informative maps, they do not pass judgement on other results from ESHM20, maintaining a neutral view of hazard values of other intensity measure types or other return periods (Labbé and Paolucci, 2022). These informative hazard maps are now subject to the inquiry and formal voting process conducted by CEN member nations. However, it is also critical to emphasize that the results obtained from ESHM20 should not be directly used as seismic design values. Instead, seismic design provisions and national annexes should be followed and enforced for seismic design purposes.

7 Summary and outlook

The European Seismic Hazard Model (ESHM20) represents a significant step forward in the assessment of seismic hazard for the Euro-Mediterranean region. It incorporates the latest datasets, as well as advanced methods for building the model and computing hazard when compared to ESHM13. ESHM20 was developed through a collaborative, regional effort that integrates the expertise and data from various European countries. The development of ESHM20 involved a rigorous process of compilation, standardization, and curation of input data, including earthquake catalogues, ground motion recordings and models, tectonic information, active fault databases, and/or seismogenic sources from various countries. A key feature of the model is its cross-border harmonization, which guarantees a consistent assessment of seismic hazard across national borders. ESHM20 supersedes ESHM13 as a reference model for seismic hazard assessment in the Euro-Mediterranean region, and it is also part of the recent update of the GEM Global Mosaic of Hazard Models (Pagani et al., 2020).

From the communication point of view, an important milestone was achieved with the first-ever release of a European regional seismic hazard and risk model to the scientific community and the general public. In May 2022, an official media release was made, accompanied by various materials such as flyers, fact sheets, posters, and video content. These materials were translated into multiple languages, facilitating the dissemination of the model's findings to a wider audience. This media event played a key role in enhancing awareness and understanding of earthquake hazard and risk in the Euro-Mediterranean region (Dallo et al., 2024).

EHSM20 results show differences from the results of national seismic hazard models mainly due to variations in datasets and methodologies used (Grünthal et al., 2018; Halldórsson et al., 2022; Meletti et al., 2021; Mosca et al., 2022; Šket Motnikar et al., 2022; Vacareanu et al., 2016; Wiemer et al., 2016). These differences should be explored and understood to fully integrate the insights of the regional models into a national hazard (Pavel et al., 2016; Trevlopoulos et al., 2023; Weatherill et al., 2023) or risk model (Papadopoulos et al., 2023). Note that, despite being of key importance, there is no straightforward way of understanding the importance and the significance of the changes between seismic hazard models. What may be considered low seismic activity in a specific region or country (e.g. southern Europe) might be classified as high in another specific region (e.g. northern Europe), and vice versa. The impact of earthquakes depends on factors such as building vulnerability, local site conditions, asset exposure, and population density (Douglas et al., 2023). Thus, to understand and compare the impact of earthquakes in different regions, the ground-shaking estimates must be analysed in the context of seismic risk (ESRM20; Crowley et al., 2021). Furthermore, the availability of products such as ESHM20 and ESRM20 opens the possibility of developing operational services in Europe, such as applications similar to the ShakeMap service, time-dependent earthquake forecasts, or rapid loss assessment. Some of these applications have been developed or are currently being developed in recent pan-European initiatives (Böse et al., 2023; Mancini and Marzocchi, 2023; Spassiani et al., 2023).

Despite its advancements, ESHM20 faces challenges typical of large-scale seismic hazard models (Gerstenberger et al., 2020). The heterogeneity of data used and their variability in completeness, particularly in regions of low seismicity, pose a significant challenge to the development of a uniform hazard model. The seismogenic source model, while comprehensive, may require future refinements as new data and models are integrated, particularly geodetic and geologic data. However, in recent years significant progress was made in regional seismic hazard models, including those in the USA (Field et al., 2017; Petersen et al., 2020), New Zealand (Gerstenberger et al., 2022), Australia (Allen et al., 2020), Italy (Meletti et al., 2021), Germany (Grünthal et al., 2018), and Switzerland (Wiemer et al., 2016) and at a global scale (Pagani et al., 2020), it is worth observing that the overall uncertainties have not seen a significant reduction over time. The complexity of the seismic hazard models steadily increased given the continuous expansion of earthquake data and information, leading also to an increase in uncertainties around these models that were previously neglected. Looking ahead, one can anticipate the development of more advanced methods for handling the uncertainties in seismic hazard datasets, components, and models. These methods are likely to involve the use of physics-based simulations (Bradley, 2019; Li et al., 2023; Paolucci et al., 2021) of both earthquake ruptures and/or ground shaking (Milner et al., 2021). The integration of physics-based simulations into seismic hazard modelling has the potential to improve the main pool of existing records, enhance ground-shaking characterization particularly in the magnitude–distance range poorly covered in current strong motion databases, improve the ground motion characteristic models, augment our understanding of earthquake scenarios, and support earthquake preparedness and mitigation strategies (Graves et al., 2011). In addition to using physics-based simulations, one can also anticipate significant progress in computational capabilities, such as high-performance computing (Folch et al., 2023), and artificial intelligence (AI)-driven analytics in the coming years. These leading-edge tools have the potential to significantly accelerate the processing of extensive, multidisciplinary datasets and complex calculations (Dal Zilio et al., 2023). However, the future application of AI and machine learning in seismic hazard modelling is not without challenges, including black box dilemma, computational demand, scalability, representation of data, bias, over-fitting, and ethical considerations (Jiao and Alavi, 2020; OECD, 2023). Furthermore, it is evident that we are entering a decade of interoperability and close interdisciplinary collaboration. Advanced research infrastructures such as the European Plate Observing System (EPOS; Haslinger et al., 2022), with their next generation of Earth science data and services, can facilitate such data interoperability for advancement in the field and support the next generation of geo-related hazard and risk models.

In conclusion, ESHM20 is foreseen to be a living and collaborative model that includes a broader European community of Earth scientists, seismic hazard experts and modellers, engineers, practitioners, and stakeholders. ESHM20 will coexist with the national hazard models, which is not intended to replace but rather advance and enhance them; this coexistence will rely on an ongoing feedback loop between the two, where new data, methodologies, and/or innovative approaches will contribute to the future versions of these hazard and risk models. Ultimately, this will support efforts to create a more earthquake-resilient society in the Euro-Mediterranean region.