the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Simulating historical flood events at the continental scale: observational validation of a large-scale hydrodynamic model
Oliver E. J. Wing
Andrew M. Smith
Michael L. Marston
Jeremy R. Porter
Mike F. Amodeo
Christopher C. Sampson
Paul D. Bates
Continental–global-scale flood hazard models simulate design floods, i.e. theoretical flood events of a given probability. Since they output phenomena unobservable in reality, large-scale models are typically compared to more localised engineering models to evidence their accuracy. However, both types of model may share the same biases and so not validly illustrate their predictive skill. Here, we adapt an existing continental-scale design flood framework of the contiguous US to simulate historical flood events. A total of 35 discrete events are modelled and compared to observations of flood extent, water level, and inundated buildings. Model performance was highly variable, depending on the flood event chosen and validation data used. While all events were accurately replicated in terms of flood extent, some modelled water levels deviated substantially from those measured in the field. Despite this, the model generally replicated the observed flood events in the context of terrain data vertical accuracy, extreme discharge measurement uncertainties, and observational field data errors. This analysis highlights the continually improving fidelity of large-scale flood hazard models, yet also evidences the need for considerable advances in the accuracy of routinely collected field and high-river flow data in order to interrogate flood inundation models more comprehensively.
- Article
(15776 KB) - Full-text XML
- BibTeX
- EndNote
The severity of riverine flood hazards is principally understood through inundation modelling. Few stretches of river contain enough observations of their flood behaviour to adequately characterise the hazard they pose alone. Instead, these limited observations are used to drive physical models to produce synthetic realisations of flooding. The output of these models is typically a series of flood maps with a defined probability of occurrence which, when intersected with socio-economic data, can be used to estimate the frequency at which people and property may be exposed to flood hazards. Such models form the cornerstone of national flood risk management frameworks, which guide planning decisions and investment in mitigatory actions.
The gold standard approach to building accurate flood models locally is from the ground up by hydraulic engineers, who principally use in situ river flow measurements, surveyed channel bathymetry, high-resolution terrain data, and the incorporation of local drainage and protection features. Scaling this local modelling approach up to obtain nationwide views of flood hazard therefore requires the building of many thousands of hydraulic models covering every river basin in the country. Even for the world's wealthiest countries, this poses a formidable modelling challenge. The flood mapping programme of the US Federal Emergency Management Agency (FEMA), for instance, has required over USD 10 billion of public funding over ∼50 years, yet it has only modelled one-third of US river reaches to date (Association of State Floodplain Managers, 2020).
In response to this dearth of flood hazard information at large spatial scales, researchers have built hydraulic models with domains covering vast regions or even the globe (Alfieri et al., 2014; Dottori et al., 2016; Hattermann et al., 2018; Sampson et al., 2015; Wing et al., 2017; Winsemius et al., 2013; Yamazaki et al., 2011). These models sacrifice some local accuracy compared to the traditional engineering approach but benefit from complete spatial coverage and the ability to be re-run as climatic and landscape conditions change, all within reasonable timescale and resource limits. One question that remains to be answered in this field of enquiry regards how much local accuracy is lost.
To answer it, these large-scale inundation models must be validated, but two critical barriers prevent this from taking place routinely and rigorously. Firstly, design flood maps of this nature do not represent something observable in reality. The 100-year flood, for instance, is not a tangible phenomenon, since real flood events do not have spatially static return periods. In producing something theoretical, it is impossible to validate it against something real. Model-to-model comparisons – where one model is deemed to be suitably accurate so as to be the benchmark, while the other is the one to be tested – are therefore necessitated. The second barrier, then, is the low availability of suitable model benchmarks. Global flood models have been compared to local engineering flood maps in Europe and the US but only for a small handful of river basins, inhibiting wide-area testing (Dottori et al., 2016; Sampson et al., 2015; Ward et al., 2017; Winsemius et al., 2016). Wing et al. (2017) presented a model of the contiguous US, adopting the higher-quality hydrographic, hydrometric, terrain, and protection data available in the US compared to available data globally. They compared their model to FEMA's large, yet incomplete, database of 100-year flood maps, charting a high degree of similarity between the large-scale model and the engineering approach espoused by FEMA. Wing et al. (2019) furthered this examination with statewide engineering models from the Iowa Flood Center, coming to similar conclusions. While these studies provide useful indications of large-scale model accuracy, they are fundamentally limited in their characterisation of skill through model intercomparisons. The benchmark data in these analyses may share many of the same biases (e.g. friction parameterisation, channel schematisation, structural error, terrain data precision, and boundary condition characterisation) as the model being tested and so not usefully describe the extent to which it is behavioural.
Model validation, rather than model intercomparison, can only be executed through benchmarking against observations. To do so, the hydraulic models must replicate real-world events rather than frequency-based flood maps. This would, by proxy, enable typical applications of design flood maps (such as planning or regulatory decisions, insurance pricing, or emergency response) generated by such a model to be carried out with a richer understanding of its biases. This is common practice in event-replicating, local-scale, engineering-grade inundation modelling studies. However, their limited spatial scale, laborious manual set-up, and the scarce availability of validation data result in observational benchmarking against only a handful of real-world flood events at most – indeed, a single test case is typical (e.g. Hall et al., 2005; Hunter et al., 2008; Mason et al., 2003; Matgen et al., 2007; Neal et al., 2009; Pappenberger et al., 2006; Schumann et al., 2011; Stephens et al., 2012; Wood et al., 2016). An analysis of simulation performance across a wider variety of temporal and spatial settings would provide a more reliable evidence case of model validity. To practicably achieve this, it is necessary to replace the onerous manual construction and parameterisation of local-scale models with a consistent regional- to global-scale model-building framework capable of deployment for any model domain within its realm.
Furthermore, the replication of historical flood events has value beyond scientific validation. While design flood maps are useful for skilled practitioners who (mostly) understand what the models purport to represent, the maps can seem abstract and unconvincing to members of the public since they simulate something intangible and theoretical; thus, knowledge of the statistical meaning and uncertain derivation of a design flood is required to correctly comprehend them (Bell and Tobin, 2007; Luke et al., 2018; Sanders et al., 2020). Producing flood maps of historical events – providing an explicit understanding of where has flooded in the past – can aid in motivating private mitigation efforts where the risk perception formed via a design flood map often fails to do so (Bubeck et al., 2012; Kousky, 2017; Luke et al., 2018; Poussin et al., 2014). As such, en masse replication of historical flood events at high resolution may have value in enhancing risk awareness and the willingness of individuals to take mitigatory action.
In this paper, we adapt the existing continental-scale design flood model framework of Bates et al. (2020) to replicate historical flood events across the contiguous US. Flood events are isolated from US Geological Survey (USGS) river gauge data, which form inflow boundary conditions to a ∼30 m resolution 2D hydrodynamic model. High water mark surveys from the USGS were sourced for nine of the simulated events which, alongside derived flood extents, were used to validate the model. Insurance and assistance claims were obtained for 35 flood events to further analyse the model's skill in the context of exposure. By validating against an order of magnitude greater number of historical flood event observations that exist in academic literature to date, the analysis provides robust evidence of large-scale model skill for the first time. To aid in enhancing risk awareness amongst the US public, these flood event footprints have been released on https://floodfactor.com/ (last access: 3 February 2021), which is a free and accessible tool for Americans to understand their flood risk. Section 2 describes the methods behind the event replication model and the validation procedures undertaken. In Sect. 3, the results of the model validation are presented and discussed. Conclusions are drawn in Sect. 4.
2.1 USGS gauge input and event selection
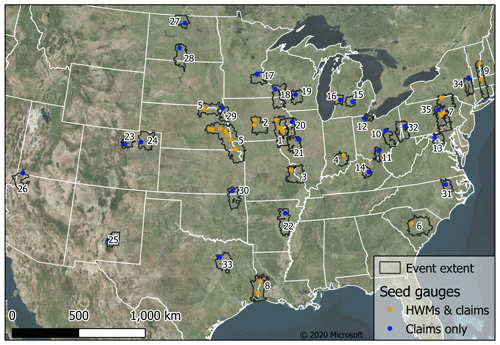
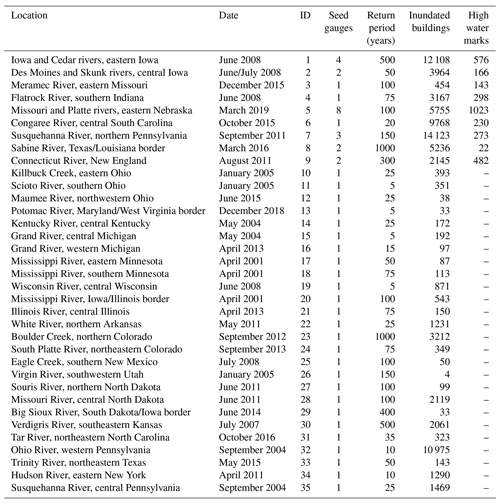
USGS river gauge data were initially filtered into those representing catchments which have an upstream area of >10 000 km2 and a record length of >50 years. Of these, one gauge was selected for each level eight USGS Hydrologic Unit (i.e. HUC8), and the largest event in the record was extracted. This filtering ensured that large loss-driving events, for which validation data were more likely to be available and whose return periods could be more robustly estimated, were captured. This yielded roughly 200 river gauge events, 50 of which had suitable validation data (see Sect. 2.3). Model domains of a 50×50 km area were constructed around these 50 seed gauges, and within each domain, all USGS river gauges within it were selected (regardless of drainage area or record length) to ensure all gauged event flows were captured. Hydrographs spanning 7 d were then extracted from each gauge for each event, with the seed gauge peak at its temporal centre. To account for the uncertainty due to stage measurement error and rating curve configuration in the generation of the gauged discharges (Coxon et al., 2015; Di Baldassarre and Montanari, 2009; McMillan et al., 2012), we simulate each event three times, i.e. the reported discharges and ±20 %, producing a 0.8*Q, 1.0*Q, and 1.2*Q model for each event. Some of these 50 gauge events were from the same (particularly widespread) flood event. Once simultaneous events were merged post-simulation, 35 discrete flood events remained. Figure 1 illustrates the location of the events, with additional information provided in Table A1.
2.2 Hydraulic model
The USGS river flows form the input to the First Street Foundation National Flood Model (FSF-NFM) built in collaboration with Fathom. The model was first presented by Wing et al. (2017), with updates specified in Bates et al. (2020), based on the original global modelling framework of Sampson et al. (2015). Terrain data are based on the USGS National Elevation Dataset (NED), with hydraulic simulations run at the native resolution of 1 arcsec (∼30 m). Other local sources of more accurate terrain data were also compiled into the data set where available, with ∼30 m water surfaces downscaled to ∼3 m in locations where such fine-resolution data are present. Gesch et al. (2014) report relative vertical errors (point-to-point accuracy; measuring random errors exclusive of systematic errors), which is more relevant control on inland flood inundation modelling accuracy than absolute vertical errors, in the NED of 1.19 m. Most, but not all, events were located in areas where the NED consists of lidar, with an associated point-to-point accuracy of ∼0.66 m (Gesch et al., 2014). The computational hydraulic engine is based on LISFLOOD-FP, which solves a local inertial formulation of the shallow water equations in two dimensions (Bates et al., 2010). River flows are routed through channels defined by the USGS National Hydrography Dataset. Channels are retained as 1D sub-grid features, permitting river widths narrower than the grid resolution (Neal et al., 2012). Channel bathymetry is estimated based on the assumption that they can convey the 2-year discharge, which is based on the Smith et al. (2015) regionalised flood frequency analysis (RFFA) but using USGS river gauges (Bates et al., 2020). Ungauged river channels within each model domain propagated the RFFA-derived mean annual flow instead. Flood protection measures are implemented directly into the model, using a database of adaptations compiled from the US Army Corps of Engineers National Levee Database and hundreds of other sub-national databases. For further information, including details on the aforementioned model-to-model validation, the reader is referred to Wing et al. (2017) and Bates et al. (2020).
2.3 Event validation
High water marks (HWMs) were obtained for nine of the simulated events from the USGS Flood Event Viewer (https://stn.wim.usgs.gov/FEV/, last access: 3 February 2021). HWMs were filtered based on (i) the presence of a nearby upstream river gauge, which ensured the model was only tested on floodplains it simulated, (ii) a designation of being high quality, and (iii) the North American Vertical Datum of 1988 (NAVD 88) being the vertical datum of the reference, consistent with the model terrain data. The number of HWMs retained for each event is shown in Table A1. The surveyed water surface elevation (WSE) from each flood event was compared to that of the nearest inundated pixel of the modelled maximum inundation extent. Performance was summarised using the following simple equations:
where N is the number of HWMs, and the subscripts “mod” and “obs” represent modelled and observed WSEs, respectively. Error indicates the absolute deviation of the modelled WSE from the observed WSE, i.e. on average, what is the magnitude of model prediction error? This is commonly referred to as the mean absolute error (MAE), which is less sensitive to outliers than the root mean squared error (RMSE). Bias illustrates whether the modelled WSEs are generally higher or lower than the observed WSE, i.e. on average, does the model over or underpredict WSEs?
To examine model skill in the context of flood extent prediction, HWMs are converted to maps of flood inundation, in line with the methods of Watson et al. (2018). Firstly, the HWMs are interpolated to produce a 2D surface of WSEs across the model domain. These are then subtracted from terrain data, resulting in a grid of water depths. Values greater than 0 m therefore fall within the flood extent. Areas of flooding disconnected from the river channel are removed. To prevent the generation of flood extents in areas for which there are no relevant HWMs, inundation maps are only produced in river basins (based on level 12 USGS Hydrologic Units) which contain at least one HWM. These observation-based flood extents are then compared with the extents simulated by the model, using the critical success index (CSI) described below:
where M and O refer to modelled and observed pixels, respectively, and the subscripts 1 and 0 indicate whether these pixels are wet or dry, respectively. This metric divides the number of correctly wet pixels by the number of pixels which are wet in either the modelled or observed data. This general fit score, falling between 0 and 1, accounts for both over- and under-prediction errors.
Beyond purely flood-hazard-based validation, we sourced counts of buildings which were inundated during the simulated events. Individual Assistance (IA) and National Flood Insurance Program (NFIP) claims data were gathered from the OpenFEMA database (https://www.fema.gov/about/reports-and-data/openfema, last access: 3 February 2021). For each event, the zip codes that intersected the event inundation layer were selected, and the IA and NFIP claims data for those zip codes were extracted from the claims data sets for the year of the simulated event. The total number of claims (IA and NFIP) were then computed for each of those zip codes. Meanwhile, the number of building centroids inundated was computed for each zip code using Microsoft Building Footprint data. Simple statistical summaries of the errors are reported, including the coefficient of determination (R2) as follows:
where C is the count of inundated buildings observed (obs) in OpenFEMA data or simulated by the model (mod) across N=35 events. This metric, bounded between −∞ and 1, indicates the predictive capabilities of the model through comparing the residual variance with the data variance. A perfect model would obtain an R2 of 1, while (subjectively) acceptable models would obtain R2>0.5.
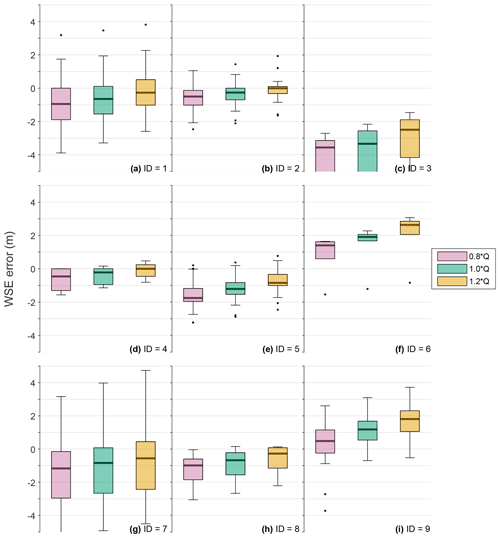
Figure 2Box plots of water surface elevation errors for each of the nine simulations. The 25th and 75th percentiles bound the shaded boxes with medians within. Whiskers are set to a maximum length of 1.5 times the interquartile range beyond the upper or lower quartiles, with outliers shown as black dots. Box shading refers to the following model discharge input: 80 % (violet), 100 % (green), and 120 % (orange) of the gauged discharge.
3.1 Water surface elevation comparison
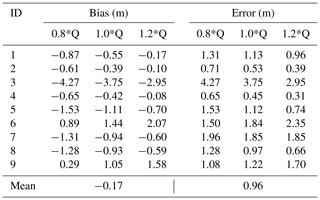
The results of the HWM validation are shown in Table 1 and visualised in Fig. 2. Biases (Eq. 2) consistently indicate a tendency towards underprediction for most events, even when simulated using 120 % of the gauged discharge. Taking the least biased of each event's three simulations, the mean bias comes to −0.17 m, ranging from −2.95 m for event 3 in Missouri (2015) to 0.89 m for event 6 in South Carolina (2015) – including a simulation of event 4 in Indiana (2008), with −0.08 m. Computing errors in line with Eq. (1), which averages the absolute deviation from the observed water surface elevation, the most accurate of each event's simulations ranges from 0.31 m (event 4) to 2.95 m (event 3), with a mean of 0.96 m. Most of the events obtain errors in line with the relative vertical accuracy of the NED, which is accurate to between 0.66 and 1.19 m, depending on the terrain data source (Gesch et al., 2014).
Surveyed water marks are an excellent tool for validating inundation models, though they are not themselves error-free. Numerous past studies sought to quantify uncertainties in these observational data, finding average vertical errors in the region of 0.3–0.5 m, though, in some cases, these can be much higher and systematically more biased for particular sites (Fewtrell et al., 2011; Horritt et al., 2010; Neal et al., 2009; Schumann et al., 2007). Given these constraints, typical reach-scale hydrodynamic models of inundation events are calibrated to <0.4 m deviation from observations of water surface elevation (Adams et al., 2018; Apel et al., 2009; Bermúdez et al., 2017; Fleischmann et al., 2019; Matgen et al., 2007; Mignot et al., 2006; Pappenberger et al., 2006; Stephens and Bates, 2015; Rudorff et al., 2014). Commonly, the calibration of such models is executed via maximising some measure of fit to the benchmark data by varying the friction parameters (e.g. Pappenberger et al., 2005). Equally, studies have calibrated models by varying other uncertain model features, including channel geometry (e.g. Schumann et al., 2013), terrain data (e.g. Hawker et al., 2018), model structure (e.g. Neal et al., 2011), or boundary conditions (e.g. Bermúdez et al., 2017). The model in this study is essentially calibrated by varying the uncertain boundary conditions – though with a sparser exploration of parameter space (i.e. only three simulations per event) than is typical – to within similar errors found in the literature for some events, though most events have significantly higher errors. The impact of discharge uncertainty is evident in the errors of each simulation per event. Assuming ±20 % error in the observation of flood peak stage and its translation to discharge (a modest assessment of their uncertainties), hydraulic model errors can increase by between 6 % and 107 % (median of 57 %). While this illustrates considerable sensitivity, different input discharge configurations within these uncertainty bounds failed to induce an inundation model replication of the HWM elevations for most events.
To further contextualise the results obtained here, we analyse the hydraulic plausibility of the surveyed HWMs along selected river reaches. Figure 3a shows the profile of the water surface elevation experienced during the 2008 event on the Cedar River. Figure 3c shows the same but for the Platte River event in 2019. It is clear that the HWMs produce some local water surfaces which qualitatively appear inconsistent and implausible at the reach scale. No hydraulic model obeying mass and momentum conservation laws could feasibly reproduce such water surfaces. For these events, local USGS river gauges are obtained (Cedar River – 05453520 and 05464000; Platte River – 06796000, 06801000, and 06805500), and a water surface for the considered reaches is linearly interpolated between these. While being an unreliable estimate of WSE far from gauged locations, this interpolated surface provides a useful indicator of how HWM WSEs vary across the river reaches (see Fig. 3b and d). Altenau et al. (2017a) measured water surface elevations at ∼100 m intervals along a 90 km reach of the Tanana River, AK, using airborne radar. The radar data, shown to be highly accurate (±0.1 m) when compared to field measurements, illustrated a smooth and approximately linear slope, even for a complex, braided river. However, this campaign did not take place during a flood event. Bed slopes akin to those on the Platte River suggest that the flood wave would be quasi-kinematic, with the bed and water slope roughly parallel (Dottori et al., 2009). A steady flow profile consistent with the observed peaks may therefore be more appropriate than linear interpolation. Given the complexity of fitting a 1D steady flow model to widespread flood observations, we do not simulate it for the purposes of this discussion. Furthermore, inconsistencies in the HWM-derived water surface may often be a question of scale, where highly granular topographic features cause a local change in water surface that is inconsistent with the reach-scale water levels. Notwithstanding the difficulties in understanding water surfaces across a river reach with relatively sparse 1D observations, these comparisons do lead one to question whether the water slopes purported by the HWMs in Fig. 3 are physically realistic. When the data points in Fig. 3 are restricted to within 1 km of gauge locations, the HWMs deviate from the interpolated surface by 0.79 m (Cedar River) and 0.94 m (Platte River) on average. These observational data, then, may have higher errors than similar data reported in the wider literature, which provides a useful context for the 0.96 m mean error obtained by the model here.
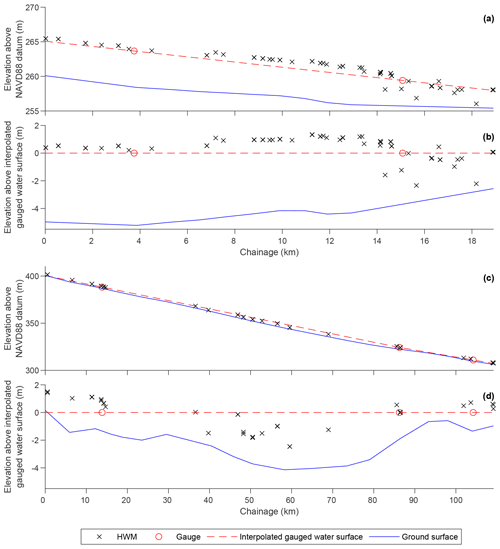
Figure 3Water surface profiles based on gauge and high water mark data for (a, b) the Cedar River between Cedar Falls and Waterloo, Iowa (event 1), and (c, d) the Platte River near Omaha, Nebraska (event 5). Profiles in (a) and (c) are referenced to mean sea level, while those in (b) and (d) adopt the interpolated gauged water surface as the vertical datum.
3.2 Flood extent comparison
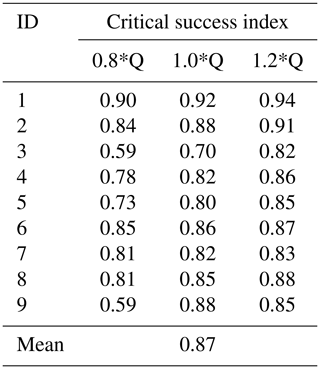
When examining the differences between the simulated maximum flood extents and those produced from interpolating the HWMs over relevant river basins in the terrain data, the model obtains a CSI of 0.87 on average (see Table 2). Event 3 in Missouri obtains the lowest maximum CSI of 0.82, while the highest, of 0.94, is held by event 1 in Iowa. Optimum simulations and their comparison to the observation-based extents are shown in Fig. 4.
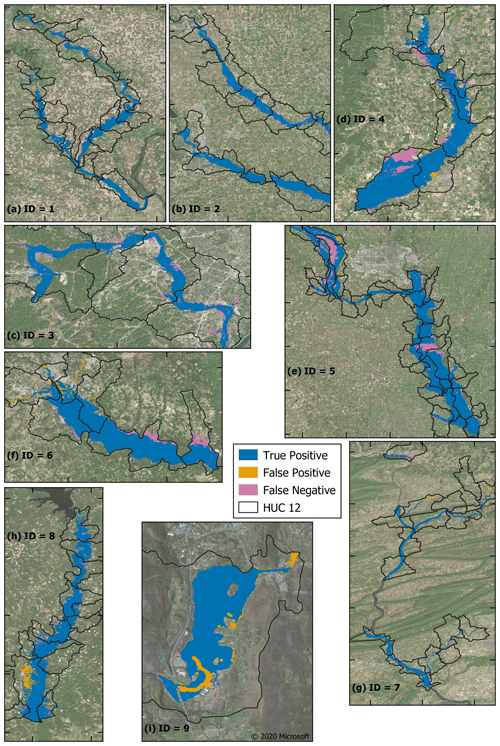
Figure 4Maps illustrating the similarity between modelled flood events and HWM-derived extents in relevant hydrologic unit code (HUC) 12 zones. Interior tick marks are spaced 0.25∘ (∼27 km) apart. Imagery sourced from © 2020 Microsoft.
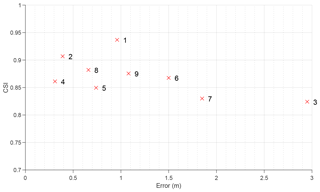
Figure 5The relationship between the WSE error and flood extent CSI for the nine events. Numbered crosses refer to the ID of the flood event.
Typical reach-scale 2D inundation models generally obtain CSIs of 0.7–0.8 when calibrated to air- or space-borne imagery of flood extents (Aronica et al., 2002; Di Baldassarre et al., 2009; Horritt and Bates, 2002; Pappenberger et al., 2007; Stephens and Bates, 2015; Wood et al., 2016). Where observations and their classification methods are of high quality, CSIs of up to 0.9 can be obtained (Altenau et al., 2017b; Bermúdez et al., 2017; Bates et al., 2006; Stephens et al., 2012). The model here obtained CSIs of 0.8–0.9 when benchmarked against interpolated HWMs rather than actual 2D observations of flood extent. Where HWMs are sparsely spaced, the interpolated flood extent may not have accurately replicated the true flood extent. Thus, while it is likely that the model has replicated the uncertain benchmark flood extents to within error, setting a precedent for CSIs in the wider literature can often provide misinformation. In Fig. 5, the relationship between minimum WSE error and maximum CSI for each of the nine events is compared. While a generally intuitive negative relationship between CSI and water level error is exhibited (Pearson's ), CSIs do not drastically reduce as water level errors increase. The reasons for this seeming CSI insensitivity relate to specific characteristics of each event. Events on the Congaree and Connecticut rivers (events 6 and 9) have fairly large water level errors in spite of excellent CSIs. This is because, in both modelled and observed floods, the floodplain was filled up, meaning that extent comparisons were less sensitive to model overprediction. These events were simulated with an overprediction bias, i.e. there was too much water on the floodplain (in three dimensions), but this made little difference to flood extent (in two dimensions). In contrast, the event on Flatrock River (event 4), which is characterised by low WSE errors, obtained a comparable CSI to events 6 and 9. While vertical errors were small, the model did not completely replicate the larger flood inundation across the low-gradient terrain represented by the benchmark flood extent for event 4. Even the event on Meramec River (event 3) obtained a CSI illustrative of high performance, despite very high water level errors. This particular flood was large in magnitude, meaning that the reward for capturing the numerous inundated areas overshadowed the penalisation for underestimating the flood edge. In the vertical plane, however, the Meramec River event simulation is shown to significantly underpredict water surface elevation. Meanwhile, the model was rightly rewarded by both metrics for correctly simulating the Iowa 2008 floods (events 1 and 2) – large floods on large rivers – by filling up the floodplains with reasonably low water level errors. These examinations build on the evidence provided by Stephens et al. (2014), who noted that similar water level errors can result in different CSIs, depending on the size of the flood, the valley gradient, and the sign of model bias. Mason et al. (2007, 2009) similarly posit that an analysis of water height offers a way of discriminating between the equifinal model structures that extent comparisons tend to result in. For this analysis of a larger sample of flood events, we reaffirm their conclusions that CSIs cannot be easily compared for events of different natures, and that a comparison against water levels is a more discriminatory metric.
The extremely large underprediction errors for the Meramec River flood event simulation (event 3) may be explained by its nature as a tributary of the Mississippi River and the arbitrary nature of the geographic domains that the automated model builder produces. Even adding 20 % to the reported USGS discharges resulted in an underprediction of water surface elevations by roughly 3 m. It is likely that this flood event was primarily driven by Meramec River flows backing up against the Mississippi River. With no Mississippi River gauge within the 50 km radius of the Meramec River seed gauge, the Mississippi River was not also in flood during the simulation. In the absence of a correct downstream boundary inducing a backwatering effect, the Meramec River flood flowed freely down the Mississippi River in the simulation rather than onto the Meramec River floodplain. The general underprediction bias across most flood events is likely explained by river gauge density. Boundary conditions are only available in the presence of a USGS gauging station, meaning ungauged tributaries and other lateral inflows within the model domain were not properly accounted for. In failing to simulate the aggregation of these flows, the volume of water within and exiting the model was likely much lower than reality for many of the flood events, resulting in a correspondingly underpredicting inundation model.
3.3 Inundated building comparison
The results after using FEMA claims data to validate the full set of 35 events are shown in Fig. 6. Only nine events simulate the correct number of claims within the discharge uncertainty bounds. When considering the closest match simulation (of the three) in terms of inundated buildings for each event, the mean error in the simulated counts of building inundation is 26 % of the observed count. The standard deviation of this quantity is 132 %, reflecting the substantial scatter evident in Fig. 6. The modelled building inundation obtains an R2 (Eq. 4) of 0.63. In general, it appears that more catastrophic events (in terms of inundated buildings) are more frequently underpredicted by the model, i.e. nine events underpredict building inundation compared to three which overpredict for events with >500 inundated buildings. Meanwhile, less catastrophic events are seemingly systematically overestimated, i.e. 10 events overpredict and four events underpredict for events with <500 inundated buildings. This is perhaps explained by the nature of the validation data. The sum of NFIP and IA claims may not account for all inundated buildings during an event. Impacted households may obtain assistance from local governments (with or without aid from the federal Public Assistance programme), low-interest disaster loans from the Small Business Administration, have private insurance, or simply require no external aid – none of which are captured by the sum of NFIP and IA claims. The validation data in this instance are almost certainly underestimates of the true count of affected buildings; the magnitude of this underestimation is unknown, though is likely non-negligible. A total of 10 of the 18 events with <500 observed inundated buildings consist entirely of NFIP claims, while only one of the 17 events with >500 observed inundated buildings share this characteristic. This is because IA can only be claimed when the associated event is declared as a disaster by the president. Typically, these are larger disasters which exceed the state or local government's capacity to respond. As such, uninsured (via the NFIP) households impacted by these smaller events (in a risk context) who are unable to claim IA will be uncounted in this analysis, as they likely received assistance from other sources. Hence, the overprediction bias for these less catastrophic events appears intuitive. Potential causes of the underprediction biases in Fig. 6 have been highlighted previously in this section. Difficulties in defining a downstream boundary may have induced a more confined flood to be modelled than reality, and low river gauge density may have resulted in some damage-causing tributary floods to remain unmodelled. As for some of the more extreme cases of underprediction, such as the flood events in South Carolina (event 6; ∼10 000 observed versus ∼1000 modelled inundated buildings) and Kansas (event 30; ∼2000 observed versus ∼400 modelled inundated buildings), these may be explained by much of the risk being pluvial driven. Since the rainfall component of the Bates et al. (2020) model was not utilised here, urban, rainfall-driven, flash flooding – which contributed to many of the inundated buildings for these events – was not captured.
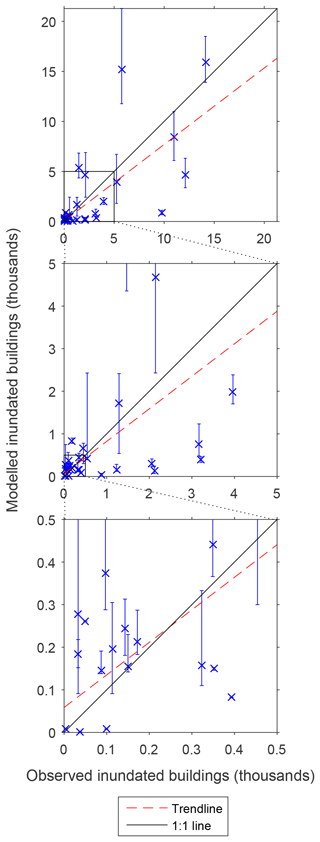
Figure 6Scatter plots illustrating the observed (NFIP and IA) versus the modelled count of inundated buildings for each of the 35 events. Blue crosses represent the simulated count in the 1.0*Q model, with error bars representing the range of counts between the 0.8*Q and 1.2*Q simulations. The trend line represents a linear polynomial fitted to the optimum of each event's three simulations. Descending panels are sequentially more magnified towards the origin.
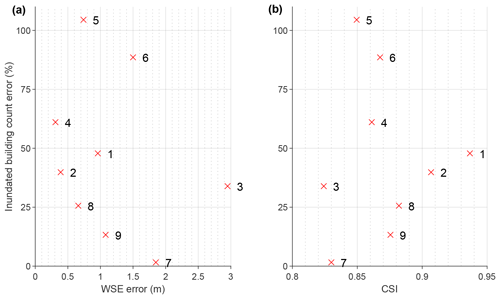
Figure 7The relationship between inundated building count errors and (a) WSE error and (b) flood extent CSI for the nine events. Numbered crosses refer to the ID of the flood event.
Furthermore, in Fig. 7 we can see that the model skill purported by the inundated building analysis bears little relation to the flood elevation and extent errors for the nine events with this information. A positive relationship would be expected in Fig. 7a, while a negative relationship would be expected in Fig. 7b. Event 7 in Pennsylvania is one of the least skilful events in the hazard-based analysis (WSE error of 1.85 m; CSI of 0.83), yet it is within discharge error of the observed inundated building count. Of course, the inundated building analysis does not measure whether the correct buildings are inundated. Instead, it tests whether the same number of buildings are inundated in aggregate, which could be a fortuitous balance of type I and II errors. In spite of this, and incorporating Fig. 5 into this discussion, it is clear that the choice of model test and the spatio-temporal setting of the test holds enormous sway over how one interprets the model's efficacy. High water level errors may have little impact on a model's ability to replicate impacted buildings; equally, inundated building counts may be highly sensitive to small water level errors. Coupled with the inconsistency in skill scores – of any metric – between flood events of different magnitudes, locations, data richness, and other characteristics, it makes obtaining an objective and generalised assessment of the US flood model employed here challenging. The likely considerable uncertainties in the data used to interrogate the model's skill are layered on top of this, for instance: (i) errors against HWMs are often high, but, from Fig. 3, we can see that these field data sometimes make little hydraulic sense, containing errors themselves perhaps approaching those obtained by the model in many instances; (ii) the resultant extents derived from these will share their biases and, particularly in areas unconstrained by HWMs, the interpolated surface may not represent reality well; and (iii) no reliable and integrated data exist on exact counts of buildings impacted by flood events, meaning the assimilation of NFIP and IA claims used here likely underpredict the true value of this quantity. Whether a model is deemed good therefore depends on what it is simulating and for what purpose, in addition to considering the influence of an unknown upper limit on the desired closeness of the match between the model and uncertain validation data.
In this analysis, we devised a framework to construct and deploy hydrodynamic models for any recorded historical flood event in the US, with minimal manual intervention, using the continental-scale design flood model described by Bates et al. (2020). We obtained hydrologic field observations for nine events simulated by this framework and recordings of inundated buildings for 35 such events in order to examine the skill of the model. Not unexpectedly, we find that model skill varies considerably between events, suggesting that the testing of flood inundation models across a spatial-scale imbalance (i.e. benchmarking continental–global-scale models against a handful of localised test cases) is prone to a misleading evaluation of its usefulness. Previous studies suggest that the continental model employed here can replicate the extent of high-quality, local-scale models of large flood events within error (Wing et al., 2017, 2019; Bates et al., 2020). Similarly, this analysis illustrates the very close match between flood extents derived from field data collected during the flood events and the maximum flood extent simulated by the continental model. However, we also highlight that tests of flood extent similarity can mask large deviations between observed and simulated water surface elevation. While all events were well replicated in terms of flood extent, water surface elevation errors were roughly 1 m on average. Some events adequately replicated the WSEs recorded in the HWM data, while others were considerably underestimated. However, most event water level errors are within the relative vertical errors of the terrain data employed. The impact of plausible (and perhaps conservative) errors in the high flow measurements used to drive the model is shown to affect its skill substantially, yet it is also clear that other errors remain. The insensitivity of extent comparison scores to changing water level errors suggests that CSIs are not readily comparable for different types of flood events; a model obtaining a CSI of 0.8 for event A may be no more skilful (in terms of water level error) than one which obtains a CSI of 0.6 for event B. We reiterate here the conclusions from other bodies of work (e.g. Mason et al., 2009; Stephens et al., 2014) which suggest that an analysis of water surface elevations provides a more rigorous and discriminatory test of a flood inundation model. In the analysis of buildings inundated by the larger set of flood events, some perfectly replicated the observed count of buildings while others starkly deviated from this. The 26 % mean error and an R2 of 0.63 still indicates reasonably strong predictive skill of these quantities by the model.
A consideration of the error in the observational validation data is often overlooked when interpreting the efficacy of a flood inundation model. If the deviation between the true maximum water surface elevation achieved during a flood event and that recorded from a high water mark is upwards of 0.5 m, obtaining model-to-observation errors of less than 0.5 m would be the result of rewarding the replication of noise. In this analysis, the magnitude of observational uncertainties is not formally examined, yet for many of the tests, the value of the validation data was close to exhaustion, i.e. a given benchmark was often replicated within its likely error. The HWMs did not always produce consistent water surfaces, interpolating between these may produce unrealistic flood extents at some locations, and the source of inundated building data may have undercounted the true number of impacted households.
In spite of this, useful interpretations of model performance can still be drawn from this analysis. The automated large-scale model is capable of skilfully replicating historical flood events, though, in some circumstances, events are poorly replicated and are generally so with an underprediction bias. This can be addressed by further developments to the event replication framework, which include the addition of a pluvial model component and restricting event domains to those which contain downstream (and not just upstream) river gauges to better represent backwatering. Furthermore, the use of hydrological models would solve the issue of gauge density and would also enable an estimation of future inundation hazards, which this framework cannot presently execute. However, the additional error induced by employing simulated, rather than observed, discharges would need to be considered. While these will be explored in future research, it is also clear from this analysis that flood inundation models can rarely be comprehensively validated when using historical data. Routinely collected terrain, boundary condition, and validation data must improve drastically for the science in this field to advance meaningfully. To do this, dedicated and specialist field campaigns are required, though it should be recognised that mobilising such a resource in time to capture transient events safely during extreme floods will be challenging. To this end, complementary data from remote sensing observations – particularly with the forthcoming launch of the NASA Surface Water and Ocean Topography (SWOT) mission – will necessarily play a role.
Historical flood events were simulated on behalf of the First Street Foundation (https://firststreet.org/, last access: 3 February 2021) and form part of their Flood Factor platform (https://floodfactor.com/, last access: 3 February 2021). Hydrodynamic modelling output is available for non-commercial, academic research purposes, only upon reasonable request from the corresponding author. USGS terrain data are available from https://ned.usgs.gov/ (last access: 3 February 2021) (US Geological Survey, 2021a). USGS river gauge data are available from https://waterdata.usgs.gov/nwis (last access: 3 February 2021) (US Geological Survey, 2021b). USGS high water mark data are available from https://stn.wim.usgs.gov/FEV/ (last access: 3 February 2021) (US Geological Survey, 2021c). Insurance and assistance claims are available from https://www.fema.gov/about/reports-and-data/openfema (last access: 3 February 2021) (Federal Emergency Management Agency, 2021). Microsoft Building Footprints are available from https://github.com/microsoft/USBuildingFootprints (last access: 3 February 2021) (Microsoft, 2021). USGS StreamStats are available from https://streamstats.usgs.gov/ (last access: 3 February 2021) (US Geological Survey, 2021d). USGS HUC zones are available from https://water.usgs.gov/GIS/huc.html (last access: 3 February 2021) (US Geological Survey, 2021e). The United States Army Corps of Engineers (USACE) National Levee Database is available at https://levees.sec.usace.army.mil/ (last access: 3 February 2021) (US Army Corps of Engineers, 2021). The USGS National Hydrography Dataset is available at https://www.usgs.gov/core-science-systems/ngp/national-hydrography (last access: 3 February 2021) (US Geological Survey, 2021f).
OEJW performed the hydraulic analyses of the models and wrote the paper. AMS and CCS developed and ran the models. MLM performed the analyses relating to the building data. JRP and MFA conceived the project. All authors aided in the conceptualisation of the analysis and commented on initial drafts.
The authors declare that they have no conflict of interest.
The authors are indebted to the US Geological Survey for their continued efforts in providing easy and open access to data sets fundamental to the construction and assessment of flood inundation models in the US.
Oliver E. J. Wing and Paul D. Bates were supported by the Engineering and Physical Sciences Research Council (EPSRC; grant no. EP/R511663/1). Paul D. Bates was supported by a Royal Society Wolfson Research Merit Award.
This paper was edited by Philip Ward and reviewed by Marc Bierkens and Francesco Dottori.
Adams, T. E., Chen, S., and Dymond, R., Results from operational hydrologic forecasts using the NOAA/NWS OHRFC Ohio river community HEC-RAS model, J. Hydrol. Eng., 23, 04018028, https://doi.org/10.1061/(ASCE)HE.1943-5584.0001663, 2018.
Alfieri, L., Salamon, P., Bianchi, A., Neal, J., Bates, P., and Feyen, L.: Advances in pan-European flood hazard mapping, Hydrol. Process., 28, 4067–4077, https://doi.org/10.1002/hyp.9947, 2014.
Altenau, E. H., Pavelsky, T. M., Moller, D., Lion, C., Pitcher, L. H., Allen, G. H., Bates, P. D., Calmant, S., Durand, M., and Smith, L. C.: AirSWOT measurements of river water surface elevation and slope: Tanana River, AK, Geophys. Res. Lett., 44, 181–189, https://doi.org/10.1002/2016GL071577, 2017a.
Altenau, E. H., Pavelsky, T. M., Bates, P. D., and Neal, J. C.: The effects of spatial resolution and dimensionality on modeling regional-scale hydraulics in a multichannel river, Water Resour. Res., 53, 1683–1701, https://doi.org/10.1002/2016WR019396, 2017b.
Apel, H., Aronica, G. T., Kreibich, H., and Thieken, A. H., Flood risk analyses – how detailed do we need to be?, Nat. Hazards, 49, 77–98, https://doi.org/10.1007/s11069-008-9277-8, 2009.
Aronica, G., Bates, P. D., and Horritt, M. S.: Assessing the uncertainty in distributed model predictions using observed binary pattern information within GLUE, Hydrol. Process., 16, 2001–2006, https://doi.org/10.1002/hyp.398, 2002.
Association of State Floodplain Managers: Flood Mapping for the Nation: A Cost Analysis for Completing and Maintaining the Nation's NFIP Flood Map Inventory, Madison, WI, USA, 2020.
Bates, P. D., Wilson, M. D., Horritt, M. S., Mason, D. C., Holden, N., and Currie, A.: Reach scale floodplain inundation dynamics observed using synthetic aperture radar imagery: data analysis and modelling, J. Hydrol., 328, 306–318, https://doi.org/10.1016/j.jhydrol.2005.12.028, 2006.
Bates, P. D., Horritt, M. S., and Fewtrell, T. J.: A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling, J. Hydrol., 387, 33–45, https://doi.org/10.1016/j.jhydrol.2010.03.027, 2010.
Bates, P. D., Quinn, N., Sampson, C. C., Smith, A. M., Wing, O. E. J., Sosa, J., Savage, J., Olcese, G., Schumann, G. J.-P., Giustarini, L., Coxon, G., Neal, J. C., Porter, J. R., Amodeo, M. F., Chu, Z., Lewis-Gruss, S., Freeman, N., Houser, T., Delgado, M., Hamidi, A., Bolliger, I. W., McCusker, K. E., Emanuel, K. A., Ferreira, C. M., Khalid, A., Haigh, I. D., Couasnon, A., Kopp, R. E., Hsiang, S., and Krajewski, W. F.: Combined modelling of US fluvial, pluvial and coastal flood hazard under current and future climates, Water Resour. Res., e2020WR028673, https://doi.org/10.1029/2020WR028673, accepted, 2020.
Bell, H. M. and Tobin, G. A.: Efficient and effective? The 100-year flood in the communication and perception of flood risk, Environ. Hazards, 7, 302–311, https://doi.org/10.1016/j.envhaz.2007.08.004, 2007.
Bermúdez, M., Neal, J. C., Bates, P. D., Coxon, G., Freer, J. E., Cea, L., and Puertas, J., Quantifying local rainfall dynamics and uncertain boundary conditions into a nested regional-local flood modeling system, Water Resour. Res., 53, 2770–2785, https://doi.org/10.1002/2016WR019903, 2017.
Bubeck, P., Botzen, W. J. W., and Aerts, J. C. J. H.: A review of risk perceptions and other factors that influence flood mitigation behavior, Risk Anal., 32, 1481–1495, https://doi.org/10.1111/j.1539-6924.2011.01783.x, 2012.
Coxon, G., Freer, J., Westerberg, I. K., Wagener, T., Woods, R., and Smith, P. J.: A novel framework for discharge uncertainty quantification applied to 500 UK gauging stations, Water Resour. Res., 51, 5531–5546, https://doi.org/10.1002/2014WR016532, 2015.
Di Baldassarre, G. and Montanari, A.: Uncertainty in river discharge observations: a quantitative analysis, Hydrol. Earth Syst. Sci., 13, 913–921, https://doi.org/10.5194/hess-13-913-2009, 2009.
Di Baldassarre, G., Schumann, G., and Bates, P. D.: A technique for the calibration of hydraulic models using uncertain satellite observations of flood extent, J. Hydrol., 367, 276–282, https://doi.org/10.1016/j.jhydrol.2009.01.020, 2009.
Dottori, F., Martina, M. L. V., and Todini, E.: A dynamic rating curve approach to indirect discharge measurement, Hydrol. Earth Syst. Sci., 13, 847–863, https://doi.org/10.5194/hess-13-847-2009, 2009.
Dottori, F., Salamon, P., Bianchi, A., Alfieri, L., Hirpa, F. A., and Feyen, L.: Development and evaluation of a framework for global flood hazard mapping, Adv. Water Resour., 94, 87–102, https://doi.org/10.1016/j.advwatres.2016.05.002, 2016.
Federal Emergency Management Agency: OpenFEMA, available at: https://www.fema.gov/about/reports-and-data/openfema, last access: 3 February 2021.
Fewtrell, T. J., Duncan, A., Sampson, C. C., Neal, J. C., and Bates, P. D.: Benchmarking urban flood models of varying complexity and scale using high resolution terrestrial LiDAR data, Phys. Chem. Earth Pt. A/B/C, 36, 281–291, https://doi.org/10.1016/j.pce.2010.12.011, 2011.
Fleischmann, A., Paiva, R., and Collischonn, W.: Can regional to continental river hydrodynamic models be locally relevant? A cross-scale comparison, J. Hydrol., 3, 100027, https://doi.org/10.1016/j.hydroa.2019.100027, 2019.
Gesch, D. B., Oimoen, M. J., and Evans, G. A.: Accuracy Assessment of the US Geological Survey National Elevation Dataset, and Comparison with Other Large-Area Elevation Datasets – SRTM and ASTER, US Geological Survey Open-File Report 2014-1008, US Geological Survey, Reston, VA, 10 pp., https://doi.org/10.3133/ofr20141008, 2014.
Hall, J. W., Tarantola, S., Bates, P. D., and Horritt, M. S.: Distributed sensitivity analysis of flood inundation model calibration, J. Hydraul. Eng., 131, 117–126, https://doi.org/10.1061/(ASCE)0733-9429(2005)131:2(117), 2005.
Hattermann, F. F., Wortmann, M., Liersch, S., Toumi, R., Sparks, N., Genillard, C., Schröter, K., Steinhausen, M., Gyalai-Korpos, M., Máté, K., Hayes, B., del Rocío Rivas López, M., Rácz, T., Nielsen, M. R., Kaspersen, P. S., and Drews, M.: Simulation of flood hazard and risk in the Danube basin with the Future Danube Model, Clim. Serv., 12, 14–26, https://doi.org/10.1016/j.cliser.2018.07.001, 2018.
Hawker, L., Rougier, J., Neal, J., Bates, P., Archer, L., and Yamazaki, D.: Implications of simulating global digital elevation models for flood inundation studies, Water Resour. Res., 54, 7910–7928, https://doi.org/10.1029/2018WR023279, 2018.
Horritt, M. S. and Bates, P. D.: Evaluation of 1D and 2D numerical models for predicting river flood inundation, J. Hydrol., 268, 87–99, https://doi.org/10.1016/S0022-1694(02)00121-X, 2002.
Horritt, M. S., Bates, P. D., Fewtrell, T. J., Mason, D. C., and Wilson, M. D.: Modelling the hydraulics of the Carlisle 2005 flood event, Proc. Inst. Civ. Eng., 163, 273–281, https://doi.org/10.1680/wama.2010.163.6.273, 2010.
Hunter, N. M., Bates, P. D., Neelz, S., Pender, G., Villanueva, I., Wright, N. G., Liang, D., Falconer, R. A., Lin, B., Waller, S., Crossley, A. J., and Mason, D. C.: Benchmarking 2D hydraulic models for urban flooding, Proc. Inst. Civ. Eng. – Water Manage., 161, 13–30, https://doi.org/10.1680/wama.2008.161.1.13, 2008.
Kousky, C.: Disasters as learning experiences or disasters as policy opportunities? Examining flood insurance purchases after hurricanes, Risk Anal., 37, 517–530, https://doi.org/10.1111/risa.12646, 2017.
Luke, A., Sanders, B. F., Goodrich, K. A., Feldman, D. L., Boudreau, D., Eguiarte, A., Serrano, K., Reyes, A., Schubert, J. E., AghaKouchak, A., Basolo, V., and Matthew, R. A.: Going beyond the flood insurance rate map: insights from flood hazard map co-production, Nat. Hazards Earth Syst. Sci., 18, 1097–1120, https://doi.org/10.5194/nhess-18-1097-2018, 2018.
Mason, D. C., Cobby, D. M., Horritt, M. S., and Bates, P. D.: Floodplain friction parameterization in two-dimensional river flood models using vegetation heights derived from airborne scanning laser altimetry, Hydrol. Process., 17, 1711–1732, https://doi.org/10.1002/hyp.1270, 2003.
Mason, D. C., Horritt, M. S., Dall'Amico, J. T., Scott, T. R., and Bates, P. D.: Improving river flood extent delineation from synthetic aperture radar using airborne laser altimetry, IEEE T. Geosci. Remote, 45, 3932–3943, https://doi.org/10.1109/TGRS.2007.901032, 2007.
Mason, D. C., Bates, P. D., and Dall'Amico, J. T.: Calibration of uncertain flood inundation models using remotely sensed water levels, J. Hydrol., 368, 224–236, https://doi.org/10.1016/j.jhydrol.2009.02.034, 2009.
Matgen, P., Schumann, G., Hentry, J.-B., Hoffmann, L., and Pfister, L.: Integration of SAR-derived river inundation areas, high-precision topographic data and a river flow model toward near real-time flood management, Int. J. Appl. Earth Obs. Geoinf., 9, 247–263, https://doi.org/10.1016/j.jag.2006.03.003, 2007.
McMillan, H., Krueger, T., and Freer, J.: Benchmarking observational uncertainties for hydrology: rainfall, river discharge and water quality, Hydrol. Process., 26, 4078–4111, https://doi.org/10.1002/hyp.9384, 2012.
Microsoft: USBuildingFootprints, available at: https://github.com/microsoft/USBuildingFootprints, last access: 3 February 2021.
Mignot, E., Paquier, A., and Haider, S.: Modeling floods in a dense urban area using 2D shallow water equations, J. Hydrol., 327, 186–199, https://doi.org/10.1016/j.jhydrol.2005.11.026, 2006.
Neal, J., Schumann, G., Fewtrell, T., Budimir, M., Bates, P., and Mason, D.: Evaluating a new LISFLOOD-FP formulation with data from the summer 2007 floods in Tewkesbury, UK, J. Flood Risk Manage., 4, 88–95, https://doi.org/10.1111/j.1753-318X.2011.01093.x, 2011.
Neal, J., Schumann, G., and Bates, P.: A subgrid channel model for simulating river hydraulics and floodplain inundation over large and data sparse areas, Water Resour. Res., 48, W11506, https://doi.org/10.1029/2012WR012514, 2012.
Neal, J. C., Bates, P. D., Fewtrell, T. J., Hunter, N. M., Wilson, M. D., and Horritt, M. S.: Distributed whole city water level measurements from the Carlisle 2005 urban flood event and comparison with hydraulic model simulations, J. Hydrol., 368, 42–55, https://doi.org/10.1016/j.jhydrol.2009.01.026, 2009.
Pappenberger, F., Beven, K., Horritt, M., and Blazkova, S.: Uncertainty in the calibration of effective roughness parameters in HEC-RAS using inundation and downstream level observations, J. Hydrol., 302, 46–69, https://doi.org/10.1016/j.jhydrol.2004.06.036, 2005.
Pappenberger, F., Matgen, P., Beven, K. J., Henry, J.-B., Pfister, L., and de Fraipont, P.: Influence of uncertain boundary conditions and model structure on flood inundation predictions, Adv. Water Resour., 29, 1430–1449, https://doi.org/10.1016/j.advwatres.2005.11.012, 2006.
Pappenberger, F., Frodsham, K., Beven, K., Romanowicz, R., and Matgen, P.: Fuzzy set approach to calibrating distributed flood inundation models using remote sensing observations, Hydrol. Earth Syst. Sci., 11, 739–752, https://doi.org/10.5194/hess-11-739-2007, 2007.
Poussin, J. K., Botzen, W. J. W., and Aerts, J. C. J. H.: Factors of influence on flood damage mitigation behaviour by households, Environ. Sci. Policy, 40, 69–77, https://doi.org/10.1016/j.envsci.2014.01.013, 2014.
Rudorff, C. M., Melack, J. M., and Bates, P. D.: Flooding dynamics on the lower Amazon floodplain: 1. Hydraulic controls on water elevation, inundation extent, and river-floodplain discharge, Water Resour. Res., 50, 619–634, https://doi.org/10.1002/2013WR014091, 2014.
Sampson, C. C., Smith, A. M., Bates, P. D., Neal, J. C., Alfieri, L., and Freer, J. E.: A high-resolution global flood hazard model, Water Resour. Res., 51, 7358–7381, https://doi.org/10.1002/2015WR016954, 2015.
Sanders, B. F., Schubert, J. E., Goodrich, K. A., Houston, D., Feldman, D. L., Basolo, V., Luke, A., Boudreau, D., Karlin, B., Cheung, W., Contreras, S., Reyes, A., Eguiarte, A., Serrano, K., Allaire, M., Moftakhari, H., AghaKouchak, A., and Matthew, R. A.: Collaborative modeling with fine-resolution data enhances flood awareness, minimizes differences in flood perception, and produces actionable flood maps, Earth's Future, 8, e2019EF001391, https://doi.org/10.1029/2019EF001391, 2020.
Schumann, G., Matgen, P., Hoffmann, L., Hostache, R., Pappenberger, F., and Pfister, L.: Deriving distributed roughness values from satellite radar data for flood inundation modelling, J. Hydrol., 344, 96–111, https://doi.org/10.1016/j.jhydrol.2007.06.024, 2007.
Schumann, G. J.-P., Neal, J. C., Mason, D. C., and Bates, P. D.: The accuracy of sequential aerial photography and SAR data for observing urban flood dynamics, a case study of the UK summer 2007 floods, Remote Sens. Environ., 115, 2536–2546, https://doi.org/10.1016/j.rse.2011.04.039, 2011.
Schumann, G. J.-P., Neal, J. C., Voisin, N., Andreadis, K. M., Pappenberger, F., Phanthuwongpakdee, N., Hall, A. C., and Bates, P. D.: A first large-scale flood inundation forecasting model, Water Resour. Res., 49, 6248–6257, https://doi.org/10.1002/wrcr.20521, 2013.
Smith, A., Sampson, C., and Bates, P.: Regional flood frequency analysis at the global scale, Water Resour. Res., 51, 539–553, https://doi.org/10.1002/2014WR015814, 2015.
Stephens, E. and Bates, P.: Assessing the reliability of probabilistic flood inundation model predictions, Hydrol. Processs., 29, 4264–4283, https://doi.org/10.1002/hyp.10451, 2015.
Stephens, E., Schumann, G., and Bates, P.: Problems with binary pattern measures for flood model evaluation, Hydrol. Process., 28, 4928–4937, https://doi.org/10.1002/hyp.9979, 2014.
Stephens, E. M., Bates, P. D., Freer, J. E., and Mason, D. C.: The impact of uncertainty in satellite data on the assessment of flood inundation models, J. Hydrol., 414–415, 162–173, https://doi.org/10.1016/j.jhydrol.2011.10.040, 2012.
US Army Corps of Engineers: National Levee Database, available at: https://levees.sec.usace.army.mil/, last access: 3 February 2021.
US Geological Survey: The National Map, available at: https://ned.usgs.gov/ (last access: 3 February 2021), 2021a.
US Geological Survey: USGS Water Data for the Nation, available at: https://waterdata.usgs.gov/nwis (last access: 3 February 2021), 2021b.
US Geological Survey: USGS Flood Event Viewer, available at: https://stn.wim.usgs.gov/FEV/ (last access: 3 February 2021), 2021c.
US Geological Survey: StreamStats: Streamflow Statistics and Spatial Analysis Tools for Water-Resources Applications, available at: https://streamstats.usgs.gov/ (last access: 3 February 2021), 2021d.
US Geological Survey: Hydrologic Unit Maps, available at: https://water.usgs.gov/GIS/huc.html (last access: 3 February 2021), 2021e.
US Geological Survey: National Hydrography, available at: https://www.usgs.gov/core-science-systems/ngp/national-hydrography (last access: 3 February 2021), 2021f.
Ward, P. J., Jongman, B., Aerts, J. C. J. H., Bates, P. D., Botzen, W. J. W., Loaiza, A. D., Hallegatte, S., Kind, J. M., Kwadijk, J., Scussolini, P., and Winsemius, H. C.: A global framework for future costs and benefits of river-flood protection in urban areas, Nat. Clim. Change, 7, 642–646, https://doi.org/10.1038/nclimate3350, 2017.
Watson, K. M., Harwell, G. R., Wallace, D. S., Welborn, T. L., Stengel, V. G., and McDowell, J. S.: Characterization of Peak Streamflows and Flood Inundation of Selected Areas in Southeastern Texas and Southwestern Louisiana from the August and September 2017 Flood Resulting from Hurricane Harvey, US Geological Survey Scientific Investigations Report 2018-5070, US Geological Survey, Reston, VA, 44 pp., https://doi.org/10.3133/sir20185070, 2018.
Wing, O. E. J., Bates, P. D., Sampson, C. C., Smith, A. M., Johnson, K. J., and Erickson, T. A.: Validation of a 30 m resolution flood hazard model of the conterminous United States, Water Resour. Res., 53, 7968–7986, https://doi.org/10.1002/2017WR020917, 2017.
Wing, O. E. J., Bates, P. D., Neal, J. C., Sampson, C. C., Smith, A. M., Quinn, N., Shustikova, I., Domeneghetti, A., Gilles, D. W., Goska, R., and Krajewski, W. F.: A new automated method for improved flood defense representation in large-scale hydraulic models, Water Resour. Res., 55, 11007–11034, https://doi.org/10.1029/2019WR025957, 2019.
Winsemius, H. C., Van Beek, L. P. H., Jongman, B., Ward, P. J., and Bouwman, A.: A framework for global river flood risk assessments, Hydrol. Earth Syst. Sci., 17, 1871–1892, https://doi.org/10.5194/hess-17-1871-2013, 2013.
Winsemius, H. C., Aerts, J. C. J. H., van Beek, L. P. H., Bierkens, M. F. P., Bouwman, A., Jongman, B., Kwadijk, J. C. J., Ligtvoet, W, Lucas, P. L., van Vuuren, D. P., and Ward P. J.: Global drivers of future river flood risk, Nat. Clim. Change, 6, 381–385, https://doi.org/10.1038/nclimate2893, 2016.
Wood, M., Hostache, R., Neal, J., Wagener, T., Giustarini, L., Chini, M., Corato, G., Matgen, P., and Bates, P.: Calibration of channel depth and friction parameters in the LISFLOOD-FP hydraulic model using medium-resolution SAR data and identifiability techniques, Hydrol. Earth Syst. Sci., 20, 4983–4997, https://doi.org/10.5194/hess-20-4983-2016, 2016.
Yamazaki, D., Kanae, S., Kim, H., and Oki, T.: A physically based description of floodplain inundation dynamics in a global river routing model, Water Resour. Res., 47, W04501, https://doi.org/10.1029/2010WR009726, 2011.