the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Deriving rainfall thresholds for landsliding at the regional scale: daily and hourly resolutions, normalisation, and antecedent rainfall
Elena Leonarduzzi
Peter Molnar
Rainfall thresholds are a simple and widely used method to forecast landslide occurrence. We provide a comprehensive data-driven assessment of the effects of rainfall temporal resolution (hourly versus daily) on rainfall threshold performance in Switzerland, with sensitivity to two other important aspects which appear in many landslide studies – the normalisation of rainfall, which accounts for local climatology, and the inclusion of antecedent rainfall as a proxy of soil water state prior to landsliding. We use an extensive landslide inventory with over 3800 events and several daily and hourly, station, and gridded rainfall datasets to explore different scenarios of rainfall threshold estimation. Our results show that although hourly rainfall did show the best predictive performance for landslides, daily data were not far behind, and the benefits of hourly resolutions can be masked by the higher uncertainties in threshold estimation connected to using short records. We tested the impact of several typical actions of users, like assigning the nearest rain gauge to a landslide location and filling in unknown timing, and we report their effects on predictive performance. We find that localisation of rainfall thresholds through normalisation compensates for the spatial heterogeneity in rainfall regimes and landslide erosion process rates and is a good alternative to regionalisation. On top of normalisation by mean annual precipitation or a high rainfall quantile, we recommend that non-triggering rainfall be included in rainfall threshold estimation if possible. Finally, while antecedent rainfall threshold approaches used at the local scale are not successful at the regional scale, we demonstrate that there is predictive skill in antecedent rain as a proxy of soil wetness state, despite the large heterogeneity of the study domain.
- Article
(2810 KB) - Full-text XML
- BibTeX
- EndNote
Landslides are a natural hazard that affects alpine regions worldwide, resulting in substantial economic losses and human casualties (Kjekstad and Highland, 2009). Landslides can be initiated by different triggering factors but mainly rainfall and earthquakes. Economic losses connected to landsliding are estimated to be between USD 0.5 billion and 5 billion annually for the European Alps region (e.g. Salvati et al., 2010; Trezzini et al., 2013; Klose, 2015; Kjekstad and Highland, 2009), and similar losses are also reported for Canada and the United States (e.g. Kjekstad and Highland, 2009; Schuster, 1996; Mirus et al., 2020). Petley (2012) carried out a global study over a 7-year period (2004–2010) and found a total of 2620 non-seismically triggered landslides causing 32 322 fatalities. Clearly, the socio-economic impact of landslides is large and this natural hazard requires attention in the form of risk mapping, better prediction, and early warning systems.
The focus in this work is on rainfall-induced shallow landslides, which are the predominant type of landslides in Switzerland and other alpine environments. These are landslides where the entire soil (upper regolith) fails along a weathered bedrock interface, and they develop quickly, leading to mass failure following soil-saturating rainfall (e.g. Highland and Bobrowsky, 2008). Despite their smaller size, these landslides can be widespread and have the potential to damage infrastructure (railways, roads), homes, and even lead to fatalities. For instance, in Switzerland, a total of EUR 520 million in damage was recorded in the period 1972–2007 and 32 people lost their life due to shallow landslides (Hilker et al., 2009).
One of the most widespread approaches for the prediction of triggering conditions leading to rainfall-induced landslides is that of rainfall thresholds (e.g. Stevenson, 1977; Caine, 1980; Guzzetti et al., 2007), which are used operationally in many countries (e.g. see reviews in Guzzetti et al., 2020; Piciullo et al., 2018). These can be based on any rainfall property but most frequently are assumed to be power law curves in the intensity-duration (ID) or the total rainfall-duration (ED) space. The reasoning behind this choice is that two different storm types may be responsible for the initiation of landslides: short and intense, or long-lasting and typically less intense. Many approaches exist to formulate and estimate ID or ED curves, and they differ in the accuracy of the landslide inventory, the rainfall records used, the definition of rainfall events, the statistical methodology for threshold definition, and the validation technique, among others (see review in Segoni et al., 2018).
One of the main aspects in which the approaches differ is the choice of rainfall temporal resolution, typically forced by data availability. The short and intense events responsible for local soil saturation and triggering of landslides are usually associated with convective activity, which can last for just a few hours (e.g. Molnar and Burlando, 2008). For this reason, hourly thresholds are expected to be more appropriate for landslide prediction. There is some evidence for this in the literature. For example, Marra (2019) shows the underestimation of rainfall thresholds as the temporal resolution of rainfall is coarsened with a numerical experiment, while Gariano et al. (2020) demonstrate a similar effect on a real case dataset where reported landslides are combined with rain gauge records aggregated to different temporal resolutions. At the same time, daily rainfall thresholds or ID curves may also exhibit good predictive power for landsliding, e.g. as shown in a comprehensive analysis in Switzerland (Leonarduzzi et al., 2017). So the following question arises: how does the temporal resolution of the rainfall data actually affect landslide prediction?
We address this question with a data analysis experiment, where we take into account realistic conditions and consequences of different temporal resolutions of data. For example, choosing a higher resolution (e.g. hourly) has several undesirable consequences: (a) rainfall records are typically shorter (hourly records are only available in automatic networks in more recent decades); (b) rainfall records are likely to be less dense in space, leading to poorer matching with landslide locations; and (c) landslide inventories are typically less rich (requiring timing and not only date of occurrence) or more uncertain, especially for older events that were reconstructed from newspaper articles or other indirect sources. All these aspects have to be taken into consideration in an objective analysis of the effects of temporal resolution on rainfall thresholds.
In this paper we undertake such an analysis with the high-quality landslide database available in Switzerland (Hilker et al., 2009) and several high-quality rainfall records available for Switzerland from MeteoSwiss. We expand the impact of temporal resolution (hourly versus daily) on landslide prediction with sensitivity to two other important aspects which appear in many landslide studies: the normalisation of rainfall, which accounts for local meteorological properties (e.g. Marc et al., 2019), and the inclusion of antecedent rainfall, which provides additional information on soil state prior to landsliding, typically studied at local scales (Glade et al., 2000; Godt et al., 2006; Mirus et al., 2018a, b). The objectives of the paper therefore are (a) to provide an extensive comparison between hourly and daily rainfall data for the definition of rainfall thresholds, considering several practical consequences of choosing a higher temporal resolution; (b) to compare different strategies for the normalisation of rainfall thresholds; and (c) to explore whether antecedent rainfall does provide added predictive power at the regional/national scale.
We use several rainfall datasets and a landslide inventory (Hilker et al., 2009) (Sect. 2.1) to derive objective landslide-triggering rainfall thresholds at the daily and hourly scale using two different statistical methods (true skill statistic maximisation and frequentist approach) (Sect. 2.2) and to address some of the issues associated with higher temporal resolution data, such as the absence of accurate timing information for landslide occurrence (Sect. 2.3) and the lower quality (density) of rainfall data (Sect. 2.4). We follow up with methods which quantify the impact of rainfall threshold normalisation (Sect. 2.5) and the added power of antecedent rainfall on landslide prediction (Sect. 2.6).
2.1 Rainfall and landslide data
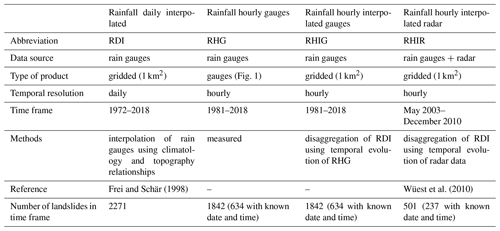
The rainfall datasets used differ by type of measurement, duration of record, and temporal and spatial resolutions (Fig. 1 and Table 1). The daily product (rainfall daily interpolated, RDI) is the longest record (1972–2018), containing daily sums (06:00 to 06:00 am) over 1 km × 1 km cells covering Switzerland. It is obtained by interpolating daily measurements from approximately 420 rain gauges, using the climatology (intended here as anomaly relative to the monthly mean precipitation over the reference period 1971–1990), and regionally varying precipitation–topography relationship (procedure explained in detail in Frei and Schär, 1998).
Frei and Schär (1998)Wüest et al. (2010)
Figure 1Map and scheme of the different rainfall datasets used in the analysis. The daily interpolated product (RDI), the hourly rain gauges (RHG), and the two derived hourly gridded products, which preserve the daily sums from RDI, but use the sub-daily temporal variability of a radar composite (RHIR) or of the hourly rain gauges (RHIG).
The hourly station rainfall dataset (rainfall hourly gauges, RHG) is the collection of the hourly rainfall time series measured continuously since 1981 at 45 gauges across the country (green dots in Fig. 1). We use two different hourly datasets that were derived by disaggregating the RDI such that the daily sums match that of the corresponding RDI cell at the same 1 km × 1 km resolution. The first dataset (rainfall hourly interpolated gauges, RHIG) is computed by disaggregating the daily sum RDI into hourly intensities by using the hourly fractions recorded at the nearest hourly gauge (RHG). The second dataset (rainfall hourly interpolated radar, RHIR) instead uses an hourly composite of radar measurements NASS (Joss et al., 1998; Germann and Joss, 2004; Germann et al., 2006) for the disaggregation (procedure explained in detail in Wüest et al., 2010). Due to the quality of the radar composite, we expect RHIR to be more accurate than RHIG between stations. In fact, the hourly gauge network measuring continuously since 1981 is quite sparse (see Fig. 1, ca. 1 rain gauge per 900 km2), and it is likely to miss heavy rainfall intensities especially during convective storms.
The four different rainfall records (RDI, RHG, RHIG, and RHIR) are combined with the landslides extracted from the Swiss flood and landslide damage database (Hilker et al., 2009). This databases collects floods, debris flows, landslides, and rockfalls that produced damage in Switzerland since 1972. Of the total reported landslides in the period 1972–2018 we selected those with known location and date. Then, depending on the rainfall dataset used, the time frame is modified, and for hourly analysis a further selection is made of the entries with known timing (number of landslides per rainfall dataset is reported in Table 1).
2.2 Rainfall thresholds
The methodology for the definition of rainfall thresholds follows the statistical procedure introduced in Leonarduzzi et al. (2017). First we separate the rainfall time series into events, by considering a minimum amount of dry hours between events. We choose 24 h for daily rainfall data and 6 h for hourly rainfall data. The hourly inter-storm period of 6 h separating events is selected as the one leading to the best performance (highest true skill statistic; see methodology explained hereafter), within a range of 2–12 h, which is the amount of dry hours expected to separate individual storms. This is longer than the requirement of statistical independence between events, which Gaál et al. (2014) showed to be at least 2 h. This difference reflects the role that antecedent rain plays in landslide generation.
Then we classify rainfall events as triggering events if a landslide happens during or immediately after the event, and non-triggering otherwise. We compute the event duration, total rainfall, mean, and maximum rainfall intensity for each event. We then define optimal thresholds for each of the precipitation characteristics by finding the threshold that maximises the true skill statistic TSS = specificity + sensitivity − 1, where sensitivity is the rate of true positives and specificity is the rate of true negatives. Additionally we also define total rainfall E versus duration D (ED) thresholds in the form of a power law function, , by optimising the two parameters a and b through TSS maximisation. As a reference, we provide also the results for the thresholds defined following the frequentist approach, first introduced in Brunetti et al. (2010), which is one of the most widely used methods for ED fitting (e.g. Peruccacci et al., 2012; Vennari et al., 2014; Gariano et al., 2015; Iadanza et al., 2016; Melillo et al., 2018; Roccati et al., 2018). The optimum threshold in this case is based on triggering events only. The exponent b is obtained by fitting the ED pairs with a line in log–log space. The intercept a is adjusted to match a chosen exceedance probability (in this paper we use the 5 % exceedance probability as a reference).
For all analyses based on the gridded rainfall products, we consider the rainfall time series for each susceptible cell, for which we define rainfall events following the procedure explained above. Susceptible cells are those rainfall cells in which at least one landslide was recorded in the respective time frame of each dataset in Table 1.
2.3 Inaccurate landslide timing: triggering and peak intensities
One problem we face when utilising hourly rainfall records is that the actual timing of historical landslides is typically not available or very uncertain/inaccurate. For instance, Guzzetti et al. (2007) report that, out of the 2626 rainfall events associated with shallow slope failures globally, only 26.3 % had information about the date of occurrence and only 5.1 % also had information about the timing. Although a common approach to compensate for the lack of accurate landslide timing is to assign the landslide to the rainiest hour within a certain time window, the effect of this approximation is not well known. Peres et al. (2018) showed the potential impact of timing and date uncertainty using synthetic databases by coupling stochastic weather generation and a physically based hydrological and slope stability model. Staley et al. (2013) showed, using a precise debris-flow database, that using peak rainstorm intensity instead of the actual triggering intensity results in an overestimation of the ID threshold.
We study the wrong timing effect similarly to Staley et al. (2013) by introducing two scenarios as alternatives to the actual landslide database: one in which we assume that when the day of a landslide is known its timing is assigned to the most intense rainy hour within the day (this is the case of Staley et al., 2013) and a second alternative in which the timing is assigned to the rainiest hour within a 48 h window centred on the actual timing recorded in the database (this is a hypothetical case which considers the fact that we may not have the right date recorded in the landslide database). Once the timing is altered accordingly, the modified landslide databases are used for the definition of ED thresholds following the same procedure as with the original true database. We carry out this exercise utilising landslides with known time of occurrence recorded between May 2003 and December 2010 (time frame of RHIR).
2.4 Rainfall quality: gauge density and interpolation
In most studies where regional rainfall thresholds are defined, landslides in a region are assigned to the closest rain gauge, sometimes taking into consideration not only distance (Finlay et al., 1997; Godt et al., 2006), but also similarities in topography or other aspects important for precipitation (e.g. Aleotti, 2004; Berti et al., 2012; Gariano et al., 2012; Rossi et al., 2012; Melillo et al., 2018; Vennari et al., 2014). Nikolopoulos et al. (2015) showed that, decreasing the density of the rain gauge network, the b parameter of the power law ID curve on average decreases, depending on whether the closest rain gauge is considered (nearest neighbour) or simple interpolation methods such as inverse distance weighting or ordinary kriging are used. In the context of comparing the impacts of daily and hourly rainfall resolutions on landslide thresholds, we recognise that gauge density is very important, and we construct an experiment to test the effects of gauge density and accuracy of spatial interpolation.
To do this, we define rainfall thresholds with the closest rain gauge based on the very sparse station-based hourly rainfall record RHG and compare it to the spatially distributed disaggregated dataset RHIG. The comparison shows the effect of improving an hourly record obtained with a very sparse network, by taking advantage of a daily dataset based on a much denser network and an advanced interpolation method in RDI (Frei and Schär, 1998), merged with hourly station data. We propose two versions of the closest-rain-gauge approach used in many studies. First we assign each landslide to the geographically closest rain gauge and then extract rainfall events for each of the gauges which have at least one landslide (maximum 45 rain gauges) from the RHG dataset. Second we assign to each susceptible rainfall cell (as defined for the gridded rainfall products) the rainfall of the closest rain gauge, and the event definition is carried out for each of these cells (maximum as many cells as the number of landslides) from the RHIG dataset.
2.5 Rainfall normalisation
One of the methods suggested to improve the predictive power of regional rainfall thresholds is to localise them. This can be done through regionalisation by dividing the area into homogeneous regions and defining a different threshold for each of them (e.g. Peruccacci et al., 2012; Leonarduzzi et al., 2017; Peruccacci et al., 2017) or by normalisation, which is defining thresholds based on the ratio between the precipitation parameters and a local scaling value, considered to be representative of local rainfall characteristics. Typically, the property chosen is the mean annual precipitation, MAP (e.g. Dahal and Hasegawa, 2008; Aleotti, 2004; Guzzetti et al., 2007; Leonarduzzi et al., 2017; Peruccacci et al., 2017); the rainy-day normal, , where n is the number of rainy days in a year (Guidicini and Iwasa, 1977; Wilson and Jayko, 1997; Guzzetti et al., 2007; Postance et al., 2018); or other precipitation characteristics (e.g. anomaly relative to 10-year return period rainfall in Marc et al., 2019).
In this paper we test in addition to the well established MAP and RDN normalisations also quantiles of event properties and of daily/hourly rainfall as scaling parameters. We consider both wet quantiles, which are computed only considering rainy days/hours, and absolute quantiles, which consider all days/hours. Note that there are fundamental differences between scaling with MAP and absolute quantiles or RDN, event properties quantiles, and wet quantiles, in that the former ignore intermittency of rainfall, while the latter are computed only from the rainy hours/days of the rainfall dataset.
2.6 Antecedent rainfall
The main criticism raised against rainfall thresholds for landsliding in general is that they only consider recent/event rainfall, without taking into account the soil status prior to it (e.g. Bogaard and Greco, 2018). To include this antecedent soil moisture state into rainfall thresholds, several ad hoc approaches have been introduced with varying levels of complexity and data demand. The simplest of these consists in accumulating rainfall over a fixed duration prior to the triggering event rainfall (e.g. Chleborad, 2003; Frattini et al., 2009). In other studies the fixed duration has been modified to account for vanishing memory in rainfall using the antecedent precipitation index (API), which gives less weight to rainfall contributions further back in time (e.g. Crozier and Eyles, 1980; Crozier, 1986), often relating the decay coefficient to the recession curves of storm hydrographs, as first suggested by Glade et al. (2000). A further development of the API is the so-called antecedent wetness index, which accounts also for other hydrological variables by removing from antecedent rainfall the potential evapotranspiration and then following the same approach as API (e.g. Godt et al., 2006). Finally, a few studies use estimates of the real antecedent soil wetness which are based on the soil water balance (Ponziani et al., 2012) or hydrological modelling (e.g. Segoni et al., 2009; Thomas et al., 2018), or obtained from on-site (e.g. Mirus et al., 2018b; Wicki et al., 2020) or remote sensing measurements (e.g. Brocca et al., 2012; Thomas et al., 2019).
Here, we follow a new approach to assess the information content of antecedent rainfall, with the goal of testing whether it is still recognisable over such a large and heterogeneous area. To do this, we follow an approach opposite to what is normally done, where events are separated into with and without antecedent rainfall a priori (e.g. Frattini et al., 2009). We start from the rainfall events, as described in Sect. 2.2. For each of those, we compute the antecedent 5 and 30 d rainfall, which is simply the sum of rainfall over the N days prior to the beginning of the rainfall event itself. All these events were either observed as triggering, if a landslide happened during them, or non-triggering. According to the optimised ED threshold, we can also separate them into predicted triggering, above the ED power law curve, or predicted non-triggering, below it. The intersection of these predictions/observations gives us four groups of events: false alarms, true positives, misses, and true negatives. If the antecedent rainfall is the parameter explaining the failures of the ED threshold, we would expect that misses were associated with high antecedent rainfall and false alarms with very low antecedent rainfall. We investigate this by averaging within each of the four groups the antecedent rainfall for each event duration (all events of duration 1 d, all events of duration 2 d, etc.). We decide to do it separately for each event duration because we suspect there could be differences related to the duration, as a proxy of storm/weather system type. Averaging antecedent rainfall over these groups of events and durations allows us to study the general tendencies (i.e. whether antecedent wetness is generally higher or lower) and possibly reduce the effect of heterogeneities unavoidable at such a regional scale.
3.1 Daily and hourly thresholds
We define several rainfall thresholds by maximising TSS for the different rainfall datasets, as well as the associated time frames (Fig. 2). Comparing the results for the three different rainfall products (comparison D in Fig. 2 and Fig. 3a) it can be seen as expected that performance is best with the high-quality hourly rainfall product which uses high-resolution radar information for the disaggregation of daily sums (RHIR). Disaggregation using the closest hourly rain gauge (RHIG) seems to lead to worse performance than the corresponding daily analysis RDI (red and blue bars in Fig. 3a). However, this may be deceptive, as the time periods as well as the number of landslides behind the rainfall datasets are different. This is a critical point we investigate below.
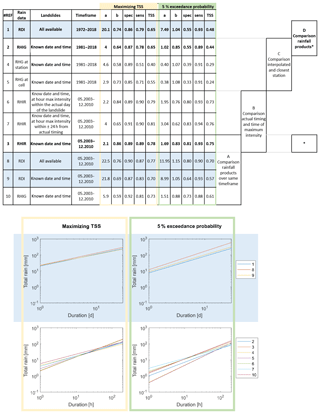
Figure 2Table containing the coefficients of the threshold power law curve in the total rainfall–duration plane obtained by maximising the TSS, or selecting the 5 % exceedance probability line following the frequentist approach, for all the different time frames and rainfall records. To facilitate reading, the different comparisons carried out are indicated, matching the respective results. In the bottom panel, all the ED threshold curves are shown, separated into daily (above) and hourly (below), obtained with TSS maximisation (left) or following the frequentist approach (right). The numbers in the legend match the “#REF” entry in the Table above.
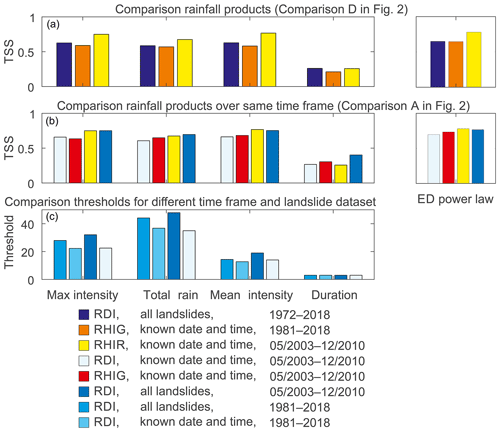
Figure 3True skill statistic for the different precipitation characteristics and all the different rainfall dataset considered. (a) Comparison of rainfall products using for each rainfall dataset the entire time frame available. (b) Comparison of the overlapping time frame (May 2003–December 2010). The right subpanels in panels (a) and (b) show the performance of the ED power law threshold for the corresponding datasets as reference. (c) The optimum thresholds obtained with daily rainfall data and considering all time frames and landslides with known date and timing (known timing) or at least date (all landslides).
A fairer comparison would be to compare performance over the same time period (May 2003–December 2010) and considering the same landslide events (comparison A in Fig. 2 and Fig. 3b). In this case, the differences in performance across the different rainfall datasets become smaller. The hourly disaggregated product using radar (RHIR) still leads to the best performance, but the performance with daily data (RDI) is improved even with the simple disaggregation using the closest rain gauge (RHIG), for all rainfall properties except maximum intensity. Remarkably, the daily rainfall dataset RDI retains reasonably good predictive power despite its coarser temporal resolution.
One additional comparison that can be made in the overlapping time frame (May 2003–December 2010) is with all landslide events, regardless of whether the timing is also known or only the date. The performance obtained with daily data and all these events is now comparable to the one with the high-quality hourly product (RHIR). The differences between the two are even more evident looking at the thresholds associated with the performance shown here (Fig. 3c). The daily thresholds considering only events with known timing rather than all landslides decrease to 22.5 mm d−1 for the maximum intensity (32.0 mm d−1 considering all landslides within the time frame), 35.0 mm for the total rainfall (47.9 mm considering all landslides within the time frame), and 14.0 mm d−1 for the mean intensity (19.0 mm d−1 considering all landslides within the time frame).
While the decrease in the thresholds and performance is consistent for all rainfall properties as the landslide dataset is reduced, this is not a general result. Rather it demonstrates that the size and accuracy of the landslide dataset is important and that results based on shorter records are likely to be less robust as they are more susceptible to individual events, years, outliers, or mistakenly reported landslides. This short-record bias is also evident when comparing daily thresholds obtained using the 1981–2018 time frame or the shorter time frame of May 2003–December 2010 for which RHIR is available (first and third bars in Fig. 3c). The thresholds obtained with the latter are higher. The reason is that in 2005, 187 landslides occurred, most of them due to a single intense summer storm in August. Considering all 38 years (1981–2018) the effect of that outlier year is reduced as it amounts to ca. 10 % of the total number of landslides available with known timing (almost 40 % within the period May 2003–December 2010).
Final visual evidence of the lower robustness of thresholds defined using hourly rainfall data is found in the relative frequency plots of triggering events for hourly rainfall data, compared to daily (Fig. 4b and d). The triggering events at the hourly resolutions (634 events) are much more sparse than the corresponding daily events (2117 events).
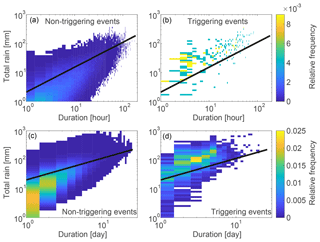
Figure 4Total rainfall–duration (ED) plots with colour scale representing the relative frequency (a, c) of non-triggering and (b, d) of triggering events. The lines represent the best power law curve thresholds obtained by maximising TSS, (a, b) with hourly (RHIR) and (c, d) with daily (RDI) rainfall data.
3.2 Inaccurate landslide timing: triggering and peak intensities
Results of two different approaches are presented here to illustrate the case when historical landslide inventories have no timing information available. The landslides are assigned to the actual timing in the database, the most intense hour within the actual day, or the most intense hour within a 48 h window centred around the actual timing.
We defined ED thresholds using each of these modified landslide datasets (comparison B in Fig. 2). Searching for the most intense hour within the actual day of the landslides (no. 6 in Fig. 2) leads to optimal thresholds that are not far off from the ones defined using the actual timing (no. 3 in Fig. 2). Instead, when the hour with the maximum intensity is found within a 48 h window centred on the actual timing (no. 7 in Fig. 2), the threshold changes, leading to a higher coefficient a and smaller slope b.
This observation is true for both threshold optimisation using TSS or following the frequentist approach, for which the change in the threshold parameters is present also when limiting the time to the day of the landslides. The explanation for this difference is that the TSS maximisation approach for the definition of ED thresholds is relatively robust, as altering the timing of the landslides some triggering events might change their total rainfall and duration values, but non-triggering events are unaffected. What is important is that for the TSS maximisation in both scenarios of unknown adjusted timing, the TSS value associated with the best threshold is higher than if the timing was known.
All the observations presented here are valid also when carrying out the same analysis over the 1981–2018 time period using RHIG. The TSS maximisation leads to basically identical thresholds in the three scenarios but the TSS increases from 0.65 (actual timing) to 0.67 (most intense hour within the actual date) or 0.70 (most intense hour within a 48 h window). Following the frequentist approach, the TSS also increases from 0.44 (actual timing) to 0.51 (most intense hour within the actual date) or 0.60 (most intense hour within a 48 h window).
This means that if we do not know the timing of landslides accurately and assign them to some a priori decided rainfall event property, then we are overestimating the landslide prediction skill of our ED curves. Extending this to a situation in which the actual timing is unknown and this technique is applied to compensate for it, while the threshold might not be very far off, the user would overestimate model performance, leading to a false overconfidence in the threshold's predictions.
Nevertheless, having to make a choice between the two methods of correcting timing, limiting the search of the rainiest hour to the actual date, seems to be slightly better, with smaller overestimation of the performance (TSS) and threshold curve parameters more similar to the ones obtained using the actual timing. Considering a 48 h window not only leads to overestimation of the TSS, but the thresholds are also affected. For both threshold definition methods, the threshold in this case gets higher (higher a) and less steep (smaller b).
3.3 Rainfall quality: gauge density and interpolation
To test the importance of the general quality of the rainfall dataset in the context of the daily–hourly temporal resolution comparison, we use here the hourly gauge measurements (RHG) in a sparse network and the hourly gridded rainfall dataset (RHIG). The latter takes advantage of the high-quality daily record (RDI), which is based on a denser daily rain gauge network and accounts for climatology and topography (Comparison C in Fig. 2).
As before, the comparison between the different rainfall datasets should not be based on the thresholds obtained, since both triggering and non-triggering events can potentially change, but rather on the landslide prediction performance associated with them. When the rain gauge rainfall record is used directly (RHG) at each (closest) landslide location (no. 5 in Fig. 2) or just using one time series per gauge (no. 4 in Fig. 2), the sensitivity drops, and so does the TSS. The two rainfall datasets (RHIG and RHG) have exactly identical hourly rainfall fractions and differ only by the daily sum, which for RHIG is forced to match the RDI daily rainfall of the corresponding cell. When using the station hourly time series, the triggering rainfall events have generally smaller event characteristics than the corresponding RHIG events. Out of total 634 events, 423 have smaller maximum intensity, 382 have smaller mean intensity, 447 have smaller total rainfall, and 461 have shorter duration. This results in a decrease in the maximum TSS of up to 0.07, mostly due to a lower sensitivity (for total rain, the sensitivity drops from 0.72 to 0.63).
The same drop in performance is observed when following the frequentist approach (comparison C in Fig. 2). The TSS, which is 0.44 for the analysis using the hourly time series adjusted with the daily product (RHIG), drops to 0.29 or 0.24, depending on whether the susceptible cells or rain gauge locations are used. In this case the effect on the threshold (ED curve) is also very consistent: the curves are lower (smaller a) and slightly steeper (higher b). This is a consequence of the fact that it is especially the short (intense) events that are missed (underestimated) when considering rainfall measurements further away from the actual location of landslides (RHG rather than RDI).
3.4 Rainfall normalisation
The improvement achieved by defining thresholds not based directly on the values of the different precipitation characteristics, but scaling them by a certain quantile of the corresponding event characteristic, a certain quantile of daily/hourly precipitation, or the mean annual precipitation is shown in Fig. 5 for the daily RDI and hourly RHIR datasets. When searching for the event property thresholds, it seems to be irrelevant which quantile is chosen, as the TSS seems to be only slightly fluctuating around a value somewhere between the no normalisation and the mean annual precipitation lines. Completely different behaviour is observed for the normalisation using quantiles of hourly/daily rainfall. In that case, performance comparable to the other cases is achieved only for the highest quantiles, especially for absolute quantiles and for hourly data (Fig. 5b, d, and f).
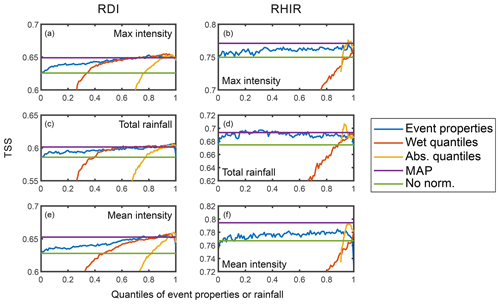
Figure 5True skill statistic (TSS) values for the best threshold for the different normalisations, (a, c, e) for the daily (RDI) and (b, d, f) for hourly (RHIR) rainfall data, (a, b) for maximum rainfall, (c, d) for total rain, and (e, f) for mean intensity. For the normalisation by event properties (event properties) and quantiles of rainfall (wet and absolute), the TSS is computed for each 0.01 quantile value (x axis). For the normalisation by mean annual precipitation (MAP) and the TSS value of the variable without normalisation (no normalisation), the constant value of the TSS is indicated as a straight line across all x values.
In general, the best performance is obtained with normalisation by mean annual precipitation. In fact, with hourly data, this level of performance can only be reached/exceeded for few very high rainfall quantiles of the total rainfall (wet or absolute quantiles, Fig. 5d) or maximum intensity (absolute quantiles, Fig. 5b). With daily data instead, performance is comparable with the mean daily precipitation over a wider range of quantiles (q>0.4 for wet quantiles) of daily rainfall and event properties. The performance seems to be only slightly better for the highest quantiles.
With daily rainfall, the performance of wet, which only considers rainy days, and absolute quantiles is only in the range of quantiles for which performance is comparable to the other normalisations (q>0.4 for wet quantiles and q>0.9 for absolute quantiles). Instead, for hourly rainfall, the normalisation with the absolute quantiles peaks around a very high quantile value (q=0.95–0.97), reaching performance similar (mean intensity, Fig. 5f) or even superior (maximum and mean intensity, Fig. 5b and d) to the MAP normalisation.
The results for the RDN normalisation (not shown here) are basically indistinguishable from the MAP, not in terms of value of optimum threshold but of performance, with differences in the TSS of the normalised optimum threshold of less than 0.01.
The improvement of landslide prediction with normalised rainfall thresholds is statistically demonstrated, but it demands a physical explanation. We hypothesise that the reason lies in the fact that the rainfall regime (climate) and the landsliding process (erosion) are connected through the landscape balance between weathering and soil formation, as well as the rainfall-driven erosion of the top soil by landsliding and other processes (e.g. Norton et al., 2014). In climates with a highly erosive rainfall regime and high topography, the rate of landsliding has on the long term adjusted to match the lower soil formation rates. Consequently, we need on average higher rainfall intensities to generate landslides there. The scaling of rainfall thresholds by a high-intensity rainfall quantile corrects for landscape-scale differences between these process rates and leads to better prediction of landslide occurrence regionally. Evidence for this hypothesis can be found in some studies (e.g. Leonarduzzi et al., 2017; Peruccacci et al., 2017) and can also be observed by comparing the differences in triggering intensities to those of mean daily precipitation values in our data (Fig. 6). Here cells in which the mean daily precipitation is higher also have generally higher triggering intensities. Accounting for this in the threshold definition, for example dividing the values of maximum intensity by the MAP of the corresponding cell, results in an improvement in the performance.
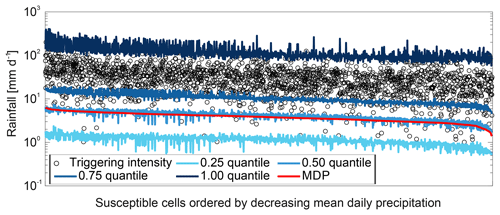
Figure 6Wet quantiles of daily intensities, mean daily precipitation (MDP = mean annual precipitation / 365) and maximum daily triggering intensities for all the susceptible cells (rainfall cells with at least one landslide). The cells are sorted (x axis) by value of MDP, left to right from the cell with the highest to lowest MDP. Markers show the daily rainfall intensities of triggering events for each cell.
It is interesting to note that most of the rainfall-triggering intensities are indeed among the strongest intensities recorded. Most of the triggering intensities (circles in Fig. 6) lie between the 0.75 and 1 wet quantiles of rainfall. This is the foundation for the success of rainfall thresholds for landslide prediction.
3.5 Antecedent rainfall
Including antecedent wetness or rainfall on a regional/national scale is not a simple task. In fact, while antecedent-triggering rainfall thresholds are successful in many local studies (e.g. for the Seattle area, Chleborad, 2003), the results shown in Sect. 3.4 are indicative of the heterogeneity at the regional/national scale which will make antecedent rainfall signals difficult to detect. For example, the approach suggested in Chleborad (2003) of defining thresholds based on the 3 and the 15 d prior cumulative rainfall applied to the RDI data 1972–2018 shows no pattern useful for the definition of thresholds. Nevertheless, the information content even in the simplest proxy of soil wetness, that is the antecedent rainfall, is clear (Bogaard and Greco, 2018).
In our experiment where we separate the events into observed triggering or non-triggering as well as predicted triggering or not-triggering (above or below the ED threshold obtained by maximising TSS) and plot the mean antecedent rainfall for 5 and 30 d periods, we can see that antecedent rainfall can explain some of the misclassifications generated by the ED threshold (Fig. 7). We expect that some of the misses (triggering events below ED curve) were actually landslides caused by low rainfall amounts on very wet soil. At the same time some false alarms (non-triggering events above ED curve) were wrongly predicted as triggering, but no landslide was observed due to the very low antecedent rainfall. These are exactly the patterns we observe in Fig. 7. Higher intensity events are generally associated with higher antecedent rainfall, due to seasonality effects (typically in the wetter periods of the year); the false alarms are associated with clearly smaller antecedent rainfall than the true positives; and, even more importantly, the misses have, for almost all durations, higher antecedent rainfall than the false alarms. As expected, the true negative events have on average the smallest antecedent rainfall for most durations.
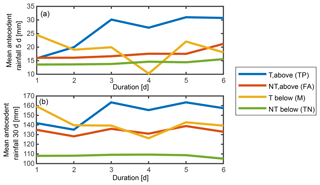
Figure 7Mean antecedent rainfall over (a) 5 or (b) 30 d before the date beginning of the event. All the rainfall events are separated into true positives (observed triggering events, T, which are above the cumulative rainfall-duration, ED, threshold), false alarms (observed non-triggering, NT, events which are above the ED threshold), misses (observed triggering events which are below the ED threshold), and true negatives (observed non-triggering which are below the ED thresholds), and the mean antecedent rainfall is computed for each of these for each rainfall event duration (1–6 d). Results are based on the RDI rainfall dataset, 1972–2018.
The highest antecedent rainfall for misses (triggering events below ED curve) for events of duration of 1 d could be indicative of the importance of antecedent conditions, either because the wrong event has been identified as triggering or because those are really triggered due to previous high soil wetness conditions rather than the event rainfall itself. However, we cannot provide evidence that this is the case. The patterns for the 5 and 30 d antecedent rainfall look very similar, showing that the antecedent conditions are consistent over longer periods. The only difference is in the true negatives, which for the 30 d, have a much smaller mean antecedent rainfall than the other events.
In the work presented here we show that the choice of the optimal temporal resolution for the definition of rainfall thresholds might not be a straightforward exercise and that many more aspects should be taken into consideration before concluding that the highest temporal resolution is best for landslide prediction.
Previous studies (e.g. Marra, 2019; Gariano et al., 2020) have focused on the effect of temporal resolution and showed that using lower temporal resolutions leads to the underestimation of the thresholds. From a theoretical point of view, we argue that hourly rainfall data are superior to daily data as they can capture the short convective events lasting a few hours, which are known to trigger landslides and which get averaged out in the daily sum. Also in the work presented here, when we consider the exact same time period and landslide events, we see that performance at the hourly temporal resolution is superior to that at the daily resolution, especially for high-quality datasets (RHIR). On the other hand, we show with this work that there are several additional factors that should be taken into consideration.
Choosing hourly rainfall data usually implies dealing with shorter historical records, lower quality (sparser) rainfall datasets, and less rich landslide databases. Typically, in the past rain gauges were mostly recording precipitation daily, which means that the daily datasets go further back in time, allowing for an analysis spanning over many more years. Taking the example of Switzerland, since 1961 ca. 420 gauges are available for generating the RDI rainfall product. The first hourly gauges start to appear around 1981, and only 45 of those are consistently measuring until 2018. The much lower density of hourly rain gauges makes the quality of the interpolated product lower, or the distance between observed landslide and measured rainfall locations greater, and therefore less representative. In recent years (ca. since 2012) the number of hourly gauges has increased dramatically, with 270 stations at the moment, but this would allow an analysis of a maximum 7 years (compared to the 48 years available at the daily resolution). The variability in the optimal threshold for the different time periods is proof of the risk of using shorter time frames (see Fig. 3c).
At the hourly resolution also the richness of the landslide database is affected, as not only the date but also the timing of the landslide must be known. Staley et al. (2013) addressed this issue and showed the overestimation of thresholds when considering peak rainstorm instead of triggering intensity. This is common practice when the actual timing of the landslides is unknown. It generally leads to overestimation of the triggering events' maximum intensity but potentially also other triggering events' parameters. Here, the optimum threshold does not seem to change much, especially when the threshold is obtained by maximising TSS. This is true if at least the landslide date is known. Constraining the timing of landslides on the actual date seems a better choice whenever possible. Allowing a larger window (48 h centred on the actual timing) leads to bigger threshold changes, both if maximising TSS or following the frequentist approach. Nevertheless, in both cases, the performance is overestimated if the peak intensity is used to time the landslide, giving the user overconfidence in the threshold values themselves.
Some last factors to take into consideration when choosing the temporal resolution are that in many countries hourly records of rainfall could be even shorter and of lower quality than in Switzerland, and choosing to work with daily data might be even more important. Furthermore, thinking of utilising rainfall thresholds in an operational setting, daily forecasts are usually more reliable than hourly forecasts (e.g. Shrestha et al., 2013).
In all the comparisons between hourly and daily rainfall, we purposely refrained from comparing the value of the optimal thresholds and of the ED curves between hourly and daily analyses. In fact, to allow this comparison, strong assumptions must be made, which are clearly not realistic, such as assuming that the daily intensity is 24 times the corresponding hourly intensity. This is in agreement with the recommendation in Gariano et al. (2020) and other studies to not extend daily ED or ID rainfall thresholds into the sub-daily domain.
Two methods for rainfall threshold estimation were presented here (TSS maximisation and frequentist approach) to show that the threshold optimisation method used does not impact the main conclusions. While our work does not intend to compare the two methods, the results presented here show clearly that accounting for non-triggering events also in the definition of the threshold (e.g. maximising TSS) increases the robustness of the obtained threshold. In fact, while the performance and the parameters of the ED curves are affected using both methods, the frequentist approach seems to be more sensitive, with greater differences in optimal thresholds and greater variability in performance (e.g. see variability of the optimum ED thresholds in Fig. 2). Nevertheless, there might be conditions in which rainfall records are not available and only triggering events can be reconstructed from newspaper and other historical records. In those conditions, a method based only on triggering events would be the only option.
Lastly, we demonstrate the benefits of normalising the rainfall thresholds using high quantiles of rainfall intensities, quantiles of event properties, MAP or RDN. These are all particularly useful when using daily data, but we suggest MAP as it is general and a widely available climatological variable.
We define and test rainfall thresholds for triggering of landslides by taking advantage of a rich landslide database and several rainfall products available in Switzerland with the main objective of providing a comparison between hourly and daily rainfall resolutions, which considers data limitations associated with choosing a higher temporal resolution. We explore the impacts of other issues, like shorter datasets, unknown landslide timing, and more sparse rain gauge networks that usually accompany higher temporal resolution data, and we test the impacts of two typical analysis steps in threshold definition: normalisation of the threshold and antecedent rainfall.
Our main findings are:
-
Although hourly rainfall is more appropriate for forecasting landslides since it better captures triggering intensities, several other aspects should be taken into consideration before utilising it exclusively for threshold definition. Generally, hourly rainfall records are shorter (only available in recent years) and of lower quality (e.g. based on sparser rain gauge networks); the landslide database only seldom contains accurate timing.
-
In ideal conditions, hourly datasets do show the best predictive performance for landslides, but daily data are not far behind, potentially since they tend to capture cumulative storm totals that may also be relevant for landslide triggering. The benefits of hourly resolutions can be masked by the higher uncertainties in threshold estimation connected to using short records and unknown timing.
-
Whenever continuous rainfall records are available together with a landslide inventory, our work underscores the importance of including non-triggering events in the definition of optimal rainfall thresholds, not only because false alarms are an essential factor in warning systems, but also to increase the robustness of the threshold estimates.
-
Localisation of rainfall thresholds through normalisation is a useful procedure, which allows us to compensate for the spatial heterogeneity in rainfall regimes and landslide erosion process rates. We recommend using mean annual precipitation or a high quantile of rainfall intensity as a normalisation factor as an alternative to regionalisation.
-
Antecedent rainfall as a proxy of soil wetness state can explain some of the false alarms in rainfall thresholds, associated with lower antecedent rainfall, and some of the misses, preceded by heavy rainfall, even when considering an entire (heterogeneous) country. Although we did not formulate new rainfall-duration curves including antecedent rainfall, it is likely that these would increase predictive skill.
The rainfall products were provided by the Swiss Federal Office of Meteorology and Climatology MeteoSwiss (available for research purposes upon request). The gauge time series were downloaded from https://gate.meteoswiss.ch/idaweb/ (MeteoSwiss, 2019). The Swiss Federal Research Institute WSL provided the landslide data (available for research purposes upon request).
EL conducted the analysis and interpreted the results. PM and EL conceived the research and prepared the paper.
The authors declare that they have no conflict of interest.
This research has been supported by the Swiss National Science Foundation (grant no. 165979).
This paper was edited by Thomas Glade and reviewed by Francesco Marra and Ben Mirus.
Aleotti, P.: A warning system for rainfall-induced shallow failures, Eng. Geol., 73, 247–265, 2004. a, b
Berti, M., Martina, M., Franceschini, S., Pignone, S., Simoni, A., and Pizziolo, M.: Probabilistic rainfall thresholds for landslide occurrence using a Bayesian approach, J. Geophys. Res.-Earth, 117, F04006, https://doi.org/10.1029/2012JF002367, 2012. a
Bogaard, T. and Greco, R.: Invited perspectives: Hydrological perspectives on precipitation intensity-duration thresholds for landslide initiation: proposing hydro-meteorological thresholds, Nat. Hazards Earth Syst. Sci., 18, 31–39, https://doi.org/10.5194/nhess-18-31-2018, 2018. a, b
Brocca, L., Ponziani, F., Moramarco, T., Melone, F., Berni, N., and Wagner, W.: Improving landslide forecasting using ASCAT-derived soil moisture data: A case study of the Torgiovannetto landslide in central Italy, Remote Sensing, 4, 1232–1244, 2012. a
Brunetti, M. T., Peruccacci, S., Rossi, M., Luciani, S., Valigi, D., and Guzzetti, F.: Rainfall thresholds for the possible occurrence of landslides in Italy, Nat. Hazards Earth Syst. Sci., 10, 447–458, https://doi.org/10.5194/nhess-10-447-2010, 2010. a
Caine, N.: The Rainfall Intensity: Duration Control of Shallow Landslides and Debris Flows, Geogr. Ann. A, 62, 23–27, 1980. a
Chleborad, A. F.: Preliminary evaluation of a precipitation threshold for anticipating the occurrence of landslides in the Seattle, Washington, Area, US Geological Survey open-file report, 3, 39, 2003. a, b, c
Crozier, M. J. and Eyles, R. J.: Assessing the probability of rapid mass movement, in: Third Australia-New Zealand conference on Geomechanics: Wellington, May 12–16, 1980, Institution of Professional Engineers New Zealand, p. 2, 1980. a
Crozier, M. J.: Landslides: Causes, Consequences & Environment, Croom Helm, London, 1986. a
Dahal, R. K. and Hasegawa, S.: Representative rainfall thresholds for landslides in the Nepal Himalaya, Geomorphology, 100, 429–443, 2008. a
Finlay, P., Fell, R., and Maguire, P.: The relationship between the probability of landslide occurrence and rainfall, Can. Geotech. J., 34, 811–824, 1997. a
Frattini, P., Crosta, G., and Sosio, R.: Approaches for defining thresholds and return periods for rainfall-triggered shallow landslides, Hydrol. Process., 23, 1444–1460, 2009. a, b
Frei, C. and Schär, C.: A precipitation climatology of the Alps from high-resolution rain-gauge observations, Int. J. Climatol., 18, 873–900, https://doi.org/10.1002/(SICI)1097-0088(19980630)18:8<873::AID-JOC255>3.0.CO;2-9, 1998. a, b, c
Gaál, L., Molnar, P., and Szolgay, J.: Selection of intense rainfall events based on intensity thresholds and lightning data in Switzerland, Hydrol. Earth Syst. Sci., 18, 1561–1573, https://doi.org/10.5194/hess-18-1561-2014, 2014. a
Gariano, S. L., Iovine, G. G. R., Brunetti, M. T., Peruccacci, S., Luciani, S., Bartolini, D., Palladino, M. R., Vessia, G., Viero, A., Vennari, C., Antronico, L., Deganutti, A. M., Luino, F., Parise, M., Terranova, O. G., and Guzzetti, F.: Populating a catalogue of rainfall events that triggered shallow landslides in Italy, Rendiconti Online della Società Geologica Italiana, 21, 396–398, 2012. a
Gariano, S. L., Brunetti, M. T., Iovine, G., Melillo, M., Peruccacci, S., Terranova, O., Vennari, C., and Guzzetti, F.: Calibration and validation of rainfall thresholds for shallow landslide forecasting in Sicily, southern Italy, Geomorphology, 228, 653–665, https://doi.org/10.1016/j.geomorph.2014.10.019, 2015. a
Gariano, S. L., Melillo, M., Peruccacci, S., and Brunetti, M. T.: How much does the rainfall temporal resolution affect rainfall thresholds for landslide triggering?, Nat. Hazards, 100, 655–670, 2020. a, b, c
Germann, U. and Joss, J.: Operational measurement of precipitation in mountainous terrain, in: Weather Radar, Springer, 52–77, 2004. a
Germann, U., Galli, G., Boscacci, M., and Bolliger, M.: Radar precipitation measurement in a mountainous region, Q. J. Roy. Meteor. Soc., 132, 1669–1692, 2006. a
Glade, T., Crozier, M., and Smith, P.: Applying probability determination to refine landslide-triggering rainfall thresholds using an empirical “Antecedent Daily Rainfall Model”, Pure Appl. Geophys., 157, 1059–1079, 2000. a, b
Godt, J. W., Baum, R. L., and Chleborad, A. F.: Rainfall characteristics for shallow landsliding in Seattle, Washington, USA, Earth Surf. Proc. Land., 31, 97–110, 2006. a, b, c
Guidicini, G. and Iwasa, O.: Tentative correlation between rainfall and landslides in a humid tropical environment, Bulletin of the International Association of Engineering Geology-Bulletin de l'Association Internationale de Géologie de l'Ingénieur, 16, 13–20, 1977. a
Guzzetti, F., Peruccacci, S., Rossi, M., and Stark, C. P.: Rainfall thresholds for the initiation of landslides in central and southern Europe, Meteorol. Atmos. Phys., 98, 239–267, https://doi.org/10.1007/s00703-007-0262-7, 2007. a, b, c, d
Guzzetti, F., Gariano, S. L., Peruccacci, S., Brunetti, M. T., Marchesini, I., Rossi, M., and Melillo, M.: Geographical landslide early warning systems, Earth-Sci. Rev., 200, 102973, https://doi.org/10.1016/j.earscirev.2019.102973, 2020. a
Highland, L. M. and Bobrowsky, P.: The landslide handbook – A guide to understanding landslides: Reston, Virginia, U.S. Geological Survey Circular 1325, 129 pp., 2008. a
Hilker, N., Badoux, A., and Hegg, C.: The Swiss flood and landslide damage database 1972–2007, Nat. Hazards Earth Syst. Sci., 9, 913–925, https://doi.org/10.5194/nhess-9-913-2009, 2009. a, b, c, d
Iadanza, C., Trigila, A., and Napolitano, F.: Identification and characterization of rainfall events responsible for triggering of debris flows and shallow landslides, J. Hydrol., 541, 230–245, 2016. a
Joss, J., Schädler, B., Galli, G., Cavalli, R., Boscacci, M., Held, E., Della Bruna, G., Kappenberger, G., Nespor, V., and Spiess, R.: Operational use of radar for precipitation measurements in Switzerland, vdf Hochschulverl. an der ETH Zürich, 1998. a
Kjekstad, O. and Highland, L.: Economic and Social Impacts of Landslides, in: Landslides – Disaster Risk Reduction, edited by: Sassa, K. and Canuti, P., Springer, Berlin, Heidelberg, 573–587, https://doi.org/10.1007/978-3-540-69970-5_30, 2009. a, b, c
Klose, M.: Landslide databases as tools for integrated assessment of landslide risk, Springer, https://doi.org/10.1007/978-3-319-20403-1, 2015. a
Leonarduzzi, E., Molnar, P., and McArdell, B. W.: Predictive performance of rainfall thresholds for shallow landslides in Switzerland from gridded daily data, Water Resour. Res., 53, 6612–6625, 2017. a, b, c, d, e
Marc, O., Gosset, M., Saito, H., Uchida, T., and Malet, J.-P.: Spatial patterns of storm-induced landslides and their relation to rainfall anomaly maps, Geophys. Res. Lett., 46, 11167–11177, 2019. a, b
Marra, F.: Rainfall thresholds for landslide occurrence: systematic underestimation using coarse temporal resolution data, Nat. Hazards, 95, 883–890, 2019. a, b
Melillo, M., Brunetti, M. T., Peruccacci, S., Gariano, S. L., Roccati, A., and Guzzetti, F.: A tool for the automatic calculation of rainfall thresholds for landslide occurrence, Environ. Modell. Softw., 105, 230–243, 2018. a, b
MeteoSwiss: Swiss ground-level monitoring networks data, available at: https://gate.meteoswiss.ch/idaweb/, last access: 18 November 2019. a
Mirus, B. B., Becker, R. E., Baum, R. L., and Smith, J. B.: Integrating real-time subsurface hydrologic monitoring with empirical rainfall thresholds to improve landslide early warning, Landslides, 15, 1909–1919, 2018a. a
Mirus, B. B., Morphew, M. D., and Smith, J. B.: Developing hydro-meteorological thresholds for shallow landslide initiation and early warning, Water, 10, 1274, https://doi.org/10.3390/w10091274, 2018b. a, b
Mirus, B. B., Jones, E. S., Baum, R. L., Godt, J. W., Slaughter, S., Crawford, M. M., Lancaster, J., Stanley, T., Kirschbaum, D. B., Burns, W. J., et al.: Landslides across the USA: occurrence, susceptibility, and data limitations, Landslides, 17, 2271–2285, https://doi.org/10.1007/s10346-020-01424-4, 2020. a
Molnar, P. and Burlando, P.: Variability in the scale properties of high-resolution precipitation data in the Alpine climate of Switzerland, Water Resour. Res., 44, 1–9, https://doi.org/10.1029/2007WR006142, 2008. a
Nikolopoulos, E. I., Borga, M., Creutin, J. D., and Marra, F.: Estimation of debris flow triggering rainfall: Influence of rain gauge density and interpolation methods, Geomorphology, 243, 40–50, https://doi.org/10.1016/j.geomorph.2015.04.028, 2015. a
Norton, K. P., Molnar, P., and Schlunegger, F.: The role of climate-driven chemical weathering on soil production, Geomorphology, 204, 510–517, 2014. a
Peres, D. J., Cancelliere, A., Greco, R., and Bogaard, T. A.: Influence of uncertain identification of triggering rainfall on the assessment of landslide early warning thresholds, Nat. Hazards Earth Syst. Sci., 18, 633–646, https://doi.org/10.5194/nhess-18-633-2018, 2018. a
Peruccacci, S., Brunetti, M. T., Luciani, S., Vennari, C., and Guzzetti, F.: Lithological and seasonal control on rainfall thresholds for the possible initiation of landslides in central Italy, Geomorphology, 139, 79–90, 2012. a, b
Peruccacci, S., Brunetti, M. T., Gariano, S. L., Melillo, M., Rossi, M., and Guzzetti, F.: Rainfall thresholds for possible landslide occurrence in Italy, Geomorphology, 290, 39–57, 2017. a, b, c
Petley, D.: Global patterns of loss of life from landslides, Geology, 40, 927–930, 2012. a
Piciullo, L., Calvello, M., and Cepeda, J. M.: Territorial early warning systems for rainfall-induced landslides, Earth-Sci. Rev., 179, 228–247, 2018. a
Ponziani, F., Pandolfo, C., Stelluti, M., Berni, N., Brocca, L., and Moramarco, T.: Assessment of rainfall thresholds and soil moisture modeling for operational hydrogeological risk prevention in the Umbria region (central Italy), Landslides, 9, 229–237, https://doi.org/10.1007/s10346-011-0287-3, 2012. a
Postance, B., Hillier, J., Dijkstra, T., and Dixon, N.: Comparing threshold definition techniques for rainfall-induced landslides: A national assessment using radar rainfall, Earth Surf. Proc. Land., 43, 553–560, 2018. a
Roccati, A., Faccini, F., Luino, F., Turconi, L., and Guzzetti, F.: Rainfall events with shallow landslides in the Entella catchment, Liguria, northern Italy, Nat. Hazards Earth Syst. Sci., 18, 2367–2386, https://doi.org/10.5194/nhess-18-2367-2018, 2018. a
Rossi, M., Peruccacci, S., Brunetti, M. T., Marchesini, I., Luciani, S., Ardizzone, F., Balducci, V., Bianchi, C., Cardinali, M., Fiorucci, F., Mondini, A. C., Reichenbach, P., Salvati, P., Santangelo, M., Bartolini, D., Gariano, S. L., Palladino, M., Vessia, G., Viero, A., Antronico, L., Borselli, L., Deganutti, A. M., Iovine, G., Luino, F., Parise, M., Polemio, M., and Guzzetti, F.: SANF: National warning system for rainfall-induced landslides in Italy, Landslides and Engineered Slopes: Protecting Society through Improved Understanding, 2, 1895–1899, 2012. a
Salvati, P., Bianchi, C., Rossi, M., and Guzzetti, F.: Societal landslide and flood risk in Italy, Nat. Hazards Earth Syst. Sci., 10, 465–483, https://doi.org/10.5194/nhess-10-465-2010, 2010. a
Schuster, R. L.: Socioeconomic significance of landslides, Landslides: Investigation and Mitigation. Washington (DC): National Academy Press, Transportation Research Board Special Report, 247, 12–35, 1996. a
Segoni, S., Leoni, L., Benedetti, A. I., Catani, F., Righini, G., Falorni, G., Gabellani, S., Rudari, R., Silvestro, F., and Rebora, N.: Towards a definition of a real-time forecasting network for rainfall induced shallow landslides, Nat. Hazards Earth Syst. Sci., 9, 2119–2133, https://doi.org/10.5194/nhess-9-2119-2009, 2009. a
Segoni, S., Piciullo, L., and Gariano, S. L.: A review of the recent literature on rainfall thresholds for landslide occurrence, Landslides, 15, 1483–1501, 2018. a
Shrestha, D. L., Robertson, D. E., Wang, Q. J., Pagano, T. C., and Hapuarachchi, H. A. P.: Evaluation of numerical weather prediction model precipitation forecasts for short-term streamflow forecasting purpose, Hydrol. Earth Syst. Sci., 17, 1913–1931, https://doi.org/10.5194/hess-17-1913-2013, 2013. a
Staley, D. M., Kean, J. W., Cannon, S. H., Schmidt, K. M., and Laber, J. L.: Objective definition of rainfall intensity-duration thresholds for the initiation of post-fire debris flows in southern California, Landslides, 10, 547–562, https://doi.org/10.1007/s10346-012-0341-9, 2013. a, b, c, d
Stevenson, P.: An empirical method for the evaluation of relative landslip risk, Bulletin of the International Association of Engineering Geology-Bulletin de l'Association Internationale de Géologie de l'Ingénieur, 16, 69–72, 1977. a
Thomas, M. A., Mirus, B. B., and Collins, B. D.: Identifying physics-based thresholds for rainfall-induced landsliding, Geophys. Res. Lett., 45, 9651–9661, 2018. a
Thomas, M. A., Collins, B. D., and Mirus, B. B.: Assessing the feasibility of satellite-based thresholds for hydrologically driven landsliding, Water Resour. Res., 55, 9006–9023, 2019. a
Trezzini, F., Giannella, G., and Guida, T.: Landslide and Flood: Economic and Social Impacts in Italy, Springer, 2, 171–176, https://doi.org/10.1007/978-3-642-31313-4_22, 2013. a
Vennari, C., Gariano, S. L., Antronico, L., Brunetti, M. T., Iovine, G., Peruccacci, S., Terranova, O., and Guzzetti, F.: Rainfall thresholds for shallow landslide occurrence in Calabria, southern Italy, Nat. Hazards Earth Syst. Sci., 14, 317–330, https://doi.org/10.5194/nhess-14-317-2014, 2014. a, b
Wicki, A., Lehmann, P., Hauck, C., Seneviratne, S. I., Waldner, P., and Stähli, M.: Assessing the potential of soil moisture measurements for regional landslide early warning, Landslides, 17, 1881–1896, https://doi.org/10.1007/s10346-020-01400-y, 2020. a
Wilson, R. C. and Jayko, A.: Preliminary maps showing rainfall thresholds for debris-flow activity, San Francisco Bay Region, California, U.S. Geological Survey, 1997. a
Wüest, M., Frei, C., Altenhoff, A., Hagen, M., Litschi, M., and Schär, C.: A gridded hourly precipitation dataset for Switzerland using rain-gauge analysis and radar-based disaggregation, Int. J. Climatol., 30, 1764–1775, https://doi.org/10.1002/joc.2025, 2010. a, b