The spatial–temporal total friction coefficient of the fault viewed from the perspective of seismo-electromagnetic theory

Recently, it has been shown theoretically how the lithospheric stress changes could be linked with magnetic anomalies, frequencies, spatial distribution and the magnetic-moment magnitude relation using the electrification of microfractures in the semibrittle–plastic rock regime (Venegas-Aravena et al., 2019). However, this seismo-electromagnetic theory has not been connected with the fault's properties in order to be linked with the onset of the seismic rupture process itself. In this work we provide a simple theoretical approach to two of the key parameters for seismic ruptures which are the friction coefficient and the stress drop. We use sigmoidal functions to model the stress changes in the nonelastic regime within the lithosphere. We determine the temporal changes in frictional properties of faults. We also use a long-term friction coefficient approximation that depends on the fault dip angle and four additional parameters that weigh the first and second stress derivative, the spatial distribution of the nonconstant stress changes, and the stress drop. We found that the friction coefficient is not constant in time and evolves prior to and after the earthquake occurrence regardless of the (nonzero) weight used. When we use a dip angle close to 30^∘ and the contribution of the second derivative is more significant than that of the first derivative, the friction coefficient increases prior to the earthquake. During the earthquake event the friction drops. Finally, the friction coefficient increases and decreases again after the earthquake occurrence. It is important to mention that, when there is no contribution of stress changes in the semibrittle–plastic regime, no changes are expected in the friction coefficient.

1 Introduction

The electromagnetic phenomena that could be linked with earthquake occurrences are usually considered within the lithosphere–atmosphere–ionosphere-coupling effect (or LAIC effect; e.g., De Santis et al., 2019a). Some of these electromagnetic phenomena have been recorded both prior to and after earthquakes using different methodologies, data, earthquakes and instrumentation. For example, some researchers have shown coseismic magnetic variations during some earthquakes (e.g., Utada et al., 2011, during the 2011 Tōhoku earthquake), while other researchers have focused on the oscillation frequency (microhertz–kilohertz range) of the magnetic field prior to the occurrence of some earthquakes (Schekotov and Hayakawa, 2015; Cordaro et al., 2018; Potirakis et al., 2018a, b, among others). One of the most recent methodologies corresponds to the measurement of magnetic anomalies, which detects the number of magnetic peaks (or events) that exceed a given threshold that represents the normal conditions of the magnetic field over long periods of time (De Santis et al., 2017). There is some research that shows that the increases in the number of anomalies could be linked with impending earthquakes. For instance, De Santis et al. (2019b) have recently found an increase in the number of daily magnetic anomalies prior to 12 major earthquakes between 2014 and 2016. These magnetic anomalies were confirmed by other researchers (e.g., Marchetti and Akhoondzadeh, 2018).

It is well known from laboratory experiments that rock samples undergoing fast changes in the semibrittle–plastic rock regime generate microfractures, displacement of dislocations and electrification (e.g. Anastasiadis et al., 2004; Zhang et al., 2020 and references therein). This physical mechanism of rock electrification is described mathematically by the motion of charged edge dislocations (MCD) model (e.g., see Vallianatos and Tzanis, 1998, 2003, for a comprehensive derivation of the MCD model). This model is a plausible electromechanical mechanism that could explain the magnetic measurements. Starting from the experimental evidence Venegas-Aravena et al. (2019) developed a seismo-electromagnetic theory based on microcracks and stress changes. This theory showed how the fractal nature of the cracks explains the observed magnetic frequency range, the coseismic magnetic field and the conditions for generating magnetic anomalies. However, this theory (like the others, e.g., Freund, 2003; De Santis et al., 2019a) does not explain any change in the parameters that control the generation of seismic ruptures using magnetic measurements. This prevents the linking of seismo-electromagnetism with classical seismology. In this work, we address this link using one of the key points that controls seismic rupture and slip on the fault: friction force and stress drop. Our model uses the tectonic geometry and stress drop of the M_w 8.8 2010 Maule (Chile) earthquake in order to provide real data and validate our analysis. The paper is divided as follows: in Sect. 2 we consider the friction coefficient, adding the brittle–plastic stress changes contribution to the usual elastic stress. In Sect. 3 we discuss the temporal variations in the brittle–plastic friction and their connections with the spatial distribution on the fault and in the lithosphere. In Sect. 4 we provide the relation between the stress drop and the coseismic magnetic field. The spatial–temporal friction coefficient along the fault is calculated by adding the elastic stress drop. In Sect. 5, the Gutenberg–Richter law is written in terms of the semibrittle–plastic shear stress. The rupture time is discussed in Sect. 6. Finally, the discussion takes place and conclusions are drawn in Sect. 7.

2 Friction coefficient in the brittle–plastic regime

The standard friction force can be understood as the complex dissipation of mechanical energy in the form of plastic or elastic deformation of asperities (mechanical interaction), thermal dissipation (heat) and the adhesion (interatomic interaction) of two sliding surfaces (e.g., Sun and Mosleh, 1994). When we consider a particular contact area between two dry surfaces, the static friction coefficient μ that describes this interaction can be written approximately as the ratio of the shear τ and the normal N stress (load) as shown by Eq. (1) (e.g., Byerlee, 1978; Chen, 2014, and references therein).

$$\begin{array}{}\text{(1)}& \mathit{\mu }={\displaystyle \frac{\mathit{\tau }}{N}}\end{array}$$

The static friction coefficient μ gives some information about the contact behavior. For instance, μ tends to be large when the contact area is increased due to the surface's plastic deformation (e.g., Chen, 2014). If we also consider the pure plastic regime, we can add a small plastic shear stress (δτ_plastic) and a small plastic normal stress (δN_plastic) contribution into Eq. (1) leading to the following expressions:

$$\begin{array}{}\text{(2)}& {\displaystyle }\mathit{\tau }={\mathit{\tau }}_{\mathrm{elastic}}+\mathit{\delta }{\mathit{\tau }}_{\mathrm{plastic}},\text{(3)}& {\displaystyle }N=N_{\mathrm{elastic}}+\mathit{\delta }{N}_{\mathrm{plastic}}.\end{array}$$

If we do not consider the pure plastic effects, the plastic contribution vanishes and the ratio of τ_elastic and N_elastic describes the usual (nonlinear) friction behaviors that occur during the complete frictional cycle: presliding (increase in friction coefficient when there is no apparent or residual displacement), gross sliding (observable displacement and decrease in friction coefficient) and healing (friction coefficient recovery; e.g., Parlitz et al., 2004; Marone and Saffer, 2015; Papangelo et al., 2015; and references therein).

Venegas-Aravena et al. (2019) state that the electrification within rocks is mainly due to a nonconstant stress change during the semibrittle–plastic transition. This means that the temporal changes in the semibrittle–plastic stress (δσ_sbp) rules the total plastic stress (δσ_plastic). Thus, it implies that the plastic shear and normal stress can be written in terms of a linear combination of the temporal changes in δσ_sbp as shown in Eqs. (4) and (5).

$$\begin{array}{}\text{(4)}& {\displaystyle }\begin{array}{rl}\mathit{\delta }{\mathit{\tau }}_{\mathrm{plastic}}& =k_{\mathrm{1}}\mathit{\delta }{\mathit{\tau }}_{\mathrm{sbp}}+k_{\mathrm{2}}{\mathit{\delta }}^{\mathrm{2}}{\mathit{\tau }}_{\mathrm{sbp}}+o\left({\mathit{\delta }}^{\mathrm{2}}\mathit{\tau }\right)\\ & =k_{\mathrm{1}}{\dot{\mathit{\tau }}}_{\mathrm{sbp}}\mathit{\delta }t+k_{\mathrm{2}}{\ddot{\mathit{\tau }}}_{\mathrm{sbp}}(\mathit{\delta }t{)}^{\mathrm{2}}+o\left((\mathit{\delta }t{)}^{\mathrm{2}}\right),\end{array}\text{(5)}& {\displaystyle }\begin{array}{rl}\mathit{\delta }{N}_{\mathrm{plastic}}& =k_{\mathrm{3}}\mathit{\delta }{N}_{\mathrm{sbp}}+k_{\mathrm{4}}{\mathit{\delta }}^{\mathrm{2}}{N}_{\mathrm{sbp}}+o\left({\mathit{\delta }}^{\mathrm{2}}N\right)\\ & =k_{\mathrm{3}}{\dot{N}}_{\mathrm{sbp}}\mathit{\delta }t+k_{\mathrm{4}}{\ddot{N}}_{\mathrm{sbp}}(\mathit{\delta }t{)}^{\mathrm{2}}+o\left((\mathit{\delta }t{)}^{\mathrm{2}}\right),\end{array}\end{array}$$

where k₁, k₂, k₃ and k₄ are dimensionless constants to be determined later, δt and (δt)² are the temporal variations from the first- and second-order time contribution, respectively. The temporal variations in the shear and normal semibrittle–plastic stress contributions are ${\dot{\mathit{\tau }}}_{\mathrm{sbp}}$, ${\ddot{\mathit{\tau }}}_{\mathrm{sbp}}$, ${\dot{N}}_{\mathrm{sbp}}$ and ${\ddot{N}}_{\mathrm{sbp}}$, respectively. The series expansions in Eqs. (4) and (5) are convenient and allow us to write the plastic contribution as a sum of stresses that depend on time. This is relevant because the seismo-electromagnetic theory seeks to relate the temporal variable of the earthquake and the stress within the lithosphere. From now on, we refer to the semibrittle–plastic stress as the uniaxial stress σ.

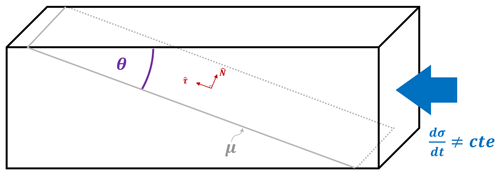
Figure 1 Schematic description of the nonconstant uniaxial stresses in presence of a fault with friction coefficient μ and dip angle θ. This schematic description is similar to the experimental setup for pressure stimulated currents (PSC; Kyriazopoulos et al., 2011).

It is possible to relate this shear, and the normal stresses from Eqs. (4)–(5), with the uniaxial stress using the geometry shown in Fig. 1. In this figure, we have a simple schematic representation of the lithosphere under uniaxial stress change dσ∕dt in the presence of a fault with a static friction coefficient μ and a dip angle of 30^∘. We can write this uniaxial stress change in terms of the dip angle θ in the normal and tangential direction (in red on Fig. 1) of the fault, as shown in the following expression:

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{\mathrm{d}\mathit{\sigma }}{\mathrm{d}t}}={\displaystyle \frac{\mathrm{d}\mathit{\sigma }}{\mathrm{d}t}}\left(-\sin \mathit{\theta }\widehat{N}+\cos \mathit{\theta }\widehat{\mathit{\tau }}\right),\end{array}$$

where dσ∕dt corresponds to the magnitude of uniaxial temporal stress change. Using this expression, we write the brittle–plastic stress contributions in terms of uniaxial stress change as

$$\begin{array}{}\text{(7)}& {\displaystyle }\dot{N}=-{\displaystyle \frac{\mathrm{d}\mathit{\sigma }}{\mathrm{d}t}}\sin \mathit{\theta },\text{(8)}& {\displaystyle }\dot{\mathit{\tau }}={\displaystyle \frac{\mathrm{d}\mathit{\sigma }}{\mathrm{d}t}}\cos \mathit{\theta }.\end{array}$$

Substituting Eqs. (2)–(8) into Eq. (1) and considering a second-order linear combination, we obtain the static friction coefficient as a function of time, the fault angle and the semibrittle–plastic changes within the lithosphere given by

$$\begin{array}{}\text{(9)}& \mathit{\mu }\left(t\right)\approx {\displaystyle \frac{{\mathit{\tau }}_{\mathrm{0}}+\left(k_{\mathrm{1}}\dot{\mathit{\sigma }}+k_{\mathrm{2}}\ddot{\mathit{\sigma }}\mathit{\delta }t\right)\cos \mathit{\theta }\mathit{\delta }t}{N_{\mathrm{0}}-\left(k_{\mathrm{3}}\dot{\mathit{\sigma }}+k_{\mathrm{4}}\ddot{\mathit{\sigma }}\mathit{\delta }t\right)\sin \mathit{\theta }\mathit{\delta }t}},\end{array}$$

where the dots above σ are the notation for the first and second temporal derivative of the uniaxial stress. According to Venegas-Aravena et al. (2019), the temporal stress change $\dot{\mathit{\sigma }}$ has approximately a sigmoidal shape, which can be written as $\dot{\mathit{\sigma }}\left(t\right)=a/(b+e^{(t_{\mathrm{0}}-t)\times w})$, where a, b, w and t₀ are constants. In Fig. 2 we represent $\dot{\mathit{\sigma }}$ and $\ddot{\mathit{\sigma }}$ as a function of time where we have used $a=b=w=\mathrm{1}$ and t₀=10 a.u. (arbitrary units). According to De Santis et al. (2019b), most of the earthquakes recorded occurred close to the center of Fig. 2, which is when t_EQ=t₀. For instance, Marchetti and Akhoondzadeh (2018) have shown that the M_w 8.2 2017 Chiapas (Mexico) earthquake occurred after this time (t_EQ>t₀). They also use daily values of magnetic anomalies ($B\propto \mathrm{d}\mathit{\sigma }/\mathrm{d}t$, which comes directly from the experimental equation $I={\mathit{\alpha }}_{\mathrm{0}}\mathrm{d}\mathit{\sigma }/\mathrm{d}t$, where I is the electric current and α₀ is a constant of proportionality; see Vallianatos and Triantis, 2008, and references therein), thus δt=1 d =86 400 s.

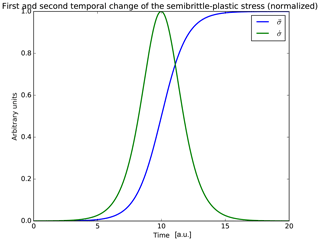
Figure 2 Dimensionless representation of normalized first and second temporal change in the uniaxial stress used by Venegas-Aravena et al. (2019). According to De Santis et al. (2019a) the earthquakes occur close to the center of figures. Here it is when $t=t_{\mathrm{0}}=\mathrm{10}$ a.u.

Let us now estimate the values of the constants of Eq. (9). First, we consider the dip or subduction angle θ. According to Maksymowicz (2015), this angle is close to 20^∘ at the depth (∼30 km) and location (35^∘54^′32^′′ S, 72^∘43^′59^′′ W) of the 2010 Maule earthquake. Maksymowicz (2015) claimed that the static friction coefficient in the Chilean convergent margin is close to μ_ch≈0.5. Lamb (2006) calculated that the initial value of τ₀ is 15.4 MPa (constant) in southern Chile. Using μ_ch, it is expected that N₀ should be approximately equal to 30.8 MPa (constant).

In addition, rock experiments show that the values of $\dot{\mathit{\sigma }}$ are close to 1 MPa s⁻¹ (e.g., Saltas et al., 2018). This implies that $\left|k_{\mathrm{1}}\right|$ and $\left|k_{\mathrm{3}}\right|$ must be close to $\sim {\mathrm{10}}^{-\mathrm{4}}$, in order to balance the δt factor. The values of k₂ and k₄ must be equal to or less than $\sim {\mathrm{10}}^{-\mathrm{9}}$, otherwise the values of the friction coefficient would be greater than 1. If we consider an initial increase in the normal stress, the sign of the constants should be negative for k₃, k₄ and positive for k₁, k₂. In Fig. 3 we can see how the friction coefficient changes in time, when using values of k₁ and k₃ described above and different values of k₂ and k₄ (second-order contribution). When we use values on k₂ and k₄ of the order of $\sim {\mathrm{10}}^{-\mathrm{9}}$, it is possible to observe how the friction decreases after the earthquake. Furthermore, it is important to note that the earthquake does not occur when the friction has its maximum value but when it is close to its maximum. When we use values of k₂ and k₄ that are similar or less than $\sim {\mathrm{10}}^{-\mathrm{10}}$, the contribution of $\ddot{\mathit{\sigma }}$ in Eq. (9) vanishes.

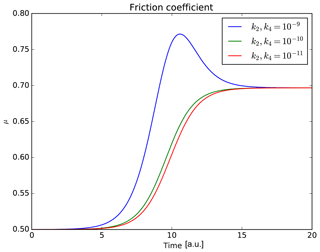
Figure 3 Temporal behavior of the semibrittle–plastic friction coefficient using different parameters. In all the cases it is possible to observe an increase in the friction before earthquake (t=10 a.u.). However, the friction decreases after the earthquake only if k₂ and k₄ have values of $\sim {\mathrm{10}}^{-\mathrm{9}}$.

Another critical point is related to the differential time. For instance, when we consider δt≤1 s, the semibrittle–plastic stress term vanishes and the usual friction is recovered. This fact is especially relevant because the semibrittle–plastic contribution to the friction coefficient seems to be relevant only on large timescales. To summarize, the friction coefficient of Eq. (9) could be seen as a generalization of the standard friction coefficient when large timescales are considered.

3 Spatial distribution of stress changes and friction

In the previous section we linked the friction coefficient to the semibrittle–plastic regime that generates microcracks and electrification within the rocks. An important caveat is that this phenomenon does not occur everywhere. For instance, Dobrovolsky et al. (1979) described a specific “preparation zone” required close to the future hypocenter in order to accumulate sufficient stress to trigger the earthquake. This criterion has been widely used by researchers to establish a threshold for determining where the magnetic measurements can be associated with earthquakes (e.g., De Santis et al., 2019a, b). In other words, the phenomenon is local. However, if this is applied, a variation in the friction coefficient related to the rock electrification phenomenon close to the fault would be expected, while a friction variation outside the zones of semibrittle–plastic influence would not.

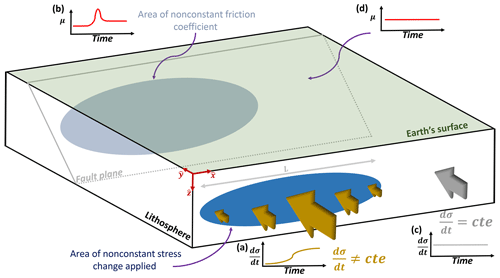
Figure 4 Schematic description of friction gradient on the fault. When a constant and nonconstant temporal stress change is applied at different places within the lithosphere, a nonzero friction coefficient gradient is expected.

In order to consider the local variations, we add to our model a separable spatial function of the uniaxial stress as given by $\stackrel{\mathrm{‾}}{\mathit{\sigma }}(x,t)=\mathit{\gamma }\left(x\right)\mathit{\sigma }\left(t\right)$ (for simplicity we choose a uniaxial dependence), where σ(t) corresponds to the same time function as considered in Sect. 2 and γ(x) is the dimensionless spatial distribution parallel to the fault (see the coordinate system in Fig. 4). Let us mention that the values of γ(x) are different when constant and nonconstant stress changes are considered. With this in mind, we can rewrite Eq. (9) as

$$\begin{array}{}\text{(10)}& \stackrel{\mathrm{‾}}{\mathit{\mu }}(x,t)\approx {\displaystyle \frac{{\mathit{\tau }}_{\mathrm{0}}+\mathit{\gamma }\left(k_{\mathrm{1}}\dot{\mathit{\sigma }}+k_{\mathrm{2}}\ddot{\mathit{\sigma }}\mathit{\delta }t\right)\cos \mathit{\theta }\mathit{\delta }t}{N_{\mathrm{0}}-\mathit{\gamma }\left(k_{\mathrm{3}}\dot{\mathit{\sigma }}+k_{\mathrm{4}}\ddot{\mathit{\sigma }}\mathit{\delta }t\right)\sin \mathit{\theta }\mathit{\delta }t}}.\end{array}$$

After straightforward derivations, we get that the gradient of the friction coefficient along the fault using Eq. (10) is given by

$$\begin{array}{}\text{(11)}& \mathrm{\nabla }\stackrel{\mathrm{‾}}{\mathit{\mu }}(x,t)={\mathit{\gamma }}^{\prime }{{\displaystyle \frac{A{N}_{\mathrm{0}}+B{\mathit{\tau }}_{\mathrm{0}}}{\left(N_{\mathrm{0}}-\mathit{\gamma }B\right)}}}^{\mathrm{2}}={\mathit{\gamma }}^{\prime }{\displaystyle \frac{\mathit{\alpha }\dot{\mathit{\sigma }}\mathit{\delta }t+\mathit{\beta }\ddot{\mathit{\sigma }}\mathit{\delta }{t}^{\mathrm{2}}}{{\left(N_{\mathrm{0}}-\mathit{\gamma }B\right)}^{\mathrm{2}}}},\end{array}$$

where $A=(k_{\mathrm{1}}\dot{\mathit{\sigma }}+k_{\mathrm{2}}\ddot{\mathit{\sigma }}\mathit{\delta }t)\cos \mathit{\theta }\mathit{\delta }t$, $B=(k_{\mathrm{3}}\dot{\mathit{\sigma }}+k_{\mathrm{4}}\ddot{\mathit{\sigma }}\mathit{\delta }t)\sin \mathit{\theta }\mathit{\delta }t$, $\mathit{\alpha }=N_{\mathrm{0}}{k}_{\mathrm{1}}\cos \mathit{\theta }+{\mathit{\tau }}_{\mathrm{0}}{k}_{\mathrm{3}}\sin \mathit{\theta }$ and $\mathit{\beta }=N_{\mathrm{0}}{k}_{\mathrm{2}}\cos \mathit{\theta }+{\mathit{\tau }}_{\mathrm{0}}{k}_{\mathrm{4}}\sin \mathit{\theta }$. Equations (10) and (11) imply that, if we distribute the constant and nonconstant temporal stress change in a nonuniform manner along the fault, then it could be said that this phenomenon is local. This can be understood using the example of Fig. 4: Fig. 4a shows a blue area of length L where we have a nonconstant temporal stress change. There one observes a change in the friction coefficient inside the projected gray area (Fig. 4b). Conversely, outside the area of length L (Fig. 4c), we assume a constant stress change, and there is no change in the friction coefficient (Fig. 4d). Let us remind ourselves that the entire fault suffered from stress accumulation during the entire process. However, only the gray area is directly affected by the friction change. This shows that the temporal friction changes are restricted only to a specific area (gray area) on the fault. Hence, one observes a nonzero friction coefficient gradient on the fault and we have a local phenomenon ($\mathrm{\nabla }\stackrel{\mathrm{‾}}{\mathit{\mu }}\ne \mathrm{0}\iff \mathrm{Local}$).

The process described in Fig. 4 reveals why the magnetic measurements are not global. It also validates the locality criteria in terms of fault properties. Furthermore, the spatial distribution of magnetic field measurements is expected to have a length scale comparable to the friction coefficient change due to the dependency of γ(x) in Eq. (10). That is, the larger the detection area of magnetic anomalies, the larger the area where fault friction is changing. In addition, Venegas-Aravena et al. (2019) described how the uniaxial stress change implies a change in the b-value of the Gutenberg–Richter law. It also implies that a significant earthquake is needed in order to satisfy this change in the Gutenberg–Richter law. Therefore, a greater expected magnitude could be related to changes in the coefficient of friction within an area within the fault. However, changes in the friction coefficient do not directly imply the earthquakes generation itself.

4 Stress drop and total friction coefficient – Spatial–temporal behavior

Up to this point, no changes in the elastic stresses have been considered in Eq. (10). This section focuses on one of the elastic parameter that is involved in the seismic rupture process: the stress drop Δτ. This parameter is one of the most relevant because it shows the shear stress differences prior to and after the onset of the earthquake within the fault rupture area (e.g., Aki, 1966). Furthermore, this parameter is also related to the seismic waves radiated (through the corner frequency of waves) and the seismic moment M₀ (e.g., Eshelby, 1957; Brune, 1970; Baltay et al., 2011, and references therein). If we consider a circular rupture area with radius d_crack, the stress drop Δτ is linked with the seismic moment M₀ through the following equation (Eshelby, 1957).

$$\begin{array}{}\text{(12)}& \mathrm{\Delta }\mathit{\tau }={\displaystyle \frac{\mathrm{7}}{\mathrm{16}}}{\displaystyle \frac{M_{\mathrm{0}}}{d_{\mathrm{crack}}^{\mathrm{3}}}}\end{array}$$

On the other hand, the seismic moment M₀ and the moment magnitude M_w in terms of the coseismic magnetic field are also related. Hence, the seismic moment is given by

$$\begin{array}{}\text{(13)}& M_{\mathrm{0}}\approx {\mathit{\mu }}_{\mathrm{sm}}{\displaystyle \frac{B_{\mathrm{cs}}{r}^{\mathrm{2}}}{{\mathit{\mu }}_{\mathrm{m}}J}}{\displaystyle \frac{(\mathrm{3}-D)}{D(D-\mathrm{2})}}\left(l_{min}^{\mathrm{2}-D}\right)\left(l_{max}^{D-\mathrm{3}}\right)d,\end{array}$$

where μ_sm is the shear modulus, d the average slip, D the fractal dimension of rock and B_cs the coseismic magnetic field; J corresponds to the total electric current density; μ_m is the magnetic permeability of the medium; r is the distance to the fault; l_max and l_min are the radius of the circular rupture area and the smallest microcrack length, respectively. The circular rupture is calculated using $l_{max}=\sqrt{S/\mathit{\pi }}$, where S corresponds to the total rupture area.

In this case, the rupture geometry is circular in both formulations, thus, $d_{\mathrm{crack}}=l_{max}$. Substituting this into Eqs. (13) and (12) we obtain

$$\begin{array}{}\text{(14)}& \mathrm{\Delta }\mathit{\tau }\approx {\displaystyle \frac{\mathrm{7}}{\mathrm{16}}}{\mathit{\mu }}_{\mathrm{sm}}{\displaystyle \frac{B_{\mathrm{cs}}{r}^{\mathrm{2}}}{{\mathit{\mu }}_{\mathrm{m}}J}}{\displaystyle \frac{(\mathrm{3}-D)}{D(D-\mathrm{2})}}\left(l_{min}^{\mathrm{2}-D}\right)\left(l_{max}^{D-\mathrm{6}}\right)d.\end{array}$$

Equation (14) relates the stress drop with the coseismic magnetic field, seismic rupture, and the electrical and mechanical properties of rocks (lithosphere). We can use the data from the Maule earthquake in order to compare the result of Eq. (14) with those found by other researchers. If we use the fault values ${\mathit{\mu }}_{\mathrm{sm}}=\mathrm{3.3}\times {\mathrm{10}}^{\mathrm{10}}$ Pa, d=4 m and $S=\mathrm{450}\times \mathrm{120}$ km² (Vigny et al., 2011; Yue et al., 2014); the granite rock and brittle properties ${\mathit{\mu }}_{\mathrm{m}}=\mathrm{13.5}\times {\mathrm{10}}^{-\mathrm{7}}$ N A⁻² (Scott, 1983), $J=\mathrm{5}\times {\mathrm{10}}^{-\mathrm{6}}$ A m⁻² (Tzanis and Vallianatos, 2002), $l_{min}={\mathrm{10}}^{-\mathrm{3}}$ m (Shah, 2011) and D=2.6 (Turcotte, 1997); and the magnetic data B_cs≈0.1 nT at r≈250 km (Fig. 5 in Venegas-Aravena et al., 2019), we obtain a stress drop Δτ≈3.4 MPa. This result is in close agreement with the result of Luttrell et al. (2011; 4 MPa). Using this value, we can calculate the elastic shear stress as

$$\begin{array}{}\text{(15)}& {\mathit{\tau }}_{\mathrm{elastic}}={\mathit{\tau }}_{\mathrm{0}}-{\mathit{\gamma }}_{\mathrm{2}}\mathrm{\Delta }\mathit{\tau }H\left(t-t_{\mathrm{0}}\right),\end{array}$$

where H(t−t₀) corresponds to the step function centered at t₀ (the moment of the earthquake occurrence) and γ₂ is a dimensionless second step function that represents the fault area where the stress drop exists. This means that γ₂=0 outside the rupture area and γ₂=1 if the point is within the rupture area. Combining this result into Eq. (10), we calculate the total friction coefficient ${\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}$ of the fault as

$$\begin{array}{}\text{(16)}& \begin{array}{rl}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}& (x,t)\approx \\ & {\displaystyle \frac{{\mathit{\tau }}_{\mathrm{0}}-{\mathit{\gamma }}_{\mathrm{2}}\mathrm{\Delta }\mathit{\tau }H\left(t-t_{\mathrm{0}}\right)+\mathit{\gamma }\left(k_{\mathrm{1}}\dot{\mathit{\sigma }}+k_{\mathrm{2}}\ddot{\mathit{\sigma }}\mathit{\delta }t\right)\cos \mathit{\theta }\mathit{\delta }t}{N_{\mathrm{0}}-\mathit{\gamma }\left(k_{\mathrm{3}}\dot{\mathit{\sigma }}+k_{\mathrm{4}}\ddot{\mathit{\sigma }}\mathit{\delta }t\right)\sin \mathit{\theta }\mathit{\delta }t}}.\end{array}\end{array}$$

This total friction coefficient ${\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}$ is especially relevant because of the dependence of the coseismic magnetic field B_cs (through the stress drop Δτ) and the magnetic anomalies (through the relation $B\propto \dot{\mathit{\sigma }}$). Furthermore, Eq. (16) explains the spatial distribution of friction along the fault in addition to its time variations. In Eq. (16), the spatial changes in friction (represented by γ) are not necessarily related to the seismic rupture area (represented by γ₂). However, in the case where they are related, one expects γ₂ to be a function of γ. That is γ₂=γ₂(γ(x)). In the general case the total friction coefficient gradient can be written as

$$\begin{array}{}\text{(17)}& \mathrm{\nabla }{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}=\mathrm{\nabla }\stackrel{\mathrm{‾}}{\mathit{\mu }}+\mathrm{\Delta }\mathit{\tau }H\left(t-t_{\mathrm{0}}\right)\mathrm{\Gamma }\left(\mathit{\gamma },{\mathit{\gamma }}_{\mathrm{2}}\right),\end{array}$$

where $\mathrm{\Gamma }(\mathit{\gamma },{\mathit{\gamma }}_{\mathrm{2}})=\mathrm{1}/(N_{\mathrm{0}}-\mathit{\gamma }B{)}^{\mathrm{2}}[{\mathit{\gamma }}_{\mathrm{2}}^{\prime }(\mathit{\gamma }B-N_{\mathrm{0}})-{\mathit{\gamma }}^{\prime }{\mathit{\gamma }}_{\mathrm{2}}B]$, $\mathrm{\nabla }\stackrel{\mathrm{‾}}{\mathit{\mu }}$ is the friction gradient already defined in Eq. (11), and the same definitions for A and B are used. The second term of Eq. (17) implies that a more complex spatial friction distribution on the fault is expected after the earthquake. When no brittle–plastic contribution is considered (γ=0), the friction is only proportional to the gradient of fault rupture distribution ($\mathrm{\nabla }{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}=-\mathrm{\Delta }\mathit{\tau }H(t-t_{\mathrm{0}}){\mathit{\gamma }}_{\mathrm{2}}^{\prime }/N_{\mathrm{0}}$). When γ₂≈γ, the two terms of the total friction coefficient will be proportional to the spatial distribution gradient ($\mathrm{\nabla }{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}\propto {\mathit{\gamma }}^{\prime }$). If the earthquake does not occur, the second term vanishes and Eq. (11) is recovered.

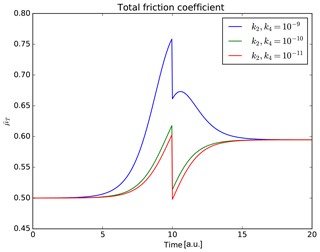
Figure 5 Total fiction coefficient from the seismo-electromagnetic theory derivation. If we consider one point within the rupture area, the highest values of friction are found before the earthquake (t=10 a.u.). The friction decreases at t=10 a.u. was calculated using the stress drop as a function of the coseismic magnetic field. The maximum value is not completely recovered after the earthquake occurs.

As an illustration, if we consider one point affected by the rupture area and the same values as in Fig. 3, we can calculate the shape of the total friction coefficient as shown in Fig. 5. The three cases show an increase in the friction coefficient prior to the earthquake, and in the three cases the friction reaches its maximum values before the earthquake (at t=10 a.u.). The subsequent decrease is due to the stress drop influence calculated using the coseismic magnetic field B_cs. After the earthquake, in none of the cases is the friction completely recovered to its values before the earthquake.

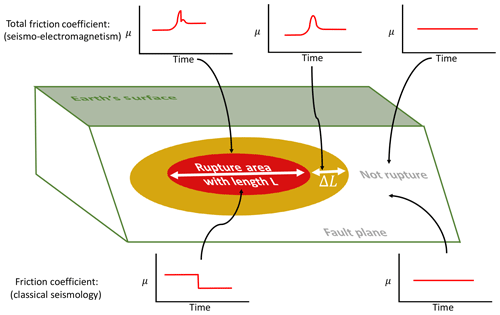
Figure 6 Schematic comparison among different friction behaviors related to seismic rupture area. At the top the result of friction in the context of the seismo-electromagnetic theory is presented. At the bottom the classical view of the friction is presented. When the rupture occurs, a friction drop is observed in the two theories. However, a friction increase exists in the case studied in this work.

As a second illustration, it is also possible to compare the temporal behavior of the friction coefficient at different points within the fault. For instance, in Fig. 6 (top) we show the different friction behaviors expected if we consider the total friction coefficient. The red area indicates the area where the friction drop occurs. A friction drop is not expected to occur outside the red zone. However, it is possible to observe differences in the coefficient of friction close to the rupture zone where γ₂≠γ (yellow area). In both the rupture zone and its surroundings (marked as red and yellow areas, respectively, in Fig. 6) there are changes in the coefficient of friction prior to the rupture. In stark contrast, the standard friction drop is expected only in the rupture zone (red area) and a nonmeasurable change in friction is expected prior to the earthquake (Fig. 6, bottom).

We can summarize our analysis by using two different distributions of γ and γ₂. For instance, in Fig. 7 we show the double-sigmoidal distribution for γ and γ₂ (black and red curves, respectively) along the fault x direction (of total length 2x_half). The dimensionless distribution is defined as a combination of the sigmoidal function used in Sect. 2 as

$$\begin{array}{}\text{(18)}& \mathit{\gamma }\left(x\right),{\mathit{\gamma }}_{\mathrm{2}}\left(x\right)=\left\{\begin{array}{ll}\frac{a}{b-e^{\left(x_{\mathrm{0}}-x\right)\times w}},& x<x_{\mathrm{half}}\\ \mathrm{1}-\frac{a}{b-e^{\left(x_{\mathrm{0}}+L-x\right)\times w}},& x\ge x_{\mathrm{half}}.\end{array}\right.\end{array}$$

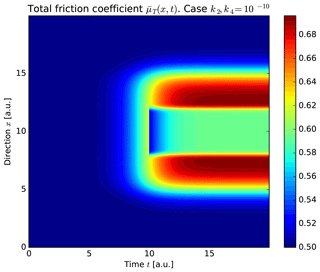
If we consider $a=b=\mathrm{1}$ and x_half=10 a.u. in both distributions; x₀=5 a.u., L=10 a.u. and w=1 a.u. for γ; and x₀=8 a.u., L=4 a.u. and w=10 a.u. for γ₂, we get the two distributions of Fig. 7. These values indicate the same situation as discussed in Fig. 6, that is a rupture length (L=4 a.u. in γ₂ represents the x direction of the red area in Fig. 6) influenced less by the friction coefficient than by semibrittle–plastic stress (here L=10 a.u. in γ represents the x direction of the yellow area in Fig. 6). Using both sets of values, those used in the stress drop (Eq. 14) and also the same k parameters used in Eq. (9), we calculate the total friction coefficient (Eq. 16) as shown in Fig. 8 (case $k_{\mathrm{2}}=k_{\mathrm{4}}={\mathrm{10}}^{-\mathrm{9}}$). At time t=0 a.u., no friction changes occur (${\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}=\mathrm{0.5}$). However, the friction increases at t=5 a.u., where the spatial distribution γ is initially defined as nonzero ($x\in [\mathrm{5},\mathrm{15}]$ a.u.). The friction increases up to t=10 a.u., the time corresponding to the earthquake occurrence. The earthquake rupture length is shown as a sudden friction decrease ($x\in [\mathrm{8},\mathrm{12}]$ a.u.) from 0.76 to 0.67. In the zone immediately next to the rupture, the friction increases even more up to the maximum values (0.77), while in the rupture section the friction decreases. After this time (t∼12 a.u.), the rupture and the surrounding section experience a friction decrease.

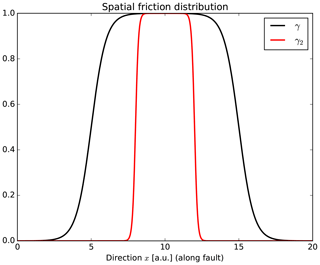
Figure 7 Spatial distribution of γ and γ₂. These functions represent the different sections (or behavior) of friction on the fault along the x direction. The distribution γ₂ represents the stress drop section and distribution γ represents the semibrittle–plastic influence region.

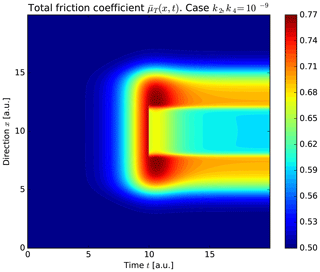
Figure 8 Spatial–temporal total friction coefficient ${\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}(x,t)$ along the fault x direction using $k_{\mathrm{2}}=k_{\mathrm{4}}={\mathrm{10}}^{-\mathrm{9}}$. The righthand color bar indicate the friction coefficient values at a certain time and position. The earthquake occurs when t=10 a.u. At this time, the stress drop (defined by the distribution γ₂) $\mathrm{\Delta }\mathit{\tau }\in [\mathrm{8},\mathrm{12}]$ a.u.

The case of $k_{\mathrm{2}}=k_{\mathrm{4}}={\mathrm{10}}^{-\mathrm{10}}$ is shown in Fig. 9. The rupture is shown as a blue area at t=10 a.u. in section $x\in [\mathrm{8},\mathrm{12}]$ a.u. At this time and location, we observe that the friction decreases to similar initial values (∼0.5). The friction of this rupture section increases after the earthquake up to ∼0.6. On the other hand, the rupture's surrounding section increases up to the maximum values (∼0.7). Despite those facts, the initial (t=0 a.u.) and final (t=20 a.u.) friction values are almost identical for both cases. For instance, the rupture area has values close to 0.6 in Figs. 8 and 9. The surrounding rupture section has values close to 0.69 in both cases, and the section away from the rupture (close to x=0 a.u. and x=20 a.u.) always has the same initial value (0.5) in both cases. However, both cases exhibit a complex time behavior after the earthquake occurrence, as Eq. (17) indicates.

Figure 9 Same spatial–temporal total friction coefficient as in Fig. 8 but using k₂, $k_{\mathrm{4}}={\mathrm{10}}^{-\mathrm{10}}$.

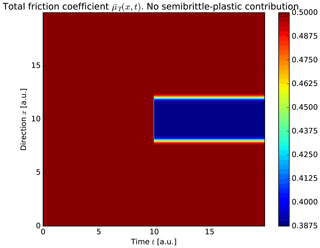
Finally when the semibrittle–plastic contribution is not considered, we get that γ=0. The result is shown in Fig. 10 and is only observed with the sudden friction decrease at t=10 a.u. (and $x\in [\mathrm{8},\mathrm{12}]$ a.u.). In this later case none of the other complex friction behaviors is observed.

Figure 10 Total friction coefficient using no semibrittle–plastic contribution. That is γ(x)=0, $\forall x\in [\mathrm{0},\mathrm{2}{x}_{\mathrm{half}}]$. The friction variation exists only when the earthquake occurs (t=10 a.u.) and at the earthquake rupture place ($\mathrm{\Delta }\mathit{\tau }\in [\mathrm{8},\mathrm{12}]$ a.u. in this case).

5 The semibrittle–plastic Gutenberg–Richter law

A general expression for friction has been obtained in Eq. (16). Following this we can adapt the Gutenberg–Richter law in this semibrittle–plastic context. Let us remind ourselves that this law establishes a relation between the number of earthquakes in a region and their magnitude (Gutenberg and Richter, 1944). Mathematically, this link is written as $\log N=a-b\times m$, where N is the number of earthquakes with magnitude equal to or greater than m and a and b are constants. However, the b-value of this law might evolve in time. Indeed, De Santis et al. (2011) determined an equation that relates the temporal evolution of the parameter b (b=b(t)) and the measure of the entropy (stress) H(t) of that region as $b\left(t\right)=b_{max}{\mathrm{10}}^{-H\left(t\right)}$, where $b_{max}=e{\log }_{\mathrm{10}}e$. The entropy H(t) is assumed to be proportional to the real stress in the lithosphere (Venegas-Aravena et al., 2019). If we consider the total shear stress τ_T in the fault described by Eq. (16), we can write

$$\begin{array}{}\text{(19)}& b\left(t\right)=b_{max}{\mathrm{10}}^{-k_{\mathrm{0}}{\mathit{\tau }}_{\mathrm{T}}},\end{array}$$

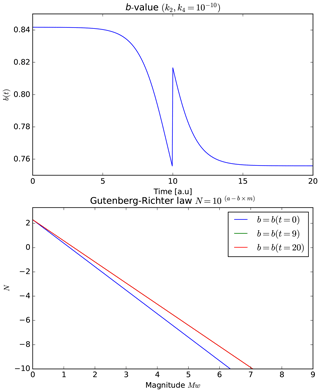
where ${\mathit{\tau }}_{\mathrm{T}}={\mathit{\tau }}_{\mathrm{0}}-{\mathit{\gamma }}_{\mathrm{2}}\mathrm{\Delta }\mathit{\tau }H(t-t_{\mathrm{0}})+\mathit{\gamma }(k_{\mathrm{1}}\dot{\mathit{\sigma }}+k_{\mathrm{2}}\ddot{\mathit{\sigma }}\mathit{\delta }t)\cos \mathit{\theta }\mathit{\delta }t$ and k₀ is a constant with dimensions of an inverse stress. If we use the same values as in Fig. 5 ($k_{\mathrm{2}}=k_{\mathrm{4}}={\mathrm{10}}^{-\mathrm{9}}$), we get the temporal evolution of the b-value (Fig. 11a). Figure 11a shows a decrease in the b-value until the earthquake occurs (at t=10 a.u.). Figure 11b shows the Gutenberg–Richter law at three instants of time (and k₀=0.01, a=1): initial (t=0 a.u.), prior to the earthquake (t=9 a.u.) and final (t=20 a.u.). This figure shows how large earthquakes (M_w∼6) are not expected at the initial moment (blue line). However, just before the earthquake, an M8-class earthquake should be expected (green line). After the earthquake one would only expect earthquakes no greater than M_w∼7 to exist (red line). Figure 12a and b show the same previous case but now considering $k_{\mathrm{2}}=k_{\mathrm{4}}={\mathrm{10}}^{-\mathrm{10}}$. In this case there is no difference between time immediately before the earthquake (t=9 a.u.) and at the final time (t=20 a.u.). In addition, using these parameters ($k_{\mathrm{2}}=k_{\mathrm{4}}={\mathrm{10}}^{-\mathrm{10}}$), smaller magnitudes are reached than when using $k_{\mathrm{2}}=k_{\mathrm{4}}={\mathrm{10}}^{-\mathrm{9}}$ (M_w∼7 and M_w∼8, respectively). This is why it is more likely that earthquakes of greater magnitude will be found when considering the contribution of the $\ddot{\mathit{\sigma }}$ term in the analysis.

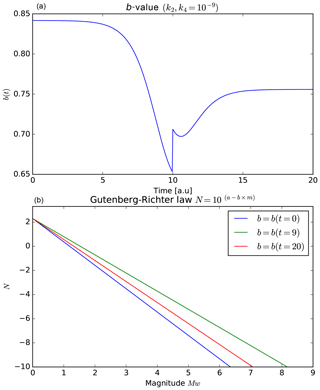
Figure 11 (a) The b-value using σ=ατ; $k_{\mathrm{2}}=k_{\mathrm{4}}={\mathrm{10}}^{-\mathrm{9}}$ and α=0.01. (b) The Gutenberg–Richter law for instants of time t=0 a.u., t=9 a.u. and t=20 a.u. The b-value decreases before the earthquake implying stronger seismic events.

Figure 12 The b-value and Gutenberg–Richter law using $k_{\mathrm{2}}=k_{\mathrm{4}}={\mathrm{10}}^{-\mathrm{10}}$. The green and red curves are the same.

6 Rupture time t₀

In Sect. 5 we determine that $k_{\mathrm{2}}=k_{\mathrm{4}}={\mathrm{10}}^{-\mathrm{9}}$ were the most adequate values. Despite this fact, the Gutenberg–Richter law does not provide an approximate time t₀ for the earthquake occurrences. If we look at Eq. (16), the term t₀ appears explicitly (in the step function). However, t₀ appears only after the earthquake, so it is not possible to find t₀ analytically before the rupture (using the rupture itself). This means that we must find an estimate using the other parameters. One way to do it is to consider the differential total friction coefficient $\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}$ to find an approximate rupture time t₀. Figure 13 shows $\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}$ considering ${\mathit{\gamma }}_{\mathrm{2}}=\mathit{\gamma }=\mathrm{1}$, $k_{\mathrm{2}}=k_{\mathrm{4}}={\mathrm{10}}^{-\mathrm{9}}$ and $k_{\mathrm{2}}=k_{\mathrm{4}}={\mathrm{10}}^{-\mathrm{10}}$. When major earthquakes ($k_{\mathrm{2}}=k_{\mathrm{4}}={\mathrm{10}}^{-\mathrm{9}}$) are considered, the rupture occurs after the maximum value ($(\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}{)}_{\mathrm{MAX}}$), when $\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}\approx \mathrm{1}/\mathrm{2}(\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}{)}_{\mathrm{MAX}}$ (Fig. 13, top). When k₂, $k_{\mathrm{4}}={\mathrm{10}}^{-\mathrm{10}}$, the rupture also occurs after the maximum value, in this case $\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}\approx \mathrm{0.9}(\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}{)}_{\mathrm{MAX}}$ (Fig. 13, bottom). Considering these two limiting cases in this framework we conclude that earthquakes occur after ($\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}{)}_{\mathrm{MAX}}$ when the differential total friction coefficient decreases to $\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}\approx C(\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}{)}_{\mathrm{MAX}}$, where $C\in [\mathrm{0.5},\mathrm{0.9}]$.

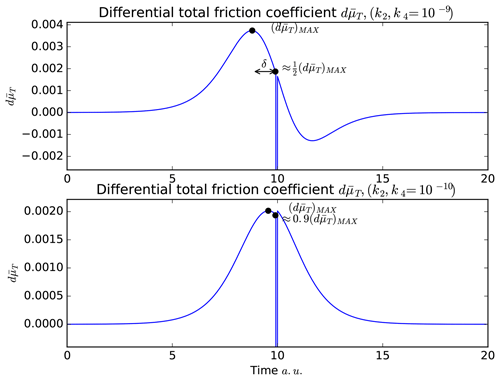
Figure 13 Different ruptures times viewed from the differential total friction coefficient $\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}$ and using different values of k₂ and k₄. The rupture occurs after the maximum differential total friction coefficient $(\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}{)}_{\mathrm{MAX}}$, when $\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}$ have values close to 0.5–0.9 times $(\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}{)}_{\mathrm{MAX}}$.

The time between $\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}\approx (\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}{)}_{\mathrm{MAX}}$ and $\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}\approx C(\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}{)}_{\mathrm{MAX}}$ can be denoted by δ. This δ parameter increases when C decreases and vice versa, so δ is inversely proportional to C ($\mathit{\delta }\propto C^{-\mathrm{1}}$). Then, we arrive at an expression for the general rupture time t₀ as follows:

$$\begin{array}{}\text{(20)}& t_{\mathrm{0}}\approx t_{C(\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}{)}_{\mathrm{MAX}}}=t_{(\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}{)}_{\mathrm{MAX}}}+\mathit{\delta },t>t_{(\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}{)}_{\mathrm{MAX}}},\end{array}$$

where $t_{(\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}{)}_{\mathrm{MAX}}}$ is the time when $\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}\approx (\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}{)}_{\mathrm{MAX}}$. Note that Eq. (20) is only valid after the maximum value ($\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}{)}_{\mathrm{MAX}}$ is reached. Equation (20) is general; however, considering the Gutenberg–Richter law, we expect that C values close to 0.5 are necessary to represent earthquakes of greater magnitude in this theoretical framework.

7 Discussion and conclusions

In this work we have linked key parameters associated with the geological fault with magnetic measurements. Both stress drops and the semibrittle–plastic stress were linked to a friction coefficient (on the fault) equation in terms of magnetic measurements (Eq. 16). One of the main points of Eq. (16) corresponds to the fact that the total friction coefficient ${\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}(x,t)$ is entirely determined by the spatial distribution of the nonconstant stress changes within the lithosphere. If the seismo-electromagnetic theory is applied, it means that the rupture process is controlled by the nonconstant stress changes that surround the fault and not by the fault itself. In this scenario, the earthquakes might occur at places on the fault that are being affected by a continuous friction increase prior to rupture (this friction increase occurs regardless of the values of k₂ and k₄ used in the analysis). In our work we have shown that the total friction coefficient depends on two different spatial distributions. The first one is associated with the uniaxial stress changes γ(x) and the second one with the rupture area γ₂(x). These two distributions are not necessarily correlated. In the case where they are comparable (that is $\left|\mathit{\gamma }\right(x)-{\mathit{\gamma }}_{\mathrm{2}}(x\left)\right|\approx \mathrm{0}$), it means that the lithosphere area affected by nonconstant uniaxial stress changes is a determining factor for predicting the earthquake magnitude and location before it occurs. This is $\mathit{\gamma }\left(x\right)\approx {\mathit{\gamma }}_{\mathrm{2}}\left(x\right)\approx \mathrm{0}$ if x belong to sections where $\dot{\mathit{\sigma }}=\mathrm{cte}$ and γ(x) and γ₂(x)≠0 if x∈L, where L is the rupture length (at places where $\dot{\mathit{\sigma }}\ne \mathrm{cte}$). The seismic moment M₀ is proportional to this length L (Aki, 1966), and the seismic moment magnitude M_w depends on the seismic moment (Hanks and Kanamori, 1979), implying that the seismic moment magnitude depends on the spatial distribution of the total friction coefficient variations. As the nonconstant uniaxial stress changes could also create magnetic signals due the microcracks of rocks (Venegas-Aravena et al., 2019, and references therein), it is reasonable to assume that a larger area of magnetic anomalies could imply a larger earthquake. This is the locality (or Dobrovolsky) criterion used by some researchers when they relate some electromagnetic measurements to earthquakes (e.g., De Santis et al., 2019a, and references therein). If in this case we also consider the initial time of friction increase (impending rupture time), the approximate magnitude, then the approximate location and the approximate imminent time could be theoretically determined through Eq. (20).

For the limiting case where $\left|\mathit{\gamma }\right(x)-{\mathit{\gamma }}_{\mathrm{2}}(x\left)\right|\gg \mathrm{0}$ we have seen that the locality criterion does not hold anymore. Hence, the earthquakes occurrences cannot be related to the nonconstant stress changes and the magnetic field. This limiting case prevents the possibility of a real earthquake prediction using this simple theoretical base. This later case may also imply that the cumulative stress on the fault is not enough to generate a seismic rupture at any point on the fault (that is γ₂(x)=0). This means that the accumulated elastic energy that is injected into the fault is not sufficient to spread the rupture (this last energy is called fracture energy G_C; see Ohnaka, 2013; Nielsen et al., 2016). This scenario could indicates that the stress changes in the semibrittle–plastic regime are not a sufficient condition for the earthquake generation; however, they could be a necessary condition.

With respect to the size of earthquakes in the present model, Sect. 5 has shown that earthquakes have greater magnitudes when $k_{\mathrm{2}}=k_{\mathrm{4}}\approx {\mathrm{10}}^{-\mathrm{9}}$. If we consider those values in Fig. 5, we see that the total friction coefficient is also higher. This is ∼0.75 when $k_{\mathrm{2}}=k_{\mathrm{4}}\approx {\mathrm{10}}^{-\mathrm{9}}$ and sensibly larger than ∼0.6 when $k_{\mathrm{2}}=k_{\mathrm{4}}\approx {\mathrm{10}}^{-\mathrm{10}}$. This indicates that there is a correlation between the size of the earthquake and the total friction coefficient. Hence, the earthquake has a greater magnitude when there is a higher total friction coefficient (or shear stress τ). This means that ${\mathit{\gamma }}_{\mathrm{2}}={\mathit{\gamma }}_{\mathrm{2}}\left({\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}\right)$; therefore, the rupture length L of Eq. (18) is proportional to ${\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}$ (that is $L=\mathit{\alpha }{\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}\left(t_{\mathrm{0}}\right)$). Note that this is independent of the value of $\left|\mathit{\gamma }\right(x)-{\mathit{\gamma }}_{\mathrm{2}}(x\left)\right|$, since it comes directly from the Gutenberg–Richter law. However, in this case ${\stackrel{\mathrm{‾}}{\mathit{\mu }}}_{\mathrm{T}}$ is homogeneous, so more studies will be needed in order to determine L.

Finally, this theoretical work has provided a possible mechanism that explains several magnetic measurements performed recently. Equally this work provides some necessary conditions of the fault in order to trigger earthquakes in terms of their magnetic properties. We think that future research of the LAIC effect community should focus on lithospheric-fault dynamics as one of the promising topics in the field. When the lithosphere part of this effect is better understood, the other effects will have a stronger theoretical basis that will help to perform measurements and/or make accurate predictions.