A study of earthquake recurrence based on a one-body spring-slider model in the presence of thermal-pressurized slip-weakening friction and viscosity

Earthquake recurrence is studied from the temporal variation in slip through numerical simulations based on the normalized form of equation of motion of a one-body spring-slider model with thermal-pressurized slip-weakening friction and viscosity. The wear process, whose effect is included in the friction law, is also taken into account in this study. The main parameters are the normalized characteristic displacement, U_c, of the friction law and the normalized damping coefficient (to represent viscosity), η. T_R, D, and τ_D are the recurrence time of events, the final slip of an event, and the duration time of an event, respectively. Simulation results show that T_R increases when U_c decreases or η increases, D and τ_D decrease with increasing η, and τ_D increases with U_c. The time- and slip-predictable model can describe the temporal variation in cumulative slip. When the wear process is considered, the thickness of slip zone, h, which depends on the cumulated slip, S(t) = ∑D(t), i.e., h(t) = CS(t) (C is a dimensionless increasing rate of h with S), is an important parameter influencing T_R and D. U_c is a function of h and thus depends on cumulated normalized slip, ∑U, with an increasing rate of C. In the computational time period, the wear process influences the recurrence of events and such an effect increases with C when C > 0.0001. When viscosity is present, the effect due to wear process becomes stronger. Both T_R and D decrease when the fault becomes more mature, thus suggesting that it is more difficult to produce large earthquakes along a fault when it becomes more mature. Neither the time-predictable nor the slip-predictable model can describe the temporal variation in cumulative slip of earthquakes under the wear process with large C.

1 Introduction

Earthquake recurrence that is relevant to the physics of faulting is an important factor in seismic hazard assessment. It is related to the seismic cycle, which represents the occurrence of several earthquakes in the same segment of a fault during a time period. Figure 1 exhibits the general pattern of time variation in slip and particle velocity during a seismic cycle. In the figure, T_R is the recurrence (also denoted by repeat or inter-event) time of two events in a seismic cycle, τ_D is the duration time of slip of an event, D is the final slip of an event, and V_m is the peak value of particle velocity of an event. The four parameters could be constants in the time history when all model parameters do not vary with time and could also vary with time, represented by T_R(t), τ_D(t), D(t), and V_m(t), when one of model parameters does vary with time. Sykes and Quittmeyer (1981) pointed out that the major factors in controlling T_R are the plate moving speed and the geometry of the rupture zone. Based on Reid's elastic rebound theory (Reid, 1910), Schwartz and Coppersmith (1984) assumed that an earthquake occurs when the tectonic shear stress on a fault is higher than a critical level, which is dependent on the physical conditions of the fault and the loading by regional tectonics. Since in their work a fault has a homogeneous distribution of physical properties under constant tectonic loading, earthquakes could happen regularly.

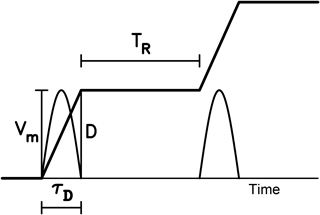
Figure 1 A general pattern of time variations in slip (thick solid line) and particle velocity (thin solid curve) during a seismic cycle: T_R is the recurrence time or the inter-event time of two events in a seismic cycle; τ_D is the duration time of slip of an event; D is the final slip of an event; and V_m is the peak particle velocity of an event.

Some observations exhibit periodicity for different size earthquakes. Bakun and McEvilly (1979) obtained T_R ≈ 23 ± 9 years for M ≈ 6 earthquakes at the Parkfield segment of the San Andreas fault, USA since 1857. Sykes and Menke (2006) estimated T_R ≈ 100 years for M ≥ 8 earthquakes in the Nankaido segments of the Nankai Trough, Japan. Okada et al. (2003) gained T_R = 5.5 ± 0.7 years for earthquakes with M = 4.8 ± 0.1 off Kamaishi, Japan, since 1957. Nadeau and Johnson (1998) inferred an empirical relation between T_R and seismic moment, M_o: T_R ∝ $M_{\mathrm{o}}^{\mathrm{1}/\mathrm{6}}$. To make this relation valid, the stress drop, Δσ, or the long-term slip velocity of a fault, v_l, must be in terms of M_o. Based on three data set from eastern Taiwan, Parkfield, USA, and northeastern Japan, Chen et al. (2007) inferred T_R ∼ $M_{\mathrm{o}}^{\mathrm{0.61}}$. Beeler et al. (2001) proposed a theoretical relation: T_R = $\mathrm{\Delta }{\mathit{\sigma }}^{\mathrm{2}/\mathrm{3}}{M}_{\mathrm{o}}^{\mathrm{1}/\mathrm{3}}/\mathrm{1.81}\mathit{\mu }{v}_{\mathrm{l}}$, where μ is the rigidity of the fault-zone materials.

However, the main factors in influencing earthquake occurrences commonly are spatially heterogeneous and also vary with time. Thus, the recurrence times of earthquakes, especially large events, are not constant inferred either from observations (Ando, 1975; Sieh, 1981; Kanamori and Allen, 1986; Wang and Kuo, 1998; Wang, 2005; Sieh et al., 2008) or from modeling (Wang, 1995, 1996; Ward, 1996, 2000; Wang and Hwang, 2001). Kanamori and Allen (1986) observed that faults with longer T_R are stronger than those with shorter T_R. Davies et al. (1989) proposed that the longer it has been since the last earthquake, the longer the expected time until the next. Wang and Kuo (1998) observed that for M ≥ 7 earthquakes in Taiwan T_R strongly follows the Poissonian processes. Enescu et al. (2008) found that the probability density distribution of T_R can be described by an exponential function. From the estimated values of T_R of earthquakes happened on the Chelungpu fault in central Taiwan from trenching data, Wang (2005) found that the earthquakes occurred non-periodically.

In order to interpret earthquake recurrences, Shimazaki and Nakata (1980) proposed three simple phenomenological models. Each model has a constantly increasing tectonic stress that is controlled by a critical stress level, σ_c, for failure and a base stress level, σ_b. The three models are (1) the perfectly periodic model (with constant σ_c, σ_b, and Δσ); (2) the time-predictable model (with constant σ_c, variable σ_b, and variable Δσ); and (3) the slip-predictable model (with variable σ_c, constant σ_b, and variable Δσ). For the first model, both T_R and D of next earthquake can be predicted from the values of T_R or D of previous ones. For the second model, T_R of next earthquake can be predicted from the values of D of previous ones. For the third model, D of next earthquake can be predicted from the values of T_R of previous ones. However, debates about the three models have been made for a long time. Some examples are given below. Ando (1975) suggested that the second model worked for post-1707 events but not for pre-1707 ones in the Nankai Trough, Japan. Wang (2005) assumed that the second model could describe the earthquakes occurred on the Chelungpu fault, Taiwan, in the past 1900 years. For the Parkfield earthquake sequence, Bakun and McEvilly (1984) took different models, while Murray and Segall (2002) considered the failure of the second model. From laboratory results, Rubinstein et al. (2012) assumed the failure of the time- and slip-predictable models for earthquakes.

Some models, for instance the crack model and dynamical spring-slider model, have been developed for fault dynamics, even though the seismologists have not a comprehensive model. There are several factors in controlling fault dynamics and earthquake ruptures (see Bizzarri, 2009; Wang, 2017b). Among the factors, friction (Nur, 1978; Belardinelli and Belardinelli, 1996) and viscosity (Jeffreys, 1942; Spray, 1993; Wang, 2007) are two significant ones.

Modeling earthquake recurrence based on different models has been long made and is reviewed by Bizzarri (2012a, b) and Franović et al. (2016). Among the models, the spring-slider model has been used to study fault dynamics and earthquake physics (see Wang, 2008). Burridge and Knopoff (1967) proposed the one-dimensional N-body model (abbreviated as the 1-D BK model henceforth). Wang (2000, 2012) extended the 1-D model to 2-D one. The one-, two-, three-, and few-body models with various friction laws have also been applied to approach fault dynamics (see Turcotte, 1992). The studies for various friction laws based on spring-slider models are briefly described below: (1) for rate- and state-dependent friction (e.g., Rice and Tse, 1986; Ryabov and Ito, 2001; Erickson et al., 2008, 2011; He et al., 2003; Mitsui and Hirahara, 2009; Bizzarri, 2012a; Abe and Kato, 2013; Kostić et al., 2013a; Bizzarri and Crupi, 2014; Franović et al., 2016); (2) for velocity-weakening friction (e.g., Carlson and Langer, 1989; Huang and Turcotte, 1992; Brun and Gomez, 1994; Wang and Hwang, 2001; Wang, 2003; Kostić et al., 2013b); (3) for simple static–dynamic friction (e.g., Abaimov et al., 2007; Hasumi, 2007).

Some results concerning earthquake recurrence are simply explained below. Erickson et al. (2008) suggested that aperiodicity in earthquake dynamics is due to either the nonlinear friction law (Huang and Turcotte, 1990) or the heterogeneous stress distribution (Lapusta and Rice, 2003). Wang and Hwang (2001) emphasized the importance of heterogeneous frictional strengths. Mitsui and Hirahara (2009) pointed out the effect of thermal pressurization. Dragoni and Piombo (2011) found that variable strain rate causes aperiodicity of earthquakes. Bizzarri and Crupi (2014) found that T_R is dependent on the loading rate, effective normal stress, and characteristic distance of the rate- and state-dependent friction law.

As mentioned previously, numerous studies have been made for exploring the frictional effect on earthquake recurrence. However, studies concerning the viscous effect on earthquake recurrence are rare. In the following, we will investigate the effects of slip-weakening friction due to thermal-pressurization and viscosity on earthquake recurrence based on the one-body spring-slider model.

2 One-body model

Figure 2 displays the one-body spring-slider model. In the model, m, K, σ_n, F, η, u, v (= du∕dt), v_p, and u_o = v_pt denote, respectively, the mass of the slider, the stiffness (or spring constant) of the leaf spring, the normal stress, the frictional force between the slider and the moving plate, the damping coefficient (to represent viscosity as explained below), the displacement of the slider, the velocity of the slider, the plate moving speed, and the equilibrium location of the slider. The frictional force F (with the static value of F_o) is usually a function of u or v. Viscosity results in the viscous force, Φ, between the slider and the moving plate, and Φ is in terms of v. A driving force, Kv_pt, caused by the moving plate through the leaf spring pulls the slider to move. The equation of motion of the model is

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }m{\mathrm{d}}^{\mathrm{2}}u/\mathrm{d}{t}^{\mathrm{2}}=-K\left(u-u_{\mathrm{o}}\right)-F(u,v)-\mathrm{\Phi }\left(v\right).\end{array}$$

When Kv_pt ≥ F_o, F changes from static frictional force to dynamic one and thus makes the slider move. Among the physical models to approach earthquake faults, the single spring-slider model, which can represent a single fault, is actually the simplest one. However, based on this simple model in the presence of thermal-pressurized friction and viscosity we can obtain good simulations of earthquake recurrences along a single fault. Results can exhibit the frictional and viscous effects on earthquake recurrence.

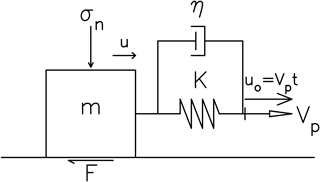
Figure 2 One-body spring-slider model. In the figure, t, m, K, η, V_p, σ_n, F, u, and u_o denote, respectively, the time, the mass of the slider, the spring constant, the damping coefficient, the driving velocity, the normal stress, the frictional force, displacement of the slider, and the equilibrium location of the slider (after Wang, 2016).

The frictional force F(u, v) is controlled by several factors (see Wang, 2016, and cited references therein). An effect combined from temperature and fluids in a fault zone can result in thermal pressurization (abbreviated as TP hereafter) which would yield a shear stress (resistance) on the fault plane (Sibson, 1973; Lachenbruch, 1980; Rice, 2006; Wang, 2009, 2011, 2016, 2017a–c; Bizzarri, 2009). Rice (2006) proposed two end-member models of TP, i.e., the adiabatic undrained deformation (AUD) model and slip-on-a-plane (SOP) model. Since the characteristic distance of the SOP model cannot be associated with the wear process, the SOP model is not used in this study. The AUD model is related to a homogeneous simple strain ε at a constant normal stress σ_n on a spatial scale of the sheared layer. Its shear stress–slip function, τ(u), is τ(u) = μ_f(σ_n − $p_{\mathrm{o}}\left)\exp \right(-u/u_{\mathrm{c}}$) (Rice, 2006), which decreases exponentially with increasing u. The characteristic displacement is u_c = ρ_fC_vh∕μ_fΛ, where ρ_f, C_v, h, μ_f, and Λ are, respectively, the fluid density, heat capacity (in J ^∘C⁻¹ kg⁻¹), the thickness, frictional strength, and the undrained pressurization factor of the fault zone. The parameter Λ is (λ_f − λ_n)∕(β_f + β_n), where β_f is isothermal compressibility of the pore fluid, β_n is isothermal compressibility of the pore space, λ_f is isobaric volumetric thermal expansion coefficient for the pore fluid, and λ_n is isobaric volumetric thermal expansion coefficient for the pore space.

Based on the AUD model, Wang (2009, 2016, 2017a–c) took a simplified slip-weakening friction law (denoted by the TP law hereafter):

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle }F\left(u\right)=F_{\mathrm{o}}\exp \left(-u/u_{\mathrm{c}}\right).\end{array}$$

The value of F(u) at u = 0 is F_o, i.e., the static friction force. An example of the plot of F(u) versus u for five values of u_c, i.e., 0.1, 0.3, 0.5, 0.7, and 0.9 m when F_o = 1N m⁻², which are taken from Wang (2016), is displayed in Fig. 3. F(u) decreases with increasing u and its decreasing rate, γ, decreases with increasing u_c. The force drop is lower for larger u_c than for smaller u_c for the same final slip. When u ≪ u_c, $\exp (-u/u_{\mathrm{c}})$ ≈ 1 − u∕u_c, thus indicating that $u_{\mathrm{c}}^{-\mathrm{1}}$ is almost γ at small u. This TP law is used in this study.

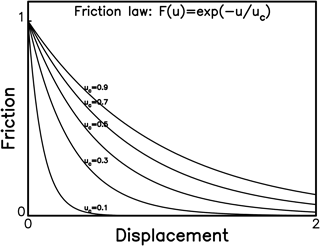
Figure 3 The plots of F(u) = $F_{\mathrm{o}}\exp (-u/u_{\mathrm{c}}$) versus u when u_c = 0.1, 0.3, 0.5, 0.7, and 0.9 m when F_o = 1N m⁻² (after Wang, 2016).

A detailed description about viscosity and the viscous force Φ(v) can be found in Wang (2016), and only a brief explanation is given below. Jeffreys (1942) first and then numerous authors (Byerlee, 1968; Turcotte and Schubert, 1982; Scholz, 1990; Rice et al., 2001; Wang, 2016) emphasized the viscous effect on faulting due to frictional melts. The viscosity coefficient, υ, of rocks is influenced by T (see Turcotte and Schubert, 1982; Wang, 2011). Spray (2005, and cited references therein) observed a decrease in υ with increasing T. He also stressed that frictional melts with low υ could produce a large volume of melting, thus reducing the effective normal stress. This behaves like fault lubricants during seismic slip.

The physical models of viscosity can be found in several articles (e.g., Cohen, 1979; Hudson, 1980). The stress–strain relationship is σ = Eε, where σ and E are, respectively, the stress and the elastic modulus for an elastic body; and σ = υ(dε∕dt), where υ is the viscosity coefficient for a viscous body. Two simple models with a viscous damper and an elastic spring are often used to describe the viscous materials. A viscous damper and an elastic spring are connected in series, leading to the Maxwell model, and in parallel, resulting in the Kelvin–Voigt model (or the Voigt model). According to Hudson (1980), Wang (2016) proposed that the latter is more suitable than the former for seismological problems and thus the Kelvin–Voigt model, whose constitution law is σ(t) = Eε(t) + υdε(t)∕dt, is taken here and displayed in Fig. 2. The viscous stress is υv.

In order to investigate the viscous effect in a dynamical system, Wang (2016) defined the damping coefficient, η, based on the phenomenon that an oscillating body damps in viscous fluids. According to Stokes' law, η = 6πRυ for a sphere of radius R in a viscous fluid of υ (see Kittel et al., 1968). Hence, the viscous force in Eq. (1) is represented by Φ = ηv. Note that the unit of η is N(m/s)⁻¹. Since υ decreases with increasing T, η decreases with increasing T. Hence, η can vary with time during faulting. This point has been studied by Wang (2017b) for the generation of nuclear phase before an earthquake ruptures. In this study, constant η is considered for each case.

Some authors (Knopoff et al., 1973; Cohen, 1979; Rice, 1993; Xu and Knopoff, 1994; Knopoff and Ni, 2001; Bizzarri, 2012a; Dragoni and Santini, 2015) considered that viscosity plays a role on causing seismic radiation to release strain energy during faulting.

3 Normalization of equation of motion

Putting Eq. (2) and Φ = ηv into Eq. (1) leads to

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }m{\mathrm{d}}^{\mathrm{2}}u/\mathrm{d}{t}^{\mathrm{2}}=-K\left(u-v_{\mathrm{p}}t\right)-F_{\mathrm{o}}\exp \left(-u/u_{\mathrm{c}}\right)-\mathit{\eta }v.\end{array}$$

Equation (3) is normalized for easy numerical computations based on the normalization parameters, which is dimensionless: D_o = F_o∕K, ω_o = $(K/m{)}^{\mathrm{1}/\mathrm{2}}$, τ = ω_ot, U = u∕D_o, and U_c = u_c∕D_o. The normalized velocity, acceleration, and driving velocity are V = dU∕dτ = $[F_{\mathrm{o}}/(mK{)}^{\mathrm{1}/\mathrm{2}}{]}^{-\mathrm{1}}$du∕dt, A = d²U∕dτ² = $(F_{\mathrm{o}}/m{)}^{-\mathrm{1}}$d²u∕dt², and V_p = v_p∕(D_oω_o), respectively. Ω = ω∕ω_o is defined as the dimensionless angular frequency, and thus the phase ωt becomes Ωτ. For the purpose of simplification, $\mathit{\eta }/(mK{)}^{\mathrm{1}/\mathrm{2}}$ is denoted by η below. Substituting all normalization parameters into Eq. (3) leads to

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle }{\mathrm{d}}^{\mathrm{2}}U/\mathrm{d}{\mathit{\tau }}^{\mathrm{2}}=-U-\mathit{\eta }\mathrm{d}U/\mathrm{d}\mathit{\tau }-\exp \left(-U/U_{\mathrm{c}}\right)+V_{\mathrm{p}}\mathit{\tau }.\end{array}$$

In order to numerically solve Eq. (4), we define two new parameters, i.e., y₁ = U and y₂ = dU∕dτ. Equation (4) can be rewritten as two first-order differential equations:

$$\begin{array}{}\text{(5a)}& {\displaystyle }& {\displaystyle }\mathrm{d}{y}_{\mathrm{1}}/\mathrm{d}\mathit{\tau }=y_{\mathrm{2}}\text{(5b)}& {\displaystyle }& {\displaystyle }\mathrm{d}{y}_{\mathrm{2}}/\mathrm{d}\mathit{\tau }=-y_{\mathrm{1}}-\mathit{\eta }{y}_{\mathrm{2}}-\exp \left(-y_{\mathrm{1}}/U_{\mathrm{c}}\right)+V_{\mathrm{p}}\mathit{\tau }.\end{array}$$

We can numerically solve Eq. (5) by using the fourth-order Runge–Kutta method (Press et al., 1986). In general, the values of D_o are several meters and ω_o are in the range of 0.1 Hz to few Hz (see Wang, 2016). This leads to that D_oω_o has an order of magnitude of 1 m s⁻¹. The value of V_p must be much smaller than 1 because of v_p ≈ 10⁻¹⁰ m s⁻¹. Since the value of V_p mainly influences the recurrence time, T_R, between two events and can only make a very small influence on the pattern of time variations in velocities and displacements of events. In order to study long-term earthquake recurrence, there must be numerous modeled events with clear and visualized time functions of displacements and velocities for an event in the computational time period. If V_p = 10⁻¹⁰ is considered, T_R is very long and thus τ_D is much shorter than T_R. This makes the time function of an event displayed in the long-term temporal variation in slip looks like just a step function for the displacements and an impulse for the velocities. Hence, in order to get fine visualization a larger value of V_p is necessary. The value of V_pτ is usually very small during an event and cannot influence the rupture because of a very tiny value of V_p. Numerical test shows that when V_p > 10⁻², the value of V_pτ is not small during an event and can influence the rupture. Hence, V_p = 10⁻² is taken in this study. The backward slip is not allowed in the simulations because of common behavior of forward earthquake ruptures.

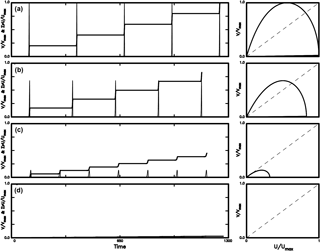
Figure 4 The time variations in V∕V_max (thin solid line) and cumulative slip ΣU∕U_max (solid line) and the phase portrait of V∕V_max versus U∕U_max (solid line) for four values of U_c: (a) for U_c = 0.2; (b) for U_c = 0.4; (c) for U_c = 0.8; and (d) for U_c = 1.0 when η = 0.0.

A phase portrait, which is a plot of a physical quantity, y, versus another, x, i.e., y = f(x), is commonly used to represent nonlinear behavior of a dynamical system (Thompson and Stewart, 1986). The intersection point between f(x) and the bisection line of y = x is defined as the fixed point, that is, f(x) = x. If f(x) is continuously differentiable in an open domain near a fixed point x_f and $\left|f^{\prime }\right(x_{\mathrm{f}}\left)\right|$ < 1, attraction can appear at the fixed point. Chaos can also be generated at some attractors. The details can be seen in Thompson and Stewart (1986). In this study, the phase portrait is the plot of V∕V_max versus U∕U_max.

4 Simulation results

Numerical simulations lead to the temporal variations in particle velocities and displacements as displayed in Fig. 1. The values of V_m and D, respectively, represent the peak value of velocity and final slip for each event. Since four cases related to our values of a particular model parameter, there are four values of V_m and D in a figure. In order to plot the temporal variations in both normalized displacements and velocities, the maximum values of V_m and D of the modeled events, i.e., V_max and U_max, respectively, are taken into account. The values of V_m and D usually appear in panel (a) of a figure. Simulation results are shown in Figs. 4–12. The temporal variations in V∕V_max (displayed by thin solid lines) and cumulative slip ΣU∕U_max (displayed by solid lines) are displayed in the left panels. The normalization scales to plot the temporal variations in slip and velocity are V_max for the velocities and the final value of ΣU∕U_max for the displacements in the computational time. Hence, the upper-bound scale is “1” for the two temporal variations. Hence, only the patterns of temporal variations of velocity and cumulative slip are concerned in these figures.

Simulation results displayed in these figures show that the maximum values of both V and U decrease from case (a) to (d) in each figure. Hence, the maximum velocity and maximum displacement, which are denoted by V_max and U_max, respectively, for case (a) can be taken as the scaled factor to normalize the waveforms from case (a) to (d). This makes it easy to compare the waveforms of the four cases in each figure.

The cases excluding the viscous effect, i.e., η = 0, are first simulated and results are shown in Fig. 4 for four values of U_c: (a) for U_c = 0.2; (b) for U_c = 0.4; (c) for U_c = 0.8; and (d) for U_c = 1.0. The results of the cases including viscosity, i.e., η ≠ 0, are displayed in Figs. 5–7 for four values of η: (a) for η = 0.20; (b) for η = 0.40; (c) for η = 0.6; and (d) for η = 0.8. The values of U_c are 0.2 in Fig. 5, 0.5 in Fig. 6, and 0.8 in Fig. 7.

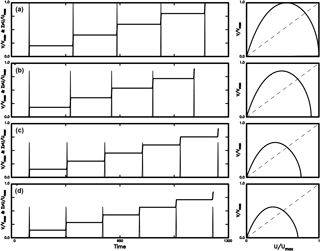
Figure 5 The time variations in V∕V_max (thin solid line) and cumulative slip ΣU∕U_max (solid line) and the phase portrait of V∕V_max versus U∕U_max (solid line) for four values of η: (a) for η = 0.2; (b) for η = 0.4; (c) for η = 0.8; and (d) for η = 1.0 when U_c = 0.2.

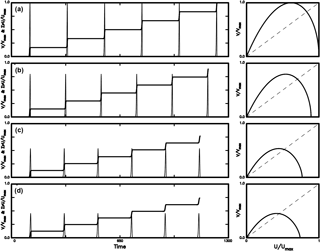
Figure 6 The time variations in V∕V_max (thin solid line) and cumulative slip ΣU∕U_max (solid line) and the phase portrait of V∕V_max versus U∕U_max (solid line) for four values of η: (a) for η = 0.2; (b) for η = 0.4; (c) for η = 0.8; and (d) for η = 1.0 when U_c = 0.5.

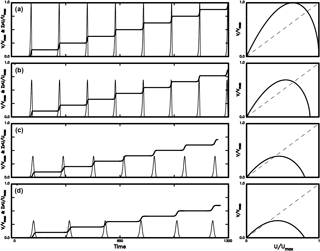
Figure 7 The time variations in V∕V_max (thin solid line) and cumulative slip ΣU∕U_max (solid line) and the phase portrait of V∕V_max versus U∕U_max (solid line) for four values of η: (a) for η = 0.2; (b) for η = 0.4; (c) for η = 0.8; and (d) for η = 1.0 when U_c = 0.8.

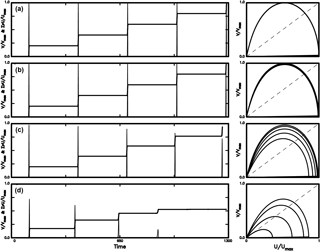
Figure 8 The time variations in V∕V_max (thin solid line) and cumulative slip ΣU∕U_max (solid line) and the phase portrait of V∕V_max versus U∕U_max (solid line) for four values of C: (a) for C = 0.0001; (b) for C = 0.001; (c) for C = 0.01; and (d) for C = 0.05 when U_co = 0.1 and η = 0.

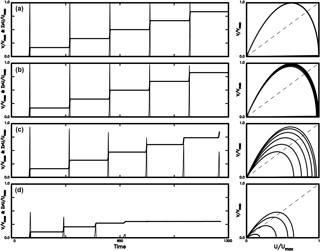
Figure 9 The time variations in V∕V_max (thin solid line) and cumulative slip ΣU∕U_max (solid line) and the phase portrait of V∕V_max versus U∕U_max (solid line) for four values of C: (a) for C = 0.0001; (b) for C = 0.001; (c) for C = 0.01; and (d) for C = 0.05 when U_co = 0.5 and η = 0.

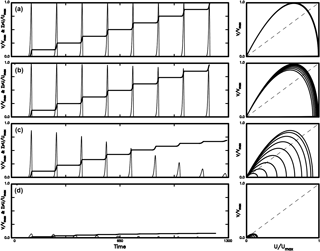
Figure 10 The time variations in V∕V_max (thin solid line) and cumulative slip ΣU∕U_max (solid line) and the phase portrait of V∕V_max versus U∕U_max (solid line) for four values of C: (a) for C = 0.0001; (b) for C = 0.001; (c) for C = 0.01; and (d) for C = 0.05 when U_co = 0.9 and η = 0.

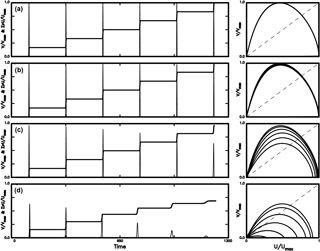
Figure 11 The time variations in V∕V_max (thin solid line) and cumulative slip ΣU∕U_max (solid line) and the phase portrait of V∕V_max versus U∕U_max (solid line) for four values of C: (a) for C = 0.0001; (b) for C = 0.0010; (c) for C = 0.0100; and (d) for C = 0.0380 when U_co = 0.1 and η = 1.

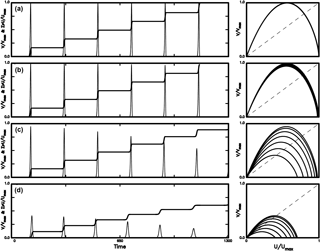
Figure 12 The time variations in V∕V_max (thin solid line) and cumulative slip ΣU∕U_max (solid line) and the phase portrait of V∕V_max versus U∕U_max (solid line) for four values of C: (a) for C = 0.0001; (b) for C = 0.0010; (c) for C = 0.0100; and (d) for C = 0.0136 when U_co = 0.5 and η = 1.

The left panels in Fig. 4 with η = 0 show that the peak velocity of an event, V_m, and final slip, D, with the respective maximum values in case (a) as mentioned above, for all simulated events decrease with increasing U_c. From Fig. 3, the force drop, ΔF, decreases with increasing U_c for a certain final slip, thus indicating that larger ΔF yields higher V_m and larger D. This interprets the negative dependence of V_m and D on U_c. When the viscous effect is absent, i.e., η = 0, the value of τ_D increases with U_c, while T_R decreases with increasing U_c. When U_c = 1, V_m and D are both very small and the system behaves like creeping of a fault. In the right panels, there are two fixed points for each case: one is called the non-zero fixed point at larger V and larger U and the other the zero fixed point at V = 0 and U = 0. The slope at a fixed point is defined to be d$(V/V_{\max })/$d(U∕U_max) = (U_max∕V_max)(dV∕dU). The absolute values of slope at the two fixed points decrease with increasing U_c, thus suggesting that the fixed point is not an attractor for small U_c and could be an attractor for larger U_c. The phase portrait for U_c = 1 is very tiny, because the final slip for U_c = 1.0 is much smaller than those for U_c = 0.2, 0.4, and 0.8. Hence, U_c = 1 will not be taken into account in the following simulations.

The left panels in Figs. 5–7 show that V_m and D decrease when either U_c or η increases, while τ_D increases with η and U_c. Meanwhile, T_R increases when either η increases or U_c decreases. The right panel shows that the phase portraits coincide for all simulated events for a certain η. The absolute values of slope at the two fixed points decrease when either U_c or η increases. This suggests that the fixed point is not an attractor for small U_c and low η, and can be an attractor for large U_c and high η. Like Fig. 4, the final slip decreases with increasing U_c.

In Figs. 5–7 we can see that the temporal variation in cumulative slip can be described by the perfectly periodic model as mentioned above. Hence, when U_c and η do not change with time, the rate of cumulative slip retains a constant in the computational time period. This is similar to the simulation results with the periodical earthquake occurrences obtained by some authors (e.g., Rice and Tse, 1986; Ryabov and Ito, 2001; Erickson et al., 2008; Mitsui and Hirahara, 2009) based on the one-body model with rate- and state-dependent friction or velocity-weakening friction. However, the present result is inconsistent with the simulation results, from which either the time-predictable model or the slip-predictable model cannot interpret the temporal variation in cumulative slip, based on the same model obtained by others (e.g., He et al., 2003; Bazzarri, 2012b; Bizzarri and Crupi, 2014; Kostić et al., 2013a, b; Franović et al., 2016). The differences between the two groups of researchers might be due to distinct additional constrains in respective studies. Although the detailed discussion of such differences is important and significant, it is out of the scope of this study and ignored here.

The phase portraits in Figs. 5–7 exhibit two kinds of fixed points as mentioned above. The absolute values of slope at the non-zero fixed point are higher than 1 and decreases with increasing η. This means that larger η is easier to generate an attractor than small η. However, the reducing rate of absolute value of slope decreases with increasing U_c. The absolute values of slope of the zero fixed point are higher than 1 and decrease with increasing η. This suggests that the zero fixed points can be an attractor. This behavior becomes weaker when U_c increases.

Figures 4–7 show that when U_c and η are constants during the computational time periods, the general patterns of temporal variations in cumulated slip do not change. Some of the previous studies (e.g., Bizzarri, 2012a, b; Franović et al., 2016) suggest that the patterns of temporal variations in cumulated slip can change with time. The changes of U_c and η with time should play the main roles. From u_c = ρ_fC_Vh∕μ_fΛ of the TP model (see Rice, 2006), the width of the slipping zone, h, where the maximum deformation is concentrated (Bizzarri, 2009), is a significant parameter in this study. From geological surveys, Rathbun and Marone (2010) observed that h is not spatially uniform even within a single fault. Hull (1988) and Marrett and Allmendinger (1990) found that the wear processes occurring during faulting could widen h, and thus h could vary with time. According to the results gained by several authors (e.g., Power et al., 1988; Robertson, 1983; Bizzarri, 2010), Bizzarri (2012b) proposed a linear dependence of h on the cumulated slip, S(t) = ∑D(t), i.e., h(t) = CS(t), where C is a dimensionless increasing rate of h with S and is considered to be a constant in each case. Based on h(t) = CS(t), the more mature the fault is, the thicker its slip zone is. Since u_c is proportional to h and U_c = u_c∕D_o, U_c is related to C. Here, we assume that U_c varies with cumulative slip in the following way: U_c = U_co + C∑U(t), where U_co is the initial value of U_c. Simulation results for four values of C are shown in Figs. 8–12: (a) for C = 0.0001, (b) for C = 0.001, (c) for C = 0.01, and (d) for C = 0.05 when η = 0 in Figs. 8–10; (a) for C = 0.0001, (b) for C = 0.001, (c) for C = 0.01, and (d) for C = 0.038 when η = 1 in Fig. 11; and (a) for C = 0.0001, (b) for C = 0.001, (c) for C = 0.01, and (d) for C = 0.0136 when η = 1 in Fig. 12. The initial values of U_c are 0.1 for Fig. 8, 0.5 for Fig. 9, 0.9 for Fig. 10, 0.1 for Fig. 11, and 0.5 for Fig. 12. Note that the value U_c varies with time due to time-varying h.

The left panels of Figs. 8–12 show that V_m, D, τ_D, and T_R are all similar when C ≤ 0.001. However, in general V_m and D decrease with increasing C, T_R slightly decreases with increasing C, and τ_D slightly increases with C. A decrease in D is particularly remarkable when C ≥ 0.01. When h is wider than a critical value with C = 0.05 for η = 0, normal earthquakes cannot occur and only creeping may happen. The critical value of h decreases when the viscous effect is present with η = 1 in this study. This decrease is also influenced by U_c: C = 0.038 when the initial value of U_c is 0.1 and C = 0.0136 when the initial value of U_c is 0.5. Obviously, T_R decreases with increasing C, thus leading to a decrease in T_R with increasing h. This is similar to the result obtained by Bizzarri (2010, 2012b). However, the viscous effect was not included in his studies.

The right panels of Figs. 8–12 show that the phase portraits for C = 0.001 are slightly different from those for C = 0.0001 even though the patterns of their variations in V and U are similar, while the phase portraits for C > 0.001 are different from those for C ≤ 0.001. An increase in h due to an increase in C with cumulative slip enlarges U_c. This can be explained from Fig. 3, which shows that larger U_c yields a lower ΔF than smaller U_c for the same final slip. Hence, an increase in U_c produces a decrease in ΔF, thus resulting in low V_m and small D. In addition, an increase in U_c makes $\exp (-U/U_{\mathrm{c}})$ approach unity, especially for small U, thus reducing the nonlinear effect caused by TP friction.

Unlike Figs. 4–7, the size of phase portraits in the right panels of Figs. 8–12 decreases with increasing C. This reflects a decrease in both T_R and D of events with increasing C as mentioned previously. The absolute values of slope at the non-zero fixed point are higher than 1 and only slightly decrease with time when C < 0.01, while the values remarkably decrease with time when C ≥ 0.01. The absolute values of slope at the zero fixed point are higher than 1 and only slightly decrease with time when C < 0.01, while those decrease with time when C ≥ 0.01. Results suggest that the non-zero fixed points for all cases in the study are not an attractor, and those at the zero fixed points can evolve to an attractor with time when C ≥ 0.01. The phenomenon is particularly remarkable for C = 0.05 in Figs. 8–10, C = 0.0380 in Fig. 11, and C = 0.0136 in Fig. 12, and the evolution is faster for large U_c than for small U_c.

5 Discussion

The simulation results as mentioned previously demonstrate that when U_c and η are constants during the computational time periods, the general patterns of temporal variations in cumulated slip cannot change. In order to investigate the effect of time-varying η and U_c on the patterns of temporal variations in cumulated slip, we must consider changes of U_c and η with time. The viscosity coefficient can actually vary immediately before and after the occurrence of an earthquake (see Spray, 1883, 2005; Wang, 2017b, c). However, a lack of long-term variation in η does not allow us to explore its possible effect on the change of general patterns of temporal variations in cumulated slip. Here, only the possible effect due to time-varying U_c.

As mentioned above, the equality U_c = u_c∕D_o leads to U_c = ρ_fC_Vh∕μ_fD_oΛ. Obviously, U_c is controlled by six factors, i.e., ρ_f, C_V, h, μ_f, D_o, and Λ. Since the tectonics of a region is generally stable over a long time, the value of D_o = F_o∕K could not change too much and thus would not influence U_c. The Debye law (cf. Reif, 1965) gives C_v ∼ (T + 273.16)³, where 273.16 is the value to convert temperature from Celsius to kelvin, at low T and C_v ≈ constant at high T. The threshold temperature, from which C_v begins to approach a constant, is 200–300 ^∘K. In this study, C_v is almost a constant because of T > 250 ^∘C = 523.16 ^∘K, which is the average ambient temperature of fault zone with depths ranging from 0 to 20 km. Hence, C_v is almost constant during a long time and thus cannot influence U_c.

The frictional strength, μ_f, is influenced by several factors including humidity, temperature, sliding velocity, strain rate, normal stress, and thermally activated rheology (Marone, 1998; Rice, 2006), and thus can change with time (Sibson, 1992; Rice, 2006). Hirose and Bystricky (2007) observed that serpentine dehydration and subsequent fluid pressurization due to coseismic frictional heating may reduce μ_f and thus promote further weakening in a fault zone. The pore fluid pressure exists in wet rocks, yet not in dry rocks. Clearly, the time variation in μ_f can affects the earthquake recurrences. However, a lack of long-term observations of μ_f during a seismic cycle makes the study of its effect on earthquake recurrence be impossible.

The fluid density ρ_f and the porosity n depend on T and p. Although there are numerous studies on such dependence (Lachenbruch, 1980; Bizzarri, 2012b; and cited references therein), observed data and theoretical analyses about the values of ρ_f and n during a seismic cycle are rare.

The porosity is associated with the permeability, κ. Bizzarri (2012c) pointed out that the time-varying permeability, κ(t), and porosity of a fault zone (cf. Mitsui and Cocco, 2010; Bizzarri, 2012b) can reduce T_R. One of the Kozeny–Carman relations (Costa, 2006, and references cited therein) is κ(t) = κ_Cφ²(t)d³(t)∕[1 − φ(t)]², where κ_C is a dimensionless constant depending on the material in consideration; φ is V_voids∕V_tot, where V_voids and V_tot are, respectively, the pore volume and the total volume of the porous materials; and d is the (average) diameter of the grains, ranging between 4 × 10⁻⁵ and 1 × 10⁻⁴ m (Niemeijer et al., 2010). Usually, κ, φ, and d can vary in the fault zone (Segall and Rice, 1995). After faulting κ and φ would change and d becomes smaller because of refining of the grains. According to this relation, Bizzarri (2012b) found that κ(t) could significantly reduce T_R in comparison with the base model with constant κ. The reason is explained below. An increase in permeability can result in an increase in pore pressure, p_f. This can reduce the frictional resistance from τ = μ(σ_n − p_f) and thus could trigger earthquakes earlier. Hence, the time-varying permeability can change T_R. Nevertheless, we cannot investigate its influence on earthquake recurrence here because there is a lack of a long-term observation of hydraulic parameters during a seismic cycle.

It is significant to explore the factors that can yield a non-perfectly periodic seismic cycle. The width of the slipping zone, h, can be a candidate as pointed out by some authors (e.g., Bizzarri, 2009; Rathbun and Marone, 2010). Since the displacement along a fault is controlled by the fault rheology, h should depend on the rheology on the sliding interface. The wear processes occurring during faulting could widen h (Hull, 1988; Marrett and Allmendinger, 1990). According to the results gained by several authors (e.g., Power et al., 1988; Robertson, 1983; Bizzarri, 2010), simulation results for various values of C and the results are shown in Figs. 8–10 with η = 0 and in Figs. 11 and 12 with η = 1. Results show that when C > 0.0001, the wear process affects the recurrence of slip and the effect increases with C and when C is larger than an upper-bound value, larger-sized events cannot occur and the earthquake recurrence does not exist. Both T_R and D decrease when the fault becomes more mature due to a thicker slip zone. Meanwhile, the viscous effect can also play a secondary role on the earthquake recurrence because it makes upper-bound value become smaller. Although either the time- or slip-predictable model can describe the temporal variations of cumulative slip of events occurring in the earlier time period, they cannot interpret those of events in the later parts. This might suggest that it is more difficult to produce large earthquakes along a fault when it becomes more mature, especially for the cases with viscosity. This implicates that seismic hazard is higher for a young fault than a mature one. Hence, it is significant and important to identify the width of slip zone of an earthquake fault for seismic hazard estimates.

6 Conclusions

To study the frictional and viscous effects on earthquake recurrence, numerical simulations of the temporal variations in cumulative slip have been conducted based on the normalized equation of a one-body model in the presence of thermal-pressurized slip-weakening friction and viscosity. The wear process, which is included in the friction law, is also taken into account. The model parameters of friction and viscosity are represented, respectively, by U_c and η, where U_c = u_c∕D_o is the normalized characteristic distance and η is the normalized damping coefficient. Numerical simulation of the time variations in V∕V_max and cumulative slip ΣU∕U_max as well as the phase portrait of V∕V_max versus U∕U_max are made for various values of U_c and η.

Results show that both friction and viscosity remarkably affect earthquake recurrences. The recurrence time, T_R, increase when η increases or U_c decreases. The final slip, D, and the duration time of slip, τ_D, of an event slightly decrease when η or τ_D increases and slightly increases with U_c. Considering the effect due to wear process, the thickness of slip zone, h, that depends on the cumulated slip, S(t) = ∑D(t), i.e., h(t) = CS(t) (C is a dimensionless constant), is an important factor in influencing earthquake recurrences. U_c increases with ∑U with an increasing rate of C. When C > 0.0001, the wear process influences the recurrence of slip and the effect increases with C. When C is larger than an upper-bound value, larger-sized events cannot occur and the earthquake recurrence does not exist. If the slip zone becomes thicker, the fault is more mature. This makes T_R and D become shorter. This might suggest that it is more difficult to produce large earthquakes along a fault when it becomes more mature. This phenomenon becomes remarkable when the viscous effect exists because the upper-bound value becomes smaller. The temporal variation in slip cannot be interpreted by the time-predictable or slip-predictable model when the fault is affected by wear process with large C. In addition, the size of phase portrait of V∕V_max versus U∕U_max decreases with increasing C. This again reflects decreases in both T_R and D of events with increasing C as inferred from the temporal variations in cumulative slip.