Prediction of the volume of shallow landslides due to rainfall using data-driven models

Landslides due to rainfall are among the most destructive natural disasters and cause property damage, huge financial losses, and human deaths in different parts of the world. To plan for mitigation and resilience and to understand the relationship between the volume of soil materials debris and their associated predictors, prediction of the volume of rainfall-induced landslides is essential. The objectives of this research are to construct a model using advanced data-driven algorithms (i.e., ordinary least squares or linear regression (OLS), random forest (RF), support vector machine (SVM), extreme gradient boosting (EGB), generalized linear model (GLM), decision tree (DT), deep neural network (DNN), k-nearest-neighbor (KNN), and ridge regression (RR) algorithms) for the prediction of the volume of landslides due to rainfall, considering geological, geomorphological, and environmental conditions. Models were trained and tested on a South Korean landslide dataset, with the EGB predictions yielding the highest coefficient of determination (R² = 0.8841) and the lowest mean absolute error (MAE = 146.6120 m³), followed by RF predictions (R² = 0.8435, MAE = 330.4876 m³), on the holdout set. The DNN, EGB, and RF models exhibited R² > 0.8 on both the training and the test sets. The differences in the coefficient of determination R² on the training and holdout set were 1.75 %, 7.72 %, and 12.17 % for RF, EGB, and DNN, respectively, signifying that these models could yield reliable volume estimates in adjacent areas with similar geomorphological and environmental settings. The volume of landslides was strongly influenced by slope length, maximum hourly rainfall, slope angle, aspect, and altitude. The anticipated volume of landslides can be important for land use allocation and efficient landslide risk management.

1 Introduction

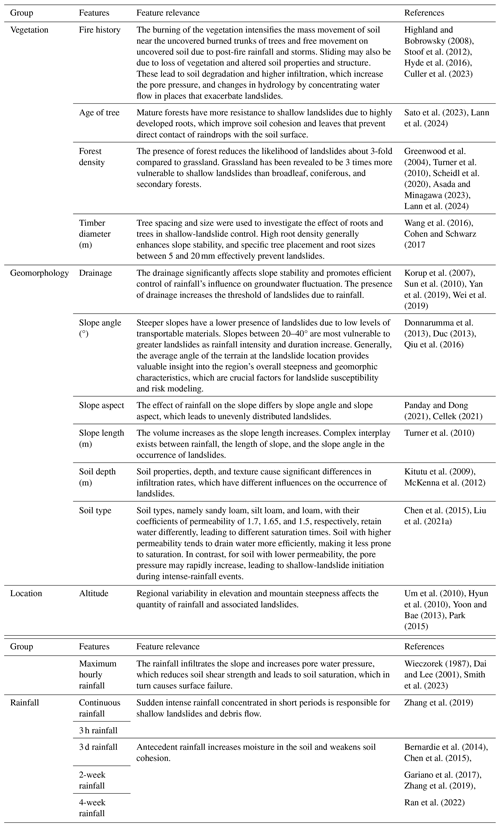
Landslides due to rainfall are phenomena that dislocate a mass of soil from its natural position, which then slides downward along a slope due to gravity forces. Intense or long-duration rainfall infiltrates the soil and increases the pore pressure, resulting in soil saturation that leads to slope failure. The saturated soil becomes weak and loses cohesion, and the slope fails when rainfall crosses a certain threshold (Bernardie et al., 2014; Martinović et al., 2018; Lee et al., 2021). The heavy rainfall saturates a slope and triggers a landslide due to the reduction in the soil's shear strength and the increase in pore water pressure (Tsai and Chen, 2010; Lacerda et al., 2014; Chatra et al., 2019; Chen et al., 2021; Luino et al., 2022). For example, steep slopes with loose soils and even moderate rainfall can lead to the displacement of an enormous quantity of soil mass. On the contrary, in slopes with more stable, cohesive soils, the surface failure might be smaller (Tsai and Chen, 2010). The rainfall quantity and duration influence the volume of the landslides; the higher the intensity and the longer the duration of rainfall, the larger the resulting surface failure (Chang and Chiang, 2009; Bernardie et al., 2014; Chen et al., 2017). The landslide occurrences can also be influenced by human activities that weaken the slope, such as excavation at the slope toe and loading caused by construction and land use such as agriculture or mining (Rosi et al., 2016). Rapid-urbanization activities in mountainous regions affect topography through hill cutting, deforestation, and water drainage (Rahman et al., 2017); these activities disturb the slope structure and change the water flow, which exacerbates the effect of landslides in regions where human engineering activities are mostly located (Holcombe et al., 2016; Chen et al., 2019). Therefore, to mitigate landslide-induced risks in runout regions, estimation of the volume of landslides due to rainfall (VLDR) plays a crucial role.

The quantification of VLDR is essential for effective risk management (Tacconi Stefanelli et al., 2020), emergency response, engineering design (Cheung, 2021), economic assessment, and environmental protection (Alcántara-Ayala and Sassa, 2023). With estimates of VLDR, morphologists can update hazard maps (Van Westen, 2000) to reflect the scale of potential mass movement in various regions and obtain regions with similar likelihoods of landslides of similar soil mass, highlighting risk zone levels, i.e., low, moderate, and high. These classifications help engineers to apply appropriate slope stabilization techniques depending on the level of risk (Dahal and Dahal, 2017). Additionally, enhancing the precision of VLDR estimations and improving predictive capabilities are essential for understanding and monitoring landscape evolution. Montgomery et al. (2009) emphasized that the volume of landslides is a key factor in determining the extent of downstream damage, particularly for large debris flows or rock avalanches, which can drastically alter the landscape and affect surrounding ecosystems and infrastructure. Similarly, Korup (2004) further explored the long-term geomorphological effects of large-volume landslides, highlighting their importance in reshaping mountainous terrains and influencing sediment transport, which is critical for understanding both immediate and future landscape changes. However, the existing landslide susceptibility models, which are mostly used for the identification of regions susceptible to landslides (i.e., landslide zonation) (Kim et al., 2014; Gutierrez-Martin, 2020; Chen et al., 2021; Li et al., 2022), are essential in emergency management because they provide a general overview of zones with a higher probability of landslide occurrence, but they do not emphasize the determination of the approximate value of the volume of failing mass in relation to excessive-rainfall events.

Numerous researchers have used landslide inventories, remote sensing data, and numerical techniques to establish the relationship between landslide geometry and influencing factors to determine landslide volumes quantitatively. For example, Saito et al. (2014) studied the relationship between rainfall-triggered landslides to test whether the volume of landslides across Japan that occurred between 2001 and 2011 could be directly predicted from rainfall metrics. The findings revealed that larger landslides occurred when rainfall exceeded certain thresholds, but there were significant discrepancies between the peaks of rainfall metrics and maximum landslide volumes, and total rainfall was found to be a suitable predictor of landslides. Dai and Lee (2001) established the frequency–volume relation for landslides in Hong Kong SAR and noticed that the relation for shallow landslides above 4 m³ followed the power law. The 12 h rolling rainfall contributed most to the prediction of the volume of landslides. Jaboyedoff et al. (2012) contributed by demonstrating the value of remote sensing technologies such as light detection and ranging (lidar) in conjunction with field data to improve the accuracy of volume estimates and capture the geomorphological changes associated with landslides. Ju et al. (2023) constructed an area–volume power law model for the estimation of the volume of landslides using high-resolution lidar data collected between 2010 and 2020 in Hong Kong SAR. Their aim was to accurately estimate the volume of small-scale landslides. Their reliance on localized datasets limits the model's applicability in regions with different geological settings, and the model does not consider all variabilities in landslide characteristics. Razakova et al. (2020) calculated landslide volume using remote sensing data to assess the efficiency of aerial photographs in environmental impact assessment and ground-based measurement. The study did not consider the effect of vegetation and topography and only focused on a single landslide case, which may be a source of bias due to differences in soil composition and environmental factors. Hovius et al. (1997) analyzed multiple sets of aerial photos and frequency–magnitude relations for landslides in Aotearoa / New Zealand. Their findings precisely determined that the landslide frequency–magnitude relationship followed a power law and their infrequent large magnitude contributed to landscape change. The study highlighted the importance of soil composition for landslide size, but the reliance on aerial photos, which may be inaccurate in dense forest areas, and the omission of climatic factors limit the generality of the findings. Guzzetti et al. (2008) applied statistical methods to regional landslide inventories and antecedent rainfall data ranging between 10 min and 35 d. Their findings revealed that the slope angle and soil type significantly influence landslide volume estimates and that the rainfall intensity is more important than duration. Chatra et al. (2019) applied numerical methods to study the effect of rainfall duration and intensity on the generation of pore pressure in the soil; their findings revealed higher instability in loose soil compared to medium-compacted soil slopes. Huang et al. (2020) introduced a hybrid machine learning model combining support vector regression (SVR) with a genetic algorithm to estimate debris-flow volumes. The model was tested on real-world case studies, showing improved accuracy in volume predictions compared to traditional methods. However, it was noticed that the study relied on a limited dataset, which may reduce the model's generalizability to other regions of different geomorphology and environmental settings. Shirzadi et al. (2017) compared the effectiveness of statistical and machine learning models in simulating landslide volume–areal relations, demonstrating that machine learning techniques outperform traditional statistical methods in terms of accuracy. The study did not consider the climatic and geomorphic factors such as rainfall, vegetation, or soil type that trigger and influence factors in landslide occurrence. It was noted that existing models only treated the interaction of soil and rainfall without considering environmental factors, human activity, and the non-linear behavior of the triggering and influencing factors.

In the present study, the volume of landslides due to rainfall is predicted using ordinary least-squares or linear regression (OLS), random forest (RF), support vector machine (SVM), extreme gradient boosting (EGB), generalized linear model (GLM), decision tree (DT), deep neural network (DNN), k-nearest-neighbor (KNN), and ridge regression (RR) algorithms, considering the details of triggering factors (i.e., rainfall) and predisposing factors (i.e., geomorphological, soil, and environmental). Here, we aim to construct a data-driven algorithm that combines input parameters for physically based and empirical models and incorporates more complex non-linear features of input variables to predict the occurrence of associated events more accurately. The main assumption behind the data-driven algorithm is that the considered feature input of the model produces a similar volume of landslides due to rainfall and follows the same pattern in a particular region with the same features under the same quantity of rainfall. Here, we examine different machine learning (ML) algorithms and compare their performance using the coefficient of determination (R²), mean square error (MAE), root mean square error (RMSE), mean absolute percentage error (MAPE), and symmetric mean absolute percentage error (SMAPE) of the predicted volume of landslides. The focus is to optimize the predictions of the volume of landslides due to rainfall, taking into account triggering and influencing factors with higher accuracy.

2 Data and study region

2.1 Study region

The region for testing the model is South Korea, characterized by mountainous (63 % of total land) relief, especially in the eastern part of the country (Lee et al., 2022). South Korea is located on the southern part of the Korean Peninsula, bordered by the Yellow Sea to the west and the East Sea (Sea of Japan) to the east. According to the Korea Meteorological Administration (https://www.kma.go.kr/, last access: 25 January 2025), the country has a temperate climate characterized by four distinct seasons: hot and humid summers, cold winters, and springs and falls with moderate temperatures. The annual rainfall varies between 1000–1400 and 1000–1800 mm for the central region and southern region, respectively (Jung et al., 2017; Alcantara and Ahn, 2020). During the summer, heavy rainfall from June to September leads to significant surface runoff, increases landslide risk, and causes approximately 95 % of all landslides each year (Lee et al., 2020; Park and Lee, 2021). In addition, the landslides may be aggravated by typhoons, which mostly occur in August and September, and it is anticipated that their frequency will increase due to climate change (Kim and Park, 2021). The rainfall trend analysis from 1971 to 2100 predicted an increase in rainfall of 271.23 mm, which indicates the growing risk of landslides associated with climate change (Lee, 2016). Temperature variations are influenced by South Korea's geographical location; the average summer temperatures vary between 25 and 30 °C, while winter temperatures can drop to −10 °C in some parts of the country (https://web.kma.go.kr/, last access: 25 January 2025). Geologically, South Korea is mainly composed of granitic and metamorphic rocks, such as gneiss, schist, and granite, which influence the stability of the landscape (Jung et al., 2024). The geomorphology is characterized by rugged mountains, river valleys, and coastal plains, with the Taebaek Mountains running along the eastern edge (Kim et al., 2020). The influence of rainfall, environmental, geomorphological, and geological factors increases the vulnerability to landslides across the country, especially in the northeastern mountainous region, as depicted in Fig. 1. The predominant soil types in South Korea include clay, sandy, and loamy soils, each with different characteristics that affect water infiltration, retention, and erosion (Kang et al., 2022; Lee et al., 2023). Clay soils, being more stable, can become highly saturated, increasing landslide risk during heavy rains. On the other hand, sandy soils are loose and more prone to shallow landslides during light rainfall. Regions with steep topography and poorly consolidated soil (loose) are mostly at risk, especially after prolonged rainfall (Kim et al., 2015).

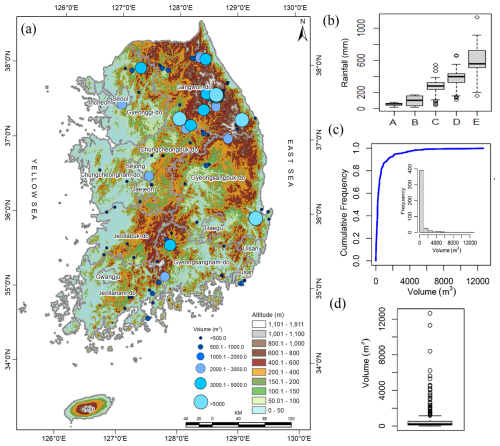
Figure 1 (a) Spatial distribution of landslides in South Korea; (b) temporal variation in rainfall – A, maximum hourly rainfall; B, 4-week rainfall; C, 3 h rainfall; D, 3 d rainfall; and E, 2-week rainfall; (c) cumulative frequency distribution of the volume of landslides; and (d) box plot of the volume of landslides (The elevation data presented in Fig. 1a are sourced from the SRTM DEM, downloaded from https://earthexplorer.usgs.gov/ (last access: 25 January 2025)).

The combination of heavy summer rainfall, geological composition, and geomorphological factors makes South Korea particularly vulnerable to shallow landslides. Thus, continuous monitoring and research are vital to understanding the complex interactions between climate, geology, soil types, and landslide occurrences in this region. Understanding the collective effects of meteorology, environment, geological stability, and geomorphological features is crucial for developing effective disaster management strategies and enhancing public safety in landslide-prone areas. As climate change continues to impact rainfall patterns, South Korea faces ongoing challenges in mitigating landslide risks and protecting vulnerable communities.

2.2 Data

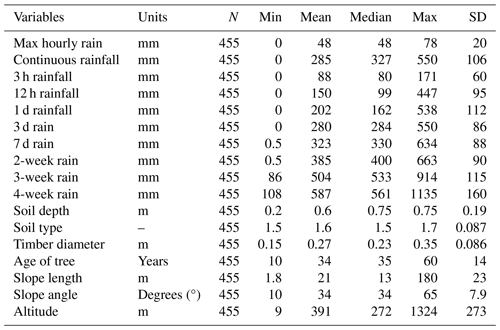
The landslide inventory dataset contains 455 landslide records from 2011 to 2012, collected from different locations in South Korea through field surveys, and vegetation and forest fire features were obtained from the Korea Forest Service database. The combined dataset tabulates information on landslide geometry, such as runout length, width, and depth and volume of the affected area, along with geomorphological composition, vegetation, and antecedent rainfall prior to landslide events. Details regarding landslide predisposing and triggering factors are summarized in Table 1.

The majority of landslides in this region were shallow, translational slope failures (Kim et al., 2021). The landslides that occurred had a volume varying between 1.5 and 12 663 m³ and predominantly occurred in the northeastern and southeastern regions (Fig. 1a, c–d). The landslides exhibited a hollowed morphology and a rightward skew in the distribution of their volumes, with 2570.7 m³ as the 95th quantile, 12 663 m³ as the largest volume, and 276 986.62 m³ as the aggregate mass of landslide due to rainfall. The estimation of the volume of removed material by landslides is important as it helps to assess the estimated damage that can be caused at the toe of the failed slope, such as blocking transportation networks, burying crops or farmland, and damaging the built environment near landslide risk areas, and it also helps in post-disaster recovery planning (Evans et al., 2006; Rotaru et al., 2007; Intrieri et al., 2019).

Table 1 Landslide influencing and triggering factors.

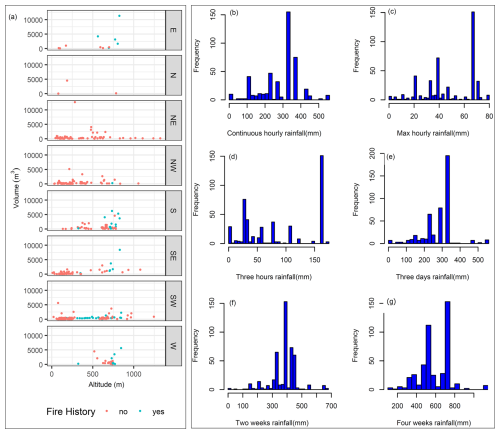
Figure 2 (a) Scatterplot showing the variation in landslide volumes with respect to slope aspect, fire history, and altitude and (b–g) histograms of rainfall distribution.

Location parameters such as altitude, latitude, and longitude are essential elements that determine the microclimate of a given region, influencing rainfall patterns (Hyun et al., 2010; Yoon and Bae, 2013; Park, 2015). The northeastern region is characterized by high-elevation terrain, including the Taebaek and Sobaek ranges, which experience dry air and orographic precipitation (Yun et al., 2009). The windward mountain versants receive a substantial amount of rainfall, which can increase the likelihood of landslides (Jin et al., 2022). This variation in rainfall with respect to direction highlights the importance of including slope aspect variables in landslide studies (Kunz and Kottmeier, 2006). Figure 2a depicts the relationship between the volume of landslides and slope aspect, altitude, and fire history and shows that larger volumes were localized in regions that faced forest fire and with altitudes between 500 and 1000 m. Additionally, topographical features such as slope length and slope angle affect the size of the landslide (Panday and Dong, 2021) and slope failure due to over-saturation from groundwater and rainfall infiltration, which destabilize the slope (Kafle et al., 2022). Furthermore, the slope length, slope angle, and slope aspect play an important role in the determination of the volume of geological material uprooted by landslides (Zaruba and Mencl, 2014; Khan et al., 2021). The slope stability depends on soil composition properties, including soil permeability indices that affect water infiltration and the saturation level (Chen et al., 2015). In the study regions, three main soil types, namely sandy loam, loam, and silt loam, were observed, and their coefficient of permeability was 1.7, 1.65, and 1.5, respectively (Lee et al., 2013). To reduce infiltration, the drainage network channels rainwater, drains the soil, and reduces saturation, which minimizes the likelihood of landslide occurrence due to groundwater discharge and surface runoff (Hovius et al., 1997; Wei et al., 2019). The vegetation protects the topsoil from the direct impact of raindrops hitting the ground, which causes erosion due to the force of gravity and reduces infiltration (Omwega, 1989; Keefer, 2000). The absence of vegetation allows rainwater to cause fine topsoil to seep away, in turn causing shallow landslides (Gonzalez-Ollauri and Mickovski, 2017). On the contrary, vegetation improves soil cohesion and prevents potential shallow landslides due to soil–root interaction (Gong et al., 2021; Phillips et al., 2021). The density of vegetation (forest) and leafage type (broadleaf, pine, or a mixture) directly affect the quantity of raindrops intercepted and prevented from directly hitting the soil, which emphasizes the contributions of vegetation in the mitigation of landslides. Further, the occurrence of forest fires can contribute to the occurrence of landslides due to the burning of vegetation covering the area, changing soil properties and increasing soil pH (Lee et al., 2013).

Table 2 Summary statistics for continuous variables.

Rainfall, a triggering factor of landslides, is the immediate cause of slope instability and failure due to infiltration and leads to saturation resulting from increased pore water pressure that reduces soil shear strength (Yune et al., 2010; Khan et al., 2012; Kim et al., 2021; Lee et al., 2021). The antecedent rainfall increases the moisture in the soil, which accelerates the soil saturation; the cumulative effect is essential to understanding the saturation levels (Ran et al., 2022). In this study, rainfall variables are grouped based on time, namely continuous rainfall, which is the cumulative value of rainfall on the day of a landslide from the rainfall start hour to the landslide event; maximum hourly rainfall; and rainfall during a fixed period such as 3 h, 1 d, 3 d, or 2 weeks (Fig. 1b). The histograms for rainfall considered in this study are depicted in Fig. 2b–g. Descriptive statistics for all continuous variables are given in Table 2.

3 Methods

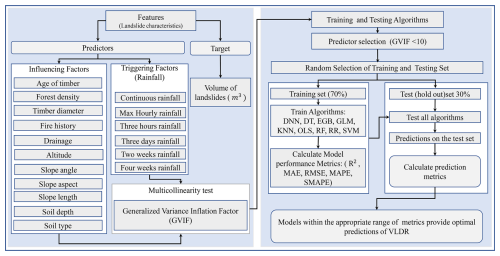
In this paper, we consider nine data-driven models, namely OLS, RF, SVM, EGB, GLM, DT, DNN, KNN, and RR, to predict the volume of landslides due to rainfall. The model is tested on South Korean landslide inventories and predisposing factors coupled with triggering factors, i.e., rainfall data. Our detailed workflow is summarized in Fig. 3. The steps for construction of these models can be briefly summarized as follows: (a) the dataset for landslide inventories is cleaned and combined with the rainfall dataset; (b) collinearity analysis is performed using the variance inflation factor; (c) continuous features are scaled (Z score) (Bonamutial and Prasetyo, 2023) to facilitate algorithms in fast convergence; (d) the dataset is split into training and test set; (e) all models are tested on the same training set and the model is evaluated on the test set using mean absolute error (MAE), coefficient of determination (R²), root mean square error (RMSE), symmetric mean absolute percentage error (SMAPE), and mean absolute percentage error (MAPE) for the comparison of actual and predicted volume by each model; (f) variable importance is calculated for the optimal model; and (g) the distance correlation is calculated for each continuous feature and the Kruskal–Wallis and Dunn tests are conducted to examine the similarity of the effects of each category on the landslide volume.

Figure 3 Workflow for the prediction of the volume of landslides due to rainfall.

3.1 Model construction

In the present investigation, we aimed to predict landslide volume using models that minimize error with interpretability and scalability. Since one model cannot have all properties simultaneously, we selected some widely used models due to their inherent interpretability and scalability properties. OLS, GLM, and DT are widely used for their high interpretability, which helps us to understand the influence of individual features on predictions (Gelman and Hill, 2007; Breiman, 2017). On the other hand, EGB, RF, SVM, RR, and KNN are used due to their robust performance in capturing complex patterns in data, which is essential for accurate predictions of landslide volumes (Liaw and Wiener, 2002; Hastie, 2009; Chen et al., 2022). Additionally, considering that the model will be used on a regional scale, which will require big data, EGB, RF, and DNN are designed to efficiently handle large datasets, making them suitable for regional-scale analysis. These last models can be scaled to incorporate more data from different geographical areas without significant adjustments, enhancing their applicability in future research (Krizhevsky et al., 2012). Accordingly, nine data-driven methods were selected and tested on a South Korean dataset to predict VLDR.

The first method considered is OLS, which is applied to estimate parameters of multilinear regression that yield the minimum residual sum of squares errors from the data (Kotsakis, 2023) under assumptions of no correlation in independent variables and error terms, constant variance in error terms, the non-linear collinearity of predictors, and the normal distribution of error terms. RF regression is a supervised data-driven technique based on ensemble learning, which constructs many decision trees during the training time of a model by combining multiple decision trees to produce an improved overall result of the model outcome. RF regression is more efficient in the analysis of multidimensional datasets (Borup et al., 2023). RF is an effective predictive model due to non-overfitting characteristics based on the law of large numbers (Breiman, 2001). DT regression is a predictive modeling technique in the form of a flowchart-like tree structure that includes all possible results, output, predictor costs, and utility. DT simplifies decision-making due to its algorithm that mimics human brain decision-making patterns (Rathore and Kumar, 2016). The KNN technique draws an imaginary boundary within which prediction outcomes are allocated as the average of k-nearest-point predictors, averaging their output variable (response). KNN calculates Euclidian distances to identify the similarity between data points, and then it groups points that have smaller distances between them (Kramer and Kramer, 2013). RR is an improved form of ordinary least squares that serves to respond to cases where collinearity is found in predictor variables. The estimated coefficients of ridges are biased estimators of true coefficients and are generated after adding a penalty to the OLS model. RR always has lower variances compared to OLS (Saleh et al., 2019). The advantage of GLM over OLS is that the dependent variables need not follow the normal distribution. GLM is composed of random and systematic components and the link function that links them. In this study, GLM with a Gaussian link function was applied. GLM is fitted using maximum likelihood estimation (Dobson and Barnett, 2018). DNN is among the data-driven models that have revolutionized different fields; DNN learns via multi-processing layers and identifies intricate patterns in the data to predict outcomes (LeCun et al., 2015). Here, the backpropagation algorithm was used to predict the estimated outcome. The advantage of DNN is that it can discover complex structures in the data using a backpropagation algorithm capable of changing the internal parameter (weight update). SVM is popular for balanced predictive performance which makes it capable of training models on small sample sizes (Pisner and Schnyer, 2020). Subsequently, SVM has been applied in many different landslide studies (Pham et al., 2018; Miao et al., 2018). SVM methods identify the optimal hyperplane in multidimensional space that separates different groups in terms of output values. EGB is the most powerful and a leading supervised machine learning method in solving regression problems. It can perform parallel processing on Windows and Linux (Chen et al., 2022). The gradient boosting trains using a differentiable loss function, and the model is fitted by minimizing the gradient. In this paper, both traditional statistical predictive models and ML models were used. The first kind is known for high clarity and explainability, and the second is famous for handling non-linearity in features. In some cases, the performance of advanced data-driven algorithms is almost similar (Chowdhury et al., 2023).

3.2 Feature selection and data splitting

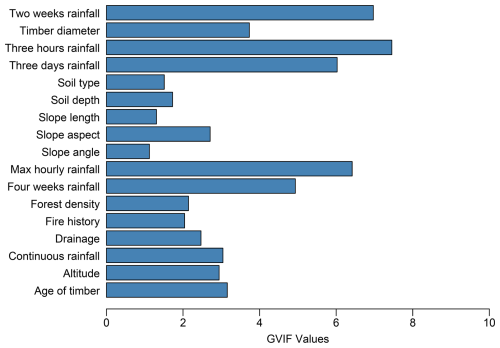
The variable selection procedure was based on previous literature and applied in the model using the generalized variance inflation factor (GVIF) (O'Brien, 2007) to eliminate collinear variables. The variable with GVIF < 10 was considered non-collinear and used in the model. Figure 4 depicts the retained features and corresponding GVIF values. The retained features have GVIFs of less than 10 (O'Brien, 2007). Accordingly, all depicted variables were considered for the model training. Further, to train the model, the datasets were split randomly, with 70 % of the data for the training set and 30 % for testing (Nguyen et al., 2021); 10-fold cross-validation was performed to obtain an optimal model. The training and test sets were scaled (Z score or variance stability scaling) to solve convergence issues that are associated with running the model without feature scaling (Singh and Singh, 2022). To run the model on the data using driven methods that accept numerical features only, the test and training sets were one-hot-encoded to create a feature matrix (Seger, 2018).

Figure 4 Generalized variance inflation factor (GVIF) bar plot for features.

3.3 Model evaluation metrics

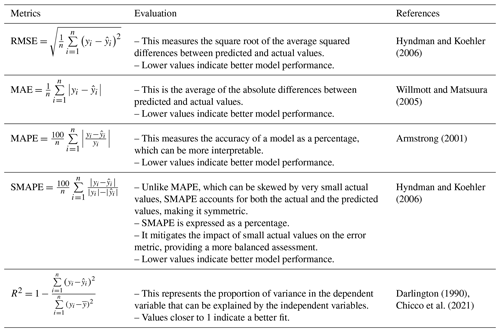
The model performance evaluation is a process of quantifying the difference between the observed value not used in the modeling process and the value predicted by the model. Different metrics are applied depending on the type of task, i.e., whether it is a classification or a regression problem. Subsequently, the widely used evaluation metrics for regression models, namely R², MAE, RMSE, MAPE, and SMAPE, were utilized to evaluate the model performance. The metric formulae and evaluation criteria are summarized in Table 3.

Table 3 Model evaluation metrics.

Note: y_i and ${\widehat{y}}_i$ represent the actual and predicted value, and $\stackrel{\mathrm{‾}}{y}$ and n stand for the mean of the actual value and number of observations in the dataset, respectively.​​​​​​​

4 Results

This section details how all analyses and model development were performed in R using various libraries. The DNN regression model was constructed using the dnn() function from the cito library (Amesoeder et al., 2024), with two hidden layers of (50, 50) nodes. The model was trained for 1500 epochs (iterations), with a learning rate of 0.01 and the MAE as the loss function. The DT regression model was constructed with tree() function from the tree library, with the recursive-partition method. The RR model was constructed using glmnet() from the glmnet package (Friedman et al., 2010), with a ridge penalty (alpha = 0). The optimal lambda was obtained by performing 10-fold cross-validation. The EGB model was built using the xgboost() function in the xgboost package (Chen et al., 2022). The optimal model was obtained at the 524th boosting iteration with max depth = 5 and other parameters set to default. The GLM regression model was constructed using the glm() function (R Core Team, 2022) with the Gaussian family and log link to constrain the model to predicting positive outcomes. KNN regression was constructed using the knnreg() function from the caret package (Kuhn, 2022), with the number of neighbors, k, at 17. The OLS model was constructed with lm() from the stats package (R Core Team, 2022). The RF model was run using randomForest() from the randomForest package (Liaw and Wiener, 2002) with default parameters, and the optimal model was reached at the 256th iteration. The SVM regression model with a linear kernel was built using the e1071 package (Meyer et al., 2021) and other parameters set to default.

Figure 5 Scatterplot of actual and predicted values for the nine tested models.

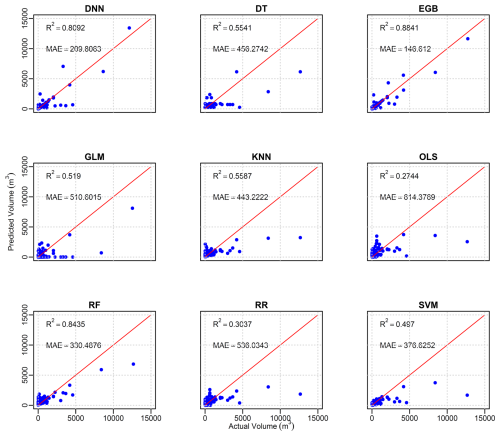
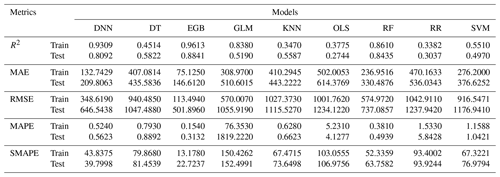
The predictive performance of all tested models on the holdout dataset is depicted by the scatterplot (Fig. 5) of the actual volume as recorded in the test set and predicted outcome values of each model. The red line represents the perfect prediction. The scatterplot of actual and predicted values of tested models shows that OLS performed least well compared to other models, with R² = 0.2744; that is, 27 % of variances in the model were explained by predictors. The second-worst-performing model was RR, with R² = 0.3034, which is a 3.6 % improvement compared to OLS. Among all models, three out of nine, namely OLS, SVM, and RR, performed at below 50 %; however, these models predicted small values of volume (below 2000 m³) well. The MAE of these three models was higher than that of the remaining six models, namely DNN, DT, GLM, KNN, RF, and EGB. Among these last models, the best performing was EGB, with R² = 0.88 being the proportion of the variance explained by predictors and MAE = 146.6 m³. The evaluation metrics for the training and test models are summarized in Table 4. Considering R², three models, namely EGB, RF, and DNN, had a value of R² above 80 % on the holdout set.

Table 4 Summary of prediction metrics for tested models on the training and test sets.

Regarding the prediction on the training set, GLM had an R² of 83 %. Nevertheless, the prediction on the holdout set was 51.9 %; this large variation in variance explained by predictors indicates that the GLM model did not catch all non-linear patterns in the holdout set. Notably, the prediction difference in R² on both the training and the test sets for the random forest exhibited a very small difference compared to EGB and DNN, that is, 1.75 % compared to 12.17 % and 7.72 % for DNN and EGB, respectively. Despite the stable prediction of RF, for the performance in terms of SMAPE, DNN gave the second-lowest symmetric mean absolute percentage error: 43.83 and 39.79 m³ on the training and test sets, respectively. According to Chicco et al. (2021), R² is more informative in regression modeling; thus, RF had better predictions than DNN.

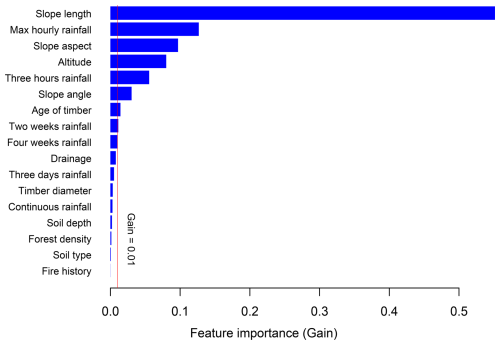
To dive deep into the prediction performance of the EGB model, we analyzed variables' importance for the prediction of the volume. It was observed that slope length was the predictor that contributed the most to the performance of the EGB model, followed by maximum hourly rainfall and slope aspect. The altitude, 3 h rainfall, slope angle, and age of timber contributed moderately to the prediction of the outcome volumes, with gains above 0.01 and less than 0.2. The antecedent rainfall from 3 d and above and continuous rainfall made minor contributions, with a gain of less than 0.01 for each. The presence of rainwater drainage channels made a moderate contribution, with a gain close to 0.01. On the other hand, the contribution of soil depth and forest density in the models was insignificant and far below 0.01. Though Fig. 2a depicts the association between larger volumes and fire history, the variable importance indicates that this relation was not significant. Some variables made minor contributions, depending on the case, and the contribution of those variables may also increase depending on other regional settings. Therefore, all variables with GVIF below 10 were kept in the model. Figure 6 illustrates the variables' importance for the EGB model. The vertical red line splits landslides prediction features into two groups, the first (to the right of the line) containing features that contributed a gain above 0.01 and the other (to the left of the line) containing those that made minor contributions.

Figure 6 Variable importance for the EGB model.

Figure 7 Distance correlation plot for the volume and continuous features.

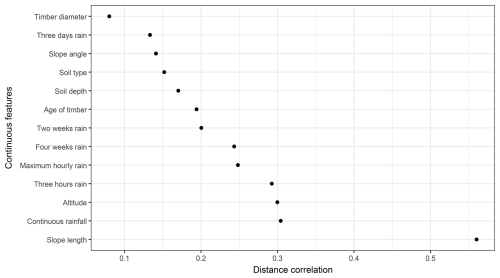
The variable importance plot depicts the overall contribution of a given feature; however, it does not provide detailed information. To gain more insight into the relationship between the volume of landslides and predictors, statistical tests for normality, namely the Shapiro–Wilk test and Dunn's test, were conducted. The Shapiro–Wilk test (Dudley, 2023) results revealed that the distribution of volume was non-normal (W = 0.40642, p value < 0.001). Noting that the volume distribution was non-normal, we opted for the non-parametric tests, which do not rely on normality to conduct the distance correlation (Székely et al., 2007) test (dcor) for continuous independent features. Figure 7 illustrates that the slope length exhibited a higher value (dcor = 0.56), followed by continuous rainfall, altitude, and 3 h rainfall, and the values kept decreasing up to timber diameter, with a distance correlation of 0.08. Overall, the distance correlation between the volume of landslides shows a moderate strength of association between continuous predictors.

Furthermore, to test for categorical features, the Kruskal–Wallis test (McKight and Najab, 2010) was used to check whether the volume of the landslide was different in each category and Dunn's tests (Dinno, 2015) were applied to examine which categories had similar means of the volume of landslides due to rainfall in different categories. The null hypothesis (H₀) was that the mean volume of landslides in different categories is the same, and the alternative hypothesis (H₁) was that the means of landslides are different in some categories. For the slope aspect, the second-most-significant predictor for the EGB model according to the results of the Kruskal–Wallis test (χ²=20.889, df = 7, p value = 0.003938), showed that there is a significant difference in the median of the volume in some categories of slope aspects. To know which classes of slope aspects had significantly different mean volumes, Dunn's test results at the 95 % confidence interval applied to pairs (east–southwest, east–southeast, east–south, east–northwest, and northwest–southeast) had significantly different means of landslides' volume (with p value < 0.05). Figure 8 shows that the southwest and southeast aspects had a higher frequency of landslides.

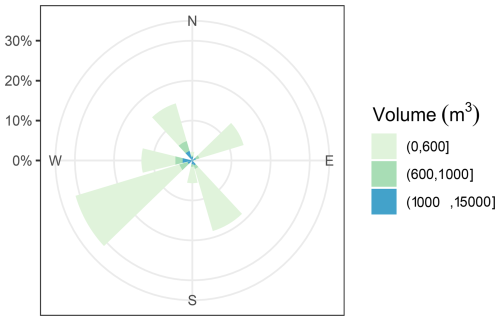
Figure 8 The distribution of the volume of landslides due to rainfall with respect to the slope aspect.

The Kruskal–Wallis test for the difference in the mean of drainage classes gave results of χ²=15.792, df = 2, and p value = 0.000372, which shows that the means of the volume per class were different. This was clarified by Dunn's test results: p values were less than 0.05 in all pairwise mean difference comparisons. The results of these tests highlighted that drainage has a remarkable influence on the occurrence of rainfall-induced landslides on the Korean Peninsula.

5 Discussion

Numerical models have traditionally been employed due to their foundation in physical principles such as slope stability and hydrological dynamics (Glade et al., 2005). These models are valuable for understanding the underlying mechanisms of landslide processes but often face limitations when applied to regions with complex or heterogeneous terrain, as they require detailed, high-quality input data that may not always be available (Caine, 1980). In the same way, statistical models, which use historical rainfall and landslide data to establish correlations, can offer useful predictions of VLDR in regions with extensive historical records (Chung and Fabbri, 2003). However, these models may struggle to account for local variations in topography or rapidly changing weather patterns, limiting their general applicability. Additionally, ML techniques have shown significant promise in improving predictive accuracy at the regional level due to the capability of processing large diverse datasets and capturing complex non-linear relationships that traditional models might fail to capture (Pourghasemi and Rahmati, 2018). Further, ML models can adapt to regional variations and continuously improve as new data are introduced, offering a more flexible and dynamic approach to predicting VLDR on a regional scale (Liu et al., 2021b). Subsequently, the aim of this study was to construct a data-driven algorithm that accurately predicts VLDR. The results of nine different tested algorithms revealed a tremendous difference between classical regression models (OLS, RR, and GLM) and other data-driven machine learning models. In this study, apart from SVM regression, DT, and KNN, the machine learning models (DNN, DT, RF, and EGB) exhibited high prediction capability with R² above 50 % (Fig. 5). The DNN, EGB, and RF models achieved R² > 0.8 on both training and test sets, with accuracy reduced to R² values of 1.75 %, 7.72 %, and 12.17 % for RF, EGB, and DNN, respectively, on the holdout set, indicating that the model could yield reliable volume estimates in adjacent areas with similar geological and environmental conditions. The random forest model performed well in predicting smaller volumes; however, as the volume increased, the model underpredicted volume values. The DNN model, with low MAE, performed quite well compared to random forest; however, the model did not perform well on moderate volume values, resulting in reduced R². The EGB model tested on the South Korean landslide inventory coupled with rainfall data at the time of landslide events and antecedent rainfall within 1 month of the event exhibited more accurate predictions compared to other constructed algorithms. The difference in performance may be due to the internal structure of each algorithm; the RF builds multiple decision trees and averages predictions to improve accuracy (Breiman, 2001), while EGB builds sequential trees in a recursive order, where the newly built tree improves error that occurred while building the previous decision tree and optimizes the loss function through a gradient descent (Chen et al., 2022).

The slope aspect played an important role in the prediction of the volume, and the landslides mostly occurred in locations oriented toward the south-southwest and southeast. This may be due to the direction taken by typhoons, which hit the southwest versants of mountains upon landfall on the Korean Peninsula and travel toward the northeast Pacific (Lee et al., 2013; Ha, 2022). The findings of this research are congruent with those of Lee et al. (2013), who also highlighted that the mountain versant oriented to strong wind directions may face more landslides. The study also highlighted that a moderate rainwater drainage channel plays an important role in the prevention of landslides due to its stabilizing effect. The landslide location and pattern follow the rainfall climate scenario, which highlighted a higher intensity of rainfall in the northeastern region of South Korea (Lee, 2016). In addition, the findings of this study are congruent with Zhang et al. (2019) observations that highlighted the low influence of soil type in landslide modeling and showed that the maximum rainfall and cumulative 3 h of rainfall were the most contributing rainfall types, which indicated that the shallow landslides of interest may have been triggered by sudden rainfall concentrated in a few hours before the occurrence of the events. The occurrence of landslides triggered by rainfall is a complex phenomenon that involves many interrelated environmental settings, human activities, geological conditions, and climatic conditions. Moreover, the occurrence of typhoons is known to aggravate the landslides' impacts on communities (Chang et al., 2008); incorporating typhoon variables in future studies to customize regional settings may improve the accuracy of models. The advantage of this research is that the constructed model has high predictive accuracy and can handle the non-linearity of predisposing factors. The model came to fill the gap in a few fields related to the prediction of the volume of landslides using data-driven techniques. This model can serve as an effective tool for policymakers to incorporate landslide volume risks into policies aimed at protecting infrastructure and residents dwelling in landslide high-risk zones.

To understand the applicability of the developed models, the trained model was tested using unknown data (test data), with volume predictions generated solely based on the predictor variables; actual volume values were utilized only for evaluating model prediction accuracy. The outcome exhibited a difference in R² on the training and holdout set of 7.72 % for the optimal model (i.e., EGB), highlighting that the model can be applied to other regions of with similar settings. It was noted that without proper model calibration with the independent dataset, it is difficult to determine whether these discrepancies in performance are due to model limitations or data differences in different regions (Huang et al., 2020). Therefore, future research will focus on developing an independent database containing recent landslide geometry data from various regions of the Korean Peninsula to enhance model accuracy, along with calibrating region-specific parameters to ensure the model's transferability to other regions.

The major limitation of this study is that the analysis is solely focused on shallow-seated landslides, specifically translational slope failures with volumes below 13 000 m³. Thus, the analysis may not fully capture the variability in landslide characteristics across different geomorphological and geological contexts. Deep-seated landslides, for instance, often exhibit distinct failure mechanisms, material compositions, and depositional patterns that influence their volumetric characteristics, and these were not considered in this investigation. Similarly, debris flows, known for their unique channelization and entrainment behaviors, were not included, potentially limiting the applicability of the optimized models to other landslide types. Further, this study was performed using point-based landslide inventory data, which may not capture all variability in influencing factors and their exact state. The incorporation of high-resolution data from remote sensing and other sources may also improve the efficiency of the predictions. These limitations may impact the broader applicability of the proposed model; however, future studies will aim to address this by conducting separate analyses for deep-seated landslides and debris flows, allowing for a more comprehensive understanding of landslide volume predictions across diverse landslide types and geomorphological settings.

6 Conclusions

In this paper, the aim was to construct a data-driven model that predicts the volume of landslides due to rainfall. To this end, nine different classical regression models and machine learning algorithms were tested on a South Korean landslide dataset containing features of landslides that occurred between 2011 and 2012. Among the tested models, the EGB model produced the most accurate prediction. This is proven by the evaluation of the difference between actual and predicted values, such as R² = 88.41 % and MAE = 146.6120 m³ on the holdout set. The analysis of feature variables in the contribution to the prediction of the model revealed that the slope length was the most influential predictor. The EGB model can be seen as a promising tool for the prediction of the volume of landslides due to its high predictive performance. The model can be customized in different environmental settings. The model can be applied to estimate the expected volume of landslides based on forecasted rainfall once the model has been well adjusted to fit the geomorphological and environmental settings of the region of interest after re-training on the regional historical data to include regional variability. Therefore, this model can be a good tool for planning for resilience and infrastructure pre-construction risk assessment to ensure that new infrastructure is placed in stable regions free from severe landslides.