the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Reduced-order digital twin and latent data assimilation for global wildfire prediction
Caili Zhong
Matthew Kasoar
Rossella Arcucci
The occurrence of forest fires can impact vegetation in the ecosystem, property, and human health but also indirectly affect the climate. The Joint UK Land Environment Simulator – INteractive Fire and Emissions algorithm for Natural envirOnments (JULES-INFERNO) is a global land surface model, which simulates vegetation, soils, and fire occurrence driven by environmental factors. However, this model incurs substantial computational costs due to the high data dimensionality and the complexity of differential equations. Deep-learning-based digital twins have an advantage in handling large amounts of data. They can reduce the computational cost of subsequent predictive models by extracting data features through reduced-order modelling (ROM) and then compressing the data to a low-dimensional latent space. This study proposes a JULES-INFERNO-based digital twin fire model using ROM techniques and deep learning prediction networks to improve the efficiency of global wildfire predictions. The iterative prediction implemented in the proposed model can use current-year data to predict fires in subsequent years. To avoid the accumulation of errors from the iterative prediction, latent data assimilation (LA) is applied to the prediction process. LA manages to efficiently adjust the prediction results to ensure the stability and sustainability of the prediction. Numerical results show that the proposed model can effectively encode the original data and achieve accurate surrogate predictions. Furthermore, the application of LA can also effectively adjust the bias of the prediction results. The proposed digital twin also runs 500 times faster for online predictions than the original JULES-INFERNO model without requiring high-performance computing (HPC) clusters.
- Article
(3152 KB) - Full-text XML
- BibTeX
- EndNote
Every year, unwanted wildland fires result in significant economic, social, and environmental impacts on a global scale (Grillakis et al., 2022). In addition, forest fires are especially sudden, extraordinarily destructive, and notably difficult to respond to timely (Grillakis et al., 2022). Globally, an average of more than 200 000 forest fires occur each year, burning more than 1 % of the world's forested area (Pais et al., 2021). Wildfires not only destroy vegetation but can also pose risks to life and property, impact human health due to smoke pollution, and feed back on climate change through the release of stored carbon (Kim, 2015; Marlier et al., 2015; Jauhiainen et al., 2012; Lasslop et al., 2019; Ward et al., 2012). Studying the influence of vegetation and climatic factors on wildfire occurrence is critical for anticipating future wildfires and preparing for their possible impacts on ecosystems and society.
Global fire frequency is related to land use, vegetation type, and meteorological factors. Arid land, hot and dry weather, and combustible vegetation are all wildfire risk factors. Therefore, data from validated natural environment models can predict forest fire risk. Numerous valid and relevant models exist, such as earth system models (Claussen et al., 2002) and dynamic global vegetation models (DGVMs) (Prentice and Cowling, 2013). The Joint UK Land Environment Simulator – INteractive Fire and Emissions algorithm for Natural envirOnments (JULES-INFERNO) (Best et al., 2011; Clark et al., 2011) is an example of a DGVM. JULES-INFERNO simulates fire burnt area and emissions over time based on geographic features such as population, land usage, and meteorological conditions (Burton, 2019; Mangeon et al., 2016). However, implementing such a DGVM simulation is time-consuming due to the complexity of the physical model and the number of associated geographical features. For example, predicting wildfire occurrence over a 100-year climate change scenario takes approximately 17 h runtime using 32 threads on the JASMIN high-performance computing (HPC) service (JASMIN Site, 2022; Lawrence, 2013) (100-year runtime estimated as average from four simulations, range of 14.3–19.7 h, using Intel Xeon E5-2640 v4 “Broadwell” or Intel Xeon Gold 5118 “Skylake” processors with ∼7 GB RAM available per thread). This is further limited by availability and queuing priority of the computer resource. Therefore, building an efficient digital twin as a surrogate model is necessary for accelerating the prediction process.
The digital twin paradigm combines process-based information and data-driven approaches to best estimate complex systems. An extensive range of scientific problems, including medical science (Quilodrán-Casas et al., 2022), nuclear engineering (Gong et al., 2022a), and earth system modelling (Bauer al., 2021), use the digital twin paradigm for modelling. Since the 1990s, researchers have studied the relationship between vegetation and wildfire using machine learning and artificial intelligence (Nadeem et al., 2020). Recent research shows that machine-learning-based reduced-order modelling (ROM) can effectively reduce the computational cost by constructing surrogate models (Mohan and Gaitonde, 2018). ROM efficiently compresses the raw data into a low-dimensional space using an encoder and then decompresses the data using a decoder. Thus, predictions and simulations can be performed in a low-dimensional latent space before being decoded into a real physical space. However, predictive models trained using large amounts of data do not necessarily guarantee long-term prediction accuracy. In fact, iterative applications of sequence-to-sequence (Seq2seq) forecasting models can lead to error accumulation, resulting in incorrect long-term predictions (Cheng et al., 2022a, b). Researchers have applied data assimilation (DA) methods to address this challenge. DA methods correct the predicted data by combining simulated data with observations through specific weighting (Gong et al., 2020). Applications of DA in high-dimensional dynamical systems include weather forecasting (Lorenc et al., 2000; Bonavita et al., 2015; Ma et al., 2014), hydrology (Cheng et al., 2020), and nuclear engineering (Gong et al., 2022b). However, wildfire data from the increasing number of meteorological satellites have high data dimensions (Jain et al., 2020). Applying DA operations on full-size data is computationally expensive, if not prohibitively so, because there are some major challenges in high-dimensional dynamical system models, such as ROM, dynamical system identification, and model error correction (Cheng et al., 2023).
Latent data assimilation (LA), which combines ROM, machine learning (ML) surrogate models, and DA, was recently proposed (Peyron et al., 2021) and applied to a wide range of engineering problems, including air pollution modelling (Amendola et al., 2021), multiphase fluid dynamics (Cheng et al., 2022a), and regional wildfire predictions (Cheng et al., 2022b). In LA, data compression happens before the DA operation (Peyron et al., 2021), significantly reducing the computational cost. Iteration of this prediction assimilation process improves the starting point of the next time-level forecast and leads to more robust long-term predictions.
The main objective of this study is to propose a digital twin model with the same burnt area output as the JULES-INFERNO system. The digital twin model combines ROM, machine learning predictive models, and LA. Data from the JULES-INFERNO simulations are used to train the machine-learning-based digital twin model. A time series of wildfire-related data is given as input to predict the occurrence of wildfires in the following years. The proposed model is tested on unseen initial conditions to predict subsequent fire conditions. This digital twin can significantly improve prediction efficiency compared to the physical model.
Two ROM approaches, convolutional autoencoder (CAE) and principal component analysis (PCA), are chosen to reduce data dimensionality. Long short-term memory (LSTM) forms the main structure for wildfire occurrence probability prediction because LSTM is suitable for dealing with dynamic simulations with long-term temporal correlations (Graves and Schmidhuber, 2005a). LA is applied to correct the model results as soon as “observation” data become available. The “observation” data used here for LA are the encoded data from the original JULES-INFERNO simulations, which we use as a proof-of-concept substitute for high-quality observation data. Compared to the traditional DA in the entire physical space, LA can considerably improve computational efficiency thanks to the ROM (Graves and Schmidhuber, 2005a). This research aims to use the initial months' output from JULES-INFERNO as input to implement a global-scale wildfire predictive model that combines ROM, recurrent neural networks (LSTM), and LA for efficient wildfire forecasting.
To summarize, the main contributions of this study are as follows.
-
This research implements a deep learning digital twin for wildfire prediction based on the JULES-INFERNO land surface model. The digital twin can greatly improve the computational efficiency of the physical model by embedding the input into a low-dimensional space before prediction.
-
We tested and compared two ROM approaches – convolutional autoencoder (CAE) and principal component analysis (PCA) – in terms of reconstruction and prediction accuracy over the simulation period of 1961 to 1990.The objective is to achieve a significant reduction in data dimensionality to improve the efficiency of subsequent predictions but maintain the original characteristics of the data. The digital twin achieves long-term predictions by making iterative predictions by using the current predicted results as the next-level input to predict the situation in the next time step.
-
LA is applied to avoid error accumulation. LA compares the predicted values against the original JULES-INFERNO outputs (considered as observations in this study) and periodically adjusts the predictions. When applying unseen scenarios to the developed model, LA adjusts the predicted values to improve the accuracy of subsequent predictions. Therefore, LA implemented in this project can effectively stabilize prediction results.
The paper is organized into the following sections: Sect. 2 explains the original physical model, JULES-INFERNO, and the dataset of this project. Section 3 describes the dimensionality reduction method used in the study (PCA and the constructed CAE structure), explains the surrogate model used in this research for wildfire prediction, and outlines the principles and applications of LA. Section 4 discusses the experimental results and analysis of the study. Finally, Sect. 5 concludes the most important findings of this research and suggests future directions for enhancement.
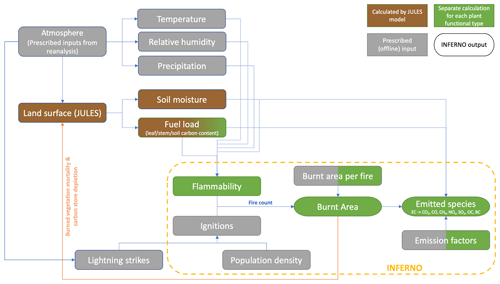
The Joint UK Land Environment Simulator (JULES) is simulating land surface vegetation, carbon stores, and hydrology, primarily using physical models to simulate the processes of land use, water and carbon fluxes with the atmosphere, and climate interactions with vegetation dynamics (Best et al., 2011; Clark et al., 2011). The INFERNO fire scheme was constructed based on a simplified parameterization of fire ignition and vegetation flammability (Pechony and Shindell, 2009). Coupled with JULES, the INFERNO scheme predicts fire burnt area and carbon emissions based on the simulated vegetation, as well as vegetation mortality due to fire, which feeds back on the vegetation distribution (Burton, 2019; Mangeon et al., 2016). More precisely, the model calculates flammability based on soil moisture, fuel density, temperature, humidity, and precipitation and then combines lightning strikes to estimate the average area burnt. Finally, emitted atmospheric aerosols and trace gases can be calculated from vegetation-dependent emission factors (Mangeon et al., 2016). Figure 1 illustrates the input variables and critical components of JULES-INFERNO. However, this model involves a large amount of data and number of parameters, leading to high computational cost. In the present paper, we propose the use of a surrogate model as a substitute for the original high-precision simulation model. The surrogate model aims to use the same input fields as the original model and to output a result that approximates the original INFERNO burnt area output but is less computationally intensive to solve.
This research considered four meteorological boundary conditions and predicted burnt area (temperature (T), humidity (H), rainfall (R), and lightning (L)) and the field of burnt area fraction (P) from the JULES-INFERNO model as input data. We used an ensemble of five JULES-INFERNO simulations which were forced using meteorological conditions from the Fire Modeling Intercomparison Project (FireMIP) last glacial maximum (LGM) scenario (Rabin et al., 2017), which uses a detrended 1961–1990 re-analysis time series, uniformly shifted to match LGM global average climate, as the atmospheric boundary conditions. Monthly-mean values were collected for each meteorological boundary condition, nominally from 1961–1990 for each simulation. Thus 360 snapshots for each variable are available, denoted as temperature (), humidity (), rainfall (), and lightning (). JULES-INFERNO was run with a resolution of 1.25∘ latitude × 1.875∘ longitude, giving each snapshot a latitude span of 144 units and a longitude span of 192 units, so the size of each snapshot is 144×192. We denote the wildfire burnt area predicted by JULES-INFERNO from each of the five ensemble members as . Although each ensemble member simulated the same nominal period (1961 to 1990) and was forced by the same detrended meteorological boundary conditions, we applied different initial internal states to sample a range of model internal variability. As shown in Table 1, P1 was randomized, and the initial internal states of the subsequent experimental results were all the last internal states of the previous one. The burnt area model output is only diagnosed over latitudes with non-zero land cover, and so the wildfire burnt area data () only spans 112 latitude units, meaning the fire snapshot size is 112×192 rather than 144×192.
In subsequent experiments, P1,P2, and portion of P3 are the training set, and another portion of P3 is the validation set during training. P4 and P5 were used as the test set for all models built in the study. In addition, to eliminate the adverse effects of odd sample data in training, this research standardized all training and test sets (climates and fire variables) by applying Eq. (1) to normalize the data to [0, 1]:
In this section, we present the main technologies used to develop the digital twin: ROM, surrogate predictive model, and LA. The computation of the digital twin starts by constructing the ROM for reducing the dimension of JULES-INFERNO data. The climate and wildfire data are then concatenated and processed into time series data and fed into the training predictive model. Afterwards, iterative forecasting tests the trained surrogate model. The test uses 12 months of unseen data as input to predict fires for the next 29 years. LA periodically adjusts the forecasting process to ensure stability, accuracy, and sustainability.
3.1 Reduced-order modelling
Assume that the original data are an n-dimensional vector denoted as ; we then denote the compressed variable (k-dimension, k < n) after dimensionality reduction as . The variable that reconstructs the compressed data to the original size is denoted as . ROM's primary purpose is to minimize the expectation of the mean square error (MSE) of reconstruction, i.e. . The meteorological boundary conditions and burnt area data obtained by dimensionality reduction can therefore be denoted by , and each reduced snapshot is k-dimensional. Decoded data are denoted as , and the dimensionality of each element is consistent with the original data (n-dimension).
3.1.1 PCA
PCA extracts essential information from the data and eliminates redundant information by analysing principal components. PCA uses the idea of dimensionality reduction to form new variables by linearly combining multiple parameter indicators and mapping the original n-dimensional features to k-dimensional features (n > k); k is known as the truncation parameter in PCA (Bianchi et al., 2015).
The compressed variable can be represented by a linear combination of as shown in Eq. (2) to make the global variance after the transformation maximal:
where is the eigenvector associated with the eigenvalues λi of the covariance matrix C.
The covariance matrix C is shown in Eq. (3), and the formula for the covariance is shown in Eq. (4):
where E(ui) represents the mathematical expectation of ui.
The contribution rate of each principal component can be calculated using the principal component explained variance formula (Eq. 5), and the principal components corresponding to the special eigenvalues are selected in descending order to construct . The cumulative explained variance is referred to in Eq. (6):
3.1.2 CAE
An autoencoder (AE) is a self-supervised deep learning method that minimizes the reconstruction error between its model input and output. The autoencoder optimizes parameters to obtain a low-dimensional data representation of high-dimensional features (Huang et al., 2017). The feature extraction method used in standard AE is fully connected and straightforward to implement. However, each neuron connects to all the neurons in the next layer. Thus, standard AE generates massive parameters, making the computation more expensive while ignoring some spatial patterns in the image (Masci et al., 2011). A convolutional autoencoder (CAE) (Masci et al., 2011), a combination of AE and convolutional neural network (CNN), has been proposed to address the drawbacks of fully connected AEs. The CAE model inherits the self-supervision function of standard AE but replaces the matrix product operation between hidden neurons with convolution and pooling operations. Compared to AE, CAE can capture local spatial patterns of monitoring data (Masci et al., 2011). Furthermore, extracting features by convolution can reduce the number of parameters and increase the training speed.
This study includes climate and fire conditions from various regions in the form of 2-dimensional images. Therefore, this research constructed a CAE model using AE reconstruction, dimensionality reduction features, and CNN local-feature extraction capabilities. The CAE model aims to achieve self-supervised learning of environmental and wildfire features.
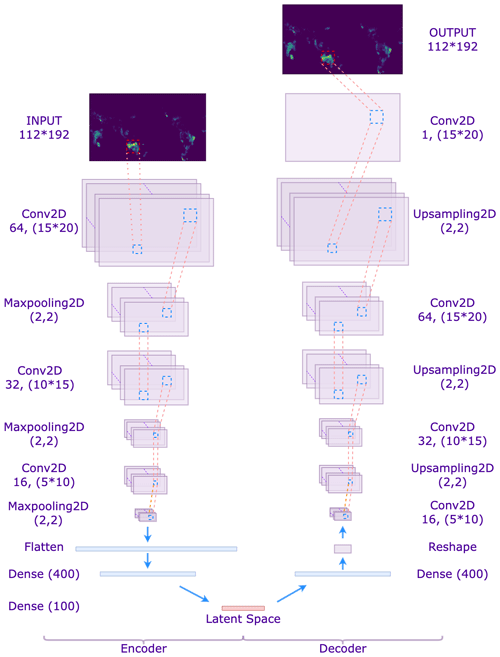
The encoder designed for this study uses three convolutional layers, three max pooling layers, and two fully connected layers. The decoder includes four convolutional layers, three up-sampling layers, and one fully connected layer. Figure 2 shows the CAE structure of this study with a latent space of dimension 100 and with Conv2d, MaxPooling2D, Dense, and UpSampling2D representing the 2D convolutional layer, max pooling layer, fully connected layer, and up-sampling layer respectively.
Firstly, the sample data, , need to be converted into a 2-dimensional matrix of p rows and q columns () according to the latitude and longitude range of the original data, and then each snapshot could be interpreted as an image. Given the input U, features are extracted by multiple convolutional kernels to obtain the output Cl of the lth layer, and then the is obtained by down-sampling through the subsequent pooling layer to retain the main features of the inflow data and prevent over-fitting. The operational methods are shown in Eqs. (7) and (8):
where Wl and bl are the weights and biases of the layer l network respectively, f(⋅) is the rectified linear unit (ReLU) function, and Maxpooling(⋅) is the maximum pooling operation.
As shown in Fig. 2, during the network training process, the encoder acquires the feature mapping of the input data layer by layer. It obtains the k-dimensional latent space data after the flatten and dense layers. In contrast, the decoder inputs the latent space data and reconstructs the data by convolution, up-sampling, etc., and evaluates the reconstruction performance of CAE on climate and wildfire data by the loss function (MSE). Equation (9) shows the square error of one sample (L(⋅)) and mean error for the training set (J(⋅)), supposing the training set is Ptr with Ntr snapshots:
3.2 Surrogate predictive model
After data compression, the proposed digital twin model combined the climate and fire data as inputs for the predictive surrogate model, denoted as and , where “s=1, 2,..5” indicates the five fire respective datasets (i.e. JULES-INFERNO simulations). The data are normalized before being fed into the model.
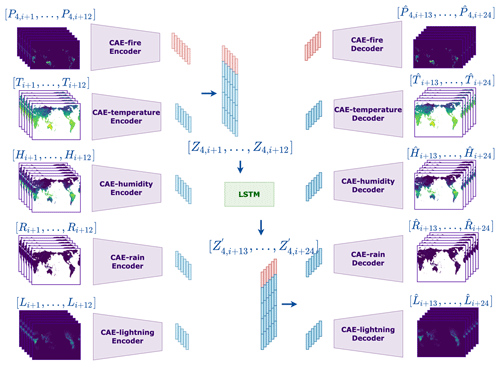
Here we aim to use ML techniques to surrogate the original physical predictive model. The recurrent neural network (RNN) is a reference method for time series prediction problems. The LSTM network, a variant of RNN, constructed the wildfire predictive model in the reduced latent space using the encoded JULES-INFERNO climate and fire data as inputs. Figure 3 shows the basic structure of the whole surrogate model.
The seq2seq prediction based on the LSTM network is implemented in this study with tin time steps as input and tout time steps as output. Here, each time step represents a month of simulation time. The length of the input and output sequences is fixed as , and the test set consists of . The input of the LSTM training can be obtained by shifting the initial time of each time series, as shown in Eq. (10). The model uses MSE loss function to evaluate the training performance:
As for the iterative predictions in the test dataset, the trained model uses the current predictive result as the input of the next prediction. The output of the predictive model can be denoted as . The first-year data of the test set is used as model input, and the prediction result set only contains data from the following 29 years. At each iteration, the model can predict the global wildfire risk for the next year, as shown in Eq. (11):
Thanks to the gate structure, LSTM networks are efficient in dealing with long-term temporal correlations that standard RNNs cannot handle (Graves and Schmidhuber, 2005b). More precisely, the essence of the gate structure of the LSTM is to use the sigmoid activation function so that the fully connected network layer outputs a value between 0 and 1, describing the proportion of the information quantity passed. The forget gate indicates the proportion of the output information quantity forgotten at the last moment, and the input gate represents the proportion of the input information quantity retained at the current moment, both updating the state value together. Finally, the output gate represents the proportion of the new state output. Suppose xt (, ) are the current inputs, ht−1 is the output of last moment, ct is the value of the new state, and ct−1 is the state value of last moment. Equations (12), (13), (14), (15), (16), and (17) represent the inner principal of the LSTM:
where , and Wo are input weighting matrix; , and Qo are loop weights; , and bo are bias values; and σ(⋅) is the sigmoid function.
3.3 Latent data assimilation
The basic principle of DA is the combination of numerical models with observation data to improve the forecast of the system under study (Vallino, 2000). When applying the developed predictive model to unseen initial conditions, we apply the DA method periodically to enhance the current prediction results with the help of the observation data. The observation data in this research is considered the original output of the JULES-INFERNO model so that we can simulate the situation where high-quality real-time observation data are available. As periodic corrections are made to the forecast data, DA allows for a more stable and accurate long-term prediction. In this study, LA was applied, which combines ROM with DA, i.e. reducing the dimensionality of the data before applying the DA method (Peyron et al., 2021). In addition, ROM could reduce the parameters for subsequent operations, which allows LA to have a significant advantage in terms of computational efficiency compared to the classical full-space DA.
Both DA and LA can be summarized as a problem of solving the minimization of an objective function JDA(⋅) characterizing the deviation between the analysis field (optimal state ) and the observation field (actual state Ztest), as well as the background field (predicted state ), as shown in Eq. (18):
where t indicates the temporal index (the tth predicted year), is the analysis variable of DA, is the background variable, and zt is the observation (original) variable. B and O represent the background and observation error covariance matrix. The modelling of these covariances determines the weight of prediction and observation in the objective function, which is crucial for DA approaches (Lawless et al., 2005). H(⋅) is the state-observation function in latent space, which maps the analysis variable to the observation variable. In this study, since we are assimilating the compressed output of the original JULES-INFERNO model, H(⋅) is the identity function.
The latent analysis field could be obtained by optimizing the objective function (Eq. 18):
Equation (18) can be solved by the best linear unbiased estimator (Fulton, 2000), since the transformation operator H=H is a linear function in the latent space:
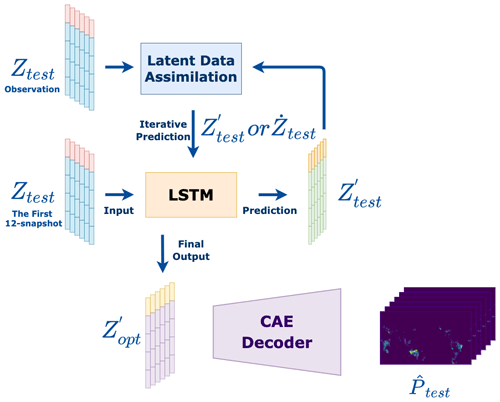
The obtained analysis state can be used as an initial point for the next-level prediction, as shown in Fig. 4, and the predicted field in the latent space could be (when applying LA at t time index) or (LSTM prediction at t time index). These processes can be repeated periodically to consistently improve the prediction performance. Furthermore, in Fig. 4, the final predicted sequence of the digital twin is the combination of and (m≠n), which could be denoted as .
In this section, we evaluate the proposed digital twin model's performance regarding prediction accuracy and computational efficiency when the digital twin model faces unseen initial conditions.
4.1 ROM results
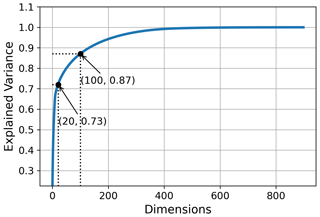
To set an optimal dimension of the latent space, we examined the explained variance of PCA for the training dataset. The training dataset consists of P1, P2, and P3 with different numbers of principal components, as shown in Fig. 5. According to the work of Li et al. (2021), 85 % to 95 % of the explained variance can reflect most data information while effectively reducing the original data dimensionality. Therefore, to reduce the latent space dimension and the computational cost of subsequent processing, we chose in this research the 100-dimension latent space with 87 % explained variance, as shown in Fig. 5. In addition, we also chose the 20-dimensional latent space for both PCA and CAE for comparison purposes.
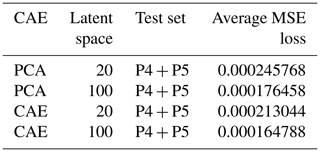
In terms of performance evaluation, the scenarios are used as the training set and P4 ∪ P5 are considered as the test set. The number of training epochs for the CAE models is fixed at 1000. The MSEs between reconstructed and original simulations for different models are shown in Table 2. To quantify the mismatch between the JULES-INFERNO output P and decoded prediction P′, we compute the MSE averaged by the number of pixels, i.e.
According to Table 2, for both PCA and CAE with 100-dimensional latent space, the reconstruction error is significantly lower compared to 20-dimensional. Furthermore, it can be evaluated from the experimental results that the CAE reconstruction MSE is lower compared to PCA. As previously described, CAE can capture feature information in 2-dimensional images during the encoding process, while PCA, which performs compression in 1-dimension space, may ignore these spatial patterns. In summary, CAE with 100-dimensional latent space has the best reconstruction performance in these experiments. As for the compression of climatic conditions , and L, 83 % of data are used for PCA and CAE model training, and the rest of the data are used for model testing, where PCA and CAE have a similar performance.
4.2 Predictive model and latent data assimilation
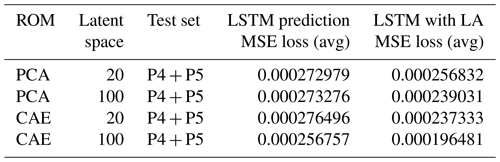
After completing the ROM, the original JULES-INFERNO data are compressed into specific latent spaces, considerably reducing the number of parameters in the predictive model. The concatenated wildfire burnt area field and the four climate variables act as inputs to the surrogate model. Thus, the surrogate model achieves the same inputs as JULES-INFERNO. The predictive model (LSTM) trains separately using encoded data from different ROMs. Similar to the ROM, P1, P2, and P3 are used as the training set, while P4 and P5 are used as the test set to evaluate the model performance. Each LSTM model has been trained over 10 000 epochs. As explained in Sect. 3.2, iterative predictions are used for the proposed digital twin. In other words, we first input the first year (12 snapshots) data and then use the current predicted result for the next-level prediction, until the 30th year's total burnt area is predicted. The MSEs for different combinations of ROM and LSTM are shown in Table 3.
Table 3 shows that the predictions obtained using PCA down to 20 and 100 dimensions and CAE reduced to 20 dimensions are similar, with an MSE close to . Same as ROM, the best performance in LSTM prediction is obtained by applying CAE with 100-dimensional latent space, with an MSE loss of approximately .
Comparing the results shown in Tables 2 and 3, there is a gap between the MSE of the predictive model and the ROM reconstruction, mainly because of the accumulation of errors during the iterative prediction process. Therefore, we periodically used the observations (raw data) and LA to adjust the forecast results to stabilize subsequent forecasts. LA is implemented every 5 years during the prediction phase in this study. According to Table 3, there is a steady reduction in forecast MSE after correction by LA. The most significant reduction in MSE is obtained with 100-dimensional CAE compared to other approaches.
To better illustrate the evolution of the prediction error, we display the MSE of the prediction against time in different predictive models. In this study, the existing climate and fire data in 1961 (provided by JULES-INFERNO) with different initial conditions are given to predict the subsequent 29 years of fire. Figure 6 shows the MSE per prediction for the different surrogate models (in red when without LA and in green when with LA) evaluated on the P4 test set, and we plotted the ROM MSE (in blue) for comparison.
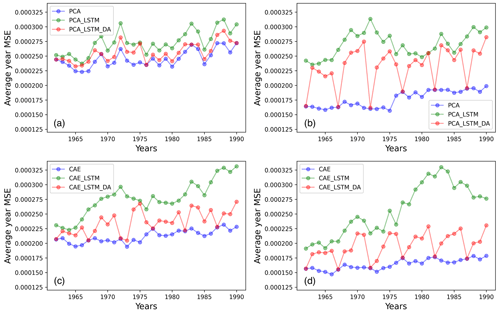
Figure 6Evolution of MSE through the years in different surrogate models: (a) 20-dimensional PCA-based model, (b) 100-dimensional PCA-based model, (c) 20-dimensional CAE-based model, and (b) 100-dimensional CAE-based model.
According to Fig. 6, using LA can effectively reduce the prediction error, as the vast majority of red points are significantly lower than the corresponding green points. Furthermore, CAE-based surrogate models can better adapt the LA, stabilizing the predictions afterwards and reducing the accumulation of errors. When applying the LA to the PCA-based surrogate models to reduce the error after the simulation, there may still be a sharply increasing forecast error in the subsequent year, as seen in Fig. 6a and b. On the other hand, CAE-based models manage to maintain the improvement in DA for future time steps, as shown in Fig. 6c and d. These results demonstrate the advantage of CAE compared to PCA in terms of generalizability when applied to unseen data. This effect has also been highlighted in the work of Peyron et al. (2021). Comparing the four cases presented in Fig. 6, the 100-dimensional CAE demonstrates the strength of both the original prediction and the assimilated one.
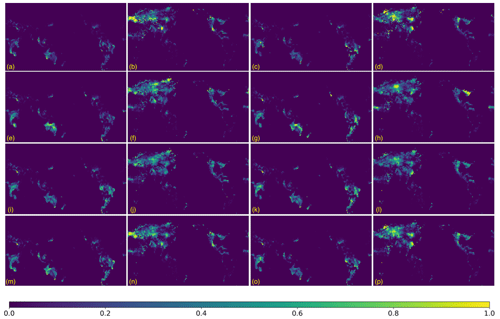
Figure 7The normalized output of 100-dimensional CAE-based digital twin: (a, b, c, d) the normalized output of original burnt area fraction, and their corresponding dates are January 1983, July 1983, January 1988, and July 1988; (e, f, g, h) the reconstructed output of the CAE model, and their corresponding dates are January 1983 , July 1983, January 1988, and July 1988; (i, j, k, l) the predicted output of CAE with the LSTM model, and their corresponding dates are January 1983, July 1983, January 1988, and July 1988; (m, n, o, p) the predicted output of CAE with the LSTM and LA models, and their corresponding dates are January 1983, July 1983, January 1988, and July 1988.
Figure 7 displays the output of the 100-dimensional CAE-based digital twin model of the years 1983 and 1988 (1 year after LA is implemented): the assimilated results (m, n, o, p) are compared with the original simulation (a, b, c, d), the CAE reconstruction (e, f, g, h), and the decoded image predicted by the LSTM model (i, j, k, l). In addition, the total burnt areas shown in Fig. 7 are normalized to the range 0 to 1. The horizontal and vertical coordinates in Fig. 7 represent latitude and longitude, and the colour values in the figure represent the grid box which indicates estimated burnt area fraction. The brighter the colour is, the larger the value is, and the colour bar is shown at the bottom of Fig. 7. It can be seen from Fig. 7 that forest wildfires in January are mainly in the Southern Hemisphere, such as Oceania (Fig. 7a) and South America in (Fig. 7c). On the other hand, the forest fires in July are mainly in the Northern Hemisphere, such as continental Europe in Fig. 7b and d.
As observed in Fig. 7, CAE and LSTM without LA can effectively reconstruct most of the features in the original image. Furthermore, comparing the LSTM-predicted images (i, j, k, l) and the optimization results after applying LA (m, n, o, p), it is found that the assimilation results are significantly closer to the JULES-INFERNO output.
Overall, in this research, we implemented four ROMs based on PCA and CAE, and the comparison reveals that the 100-dimensional CAE has the best reconstruction performance. Then, after combining the ROMs with predictive models (LSTM), a gap between the prediction results and the ROM reconstruction results is noticed. Eventually, the predictions of the surrogate model are made more stable after regular applications of LA to adjust the prediction outputs.
Table 4 compares the prediction time costs of the surrogate models using PCA and CAE downscaled to a 100-dimensional latent space without and with LA respectively. The prediction time of JULES-INFERNO in HPC is also shown as a reference. As can be seen in Table 4, the difference between PCA and CAE on the running time of the models is not significant; the application of LA slows down the prediction but still reduces the computing time cost significantly (around 500 times) compared to the original JULES-INFERNO fire predictive model.
In this study, the training of CAE and LSTM is performed with one NVIDIA P100 GPU (16 GB VRAM) in the Google Colab environment. All the online computations, including decoding, prediction and assimilation, are performed with Google Colab Intel CPUs as shown in Table 4. It is important to highlight that the application of such a digital twin does not require any HPC or GPU resources. Thus, a personal laptop can also run the model successfully.
This study implemented a deep-learning-based digital twin for global wildfire prediction using the same input and output fields to replace the physical wildfire model JULES-INFERNO. The proposed model builds ROMs to encode the data into latent space to reduce subsequent processes' computational costs. Then it makes use of the compressed data to train a predictive model based on RNN. Finally, it applies LA to stabilize the prediction results when using the predictive model for iterative prediction to avoid error accumulation. According to the numerical results, the digital twin built using CAE is more accurate compared to the ones using PCA and can effectively capture the features of the original image for encoding and decoding. Applying LA periodically to optimize the prediction results can address the issue of error accumulation and achieve stable long-term predictions. Ultimately the research achieved a much more efficient wildfire-prediction digital twin based on JULES-INFERNO. The proposed model takes only 35 s on a laptop to predict 30 years of burnt area fractions, compared to ∼5 h using the original physical model on a 32-thread HPC node. The present research clearly brings additional insight to the computing of reduced-order digital twins for high-dimensional dynamical systems. Future work can consider further improving the generalizability of the proposed approach, by, for instance, training the model with scenarios of different time periods or fine tuning the model when the initial conditions are outside the range of the training set. In addition, it is reported in recent works (Teckentrup et al., 2019) that long-term predictions of JULES-INFERNO can introduce forecast bias. Further efforts can be considered to apply a latent data assimilation framework developed in this paper with real-time satellite observations.
The code and the generated data used in this study are available at https://github.com/DL-WG/Digital-twin-LA-global-wildfire (last access: 30 April 2023; https://doi.org/10.5281/zenodo.7866704, acse-cz421, 2023).
The datasets used in this study are available at https://github.com/DL-WG/Digital-twin-LA-global-wildfire/tree/main/Prepocessed_data (https://doi.org/10.5281/zenodo.7866704, acse-cz421, 2023).
CZ: methodology, software, writing, and editing. SC: conceptualization, methodology, writing, and editing. MK: data curation, reviewing, and editing. RA: funding acquisition, reviewing, and editing.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the special issue “Advances in machine learning for natural hazards risk assessment”. It is not associated with a conference.
The authors would like to thank Zhengdan Shang at Imperial College London for the proofreading of this article. This research is funded by the Leverhulme Centre for Wildfires, Environment and Society through the Leverhulme Trust, grant number RC-2018-023. This work is partially supported by the EP/T000414/1 PREdictive Modelling with QuantIfication of UncERtainty for MultiphasE Systems (PREMIERE). JULES-INFERNO simulations were carried out using JASMIN, the UK's collaborative data analysis environment (https://jasmin.ac.uk, last access: 26 October 2022).
This research has been supported by the Leverhulme Centre for Wildfires, Environment and Society through the Leverhulme Trust (grant no. RC-2018-023). This work has been partially supported by the EP/T000414/1 PREdictive Modelling with QuantIfication of UncERtainty for MultiphasE Systems (PREMIERE).
This paper was edited by David Lallemant and reviewed by two anonymous referees.
acse-cz421: DL-WG/Digital-twin-LA-global-wildfire: Reduced-order digital twin and latent data assimilation for global wildfire prediction (v1.1.1), Zenodo [data set] and [code], https://doi.org/10.5281/zenodo.7866704, 2023.
Amendola, M., Arcucci, R., Mottet, L., Casas, Q. C., Fan, S., Pain, C., Linden, P., and Guo, Y.: Data Assimilation in the Latent Space of a Convolutional Autoencoder, ICCS 2021, Lect. Notes Comput. Sc., 12746, 373–386, https://doi.org/10.1007/978-3-030-77977-1_30, 2021.
Bauer, P., Stevens, B., and Hazeleger, W.: A digital twin of Earth for the green transition, Nat. Clim. Change, 11, 80–83, https://doi.org/10.1038/s41558-021-00986-y, 2021.
Best, M. J., Pryor, M., Clark, D. B., Rooney, G. G., Essery, R. L. H., Ménard, C. B., Edwards, J. M., Hendry, M. A., Porson, A., Gedney, N., Mercado, L. M., Sitch, S., Blyth, E., Boucher, O., Cox, P. M., Grimmond, C. S. B., and Harding, R. J.: The Joint UK Land Environment Simulator (JULES), model description – Part 1: Energy and water fluxes, Geosci. Model Dev., 4, 677–699, https://doi.org/10.5194/gmd-4-677-2011, 2011.
Bianchi, F. M., De Santis, E., Rizzi, A., and Sadeghian, A.: Short-Term Electric Load Forecasting Using Echo State Networks and PCA Decomposition, IEEE, 3, 1931–1943, https://doi.org/10.1109/ACCESS.2015.2485943, 2015.
Bonavita, M., Hólm, E., Isaksen, L., and Fisher, M.: The evolution of the ECMWF hybrid data assimilation system, Royal Meteorological Society, 142, 287–303, https://doi.org/10.1002/qj.2652, 2015.
Burton, C., Betts, R., Cardoso, M., Feldpausch, T. R., Harper, A., Jones, C. D., Kelley, D. I., Robertson, E., and Wiltshire, A.: Representation of fire, land-use change and vegetation dynamics in the Joint UK Land Environment Simulator vn4.9 (JULES), Geosci. Model Dev., 12, 179–193, https://doi.org/10.5194/gmd-12-179-2019, 2019.
Cheng, S., Argaud, J. P., Iooss, B., Lucor, D., and Ponçot, A.: Error covariance tuning in variational data assimilation: application to an operating hydrological model, Stoch. Env. Res. Risk. A., 35, 1019–1038, https://doi.org/10.1007/s00477-020-01933-7, 2020.
Cheng, S., Prentice, I. C., Huang, Y., Jin, Y., Guo, Y. K., and Arcucci, R.: Data-driven surrogate model with latent data assimilation: Application to wildfire forecasting, J. Comput. Phys., 464, 111302, https://doi.org/10.1016/j.jcp.2022.111302, 2022a.
Cheng, S., Chen, J., Anastasiou, C., Angeli, P., Matar, K. O. Guo, Y. K. Pain, C. C., and Arcucci, R.: Generalized Latent Assimilation in Heterogeneous Reduced Spaces with Machine Learning Surrogate Models, J. Sci. Comput., arXiv [preprint], https://doi.org/10.48550/arXiv.2204.03497, 2022b.
Cheng, S., Quilodrán-Casas, C., Ouala, S., Farchi, A., Liu, C., Tandeo, P., Fablet, R., Lucor, D., Iooss, B., Brajard, J., Xiao, D., Janjic, T., Ding, W., Guo, Y., Carrassi, A., Bocquet, M., and Arcucci, R.: Machine learning with data assimilation 65 and uncertainty quantification for dynamical systems: a review, arXiv [preprint], https://doi.org/10.48550/arXiv.2303.10462, 2023.
Clark, D. B., Mercado, L. M., Sitch, S., Jones, C. D., Gedney, N., Best, M. J., Pryor, M., Rooney, G. G., Essery, R. L. H., Blyth, E., Boucher, O., Harding, R. J., Huntingford, C., and Cox, P. M.: The Joint UK Land Environment Simulator (JULES), model description – Part 2: Carbon fluxes and vegetation dynamics, Geosci. Model Dev., 4, 701–722, https://doi.org/10.5194/gmd-4-701-2011, 2011.
Claussen, M., Mysak, L., Weaver, A., Crucifix, M., Fichefet, T., Loutre, M. F., Weber, S., Alcamo, J., Alexeev, V., Berger, A., Calov, R., Ganopolski, A., Goosse, H., Lohmann, G., Lunkeit, F., Mokhov, I., Petoukhov, V., Stone, P., and Wang, Z.: Earth system models of intermediate complexity: closing the gap in the spectrum of climate system models, Clim. Dynam., 18, 579–586, https://doi.org/10.1007/s00382-001-0200-1, 2002.
Fulton, W.: Eigenvalues, invariant factors, highest weights, and Schubert calculus, B. Am. Math. Soc., 37, 209–250, https://doi.org/10.1090/S0273-0979-00-00865-X, 2000.
Gong, H., Yu, Y., Li, Q., and Quan, C.: An inverse-distance-based fitting term for 3D-Var data assimilation in nuclear core simulation, Ann. Nucl. Energy, 141, 107346, https://doi.org/10.1016/j.anucene.2020.107346, 2020.
Gong, H., Cheng, S., Chen, Z., and Li, Q.: Data-Enabled Physics-Informed Machine Learning for Reduced-Order Modeling Digital Twin: Application to Nuclear Reactor Physics, Nucl. Sci. Eng., 196, 668–693, https://doi.org/10.1080/00295639.2021.2014752, 2022a.
Gong, H., Cheng, S., Chen, Z., Li, Q., Quilodrán-Casas, C., Xiao, D., and Arcucci, R.: An efficient digital twin based on machine learning SVD autoencoder and generalised latent assimilation for nuclear reactor physics, Ann. Nucl. Energy, 179, 109431, https://doi.org/10.1016/j.anucene.2022.109431, 2022b.
Graves, A. and Schmidhuber, J.: Framewise phoneme classification with bidirectional LSTM and other neural network architectures, Neural Networks, 18, 602–610, https://doi.org/10.1016/j.neunet.2005.06.042, 2005a.
Graves, A. and Schmidhuber, J.: Framewise phoneme classification with bidirectional LSTM networks, Neural Networks, 4, 2047–2052, https://doi.org/10.1109/IJCNN.2005.1556215, 2005b.
Grillakis, M, Voulgarakis, A., Rovithakis, A., Seiradakis, K. D., Koutroulis, A., Field, R. D., Kasoar, M., Papadopoulos, A., and Lazaridis, M.: Climate Drivers of Global Wildfire Burned Area, 17, 045021, https://doi.org/10.1088/1748-9326/ac5fa1, 2022.
Huang, Z., Xue, W., Mao, Q., and Zhan, Y.: Unsupervised domain adaptation for speech emotion recognition using PCANet, Multimed. Tools Appl., 76, 6785–6799, https://doi.org/10.1007/s11042-016-3354-x, 2017.
Jain, P., Coogan, P. S., Subramanian, G. S., Crowley, M., Taylor, S., and Flannigan, D. M.: A review of machine learning applications in wildfire science and management, Environ. Rev., 28, 478–505, https://doi.org/10.1139/er-2020-0019, 2020.
Jauhiainen, J., Hooijer, A., and Page, S. E.: Carbon dioxide emissions from an Acacia plantation on peatland in Sumatra, Indonesia, Biogeosciences, 9, 617–630, https://doi.org/10.5194/bg-9-617-2012, 2012.
JASMIN Site: JASMIN The UK's data analysis facility for environmental science, https://jasmin.ac.uk/, last access: 26 October 2022.
Kim, S.: Particulate Matter and Ozone: Remote Sensing and Source Attribution, ProQuest Dissertations Publishing, https://dash.harvard.edu/handle/1/17467177 (last access: 21 April 2023), 2015.
Lasslop, G., Coppola, A. I., Voulgarakis, A., Yue, C., and Veraverbeke, S.: Influence of Fire on the Carbon Cycle and Climate, Current Climate Change Reports, 5, 112–123, https://doi.org/10.1007/s40641-019-00128-9, 2019.
Lawless, A. S., Gratton, S., and Nichols, N. K.: Approximate iterative method for variational data assimilation, Int. J. Numer. Meth. Fl., 1, 1129–1135, https://doi.org/10.1002/fld.851, 2005.
Lawrence, B. N. and Bennett, V. L. and Churchill, J. and Juckes, M. and Kershaw, P. and Pascoe, S. and Pepler, S. and Pritchard, M., and Stephens, A.: Storing and manipulating environmental big data with JASMIN, 2013 IEEE International Conference on Big Data, Silicon Valley, CA, USA, 6–9 October 2013, https://doi.org/10.1109/BigData.2013.6691556, 2013.
Li, H., Li, Y., Wang, Z., and Li, Z.: Remaining Useful Life Prediction of Aero-Engine Based on PCA-LSTM, 2021 7th International Conference on Condition Monitoring of Machinery in Non-Stationary Operations (CMMNO), IEEE, Guangzhou, China, 11–13 June 2021, 63–66, https://doi.org/10.1109/CMMNO53328.2021.9467643, 2021.
Lorenc, C. A., Ballard, P. S., Bell, S. R., Ingleby, B. N., Andrews, F. L. P., Barker, D. M., Bray, R. J., Clayton, M. A., Dalby, T., Li, D., Payne, J. T., and Saunders, W. F.: The Met. Office global three-dimensional variational data assimilation scheme, Royal Meteorological Society, 126, 2991–3012, https://doi.org/10.1002/qj.49712657002, 2000.
Ma, X., Lu, X., Yu, Y., Zhu, J., and Chen, J.: Progress on hybrid ensemble-variational data assimilation in numerical weather prediction, J. Trop. Meteorol., 20, 1188–1195, 2014.
Mangeon, S., Voulgarakis, A., Gilham, R., Harper, A., Sitch, S., and Folberth, G.: INFERNO: a fire and emissions scheme for the UK Met Office's Unified Model, Geosci. Model Dev., 9, 2685–2700, https://doi.org/10.5194/gmd-9-2685-2016, 2016.
Marlier, E. M., DeFries, S. R., Kim, S. P., Koplitz, N. S., Jacob, J. D., Mickley, J. L., and Myers, S. S.: Fire emissions and regional air quality impacts from fires in oil palm, timber, and logging concessions in Indonesia, Environ. Res. Lett., 10, 85005, https://doi.org/10.1088/1748-9326/10/8/085005, 2015.
Masci, J., Meier, V., Ciregan, D., and Schmidhuber, J.: Stacked convolutional auto-encoders for hierarchical feature extraction, International Conference on Artificial Neural Networks 2011, 6791, 52–59, https://doi.org/10.1007/978-3-642-21735-7_7, 2011.
Mohan, A. and Gaitonde, D.: A Deep Learning based Approach to Reduced Order Modelling for Turbulent Flow Control using LSTM Neural Networks, arXiv [preprint], https://doi.org/10.48550/arXiv.1812.04951, 2018.
Nadeem, K., Taylor, S. W., Woolford, D., and Dean, C.: Mesoscale spatiotemporal predictive models of daily human- and lightning-caused wildland fire occurrence in British Columbia, Int. J. Wildland Fire, 29, 11–27, https://doi.org/10.1071/WF19058, 2020.
Pais, C., Miranda, A., Carrasco, J., and Shen, Z. M.: Deep Fire Topology: Understanding the role of landscape spatial patterns in wildfire susceptibility, Environ. Modell. Softw., 143, 105–122, https://doi.org/10.1016/j.envsoft.2021.105122, 2021.
Pechony, O. and Shindell, D. T.: Fire parameterization on a global scale, J. Geophys. Res., 114, D16115, https://doi.org/10.1029/2009jd011927, 2009.
Peyron, M., Fillion, A., Gürol, S., Marchais, V., Gratton, S., Boudier, P., and Goret, G.: Latent space data assimilation by using deep learning, arXiv [preprint], https://doi.org/10.48550/arXiv.2104.00430, 2021.
Prentice, C. I. and Cowling, A. S.: Dynamic Global Vegetation Models, Encyclopedia of Biodiversity, 2, 670–689, https://doi.org/10.1016/B978-0-12-384719-5.00412-3, 2013.
Quilodrán-Casas, C., Silva, V., Arcucci, R., Heaney, C., Guo, Y., and Pain, C.: Digital twins based on bidirectional LSTM and GAN for modelling COVID-19, Neurocomputing, 470, 11–28, https://doi.org/10.48550/arXiv.2102.02664, 2022.
Rabin, S. S., Melton, J. R., Lasslop, G., Bachelet, D., Forrest, M., Hantson, S., Kaplan, J. O., Li, F., Mangeon, S., Ward, D. S., Yue, C., Arora, V. K., Hickler, T., Kloster, S., Knorr, W., Nieradzik, L., Spessa, A., Folberth, G. A., Sheehan, T., Voulgarakis, A., Kelley, D. I., Prentice, I. C., Sitch, S., Harrison, S., and Arneth, A.: The Fire Modeling Intercomparison Project (FireMIP), phase 1: experimental and analytical protocols with detailed model descriptions, Geosci. Model Dev., 10, 1175–1197, https://doi.org/10.5194/gmd-10-1175-2017, 2017.
Teckentrup, L., Harrison, S. P., Hantson, S., Heil, A., Melton, J. R., Forrest, M., Li, F., Yue, C., Arneth, A., Hickler, T., Sitch, S., and Lasslop, G.: Response of simulated burned area to historical changes in environmental and anthropogenic factors: a comparison of seven fire models, Biogeosciences, 16, 3883–3910, https://doi.org/10.5194/bg-16-3883-2019, 2019.
Vallino, J. J.: Improving marine ecosystem models: Use of data assimilation and mesocosm experiments, J. Mar. Res., 58, 117–164, https://doi.org/10.1357/002224000321511223, 2000.
Ward, D. S., Kloster, S., Mahowald, N. M., Rogers, B. M., Randerson, J. T., and Hess, P. G.: The changing radiative forcing of fires: global model estimates for past, present and future, Atmos. Chem. Phys., 12, 10857–10886, https://doi.org/10.5194/acp-12-10857-2012, 2012.