the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A Bayesian network approach to modelling rip-current drownings and shore-break wave injuries
Elias de Korte
Bruno Castelle
Eric Tellier
A Bayesian network (BN) approach is used to model and predict shore-break-related injuries and rip-current drowning incidents based on detailed environmental conditions (wave, tide, weather, beach morphology) on the high-energy Gironde coast, southwest France. Six years (2011–2017) of boreal summer (15 June–15 September) surf zone injuries (SZIs) were analysed, comprising 442 (fatal and non-fatal) drownings caused by rip currents and 715 injuries caused by shore-break waves. Environmental conditions at the time of the SZIs were used to train two separate Bayesian networks (BNs), one for rip-current drownings and the other one for shore-break wave injuries. Each BN included two so-called “hidden” exposure and hazard variables, which are not observed yet interact with several of the observed (environmental) variables, which in turn limit the number of BN edges. Both BNs were tested for varying complexity using K-fold cross-validation based on multiple performance metrics. Results show a poor to fair predictive ability of the models according to the different metrics. Shore-break-related injuries appear more predictable than rip-current drowning incidents using the selected predictors within a BN, as the shore-break BN systematically performed better than the rip-current BN. Sensitivity and scenario analyses were performed to address the influence of environmental data variables and their interactions on exposure, hazard and resulting life risk. Most of our findings are in line with earlier SZI and physical hazard-based work; that is, more SZIs are observed for warm sunny days with light winds; long-period waves, with specifically more shore-break-related injuries at high tide and for steep beach profiles; and more rip-current drownings near low tide with near-shore-normal wave incidence and strongly alongshore non-uniform surf zone morphology. The BNs also provided fresh insight, showing that rip-current drowning risk is approximately equally distributed between exposure (variance reduction Vr=14.4 %) and hazard (Vr=17.4 %), while exposure of water user to shore-break waves is much more important (Vr=23.5 %) than the hazard (Vr=10.9 %). Large surf is found to decrease beachgoer exposure to shore-break hazard, while this is not observed for rip currents. Rapid change in tide elevation during days with large tidal range was also found to result in more drowning incidents. We advocate that such BNs, providing a better understanding of hazard, exposure and life risk, can be developed to improve public safety awareness campaigns, in parallel with the development of more skilful risk predictors to anticipate high-life-risk days.
- Article
(6111 KB) - Full-text XML
- BibTeX
- EndNote
Wave-dominated beaches offer a playground for a variety of activities, but at the same time they pose a threat to water users. Following Stokes et al. (2017), a conceptual definition of life risk at beaches can simplify in terms of the number of people exposed to life-threatening hazards. As a result, a beach with a relatively high hazard level could exhibit a low level of risk if the number of beach users is low and vice versa. This way, the level of life risk can be modelled indirectly by estimating hazard and exposure.
There are two primary causes of surf zone injuries (SZIs), which can sometimes co-exit at the same beach (Castelle et al., 2018): (i) rip currents resulting in drowning incidents and (ii) shore-break waves which can result in, e.g., spine and shoulder dislocations. Rip currents are intense seaward-flowing narrow currents which can form through different driving mechanisms related to breaking waves (Dalrymple et al., 2011; Castelle et al., 2018). They form close to the shoreline and often extend beyond the surf zone. Therefore they can transport unsuspecting bathers offshore, who potentially panic and drown (Drozdzewski et al., 2012; Brighton et al., 2013). The shore-break wave hazard has received little attention in the literature compared to rip-current hazard. However, shore-break waves can cause a large number of injuries (Puleo et al., 2016), including severe spine injuries (Robbles, 2006). At certain beaches, shore-break waves can even be the primary cause of SZIs, e.g. up to 88 % at Ocean City, Maryland (Muller, 2018).
Rip flow speed, which is a proxy of rip-current hazard, has been addressed on many beaches through both field measurements and numerical modelling (see Castelle et al., 2016, for a review). In brief, rip flow speed generally increases with increasing wave height and period (e.g. MacMahan et al., 2006), more shore-normal incidence (e.g. MacMahan et al., 2005), generally lower tide levels (e.g. Brander and Short, 2001; Austin et al., 2010; Bruneau et al., 2011; Houser et al., 2013; Scott et al., 2014) and more alongshore-variable surf zone morphology (Moulton et al., 2017). It is also well known that shore-break waves are associated with steep beaches and longer-period waves (Battjes, 1974; Balsillie, 1985). In addition, the number of SZIs is also greatly influenced by the number of beachgoers exposing themselves to surf zone hazards. Given that warm sunny days with low winds typically result in increased beach attendance (Ibarra, 2011; Dwight et al., 2007), it is expected that during such days the life risk, and thus the number of SZIs, is increased.
Prominent environmental controls on SZIs were identified by comparing the frequency distribution of an environmental variable (e.g. significant wave height Hs, tide elevation η) during an injury, with the background frequency distribution of that variable (Scott et al., 2014; Castelle et al., 2019). The difference between two frequency distributions shows the disproportionate number of conditions that are associated with SZIs. At two different beaches along the Atlantic coast of Europe, Scott et al. (2014) and Castelle et al. (2019) showed that the number of drowning incidents increases disproportionately during warm sunny days with light wind, maximising beach attendance, and shore-normally incident long-period waves, maximising rip-current activity. Although such analysis provides an indication of the prominent environmental controls, it does not uncover the interplay between variables and the relative magnitude of each variable. A related challenge based on current research is filtering the effect of how water users' choices are influenced by environmental conditions (e.g. wave height Hs). For instance Stokes et al. (2017) found that beach morphology type has an impact on the number of water users. It can also be hypothesised that high surf and heavy shore-break waves discourage a number of the beachgoers from entering the water, even on warm sunny days, resulting in less exposure. Finally, the respective contributions of hazard and exposure to the overall life risk for shore-break waves and rip current are virtually unknown.
Prediction of SZIs together with a better understanding of the interplay between weather and marine conditions and effect on life risk at the beach could help to better anticipate high-risk days and further improve public safety awareness campaigns on surf zone hazards. This requires a high-order statistical approach like a Bayesian network (BN). BNs are probabilistic graphical models that are based on a joint probability distribution of a set of variables with a possible mutual causal relationship. BNs have been previously successfully used in coastal science, estimating morphological changes, changes in wave parameters in the surf-zone and coastal flood risks (Gutierrez et al., 2011; Plant and Holland, 2011; Fienen et al., 2013; Pearson et al., 2017). Stokes et al. (2017) compared a BN to a multiple linear regression approach to model exposure, hazard and, in turn, life risk to beach users at 113 beaches with lifeguards in UK. Even though the multiple linear regression method moderately outperformed the BN, Stokes et al. (2017) acknowledged the benefits of a BN approach to identify the characteristics of high-risk beaches from a large dataset. More recently, Doelp et al. (2019) used a BN to predict SZIs on the Delaware coast, which are primarily caused by shore-break waves (Puleo et al., 2016). They showed that a BN approach can improve predictions 69.7 % of the time but also acknowledged limitations in predicting anomalous injuries. A BN approach has the potential both to show good prediction skill to assist decision-making and to provide a better understanding of rip-current and shore-break hazards.
In this paper, a dataset (2011–2017) of 442 drowning injuries (fatal and non-fatal) and 715 shore-break injuries occurring in boreal summer (15 June–15 September) and corresponding environmental conditions along the Gironde coast in southwest France are used to create BNs for rip-current-related drownings and shore-break injuries. The study area and SZI dataset are described in Sect. 2. Section 3 presents the development of the BNs and the method used to train them and address their performance. Results are shown in Sect. 4 and are further discussed in Sect. 5 before conclusions are drawn.
2.1 Study area
The Gironde coast is located in southwest France and stretches approximately 140 km from the La Salie Beach (La Teste) in the south to the Gironde Estuary in the north and is interrupted by the Arcachon tidal inlet (Fig. 1a). It is a meso-macrotidal environment with spring tidal range reaching 5 m. Wave conditions vary seasonally with a 99.5 % exceedance significant wave height Hs of 5.6 m, and occasional severe storms with Hs>8 m. Summers are associated with smaller waves with a mean Hs of around 1.2 m and a dominant W-NW incidence (Castelle et al., 2019).
The coast is composed of high-energy sandy beaches backed by high and wide coastal dunes. Beaches are intermediate double barred, with deep and more or less regular rip channels incising the intertidal inner bar with an average spacing of approximately 400 m (Fig. 1a and b). Intense rip currents can flow through the rip channels, with rip flow intensity potentially exceeding 1 m/s even for low-energy (Hs<1 m) long-period waves (Castelle et al., 2016). Rip-current flow is strongly modulated by the tide level, with maximum rip-current activity occurring between low and mid-tide in typical summer wave conditions (Bruneau et al., 2011). In winter, more energetic wave conditions drive a more dissipative gently sloping beach face. In contrast, the upper part of the beach is steeper in summer due to smaller waves. Beach slope and rip channel morphology also show a large interannual variability enforced by large interannual variability in the wave climate (Dodet et al., 2019). Overall, beach states are similar along the coast but with increasingly steep beach face and deeper and more spaced rip channels southwards. Noteworthy is that beach morphology dramatically changes along sectors adjacent to the Arcachon lagoon and Gironde estuary where rip-current activity decreases, but tide-driven currents become substantial (>0.2 m/s during ebb and flood).
The Gironde coast is known for a large population of tourists visiting the beaches, which results in large numbers of injuries sustained by beachgoers and surfers of all levels (Fig. 1c) (Castelle et al., 2018; Tellier et al., 2019). Beaches are patrolled by lifeguards during the summer months of July and August. Patrolled periods are extended approximately from 15 June to 15 September at the busiest beaches. A designated and supervised bathing zone is delimited by two blue flags. However, many remote beach access paths through coastal dune tracks and many access points are situated on unpatrolled sections of beaches, kilometres away from any lifeguard presence (Castelle et al., 2019).

Figure 1(a) Location map of the Gironde Coast, southwest France. Black circles indicate municipalities where injuries were reported. Locations of Truc Vert beach and wave and tide data used in this study are also indicated; (b) aerial photograph of Truc Vert beach at low tide, exposing rip channels (Vincent Marieu); (c) crowded Lacanau beach in summer during a high tide (Julien Lestage).
2.1.1 SZI data
The SZI dataset used herein is detailed in Tellier et al. (2021). In short, SZIs were recorded by the medical emergency call centre SAMU (Service d'Aide Médicale d'Urgence) of Bordeaux for the Gironde department. Calls from beachgoers and lifeguards dealing with drowning or rescues received between January 2011 and November 2017 were used here. Excluding training calls, duplicates and calls lacking victims, a total of 5022 injuries were collected. Table 2 shows that the discrepancy between the total number of injuries and the combined shore-break- and rip-current-related SZIs is due to the large number of calls with insufficient information collected. Noteworthy is that the 916 surfing-related injuries (Table 1) occurring during this period were also disregarded for analysis. The reason for this is that a large number of surfer injuries involve collision with other surfers and are likely influenced by other factors (e.g. surf break quality, surf school activity) which are not related to physical hazards.
A SZI was classified as shore-break when the medical file explicitly stated “shore-break” or a French equivalent. Given that along this coast approximately 80 % of the drowning incidents involving bathers are caused by rip currents (Castelle et al., 2018), rip-related SZIs (drownings) were determined if a drowning stage (according to standardised medical classification) was reported in the medical file, with two notable exceptions. Drownings that were related to shore-break waves were classified as shore-break, because they were presumably not associated with rip currents. Similarly, surfing-related drownings were excluded as there is no evidence that most of the drownings of surfers are related to rip currents. Six mutually exclusive classes were found based on activity (see Table 2). Even though the activity was unknown for 1943 of the SZIs, drowning stage and the shore-break classifier provided the information to classify some of these SZIs as shore-break- or rip-related drowning. Amongst the population, 45 % was male and 33 % female, and for 21 % the sex was not recorded. The population is relatively young, with 43 % between 6 and 19 years old. A slightly elevated number of SZIs was found for the age group between 36–45 years old (see Fig. 2). This demographic is in line with another, shorter, dataset described in Castelle et al. (2018). By far most SZIs occurred at Lacanau beach (26 %), which is one of the most popular beaches that consequently attracts crowds in summer (see Fig. 2).
Table 1Activity distribution SZIs as indicated in the medical files between 8 January 2011 and 18 November 2017.
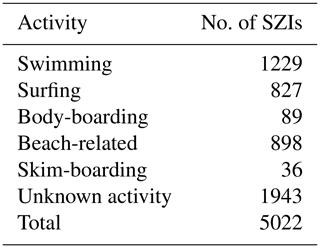
Table 2Post-processed categories to distinguish between rip-related drownings and shore-break injuries.

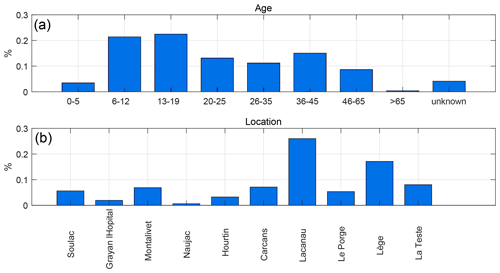
Figure 2Distribution of (a) age and (b) location of SZIs between 8 January 2011 and 18 November 2017. Beaches are ordered from north (left) to south (right).
For the purpose of this study, only summer periods between 15 June and 15 September were taken for each year because outside of this period SZIs become extremely rare events, which poses challenges for BN training. In the summer periods 442 drowning SZIs and 715 shore-break SZIs were found. This is the final population that was used in the Bayesian network.
2.2 Environmental data
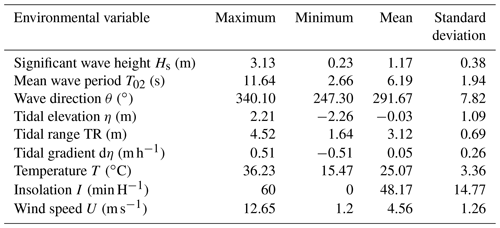
Environmental conditions were estimated at the time of each SZI by using a dataset comprising tide, wave and weather data. The dataset is described in detail in Castelle et al. (2019). Hourly weather data were collected at the Météo-France weather station Cap Ferret (Fig. 1a) from the RADOME (Réseau d'Acquisition de Données d'Observations Météorologiques Etendu). A tidal component analysis of a 3-month time series of continuous, storm-free Eyrac tide gauge data (Fig. 1) was performed to reconstruct a tide level time series at 10 min intervals. The average phase lag between the Eyrac tide gauge and beaches of the study area was estimated using tide charts from the Service Hydrographique et Océanographique de la Marine (France), resulting in an estimated maximum tide elevation error of 0.3 m at all sites, which is conservative. A wave model hindcast was used to provide continuous wave conditions at the coast. The WaveWatch 3 (Tolman, 2014) hindcast was performed on an unstructured grid with a resolution increasing from 10 km offshore to 200 m near the coast (Boudière et al., 2013). Wave conditions were extracted at an in situ directional wave buoy location c. 10 km offshore of Truc Vert at ca. 50 m depth and have been extensively validated with field data (e.g. Castelle et al., 2020). The primary metocean variables used are tidal elevation (η), significant wave height (Hs), mean wave period (T02), wave direction (θ), temperature (T), wind speed (U) and insolation (I). From tidal elevation, tidal range (TR) and tidal gradient (dη) were derived. Maximum, minimum, mean and standard deviation summer statistics are summarised in Table 3.
Table 3Statistics of environmental conditions of SZI records during summers between 15 June–15 September.
Previous work along this stretch of coast showed, qualitatively, the importance of upper beach slope and rip channel development on shore-break-related injuries and drowning incidents, respectively (Castelle et al., 2019). To further quantitatively address this link with the longer dataset used herein, we used monthly to bimonthly topographic surveys performed at Truc Vert beach since 2003 (the reader is referred to Castelle et al., 2020, for a detailed description of this beach monitoring program). This dataset was used to derive two morphological metrics. First, the inverse foreshore slope (IFS) was calculated as
where tan(β) is the beach slope between 1 and 3 m above mean sea level (a.m.s.l.) from a linear regression. To filter out extreme alongshore variations in IFS, the slope was averaged over four cross-shore transects that were systematically surveyed during the monitoring programme (Fig. 3).
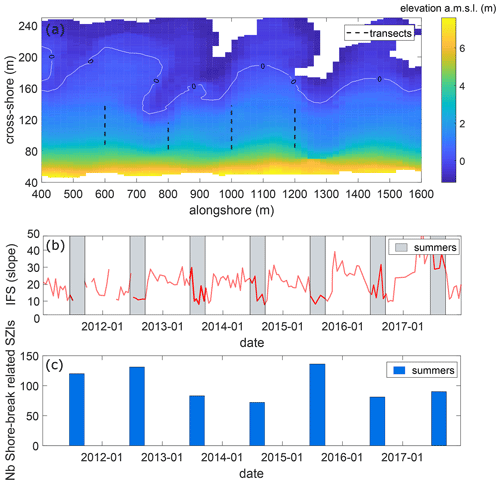
Figure 3(a) Example of a digital elevation model of Truc Vert beach on 29 April 2013, with the colour bar showing elevation above mean sea level. The four cross-shore transects used to compute the inverse beach slope IFS between 1 and 3 m a.m.s.l. are indicated by the dashed black lines. (b) Time series of IFS and (c) summer shore-break-related injuries.
Sinuosity (S) of the mean sea level iso-contour line was used to provide a measure rip channel development. It was defined as
where Lt is the true length, and Ls is the shortest Euclidean distance between the first and last points of the contour line (Fig. 4). A value larger than 1 indicates a high degree of sinuosity, whereas values close to 1 indicate a low degree of sinuosity. Before calculating the sinuosity of the shoreline, a high-pass filter was used to remove sinuous signals larger than 400 m. This was done to filter out larger-scale undulating patterns that are not enforced by the inner-bar rip channels (Castelle et al., 2015).
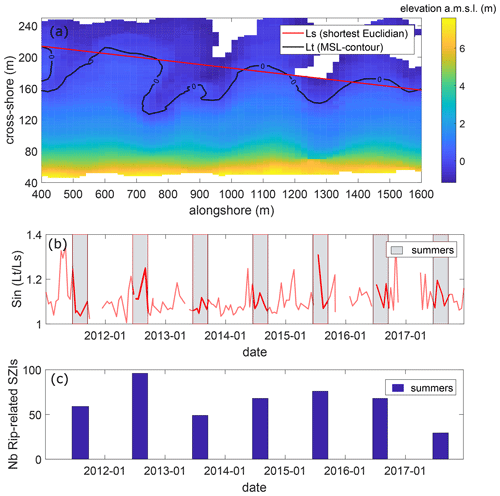
Figure 4(a) Example of a digital elevation model of Truc Vert beach on 29 April 2013, with the colour bar showing elevation above mean sea level. The red line indicates the shortest Euclidean distance. Time series of (b) sinuosity S and (c) number of summer rip-current-related drownings.
The metocean and topographic data collected at Cap Ferret or near Truc Vert are both located approximately in the centre of the study area. This data were assumed to be representative of wave and weather conditions along the entire study area. When constructing a BN (see next section), probabilities of a SZI occurrence must be compared to a probability of non-SZI. Therefore, a discretisation in time is needed. A 1 h time window was chosen to count the number of SZIs. To avoid a spurious distribution of non-SZIs, only daily hours between 7:00 and 19:00 were used.
3.1 Bayes' theorem and BN structure
Bayesian networks (BN) are based on Bayes' theorem (Korb and Nicholson, 2010). This theorem states that probabilities of a certain event can be updated, given new evidence, and can be stated as (Bayes, 1763)
where P(h|e) is the probability for a hypothesis h, given the evidence e. In Eq. (3), P(e|h) resembles the likelihood and P(h) corresponds to the prior probability of h before any evidence was given. Dividing the numerator by P(e) is a means of normalising, so that conditional probabilities sum to 1. For example P(h|e) could be the probability of a rip-current hazard, given that the tide was low.
A BN is a graphical representation of the probabilistic relations between a set of variables, using Bayes' theorem to describe the relation between variables (Korb and Nicholson, 2010). The links between nodes represent the direct dependency between variables (or nodes). A constraint on linking variables is that links cannot return to the beginning node, completing the cycle. Therefore the graphical representation of a BN is often referred to as a directed acyclic graph. If there is an arc from variable A to B, variable A is termed the parent variable and variable B the child variable. The relation between variables is often assumed to be causal, but is not necessarily the case. Once the structure is established, relations between variables are quantified according to conditional probability tables (CPTs), in the case of discrete variables. The probability of a value for a child variable is calculated for each possible value that the parent variable can take. Given that this is done for all variable nodes in the BN, two types of probabilistic reasoning become possible. Firstly, there is predictive reasoning, where a value is specified for each input variable. This results in a predicted probability for a target variable. Secondly, diagnostic reasoning is the other type for which, for example, given a SZI the BN can specify the probability that it was low tide.
3.2 Construction of the rip-current- and shore-break-related BNs
Constructing a BN requires a trade-off between complexity and predictability. This is determined by the number of variables chosen, the way variables are discretised and how the variables are linked. In general a simpler model is preferred over a complex model with the same performance, according to the principle of Ockham's razor (Jefferys and Berger, 1992). In this section we describe the choices that were made related to this trade-off, using the BN software package Netica v.6.05 (Norsys, 1998).
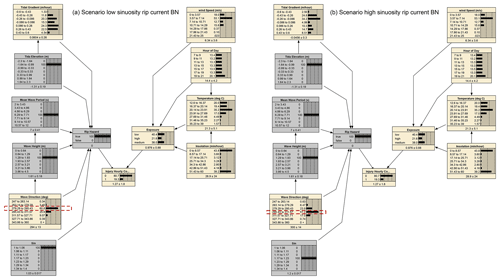
Based on earlier work on the environmental controls on SZIs in southwest France (Castelle et al., 2019) and some preliminary BN tests, the rip-current BN is made of (i) a hazard component that depends on hydrodynamic forcing parameters Hs, T02, θ, η and dη and a morphological component S and (ii) an exposure component that depends on the hour of the day H, temperature T and hourly insolation I defined as sunshine duration (see Fig. 5). The shore-break BN has a similar set-up, but the shoreline sinuosity is replaced by the inverse foreshore slope (IFS), and the tidal gradient (TG) is replaced by tidal range (TR). Such a structure was motivated by the fact that sometimes a simpler and computationally less expensive network can be obtained by adding so-called hidden or latent variables that limit the number of links between variables or the number of variables to include in the network (Russel and Norvig, 2010, p. 817). In this case, we used two hidden exposure and hazard variables which are known to control life risk and the number of SZIs (Stokes et al., 2017).
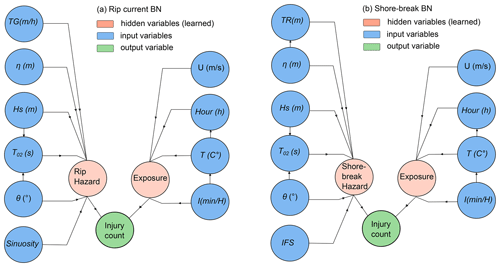
Figure 5Bayesian networks for (a) rip-current-related injuries and (b) shore-break injuries. Both BNs are defined by input variables, hidden variables, an output variable and their linkages.
In order to compare the probability of an injury with the probability of a non-injury, injuries were counted per hour for all summers. Consequently, the variable injury count was discretised as a binary variable with two possibilities: no injury or an injury. Where the number of injuries per hour exceeded 1, the cases were duplicated proportionally. Often hidden learned variables tend to be discretised with a small number of bins, as they do not have any prior information available. After testing both BNs, three dummy bins were chosen for the exposure variable and two dummy bins for the hazard variable. The number of bins chosen for the input variables determines the performance of the model to a larger extent. Therefore, different discretisation options were tested, keeping an equal bin width. This is shown in Sect. 3.4.
3.3 Bayesian network training
The probability tables of the hidden variables were calculated by using an algorithm that calculates the most likely distribution of the data, given the probability distributions of the other variables. The expectation maximisation (EM) algorithm is widely used in BNs to determine the most likely model given the data (Russel and Norvig, 2010). In a similar manner the algorithm finds the most likely value for occasionally missing data. The algorithm proceeds in the direction of the steepest gradient to find the minimum negative log likelihood for a model, given the data. The number of bins used to discretise variables in the BN determines how well data are described. The larger the number of bins, the better it describes the data until the point where there might be a bin for each value. On the other hand, a larger number of bins degrades the prediction skill of the BN, as it becomes harder to predict the correct bin. A BN might be trained slightly differently from one run to another, because it is a probabilistic process. Therefore, we used K-fold cross-validation to eliminate any bias that single model runs might hold. After Fienen and Plant (2015), Gutierrez et al. (2015), and Pearson et al. (2017) the cases were separated into k random partitions, where cases were used for training and calibration, and cases were left out for testing/validation. We used k=10 so that test cases make up 10 % of the total dataset. After 10 folds, mean values of performance metrics were taken to evaluate the performance of the BN.
3.4 BN performance metrics
Different performance metrics were used to address BN predictive performance. Here we used three relevant metrics: skill sk, log likelihood ratio LLR and area under ROC (receiver operating characteristic) AUC.
Skill was adapted from Fienen and Plant (2015) and was computed as
where σe is the mean squared error between observations and the BN forecast, and σo is the variance of observations. The skill metric in Eq. (4) expresses how close predictions of an injury match with observations of an injury, with sk=1 meaning perfect prediction.
Because skill is not an optimal measure for binary output variables, the AUC (area under ROC curve) was chosen as a complementary metric (Marcot, 2012). AUC is based on the ratio between the true positive predictions of the BN and the false positive predictions. Figure 6a shows the sensitivity on the y axis (true positive rate) and the specificity on the x axis (false positive rate) of a typical ROC curve from one of the model runs. If the dashed random classification line is equal to the ROC curve, this indicates that the model is not able to distinguish an injury from a non-injury. This corresponds to AUC=0.5. Figure 6b shows the confusion matrix on which the sensitivity and specificity are based.
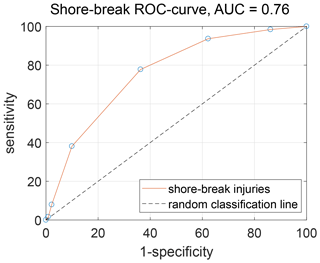
Figure 6Receiver operating characteristic curve (ROC) of the shore-break BN of one of the fold runs.
The third metric is the log likelihood ratio (LLR), adapted from Plant and Holland (2011) and Fienen et al. (2013). The LLR compares the prior probability of an injury with the posterior probability of a prediction, given the evidence (the input variables), which reads
where Fi is a forecast, in this case of a SZI, and Oj is an independent observation that was withheld from the forecast (e.g. a tidal elevation of −2.0 m). The LLR expresses the change in likelihood due to certain evidence in the form of observations. A LLR that exceeds zero indicates that the BN offers a better forecast than the prior probability. A LLR that is lower than zero indicates that the prior probability is a better forecast than the BN forecast. The LLR can be calculated for each predicted case and each variable and can then be summed over the entire BN (∑LLR). The LLR penalises wrong but confident predictions more than wrong predictions that are uncertain (Plant and Holland, 2011; Pearson et al., 2017). Therefore, it is a suitable metric to verify whether the BN is over-fitting or not.
Finally, in order to address how each input variable influences the target variable (SZI), the percentage of variance reduction Vr that was caused by updating the BN based on the evidence was computed as
where V(F) is the variance of a forecast prior to any evidence, and V(F|O) is the variance of the forecast, given the new evidence. V(F) and V(F|O) are calculated as
where p(fj) is the prior probability of the jth forecast, fj is the current value of the jth forecast, E(fj) is the expected value predicted by the BN of the jth forecast, p(fj|oi) is the predicted value of the jth forecast given the ith evidence case, E(fj|oi) is the predicted value of the jth forecast given the ith evidence case, M represents the number of evidence data and N is the number of predictions.
4.1 BN performance
To find the best BNs, a varying number of bins was tested to evaluate the trade-off between calibration and validation. For calibration, the BN was trained to make predictions of an injury based on the input variables of 90 % of the training cases. For validation, predictions of an injury were made based on the input variables of the 10 % left-out cases. Generally an increase in level of definition, i.e. number of bins, leads to a decrease in predictive capability and vice versa (Fienen and Plant, 2015; Fienen et al., 2013). Figures 7 and 8 show performance metrics for both the shore-break and rip-current BNs, respectively, as a function of the number of bins for the input variables.
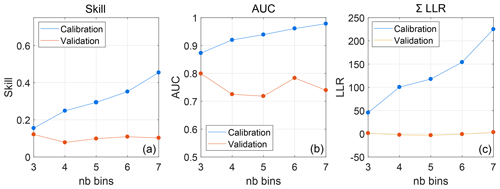
Figure 7Performance metrics of shore-break BN as a function of the number of bins of the input variables and for validation and calibration: (a) skill sk, (b) area under ROC curve AUC and (c) the summed log likelihood ratio ∑LLR.
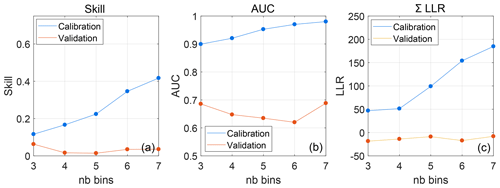
Figure 8Performance metrics of rip-current BN as a function of the number of bins of the input variables and for validation and calibration: (a) skill sk, (b) area under ROC curve AUC and (c) the summed log likelihood ratio ∑LLR.
It can be observed that the shore-break BN performs slightly better than the rip-current BN, as all performance metrics score better. Calibration results of the BNs are fair, with sk and AUC ranging from 0.15–0.43 and 0.89–0.98, respectively. Validation sk is smaller and ranges from 0.078–0.12 and 0.035–0.06 for the shore-break and rip-currents BNs, respectively. Validation AUCs are better, ranging from 0.71–0.8 and 0.63–0.68 for the shore-break and rip-current BNs, respectively. The sum of the LLR is systematically smaller than 0 for the validation of both BNs. This is either an indication that the prior estimate is on average better than the prediction of the model or that there are anomalous cases where the wrong but confident prediction is heavily punished by highly negative LLR values that result in a negative or near-zero LLR sum.
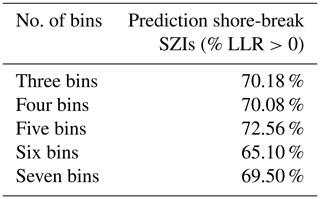
Tables 4 and 5 show that, depending on the number of bins chosen, model predictions are better than the prior probability estimate 62.21 %–79.9 % of the time. When five bins are chosen for the rip-current BN, 79 % of the time the model prediction is of added value. When five bins are chosen for the shore-break BN, 72 % of time the model prediction performs better. This shows that the negative and near-zero sums of the LLR displayed in Figs. 7 and 8 must be caused by anomalous events (the remaining percentages) that are confidently predicted wrong.
Table 4The percentage of LLR>0 for rip-current SZIs, indicating whether the prediction of the model is better than the prior probability.
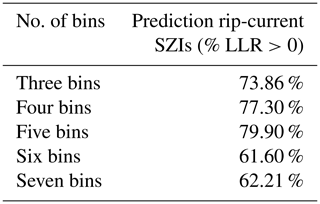
Table 5The percentage of LLR>0 for shore-break SZIs, indicating whether the prediction of the model is better than the prior probability.
The number of bins was varied from three to seven bins to choose the best trade-off between complexity and accuracy. Only the number of input variable bins was adjusted, keeping the output variables exposure, hazard and injury the same. In general, an increase in the number of bins leads to a better descriptive capability and a worse predictive capability (Fienen and Plant, 2015). When the number of bins is increased from three to four, a small decrease in sk and AUC can be noticed. However, a further increase in the number of bins does not significantly lead to worse sk, AUC or ∑LLR. AUC and sk show a small increase at six bins for the shore-break BN (Fig. 7a, b) and at six to seven bins for the rip BN (Fig. 7). Contrary to what is generally observed, validation sk, AUC and ∑LLR did not drop dramatically when complexity was increased. However, the percentage LLR>0 did drop for both BNs, when increasing the number of bins, which is in line with expectations.
4.1.1 Input variable sensitivity
Figure 9a shows the sensitivity of the shore-break BN to the input variables (six bins) and to the hidden variables exposure and shore-break hazard. For the shore-break BN, the learned variable exposure (Vr=23.5 %) has the strongest influence followed by the shore-break hazard variable (Vr=10.9 %). This suggests that exposure of water users has a more dominant control on the injury count than the shore-break hazard forcing variables. This is also reflected in Fig. 9b, where the hour of the day, temperature and insolation have larger values for Vr. These variables are followed by tide elevation, which is the most important shore-break hazard control (Vr=0.17 %). Consequently, mean wave period (Vr=0.07 %), tidal range (Vr=0.06 %), significant wave height (Vr=0.05 %) and wind speed (Vr=0.039 %) follow. The inverse foreshore slope IFS averaged over four profiles distributed along the coast has a noticeable impact (Vr=0.065 %) on the shore-break hazard. Wave direction is least sensitive to the injury count with Vr=0.025 %.
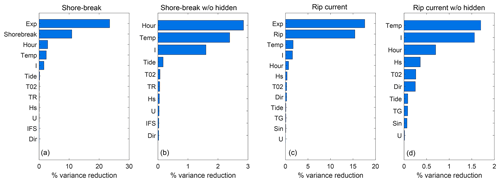
Figure 9Variance reduction (Vr) without hidden learned variables for the shore-break BN (seven bins) (a) with hidden learned variables and (b) without learned hidden variables and for the rip-current BN (six bins) (c) with hidden learned variables and (d) without hidden learned variables.
Figure 9c shows the sensitivity of the rip-current BN to the input variable (seven bins) including the hidden variables exposure and rip-current hazard. Rip-current exposure (Vr=17.6 %) and hazard (Vr=15.4 %) have similar influence, even though parents of exposure (insolation, temperature and hour) are more dominant in Fig. 9d. This suggests that it is the combined effects of input variables that cause a rip current (e.g. tide, wave direction and wave height) that have a strong influence on the occurrence of drowning incidents. This is different from what was observed for the shore-break BN. Within the exposure variables, the most sensitive for the rip-current BN are insolation (Vr=1.67 %), temperature (Vr=1.7 %) and hour of the day (Vr=1.56 %). Within hazard-related variables Hs and T02 have the highest Vr with 0.36 % and 0.26 %, closely followed by wave direction with 0.25 %, suggesting that incident wave conditions are the most important control on rip-current hazard. Shoreline sinuosity S reduces variance by 0.065 %. Interestingly enough, the percentage of variance reduction of exposure variables is of similar magnitude, although with different ordering, in both hazards (Fig. 9b, d).
4.2 Scenario analysis
Apart from the predictive ability of a BN, probabilistic scenario analysis can be a useful tool to understand how multiple variables interact. Figure 10a shows the prior joint probability distribution of the shore-break BN without updating based on any evidence. The two hidden variables, exposure (three bins) and hazard (two bins) do not contain any prior information and thus have equal probabilities for each bin. Figure 10b shows the joint probability distribution for a trained shore-break BN updated for the evidence that there was a shore-break SZI. In the latter, the distribution of tidal elevation shifts towards high tide. Additionally, there is a shift towards higher mean wave periods (T02) and a slight increase in probabilities of larger wave heights (Hs). Furthermore, temperature, hour of the day and insolation show a pronounced shift towards higher temperatures, less cloud cover and the afternoon between 14:00 and 16:30. Noteworthy is that when the BN was updated for larger wave heights, the probability of a shore-break-related injury increased. However, when the BN was updated with the evidence of an injury, intermediate wave height bins 0.75–1.5 and 1.5–2.25 m showed increased probability. This supports our hypothesis that large shore-break waves (Hs>2.5 m) can discourage bathers from entering the water, which results in fewer SZIs despite that the shore-break hazard is increased.
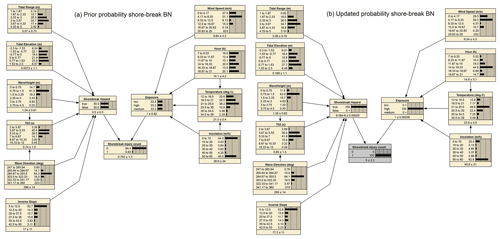
Figure 10(a) Prior probability distribution of the shore-break BN. (b) Updated probability distribution where the probability of an injury occurring was set to 100 %.
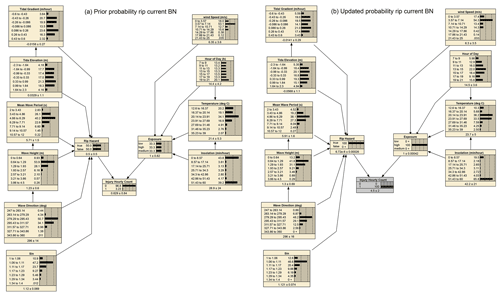
Figure 11(a) Prior probability distribution of the rip-current BN; (b) updated probability distribution of the rip-current BN when the probability of an injury occurring was set to 100 %.
A similar scenario analysis was performed for the rip-current BN. Figure 11a shows prior probabilities of the rip-current BN. The rip-current BN shows that according to the prior probability a shore-break-related injury (5.60 %) is more likely than a rip-current-related (fatal or non-fatal) drowning (3.23 %). Figure 11b shows the updated probability distributions for the rip-current BN, given that there is a 100 % chance of an injury. Although the probability distribution of the central bins of tidal gradients is similar in pattern, extreme tidal gradients ( > 0.43 m/h) show an increase in probability by about 50 %. Larger tidal gradients (both negative and positive) show a slight increase in probability, supporting the hypothesis that a rapid change in tidal elevation can surprise water users by driving the rapid onset of rip-current activity. Rip-current-related drownings are slightly more likely to occur when tides are low, with increased probabilities for larger Hs and T02. Wave direction shows a small increase in drowning probability for the NW-oriented directions. More sinuous shorelines (larger S values) show slightly increased probability of rip-current-related drowning (see for S>1.23 in Fig. 11b), suggesting that more alongshore-variable surf zone morphology increases the rip-current hazard. Wind speed has only little influence, although low wind speeds are slightly more likely during a drowning incident. Furthermore, the hour of the day shows a distribution that corresponds with the expected beach attendance. However, there is a disproportionate peak in the evening between 19:00 and 21:00. Furthermore, the highest peak is earlier between 13:00–15:00 (Fig. 11b) compared to shore-break injuries, although the bins slightly overlap (14:00–16:33, Fig. 10b). Temperature and insolation show comparable patterns to the shore-break BN, with warm sunny days between 20–28 ∘C having the highest probability.
Other rip-current BN scenarios were tested, providing insight into variable interactions. For instance, an interaction between the magnitude of shoreline sinuosity S and wave angle of incidence was explored, given average wave conditions (wave height and period) and a 100 % chance that there was a rip hazard (Fig. 12a and b). It can be observed that a low beach sinuosity (1–1.06) is correlated with higher probabilities for the shore-normally incident waves (around 279∘), while large beach sinuosity is associated with a larger probability for more NW angles of incidence (295.43–311.57∘). This indicates that for reasonably alongshore-uniform beaches more shore-normally incident wave conditions are required to have a rip-current hazard, which is not necessary for rip-channelled beaches.
5.1 BNs as a predictive tool for SZIs
Two separate BNs were created for shore-break SZIs and rip-current SZIs. This allowed use of different beach morphology metrics based on prior understanding of the physics of shore-break waves and rip-current dynamics. In addition, two hidden variables (exposure and hazard) were introduced for both BNs to decrease the number of connections and increase BN efficiency. Doelp et al. (2019) used population data to test a SZI ratio, normalised by the population, in addition to the binary injury likelihood. Although results were not dramatically improved in Doelp et al. (2019), including accurate water user data should improve BN model predictions along the Gironde coast. However, such data do not exist and will require future research effort.
Performance metrics indicate that the BNs improve prior estimates, but that BNs still have a significant percentage of wrong but confident predictions. This is due to over-fitting, which is a common issue with training a BN on rare events (unbalanced dataset) (Cheon et al., 2009). When the primary objective of a BN is prediction rather than description, a synthetic dataset can be created with an even distribution of events, although it degrades the BN descriptive ability. A similar suggestion to cope with this problem is to remove anomalous confident but wrong predictions (Doelp et al., 2019). Another issue limiting the BN predictive ability is that simple beach morphology parameters S and IFS were derived from a single site (Truc Vert). Summer beach morphologies surveyed along different beaches distributed along the coast should help improve IFS and S estimation and, in turn, prediction of rip-current drowning incidents and shore-break-related injuries. Similarly, optical satellite images should be explored to derive beach sinuosity S at the different beaches along the coast (Castelle et al., 2021). As indicated earlier, an estimation of beach attendance or water users should also improve BN predictive ability. Therefore, at this stage other tools should be used for life-risk prediction, like for instance models based on simple correlations between meteorological and oceanographic conditions and the incidence (Lushine, 1991; Lascody, 1998; Dusek and Seim, 2013; Scott et al., 2014), on the numerical modelling of rip flow speed (Austin et al., 2013), or on the combination of video images and numerical modelling (Jiménez et al., 2007). Recently, using the same SZI dataset, a logistic regression model was found to predict the risk of drowning along the Gironde coast up to 3 d in advance with good skill (Tellier et al., 2021).
Lastly, there were 1565 unknown injuries that could not be attributed to either a shore-break- or a rip-current-related injury. Theoretically, a well-trained BN could estimate which of the SZIs is more likely based on the environmental conditions. However, since the BNs are still limited in prediction, this should be explored in the future using improved BNs. Such a BN could help to retrospectively improve SZI statistics along surf coasts.
5.2 Environmental controls on SZIs and implications for beach safety management
In other studies frequency analysis was used to identify disproportionate environmental conditions during SZIs (Scott et al., 2014; Castelle et al., 2019). Some of the BN results are essentially in line with previous work. In short, more SZIs are observed for warm sunny days with light winds. Rip-current-related drowning incidents increase with increasing incident wave energy (height and period), more shore-normal incidence and lower tide level. In contrast, shore-break-related injuries are sustained at high tide levels and moderate wave height. In addition to previous work, here we proposed a method to quantify the role of beach morphology in SZIs. Beach sinuosity S, which is a measure of the alongshore variability of surf zone morphology, and inverse beach slope IFS were found to influence the occurrence of rip-current-related drowning incidents and shore-break-related injuries, respectively. These results are in agreement with current knowledge of rip flow intensity increasing with increasingly alongshore-variable surf zone morphology (Moulton et al., 2017) and shore-break waves occurring for steeper beach face (Battjes, 1974; Balsillie, 1985). We also found that rapid, positive or negative, change in tide level elevation (large dη) increase the probability of drowning incidents, with no difference between ebb and flood. Given that tide-driven current is negligible compared with rip currents along most of the beaches in southwest France, this suggests that rapid changes in tidal elevation driving the rapid onset of rip-current activity can surprise unsuspecting bathers and carry them offshore. However, another explanation is that some of the drowning incidents occurred in sectors adjacent to the Arcachon lagoon and Gironde estuary where tide-driven currents, which are maximised during ebb and flood (large ), can be intense.
In addition to the primary environmental controls on SZIs, in this study for the first time it was possible to identify the interaction between multiple input variables. For instance, it was found that it is the combined effects of tide elevation, wave direction and wave height that control rip-current hazard. In other words, even if you have shore-normally incident waves near low tide, if wave height is very small, there is no hazard and consequently a low probability of rip-current-related drownings. Such interactions, which were not possible to address in previous work (Scott et al., 2014; Castelle et al., 2019), are in line with the understanding of rip flow response to wave and tide conditions (Castelle et al., 2016). Our scenario analysis also indicates that, for reasonably alongshore-uniform beaches, more shore-normally incident wave conditions are required to have a rip-current hazard compared with rip-channelled beaches. This is also in line with observations and model outputs showing that, for the same obliquely incident wave conditions, rip cell circulation is transformed into an undulating, less hazardous longshore current for weakly (small S) alongshore-variable surf zone morphology, while rip cell circulation can be sustained for deep rip channels (MacMahan et al., 2008; Dalrymple et al., 2011). This shows that BNs including a pre-defined hidden hazard variable can provide insight into the influence of the primary input variables and their interactions on the hazard posed. Therefore, it could also be applied to other injuries, e.g. related to surfing activity, for which the causes (e.g. environmental, behavioural) and their interplay are poorly understood.
Studies addressing the environmental controls on shore-break-related SZIs are scarce (Puleo et al., 2016; Doelp et al., 2019) compared to drowning studies. The shore-break BN developed herein for the Gironde coast suggests that the predicted decrease in exposure for Hs>2.5 m, representing heavy shore-break waves at the shoreline, is thought to discourage beachgoers from entering the water near high tide. Importantly, this was not observed for rip-current-related drownings, which have a tendency to occur at low tide with the inner surf zone located on a much more gently sloping part of the beach profile. We hypothesise that in such less adverse conditions, beachgoers are less discouraged to enter the water, as opposed to facing large shore-break waves. However, further investigation on beachgoer behaviour in the presence of shore-break waves is required to test this hypothesis. This will also involve estimation of beachgoer affluence and estimation of the number of people in the surf exposing themselves to the physical hazards.
In addition, our variable sensitivity analysis indicates the shore-break-related injuries are more controlled by exposure-related variables than by hazard-related variables, contrary to rip-current-related drowning for which life risk is approximately equally distributed between hazard and exposure. This indicates that shore-break injuries are more likely to occur during busy days, whether moderate or heavy shore-break conditions are present. In contrast, the presence of intense rip currents is critical to drowning incidents.
A Bayesian network (BN) approach was used to model life risk and the controls and interactions of environmental (metocean and morphological) data on SZIs along a high-energy meso-macrotidal coast where shore-break and rip-current hazards co-exist. In line with previous work, the BNs show limited predictive skill. Although the shore-break and rip-current BNs improve prior estimates, they still have a large percentage of wrong but confident predictions, which is not tenable for life-risk prediction on beaches. However, the BNs provide fresh insight into the different environmental controls, their interactions, and their respective contribution to hazard and exposure. For the first time, the respective contributions of exposure and hazards to the overall life risk were quantified, showing the shore-break-related injuries are more controlled by the exposure than by hazard, contrary to rip-current-related drowning for which contributions are approximately equal. These results can guide the future development, or modification, of public education messaging, particularly on shore-break hazard, which has received little attention so far compared to rip currents, despite the large number of severe injuries sustained in shore-break waves along the Gironde coast. We advocate that such BNs should be developed in parallel with other risk predictors showing high predictive skill but providing much less diagnostic capability (Tellier et al., 2021).
The wave buoy data are publicly available through the French Candhis network operated by CEREMA. Weather station and tide gauge data are available from the Météo France Radome network and the SHOM, respectively. Wave hindcast is available from the MARC platform (Modelling and Analysis for Research in Coastal environment) at https://marc.ifremer.fr (MARC, 2019). The injury data collected on beaches are not publicly available due to restriction from the French National Committee for the Protection of Data Privacy.
BC and ET designed the research presented here. EdK designed the experiments, performed the modelling experiments and analysed all the results. BC and ET consulted on the experiments. EdK prepared the manuscript, and BC and ET reviewed and edited the manuscript.
The authors declare that they have no conflict of interest.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank Bruno Simonnet, who contributed to the injury data collection. Constructive suggestions to improve readability by Rieke Santjer were much appreciated. This study includes the beach monitoring study site of Truc Vert labelled by the Service National d'Observation (SNO) Dynalit, whose surveys are financially supported by Observatoire de la Côte Aquitaine (OCA) and SNO Dynalit.
This research has been supported by the Agence Nationale de la Recherche (grant no. ANR-17-CE01-0014).
This paper was edited by Mauricio Gonzalez and reviewed by Christopher Stokes and Jose A. Jiménez.
Austin, M., Scott, T. M., Brown, J. W., Brown, J. A., MacMahan, J. H., Masselink, G., and Russell, P.: Temporal observations of rip current circulation on a macro-tidal beach, Cont. Shelf. Res., 30, 1149–1165, https://doi.org/10.1016/j.csr.2010.03.005, 2010. a
Austin, M., Scott, T. M., Russell, P. E., and Masselink, G.: Rip Current Prediction: Development, Validation and Evaluation of an Operational Tool, J. Coast. Res., 29, 283–300, https://doi.org/10.2112/JCOASTRES-D-12-00093.1, 2013. a
Balsillie, J. H.: Redefinition of shore-breaker classification as a numerical continuum and a design shore-breaker, J. Coast. Res., 1, 247–254, 1985. a, b
Battjes, J. A.: Surf similarity, in: 14th Int. Conf. on Coastal Eng., 466–480, ASCE, New York, 1974. a, b
Bayes, T.: An Essay Towards Solving a Problem in the Doctrine of Chances, Philos. Trans. R. Soc. Lond., 53, 370–418, 1763. a
Boudière, E., Maisondieu, C., Ardhuin, F., Accensi, M., Pineau-Guillou, L., and Lepesqueur, J.: A suitable metocean hindcast database for the design of Marine energy converters, Int. J. Mar. Ener., 3–4, e40–e52, https://doi.org/10.1016/j.ijome.2013.11.010, 2013. a
Brander, R. W. and Short, A. D.: Flow kinematics of low-energy rip current systems, J. Coast. Res., 17, 468–481, 2001. a
Brighton, B., Sherker, S., Brander, R., Thompson, M., and Bradstreet, A.: Rip current related drowning deaths and rescues in Australia 2004–2011, Nat. Hazards Earth Syst. Sci., 13, 1069–1075, https://doi.org/10.5194/nhess-13-1069-2013, 2013. a
Bruneau, N., Bonneton, P., Castelle, B., and Pedreros, R.: Modeling rip current circulations and vorticity in a high-energy mesotidal-macrotidal environment, J. Geophys. Res.-Oceans, 116, C07028, https://doi.org/10.1029/2010JC006693, 2011. a, b
Castelle, B., Marieu, V., Bujan, S., Splinter, K. D., Robinet, A., Sénéchal, N., and Ferreira, S.: Impact of the winter 2013–2014 series of severe Western Europe storms on a double-barred sandy coast: Beach and dune erosion and megacusp embayments, Geomorphology, 238, 135–148, https://doi.org/10.1016/j.geomorph.2015.03.006, 2015. a
Castelle, B., Scott, T., Brander, R., and McCarroll, R.: Rip current types, circulation and hazard, Earth Sci. Rev., 163, 1–21, https://doi.org/10.1016/j.earscirev.2016.09.008, 2016. a, b, c
Castelle, B., Brander, R., Tellier, E., Simonnet, B., Scott, T., McCarroll, J., Campagne, J.-M., Cavailhes, T., and Lechevrel, P.: Surf zone hazards and injuries on beaches in SW France, Nat. Hazards, 93, 1317–1335, https://doi.org/10.1007/s11069-018-3354-4, 2018. a, b, c, d, e
Castelle, B., Scott, T., Brander, R., McCarroll, J., Robinet, A., Tellier, E., de Korte, E., Simonnet, B., and Salmi, L.-R.: Environmental controls on surf zone injuries on high-energy beaches, Nat. Hazards Earth Syst. Sci., 19, 2183–2205, https://doi.org/10.5194/nhess-19-2183-2019, 2019. a, b, c, d, e, f, g, h, i
Castelle, B., Bujan, S., Marieu, V., and Ferreira, S.: 16 years of topographic surveys of rip-channelled high-energy meso-macrotidal sandy beach, Sci. Data, 7, 410, https://doi.org/10.1038/s41597-020-00750-5, 2020. a, b
Castelle, B., Masselink, G., Scott, T., Stokes, C., Konstantinou, A., Marieu, V., and Bujan, S.: Satellite-derived shoreline detection at a high-energy meso-macrotidal beach, Geomorphology, 383, 107707, https://doi.org/10.1016/j.geomorph.2021.107707, 2021. a
Cheon, S.-P., Kim, S., Lee, S.-Y., and Lee, C.-B.: Bayesian networks based rare event prediction with sensor data, Knowl. Based Systs., 22, 336–343, https://doi.org/10.1016/j.knosys.2009.02.004, 2009. a
Dalrymple, R. A., MacMahan, J. H., Reniers, A. J., and Nelko, V.: Rip Currents, Annu. Rev. Fluid Mech., 43, 551–581, https://doi.org/10.1146/annurev-fluid-122109-160733, 2011. a, b
Dodet, G., Castelle, B., Masselink, G., Scott, T., Davidson, M., Floc'h, F., Jackson, D., and Suanez, S.: Beach recovery from extreme storm activity during the 2013–14 winter along the Atlantic coast of Europe, Earth Surf. Process. Landf., 44, 393–401, https://doi.org/10.1002/esp.4500, 2019. a
Doelp, M. B., Puleo, J. A., and Plant, N. G.: Predicting surf zone injuries along the Delaware coast using a Bayesian network, Nat. Hazards, 98, 379–401, https://doi.org/10.1007/s11069-019-03697-y, 2019. a, b, c, d, e
Drozdzewski, D., Shaw, W., Dominey-Howes, D., Brander, R., Walton, T., Gero, A., Sherker, S., Goff, J., and Edwick, B.: Surveying rip current survivors: preliminary insights into the experiences of being caught in rip currents, Nat. Hazards Earth Syst. Sci., 12, 1201–1211, https://doi.org/10.5194/nhess-12-1201-2012, 2012. a
Dusek, G. and Seim, H.: A probabilistic rip current forecast model, J. Coast. Res., 29, 909–925, https://doi.org/10.2112/JCOASTRES-D-12-00118.1, 2013. a
Dwight, R. H., Brinks, M. V., SharavanaKumar, G., and Semenza, J. C.: Beach attendance and bathing rates for Southern California beaches, Ocean Coast. Manage., 50, 847–858, https://doi.org/10.1016/j.ocecoaman.2007.04.002, 2007. a
Fienen, M. N. and Plant, N. G.: A cross-validation package driving Netica with python, Environ. Model. Softw., 63, 14–23, https://doi.org/10.1016/j.envsoft.2014.09.007, 2015. a, b, c, d
Fienen, M. N., Masterson, J. P., Plant, N. G., Gutierrez, B. T., and Thieler, E. R.: Bridging groundwater models and decision support with a Bayesian network, Water Resour. Res., 49, 6459–6473, https://doi.org/10.1002/wrcr.20496, 2013. a, b, c
Gutierrez, B. T., Plant, N. G., and Thieler, E. R.: A Bayesian network to predict coastal vulnerability to sea level rise, J. Geophys. Res.-Earth, 116, F02009, https://doi.org/10.1029/2010JF001891, 2011. a
Gutierrez, B. T., Plant, N. G., Thieler, E. R., and Turecek, A.: Using a Bayesian network to predict barrier island geomorphologic characteristics, J. Geophys. Res.-Earth, 120, 2452–2475, https://doi.org/10.1002/2015JF003671, 2015. a
Houser, C., Arnott, R., Ulzhofer, S., and Barrett, G.: Nearshore circulation over transverse bar and rip morphology with oblique wave forcing, Earth Surf. Process. Landf., 38, 1269–1279, https://doi.org/10.1002/esp.3413, 2013. a
Ibarra, E.: The use of webcam images to determine tourist-climate aptitude: Favourable weather types for sun and beach tourism on the Alicante coast (Spain), Int. J. Biometeorol., 55, 373–385, https://doi.org/10.1007/s00484-010-0347-8, 2011. a
Jefferys, W. H. and Berger, J. O.: Ockham's razor and Bayesian analysis, Am. Sci., 80, 64–72, 1992. a
Jiménez, J., Osorio, A., Marino-Tapia, I., Davidson, M., Medina, R., Kroon, A., Archetti, R., Ciavola, P., and Aarnikhof, S.: Beach recreation planning using video-derived coastal state indicators, Coast. Eng., 54, 507–521, 2007. a
Korb, K. B. and Nicholson, A. E.: Bayesian artificial intelligence, CRC press, London, UK, https://doi.org/10.1201/b10391, 2010. a, b
Lascody, R. L.: East central Florida rip current program, Natl. Weather Dig., 22, 25–30, 1998. a
Lushine, J. B.: A study of rip current drownings and related weather factors, Natl. Weather Dig., 16, 13–19, 1991. a
MacMahan, J. H., Thornton, E. B., Stanton, T. P., and Reniers, A. J. H. M.: RIPEX-observations of a rip current system, Mar. Geol., 218, 113–134, https://doi.org/10.1016/j.margeo.2005.03.019, 2005. a
MacMahan, J. H., Thornton, E. B., and Reniers, A. J. H. M.: Rip current review, Coast. Eng., 53, 191–208, https://doi.org/10.1016/j.coastaleng.2005.10.009, 2006. a
MacMahan, J. H., Thornton, E. B., Reniers, A. J., Stanton, T. P., and Symonds, G.: Low-Energy Rip Currents Associated With Small Bathymetric Variations, Mar. Geol., 255, 156–164, https://doi.org/10.1016/j.margeo.2008.08.006, 2008. a
Marcot, B. G.: Metrics for evaluating performance and uncertainty of Bayesian network models, Ecol. model., 230, 50–62, https://doi.org/10.1016/j.ecolmodel.2012.01.013, 2012. a
MARC: https://marc.ifremer.fr, last access: 1 April 2019. a
Moulton, M., Elgar, S., Raubenheimer, B., Warner, J. C., and Kumar, N.: Rip currents and alongshore flows in single channels dredged in the surf zone, J. Geophys. Res.-Oceans, 122, 3799–3816, https://doi.org/10.1002/2016JC012222, 2017. a, b
Muller, M. W.: Beach replenishment and surf-zone injuries along the coast of Delmarva, USA, Ocean Cast. Manage., 151, 127–133, https://doi.org/10.1016/j.ocecoaman.2017.10.013, 2018. a
Norsys, N. A.: Norsys Software Corp, available at: https://www.norsys.com (last access: 1 June 2019), v6.05, 1998. a
Pearson, S., Storlazzi, C. D., van Dongeren, A., Tissier, M., and Reniers, A.: A Bayesian-based system to assess wave-driven flooding hazards on coral reef-lined coasts, J. Geophys. Res.-Oceans, 122, 10099–10117, https://doi.org/10.1002/2017JC013204, 2017. a, b, c
Plant, N. G. and Holland, K. T.: Prediction and assimilation of surf-zone processes using a Bayesian network: Part I: Forward models, Coast. Eng., 58, 119–130, https://doi.org/10.1016/j.coastaleng.2010.09.003, 2011. a, b, c
Puleo, J., Hutschenreuter, K., Cowan, P., Carey, W., Arford-Granholm, M., and McKenna, K.: Delaware surf zone injuries and associated environmental conditions, Nat. Hazards, 81, 845–867, https://doi.org/10.1007/s11069-015-2108-9, 2016. a, b, c
Robbles, L.: Cervical spine injuries in ocean bathers: wave-related accidents, Neurosurgery, 58, 920–923, https://doi.org/10.1227/01.NEU.0000209941.18102.35, 2006. a
Russel, S. and Norvig, P.: Artificial Intelligence: A Modern Approach, Third Edition, Person Education, Boston, Munich, https://doi.org/10.1016/j.artint.2011.01.005, 2010. a, b
Scott, T., Masselink, G., Austin, M. J., and Russell, P.: Controls on macrotidal rip current circulation and hazard, Geomorphology, 214, 198–215, https://doi.org/10.1016/j.geomorph.2014.02.005, 2014. a, b, c, d, e, f
Stokes, C., Masselink, G., Revie, M., Scott, T., Purves, D., and Walters, T.: Application of multiple linear regression and Bayesian belief network approaches to model life risk to beach users in the UK, Ocean Coast. Manage., 139, 12–23, https://doi.org/10.1016/j.ocecoaman.2017.01.025, 2017. a, b, c, d, e
Tellier, E., Simonnet, B., Gil-Jardine, C., Castelle, B., Bailhache, M., and Salmi, L. R.: Characteristics of drowning victims in a surf environment: a 6-year retrospective study in southwestern France, Inj. Epidemiol., 6, 17, https://doi.org/10.1186/s40621-019-0195-x, 2019. a
Tellier, É., Simonnet, B., Gil-Jardiné, C., Lerouge-Bailhache, M., Castelle, B., and Salmi, R.: Predicting drowning from sea and weather forecasts: development and validation of a model on surf beaches of southwestern France, Inj. Prev., https://doi.org/10.1136/injuryprev-2020-044092, 2021. a, b, c
Tolman, H. L.: User manual and system documentation of WAVEWATCH III version 4.18, in: NOAA/NWS/NCEP/MMAB Technical Note 316, 194 pp., 2014. a