the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Probabilistic modelling of the dependence between rainfed crops and drought hazard
Andreia F. S. Ribeiro
Ana Russo
Célia M. Gouveia
Patrícia Páscoa
Carlos A. L. Pires
Extreme weather events, such as droughts, have been increasingly affecting the agricultural sector, causing several socio-economic consequences. The growing economy requires improved assessments of drought-related impacts in agriculture, particularly under a climate that is getting drier and warmer. This work proposes a probabilistic model that is intended to contribute to the agricultural drought risk management in rainfed cropping systems. Our methodology is based on a bivariate copula approach using elliptical and Archimedean copulas, the application of which is quite recent in agrometeorological studies. In this work we use copulas to model joint probability distributions describing the amount of dependence between drought conditions and crop yield anomalies. Afterwards, we use the established copula models to simulate pairs of yield anomalies and drought hazard, preserving their dependence structure to further estimate the probability of crop loss. In the first step, we analyse the probability of crop loss without distinguishing the class of drought, and in the second step we compare the probability of crop loss under drought and non-drought conditions. The results indicate that, in general, Archimedean copulas provide the best statistical fits of the joint probability distributions, suggesting a dependence among extreme values of rainfed cereal yield anomalies and drought indicators. Moreover, the estimated conditional probabilities suggest that when drought conditions are below moderate thresholds, the risk of crop loss increases between 32.53 % (cluster 1) and 32.6 % (cluster 2) in the case of wheat and between 31.63 % (cluster 2) and 55.55 % (cluster 2) in the case of barley. From an operational point of view, the results aim to contribute to the decision-making process in agricultural practices.
- Article
(2445 KB) - Full-text XML
- BibTeX
- EndNote
Agriculture is one of the activities most directly influenced by climate variability (Lesk et al., 2016; IPCC, 2012) and by extreme weather events in particular (IPCC, 2012). The latter are a major source of risk in agricultural systems, often entailing substantial crop yield losses (Bokusheva et al., 2016; Kogan et al., 2015; Saadi et al., 2015). Despite the constraints associated with the application of certain governmental policies in agricultural systems, the success of mitigating the consequences of climate extremes is largely dependent on the development of appropriate risk management strategies (Paredes et al., 2014; Quiroga et al., 2011). For this purpose, probabilistic information of the agricultural risk associated with certain meteorological conditions is currently a major requirement (Madadgar et al., 2017; Jayanthi et al., 2014; Iglesias and Quiroga, 2007), particularly within the scope of projected climate changes (Hernández-Barrera and Rodríguez-Puebla, 2017; Ferrise et al., 2011).
From both researcher's and stakeholder's perspectives, the management of agricultural drought risk has been a challenging task for decades, mainly in regions dominated by high precipitation variability and recurrent dry and warm episodes, such as the Mediterranean region and the Iberian Peninsula (IP) in particular (Vicente-Serrano et al., 2014; Sousa et al., 2011; Martin-Vide and Lopez-Bustins, 2006). Recent work has found significant negative trends of drought indexes in the IP, based on long-term time series including the entire 20th century, particularly in southern regions (Páscoa et al., 2017a; Sousa et al., 2011), and the expected declining of crop yields due to future warming conditions has also been pointed out (Hernández-Barrera and Rodríguez-Puebla, 2017; Ferrise et al., 2011).
The assessment of yield variability based on crop and meteorological information is crucial for a more stable farmer income and management (Reidsma et al., 2010). The recently developed drought index SPEI (Standardized Precipitation Evapotranspiration Index; Vicente-Serrano et al., 2010) is found to be particularly suitable for agricultural drought applications in Mediterranean regions (Zampieri et al., 2017) and shows significant correlations with crop yields in the IP (Ribeiro et al., 2019a; Páscoa et al., 2017b). On the other hand, crop models describing the biological processes are one of the existing tools used to assess crop productivity, e.g. CERES (Crop Environment REsource Synthesis) models (Capa-Morocho et al., 2016; Hlavinka et al., 2010) and AquaCrop (Paredes et al., 2016; Vergni et al., 2015). These crop models are important tools in agrometeorological studies as they are able to compute irrigation requirements and yield simulations, and they have been particularly useful for assessing the impacts of climate change on agricultural productions (Leng and Hall, 2019; Hlavinka et al., 2010). However, such models are limited in their ability to quantify the impact of climate variability on crop yields over larger scales (Estes et al., 2013), and the detailed representation of crop's biophysical interactions requires demanding parameterization settings and input data (Giménez et al., 2016; Paredes et al., 2014, 2016). Thus, empirical modelling constitutes an alternative for representing the large-scale impacts of drought conditions in the agricultural sector (Bokusheva et al., 2016; Kogan et al., 2015; Matsumura et al., 2015; Vicente-Serrano et al., 2006), requiring lower computation costs than mechanistic modelling (Estes et al., 2013; Ferrise et al., 2011).
In addition, the use of satellite-based data is increasing for agricultural purposes (Kogan et al., 2015; Rojas et al., 2011) and considerable correlations between remote sensing of vegetation and crop yield are found in the IP (Ribeiro et al., 2019a; Gouveia and Trigo, 2008; Vicente-Serrano et al., 2006). Some studies have considered the use of different remote sensing drought indicators to account for different crop sensitivities to drought, such as to moisture and thermal conditions over the vegetative cycle (Ribeiro et al., 2019a; Bokusheva et al., 2016; Zarei et al., 2013; Kogan, 2001). Moreover, the establishment of models for estimating crop yield under drought influence, using the combination of different drought indicators and different timescales of drought occurrence, have shown an added value in the performance of the crop yield simulations over the IP (Ribeiro et al., 2019a; Hernandez-Barrera et al., 2017; Vicente-Serrano et al., 2006).
The statistical modelling of crop yield variability under drought conditions has been previously done to estimate drought-related crop losses (Ribeiro et al., 2019a; Zampieri et al., 2017; Kogan et al., 2015). Some authors have estimated crop yield probability distribution functions to find crop-specific risk levels and have applied Monte Carlo methods to generate large sample sizes of yield distributions over Mediterranean areas (Resco et al., 2010; Iglesias and Quiroga, 2007). At the country level in Europe, Naumann et al. (2015) have developed drought damage functions using a single power law dependence between drought severity and the associated damage. At a regional level in the IP, regression techniques (Ribeiro et al., 2019a; Hernandez-Barrera et al., 2017; Hernández-Barrera and Rodríguez-Puebla, 2017) and artificial neural network (ANN) models (Ribeiro et al., 2019a) have been used to model the response of rainfed winter cereal yields to drought conditions. A major conclusion in Ribeiro et al. (2019a) was that there are stronger relationships between remote sensing indices and cereal yield in the northern sector of the IP and between SPEI and cereal yield in the southern sector of the IP. This character of the response of crop yields to climate conditions highlights how it varies according to the location, type of crop, moment of the vegetative cycle, drought indicator and temporal scale.
More recently, copula-based models have been applied for agricultural purposes, to model the dependence structures between crop yields and environmental conditions using joint distributions (Ribeiro et al., 2019b; Madadgar et al., 2017; Bokusheva et al., 2016; Li et al., 2015). The concept of copulas is quite popular in financial risk modelling and has been becoming a valuable tool to model the risks associated with climate hazards, such as droughts (Ganguli and Reddy, 2012; Mirabbasi et al., 2012; Serinaldi et al., 2009). Based on the Sklar's theorem (Sklar, 1959) a copula approach “joins” the probability of drought occurrence and the probability of crop losses caused by the drought event. A detailed description about the use of copulas is provided by Nelsen (2006).
A major advantage of copula methods is the generation of joint distributions independently of their marginal distribution functions (Maity, 2018; Nelsen, 2006). Copula functions show a great flexibility in modelling the dependence between individual variables (such as crop yield and drought indicators) with complex relationships without making significant assumptions. In addition, copula functions are adequate for modelling rare events in multivariate distributions and generating large samples, allowing us to find the probability that individual variables will not exceed a certain extreme (tailed) value (Madadgar et al., 2017). A recent study by Madadgar et al. (2017) has produced probability distributions of rainfed crop yields in Australia under drought impacts based on copula-based techniques, using the Standardized Precipitation Index (SPI) and the Standardized Soil moisture Index (SSI). For crop insurance purposes at the farm level in Kazakhstan, Bokusheva et al. (2015) modelled the joint distributions of wheat yields and two satellite-based drought indices (vegetation condition index, VCI, and temperature condition index, TCI). At the global scale, Leng and Hall (2019) have also used copulas to assess the likelihood of yield loss in response to droughts based on SPI for the a historical (1961–2016) and a future period (2071–2100) under the RCP8.5 emission scenario to investigate future changes in yield loss risk. The authors found that global wheat is more vulnerable to droughts than maize, rice, and soybeans and that global warming is expected to amplify drought-driven yield loss risk.
In this study, a copula-based approach is adopted to model the joint probability density function of crop yield and the drought conditions for probabilistic yield assessment, based on the data and empirical analysis previously considered in Ribeiro et al. (2019a). This method allows us to estimate the dependence structures between the probability distributions of crop yield and drought indicators using copula functions. The novelty and interest of this approach relates to the fact that this methodology will allow us to estimate the likelihood of crop loss and compare the expected losses under drought conditions and non-drought conditions in the IP. This key question is posed based on the current demand, of the most interest to stakeholders such as farmers and insurance companies, to mitigate agricultural drought risk over the major agricultural areas in the IP.
2.1 Study area and data
The exposure analysis performed by Ribeiro et al. (2019a) allowed the identification of two clusters of provinces in the IP dominated by rainfed agricultural practices (Fig. 1), located approximately in the regions of Castilla and Léon (cluster 1 – northern region) and Castilla–La Mancha (cluster 2 – southern region). Given the suitability of using these two clusters for an agricultural drought analysis at the regional level, here we have considered the same area selection criteria: provinces with more than 50 % of the territory occupied by agricultural areas and more than 50 % of rainfed crops according to the CORINE Land Cover (2012) (for more details please see Ribeiro et al., 2019a). Considering previous requirements, and for sequential purposes, the crop and drought hazard data used in Ribeiro et al. (2019a) have been incorporated in the present study to analyse the distributions of probabilities. Spatial averages of annual yield anomalies (t ha−1) of barley and wheat were computed over the two clusters during the period 1986–2012, based on production (t) and area (ha) information obtained from the Portuguese National Statistics Institute and the Spanish Agriculture, Food and Environment Ministry.
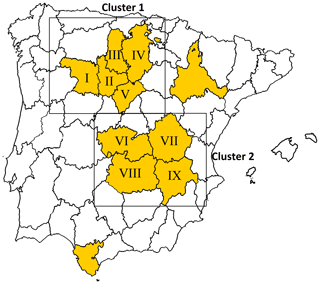
Figure 1Provinces with more than 50 % of the territory occupied by agricultural areas and more than 50 % of rainfed crops (yellow), according to CLC (2012), and selected clusters of provinces. Cluster 1 provinces: Zamora (I), Valladolid (II), Palencia (III), Burgos (IV) and Segovia (V). Cluster 2 provinces: Toledo (VI), Cuenca (VII), Ciudad Real (VIII) and Albacete (IX).
Drought conditions were investigated using the hydro-meteorological drought indicator SPEI and three satellite-based indices obtained from NOAA-AVHRR since 1981, namely the VCI (Kogan, 1990), the TCI (Kogan, 1995) and the Vegetation Health Index (VHI) (Kogan, 1995). The monthly drought index SPEI gridded values, with a spatial resolution of 0.5∘, were computed based on precipitation and temperature values from the Climate Research Unit TS3.21 database (Harris et al., 2014) using a variety of timescales (1 to 12 months). The weekly global maps of VCI, TCI and VHI were retrieved at 4 km spatial resolution from NOAA's ftp server (ftp://ftp.star.nesdis.noaa.gov/pub/corp/scsb/wguo/data/VHP_4km/geo_TIFF/, last access: 21 June 2018). While SPEI computation uses climatic water balance anomalies incorporating the role played by the evaporative demand on the occurrence of dry events (Vicente-Serrano et al., 2010), the remote sensing indices characterize the moisture, through the VCI, the temperature-induced stress, through the TCI, and health of vegetation, through the VHI.
Considering the vegetative cycle of wheat and barley, and in accordance with the results obtained by Ribeiro et al. (2019a), the data of VCI, TCI and VHI used in this work covered the period from week 35 (early September) to week 25 (late June) and data of SPEI covered January to June. Spatial averages of all of these indicators were computed for each provincial cluster and used for further modelling of the joint probability between the drought hazard and cereal yield anomalies over the period 1986–2012. Stepwise regression models (95 % confidence level) were established to select the timescales and months of SPEI, together with the weeks of VCI, TCI and VHI, better related with wheat and barley annual yield (Ribeiro et al., 2019a). The selection of the most relevant drought indicator for each cereal and cluster was performed based on the largest absolute value of the standardized regression coefficients from the models developed in Ribeiro et al. (2019a), in order to constitute pairs of cereal yield anomalies and drought indicators. Afterwards, for each cereal time series, the joint probability with drought conditions was estimated using one drought indicator.
2.2 Copula-based method
2.2.1 The concept of copula
Copula functions are powerful tools used to estimate the joint distribution between variables (Madadgar et al., 2017; Bokusheva et al., 2016; Zhang et al., 2011). The concept of copula was firstly introduced by Sklar (1959) to decompose a joint cumulative distribution function FXY(x, y) into two parts (Eq. 1): the marginal distribution functions FX(x)=u and FY(y)=v and the copula C describing the dependence between u and v,
where the margins u and v are uniformly distributed on the interval [0, 1] (Nelsen, 2006). This study adopts a bivariate modelling approach such that for each pair (X, Y) of cereal and drought indicators over each cluster we considered bivariate copula functions to estimate the joint probability distributions. Trivariate copulas have been proposed in the analysis of hydrological extremes (Afshar et al., 2016; Bezak and Brilly, 2014; Saghafian and Mehdikhani, 2014), but the development of higher-dimensional copulas exhibits very complex structures and further studies and evaluations are required. In comparison to high-dimensional copulas, the two-dimensional copulas involve much less computational cost and allow for more easily interpretable and illustratable relationships between the interval margins. For this reason, in the present study we restricted the analysis to the bivariate case using two-dimensional copulas, simplifying the interpretation of the results .
There is a range of copula families described in the literature that are able to estimate the dependence between the univariate variables (Nelsen, 2006). The most commonly used copula families focus on the Archimedean and elliptical classes (Maity, 2018). There are three Archimedean copulas that are particularly popular, given their simple functional form and their different patterns of dependence captures, i.e. Clayton, Gumbel and Frank, while there the two most popular elliptical copulas are derived from elliptical distributions, i.e. Gaussian and t copulas. These five copula functions are well-documented and have been employed in recent agrometeorological studies with a number of annual observations similar to our study (Madadgar et al., 2017; Zscheischler et al., 2017; Bokusheva et al., 2016). Table 1 summarizes the mathematical expressions of the referred copula functions considered in the present study.
Table 1Equations of the copula functions, where u and v are univariate variables, Φ−1 is the inverse of standard Gaussian CDF, is the inverse Student's t CDF, “df” is the degree of freedom, and ρ and θ are dependence parameters.

An important concept for studying extreme events is the tail dependence, whose importance is more critical than the overall dependence structure for risk analysis (Bokusheva, 2014). The joint tail behaviour describes the amount of dependence in the corners of upper-right and lower-left quadrants (i.e. joint extreme events) and its representation depends on the type of copula (Nelsen, 2006). The Frank, Gaussian and t copulas describe a joint symmetric structure with a symmetric tail dependence, i.e. the same degree of dependence in both pairs of extremes. The Clayton and Gumbel copulas have an asymmetric tail dependence with greater dependence in the lower or upper tail, suggesting greater probabilities of joint lower or upper extremes (i.e. lower or higher values of yield anomalies, given lower or higher values of drought indicators).
2.2.2 Fitting of the copula functions
The estimation of the copula parameters can be performed using different methods based on maximum likelihood, such as maximum likelihood estimate (MLE), inference functions for margins (IFM) or canonical maximum likelihood (CML) (Maity, 2018). With MLE, both individual margins and copula parameters are estimated together, whereas with IFM the marginal parameters are first estimated individually. In this study the statistical inference of the copula functions is performed with the CML method, which stands for a nonparametric estimation of the margins. In this way, the individual variables were first transformed to the unit scale (pseudo-observations) using the kernel density estimator of the cumulated distribution function (CDF) without making assumptions about the marginal distributions (Fig. 2). The drawback of the shorter sample size is surpassed by the nonparametric estimation of the margins, which avoids significant assumptions about their distributions, even when the available sample is rather small (Fahr, 2017; Corder and Foreman, 2011). The fitting of the bivariate copula functions was then applied to the pseudo-observations, and the dependence parameters were estimated by means of maximum likelihood (Fig. 2). Figure 2 summarizes the main steps of the copula-based approach adopted in the present study. For a detailed description on fitting methods please see Maity (2018).
Akaike's Information Criterion (AIC) is frequently employed as a model selection tool in copula modelling (Li et al., 2015; Mirabbasi et al., 2012). Therefore, the selection of the best copula function for each pair of cereal and drought indicators was made based on the evaluation of AIC values, calculated as AIC = (sum of log-likelihood) + 2 × (number of parameters) (Fig. 2). The copula function minimizing the AIC value was selected for each case. For verification purposes, the leave-one-out cross-validated log likelihood was also computed during the estimation of the parameters. This step was performed to confirm the reliability of the selected copula models and we found that, in general, the same functions are selected with both the AIC and the cross-validated log-likelihood criteria. For this reason, and given the wide use of the AIC, only the results for model selection based on the AIC will be presented.
2.2.3 Probability of non-exceedance and conditional probability of non-exceedance
After the estimation of the copula parameters, the established models are used to simulate 1000 pairs of uniformly distributed data (Fig. 2). In the present study, let denote the simulated CDF of yield x and the simulated CDF of drought indicator y. The data generation using the joint relationship preserves the dependence structure between the margins. The simulated data in the range [0, 1] are transformed back to the original scale using the kernel estimations of the inverse CDF, providing Xsim and Ysim, respectively.
First the copula simulations were used to estimate the risk of crop loss in terms of the probability of not exceeding a threshold value of yield, i.e. probability of non-exceedance (PNE) (Fig. 2). In this study we considered the threshold of minus one standard deviation (−XSD) of each cereal yield anomaly time series, as we are focused on real losses of yield and not just values below the mean (Eq. 2).
The PNE gives information about how likely the occurrence of a yield value below a certain threshold is. In other words, it gives the expected chance in percentage that the negative yield anomaly will not exceed (i.e. is not higher than) minus one standard deviation (−1 SD).
Afterwards we partitioned the simulated data points of Xsim into those corresponding to drought (e.g. SPEI −0.84; Agnew, 2000, and/or VHI 40; Kogan, 2001) and non-drought conditions (e.g. SPEI > −0.84 and/or VHI > 40) (Fig. 2). The respective CDFs were used to estimate the risk of crop loss in terms of the conditional probability of non-exceedance (CPNE) given by Eqs. (3) and (4), where Yth-dr is the drought threshold amounting to −0.84 and 40, respectively, when the SPEI and VHI or TCI are used.
For the purpose of validation and estimation of confidence intervals, the theoretical values of the above CPNE were inferred from the copula functions using the Eqs. (5) and (6) (deduced from the definition of conditional probability),
where and vth-dr=FY(Yth-dr) are the marginal probabilities of crop loss and drought occurrence obtained from the kernel-based univariate CDFs. The lower and upper bound of the 95 % confidence interval (ci) of the estimated copula dependence parameters were considered using the Eqs. (5) and (6) in order to obtain the confidence interval of CPNE coming from the inaccuracy of the copula parameter and to address if the CPNE using simulations (Eqs. 3 and 4) lies within the 95 % confidence level.
In sum, first we describe the joint probability of drought hazard and yield anomalies and simulate pairs of data preserving their dependence structure. After that, probability of crop loss (PNE) and conditional probability of crop loss (CPNE) are estimated, addressing whether the probability of crop loss under drought conditions is higher than during non-drought conditions and if distinguishing drought severity is important. The probability distributions (based on a normal kernel function) of the generated yield anomalies are also analysed for graphical visualization of the area corresponding to crop loss.
3.1 Fitting copula models
The estimates of the dependence between the yield anomalies and drought hazard were performed using the selected drought indicators outlined in Table 2. This selection of drought indicators highlights that the response of crop yields to climate conditions varies according to the location, type of crop, moment of the vegetative cycle and chosen temporal scale. While annual yield anomalies in cluster 1 are better characterized by short-term responses to the drought conditions based on the weekly values of TCI and VHI, the annual yield anomalies in cluster 2 are better characterized by the monthly response to the dry conditions based on the SPEI. In terms of predictability, the effects of temperature (TCI) and vegetation health (VHI) during late growth stages (weeks 23 and 22 correspond approximately to end of May and beginning of June, respectively, for wheat and barley) are the most influential conditions in the northern cluster. On the other hand, the yields in cluster 2 are influenced by drought conditions described by SPEI much earlier, in the beginning of the intermediate growth stages (February and April with 5 and 1 month timescales, respectively, for wheat and barley). In this way, the importance of including multiple drought response timescales is evidenced for predictability purposes and assessment of drought-related crop losses.
Table 2Variables used for copula application. In the first column, the numbers 1 and 2 correspond to the respective provincial cluster (clusters 1 and 2). In the second column, the numbers correspond to the selected weeks in the case of the remote sensing indices and to the selected months and timescales (in months) in the case of SPEI. The values of the standardized regression coefficients were determined by Ribeiro et al. (2019a).
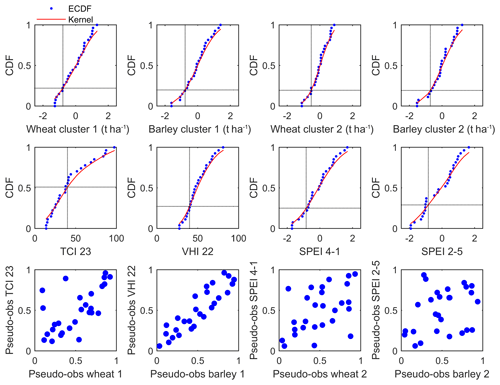
Figure 3Empirical cumulative distribution functions (ECDF, blue points), kernel density estimation of the CDF (red line), crop loss and drought thresholds (dotted black vertical line), respective marginal probabilities of crop loss and drought occurrence (dotted black horizontal line), and pseudo-observations (scatter) of the margins on the interval [0, 1].
Figure 3 shows the non-parametric estimations of the CDF of the individual variables from Table 2, here used to transform the variables to the unit scale (pseudo-observations) for the copula modelling. A good agreement with the ECDF is suggested (Fig. 3) and the crop loss and drought thresholds used in this study (−XSD and Yth-dr, respectively) are illustrated. A straightforward way of visualizing the association between the cereal yields and drought conditions was first carried out based on the scattering of the uniform pseudo-observations of the margins (Fig. 3, bottom panels). Most of the transformed data points are concentrated along the diagonal line (Fig. 3, bottom panels), mainly due to the correlations between the yield and selected drought indicators (Ribeiro et al., 2019a). Most of the work based on copulas has estimates of the marginal distribution functions (Afshar et al., 2016; Bokusheva et al., 2016; Mirabbasi et al., 2012), whereas this procedure has no requirement for prior knowledge of the marginal distributions, therefore incurring less significant assumptions.
The estimates of the dependence between the yield anomalies and drought indicators were performed using the copula functions from Table 1 (Gaussian, t copula, Clayton, Frank and Gumbel). Table 3 indicates each copula dependence parameter estimate (ρ, df or θ) and respective AIC values. Based on the values of AIC, a Gaussian copula, a Clayton copula and two Gumbel copulas were eligible to perform the best fits (Table 3). In general, the Archimedean copulas are better suited to estimate the joint distributions between crop yield and drought indicators in most of the cases (Table 3), with the exception of barley in cluster 1, which is better fitted by a Gaussian copula. Given that AIC penalizes the number of estimated parameters (Wilks, 2006), t copulas are not expected to be chosen, since they have two parameters that control the tail dependence.
Table 3Copula dependence parameter estimates (ρ, df or θ), with the 95 % confidence interval (ci) in parenthesis, and AIC values. The ci 95 % denoted by “−” indicates that the model was unable to compute the ci using the profile likelihood of the parameter. The selected models according to the lowest value of AIC are in bold.

The selected copula functions (Table 3) suggest that, in general, the relationship between yield and drought conditions is described by an asymmetric dependence in the tails of the joint distributions, except in the case of barley in cluster 1. This feature is illustrated in Fig. 4, showing the different shapes and contours of the selected copula densities. While wheat in cluster 1 and 2 shows a stronger dependence in the upper tail of the joint distributions based on Gumbel copulas (suggesting higher probability of observing a higher value of yield anomalies given a high value of the drought indicators), barley in cluster 2 shows stronger dependence in the lower-left tail based on a Clayton copula, suggesting higher probability of finding a lower value of yield anomalies given a low value of the drought indicators. The randomly generated yield and drought data were transformed back to the original scales (Fig. 4, bottom row) and the respective scatter plots indicate that more extreme values are generated using the joint distribution relationships. In general, the modelling of the joint distributions leads to results close to the real observations (Fig. 4, bottom panel).
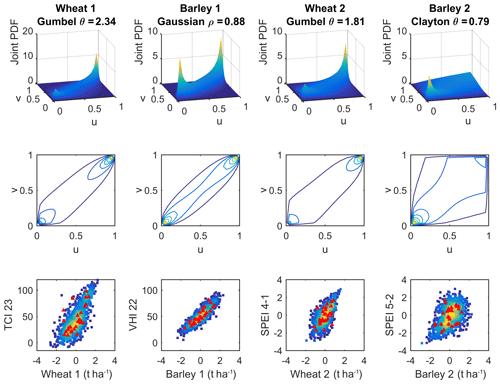
Figure 4Selected joint probability distribution functions (PDFs) where u and v are scalar values on the interval [0, 1] (top row), contours showing the two-dimensional view of PDFs (middle row) and observed (red triangles), and copula-based simulation (density squares) scatter plots of crop yields and drought indicators (bottom row).
3.2 Probability of non-exceedance and conditional probability of non-exceedance using copula simulations
After estimating the joint distribution functions and simulating pairs of data preserving the modelled dependence structures, we evaluate and compare the probability of non-exceedance (PNE) and conditional probability of non-exceedance (CPNE) as a function of the crop loss threshold. In this way, we evaluate if distinguishing drought severity leads to different risk values of crop loss in comparison to disregarding a drought threshold (using only simulations of yield) and compare the probability of crop loss under drought and non-drought conditions (by means of both simulations of yield and respective drought indicator). One of the key advantages of estimating the values of PNE and CPNE by means of the copula simulations is the use of larger samples that are comprised of more joint extreme values based on the joint behaviour of crop yields and drought hazard.
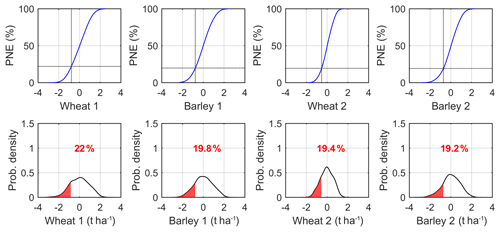
Figure 5Probability of non-exceedance (PNE) function (%) of yield anomalies (top row) in both clusters based on the derived simulations from the estimated copulas and respective probability density estimates (bottom row). In the bottom row, the red values indicate the probability of crop loss, which is also indicated in the top row by the intersected dashed lines, indicating the threshold of crop loss and respective PNE value.
Figure 5 shows the PNE curves and the distributions of the simulations of yield anomalies, with the respective crop loss area correspondent to the probability (%) of the yield anomaly not exceeding −1 SD. The PNE curves indicate a more than 19 % chance of having crop losses in all cases. According to Fig. 5, wheat at cluster 1 is the cereal with the highest risk level (22 %), followed by barley in cluster 1 (19.8 %), wheat in cluster 2 (19.4 %) and barley in cluster 2 (19.2 %) (Fig. 5). As mentioned before, the wheat's left tail area (negative yield anomalies) is slightly higher in cluster 1, suggesting a higher risk of wheat loss in the northern sector of the IP.
The following target was to compare the likelihood of crop loss under drought and non-drought conditions. Figure 6 shows the simulated crop yield anomalies during drought (orange boxplots) and non-drought (blue boxplots) events. As expected, the boxplots show lower (and negative in average) values of yield anomalies during drought events in comparison with non-drought episodes. Although the number of samples simulated under drought conditions is smaller than under non-drought conditions (Fig. 6), the use of copula simulations enhances the amount of simulated joint low extremes (i.e. co-occurrence of crop loss and drought events).
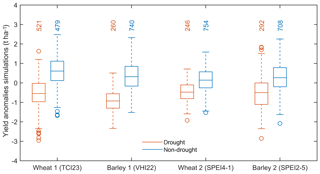
Figure 6Wheat and barley yield simulations, differentiating drought (orange) and non-drought conditions (blue) according to the respective drought indicator denoted in parenthesis in the x tick label. The numbers on top of the boxplots denote the sample size of the simulations under the different climatic conditions.
The differences in terms of crop losses between cereals and regions is much evident when differentiating the climatic conditions (Fig. 7), particularly during drought conditions. Figure 7 shows that the values of CPNE under drought (non-drought) conditions are above (below) the values of PNE illustrated in Fig. 5. In comparison with the distributions of yield simulations without conditioning to specific thresholds of the drought indicators shown in Fig. 5, in Fig. 7 the distributions of the yield simulations during drought events show a shift to the left towards negative values of yield anomalies, while the distributions of yield simulations during non-drought events show a shift to the right towards positive values of yield anomalies (Fig. 7). The case of barley in cluster 1 is quite distinct exhibiting a drought-related barley loss almost 3 times higher than the value illustrated in Fig. 5 (19.8 %), supporting the importance of conditional probabilities for agricultural drought risk purposes. The conditional probability of wheat loss (Fig. 7), is also higher when focusing on drought conditions, although it is less than 2 times the values shown in Fig. 5.
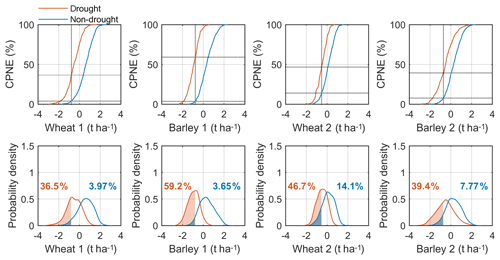
Figure 7Conditional probability of non-exceedance (CPNE) function (%) based on the derived copula simulations (top row) and respective probability density estimates (bottom row) under drought (orange) and non-drought conditions (blue). In the bottom row, the orange and blue values indicate the probability of crop loss under the different climatic conditions, which is also indicated in the top row by the intersected dashed lines, which indicate the threshold of crop loss and respective CPNE value.
Regarding the drought-related barley loss, the distribution of barley in cluster 1 is more shifted to negative yield anomalies, stressing that the drought risk of barley loss is higher on cluster 1 (59.2 %) than on cluster 2 (39.4 %), while it is quite similar on both clusters in Fig. 5. While barley suggests higher conditional probabilities of crop loss under drought conditions in cluster 1, wheat suggests higher conditional probabilities of crop loss under drought conditions in cluster 2 (46.7 %) in comparison to cluster 1 (36.5 %). Among all the cases, the highest level of drought-related crop loss is 59.2 %, observed in the case of barley in cluster 1, followed by wheat in cluster 2 with 46.7 % chance of crop loss under dry conditions.
The theoretical CPNE based on Eqs. (5) and (6) (Table 4) agrees quite well with the estimates of the CPNE in Fig. 7, thus corroborating the representativeness of the copula experiment using 1000 simulations. Nevertheless, the use of simulations allows us to increase the sample size and to generate more joint extreme values based on the dependence structures characterized by the selected copulas. In addition, the effect of the copula parameter (ρ or θ) inaccuracy due to the finiteness of available sample is considered in Table 4 in terms of the 95 % confidence level interval of CPNE based on the confidence interval of the copula parameters taken from Table 3. Table 4 shows that the theoretical CPNE under drought conditions still remains well above the CPNE under non-drought conditions, with their difference taking the smallest value at the lower bound of the copula parameter confidence interval. In most cases, those differences are positive, as expected from the effect of drought on crop yield, despite the relative finiteness of the sample to fit the copula models.
Table 4Theoretical CPNE (%) during drought and non-drought conditions (Eqs. 9 and 10) and respective lower and upper bounds of the 95 % confidence interval, where u−SD and vth-dr are the marginal probabilities of crop loss and drought occurrence and θ or ρ are the estimated copula parameters with 95 % confidence limits (Table 3). The only exception that gives greater values of CPNE during non-drought conditions rather than drought is denoted by “*”.
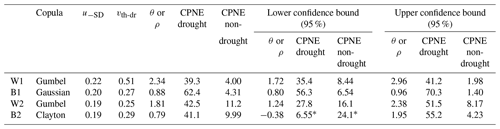
The results show that CPNE based on simulations (Fig. 7) and theoretical equations (Table 4) indicate that the probabilities of crop loss increase when drought conditions occur, even considering the two-sided confidence bound values of the copula parameters. Moreover, the results indicate that the CPNE using the simulations (Fig. 7) lies within the estimates of CPNE using the two-sided confidence bound values of the copula parameter at the 95 % level of confidence (Table 4). The only exception is the case of barley in cluster 2 considering the lower bound of θ, which gives greater probabilities of crop loss during non-drought conditions rather than during drought conditions, suggesting that factors other than water stress are the cause of crop failure. This result has to do with the negative value of the copula parameter in the lower confidence bound (), thus suggesting a weak dependence between crop loss and drought conditions in this case. However, at the 80 % confidence level (θ∈[0.03, 1.55]) the values of the copula parameter confidence bounds are both positive and give higher CPNE under drought conditions. This lack of accuracy of the CPNE at the 95 % in the case of barley in cluster 2 may be the reason why the CPNE under drought conditions are not the highest of all cases, as would be expected from a Clayton copula (which is known for capturing lower tail dependence).
This study investigated the usefulness of copula methods in estimating the likelihood of drought risk in wheat and barley cropping systems, when applied to two regions in the IP. Here we proposed modelling the joint probability of yield and drought hazard using copulas, based on a prior analysis of the association between drought and crop loss (Ribeiro et al., 2019a). The advantage of using a probabilistic approach is to meet the ambitious challenge of helping farmers and stakeholders in managing their operations by identifying the probability of crop loss under specific drought conditions. Hernández-Barrera and Rodríguez-Puebla (2017) and Ferrise et al. (2011) have shown that the projected warmer and drier climate will lead to wheat yield shortfall over the IP and Mediterranean, respectively, highlighting the importance of establishing novel statistical approaches for agricultural drought risk analysis. Other crops rather than rainfed cereals are also expecting significant losses during the next century in the IP (Saadi et al., 2015; Resco et al., 2010; Quiroga and Iglesias, 2009), and the here-proposed crop-specific approach could be applied to other agricultural systems under drought conditions for different regions around the world.
The novelty of the presented models, in comparison to other works addressing climate risk in the IP (e.g. Ribeiro et al., 2019a; Resco et al., 2010; Iglesias and Quiroga, 2007), is the focus on the impacts associated with droughts and on the joint probability of rainfed yield anomalies and drought hazards. Previous works using copulas in hydro-climatology studies have tended to focus on the joint distribution of different characteristics of the hazardous events, such as frequency, intensity, severity, and duration, among others (Li et al., 2015; Chen et al., 2013; Mirabbasi et al., 2012). Moreover, the restriction to the bivariate case allowed for a simpler interpretation of the results, in contrast to higher-dimension copulas (Afshar et al., 2016; Ganguli and Reddy, 2013), for instance by adding other factors influencing crop yield beyond drought as copula variables.
More recently, copulas have been applied to estimate the joint behaviour of drought conditions and the associated impacts in agricultural systems (Leng and Hall, 2019; Ribeiro et al., 2019b; Madadgar et al., 2017; Bokusheva et al., 2016), instead of using drought information only. We have adopted a similar approach to reproduce time-, regional- and crop-specific dependence of drought conditions, and the probability distribution of crop yield anomalies under drought conditions was estimated for risk analysis. In addition, the use of different drought indicators in this study represents an advantage since crops react differently to several factors at distinct moments and locations, highlighting the importance of quantifying the contributions of different drought indices on a regional scale (Peña-Gallardo et al., 2019; Zarei et al., 2013). A recent study by Peña-Gallardo et al. (2019) focused on the responses of wheat and barley cropping systems to different drought indices over Spain, have shown the different efficacies of several drought indices, stressing the importance of the multiscalar character of droughts, in particular of the SPEI. Similarly, and in accordance to previous work by the authors (Ribeiro et al., 2019a), the present study shows the adequacy of SPEI for the assessment of the agricultural risks associated with droughts in the IP and advances the added value of using the remote sensing of vegetation.
Overall, the results of the estimated copula functions have shown that Archimedean copulas are suitable to model the joint behaviour of yield anomalies and droughts, suggesting a dependence between extreme values of rainfed cereal yield anomalies and drought indicators, and the subsequent simulated distributions of crop yield anomalies are quite consistent with the observations. The results highlighted that the use of copulas for probabilistic assessment allows the estimation of the dependence in the tails of the distribution and was able to give the likelihood of crop loss under drought conditions. This feature is of the most interest in risk analysis given that it models the joint probability of occurrence of crop loss and drier events. Moreover, this study suggests the relevance of impact-centric approaches (also referred to the literature as “bottom-up” approaches; Zscheischler et al., 2018) to identify and characterize the hazards that lead to the larger impacts.
Moreover, it is important to stress that crop anomalies decline much more when drought conditions are below the mild or moderate threshold, suggesting a high agricultural drought risk level of wheat and barley in both clusters. While values of PNE in the crop loss threshold were low and similar for wheat in cluster 1 and barley in cluster 2, the values of CPNE in the crop loss threshold during drought years are considerably larger. The higher probability of crop loss obtained when analysing only drought conditions agrees with Páscoa et al. (2017b), which show a very high agreement between low wheat yield anomalies and drought conditions in the IP, even on provinces where the linear correlation is not significant.
Although there is a greater risk of crop loss during drought conditions, some losses can still be expected during non-drought events, particularly in cluster 2 (14.1 % and 7.77 % in the cases of wheat and barley, respectively). In the northern sector (cluster 1) the probabilities of crop loss under non-drought conditions have the lower values, displaying 3.97 % in the case of wheat and 3.65 % in the case of barley. Some studies point to crop damage attributable to excessively wet soils (Zampieri et al., 2017; Rosenzweig et al., 2002), due to delayed planting or later harvest, nutrient runoff and development of pests and diseases, among other factors, highlighting the complexity of quantifying agricultural risk levels for management purposes and the non-linear relation between crop yield and climate conditions. The lower values of CPNE under non-drought conditions in cluster 1 support the fact that the slightly high values of PNE in cluster 1 are mainly dominated by drought conditions.
With the present study it is not possible to establish sharp conclusions about the adequacy of the copula models to a specific type of drought indicator (remote sensing or hydro-meteorological), since only one type of drought indicator was considered for each cereal. In contrast, Bokusheva et al. (2016) have found that Gumbel copulas provided better fits representing the joint distribution of VCI and wheat, while Frank copulas better described the dependence between TCI and wheat yields in Kazakhstan. Madadgar et al. (2017) modelled the conditional probability density functions of crop yields under wet and dry conditions using SPI and SSI and found that a Clayton copula was the best function to model the dependence structures. Similarly, Leng and Hall (2019) have also used the same copula families and found that from 10 countries studied 5 used Clayton copulas to fit the joint distribution between wheat production and SPI. However, the referred studies were somehow more restrictive as they do not take advantage of using both remote sensing and hydro-meteorological drought indicators and do not select the most important one a priori.
To further the research, the application of SPEI methodology to climate projections of precipitation and temperature holds an added value to the estimation of drought risk levels for the next century. Likewise, the use of seasonal drought forecasts is also quite plausible in the approach presented in this study. Nevertheless, the presented results indicated the likelihood of crop loss based on drought conditions observed much earlier than the harvest time, particularly in cluster 2 using SPEI (February and April with 5 and 1 month timescales). Hence, given the uncertainty associated with the seasonal forecasts for regional drought predictability in the IP, the use of past information for predictability studies is still successfully used (Pires and Ribeiro, 2016) and continues to be a source of information from an operational point of view. Another potential use of this methodology for future research is the evaluation of its suitability at the province level and the assessment of whether other hazards (such as heat waves) are amplifying the impact of droughts on crop harvests.
The agricultural drought risk levels estimated in the present work aimed to improve the effectiveness of the agricultural management of rainfed cereals in the major agricultural areas of the IP. The main findings of this study are summarized below.
-
The dependence structure between crop yield anomalies and drought conditions is mainly asymmetrical, suggesting the existence of dependence among extreme values of yield anomalies and drought indicators.
-
The differences between the unconditional and the conditional probability suggest that the risk of wheat loss and barley loss can be underestimated without conditioning the probabilities of non-exceedance crop thresholds to specific drought levels.
-
The conditional probabilities of non-exceedance suggest that the risk of wheat loss and barley loss increases when drought events aggravate from normal or wet to moderate or severe conditions.
-
The values of conditional probabilities of crop loss under dry conditions suggest that the risk of drought-related barley loss is more likely to occur in the northern sector, while the risk of drought-related wheat loss is more likely in the southern sector, suggesting that sowing in cluster 1 (cluster 2) could be more focused on wheat (barley).
-
The overall results show the importance of the concept of conditional probability for distinguishing different meteorological settings associated with crop losses and the applicability of the copula theory. The use of copula simulations for the analysis of the co-occurrence of dry and low-yield extreme events has shown the additional value of this methodology for the estimation of drought-related crop failure.
-
Nevertheless, minor wheat and barley losses can still be expected during normal or wet conditions, stressing the complexity of the interactions between the agricultural systems and the climate. Particularly under the current climate change context, further high-impact-centric analysis are required, involving the cascading effects of different climate hazards.
The Portuguese crop yield database is published by the Portuguese National Statistics Institute and is available at https://ine.pt/xportal/xmain?xpid=INE&xpgid=ine_base_dados (last access: 9 November 2019) by selecting “main crops production (t) by geographic localization (Agrarian region) and species; annual (1)” and afterwards by selecting the species of wheat and barley. The Spanish crop yield is published by the Spanish Agriculture, Food and Environment Ministry in their Statistical Yearbook, which can be consulted at https://www.mapa.gob.es/es/estadistica/temas/publicaciones/anuario-de-estadistica/ (last access: 9 November 2019) by selecting the desired year, the chapter entitled “surfaces and crop productions”, and the species wheat and barley. The CORINE Land Cover datasets are publicly available at https://land.copernicus.eu/pan-european/corine-land-cover (last access: 9 November 2019). The remote sensing indices (VCI, TCI and VHI) database was accessed for the last time on 21 June 2018 at ftp://ftp.star.nesdis.noaa.gov/pub/corp/scsb/wguo/data/VHP_4km/geo_TIFF/ and the webpage has recently been updated to ftp://ftp.star.nesdis.noaa.gov/pub/corp/scsb/wguo/data/Blended_VH_4km/geo_TIFF/. The precipitation- and temperature-gridded values are publicly available from the Climate Research Unit (CRU) TS3.21 dataset by Harris et al. (2014) (https://doi.org/10.1002/joc.3711).
AFSR, AR and CMG conceived the idea of the present study. AFSR analysed the data, performed the statistical analysis, produced the figures and drafted the manuscript. AR and CMG supervised the work. CALP verified the analytical methods and designed the estimation of the conditional probabilities' uncertainty. AR performed the computations of SPEI. PP instructed the acquisition and analysis of the crop yield data. CMG instructed the acquisition and analysis of the remote sensing data. All the authors provided helpful insight in the discussion of the results and contributed to the design of the research and to the final paper.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Hydroclimatic extremes and impacts at catchment to regional scales”. It is not associated with a conference.
This work was partially supported by national funds through the FCT (Fundação para a Ciência e a Tecnologia, Portugal) under the projects CLMALERT (ERA4CS/0005/2016) and IMPECAF (PTDC/CTA-CLI/28902/2017). Ana Russo and Andreia Ribeiro thank FCT for grants SFRH/BPD/99757/2014 and PD/BD/114481/2016, respectively. The authors are also sincerely thankful to Ricardo Trigo (Instituto Dom Luiz) for his valuable suggestions and support.
This research has been supported by the FCT (Fundação para a Ciência e a Tecnologia, Portugal) (grant nos. SFRH/BPD/99757/2014, PD/BD/114481/2016, ERA4CS/0005/2016, WaterJPI/0004/2014 and PTDC/CTA-CLI/28902/2017).
This paper was edited by Fernando Domínguez-Castro and reviewed by three anonymous referees.
Afshar, M. H., Sorman, A. U., and Yilmaz, M. T.: Conditional copula-based spatial-temporal drought characteristics analysis – A case study over Turkey, Water (Switzerland), 8, 1–16, https://doi.org/10.3390/w8100426, 2016.
Agnew, C. T.: Using the SPI to Identify Drought, Drought Netw. News, 12, 6–12, 2000.
Bezak, N. and Brilly, M.: Applicability of copula functions in analysis of extreme hydrological, in: Proceedings of the Mediterranean Meeting on Monitoring, modelling and early warning of extreme events triggered by heavy rainfalls, PON 01_01503 – MED-FRIEND project, University of Calabria, 26–28 June 2014, Cosenza, Italy, 2014.
Bokusheva, R.: Improving the Effectiveness of Weather-based Insurance: An Application of Copula Approach, MPRA Pap. 62339, available at: https://mpra.ub.uni-muenchen.de/62339/ (last access: 9 November 2019), 2014.
Bokusheva, R., Kogan, F., Vitkovskaya, I., Conradt, S., and Batyrbayeva, M.: Satellite-based vegetation health indices as a criteria for insuring against drought-related yield losses, Agr. Forest Meteorol., 220, 200–206, https://doi.org/10.1016/j.agrformet.2015.12.066, 2016.
Capa-Morocho, M., Ines, A. V. M., Baethgen, W. E., Rodriguez-Fonseca, B., Han, E. and Ruiz-Ramos, M.: Crop yield outlooks in the Iberian Peninsula: Connecting seasonal climate forecasts with crop simulation models, Agric. Syst., 149, 75–87, https://doi.org/10.1016/j.agsy.2016.08.008, 2016.
Chen, L., Singh, V. P., Chen, L., Singh, V. P., Asce, F., Guo, S., Mishra, A. K., and Guo, J.: Drought Analysis using copulas, J. Hydrol. Eng., 18, 797–808, https://doi.org/10.1061/(ASCE)HE.1943-5584.0000697, 2013.
CLC 2012: Copernicus Programme Land Monitoring Service, available at: https://land.copernicus.eu/pan-european/corine-land-cover/clc-2012 (last access: 9 November 2019), 2012.
Corder, G. W. and Foreman, D. I.: Nonparametric Statistics: An Introduction, in: Nonparametric Statistics for Non-Statisticians: A Step-by-Step Approach, John Wiley & Sons, Inc., 1–11, https://doi.org/10.1002/9781118165881, 2011.
Estes, L. D., Bradley, B. A., Beukes, H., Hole, D. G., Lau, M., Oppenheimer, M. G., Schulze, R., Tadross, M. A., and Turner, W. R.: Comparing mechanistic and empirical model projections of crop suitability and productivity: Implications for ecological forecasting, Global Ecol. Biogeogr., 22, 1007–1018, https://doi.org/10.1111/geb.12034, 2013.
Fahr, A.: Nonparametric Analysis, Int. Encycl. Commun. Res. Meth., 3, 1297–1303, https://doi.org/10.1002/9781118901731.iecrm0168, 2017.
Ferrise, R., Moriondo, M., and Bindi, M.: Probabilistic assessments of climate change impacts on durum wheat in the Mediterranean region, Nat. Hazards Earth Syst. Sci., 11, 1293–1302, https://doi.org/10.5194/nhess-11-1293-2011, 2011.
Ganguli, P. and Reddy, M. J.: Risk Assessment of Droughts in Gujarat Using Bivariate Copulas, Water Resour. Manage., 26, 3301–3327, https://doi.org/10.1007/s11269-012-0073-6, 2012.
Ganguli, P. and Reddy, M. J.: Probabilistic assessment of flood risks using trivariate copulas, Theor. Appl. Climatol., 111, 341–360, https://doi.org/10.1007/s00704-012-0664-4, 2013.
Giménez, L., Petillo, M. G., Paredes, P., and Pereira, L. S.: Predicting Maize Transpiration , Water Use and Productivity for Developing Improved Supplemental Irrigation Schedules in Western Uruguay to Cope with Climate Variability, Water, 8, 1–22, https://doi.org/10.3390/w8070309, 2016.
Gouveia, C. and Trigo, R. M.: Influence of climate variability on European agriculture-analysis of winter wheat production, in: geoENV VI – Geostatistics Environ. Appl., Springer Netherlands, 27, 335–345, https://doi.org/10.3354/cr027135, 2008.
Harris, I., Jones, P. D., Osborn, T. J. and Lister, D. H.: Updated high-resolution grids of monthly climatic observations – the CRU TS3.10 Dataset, Int. J. Climatol., 34, 623–642, https://doi.org/10.1002/joc.3711, 2014.
Hernández-Barrera, S. and Rodríguez-Puebla, C.: Wheat yield in Spain and associated solar radiation patterns, Int. J. Climatol., 37, 45–58, https://doi.org/10.1002/joc.4975, 2017.
Hernandez-Barrera, S., Rodriguez-Puebla, C., and Challinor, A. J.: Effects of diurnal temperature range and drought on wheat yield in Spain, Theor. Appl. Climatol., 129, 503–519, https://doi.org/10.1007/s00704-016-1779-9, 2017.
Hlavinka, P., Trnka, M., Eitzinger, J., Smutný, V., Thaler, S., Žalud, Z., Rischbeck, P., and Křen, J.: The performance of CERES-Barley and CERES-Wheat under various soil conditions and tillage practices in Central Europe, Bodenkultur, 61, 5–17, 2010.
Iglesias, A. and Quiroga, S.: Measuring the risk of climate variability to cereal production at five sites in Spain, Clim. Res., 34, 47–57, https://doi.org/10.3354/cr034047, 2007.
IPCC: Managing the risks of extreme events and disasters to advance climate change adaptation, Cambridge University Press, available at: https://www.ipcc.ch/site/assets/uploads/2018/03/SREX_Full_Report-1.pdf (last access: 9 November 2019), 2012.
Jayanthi, H., Husak, G. J., Funk, C., Magadzire, T., Adoum, A., and Verdin, J. P.: A probabilistic approach to assess agricultural drought risk to maize in Southern Africa and millet in Western Sahel using satellite estimated rainfall, Int. J. Disast. Risk Reduct., 10, 490–502, https://doi.org/10.1016/j.ijdrr.2014.04.002, 2014.
Kogan, F., Guo, W., Strashnaia, A., Kleshenko, A., Chub, O., and Virchenko, O.: Modelling and prediction of crop losses from NOAA polar-orbiting operational satellites, Geomatics, Nat. Hazards Risk, 7, 886–900, https://doi.org/10.1080/19475705.2015.1009178, 2015.
Kogan, F. N.: Remote sensing of weather impacts on vegetation in non-homogeneous areas, Int. J. Remote Sens., 11, 1405–1419, https://doi.org/10.1080/01431169008955102, 1990.
Kogan, F. N.: Application of vegetation index and brightness temperature for drought detection, Adv. Space Res., 15, 91–100, https://doi.org/10.1016/0273-1177(95)00079-T, 1995.
Kogan, F. N.: Operational space technology for global vegetation assessment, B. Am. Meteorol. Soc., 82, 1949–1964, 2001.
Leng, G. and Hall, J.: Crop yield sensitivity of global major agricultural countries to droughts and the projected changes in the future, Sci. Total Environ., 654, 811–821, https://doi.org/10.1016/j.scitotenv.2018.10.434, 2019.
Lesk, C., Rowhani, P., and Ramankutty, N.: Influence of extreme weather disasters on global crop production, Nature, 529, 84–87, 2016.
Li, Y., Gu, W., Cui, W., Chang, Z., and Xu, Y.: Exploration of copula function use in crop meteorological drought risk analysis: a case study of winter wheat in Beijing, China, Nat. Hazards, 77, 1289–1303, https://doi.org/10.1007/s11069-015-1649-2, 2015.
Madadgar, S., AghaKouchak, A., Farahmand, A., and Davis, S. J.: Probabilistic estimates of drought impacts on agricultural production, Geophys. Res. Lett., 44, 7799–7807, https://doi.org/10.1002/2017GL073606, 2017.
Maity, R.: Statistical Methods in Hydrology and Hydroclimatology, Springer, https://doi.org/10.1007/978-981-10-8779-0, 2018.
Martin-Vide, J. and Lopez-Bustins, J.: The Western Mediterranean Oscillation and rainfall in the Iberian Peninsula, Int. J. Climatol., 26, 1455–1475, 2006.
Matsumura, K., Gaitan, C. F., Sugimoto, K., Cannon, A. J., and Hsieh, W. W.: Maize yield forecasting by linear regression and artificial neural networks in Jilin, China, J. Agric. Sci., 153, 399–410, https://doi.org/10.1017/S0021859614000392, 2015.
Mirabbasi, R., Fakheri-Fard, A., and Dinpashoh, Y.: Bivariate drought frequency analysis using the copula method, Theor. Appl. Climatol., 108, 191–206, https://doi.org/10.1007/s00704-011-0524-7, 2012.
Naumann, G., Spinoni, J., Vogt, J., and Barbosa, P.: Assessment of drought impacts and their uncertainties in Europe, Environ. Res. Lett., 10, 124013, https://doi.org/10.1088/1748-9326/10/12/124013, 2015.
Nelsen, R. B.: An introduction to copulas, Springer Series in Statistics, 1–269, 2006.
Paredes, P., Rodrigues, G. C., Alves, I., and Pereira, L. S.: Partitioning evapotranspiration, yield prediction and economic returns of maize under various irrigation management strategies, Agric. Water Manage., 135, 27–39, https://doi.org/10.1016/j.agwat.2013.12.010, 2014.
Paredes, P., Rodrigues, G. C., Cameira, M. do R., Torres, M. O., and Pereira, L. S.: Assessing yield, water productivity and farm economic returns of malt barley as influenced by the sowing dates and supplemental irrigation, Agric. Water Manage., 179, 132–143, https://doi.org/10.1016/j.agwat.2016.05.033, 2016.
Páscoa, P., Gouveia, C. M., Russo, A., and Trigo, R. M.: Drought trends in the Iberian Peninsula over the last 112 years, Adv. Meteorol., 2017 4653126, https://doi.org/10.1155/2017/4653126, 2017a.
Páscoa, P., Gouveia, C. M., Russo, A., and Trigo, R. M.: The role of drought on wheat yield interannual variability in the Iberian Peninsula from 1929 to 2012, Int. J. Biometeorol., 61, 439–451, https://doi.org/10.1007/s00484-016-1224-x, 2017b.
Peña-Gallardo, M., Vicente-Serrano, S. M., Domínguez-Castro, F., and Beguería, S.: The impact of drought on the productivity of two rainfed crops in Spain, Nat. Hazards Earth Syst. Sci., 19, 1215–1234, https://doi.org/10.5194/nhess-19-1215-2019, 2019.
Pires, C. A. L. and Ribeiro, A. F. S.: Separation of the atmospheric variability into non-Gaussian multidimensional sources by projection pursuit techniques, Springer, Berlin, Heidelberg, 2016.
Quiroga, S. and Iglesias, A.: A comparison of the climate risks of cereal, citrus, grapevine and olive production in Spain, Agric. Syst., 101, 91–100, https://doi.org/10.1016/j.agsy.2009.03.006, 2009.
Quiroga, S., Fernández-Haddad, Z., and Iglesias, A.: Crop yields response to water pressures in the Ebro basin in Spain: Risk and water policy implications, Hydrol. Earth Syst. Sci., 15, 505–518, https://doi.org/10.5194/hess-15-505-2011, 2011.
Reidsma, P., Ewert, F., Lansink, A. O., and Leemans, R.: Adaptation to climate change and climate variability in European agriculture: The importance of farm level responses, Eur. J. Agron., 32, 91–102, https://doi.org/10.1016/j.eja.2009.06.003, 2010.
Resco, P., Quiroga, S., Iglesias, A., and Sotés, V.: Risk of Climate Change for Grapevine Production in Mediterranean Areas, Le Bull. l'OIV, 83, 1–8, 2010.
Ribeiro, A. F. S., Russo, A., Gouveia, C. M., and Páscoa, P.: Modelling drought-related yield losses in Iberia using remote sensing and multiscalar indices, Theor. Appl. Climatol., 136, 203–220, https://doi.org/10.1007/s00704-018-2478-5, 2019a.
Ribeiro, A. F. S., Russo, A., Gouveia, C. M., and Páscoa, P.: Copula-based agricultural drought risk of rainfed cropping systems, Agric. Water Manage., 223, 105689, https://doi.org/10.1016/j.agwat.2019.105689, 2019b.
Rojas, O., Vrieling, A., and Rembold, F.: Assessing drought probability for agricultural areas in Africa with coarse resolution remote sensing imagery, Remote Sens. Environ., 115, 343–352, https://doi.org/10.1016/j.rse.2010.09.006, 2011.
Rosenzweig, C., Tubiello, F. N., Goldberg, R., Mills, E., and Bloomfield, J.: Increased crop damage in the US from excess precipitation under climate change, Global Environ. Change, 12, 197–202, https://doi.org/10.1016/S0959-3780(02)00008-0, 2002.
Saadi, S., Todorovic, M., Tanasijevic, L., Pereira, L. S., Pizzigalli, C., and Lionello, P.: Climate change and Mediterranean agriculture: Impacts on winter wheat and tomato crop evapotranspiration, irrigation requirements and yield, Agric. Water Manage., 147, 103–115, https://doi.org/10.1016/j.agwat.2014.05.008, 2015.
Saghafian, B. and Mehdikhani, H.: Drought characterization using a new copula-based trivariate approach, Nat. Hazards, 72, 1391–1407, https://doi.org/10.1007/s11069-013-0921-6, 2014.
Serinaldi, F., Bonaccorso, B., Cancelliere, A., and Grimaldi, S.: Probabilistic characterization of drought properties through copulas, Phys. Chem. Earth, 34, 596–605, https://doi.org/10.1016/j.pce.2008.09.004, 2009.
Sklar, A.: Fonctions de Répartition à n Dimensions et Leurs Marges, Inst. Stat. l'Université Paris, 8, 229–231, 1959.
Sousa, P. M., Trigo, R. M., Aizpurua, P., Nieto, R., Gimeno, L., and Garcia-Herrera, R.: Trends and extremes of drought indices throughout the 20th century in the Mediterranean, Nat. Hazards Earth Syst. Sci., 11, 33–51, https://doi.org/10.5194/nhess-11-33-2011, 2011.
Vergni, L., Todisco, F., and Mannocchi, F.: Analysis of agricultural drought characteristics through a two-dimensional copula, Water Resour. Manage., 29, 2819–2835, https://doi.org/10.1007/s11269-015-0972-4, 2015.
Vicente-Serrano, S. M., Cuadrat-Prats, J. M., and Romo, A.: Early prediction of crop production using drought indices at different timescales and remote sensing data: application in the Ebro Valley (north-east Spain), Int. J. Remote Sens., 27, 511–518, https://doi.org/10.1080/01431160500296032, 2006.
Vicente-Serrano, S. M., Begueria, S., and Lopez-Moreno, J. I.: A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index, J. Climate, 23, 1696–1718, https://doi.org/10.1175/2009JCLI2909.1, 2010.
Vicente-Serrano, S. M., Lopez-Moreno, J.-I., Beguería, S., Lorenzo-Lacruz, J., Sanchez-Lorenzo, A., García-Ruiz, J. M., Azorin-Molina, C., Morán-Tejeda, E., Revuelto, J., Trigo, R., Coelho, F., and Espejo, F.: Evidence of increasing drought severity caused by temperature rise in southern Europe, Environ. Res. Lett., 9, 044001, https://doi.org/10.1088/1748-9326/9/4/044001, 2014.
Wilks, D. S.: Statistical Methods in the Atmospheric Sciences, 2nd Edn., Academic Press, Oxford, UK, 2006.
Zampieri, M., Ceglar, A., Dentener, F., and Toreti, A.: Wheat yield loss attributable to heat waves, drought and water excess at the global, national and subnational scales, Environ. Res. Lett., 12, 064008, https://doi.org/10.1088/1748-9326/aa723b, 2017.
Zarei, R., Sarajian, M., and Bazgeer, S.: Monitoring Meteorological Drought in Iran Using Remote Sensing and Drought Indices, Desert, 18, 89–97, 2013.
Zhang, Q., Chen, Y. D., Chen, X., and Li, J.: Copula-Based Analysis of Hydrological Extremes and Implications of Hydrological Behaviors in the Pearl River Basin, China, J. Hydrol. Eng., 16, 598–607, https://doi.org/10.1061/(asce)he.1943-5584.0000350, 2011.
Zscheischler, J., Orth, R., and Seneviratne, S. I.: Bivariate return periods of temperature and precipitation explain a large fraction of European crop yields, Biogeosciences, 14, 3309–3320, https://doi.org/10.5194/bg-14-3309-2017, 2017.
Zscheischler, J., Westra, S., Van Den Hurk, B. J. J. M., Seneviratne, S. I., Ward, P. J., Pitman, A., AghaKouchak, A., Bresch, D. N., Leonard, M., Wahl, T., and Zhang, X.: Future climate risk from compound events, Nat. Clim. Change, 8, 469–477, https://doi.org/10.1038/s41558-018-0156-3, 2018.






