the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Estimates of tropical cyclone geometry parameters based on best-track data
Kees Nederhoff
Alessio Giardino
Maarten van Ormondt
Deepak Vatvani
Parametric wind profiles are commonly applied in a number of engineering applications for the generation of tropical cyclone (TC) wind and pressure fields. Nevertheless, existing formulations for computing wind fields often lack the required accuracy when the TC geometry is not known. This may affect the accuracy of the computed impacts generated by these winds. In this paper, empirical stochastic relationships are derived to describe two important parameters affecting the TC geometry: radius of maximum winds (RMW) and the radius of gale-force winds (ΔAR35). These relationships are formulated using best-track data (BTD) for all seven ocean basins (Atlantic; S, NW, and NE Pacific; and N, SW, and SE Indian oceans). This makes it possible to (a) estimate RMW and ΔAR35 when these properties are not known and (b) generate improved parametric wind fields for all oceanic basins. Validation results show how the proposed relationships allow the TC geometry to be represented with higher accuracy than when using relationships available from literature. Outer wind speeds can be reproduced well by the commonly used Holland wind profile when calibrated using information either from best-track data or from the proposed relationships. The scripts to compute the TC geometry and the outer wind speed are freely available via the following URL: https://bit.ly/2k9py1J (last access: October 2019).
- Article
(3313 KB) - Full-text XML
- BibTeX
- EndNote
Tropical cyclones (TCs) are among the most destructive natural hazards worldwide. TCs can cause hazardous weather conditions including extreme rainfall and wind speeds, leading to coastal hazards, such as extreme storm surge levels and wave conditions. The impacts of TCs are different in developed and developing countries. Generally, the worst effects in the developed world are direct economic losses. In the United States (US) alone, the mean annual damage due to TCs was estimated by Willoughby (2012) as USD 11.0 billion (year 2015). In the developing world, TCs result in immense social costs in terms of destruction and mortality. For example, between 1960 and 2004 more than half a million inhabitants of Bangladesh died as a consequence of TCs, primarily due to storm surges (Shultz et al., 2005). Peduzzi et al. (2012) showed that over the next 20 years the number of people exposed to TC risk will increase despite governmental efforts and implementation of adaptation measures. Additionally, TCs can also have devastating effects on nature, geomorphology, agriculture and freshwater supply. Thus, due to the extensive costs in lives, property and other damage, the ability to effectively model these storms is essential.
Numerical models can be applied to quantify the effects of TCs (e.g., Bloemendaal et al., 2018; Giardino et al., 2018; Vousdoukas et al., 2018). In hindcasting studies, this is generally done by using surface winds derived through data assimilation techniques (e.g., HRD Real-time Hurricane Wind Analysis System or H*WIND; e.g., Powell et al. 1998). However, in multi-hazard risk assessments, the spatial distribution of surface winds is generally not known. Therefore, wind fields based on best-track data (BTD) or synthetic tracks are generated using parametric wind profiles. Several (horizontal) parametric wind profiles (e.g., Fujita, 1952; Willoughby et al., 2006; Chavas et al., 2015) exist in literature, with the original Holland wind profile (Holland, 1980; hereafter H80) being the most widely used due to its relative simplicity. However, without calibration, parametric wind profiles are often unable to accurately reproduce the spatial distribution of winds in TCs (e.g., Willoughby and Rahn, 2004). This potentially leads to an under- or overestimation of wind speeds and associated coastal hazards. Calibration of TC formulations is possible by applying additional relationships, supported by the use of suitable data. In particular, information on the wind radii of cyclones can constrain the decay of wind speeds away from the eye wall and can be included in the most recent version of the Holland wind profile formulation (Holland et al., 2010; hereafter H10).
The radius of maximum winds (RMW), which describes the distance from the center to the strongest axially symmetric wind in the core of the cyclone, is one of the most important parameters to define a parametric wind profile. Moreover, the RMW plays an important role in the assessment of hazards induced by TCs since the storm surge level increases as a function of the RMW (Loder et al., 2009). Several relationships exist in literature to estimate the RMW (e.g., Willoughby et al., 2006; Vickery and Wadhera, 2008; Knaff et al., 2015). However, these relationships are derived for either the Atlantic or eastern Pacific Ocean (i.e., US coast) and are therefore not necessarily valid for other ocean basins. Each ocean basin has its own climatological properties and, for example, there seems to be an observational relationship between (mean) storm size, in terms of precipitation area (Lin et al., 2015) or wind speeds (Chavas et al., 2016), and the relative sea surface temperature (SST). The reason that most relationships are derived for the US coast is because of the high-quality data available (i.e., aircraft reconnaissance data). Relationships that estimate wind radii at different wind speeds are scarcer. Knaff et al. (2007) explicitly describe the TC surface winds using a modified Rankine vortex, which also makes it possible to compute different wind radii corresponding to different wind speeds (i.e., 34, 50, 64, 100 kn). However, these results are derived from BTD of the Atlantic, northeast Pacific and northwest Pacific oceans.
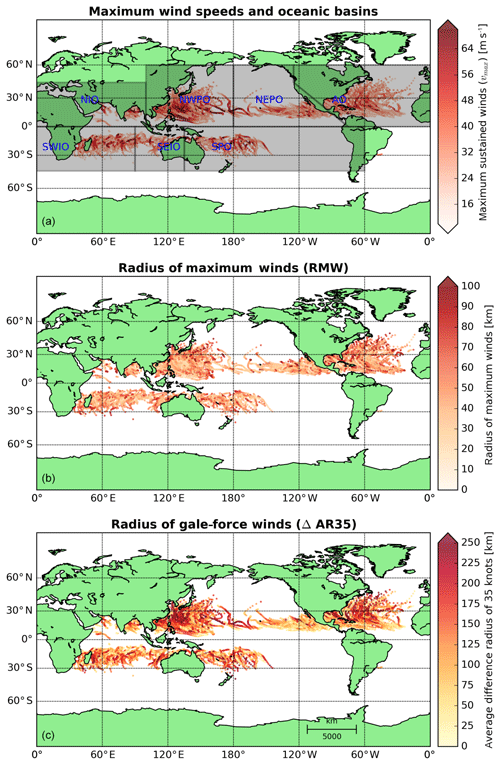
In the last decades, a large amount of higher-quality data have become available, which can be used to improve and validate the relationships and parametric wind profiles found in literature. In addition to the RMW, the wind radii of 35 (or 34), 50, 65 (or 64) and 100 kn (hereafter referred to as R35, R50, R65, R100) for the four geographical quadrants around the cyclone are currently recorded (see also Fig. 1a). There are numerous sources that can provide information on the spatial distribution of surface winds ranging from in situ observations (e.g., surface reports and buoy observations) to scatterometry (e.g., QuikSCAT; see Chavas and Vigh, 2014). Some methods are more reliable than others, but a posteriori it is not clear which sources were used for individual wind radii estimates in the best-track data (BTD). However, the currently operationally available satellite-based wind radii estimates are characterized by higher accuracy than in the past (Sampson et al., 2017).
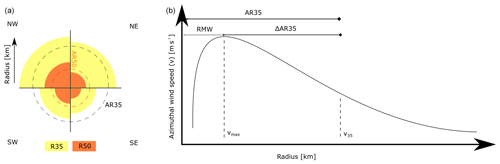
Figure 1Sketch of the terminology used in this paper. (a) The difference in wind radii for several wind values observed from different quadrants (NW, NE, SE, SW) and the average (AR) are shown. (b) RMW, AR35 and ΔAR35 are shown.
In this paper, new relationships are proposed to estimate the median RMW and radius of gale-force winds (ΔAR35) for each ocean basin. In addition, the standard deviation of the TC geometry is described explicitly, making it possible to treat the TC geometry stochastically with a certain probability distribution. This means that TC geometry is a random variable whose possible values are an ensemble of different outcomes. This is useful when TC size is not known and the probability of a relatively large and/or small TC and consequent risks need to be assessed (e.g., in a Monte Carlo analysis with synthetic tracks). Moreover, the paper demonstrates how the proposed relationships lead to improved error statistics compared to those found in literature. In addition, validation with QSCAT-R shows that outer wind speeds can be reproduced well by a parametric wind profile while using the newly developed relationships or observed values for RMW and wind radii.
This paper is outlined as follows: Sect. 2 describes the data used for the study. The new relationships describing the radius of maximum winds and radius of gale-force winds are derived in Sect. 3 and then validated in Sect. 4. Finally, Sects. 5 and 6 discuss and summarize the main conclusions of the study.
2.1 Best-track data (BTD)
Two data sources were used to describe the RMW and R35: data from the North Atlantic and Northeast and North Central Pacific database from the National Hurricane Center (NHC) and the dataset from the Joint Typhoon Warning Center (JTWC). The second dataset includes data from different ocean basins (northwest Pacific Ocean, the South Pacific Ocean and Indian Ocean). Note that the estimation of wind radii is rather subjective and strongly dependent on data availability as well as different climatology and analysis methods (e.g., aircraft observations versus the Dvorak method). In this paper, all the available data were used and potential shortcomings in the data are disregarded in order to fit new empirical stochastic relationships with the largest possible dataset and for every ocean basin separately. This approach, with its advantages and disadvantages, is discussed in Sect. 5.1. Some of the historical records do not contain values for either the RMW or R35, and therefore these records are discarded. Although these BTD are used as the ground truth, the errors in the best-track wind radii are estimated to be as high as 10 %–40 % (e.g., Knaff and Sampson, 2015). The accuracy of a single record depends on the quality and quantity of the available observational data. For example, if in situ observations were available in proximity to the TC or if a complete scatterometer passed over the TC, the accuracy may increase. However, information on the accuracy is not available per single data entry.
The archives from the NHC and JTWC contain 6-hourly storm positions and maximum intensity estimates of tropical and subtropical systems. For this analysis, all data points with a wind speed of 20 m s−1 or higher were included in the study since the focus is on tropical storms. Moreover, it is expected that parametric wind profiles cannot capture subtropical systems. Also, data points with an RMW larger than 100 km were excluded from the analysis because, generally, those points refer to tropical depressions, with large spatial coverage, which are outside the scope of this study. Moreover, the averaged value of R35 () over the four quadrants, similarly to Carrasco et al. (2014), was used. Only data entries with an estimate of R35 for all four quadrants were used. Therefore, all data entries additionally have an estimate for both RMW and , and using all the 6-hourly storm positions and maximum intensity estimates in the calibration and validation assumes statistical independence.
In this paper, TC geometry variables RMW and R35 were treated as stochastic variables. This means that, although physically not realistic, RMW could assume larger values than R35. In order to overcome this, a new variable was defined: the average difference in radius of 35 kn (ΔAR35; similar to Xu and Wang, 2015), or radius of gale-force winds, describing the difference between the RMW and the average radius of 35 kn (AR35); see Eq. (1). In practical applications, one would first retrieve the RMW based on data or estimate the RMW based on an empirical relationship. Secondly, the R35 would be calculated by adding up the RMW with the ΔAR35 (see also Fig. 1b). An additional advantage of introducing this new variable is that ΔAR35 contains considerably less scatter. This might imply a correlation between R35 and RMW, but is not further explored in this paper.
The BTD are divided into a calibration period (2000–2014) and a validation period (2015–2017). The combined BTD from the NHC and JTWC contain a total of 18 903 unique historical TC data entries, of which 14 800 were used for the calibration of the new empirical (stochastic) relationships, and 4103 were used for the validation of the estimated wind radii.
2.2 QSCAT-R
The QuikSCAT-based QSCAT-R database (Chavas and Vigh, 2014), with data for the period 1999–2008, was used to validate the computed outer (azimuthal) winds using H10 wind profile and the new proposed empirical relationship. The dataset, developed by researchers at the NASA Jet Propulsion Laboratory (JPL), is derived from the latest version of the QuikSCAT near-surface ocean wind vector database. It includes 690 unique TC profiles and it is optimized specifically for tropical cyclones with higher wind speeds. QuikSCAT measurements are accurate in all weather conditions for winds up to 40 m s−1 (Stiles et al., 2014), while their precision decreases for the inner wind speeds in the TC core (Hoffman and Leidner, 2005). Therefore, QSCAT-R data were only used to validate the outer wind speeds, and not the inner wind speeds or TC core. The tropical cyclone dataset carries a 1–2 m s−1 positive bias and a 3 m s−1 mean absolute error, which are not further discussed or taken into account in the analysis.
2.3 Ocean basins
According to the WMO (World Meteorological Organization), areas of TC formation were divided into seven basins (Fig. 2a). These include the North Atlantic Ocean (NAO), the northwest Pacific Ocean (NWPO), the northeast Pacific Ocean (NEPO), the South Pacific Ocean (SPO), the southwest Indian Ocean (SWIO), the southeast Indian Ocean (SWEI) and the north Indian Ocean (NIO). Other ocean basins (e.g., the South Atlantic Ocean) were not included in this study since weather systems in these areas rarely form a TC.
2.4 Data conversion
Data were converted to the International System of Units (SI) units (wind speeds in meters per second from knots with a conversion of 1 kn = 0.514 m s−1 and wind radii in kilometers from nautical mile with a conversion of 1 nm = 1.852 km). Throughout this study, a maximum sustained cyclone wind vmax has been determined at a 10 m elevation over open sea and 1 min average. The reason for this averaging is to be consistent with the JTWC and NHC, which also report the maximum sustained surface winds in terms of 1 min mean wind speed. Other nations, however, report maximum sustained surface winds averaged over a different time interval, which in some cases is 10 min. Also, numerical models often require 10 min averaged winds. For the conversion of 1 to 10 min averaged wind speed, a conversion factor equal to 0.93 can be used, based on WMO guidelines (Harper et al., 2010). However, in this study, conversions between 1 and 10 min wind speeds were not needed.
In this section, empirical relationships to estimate the radius of maximum winds (RMW; Sect. 3.1; see Fig. 2b) and the radius of gale-force winds (ΔAR35; Sect. 3.2; see Fig. 2c) were derived based on BTD from the calibration period (2000–2014).
3.1 Radius of maximum winds (RMW)
The Vickery and Wadhera (2008) relationship, derived for all major hurricanes (Δpc>30 hPa or vmax>35 m s−1) in the Gulf of Mexico and Atlantic Ocean (hereafter VW08), is one of the several relationships in literature providing an estimate of the RMW. VW08, derived based on H*WIND data, relates RMW to pressure drop in the eye and latitude. While we acknowledge the existence of several other relationships to estimate the RMW, VW08 was used due to its relative simplicity. Figure 3 compares RMW data from the BTD during the calibration period with results from VW08 in the form of a scatter plot with the maximum sustained wind speed (vmax) indicated by color intensity. The data show a large amount of scatter, for both lower and higher RMW values. However, there is a clear pattern visible that larger maximum sustained wind speeds result in a smaller RMW. This is in line with other observations (e.g., Willoughby and Rahn, 2004) or based upon idealized Sawyer–Eliassen models (e.g., Schubert and Hack, 1982; Willoughby et al., 1982) that TC eye walls generally contract during intensification. There is also a tendency in the dataset for TCs at higher latitudes to have larger eye diameters (e.g., Knaff et al., 2015; not shown here). The large negative bias of 17 km, computed as a difference between observed and computed RMW, is noteworthy, indicating that VW08 often underestimates the RMW, especially for lower maximum sustained wind speeds. Furthermore, the root-mean-square deviation (RMSD) of almost 29 km is also large compared to the observed mean. In particular, the scatter index (RMSD divided by the mean) and relative bias (bias divided by the mean) result in a scatter index of 53 % and a relative bias of −32 %.
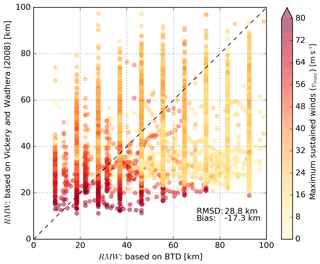
Figure 3Scatter plot describing BTD RMW (x axis) versus computed RMW based on VW08 (y axis). Data points are colored-coded based on the maximum sustained wind speeds in the BTD. The dashed line represents a perfect fit between BTD and computed data based on VW08.
Given the large spread in the data, as also shown in Fig. 3, it was decided to treat RMW as a stochastic variable. Instead of directly deriving an empirical equation which relates RMW to vmax using a least-square fitting procedure as typically done in similar studies, the following approach was used. At first, parameters of a probability density function (PDF) that fits the variation in RMW for a range of vmax and latitude values were fitted. Then empirical equations were derived that relate these parameters to vmax and latitude. The benefit of this approach is that it can produce an estimate of the most probable value for RMW (i.e., mode) or median and mean as well as its variance (e.g., 90 % prediction interval, PI).
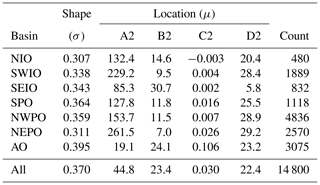
First, the RMWs for each TC category were fitted to various parent distributions. In particular, the following fitting parent distributions were tested by visual comparison and by applying the Kolmogorov–Smirnov test: normal, lognormal, Gumbel, Rayleigh and gamma. The lognormal distribution was found to provide the best fit with the measured data, and therefore further used to describe the distribution of RMW. This is also consistent with the distribution used for describing ΔAR35 and findings in literature (e.g., Dean et al., 2009). Secondly, the chosen parent distribution was used to fit the BTD in order to derive shape (σ) and location parameter (μ) of the lognormal distribution, dependent on latitude and wind speed. In particular, the BTD from the calibration period were divided based on a moving window with a bin of 10 m s−1 for wind speed and 10∘ for latitude (0–10, 1–11, 2–12, etc.). For each ocean basin fitting coefficients were determined for a constant shape parameter and a location parameter with exponential decay. This resulted in Eq. (2) for the μ parameter, which, for a lognormal distribution, corresponds to the median value:
where μRMW represents the location parameter of the lognormal distribution for RMW, vmax is the maximum (1 min averaged) wind speed, θ is the latitude in degrees, and A2, B2, C2 and D2 are fitting coefficients.
As observed in literature (e.g., Knaff et al., 2015), the median RMW (μRMW) in Eq. (2) depends on vmax (i.e., higher wind speeds result in lower RMW) and latitude (i.e., higher latitude results in higher RMW). The addition of storm duration or the use of the axisymmetric component of the wind speed only as input parameters resulted in very limited skill improvement in the estimation of RMW; therefore these variables were discarded. This procedure was applied to the combined JTWC and NHC BTD from the calibration period at all basins, and then for each individual ocean basin. Table 1 contains the shape and location values for the fitting parameters to be used in Eq. (2).
A scatter plot describing the RMW derived from BTD as a function of the maximum wind speed and for (an arbitrarily chosen) latitude of 10∘ and computed according to Eq. (2) is shown in Fig. 4. The green line shows the median RMW based on the BTD, whereas the solid blue line represents the mean RMW obtained from Eq. (2). The black lines indicate the 5 % and 95 % exceedance values computed based on BTD. Finally, the 90 % prediction interval is shown using red shading. The figure shows how the variance in RMW decreases (both in the data and in the empirical relationship) as a function of vmax, indicating that faster-rotating cyclones are characterized by less noise. The new empirical equation for RMW is evaluated in Sect. 4.
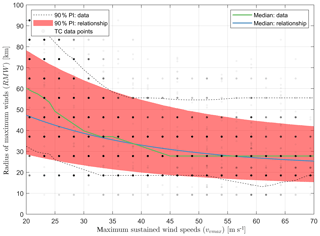
Figure 4Scatter plot describing RMW (BTD and computed; y axis) as function of the maximum sustained wind speeds (x axis; and the latitude; not shown). The blue line is the median of the proposed relationship derived for all basins at an arbitrarily chosen latitude of 10∘. The green line is the median of the BTD. The red area shows the 90 % prediction interval (PI) based on the proposed relationship for all basins. The 5 % and 95 % exceedance values from the BTD are presented as black dashed lines. The gray dots are observation points in which more frequent observations are shown as darker points and less frequent observations as lighter points.
3.2 Radius of gale-force winds (ΔAR35)
By applying a parametric wind profile, it is possible to derive the ΔAR35. Here, the H10 wind profile was applied, in which the B parameter was computed based on H80 (Eq. 3a), and in which information on the wind radii of cyclones was used to constrain the decay of wind speeds away from the eye wall (Eq. 3b). When no additional information on the wind radii is provided, H10 reduces to the original H80 wind profile, which is often unable to accurately reproduce the spatial distribution of winds in TCs (e.g., Willoughby and Rahn, 2004).
Here B represents the Holland pressure profile parameter, ρa is the air density (assumed constant at 1.15 kg m−3), e is the base of natural logarithms, Δpc is the pressure drop in the core of the TC in hectopascals, x is the exponent used to compute the wind profile in H80–H10 and xn represents the adjusted exponent to fit the peripheral observations at radius rn.
Knaff et al. (2007) relationships (hereafter CLIPER, climatology and persistence models), derived for the NAO, NWPO and NEPO, are among the few in literature providing an estimate of the TC surface winds. Knaff et al. (2007) fitted a modified Rankine vortex on the BTD of NHC and JTWC, which also makes it possible to retrieve the ΔAR35. Figure 5 compares ΔAR35 from the BTD, derived from the calibration period, with results from CLIPER, in which vmax is indicated by color intensity in the scatter plot. The data show a large amount of scatter and bias with a computed scatter index of 67 % and a relative bias of −18 %. However, there is a clear pattern showing that larger maximum sustained wind speeds result in a larger ΔAR35. There is also a tendency in the dataset for TCs at higher latitudes to have a larger ΔAR35 (not shown here).
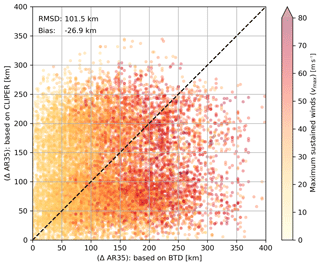
Figure 5Scatter plot describing BTD ΔAR35 (x axis) versus computed ΔAR35 based on CLIPER (y axis). Data points are colored-coded based on the maximum sustained wind speeds in the BTD. The dashed line represents a perfect fit between the BTD and the computed data based on CLIPER.
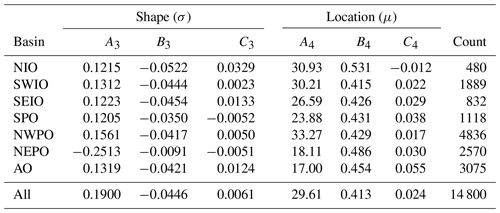
In order to improve the estimate of the ΔAR35, generic relations were derived as part of this study based on BTD from the calibration period from all ocean basins, as well as data from each individual basin separately. The method followed is similar to the one applied to estimate RMW. First, a representative parent distribution of the data was sought, secondly the parameters of the PDF were determined, and thirdly the parameters of the PDF were fitted for a range of vmax and latitude values. The same parent distributions were tested and the lognormal distribution was again chosen as most representative, which is in line with Chavas et al. (2016).
Similarly to RMW, the BTD from the calibration period were divided based on a moving window with a bin width of 10 m s−1 for wind speed (0–10, 1–11, 2–12, etc.) and 10∘ for latitude. This led to Eq. (4) in which exponential functions, dependent on the wind speed per oceanic basin, were used to describe the location parameter and the shape parameter. Additionally, the analysis of the data showed that ΔAR35 is dependent on the latitude, with TCs generally increasing in size at higher latitudes. Adding additional parameters (e.g., storm duration or intensity change of the wind speed) resulted in very limited skill improvement for the estimate of ΔAR35. This procedure was applied to both the combined JTWC and NHC BTD from the calibration period of all basins, and for each individual ocean basin. Table 2 contains the values for the fitting parameters for the ΔAR35 of Eq. (4).
Here μΔAR35 and σΔAR35 represent, respectively, the location and shape parameter of the lognormal distribution for ΔAR35, and A3, A4, B3, B4, C3 and C4 are fitting coefficients.
A scatter plot describing the ΔAR35 derived from BTD as a function of the vmax and latitude and computed according to Eq. (4) is shown in Fig. 6. The green line shows the median ΔAR35 based on the BTD, whereas the solid blue line represents the mean ΔAR35 obtained from Eq. (4). The black lines indicate the 5 % and 95 % exceedance values computed based on BTD. Finally, the 90 % prediction interval is shown using a filled red color. The figure shows how the median ΔAR35 increases as a function of vmax while the variance stays fairly constant. The new empirical equation for ΔAR35 is evaluated in the next section.
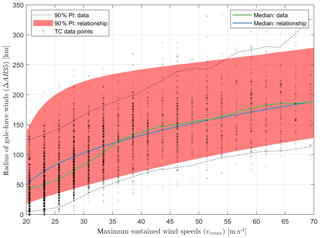
Figure 6Scatter plot describing ΔAR35 (BTD and computed, y axis) as a function of the maximum sustained wind speeds (x axis; and the latitude; not shown). The blue line is the median of the proposed relationship derived for all basins at an arbitrarily chosen latitude of 10∘. The green line is the median of the BTD. The red area shows the 90 % prediction interval based on the proposed relationship for the standard deviation. The 5 % and 95 % exceedance values from the BTD are presented as black solid lines. The gray dots are observation points in which more frequent observations are shown as darker points and less frequent observations as lighter points.
In this section, empirical relationships to estimate the RMW and ΔAR35 were validated based on BTD from the validation period (2015–2017) (Sect. 4.1). Moreover, the outer wind profile based on the Holland wind profile, in combination with observed wind radii, were further validated using the QSCAT-R database (Sect. 4.2).
4.1 Wind radii
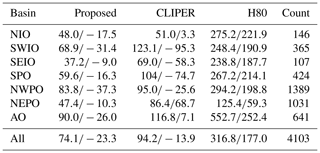
A subset of the BTD (from 2015 to 2017) was used to validate the wind radii. Error statistics are summarized in Table 3. The values indicate that, for all basins combined, the RMSD between the BTD and the proposed relations for the RMW is 17 % lower than compared to VW08 (RMSD of 18 km compared to 21 km). In the NEPO basin, VW08 performs relatively better than at other basins. When comparing the performance of the proposed relations and VW08, it is important to note that the relation of VW08 was derived for storms with central pressures lower than 980 hPa, thereby explicitly focusing on the most severe TCs. When the data were filtered to include only data points with a pressure drop (Δpc) larger than 30 hPa, the RMSD decreases and differences become much smaller (0 %–10 % decrease in RMSD). Moreover, the bias also decreases.
Table 3Root-mean-square difference (RMSD; first number) and bias (second number) for RMW in kilometers for the validation period for both the proposed relationships as for VW08. Statistics are presented for all data points, as well for data points with a pressure drop (Δpc) larger than 30 hPa.
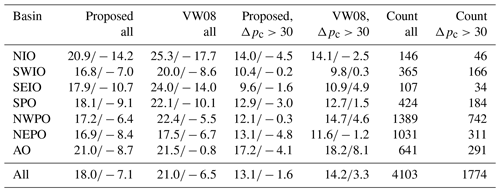
Table 4 shows the error statistics related to the estimation of ΔAR35. In particular, the RMSD between the proposed relations and the BTD for all basins combined is 25 % lower compared to CLIPER (RMSD of 74 km compared to 94 km) and there is a negative bias ranging between 9 and 37 km. Remarkably, the deviations of the ΔAR35 based on BTD in the NIO and SEIO from CLIPER are significantly smaller compared to the differences for the AO for which CLIPER was derived. When the H10 wind profile is applied without additional information to compute the decay of wind speeds away from the eye wall (H80), the ΔAR35 is strongly overestimated (overall bias of 177 km).
4.2 Outer wind speeds
The QSCAT-R database was used to validate the computed (outer) azimuthal wind speeds while using the H10 wind profile in combination with several sources to constrain the decay of wind speeds. QuikSCAT includes 690 unique tropical cyclones and is known to provide reliable results for outer wind speeds of lower intensity. Figure 7 displays the error profile, representing the difference between modeled wind speed and measured data based on QuikSCAT, as a function of the normalized radius. This means that for all validated TCs the radius on the x axis is divided by the RMW. A horizontal line equal to zero indicates no difference between modeled and measured wind speed data, while the solid colored lines represent the median difference. The filled area indicates the interquartile range (IQR).
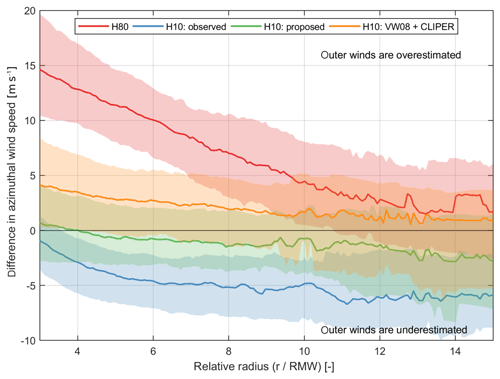
Figure 7Wind speed error (observed QSCAT-R minus modeled) profiles for different models as a function of relative TC radius (r∕RMW). A value equal to zero on the y axis indicates a perfect match between model and observations. Interquartile ranges are shown with shaded colors and the solid line represents the median. Note: for the proposed relationships the most probable value for RMW and AR35 was used (i.e., mode).
The figure shows that in combination with the H10 wind profile the proposed relationships result in the smallest difference with respect to the measured wind speeds (green line). However, applying the H10 wind profile with observed values for the wind radii (i.e., based on BTD values) results in an underestimation of the modeled outer winds (blue line). On the other hand, applying the H10 wind profile, without additional information on the gale-force winds (H80), results in a strong overestimation of the outer winds (red line). Similarly, a combination of other existing relationships for RMW (VW08) and ΔAR35 (CLIPER) results in an overestimation of the outer winds but to a lesser degree (orange line).
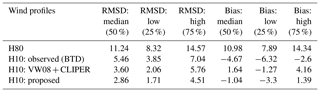
The same information is also shown in Table 5, where the root-mean-square differences and bias between modeled wind speeds and measurements are summarized. Using the proposed relationship with the H10 wind profile results in the lowest RMSD and smallest bias.
Table 5Root-mean-square difference (RMSD) and bias (m s−1) between modeled and measured azimuthally averaged wind speeds based on QSCAT-R data. The data analyzed in the table refer to all TCs with wind speeds between 40 and 5 m s−1 and a normalized radius between 3 and 16. Statistics are shown for median values (50 %) and the IQR range (25 %–75 %). With “H10: observed” the authors refer to the Holland et al. (2010) wind profile in combination with the RMW and AR35 from the BTD.
For clarity, discussion points have been grouped under three main topics, which are as follows.
5.1 Data
In this study, all available BTD from NHC and JTWC were used and combined into one dataset. This approach was followed to create the largest sample size possible, in order to derive empirical (stochastic) relationships valid for each ocean basin, various latitudes, different TC geometries and strengths. This approach is limited by the debatable assumption that each 6-hourly data point is statistically independent. Moreover, errors in the BTD can be quite significant, so previous studies (e.g., Holland, 2008) selected a specific subset of the BTD in order to ensure the quality of the data and remove potential inconsistencies. However, the advantage of including all data entries is that the derived relationships are more widely applicable (i.e., larger parameter space). Moreover, as they are based on larger datasets, it is possible to treat TC geometry variables using a stochastic rather than a deterministic approach.
5.2 Methodology
In order to derive the new empirical relationship for RMW and ΔAR35, the maximum sustained wind speed and latitude were used. Although other authors used additional parameters to describe the TC geometry (e.g., pressure drop, storm duration, rapid intensification), limited predictive skill improvement was found by incorporating those additional parameters. This makes the derived relationships relatively simple for practical applications. Moreover, lognormal statistical distributions in combination with exponential functions were used to fit all available data and derive those relationships. For our application, exponentially shaped functions resulted in the best fit compared to the available data. The choice of lognormal statistical distributions was based on comparison of the different cumulative distribution functions (CDFs) derived using different distributions and the Kolmogorov–Smirnov test and supported by findings from literature (e.g., Dean et al., 2009; Chavas et al., 2016). However, different statistical distributions and functions are available in literature to fit and describe TC geometry data. The strength of using statistical distributions to derive these relationships is that TC geometry is treated stochastically, therefore providing not only mean and median values but also prediction intervals. This is especially of importance when the TC geometry is not known (e.g., for older BTD and/or Monte Carlo analysis with synthetic tracks) with numerical models. Another possibility would be the derivation of wind speed probability estimates. A possibility to further improve these relationships would be to use machine learning techniques such as Bayesian neural networks to estimate TC geometry parameters when enough data are available (via either additional observations or surrogate data derived by numerical models).
5.3 Differences in measured and modeled outer wind profiles
QuikSCAT data were used to validate the (outer) azimuthal wind speeds derived using the new empirical relationships in combination with the H10 wind profile. The analysis has shown how the proposed relationships in combination with the H10 wind profile result in the lowest RMSD and smallest bias for the outer winds, compared to other existing relationships (see Fig. 7). This gives confidence that parametric wind models can be used to compute the outer wind speeds. This is of particular importance for the estimation of coastal hazards (i.e., storm surge and wave heights).
However, differences were also found for individual TCs, where the Holland wind profile in combination with the empirical relationships derived in this paper did not result in a good reproduction of the outer wind speeds. As an example, Fig. 8a shows computed and measured wind speeds for TC Vaianu (2006), which was characterized by an extremely large radius of gale-force wind (R35 equal to 292 km ≈ 10 % probability of exceedance). Measured values are shown in Fig. 8 by the black circles. When applying the proposed relationships to compute the most probable values of the wind radii (red line), a R35 value equal to 162 km is obtained, resulting in an overall underestimation of the measured outer wind speeds. Also, when using the observed wind radii information (blue line), TC outer winds are not well reproduced, which shows that even with the correct wind radii value, parametric wind models can have the wrong shape. This approach is also limited when measured wind speeds cannot be represented by an exponential decay, as is assumed by the Holland wind profile. For example, TCs characterized by two wind maxima cannot be reproduced by an exponential decay of wind speed (Fig. 8b). However, the Holland wind profile is widely used due to its relative simplicity and does, most of the time (80 % of the TCs are reproduced with a RMSE of less than 5 m s−1), reproduce the decay of wind speed fairly well as shown in the evaluation of 690 unique TCs in Fig. 7.
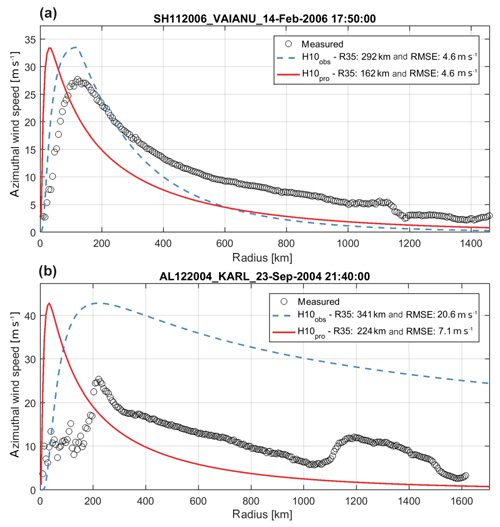
Figure 8Radial wind profiles for measured wind speeds (black circles), computed wind speeds based on relationships for wind radii (red lines) and computed based on observed wind radii for tropical cyclones Vaianu (14 February 2006) (a) and Karl (23 September 2004) (b). Measured data are based on QSCAT-R data, while computed values are based on the H10 wind profile calibrated with the relationships proposed in this paper (red line) or observed data (blue line). Panels (a) and (b) are examples indicating when a difference between measured wind speeds and TC size can be encountered.
In this paper, new empirical relationships are derived which estimate tropical cyclone (TC) geometry with simple and generic equations and with higher accuracy with respect to other well-known empirical relationships available from literature. Those new relationships are valid for any ocean basin (Atlantic; S, NW, and NE Pacific; N, SE, and SW Indian oceans). Moreover, the new relationships include a stochastic description for both the radius of maximum winds (RMW) and the radius of gale-force winds (ΔAR35). This allows the quantification of the prediction interval around the median estimates, making the estimation more useful.
According to the derived relationships, the RMW is described as a function of the maximum sustained wind speeds and latitude. The radius of gale-force winds is estimated using a newly introduced ΔAR35 parameter (average difference between radius of 35 kn and radius of maximum wind), and is also dependent on the maximum sustained winds and latitude. Both parameters are fit through simple exponential functions. Compared to best-track data, the proposed relationships improve the estimation of RMW and ΔAR35 by reducing the root-mean-square difference (RMSD) up to 25 %. Larger improvements were found in particular for non-US TCs since most of the existing relationships are based on data from the Atlantic Ocean, northeastern Pacific Ocean and/or northwestern Pacific Ocean.
The new relationships, in combination with the Holland wind profile, were validated using a subset of the BTD and (outer) azimuthal wind speeds from the QSCAT-R database. The results showed that (outer) azimuthal wind speeds of the TC can be reproduced with the H10 wind profile when using either the BTD (“observed”) for RMW and ΔAR35 or the relationships derived in this paper. When no additional information on wind radii was used to calibrate the H10 wind profile, which is generally done when the radius of gale-force wind is not known, surface wind speeds were overestimated.
The derived empirical relationships can be used in a variety of applications. For example, a better estimate of TC pressure and surface wind speeds for Monte Carlo analysis with synthetic tracks for risk assessments with numerical models can result in a more accurate description of wave and surge conditions resulting from the TC. As a result, this can lead to a better quantification of coastal hazards, and consequent risks and damages. Similarly, an improved assessment of those hazards can help the design of appropriate adaptation measures. Other fields of application may vary from improved design parameters for offshore structures to navigation. The application of the new empirical relationships will be presented as part of a separate paper currently under preparation.
The best-track data (BTD) are freely available and collected from the National Hurricane Center (NHC) and the Joint Typhoon Warning Center (JTWC). Upon request this combined dataset can be shared with other researchers. Moreover, the QSCAT-R (open) database (https://doi.org/10.5065/D6J67DZ4) (Chavas and Vigh, 2014), with data for the period 1999–2008, was used to validate the computed outer winds. The MATLAB script to compute the tropical cyclone geometry is freely available via the following URL: https://bit.ly/2k9py1J (last access: October 2019).
KN and MvO analyzed the data and developed the MATLAB code for computing (stochastic) tropical cyclone geometry. AG and DV provided the idea and wrote the paper.
The authors declare that they have no conflict of interest.
The authors thank the Deltares research program “Hydro- and morphodynamics during extreme events” and “Enabling Technologies”, which provided financing to write this paper. Final thanks are due to Stuart Pearson for proofreading a previous version of the article and providing valuable comments, which have led to an improved paper.
This research has been supported by the Deltares research programs (Extreme hydro and morphodynamic events and Enabling Technologies).
This paper was edited by Gregor C. Leckebusch and reviewed by two anonymous referees.
Bloemendaal, N., Muis, S., Haarsma, R. J., Verlaan, M., Irazoqui Apecechea, M., de Moel, H., Ward, P., and Aerts, J.: Global modeling of tropical cyclone storm surges using high-resolution forecasts, Clim. Dynam., 52, 5031–5044, https://doi.org/10.1007/s00382-018-4430-x, 2018.
Carrasco, C. A., Landsea, C. W., and Lin, Y.-L.: The Influence of Tropical Cyclone Size on Its Intensification, Weather Forecast., 29, 582–590, https://doi.org/10.1175/WAF-D-13-00092.1, 2014.
Chavas, D. and Emanuel, K. A.: A QuikSCAT climatology of tropical cyclone size, Geophys. Res. Lett., 37, 10–13, https://doi.org/10.1029/2010GL044558, 2010.
Chavas, D. and Vigh, J.: QSCAT-R: The QuikSCAT Tropical Cyclone Radial Structure Dataset, https://doi.org/10.5065/D6J67DZ4, 2014.
Chavas, D., Lin, N., and Emanuel, K.: A Model for the Complete Radial Structure of the Tropical Cyclone Wind Field. Part I: Comparison with Observed Structure, J. Atmos. Sci., 72, 3647–3662, https://doi.org/10.1175/JAS-D-15-0014.1, 2015.
Chavas, D., Lin, N., Dong, W., and Lin, Y.: Observed tropical cyclone size revisited, J. Climate, 29, 2923–2939, https://doi.org/10.1175/JCLI-D-15-0731.1, 2016.
Dean, L., Emanuel, K. A., and Chavas, D.: On the size distribution of Atlantic tropical cyclones, Geophys. Res. Lett., 36, 1–5, https://doi.org/10.1029/2009GL039051, 2009.
Fujita, T.: Pressure Distribution Within Typhoon, Geophys. Mag., 23, 437–451, 1952.
Giardino, A., Nederhoff, K., and Vousdoukas, M.: Coastal hazard risk assessment for small islands: assessing the impact of climate change and disaster reduction measures on Ebeye (Marshall Islands), Reg. Environ. Change, 18, 223, https://doi.org/10.1007/s10113-018-1353-3, 2018.
Harper, B. A., Kepert, J. D., and Ginger, J. D.: Guidelines for converting between various wind averaging periods in tropical cyclone conditions, World Meteorological Organization, available at: https://www.wmo.int/pages/prog/www/tcp/documents/WMO_TD_1555_en.pdf (last access: 9 February 2019), 2010.
Hoffman, R. N. and Leidner, S. M.: An Introduction to the Near–Real–Time QuikSCAT Data, Weather Forecast., 20, 476–493, 2005.
Holland, G. J.: An analytical model of the wind and pressure profiles in hurricanes, Mon. Weather Rev., 108, 1212–1218, https://doi.org/10.1175/1520-0493(1980)108<1212:AAMOTW>2.0.CO;2, 1980.
Holland, G. J.: A Revised Hurricane Pressure – Wind Model, Mon. Weather Rev., 2, 3432–3445, https://doi.org/10.1175/2008MWR2395.1, 2008.
Holland, G. J., Belanger, J., and Fritz, A.: A Revised Model for Radial Profiles of Hurricane Winds, American Meteorological Society, 4393–4401, https://doi.org/10.1175/2010MWR3317.1, 2010.
Knaff, J. and Sampson, C.: After a Decade Are Atlantic Tropical Cyclone Gale Force Wind Radii Forecasts Now Skillful?, Weather Forecast., 30, 702–709, https://doi.org/10.1175/WAF-D-14-00149.1, 2015.
Knaff, J., Sampson, C., DeMaria, M., Marchok, Timothy, P., Gross, J. M., and McAdie, C. J.: Statistical Tropical Cyclone Wind Radii Prediction Using Climatology and Persistence, Weather Forecast., 22, 781–791, https://doi.org/10.1175/WAF1026.1, 2007.
Knaff, J., Longmore, S. P., DeMaria, R. T., and Molenar, D. A.: Improved tropical-cyclone flight-level wind estimates using routine infrared satellite reconnaissance, J. Appl. Meteorol. Clim., 54, 463–478, https://doi.org/10.1175/JAMC-D-14-0112.1, 2015.
Lin, Y., Zhao, M., and Zhang, M.: Tropical cyclone rainfall area controlled by relative sea surface temperature, Nat. Commun., 6, 1–7, https://doi.org/10.1038/ncomms7591, 2015.
Loder, N. M., Irish, J. L., Cialone, M. A., and Wamsley, T. V.: Sensitivity of hurricane surge to morphological parameters of coastal wetlands, Estuar. Coast. Shelf Sci., 84, 625–636, https://doi.org/10.1016/j.ecss.2009.07.036, 2009.
Peduzzi, P., Chatenoux, B., Dao, H., De Bono, A., Herold, C., Kossin, J., Mouton, F., and Nordbeck, O.: Global trends in tropical cyclone risk, Nat. Clim. Change, 2, 289–294, https://doi.org/10.1038/nclimate1410, 2012.
Powell, M. D., Houston, S. H., Amat, L. R., and Morisseau-Leroy, N.: The HRD real-time hurricane wind analysis system, J. Wind Eng. Indust. Aerodynam., 77–78, 53–64, https://doi.org/10.1016/S0167-6105(98)00131-7, 1998.
Sampson, C., Fukada, E. M., Knaff, J., Strahl, B. R., Brennan, M. J., and Marchok, T.: Tropical Cyclone Gale Wind Radii Estimates for the Western North Pacific, Weather Forecast., 32, 1029–1040, https://doi.org/10.1175/WAF-D-16-0196.1, 2017.
Schubert, W. and Hack, J.: Inertial Stability and Tropical Cyclone Development, J. Atmos. Sci., 39, 1687–1697, 1982.
Shultz, J. M., Russell, J., and Espinel, Z.: Epidemiology of tropical cyclones: The dynamics of disaster, disease, and development, Epidemiol. Rev., 27, 21–35, https://doi.org/10.1093/epirev/mxi011, 2005.
Stiles, B., Danielson, R., Poulson, W., and Brennman, M.: Optimized Tropical Cyclone Winds From QuikSCAT: A Neural Network Approach, IEEE T. Geosci. Remote, 52, 7418–7434, https://doi.org/10.1109/TGRS.2014.2312333, 2014.
Vickery, P. J. and Wadhera, D.: Winds of Hurricanes from Flight-Level Pressure and H* Wind Data, J. Appl. Meteorol. Clim., 47, 2497–2517, https://doi.org/10.1175/2008JAMC1837.1, 2008.
Vousdoukas, M. I., Mentaschi, L., Voukouvalas, E., Verlaan, M., Jevrejeva, S., Jackson, L. P., and Feyen, L.: Global probabilistic projections of extreme sea levels show intensification of coastal flood hazard, Nat. Commun., 9, 1–12. https://doi.org/10.1038/s41467-018-04692-w, 2018.
Willoughby, H.: Distributions and Trends of Death and Destruction from Hurricanes in the United States, 1900–2008, Nat. Hazards Rev., 13, 57–64, https://doi.org/10.1061/(ASCE)NH.1527-6996.0000046, 2012.
Willoughby, H. and Rahn, M. E.: Parametric Representation of the Primary Hurricane Vortex. Part I: Observations and Evaluation of the Holland (1980) Model, Mon. Weather Rev., 132, 3033–3048, https://doi.org/10.1175/MWR2831.1, 2004.
Willoughby, H., Clos, J. A., and Shoreibah, M. G.: Concentric Eye Walls, Secondary Wind Maxima and the Evolution of the Hurricane Vortex, J. Atmos. Sci., 39, 395–411, 1982.
Willoughby, H., Darling, R. W. R., and Rahn, M. E.: Parametric Representation of the Primary Hurricane Vortex. Part II: A New Family of Sectionally Continuous Profiles, Mon. Weather Rev., 134, 1102–1120, 2006.
Xu, J. and Wang, Y.: A Statistical Analysis on the Dependence of Tropical Cyclone Intensification Rate on the Storm Intensity and Size in the North Atlantic, Weather Forecast., 30, 692–701, https://doi.org/10.1175/WAF-D-14-00141.1, 2015.