Laboratory and field tests and distinct element analysis of dry granular flows and segregation processes

Natural as well as fill slopes are commonly found in Hong Kong, China, and many other countries, and slope failures with the subsequent debris flows have caused a serious loss of life and property in the past until now. There are various processes and features associated with debris flow which engineers need to know so as to design for the precautionary measures. In this study, experiments on flume tests, friction tests, deposition tests, and rebound tests were carried out for different sizes of balls to determine the parameters required for the modelling of dry granular flow. Different materials and sizes of balls are used in the flume tests, and various flow pattern and segregation phenomena are noticed in the tests. Distinct element modelling (DEM) of dry granular flow is also carried out for the flow process. It is found that for simple cases, the flow process can be modelled reasonably well by DEM, which is crucial for engineers to determine the pattern and impact of granular flow, which will lead to further study in more complicated debris flow. From laboratory tests, large-scale field tests, and numerical simulations of single- and multiple-material tests, it is also found that the particle size will be the most critical factor in the segregation process during granular flow. It is also found from the laboratory tests and numerical simulations that a jump in the flume can help to reduce the final velocity of the granular flow, which is useful for practical purposes.

1 Introduction

The terrain of Hong Kong is hilly. Many slopes (fill, cut, and natural) and roads are formed to cope with the rapid development of Hong Kong, China, and many other developed cities. Hong Kong has a high amount of rainfall, with an annual average of 2300 mm which falls mostly in summer between May and September. The stability of man-made and natural slopes is of major concern to the government and the public. Landslides and the subsequent debris flows have caused loss of life and significant amounts of property damage in the past. In Hong Kong, for the 50 years after 1947, more than 470 people died due to slope failures and debris flow associated with man-made cut slopes, fill slopes, and retaining walls.

There have been many reported serious slope failures and debris flow problems in China in the past 10 years, due to the significant amount of construction and inadequate stabilization to many temporary or permanent fill or natural slopes. The destructive power of large-scale debris flow is well known, and the prevention of slope instability and the reduction of debris flow's destructive power by the use of rigid, flexible barriers or other means are well practised in many countries. There are many cases where the slopes fail with subsequent debris flows in Hong Kong and China (Scott and Wang, 1997), which have created various serious problems. Based on a conservative estimate, over 60 countries in the world have faced the problems of debris flow over the years. With reference to Fig. 1, the debris flows in Hong Kong and China have created traffic problems, a serious loss of life and property, and currently there are many active research works in the area of debris flow in Hong Kong and China. The research works include three-dimensional analyses of slope stability, debris flow processes, impact loads on flexible and rigid barriers, and others. An example of a three-dimensional slope stability analysis using 16 000 columns was carried out in 2016–2017, which is shown in Fig. 2a (Lo et al., 2018). The analysis of non-spherical surfaces was achieved by the use of the NURBS function as discussed by Cheng et al. (2005). Upon the determination of the critical failure mass, the flow path of the soil can be estimated from a distinct element analysis using the method discussed by Cheng et al. (2015). The slope failure and the subsequent debris flow (2100 m³ of debris) as shown in Fig. 2b are ultimately controlled by the use of three levels of flexible barriers. We also consider using a meshless method in the assessment of debris flow, which will be the next stage of the present work (Wong, 2018).

Figure 1 Representative debris flow in Hong Kong and Shenzhen, China (a) Tsing Shan debris flow in 1990 (King, 2013); (b) debris flow in Shenzhen 2015.

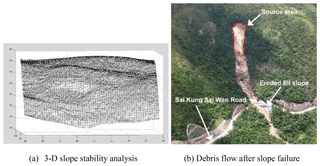
Figure 2 Three-dimensional slope stability analysis from Lo et al. (2018) (the triangulation represents the geometry as defined by the geographic information system (GIS) information) and the subsequent debris flow for a slope in Hong Kong that has blocked the Sai Wan Road traffic.

Granular flow, as a pilot study for debris flow, has some fundamental difficulties in the physical tests as well as numerical analyses. In general, various particle sizes are present in a flow, and the debris mix is usually far from uniform in composition. For physical tests, it is difficult to apply a representative debris flow mix, and the flow process is further complicated by the presence of water. For numerical simulations, it is virtually impossible to accommodate so many particles in a model when they can range from very small particles to cobbles or even boulders, in the extreme range. Even if such a numerical model can be established, there will be serious numerical problems if the particle sizes differ too much in the system. Granular flow can be induced by gravity, driven by fluid dynamics, or by both factors. The classification of debris was given by Varnes (1978), and later modified by Furuya (1980), Ohyagi (1985), Pierson and Costa (1987), Coussot and Meunier (1996), Cruden and Varnes (1996), Hungr et al. (2001), Takahashi (2001, 2006), and others. A detailed theoretical treatment of dry granular flow similar to some of the single material tests in the present study was given by Takahashi (2014) and will not be repeated here. In this study, we will concentrate mainly on the force of gravity, while the effects of water are under our study as the next stage of research work.

Many scientists have carried out granular flow analyses. Lo (2004) compared different compositions of granular flow in landslides in Hong Kong and examined the coarse and fine particle concentration. Hutter et al. (2005) considered the flow envelops and the deposition of the flow. In year 1991, the US Geological Survey made a large-scale flume for detailed experimental tests on debris flows. Mizuyama and Uehara (1983) made a flume which is 20 cm wide and 25 m long, and the slope angle ranged from 5 to 25^∘. Liu (1996) made a 18 cm deep, 16 cm wide, and 150 cm long flume in Yunnan, China, and the flume inclination could be adjusted from 10 to 34^∘. Lin et al. (2009) made a 20 cm wide by 8 m long flume with a 2.2 m wide by 3 m long catchment. There are also various flume tests that have been carried out by various researchers in Hong Kong and many other countries.

During the transportation period, segregation occurs when debris starts to flow. Iverson et al. (1997) studied the factors that influence the segregation process. He found that particle size has a great effect on the segregation process, and debris with a larger particle size moves upward while fine particles go downwards. This phenomenon is the opposite of “normal grading”, in which the finer particles are found in the upper layers in the lake or river, and large particles rest at the bottom. The main reason for the segregation is kinetic sieving, where finer particles can go through the gaps between particles more easily than the larger particle. Large particles can also be found at the front of the flow because of the relatively high velocity of the larger particles in the upper layer, compared with the finer particles with lower velocity in the lower layer. When a stable contact network for large particle is formed at the free surface, the segregation ceases to occur and the balls finally deposit at the catchment area.

For distinct element modelling (DEM) of granular flow, Jiang et al. (2003) studied the methods of the generations of balls in PFC2D (Cundall, 1971, 1988; Cundall and Hart, 1992; Cundall and Strack 1979), namely the expansion method and isotropic compression method. Zohdi (2007) and Halsey and Mahta (2002) discussed about the physics of granular flow, the contact model, and the limits of the friction coefficient. Sullivan (2011) also compared the theory and computation in distinct element analysis. It is well known that the use of DEM can only provide qualitative rather than quantitative analysis in studies up to the present (see also the Discussion), so most researchers adopt DEM for qualitative analysis only.

In the present study, dry granular flow experiments will be conducted under different conditions using glass and rubber balls as a basic study on the flow process and segregation. Both glass and rubber balls of different diameters were used in the tests, and a combination of different sizes and materials have also been tried in the tests for an illustration of the segregation problem. The experimental results are also analysed by distinct element analysis using the program PFC2D. It is true that 3-dimensional distinct element modelling can be a better tool for the present problems, but our previous experience in 3-dimensional distinct element modelling suggests that the amount of computational time can be significant. For the present study, the flumes in both the laboratory and field tests are relatively narrow, and off-track movement of the balls and grains is not major. In view of that, 2-dimensional modelling was adopted in the present study, and good results were actually obtained. The tests are performed at relatively simple conditions so that the basic problem of flow and segregation can be studied easily. It should also be mentioned that more than 10 000 photos were taken from the laboratory and field tests, and such an amount of information cannot be fed into a paper. In light of that, only representative intermediate photos which are used for illustration are given in the present paper, while some of the observed phenomena are simply described without the support of the photos.

2 Physical flume modelling of granular flow

2.1 Instrumentation and test material

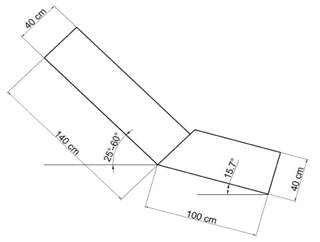
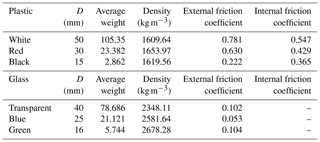
To enhance the knowledge on the granular flow mechanism, many laboratory and large-scale field tests were carried out. The laboratory model is about 1.5 m long and 1.3 m high (adjustable). The flume in the laboratory is made of polystyrene and is designed to be flexible, and the angle of inclination can be adjusted if necessary. The flume model is 40 cm deep by 40 cm wide by 140 cm long for the upper flume and 100 cm for the lower flume with a 60 cm×60 cm catchment area at the bottom. Figures 3 and 4 show the schematic design of flume and flume model in the laboratory tests. In order to record the motion of the particles, two high-speed cameras are adopted. The first one is mounted on the upper flume while the second one is fixed to the bottom flume. In the laboratory tests, different sizes of glass beads and rubber beads are used to replace the use of sand, and this simplification can help to assess the effects of shape and material on the segregation process. In the large-scale field test, real sand is used. For the material parameters, the dynamic friction angle is measured by using the tilting test (Pudasaini and Hutter, 2007; Mancarella and Hungr, 2010). The properties of the glass and rubber beads are determined experimentally, and the details are given in Table 1.

Figure 3 Schematic design of the flume.

Table 1 The properties of the glass balls and plastic balls in the laboratory granular flow test.

2.2 Test programme

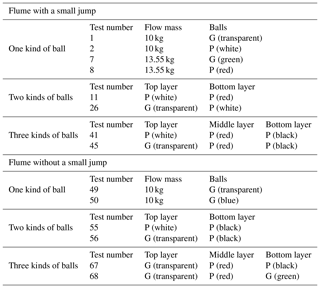
In the present study, the angle of the flume in the laboratory is kept at 45^∘. The effect of the slope inclination will not be discussed in this paper, but the test results show that the segregation process will basically remain unchanged with a different flume inclination. The flume inclination can affect the degree of segregation as well as impact forces, which will be covered by a separate paper later. A total of 68 laboratory tests were carried out. The 68 tests are divided into two groups; the first group of tests was conducted on the flume with a small jump, and the second group of tests was carried out on the flume without a jump. Such a jump is also commonly adopted in Hong Kong, and this helps to lower the velocity of the granular flow (for small-scale flow). Figure 5 shows the flume in the laboratory with a small jump. The effects of the particle size and the flowing mass are also studied through the use of a combination of balls with different diameters, and mass. Table 2 shows only some of the test programme. Test 1 to test 48 belong to the first test group with a small flume jump. Test 1 to test 6 were carried out by using six different kinds of balls separately with the same mass of 10 kg. The mass of the balls was then changed to 13.55 kg, and the above tests were repeated again (for tests 7 to 10). In order to study the segregation process for tests 11 to 40, two kinds of balls with different diameters were combined, and for the same purpose in tests 40 to 48, three kinds of balls were combined. Test 49 to test 68 belong to the group without a small flume jump. Same as the first group of tests with a small flume jump, test 49 to test 55 were carried out for same material but different sizes of balls. In test 56 to test 63, a combination of two kinds of balls were tried. The last five tests were a combination of three kinds of balls.

Figure 4 Flume model in the laboratory.

Figure 5 Flume model with a small jump in the laboratory.

Table 2 Test programme.

P refers to plastic balls, G refers to glass beads.

2.3 Test procedure and test results

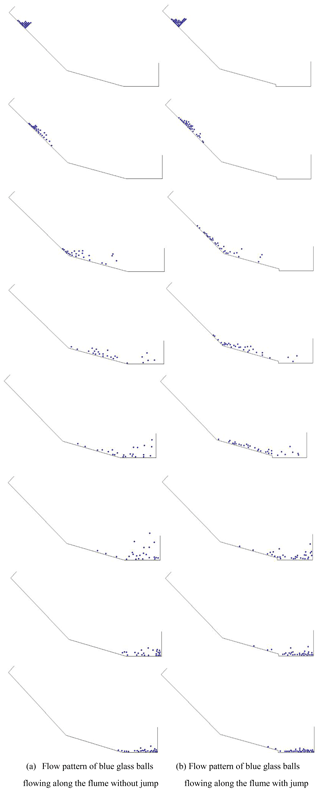
Test materials with different particle size combinations (single types of balls to multiple types of balls) were put into the container which is on the top of the flume. Figure 7 shows the flow pattern of single-type dry granular material flowing along the flume. The video captured by high-speed camera can show this process clearly. When the gate of the container was pulled up, the front part of the flow mass became loose and started to flow along the upper flume under the force of gravity, while the latter part of flow mass followed behind. Flow mass elongated when it moved forward, and the shape of the flow front is wedge-like. At the moment when the particles reached the bottom of the flume, the velocity direction of the balls changed because of the angle difference between the upper flume and the lower flume. During the transportation period, a large amount of potential energy of the initial flow mass was transferred to momentum accompanied by energy dissipation through the grains' collision and friction. Particles at the front of the flow reflected back when they impacted on the wall of the deposition zone and collided with the subsequent particles immediately, which consumed the residual momentum of flow particles. Finally, all of the particles rested in the deposition zone.

Figure 6 The plastic and glass balls used in the laboratory tests.

Figure 7 Flow pattern of mono-size particle flow in the physical model.

In reality, there are sediments and water in debris flow. The effect of water is complicated and will not be studied in the present work. The grain size distribution is usually not uniform as in the present laboratory tests. Consequently, a good understanding of the particle flow under a mixture of ball sizes is important. Particle size is a vital parameter for the good understanding of multi-size particle flow because it not only has an effect on the flow dynamics, but also influences the energy attenuation during the whole flow process. Furthermore, the tilting test that is mentioned above demonstrates that the dynamic friction angle depends on the particle size; specifically, larger particle sizes will have a smaller dynamic friction angle while smaller particle sizes will have a larger dynamic friction angle. The flow pattern of multi-size particle flow is more complicated when compared with the single-size particle flow.

Figure 8 shows the flow pattern of multi-size particle flow. Segregation occurred when the combined particles started flowing along the flume. Figure 8a demonstrates the flow pattern of multi-size particle flow composed of white and black plastic balls. The diameter of the white plastic ball is much larger than the black plastic ball, as shown in Table 1. From the video captured by the high-speed camera, it is easy to observe that during the transportation period, white plastic balls flowed on the upper layer while black plastic balls stayed in the bottom layer. This phenomenon is consistent with the segregation theory of Savage and Lun. (1988). Besides, it is not difficult to find that white plastic balls always stayed at the front of the flow where the velocity was the highest; in other words, the velocities of the white plastic balls with relatively larger diameters are higher than the black plastic balls. Besides, at the upper layer where larger white plastic balls are located, the inertial force dominated the flow dynamics and the energy dissipation was less than that of the lower layer where the flow motion is mainly controlled by the contact forces. For the aforementioned reasons, it can be seen that large particle size leads to higher velocity during the flow.

Figure 8 Flow pattern of multi-size particle flow.

Figure 8b shows the flow pattern of multi-size material composed of green glass balls and black plastic balls. The diameter of green glass ball is similar to the diameter of black plastic ball, while the density of green glass balls is almost 2 times larger than black plastic ball. In the upper container, green glass balls were put statically on top of the black plastic balls. After pulling up the door, the black plastic balls flowed out first and stayed in the bottom layer due to the arrangement of the initial position of balls in the container, green glass balls quickly moved downwards under the force of gravity, which led to the green glass balls in the upper layer to be subsequently replaced by black plastic balls. When the black plastic balls form a stable contact network in the upper layer of the flow, the position transition or segregation process stopped. In this case, the difference of particle sizes between two kinds of balls is not obvious, and segregation was initiated due to the density difference only. During the segregation process in which green glass balls moved downwards and black plastic balls migrated upwards, the momenta of these two kinds of balls were transferred to each other at neighbouring locations, and therefore green glass balls and black plastic balls arrived at the catchment area almost at the same time. While for the test in which balls were arranged in an opposite order (black plastic balls on top and green glass balls on bottom), the green glass balls moved faster and deposited earlier at the catchment area compared with the black plastic balls. This was due to the smaller dynamic friction angle as well as the larger kinetic energy of the green glass balls.

Similar to the above two figures, Fig. 7c shows the flow pattern of transparent glass balls and black plastic balls. In this case, both the density and particle size of the transparent glass balls are larger than those of the black plastic balls. As shown in high-speed camera video, during the flow process, the transparent glass balls flowed upwards and moved faster in comparison with the black plastic balls. Hence, although the density of the transparent glass balls is larger than the black plastic balls, the transparent glass balls still stay in the upper layer of the granular flow due to their relatively large particle sizes, which means that particle size has greater contribution for the segregation process than density in the analysis of granular flow.

3 Numerical modelling of granular flow

3.1 Model generation

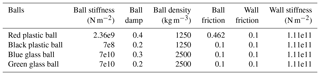
Previous model tests by Chan (2001) for the runout were calibrated by the DAN-W model, where the problem of segregation and flume jump were not considered. In general, the results are in agreement with those from Rickenmann (1999) and Jackob and Hungr, (2005). For the present studies where multi-size particles are considered, the use of the simple DAN-W model is insufficient. The use of a meshless method to model debris flow has recently been considered by Wong (2018). While the meshless method can give a prediction of the debris flow process, the segregation phenomenon is totally neglected in the analysis, and such phenomena are found to be critical for many cases in Hong Kong. In view of the limitations of these numerical methods, the laboratory tests in the present study are modelled using the distinct element method, which is more appropriate for the large deformation, segregation, and separation phenomena during the transportation process. Once the appropriate numerical model is established, the numerical technique will be extended to the field tests for which natural sand is adopted. In this paper, the commercial program PFC2D using DEM was adopted to implement the numerical simulation of dry granular flow. In total, there are five different methods of model generation in PFC2D program, and based on the consideration of time requirements, the rain method was adopted in the end. The parameters used in the numerical simulations are the micro-properties which are difficult to determine. Benchmark tests were carried out in order to calibrate the micro-mechanical properties of the dry granular material. Some of the micro-parameters of the balls are determined through changing their values so that the macroscopic behaviours in numerical simulation are consistent with those in physical tests. The detailed micro-properties of the balls are shown in Table 3. Except for the wall friction (which should be small as the walls are relatively smooth) and wall stiffness, all of the other parameters in Table 3 are determined by laboratory tests. In order to get different frictional coefficients among the balls, two pieces of wood which have plastic balls attached to their surfaces regularly and have shear force applied. Furthermore, depositional tests and rebound tests are carried out to measure the frictional angle and rebound coefficients of the balls. For each parameter, five laboratory tests were carried out, and the mean values are presented in Table 3. It should be noted that there is not a wide distribution in the laboratory-determined parameters; hence the range of these parameters is not shown for clarity. The diameters of the particles in the numerical analysis are the same as those used in the physical tests.

Table 3 Microscopic parameters of the balls for granular flow analysis.

3.2 Numerical test results

A detailed comparison of the granular flow pattern modelled by the physical tests and discrete element analysis is shown in Fig. 9. Figure 9a shows the physical test in which both the red plastic balls and green glass balls were used (too many test results are available, and only selected results are used for illustration in this paper). Large blue balls and small red balls in the numerical model represent the actual red plastic balls and green glass balls in the physical model tests respectively. A full-scale numerical simulation is rarely conducted for discrete element analysis due to the limitation of computational resources, but this is considered to be necessary and acceptable for the present study. Figure 9b shows the numerical results of the flow pattern of the multi-size particles. Particles started to flow along the flume after the initiation of the flow. During the flow process, the flow mass became longer under the action of shear force. Particles moved apart from each other and pushed other particles forward. During this process, the momenta of the balls were exchanged and transferred to other balls at neighbouring locations. The flow velocity kept increasing until the front of the flow hit on the wall of the deposition zone. When the kinetic energy of the balls was exhausted, the balls eventually ceased to move at the catchment area. Figure 10 shows the flow pattern of multi-size particles, composed of black plastic balls and green glass balls, of which the diameters are relatively smaller than the other balls considered in the present paper. Pronounced saltation was observed as balls flowed, implying a collisional character of the flow mass where the Savage number is larger than 0.1 (if the Savage number is smaller than 0.1, the flow belongs to frictional flow, Iverson, 1997). The Savage number is the ratio between inertial force and frictional force. The comparison between Figs. 10 and 9b indicates that the larger the ball size, the more collisional the flow mechanism would be. As a result, the inertial forces dominate the flow dynamics compared with the frictional forces in the present tests. Furthermore, the balls in the upper region of the flow associated with higher velocity had more collisions and moved freely compared with those in the bottom region. The balls in the lower region were compacted with lower flow velocities. By comparison, the numerical simulation results of the flow pattern are in very good agreement with the physical test results when the micro-parameters were selected suitably.

Figure 9 Flow pattern of multi-size particle flow composed of red plastic balls and green glass balls.

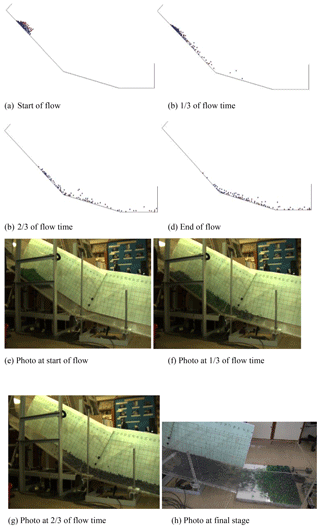
Figure 10 Flow pattern of multi-size particle flow composed of black plastic balls and green glass balls.

As shown in Figs. 9b and 10, segregation was also observed in the numerical model after the dry granular balls started to move. In Fig. 9b, it was evident that the blue balls with a larger ball size moved upwards and forwards, while the red balls with a smaller ball size went to the lower layer and stayed at the rear of the flow, which was consistent with the results in the physical model tests. Smaller particles are more likely to move through the voids between the larger particles, and this will in turn squeeze the large particles to the upper layer of the flow. Because of the momentum exchange between the balls and the flow mass dilation resulting from the shear deformation, a dispersive pressure was caused, which resulted in larger dry granular balls moving faster than the finer particles and going upwards and led to the results that larger balls flowed to the upper layers, where the shear strain is low, and accumulated at the front of the flow, while the finer balls tended to move downwards and accumulated at the bottom of the flow (Takahashi, 1981). Besides, the difference of the ball sizes induced an imbalance in the forces on the balls which restricted the vertical movement of the balls and also affected the flow segregation in the vertical direction. Furthermore, the density difference between the balls in the numerical model was another factor that influenced the segregation process. Particles with lower density are more likely to rise to the free surface, while particles with higher density are more likely to segregate to the bottom of the flow. From Fig. 5b, it can be noticed that it is easy for the red balls with higher density to travel through the gap generated by the shear deformation and squeeze the particles with lower density up to the upper flowing layer. The balls with higher density at the bottom pushed the balls with lower density forward. It is worth mentioning that from the simulation results, the velocities of the blue balls at the free surface are the largest, which results in the balls with large sizes migrating to the front of the flow. The segregation mechanism simulated in the numerical model is consistent with what is mentioned previously in the physical model tests. Ashwood and Hungr (2016), Choi et al. (2014, 2015), Kwan (2012), Lo (2000), and Ng et al. (2014, 2017) have investigated the impact forces on the barrier, which are, however, not considered in the present study, as they are not the main theme of the present work.

3.3 The effect of the flume jump

To reduce the impact force and velocity of the granular flow mass, we have proposed to add a jump in the flume as a pilot test in this study. From the results in this study, it is found that the construction of a jump, which has a very low cost, has some small advantage in reducing the impact from debris flow. Based on the present results, some rigid barriers in Hong Kong have started to include a jump as a small benefit to the control of debris flow, and this is the reason for carrying out such a test in the present research programme which was seldom considered in the past. Figure 11 shows the numerical results of the flow pattern of the blue glass balls flowing on the flume with or without a jump. The flow pattern of the blue glass balls flowing on the flume without a jump in the numerical model is almost the same as the flow pattern of the red plastic balls in the aforementioned physical tests. From the comparison of the flow pattern between Fig. 11a and b, an important phenomenon was observed. The run-up height of the balls flowing on the flume with a jump is obviously lower than the run-up height of the particles flowing on the flume without a jump, which indicates that the flume jump is able to facilitate the process of energy attenuation and thereby has a good effect on suppressing the run-up height of granular flow.

Figure 11 Flow pattern of blue glass balls flowing on the flume with or without a jump.

Figure 12 Maximum velocity of blue glass balls in the numerical model.

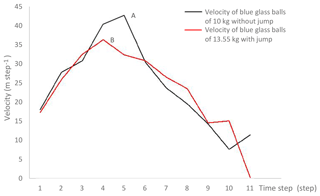
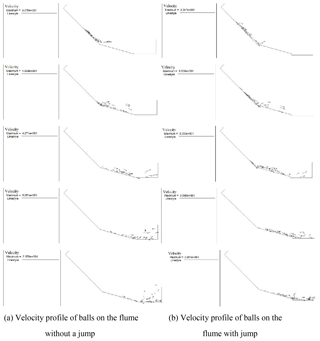
Figure 12 exhibits the velocity of the blue glass balls at different time steps. In PFC2D, we developed the code to monitor the maximum velocity of the balls for comparison purposes, and the monitored results are used to produce Fig. 12. The black line represents the maximum velocity of the blue glass balls of 10 kg weight flowing on the flume without a jump at different time steps, while the red line represents the same kind of balls of 13.55 kg weight on the flume with a jump. The comparison of the velocities at point A and point B indicates that the peak velocity of the balls flowing on the flume with a jump is pronouncedly smaller than that on the flume without a jump, and the peak speeds of the balls on the flume with a jump were achieved earlier than balls on the flume without a jump. It is worth mentioning that the velocity of the balls is independent of the mass of the test material, except at the peak period. Figure 13 shows the velocity profile of mono-size particles (blue glass balls) along the flume with or without a flume jump. The length of the velocity vector represents the speed of the particles. From Fig. 13, it can be noticed that the frontal flow velocities are the largest compared with the velocities of the particles at the rear of the flow. When these particles approached the lower part of the flume, the velocity directions changed due to the difference of the flume angles. This is in good agreement with the laboratory results mentioned above. Figure 13b shows that the velocity of mono-size particles on the flume with a jump increased after the initial state. The largest flow velocity was achieved at the moment when these particles intended to jump into the deposition zone. The directions of flow velocities changed, and the speed of particles decreased as soon as they fell into the deposition zone. As with those particles moving on the flume with a jump, the velocity of the particles flowing along the flume without a jump increased when they approached the deposition zone; however, the velocity of these particles kept increasing when they flowed into the deposition area, and the peak speed was achieved at the moment just before they reached the boundary of the deposition area. When the granular front impacted on the wall of the deposition area, the particles at the front of the flow reflected back and collided with the following particles, and that is the moment when the flow speed decelerated.

Figure 13 Velocity profile of blue glass balls in the numerical model.

According to Figs. 12 and 13, the peak velocity of the balls on the flume with a jump was achieved before they impacted the wall of the deposition zone, contrasting with the balls on the flume without a jump, and this is meaningful to the engineers because the flume jump can effectively reduce the impact force on the barrier. Besides, the jump of the flume is capable of reducing the peak velocity of the dry granular particle flow as well. To sum up, flume jumps play a useful role in attenuating granular flow, and therefore flume jumps are recommended to be applied in the design of debris flow barriers (which is actually sometimes adopted in Hong Kong).

It should be noted that the actual flow velocity of the balls can be traced back from the high-speed camera photos and the video, but we do not present the results here because it is not the main theme of the present study. Most importantly, DEM usually cannot give a good quantitative prediction unless the micro-parameters are finely tuned. We do not prefer such tuning of the parameters, as such tuning cannot be performed before the tests. However, the qualitative results from the DEM analysis and the laboratory tests are reasonable as found from the present study; hence we can still accept the results from DEM in our discussion. Actually, we have carried out limited tuning of the micro-parameters (not shown in this paper) in our internal studies. Since the flow and segregation process are practically unaffected by the change of these micro-parameters (but the actual value of the flow velocity, run-out, etc. are affected), we have not included these results in the present paper, and we prefer to concentrate on the segregation and jump for a flume test.

4 Large-scale field tests

After the laboratory studies using a 1.5 m long flume and glass and rubber balls, we carried out a large-scale flume test which is shown in Fig. 14. The flume is about 6 m long, and five types of sand, as shown in Fig. 15, are used in the field tests. The particle sizes within each type are relatively uniform, and they ranged from 1 to 3 (type 1), 3 to 5 (type 2), 5 to 7 (type 3), 7 to 8 (type 4) and above 8 mm (type 5). The friction angles for the five types of sand as determined from the deposition tests as shown in Fig. 15b are given by 28, 30.3, 29.1, 31.5, and 33.7^∘ respectively.

Figure 14 Large-scale flume for the field test.

Figure 15 (a) Sand used for the granular flow tests. (b) Deposition tests for sand.

A series of tests with single, double, and triple types of sand were carried out, and only some of the results are shown in this paper for comparisons with the laboratory tests. As shown in Fig. 16, the final deposition profile using type 1 (1–3 mm) and type 4 (7–8 mm) sands is shown. It is noticed that the coarse-grain sand moves to the top of the flow, which is illustrated by Fig. 17a to c. Such results comply with the laboratory studies well. The control tests using coarse and finer sands are shown in Fig. 18. A closer look into the difference between Figs. 18a and 16 shows that the profile in the rear can reveal an important difference. For granular flow with two types of materials, the difference in the height of the deposit for the first metre as measured from the left is greater than that for the test with a single material (true for all single-sand tests). Such a phenomenon can be attributed to the effect of the difference in the velocity flows between type 1 and 4 materials, with type one material depositing at the bottom during the flow. Based on the field tests, the importance of the particle size during the segregation process as derived from the laboratory tests can be further verified.

Figure 16 Final deposition after the granular flow for two types of material (coarse and fine).

Figure 17 (a) Deposition at the rear of the deposit. (b) Deposition at the front of the deposit. (c) Front view of the deposition (two types of material).

With reference to Fig. 19, it is clear that the formation of the flow front, flow head, channelized flow, and levee from the present field test is very similar to that by Johnson et al. (2012). The surface trajectories of the particles by Johnson et al. (2012) are also captured by the high-speed camera in the present laboratory and field tests. A coarse enriched surface layer was obtained by Johnson et al. (2012), and such phenomena are also obtained from the laboratory and field tests and are clearly illustrated in Fig. 17. Iverson (1997) has also found similar segregation from the granular flow in Oregon in 1996. It should be noted that for all of the granular flow tests in the present study, such segregation phenomena are always obtained as long as there is more than one material in the problem.

5 Discussion

Laboratory tests were carried out with numerical simulations through the distinct element method to study the flow pattern of dry granular flow. The study is important for the basic understanding of the granular flow segregation problem and the importance of providing a jump in the flume in actual protective measures. For the present tests, the flume base is even and smooth which results in a relatively small dynamic frictional angle and less energy attenuation compared with the real granular flow. Besides, the surfaces of the glass and plastic balls used in the experiments are regular and smooth, while for debris flow occurring in nature, the debris materials are always irregular and rough, which cause the dynamic internal frictional shear force between real-scale debris flow particles to be relatively large with a lower run-up height. As a consequence, the present tests are a conservative approach to study the flow pattern of granular flow. Such an arrangement is necessary to separate the contribution of particle size distribution from other parameters in the segregation process.

Physical tests were conducted to study the flow pattern of mono- as well as multiple-size particle flows. In general, the results from the present study comply with those from the literature well. Test results indicate that flow mass is elongated under the action of shear force when the particles flowed on the flume. For particles with different particle sizes, segregation always occurs. Particles with larger diameters migrated upward and small particles moved downwards because particles with smaller diameters can go through the gaps between the larger particles. In addition, the density of the particles is another factor that plays a role in the segregation process. Under the force of gravity, particles with higher density moved downwards faster, and other particles with lower density were squeezed upwards. For the real scale debris flow, the debris material ranges from clay and silt to boulders, while the differences in the densities between different types of particles are relatively small; hence, particle size is the most dominant factor which influences the segregation process. The top view from the high-speed camera indicates that the velocities of the large particles are higher than the velocities of the small particles. Granular particles with larger particle sizes travelled to the front of the flow where the velocities are higher. Larger particle size is observed to lead to a higher velocity. Such results are also in general agreement with the results by Takahashi (1981).

For the present work, the detailed movement of individual particles is hard to trace even with the help of a high-speed camera. Instead of that, we choose to trace the segregation process through the macro-phenomena such as grain migration, segregation, and the formation of a levee. Combined with the DEM analysis, the interpretation of individual grain movement as well as the formations of the segregation and levee can be assessed. Based on the various laboratory and field tests on flow with mixtures of different material sizes, stiffness, and densities, it is established that the grain size distribution is the most critical factor in the flow process, as grain movement occurs and controls the flow process for about half of the flow time. The formation of a force chain which actually affects the flow process is also controlled by the grain size distribution. This result has an important implication in that most of the natural flow processes involve debris of different grain sizes.

For the flow pattern of dry granular particles simulated through the distinct element method, the simulation results of flow pattern are almost the same as the physical tests. Berger (2016), Chen and Lee (2000), and Ghilardi et al. (2001) also obtained a reasonably good numerical modelling of the flow process for the relatively simple flow problem, which supports the use of numerical analysis for the granular flow problem. In the present numerical model, a pronounced segregation process was observed as well, which complies well with many previous studies by Gray et al. (2003), Hákonardóttir et al. (2003), Iverson (1997), Johnson et al. (2012), and many others. Large particles went upwards while small particles went downwards. From the velocity vector figure, the velocities of the particles in the upper layer as well as the velocities at the front of the flow were the largest. Savage numbers of the dry granular particles in present tests were larger than 0.1, which represents the collisional characteristics of the flow. The flow behaviour was hence more inertial than frictional. Flume jumps have a significant influence on impeding the granular flow. When the particles flowed through the jump, a large quantity of kinetic energy was consumed during the process. The peak velocities of the particles flowing on the flume with a jump were lower than those without a flume jump. Besides, the peak velocities of the particles on the flume with a jump were achieved earlier, and after that the flow velocity started to decrease, which make a great contribution for reducing the impact load. The run-up height of the particles on the flume with a jump was apparently lower than that without a jump. Thus, a flume jump can help to reduce the flow velocity as well as suppress the run-up height. In previous sections, detailed discussions about the formation of a force chain from DEM are investigated, and such a force chain has a major effect on the flow and segregation processes, which is actually observed from the tests. Without the DEM results, these phenomena cannot be explained clearly. In this respect, the use of numerical modelling has provided an important aid in understanding the flow and segregation processes.

Comparing the physical and numerical test results, the macroscopic flow behaviour in numerical models is consistent with the physical tests. Through a good selection of the model generation method and micro-parameters, the distinct element method can produce a reasonable qualitative simulation of the behaviour of dry granular flow for the consideration of engineers. These results have useful contributions for better understanding the granular flow behaviour, which is not possible for the other classical methods. Up to the present, engineers are still relying on some empirical methods such as using the dynamic impact earth pressure coefficient (Kwan, 2012) or other similar approaches for the design of a flexible or rigid barrier, as granular flow processes are complicated by many geotechnical and geographical complexities. The design of a barrier is still more of an art than science in the present, though some guidelines are available to help engineers in the design. However, the DEM analysis in this study can supplement the field and laboratory studies for which the internal forces between the particles cannot be determined.

The flow processes and segregation processes from laboratory and field tests are similar in many respects – they are largely controlled by the particle size distribution. This is clearly illustrated from about 50 tests in our study. A limited number of photos are shown in this paper to limit the length of the paper. Thousands of photos and about a hundred video files were obtained from the laboratory and field tests in this study, and only selected photos which are sufficient to illustrate the main purposes of the present work are shown in the present paper. We are, however, happy to share these materials upon request at ceymchen@polyu.edu.hk.

In the present paper, the effect of the flume inclination has not been investigated. However, we have carried out some other tests on the effects of flume inclination. For the segregation process, the test results indicate that the basic conclusions from the present work remains unchanged for practical purposes. Flume inclination has more important effects on the impact forces and erosion, which are to be covered by the next stage of the present research work.

Figure 18 (a) Front view of the deposition (type 4 material). (b) Close-up view of the deposition.

Figure 19 Front of the runout.

6 Conclusions

In the present study, two important phenomena in granular flow are studied. The first problem is the segregation process which is captured in all of the tests in the present studies. The segregation phenomenon can affect the design of the barrier in different ways. Finer materials are deposited at the bottom of the runout, and the relatively lower permeability of this layer tends to drive the water level upward (somewhat similar to the perched water table phenomenon). This may increase the destructive power of water. For the design of rigid barriers, the use of a suitable water table will also be crucial to maintain an adequate factor of safety of the barrier. Since segregation practically occurs for the majority of the debris flow problems, this effect should be well studied and considered in the design of flexible and rigid barriers.

We chose flexible, spherical rubber beads as well as rigid glass beads for the laboratory, and the range of stiffness was sufficient to cover most of the natural flow materials. The segregation process as found from the laboratory test was actually similar to that in the field tests using non-spherical sand. Through such selection, it is clearly demonstrated that particle size distribution is a very critical factor in the segregation process, and it appears that it is more critical than particle shape or stiffness.

To reduce the destructive power of the debris, a small jump in the flow channel is sometimes applied in Hong Kong if the site conditions allow. In general, the effect of this jump is small, and is effective only for low-volume debris flow, which is the common case for Hong Kong. Nevertheless, such provision can slightly reduce the destructive power of the debris. It is interesting to note that there are virtually no studies about the effect of a jump in the past, and the present study provides some useful pilot work, for which more works may come out in the future.

One of the main limitations for the present study is that the flow material is limited to granular but not cohesive material. The reason is that practically all of the debris flows in Hong Kong are granular debris flows. The most critical factors in debris flow for Hong Kong also include different particle size distribution (studied in the present work), topography, and the effects of water. The present work does not aim to consider all of these effects simultaneously but is confined to address the critical issues found in Hong Kong. Nevertheless, the present work will still be useful for many countries where the flow material is mainly granular.

We are currently considering the next stage of field tests, for which the wet test will be carried out (limited tests have been so far), and more equipment and measurements will also be used. Currently, we are constructing a laboratory flume where the base is rough. An investigation of combined effects of base roughness and flume inclination angle will be carried out soon, and hopefully the results will form an extension of the present paper. For the field test, most of the researchers will place a container of a wet sample and let the sample flow down. This approach is simple in execution, but the actual debris flow may not be. From the observations of several debris flows in Hong Kong, we have noticed that erosion processes are sometimes an important phenomenon, which is not simple to reproduce in a field flume. The composition of the flow material actually changes during the flow process. More thought will be given to the setup of the wet field test in the future, and the base of the flume may be specially prepared with some soil bedding to allow for erosion in the future tests.