Tree fall along railway lines: modelling the impact of wind and other meteorological factors

Strong winter wind storms can lead to billions of euros in forestry losses, disrupt train services and necessitate millions of euros in spending on vegetation management along the German railway system. Therefore, understanding the link between tree fall and wind is crucial.

Existing tree fall studies often emphasize tree and soil factors more than meteorology. Using a tree fall dataset from Deutsche Bahn (DB; 2017–2021) and meteorological data from the ERA5 reanalysis and RADOLAN (Routineverfahren zur Online-Aneichung der Radarniederschlagsdaten mit Hilfe von automatischen Bodenniederschlagsstationen (Ombrometer)) radar, we employed stepwise model selection to build a logistic regression model predicting the risk of a tree falling on a railway line in a 31 km grid cell.

While the daily maximum gust speed (the maximum wind speed in a model time step at 10 m height) is the strongest risk factor, we also found that the duration of strong wind speeds (wind speeds above the local 90th percentile), the gust factor (the ratio of the maximum daily gust wind speed to the mean daily gust speed), precipitation, soil water volume, air density and the precipitation sum of the previous year are impactful. Therefore, our findings suggest that high wind speeds, a low gust factor and a prolonged duration of strong winds, especially in combination with wet conditions (high precipitation and high soil moisture) and high air density, increase tree fall risk. Incorporating meteorological parameters linked to local climatological conditions (through anomalies or in relation to local percentiles) improved the model accuracy. This indicates the importance of considering tree adaptation to the environment.

1 Introduction

Strong wind speeds are a major factor leading to tree fall and are therefore a risk both to the railway service and forestry. Strong winter wind storms can cause billions of euros in damages for forestry (Gliksman et al., 2023). These losses have been increasing over recent decades (Gregow et al., 2017). Additionally, there is an interconnection between storm damage and other ecological risks like droughts and bark beetle infestation in summer or the unfreezing of soils in winter which put further stress on forest ecosystems and are likely to change in a warming climate (Gregow, 2013; Temperli et al., 2013; Seidl et al., 2014; Stadelmann et al., 2014; Venäläinen et al., 2020). In 2018, Deutsche Bahn (DB) increased its budget for vegetation management to enhance storm safety, now spending approximately EUR 125 million annually (DB, 2023). And yet the cost of tree fall remains of the order of millions of euros per year (Meßenzehl, 2019). With 68 % of railway tracks lined by trees and forests, ongoing management is necessary. Since 2018, over 1000 workers have been employed to monitor and maintain railway vegetation (DB, 2023). Despite these efforts, there was an annual average of approximately 3000 tree fall incidents from 2017 to 2021, causing service disruptions and infrastructure damage. In recent years interest in the topic has increased. A number of studies on tree fall hazards show that this problem is also present outside the German railway network (Bíl et al., 2017; Koks et al., 2019; Kučera and Dobesova, 2021; Szymczak et al., 2022). Therefore, it is vital to study the relationship of tree fall and wind. Such research aids the management of vegetation alongside transportation routes as well as the development of climate-resilient forests. There are many studies which investigate the impact of wind speed on tree fall, including tree motion measurements and tree-pulling experiments (Peltola et al., 2000; Kamimura et al., 2012; Schindler and Kolbe, 2020; Jackson et al., 2021), mechanistic modelling (Gardiner et al., 2008; Hale et al., 2015; Kamimura et al., 2016; Costa et al., 2023), and statistical and machine learning approaches (Schindler et al., 2009; Schmidt et al., 2010; Hanewinkel et al., 2014; Hale et al., 2015; Jung et al., 2016; Kamimura et al., 2016; Kamo et al., 2016; Hart et al., 2019; Valta et al., 2019; Zeppenfeld et al., 2023). One issue the field of tree and forest damage modelling faces is the lack of highly resolved gust and airflow data. Great efforts have been made in recent years to develop small-scale gust speed products which can also be used for impact modelling (Primo, 2016; Albrecht et al., 2019; Schulz and Lerch, 2022). Additionally, there are a number of studies that identify, track and classify the storms most damaging to forests and infrastructure (Mohr et al., 2017; Jung and Schindler, 2019; Tervo et al., 2021). Among the statistical modelling approaches, logistic regression models are very common and are also used in our study. Numerous existing studies on storm damage focus on a single storm event or a small spatial region (Albrecht et al., 2012; Hale et al., 2015; Kamimura et al., 2016; Hart et al., 2019; Hall et al., 2020; Zeppenfeld et al., 2023). Consequently, there is a need for long-term and large-scale investigations in this field.

Additionally, previous studies have mainly analysed the impact of tree-, stand- and soil-related factors on wind-induced damages but often excluded metrology. Those which consider meteorological predictors often focus on the relationship between tree damage and mean or maximum wind speeds (Schindler et al., 2009; Jung et al., 2016; Morimoto et al., 2019). Yet, there are some other meteorological predictors which are considered in previous works and which we will consider as well.

To account for the turbulent aspect of wind, some studies employ the gust factor. There are different understandings of the term gust factor in the fields of meteorology and forestry. In forestry the gust factor is often referred to as the ratio of the maximum to mean bending moment experienced by a tree (Gardiner et al., 1997). In other works the gust factor is defined as the ratio of the maximum short-term-averaged wind speed over a shorter duration t_s to a long-term-averaged wind speed over a longer duration t_l (Ancelin et al., 2004; Gromke and Ruck, 2018). The durations t_s and t_l then need to be adapted to the specific research questions. Wind load is the wind force per area applied to a tree and the product of a tree's specific drag coefficient, air density, a tree's exposed frontal area and wind speed (see Eq. 13). Wind load and air density are considered in a few studies on tree fall and storm damage (Schelhaas et al., 2007; Ciftci et al., 2014; Gromke and Ruck, 2018; Sterken, 2021) as well as the wind direction (Akay and Taş, 2019; Valta et al., 2019). The role of the wind event duration is also discussed in some literature (Gardiner et al., 2013; Mitchell, 2013; Kamimura et al., 2022) but is not studied in detail. Next to wind, snow, frozen soils and precipitation have been identified as impactful meteorological factors (Peltola et al., 2000; Gardiner et al., 2010; Pasztor et al., 2015; Kamo et al., 2016). For example, heavy rain or snow during a storm event may add considerable weight to the crowns and increase tree fall risk (Gardiner et al., 2010). A decrease of frozen soils in the past as well as in future climate scenarios has been found for example for Finland, where it was connected to higher risks of uprooting (Gregow, 2013; Lehtonen et al., 2019). Soil moisture is also sometimes considered (Kamo et al., 2016; Csilléry et al., 2017), as excessive water in the soil is expected to weaken root anchorage (Kamimura et al., 2012; Défossez et al., 2021). However, the role of soil moisture on tree fall risk is not completely clear and only a few field experiments have been done on the topic (Gardiner, 2021). Both very wet and very dry soils might have a negative impact. The legacy effects of drought may cause lasting changes in tree physiology and weaken the tree (Kannenberg et al., 2020; Zweifel et al., 2020; Haberstroh and Werner, 2022). Therefore, droughts are expected to increase damage caused by wind (Gardiner et al., 2013). Yet, Csilléry et al. (2017) found both positive and negative effects on tree damage. They suggest that in some stands drought weakens the trees and makes them more vulnerable to wind loading, while in others dry soils make them less vulnerable to overturning.

We aim to develop a meteorology-based tree fall impact model, which is a first step toward a more complex predictive tree fall model. On the one hand, such a predictive model could be used to identify areas at risk and support management decisions, for example, which trees to cut down, especially when environmental and forest data become available and can be taken into account in the future. On the other hand, the model can be applied to climate model data to identify future changes in tree fall risk. To accomplish this, we need to identify meteorological parameters and parameter combinations that impact tree fall risk alongside railway lines in Germany over the long term and across a large-scale area. We aim to deepen the understanding of tree fall risk and wind and to explore how far wind-related parameters like the daily maximum gust speed, the gust factor, air density, wind load, the duration of strong wind speeds or wind direction have an impact on tree fall. We also examine the impacts of other predictors related to meteorology that have been included in previous studies, such as soil moisture, precipitation, snow or soil frost. Additionally, we study legacy effects of dry and wet spells by including the soil water volume and precipitation in antecedent time periods.

We will introduce both the tree fall data as well as the meteorological data used in this study (Sect. 3). We will describe the background theory and the selection process for the logistic regression model (Sect. 4), and we will finally present (Sect. 5) and discuss (Sect. 6) our results and conclude with our most important findings (Sect. 7).

2 Data

2.1 Tree fall data

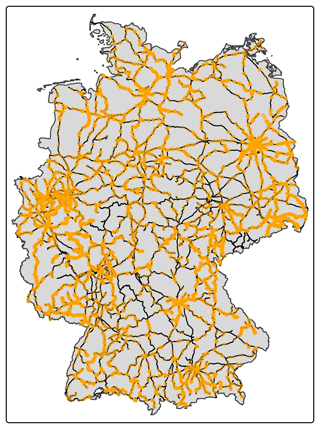
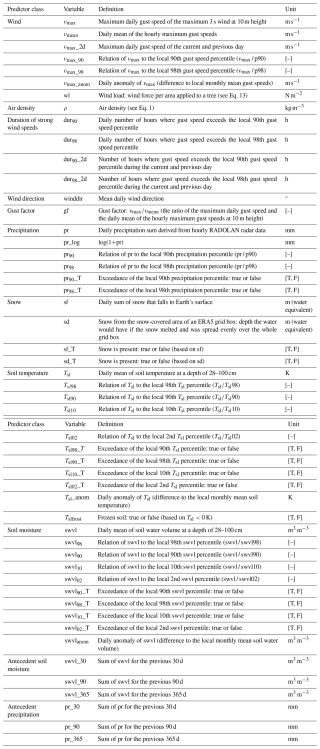
Figure 1 All tree fall events (orange dots) alongside railway lines (black lines) in Germany in the extended winter season (October–March) of 2017–2021.

Figure 2 Percentage of tree fall events per month alongside German railway lines for the period 2017–2021.

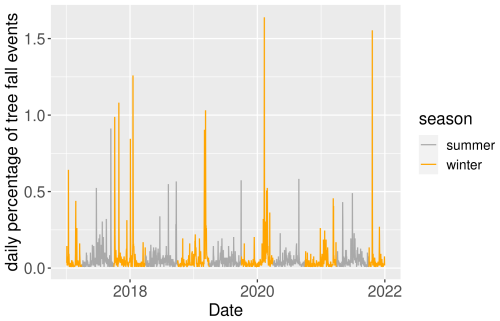
Figure 3 Percentage of tree falls per day relative to the total number of tree falls over the entire period alongside German railway lines. Summer and winter are colour-coded. Most extreme peaks of event numbers are caused by winter wind storms, for example Friederike (18 January 2018), Sabine (20 February 2020) and Hendrik (21 October 2021).

Tree fall events along the German railway network were derived from a dataset created by Deutsche Bahn (Fig. 2). The data consist of disturbance events reported by rail drivers and local inspectors. These reports were later merged into one dataset by the railway infrastructure company InfraGO AG (formerly called Netz AG) of Deutsche Bahn. For each tree fall event, the date and time of the report, the coordinates of the event, and further railway-related information like the route section number are included.

The highest number of monthly tree fall events occurs from January to March and from June to August. There is also a peak in October (Fig. 3). The most extreme daily number of tree fall occurs during the winter season and is connected to winter wind storm events due to extra-tropical cyclones (Fig. 4).

2.2 Meteorological data

We used hourly ERA5 data (Hersbach et al., 2020; Hersbach et al., 2023) for all meteorological parameters, except precipitation. ERA5 (provided by the ECMWF, European Centre for Medium-Range Weather Forecasts) is a reanalysis dataset from 1940 to the present with a spatial resolution of ∼31 km. It was accessed using the ClimXtreme Central Evaluation System framework (Kadow et al., 2021). We performed our analysis only for the extended winter season (October to March) to focus on winter wind storms, which cause the most extreme peaks in tree fall events. We used hourly data to calculate daily means, sums or maxima for each predictor (see Table 1) as well as local percentiles (2nd, 10th, 90th and 98th) in each grid cell over the years 2000 to 2019 for some predictors. The CDO module (Climate Data Operators; Schulzweida, 2023) was used for each of these operations. The advantage of using wind speeds from ERA5 is the coverage of the complete area and period under investigation. For these reasons ERA5 and similar reanalysis products are already used as input data in many forecast and impact models (Pardowitz et al., 2016; Valta et al., 2019; Battaglioli et al., 2023; Cusack, 2023). Previous versions of the ECMWF reanalysis have successfully been used to reproduce windstorm-related damage as recorded by the German Insurance Association (Donat et al., 2010; Prahl et al., 2015), suggesting the usability of these data in spite of deviations with local station measurements (Minola et al., 2020). Studies comparing wind speed observation with the ERA5 reanalysis find good correlations (Minola et al., 2020; Molina et al., 2021).

For precipitation data we used RADOLAN (Routineverfahren zur Online-Aneichung der Radarniederschlagsdaten mit Hilfe von automatischen Bodenniederschlagsstationen (Ombrometer)) data provided by the German Weather Service (Bartels et al., 2004; DWD, 2004) with a spatial resolution of 1 km. RADOLAN combines radar reflectivity, measured by the 16 C-band Doppler radars of the German weather radar network, and ground-based precipitation gauge measurements.

3 Methods

In this section, we describe data pre-processing as well as the theoretical background and the model selection process for the logistic regression model. The aim of this model is to calculate the probability of at least one tree falling on a given day in a 31 km grid cell, depending on meteorological parameters. It is used to analyse the impact of a set of predictor variables.

3.1 Data pre-processing

A shapefile of the German railway lines (DB, 2019) was used to mask the ERA5 grid and select all grid cells in Germany that are crossed by at least one railway line. We calculated the rail density (total length of all railway lines in kilometres) for each grid cell in order to quantify the length of exposed railway lines.

Daily mean air density ρ was calculated as

$$\begin{array}{}\text{(1)}& \mathit{\rho }=p/R\cdot T,\end{array}$$

where p is the daily mean surface air pressure (hPa), T is the daily mean near-surface air temperature (K) (both derived from ERA5 hourly data) and R is the universal gas constant (8.314 J K⁻¹ mol⁻¹).

Daily precipitation sums were calculated from the hourly data. We then remapped the precipitation radar data to the ERA5 grid using bilinear interpolation by applying the remapbil function of the CDO module and thus ascribing daily precipitation sums to each grid cell. We calculated percentile exceedance of the 2nd, 10th, 90th and 98th percentile for gust speed maxima, the soil water volume, and precipitation via the relation of the daily value and the local percentile.

Finally, we collected all these data for the months of October to March in 2017 to 2021 in a dataset containing grid cell IDs, a variety of daily meteorological predictors (see Table 1), rail density, and the daily occurrence of at least one tree fall event in the grid cell given as true or false. This dataset contains only grid cells crossed by at least one railway line.

3.2 Logistic regression

Logistic regression was used to relate the probability of an event to a linear combination of predictor variables, which is converted with the logit link function into the scale of a probability:

$$\begin{array}{}\text{(2)}& \mathrm{logit}\left(\mathrm{\Theta }\right)=\ln \left({\displaystyle \frac{\mathrm{\Theta }}{\mathrm{1}-\mathrm{\Theta }}}\right)=a+b_{\mathrm{1}}\cdot x_{\mathrm{1}}+b_{\mathrm{2}}\cdot x_{\mathrm{2}}+\mathrm{\dots }+b_k\cdot x_k.\end{array}$$

Here, θ is the probability of an event, x_1−k is the predictor variables, b_1−k are the estimated coefficients and a is the intercept term. Equation (2) can be rearranged in the following way to calculate the event probability (MacKenzie et al., 2018):

$$\begin{array}{}\text{(3)}& \mathrm{\Theta }={\displaystyle \frac{\exp \left(a+b_{\mathrm{1}}\cdot x_{\mathrm{1}}+b_{\mathrm{2}}\cdot x_{\mathrm{2}}+\mathrm{\dots }+b_k\cdot x_k\right)}{\mathrm{1}+\exp \left(a+b_{\mathrm{1}}\cdot x_{\mathrm{1}}+b_{\mathrm{2}}\cdot x_{\mathrm{2}}+\mathrm{\dots }+b_k\cdot x_k\right)}}.\end{array}$$

Interactions allow for expressing the dependence of two or more variables on each other in a model. The effect (a.k.a. the estimated coefficient) for one predictor might change depending on the value of another predictor. Compared to a model without interaction (see Eq. 2), two predictors that are assumed to have an influence on each other are multiplied and a coefficient is estimated for this new term, resulting in

$$\begin{array}{}\text{(4)}& \mathrm{\Theta }={\displaystyle \frac{\exp \left(\mathrm{a}+{\mathrm{b}}_{\mathrm{1}}\cdot {\mathrm{x}}_{\mathrm{1}}+{\mathrm{b}}_{\mathrm{2}}\cdot {\mathrm{x}}_{\mathrm{2}}+{\mathrm{b}}_{\mathrm{3}}\cdot {\mathrm{x}}_{\mathrm{1}}\cdot {\mathrm{x}}_{\mathrm{2}}\mathrm{\dots }+{\mathrm{b}}_{\mathrm{k}}\cdot {\mathrm{x}}_{\mathrm{k}}\right)}{\mathrm{1}+\exp \left(\mathrm{a}+{\mathrm{b}}_{\mathrm{1}}\cdot {\mathrm{x}}_{\mathrm{1}}+{\mathrm{b}}_{\mathrm{2}}\cdot {\mathrm{x}}_{\mathrm{2}}+{\mathrm{b}}_{\mathrm{3}}\cdot {\mathrm{x}}_{\mathrm{1}}\cdot {\mathrm{x}}_{\mathrm{2}}+\mathrm{\dots }+{\mathrm{b}}_{\mathrm{k}}\cdot {\mathrm{x}}_{\mathrm{k}}\right)}},\end{array}$$

where b₃ is the estimated coefficient for the interaction of the predictors x₁ and x₂. It represents how the effect of x₁ on the event probability changes with x₂ (and vice versa). A significant b₃ would indicate that the effect of x₁ on the probability is different at different levels of x₂.

For quantifying the model's forecast quality we use the Brier skill score (BSS), which is based on the Brier score (BS) (Wilks, 2011):

$$\begin{array}{}\text{(5)}& \mathrm{BS}={\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^N(f_i-o_i){}^{\mathrm{2}},\end{array}$$

where N is the number of observations, f is the forecast probability and o is the outcome (either 1 or 0). The BSS is then calculated as

$$\begin{array}{}\text{(6)}& \mathrm{BSS}=\mathrm{1}-\mathrm{BS}/{\mathrm{BS}}_{\mathrm{ref}},\end{array}$$

where BS is the modelled Brier score and BS_ref is the score of a reference model, in this case a model that simply assumes the mean tree fall probability in each grid cell. This mean probability is used as the forecast probability f in BS_ref and compared to the outcome o. The BSS ranges from −∞ to 1, where a positive value indicates that the model is better than the reference model. For calculating the BSS we use 10-fold cross validation. Here, the dataset is randomly divided into 10 equal sequences. The model is trained on 9 sequences, while the BS score is calculated for the 10th sequence and used for validation. This is repeated 10 times, each time using a different sequence for the validation.

We selected a set of meteorological parameters based on the literature cited in the Introduction and grouped them into 11 predictor classes, e.g. “wind”, “snow” and “precipitation” (see Table A1 for full list of predictors and classes). To test for legacy effects we also include the precipitation sum and soil water volume from antecedent time periods of 3 months, 9 months and 1 year. The goal is not to build the “perfect” model but to examine which predictor classes influence tree fall, which are not influential and which are most clearly improving the skill of the model against the basic reference model.

Since the length of railway lines in a grid cell is highly influential regarding the tree fall probability, this variable is included as well.

We were interested in the impact of each predictor class and also the predictor modifications (for example anomalies or relations to local percentiles) which improve the model skill the most. At the same time we wanted to avoid multicollinearity. Therefore, model selection followed three criteria:

1. There must be exactly one predictor from each predictor class in the model (see Table A1 for a full list of predictors and classes).

2. Only the predictor of each class improving the model's BSS the most is added to the model.

3. The predictor has to be significant with p<0.05 based on Student's t test.

We then moved gradually from class to class. We added and removed each of the predictors in the class in a stepwise approach, keeping only the class predictor with the best BSS performance.

We assume gust speeds to be the key predictor, but interactions with other predictors that influence a tree's vulnerability are likely. Therefore, we added interaction terms between the daily maximum gust speed and each other model predictor in the model in the same stepwise approach. Again, we only kept the interaction term if it improved the model's BSS.

After adding all predictors to the model we tested for multicollinearity. Multicollinearity exists when two or more predictors in a regression model are moderately or highly correlated with one another. We used the variance inflation factor (VIF) to test for multicollinearity:

$$\begin{array}{}\text{(7)}& {\mathrm{VIF}}_j={\displaystyle \frac{\mathrm{1}}{\mathrm{1}-R_j^{\mathrm{2}}}},\end{array}$$

where $R_j^{\mathrm{2}}$ is the R² value obtained by regressing the jth predictor on the remaining predictors. All predictors with VIF < 5 were considered to have no critical multicollinearity (Sheather, 2009).

We calculated the standardized effect size for each predictor to estimate their effects on tree fall probability compared to each other. For this, we standardized the absolute value of the predictor's estimated coefficient by calculating the standardized coefficient or beta coefficient:

$$\begin{array}{}\text{(8)}& \mathit{\beta }=b_j{\displaystyle \frac{s_{xj}}{s_y}},\end{array}$$

where b_j is the estimated coefficient for the jth predictor, s_xj is the standard deviation of the independent predictor x_j and s_y is the standard deviation of the dependent variable y.

Finally, we tested the significance of each independent variable in the model. We kept only those independent variables that are significant (with p<0.05 based on Student's t test) and then continued analysis with this reduced model.

4 Results

In this section we describe the selected model and the impact of the model predictors on tree fall risk.

As can be seen in Figs. 3 and 4, winter wind storms cause the highest number of tree fall events, while a very high monthly number of tree fall events occurs from January to March, the season of winter wind storms. However, meteorological predictors other than wind speed caused by storms factor into tree fall risk: according to the selection criteria described in Sect. 4 the resulting model (using the McCullagh and Nelder, 1989, model notation) is

$$\begin{array}{}\text{(9)}& \begin{array}{rl}& \text{tree fall}\sim \mathrm{rd}+v_{\max \mathrm{\_}\mathrm{anom}}+{\mathrm{dur}}_{\mathrm{90}}+\mathrm{gf}\\ & +\sin \left(\mathrm{2}\cdot \mathrm{pi}/\mathrm{360}\cdot \mathrm{winddir}\right)+\cos (\mathrm{2}\cdot \mathrm{pi}/\mathrm{360}\cdot \mathrm{winddir})\\ & +\mathrm{sd}+T_{\mathrm{slfrost}}+{\mathrm{pr}}_{\mathrm{90}}+{\mathrm{swvl}}_{\mathrm{anom}}+\mathrm{pr}\mathit{\_}\mathrm{365}+\mathrm{swvl}\mathit{\_}\mathrm{365}\\ & +\mathit{\rho }+v_{\max \mathrm{\_}\mathrm{anom}}:{\mathrm{dur}}_{\mathrm{90}}+v_{\max \mathrm{\_}\mathrm{anom}}:\mathrm{gf}.\end{array}\end{array}$$

Explanations for the different predictor abbreviations are given in Tables 1 and A1. This model predicts the tree fall risk for each grid cell using the meteorological variables of each cell as input. The terms v_{max_anom}:dur₉₀ and v_{max_anom}:gf represent the interactions of the gust speed with duration and the gust factor. They serve to account for the fact that the individual parameters do not change tree fall risk independently. Their impact in the model becomes apparent mainly on days with relatively high wind speeds. See Sect. 6.3 for further discussion of this effect. Sine and cosine terms are used for winddir to ensure that the tree fall probability as a function of winddir has the same values at 0 and 360°. The model's BSS is 0.069, compared to a BSS of 0.0637 for

$$\begin{array}{}\text{(10)}& \mathrm{tree}\mathrm{fall}\sim \mathrm{rd}+v_{\max },\end{array}$$

showing an improvement of model skill when using additional meteorological predictors compared to just rail density rd and the daily maximum gust speed v_max.

In Table 1 the predictors, their definitions, and corresponding model coefficients and metrics are listed. All coefficients except for those of snow depth (sd), soil frost (T_slfrost) and the mean soil water volume during the previous year (swvl_365) are significantly different from 0. We find the highest effect sizes (with absolute standardized coefficients greater than 1) for the gust speed anomaly (v_{max_anom}), the interaction of the gust speed anomaly and the duration of strong wind speeds (dur₉₀), the interaction of the gust speed anomaly and the gust factor (gf), rail density (rd), and the duration of strong wind speeds. Interactions between the gust speed anomaly and other predictors (except the duration of strong wind speeds and the gust factor) do not improve the model's BSS.

For daily precipitation, the daily soil water volume and the daily maximum gust speed we compare unmodified predictors and predictors related to local conditions (using anomalies or percentiles) and find that the latter improve the BSS more, with pr₉₀, swvl_anom and v_{max_anom} being the best predictors.

To test for multicollinearity, we use the VIF and find all values to be below 5 and therefore not critically correlated with each other. Interaction terms are excluded from this as they are naturally highly correlated with the interaction partners.

In a second step we adapt the model and identify all non-significant predictors: sd, T_slfrost and swvl_365. To reduce model complexity we remove these predictors. After removing the three non-significant predictors the BSS remains at 0.069. This results in the following model:

$$\begin{array}{}\text{(11)}& \begin{array}{rl}& \mathrm{tree}\mathrm{fall}\sim \mathrm{rd}+v_{\max \mathrm{\_}\mathrm{anom}}+{\mathrm{dur}}_{\mathrm{90}}+\mathrm{gf}\\ & +\sin (\mathrm{2}\cdot \mathrm{pi}/\mathrm{360}\cdot \mathrm{winddir})+\text{cos}(\mathrm{2}\cdot \mathrm{pi}/\mathrm{360}\cdot \mathrm{winddir})\\ & +{\text{pr}}_{\mathrm{90}}+{\text{swvl}}_{\mathrm{anom}}+\text{pr\_365}+\mathit{\rho }+v_{\text{max\_anom}}{\text{: dur}}_{\mathrm{90}}\\ & +v_{\text{max\_anom}}\text{:gf}.\end{array}\end{array}$$

We find that the rail density, anomaly of daily maximum gust speeds v_{max_anom}, duration of strong wind speeds based on the local 90th gust speed percentile dur₉₀, gust factor gf, wind direction winddir, precipitation related to the local 90th percentile pr₉₀, soil water volume anomaly swvl_anom, precipitation sum in the previous year pr_365, air density ρ, and the two interactions of the gust speed anomaly with either the gust factor or duration of strong wind speeds were significant, improved the model's BSS and therefore meet the model selection criteria. This model is used to plot the functional relationships between the tree fall probability and meteorological predictors (Fig. 5). For these plots one model parameter is varied, while the others are fixed to a certain value (detailed in the caption of Fig. 5) that was determined during previous data exploration. For the fixed values of v_max anom and dur₉₀ we picked 18 m s⁻¹ and 5 h, which represent values of a short but strong winter storm. A wind speed of 18 m s⁻¹ is exceeded on about 0.5 % of days and thus occurs approximately 2 days a year. For swvl_anom and pr₉₀ we selected values that represent a dry situation, thus very low soil moisture and very low precipitation. For wind direction we picked a north-easterly wind. For the other variables (pr_365, ρ) we chose the average over the time period 2017–2021. Based on these plots and the standardized coefficients (Table 1) we find a relatively strong increasing impact on tree fall risk for v_{max_anom}, dur₉₀ and rd. We find a relatively weak but still significant increasing impact for swvl_anom, pr₉₀, ρ and pr_365. We find a relatively strong decreasing effect for gf and a relatively weak impact for winddir with easterly to south-easterly winds having a decreasing and westerly to north-westerly winds having an increasing impact respectively.

Based on these findings, we propose that high and prolonged wind speeds, especially in combination with wet conditions (high precipitation and high soil moisture) and high air density, increase tree fall risk.

Table 1 Model predictors (ordered by their effect size) and their corresponding model coefficients and metrics. Bold numbers indicate values below the required threshold for significance and multi-correlation (with p<0.05 based on Student's t test and VIF < 5). See Table A1 for further details.

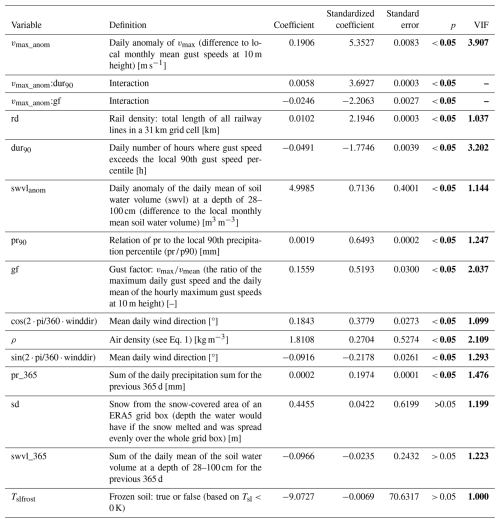
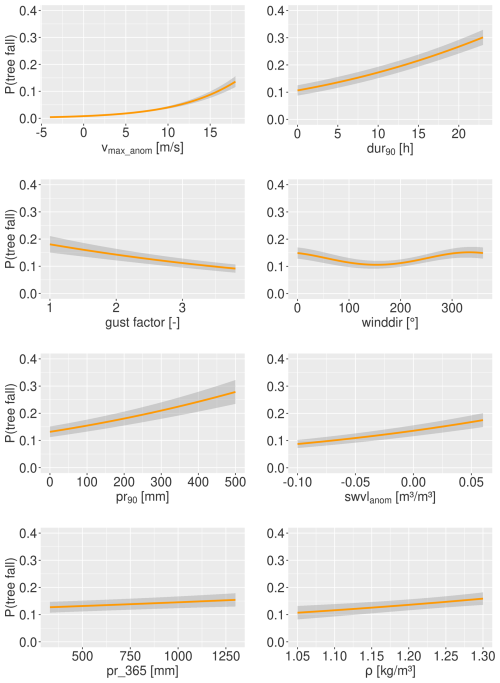
Figure 4 Changes in tree fall probability in an ERA5 grid cell with 100 km railway length (urban conditions) depending on different parameters. In each figure one model parameter is varied, while the others are fixed to a certain value: v_{max_anom}=18 m s⁻¹, dur₉₀=5 h, gf = 2.2, pr₉₀=20 mm, winddir = 41°, swvl_anom=0 m³ m⁻³, pr_365 = 663 mm and ρ=1.2 kg m³. Grey areas signify the confidence interval with a level of 95 %.

5 Discussion

There are a vast number of studies which contributed significantly to understanding storm impacts on forests, particularly in areas such as impact modelling (Gardiner et al., 2008; Hale et al., 2015; Kamimura et al., 2016; Valta et al., 2019; Costa et al., 2023), wind climatology (Mohr et al., 2017; Jung and Schindler, 2019; Tervo et al., 2021), or field campaigns and pulling experiments (Kamimura et al., 2016; Kamo et al., 2016; Schindler and Kolbe, 2020). A key goal of these research efforts is to develop functional forecast models which can predict tree and forest damage. Such a model should be applicable to major tree species, diverse landscapes and various forest types. It would help to identify areas of risk, estimate damages in a future climate scenario or during possible extreme events, and assess management strategies for foresters and infrastructure providers like Deutsche Bahn (Akay and Taş, 2019; Albrecht et al., 2019). However, there are several hurdles on the way to this goal. (1) There are a lack of damage data covering large areas and longer time periods which are needed to train these models and often a lack of environmental data to feed into them (Hart et al., 2019; Maringer et al., 2020). (2) There is also a lack of highly resolved gust speed data. Such data are needed to fully understand and model tree damage (Jung and Schindler, 2019; Gregow et al., 2020). (3) Many of the existing studies focus on a partial aspect of the issue, for example on a small spatial region, a single damaging storm event or one tree species (often due to the lack of bigger data). (4) And finally such a model would need to incorporate parameters from many relevant fields (such as tree biology, forestry, meteorology, fluid dynamics, pedology and others) as well as their interactions. So far, many studies have focused on the parameters from their respective fields. These issues make it difficult to apply existing works to different tree species or forest types and also to use the existing impact models on data from climate models. Several works call for more impact data and longer time series, addressing the interaction of multiple risks, and inter-disciplinary approaches and cooperation (Valta et al., 2019; Gregow et al., 2020; Venäläinen et al., 2020; Gardiner, 2021). Additionally, there is ongoing work dedicated to developing more accurate small-scale gust speed products (Primo, 2016; Schulz and Lerch, 2022).

In the field of forest impact modelling many models focus on biological and environmental predictors such as tree, stand and soil properties (Mayer et al., 2005; Schindler et al., 2009; Kamo et al., 2016; Kabir et al., 2018; Díaz-Yáñez et al., 2019; Hart et al., 2019; Wohlgemuth et al., 2022). Meteorological predictors like precipitation or soil moisture are considered less often (Schmidt et al., 2010; Hall et al., 2020). Wind is mostly considered regarding the mean or maximum wind speed (Hale et al., 2015; Morimoto et al., 2019; Hall et al., 2020). This focus on environmental predictors and mean wind speeds is often also true for studies that consider tree fall on railway lines (Bíl et al., 2017; Kučera and Dobesova, 2021; Gardiner et al., 2024).

Many impact studies focus on singular and very damaging storm events (Hale et al., 2015; Kabir et al., 2018; Hart et al., 2019; Hall et al., 2020; Zeppenfeld et al., 2023). Those who study longer time periods are often focused on small areas such as experimental plots (Albrecht et al., 2012; Kamimura et al., 2016) or smaller administrative units (Jung et al., 2016). In this study, we try to contribute to this ongoing research using data covering a large area over several years (2017 to 2021) and exploring the impact of different meteorological factors. In a next step, our model can be applied to gridded climate model data to estimate risks for trees in future climate scenarios.

We focused on not only different types of meteorological predictors, including those that describe wind characteristics, but also predictors describing precipitation and soil conditions. We showed that meteorological predictors other than the mean or maximum wind speed have a significant effect on tree fall risk and improve the model's predictive skill.

5.1 Model building and predictor selection

The model selection process resulted in a model with 10 independent variables and 2 interactions, raising the possibility of over-complexity. To account for this we calculated the Akaike information criterion (AIC), which is a relative measure showing how well different models fit the data. It penalizes numbers of independent variables that are too high. The model with the lowest AIC value is considered the best. We calculated the AIC for the resulting model as well as reduced versions of the model in which we left out (1) the interactions, (2) all predictors with an absolute standardized coefficient < 1 and (3) all predictors with an absolute standardized coefficient < 0.5. We find that our selected model has the lowest AIC (56 985.43) compared to options 1 to 3 (57 339.14, 57 512.49 and 57 062.27 respectively).

In our model the influence of the wind direction on tree fall risk is relatively small compared to the effect of the wind speed itself. Nonetheless, it appears that north-westerly winds slightly increase tree fall risk. This seems counter-intuitive as this is the predominant wind direction in Germany. It is assumed that trees adapt to the dominant wind direction and that untypical wind directions, in this case easterly winds, increase tree fall risk (Bonnesoeur et al., 2016; Valta et al., 2019). An explanation might be that westerly winds are on average stronger. ERA5 is not a perfect representation of local winds and sometimes underestimates gust speeds (Molina et al., 2021). Thus, in cases where ERA5 underestimates the real gust speeds but shows westerly winds the wind direction might become a proxy for stronger winds. While Akay and Taş (2019) found the wind direction at three stations to be one of the predictors with the highest impact on storm damage risk, it has a relatively small effect in our model. Their result may be related to the role of wind direction on wind speeds at stations located in an area with high orography, which is much weaker in the rather coarse ERA5 data. Certainly there can also be a relationship between the wind direction and a tree's exposure, for example depending on the topography, the tree's acclimation to the average local wind direction (Mitchell, 2013) or the location of the tree to an exposed edge (Quine et al., 2021). We did not account for these factors. Future modelling might benefit by adding local tree wind exposure.

Duration of strong winds is important because trees do not fail instantly but fail with repeated swaying that fractures the root–soil system, and this process can take many hours (Kamimura et al., 2022). The gust factor and air density are also known to be critical components in calculations of tree wind damage risk (see Eqs. 4.4, 4.12 and 4.15 in Quine et al., 2021).

We found that both the soil water volume anomaly and daily precipitation sum have an increasing impact on tree fall probability, which is in agreement with previous studies (Kamimura et al., 2016; Hall et al., 2020). This could be due to the fact that heavy precipitation can contribute to the accumulation of weight on tree crowns, consequently increasing wind-induced stress (Neild and Wood, 1999; Gardiner et al., 2010; Hale et al., 2015). Additionally, water-logged soils can have a negative affect on root anchorage (Kamimura et al., 2012). The influence of precipitation and soil moisture on tree fall during winter will likely increase in northern forest areas. Here rising temperatures and shortened winter decrease soil frost and thus root anchorage (Gregow et al., 2017, 2020; Lehtonen et al., 2019; Venäläinen et al., 2020).

We also included predictors describing antecedent soil moisture and precipitation conditions, namely mean soil water volume accumulation and the precipitation sum of the previous 12 months. The antecedent soil water volume is not significant in our model, but the precipitation sum of the previous year is, showing a weak increasing impact on tree fall risk. The role of droughts in other hazards such as fires or bark beetle infestation is well studied (Venäläinen et al., 2020; Singh et al., 2024). However, research on the impact of drought on wind-induced tree damage is inconclusive. Csilléry et al. (2017) found both positive but mainly negative effects on tree damage. They suggest that in some stands drought weakens the trees and makes them more vulnerable to wind loading, while in others dry soils make them less vulnerable to overturning. We suggest that further research should consider antecedent weather situations in more detail, for example, by including indices like the standardized precipitation–evapotranspiration index (SPEI), which has been used in recent research on forest disturbance (Klein et al., 2019; Gazol and Camarero, 2022). It is also likely that trees react very differently to dry and wet conditions depending on their species, height or soil type. Whenever such information is available, it should be included in the analysis.

Several studies have found snow and frozen soil to be influential (Peltola et al., 2000; Hanewinkel et al., 2008; Kamimura et al., 2012; Kamo et al., 2016). Snow loading can apply stress on the canopy and branches, and this stress can be increased by additional wind (Kamo et al., 2016; Zubkov et al., 2023). Frozen soil has been shown to prevent uprooting (Gardiner et al., 2010; Pasztor et al., 2015). Yet, in our study snow and soil frost did not prove to be significant. This is likely connected to the rare occurrence of such conditions in Germany between 2017 and 2021. On average, over all model grid cells snow depth exceeded 0.05 m water equivalent only on 1.3 % of all winter days and soil frost occurred only on 0.03 % of the days. Our snow data are derived from ERA5 and are therefore modelled data. In their evaluation of snow cover properties in ERA5, Kouki et al. (2023) found that ERA5 generally overestimates snow water equivalent in the Northern Hemisphere. Thus, snow coverage might even be lower than shown in our data. Using measured instead of modelled snow data could potentially improve the modelling results.

For wind speed, precipitation and soil water volume we compared unaltered predictors with anomalies and percentile exceedances. For all three parameter types, we found that predictors based on percentile exceedances (pr₉₀) or anomalies (swvl_anom, v_{max_anom}) improve the model's BSS the most and, thus, reflect the trees' ability to acclimate. Trees adapt to the local climate (Mitchell, 2013; Gardiner et al., 2016), and what might be windy or dry conditions for a tree in one region might be average in another. When modelling tree damage over larger spatial regions, we therefore suggest relating meteorological predictors to local climatological conditions, for example using anomalies or percentiles.

We found that air density has a positive impact on tree fall risk. As our model includes both the maximum gust speed and air density we considered wind load as a model predictor. Wind load is proportional to air density and the square of wind speed:

$$\begin{array}{}\text{(12)}& \mathrm{wl}=\mathrm{1}/\mathrm{2}C\mathit{\rho }A{v}^{\mathrm{2}},\end{array}$$

where C is a non-dimensional drag coefficient, ρ is the air density (kg m⁻³), A is the frontal area and v is the wind speed (m s⁻¹) (Ciftci et al., 2014; Gardiner et al., 2016; Quine et al., 2021). Therefore, wind load is highly correlated with wind speed. In our data, v_{max_anom} and wind load have a high Pearson correlation coefficient of 0.95. Due to this, they should not be used together in a single model since a high correlation between parameters makes model interpretation difficult. As both the drag coefficient and the tree's frontal area are unknown, we reduced the equation to

$$\begin{array}{}\text{(13)}& \mathrm{wl}=\mathrm{1}/\mathrm{2}\mathit{\rho }{v}^{\mathrm{2}}.\end{array}$$

We tested a model that used wind load instead of air density and v_{max_anom}. We removed air density from the predictors of Eq. (11) and exchanged v_{max_anom} with wind load. We found a lower BSS for this model of 0.0678 compared to 0.069. Yet, wind load is highly significant and has a strong effect size with a standardized coefficient of 4.07. Additionally, the wind load model has a marginally lower AIC (56 980.45) than the original model (56 985.43). Due to the lower BSS, wl did not meet the selection criteria in our modelling process. Yet, it is certainly influential regarding tree fall and might add value to other impact models. We suggest considering it in future studies.

5.2 The effect of interaction terms

Interactions can show the combined effect predictors may have on model outcome and how the effect of one predictor changes depending on the value of the other. We tested if interaction terms with the gust speed anomaly add to the model skill and found positive results for the interaction with the duration of strong wind speeds as well as gust factor. Both predictor interactions improve the BSS and are highly significant (see Table 1).

A low gust factor could be the result of a day with a high maximum gust speed and a high mean gust speed as well as the result of a low maximum gust speed and a low mean gust speed. Thus, this predictor lacks information without the interaction with the maximum gust speed. The duration of strong wind speeds depends on the local 90th gust speed percentile. As the average 90th percentile in our data is 12 m s⁻¹, a wide range of gust speeds exceed the percentile since a v_max greater than 30 m s⁻¹ is possible during strong storms. Here too, the interaction adds missing information to the model. The duration and gust factor are not strongly correlated (with a Spearman's correlation coefficient of 0.15) and therefore provide complementary information as long durations are accompanied by a vast range of gust factor values.

In Fig. 5 the effect of the duration of strong wind speeds and gust factor for the model with and without interaction terms is compared. When the interactions are removed, the decreasing impact of the gust factor on tree fall probability is much smaller, while the duration of strong wind speeds seems to be not at all connected to tree fall probability. The effect size of these predictors also decreases strongly: in a model without interactions, the standardized coefficient of the gust factor is −0.3181 and that of the duration of strong wind speeds is 0.0275 (compare to Table 1). Only when we add the interaction does the impact of these predictors become visible, thus showing their combined effect. Furthermore, the model without interactions has a BSS of only 0.0678 compared to 0.069 for the model that includes interactions (Eq. 11).

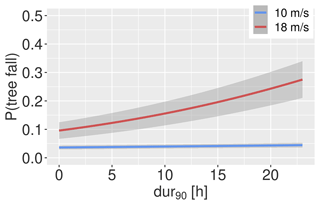
The combined effect of the predictors is illustrated in Fig. 6. We compare the model outcome depending on the duration of strong wind speeds for two values of v_{max_anom}, 10 and 18 m s⁻¹. Both represent values that exceed the 98th percentile of daily gust speeds in most grid cells, but one represents a low exceedance, while the other is very high. The duration of strong wind speeds has a much stronger increasing impact on tree fall probability in the second scenario. This also fits with the observations of Kamimura et al. (2022), who showed that even in a typhoon with very high wind speeds the duration of the storm was important regarding the occurrence of damage.

A high maximum daily gust speed could be not only the result of just one strong gust but also the result of a stormy day with lasting high wind speeds. Adding additional wind properties like the gust factor or duration of strong wind speeds can help differentiate between these scenarios. Figure 7 illustrates this. Here, we compare modelled tree fall probabilities for a day with a high gust factor and low duration of strong wind speeds (a gusty day) and a day with a low gust factor and long duration of strong wind speeds (a day of sustained high wind speeds). The relationship between v_{max_anom} and the tree fall probability is much weaker on the gusty day, showing how strongly the interaction with additional wind properties can change tree fall risk.

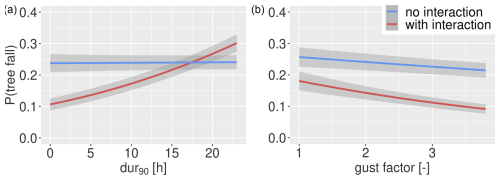
Figure 5 Comparison of the effects of the duration of strong wind speeds (dur₉₀, a) and the gust factor (gf, b) on tree fall risk for the model with and without interaction terms. Parameters are fixed to the same values as in Fig. 4 with v_{max_anom}=18 m s⁻¹. Grey areas signify the confidence interval with a level of 95 %.

Figure 6 Interaction effect of v_{max_anom} and storm duration for two different values of v_{max_anom} (10 and 18 m s⁻¹). All other parameters are fixed to the same values as in Fig. 4. Grey areas signify the confidence interval with a level of 95 %.

5.3 Limitations

This study aimed, among other things, to create a meteorological basis for a predictive tree fall model that can support decisions regarding the management of vegetation alongside transportation routes, as well as climate-resilient forests. However, local ecological information (soil, tree species, stand structure, etc.) is not taken into account. Thus, the results are not representative of every individual setting but rather for an average setting across Germany.

Many studies have pointed out the influence of tree, stand and soil factors (Mayer et al., 2005; Kamo et al., 2016; Kabir et al., 2018; Díaz-Yáñez et al., 2019; Hart et al., 2019; Gardiner, 2021; Wohlgemuth et al., 2022) on wind damage vulnerability. Thus, model results could vary if such information were to be incorporated. The tree fall risk according to this model might vary at the same gust speed level for different trees and different stands. For example, Gardiner et al. (2024) demonstrated how critical wind speeds for tree fall along railway lines vary significantly depending on factors such as tree height, canopy shape, and whether the tree is coniferous or deciduous. However, our results show clear evidence for the importance of specific meteorological predictors in tree fall and storm damage modelling. Finding the specific relationships for meteorological predictors and different tree species, forest types and soil types should be the next step in understanding the impact of different meteorological conditions on wind damage.

In the dataset about 25 % of tree fall events occur at a maximum daily gust speed below 11 m s⁻¹. These tree fall events might be caused by processes unrelated to meteorology. Valta et al. (2019) point out that an individual tree fall instance is already possible at low wind speeds such as 15 m s⁻¹. Events at an even lower speed cannot be ruled out. On the other hand, these events might be related to wind events not resolved by the ERA5 reanalysis and thus caused by wind speeds that were higher in reality than shown in the data. For example, convection is not explicitly resolved by the underlying atmospheric model of ERA5. Therefore, the wind speeds caused by convective events are likely to be underestimated. Additionally, the coarse resolution of ERA5 is generally suboptimal when trying to connect small-scale events such as a single tree fall instance with meteorological data. Yet, at the time of our research ERA5 was the only reanalysis dataset covering the years 2017 to 2021. While evaluations of ERA5 gust speeds with observational data point out some limitations, they also find the data in general to be a good representation of local measurements. Molina et al. (2021) compare hourly 10 m wind speed from ERA5 with wind observations from 245 stations across Europe. They find that “Most of the stations exhibit hourly [Pearson correlation coefficients] ranging from 0.8 to 0.9, indicating that ERA5 is able to reproduce the wind speed spectrum range ... for any location over Europe”. Minola et al. (2020) compare ERA5 with hourly near-surface wind speed and gust observations across Sweden for 2013–2017. They, too, find Pearson correlations of 0.8 and higher for daily maximum gust speeds. However, they do point out that “evident discrepancies are still found across the inland and mountain regions” and that higher wind speeds and gust speeds display stronger negative biases. Data with higher spatial resolutions that include convective effects might help in understanding the effects of thunderstorms and other small-scale phenomena in future research. There is already some concern that such phenomena are becoming more problematic in Europe (Suvanto et al., 2016; Sulik and Kejna, 2020).

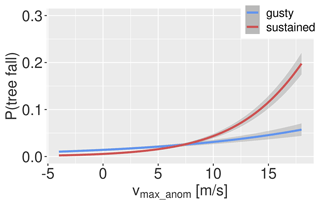
Figure 7 Comparison of the interaction effect. Gusty day: dur₉₀=2 h and gf = 5; sustained day: dur₉₀= 12 h and gf = 2. All other parameters are fixed to the same values as in Fig. 4. Grey areas signify the confidence interval with a level of 95 %.

The addition and removal of model predictors during the stepwise model selection process caused only very small changes in the model's BSS, which was very low to begin with. This is quite likely connected to all of the limitations listed above. Models which are able to add tree, soil or stand data or have access to meteorological data of a higher spatial resolution will likely produce a better model skill rating and be able to examine the relationships of tree fall and meteorology in more detail. Nonetheless, our approach provides clear evidence about which meteorological predictors have a significant impact and indicates the magnitude of their effect.

6 Conclusions

Our aim was to investigate the relationship between tree fall and wind as well as other meteorological conditions. For this, we used a stepwise approach to build a logistic regression model predicting tree fall risk.

We showed that high and prolonged wind speeds, especially in combination with wet conditions (high precipitation and high soil moisture) and a high air density, increase tree fall risk. We find a relatively strong increasing impact on tree fall risk for the daily maximum gust speed anomaly and duration of strong wind speeds. We find a relatively weak but still significant increasing impact for the daily soil water volume anomaly, the daily precipitation exceedance of the 90th percentile, daily air density and the precipitation sum of the previous year. We find a relatively strong decreasing effect for the gust factor and a relatively weak impact for wind direction, with easterly to south-easterly winds having a decreasing and westerly to north-westerly winds having an increasing impact. Snow and soil frost predictors, which were found to be important in past research, have no significant impact in our model. To account for the potential acclimation of trees to the local climate we compared unmodified predictors and predictors related to local conditions (using anomalies or percentiles) for the daily precipitation, daily soil water volume and daily maximum gust speed. We find that the latter predictors, which reflect acclimation, improve the model's skill the most. Finally we showed that the inclusion of interaction terms improved the model's skill score, changed modelled risk probabilities and helped to illustrate the combined effect meteorological predictors may have on tree fall probability.

Many previous studies on tree fall and forest storm damage are restricted to a single event or small research region. Additionally, past research has primarily focused on tree, soil and stand parameters. When studies have taken meteorology into account, they often implemented only mean or maximum gust speeds. We were able to conduct a long-term and large-scale study on tree fall risk and were able to show that other wind-related parameters such as the gust factor, duration of strong wind speeds or air density as well as other predictors related to meteorology, including precipitation and soil moisture, have a significant impact on tree fall risk. Our results also highlight the importance of using anomalies or relations to local percentiles for meteorological predictors in large-scale studies to account for the acclimation of trees to their local climatic conditions.

This work is a step towards future research on the topic of wind damage and tree fall. It shows how meteorological factors can be incorporated into a probabilistic tree fall model. Such a model can be applied to climate model data to estimate changes in tree fall risk in future climate scenarios and during potential extreme events. We aim to elaborate on these goals in future research.

Appendix A

Table A1 List of meteorological predictors tested in the logistic regression model.