Classification of North Atlantic and European extratropical cyclones using multiple measures of intensity

The question of how to quantify the intensity of extratropical cyclones (ETCs) does not have a simple answer. To offer some perspective on this issue, we analyse multiple measures of intensity for North Atlantic and European ETCs for the extended winter season between 1979 and 2022 using ERA5 reanalysis data. The most relevant intensity measures are identified by investigating relationships between them and by performing a sparse principal component analysis on the set of measures. We show that dynamical intensity measures correlate strongly with each other, while correlations are weaker for impact-relevant measures. Based on the correlations and the sparse principal component analysis, we find that five intensity measures, namely 850 hPa relative vorticity, 850 hPa wind speed, wind footprint, precipitation, and a storm severity index, describe ETC intensity comprehensively and non-redundantly. Using these five measures as input, we objectively classify the ETCs with a cluster analysis based on a Gaussian mixture model. The cluster analysis is able to produce four clusters between which ETCs differ in terms of their intensity, life cycle characteristics such as deepening rate and lifetime, and geographical location. A fourth of all ETCs belong to the weakest cluster and occur mostly over Europe and in the Mediterranean area. Nearly half of all ETCs belong to the average-intensity cluster and occur mostly at the northeastern parts of the main North Atlantic storm track. A fifth of all ETCs belong to the second most intense cluster and occur mostly at the start of the North Atlantic storm track. Finally, less than a 10th of all ETCs belong to the most intense cluster and occur almost equally everywhere. This last cluster includes a clear majority of a set of investigated impactful storms (17 out of 21), which demonstrates the ability of the method to identify potentially damaging ETCs.

1 Introduction

Extratropical cyclones (ETCs), also referred to as mid-latitude cyclones or low-pressure systems, constitute a substantial part of the atmospheric circulation in the mid-latitudes and transport large amounts of heat, moisture, and momentum polewards (Hartmann, 2015). ETCs are also responsible for most of the day-to-day variability in weather in the mid-latitudes and are the dynamical cause for most of the precipitation (Hawcroft et al., 2012). Furthermore, the most extreme ETCs can be associated with heavy precipitation and strong winds responsible for flooding, landslides, damage to infrastructure, or diverse economic losses.

No two ETCs are the same, and there is great variability in their shape, size, lifetime, and intensity (Nielsen and Dole, 1992). Thus, many attempts of classifications have been made and have often been driven by the desire to better understand the development or the structure of certain types of ETCs. For example, Zillman and Price (1972) and Browning (1990) classified ETCs based on their cloud patterns, whereas Field and Wood (2007) grouped ETCs based on their low-level wind speed and their water vapour path in an attempt to understand ETC precipitation. Attempts have also been made to classify ETCs by their dynamical forcing. For example, Thorncroft et al. (1993) and Schultz et al. (1998) separated ETCs that develop in different background flows, whereas Petterssen and Smebye (1971), Deveson et al. (2002), and Dacre and Gray (2009) grouped ETCs that are dominated either by low-level thermal advection or by upper-level vorticity advection. However, perhaps the most common approach to group or classify ETCs is based on a measure of their intensity. Previous studies have grouped ETCs either by their maximum 850 hPa relative vorticity (VO), often focusing on the strongest storms (e.g. Catto et al., 2010; Sinclair et al., 2020), or by the decrease in minimum mean sea level pressure (MSLP) over a 24 h period, again commonly focusing on the most rapidly deepening storms (e.g. Sanders and Gyakum, 1980; Reboita et al., 2021).

Quantifying the intensity of any given ETC in a concise yet accurate manner is, however, a challenging task. Meteorologists and climate scientists have faced this challenge for many decades, and as such many methods and diagnostics exist, but there is no clear “correct” way or “best” diagnostic. The most common metrics used to quantify ETC intensity, MSLP and VO, describe the synoptic-scale dynamics of the ETCs and are strongly related to the horizontal pressure gradient and large-scale winds. Historically, MSLP has been provided by records from surface stations, while nowadays VO is also commonly available from large gridded datasets such as reanalyses. However, in many cases, neither the minimum MSLP nor maximum VO correlates well with the impacts of a given ETC (e.g. Field and Wood, 2007; Roberts et al., 2014; Sinclair and Catto, 2023). This is mainly due to the presence of mesoscale features such as fronts, low-level jets, and convergence bands which strongly influence the wind and precipitation fields (Hewson and Neu, 2015). Therefore, impact-relevant metrics which have no direct theoretical link to the traditional dynamically based metrics of MSLP and VO have been introduced. Such metrics include precipitation rates and accumulations (Hawcroft et al., 2012), sizes of wind footprints (Roberts et al., 2014), and storm severity indices (Leckebusch et al., 2008a).

Though challenging, quantifying the intensity of ETCs is crucial for climate studies. Firstly, many studies have used reanalysis datasets to quantitatively describe the state of the current climate in terms of number, location, and intensity of ETCs (e.g. Hoskins and Hodges, 2002; Rudeva and Gulev, 2007; Jeglum et al., 2010; Laurila et al., 2021a). Secondly, a manageable number of metrics which are easy to compute (concise metrics) are needed to identify whether any trends in ETC intensity have already occurred or may do in the future as the climate changes. For example, simulations from the Coupled Model Intercomparison Project (CMIP) have been extensively analysed to determine how the intensity of ETCs may change in the future (e.g. Zappa et al., 2013b; Colle et al., 2013; Seiler and Zwiers, 2016; Chang, 2018; Priestley and Catto, 2022; Dolores-Tesillos et al., 2022). Thirdly, concise metrics of ETC intensity enable the comparison of the representation of ETCs in different datasets. For example, ETC climatologies can differ between different reanalysis datasets because ETCs differ in the underlying models, data assimilation methods, or the spatial and temporal resolution of the reanalyses (Wang et al., 2016). Furthermore, by comparing ETCs in historical simulations to ETCs in reanalysis datasets, it is possible to determine how accurately climate models reproduce the current climate (Catto et al., 2010; Priestley et al., 2020).

Up to now, most studies have only quantified ETC intensity using a single metric, or, if more than one has been considered, they have been used independently of each other. This may result in some information being omitted, as each metric only gives information about one aspect of ETCs. For example, two ETCs with the same minimum MSLP may have considerably different wind gusts associated with them or be very different in size (Sinclair, 1997). Considering a vast number and diversity of measures would likely give an in-depth description of all ETCs, but this would become impractical to deal with, hard to visualize, and challenging for forecasters and researchers to easily comprehend. Therefore, an optimal balance should be sought. In this context, automated and objective methods need to be applied to group ETCs using more than one metric or the spatial variation in a variable. For this purpose, machine learning methods have gained popularity in recent years due to their predictive and classification abilities (e.g. Catto, 2018; Sinclair and Catto, 2023; Wang et al., 2024). Of the many ways to classify meteorological datasets, unsupervised learning (i.e. clustering) is often prioritized to group elements of the dataset without any a priori knowledge. One such method is the Gaussian mixture model (GMM) which has been used in meteorological applications before (e.g. Vrac et al., 2005; Watanabe et al., 2020) but not widely in the context of ETCs.

The purpose of the study is to classify ETCs using multiple measures of intensity. The first aim is to identify how a number of commonly used ETC intensity measures relate to each other and then to identify the optimal metrics which, when considered together, fully describe the intensity of ETCs. The second aim is to classify the wintertime ETCs in the North Atlantic and in the European region based on this subset of intensity measures and to quantify the characteristics of each cluster. The last aim of this study is to show where some of the previously studied high-impact ETCs occur in our phase space of intensity and ETC classification.

The paper is structured as follows. Section 2 explains how the dataset of ETC tracks and intensity measures was created. Section 3 describes the methods used in the analysis of the data. Section 4 contains the results of the study which are then discussed in Sect. 5. Finally, Sect. 6 concludes the results.

2 Creation of ETC intensity dataset

2.1 ERA5 reanalysis

ERA5 (Hersbach et al., 2020) is an open-access global reanalysis dataset provided by the European Centre for Medium-range Weather Forecasts (ECMWF). It has a horizontal spectral resolution of T_L639, which corresponds to a grid spacing of $\mathrm{0.28}\mathit{°}/\mathrm{31}\mathrm{km}$ at the Equator on the native regular Gaussian grid of ERA5. We use ERA5 pressure level data and selected surface fields with 3-hourly resolution from 1979–2022 to both create ETC tracks (Sect. 2.2) and extract the ETC intensity measures (Sect. 2.3).

2.2 ETC tracking

ETC tracks are identified with the objective feature tracking software TRACK (Hodges, 1994, 1995, 1999b). TRACK uses a Lagrangian approach of tracking individual cyclones by identifying extrema in a given field and following them through time. To track ETCs, we use the 3-hourly VO field at the native horizontal resolution of ERA5 which is first truncated to T42 spectral resolution (310 km at the Equator) to exclude small-scale features and ensure that only synoptic-scale ETCs are identified. Wave numbers less than five are also removed to filter out planetary-scale waves. For the remaining wave numbers, local maxima are identified in the filtered VO field and a nearest-neighbour approach is used to connect them into ETC tracks. TRACK produces output which consists of the horizontal location (longitude and latitude) and magnitude of the T42 VO maxima for each time step in each ETC track.

We further filter the ETC tracks using the following criteria:

1. To exclude stationary and short-lived systems, the tracks need to be at least 1000 km long and last for at least 2 d (16 time steps in the 3-hourly data).

2. Weak systems are excluded by using a minimum threshold of $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}{\mathrm{s}}^{-\mathrm{1}}$ for the T42 VO.

3. Like in Sinclair and Catto (2023), the maximum T42 VO of the track must occur 24 h after genesis (the first time step) or later.

4. The maximum T42 VO needs to occur inside the area 80° W to 40° E in longitude and 30° N to 75° N in latitude (the magenta box in Fig. 1).

In total, in the 43 extended winters we find 7361 tracks meeting these criteria.

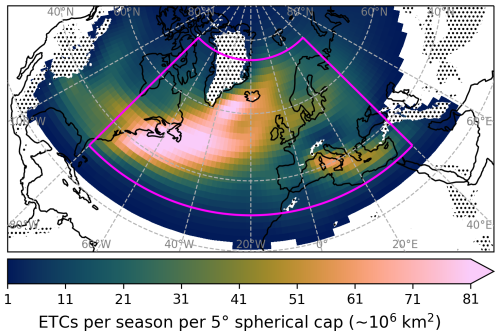
Figure 1 Climatology of ETC track density for the 43 October–March seasons in areas, where on average at least one track per 5° spherical cap (∼ 10⁶ km²) occurs per season. The magenta box bounded by 80° W, 40° E, 30° N, and 75° N shows the area inside which the ETCs need to have their maximum T42 VO. The hatching indicates areas where the average monthly mean value of surface pressure between October 1979 and March 2022 is below 850 hPa and the tracks may therefore be non-physical.

Statistical diagnostic fields of ETC tracks, such as track density, are calculated by using spherical kernel estimators provided by TRACK (Hodges, 1996, 1999a, 2008). Figure 1 shows the climatology of track density of the 7361 ETC tracks. In Fig. 1 we see that track density is the largest along the North Atlantic storm track, beginning at the eastern coast of North America and extending northeastward towards northern Europe. A local maximum in track density can also be seen in the Mediterranean basin. This is despite the fact that the tracking algorithm we use and the filters we applied are more designed to identify ETCs in the main storm tracks than in the Mediterranean, where ETCs tend to be smaller and shorter-lived (Campins et al., 2011). Similar distributions of track density during winter (DJF) were identified previously by Priestley et al. (2020) in historical CMIP6 simulations and by Hoskins and Hodges (2002) in ECMWF analyses using the same tracking algorithm. Campins et al. (2011), Aragão and Porcù (2022), and Doiteau et al. (2024), who focused on the Mediterranean region, determined the Gulf of Genoa as the location of maximum track density during DJF, whereas we have a maximum over the Tyrrhenian Sea. This difference can be explained by the sensitivity of the tracking method in this particular basin (see Flaounas et al., 2023, for details). However, the overall number of tracks in the Mediterranean area in these previous studies is in agreement with our distribution.

2.3 Intensity measures

We use ERA5 reanalysis data to create a set of intensity measures for the tracked ETCs. We reduce the amount of data to obtain one value per intensity measure per track. All the intensity measures can be calculated from any other reanalysis dataset.

The intensity measures can be divided into two categories. The first category consists of dynamical measures which describe physical aspects of ETCs and can be obtained from the reanalysis with no or minimal post-processing. The second category consists of what we call impact-relevant measures. These are diagnostic variables which are designed to quantify the aspects of ETCs that possibly have societal impacts. We emphasize that the impact-relevant measures do not necessarily directly translate into impacts but are based on variables which quantify the ETC features that have been found to cause the most damage to infrastructure.

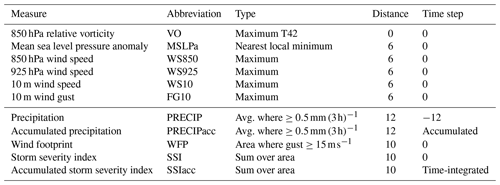
All intensity measures and the details of how they are produced are described in detail in the following subsections (Sect. 2.3.1 and 2.3.2), and the measures are summarized in Table 1. Most of the variables are on the native ERA5 grid with the horizontal resolution of 0.28°. The exceptions are 850 hPa wind speed and 10 m wind speed, which are on a 0.25° regular longitude–latitude grid. This is solely because we already had these data locally available. However, this difference in resolution is small and very unlikely to affect the results.

Table 1 Summary of all 11 intensity measures. The columns are the full name, abbreviated name, the type of value extracted, the maximum distance from the VO maximum (in geodesic degrees) to which the values are searched for, and time step with respect to the time of VO maximum (in hours). The horizontal line separates the measures into dynamical and impact-relevant ones.

2.3.1 Dynamical measures

The baseline for the intensity measures is VO, a widely used measure of ETC intensity. We use VO at the T42 resolution directly from the output of TRACK. For the sake of simplicity, we refer to the location of the VO maximum as the ETC centre, although the physical centre of the ETC is not necessarily located exactly at the same point.

The next dynamical variable we include is based on MSLP, which along with VO is a widely used measure of ETC intensity (e.g. Priestley et al., 2020). To account for the effect of the background environment on the MSLP values (i.e. large-scale temporal variations and climatological dependence of latitude; Anderson et al., 2003), we subtract a monthly mean value from the MSLP field to obtain an MSLP anomaly (MSLPa). We use the MSLPa field to find the nearest local minimum around the VO maximum. This is done by using bilinear spline interpolation and a steepest-descent method with TRACK. The local minimum MSLPa is found inside a circle centred around the VO maximum and has a radius of 6 geodesic degrees (equivalent to about 670 km). Various values were tested for the radius, and 6 geodesic degrees was discovered to be the most suitable (not shown). This value is also used by e.g. Li et al. (2014). Most of the MSLPa minima are within 100 km of the VO maxima, and very few values are actually found at a distance of 670 km (see Fig. S1 in the Supplement). For a small number (3 %) of maximum VO values, TRACK is unable to find an associated MSLPa value. These ETCs are omitted from the dataset.

Finally, we include winds from multiple levels as dynamical intensity measures. For a comprehensive overview of winds associated with ETCs, we include the maximum wind speed at 850 hPa (WS850), 925 hPa (WS925), and 10 m (WS10) within 6 geodesic degrees from the VO centre, a radius also used by Zappa et al. (2013a) and Gramcianinov et al. (2020). We also include the wind gusts at 10 m (FG10) as the maximum within 6 geodesic degrees, but unlike for the other three wind variables, we do not use an instantaneous value. Wind gust is highly variable in time, and therefore we take the maximum value of the previous 3 h. As for MSLPa, various values were explored for the radius of the area for all wind speed measures (not shown).

2.3.2 Impact-relevant measures

The first impact-relevant intensity measure is based on precipitation, which is an hourly accumulated field in ERA5. We sum precipitation values over 3 h to correspond to our time interval and define a precipitation diagnostic (PRECIP) as the average precipitation rate within an area, with a definition adapted from Sinclair and Catto (2023):

$$\begin{array}{}\text{(1)}& \mathrm{PRECIP}={\displaystyle \frac{\mathrm{1}}{A_{\mathrm{T}}}}\sum _{i=\mathrm{1}}^m{P}_i{A}_i,\end{array}$$

where P_i is the 3-hourly precipitation rate at grid point i, A_i is the area of the grid point, m is the number of grid points in which P_i exceeds a specific threshold value, and A_T is the total area of the m grid points. The precipitation is considered and averaged only within a specific geodesic radius around the ETC centre. We use the same values as Sinclair and Catto (2023) adapted to our grid and time resolution, i.e. a geodesic radius of 12° and a minimum precipitation rate of 0.5 mm (3 h)⁻¹.

Next, we construct a wind footprint diagnostic to measure the area of the ETC wind field. The wind footprint (WFP) is defined as

$$\begin{array}{}\text{(2)}& \mathrm{WFP}=\sum _{i=\mathrm{1}}^m{A}_i,\end{array}$$

where A_i is the area of grid point i and m is the number of grid points within a given radius from the ETC centre in which the 3-hourly maximum of 10 m wind gust exceeds a specific threshold. A geodesic radius of 10° was found to be the best compromise for capturing winds associated with a given ETC from an area as large as possible without contaminating the WFP with winds related to neighbouring ETCs (see Fig. S2). For the threshold, we use a relatively small value of 15 m s⁻¹ to have a non-zero WFP for moderate ETCs as well. The value was chosen by considering thresholds used by various national weather services in Europe to issue the lowest-level (yellow) wind warnings over land. In Finland this value is 15 m s⁻¹ in summer and 20 m s⁻¹ in winter (FMI, 2018), whereas the corresponding values in Norway are 17 and 19 m s⁻¹ (METNorway, 2021). In Ireland this value is 25 m s⁻¹ (MetÉireann, 2024), whereas in Germany the threshold is 14 m s⁻¹ (DWD, 2015). The low threshold selected here is also justified based on the fact that in ERA5, the wind gust may be underestimated in some areas (Chen et al., 2024; Minola et al., 2020).

Finally, we include a storm severity index (SSI) to quantify the possible impact from wind associated with ETCs. Different SSI metrics have been previously used to successfully estimate the societal impact of ETCs (Klawa and Ulbrich, 2003; Pinto et al., 2007; Leckebusch et al., 2007). We use an SSI metric adapted from Leckebusch et al. (2008a). Here, SSI is calculated at each grid point within a circular area with a fixed radius around the ETC centre throughout the ETC life cycle. Our definition of SSI is as follows:

$$\begin{array}{}\text{(3)}& \mathrm{SSI}={\displaystyle \frac{\mathrm{1}}{A_{\mathrm{ref}}}}\sum _{i=\mathrm{1}}^m\max (\mathrm{0},{\displaystyle \frac{v_i}{v_{\mathrm{98},i}}}-\mathrm{1}{)}^{\mathrm{3}}{A}_i,\end{array}$$

where v_i is the maximum 10 m wind gust within 3 h and v_98,i is the climatological 98th percentile value of 10 m wind gust at grid point i, A_i is the area of the grid point, m is the number of grid points within a certain geodesic radius from the ETC centre, and A_ref is the area of the largest point in the grid (at the Equator). Scaling SSI values with the relative area of each grid point ensures that an ETC is considered more severe because the impacted area is larger, independent of latitude. We use a geodesic radius of 10° to compute the SSI. This value was discovered to be the most suitable based on a similar analysis as the one performed for the WFP (see Fig. S4).

The climatology of 10 m wind gust is calculated for the whole period from October 1979 to March 2022, including the summer months as well. We include summer months in the climatology since the justification for using the 98th percentile as a threshold for the wind gust is based on the finding that damage from winds occurs locally on 2 % of all days (Palutikof and Skellern, 1991). In some regions (e.g. parts of Scandinavia, in the Mediterranean, or southeastern Europe) the climatological 98th percentile values of 10 m wind gust are quite small (Fig. S3) and unlikely to cause severe damage. Karremann et al. (2014) avoided this discrepancy between the definition of SSI and actual wind gust values by implementing a fixed minimum threshold. For impactful events in the Mediterranean region, Nissen et al. (2010) required a minimum duration of 18 h and minimum affected area of around 36 000 km². We do not use a minimum wind gust or area threshold for the SSI, since such an approach is already evaluated by the WFP, which is based on a fixed gust threshold.

For each ETC track, we restrict the analysis to only one time step per intensity measure. For all intensity measures other than PRECIP, the value at the time of maximum VO along the track is chosen, since the maximum value of the intensity measures also occurs at the same time or at the adjacent time step on average (see Fig. S5). The maximum precipitation rate occurs on average 12 h before the time of maximum VO (see Fig. S5f). For this reason, PRECIP is evaluated at this time step.

We also include accumulated versions of PRECIP and SSI. We construct an accumulated precipitation measure (PRECIPacc) by summing together all PRECIP values along each track and an accumulated SSI measure (SSIacc) by time-integrating successive SSI values along each track.

3 Methods

3.1 Correlation analysis

We use two different correlation metrics to quantify co-occurrence relationships between the intensity measures. The first one is the widely used Pearson's correlation coefficient, r, which evaluates linear dependence. The second one is mutual information (MI), which we use to quantify non-linear dependencies. MI is a measure of dependence between two random variables based on their joint and marginal entropies (Cover and Thomas, 2006). In other words, it quantifies how much information can be obtained about one random variable by observing another random variable. MI has values in the interval [0, ∞), but it can be converted into a correlation coefficient, ρ, by normalizing it to a range [0, 1]. The normalization is computed using the Python package ennemi (Laarne et al., 2021, 2022) as follows:

$$\begin{array}{}\text{(4)}& \mathit{\rho }=\sqrt{\mathrm{1}-\exp (-\mathrm{2}\mathrm{MI})}.\end{array}$$

Using two different kinds of correlation metrics is beneficial because in addition to quantifying the strength of the relationship, we can learn about its type as well. Because MI is able to quantify non-linear relationships in addition to linear ones, similar values of r and ρ indicate a linear relationship between two variables, whereas higher ρ than r values indicate a relationship with a non-linear component.

3.2 Principal component analysis

Principal component analysis (PCA) aims to find an orthogonal linear transformation that maximizes the variance projected onto each of the newly found axes. This method is used in all fields of science, including meteorology (Statheropoulos et al., 1998; Nagendra and Khare, 2003), and has also been applied in studies on cyclones (Lou et al., 2012; Nakajo et al., 2014; Chen et al., 2019). One of the main features of PCA is its ability to reduce the dimensionality of a given problem by ignoring the axes explaining a negligible amount of the original variance. However, one of its main drawbacks is the interpretability of the results as each axis is expressed by a linear combination of the original feature space, often mobilizing the entire space. Sparse PCA (sPCA) alleviates this issue by proposing a PCA with sparse loadings, i.e. setting some of the coefficients in the linear expression of the PCA's axes to zero (Zou et al., 2006; Zou and Xue, 2018). However, sPCA is a lossy compression technique with an important dependency on the dimension of the projective hyperplane.

Consequently, in this study we will guide the sPCA by a classical PCA analysis (respectively scikit-learn's SparsePCA and PCA; Pedregosa et al., 2011). We apply the PCA to estimate the explained variance against the number of principal components (PCs). Then, we select the number of components which explains more than 90 % of the variance. This number of components is then used as the main parameter of the sPCA and is applied to the same dataset. Therefore, we minimize the risk of losing too much information with PCA by conserving a satisfying interpretability with sPCA. Based on the correlations and the sPCA results, we select a reduced subset of intensity measures to use as input for the cluster analysis. This subset is conceived to reduce information redundancy whilst maintaining the interpretability of the original set of measures.

3.3 Cluster analysis

A cluster analysis using the GMM aims to fit several multivariate Gaussian distributions to a dataset. As such, each cluster may be represented as a multidimensional Gaussian probability density function extending throughout the whole feature space, in our case the small subset of intensity measures produced by the sPCA analysis. The main drawback of the GMM is that the number of clusters has to be input, and the optimal number of clusters cannot be known in advance. The elbow method is used to disambiguate this choice and select the number of clusters which (1) maximizes Silhouette score (Shahapure and Nicholas, 2020) and (2) does not fall in the over-fitting learning plateau (i.e. when the Silhouette score is constant). In other words, the optimal number of clusters is the case avoiding both under- and over-fitting.

We use the GMM (scikit-learn's GaussianMixture; Pedregosa et al., 2011) on the reduced subset of intensity measures selected by our sPCA method. To choose the correct number of clusters to be found, we first use the elbow method to select two values to test before the over-fitting plateau is reached, as shown in Fig. S6. Then, we use the following stability test to refine our decision to one value. Our stability test aims to verify if the clusters' centroids predicted by several instances of the GMM are intercomparable. We first compute the Euclidean distance between the reference centroids and the centroids predicted by 1000 other instances. Then, the arguments of the minimum of the Euclidean distances are taken for each predicted clusters. If the arguments of the minimum are not repeating, it means a permutation of the clusters is able to successfully compare two instances of the GMM. In other words, we test the sensitivity of our cluster analysis to the chosen number of clusters. A stability score has been defined as the average number of clusters which are not intercomparable between two instances of the GMM. Thus, a stability score of zero is considered optimal. Stability scores are shown in Table S1 in the Supplement. As a result, we select n=4 as our optimal number of clusters as this value falls in the elbow criteria and has the lowest stability score.

4 Results

4.1 Relationships between intensity measures

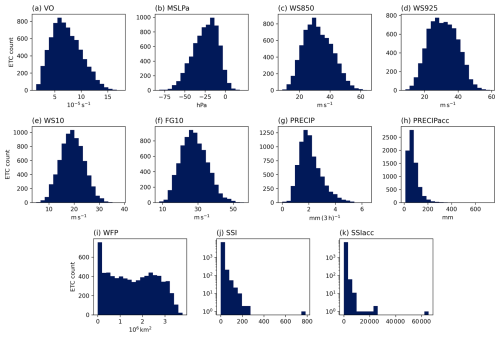
Distributions of all 11 intensity measures are shown in Fig. 2. We see in Fig. 2a–f that the dynamical intensity measures have Gaussian-like distributions. Distributions of VO, MSLPa, and WS850 (Fig. 2a–c) are slightly skewed towards more intense values, whereas WS925, WS10, and FG10 have more symmetric distributions (Fig. 2d–f). Similar distributions for these measures have been previously found by e.g. Bengtsson et al. (2006, 2009), Zappa et al. (2013a), and Gramcianinov et al. (2020). Compared to the dynamical intensity measures, the distributions of the impact-relevant measures are much less Gaussian-like (Fig. 2g–k). Out of these, PRECIP has the most Gaussian-like distribution (Fig. 2g) but is more positively skewed than any of the dynamical measures' distributions. With a slightly different definition, Zappa et al. (2013b) found a similar distribution for precipitation. The distribution of PRECIPacc (Fig. 2h) is even more positively skewed than that of PRECIP as the differences between ETCs are emphasized with the added effect of the duration of the track. WFP (Fig. 2i) has a very different distribution to the other intensity metrics with a large peak at the smaller end of the distribution and is very flat almost until the largest values. Only around 80 ETCs have a WFP of zero (not shown), which means that the first bin has the most ETCs with non-zero WFP. The WFP values decrease rapidly at the large end of the distribution as the radius threshold is reached (the theoretical maximum value of WFP is around 3.9×10⁶ km²). The shapes of the SSI distributions are even more extreme (Fig. 2j–k, shown on semi-log axes). The cube of the wind exceedance in Eq. (3) for SSI emphasizes differences between small and large values. Therefore, there are many very small values and few large values. For example, there are outlier ETCs in which the values of SSI and SSIacc are more than twice the value of the next largest one. These outlier ETCs are the 1993 Storm of the Century (Huo et al., 1995) and ex-hurricane Wilma (Pasch et al., 2006), respectively.

Figure 2 Distributions of intensity measures at the selected times along the tracks (see text in Sect. 2.3 and Table 1 for details). Note that panels (j) and (k) are shown on the logarithmic y axes.

We investigate the Pearson correlation coefficients (r) in Fig. 3a and correlation coefficients from MI (ρ) in Fig. 3b for relationships between all 11 intensity measures. The relationships can be roughly divided into two groups based on their strength: the first group contains the six dynamical measures and WFP, and the second one the two SSI and two precipitation measures. All the Pearson correlations are statistically significant (not shown).

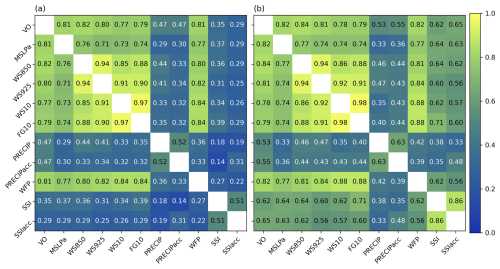
Figure 3 (a) Pearson's r and (b) MI correlation coefficients ρ for the ETC intensity measures. All values of Pearson's r involving MSLPa are negative, but an absolute value is shown for them to aid comparison with other coefficients.

Correlations between all measures in the group consisting of the dynamical measures and WFP are strong, with a Pearson's r of at least 0.7 for every combination (Fig. 3a). The strongest correlations are between the four wind speed measures (WS850, WS925, WS10, and FG10). A particularly strong correlation is between WS10 and FG10, with a Pearson's r of 0.97. This is surprising, given that in the Integrated Forecast System, which is used to produce ERA5, the parameterization for wind gusts includes a term to represent the contribution of convective downdraughts and a term to account for surface roughness, in addition to the 10 m wind speed term (Bechtold and Bidlot, 2009). The very strong correlation between WS10 and FG10 found here indicates that the convective downdraughts and surface friction contribute a minimal amount to the wind gusts in ETCs in ERA5. The weakest correlations in the first group of measures are between MSLPa and the wind speed measures, with r values between 0.71 and 0.76. Correlation coefficients from MI (Fig. 3b) are consistently, yet only slightly, larger than Pearson's r for the measures in the first group. The small differences between the two correlation coefficients suggest that the relationships are linear.

Relationships of the measures in the second group, SSI and precipitation measures, are weaker than those of the measures in the first group. This can be explained by the different shapes of the distributions in Fig. 2. For both SSI and precipitation measures, the largest values of Pearson's r (around 0.5) are between the corresponding accumulated and instantaneous versions. For any of the measures in the second group, the strongest correlation with a measure in the first group is between PRECIP and VO, with a value of r=0.47. This may be explained by precipitation-related diabatic heating producing a low-level potential vorticity anomaly which feeds back to the 850 hPa relative vorticity (Davis and Emanuel, 1991).

Correlations between SSI and precipitation measures are the weakest in terms of r and among the weakest in terms of ρ. For these measures, the ρ values are consistently larger than r values, and the difference is larger than for measures in the first group. The relationships are thus more non-linear. The difference is also larger for SSI than precipitation measures. This is not unexpected given the highly non-Gaussian distribution of the SSI measures. However, the ρ values are still not as large as for the first group, with the strongest correlation coefficients from MI between FG10 and SSI having ρ=0.71.

4.2 PCA and sparse PCA

The result of the PCA is obtained with the 11 intensity measures as input (Fig. 4). The weights of the intensity measures in the first four PCs (Fig. 4b–e) indicate that there are multiple measures with a contribution of similar magnitude in each PC. For example, in the first PC (Fig. 4b) WFP has the largest weight, but VO, MSLPa, and all wind speed measures have similar, non-negligible weight. In Fig. 4a, which shows ETCs projected onto the first three PCs of the PCA space, this can be seen in the even spread of points all over the axes. Based on the result of the PCA, it is not straightforward to determine which intensity measures have redundancy between them and which do not. Therefore, it is difficult to use only the PCA for dimensionality reduction in the original dataset. However, we can use the fact that the first four PCs of the PCA contain 94 % of explained variance in the dataset to constrain the sPCA. The result of the sPCA constrained to 4 PCs with the 11 intensity measures as input is shown in Fig. 5. As opposed to the result of the PCA, now each of the four PCs consists almost completely of either a single intensity measure or a group of similar intensity measures. We see this in their larger weight compared to the other measures, which have a weight close to or exactly zero in the same PC (Fig. 5b–e). The PCs can therefore be labelled as mainly consisting of (1) the four dynamical wind speed measures (WS850, WS925, WS10, and FG10), (2) PRECIP, (3) WFP, and (4) VO and MSLPa. Minor contributions in terms of weight come from (1) VO, (2) PRECIPacc and VO, (3) WS10 and FG10, and (4) WS850. The only measures which have no weight in any of the PCs are the two SSI measures.

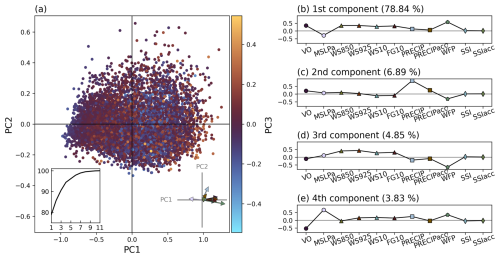
Figure 4 (a) ETCs projected onto the PCA space. PC1 and PC2 are the horizontal and vertical axes, respectively, and PC3 is shown in colours. Inset in the bottom left corner shows cumulative proportion of explained variance (percent) as a function of number of PCs. Inset in the bottom right corner shows loadings of PC1 and PC2 as vectors. (b–e) Weights of input measures in the first four PCs. Weights with larger magnitudes indicate more contribution of the specific intensity measure to the PC. The numbers in parentheses indicate the proportion of total explained variance in a given PC.

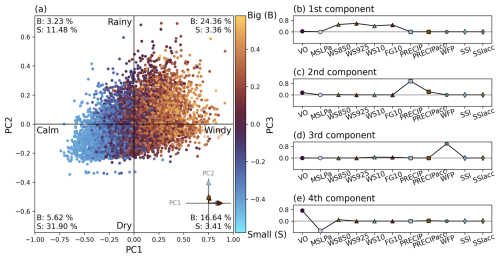
Figure 5 (a) ETCs projected onto the sPCA space. PC1 and PC2 are the horizontal and vertical axes, respectively, and PC3 is shown in colours. Inset in the bottom right corner shows loadings of PC1 and PC2 as vectors. The percentages indicate how large a proportion of all tracks falls into each sector (on which side of the mean, i.e. negative or positive value of PC). The labels “calm” and “windy”, “dry” and “rainy”, and “small” and “big” refer to the qualitative interpretation of PC1, PC2, and PC3, respectively. (b–e) Weights of input measures in the four PCs.

The PCs now have a straightforward physical interpretation, and we can label the axes in the sPCA space according to ETC features quantified by the most important intensity measures in the PCs (e.g. windiness). In Fig. 5a the ETCs are shown projected onto the first three PCs of the sPCA space in which PC1 goes from “calm” to “windy”, PC2 goes from “dry” to “rainy”, and PC3 goes from “small” to “big”. For reference, the most “average” ETC in the sPCA space (the smallest Euclidean distance from origin) has a WS850 value of 30.2 m s⁻¹, PRECIP of 2.3 mm (3 h)⁻¹, WFP of 1.7×10⁶ km², and VO of $\mathrm{6.8}\times {\mathrm{10}}^{-\mathrm{5}}{\mathrm{s}}^{-\mathrm{1}}$. Compared to the projection of the PCA space in Fig. 4a, the ETCs fall into the sPCA space much less symmetrically. The strong correlation between the wind speeds (PC1) and WFP (PC3) is evident as most of the tracks are on the same side of the mean of the PC (value 0) for PC1 and PC3 (either calm and small or windy and big). Precipitation (PC2) has a weaker correlation with the winds and WFP, which can be seen in the more even distribution of positive and negative PC3 values on either side of the PC2 mean than of the PC1 mean. However, more than half of the ETCs (56 %) are in sectors in which all the three PCs are on the same side of the mean, i.e. in the qualitative binary representation of the sPCA space either calm, dry, and small (32 %) or windy, rainy, and big (24 %).

We use the result of the sPCA to reduce the number of necessary intensity measures in the dataset for the comprehensive description of ETC intensity. Despite strong correlations between the winds, WFP, and VO, we retain them separately in the reduced set as they appear each on their own in the sPCA. We choose to keep five intensity measures in the final set for the comprehensive and non-redundant representation of ETC intensity.

1. WS850. All four wind speed measures are highly correlated with each other and grouped in PC1 of the sPCA. WS850 is chosen because of its link to VO in PC4.

2. PRECIP. PRECIP is from sPCA.

3. WFP. WFP is from sPCA.

4. VO. VO is from sPCA. It is preferred over MSLPa because of its minor weight in PC1 and PC2.

5. SSI. Although SSI has zero weight in sPCA, it is included since it is weakly correlated with the other intensity measures and has a more non-linear relationship with them. It can therefore be used to better separate the feature space (non-linearly).

4.3 Cluster analysis

The cluster analysis was performed using the method described in Sect. 3.3 with the reduced set of intensity measures identified in Sect. 4.2 as input. The number of clusters was chosen to be four. Each ETC is assigned into the most probable cluster based on the multivariate Gaussian probability density distribution. The clusters are named based on the average magnitudes of the input measures and the average geographical locations of ETCs in them. These are explained in detail in the following sections. The four obtained clusters are denoted as

1. HighSSI (proportion of total ETCs in the cluster: 8.57 %)

2. Intense (21.46 %)

3. AvgMST (average main storm track, 44.42 %) and

4. Weak (25.54 %).

4.3.1 ETC intensity measures

Distributions of all 11 intensity measures for ETCs in each of the clusters are shown in Fig. 6. For each intensity measure, the distributions are significantly different between the four clusters at the 5 % level based on the Mann–Whitney U test (Mann and Whitney, 1947, not shown). The shapes of the intensity measures' distributions in different clusters are largely similar in nature to the full distributions shown in Fig. 2. For example, in each cluster the distribution of VO is Gaussian-like (Fig. 6a). In terms of both the mean and the median, the average magnitude of VO in the clusters in decreasing order is HighSSI, Intense, AvgMST, and Weak. All distributions of WS850 (Fig. 6b) and WS10 (Fig. 6h) are also Gaussian-like with similar shapes between the clusters. The order of the average magnitudes is the same as for VO. For MSLPa (Fig. 6f) and WS925 (Fig. 6g) the shapes of HighSSI, Intense, and AvgMST distributions are more similar between each other than for the previously mentioned intensity measures. However, the order of the average magnitudes of the intensity measures is the same. Finally, clusters HighSSI and Intense both have broad, non-Gaussian distributions with almost flat tops (Fig. 6i). The order of the average magnitudes is, however, the same as for the other dynamical measures.

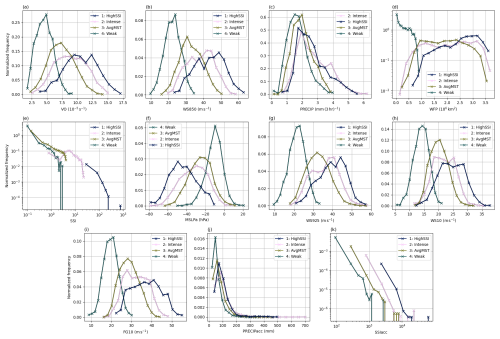
Figure 6 Probability densities of the intensity measures in ETC clusters. The legend in each panel is ordered based on the means of the distributions from largest to smallest. Note that panels (e) and (k) are shown on logarithmic axes.

Like the full distributions in Fig. 2, the distributions of the impact-relevant intensity measures in the clusters are less Gaussian-like than those of the dynamical measures. In the distributions of WFP for the different clusters, the order of average magnitudes is the same as in the dynamical measures, but there is more overlap between the three most intense clusters (Fig. 6d). For PRECIP, clusters Weak and AvgMST have narrow Gaussian-like distributions, while distributions of clusters Intense and HighSSI are positively skewed (Fig. 6c). The PRECIP distributions largely overlap, especially between clusters Intense and HighSSI. In fact, PRECIP is the only intensity measure for which the mean value is the largest for cluster Intense instead of cluster HighSSI. SSI distributions of clusters Weak and AvgMST heavily overlap and comprise most of the smallest SSI values (Fig. 6e). There is little overlap with the other two clusters, as most SSI values in cluster Intense are larger than any value in the two weaker clusters (Weak and AvgMST), and almost all values in cluster HighSSI are larger than any value in the other three clusters. These three distinct ranges of SSI values are probably an effect of the highly skewed distribution of SSI, and they indicate that SSI creates a lot of separation between the clusters. For SSIacc there is a clear separation between the mean values in the clusters, but there is much more overlap between distributions than for SSI.

4.3.2 ETC characteristics

In addition to the intensity measures, we compare various ETC characteristics between the four clusters. Figure 7 shows the distributions of latitude of genesis, meridional displacement (latitude of lysis minus latitude of genesis), latitude of maximum VO, deepening rate (difference in MSLPa 24 h before and at time of minimum MSLPa), lifetime, and mean displacement speed (averaged over the whole life cycle) of ETCs in the four clusters. In general, compared to the intensity measures, the distributions of ETC characteristics have more overlap between the clusters. As was the situation with the intensity measures, in almost all ETC characteristics clusters HighSSI and Intense have the most similar distributions between each other. Despite this, all distributions are statistically different at a significance level of at least 5 % in a Mann–Whitney U test, except for the latitude of genesis of clusters HighSSI and Intense (not shown). This indicates that cluster analysis based on intensity measures is able to identify ETCs which are different in terms of their life cycle characteristics in addition to their intensity. These differences are described in detail in the following paragraphs.

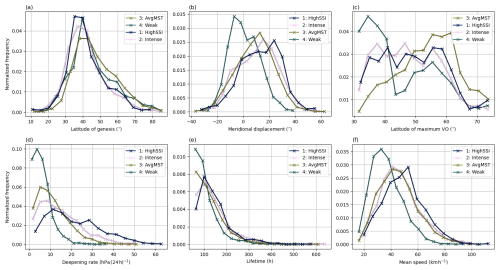
Figure 7 Probability densities of the ETC characteristics for the clusters. The legend in each panel is ordered based on the means of the distributions from largest to smallest.

The distributions of genesis latitude overlap considerably between the clusters, and they all peak around 40° N (Fig. 7a). Compared to the latitude of genesis, there is more variation between clusters in the meridional displacement of ETCs (Fig. 7b). The largest meridional displacement is on average in cluster HighSSI with a peak around 25°. Slightly smaller displacements are found in clusters Intense and AvgMST, while cluster Weak has the most negative displacement values (i.e. equatorward displacement) with a peak in the distribution around −5°. This causes ETCs in cluster Weak to have the smallest latitude of maximum VO on average, with a peak around 35° (Fig. 7c). Although ETCs in clusters HighSSI and Intense have on average a lower latitude of genesis compared to cluster Weak, their larger meridional displacement causes them to have on average a higher latitude of maximum VO. In contrast, despite the slightly smaller meridional displacement values compared to clusters HighSSI and Intense, the highest latitudes of genesis cause ETCs in cluster AvgMST to have on average the highest latitude of maximum VO, with a peak in the distribution around 60° N.

All the distributions of deepening rate (Fig. 7d), lifetime (Fig. 7e), and mean speed (Fig. 7f) are skewed to the right. All of them also have the same order of average magnitude between the clusters: (1) HighSSI, (2) Intense, (3) AvgMST, and (4) Weak. This order is the same as in most of the intensity measures in Fig. 6 as well as meridional displacement (Fig. 7b). An explanation for this similarity on the order of average magnitude between intensity and the characteristics is that, for example, higher wind speeds tend to relate to higher displacement speeds, while larger deepening rates are likely to result in deeper ETCs in terms of MSLPa.

4.3.3 Geographical distribution of ETCs

Figure 8 shows the geographical distribution of ETCs in the different clusters compared to the full climatology, and Fig. 9 shows the proportion of ETCs in each cluster in the boxes shown in Fig. 8e, which offers more insight into the geographical distribution. In Fig. 8d we see that ETCs in cluster Weak are mostly absent from the main North Atlantic storm track area (the southwest to northeast tilted area of large track densities in the North Atlantic in Fig. 8e). They are inversely the most abundant in the Mediterranean basin. Mediterranean cyclones are generally smaller and have shorter life cycles than ETCs in other larger basins (Campins et al., 2011), which may explain the larger number of Weak cyclones in this region as their WFPs tend to be smaller. The high density of cluster Weak ETCs in the Mediterranean is also consistent with small values of latitude of maximum VO (Fig. 7c) and meridional displacement (Fig. 7b), given the location and orientation of the Mediterranean basin. In addition to the Mediterranean basin, ETCs in cluster Weak comprise most of the tracks in continental Europe (Fig. 8d). The occurrence in this area also explains the smaller WFP values, as near-surface wind speeds and gusts are lower over land than over sea areas (Laurila et al., 2021b). However, it does not explain the small SSI values, which depend on local FG10 values instead of an absolute threshold.

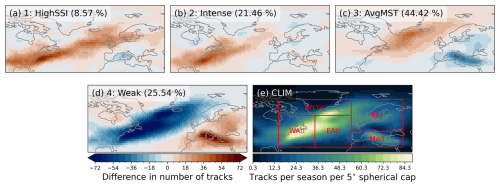
Figure 8 (a–d) Anomalies of track density in the clusters compared to (e) the full climatology. Track densities are calculated separately for the clusters; normalized by multiplying them with $N_{\mathrm{tot}}/N_{\mathrm{c}}$, where N_c is the number of tracks in a cluster and N_tot is the total number of tracks; and the track density of the full climatology subtracted from them. The percentages in parentheses indicate the proportion of all tracks in each cluster.

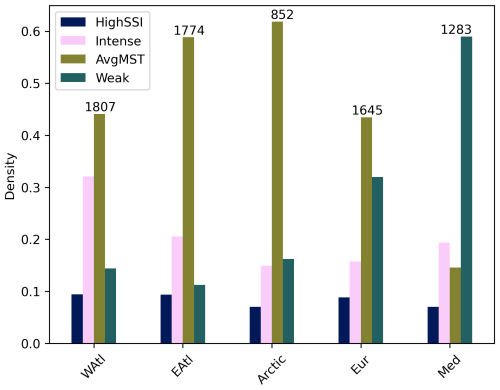
Figure 9 Proportion of ETCs in each cluster in the area boxes shown in Fig. 8e. The occurrence area of an ETC is allocated based on its location at time of maximum VO. The values are normalized by the number of ETCs occurring in each box, which is shown by the numbers at the top of the bars. Thus, the four bars for each area sum up to one. Explanations for the abbreviations are as follows: WAtl is western North Atlantic, EAtl is eastern North Atlantic, Eur is Europe, and Med is Mediterranean.

From a qualitative perspective, the occurrence areas of ETCs in cluster AvgMST (Fig. 8c) are a mirror image of the ones in cluster Weak. As the name suggests, ETCs in cluster AvgMST mostly occur along the main storm track with a maximum between Greenland and Iceland. In Fig. 9 we see that over the North Atlantic Ocean most ETCs are in this cluster, especially in the “Arctic” area where their proportion is more than 60 %. However, we also see that in Europe almost half of ETCs are in cluster AvgMST. In general, ETCs in this cluster occur more in the northern parts of the domain and are largely absent south of 45° N. This can be seen also in the northernmost values of genesis latitude (Fig. 7a) and latitude of maximum VO (Fig. 7c).

ETCs in cluster Intense have a maximum in track density over the eastern coast of the United States (Fig. 8b). Most of them occur at the start of the storm track. Elsewhere in the domain, differences are small compared to the full climatology. The location of the tracks in cluster Intense partly explains the large precipitation values in many of its ETCs, as they occur in the southwestern parts of the domain at the start of the storm track, which is an area with large ETC-associated precipitation (Hawcroft et al., 2012), and over oceans where surface moisture is abundant. Finally, Fig. 9 shows that also approximately 20 % of Mediterranean ETCs belong to cluster Intense, indicating that strong ETCs do develop in this region.

Due to the small size of cluster HighSSI (8.57 % of all tracks), the normalization of the track density by the total number of tracks in the full climatology affects the distribution greatly, with individual tracks having a larger contribution than in the other clusters. Despite this, the distribution of track density in cluster HighSSI (Fig. 8a) looks like what one would expect based on its similarity to cluster Intense in terms of intensity and ETC characteristics. As in cluster Intense, the highest track densities occur at the start of the storm track. However, the area of higher track density extends more to the northeast along the storm track (i.e. over Ireland, Great Britain, and southern Scandinavia) than in cluster Intense, but the values in this area are more discontinuous with multiple local maxima, which is likely due to the effect of normalization. The normalization also obscures the fact that each area in Fig. 9 has a similar proportion of cluster HighSSI ETCs (around 10 %).

4.3.4 Temporal occurrence of ETCs

We investigate the temporal occurrence of the total number of ETCs and the number of ETCs in each cluster with a trend analysis. First, time series of ETC occurrence in each extended winter are smoothed by taking a 5-year running mean. A Mann–Kendall test (Mann, 1945; Kendall, 1970) is performed on these smoothed time series to detect trends using the Python package pyMannKendall (Hussain and Mahmud, 2019). We find that there is no trend in the total number of ETCs within the study period (not shown). The time series of the number of ETCs in each cluster and the results of the Mann–Kendall test are shown in Fig. 10. There is large interannual variability in the number of ETCs per season, especially in clusters Intense (Fig. 10b) and AvgMST (Fig. 10c), which is a similar result to that found by Laurila et al. (2021a). The slope of the trend is positive in cluster HighSSI (0.024 ETC yr⁻¹; Fig. 10a) and negative in cluster AvgMST ($-\mathrm{0.073}\mathrm{ETC}{\mathrm{yr}}^{-\mathrm{1}}$; Fig. 10c), but these trends are not statistically significant. In contrast, statistically significant (at 1 % significance level) increasing and decreasing trends are identified in clusters Intense (0.104 ETC yr⁻¹; Fig. 10b) and Weak ($-\mathrm{0.080}\mathrm{ETC}{\mathrm{yr}}^{-\mathrm{1}}$; Fig. 10d), respectively. To understand why, we computed the trends in all 11 intensity measures for all ETCs (not shown). PRECIP, PRECIPacc, and SSIacc have significantly increasing trends (at the 5 % level), while none of the other intensity measures has a trend. The increase in the number of cluster Intense ETCs, which have the highest PRECIP values on average and the largest PRECIPacc values for single ETCs, is thus consistent with the increasing trend in precipitation in all ETCs. We can therefore say that within our study period, the intensity of ETCs has increased mostly in terms of precipitation.

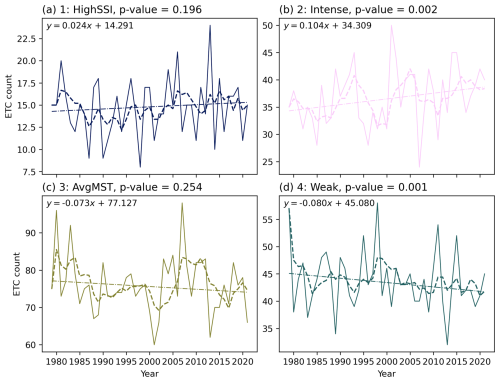
Figure 10 Temporal trends of the number of ETCs in each cluster. The solid lines show the number of ETCs in each extended winter season, and the dashed lines show 5-year running means. The dash-dotted lines show the slopes of the trend of the 5-year running means from a Mann–Kendall test. The trend is given by the equation $y=ax+b$, where y is ETC count, x is the year minus 1979, a is the slope (in  ETC yr⁻¹), and b is the intercept in 1979 (in number of ETCs). Note that the vertical axes have different scales in each panel.

4.4 Case study ETCs

In addition to the statistical approach, we investigate the clusters in terms of individual ETCs. We select named ETCs which mainly affected Europe and either occur in the Extreme Wind Storms (XWS) catalogue (Roberts et al., 2014) or a list of strong storms in Finland maintained by the Finnish Meteorological Institute (FMI, 2024) or are well-known intense Mediterranean cyclones. The 21 selected ETCs are listed in Table 2, and their tracks are shown in Fig. S7. Figure 11 shows these storms projected onto the first two PCs of the sPCA space and coloured by either their cluster (Fig. 11a) or the value of PC3 of the sPCA (Fig. 11b).

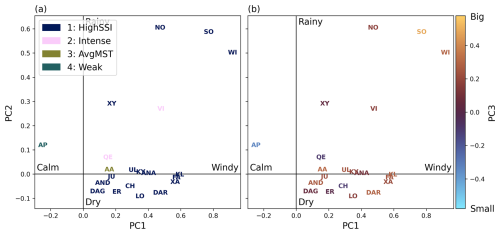
Figure 11 Case study storms in the sPCA space, coloured by (a) their predicted cluster and (b) their PC3 value. See Table 2 for abbreviations of storm names.

ECMWF (2021)Ulbrich et al. (2001)Kouroutzoglou et al. (2013)Menna et al. (2023)Hewson et al. (2014)Weijenborg and Spengler (2020)McCallum (1990)Suursaar et al. (2006)Baker (2009)Stojanovic et al. (2021)Metheniti (2012)Liberato et al. (2011)Bertotti et al. (2012)Fink et al. (2009)Ulbrich et al. (2001)Wernli et al. (2002)Brennan et al. (2009)Coll-Hidalgo et al. (2022)Huo et al. (1995)Fox et al. (2012)Smart and Browning (2014)Schüepp et al. (1994)Pasch et al. (2006)Hewson et al. (2014)Liberato et al. (2013)Ludwig et al. (2014)

Table 2 The named case study ETCs included in Fig. 11. The columns are the name of the ETC, abbreviation used in Fig. 11, time of occurrence, the area the ETC mostly affected, and a reference study for the ETC.

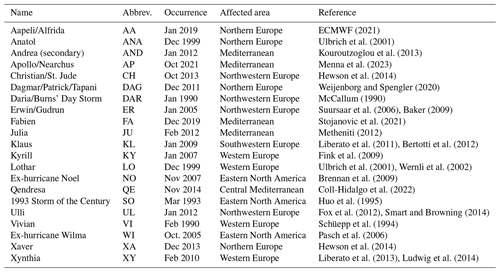
Figure 11a shows that cluster HighSSI is disproportionately represented in the set of named storms. Out of the 21 storms, 17 are assigned to cluster HighSSI despite it consisting of less than 10 % of all ETC tracks in the dataset. The four storms which do not belong to cluster HighSSI (Apollo, Aapeli, Vivian, and Qendresa) have the smallest SSI values of the 21 case studies, which cannot be seen in the PCs in Fig. 5. These four are among the five storms with the smallest PC4 values of the 21 case studies, which means they have low VO and/or high MSLPa values (not shown). In Fig. 11b we see that most of the 21 storms fall close to the mean value of PC2, meaning that they have near-average precipitation. Most storms which affected Europe are relatively close to one another in the sPCA (e.g. Anatol, Kyrill, and Ulli), except for Vivian, Xynthia, and Apollo which had more precipitation and/or lower wind speeds. Although cluster HighSSI is overwhelmingly the most common cluster among the named storms, only 9 of the 21 storms have a positive value in all four PCs (e.g. Christian/St. Jude has negative PC2 and PC3 values and a small PC4 value but still is a HighSSI storm). This demonstrates the need to use more than one measure to quantify ETC intensity.

At the same time, there is only one storm, Medicane Apollo, which has a negative PC1 value, i.e. smaller than average wind speed, and a PC3 close to the negative end, i.e. small WFP. Apollo, however, has the sixth-largest PC2 value of the 21 case study ETCs, which is to be expected since most of the damage was caused by precipitation rather than wind. Apollo belongs to cluster Weak, since the cluster analysis discriminates intensity more based on wind than precipitation (cf. e.g. Fig. 6b and c). However, this may also be due to the underestimation of the intensity of medicanes in ERA5 (Pantillon et al., 2024).

There are a couple of reasons why most of the selected storms are more extreme in terms of wind (PC1) than precipitation (PC2). Firstly, the majority come from the XWS catalogue (Roberts et al., 2014), in which the storms are selected using wind-based diagnostics. Secondly, ETCs with the highest PC2 values, and thus the most precipitation, occur mostly over the ocean, where their effects are not felt and storms do not get named. Thirdly, in our dataset ETCs which do have high precipitation values over land areas occur mostly over North America. This is demonstrated by the presence of three North American storms in the top right corner of the sPCA space in Fig. 11: ex-hurricanes Noel and Wilma and the northeaster 1993 Storm of the Century. The remaining selected storms with high PC2 values, Xynthia and Vivian, had compound impacts with both heavy rainfall and strong winds.

5 Discussion

Similar classes of ETCs have been found with cluster analysis methods in previous studies. Blender et al. (1997) used k-means clustering and found three clusters of North Atlantic ETC track orientations: stationary, northeastward, and zonal. Qualitatively, our findings match theirs well. Their stationary ETCs occurred mostly in the Mediterranean, Greenland, and northern Canada and, as the name suggests, had small propagation speeds. This is similar to our cluster Weak. Likewise, their northeastward ETCs are similar to our clusters HighSSI and Intense, with large meridional displacements and propagation speeds. While their zonal ETCs match our cluster AvgMST in terms of the more moderate meridional movement, their zonal tracks are not concentrated at the end of the storm track in the northeastern Atlantic like our AvgMST ETCs are. In addition to the similarity in track orientations, ETCs in their clusters had similar average intensities to ours. In terms of geopotential height at 1000 hPa (Z₁₀₀₀), their stationary ETCs had on average the weakest Z₁₀₀₀ gradient (comparable to low-level winds) and the highest Z₁₀₀₀ (comparable to MSLP), while northeastward ETCs had the strongest Z₁₀₀₀ gradient and the lowest Z₁₀₀₀ values.

Similarly, Gaffney et al. (2007) performed cluster analysis on North Atlantic ETC tracks with regression mixture models, which are probabilistic methods like GMMs. Like Blender et al. (1997), they found clusters with northeastward and zonal track orientations. They, however, identified also a cluster with northward track orientations but did not find a cluster of stationary ETC tracks. Their northward-oriented cluster tracks were mostly found near the eastern coast of North America and were among the most intense ETCs in terms of MSLP. This indicates that the northward-oriented tracks could contain many of the same tracks as our clusters HighSSI and Intense (e.g. post-tropical cyclones). They also found that the northeastward-oriented ETCs were the fastest-moving, while they found no significant differences in ETC lifetime between any of the clusters. This result is different from ours, as we found a link between average dynamical intensity and ETC speed and lifetime.

Leckebusch et al. (2008b) used similar methods to those we used to relate large-scale flow patterns to different types of ETCs. From a PCA performed on a Z₁₀₀₀ field they identified six large-scale flow patterns over Europe which they used to classify winter storm situations with k-means clustering. Of 55 identified pressure pattern clusters, 4 were classified as primary storm clusters. These primary storm clusters were associated with more extreme ETCs, as 72 % of 46 important European winter storms occurred during these clusters, while the overall relative frequency of occurrence of the four clusters was only 5 %. This result is reminiscent of our finding that the majority of well-known impactful storms are found in cluster HighSSI despite its small proportion of all ETCs.

Others have also previously used phase spaces consisting of different variables to categorize ETCs. Many have subjectively divided phase spaces into various parts and analysed ETCs in each part of the phase space separately. Graf et al. (2017) performed PCA on 30 ETC precursors to classify northern hemispheric cyclogenesis events. Although they found no obvious clusters in the continuous phase space determined by the genesis events, they were able to formulate five ETC classes by using the first two components of the PCA. The first PC determined whether an ETC genesis was characterized by strong or weak moist processes, and the second PC split the genesis events based on the type of forcing mechanisms, as in Petterssen and Smebye (1971). Their PCA classification was robust to the number of input features, with 5 precursors producing similar results to the initial 30. They also determined that a majority (67 %) of investigated well-known ETCs belonged to a single class. Furthermore, all four case study ETCs that are shared between their and our studies (Klaus, Kyrill, Lothar, and Xynthia) belonged to this class, while in our investigation they were all found in cluster HighSSI. While they note that their analysis cannot be used to directly attribute cyclogenesis events to specific cyclone evolution, this is an interesting result.

Besson et al. (2021) investigated dry-dynamic forcing of northern hemispheric ETCs by studying their Eady growth rate and upper-level-induced quasi-geostrophic ascent. They defined four categories of ETC forcing by selecting values at the extreme corners of a two-dimensional phase space determined by the two variables. They found that these four categories of ETC forcing occur in different geographical areas and lead to ETCs which differ in their deepening rates and have differences in their upper-level structure. Similarities between their categories and our clusters can be seen in the link between ETC deepening rates and occurrence areas of the four categories of ETC forcing. For example, a combination of the two forcing mechanisms leading to large deepening rates is found mostly at the start of the North Atlantic storm track (see clusters HighSSI and Intense), while combinations leading to the smallest deepening rates occur more at the southern and southeastern parts of the North Atlantic (see cluster Weak). Deepening rates in between these extremes are associated with a combination of forcing mechanisms which occurs mostly in the northern parts of the North Atlantic with a maximum density between Greenland and Iceland (see cluster AvgMST). Similar analyses were done by Binder et al. (2016) and Binder et al. (2023), who determined three categories of ETC intensification for northern hemispheric ETCs from a phase space of ETC deepening rate and low-level warm conveyor belt air mass.

While these types of analyses are suitable for studying the precursors and forcing mechanisms of ETCs, we demonstrate that the classification of ETCs based on their intensity benefits from an added level of objectivity via the cluster analysis. This can be seen in the overlap between the intensity measure distributions for different clusters in Fig. 6. Despite this overlap introduced by the objective method, our clusters can be at least qualitatively linked to classes of ETCs obtained with more subjective methods as described above. In fact, a possible course of future study is the identification of the variability in the ETC precursors and forcing mechanisms within our clusters. We believe that this form of analysis, which links the intensity and relevance for impacts to the genesis environment of ETCs, would offer a new perspective on the classification of ETC life cycles and possibly improve the predictability of ETC intensity.

An investigation of well-known case study ETCs showed that proportionally, the majority of impactful storms belong to cluster HighSSI (17 out of 21). This highlights the ability of the cluster analysis to identify intense storms. However, we cannot say that all ETCs in cluster HighSSI are impactful or damaging. In addition to the statistical nature of the cluster analysis, this is due to the fact that apart from SSI, which is based on local climatological values, the impact-relevant intensity measures do not discriminate between land and sea areas. ETCs have on average larger WFP values and/or more precipitation over the ocean and on the eastern coast of North America (Hawcroft et al., 2012; Laurila et al., 2021b), which inevitably leads to some non-impactful ETCs being classified as Intense or HighSSI. It also explains why many European storms in Fig. 11 have below-average precipitation and why Medicane Apollo is classified as a cluster Weak storm. On the other hand, the analysis showed that SSI, which does not by definition have larger values over sea than land, is an important measure in determining the cluster of an ETC whose other intensity measures have close to average values. However, SSI alone cannot be used to identify impactful storms since it is relevant for impacts due to wind only, while other factors in ETCs such as precipitation can also cause significant damage (e.g. Medicane Apollo). This emphasizes the fact that multiple intensity measures should be used to quantify the intensity of ETCs.

A limitation of our study is the use of only one data source (ERA5) and one ETC tracking algorithm (TRACK). Firstly, the representation of ETCs has been found to vary between reanalysis datasets (Hodges et al., 2011; Wang et al., 2016). Secondly, ERA5 underestimates precipitation and strong low-level winds in some areas (Chen et al., 2024; Minola et al., 2020). This underestimation may cause our precipitation or wind distributions to be too narrow, which may have an effect on the cluster analysis through, for example, creating more overlap in precipitation between the clusters than without the bias. Thirdly, earlier studies have shown that ETC climatologies may differ in distributions and trends due to sensitivity to the tracking algorithm because using different variables and thresholds leads to identifying different categories of ETCs (Raible et al., 2008; Neu et al., 2013; Flaounas et al., 2023). Another limitation of our study is that the criteria used for the ETC tracking are optimized for the North Atlantic. Therefore, some Mediterranean ETCs are excluded from our set of tracks since they can be more stationary, have shorter lifetimes, and have their maximum vorticity within the first 24 h. Flaounas et al. (2023) compared 10 ETC tracking algorithms in the Mediterranean area, one of which was TRACK. In their comparison, TRACK produced the longest lifetimes and largest propagation speeds for ETCs in the Mediterranean. Despite these limitations, our study brings valuable new knowledge on which intensity measures should be used to comprehensively and non-redundantly quantify the intensity of ETCs.

6 Conclusions

We created a dataset of extratropical cyclone (ETC) intensity measures for 43 extended winters of North Atlantic and European ETC tracks and performed sparse principal component analysis (sPCA) to identify the measures which explain most of the variability in the dataset. Using the results of the sPCA and correlations between the intensity measures, we determined five measures for the comprehensive and non-redundant representation of ETC intensity: 850 hPa relative vorticity, 850 hPa wind speed, wind footprint, precipitation, and a storm severity index (SSI).

Our analysis shows that while there is strong correlation between different dynamical ETC intensity measures, there is a much weaker link between the dynamical intensity and impact-relevant measures. A correlation of similar strength between wind speed and precipitation was found previously by Pfahl and Sprenger (2016), who determined a correlation coefficient of 0.36. Therefore, when using ETC intensity as a broad term, i.e. including the impacts as well as the meteorological intensity in the definition, we need to consider the non-linear and weakly correlated relationship between the two and use more than one or two measures to describe the intensity. We recommend studies which aim to quantify future changes in ETC intensity to consider the five variables we determined.

We used these five intensity measures as input to a cluster analysis performed with a Gaussian mixture model (GMM) to create classes of ETCs. We found four clusters in which ETCs are significantly different in terms of their intensity. Cluster Weak has on average the weakest ETCs (25.54 % of all ETCs), cluster AvgMST contains average-intensity ETCs (44.42 %), and clusters Intense and HighSSI are composed of more intense ETCs (21.46 % and 8.57 %, respectively). For all intensity measures except for precipitation, the clusters are in the same relative order in terms of average magnitude: HighSSI, Intense, AvgMST, and Weak. However, the clusters are not discrete in the feature space defined by the intensity measures since there is overlap in the distributions of the intensity measures between the clusters. The most overlap is between clusters Intense and HighSSI. This overlap, the small size of cluster HighSSI, and the large SSI values in its ETCs indicate that cluster HighSSI, which contains the most extreme and potentially impactful ETCs, is a subset of cluster Intense. Of all intensity measures, there is the least overlap between clusters in the distributions of the SSI. This, along with the fact that a large majority of the named impactful storms considered in this study (17 out of 21) belong to cluster HighSSI despite the cluster accounting for less than 10 % of all ETCs, suggests that SSI is useful in identifying impactful ETCs, which is in agreement with previous studies (Klawa and Ulbrich, 2003; Leckebusch et al., 2007, 2008a; Donat et al., 2011).

The clusters are different in terms of their characteristics and geographical location of occurrence as well. The average intensity of ETCs in the clusters can be qualitatively linked to their deepening rate, lifetime, and mean propagation speed. The weaker ETCs occur more frequently in Europe and in the Mediterranean basin than over the Atlantic Ocean, but HighSSI ETCs are almost as frequent everywhere when normalized with respect to the climatological distribution of ETC occurrence. The number of ETCs in cluster Intense increased from 1979 to 2022, while the number of ETCs in cluster Weak decreased, which is mostly caused by a positive trend in precipitation. This increasing trend in ETC precipitation is in agreement with Li et al. (2014), who compared a recent warmer period (in average sea surface temperature) as an analogue of future climate change to an earlier base period and found that while precipitation was larger in the warmer period than the base period, there was no consistent change in vorticity or wind speed. There is also a significant increase in accumulated SSI (SSIacc) which, without an increase in maximum wind gusts at 10 m (FG10), can be explained by an increase in extreme wind gust values in North Atlantic ETCs from 1979 to 2021 found by Karwat et al. (2022).

Our objective classification of ETCs based on their intensity offers a new perspective on the multitude of ETC classifications reviewed in Catto (2016). Our classification is performed using variables which are available or easy to compute from both model and reanalysis data. Both the sPCA model and the GMM instance trained with our dataset are provided as downloadable Python objects in a repository (Cornér et al., 2024). For any dataset including ETC tracks and an associated value of each of the intensity measures per track, the sPCA model can be used to project ETCs onto the sPCA space shown in Fig 5a. Moreover, to predict the cluster of each ETC in the same or a similar dataset, the GMM instance can be used with the five intensity measures listed above as input. Building on the work of Bengtsson et al. (2009) and Champion et al. (2011), who studied the intensity and extreme weather from ETCs in future climates, utilizing this kind of classification in climate projection studies could give insight into how different kinds of ETCs respond to climate change. In addition to climate applications, quantifying the intensity of ETCs is also important in terms of numerical weather prediction. This is especially true in the current age, when ensemble prediction systems are key to produce probabilistic forecasts and vast amounts of data. Being able to identify ETCs in each ensemble member and compute their intensity allows for an accurate estimate of the uncertainty in how strong and how potentially impactful a specific ETC will be. Furthermore, this allows a vast amount of information to be condensed to a level that is manageable for operational forecasters, who often are working under time pressure.