Testing the 2020 European Seismic Hazard Model (ESHM20) against observations from Romania

Evaluating the performance of probabilistic seismic hazard models against recorded data and their potential to forecast future earthquake ground shaking is an emerging research topic. In this study, we evaluate and test the results of the recently released 2020 European Seismic Hazard Model (ESHM20; Danciu et al., 2021a, 2024) against observations for several cities in Romania. The dataset consists of ground-shaking recordings and macroseismic observations that extend the observational time period to a few hundred years. The full distribution of the hazard curves, depicting the epistemic uncertainties in the hazard at the given location was considered, and the testing was performed for peak ground acceleration (PGA) values of 0.1 and 0.2 g.

The results show consistency between ESHM20 and the ground motion observations for the cities located near the Vrancea intermediate-depth source (VRI) for both selected PGA levels. ESHM20's estimated values appear to be over the recorded VRI ground motions along the Carpathian Mountains and below those at the far-field locations outside the Carpathians yet inside the expected model variability. Some of these differences might be attributed to the uncertainties in data conversion, local site effects, or differences in the attenuation patterns of the ground motion models. Our analysis suggests that the observed exceedance rates for the selected PGA levels are consistent with ESHM20 estimates, but these results must be interpreted with caution given the limited time and spatial coverage of the observations.

1 Introduction

Probabilistic seismic hazard analysis (PSHA) is an important framework in seismology and earthquake engineering, widely used worldwide to quantify the uncertainty inherent in both the occurrence and the effects of earthquakes. PSHA underpins a wide range of applications, including the development of modern seismic design building codes and seismic risk assessments. It also informs various public policy and risk management strategies aimed at mitigating the impacts of seismic events.

Despite the widespread adoption of PSHA, testing its results is not straightforward. The sporadic nature of earthquakes, coupled with their low rate of occurrence and being categorised as low-probability–high-consequence events, makes the empirical validation of PSHA models and results a task that would typically require observations spanning multiple human lifetimes (e.g. Vanneste et al., 2018; Gerstenberger et al., 2020; Allen et al., 2023). For instance, in regions like France or Germany, where the installation of accelerometric stations began in the mid-1990s, the availability of the instrumental records is limited to a short temporal window. Even in more seismically active regions like Italy, Türkiye, or Greece, which are subject to more frequent damaging events, validating probabilistic hazard models is challenging for the same reasons. In recent years, several procedures aimed at testing seismic hazard estimates against past observations have emerged (e.g. Hanks et al., 2012; Marzocchi and Jordan, 2018). These procedures are typically performed for short (e.g. Stirling and Gerstenberger, 2010; Tasan et al., 2014; Mousavi and Beroza, 2018; Mak and Schorlemmer, 2016; Iervolino et al., 2023; Stirling et al., 2023) or long (e.g. Rey et al., 2018; Salditch et al., 2020; Meletti et al., 2021) return periods, depending on the aim of the application.

The current study aims to compare the recently released 2020 European Seismic Hazard Model (ESHM20; Danciu et al., 2021a, 2024) results against instrumental recordings and detailed macroseismic observations specific to Romania. This region offers a distinctive seismo-tectonic landscape, dominated by the Vrancea intermediate-depth seismic source (VRI). The VRI has a concentrated nest of seismicity at depths between 60 and 200 km, which is associated with the current dehydration of an oceanic subducted plate, as noted by Ferrand and Manea (2021) and Craiu et al. (2022). Macroseismic-intensity maxima of strong VRI events are often observed/reported outside of the epicentral area: values of IX+ (MSK-64 scale) for the 1940 event with a moment magnitude (M_w) of 7.7 and VIII+ (MSK-64 scale) for the 1977 event with M_w=7.4 (e.g. Kronrod et al., 2013).

The largest intensity values are found outside of the Carpathian belt, where a substantial number of sedimentary structures are located (Marmureanu et al., 2016a, 2017; Manea et al., 2019). Besides this, the source properties imprint an asymmetric shape on the macroseismic field, elongating it in the NE–SW direction (Marmureanu et al., 2016b). In contrast, strong back-arc attenuation features are recorded within the Carpathian region and prescribe the current pattern of the macroseismic fields (e.g. Vacareanu et al., 2015; Manea et al., 2022). The VRI impact extends beyond the national borders, and significant damage has been reported in neighbouring countries, with observed intensities of VII–VIII at epicentral distances of more than 250 km during the 1940 M_w 7.7 event (Cioflan et al., 2016).

Furthermore, while the shallow crustal seismic activity in Romania is not as frequent as that at intermediate depths in the Vrancea region, it still makes a significant contribution to the regional seismic hazard (Marmureanu et al., 2016a). The main seismic sources for such events are located along the Carpathian Mountains, particularly in the Făgăraș–Câmpulung zone, as well as in the foreland regions of southwestern Romania, including Banat and Danubius, and extending northwest to Crișana–Maramureș. Despite the lower rate of crustal activity in these areas compared to the Vrancea region, historical accounts and pre-instrumental catalogues document significant earthquakes with M_w≥5 and epicentral intensities (I₀) ≥ VI on the MSK-64 scale (e.g. Radu, 1979; Oncescu et al., 1999). Thus, in this study, we consider intensity data spanning more than 3 centuries from 12 important cities in Romania (see their locations in Fig. 1). These urban areas are selected for their significant population and different exposure levels to seismic hazard. The present study begins with an overview of ESHM20 and its specific relevance to Romania, and then the main components of the model and the results relevant at the regional level are discussed (Sect. 2). The next section (Sect. 3) describes the main data and the curation and conversion procedure, which includes how historical macroseismic data were collected and converted into peak ground acceleration (PGA) values for different Romanian cities. Subsequently, a summary of the statistical testing process is given (Sect. 4), detailing the approaches taken to contrast the recorded seismic activity with the ESHM20 estimates. Next, the main outcomes of the statistical testing at two reference values for PGA, 0.1 and 0.2 g, are illustrated and interpreted (Sect. 5); this is followed up by discussion and conclusions of our findings (Sect. 6).

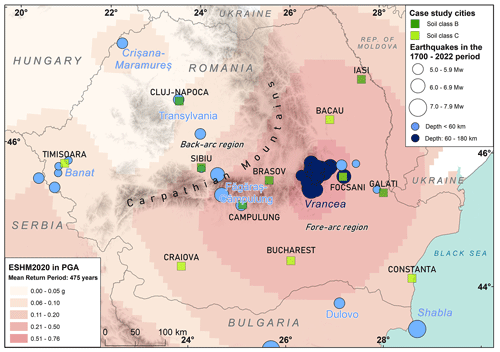
Figure 1 Location of the selected 12 cities and the post-1700 earthquakes (according to the Unified Earthquake Catalogue of the European Seismic Hazard Model 2020 – ESHM20; Danciu et al., 2021a) used in this study. Only events with M_w≥5 for which at least one macroseismic-intensity result exceeding VI (MSK-64) is recorded at the selected locations were considered. The background is ESHM20's ground-shaking map in terms of peak ground acceleration (PGA) for a return period of 475 years.

2 ESHM20 results for Romania

The 2020 European Seismic Hazard Model (ESHM20; Danciu et al., 2021a, 2022) is the latest revision and update of the seismic hazard assessment for the Euro-Mediterranean region. ESHM20 is constructed using harmonised datasets that include information on ground motion, earthquake catalogues, active faults, and tectonic data across different borders. The ground-shaking hazard in the region is estimated by combining a complex seismogenic source model, which includes distributed seismicity, active faults, and subduction sources, with regionally scaled backbone ground motion models (Weatherill et al., 2024). More specifically, the seismogenic source model consists of two branches of sources: the area source models and a hybrid combination of active faults and background smoothed seismicity. In Romania, due to the lack of available data on active faults, the seismogenic source model is based on an area source model and a smoothed seismicity with an adaptive kernel. Furthermore, the seismogenic sources depicting the nested seismicity with depth in the Vrancea region are also considered and modelled with a set of uniform-area source zones located between 70 and 150 km depth. The ground motion characteristic models for Romania are scaled based on regional factors to capture the ground-shaking characteristics of both the active shallow crust and the non-subduction deep seismicity. These models are described by Weatherill et al. (2020, 2024). A complex logic tree was developed to address the spatial and temporal variability in the earthquake rate forecast as well as the regional backbone ground motion models. The computation was performed using OpenQuake (Pagani et al., 2014), and the full logic tree was sampled to obtain the distribution of the hazard results. For this analysis, we selected 12 major cities in Romania, as illustrated in Fig. 1, where we superimposed the ESHM20 ground-shaking map in terms of peak ground acceleration (PGA) for a return period of 475 years. Additionally, the relevant earthquakes with moment M_w≥5 for which at least one macroseismic-intensity result exceeding VI (MSK-64) is recorded at the selected locations are also plotted on the same map. The highest PGA mean value is observed in proximity to the Vrancea source, a region of high seismicity as also indicated by the density of the seismic events (Fig. 1). The pattern of PGA values follows the Carpathian arc, with values decreasing in the back arc towards the northwestern part of the region. The range of PGA values is rather large, spanning 0.15 g in Cluj-Napoca to 0.9 g observed for Focșani. The ESHM20 hazard curves for the mean PGA values at the selected cities in Romania are presented in Fig. 2a and show that the decay of the hazard curves is different, with a fast decay indicating lower hazard and vice versa. A significant spreading of the mean hazard curves is present between the locations outside and within the Carpathian arc, following the same pattern as the ESHM20 475-year mean ground-shaking map (Fig. 2a). The highest annual probabilities of exceedance (APEs) are seen at locations in proximity to the Vrancea source, which dominates the hazard at all the return periods, while the lowest values are observed at cities located in the far-field extent of this region, where low-recurrence shallow seismicity is present. The full distribution of hazard curves for 10 000 randomly sampled hazard curves from the ESHM20 logic tree for Bucharest, together with the mean and the 5th and 95th percentiles, is shown in Fig. 2b.

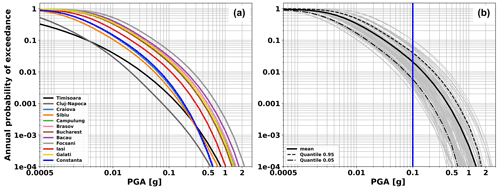
Figure 2 (a) The ESHM20 annual probability of exceedance as a function of PGA (so-called hazard curves) at the selected cities in Romania. (b) Full distribution of hazard curves for 10 000 samples extracted across all the ESHM20 hazard branches for the city of Bucharest. The mean hazard is presented as a continuous black line, while the dashed lines represent the 5th and 95th percentiles.

At the Bucharest location, the variability in the hazard curves presents a narrow range and depicts the combined uncertainties mainly in the Vrancea source and ground motion (Danciu et al., 2024). Finally, we used the full distribution of the ESHM20 hazard curves to retrieve the statistical testing input, as described in the “Statistical testing procedure” section.

3 Available data and conversion

Macroseismic-intensity observations recorded over several hundreds of years (starting with 1700) at the main cities across Romania are used to test ESHM20's results. The selected cities are among the most highly populated urban areas across Romania and are well distributed with respect to the various seismic hazard levels and source characteristics shown by the ESHM20 PGA hazard map for the 475-year return period (see Fig. 1). It is noteworthy that these observations were collected within this study and were not directly used in the derivation of the ground motion component of ESHM20, securing their independence for statistical testing. Intensity data points (IDPs) were acquired from multiple available sources: Atanasiu (1961), Constantin and Pantea (2013), Constantin et al. (2011, 2016, 2023), Kronrod et al. (2013), Marmureanu et al. (2018), Rogozea (2014, 2016), and Shebalin et al. (1974). Besides compiling original information (i.e. intensity values), most of these studies also provide new evaluations at locations where new macroseismic information has become available. Note that, while IDPs of the 17th–18th centuries were evaluated from scarce information, the ones related to strong Vrancea earthquakes of the 20th century were collected through wide national campaigns (see details in Kronrod et al., 2013; Constantin et al., 2016). Several IDPs of our initial dataset have a very local character as they strictly reflect the effects of strong intermediate-depth earthquakes on specific buildings that existed at the time of the respective earthquakes (e.g. churches, monasteries; Marmureanu et al., 2018). Where available, such site-specific intensity estimations are averaged with macroseismic data from other authors and various sources (especially isoseismal maps). Additionally, maps published before 2000 have been checked against the information available in the European Archive of Historical Earthquake Data (AHEAD) platform (Rovida et al., 2020), which also helped us to fill in the data gaps for some cities. If an IDP was not available at the specific location, a natural-neighbour interpolation scheme (Sibson, 1981) was used to extract it from georeferenced isoseismal maps selected from the above-mentioned sources. Some of the collected IDPs were reported on the Rossi–Forel intensity scale (e.g. 1908 M_w 7.1 VRI earthquake) and were homogenised to MSK-64 using the conversions proposed by Musson et al. (2010). Thus, we also treat MMI and EMS-98 values as equivalent to MSK-64 ones. MSK-64 is preferred as the VRI's intensity–ground motion conversion equations (IGMCEs) were developed using this intensity scale for Romania.

From this collected dataset, we considered only IDP data from events with M_w≥6 for the VRI and M_w≥5 for shallow seismicity (see their locations in Fig. 1) and with a minimum observed epicentral intensity (I₀) of VII (MSK-64), which corresponds to a PGA value of 112 cm s⁻² for the VRI (e.g. Ardeleanu et al., 2020) and/or 154 cm s⁻² (Caprio et al., 2015) for shallow seismicity. The testing dataset for the 12 major cities contains 199 IDPs recorded from 58 earthquakes (see Fig. 1), of which 39 are located in the VRI region. For each city, the time window of data completeness (Table 1) is visually evaluated based on IDPs higher than or equal to V (see Fig. 3) from events considered mainshocks in the declustered ESHM20 catalogue (Danciu et al., 2021a, 2022). Where available, the converted PGA values were replaced by the recorded ones from the post-1977 VRI event dataset of Manea et al. (2022). We did not include any intensity measure which is related to the events identified as foreshocks, aftershocks, or swarm events. Depending on the available data, the intensity values were translated to PGA values using the latest conversion equations proposed by Ardeleanu et al. (2020) for the VRI and Caprio et al. (2015) for global crustal activity as no local shallow models are available. A different conversion equation was used for the VRI as the observed macroseismic field presents unique features which are not seen for shallow seismicity, such as an azimuthal asymmetric shape due to the source properties (Marmureanu et al., 2016b; Craiu et al., 2023), different apparent attenuation patterns due to the unique tectonic environment (e.g. Manea et al., 2022), and strong far-field site effects (Cioflan et al., 2022). The equation of Ardeleanu et al. (2020) was selected as it is the most recent intensity–PGA conversion equation proposed for the VRI and its predictions agree with the ones from previous studies, such as Vacareanu et al. (2015) and Marmureanu et al. (2011). The distribution of the MSK-64–PGA conversions and their corresponding standard deviations up to X (MSK-64) are presented in Fig. S1, which can be found in the Supplement. Each IDP was translated into three PGA values, i.e. the mean IGMCE model and its standard deviation, to consider the variability in this conversion in the final results. IDPs were translated into PGA values as this is simply less challenging and more efficient than converting all the PGA hazard curves to intensity values.

Table 1 Observed and the ESHM20-predicted exceedances for 0.1 and 0.2 g PGA at 12 Romanian cities.

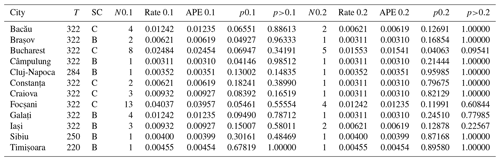
T is the time window of completeness [years]; SC is the EC8 site class (CEN, 2004); N0.1 (N0.2) is the number of observed exceedances in T for 0.1 (0.2) g PGA; Rate 0.1 (Rate 0.2) is the observed annual rate of exceedance for 0.1 (0.2) g PGA; APE 0.1 (APE 0.2) is the annual probability of exceedance for 0.1 g – calculated from the observed rate; p0.1 (p0.2) is the p value that the observed number of exceedances within T could be drawn from in ESHM20 for 0.1 (0.2) g; p>0.1 (p>0.2) is the p value where there are N observations or more that the observed number of exceedances within T could be drawn from in ESHM20 for 0.1 (0.2) g PGA.

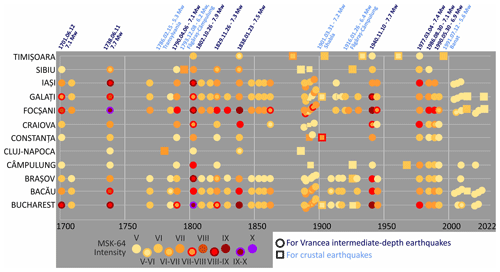
Figure 3 The distribution of the selected intensity data points used for the ESHM20 hazard testing at the 12 cities, with a threshold above V (MSK-64). The timeline and primary source information for the major earthquakes that significantly affected Romanian territory are presented at the top of the plot.

To align with the ESHM20 rock conditions, for which the time-averaged shear-wave velocity to 30 m depth (V_s30) is set to 800 m s⁻¹, the ground motion amplitudes were corrected for site effects considering amplification in each city by means of soil factors recommended in Eurocode 8 (EC8; Comité Européen de Normalisation (CEN), 2004) for crustal seismicity and the ones adjusted for Vrancea earthquakes proposed by Vacareanu et al. (2014). The EC8 site classes were gathered from Manea et al. (2022) and Coman et al. (2020) and are presented in Table 1. The use of observational intensity data for comparison with hazard curves introduces additional layers of uncertainty. One must acknowledge the complex process of converting subjective intensity measures into objective ground acceleration values, given the uncertain nature of intensity observations and the variability in the human experience of ground shaking (e.g. Rey et al., 2018). Furthermore, the determination of complete and reliable historical records for specific macroseismic-intensity levels is equally challenging, presenting a considerable difficulty when it comes to aligning past seismicity with probabilistic forecasts. We incorporated the full uncertainty variability within the PGA calculations by considering the uncertainty in the conversion from intensity to PGA to evaluate how much these uncertainties impacted the results of the hazard testing.

4 Statistical testing procedure

In the following section, we provide an overview of our methodology for evaluating the performance of the ESHM20 ground-shaking estimates by comparing them to instances of ground motion exceedances at 12 main cities in Romania. The statistical testing relies upon comparing the actual occurrences of ground acceleration surpassing specific thresholds (0.1 and 0.2 g PGA) with the ESHM20 estimates by considering the associated uncertainties. The selected ground motion levels are of relevance to PSHA in Romania, with 0.1 g approximating the lower bound of damaging ground motions. First, we compile the full dataset of ground shaking that includes both the recordings (where available) and the macroseismic observations converted to PGA by considering uncertainties in the conversion process and the influence of site conditions. Next, we determine the specific time period of this dataset and count the instances where the acceleration thresholds are surpassed to obtain the distribution of the observed number of exceedances over the time period of completeness.

Subsequently, we closely follow the statistical testing approach proposed by Marzocchi and Jordan (2014, 2017, 2018), which accounts for both the aleatory and the epistemic uncertainties in the hazard (Meletti et al., 2021; Stirling et al., 2023). The above-mentioned methodology assumes that the exceedance rate variability is well represented by a binomial distribution. We forecast the anticipated number of exceeding occurrences for each logic-tree branch using the proposed binomial distribution (Stirling et al., 2023) and build the sum of all the weighted distributions by considering each branch weight to evaluate the likelihood of observing the exact number of exceedances.

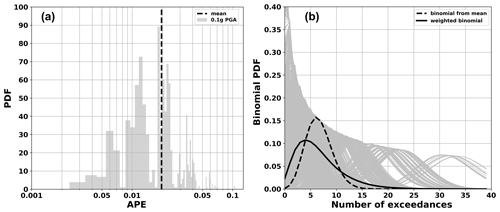
Figure 4 (a) Probability density functions (PDFs) computed for the 0.1 g PGA level versus the annual probability of exceedance – APE. The black vertical line indicates the traditional hazard mean value. (b) The variability in the computed binomials for all the hazard ensemble curves (grey lines) shown together with the final weighted mean curve considering the full distribution of the uncertainties and with the one computed from the commonly used mean hazard curve.

The variability in the 10 000 random samples of the hazard curves for Bucharest, capital of Romania, is presented in Fig. 2b, while the contribution of various logic-tree branches to the hazard at 0.1 g PGA is illustrated in Fig. 4a. The latter shows that the mean hazard value does not explain the APEs asymmetric distribution. Thus, for this analysis we use the weighted binomial distribution considering the APE distribution of all the ESHM20 logic-tree branches. The variability in all the computed binomials for the entire ensemble of the hazard curves is presented in Fig. 4b, alongside the final weighted mean considering the full distribution of the uncertainties and the resulting binomial retrieved from the statistical mean. The distribution of the APEs reflects the contribution of various logic-tree branches, and the differences between the two statistical descriptors, i.e. the weighted mean versus the statistical mean, are evident in Fig. 4b.

Based on the above-mentioned methodology, we perform point-based testing at each of the 12 cities using the following steps:

1. Estimate the time period of available ground motion data for each city in the compiled ground motion dataset (in terms of PGA-corrected values for site effects).

2. Count the observed exceedances of PGA at 0.1 and 0.2 g levels for each city's complete time window, and calculate their corresponding standard deviations considering the uncertainties in the intensity–PGA conversions.

3. Calculate the predicted number of exceedances for each of the PGA thresholds considering every end branch of the ESHM20 logic tree (i.e. annual probability of exceedance × total time period).

4. Compute the weighted mean binomial distribution by combining all the binomial distributions applied to (3) considering the full distribution of the hazard uncertainties. Calculate the probability (p value) of the observed number of exceedances being drawn from the weighted mean binomial distribution.

5. Compute the p value where there will be N observations or more than the observed number of exceedances from the weighted mean binomial distribution.

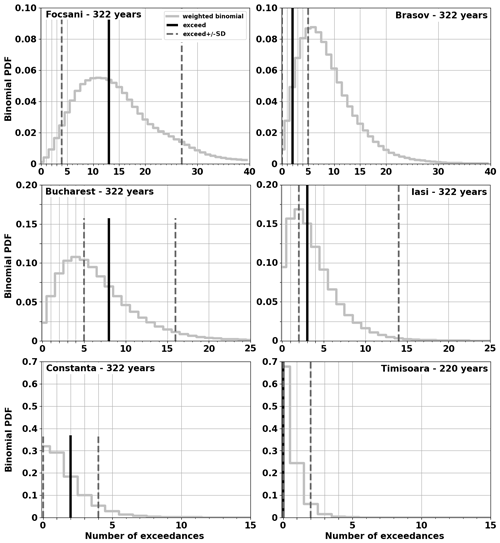
Figure 5 Consistency test results of ESHM20 with the observed PGA values at 0.1 g for each of the following six cities: Focșani, Brașov, Bucharest, Iași, Constanța, and Timișoara. The histogram depicts the ESHM20 weighted mean; the observed number of exceedances over the time window of completeness is given as the black vertical line and its 1σ variability is given as dashed vertical lines; the total completeness time is specified in each panel for the respective city.

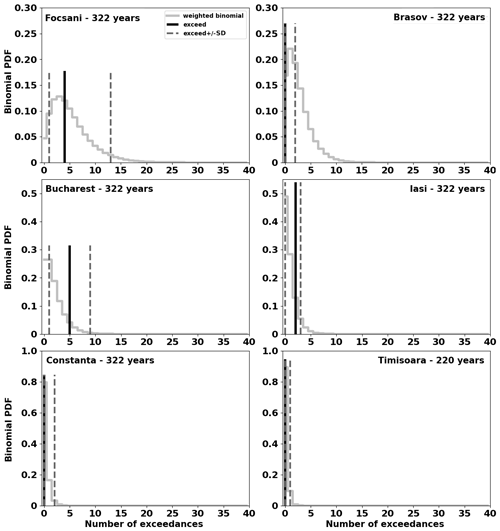
Figure 6 Consistency test results of ESHM20 with the observed PGA values at 0.2 g for six representative cities. The histogram depicts the ESHM20 weighted mean; the observed number of exceedances over the time window of completeness is given as the black vertical line, and its 1σ variability is given as dashed vertical lines; the total completeness time is specified in each panel for the respective city.

5 Statistical testing procedure: results

The results of the statistical testing of ESHM20 at 0.1 and 0.2 g PGA are illustrated in Figs. 5 and 6 for six cities (Focșani, Brașov, Bucharest, Iași, Constanța, and Timișoara), while the others (Bacău, Câmpulung, Cluj-Napoca, Craiova, Galați, Sibiu) are given in Figs. S2 and S3 of the Supplement. These plots depict the histogram of the weighted mean of ESHM20 and the observed number of exceedances (i.e. black vertical line) and their 1σ variability (i.e. dashed vertical lines). The total time of the observations is specified in each panel for the respective city. As mentioned before, the average time period of the observations of both ground-shaking recordings and macroseismic data spans 322 years for all the cities, except the ones within the Carpathian region, such as Sibiu and Cluj-Napoca, as well as Timișoara, the westernmost city. For these cities, the time period is about 220 years. Overall, there is a consistent alignment of estimated ground-shaking hazard of ESHM20 with the observed data at the 0.1 g PGA level, as shown by Fig. 5. Notably, cities located along the northeast–southwest trajectory outside the Carpathians – such as Iași, Focșani, and Bucharest (see Fig. 5) – show a robust correlation with the ESHM20 PGA estimates. Of particular interest is the consistency of ESHM20 with observations for Focșani, a city that is in proximity to the Vrancea deep-seismicity sources, the main seismogenic source of the region. A slight shift from the ESHM20 prediction is observed for the capital city of Romania, i.e. Bucharest, where more intensities over VII (MSK-64) were recorded than predicted; this fact might reflect the way humans experience ground shaking within different typologies of buildings in megacities (Rogozea, 2016; Cioflan et al., 2016). Additionally, such a shift might be attributed to the effect of different source and path features, such as directivity, or uncertainties in correcting for site effects. Furthermore, the values expected from ESHM20 are higher than the observed ones for cities along and in proximity to the Carpathian bend, e.g. Bacău, Brașov, and Câmpulung, and might suggest that a local attenuation effect is not currently captured or modelled using the ESHM20-scaled backbone logic tree for the Vrancea in-slab region (Weatherill et al., 2020). The impact of different attenuation patterns due to complex tectonic configuration was previously seen in both human-felt and instrumental observations (e.g. Radulian et al., 2006; Ivan, 2007; Marmureanu et al., 2016b) and captured within recent region-specific ground motion models (GMMs; e.g. Vacareanu et al., 2015; Manea et al., 2022). The results at the cities beyond the Carpathian Mountains (e.g. Sibiu, Cluj-Napoca, Timișoara) exhibit hazard predictions that reflect frequent crustal seismic activity because significant attenuation behind the arc reduces VRI-related ground motion. It appears that a more comprehensive dataset covering a longer period of time may be required to accurately assess the distribution of ground-shaking hazard levels. For cities located in the far-field area of the VRI and outside of the Carpathian arc (fore-arc region), such as Constanța and Craiova, the computed hazard is slightly lower than the recorded data. The same feature can be seen from the 475-year return period PGA map (see Fig. 1), and it contrasts the recorded ground motion field and pre-instrumental intensity data (e.g. Cioflan et al., 2022). Manea et al. (2022) provide insights into the apparent attenuation of the ESHM20 ground motion model for the fore-arc area, and future adjustments of ESHM20 are recommended to capture the ground motion characteristics within this region of Romania. However, the estimates of ESHM20 at 0.1 g PGA appear overall to be consistent with the data, given all the uncertainties involved in this analysis. Similarly, for the 0.2 g PGA level, the results suggest a strong correlation in areas near the VRI (see Figs. 6 and S3). Focșani experiences multiple instances of surpassing the 0.1 g PGA level, and the observed exceedances are within the ESHM20-estimated binomial distribution. Nevertheless, for the remaining cities, ESHM20 exceedances are slightly below observed exceedances in Bucharest and Iași, due to the influence of source/path effects and/or uncertainties in correcting for site effects. For the cities located along the Carpathian arc (Bacău, Brașov, and Câmpulung), the trend is reversed, with ESHM20 exceedances being higher than the observed ground-shaking recurrences. For the rest of the cities (Galați, Craiova, Timișoara, Sibiu, Constanța, Cluj-Napoca), the ESHM20 estimates fit the observations relatively well. The comparison between the observations and the weighted mean and the range of annual probabilities of exceedance from ESHM20 hazard curves is consistent for the 0.1 g PGA level. For the 0.2 g PGA level, the consistency is valid for the cities located in proximity to the VRI.

The overall results are listed in Table 1, and the probability that the observed record could be drawn from the combined distribution (p value) is presented at each location as “p0.1” and “p0.2”. These results show that 9 out of 12 locations provide no evidence for poor performance of ESHM20 for 0.1 g PGA (poor performance – p value < 0.05), while only at 1 location does the hazard not pass the test at 0.2 g. Overall, the testing results suggest that there are no reasons to reject ESHM20 in Romania for 0.1 and 0.2 g PGA.

6 Conclusions

Evaluating the performance of seismic hazard models against recorded data is an emerging research topic. In this study, we evaluated the performance of the recent update of ESHM20 (Danciu et al., 2021a) in Romania. The compiled ground-shaking database combines strong-motion records and macroseismic-intensity data. The inclusion of the macroseismic-intensity data allows expansion of the observational time period to over 200–300 years at the cost of increased uncertainties in the ground motion estimates. The result of the statistical testing suggests that ESHM20 is consistent with the observations for two PGA levels at the locations of the 12 cities selected across Romania. We found strong consistency between the weighted mean of ESHM20 and the exceedances of the observations for the cities (Focșani and Galați) located in proximity to the VRI for both PGA levels, i.e. 0.1 and 0.2 g.

For cities located along the Carpathian arc (Bacău, Brașov, and Câmpulung), the ESHM20 exceedances are above the recorded ground motions and suggest that the along-arc attenuation effect (Manea et al., 2022) might not be captured or modelled in the ESHM20 ground motion model (Weatherill et al., 2020). Furthermore, the testing results at cities located in the VRI far-field area and outside of the Carpathian arc (Constanța, Craiova) might suggest that the ground motion models used in ESHM20 attenuate too fast compared to the recorded PGA, as observed by Manea et al. (2022). For the Iași and Bucharest sites, located along the NE–SW direction from the VRI, the ESHM20 estimates appear to be below the values of the recorded data at the 0.1 g PGA level, and this feature becomes more prominent at 0.2 g; these differences might be attributed to (1) source directivity effects, which are significant for major events occurring in Vrancea (Cioflan et al., 2022); (2) potential bias in the conversion of the intensity to PGA; or (3) possible complex local site effects which might not have been completely removed from the observations. While informative conclusions could be drawn from evaluating the comparison at cities along and outside of the Carpathian range, limited conclusions can be derived for locations in regions of low seismic hazard, such as Sibiu and Cluj-Napoca or Timișoara in western Romania. The seismic hazard of these regions is dominated by episodic clusters of small to moderate shallow seismicity with regional effects, which are not well captured in the macroseismic data or the strong-motion recordings. We acknowledge that even with a time period of 2 to 3 centuries, the observations remain largely incomplete in time and space. The Romanian seismic network (Marmureanu et al., 2021) has evolved over time; however few ground motion data are available due to a lack of significant earthquakes occurring in recent decades. Uncertainties associated with the ground motion dataset increase with the conversion of the macroseismic data, as illustrated in the results given in Figs. 5 and 6. Moreover, the statistical testing is limited in scope given that all the uncertainties are also associated with the distribution of the hazard results; configuration of the logic tree; sampling technique; and/or use of a certain distribution, i.e. binomial or log-normal. All these factors contribute to the overall stability of the statistical testing.

In conclusion, our analysis suggests that observed exceedance rates for these two PGA levels, i.e. 0.1 and 0.2 g, are consistent with ESHM20 estimates. These results must be interpreted with caution given the above-mentioned limitations to the time and spatial coverage of the observations for both the ground-shaking and the macroseismic-intensity dataset.