Dynamical changes in seismic properties prior to, during, and after the 2014–2015 Holuhraun eruption, Iceland

When a volcano is monitored using only a single discipline or a single seismic station, it becomes important to harvest information from the limited data set. Changes in the seismic complexity could reveal a dynamic change due to magma propagation. We evaluated permutation entropy (PE) and phase permutation entropy (PPE) to monitor the 2014–2015 Holuhraun eruption in Iceland. These methods provide fast and robust quantification of time series complexity. We additionally calculated the instantaneous frequency (IF), commonly used to monitor the frequency changes in a non-stationary signal; the root-mean square (RMS); and the root-median square (RMeS) of the seismic amplitude. We observed distinct changes in the temporal variation in PE, PPE, and IF, which are consistent with the changing state from quiescence to magma propagation and then to eruption. During the eruption, PE and PPE fit the lava discharge rate, showing their potential to forecast the duration of the eruption. While one parameter may be more sensitive to one stage, the other may respond better to another stage. Therefore, combining them may provide more reliable information. Cluster analysis of these combined parameters shows clusters consistent with the expert interpretation, confirming the power of these parameters to distinguish different eruption stages.

1 Introduction

A volcano should be monitored using at least four to six seismic stations (Wassermann, 2012; Saccorotti and Lokmer, 2021; Moran et al., 2008). Yet many volcanoes are only monitored by a few seismic stations (Thompson et al., 2015). Monitoring a volcano using one seismic station hinders the classification of the recorded volcano–seismic signals and their location. However, it provides the opportunity to monitor the temporal evolution of both transient and continuous seismic features, which can give an overview of the state of a volcano. Furthermore, when a volcano observatory starts operating with a single seismic station and more seismometers are only added later, seismic analysis of a single station is important to establish a continuous baseline of monitoring.

An example of single-station monitoring is estimating the temporal change in seismic velocity (d$v/v$), which can be influenced by magma intrusion, using ambient noise interferometry (Brenguier et al., 2008). Ambient noise interferometry can be applied to data from a single station using either cross-component correlation (De Plaen et al., 2016) or autocorrelation (De Plaen et al., 2019). As a volcanic state can change quickly in a crisis, a high temporal resolution of monitoring is crucial for making a short-term prediction. The estimation of d$v/v$ can be done in a short time window, such as minutes; however, it requires a dense network (Illien et al., 2023). The d$v/v$ changes also do not always relate to magma intrusions, as the physical properties of the crustal rocks can also be influenced by atmospheric pressure and temperature (Hillers et al., 2015), changes in groundwater level (Sens-Schönfelder and Wegler, 2006), and ground freezing (Steinmann et al., 2020).

Entropy is a term that is broadly used to measure the level of disorder of a system, e.g., in thermodynamics (Cropper, 1986), statistical mechanics (Wehrl, 1978), and information theory (Shannon, 1948). In nature, a state that is not balanced will always shift to reach equilibrium, and this process can be associated with increasing entropy (Posadas et al., 2023). In seismology, increasing entropy can be related to the irreversible transition of unbalanced stress and strain in the crust, culminating in earthquakes (De Santis et al., 2011; Posadas et al., 2021, 2023). The changes in entropy can be linked to the seismic cycle of earthquakes (Posadas et al., 2023), where the entropy increases and reaches its maximum value at or shortly after the main shock, followed by a drop and then stabilization during the relaxation period (De Santis et al., 2011; Posadas et al., 2021, 2023).

One of the methods to estimate entropy using the amplitude of a time series is permutation entropy (Bandt and Pompe, 2002). Glynn and Konstantinou (2016) calculated permutation entropy (PE) based on seismic time series to find a precursor prior to the 1996 Gjálp eruption in Iceland. In principle, PE is estimated using one station. When several stations are available, PE can be estimated from them to verify whether its temporal evolution is consistent at all stations. During the propagation of magma to the surface, magma will interact with the varying surrounding rocks at depth and create different seismic signals with different complexities. As magma reaches the surface, magma interaction with the shallow subsurface can generate a tremor and/or a long-period signal. When a pre-eruptive tremor and/or long-period signal is present, it exhibits a more regular oscillation and is narrow banded in frequency, and hence PE is reported to drop (Konstantinou et al., 2022).

While PE can detect a seismic precursor occurring days before an eruption (Glynn and Konstantinou, 2016), PE is also reported to be sensitive to fast changes. Sudibyo et al. (2022) calculated PE for 63 eruptions of Strokkur Geyser in Iceland, where the duration of a typical eruptive cycle is 3.7±0.9 min (Eibl et al., 2020). PE can resolve the typically observed four phases of Strokkur's eruptive cycle, which last several seconds to several minutes (Eibl et al., 2021), and the 1 s long processes therein at a high resolution (Sudibyo et al., 2022).

Apart from the amplitude, another useful property of the continuous seismic recording is the phase information. Instantaneous phase, along with the other seismic attributes, has been utilized in seismic reflection to map geological discontinuities in the shallow subsurface since the 1970s (Taner et al., 1979). In seismology, the instantaneous phase is used, e.g., in seismic tomography (Bozdağ et al., 2011) and noise suppression in ambient noise cross-correlation (Schimmel et al., 2011; De Plaen et al., 2019). Kang et al. (2021) introduced the use of the instantaneous phase to calculate phase permutation entropy (PPE), which has also been shown to be sensitive to dynamic changes in a signal. Here we use the application of PE and PPE to detect the dynamic changes before, during, and after the 2014–2015 Holuhraun eruption, Iceland.

Different observable parameters from various methods are required to form a robust forecasting framework. Understanding which parameters to use and how they can represent the process in the system can help improve the framework's accuracy and reduce the computational cost. Here we also assess the derivative of the instantaneous phase known as instantaneous frequency, IF (Boashash, 1992), which is commonly used to perform time–frequency analysis for a non-stationary signal.

From 16 August 2014, seismicity migrated for 2 weeks from the subglacial Bárðarbunga volcano in northeastern Iceland: first to the southeast, then to the northeast for about 48 km, at a depth of 5 to 9 km (Ágústsdóttir et al., 2016, 2019). This seismicity is interpreted as having been induced by a dike intrusion, which is divided into four segments, S1 to S4 (Woods et al., 2019), and which culminated in an eruption that formed the Holuhraun lava flow field (see Fig. 1a and b). Along the dike path, three cauldrons formed on the ice surface, possibly indicating small subglacial eruptions (Eibl et al., 2017b; Reynolds et al., 2017). After the dike reached Holuhraun, a short-lived eruption occurred during the night on 29 August 2014 and was followed by a 6-month-long eruption from 31 August 2014 at the same site. Another subglacial eruption possibly occurred on 3 September 2014 (Eibl et al., 2017b), and another subaerial eruption took place from 5 to 7 September 2014 between the ice cap and the main lava flow field (Pedersen et al., 2017; Eibl et al., 2017a). The spatial chronology is shown in Fig. 1a, while the chronology timeline is shown in Fig. 1b.

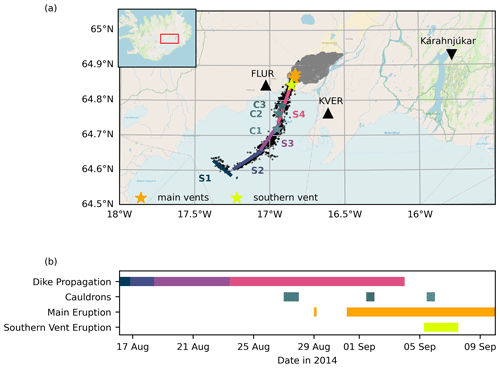
Figure 1 Overview of the unrest, followed by the 2014–2015 Holuhraun eruption, Iceland. (a) The recorded earthquakes from the catalog of Ágústsdóttir et al. (2019) are represented by the black dots, the activated dike segments reported by Woods et al. (2019) are represented by the lines S1 to S4, the erupted lava flow field from Voigt et al. (2021); Voigt and Hamilton (2021) is shown by the gray shaded area, the main vents are the yellow stars, the southern vent is the light-green star, the location of the seismic stations FLUR and KVER are marked by the black triangles, and the weather station at Kárahnjúkar is shown by the black inverted triangle. Panel (b) shows the temporal information on the dike propagation (Woods et al., 2019), observation of the cauldrons (Eibl et al., 2017b; Reynolds et al., 2017), the main eruption, and the southern vent eruption (Eibl et al., 2017a).

This 2014–2015 Holuhraun eruption was exceptionally well monitored by combining a variety of disciplines. In terms of eruption forecasting, this eruption is interesting due to several subglacial eruptions, three subaerial eruptions, and the extensive dike formation. In addition, a dense network of 72 seismometers (Woods et al., 2018) was distributed around the growing lava flow field, providing a wealth of data. The lack of recorded shallow seismicity prior to the eruptions (Sigmundsson et al., 2015) raises the question of whether the final magma movement is aseismic or generated a pre-eruptive tremor as suggested by Eibl et al. (2017b).

In this paper, we first introduce PE (Sect. 2.2) and PPE (Sect. 2.3), along with other quantification methods consisting of instantaneous frequency (IF) (Sect. 2.4), the root-mean square (RMS), and the root-median square (RMeS) of seismic amplitude (Sect. 2.5); the time-averaged discharge rate (TADR) (Sect. 2.6); and k-means clustering (Sect. 2.7). Synthetic tests to evaluate the performance of PE and PPE are provided in Sect. 3.1. Additionally, we provide an explanation of the parameters utilized to calculate PE and PPE (Sect. 3.2) as well as IF, RMS, and RMeS (Sect. 3.3). We calculated PE, PPE, IF, RMS, and RMeS from February 2014 to December 2015 (Sudibyo et al., 2024). We then compare the temporal variations in PE, PPE, and IF with the RMS of the seismic amplitude and the hypocentral distances to the station (Sect. 4). Furthermore, we discuss the temporal variation in PE, PPE, and IF during the repose time (Sect. 5.2), during the dike propagation (Sect. 5.3), and during the eruption (Sect. 5.4). During the eruption, we compare them with the lava effusive rate (also Sect. 5.4). We show the clustering of PE, PPE, IF, and log(RMeS) in Sect. 5.5 before we provide our conclusion.

2 Method

2.1 Seismic network

A dense seismic network (network code Z7) was maintained in the area of the 2014–2015 Holuhraun eruption (White, 2010). A total of 50 stations were running long enough to record the seismicity from the first half of 2014 to the end of 2015. Based on its proximity to the dike and eruption vents and on the data availability, we chose the FLUR station for further analysis. This station is located about 32.7 km north of Bárðarbunga and about 9.1 km southwest of the Holuhraun lava flow field. At FLUR, a Guralp CMG-3ESP broadband sensor recorded at a sampling frequency of 100 Hz. For comparison we used the KVER station, which is located about 14 km southeast of the lava flow field. At KVER, a Guralp CMG-6T broadband seismometer recorded at a 100 Hz sampling rate. The locations of these two stations are shown in Fig. 1a.

2.2 Permutation entropy (PE)

PE quantifies the probability distribution of ordinal patterns in a time window. An ordinal pattern is a vector representing the relative order of the amplitudes. For example, a sequence of {0.32, 1.0, 2.7, 3.5, 5.0} is represented by the ordinal pattern of {0, 1, 2, 3, 4}, while {3.1, 2.2, 1.1, 3.8, 5.0} is represented by {2, 1, 0, 4, 5}. To reconstruct an ordinal pattern, we down sample the time series using an embedding dimension m and a delay time τ. The embedding dimension m is the total number of samples in the sequence, and the delay time τ is the time gap between samples. The vector of the ordinal pattern is first constructed, $[x_{\mathrm{s}},(x_{\mathrm{s}}+\mathit{\tau }),\mathrm{\dots },(x_{\mathrm{s}}+(m-\mathrm{1})\mathit{\tau }\left)\right]$. The next ordinal patterns then are reconstructed by continuously shifting x_s one sample forward until the last ordinal pattern reaches the end of the window.

Then, we calculate PE as

$$\begin{array}{}\text{(1)}& \mathrm{PE}={\displaystyle \frac{-\mathrm{1}}{\log m\mathrm{!}}}\sum _{k=\mathrm{1}}^{m\mathrm{!}}{p}_k\log p_k,\end{array}$$

where p_k is the probability of the ordinal pattern k. p_k is determined by the relative frequency $N_k/N$, where N_k is the number of patterns k observed in the window and N the total number of ordinal patterns in the window. Equation (1) is then normalized by the maximum number of different ordinal patterns log m!, leading to a PE between 0 and 1.

An example of the PE calculation is illustrated in Fig. 2. Figure 2a shows a 5 h long seismic time series recorded by the vertical component at the FLUR station, Iceland. This seismic waveform has been bandpass-filtered between 0.5 and 10 Hz. We first divided the time series into 1 h long windows without overlap. We then used m=7 and τ=0.04 s to reconstruct the ordinal patterns (Fig. 2b). Note that the τ used in Fig. 2 is for illustration purposes, while the real analysis in this paper uses the parameters mentioned in Sect. 3.2. Finally, in each 1 h window, we calculated the respective PE (Fig. 2e).

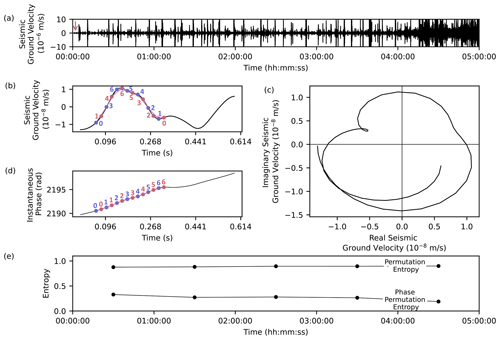
Figure 2 The overview of PE and PPE calculation. (a) A seismic time series of 5 h from the vertical component of the FLUR station, filtered between 0.5 and 10 Hz. (b) The amplitude of the waveform starting at the red arrow in panel (a) with two consecutive ordinal patterns {0, 3, 6, 5, 4, 2, 1} and {1, 4, 6, 5, 3, 2, 0}. (c) The analytic signal reconstructed from the same part of the signal in the complex plane. (d) The unwrapped instantaneous phase of the analytical signal in panel (c) with two examples of consecutive ordinal patterns {0, 1, 2, 3, 4, 5, 6}. Note that the linear trend of the instantaneous phase leads to fewer different ordinal patterns than the seismic amplitude data. (e) The estimated PE and PPE for the waveform in panel (a).

2.3 Phase permutation entropy (PPE)

A seismic time series, denoted as x(t), can be regarded as the real component of the seismic analytic signal $X\left(t\right)=x\left(t\right)+iy\left(t\right)$, where y(t) is the imaginary component obtained by applying the Hilbert transform to x(t) (Gabor, 1946; Taner et al., 1979; Barnes, 1992). The Hilbert transform is the equivalent of a linear filter, where the amplitudes of a signal are unchanged but their phases are shifted by $-(\mathit{\pi }/\mathrm{2})$ (Feldman, 2011). Scipy is a free and open source Python library (Virtanen et al., 2020) that provides a tool to compute the analytic signal from a time series. The function scipy.signal.hilbert implements the step defined by Gabor (1946) in computing an analytic signal X(t) as follows:

1. Fourier transforming the real component,

2. zeroing the amplitude for negative frequencies and doubling the amplitude for positive frequencies, and

3. inverting the Fourier transform.

The instantaneous phase can be defined as the degree of the X(t) rotation. The instantaneous phase θ(t) is calculated using

$$\begin{array}{}\text{(2)}& \mathit{\theta }\left(t\right)={\tan }^{-\mathrm{1}}\left({\displaystyle \frac{y\left(t\right)}{x\left(t\right)}}\right).\end{array}$$

PPE was introduced by Kang et al. (2021) to calculate a wave complexity using the instantaneous phase of an analytic signal. In calculating PPE, we reconstruct the ordinal pattern using the instantaneous phase, which is obtained from Eq. (2). Unlike Kang et al. (2021), who used the wrapped instantaneous phase from −π to π to construct the ordinal pattern, here we use the unwrapped instantaneous phase. For reference, a sine wave will have a linear increase in the unwrapped instantaneous phase, producing only one ordinal pattern. Its respective PPE value is thus 0.

An example of PPE calculation for a seismic time series (Fig. 2a) is shown in Fig. 2c, d, and e. We first obtain the analytic signal (Fig. 2c). We then estimate the instantaneous phase and reconstruct the ordinal patterns (Fig. 2d). Finally, we estimate the PPE from the probability of the reconstructed ordinal patterns (Fig. 2e).

2.4 Instantaneous frequency (IF)

The instantaneous frequency (IF(t)) is defined as the derivative of the instantaneous phase θ(t),

$$\begin{array}{}\text{(3)}& \mathrm{IF}\left(t\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\mathit{\theta }\left(t\right).\end{array}$$

2.5 Root-mean square (RMS) and root-median square (RMeS) of the seismic amplitude

The root-mean square (RMS), the root of the mean squared seismic amplitude, is commonly used in volcano monitoring to continuously estimate the average seismic energy.

$$\begin{array}{}\text{(4)}& \mathrm{RMS}=\sqrt{{\displaystyle \frac{\mathrm{1}}{n}}\sum _i{x}_i^{\mathrm{2}}}\end{array}$$

In some cases where both volcano–tectonic (VT) events and tremors are present, VT events will dominate the RMS and conceal the tremor in the RMS time series. Calculating the root of the median squared seismic amplitude (RMeS) will emphasize the tremor energy more (Eibl et al., 2017a). RMS and RMeS are calculated using a 1 h window length without overlapping. For x² values sorted by size, RMeS is calculated as follows:

$$\begin{array}{}\text{(5)}& \mathrm{RMeS}=\left\{\begin{array}{ll}\sqrt{x_{(n+\mathrm{1})/\mathrm{2}}^{\mathrm{2}}}& \text{if}n\text{is odd}\\ \sqrt{\mathrm{0.5}(x_{n/\mathrm{2}}^{\mathrm{2}}+x_{n/\mathrm{2}+\mathrm{1}}^{\mathrm{2}}})& \text{if}n\text{is even}.\end{array}\right.\end{array}$$

2.6 Time-averaged discharge rate (TADR)

Coppola et al. (2016) exploited the intermediate-infrared data acquired by multiple sensors from multiple satellites. These infrared data can be used to identify the thermal radiation emitted by volcanic eruption processes. The intensity of the thermal anomaly is known as volcanic radiative power (VRP). During an effusive eruption, VRP can be used to calculate the time-averaged lava discharge rate (TADR) in m³ s⁻¹:

$$\begin{array}{}\text{(6)}& \mathrm{TADR}={\displaystyle \frac{\mathrm{VRP}}{c_{\mathrm{rad}}}},\end{array}$$

where c_rad (J m⁻³) is the radiant density representing the efficiency of the lava body at modulating the heat.

2.7 k-means clustering

k-means is a non-supervised clustering method to find K numbers of clusters, each consisting of sets of points that are evenly spaced in a D-dimensional Euclidian space (Bishop, 2006). The D dimension is determined from D numbers of seismic parameters used. We describe the data set of each seismic parameter as $x_n=X_{\mathrm{1}},\mathrm{\dots },X_N$. The steps to assign each data point of D seismic parameters into k clusters are elaborated as follows. We introduce an initial set of D-dimensional vectors μ_k, which represent the center of the cluster k, where $k=\mathrm{1},\mathrm{\dots },k$. We then need to find an assignment such that the sum of the squares of the distances (J) of the data points $X_{\mathrm{1}},\mathrm{\dots },X_N$ to its closest vector μ_k is at a minimum:

$$\begin{array}{}\text{(7)}& J=\sum _{n=\mathrm{1}}^N\sum _{k=\mathrm{1}}^K{r}_{nk}\left|\right|x_n-{\mathit{\mu }}_k|{|}^{\mathrm{2}},\end{array}$$

where r_nk=1 if the data points x_n are assigned to cluster k and r_nk=0 otherwise.

Finding the values of r_nk and μ_k where J is at a minimum is done by iteration using three successive steps. Initially, we randomly choose the initial value of μ_k. Second, we minimize J with respect to r_nk while keeping a fixed μ_k. Then, we minimize J with respect to μ_k while keeping r_nk fixed (Bishop, 2006).

2.8 Weather data

A weather station located in Kárahnjúkar, about 59.7 km from the FLUR station (Fig. 1a), provides weather data as a reference for the analysis during the repose time. The station was installed at 639 m above sea level and measures 10 m above the Earth's surface. It measures the average of the last 10 min wind speed and the last 1 min temperature. The data are provided by the Icelandic Meteorological Office and are available by email request.

3 Synthetic tests and the application to seismic data

3.1 Synthetic tests

Sudibyo et al. (2022) tested different delay times τ to obtain optimum PE for stationary signals with different bandwidths. For a noisy stationary signal, PE is less affected by noise when τ is not too small nor equal to the fundamental period. τ is related to the frequency of the signal. When the frequency of a non-stationary signal changes, it will influence the calculated PE, as the calculation uses a fixed τ. This behavior was not investigated in detail in the previous study.

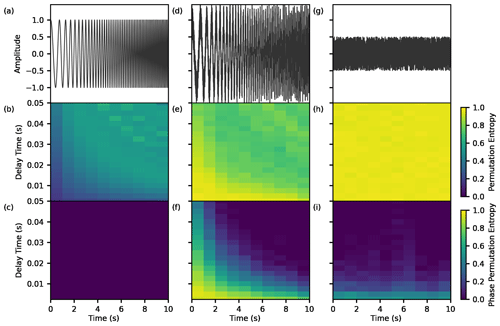
Figure 3 Synthetic test (a) time series of a chirp signal, (b) PE, and (c) PPE. (d–f) The same as panels (a)–(c) but for a noisy chirp signal. (g–i) The same as panels (a)–(c) but for noise.

Here we investigated the effects of the differences in PE and PPE calculation on three different synthetic signals. First, we generated a chirp signal with increasing frequency from 1 to 10 Hz and a sampling rate of 400 Hz (Fig. 3a) and then added a de-meaned uniform noise (Fig. 3d). Furthermore, we also tested the noise itself (Fig. 3g). We used the Numpy library (Harris et al., 2020) to create the chirp signal and the noise and then calculated the PE and PPE for every 1 s window length. We use m=5, which is the highest m possible to calculate PE and PPE based on the number of samples for the 1s window length.

In this test, we focus on how changing the frequency could affect the PE and PPE calculation. We tested different τ from the shortest possible length to 0.5 s, which is the Nyquist period of the high-frequency corner of the signal. Figure 3b and e show that using τ>0.25 s, which is half of the Nyquist period, generates artifacts in the PE of the higher frequencies. Figure 3b shows that the PE of the chirp signal increases when the frequency increases. This is due to the less repeating ordinal patterns reconstructed when the frequency increases. The opposite behavior is shown in Fig. 3e for the noisy chirp. Noise increases the PE (Fig. 3h). Due to the fixed τ, the ordinal pattern samples relatively more noise at lower frequencies. When the frequency increases, the length of the ordinal patterns gets closer to the signal's wavelength and the signal-to-noise ratio increases, resulting in a lower PE at a higher frequency.

PPE utilizes the instantaneous phase. The unwrapped instantaneous phase of a chirp signal is always increasing (Fig. S1a in the Supplement), producing only one ordinal pattern, resulting in PPE = 0. In the case of the noisy chirp, the noise contains non zero-crossing amplitude and generates tangled rotation in its analytical signal, as shown in Figs. 2c, S1f, and S1j. These tangled rotations have decreasing phase angles, which generate different ordinal patterns (Fig. S1h and S1l), hence increasing PPE.

A common practice to reduce noise and isolate the signal of interest is filtering. We tested how PE and PPE change if noise gets filtered. Figure S2 shows a decrease in PE and PPE in the filtered noise, with a wider bandwidth possessing higher PE and PPE than a narrower bandwidth.

3.2 Parameter selection in calculating PE and PPE of seismic time series

The parameters required to calculate PE and PPE are window length, embedding dimension m, and delay time τ. To determine the window length, we need to fulfill two requirements: the minimum number of samples required by the embedding dimension m and the targeted resolution in the temporal variation in PE and PPE. To calculate PE and PPE, the number of samples in a window has to be more than m!, where m! is the maximum number of possible ordinal patterns reconstructed from the embedding dimension m. In the case of a noisy signal, it is advised to use a window length longer than 5⋅m! (Amigó et al., 2008) to cover all possible patterns generated by the noise. Following their suggestion, for m=7 we need a minimum sample of 25 200 points or 252 s. As seismic precursors can range from hours to days prior to an eruption, we chose a 1 h window length, which also fulfills the requirements of the number of samples needed by the embedding dimension mentioned. The delay time τ needs to be smaller than the Nyquist period of the targeted signal (Berger et al., 2017), and our synthetic test recommends a τ < 0.5 Nyquist period (see Fig. 3b and e). Our interest lies in the frequency between 0.5 and 10 Hz, which covers the frequency band of the tremor between 0.8 to 2.5 Hz (Eibl et al., 2017b) and excludes the repeating noise at frequencies above 10 Hz. The Nyquist period for a 10 Hz signal is 0.05 s, and we chose τ= 0.02 s.

We processed 2 years of seismic data recorded at the vertical component of the FLUR station from January 2014 to December 2015, covering the repose period, the unrest, and the eruption. We used Obspy to read the seismic data and to apply a fourth-order Butterworth bandpass filter. A Butterworth filter does not create ripples in the passband, which is important to avoid artificial ordinal patterns. We activated the zero-phase option in the Butterworth filtering to obtain no phase shift in the filtered seismogram. All plotting is done using Matplotlib. A comparison between the two stations, FLUR and KVER, shows similar temporal variations in PE and PPE at both stations (Fig. S3).

3.3 Calculation of IF, RMS, and RMeS

We also used the vertical component from the FLUR station for the IF, RMS, and RMeS calculations and adapted the same 0.5–10 Hz frequency band used for the IF calculation. First, we estimated the instantaneous phase for every seismic data sample, and then we calculated IF from every two consecutive instantaneous phases. We then calculate the mean IF for every 1h window to obtain the same resolution as the PE and PPE. In this paper, we refer the hourly mean IF as the IF. The calculation of RMS and RMeS also uses the same 1h window length and is within the frequency from 0.5 to 10 Hz.

3.4 Parameter selection in k-means clustering

We performed a clustering analysis to assess the ability of the seismic parameters calculated to discriminate between the different processes before and during the eruption. We used PE, PPE, and IF to generate a three-dimensional Euclidian space and added RMS or RMeS to generate a four-dimensional Euclidian space. The lava discharge rate is not used in the clustering since it is only available during the eruption. We generated three clusters representing the major events: quiescence, dike propagation, and eruption in these spaces using scikit-learn (Pedregosa et al., 2011). To validate the result, we also clustered the data based on the timeline of the eruption processes consisting of (i) quiescence, (ii) the propagation of four dike segments (Woods et al., 2019), and (iii) the presumed sub-glacial eruption (Eibl et al., 2017b) and the subaerial eruption (Eibl et al., 2017a). We then calculated by expert interpretation how many points in clusters fall into the equivalent k-means clusters and normalized them by the total points in each interpreted cluster. This quantification is expressed in the confusion matrix. By choosing the confusion matrix with the highest score, we can choose the best clustering result. The resulting confusion matrices for different combinations of seismic parameters are shown in Tables S1 to S5 of the Supplement.

4 Results

In the following, we will describe the temporal variation in various features of the seismic waveform in the last 5 d of the repose time, in the 14 d of earthquake migration, and in the first 15 d of the main eruption (Fig. 4). We will also describe the further evolution until March 2015, when the eruption ended (Fig. 5).

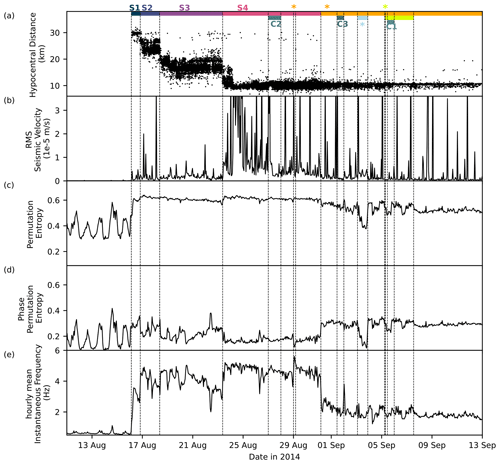
Figure 4 Overview of the seismic characteristics during the quiescence, eruption-preceding seismicity, and the first 15 d of the eruption: (a) hypocentral distances of the earthquakes from the FLUR station, (b) RMS, (c) PE, (d) PPE, and (e) IF. RMS, PE, PPE, and IF are calculated from seismic time series recorded at the vertical component of the FLUR station, filtered between 0.5 and 10 Hz. The segmentation of the dike (S1–S4, dark-blue to pink horizontal lines), cauldrons observed on the glacier surface (C1–C3, horizontal dark-green lines), the tremor on 3 September 2014 interpreted as a subglacial eruption (Eibl et al., 2017b) (light blue), the eruption from the southern vent (horizontal light-green line and light-green star), and the main eruption (horizontal yellow line and yellow stars) are marked in panel (a) and indicated by dashed vertical lines in all panels.

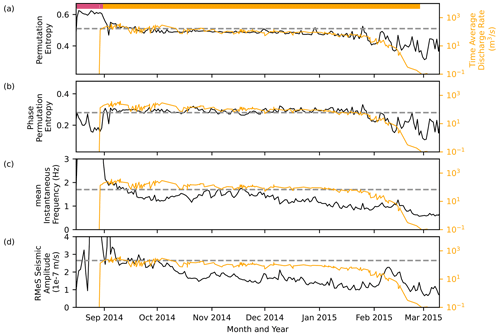
Figure 5 Overview of the 6-month-long subaerial eruption. Comparison of (a) PE, (b) PPE, (c) IF, and (d) RMeS seismic velocity (all black) on a linear y axis, with the lava effusion rate (Coppola et al., 2017) plotted on a logarithmic y axis (orange line, scale on right). Note the different y-axis scales for PE and PPE. All values were calculated using 1 d window length. The dashed line marks the reference line, obtained from the values of PE, PPE, IF, and RMeS on 8 September 2014, when the eruption starts to stabilize.

4.1 The earthquake hypocentral distances and RMS of seismic amplitude

More than 30 000 earthquakes are listed in the earthquake catalog by Ágústsdóttir et al. (2019). They migrate from the southeastern rim of the subglacial Bárðarbunga volcano at 29–32 km from the FLUR station and then progress to the Holuhraun lava field at about 8–12 km from the FLUR station (Figs. 1a and 4a). The dike segments S1 to S4 (Woods et al., 2019) feature distinctly different distance ranges. The hypocentral distance to our station decreased most quickly at the beginning of each segment when it formed, and the distance stalled towards the end of a segment. In segment S3, the earthquakes moved in several episodes on 18–20 August 2014, and later a short quiescence occurred on 22 August 2014 at 10:00 UTC. While in segment S4, the earthquakes kept moving to the northeast; they remained around 10 km distant from the FLUR station. After the onset of the main eruption on 31 August 2014, the number of earthquakes became fewer, and the seismic time series was dominated by the eruptive tremor.

Consequently, the seismic waveform not only is dominated by earthquakes but also features the seismic volcanic tremor. During repose time, the RMS is mostly below $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{7}}$ m s⁻¹. During dike formation, the RMS of the seismic amplitude is very spiky and is affected by the earthquakes (Fig. 4b). RMS increases significantly after S4 starts on 23 August 2014 and is also dominated by spikes throughout the segment and the eruptive period. Throughout S4, the RMS exhibits few fluctuations during 23–24 August, 24–26 August, and 26 August–1 September 2014. In the eruptive period, there is an increase between 2 and 4 September. Afterward, the RMS amplitude is mostly low and decreases over time, with spikes throughout the eruptive period.

4.2 The temporal evolution of permutation entropy (PE)

During the repose time, PE displays strong daily variation (Fig. 4c). A sharp increase is observed on 16 August 2014 when the earthquakes occur and start to migrate. PE stays high, mostly above 0.6 during the 2 weeks of the earthquake migration. Prior to the main eruption on 31 August 2014, PE exhibits three decreasing trends: segment S1 to S2, S2 to S4, and a more gentle slope during S4 to the onset of the main eruption. After the main eruption begins, there is a notable decrease in PE, followed by a strong drop on 3 September 2014, when PE reaches a value of 0.37. The drop on 3 September represents a local minimum that persists for 1 d. PE then fluctuates between 4 and 7 September and subsequently gets more steady after 10 September 2014. PE generally declines toward the end of the eruption (Fig. 5a). The comparison of PE with TADR from Coppola et al. (2017) reveals a similar shape for both (Fig. 5a). Note that TADR is plotted on a log scale, while PE is on a linear scale.

4.3 The temporal evolution of phase permutation entropy (PPE)

Similar to PE, PPE also exhibits strong daily variation during the repose time (Fig. 4d). Interestingly, during the earthquake migration, PPE follows a pattern that is anti-correlated to that of PE and IF. PPE increases from 0.27 in S1 to 0.32 in S2 but drops to 0.224 in the next 2 h. PPE then drops to 0.14 on 20 August, followed by a sharp increase until 23 August 2014. An abrupt drop occurs on 23 August 2014 when the time segment S4 starts, followed by two successive increasing trends, which culminate in the eruptions on 29 and 31 August 2014. Before the eruption, another peak is observed on 22 August 2014 at 10:00 and 26 August at 07:00. These peaks occurred 1 d before the presumed subglacial eruptions on 23 and 27 August 2014. PPE increases abruptly right after the main eruption starts. Interestingly, this is then followed by a pattern that is similar to the pattern in PE. PPE also drops and reaches the minimum value on 3 September 2014 for 1 d and generally declines towards the end of the eruption. The trend observed in PPE also aligns well with the shape of the lava effusion rate (Fig. 5b), with PE plotted on a linear scale and TADR on a log scale.

4.4 The temporal evolution of the mean instantaneous frequency (IF)

Before the start of the 2-week migration of earthquakes, the IF is mostly low, between 0.5 to 0.8 Hz, and exhibits daily variation (Fig. 4e). An abrupt increase in IF is observed when the swarm starts on 16 August 2014. IF generally increases from 16 to 20 August 2014, with values from 3 to 5 Hz during the propagation of segments S1 to S3. Even though it generally increases, IF exhibits a quasi-periodic fluctuation with each period varying from 4 to 12 h. There are two decreasing trends within this fluctuation, which fit the time lengths of segments S1 and S2. IF was the highest at the beginning of both segments and dropped continuously towards the end of the segments. IF is generally higher during S2 than during S1. IF continues to increase from the beginning of S3 for 2 d before decreasing towards the beginning of S4. During the propagation of S4, IF decreases quickly before the onset of the eruption on 29 August and continues to decrease more slowly towards the main eruption on 31 August. During the earthquake migration, IF is anti-correlated with PPE.

Two sharp drops in IF are also observed at 10:00 on 22 August and at 07:00 on 26 August 2014, at the same time as the two peaks in PPE are observed. Another drop is also observed on 28 August 2014 at 22:00, followed by a sharp increase to the maximum value of 5.6 Hz, marking the onset of the short eruption on 29 August 2014. After the onset of the main eruption on 31 August 2014, IF drops from 4.2 to 2 Hz. IF increases slightly from October to November 2014, then in general decreases to the end of the eruption on 28 February 2015 (Fig. 5c).

5 Discussion

5.1 Factors affecting the complexity quantification in PE and PPE

The synthetic tests in Sect. 3.1 show that PE, calculated using fixed m and τ, is higher for a signal with higher-frequency content compared to one with lower frequencies. A signal with energy in a broad frequency bandwidth usually possesses a higher PE (Dávalos et al., 2021; Sudibyo et al., 2022) and PPE (Fig. S2). Independent of its frequency content, PPE is more affected by the presence of non-zero-crossing oscillation in its signal. When a low-frequency signal is superposed by a weaker signal with a higher frequency, most oscillations of the higher-frequency part do not cross the zero amplitude. This oscillation type will cause more complex rotation in its analytical signal (Fig. S1f), resulting in more ordinal patterns and higher PPE.

5.2 The influence of atmospheric processes on PE, PPE, and IF

We investigated the influence of temperature and wind on the hourly PE, PPE, and IF during different seasons from 2014 to 2015. Seasonal variation including temperature, wind speed, and air pressure is commonly observed in seismic ambient noise (Bormann and Wielandt, 2013). Atmospheric pressure and temperature can generate noise at frequencies below 0.05 Hz (Bormann and Wielandt, 2013), while wind can generate noise at higher bandwidths between 0.5 to 60 Hz (Bormann and Wielandt, 2013; Withers et al., 1996). Here we observe strong effects of atmospheric signals on the seismic characteristics in the repose time before the magma propagation and after the eruption. It should be noted that the seismic station FLUR and the weather station Kárahnjúkar are about 57.9 km apart. While we noticed a shift between the variations in wind speed in comparison with PE, PPE, and IF of about 1–2 h in the hourly window, this can be considered negligible.

Wind speed is found to be strongly correlated with the background noise at frequencies higher than 1 Hz (Withers et al., 1996). We observed the strong influence of wind speed on the RMS of the seismic amplitude during the whole repose period (Figs. S5h–S12h). Interestingly, we did not observe the influence of wind on PE, PPE, and IF in summer. The influence of wind speed on PE, PPE, and IF could be seen clearly in spring, especially from February to May (Figs. S5e–S5g, S9e–S9g, S10e–S10g) when the fastest wind speed reaches 40 m s⁻¹ in March 2014, in autumn from September to October (Fig. S11e–S11g), and in winter (Fig. S12e–S12g). Wind seems to already influence PE and PPE at the end of the eruption from January to February 2015 when the wind speed reaches about 25 m s⁻¹ and the tremor amplitude is low, while the IF is less affected (Figs. S8e–S8g and S9e–S9g). Nevertheless, the wind effects on PE, PPE, and IF are found to be negligible during the magma propagation and the main eruption phases.

During the repose time, PE, PPE, and IF show clear daily cycles with high correlations with the temperature changes, as shown in Fig. S6a–S6c for the temperatures between June and August 2014. Similar results are observed for the summer months of 2015 (Figs. S10a–S10c and S11a–S11c). This is surprising because the influence of temperature on seismic waves with frequencies higher than 50 MHz is usually very small and is negligible for most seismological processing. For example, temperature does not seem to influence the temporal variation in the RMS of seismic amplitude for the whole observation period (Figs. S5d–S12d). However, PE and PPE depend only on the order of the consecutive values of the amplitude and instantaneous phase but not on the magnitudes. A very small difference in the consecutive values can change the order and create a different ordinal pattern, thus increasing the calculated entropy. Temperature affects both the thermo-elasticity of the seismometer, especially the analyzed vertical component (Bormann and Wielandt, 2013), and the underlying rocks (Prawirodirdjo et al., 2006), generating a temporal variation that is emphasized in PE and PPE. However, the temperature effect on PE, PPE, and IF are found to be negligible during the magma propagation and the main eruption.

Donaldson et al. (2019) estimated more than 10 years of variation in relative velocity changes (d$v/v$) in the crustal rock of central Iceland, including Bárðarbunga and Holuhraun. They observed the d$v/v$ to be high in the winter and spring and low in the summer and fall. This seasonal variation is associated with (i) the changes in the elastic loading on the rocks due to the seasonal changes in snow thickness and the atmospheric pressure and (ii) the annual variation in the groundwater level. They did not compare d$v/v$ with the wind speed and temperature. Wind speed is usually not considered an influence on d$v/v$, while the atmospheric temperature can still affect the d$v/v$ through the thermo-elasticity of the crustal rocks (Hillers et al., 2015; Prawirodirdjo et al., 2006). In our 2-year observation, we did not observe a clear change due to these long-period seasonal variations. While these seasonal changes in the crustal properties might affect the variation in PE, PPE, and IF, it seems to be much weaker compared to the daily variation due to the atmospheric noise.

5.3 The influence of the magma propagation on PE, PPE, and IF

PE and IF increase sharply on 16 August 2014. Both values remain at elevated levels until the onset of the main eruption on 31 August 2014. In contrast, PPE does not increase, but its fluctuation gradually decreases until the main eruption. The high PE and IF are caused by the high dominant frequencies of earthquakes and their energy distributions in a broad frequency range. We investigated the rotation of their analytic signals in a complex plane (Fig. S4b). Compared to ambient noise (Fig. S4a), earthquakes exhibit less complex rotation and therefore lower PPE.

PE and IF increase at the initial start of not only the magma propagation (segment S1) but also other segments, followed by a gentle, gradual decrease towards the end of each segment (Fig. 4a, c). Only for S3 does PE not show this pattern, while IF shows it for all segments. This pattern may reflect the magma propagation in the initial phase of each segment releasing more fracture energy to open the pathways, and less energy was needed later when the dike only continued to open until it extended into another segment (Sigmundsson et al., 2015; Ágústsdóttir et al., 2016, 2019). We checked the distribution of the earthquake magnitudes and observed that the magnitudes mostly became smaller temporally when the segment was ending. However, the RMS signal is too spiky to clearly show the same trend (Fig. 4d). An equivalent case is observed in the seismic cycle of tectonic earthquakes, where the Shannon entropy is found to gradually drop to its initial state after the main shock during the post-seismic states (De Santis et al., 2011; Posadas et al., 2023). Here, the main shock corresponds to the dike migration phase in a segment, and the post-seismic state corresponds to the dike thickening after its extension.

The PPE of earthquakes is found to be lower than the PPE of the ambient noise. Its temporal evolution during the earthquake migration exhibits stronger changes than PE. At the beginning of segments S1 to S4, PPE is low and then increases to the end of the segment. As most of the seismic moment is released and more earthquakes are generated at the beginning of each dike segment, PPE first drops and then increases towards the end of the segment when the number of earthquakes becomes fewer. During segment S3, PPE did not drop suddenly but decreased over 2 d until 20 August 2014 before increasing to the end of the segment. An anti-correlated trend is shown by the IF: while it increased from 18 to 20 August 2014, it decreased back to the end of segment S3. From 19 to 23 August 2014, the earthquake migration was reported to stop before changing its direction from southeast to northeast (Sigmundsson et al., 2015).

A single peak in PPE and a drop in IF are observed on 22 August 2014 at 07:00 to 13:00. These are associated with small earthquakes during these hours. When the S4 dike segment formed, the earthquakes reached the closest distance to the FLUR station, which is about 10 km (Fig. 4e). These earthquakes dominate the time series, causing PPE to reach the lowest point, while the RMS reaches the highest value (Fig. 4d).

After stopping for 81 h, the dike started to move again and generated segment S4 on 23 August 2014; it was accompanied by a pre-eruptive tremor (Eibl et al., 2017b). This tremor could also be associated with the formation of cauldron C1, which was visually observed on 27 August 2014 (Reynolds et al., 2017). However, this tremor was concealed by a high seismicity rate during the lateral movement of segment S4 (Fig. 1). Therefore, it is not seen in PE, PPE, and IF.

There was a lack of shallow seismicity prior to the eruption (Ágústsdóttir et al., 2019; Eibl et al., 2017b). Following the earthquakes moving horizontally at depths of 5 to 8 km (Ágústsdóttir et al., 2019; Woods et al., 2019), long-period (LP) events were detected for about 10 d, starting on 25 August 2014. These LP events had a dominant frequency of ∼1Hz, had clear P- and S-wave onsets, and occurred at ∼ 4 km in depth (Woods et al., 2018). Eibl et al. (2017b) suggested the possibility of a pre-eruptive tremor that is formed by repetitive microearthquakes at less than 3 km in depth followed by silent magma migration to the surface. However, by utilizing PE, PPE, and IF, we were not able to observe any changes that could be related to the pre-eruptive tremor before the eruption onsets on 29 and 31 August 2014. The seismic wave generated by earthquakes seems to be dominating the time series, masking other processes, especially during the last dike segment, S4, when the earthquakes reach the closest distance to the station and the changes in PE, PPE, and IF become less significant than in the earlier segments.

Eruption forecasting is easier when the pre-eruptive process generates a pattern of distinct seismic events that are chronologically changing in time and depth. In the case of Strokkur Geyser, the PE variation can characterize the four different phases in the geyser's eruptive cycle (Sudibyo et al., 2022), which are eruption, conduit refilling, gas accumulation in the bubble trap, and the collapse of the bubbles in the shallow conduit (Eibl et al., 2021). These different processes generate distinct signals with different complexities, thus resulting in distinct values of the corresponding PE. Furthermore, each phase takes place at separate locations and depths (Eibl et al., 2021). Therefore, Sudibyo et al. (2022) not only observed a high correlation between PE and the hypocentral distance between seismic event's source and the seismic station but also used PE to accurately predict the geyser's eruptions. Konstantinou et al. (2022) reported a consistently decreasing PE prior to and during three eruptions in Shinmoedake, a stratovolcano in Japan, which is associated with the dominant occurrence of the pre-eruptive and eruptive tremor. In Shinmoedake, as magma moves to a shallower depth and the higher frequency of the seismic events becomes attenuated, PE drops before the eruption starts. In contrast, the 2014–2015 Holuhraun eruption is preceded by 2 weeks of lateral dike propagation dominated by high-frequency events. Changes in the types of seismic events are minor during the pre-eruptive process, and the majority of the events do not move to shallower depth, causing less significant evolution in the seismic parameters towards the eruption's onset.

5.4 PE, PPE, and IF reflecting the dynamics of eruptive tremor

In contrast to the pre-eruptive tremor, the dynamic of the eruptive tremor is reflected well by the properties of PE, PPE, and IF. After the main eruption starts, the eruptive tremor dominates the 6 months of eruption, and we observed decreasing values of PE and IF, while PPE increases. Volcanic tremors have been reported to have a low PE due to their low dominant frequency and narrow spectral distribution (Konstantinou et al., 2022). The eruptive tremor in Holuhraun has most energy in a low and narrow frequency band ranging from 0.8 to 2.5 Hz (Eibl et al., 2017b). We investigated the seismic analytic wave of the eruptive tremor and found that its rotation is more complex compared to earthquakes (Fig. S4d). While the presence of noise could increase the complexity of phase angle rotation, the trend in PPE does not align with the trend in the ambient noise (Figs. S7 and S8). Therefore, it is more likely that the calculated PPE represents the characteristics of the eruptive tremor itself.

Eibl et al. (2017a) have identified multiple sources generating the eruptive tremor accompanying the Holuhraun eruption. These sources are associated with fissure locations and the height of the lava fountain, the growth of the lava flow field, and intrusions at depth. Hibert et al. (2015) found a linear correlation between the seismic energy of the tremor and the lava effusive rate in Piton de la Fournaise volcano on Réunion Island. Figure 5 shows the comparison of the magma effusion rate estimated by Coppola et al. (2017) with the temporal variations in PE, PPE, IF, and seismic root-median square (RMeS), where we fitted a horizontal dashed line to the early values of each parameter as a reference and observed the decreases in the values with time. Both PE and PPE show an alignment with the magma effusion rate (Fig. 5b and c). Starting from January 2015, PE and PPE start to decline faster, which indicates that the eruption is ending. A similar pattern was observed by Sudibyo et al. (2022), when studying the temporal variation in PE during 63 eruptions of Strokkur Geyser, Iceland. During eruptions with two to four water fountains in quick succession, PE stayed high and only dropped after the end of the last water fountain of one eruption.

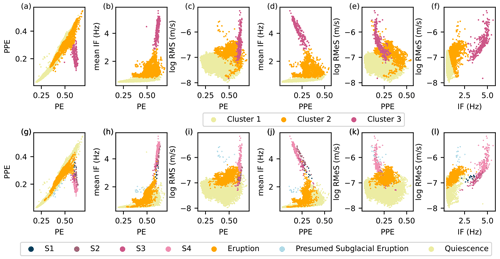
Figure 6 Clustering plots based on the k-means algorithm (a–f) and an expert interpretation (g–l) using PE, PPE, IF, and log(RMeS). Cluster 1 is associated with quiescence; cluster 2 is associated with the eruption and presumed subglacial eruption; and cluster 3 is associated with the dike segments S1, S2, S3, and S4.

On 3 September 2014, a strong tremor was recorded for about 21 h (Eibl et al., 2017b; Woods et al., 2018), which is assumed to have preceded a sub-glacial eruption deepening either the C2 (Eibl et al., 2017b) or C1 cauldron (Woods et al., 2018). We noticed the drop in PE and PPE on 3 September 2014. PE and PPE reach the minimum value at 12:00 for 6 h before they start increasing back to the previous level at 18:00. The analytic signal shows fewer entangled rotations (Fig. S4c) than the main eruption tremor, which is similar to earthquakes (Fig. S4b) and causes low PPE. The PE and IF are also low, suggesting that the energy of the tremor is concentrated in a low and narrow frequency band. This result supports Eibl et al. (2017b), who suggested that the tremor is comprised of swarms of microseismicity associated with the fracturing of the shallow crust above the dike.

Woods et al. (2018) observed that the tremor on 3 September has a similar spectral content as the LP swarms that were recorded from 25 August to 2 September 2014. They suggested that the LP swarms could represent magma moving above the dike, which culminates in a tremor, producing the sub-glacial eruption. As we cannot resolve the LP swarms during the mentioned period, we can neither confirm nor reject their interpretation.

PE, PPE, and IF then undergo a fluctuation from 4 to 7 September 2014 (Fig. 4b and c). This fluctuation could be associated with the opening of two fissures located to the south of the main eruption, resulting in a minor eruption from 5 to 7 September 2014. Thereafter, the PE, PPE, and IF started to be more stable throughout the eruption (Fig. 5a, b and c).

5.5 Cluster analysis

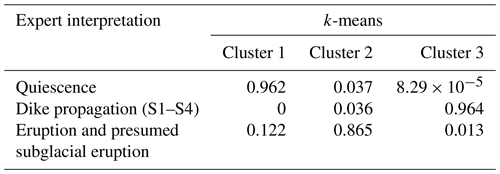
Analyzing the seismic parameters separately could produce a limitation when each parameter responds differently to the different stages of eruption. In this case, combining them could provide more information on the temporal changes in the volcano. Figure 6 compares the clusters generated by the k-means algorithm (panels a–f) and the expert interpretation (panels g–l) using the parameters of PE, PPE, IF, and log(RMeS). Visually they are highly similar, with cluster 1 corresponding to the quiescence, cluster 3 corresponding to the dike segments S1 to S4, and cluster 2 corresponding to the subaerial eruption and presumed subglacial eruption. The confusion matrix shows that 96.2 % of the data points during quiescence are classified into cluster 1, 96.4 % of the data points during dike propagation are classified into cluster 3, and 86.5 % of the data points in the eruption phase are classified into cluster 2 by the k-means algorithm (see Table 1). This score, 86.5 %, is the highest score in the eruption cluster in comparison to other clustering results using different combinations (see Tables S1 to S4).

Table 1 Confusion matrix between clusters formed by k-means and expert interpretation using PE, PPE, IF, and log(RMeS) in Fig. 6. It shows that 96.2 % of the data points during quiescence are classified into cluster 1, 96.4 % of the data points during the dike propagation are classified into cluster 3, and 86.5 % of the data points during the eruption and presumed subglacial eruption are classified into cluster 2. The sum of the values in each row is equal to 1.

6 Conclusions

In this study, we assessed the ability of PE, PPE, and IF estimated from continuous seismic recordings to characterize the changing state before, during, and after the 2014–2015 Holuhraun eruption in Iceland. We observed that temperature and wind strongly influence PE and PPE during the repose time, but their effects are minor during the dike migration and eruption. Intense volcano–tectonic earthquakes occurred during the dike propagation with high-frequency content, complex amplitude motion, and more regular motion of the instantaneous phase. After the main eruption started, the signal was dominated by a volcanic tremor with low-frequency content and more regular amplitude motion but with more complex motion of the instantaneous phase. The intense volcano–tectonic earthquakes before the eruption onset complicate the prediction of the eruption onset prior to its occurrence, which could be different when the tremor and/or low-frequency events are more dominant.

The changes in IF and PPE were stronger than PE prior to the eruption, but the variations in PE and PPE became more stable after the eruption started, and their decay indicated the end of the eruption. Limiting the analysis to only one or two parameters may not be sufficient, as they capture different parts of the eruptive process differently. One parameter can be more sensitive to a certain process than others, and parameter combinations may improve the monitoring of potential changes in a volcanic system. Using clustering analysis, we tested which parameter combination best separates different processes. We found that including log(RMeS) provides more accurate cluster separation than only using PE, PPE, and IF. We did not investigate how the clusters temporarily evolve with respect to different eruption stages or whether there is a sign when the cluster is about to change. Analyzing the temporal change in a multi-dimensional space requires different approaches and is reserved for future studies.