The European Fault-Source Model 2020 (EFSM20): geologic input data for the European Seismic Hazard Model 2020

Earthquake hazard analyses rely on seismogenic source models. These are designed in various fashions, such as point sources or area sources, but the most effective is the three-dimensional representation of geological faults. We here refer to such models as fault sources. This study presents the European Fault-Source Model 2020 (EFSM20), which was one of the primary input datasets of the recently released European Seismic Hazard Model 2020. The EFSM20 compilation was entirely based on reusable data from existing active fault regional compilations that were first blended and harmonized and then augmented by a set of derived parameters. These additional parameters were devised to enable users to formulate earthquake rate forecasts based on a seismic-moment balancing approach. EFSM20 considers two main categories of seismogenic faults: crustal faults and subduction systems, which include the subduction interface and intraslab faults. The compiled dataset covers an area from the Mid-Atlantic Ridge to the Caucasus and from northern Africa to Iceland. It includes 1248 crustal faults spanning a total length of ∼95 100 km and four subduction systems, namely the Gibraltar, Calabrian, Hellenic, and Cyprus arcs, for a total length of ∼2120 km. The model focuses on an area encompassing a buffer of 300 km around all European countries (except for Overseas Countries and Territories) and a maximum of 300 km depth for the subducting slabs. All the parameters required to develop a seismic source model for earthquake hazard analysis were determined for crustal faults and subduction systems. A statistical distribution of relevant seismotectonic parameters, such as faulting mechanisms, slip rates, moment rates, and prospective maximum magnitudes, is presented and discussed to address unsettled points in view of future updates and improvements. The dataset, identified by the DOI https://doi.org/10.13127/efsm20 (Basili et al., 2022), is distributed as machine-readable files using open standards (Open Geospatial Consortium).

1 Introduction

Seismogenic fault-source models are mathematical representations of the characteristics and behavior of earthquake faults. They are used to simulate how earthquakes might occur in any given region and to estimate the expected ground shaking intensity. Fault-source models can also be used to simulate earthquake-triggered tsunamis, ground-surface displacement, and various secondary effects (e.g., landslides, liquefactions). Considering that seismic sources in earthquake hazard studies are modeled in different fashions, such as point or area sources, we here refer to a fault source to designate the geological fault capable of being reactivated and generating earthquakes.

In this context, geological and paleo-seismological data provide a framework to estimate the average long-term recurrence time of possible earthquakes on known faults. These earthquakes often have recurrence intervals that are longer than instrumental and historic seismic catalogs, so geologic-fault information can effectively complement the recurrence statistics of earthquake catalogs where they lack more data. The combination of the spatial scale in fault mapping and the temporal scale of their recurrent behavior in generating earthquakes makes the geologic-fault data more important, relative to other datasets, in forecasting larger-magnitude earthquakes.

This work documents the European Fault-Source Model 2020, EFSM20 (Basili et al., 2022), a data product of the EU H2020 project SERA (Work Package 25, WP25, Joint Research Activity 3, JRA3), designed to fulfill the requirements related to active faulting of the 2020 update of the European Seismic Hazard Model, ESHM20 (Danciu et al., 2021, 2022), following the probabilistic framework established for the 2013 European Seismic Hazard Model, ESHM13 (Woessner et al., 2015). To this end, the model aimed to cover a target area for foreseen ground motion that encompasses a buffer of 300 km around all European countries except for Overseas Countries and Territories (OCTs). The 300 km value estimate comes from the distance at which the ground motion propagated from a given source becomes negligible at the target site, based on ESHM13 ground motion model selection and outcomes (Delavaud et al., 2012; Woessner et al., 2015). We extend this concept also to the depth direction for deep earthquakes. The model, however, extends beyond this area to gain insights from the good continuity of plate boundaries.

We defined two fault-source categories: crustal faults and subduction systems. A crustal fault is a fracture or a system of fractures that separates different blocks of the Earth's crust. This category includes faults in various tectonic contexts, including onshore and offshore active plate margins and interiors. A subduction system is a combination structures formed where one plate (the slab) moves under another (the upper plate) and sinks into the mantle beneath it. This process results in a convergent movement of the two involved plates, which is known to generate earthquake ruptures of different types (Satake and Tanioka, 1999). This category includes the detachment at the base of the accretionary wedge, the interface between the two plates at crustal depth, and the dipping slab at mantle depth. These three elements are all part of the lower plate. The possible splay faults, branching upward into the upper plate from the subduction interface, are included in the crustal faults category.

The EFSM20 compilation is entirely based on published reusable data. Details about these data and how they were used are given in Sects. 2 and 3. We then performed data curation and harmonization (i.e., treating the complementary compartments of the different datasets to have them working together) to provide the user with all the necessary elements to develop a seismic source model and, ultimately, build an earthquake rate forecast. Although EFSM20 was designed for developing earthquake hazard models, it can also assist post-earthquake analyses and tectonic or geodynamic modeling.

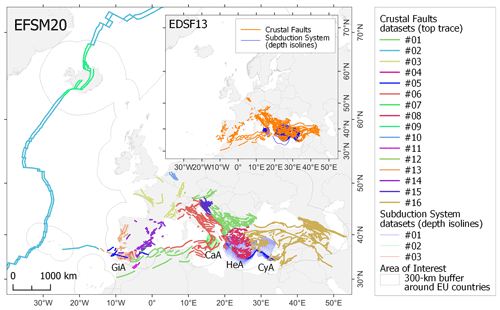
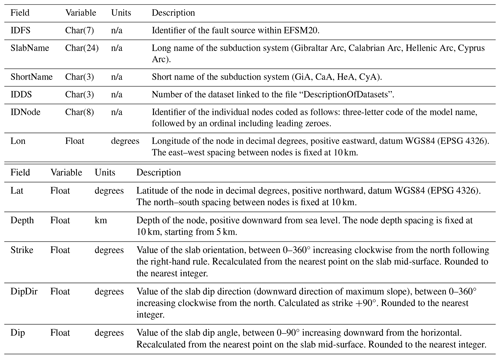
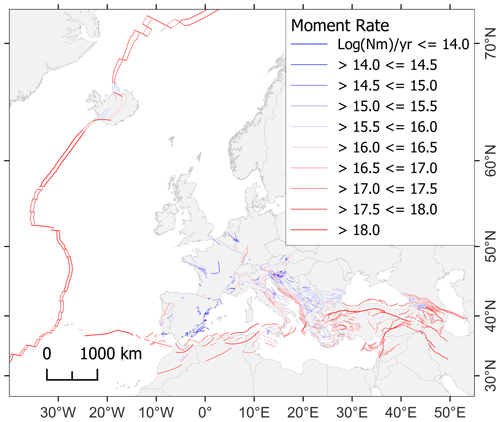
Figure 1 Map of collated fault datasets for developing the European Fault-Source Model 2020 (EFSM20). The colors in the legend identify the various datasets (see Sect. 3 for their descriptions). From west to east, the subduction systems are the Gibraltar Arc (GiA), Calabrian Arc (CaA), Hellenic Arc (HeA), and Cyprus Arc (CyA). The inset map shows the European Database of Seismogenic Faults 2013 (EDSF13) for comparison.

The EFSM20 dataset includes 1248 crustal faults spanning a total length of ∼95 100 km – with an individual end-to-end length range of ∼4–900 km – and four subduction systems, namely Gibraltar, Calabrian, Hellenic, and Cyprus arcs, spanning a total length of ∼2120 km – with an individual end-to-end length range of ∼220–1010 km (Fig. 1). The dataset distribution includes several layers providing different map feature implementations linked to relevant parameters. Such data layers are made available through the European Databases of Seismogenic Faults portal with a dedicated web page (https://seismofaults.eu/efsm20, last access: 14 November 2024) that directs the users to Open Geospatial Consortium (OGC; https://www.ogc.org/, last access: 14 November 2024) web services (Web Feature Service, WFS, and Web Map Service, WMS), with downloadable GIS files in various formats (GeoJSON, ESRI shapefile, MapInfo tables). The dataset files, web services, structure, and description of all fault-source attributes in tabular form are shown in Appendix A. EFSM20 is part of the European Plate Observing System (EPOS), Thematic Core Services (TCS) Seismology, European Facilities for Earthquake Hazard and Risk (EFEHR) portfolio (Haslinger et al., 2022) and is already accessible through the EPOS Integrated Core Services data portal (https://www.ics-c.epos-eu.org/, last access: 14 November 2024). The geographic distribution and comparison of the derived parameters most related to the seismogenic process, such as fault type, slip rate, moment rate, and maximum magnitude, are discussed in Sect. 4.

Although the continent scale of the collection prevented us from exploring each fault in great detail and several fault parameters are affected by significant approximations, EFSM20 covers the major plate boundaries around the European plates and their interiors. The machine-readable fault attributes allow users to develop earthquake rate forecasts straightforwardly, promoting future updates to address unsettled points and meta-analyses and curiosity-driven studies to enhance our understanding of the seismogenic processes.

2 Data and methods

The EFSM20 compilation was entirely based on reusable data. We started the initial collection from the pan-European compilation EDSF13 (Basili et al., 2013) and progressively replaced it with up-to-date regional datasets.

We considered primarily the compilations that covered significantly large regions with a consistent approach, relying on the work of the authors of each compilation regarding the accuracy and recency of the information. We resorted to using smaller-scale studies only in case of undefined situations, e.g., area of overlap between two regional datasets or cases where a significant update was available or where the fault information was not covered by the initial pan-European dataset but deemed necessary. Regardless of size and coverage, all considered datasets must comply with a series of requirements. Each crustal fault must have been declared active under one of the many existing definitions by the dataset authors or contributors. On the one hand, reviewing the definition of active fault was beyond the scope of this work. On the other hand, we recall that the definition of active faults may even differ in different tectonic settings. Subduction systems, instead, are included in the compilation regardless of the activity definition. The minimum set of basic fault parameters required for constructing a seismogenic source model refers to geometry (location: latitude, longitude, and depth; size: length and width; orientation: strike and dip) and behavior (rake and slip rate). These are indispensable elements for devising and applying a fault recurrence model to be expressed by a frequency–magnitude distribution (FMD). Not all fault compilations fully provide this characterization, and strategies were devised to fill in the missing information and harmonize it.

We assigned a unique identifier (ID) to each retained record in the collated dataset to avoid possible ambiguities in identifying the faults. The ID is a seven-character string, in which the first two positions are occupied by the letters “CF” for crustal faults and “SS” for subduction systems, followed by the standard ISO 3166 two-letter code, which identifies the country where most of the fault is located, followed by an alphanumeric three-letter code (e.g., CFCH0B5 identifies the crustal fault 0B5, which is in Switzerland). To track the provenance of each record, we assigned an identifier to the original dataset and stored the original fault identifier in that dataset. See Appendix A for a complete description of all fault parameters.

The next subsections summarize the main adopted datasets (Fig. 1; each record in EFSM20 reports its provenance to one of them) and describe the procedures to retrieve the initial geometry and relevant parameters, as well as the additional data used to harmonize the collation and estimate the derived parameters. Crustal faults and subduction systems are treated separately.

2.1 Crustal-fault datasets

Dataset no. 01. This is the original database EDSF13, compiled in the framework of the Seismic Hazard Harmonization in Europe (SHARE) project (Basili et al., 2013), which covered Europe and the Mediterranean region. This dataset was adopted as the starting point to build the new crustal-fault-source model. The largest regions that remained unmodified are the Balkans and northern Africa. According to individual studies, most regions were entirely replaced by new datasets or partly revisited. Elements added in regions that EDSF13 did not cover are in Iceland, France, and the northern mid-Atlantic plate boundary. The major regional updates are summarized below.

Dataset no. 02. This dataset covers the Mid-Atlantic Ridge and transforms. The initial geometry was derived from a global plate-boundary model (Bird, 2003), and the rest of the characterization was based on the oceanic crust age and spreading rate (Müller et al., 2008). For the transform faults, the slip rate was directly derived from the spreading rate, aided by more local data for the Gloria Fault (Fadil et al., 2006; Koulali et al., 2011). For the normal faults, the slip rate was obtained by combining the spreading rate with local information about fault spacing and heave (MacDonald and Luyendyk, 1977; Escartín et al., 1999).

Dataset no. 03. This dataset covers the French region and is derived from BDFA (Jomard et al., 2017). Due to the different strategies of fault mapping used in BDFA, we redrew the fault traces by interpolation and reassigned some parameters, particularly slip rates, based on recent regional works.

Dataset no. 04. This dataset includes a few faults in the Gulf of Corinth. The initial geometry of the faults is based on GreDaSS (Caputo and Pavlides, 2013), and the slip rates were updated based on recent works not included in the GreDaSS compilation (Bell et al., 2009; Fernández-Blanco et al., 2019).

Dataset no. 05. This dataset covers the offshore parts of the Gulf of Cádiz and the Alboran Sea. In this area, we updated EDSF13 based on several recent works, providing updated geometries and/or slip rates (Koulali et al., 2011; Martínez-Loriente et al., 2013, 2018; Neres et al., 2016; Perea et al., 2018; Gómez de la Peña et al., 2018).

Dataset no. 06. This dataset covers the Italian territory and some surrounding regions. It is mainly based on the most recent version of the DISS (Basili et al., 2008; DISS Working Group, 2021).

Dataset no. 07. This dataset includes a few faults in the eastern Betic region. Such faults represent modifications of QAFI (see Dataset no. 14) according to recent works with substantial updates of fault geometries and slip rates (Borque et al., 2019; Gómez-Novell et al., 2020a, b; Herrero-Barbero et al., 2020).

Dataset no. 08. This dataset covers the Aegean region. It is mainly based on the most recent version of GreDaSS (Caputo and Pavlides, 2013).

Dataset no. 09. In Iceland, we started from the same approach as the Mid-Atlantic Ridge and transform faults (see dataset no. 02) and added data and considerations based on local studies (Bergerat et al., 1990; Forslund and Gudmundsson, 1991; Rögnvaldsson et al., 1998; Garcia et al., 2002; LaFemina et al., 2005; Árnadóttir et al., 2008; Rust and Whitworth, 2019).

Dataset no. 10. This dataset deals with the Lower Rhine Graben. In this area, we started from EDSF13, already based on a local fault model (Vanneste et al., 2013), and updated the slip rate of several faults based on more recent data (Gold et al., 2017).

Dataset no. 11. This dataset covers the northwestern African region (Morocco, Algeria, and Tunisia). In this region, we mainly relied on EDSF13 with updates of a few faults in the Moroccan region based on the GEM Global Active Faults Database (Styron and Pagani, 2020) and various other works (Gomez et al., 1996; Akoglu et al., 2006; Rigby, 2008; van der Woerd et al., 2014; Pastor et al., 2015) for refining several fault parameters.

Dataset no. 12. The NOAFAULTS database (Ganas, 2022) was used to integrate the dataset in the Aegean region for faults not already included in GreDaSS. This dataset was built gradually since 2013 (Ganas et al., 2013) following a fault trace (polyline) approach with significant upgrades whenever compiled fault maps were available, including faults activated during seismic sequences in the Aegean (Ganas et al., 2018).

Dataset no. 13. This dataset covering Portugal and offshore regions was updated based on recent works in the Lower Tagus Valley Fault Zone (LTVFZ) (Canora et al., 2015) and Algarve (Sanz de Galdeano et al., 2020).

Dataset no. 14. This dataset covers most of the Iberian region, including the Pyrenees. In this region, we relied on the Quaternary Active Faults Database of Iberia (QAFI; García-Mayordomo et al., 2012, 2017; IGME, 2015). Due to the different strategies of fault mapping used in QAFI, we redrew the fault traces by interpolation.

Dataset no. 15. This dataset deals with Slovenia and its surroundings. In this area, we relied on the recently published Database of Active Faults in Slovenia (Atanackov et al., 2021) and the seismogenic fault-source model (Atanackov et al., 2022) prepared for the 2021 seismic hazard model for Slovenia (Šket Motnikar et al., 2022). This dataset provides the seismic component of the slip rates.

Dataset no. 16. This dataset covers Anatolia and parts of the Middle East. In this region, we relied on recent data from the Earthquake Model of the Middle East (EMME) project and data from the national update of the Turkish hazard model (Danciu et al., 2018; Demircioğlu et al., 2018; Emre et al., 2018).

2.2 Procedures for crustal faults

The location and geometry of the mapped feature must be available through a set of coordinate pairs in a recognizable geographic coordinate system. The depth extent of the fault plane must have also been provided or derivable. The strike or dip direction, or any alternative strategy to provide data complying with the right-hand rule (e.g., ordered sequence of nodes forming the mapped feature), and the dip angle were also indispensable to complete the geometric reconstruction of the fault plane in three dimensions. Regarding the fault behavior, the required parameters were the rake angle (or at least the prevailing sense of movement) and the slip rate.

The strategy outlined above also adopted a set of prioritization criteria. The highest priority for collating the different datasets was given to the pan-European dataset because it guaranteed maximum spatial coverage with minimum effort. Then, in replacing or extending this initial dataset, we incorporated new data, with progressively lower priority given to data that were publicly available within the time frame of the project, followed by voluntarily contributed datasets from the community and lastly by solicited local contributions where necessary. In handling the possible multiple contributions over the same areas, we prioritized newer data, national data when the dataset covered a specific country, level of accuracy and justification for the requirements listed above, and coherence with surrounding datasets.

Thus, these criteria were applied to collate and harmonize the datasets, fill gaps, resolve overlaps, and remove inconsistencies. Once the collated dataset was obtained, the performed data processing aimed to extract relevant information from the different datasets and convert it into the EFSM20 format, identify the possible duplicates, and assign an ID to each retained record.

The mapped features were resampled to obtain an evenly spaced single-trace polyline with an average distance between consecutive nodes of ∼5 km (Fig. 2). Based on common fault scaling relationships (Wells and Coppersmith, 1994; Leonard, 2010, 2014; Allen and Hayes, 2017; Thingbaijam et al., 2017), this length enables us to capture with sufficient accuracy the smallest earthquake ruptures commonly modeled in most hazard analyses using fault sources. The even spacing also ensures that the fault-source total length is measured consistently, regardless of the subjective mapping strategy adopted in the original datasets. The fault trace nodes were sorted based on the average strike (or dip direction) to comply with the right-hand rule (Aki and Richards, 1980). The strike values were then recalculated to reflect the variability of the re-mapped fault.

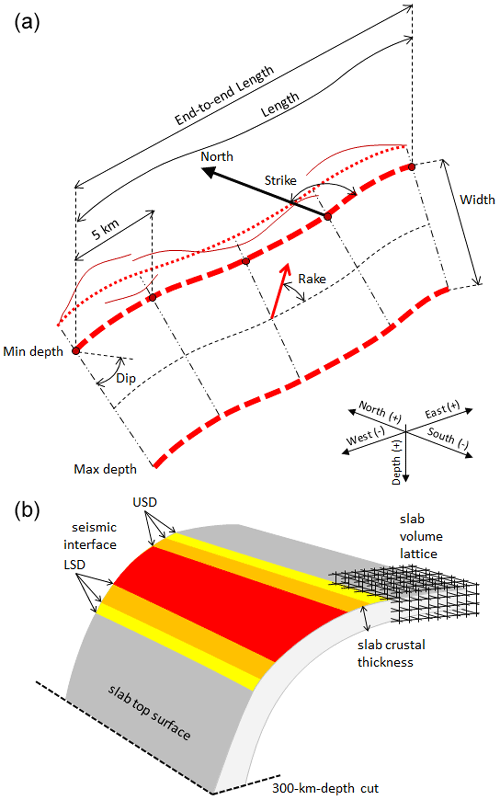
Figure 2 Illustration showing the main geometric elements of crustal faults (a) and subduction systems (b). See the main text for a complete list of parameters and their descriptions.

With this revised geometry, we determined the complexity index c, which is calculated as

$$\begin{array}{}\text{(1)}& c=(\mathrm{1}-L^{\prime }/L)\cos \mathit{\delta },\end{array}$$

where L^′ is the end-to-end fault length, L is the fault trace length, and δ is the reported dip angle (Fig. 2). This complexity index tends to be close to zero when the fault tends to be nearly straight or vertical. It can contribute to better evaluating whether to adopt the simple- or complex-fault models when using the OpenQuake software (Pagani et al., 2014) for modeling seismic hazards. The crustal-fault complexity index returned 174 faults with a value equal to zero. This value is due to a dip equal to 90° for 62 cases and a rectilinear trace for the remaining 112. Only 6 faults have a complexity index larger than 0.1.

We verified the depth datum (local ground surface or mean geoid/spheroid), checked the possible intersections of the reported upper depth with the topo-bathymetry using the ETOPO1 Global Relief Model (Amante and Eakins, 2009; NOAA National Geophysical Data Center, 2009), and checked the reported lower depth with the base of the crust using the European Moho (short for Mohorovičić discontinuity; Grad et al., 2009). We also searched for possible down-dip intersections of different fault planes (e.g., two faults cross-cutting each other at depth). Occasionally, when the faults determined an unrealistic structural configuration, we removed or modified parts of the interested faults.

A one-letter or two-letter code indicates the fault sense of movement: N for normal (−135° ≤ rake ≤ −45°), R for reverse faulting (45° ≤ rake ≤ 135°), RL for right-lateral transcurrent (135° < rake < −135°), and LL for left-lateral transcurrent (45° > rake > −45°). These four classes were also reduced to two classes, using the two-letter code DS for dip-slip faulting (normal and reverse) and SS for strike-slip faulting (right lateral and left lateral) to ease the application of the fault scaling relations.

The tectonic characterization of crustal faults includes defining three types of tectonic settings – interplate region, stable continental region, and Mid-Atlantic Ridge – identified by the three-letter codes INT, SCR, and MAR, respectively. For the geographic distribution of the SCR, we started from the mapping made by Johnston (1994) and refined the INT and MAR based on the plate tectonic model by Kagan et al. (2010) and local geology where needed.

Since some of the original datasets only reported a single value of the dip angle for several faults, we extrapolated the dip angle variability from all the other records in the fault collection. We thus calculated the dip angle variation ratio of reported values and then applied it to extrapolate the dip uncertainty range around single-value dip angles, assuming the reported single value as the average dip. The dip variation ratio (Rδ) for each fault is calculated as

$$\begin{array}{}\text{(2)}& R\mathit{\delta }={\displaystyle \frac{{\mathit{\delta }}_{\max }-{\mathit{\delta }}_{\min }}{\mathrm{2}}}/{\mathit{\delta }}_{\mathrm{avg}},\end{array}$$

where δ is the dip angle value of all faults with ${\mathit{\delta }}_{\max }-{\mathit{\delta }}_{\min }>\mathrm{0}$. We performed this calculation separately for dip-slip and strike-slip faults. The dip harmonization procedure used 660 dip-slip faults to determine an average dip variation ratio of 0.21 and 236 strike-slip faults to determine an average dip variation ratio of 0.12. These two values were then applied to incorporate the range of dip variability in the remaining 195 dip-slip faults and 157 strike-slip faults.

Once the minimum and maximum depths and dip angles are determined, the fault width can be calculated using simple trigonometry.

Also, in the case of the slip rate, several records of the original datasets only reported a single value, and thus we adopted the same approach. The slip-rate variation ratio ($R\dot{D}$) for each fault is calculated as

$$\begin{array}{}\text{(3)}& R\dot{D}={\displaystyle \frac{{\dot{D}}_{\max }-{\dot{D}}_{\min }}{\mathrm{2}}}/{\dot{D}}_{\mathrm{avg}},\end{array}$$

where $\dot{D}$ is the slip-rate value of all faults with ${\dot{D}}_{\max }-{\dot{D}}_{\min }>\mathrm{0}$ and ${\dot{D}}_{\min }>\mathrm{1}\times {\mathrm{10}}^{-\mathrm{4}}$ mm yr⁻¹ (the latter assumed as a lower threshold for considering the fault activity. We performed this calculation separately for the four different combinations of slip type (DS and SS) and tectonic setting (INT and SCR). Then we calculated the weighted average based on the number of faults in the four groups. The slip-rate harmonization procedure used 970 faults out of the 1109 INT and SCR faults to determine a weighted-average slip-rate variation ratio of 0.51 that was then applied to the remaining 139 faults, including the Gloria Fault (dataset no. 02). The 138 MAR faults were excluded from the slip-rate harmonization because of their peculiar tectonic setting, which, differently from the rest of crustal faults, involves exclusively oceanic crust. The weighted-average slip-rate variation ratio for these faults is 0.46.

The maximum earthquake magnitude of a crustal fault is estimated as the magnitude value, in the moment magnitude scale, that corresponds to the largest possible rupture that the fault can host based on its dimensions and the magnitude scaling relations by Leonard (2010, 2014), which also incorporate the rupture aspect ratio. In the adopted scaling relations, the moment magnitude (M_w) is determined by an equation in the form of

$$\begin{array}{}\text{(4)}& M_{\mathrm{w}}=a+b\log \left(S\right),\end{array}$$

where S is the size of any of the rupture dimensions – end-to-end length, width, area, or displacement – and the parameters a and b take different values depending on the S type, the sense of slip (DS and SS), and the seismotectonic context (INT or MAR, and SCR). Estimating the maximum earthquake magnitude of fault sources takes three steps. In the first step, we retrieve the fault width (W) and preliminarily assume that this value can be the maximum rupture width. Bringing in the rupture aspect ratio, we obtain the rupture length (L) required by a rupture of the retrieved width using the scaling relations (Leonard, 2010, 2014). Then we calculate the maximum rupture area (A) based on the obtained length and width. These calculations are repeated for the minimum, average, and maximum fault dimensions and retain three magnitude values corresponding to the scaling expected value, plus and minus 1 standard deviation. In the second step, we calculate the distribution of magnitude deviations ($\mathrm{\Delta }{M}_{\mathrm{w}}^{-}=\mathrm{avg}{M}_{\mathrm{w}}-\min M_{\mathrm{w}}$) and ($\mathrm{\Delta }{M}_{\mathrm{w}}^{+}=\max M_{\mathrm{w}}-\mathrm{avg}{M}_{\mathrm{w}}$) from the average for all faults. A preliminary inspection of these deviations showed that the ΔM_w distributions were strongly skewed; therefore, we considered values above the 95th percentile (corresponding to $\mathrm{\Delta }M\mathrm{w}>\left|\mathrm{0.5}\right|$) to be outliers and removed them. In the third step, we obtained the updated distributions of percentile ranks and extracted the 2nd and 5th percentiles of the negative deviations and the 95th and 98th percentiles of the positive deviations and applied them to the average magnitude already calculated.

Finally, the seismic-moment rate (${\dot{M}}_{\mathrm{s}}$) can be calculated based on the following classic formulation:

$$\begin{array}{}\text{(5)}& {\dot{M}}_{\mathrm{s}}=\dot{\mathit{\chi }}{M}_{\mathrm{g}}=\mathit{\chi }\mathit{\mu }LW\dot{D},\end{array}$$

where χ is the seismic efficiency, or seismic coupling (Kagan and Jackson, 2013); ${\dot{M}}_{\mathrm{g}}$ is the geologic moment rate; μ is the rigidity; L and W are the fault length and width, respectively; and $\dot{D}$ is the long-term slip rate. The applied rigidity is the global crustal average of 33 GPa (Dziewonski and Anderson, 1981), which is also the rigidity used for deriving the magnitude scaling relations (Leonard, 2010, 2014). We use the term seismic efficiency to indicate a coefficient between 0 and 1 that quantifies how much of the total moment rate is to be converted into a seismic-moment rate and ultimately into an earthquake rate forecast. This coefficient is often called seismic coupling, but we avoid using it because it also has various meanings (Wang and Dixon, 2004). The information on slip-rate values was adopted in bulk from large datasets of regional compilations, and it is therefore obtained using very heterogeneous estimation approaches. In some datasets, slip-rate values correspond to the total (seismic and aseismic) slip, whereas fault slip rates of other datasets correspond to only their seismic part. Therefore, the seismic efficiency was not assigned to individual faults in this dataset. This implicitly means that for the moment rate calculations, the seismic efficiency is as if it was equal to 1, and it is thus left to the users to choose a value to apply in their applications.

2.3 Subduction system datasets

Dataset no. 01. This is the original database EDSF13, compiled in the framework of the SHARE project (Basili et al., 2013), which covered the subduction systems in the eastern Mediterranean region. This dataset was adopted as the starting point to build the new subduction system models for the Hellenic and Cyprus arcs. The geometry of both slabs was recently revisited in the framework of a tsunami hazard project (Basili et al., 2021). These datasets have also been re-examined in light of the SLAB 2 model (Hayes et al., 2018) and several other slab geometry reconstructions (Ganas and Parsons, 2009; Halpaap et al., 2018, 2019; Sachpazi et al., 2016).

Dataset no. 02. This dataset corresponds to the most recent version of the DISS (DISS Working Group, 2021), which includes an updated reconstruction of the Calabrian Arc slab geometry based on a rich dataset of seismic reflection profiles for the shallower part (<20 km depth) and the seismicity distribution for the deeper part (Maesano et al., 2017).

Dataset no. 03. This dataset is an original elaboration of the Gibraltar Arc based on published works. The geometry of the slab was reconstructed using different datasets at different depths. For the shallowest depths, we used data from bedrock markers based on interpreting multichannel seismic reflection profiles and wide-angle seismic surveys (Gutscher et al., 2009), assuming that the top of the slab coincides with the top of the basement. For the intermediate depths (12–40 km), we used a model of the Moho obtained from a set of diverse datasets using a probabilistic surface reconstruction algorithm (Arroucau et al., 2021) and considering typical values for the old Tethys oceanic crust in the range of 7–9 km (Sallarès et al., 2011). Then, we obtained the slab position between 40–70 km depth by interpolating seismicity clusters from the ISC earthquake catalog (ISC, 2019). Within the 140–200 km depth range, the slab was assumed to be vertical based on a tomographic model (Civiero et al., 2018), which shows a nearly vertical high-velocity P-wave anomaly down to 600 km deep.

2.4 Procedures for subduction systems

Subduction systems form at convergent plate boundaries where one plate, the slab, sinks below the other. In these complex systems, different types of earthquake sources co-exist (Satake and Tanioka, 1999).

In this compilation, we assume that the crustal-fault sources deal with the earthquakes occurring in the upper plate of a subduction system. We thus designed the subduction system model to address both the subduction interface and the intraslab seismicity (Fig. 2). To this end, we first focused on reconstructing the three-dimensional geometry of the lower-plate top surface and its crustal thickness. Then, we added a set of basic parameters required for addressing the tectonic behavior, such as the upper and lower depths of the seismic interface and the net convergence direction and rate.

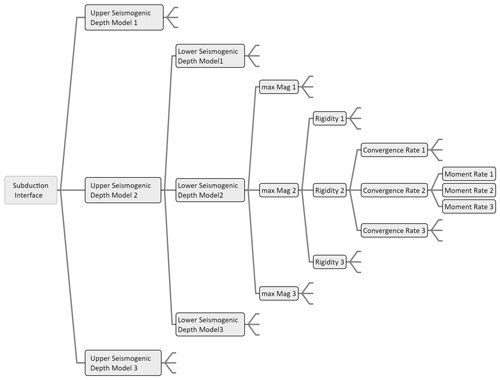
Figure 3 Logic tree to handle the parameter uncertainty in the different realizations of the subduction interfaces. This scheme implies nine geometric realizations with different areas spanning different depth ranges, implying 27 alternatives of maximum magnitude and rigidity. Considering the three alternative convergence rates yields 81 moment rate alternatives. The logic-tree outcomes provide 243 moment rate and maximum-magnitude combinations for exploring the earthquake rate forecasts based on seismic-moment-balanced recurrence models. (Figure prepared with XMind software.)

This type of reconstruction is typically performed using data from geology, exploration geophysics, seismicity distribution, and seismic tomography. The mapped feature must be available through a set of coordinate triplets, typically latitude, longitude, and depth, in a recognizable geographic coordinate system (e.g., scattered points, lattice, isolines, triangular meshes). The adopted 3D geometries were resampled at regular spacing and smoothed to ensure the same spatial resolution in the different models. Evenly spaced isolines were then used to represent the slab top surface. The average distance between consecutive nodes of each isoline was set at 5 km. The isoline depth interval was set at 1 km above 40 km depth and 10 km below 40 km. The deepest slab isoline was fixed at 300 km depth. The slab geometry is completed by assessing the crustal thickness of the lower plate measured in the outermost part of the subduction zone, near the tip of the accretionary wedge, by taking the base of the crust as a reference from the European Moho (Grad et al., 2009) model for consistency with that used for the crustal faults. For the sake of simplicity, the crustal thickness so measured is assumed to be constant in the rest of the subducted slab to derive the lower-plate bottom surface. The volume between the lower-plate top and bottom surfaces is then resampled by a lattice of evenly spaced nodes at a 10 km distance in all directions. The uppermost depth of the lattice was fixed at 5 km to ensure a consistent sampling of the shallower and gentler part of the slab.

The subduction interface parameterization includes the treatment of uncertainties based on the logic tree schema shown in Fig. 3, including three alternative estimates of each parameter.

To estimate the upper depth of the seismic interface, we considered data about the location of the 100–150 °C isotherm, the position of the contact between the lower plate and the overlaying softer sediments, the position of splay-fault branching, and the seismicity cutoff depth, whereas to estimate the lower depth of the seismic interface, we considered the location of the intersection of the lower plate with the Moho of the upper plate, the location of the 350–450 °C isotherm, and the seismicity cutoff (Di Stefano et al., 1999; Gutscher et al., 2006; Thiebot and Gutscher, 2006; Grad et al., 2009; Syracuse et al., 2010; Heuret et al., 2011; Davies, 2013). When multiple estimates from different data types were available, we assigned a higher weight to the Moho intersection and a lower weight to thermal and other models. We then obtained a weighted average of the minimum, intermediate, and maximum values retrieved from various literature sources.

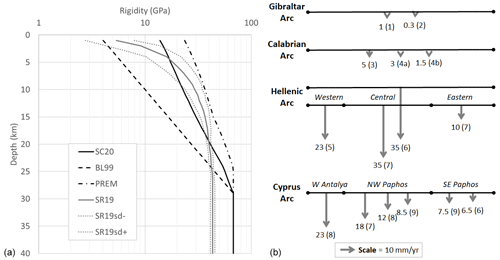
Figure 4 (a) Depth-dependent rigidity in subduction zones from various authors. SC20, BL99, PREM, and SR19 (Dziewonski and Anderson, 1981; Scala et al., 2020; Bilek and Lay, 1999; Sallarès and Ranero, 2019). (b) Synoptic view of the velocity vectors in the four subduction systems. Arrow sizes are scaled according to the reported velocity (all in mm yr⁻¹). Number in parentheses represents different works: (1) Stich et al. (2006); (2) Palano et al. (2015); (3) Devoti et al. (2008); (4a, b) Carafa et al. (2018); (5) Hollenstein et al. (2008); (6) Nocquet (2012); (7) Reilinger et al. (2006); (8) Howell et al. (2017); (9) Wdowinski et al. (2006). For the Calabrian Arc, the reported velocities from Carafa et al. (2018) refer to the case of a creeping subduction (4a) or temporarily locked subduction (4b), respectively.

The maximum earthquake magnitude of the seismic interface is estimated as the magnitude value, in the moment magnitude scale, that corresponds to the largest possible rupture that the seismic interface can host based on its area and magnitude scaling relations (Allen and Hayes, 2017).

The rigidity (shear modulus) depth dependence from different datasets (Dziewonski and Anderson, 1981; Scala et al., 2020; Bilek and Lay, 1999; Sallarès and Ranero, 2019) is reported in Fig. 4 (left), showing the rigidity variation within the common depth interval of the subduction interface of the four subduction systems.

The convergence direction and rate were estimated by geodetic measurements (velocity vectors) and/or by modeling the relative motion of the upper and lower plates across the subduction interface, as available in the literature (Carafa et al., 2018; Devoti et al., 2008; Hollenstein et al., 2008; Howell et al., 2017; Nocquet, 2012; Palano et al., 2015; Reilinger et al., 2006; Stich et al., 2006; Wdowinski et al., 2006) across the subduction systems (Fig. 4, right). The values from different sources were weight-averaged based on the length of the subduction interface sector over which the values were measured or estimated. The goal was to agnostically capture the plate convergence order of magnitude and its possible variability range, rather than finding the best estimates. Assuming that the subduction interface cannot be faster than the plate motion, these values were used as simple indicators without any further processing, and the modeled convergence was not differentiated based on the modeling approach (e.g., block modeling vs. kinematic finite-element modeling).

Similarly to crustal faults, the seismic-moment rate is estimated using the classic formulation reported in Eq. (5). However, in the subduction case, $\dot{D}$ is the long-term convergence rate, and the rigidity (m) varies with depth within the upper and lower depth limits of the subduction interface. The seismic efficiency was not assigned in this dataset; thus, the distributed dataset reports the total moment rate. This implicitly means that for the moment rate calculations, the seismic efficiency is as if it was equal to 1, and it is thus left to the users to choose a value to apply in their applications.

3 Results

3.1 EFSM20 data compilation

The EFSM20 final compilation covers an area spanning from the Mid-Atlantic Ridge to the Caucasus and from northern Africa to Iceland, counting 1248 crustal faults – for a total length of ∼95 100 km. Thanks to the continuous work on active faults in many regions and the continual update of regional databases, we were able to obtain a much richer fault-source model with respect to EDSF13, which counted 1128 crustal faults – for a total length of ∼63 775 km. Of the cumulative EFSM20 crustal-fault length, 55 401 km is onshore. Of the 39 699 km offshore, 22 846 km is in the Atlantic Ocean and 16 853 km in the Mediterranean Sea, the Black Sea, and the Caspian Sea. EFSM20 also includes four subduction systems, for a total length of the subduction interface of ∼2120 km. Three subduction systems in the eastern Mediterranean Sea were already present in the EDSF13 starting dataset, and a new one was added in the Strait of Gibraltar. The classification per tectonic setting and slip type is summarized in Table 1.

Table 1 EFSM20 fault-source summary.

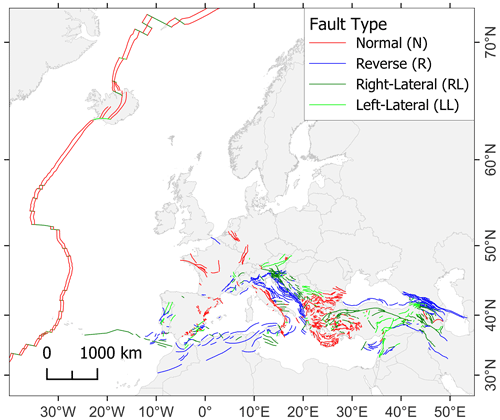
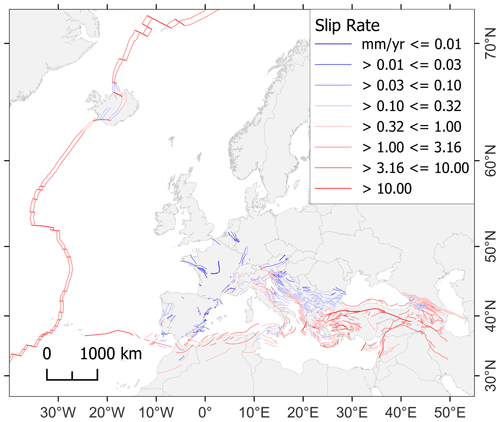
Figure 5 shows the crustal faults' geographic distribution and frequency of relevant behavior parameters (faulting type, slip rate, moment rate, and maximum magnitude). Slip rates and moment rate maps provide an overview of the location of the most-active faults, generally aligned with the major plate boundaries. Conversely, moving away from the plate boundary toward the plate interiors, one finds progressively less active faults. The average maximum-magnitude distribution (Fig. 5, lower-left panel) is somehow left-skewed, indicating that the crustal faults hosting the largest magnitude potential are very rare. Although most of the highest maximum-magnitude values are found on faults aligned with plate boundaries, several large values are also found in the plate interiors. This circumstance occurs because the adopted method reflects the size of the fault and not any other property.

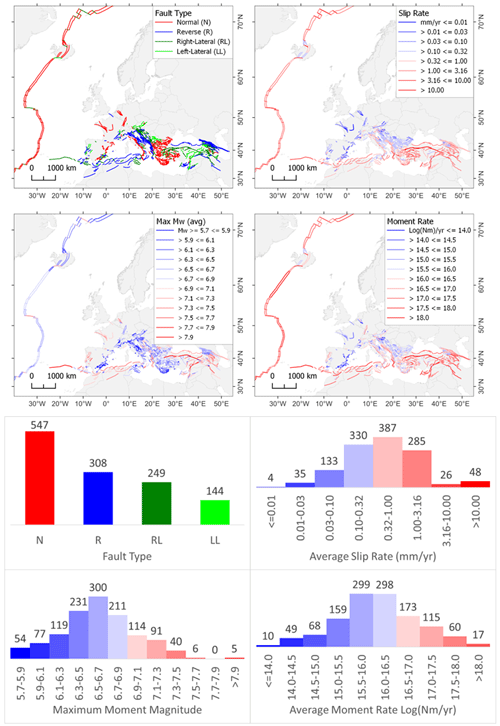
Figure 5 Maps (upper panels) and histograms (lower panels) of the EFSM20 crustal faults color-coded according to faulting type (upper left), average slip rate (upper right), maximum moment magnitude (lower left), and average moment rate (lower right). Color classes are the same as those distributed by OGC WMS web services. (See Appendix B for a large version of these maps.)

Figure 6 shows the 3D geometric reconstruction of the four slabs. Overall, the seismic interface is confined at depths between 6 and 39 km. The 3D geometry and the upper and lower depths of the seismic interface were the main constraints for determining the size of the largest rupture and its associated moment magnitude based on the scaling relations. The obtained maximum-magnitude values vary from a minimum of ∼7.8 in the Cyprus Arc to a maximum of ∼9.2 in the Hellenic Arc.

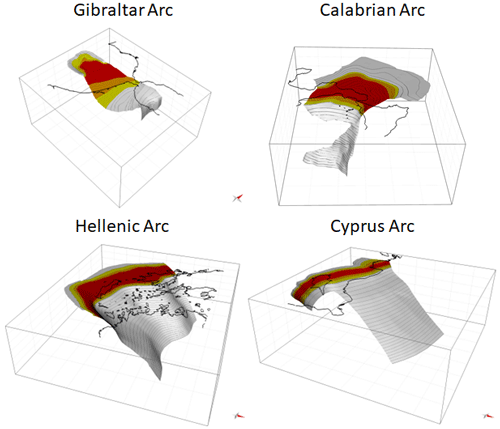
Figure 6 Oblique views of the three-dimensional geometry of the four slab models. The vertical extent of all boxes is 300 km. The colored part of the slab top surface represents the extent of the seismic interface, including the uncertainty of the upper and lower seismogenic depths represented by color bands as indicated in Fig. 2.

The uncertainties of the area and the scaling relations provide 27 combinations per subduction interface, yielding an overall variability between 0.65–0.85 magnitude units. Regarding convergence rates, we recall that although some reported values concern different sectors of the subduction interface, EFSM20 reports a single value and associated uncertainty for the entire arc. The obtained average values vary from a minimum of ∼1 mm yr⁻¹ in the Gibraltar Arc to a maximum of ∼24 mm yr⁻¹ in the Hellenic Arc. Combining the variability associated with the calculation (rigidity, area, and convergence rate) leads to 81 alternatives for each subduction interface. The resulting moment rates vary from a minimum of $\mathrm{4.4}\times {\mathrm{10}}^{+\mathrm{17}}$ N m yr⁻¹ in the Gibraltar Arc to a maximum of $\mathrm{1.8}\times {\mathrm{10}}^{+\mathrm{20}}$ N m yr⁻¹ in the Hellenic Arc. Each subduction system's largest moment rate value is 3–5 times larger than its smallest value. Figure 7 summarizes the moment rate and maximum magnitudes for crustal faults, grouped in various classes, and subduction interfaces showing the overall variability of these key parameters for the entire dataset.

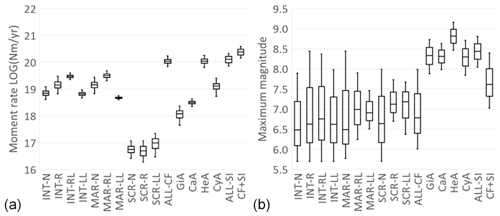
Figure 7 Box-and-whisker charts of the moment rate (a) and maximum magnitudes (b) for crustal faults, grouped in various classes, and subduction interfaces. Boxes indicate the variability between the median and the upper and lower quartiles; whiskers indicate the variability outside the quartiles. Legend: INT, interplate; MAR, Mid-Atlantic Ridge; SCR, stable continental region; N, normal; R, reverse; RL, right lateral; LL, left lateral; CF, crustal faults; GiA, Gibraltar Arc; CaA, Calabrian Arc; HeA, Hellenic Arc; CyA, Cyprus Arc (CyA); SI, subduction interfaces.

3.2 EFSM20 data product sharing portfolio

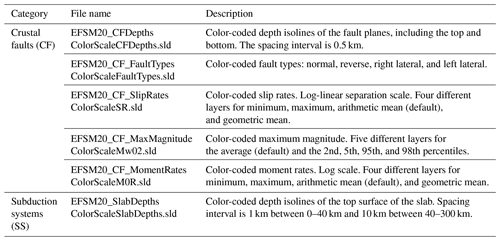
The outcomes of collation, harmonization, and derived-parameter characterization of all fault sources form a portfolio of datasets publicly shared for download (GeoJSON files, ESRI shapefiles, MapInfo tables) and via web services (WFS and WMS) adopting the OGC standards (Tables A1 and A2).

Crustal-fault sources also include the geometric extrusion of the fault plane within the minimum and maximum depths in the direction normal to the fault trace. Key elements of the fault plane are the vertical projection onto the ground surface of the top and bottom traces, the midline trace, the polygon enclosing the fault plane, and depth isolines. These geometric features are provided in different files, including all the key parameters illustrated in the previous section as tabulated attributes. The depth isolines have a 0.5 km spacing interval and include the nominal depth as an attribute.

The subduction systems include the geometric representation of the slab top surface by depth isolines and the slab by a cubic lattice. The depth isolines are at 1 km spacing between 0–40 km depth and 10 km spacing between 40–300 km depth. The side of the cubic lattice is 10 km, and each lattice node also provides the slab strike, dip direction, and dip. The subduction systems, in addition to the geometry of the top surface of the slabs, include datasets for the subduction interface parameters, the discretization, and the various realizations considered using the logic tree shown in Fig. 3.

Table A1 summarizes the content of these datasets, including a link to the attribute definitions of each file (Tables A3–A9).

Table A2 summarizes the data made available only via OGC WMS. These are styled map layers ready to use to display color-coded relevant parameters of the fault sources. The adopted styles are provided to the users in the Styled Layer Descriptor (SLD) format. These style files can be re-applied to the downloaded files or to the WFS layers to recreate the styled maps.

The main access point to this dataset is the European Databases of Seismogenic Faults portal (https://seismofaults.eu/efsm20, last access: 14 November 2024). Other access points for the dataset are the EFEHR portal (http://www.efehr.org/start/, last access: 14 November 2024) and the EPOS ICS-C data portal (Bailo et al., 2023) (https://www.ics-c.epos-eu.org/, last access: 14 November 2024).

4 Discussion

4.1 Lessons learned from the compilation and harmonization

The compilation of EFSM20 represents a substantial update and advancement of EDSF13. EFSM20 improved along the boundary around the European plate and within the plate interiors, focusing on the region within a 300 km wide buffer around European countries. Within this buffer, the compilation was simplified in Iceland and certainly lacking in the Azores, mainly due to the complex volcano-tectonic processes and limited knowledge of active structures. Also lacking is the region of the Hellenic Arc and Cyprus Arc accretionary wedge, where seismic sources, such as splay thrust faults and back thrusts, are known to exist, but their systematic mapping would require a dedicated effort due to the large extent of the region, its offshore location, and complex deformation that characterize accretionary wedges in general, as well as a very broad and fast-growing one in this case (>300 km at 10 mm yr⁻¹) due to the long duration (>35 Myr) of the subduction process (Kastens, 1991).

Concerning crustal faults, we identified several regional datasets that vary in date of the latest release, geographical extent, level of fault characterization, and data formats. In addition to those listed in the final compilation, several other datasets were considered, such as those covering Romania and the northern Black Sea (Diaconescu et al., 2019a, b, 2021), Iceland (Bayat et al., 2022), or the Caucasus (Onur et al., 2019, 2020). Although these datasets represented a significant advancement relative to EDSF13, they could not be used because we could not work out the compliance with the requirements above recalled within the project time frame.

The fault information in certain areas has already improved due to recent work not included in this release, such as the northern Adriatic region (Panara et al., 2021), which included a better-constrained version of the fault that ruptured in the M_w 5.5 earthquake (Maesano et al., 2023) on 9 November 2022 in the northern Adriatic Sea. The depth extent of the Hellenic Arc subduction interface and its relation with the maximum depth of the crustal faults in the Aegean region could be improved using rheological models (Maggini and Caputo, 2020, 2021). Likewise, newer geodetic data are now available to help refine the convergence rate across the Hellenic Arc (Briole et al., 2021). Other improvements or corrections can also be expected from post-earthquake surveys and analyses of significant recent seismic events such as, among others, the Petrinja (Croatia) M_w 6.4 earthquake on 29 December 2020, the Marrakesh–Safi (Morocco) M_w 6.8 earthquake on 8 September 2023, or the M_w 7.8 earthquake the on 6 February 2023 that struck the Türkiye–Syria border region. Also, some known errors are present, such as the case of the Averroes fault in the Alboran Sea (IDFS: ESCF03E; IDDS: no. 4). This fault was introduced as reported in an earlier version of QAFI and escaped a recent update that, although confirming the fault trace, revised the dip, dip direction, and kinematics (Perea et al., 2018). These and possibly other cases should be taken into consideration for future updates.

The total moment rate in EFSM20 of crustal faults and subduction interfaces combined is in the order of $\mathrm{2.4}\times {\mathrm{10}}^{+\mathrm{20}}$ N m yr⁻¹ (Fig. 7). The crustal faults take up to about 46 % and the subduction interfaces 54 % of this amount. Among the former, the moment rate attributable to the SCR is 0.2 %, and the rest is almost equally partitioned between the MAR and the rest of the INT. Among the latter, instead, more than 85 % of the total subduction interface moment rate is taken up by the Hellenic Arc. The contribution of intraslab tectonics is excluded from the total moment rate because intraslab faults were neither individually mapped nor was their slip rate determined.

We recall that slip rate is the amount of slip as a function of geologic time; in other words, slip rate is obtained by dividing the amount of fault displacement, as determined from geodetic measurements, from offset human-made structures, or from offset geologic features, by time interval during which that offset has taken place (Morell et al., 2020). Generally, reported slip rates from geologic studies include the cumulative slip of individual seismic events and any aseismic slip on the fault (e.g., pre- and/or post-seismic slip and aseismic slip at the surface). These components are hardly distinguishable in the geologic record. In common practice encountered in the collected datasets, slip-rate data come from a limited number of point observations that are accepted as representing some presumed average displacement along strike. Studies that report accurate slip-rate variations along strike are relatively rare, and those that report the slip variations with depth or along dip are even much rarer (Finocchio et al., 2016). Therefore, moment rate estimates in EFSM20 generally refer to the tectonic component, and the actual seismic-moment rate to be converted in an earthquake rate forecast could be somewhat smaller depending on the seismic efficiency in Eq. (5). This parameter is not explored here. Users are thus cautioned about the possibility that some crustal-fault slip rates, as in the case of dataset no. 15 or others derived from the literature, could have already been “cleaned” by a predetermined or modeled seismic efficiency. This occurrence may not have been evident when the information on slip-rate values was adopted in bulk from a large dataset of a regional compilation. In this respect, it is worth recalling that seismic efficiency can dramatically influence earthquake productivity, especially for the subduction interfaces. For example, the seismic efficiency of the Hellenic Arc is generally considered weak (Shaw and Jackson, 2010; Heuret et al., 2011; Reilinger et al., 2010; Becker and Meier, 2010; Rontogianni, 2010), as moment rate based on seismicity accounts only for about 20 % of the moment rate based on the convergence rate shown by geodetic data. However, complete seismic coupling was proposed for the northwestern termination of the subduction beneath the Ionian Islands (Laigle et al., 2002; Ganas et al., 2020; Briole et al., 2021), suggesting possible lateral variations of seismic coupling along the Hellenic Arc (Laigle et al., 2004), in contrast with proposals of full coupling characterizing the entire Hellenic Arc (Ganas and Parsons, 2009). The seismic efficiency of the Calabrian Arc is also very variable. Based on geodetic observations and geodynamic modeling, the Calabrian Arc was hypothesized to be either locked or partly locked (Carafa et al., 2018) or negligibly active (Nijholt et al., 2018). Also, different interpretations exist on the activity of the Gibraltar Arc subduction interface. For example, the QAFI dataset does not include the Gibraltar subduction system, and other studies on geodetic observations do not consider the subduction process active (Stich et al., 2006) or consider it at all (Palano et al., 2015). The convergence rates reported in EFSM20 are thus meant to provide reasonable values in the hypothesis that the subduction interface is active, although EFSM20 remains neutral in this respect. The slab geometric reconstruction can still be useful for separating crustal seismicity from intraslab seismicity either for geodynamic studies (Goes et al., 2017) or other hazard applications (Basili et al., 2021), since the intraslab tectonic rates were not estimated.

The rigidity treatment is the main difference between crustal faults and subduction interfaces in estimating the moment rate. For crustal faults, we considered a uniform rigidity of 33 GPa, according to global estimates and consistency with fault scaling relations (Dziewonski and Anderson, 1981; Leonard, 2010), whereas for the subduction interfaces, we used the depth-dependent rigidity variation as observed in subduction zones from around the world (Bilek and Lay, 1999; Sallarès and Ranero, 2019) and already used to model earthquake ruptures for tsunami simulations and hazards (Geist and Bilek, 2001; Scala et al., 2020). We know that using a uniform rigidity value for crustal faults is not appropriate in certain cases. For instance, evidence shows that the basement offshore SW Iberia is mainly made of exhumed mantle rocks (Sallarès et al., 2013; Martínez-Loriente et al., 2014). However, we decided to use a homogeneous rigidity value due to the large volume of data and the need to homogenize its treatment. Noteworthily, depth-dependent rigidity in EFSM20 subduction systems implies a variation of up to ±30 % on the moment rate estimates compared to the uniform rigidity approach.

The subduction interfaces have systematically higher maximum magnitude than crustal faults (Fig. 7), reflecting the larger area of subduction interfaces, which can host larger ruptures. The maximum magnitude informs us of the size of the largest possible rupture that each fault-source can individually host (i.e., excluding the possible interactions among multiple faults) but tells nothing about the likelihood of that magnitude earthquake being released. To that end, a recurrence model should be developed based on the provided characteristics. Notice that the scaling relations of interface earthquakes predict rupture areas about 1.7 times larger, and their average slip is about 0.5 times smaller than those of crustal earthquakes with the same seismic moment. This consideration applies to most scaling relations, not just those used here (Skarlatoudis et al., 2016), and has implications for how the moment rate is partitioned into earthquakes of different sizes and, ultimately, in their recurrence. This reasoning particularly affects the crustal faults in the SCR, where the very low moment rate implies that the occurrence of the largest earthquakes is extremely unlikely and possibly their recurrence of little to no practical impact on seismic hazard estimates at standard average return periods (475 years).

4.2 Outlook

EFSM20 was designed to fulfill the specific needs of a hazard application at the scale of a continent and has thus been one of the main input datasets used for the 2020 update of the European Seismic Hazard Model (ESHM20) (Danciu et al., 2021, 2022). Its predecessor EDSF13 (Basili et al., 2013) was used for the 2013 European Seismic Hazard Model (ESHM13) (Woessner et al., 2015), the first regional tsunami hazard model NEAMTHM18 (Basili et al., 2021), and several other hazard analyses at different scales, post-earthquake analyses, and tectonic modeling. Likewise, EFSM20 is aimed to serve the same scope. To this end, it is distributed as machine-readable files using open standards (OGC), which allow users to port the datasets on various platforms and use them programmatically.

Being a continent-scale compilation, however, EFSM20 implied data selections and simplifications, which may hinder its application at a more local scale. We thus recommend that the users resort to the original datasets and pertinent literature when performing analysis at a local scale, such as site-specific hazard applications or near-field seismic scenarios. In these regards, one first-order aspect is fault geometry. The down-dip planar simplification is known to generate bias when reconstructing the earthquake ruptures (Dutta et al., 2021) or to underestimate the near-field ground motion (Passone and Mai, 2017). Similarly, tsunami modeling requires full knowledge of the 3D geometry of faults (Gómez de la Peña et al., 2022; Serra et al., 2021; Tonini et al., 2020).

The compilation of EFSM20 relied on the efforts made by many scientists in collecting and systematizing data about active faults with a region-wide perspective. Scientists collect most data on potential fault sources country by country for practical and organizational reasons. This practice may hardly change, but multilateral collaborations at the country boundaries may decrease the need for ex post data harmonization. The regional element is key for earthquake hazard analyses, which need fault-source characterization also in remote or less tectonically active areas. From a review of the literature, we realized that most works concentrate on the most-active, most-evident geological structures. A more balanced approach seems instead necessary to complement our in-depth knowledge of the most obvious structures along major plate boundaries with a better understanding of the least obvious ones. For example, the plate interiors account for less than 4 % of all global seismicity (Kagan et al., 2010), and this estimate from fault sources in EFSM20 is much lower, suggesting that we might still be missing important intraplate faults or misjudging their activity rate or recurrence (Calais et al., 2016). Mitigating earthquake risk in such areas is thus extremely challenging and important (England and Jackson, 2011).

Active fault identification and characterization are challenging in many respects. In continental interiors, climatic processes and human activities can easily obliterate the most recent active faulting due to the long earthquake recurrence intervals (Grützner et al., 2017). In moderately active regions along plate boundaries, sedimentation rates can overtake tectonic rates and conceal the fault activity under a thick sedimentary cover (Panara et al., 2021).

Nonetheless, even very active plate boundaries are not easily accessible for in-depth analyses. Although EFSM20 includes a large proportion of offshore faults, there is no doubt that offshore fault-source identification and characterization have considerable room for improvement (Perea et al., 2021), not only to improve the use of fault sources in tsunami hazard analyses but also to improve the modeling of tectonic systems and the tectonic deformation partition at the transition between onshore and offshore structural systems.

Appendix A

Table A1 Files distributed for download (GeoJSON files, ESRI shapefiles, MapInfo tables) and via OGC WFS. The rightmost column indicates the relevant table number, with the attribute descriptions provided below in this appendix.

Table A2 Files distributed via OGC WMS only.

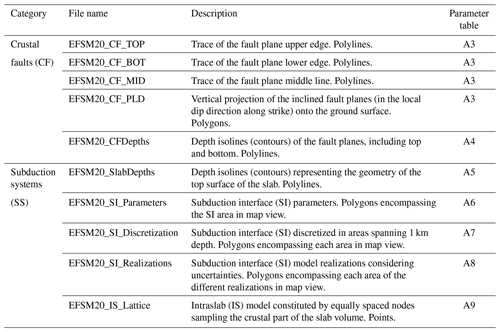
Table A3 Definition of the crustal-fault attributes. These attributes are the same for EFSM20_CF_TOP, EFSM20_CF_BOT, EFSM20_CF_MID, and EFSM20_CF_PLD files, in any of the distributed format or WFS service. n/a stands for not applicable.

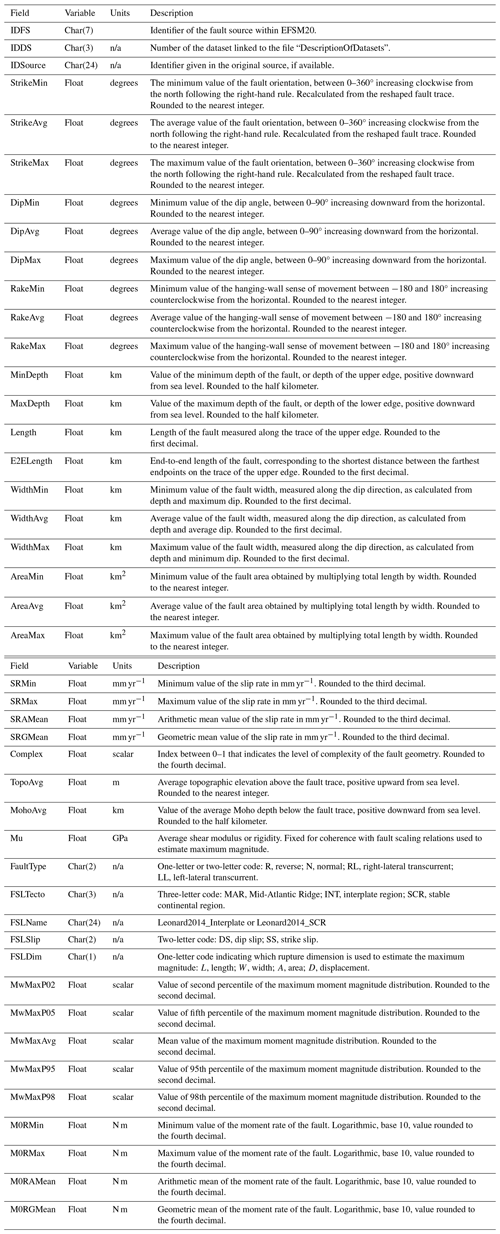
Table A4 Definition of the crustal-fault attributes for the EFSM20_CFDepths files. n/a stands for not applicable.

Table A5 Attributes of the slab depths. n/a stands for not applicable.

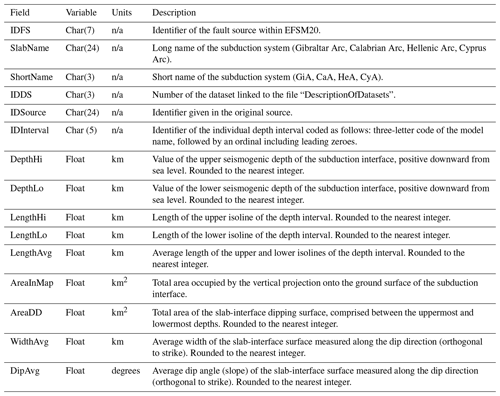
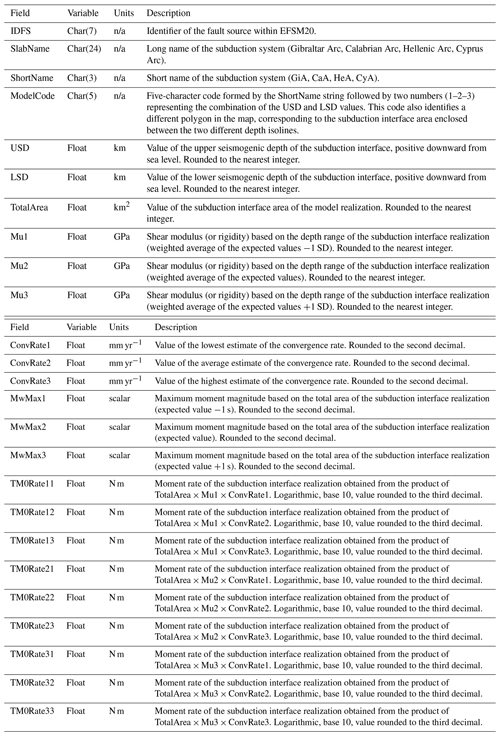
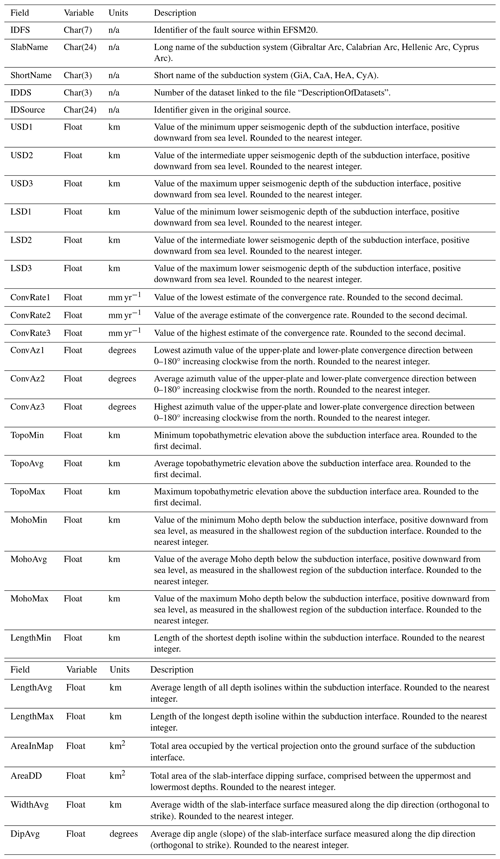
Table A6 Attributes of the subduction interface. Geometry and behavior parameters. n/a stands for not applicable.

Table A7 Attributes of the subduction interface discretization. n/a stands for not applicable.

Table A8 Attributes of the subduction interface realizations. n/a stands for not applicable.

Table A9 Attributes of the intraslab geometric parameters. n/a stands for not applicable.

Appendix B

Large version of the maps shown in Fig. 5 in the main text (the color classes used in these figures are the same as those distributed by OGC WMS web services).

Figure B1 EFSM20 crustal faults color-coded according to faulting type.

Figure B2 EFSM20 crustal faults color-coded according to average slip rate.

Figure B3 EFSM20 crustal faults color-coded according to maximum moment magnitude.

Figure B4 EFSM20 crustal faults color-coded according to average moment rate.