Review article: Towards improved drought prediction in the Mediterranean region – modeling approaches and future directions

There is a scientific consensus that the Mediterranean region (MedR) is warming and as the temperature continues to rise, droughts and heat waves are becoming more frequent, severe, and widespread. Given the detrimental effects of droughts, it is crucial to accelerate the development of forecasting and early warning systems to minimize their negative impact. This paper reviews the current state of drought modeling and prediction applied in the MedR, including statistical, dynamical, and hybrid statistical–dynamical models. By considering the multifaceted nature of droughts, the study encompasses meteorological, agricultural, and hydrological drought forms and spans a variety of forecast scales, from weekly to annual timelines. Our objective is to pinpoint the knowledge gaps in literature and to propose potential research trajectories to improve the prediction of droughts in this region. The review finds that while each method has its unique strengths and limitations, hybrid statistical–dynamical models appear to hold the most promising potential for skillful prediction with seasonal to annual lead times. However, the application of these methods is still challenging due to the lack of high-quality observational data and the limited computational resources. Finally, the paper concludes by discussing the importance of using a combination of sophisticated methods such as data assimilation techniques, machine learning models, and copula models and of integrating data from different sources (e.g., remote sensing data, in situ measurements, and reanalysis) to improve the accuracy and efficiency of drought forecasting.

1 Introduction

Drought is a recurrent phenomenon in the Mediterranean region (MedR). Throughout time, adaptation to this kind of climate event has been an important issue for the development of many countries in the region. Yet, with the disruptive accelerated impact of global warming, already reflected in more regular and intense droughts around the Mediterranean in the last few decades, building resilience to extreme weather conditions remains a true challenge (Satour et al., 2021). For these reasons among others, the region is often described as a hotspot for climate change (Tuel and Eltahir, 2020). The Intergovernmental Panel on Climate Change (IPCC) pointed out in the Sixth Assessment Report (AR6) that global warming has been more rapid in the Mediterranean than in the rest of the world (IPCC, 2021). This report projected an increase in the frequency and/or severity of agricultural and ecological droughts across the Mediterranean and western Africa (IPCC, 2021). A global increase of 2 ^∘C is thought to correspond to a 3 ^∘C increase in the daily maximum temperature in the MedR (Seneviratne et al., 2016; Vogel et al., 2021). If this increase in temperature continues at the same pace, the MedR is susceptible to experiencing fearful desertification by the end of the 21st century, driving an increase in aridity (Carvalho et al., 2022).

Figure 1 Topography of the Mediterranean Region (30–46^∘ N in latitude and 10^∘ W–40^∘ E in longitude).

This will surely lead to irreversible biodiversity loss and diminish the capability of semi-arid Mediterranean ecosystems to function as effective carbon sinks in the future (Valentini et al., 2000; Briassoulis, 2017; Zeng et al., 2021). These conditions exacerbate water stress, which, in turn, enhances the probability of wildfire (Turco et al., 2017a), a phenomenon already witnessed in two recent summers (2021 and 2022) in several Mediterranean countries (Türkiye, Greece, Italy, Algeria, and Morocco) that displaced thousands, killed hundreds, and caused irreparable damage (Rodrigues et al., 2023; Yilmaz et al., 2023; Eberle and Higuera Roa, 2022).

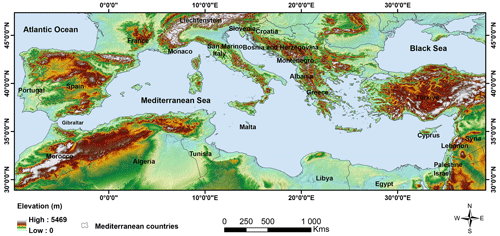
The Mediterranean Sea (MEDS), lying between Africa, Europe, and Asia, serves as a substantial source of moisture and heat, affecting atmospheric circulation and weather patterns (Mariotti et al., 2008). Its narrow connection to the Atlantic Ocean via the 14 km wide Strait of Gibraltar and the surrounding varied topography (Fig. 1), with vegetated areas to the north and desert areas to the south and east, contribute to the region's complex climate dynamics (Michaelides et al., 2018).

The MedR is characterized by a mid-latitude temperate climate with mild, rainy winters and hot, dry summers (Lionello et al., 2023). Notably, this area is positioned in a transitional band between the mid-latitude and subtropical regions, which makes climate modeling for this region quite challenging (Planton et al., 2012). The Mediterranean climate exhibits a strong spatial gradient in precipitation, with generally decreasing precipitation values towards the south and hardly any precipitation during the summer (Lionello, 2012). Such conditions pose challenges in climate modeling and can lead to severe impacts on water supply and agriculture, especially in regions relying on rain-fed agriculture (Tramblay et al., 2020).

Water availability is unevenly distributed among the Mediterranean countries with 72 % in the temperate countries of the north against 5 % in the south and 23 % in the east (Milano et al., 2013). Accordingly, several countries such as Algeria, Morocco, Egypt, Libya, and Malta and some countries of southern Europe such as Portugal and Spain are experiencing a structural water shortage that is likely to increase with the expected population growth (Sanchis-Ibor et al., 2020). This situation is further aggravated when multi-annual droughts hit the region. In this challenging context, drought forecasting that provides seasonal to annual lead times becomes critically important for proactive agricultural and water resource management.

Growing concern about the drought phenomenon in the last few decades has spurred the development of improved systems that predict the full cycle of drought (onset, duration, severity, and recovery) via a large number of indices and models. Common approaches to predicting drought can be subdivided into two categories of models: statistical models and dynamical models. Statistical models, also named data-driven models, rely on the estimated correlations between several predictors (large-scale climate variables) and predictands (local climate variables represented by historical observations). The climatology-based or persistence-based models, like the ensemble streamflow prediction (ESP) system, form an essential tool in this category, leveraging both historical and near-real-time data to generate a probabilistic forecast of future drought events (AghaKouchak et al., 2014; Turco et al., 2017b; Torres-Vázquez et al., 2023). Meanwhile, dynamical drought prediction relies on the use of global climate models (GCMs) to simulate the dynamical processes that govern hydroclimatic variability. Nevertheless, despite the usefulness of these models in drought prediction and early warning systems, their forecast accuracy remains limited for longer lead times (exceeding 1 month) (Wood et al., 2015). Post-processing and multi-model ensemble techniques are usually used to improve prediction skills by avoiding systematic bias related to the coarse resolution of GCMs (Han and Singh, 2020). Recently, drought prediction has also been tackled by hybrid statistical–dynamical models which combine the two approaches mentioned above. These models constitute a promising tool for long-lead-time drought forecasting (Ribeiro and Pires, 2016).

Despite the efforts made to predict drought phenomena, they remain largely little understood due to drought's multiple causative mechanisms and contributing factors (Kiem et al., 2016; Hao et al., 2018). The complexity and variability depicted by many physical mechanisms such as sea surface temperature (SST), the North Atlantic Oscillation (NAO), the El Niño–Southern Oscillation (ENSO), the Mediterranean Oscillation (MO), and land–atmosphere feedback are also responsible for the low performance of drought monitoring and forecasting (Ayugi et al., 2022). Understanding the synoptic conditions leading to drought phenomena becomes increasingly important given the upward trend in temperature in the MedR. Further investigations to assimilate how large-scale teleconnections affect local weather and climate anomalies, as well as how these later feed back into the larger context, are much needed in this context.

To address these questions, numerous review papers have sought to consolidate the scientific advances in drought prediction from different regions of the world (e.g., Mishra and Singh, 2011; Hao et al., 2018; Fung et al., 2019; Han and Singh, 2020). While these studies provided a comprehensive overview of drought prediction at a global scale, our paper offers an in-depth analysis of drought prediction methodologies specifically applied to the Mediterranean context. This is achieved through an examination of the applicability, strengths, and limitations of statistical, dynamical, and hybrid statistical–dynamical models, in line with the regional specifics of the MedR. This specificity is vital given that drought, as a phenomenon, is highly region dependent. The unique meteorological conditions of the MedR necessitate dedicated studies, as solutions developed for other regions may not be applicable or effective here.

Tramblay et al. (2020) emphasized the urgent need for drought modeling and forecasting methods designed for the Mediterranean context, particularly as climate change continues to exacerbate drought conditions in this region. Building on this, our work not only emphasizes the complexities of drought assessment but also conducts a critical review of recent drought forecasting methodologies applied specifically to the MedR. In addition to shedding light on the merits and limitations of these methods, our investigation also helps identify underexplored areas that warrant further research. Detecting these gaps is a crucial aspect of our work, as it directs future research towards these relatively unexplored realms of drought prediction.

The structure of this paper is as follows: Sect. 2 highlights the difficulty related to the definition of drought from different perspectives. The causes of drought in the MedR are provided in Sect. 3. Sections 4, 5, and 6 present the recent advances in drought prediction with statistical, dynamical, and hybrid statistical–dynamical models, respectively. Section 7 discusses the results found in this review, providing insights into the current state of drought forecasting in the MedR and highlighting potential areas for improvement. The challenges in drought prediction are reviewed with its prospects in Sect. 8. Finally, Sect. 9 presents the conclusions of the whole paper.

2 Drought definitions, classification, and indices

Drought is a compound phenomenon of a creeping nature. Establishing accurate predictions that describe its starting date and duration well is extremely hard. The multidisciplinary and multiscale nature of drought renders the understanding of this phenomenon very challenging (AghaKouchak et al., 2021). As a matter of fact, the literature gives numerous definitions for drought.

In the 1980s, Wilhite and Glantz (1985) found more than 150 published definitions of drought that can be categorized into four broad groups: meteorological, agricultural, hydrological, and socioeconomical. This classification based on both physical and socioeconomic factors is still adopted today. As this classification is human-centered, some recent works emphasized the need to consider ecological drought as well, which creates multiple stresses in natural ecosystems; see for example Crausbay et al. (2017), Vicente-Serrano et al. (2020), Bradford et al. (2020), and Zhang et al. (2022). Since the aim of this study is to review forecasting drought methods, we will focus only on the first three categories, which provide direct methods to quantify drought as a physical phenomenon.

In an attempt to associate a mathematical definition with each drought type, several drought indices have emerged. These indices are typically based upon some hydroclimatic variables or parameters (indicators) such as temperature, precipitation, soil moisture, streamflow, and snowpack to describe three major characteristics of the drought event: severity, duration, and frequency. However, the lack of a universal definition of drought is also apparent in the huge variety of indices (more than 100) that have been developed for drought prediction (Lloyd-Hughes, 2014). Unfortunately, this plethora of indices creates more confusion than clarity (Lloyd-Hughes, 2014) and makes the choice of the most suitable indices a difficult task.

2.1 Meteorological drought

The World Meteorological Organization (WMO) characterizes meteorological drought as “a prolonged absence or marked deficiency of precipitation”. Similarly, the IPCC defines meteorological drought as “a period of abnormally dry weather in a region over an extended period”. The threshold to distinguish between a dry or wet period often depends on the average rainfall typical of the specific area under study. This gives rise to a variety of meteorological definitions, each tailored to the distinct conditions of diverse regions or countries (Isendahl, 2006). Regarding the MedR, creating a single encompassing definition of meteorological drought is particularly challenging. This complexity stems from the diverse climate conditions across the region, particularly the pronounced variability between eastern and western meteorological conditions that contribute to drought.

The Standardized Precipitation Index (SPI) (McKee et al., 1993) and the standardized precipitation evapotranspiration index (SPEI) (Vicente-Serrano et al., 2010a) are two of the most prevalent indicators used to describe meteorological drought. They owe their popularity to the recommendation of the WMO (Svoboda et al., 2012). SPI has been extensively used in previous studies for its ease of computation, its probabilistic nature, and its ability to detect drought on multiple timescales (Madadgar and Moradkhani, 2013; Chen et al., 2013; Li et al., 2020; Mesbahzadeh et al., 2020; Das et al., 2020). By fitting a probability distribution to observed precipitation data, SPI is calculated and subsequently transformed into a standard normal distribution with a mean of 0 and a standard deviation of 1 (Livada and Assimakopoulos, 2007). Consequently, SPI values can be compared across various regions and time frames (e.g., 1, 3, 6, 12, or 24 months). This multiscale nature of SPI enables it to capture diverse aspects of drought depending on the selected timescale. The shorter timescales (1–3 months) are suitable for monitoring agricultural drought, while longer timescales (6–12 months or more) are better suited for evaluating hydrological drought. However, it should be noted that SPI considers only precipitation data and neglects the variability in temperature and potential evapotranspiration (PET), ignoring the effect of warming on droughts. Indeed, in relatively wet regions, the precipitation deficit can constitute an important indicator for drought (Gamelin et al., 2022). Yet, in mid-latitude (or extratropical) regions such as the Mediterranean where the climatological precipitation is modest or low, the precipitation deficit may not be sufficient to measure extreme droughts. Furthermore, knowing the upward trend in temperature and the influence of high atmospheric evaporative demand (AED) on the increasing severity of recent drought events in the MedR (Tramblay et al., 2020; Mathbout et al., 2021; Bouabdelli et al., 2022), the choice of drought indices needs to prioritize those including these variables in their formulation, such as SPEI, the Palmer drought severity index (PDSI) (Palmer, 1965), or the Reconnaissance Drought Index (RDI) (Tsakiris and Vangelis, 2005) to mention but a few.

SPEI was developed by Vicente-Serrano et al. (2010a) using the climatic water balance concept of climatic water supply and AED. It is based on precipitation and PET and has the advantage of combining the multiscalar character of SPI with the ability to include the effects of temperature variability (Vicente-Serrano et al., 2010a).

A global assessment of drought indices conducted by Vicente-Serrano et al. (2012) found that SPEI provided a superior capability in capturing drought impacts, particularly during the crucial summer season. Bouabdelli et al. (2022) used SPI and SPEI and copula theory to study the impact of temperature on agricultural-drought characteristics under future climate scenarios over seven vast Algerian plains located in the MedR. The results of this study confirmed that the frequency of drought events is much higher using SPI, while their duration and severity are more intense using SPEI. Russo et al. (2019) performed drought characterization in the MedR using both SPEI and SPI, considering the period 1980–2014. Their findings indicated that SPEI exhibits a stronger correlation with drought conditions over a 3-month timescale, while SPI shows a better correlation for a 9-month duration. This result highlights the ability of SPEI to capture the early shifts in the balance between evapotranspiration and precipitation more efficiently than SPI (Russo et al., 2019).

Despite the utility of SPEI in drought characterization, it does have a noteworthy limitation. The effectiveness of SPEI significantly relies on the method used for estimating PET such as the Penman–Monteith equation, the Thornthwaite method, the Hargreaves method, and the Priestley–Taylor method. These estimation methods can yield varying results, leading to inconsistencies in SPEI values. In essence, the sensitivity of SPEI to the PET estimation method used could potentially affect the accuracy and reliability of the index in representing drought conditions (Vicente-Serrano et al., 2010b; Stagge et al., 2014).

PDSI has also been widely used to quantify the drought characteristics for a given location and time. It includes precipitation, temperature, and soil moisture data to estimate water supply and demand and to reflect long-term drought. But it has shown some inconsistencies when used at various locations (Wells et al., 2004). A self-calibrating variant of this index (sc-PDSI) was proposed by Wells et al. (2004) to automatically calibrate the behavior of the index by replacing empirical constants in its computation with dynamically estimated values to account for the variability in precipitation and the climate characteristics between locations (Wells et al., 2004). Ionita and Nagavciuc (2021) evaluated the drought characteristics at the European level over the period 1901–2019 using SPI, SPEI, and sc-PDSI. The results based on SPEI and sc-PDSI show that the increase in mean air temperature and PET are making central Europe and the MedR drier, whereas northern Europe is getting wetter. In contrast, results based on SPI using only precipitation data did not reveal this drought variability. This underscores the findings of Vicente-Serrano et al. (2012), who emphasized the benefits of using more integrative indices like SPEI to understand and predict drought variability more effectively.

MedPDSI, which is an update of the PDSI formulation in terms of its soil water balance to consider real evapotranspiration (based on reanalysis data instead of PET) in the MedR, has allowed an earlier identification of longer and more severe droughts (Paulo et al., 2012). Paulo et al. (2012) compared SPI, SPEI, PDSI, and MedPDSI in detecting drought characteristics in Portugal for the period 1941 to 2006. They concluded that PDSI and MedPDSI are likely to better identify the supply–demand dynamics and that they may be of great interest for drought warning applications aimed primarily at agriculture (Paulo et al., 2012).

2.2 Agricultural drought

Agriculture is very sensitive to climate variation, especially extreme weather. Due to its dependency on water availability, this sector is strongly impacted by drought events. In the Mediterranean Basin, agricultural practices span both rain-fed and irrigated systems. Rain-fed agriculture is prevalent, particularly for crops such as wheat and barley, while crops like olives and citrus fruits such as oranges often utilize controlled irrigation systems to supplement natural precipitation (Rodrigo-Comino et al., 2021). Regardless of the system employed, if meteorological drought lasts for a prolonged period, it can lead to a reduction in soil moisture to such a level that it harmfully affects crop production, especially during the active plant growth season (Wilhite and Glantz, 1985; Mishra and Singh, 2010). At this stage agricultural drought sets in.

Therefore, in addition to meteorological factors, the agricultural-drought definition is also related to the retention capacity of soil in the crop growth season (Kuśmierek-Tomaszewska and Żarski, 2021), which depends on crop types, soil characteristics, and soil management. All these indicators can be employed to develop relevant agricultural drought indices. Among them, we cite the crop moisture index (CMI) (Palmer, 1968), soil moisture deficit index (SMDI), evapotranspiration deficit index (ETDI) (Narasimhan and Srinivasan, 2005), normalized soil moisture index (NSMI) (Dutra et al., 2008), and Empirical Standardized Soil Moisture Index (ESSMI) (Carrão et al., 2016).

The formulation of these indices integrates soil moisture data, leveraging a variety of assessment techniques, each with unique advantages. These include in situ soil moisture probes, cosmic-ray neutron probes, and physically driven models such as the ISBA land surface model (Tramblay et al., 2019). Each of these techniques has distinct advantages and is suitable for different application contexts (Miralles et al., 2010; Martens et al., 2017). However, when faced with the scarcity of observed soil moisture data, remote sensing comes to the forefront. It furnishes extensive and frequent measurements of soil moisture characteristics, effectively supplementing areas where observed data fall short. Yet, it is crucial to be aware of the limitations of remote sensing tools. Despite its indispensable role, remote sensing is constrained by factors such as coarse temporal and spatial resolutions, limited penetration depth, and incompatible governing hydrologic principles (Mohanty et al., 2017; Gruber and Peng, 2022). As an alternative, hydrological models have been commonly used to simulate and calibrate this variable in the context of agricultural-drought forecasts (Hao et al., 2018). Mimeau et al. (2021) used a modeling framework to estimate soil moisture sensitivity to changes in precipitation and temperature at 10 plots located in southern France. They concluded that the current climate change scenarios may induce longer periods of depleted soil moisture content, corresponding to agricultural-drought conditions.

In general, when soil moisture in the root zone reaches a critical level, farmers resort to irrigation to save crops (Kang et al., 2000). However, nowadays agriculture consumes approximately 85 % of global fresh water for irrigation (D'Odorico et al., 2019; Tatlhego et al., 2022), which is expected to increase in the years to come because of growing populations, increasing food consumption, and rising temperatures that accelerate PET and promote hydrological stress.

2.3 Hydrological drought

Unlike agricultural drought, which is mainly affected by the depletion of soil moisture after a dry period, a lack of precipitation impacts many components of the hydrological system in a river basin or watershed (streams, reservoirs, and lakes). These define the availability of water that can be used for commercial navigation, generation of hydroelectric power, irrigation of farmlands, industry, and domestic activities for several months after the deficiency in precipitation. Consequently, hydrological drought lags behind the occurrence of meteorological and agricultural droughts. This lag time is a characteristic of the watershed, which is defined based on many physical drivers such as evapotranspiration capacity, soil properties, vegetation types, snow accumulation and melt, local water management such as dams' construction and control, water supply operation rules, and irrigation strategy (Van Loon and Laaha, 2015).

A hydrological drought is generally proclaimed when the water levels in streamflow, reservoirs, lakes, aquifers, and other water storage systems fall below a specific threshold. Therefore, hydrological-drought prediction necessitates the analysis of climate variables such as precipitation and temperature and of initial catchment conditions (e.g., snow cover and soil moisture) (Hao et al., 2018).

In the Mediterranean Basin, a common tendency for water levels to drop in shallow lakes and aquifers has motivated many researchers to study the hydrological drought in this region: Greece (Myronidis et al., 2012), Türkiye (Akyuz et al., 2012), Tunisia (Hamdi et al., 2016), Lebanon (Al Sayah et al., 2021), Italy (Di Nunno et al., 2021), Portugal (Mendes et al., 2022), Algeria (Bouabdelli et al., 2022), and Syria (Mohammed et al., 2022). The most common hydrological drought indices include the Palmer hydrological drought index (PHDI) (Palmer, 1965), the streamflow drought index (SDI) (Nalbantis, 2008), and the standardized runoff index (SRI) (Shukla and Wood, 2008).

As part of the effort made by Wayne Palmer in the 1960s, PHDI has been developed using the same two-layer soil model as PDSI, but it applies a stricter criterion for determining the ends of drought to account for long-term drought events that reduce surface and groundwater supply. Vasiliades and Loukas (2009) tested the Palmer indices in a Mediterranean Basin (in Greece), and they concluded that these indices were successful in the identification of the drought severity of historical events but were unable to identify drought duration.

SRI is an index that uses the same computational principles as SPI but uses monthly mean streamflow rather than precipitation only to account for the hydrological process that determines seasonal lags in the influence of climate on streamflow (Shukla and Wood, 2008). Shukla and Wood (2008) compared the SRI and the SPI results during drought events in a snowmelt region. They concluded that SRI can be used as a complement to SPI for depicting hydrologic aspects of drought.

SDI is also a simple index that uses the cumulative monthly streamflow volumes for a given hydrological year to predict wet and dry periods and identify the severity of a hydrological drought (Nalbantis, 2008). Bouabdelli et al. (2020) conducted a comparison study of SPI and SDI, focusing on the indices' characteristics across three watersheds in northwestern Algeria. Their analysis revealed a substantial similarity between meteorological-drought events (as represented by SPI-12) and hydrological-drought events (as indicated by SDI-6). This correlation emphasizes the sensitive and responsive nature of these basins to dry conditions, further illustrated by the swift transition from meteorological-drought to hydrological-drought events in the studied basins (Bouabdelli et al., 2020).

The application of hydrological drought indices appears to be very valuable. However, the main challenge in applying these indices lies in the requirement for a long-term series of climatic data. According to the WMO, up to 30 years of continuous rainfall data may be necessary for accurate drought index calculations (WMO, 1994). This condition is not always fulfilled, which makes the rainfall–runoff transformation a difficult task (De Luca et al., 2022). Modern hydrological models can offer a valuable counterpart to existing climate-based drought indices by simulating hydrologic variables such as land surface runoff (Shukla and Wood, 2008).

3 Overview of the physical mechanisms causing drought in the Mediterranean region

It is difficult to determine the physical mechanisms causing droughts in the Mediterranean Basin, since the region covers a complex landscape with high topographic and climatic heterogeneity, strong land–sea contrasts, and high anthropic pressure (De Luca et al., 2022).

Considering the various forms of drought, meteorological droughts, characterized by a deficit in precipitation, are commonly recognized as marking the onset of drought conditions. This initial stage is intrinsically linked to precipitation predictability, which is driven by large-scale atmospheric motions such as Walker circulations and Rossby waves, influenced by factors like SST anomalies, radiative forcing changes (both natural and anthropogenic), and land surface interactions (Hao et al., 2018; Wood et al., 2015). However, due to the inherently chaotic nature of atmospheric circulation, predictability, particularly for meteorological droughts, tends to diminish beyond a 1-month lead time. It is crucial to note that the reliability of these predictions can differ when considering other drought types (such as agricultural or hydrological droughts) or altering the forecast scale, with seasonal forecasts often displaying more reliability months in advance, while daily forecasts may face limitations from around 2 weeks.

The discovery of teleconnections between SST anomalies and hydroclimatic phenomena constitutes a major advance in drought forecasting and early warning (Wood et al., 2015). Notably, it is widely established within the scientific community that certain ocean–atmospheric teleconnections, such as ENSO, can profoundly influence the onset of drought conditions in various regions worldwide, particularly in the tropics (Ropelewski and Halpert, 1987; Shabbar and Skinner, 2004; Hoell et al., 2014; Vicente-Serrano et al., 2017). For instance, during the peak phase of El Niño or La Niña in the tropical Pacific, a corresponding change in precipitation patterns can be observed several months later in the North American winter climate (Livezey and Smith, 1999; Hoerling and Kumar, 2003). This delayed impact provides a crucial window for predicting potential drought conditions with a long lead time exceeding 1 month (Johnson and Xie, 2010). Moreover, this lagged correlation allows for proactive drought management strategies, with the ability to anticipate and prepare for drought conditions based on forecasted ENSO conditions. Nevertheless, drought predictability is seasonally and spatially variable. Typically, the accuracy of seasonal drought prediction is superior in the tropics, while it is still challenging in the extratropics (Doblas-Reyes et al., 2013).

In the MedR, the response of climate to ENSO is complex. It varies over time and depends on the maturity of the ENSO state and the co-occurrence with NAO (Kim and Raible, 2021; Brönnimann et al., 2007; Mariotti et al., 2002). Although many authors have found a non-negligible correlation between ENSO and precipitation anomalies in the MedR, it remains insignificant compared to in the tropics (Mariotti et al., 2002).

In contrast, the NAO is commonly identified as a prominent factor influencing Mediterranean climate variability during the winter season (Ulbrich and Christoph, 1999; Vicente-Serrano et al., 2011; Kahya, 2011; Santos et al., 2014; Cook et al., 2016). It is important to note, however, that while acknowledging the profound impact of the NAO on the climate dynamics of the MedR, its predictability, especially on seasonal scales, continues to be a considerable challenge in the field of climate science (Czaja and Frankignoul, 1999; Saunders and Qian, 2002; Scaife et al., 2014; Dunstone et al., 2016).

During the positive phase of the NAO, below-average precipitation rates are observed over large parts of the northern and western MedR. While in the negative phase of the NAO, the climate is wetter and warmer (Lionello, 2012). Kim and Raible (2021) analyzed the dynamics of multi-year droughts over the western and central Mediterranean for the period of 850–2099 CE. This analysis suggests Mediterranean droughts from 850–1849 CE were mainly driven by the internal variability in the climate system, including elements like barotropic high-pressure systems, positive NAO phases, and La Niña-like conditions. Conversely, external forcing such as volcanic eruptions was found to be associated with wetter Mediterranean conditions. In the period 1850–2099 CE, however, anthropogenic influences amplified land–atmosphere feedback, leading to persistent dry conditions in the Mediterranean (Kim and Raible, 2021).

Paz et al. (2003) analyzed monthly mean sea level pressure (SLP) anomalies from the 1958–1997 record over the Mediterranean Basin. They identified a significant anomalous SLP oscillation between north Africa and west Asia and concluded that the regional trend of the north Africa–west Asia (NAWA) index could explain increased drought processes in the eastern Mediterranean after the late 1970s, in relation to northern hemispheric circulation.

The climate heterogeneity in the Mediterranean area may also be explained by the regional Mediterranean Oscillation (MO), characterized by opposite precipitation patterns between the eastern and western regions (Dünkeloh and Jacobeit, 2003). More recently, Redolat et al. (2019) proposed a new version of MO that uses areas instead of observatories or isolated points. The new index, which is referred to as the Upper-Level Mediterranean Oscillation index (ULMOi), is based on the differences in geopotential height at 500 hPa to improve the predictability of seasonal anomalies in the Mediterranean climate (Redolat et al., 2019). According to this study, ULMOi has reported higher confidence than the MO index for rainfall predictability (Redolat et al., 2019). Other teleconnections influencing the climate of the MedR can be found in the reviews done by Paz et al. (2003) and Lionello (2012). Recent works have also shed light on the impact of the Madden–Julian Oscillation (MJO) on water availability in the region, especially during heavy-rain episodes; see for example Chaqdid et al. (2023).

In conclusion, several complex factors that influence the predictability of drought are not yet fully understood, especially those related to climate change. Therefore, more research on the physical mechanisms causing drought in the MedR is needed to improve the predictability of drought forecasts.

Expanding our grasp of the physical factors causing drought in the MedR, we will now delve into drought forecasting models. By leveraging insights from these mechanisms, scientists have developed numerous approaches and techniques including statistical, dynamical, and hybrid statistical–dynamical models to boost the accuracy and trustworthiness of drought predictions.

4 Statistical drought prediction methods

Once the major sources of predictability are identified, the task of the statistical models is to uncover the spatial and/or temporal relationship between a set of these potential predictors and the predictand. When a large number of predictors are identified within the same region, dimension reduction techniques like principal component analysis (PCA) or linear discriminant analysis (LDA) can improve model accuracy and efficiency by reducing the number of dimensions while preserving essential information. On the other hand, feature selection methods such as decision trees or random forests can help eliminate irrelevant predictors. These approaches can prevent overfitting, leading to enhanced model performance and interpretability (Hao et al., 2018; Ribeiro and Pires, 2016).

The next sections will present the frequently used data-driven models and how they have been employed to predict different types of drought at different spatiotemporal resolutions in the MedR.

4.1 Time-series models

During the last few decades, several methods have been developed to analyze the stochastic characteristics of hydrologic time series (Morid et al., 2007; Rafiei-Sardooi et al., 2018; Band et al., 2022; Zarei and Mahmoudi, 2020). The moving average (MA), autoregressive (AR), and autoregressive integrated moving average (ARIMA) models are all linear models that analyze past observations of the same variable to predict its future values. Normality and stationarity of observations are two of the basic assumptions of these time-series models. Therefore, if some trends or seasonality is detected in observations, it should be removed before the modeling to avoid any drift in the concepts to be captured.

ARIMA is the most frequently used time-series model (Zhang, 2003). The popularity of this model is related to its ability to search systematically for an adequate model at each step of the model building (identification, parameter approximation, and diagnostic check). This method is based on the concept that nonstationary data could be made stationary by “differencing” the series (Box et al., 2015). The approach involved considering a value Y at time point t and adding/subtracting based on the Y values at previous time points and adding/subtracting error terms from previous time points. The formula can be written as

$$\begin{array}{}\text{(1)}& Y_t=c+{\mathit{\phi }}_{\mathrm{1}}{Y}_{t-\mathrm{1}}+\mathrm{\dots }+{\mathit{\phi }}_p{Y}_{t-p}+{\mathit{\theta }}_{\mathrm{1}}{e}_{t-\mathrm{1}}+\mathrm{\dots }+{\mathit{\theta }}_q{e}_{t-q}+e_t,\end{array}$$

where Y_t is the value of the variable at time t; c is a constant term; p and q are the orders of AR and MA models, respectively; φ_i and θ_i are model parameters; and e_t−1, …, e_t denotes the error terms.

The AR component captures the impact of past values on the current value, the I component handles any nonstationarity in the data (i.e., changes in the mean or variance over time) by differencing the time series, and the MA component captures the impact of random shocks or errors in the data.

The ARIMA model is generally expressed with the three terms p, d, and q. The order of differencing in the I component is denoted by the value of (d) in the ARIMA ($p,d,q$) notation. It represents the number of times that the data must be differenced to produce a stationary signal. The lag order (p) represents the number of prior observations that have a strong correlation with the current observation, while q is the size of the moving window and is identified by determining the number of lag errors that have a significant impact on the current observation.

SARIMA is a more specific version of ARIMA that includes a seasonal component, which takes into account the repeating patterns that occur at regular intervals (e.g., daily, weekly, monthly) in the data. This makes it more appropriate for forecasting seasonal time-series data.

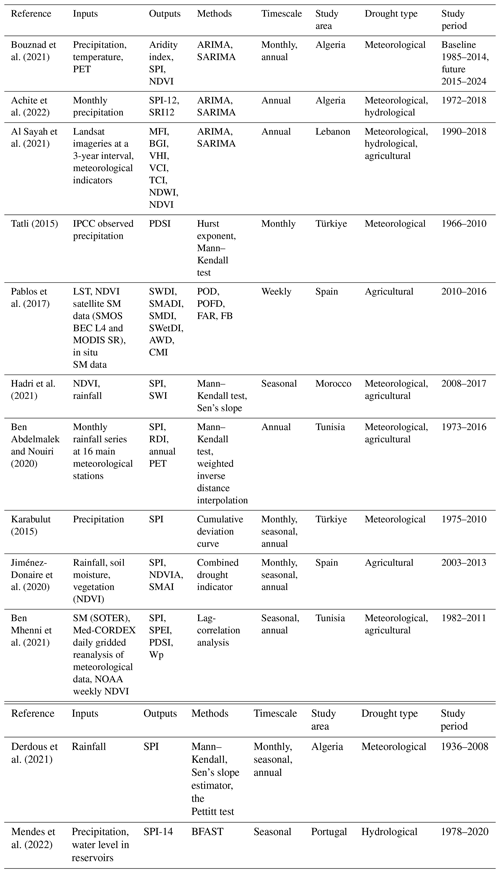
Bouznad et al. (2021) conducted a comparative analysis of ARIMA and SARIMA models using precipitation, temperature, and evapotranspiration data to assess seasonal drought conditions in the Algerian highlands. These models were compared based on their ability to replicate and forecast the data series accurately. The SARIMA model emerged as the better choice as it exhibited significant p values for all variables under study. This implies that the model was statistically significant in predicting the variables and thus outperformed the ARIMA model in this specific context. In the same country, Achite et al. (2022) investigated meteorological and hydrological drought in the Wadi Ouahrane Basin using ARIMA and SARIMA models applied to SPI and SRI. A validation based on R² revealed high accuracy for SPI and SRI of 0.96 and 0.97, respectively, at a 1-month lag. Additional examples of the use of the time-series model in drought forecasting in the MedR can be found in Table 1.

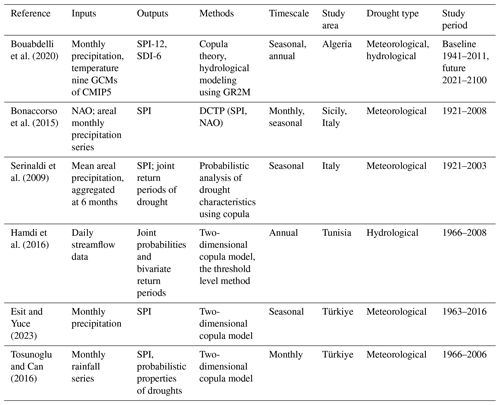
Table 1 Main studies using the time-series model to forecast drought in the MedR. For all tables, refer to the Appendix for abbreviations not defined in the main text.

Although time-series models have shown good predictability of drought characteristics, these methods present certain limitations as they are based solely on the persistence of some drought indicators (trend, seasonality) without worrying about their interactions.

4.2 Regression analysis

Regression models are commonly applied in drought forecasting due to their straightforwardness, interpretability, and proficiency in revealing potential connections between hydroclimatic variables. These models use various predictors (independent variables), including precipitation, temperature, and other relevant climate indices, to approximate drought indices or related target variables (dependent variables).

Simple and multivariate linear regression (MLR) models have been broadly applied for projecting extreme hydrological phenomena such as droughts (Sharma et al., 2018). These models shed light on the linear connections between various predictors and predictands, offering a valuable method to understand the primary factors of drought conditions and their interactions (Mishra and Singh, 2011).

An MLR model that predicts drought from multiple drought predictors X₁, X₂, …, X_n can be formulated as

$$\begin{array}{}\text{(2)}& Y={\mathit{\beta }}_{\mathrm{0}}+{\mathit{\beta }}_{\mathrm{1}}{X}_{\mathrm{1}}+{\mathit{\beta }}_{\mathrm{2}}{X}_{\mathrm{2}}+\mathrm{\dots }+{\mathit{\beta }}_n{X}_n+\mathit{\epsilon },\end{array}$$

where β₀ is the y intercept or the constant term, ${\mathit{\beta }}_{i(i=\mathrm{1},\mathrm{2},\mathrm{\dots },n)}$ denotes the regression coefficient for each independent variable $X_{i(i=\mathrm{1},\mathrm{2},\mathrm{\dots },n)}$, and ε is the model's error term.

On the other hand, when drought forecasts have a binary or dichotomous nature, such as drought vs. no drought, logistic regression models can be particularly useful. In these cases, the dependent variable (drought) is expressed as a probability or likelihood of occurrence. The main goal of logistic regression is to estimate the relationship between a set of predictors and the probability of the binary outcome (Rahali et al., 2021; Hosmer et al., 2013).

Some of the applications of regression analysis for drought forecasting in the MedR are discussed below and are summarized in Table 2.

Table 2 Main studies using regression analysis to forecast drought in the MedR.

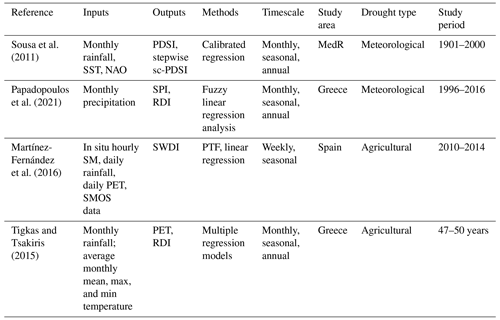
Sousa et al. (2011) analyzed the spatiotemporal evolution of drought conditions across the MedR during the 20th century using monthly precipitation, the NAO, and SST as independent variables and sc-PDSI as a dependent variable. Their study successfully developed a robust stepwise regression model capable of predicting summer drought conditions 6 months in advance with a high correlation of 0.79 between simulated and observed sc-PDSI time series, thus demonstrating its utility in forecasting future drought conditions in the region. Tigkas and Tsakiris (2015) used the MLR model with variables that include the minimum temperature and RDI as the main independent variable for the assessment of drought effects on wheat yield in two rural areas of Greece. The results of this analysis showed a high correlation between RDI and the wheat yield during the winter months, which proves that satisfactory prediction of the drought impacts on wheat yields 2 to 3 months before the harvest can be achieved using the MLR model. Martínez-Fernández et al. (2016) conducted a study in the REMEDHUS (Soil Moisture Stations Network) area in Spain, aiming to monitor agricultural drought on a weekly timescale and provide early warning to farmers for adapting irrigation strategies. They computed a specific agricultural drought index (SWDI) using data from the SMOS satellite. Within this study, various computation approaches were analyzed, and the ones that yielded the most promising results were those directly based on soil attributes or parameters extracted from pedotransfer functions (PTFs). These approaches utilized a multiple regression analysis, with soil water parameters as dependent variables, and incorporated other relevant soil characteristics such as texture, bulk density, and porosity.

Although regression models have been valuable in drought forecasting, they exhibit certain limitations such as the linearity assumption, limited interactions between variables, sensitivity to overfitting, and multicollinearity (Rafiei-Sardooi et al., 2018). Consequently, their ability to accurately represent complex real-world phenomena is often insufficient (Zhang, 2003). To address these shortcomings, more advanced models capable of capturing nonlinear relationships and interactions are required, ultimately improving the forecasting of complex hydroclimatic events such as droughts.

Figure 2 Drought forecasting based on a simple ANN architecture.

4.3 Machine learning and hybrid models

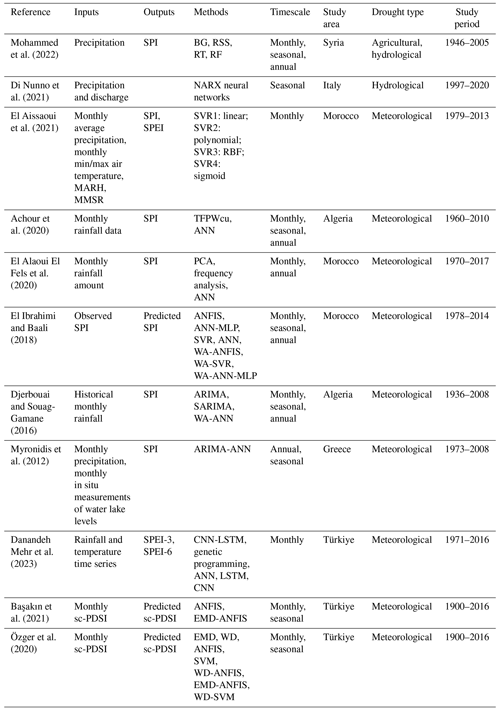
One of the big challenges in drought prediction is the random and nonlinear nature of the hydroclimatic variables (Agana and Homaifar, 2017). Over the last 2 decades, intelligent techniques such as artificial neural networks (ANNs), support vector machines (SVMs), and fuzzy logic (FL) have proven to be very promising tools for modeling nonlinear and dynamic time series (Mokhtarzad et al., 2017; Dikshit et al., 2022; Prodhan et al., 2022). These algorithms have thus garnered significant interest in the realms of drought modeling and forecasting (Prodhan et al., 2022). In the context of modeling, they are used to develop mathematical representations of complex drought systems, capturing the interplay of various atmospheric, hydrological, and land surface processes that lead to these phenomena. In forecasting, the models derived from these algorithms are employed to anticipate future drought conditions, assisting in risk assessment and mitigation strategies. Table 3 highlights key studies that utilize machine learning models for drought prediction in the MedR.

Table 3 Main studies using artificial intelligence models to forecast drought in the MedR.

Prodhan et al. (2022) stated in their review of machine learning methods for drought hazard monitoring and forecasting on a global scale that the ANN model was the most popular model in peer-reviewed literature, and they suggested that higher use of the ANN model is anticipated because it has nonlinear properties that make it more robust for identifying all possible interactions between predictors.

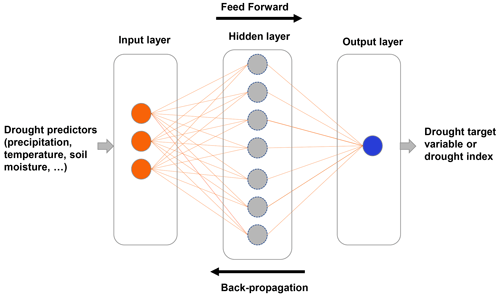
The ANN model is a mathematical model inspired by biological brain neural networks. It consists of an interconnected group of nodes (artificial neurons) and processes information using a connectionist computation (Fig. 2). In the case of drought forecasting, ANN architecture is usually made of three layers: an input layer which consists of the drought predictors, a hidden layer or layers which comprise a function that applies weights to the input variables and passes them using a non-linear activation function, and an output layer which consists of the drought target variable or drought index (Han and Singh, 2020).

For the proper functioning of a neural network, the optimization of network weights (known as the learning or training process) is an essential step (Dikshit et al., 2022). Back propagation, feed forward, gradient descent, stochastic gradient descent, Adam, and Levenberg–Marquardt algorithms are among the common training algorithms (Bergou et al., 2020). The role of these algorithms is to minimize the difference between predicted and observed values by adjusting the network weights and biases of the model.

Di Nunno et al. (2021) used a nonlinear autoregressive with exogenous inputs (NARX) neural network (a particular type of recurrent dynamic ANN) to predict spring flows in the Umbria region (Italy). The results of this study show a good performance of the NARX model in predicting spring discharges for both a short lag time (1 month: R²=0.90 to 0.98, RAE = 0.09 to 0.25) and a long-term lag time (12 months: R²=0.90 to 0.98, RAE = 0.09 to 0.24). Achour et al. (2020) also confirmed the performance of the ANN model with multilayer perceptron networks architecture and a Levenberg–Marquardt calibration algorithm in predicting drought in seven plains located in northwestern Algeria with a 2-month lead time (R²=0.81, RMSE < 0.41, and MAE < 0.23).

SVM models are also robust supervised learning models that investigate data for classification and regression analysis. It designates the best separating line to classify the data with more safety margins. Besides its good performance in solving linear problems, SVM could also transfer a nonlinear classification to a linear one using the kernel function and be able to solve high-dimensional problems (El Aissaoui et al., 2021).

In the context of drought studies, SVMs are particularly beneficial due to their ability to handle many inputs, ability to use a small dataset for training, and resistance to overfitting compared to ANN models (Hao et al., 2018). These features make SVMs less sensitive to the data sample size, enhancing the robustness of the drought model. Regarding the forecasting aspect, SVMs employ a kernel function to map predictors in a high-dimensional hidden space, subsequently transforming the predictand to the output space (El Aissaoui et al., 2021). This process allows the SVM model to generate effective and accurate forecasts about potential future drought events given the input variables.

El Aissaoui et al. (2021) used the support vector regression (SVR) model with three kernel functions (linear, sigmoid, polynomial, and radial basis function (RBF)) for the prediction of drought in the region of upper Moulouya (Morocco) through SPI and SPEI. Their research underscores the SVR model's effectiveness, particularly with the RBF kernel function, in forecasting the drought indices SPI (R=0.92) and SPEI (R=0.89). Mohammed et al. (2022) evaluated the applicability of four machine learning algorithms, namely bagging (BG), random subspace (RSS), random tree (RT), and random forest (RF), in predicting agricultural- and hydrological-drought events in the eastern MedR based on SPI. The results of this study revealed that hydrological drought (SPI-12, SPI-24) was more severe over the study area and BG was the best model in the validation stage with RMSE ≈ 0.62 to 0.83 and r≈0.58 to 0.79.

To further improve the prediction accuracy of artificial intelligence (AI) models, pre-processing of data using wavelet decomposition (WD), PCA, or empirical mode decomposition (EMD) is recommended. These techniques known as hybrid models have gained attention due to their potential to improve prediction accuracy and better capture complex relationships in the data (Yoo et al., 2015; Liu et al., 2020). The pre-processing techniques are used to extract and represent the essential features and patterns within the data and statistical methods, such as ANN, SVM, or RF, and model the relationship between the input variables and the target drought index. El Ibrahimi and Baali (2018) explored the prediction of short-term (SPI-3) and long-term (SPI-12) drought conditions using six models – SVR, ANN-MLP, adaptive neuro-fuzzy inference systems (ANFISs), WA-SVR, WA-MLP, and WA-ANFIS – in the Saïss Plain (Morocco). They argued that ANN models were more efficient than SVR models and that the use of wavelet analysis has enhanced the prediction skill of ANN models, which is probably due to their capacity to detect local discontinuities and nonstationary characteristics of the data.

Özger et al. (2020) evaluated the effect of using EMD and WD for decomposing time-series data on drought prediction using the self-calibrated Palmer drought severity index (sc-PDSI) and ANN and SVM machine learning models. They found that the accuracy of standalone machine learning models in midterm sc-PDSI predictions was unsatisfactory, but it significantly improved when EMD and WD techniques were introduced, particularly for hybrid wavelet models.

In summary, machine learning and hybrid models, which combine pre-processing techniques with statistical methods, have demonstrated their efficiency in drought forecasting, as they can effectively handle intricate, nonlinear relationships and adjust to a diverse range of input data characteristics. However, the applicability of these models may be challenging when input variables exhibit strong dependence on each other. This dependency can lead to several issues such as multicollinearity, overfitting, and diminishing returns (Maloney et al., 2012). To address these limitations and improve drought forecasting performance, it is essential to consider joint probability models (Madadgar and Moradkhani, 2014; Hao et al., 2018).

4.4 Joint probability models

The probabilistic analysis of drought events plays a significant role in the planning and management of water resource systems, particularly in arid or semi-arid Mediterranean regions known for low annual and seasonal precipitation. Drought return periods, which estimate the frequency of drought events, can provide valuable information for responsible water management during drought conditions. The univariate frequency analysis is a common method for analyzing drought events. As mentioned above, drought is usually characterized by its severity, duration, and frequency, which can be extracted using the theory of runs introduced by Yevjevich (1967). These characteristics present a dependence structure that can be ignored by the univariate approach, resulting in an under-/overestimation of drought risks. As such, several joint probability theories have been recently incorporated into drought risk analysis that include two or more variables. One of the most important joint probability models that has garnered increasing attention in the hydrologic community over the last decade is the copula model (Jehanzaib et al., 2021; Pontes Filho et al., 2020; Das et al., 2020; Zellou and Rahali, 2019; Mortuza et al., 2019; Ozga-Zielinski et al., 2016; Xu et al., 2015; AghaKouchak, 2014; Madadgar and Moradkhani, 2013; Chen et al., 2013).

There are numerous copula families and classes, such as elliptic, Archimedean (Clayton, Frank, Gumbel, Joe), extreme value, and Bayesian to cite but a few. The choice of the most suitable copula family depends on the specific modeling goals and the structure of the data being modeled (Genest and Favre, 2007; Joe, 2014).

A brief overview of the bivariate copula theory is given here to initiate readers with its concept and application. However, for additional details on the theory and concepts of the copula, readers may refer to the monographs by Joe (1997) and Nelsen (2007). Furthermore, comprehensive methodological understanding of constructing high-dimensional copulas, such as pair copula construction (PCC) and nested Archimedean construction (NAC), can be garnered from the works of Aas and Berg (2009) and Savu and Trede (2010).

Let F be a two-dimensional distribution function, with univariate margins F₁ and F₂ for random variables U and V, respectively. According to Sklar's theorem (Sklar, 1959), there exists a copula C such that

$$\begin{array}{}\text{(3)}& F(U,V)=C\left(F_{\mathrm{1}}\left(U\right),F_{\mathrm{2}}\left(V\right)\right)U,V\in R,\end{array}$$

with C being unique when F₁(U) and F₂(V) are continuous marginal distributions, so $C:[\mathrm{0},\mathrm{1}{]}^{\mathrm{2}}\to [\mathrm{0},\mathrm{1}]$ that satisfies the boundary conditions $C(u,\mathrm{0})=C(\mathrm{0},v)=\mathrm{0}$ and $C(u,\mathrm{1})=C(\mathrm{1},u)=u$ (uniform margins) for any values of $u\in [\mathrm{0},\mathrm{1}]$ and the so-called 2-increasing property (Papaioannou et al., 2016).

The main advantage of the copula over the traditional multivariate distributions is its ability to model the nonlinear dependence structure between variables independently from the choice of their marginal distributions (Salvadori and De Michele, 2004). This concept simplifies the joint probability analysis, and its application in high dimensions (with a large number of variables or predictors) becomes possible.

Serinaldi et al. (2009) constructed a four-dimensional joint distribution using the copula approach and SPI to model the stochastic structure of drought variables in Sicily (Italy). Drought return periods were next computed as the mean interarrival time, taking into account two drought characteristics at a time by means of the corresponding bivariate marginals of the fitted four-dimensional distribution. Bouabdelli et al. (2020) investigated the joint probability and joint return period of drought severity and duration using copula theory to assess the hydrological-drought risk in the reference period and its probability of occurrence in the future under two climate change scenarios in three basins located in northern Algeria. Bonaccorso et al. (2015) evaluated the conditional probability of future SPI classes under the hypothesis of multivariate normal distribution of NAO and SPI series in Sicily (Italy). The results of this study indicated that transition probabilities towards equal or worse drought conditions increase as the NAO tends towards extremely positive values. Table 4 displays additional examples of the application of the joint probability models to forecast drought in the MedR.

Table 4 Main studies using joint probability models to forecast drought in the MedR.

All the abovementioned studies confirm that copulas can accurately capture the joint distribution and dependence structure between multiple drought predictors without making strong assumptions about their marginal distributions. By combining the strengths of machine learning models with the flexibility of copulas, researchers can develop more accurate and reliable hybrid methods that better represent the intricacies of hydrological processes and climatic variables, even in the presence of strong dependence among the input variables (Jiang et al., 2023; Li et al., 2022; Wu et al., 2022; Zhu et al., 2020).

4.5 Ensemble streamflow prediction

The ESP method, a commonly used technique in hydrological forecasting, was primarily intended for medium- to long-term streamflow prediction (Day, 1985). However, its utility extends to the prediction of hydrological droughts, characterized by low streamflows (KyungHwan and DegHyo, 2015; Sutanto et al., 2020; Troin et al., 2021).

ESP operates on the principle of employing historical data to generate an ensemble of possible future climate conditions (Turco et al., 2017b). The process begins by determining the current state of the system, considering parameters such as current streamflow, soil moisture levels, and reservoir levels, which serve as the initial conditions for the forecast (Wanders and Wood, 2016). The generation of the ensemble involves choosing a historical record at each time (day, week, or month) of forecast that will provide the meteorological inputs (Day, 1985). By repeating this process for every time in the historical record, an ensemble of forecasts is produced, each member representing a potential future scenario. The hydrological model is run for each ensemble member, using the chosen meteorological inputs and initial conditions to generate a range of potential future states of the system (Harrigan et al., 2018). The ensemble of forecasts is then analyzed to derive probabilistic predictions.

As new data become available, forecasts can be updated by re-initializing the system's state and generating a new ensemble of forecasts. A significant advantage of this method is that it enables the uncertainty prediction by producing a variety of potential future streamflow forecast scenarios which can increase the confidence of this approach, specifically for its operational use in water management (Troin et al., 2021).

However, the limitations of the ESP method must be noted. For instance, it presupposes that future behavior will mirror past behavior, a concept that may not hold under changing climatic conditions (Wanders and Wood, 2016). Furthermore, the method's performance is heavily reliant on the quality and duration of the historical meteorological records used in the ensemble generation process (Turco et al., 2017b).

ESP is frequently employed as a benchmark for comparison with more sophisticated forecasting methods, such as dynamical climate models or hybrid statistical–dynamical models (AghaKouchak et al., 2014; Turco et al., 2017b; Torres-Vázquez et al., 2023). Although these more complex methods can outperform ESP in some instances, the computationally efficient ESP method often exhibits comparable performance, particularly when forecasting a few months ahead (Turco et al., 2017b; Torres-Vázquez et al., 2023).

4.6 Markov chain models

Markov chains are effective tools to understand the stochastic characteristics of drought events and their temporal dependency. These models assume that future states depend only on the current state.

Mathematically, the Markov chain is a stochastic process X such that at any time t, X_t+1 is conditionally independent from X₀, X₁, X₂, …, X_t−1, given X_t; the probability that X_t+1 takes a particular value j depends on the past only through its most recent value X_t:

$$\begin{array}{}\text{(4)}& \begin{array}{rl}P\left\{X_{t+\mathrm{1}}=\right.& \left.j\mathrm{|}{X}_{\mathrm{0}},X_{\mathrm{1}},\mathrm{\dots },X_t\right\}=P\left\{X_{t+\mathrm{1}}=j\mathrm{|}{X}_t=i\right\}\\ & \forall i,j\mathit{ϵ}S,t\in T.\end{array}\end{array}$$

A Markov chain is characterized by a set of states, S, and by the transition probability, P_ij, between states. The transition probability P_ij is the probability that the Markov chain is at the next time point in state j, given that it is at the present time point in state i.

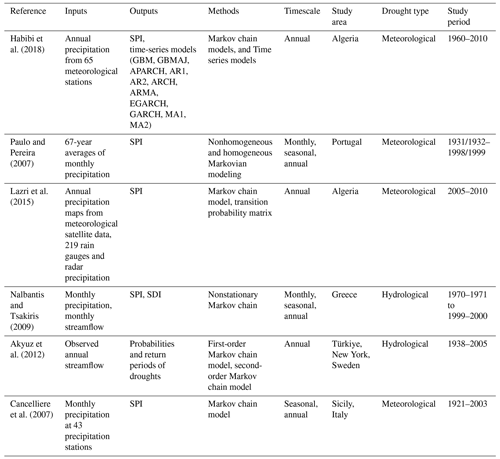
The drought prediction using this concept can be expressed as the transition from a wet or normal state to a dry state (or the other way around) or the transition from one drought severity state to another (e.g., no drought, mild drought, moderate drought, extreme drought). Habibi et al. (2018) studied meteorological drought in northern Algeria's Chéliff–Zahrez Basin, employing both localized and spatially distributed probabilities for temporal transitions using Markov chains and recurrence probabilities using an optimal time-series model, the APARCH approach. Paulo and Pereira (2007) used Markov chains, incorporating homogeneous and nonhomogeneous formulations, to predict drought transitions up to 3 months ahead, based on SPI derived from 67 years of data in southern Portugal. The nonhomogeneous Markov model outperformed its counterpart by considering the initial month and seasonal rainfall variations. Table 5 lists additional studies that apply Markov chain models for MedR drought forecasting.

Table 5 Main studies using Markov chain model to forecast drought in the MedR.

These studies generally support the effectiveness of Markov chain models in providing valuable drought insights. However, it is essential to consider the challenges associated with applying Markov chains within the MedR, as the region's complex topography, considerable interannual climate fluctuations, limited data availability, and nonstationarity resulting from climate change can adversely affect the models' core assumptions and constrain their long-term forecasting accuracy. Addressing these challenges calls for the adoption of more sophisticated techniques that encompass both stochastic and physically based approaches, ultimately enhancing the accuracy and reliability of drought predictions in this region (Paulo and Pereira, 2007).

5 Dynamical drought prediction methods

Dynamical drought prediction methods are generally based on the use of seasonal climate forecasts derived from comprehensive GCMs. The European Centre for Medium-Range Weather Forecasts (ECMWF) System 4 (SYS4), the Hadley Centre Global Environmental Model (HadGEM), the Community Earth System Model (CESM), and the National Centers for Environmental Prediction (NCEP) Climate Forecast System (CFS) are some widely recognized examples. Designed to emulate physical processes across the atmosphere, ocean, and land surface, these GCMs can produce near-term forecasts for various climatic factors such as precipitation, temperature, surface pressure, and winds. However, these models typically provide a global overview and possess a relatively coarse resolution, which spans 150 to 300 km horizontally and encompasses 10 to 20 vertical atmospheric layers and up to 30 oceanic layers. This level of detail may not offer the specificity necessary for local-scale impact assessments. To counter this, post-processing steps, encompassing downscaling and bias correction, are crucial when employing GCM forecasts (Tuel et al., 2021; Gumus et al., 2023). The main objective here is to refine the global, coarse-grained GCM data into higher-resolution forecasts. These refined forecasts are far more pertinent for predicting seasonal drought events at a regional and local scale within the MedR.

The most common approaches to downscale GCM forecasts include statistical models, dynamic or nested models, and hybrid statistical–dynamical models (Wilby et al., 2004). In statistical downscaling, large-scale variables are used as the predictors and desired near-surface climate variables are the predictands (Aguirre-Gutiérrez et al., 2019). The role of statistical models is then to measure the correlations between predictors and predictands, whereas dynamical downscaling refers to the use of high-resolution regional simulations to dynamically extrapolate the effects of large-scale climate processes to regional or local scales based on a nesting approach between GCMs and regional climate models (RCMs) (Giorgi and Gutowski, 2015). However, it is known that GCMs contain significant systematic biases that may propagate into RCMs through the lateral and lower boundary conditions and thus degrade the dynamically downscaled simulations and lead to large uncertainties (Maraun, 2016). Besides, climate predictions from a single climate model simulation are sensitive to initial oceanic and atmospheric states and can represent only one of the possible pathways the climate system might follow.

5.1 Multi-model ensemble

To allow probabilistic estimates of climate variables with uncertainties in quantification, it is necessary to carry out an ensemble of simulations with different initial conditions from each model and to combine various models as ensemble members. The frequently used multi-model ensemble (MME) and bias correction methods include quantile mapping (Wood et al., 2002) and Bayesian model averaging (Krishnamurti et al., 1999; Seifi et al., 2022). These methods proceed by adjusting the modeled mean, variance, and/or higher moments of the distribution of climate variables to match the observations. However, such MME simulations can be very computationally demanding. Therefore, some international dynamical downscaling intercomparison projects were carried out such as the Coordinated Regional Climate Downscaling Experiment (CORDEX; Wilby et al., 1998) and its Mediterranean initiative Med-CORDEX (Ruti et al., 2016) to provide present and future climate simulations with a high spatial resolution (∼12 km). In a study conducted by Turco et al. (2017b), the accuracy and reliability of ECMWF's System 4 (SYS4) in forecasting drought conditions, characterized by a 6-month SPEI-6, across Europe from 1981 to 2010 were evaluated. The authors found that the SYS4 model effectively projected the spatial patterns of SPEI-6 and various drought conditions (ranging from extreme to normal) with a reasonable degree of precision up to a lead time of 2 months. In the same geographical context, Ceglar et al. (2017) demonstrate the power of dynamical models in the agricultural sector by investigating the relationship between large-scale atmospheric circulation and crop yields in Europe. Their research highlights the significant potential of such models in developing effective seasonal crop yield forecasting and, consequently, in advancing dynamic adaptation strategies to climate variability and change.

All these studies confirmed the good performance of MME methods in providing probabilistic drought forecasts for 1 to 2 months of lead time and improving drought onset detectability. However, much effort should be made in selecting the most skilled GCM ensembles in reproducing the large- and synoptic-scale atmospheric and land surface conditions associated with drought development in the MedR. By prioritizing ensembles that adequately capture the region's distinct climate characteristics, spatial–temporal variability, and land–atmosphere interactions, the MME forecasts can mitigate biases related to key meteorological variables such as temperature or precipitation and significantly improve the precision and reliability of drought predictions (Li et al., 2023; Ahmed et al., 2019).

5.2 Coupled hydrological models

On the other hand, GCMs often struggle to accurately represent some complex elements of the hydrological cycle, such as soil moisture, streamflow, groundwater level, and PET. The inherent complexities of these variables and the broad spatial scale of GCMs make it challenging to fully capture their behavior. This gap can limit the effectiveness of GCMs in drought prediction and modeling (Balting et al., 2021). Consequently, to dynamically forecast agricultural and hydrological droughts, the water balance should be correctly simulated by hydrological models forced by climate forecasts (Wanders and Wood, 2016). Among the most used models to forecast hydrological drought, we cite the Soil & Water Assessment Tool (SWAT) (Arnold et al., 1998), the variable infiltration capacity (VIC) model (Liang et al., 1994), and the Community Land Model (CLM) (Oleson et al., 2004). These models can incorporate data on soil moisture, vegetation, snow water equivalent, groundwater level, and other initial hydrologic conditions with climate forecasts to simulate the movement of water through the hydrological cycle, including the processes of precipitation, evaporation, infiltration, and runoff. Crop growth models can also be coupled with hydrological models to make an accurate prediction of agricultural drought and its impact on crop yields (Narasimhan and Srinivasan, 2005; Abhishek et al., 2021).

Coupled hydroclimatic models can improve drought forecasting by allowing for the consideration of feedback between the hydrological and climatological components of the Earth system. Indeed, drought conditions can affect the availability of water for evapotranspiration, which in turn can affect the amount of moisture in the atmosphere and the likelihood of precipitation. By incorporating this feedback into the model, it is possible to produce more accurate forecasts of drought conditions.

In a recent study, Brouziyne et al. (2020) combined meteorological and hydrological drought indices (SPI and SDI) with a SWAT model forced by bias-corrected CNRM-CM5 data to predict future droughts under two representative concentration pathways (RCPs; RCP4.5 and RCP8.5) in the Bou Regreg watershed, Morocco. They confirmed that using multiple drought indices and a comprehensive water budget indicator such as total water yield provided a valid approach to evaluating drought conditions in a Mediterranean context. Marx et al. (2018) analyzed a multi-model ensemble of 45 hydrological simulations based on three RCPs (RCP2.6, RCP6.0, and RCP8.5), five GCMs (CMIP5), and three state-of-the-art hydrological models (mHM, Noah-MP, and PCR-GLOBWB) to investigate how hydrological low flows are affected under different levels of future global warming. Based on the analysis of the results, the authors recommended using multiple hydrological models in climate impact studies and embracing uncertain information in the multi-model ensemble as well as its single members in the adaptation process.

5.3 Long-term drought projection under climate change

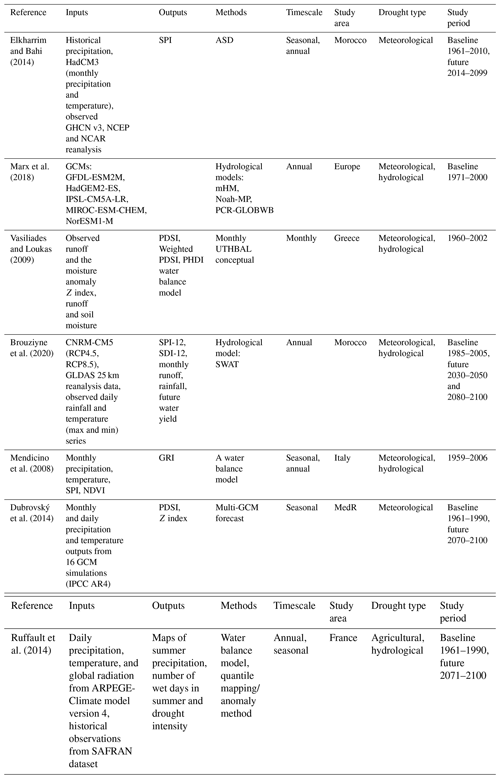
As climate change continues to influence drought events in the MedR, it is vital to integrate long-term climate projections into drought forecasting strategies (Tramblay et al., 2020). In this regard, GCMs are essential for projecting future climate changes under varying scenarios, such as Representative Concentration Pathways (RCPs) or Shared Socioeconomic Pathways (SSPs).¹ Coupled with downscaling techniques, these models offer region-specific projections of critical climate variables including precipitation, temperature, surface pressure, and winds. These projections are instrumental in estimating long-term drought events, facilitating a more comprehensive risk assessment for stakeholders and decision-makers. Baronetti et al. (2022) analyzed the expected characteristics of drought episodes in the near (2021–2050) and far (2071–2100) future compared to the baseline conditions (1971–2000) for northern Italy using EURO-CORDEX and Med-CORDEX GCM–RCM pairs at a spatial resolution of 0.11^∘ for the RCP4.5 and RCP8.5 scenarios. The results indicated that the GCM–RCM pairs performed generally well, while in complex environments such as coastal areas and mountain regions, the simulations were affected by considerable uncertainty. Dubrovský et al. (2014) used an ensemble of 16 GCMs to map future drought and climate variability in the MedR. Bağçaci et al. (2021) compared the capacity of the Coupled Model Intercomparison Project Phase 6 (CMIP6, the latest release) model ensembles in representing the near-surface temperature and precipitation of Türkiye in comparison with its predecessor CMIP5 to better understand the vulnerability degree of the country to climate change. In a study conducted by Cos et al. (2022), the authors compared climate projections from CMIP5 and CMIP6 models to assess the impacts of climate change in the MedR. The findings reveal a robust and significant warming trend across all seasons, with CMIP6 models projecting stronger warming compared to CMIP5. While precipitation changes show greater uncertainties, a robust and significant decline is projected over large parts of the region during summer by the end of the century, particularly under high-emission scenarios. Seker and Gumus (2022) used 22 global circulation models from CMIP6 to project future precipitation and temperature changes in the MedR. The MMEs outperform individual GCMs in simulating historical data, and the projections indicate a decrease in precipitation by 15 % for SSP2-4.5 and 20 % for SSP5-8.5. Table 6 shows the main studies using dynamical models to forecast drought in the MedR.

Table 6 Main studies using dynamical models to forecast drought in the MedR.

In summary, recent advancements in seasonal drought forecasting with dynamical models encompass increased climate resolution, improved representation of physical processes, improved initialization methods using data assimilation techniques (Zhou et al., 2022), use of multi-model ensembles (Wanders and Wood, 2016; Seker and Gumus, 2022), coupled modeling approaches (Guion et al., 2022), and the development of sub-seasonal to seasonal predictions (Zhou et al., 2021). These steps have contributed to more accurate and reliable drought predictions. However, even with these improvements, predicting drought months in advance remains a significant challenge due to the inherent complexity and chaos of the climate system.

6 Hybrid statistical–dynamic methods

While statistical models, when appropriately fine-tuned, can effectively predict seasonal drought events, a significant limitation arises from the nonstationary relationship between the predictors and predictands used in the forecasting process (AghaKouchak et al., 2022). This can limit their ability to accurately predict unprecedented drought events, which fall beyond the scope of their historical training data (Hao et al., 2018). On the other hand, dynamical models are proficient at capturing the nonlinear interactions among the atmosphere, land, and ocean, enhancing their ability to detect the onset of droughts (Turco et al., 2017b; Ceglar et al., 2017). However, despite their advanced capabilities, their forecast proficiency is generally constrained to a few months of lead time (Turco et al., 2017b). To address the shortcomings associated with seasonal forecasting skills, hybrid models employ statistical or machine learning methods to merge a broad variety of forecasts from statistical and dynamical models into a final probabilistic prediction product (Slater et al., 2023). The frequently used merging methods include regression analysis, BMA, and the Bayesian post-processing method (Hao et al., 2018; Strazzo et al., 2019; Han and Singh, 2020; Xu et al., 2018). The BMA method involves the estimation of the posterior probability density function (PDF) of model parameters based on the observed data and uses this PDF to weight each individual model forecast (Tian et al., 2023). The hybrid forecast is then generated as the weighted average of the individual forecasts from statistical and dynamical models. The BMA weights' estimation with simultaneous model uncertainty quantification can also be used in selecting the best-performing ensemble members to reduce the cost of running large ensembles (Raftery et al., 2005). There is also an opportunity to enhance the probabilistic seasonal forecast skill through Bayesian post-processing methods such as the calibration, bridging, and merging (CBaM) technique (Schepen et al., 2014, 2016; Strazzo et al., 2019). The calibration step consists in optimizing the dynamical forecasts from multiple GCMs by analyzing their correlation to observed data through a statistical model. In the bridging step, the dynamical forecasts from GCMs are calibrated using some large-scale climate indices (e.g., ENSO, NAO, PDO, AO), and finally, the merging component combines the forecasts of the two previous steps.

These hybrid statistical–dynamical models combine the strengths of both modeling approaches and offer several advantages compared to either statistical or dynamical models alone. Thereby, seasonal drought forecasting using hybrid models has recently become an active area of research (Madadgar et al., 2016; Strazzo et al., 2019; AghaKouchak et al., 2022). On a global scale, Yuan and Wood (2013) analyzed the capability of seasonal forecasting of global drought onset and found that despite climate models increasing drought detection, a significant proportion of onset events are still missed. Their findings underscore the urgent need for implementing reliable, skillful probabilistic forecasting methods to better manage the inherent uncertainties and potentially improve drought predictability. Dutra et al. (2008) confirmed that the uncertainty in long-lead-time forecasts suggests that drought onset might fundamentally be a stochastic problem. Mo and Lyon (2015) also found that improvements in near-real-time global precipitation observations could yield the most substantial advances in global meteorological-drought prediction in the near term. This reinforces the notion that the effectiveness of dynamical models is fundamentally associated with the quality of the initial data and the inherent stochastic nature of drought onset.

In line with these findings, a unique approach was undertaken by Ribeiro and Pires (2016) in the MedR. They proposed a hybrid scheme that combines dynamical forecasts from the UK Met Office (UKMO) operational forecasting system with past observations as predictors in a statistical downscaling approach based on the MLR model for long-range drought forecasting in Portugal (Table 7). They concluded that hybridization improves drought forecasting skills in comparison to dynamical forecasts.

Table 7 Main studies using hybrid statistical–dynamical models to forecast drought in the MedR.

Leveraging these advantages of hybrid statistical–dynamical models, the prediction of flash droughts has become possible. Indeed, these events can develop rapidly by a quick decline in soil moisture and streamflow that may cause devastating economic and ecological impacts in a short period (from a few days to 1–2 months) (Mo and Lettenmaier, 2015), which makes them particularly challenging to forecast. By providing a more nuanced understanding of the drought contributing factors, hybrid statistical–dynamical models help to identify potential warning signs of an imminent drought event, improve drought early warning systems, and reduce the false alarm rate of drought onset (Xu et al., 2018), thus tackling some of the limitations and challenges highlighted in the earlier studies.

Figure 3 Pie chart showing the proportion of the use of indices in the surveyed studies in the MedR for different drought types.

7 Discussion

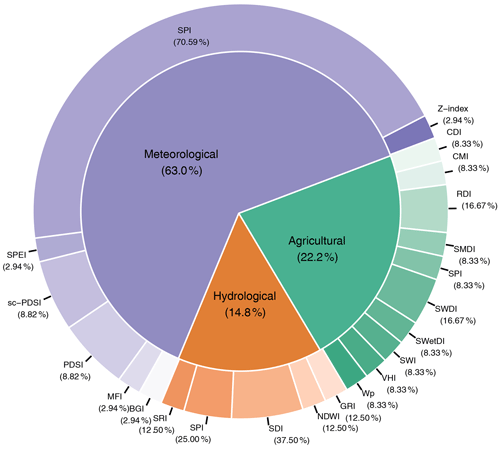
7.1 Drought types and indices

The indices adopted by the surveyed studies were grouped according to three distinct drought categories: meteorological, agricultural, and hydrological. Figure 3 illustrates the percentage of usage for each index by category. Meteorological droughts were the most common, appearing in 63.00 % of the examined studies, followed by agricultural droughts with approximately 22.20 %, whereas hydrological droughts were the least prevalent, making up only 14.80 %.

SPI was the primary indicator, used in 70.59 % of meteorological-drought studies. But it also served as an indicator for hydrological and agricultural droughts, with usage rates of around 25.00 % and 8.33 %, respectively.

Despite the apparent versatility of SPI, its reliance on precipitation data limits its ability to account for other influential factors such as evapotranspiration, soil moisture, land usage, and water management practices. Consequently, an overemphasis on SPI could potentially constrain our comprehension of drought phenomena in the MedR. To enrich this understanding, it is recommended to incorporate a broader range of indicators and models that include a more diverse set of variables. Using multivariate drought indices such as SPEI, PDSI, or sc-PDSI or, alternatively, a combination of multiple indices can contribute to a more comprehensive view by including regional feedback mechanisms in the forecast process. This approach also enhances our capacity to evaluate the impacts of global warming on drought severity and intensity in the MedR (see Marcos-Garcia et al., 2017; Gouveia et al., 2017).

On the other hand, SDI was the most applied index in hydrological-drought studies in the MedR (37.50 %). It is calculated by comparing the current streamflow to the long-term average or median streamflow for a specific location and time of year (Nalbantis and Tsakiris, 2009). Despite its usefulness, there are some limits to using SDI in the MedR. Indeed, this region is known for highly variable climates with strong seasonality (wet winters and dry summers) and the presence of transient streams or intermittent rivers that flow only during and after rainfall events, especially in sub-humid and semi-arid areas. Groundwater recharge principally occurs during the wet season, when precipitation infiltrates the soil and replenishes aquifers (Scanlon et al., 2006). In these regions, SDI may not provide an accurate representation of the hydrological drought as it relies solely on streamflow data. Therefore, the use of SDI should be made in combination with other drought indices that consider variables such as groundwater, soil moisture, runoff, and regional variations in precipitation and streamflow patterns for accurate hydrological-drought assessment.

One can notice from Fig. 3 that the agricultural-drought studies are characterized by more diversity of indices. This diversity can be explained by the varied range of agro-climatic conditions that characterize the MedR, including a wide range of soil types, topography, and vegetation cover. These diverse conditions can result in varying impacts of drought on agricultural production, which require different drought indices to accurately capture the extent and severity of the drought. In addition, the MedR is also home to a diverse range of crops, each with different sensitivities to drought (Fereres and Soriano, 2007). This diversity of crops can require different indices to assess the impact of drought on each crop.

Overall, a suitable index should be able to capture the impacts of drought, detect changes over time, and differentiate between different levels of severity while also being accurate and easily interpretable by stakeholders.

7.2 Drought forecasting accuracy

Key obstacles in drought modeling include the absence of a one-size-fits-all model, choosing suitable inputs, determining an index that accurately represents drought tracking in various regions, and the uneven geographical influence that leads to discrepancies in model accuracy (Mishra and Desai, 2006; Murray and Ebi, 2012). Consequently, contrasting different methodologies is crucial for developing a reliable prediction model.

The accuracy of drought prediction depends on various factors such as the quality and availability of data, spatial and temporal scales, prediction lead time, and model complexity, to cite but a few (Wilhite et al., 2014; Mishra and Singh, 2010). For consistency, this analysis only includes studies that use R² as an evaluation criterion of the forecast with a lead time of 1 month. Joint probability models were excluded from this analysis, since the accuracy evaluation criteria were different. Moreover, the concept of lead time is not addressed in most of the surveyed studies. It is also important to note that this analysis does not include hybrid statistical–dynamical models, as the number of studies applying this approach in the MedR was quite limited. Consequently, the available research is insufficient to offer a comprehensive understanding of the applicability and effectiveness of these models in the region.

Figure 4 shows a box-and-whisker plot of drought forecasting model accuracy based on R² in the surveyed studies in the MedR (see Appendix). According to the graph, hybrid models appear to be the most accurate and consistent, with the highest median and shortest box height. Markov chains and AI models also have relatively short box heights, indicating high agreement and accuracy across studies. Meanwhile, dynamical and regression models exhibit moderate to high accuracy (both have a median equal to 0.79), but the height of the dynamical model box is shorter than that of the regression models, suggesting greater consistency. Time-series models also show moderate to high accuracy, with a median equal to 0.82.

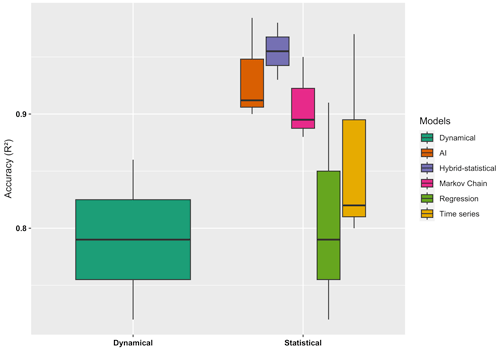
Figure 4 Box-and-whisker plot to show the performance of drought prediction models denoted by the coefficient of determination (R²) for the surveyed studies in the MedR. The lower edge of the box shows the 25th percentile, the upper edge of the box shows the 75th percentile, and the median (50th percentile) is represented by the black line inside the box. The whiskers show the extent of the minimum and maximum values within 1.5 times the interquartile range (IQR) of the box.

Nonetheless, Fig. 4 provides valuable information about the relative performance of different models across multiple studies in the MedR. The consistently high median of hybrid models suggests that they are particularly effective for drought forecasting in the region. Similarly, the consistent performance of the AI and Markov chain models suggests that these models also show promise. The variability in the performance of the regression, as well as the time series, as indicated by their taller boxplots, suggests that there may be more variability in the effectiveness of these models across different studies and regions. The results also show that dynamical models can provide valuable insights into drought conditions. However, the high variability in their performance suggests that there may be room for improvement in the development and implementation of these models in the MedR.

This analysis concludes that simple statistical models such as Markov chains, regression, and time series can still be useful in some situations and are generally more transparent and easier to interpret. For example, when focusing on a single variable to forecast drought (e.g., precipitation using SPI), simple models like ARIMA can effectively capture the temporal patterns and provide reasonable forecasts. Or, when drought conditions can be effectively represented by discrete states or categories, Markov chains can be employed to model the transition probabilities between these states and forecast future drought conditions (Habibi et al., 2018; Nalbantis and Tsakiris, 2009; Paulo and Pereira, 2007). Also, when working with a limited number of variables and moderate interactions, simple regression models like linear or logistic regression can provide adequate predictions of drought conditions (Sharma et al., 2018). The effectiveness of simple models in these situations depends on the specific context and the data quality and quantity. When more complex relationships or high-dimensional data are involved, it may be necessary to employ more advanced models like dynamical models or combine simple models with techniques like machine learning, copulas, or hybrid approaches to improve forecasting performance. Hybrid statistical–dynamical models present a promising avenue for enhancing forecast accuracy, particularly for extended lead times and in situations where intricate processes and interactions are critical (AghaKouchak et al., 2021; Mehran et al., 2017; Madadgar et al., 2016). The relatively nascent emergence of these hybrid techniques has resulted in only a limited number of studies applying them in the MedR. This can be ascribed to factors such as data constraints, computational complexity, and model uncertainty. Moreover, proficiency in both statistical and dynamical modeling is needed, and interdisciplinary cooperation is frequently deficient. Notwithstanding these challenges, there is an increasing interest not only in enhancing traditional dynamical models but also in the development and utilization of hybrid models. As research progresses and resources become more accessible, these hybrid models may see wider adoption for their potential to improve predictive accuracy.

7.3 Spatial and temporal scales of drought

Figure 5 displays the spatial and temporal scales of drought forecasting studies in the MedR with pie charts indicating the percentage of use of the drought forecasting methods – statistical, dynamical, and hybrid statistical models – for each spatiotemporal scale. This figure shows that the number of drought forecasting studies tends to decrease as the spatial scale increases and increases as the timescale increases. We can also notice from this figure that the majority of studies in the MedR focused on the local scales (e.g., city or catchment), particularly at annual and seasonal timescales. In contrast, very few studies were conducted at the MedR scale, and only a few studies were conducted at the country scale.

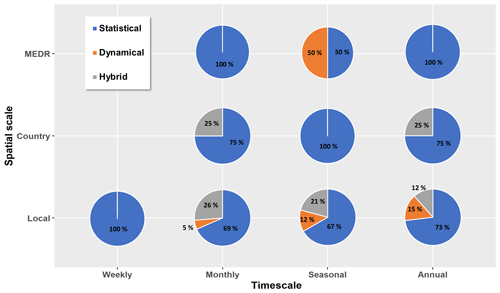
Figure 5 Spatial and temporal scales of drought forecasting studies in the Mediterranean region with pie charts indicating the percentage of use of the drought forecasting methods – statistical, dynamical, and hybrid statistical models – for each spatiotemporal scale.

When considering the spatial scale, drought forecasting becomes more challenging at larger scales due to various factors. One of the major challenges is the complexity of the interactions between different factors that contribute to droughts, such as precipitation, temperature, soil moisture, and vegetation cover (Sheffield and Wood, 2011). These interactions are nonlinear and difficult to capture accurately, especially at larger scales where there is more variability and heterogeneity (AghaKouchak et al., 2015). For instance, at the country scale, there could be different microclimates, topography, and land use practices that affect these factors differently (Vicente-Serrano et al., 2010a). This heterogeneity tends to increase as the spatial scale increases, making it harder to calibrate and validate drought forecasting models. On the other hand, the small number of studies that focused on large geographic areas is probably due to the challenge of data availability and homogeneity, which arises due to limitations in data collection and standardization, particularly at larger spatial scales (Dai, 2011). This can lead to incomplete or inconsistent datasets, which in turn can impact the accuracy of drought forecasting models. Remote sensing technologies can provide a solution to this problem by allowing for the collection of large-scale, high-resolution data that can improve the accuracy of forecasting models (Gouveia et al., 2017). The role of remote sensing data in improving drought prediction will be further discussed in Sect. 8.2.

When considering the timescale, the number of drought forecasting studies tends to increase as the scale increases. Drought research often emphasizes seasonal, annual, or decadal scales due to various factors. The slow-onset nature of droughts necessitates studying their progression and recovery over extended periods (Mishra and Singh, 2010). Investigating longer timescales also allows researchers to analyze the impact of large-scale climate drivers, such as the ENSO or NAO, on drought events (Dai, 2011). Moreover, focusing on these timescales enables a better assessment of drought consequences for water resources, agriculture, and ecosystems, which are more pronounced over extended periods (Wilhite and Pulwarty, 2017). Additionally, data availability and reliability tend to be higher for longer timescales, facilitating more robust analyses. Long-term trends and climate change impacts on droughts can also be better understood at longer timescales (Trenberth et al., 2014).

Notably, only one study focused on the weekly timescale. Drought forecasting at small scales or weekly timescales offers several advantages, including early warning and improved water management (Pulwarty and Sivakumar, 2014), quick response to flash droughts (Mo and Lettenmaier, 2015), support for agricultural decision-making (Hansen et al., 2011), improved accuracy of longer-term forecasts (Yuan et al., 2015), and model improvement and validation (Wood et al., 2016). However, drought forecasting at such a small scale may be more challenging due to the chaotic nature of the atmosphere, making it difficult to accurately model complex interactions between atmospheric conditions, land surface characteristics, and water management practices over short periods (Lorenz, 1963; Seneviratne et al., 2012).

On the other hand, the most commonly used forecasting methods were statistical and hybrid statistical models, with only a few studies applying dynamical models and the percentage of studies applying this last approach increases with an increase in the temporal scale. There could be several reasons for these findings. Dynamical models require large quantities of high-quality input data, which may not be readily available for the MedR due to limitations in historical data and spatial coverage (Giorgi and Lionello, 2008). Statistical and hybrid statistical models often have lower data requirements and are generally computationally more efficient than dynamical models, making them more suitable for regions with limited data availability and with computational constraints. Furthermore, the percentage of studies applying dynamical models increases with an increase in the temporal scale because these models are better suited for capturing long-term climate variability and the influence of large-scale climate drivers (Dai, 2011; Sheffield et al., 2012). Statistical and hybrid statistical models, conversely, are more effective at capturing short-term variability and local-scale processes, which are often more relevant for drought forecasting in the MedR (Mehran et al., 2014). Lastly, data availability at shorter temporal scales can be a limiting factor for developing and validating dynamical models (Shah and Mishra, 2020).

In summary, while increasing the spatial scale can decrease the accuracy of drought forecasting studies, increasing the timescale can improve the accuracy by allowing for a more comprehensive understanding of the various factors that contribute to drought conditions. It is essential to consider both spatial and temporal scales when conducting drought forecasting studies to ensure the most accurate predictions possible.

8 Challenges and future prospects

In the earlier discussion (Sect. 7), we analyze drought indices, factors affecting the accuracy of drought forecasts, and the significance of spatial and temporal scales in drought predictions within the MedR context. Building on this understanding, the following sections focus on the challenges and prospects within the realm of drought forecasting, which will help to pinpoint potential avenues for progress and innovation in this area.

8.1 Data assimilation

The lack of in situ measurement networks and coarse global seasonal forecast skills has hindered drought forecasting facilities, especially in data-poor regions (Pozzi et al., 2013; Haile et al., 2020). In this regard, data assimilation (DA) provides a powerful approach to enhancing drought forecasting accuracy by incorporating different observations and climate forecasts into a hydrological model to generate more precise initial conditions (Hao et al., 2018; Tang et al., 2016). Therefore, many studies have referred to this method to better forecast hydroclimatic variables (e.g., Bazrkar and Chu, 2021; Peng, 2021; Xu et al., 2020; Liu et al., 2019; Steiger et al., 2018; Steiger and Smerdon, 2017). The ensemble Kalman filter (EnKF) (Evensen, 1994) algorithm is one of the most popular DA techniques applied by the hydrologic community. However, this assimilation method is subject to some inherent drawbacks, especially in nonlinear dynamic systems, thus resulting in suboptimal performance and violation of water balance (Abbaszadeh et al., 2018). Given these limitations, emphasis should be placed on the development of improved DA algorithms that are better adapted to hydrological models, which allow the modeling of different temporal and spatial scales and the improvement of water balance. This can be achieved by modifying the standard approaches such as the ensemble Kalman filter or variational algorithms so that accurate predictions can be obtained at a reasonable computational cost. These include among others hybrid EnKF–Var methods (Bannister, 2017; Bergou et al., 2016; Mandel et al., 2016) and AI algorithms for ensemble post-processing (Grönquist et al., 2021). One recent advance in data assimilation techniques for drought forecasting is the use of machine learning algorithms to improve the accuracy of predictions. For example, researchers have used machine learning techniques to develop models that can analyze large quantities of data from a variety of sources and generate more accurate forecasts of drought conditions (Aghelpour et al., 2020; Rhee and Im, 2017; Feng et al., 2019). These models can also be updated in real time as new data become available, allowing for more accurate and up-to-date forecasts. Another advance in data assimilation techniques for drought forecasting is the use of remote sensing data and reanalysis to improve the accuracy of predictions, which may be particularly beneficial in areas where ground-based observations are limited (Shahzaman et al., 2021b; Shi et al., 2011).

8.2 Remote sensing and reanalysis

Various challenges in drought modeling in the MedR are related to data availability: the lack of climatic and hydrological observations in ungauged catchments, low station density, short data records, data gaps, and limited data access in some Mediterranean countries. All these challenges can limit the accuracy and reliability of drought predictions. Although many efforts are being deployed by developing new complete datasets in the MedR (Tuel and El Moçayd, 2023), finding alternative data sources and modeling techniques is essential to tackle these challenges.

Remote sensing data can provide real-time information about the Earth's surface, facilitating effective drought forecasting, monitoring, and early warning (Zhang et al., 2016). Agricultural drought can be assessed by analyzing changes in vegetation cover over time. Indeed, drought can lead to marked changes in the health and vigor of vegetation, and these changes can be detected using remote sensing data (Belal et al., 2014). By analyzing changes in vegetation greenness over time, it is possible to identify areas that are experiencing or are at risk of experiencing drought stress. Moreover, drought conditions related to vegetation or evapotranspiration can also be monitored with drought indices from remote sensing products, such as the normalized difference vegetation index (NDVI) or evaporation stress index (ESI) (Shahzaman et al., 2021a). Microwave satellite data can also be used to estimate soil moisture levels during the crop growing season, which can be used to predict and monitor potential agricultural droughts (Le Page and Zribi, 2019; Yuan et al., 2015).

In addition, satellite observations of precipitation and soil moisture such as IMERG (Huffman et al., 2015), PERSIANN-CCS (Sadeghi et al., 2021), CHIRPS (Funk et al., 2015), SMAP (Entekhabi et al., 2010), MSWEP V2 (Beck et al., 2019), GLEAM v3 (Martens et al., 2017), and DROP (Turco et al., 2020) can be used in conjunction with in situ observations and ground-based radar observation data to fill observational gaps.

Moreover, data from numerical weather forecasting reanalysis such as ERA5-Land were used instead of or along with direct observations to forecast drought in many studies (Babre et al., 2020; Junqueira et al., 2022; Parker et al., 2021). ERA5-Land is a state-of-the-art global reanalysis dataset that can provide a consistent view of the evolution of land variables (e.g., precipitation, temperature) over several decades at an enhanced resolution (∼10 km). This product obtained by assimilating observations through a 4D-VAR data assimilation technique can be used as ground truth in data-poor regions. For example, ERA5-Land can be used to calibrate and validate climate forecasts and to choose an ensemble of the most skilled GCMs in reproducing the actual observed climate in a specific region.

Similarly, SAFRAN, a high-resolution meteorological reanalysis, has shown its utility in regions with sparse observational data. Tramblay et al. (2019) used SAFRAN to generate a high-resolution (5 km) gridded daily precipitation dataset for Tunisia between 1979 and 2015. Their study, which combined data from 960 rain gauges with the SAFRAN analysis, demonstrated that SAFRAN surpassed other standard interpolation methods like inverse distance, nearest neighbors, ordinary kriging, or residual kriging with altitude. The outcome was a highly accurate gridded precipitation dataset that could be instrumental for climate studies, model evaluation, and hydrological modeling to support the planning and management of surface water resources.

Finally, remote sensing data and reanalysis remain valuable tools for drought forecasting and monitoring, as they provide timely land surface information that can fill the observational gaps, help to identify areas at risk of potential drought conditions, and monitor the progression of drought over time.

8.3 Uncertainty analysis in drought forecasting

In spite of the large number of studies that have been carried out on the probabilistic characterization of drought, the quantification of uncertainty in these forecasts is still ignored in major studies. Uncertainty analysis is an important aspect of probabilistic drought forecast, as it allows users to understand the degree of confidence associated with the forecasted probabilities (Hao et al., 2016; Dehghani et al., 2014). Therefore, more efforts should focus on quantifying the uncertainty beyond just an ensemble of model simulations (AghaKouchak et al., 2022).

Drought forecasting is subject to epistemic and aleatory uncertainties. The first one arises from incomplete knowledge of drought processes and can be reduced with improved understanding, more data, and good model calibration and validation. The second one is related to the inherent variability and randomness in natural systems and is often difficult to reduce (Pappenberger and Beven, 2006). In addition, uncertainties in drought forecasting can vary by region, spatial scale, and temporal scale. As we discussed in Sect. 7.3, even when well calibrated and validated, the drought forecasting model will not necessarily perform equally well in all periods or locations. By considering the uncertainty in the drought model a nonstationary process in space and time, researchers can gain new insights into the variability in uncertainty and its underlying causes (AghaKouchak et al., 2022). This perspective can help identify regions or periods where the uncertainties are particularly high, which can guide further research, data collection, and model development efforts. Additionally, understanding the space–time variability in uncertainty can inform the development of more robust and reliable forecasting and decision-making approaches that account for the changing nature of uncertainty.

Various techniques can be employed to quantify drought forecast uncertainty, including ensemble forecasting (Palmer et al., 2004), Bayesian methods (Vrugt et al., 2005), sensitivity analysis (Saltelli et al., 2008), and probabilistic forecasting (Gneiting et al., 2005). Probabilistic drought prediction can also involve the use of data assimilation techniques to integrate different data sources, including remote sensing data, ground-based observations, and output from meteorological and hydrological models. Lately, hybrid statistical–dynamical models have shown their potential in reducing uncertainties associated with both statistical and dynamical methods (Yuan et al., 2015; Madadgar et al., 2016). For example, shortcomings in dynamical model physics or data can be counterbalanced by the empirical associations in statistical models, while uncertainties in statistical models resulting from shifting climate conditions can be tackled by the physically based dynamical models (Yuan et al., 2015).

In summary, probabilistic drought prediction with uncertainty analysis can comprise useful tools for decision-makers, as it provides a more comprehensive view of the potential impacts of drought and allows for more informed risk management decisions. However, what is missing in the current drought forecasting models is not just uncertainty quantification, but also a lack of awareness of it (AghaKouchak et al., 2022).

8.4 Drought information systems

A critical component of proactive approaches to drought preparedness is providing timely and reliable climate information, including seasonal forecasts, that helps decision-makers prepare management policies (Manatsa et al., 2017). Identifying drought risk in a timely manner depends on our ability to monitor and forecast its physical causative mechanisms at the relevant spatiotemporal scale. An integrated national drought monitoring and early warning system has been implemented in many regions and countries such as the United States, New Zealand, South Asia, India, and Europe (Prabhakar and Rama, 2022) but has not taken place until recently in developing countries (e.g., the southern and eastern Mediterranean countries). This is probably due to the lack of a drought information system, the sparse observation networks, and the low predictability of seasonal precipitation in these countries. To overcome these limitations, there is a need for developing a drought information system with a complete approach allowing data collection and pre-processing; accurate probabilistic drought risk prediction using a combination of ensemble climate seasonal forecasts, ground-based observations, reanalysis, conventional and remote sensing observations, artificial intelligence, data assimilation, and hydrological models; and drought information dissemination through a web-based drought early warning system (DEWS).

9 Conclusions

This study reviewed the recent statistical, dynamical, and hybrid statistical–dynamical methods used to forecast droughts and their application in the MedR. Drought definitions, classification, indices, and causative physical mechanisms were also presented in the context of the MedR. The main conclusions of this review are as follows:

1. There are only a few studies on the analysis of physical mechanisms causing droughts in the MedR. A review of these studies has confirmed that seasonal drought predictability skills are still very limited across the region due to its relatively poor teleconnection with ENSO compared to the tropical and subtropical regions. Besides, the MedR is strongly influenced by other climate patterns, such as the NAO, regional MO, ULMOi, and NAWA, which can also affect the region's weather and climate, but their relationship to drought onset is rather weak and could not explain major droughts in the region. Land surface memory can also contribute to the predictability of seasonal and sub-seasonal droughts. Thereby, an accurate representation of these land–atmosphere processes is needed to improve drought forecasting skills in mid-latitude regions such as the Mediterranean.

2. Statistical models were largely used to forecast droughts in the MedR. One of the major limitations of these models is that they often assume a stationary relationship between the predictors and the predictands, which can lead to potentially inaccurate forecasts. In this regard, AI models such as SVR, SVM, and ANN models have been proven to have good capacity in detecting local discontinuities and nonstationary characteristics of the data and show satisfactory forecasting skills at lead times of less than 6 months. Moreover, sophisticated statistical models, incorporating a data pre-processing technique such as wavelet analysis, EMD, or PCA with AI models, have proven to be more efficient than using a single model and can extend the lead time of the drought forecast to up to 12 months. The copulas can also provide valuable insights into the complex relationships between different drought predictors. The use of copulas enables a more in-depth analysis of the nonlinear dependencies between variables such as temperature, precipitation, and soil moisture, yielding a more comprehensive understanding of the factors that contribute to drought risk in a specific region. This leads to a more sophisticated and reliable forecast of drought probability. Thus, copulas are a highly useful resource in the ongoing effort to understand and manage the consequences of drought.

3. Dynamical models, given their ability to capture nonlinear interactions across the atmosphere, land, and ocean, offer considerable potential for more accurate and reliable seasonal drought predictions. However, the inherent chaotic nature of the atmosphere restricts their forecast skill to a few months in advance. Dynamical drought forecasting has seen notable advancements, such as enhanced climate model resolution, refined representation of physical processes, improved initialization methods, the application of multi-model ensembles, and the development of coupled modeling approaches. These developments have indeed bolstered the accuracy and reliability of drought predictions. Nevertheless, the implementation of these models in the MedR is constrained by challenges such as limited data availability, computational complexity, and inherent model uncertainties.

4. Hybrid statistical–dynamical models can be promising tools to potentially enhance the accuracy and reliability of drought forecasting in the MedR. By merging a broad variety of forecasts from statistical and dynamical models into a final probabilistic prediction, hybrid models benefit from the strengths of both modeling approaches and improve the forecast skill compared to an individual model. But their applicability remains challenging due to several constraints. Indeed, the hybrid model may require careful calibration and validation to ensure that it is performing optimally, which can be time-consuming, requiring a large number of data, specialized expertise, and a high level of computational resources.

5. One of the major challenges in drought forecasting in the MedR is the lack of long-term, high-quality hydroclimatic observations to convey nonstationary patterns and the variability in the climate. In addition, hydrological model predictions are often poor, due to model initialization, parametrization, and physical errors. To address these challenges, it is important to improve the availability and quality of data for drought forecasting in this region. This could involve implementing better monitoring systems and increasing the number of weather stations in the region. In addition, efforts should be made to improve the performance of drought forecasting models, using more advanced data assimilation and machine learning techniques, and to incorporate data from other sources such as state-of-the-art satellite observations and reanalysis with relatively high spatiotemporal analysis to provide superior hydrologic and climate state estimates and consequently skillful agricultural- and hydrological-drought forecasting.

6. Drought mapping is the final stage in which drought risk information is disseminated and communicated to end users. Major studies in the MedR analyze drought risk using some drought indices without applying a visualization via maps or presenting the risk on a single map that shows the overall risk situation. An informative visualization of results via probabilistic drought risk maps is recommended, whereby color gradations or contouring is used to effectively illustrate the range of probabilities. Ensuring cartographic rigor, such maps should maintain spatial accuracy, use appropriate scaling, and include a clearly defined legend to decrypt different probability levels. Uncertainties related to drought modeling and prediction also need to be perspicuously defined, discussed, and communicated to increase their intelligibility and comprehensibility for decision-makers, farmers, and other end users.

7. Finally, much effort should be made to improve the communication and dissemination of drought forecasts, extending their lead time and ensuring that decision-makers and stakeholders have access to the most up-to-date information.

Appendix A: Index of acronyms and abbreviations

Adaptive neuro-fuzzy inference systems	ANFISs
Arctic Oscillation	AO
Artificial neural network of multilayered perceptron	ANN-MLP
Asymmetric power autoregressive conditional heteroskedasticity	APARCH
Atmospheric water deficit	AWD
Automated statistical downscaling	ASD
Autoregressive	AR
Autoregressive conditional heteroskedasticity time series of order 1	ARCH
Autoregressive integrated moving average	ARIMA
Autoregressive moving average	ARMA
Autoregressive moving average time series of order 1	MA1
Autoregressive moving average time series of order 2	MA2
Autoregressive time series of order 1	AR1
Autoregressive time series of order 2	AR2
Bagging	BG
Bagnouls–Gaussen aridity index	BGI
Barcelona Expert Centre	BEC
Bayesian model averaging	BMA
Breaks for additive season and trend	BFAST
Convolutional neural network long short-term memory	CNN-LSTM
Combined Drought Indicator	CDI

Co-ordinated regional climate downscaling experiment for the Mediterranean area	Med-CORDEX
Corrected and unbiased trend-free pre-whitening	TFPWcu
Coupled Model Intercomparison Project	CMIP
Crop moisture index	CMI
Drought class transition probabilities	DCTP
Empirical mode decomposition	EMD
Exponential general autoregressive conditional heteroskedasticity	EGARCH
False alarm ratio	FAR
Frequency bias	FB
Generalized autoregressive conditional heteroskedasticity	GARCH
Geometric Brownian motion	GBM
Geometric Brownian motion time-series model with asymmetric jumps	GBMAJ
Global Historical Climatology Network monthly	GHCN
Global Land Data Assimilation System	GLDAS
Groundwater resource index	GRI
Hadley Centre Coupled Model version 3	HadCM3
Land surface temperature	LST
Mean absolute error	MAE
Moderate Resolution Imaging Spectroradiometer	MODIS
Modified Fournier index	MFI
Monthly average relative humidity	MARH
Monthly mean solar radiation	MMSR
Moving average	MA
Multiple linear regression	MLR
National Center for Atmospheric Research	NCAR
National Centers for Atmospheric Prediction	NCEP
National Oceanic and Atmospheric Administration	NOAA
NDVI anomaly index	NDVIA
Nonlinear autoregressive with exogenous inputs	NARX
Normalized difference vegetation index	NDVI
Normalized difference water index	NDWI
North Atlantic Oscillation	NAO
Pacific Decadal Oscillation	PDO
Pedotransfer function	PTF
Principal component analysis	PCA
Probability of detection	POD
Probability of false detection	POFD
Random forest	RF
Random subspace	RSS
Random tree	RT
Reconnaissance Drought Index	RDI
Relative absolute error	(RAE)
Root mean squared error	RMSE
Sea surface temperature	SST
Seasonal ARIMA	SARIMA
Soil and Terrain Database	SOTER
Soil moisture	SM
Soil moisture agricultural drought index	SMADI
Soil moisture and ocean salinity	SMOS
Soil moisture anomaly index	SMAI
Soil moisture deficit index	SMDI
Soil moisture percentiles	Wp
Soil water deficit index	SWDI
Soil wetness deficit index	SWetDI
Standardized water-level index	SWI

Streamflow drought index	SDI
Support vector regression	SVR
Surface reflectance	(SR)
Temperature condition index	TCI
The University of Thessaly monthly water balance	UTHBAL
Vegetation condition index	VCI
Vegetation health index	VHI
Wavelet analysis	WA
Wavelet decomposition	WD