the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Temporal changes in rainfall intensity–duration thresholds for post-wildfire flash floods in southern California
Tao Liu
Luke A. McGuire
Nina Oakley
Forest Cannon
Rainfall intensity–duration (ID) thresholds are commonly used to assess flash flood potential downstream of burned watersheds. High-intensity and/or long-duration rainfall is required to generate flash floods as landscapes recover from fire, but there is little guidance on how thresholds change as a function of time since fire. Here, we force a hydrological model with radar-derived precipitation to estimate ID thresholds for post-fire flash floods in a 41.5 km2 watershed in southern California, USA. Prior work in this study area constrains temporal changes in hydrological model parameters, allowing us to estimate temporal changes in ID thresholds. The results indicate that ID thresholds increase by more than a factor of 2 from post-fire year 1 to post-fire year 5. Thresholds based on averaging rainfall intensity over durations of 15–60 min perform better than those that average rainfall intensity over shorter time intervals. Moreover, thresholds based on the 75th percentile of radar-derived rainfall intensity over the watershed perform better than thresholds based on the 25th or 50th percentile of rainfall intensity. Results demonstrate how hydrological models can be used to estimate changes in ID thresholds following disturbance and provide guidance on the rainfall metrics that are best suited for predicting post-fire flash floods.
- Article
(10602 KB) - Full-text XML
-
Supplement
(1230 KB) - BibTeX
- EndNote
Heightened hydrological responses are common within and downstream of recently burned areas, resulting in an increased likelihood of flash floods. Rainfall intensity–duration (ID) thresholds are commonly used to assess the potential for flash floods (Moody and Martin, 2001; Cannon et al., 2008). Many past studies aimed at defining thresholds for flash floods focus on the first 1–2 years following fires (Cannon et al., 2008; Wilson et al., 2018). Since the hydrologic impacts of fire are transient, rainfall ID thresholds associated with flash floods are likely to change as a watershed recovers (Ebel and Martin, 2017; Ebel and Moody, 2017; Moreno et al., 2020; Ebel, 2020). It may take more than a decade for hydrological responses to return to pre-fire levels, yet there is limited guidance on how the magnitude and utility of rainfall ID thresholds change with time since fire. Given the increased frequency and size of fires in many geographic and ecological zones (e.g. Gillett et al., 2004; Westerling et al., 2006; Kitzberger et al., 2017), it is of growing importance to quantify the best metrics for assessing flash-flood potential in the immediate aftermath of fire as well as how these metrics change throughout the recovery process (e.g. Ebel, 2020).
Rainfall ID thresholds for flash floods are typically defined using historic data that relate rainfall over different intensities and durations to an observed hydrological response, namely the presence or absence of flooding (e.g. Cannon et al., 2008). Due to the stochastic nature of rainfall over burned areas and limited observations throughout the recovery process, there is a paucity of data that can be used to derive empirical thresholds for flash flooding beyond 1 year of recovery. Hazards associated with flash flooding, however, may exist downstream of burned areas well beyond 1 year of recovery. Wildfires alter rainfall-runoff partitioning and flood routing by incinerating vegetation and reducing interception capacity (Stoof et al., 2012; Saksa et al., 2020), decreasing hydraulic roughness, and reducing soil infiltration capacity (Larsen et al., 2009; Ebel and Moody, 2013). Reductions in infiltration capacity are often attributed to fire-induced soil-water repellency (Ebel and Moody, 2013), which is generally strongest immediately following a fire and then decays over timescales ranging from 1 year to more than 5 years (Dyrness, 1976; Huffman et al., 2001; Larsen et al., 2009), though surface soil sealing (Larsen et al., 2009) and hyper-dry conditions (Moody and Ebel, 2012) are also known to play important roles. Vegetation recovery, which may influence temporal changes in hydraulic roughness and canopy interception, can take 5 years or longer. Cannon et al. (2008) collected sufficient data over a 2-year time period following fires in southern California, USA, to define separate rainfall ID thresholds for post-fire debris flows and flash floods in the first and second years following fires. They found that the ID thresholds for flash floods and debris flows may increase by as much as 25 mm h−1 after 1 year of recovery, a change that they attributed to a combination of vegetation growth and sediment removal as a result of rainstorms during the first post-fire year.
Rainfall ID thresholds are often defined over a range of durations, though averaging rainfall intensity over a particular duration may provide a more reliable threshold. The post-fire hydrological response in the first few years is often best related to rainfall intensity over short durations (less than 60 min) (Staley et al., 2017; Moody and Martin, 2001). In their efforts to define rainfall ID thresholds for post-fire debris flows, Staley et al. (2013) showed that averaging rainfall intensities over durations between 15 and 60 min resulted in thresholds that performed better relative to those associated with longer durations. One potential explanation for this observation is that post-fire debris flows are often triggered by runoff in steep, low-order drainages, which both Kean et al. (2011) and Raymond et al. (2020) have found to be highly correlated with rainfall intensities averaged over similarly short time intervals (10–15 min). Moody and Martin (2001) have also documented a substantial increase in peak discharge following wildfires once the 30 min rainfall intensity (I30) crossed a threshold value, suggesting that I30 may be a consistent predictor of flash flood activity in recently burned watersheds. Moody and Martin (2001) suggest that peak I30 can be used to set the threshold for early warning flood systems. The optimal duration for defining post-fire flash floods thresholds, as well as how it may change with time, remains relatively unexplored.
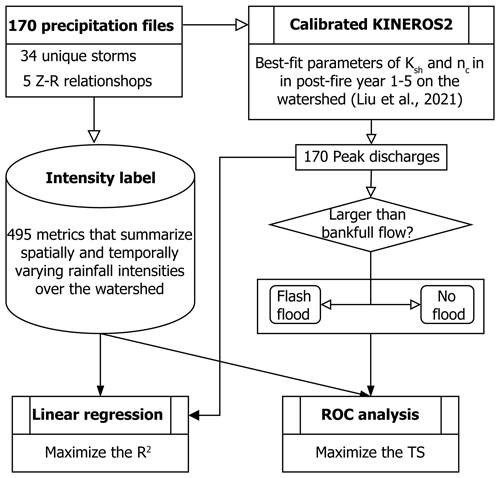
Rain gage records are typically used to derive rainfall ID thresholds for flash flood and post-fires debris flows (Staley et al., 2013, 2017). Post-fire debris flows, however, tend to initiate in small (<1 km2), steep watersheds. In these small watersheds, the rainfall intensity responsible for initiating a debris flow can be characterized by a single rain gage installed near the initiation zone. Flash floods differ in that they tend to occur at larger spatial scales where rainfall is spatially variable and may not be adequately characterized by data from a single rain gage. Radar-derived precipitation estimates, which can provide high spatiotemporal rainfall intensity resolution, present opportunities to develop basin-specific thresholds for post-fire flash floods. However, high spatiotemporal variability in rainfall intensity also brings new challenges when employing radar-derived precipitation in flood warning practice. In particular, what is the best way to summarize spatially and temporally variable rainfall intensity information with a single metric that can be used as a threshold? How does hydrological recovery following fires influence the generation of flash floods and the metrics that are best suited for their prediction? Data-driven approaches to answering these and related questions may be hampered by limited monitoring of post-fire hydrological response throughout the recovery period and the stochastic occurrence of rainfall over burned areas, which limits opportunities for observations. Given a well-constrained hydrological model that accounts for changes associated with post-fire recovery, it is possible to use numerical experiments to understand relationships between time since fire, the spatiotemporal patterns of rainfall over a watershed, and the occurrence of flash floods.
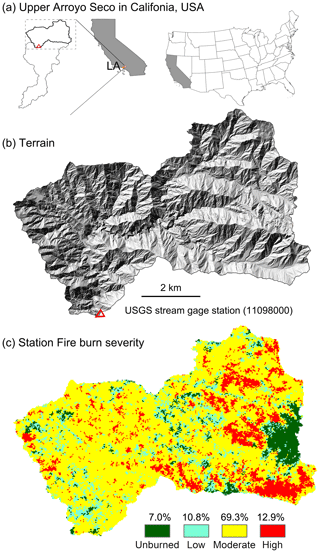
Figure 1Modified from Fig. 1 in Liu et al. (2021) (a) The location of the upper Arroyo Seco watershed within California. The red triangle indicates the location of the USGS stream gage (11098000); (b) Shaded relief showing the study watershed with the USGS stream gage (red triangle; 34∘13′20′′, −118∘10′36′′); (c) Soil burn severity for the 2009 Station fire. Burn severity percentages are for planform area within each category.
Here, we use observed patterns of spatially and temporally varying radar-derived rainfall estimates over a 41.5 km2 watershed in the San Gabriel Mountains of southern California, USA, to (1) determine the optimal method to define a rainfall ID threshold for flash floods, and (2) identify changes in rainfall ID thresholds for flash floods as a function of time since fire. The watershed, which we refer to as the upper Arroyo Seco, burned during the 2009 Station Fire (USDA Forest Service, 2009). Liu et al. (2021) used rain and stream gage data collected at different times following the fire to calibrate the KINEROS2 hydrological model for this watershed, enabling them to quantify temporal changes in model parameters as a function of time since fire. Combining this calibrated model with spatially explicit, radar-derived estimates of rainfall intensity during 34 rainstorms, we explore the utility of different rainfall ID metrics as flash flood thresholds and quantify temporal changes in those thresholds through the first 5 years of recovery. Results provide insight into the magnitude of temporal changes in flash flood thresholds in the densely populated, fire-prone region of southern California. Findings also provide guidance for the magnitude of change expected in rainfall ID thresholds for flash floods during the post-fire recovery period in chaparral-dominated environments similar to southern California. More generally, results support the development of early warning systems for flash floods by identifying specific metrics that can be computed using spatially variable rainfall intensity estimates to assess the potential for flash flooding. The optimal rainfall ID metrics identified in this study could be helpful when issuing flash flood warnings based on radar-derived precipitation estimates or data from several real-time rain gages within a watershed.
The upper Arroyo Seco watershed drains the 41.5 km2 area above USGS stream gage station (11098000) near Pasadena in the San Gabriel Mountains (Fig. 1). The upper Arroyo Seco was burned in the August–October 2009 Station Fire, which burned more than 80 % of the watershed at moderate-to-high soil burn severity (USDA Forest Service, 2009). Dominant shrubs and chaparral, such as chamise (Adenostoma fasciculatum) and manzanita (Arctostaphylos spp.), were completely consumed with severe soil heating in isolated patches throughout many areas burned at moderate-to-high severity (USDA Forest Service, 2009). Soils in this area are typically sand and silty–sand textured and thin (<1 m) with partial exposure of bedrock (Staley et al., 2014). The majority of rainfall in the study area typically occurs in the cool season, between December and March, while warm, dry conditions dominate from April to early November. The San Gabriel Mountains also experience some of the most frequent short-duration, high-intensity rainfall event in the state (Oakley et al., 2018a).
Due to wildfire-induced changes in surface conditions, including canopy cover and soil-hydraulic properties, runoff generation in the first year following the fire was likely dominated by infiltration excess overland flow (Schmidt et al., 2011; Liu et al., 2021). Enhanced soil-water repellency (SWR), which helps promote low infiltration capacity, and extensive dry ravel, which loads channels with fine-grained hillslope sediment, are both commonly observed after fires in the San Gabriel Mountains (e.g., Watson and Letey, 1970; Hubbert and Oriol, 2005; Lamb et al., 2011; Hubbert et al., 2012). Rengers et al. (2019) calibrated a hydrologic model using data from small watersheds (0.01–2 km2) burned by the Station Fire and found relatively low values for saturated hydraulic conductivity (Ks), generally between 2 and 10 mm h−1. These results are consistent with values for saturated hydraulic conductivity inferred by Liu et al. (2021) via model calibration in the upper Arroyo Seco watershed. The impact of dry ravel, which reduces grain roughness in the channel network, and reduced vegetation density led to estimates of Manning's n in the channels of the upper Arroyo Seco of approximately 0.09 s m in the first year following fires (Liu et al., 2021). These hydrologic changes led to widespread flooding and debris flows during multiple rainstorms in the first winter after the fire (Kean et al., 2011; Oakley et al., 2017). As hydrological recovery began over the next several years, the watershed-scale Ks and Manning's n generally increased and likely started to mitigate the flash flood risk (Liu et al., 2021).
3.1 Radar-derived precipitation
Weather radar coverage is adequate for estimating rainfall over the study area (NOAA, 2021a, b), and radars have been operational since the mid-1990s. This allows us to utilize observed data to capture temporal and spatial characteristics of storms impacting the study area, a region of complex terrain. We sought to identify storms in the study area that produced moderate-to-high intensity rainfall to use as inputs to a hydrological model to simulate flood responses. Storm events were selected within the period for which observations are archived for the two operational NWS Next-Generation Weather Radar installations (NEXRAD; NOAA, 1991) that cover the study area, KSOX (Santa Ana) and KVTX (Ventura). Archives for the radars begin in 1997 and 1995, respectively.
We compiled storm events starting with those known to have produced high intensity rainfall and a debris flow response in the San Gabriel Mountains (e.g., Table 1 in Oakley et al., 2017) as well as other storms that produced high-intensity rainfall in the region (e.g., Oakley et al., 2018b; Cannon et al., 2018). We then used hourly rainfall observations from the Clear Creek (2002–present), San Rafael Hills (2005–present), and Henninger Flats (2010–present) Remote Automated Weather Stations (RAWS, acquired from https://raws.dri.edu/, last access: 2 February 2022) as indicator gages for the study area. This further limited us to post-2002 events outside of the literature. All gages are <10 km from the watershed of interest; there were no long-record gages within the watershed. We used 15 mm h−1 as a threshold for moderate-to-high intensity rainfall and extracted all events from the gage record meeting or exceeding this value to develop a list of events of interest. This threshold generally corresponds with a 1-year average recurrence interval storm event in the study area (NOAA, Atlas 14). This value falls between the California–Nevada River Forecast Center's flash flood guidance for unburned areas in the region (∼ 22–25 mm h−1; CNRFC, 2022) and regional thresholds for post-wildfire debris flows in this region at a point (12.7 mm h−1, Cannon et al., 2008; Staley et al., 2013). This threshold allows us to focus on storms that have a high potential to generate floods, while keeping the number of storms to a manageable level for data processing. We reviewed the radar data for these events, at which point some of the selected events could not be utilized due to radar outages or poor data quality. This exercise presented us with 34 storm events (Table S1 in the Supplement).
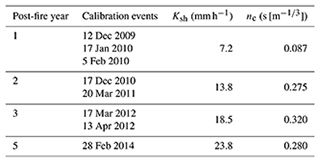
Table 1Summary of model parameters for post-fire years 1, 2, 3, and 5. The saturated hydraulic conductivity on hillslopes (Ksh) and hydraulic roughness in channels (nc) are the average of values calibrated in post-fire years 1, 2, 3, and 5 (Liu et al., 2021).
Various atmospheric processes may contribute to generation of moderate-to-high rainfall intensities (e.g., Oakley et al., 2017), resulting in differing spatial and temporal precipitation patterns over a burn area. To ensure the events selected captured the variability in spatial and temporal precipitation characteristics, we evaluated the spatial characteristics of the events. We found rainfall patterns could generally be categorized into four main spatial patterns at the scale of several tens of kilometers: (1) a broad pattern, with a contiguous area of moderate-to-high intensity precipitation (>45 dBZ) spanning tens of kilometers; (2) a scattered pattern with numerous cells of moderate-to-high precipitation that are not spatially continuous; (3) an isolated pattern, with one to a few isolated cells of moderate-to-high intensity rainfall separated by non-precipitating areas several to tens of kilometers in extent; (4) a narrow cold frontal rainband (NCFR) – a north–south oriented narrow band (∼ 3–5 km wide, tens to 100 km in length) of very high intensity rainfall (e.g., Oakley et al., 2018b; Cannon et al., 2020; Figure S1). At the <10 km horizontal scale (the scale of the watershed), it was harder to identify meaningful patterns and distinctions, though the larger-scale signals imply varying spatial and temporal patterns of precipitation as each pass over the watershed. A table of storm events and their characteristics is available in Table S1.
An approximate start and end time were determined for each event using the Clear Creek RAWS gauge as an indicator. Start time was determined by identifying the time of maximum 1 h rainfall in the event and going back in time to the first of three consecutive hours of >1.5 mm h−1 precipitation. The end of an event was determined as the last hour where precipitation dropped below 3 mm h−1 for at least two consecutive hours.
Level-II base reflectivity (https://www.ncdc.noaa.gov/wct/, last access: 2 February 2022) between the start and end time of each event was downloaded from both the KSOX and KVTX radars. The data were used to generate spatially distributed precipitation over the study area. Radar imagery concurrent with the gauge-based record of high intensity rainfall events was converted to a composite maximum reflectivity product at 250 m spatial and 5 min temporal resolution. Conversion of radar reflectivity to rain rate required the application of an empirically derived reflectivity (Z) to rain rate (R) relationship (e.g. Marshall and Palmer, 1948). The Z-R relationship is conventionally represented by the equation Z=aRb, which includes parameters a and b to account for variations in precipitation for a given reflectivity arising from differences in the drop size distribution. Due to the lack of previous studies investigating Z-R relationships in precipitating conditions over the region of interest, there are no standard a and b parameters to apply to the reflectivity data analyzed here. Thus, five well-known and previously published Z-R relationships were applied to the gridded reflectivity values. Supplement S3 lists the different Z-R relationships applied here and the general conditions for which they are suitable. Although the Z-R relationships used here are not based on observations from the present study's region of interest, the variation of a and b parameters yields an estimate of precipitation uncertainty. It is worth noting that a number of additional sources of radar measurement uncertainty exist that are not evaluated in depth here, including beam broadening, topographic blocking, and scan elevation. However, this was not of primary concern since the goal of this study was to generate realistic spatial and temporal patterns of rainfall over the watershed with varying intensity that could be used to force the KINEROS2 hydrological model. The goal was not to reproduce the observed hydrological response resulting from a particular set of rainstorms.
As a range of precipitation intensities for each storm result from the application of the five different Z-R relationships (e.g., Fig. S2), we utilize these as plausible storms of varying precipitation intensity to increase our storm sample size, such that we apply 34 storms ⋅ 5 Z-R relations = 170 precipitation scenarios as inputs to KINEROS2. These 170 scenarios were then processed for ingestion into KINEROS2 (Fig. 2).
3.2 Summary metrics for spatially and temporally varying rainfall
In search of a spatiotemporal summary metric that may serve as a reliable flash flood threshold, we begin by describing a methodology to summarize spatially and temporally varying rainfall over a watershed. For a given rainstorm, the rainfall intensity time series at a single point, such as a single radar pixel, can be summarized by computing a moving average of intensity over a specified duration, D. Letting t denote time and R denote the cumulative rainfall (mm), we define the rainfall intensity over a duration D at any given pixel within the watershed as
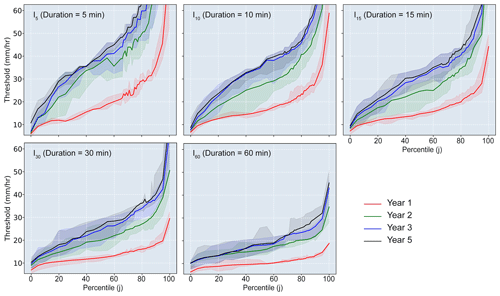
Here, we compute ID(t) for each pixel for durations of 5, 10, 15, 30, and 60 min. Since the intensity in each radar pixel could have a unique value, we also need a way to summarize ID(t) in space. One option would be to take the median of ID(t) to determine a typical value of ID within the watershed at each time, t. However, the median may not be a good predictor of flash flooding since one could envision a scenario where it is only raining over of the watershed, yet it is raining with sufficient intensity to generate a flash flood. We therefore compute the jth percentile of ID(t) at each time, t, for j between 1 and 99. We denote the jth percentile of ID(t) as . For each rainstorm, we focus our analysis on the peak value of which we denote as . As an example, would be computed by defining I30 for all radar time steps within a rainstorm, determining the median value of I30 over the watershed at each of those time steps, and then taking the maximum of that time series of median I30 intensities. This analysis yields 495 different metrics ( for and ) that summarize spatially and temporally varying rainfall intensities over the watershed. In the following sections, we describe how we test the utility of each of these 495 different metrics as a flash flood threshold. A threshold defined by would denote a threshold where (100–j)% of the watershed experiences rainfall of duration D with an intensity of I or greater.
3.3 Hydrological modeling
We used the KINEROS2 (K2) hydrological model to simulate the rainfall partitioning, overland flow generation, and flood routing in the upper Arroyo Seco watershed. K2 is an event-scale, distributed-parameter, process-based watershed model, which has been used extensively for rainfall-runoff processes in semi-arid and arid watersheds (Smith et al., 1995; Goodrich et al., 2012). Liu et al. (2021) used rain gage data in combination with the USGS stream gage installed at the outlet of the upper Arroyo Seco watershed to calibrate K2 during different stages of the post-fire recovery process. We use the same model setup for simulations in this study. In particular, the 41.5 km2 watershed was discretized into 1289 hillslope planes and these planes were connected by a stream network of 519 channel segments based on a 1 m lidar-derived digital elevation model (DEM). After accounting for a fixed interception depth of 2.97 mm based on the land cover look-up table in the Automated Geospatial Watershed Assessment toolkit (AGWA; Miller et al., 2007), infiltration of rainfall into soil is represented using the Parlange et al. (1982) approximation. Overland flow and channel flow are modeled by kinematic wave equations. Both saturated hydraulic conductivity on hillslopes (Ksh) and hydraulic roughness in channels (nc) primarily determine runoff generation and the shape of hydrograph, including total runoff volume, peak discharge rate, and time to peak (Canfield et al., 2005; Yatheendradas et al., 2008; Meles et al., 2019). Other parameters, such as hydraulic roughness (nh) and capillary drive (Gh) on hillslopes, had a relatively minor impact on modeled runoff after the Station Fire in the upper Arroyo Seco watershed (Liu et al., 2021).
Liu et al. (2021) found that both Ksh and nc were lowest immediately after the fire. Ksh increased, on average, by approximately 4 mm h−1 yr−1 during the first 5 years of recovery, whereas nc increased by more than a factor of 2 after 1 year of recovery and then remained relatively constant. We focus here on simulating the response to rainfall in the first 5 years following the fire, when the watershed is likely most vulnerable to extreme responses. To represent the temporal changes in Ksh and n documented by Liu et al. (2021) following the fire, we used different values of Ksh and nc for each post-fire year (i.e. post-fire years 1, 2, 3, and 5) based on the values calibrated by Liu et al. (2021) in post-fire years 1, 2, 3, and 5 (Table. 1). Liu et al. (2021) were unable to calibrate the necessary K2 parameters in post-fire year 4 so we do not perform any simulations to constrain flash flood thresholds in that year. Initial soil moisture is set to a volumetric soil-water content of 0.1, following Liu et al. (2021). Other parameters were also given the same values as the calibrated K2 model, including saturated hydraulic conductivity of channels (1 mm h−1), net capillary drive of channels (5 mm), hydraulic roughness of hillslopes (0.1 s m, net capillary drive of hillslopes (50 mm), and soil porosity (0.4). With this model setup, we simulate the response to each of the 170 rainstorms for post-fire years 1, 2, 3, and 5.
3.4 Rainfall intensity–duration thresholds
Each K2 simulation results in a modeled hydrograph at the watershed outlet. As a first step towards defining a flash flood threshold, it is necessary to determine, based on the modeled time series of discharge, whether or not a flash flood would have occurred. We defined the flash flood level as the discharge required to exceed bankfull flow (Sweeney, 1992), which we assumed was equal to the 2-year flood (Leopold et al., 1964). To determine the discharge associated with the 2-year flood, we performed a flood frequency analysis using HEC-SSP v2.2 (Bartles et al., 2019) based on annual maximum records at the USGS stream gage station (11098000). The discharge associated with the 2-year flood at the stream gage station is 15.3 m3 s−1, with a 95 % confidence interval of 12.3–19.2 m3 s−1 (Fig. S3). A flash flood threshold by this definition can be viewed as conservative since it may only indicate the onset of minor flooding as water begins to spill out of the channel. Based on this definition, we then used two approaches to identify the rainfall ID threshold for flash floods (Fig. 2).
The first approach is based on a linear regression analysis that relates peak discharge with different rainfall ID metrics, namely for different values of j and D. Using simulations of 170 rainfall-runoff events in each post-fire year, it is possible to determine a relationship for peak discharge (Q) as a function of . Then, the rainfall ID threshold can be found by determining the rainfall intensity at which the peak discharge exceeds the bankfull capacity. The simplest quantitative relation is a linear regression:
where Q is the peak discharge (m3 s−1) of a simulated hydrograph at the outlet, denotes rainfall intensity (mm h−1) for the rainstorm that produced the hydrograph, and m and k denote the slope and y intercept of the linear regression, respectively.
Considering the channel dimensions and resolution of the DEM used in the K2 model, we selected intensity–discharge () pairs associated with a Q greater than 2 m3 s−1. The flow depth associated with a Q less than 2 m3 s−1 would be very small and any impact from such flow would be negligible. The parameters in the linear Eq. (1) with the maximum determination coefficient () were estimated using least-squares linear regression in the SciPy Python library for the selected pairs. A total of 495 linear regressions were produced for each year because can take on 495 different values (five durations, 99 percentiles) for each rainstorm. For each post-fire year, we then identified the maximum R2 value for each duration as a function of percentile from 1st to 99th (Fig. 3). The rainfall ID threshold for flash flooding in each year was found, for each duration, from the linear relation associated with the largest R2 (Fig. 4).
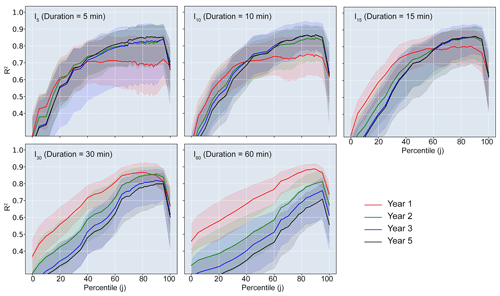
Figure 3The determination coefficient (R2) and 95 % confidence interval associated with the linear regression between and peak discharge in post-fire years 1, 2, 3, and 5. Data used to fit the linear relation are from events with peak discharge greater than 2 m3 s−1.
We also estimated the 95 % confidence interval (CI) of both R2 and the rainfall ID threshold by performing bootstrapping resampling on 170 rainfall-runoff events for each year. The number of replications is 50. The 95 % CI was constructed with the 2.5 percentile and the 97.5 percentile of the ranked R2 or rainfall ID threshold.
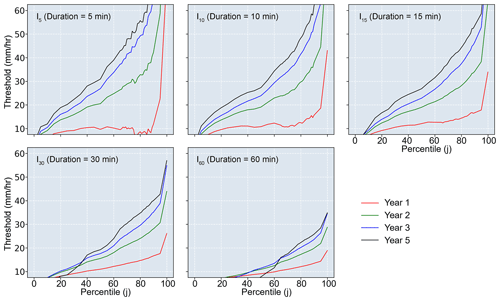
Figure 4The rainfall intensity–duration threshold for flash floods derived from the best linear relation for different durations and percentiles of the most intense rainfall field in post-fire years 1, 2, 3, and 5.
The second approach for determining rainfall ID thresholds is based on a receiver operating characteristic (ROC) analysis following Staley et al. (2013). We assess the utility of a potential threshold (e.g. ), by computing the threat score (TS) associated with using that threshold to define the transition between rainstorms that produce flash floods and those that do not. The TS, as one of the ROC utility functions, measures the fraction of forecast events that were correctly predicted:
where TP, FP, and FN denote a true positive, false positive, and false negative, respectively. Flash flood occurrence (true or false) is determined by comparing the peak discharge of each simulated hydrograph with the flash flood level (15.3 m3 s−1). A TP represents an event where rainfall rates exceed the threshold (e.g. ), and a flash flood occurred. An FP represents an event where rainfall rates exceed the threshold, but no flash flood occurred. FN events occur when rainfall rates were below the threshold, yet a flash flood occurred. The optimal TS is 1, meaning use of the threshold resulted in no false positives or false negatives.
For a given rainfall intensity metric (e.g. the peak 75th percentile of I30, , in year 1), we calculated TS for intensities ranging from 0–100 mm hr−1 at 0.01 mm h−1 intervals (Fig. 5). We then identified the threshold associated with the maximum TS (TSmax). The intensity associated with TSmax is the optimal threshold for that rainfall metric (Fig. 6). We determined the optimal threshold associated with each of the 495 rainfall metrics for each post-fire year (1, 2, 3, and 5) (Fig. 7). We also estimated the 95 % CI of TS and rainfall ID threshold for each year by performing bootstrapping resampling with 50 replications.
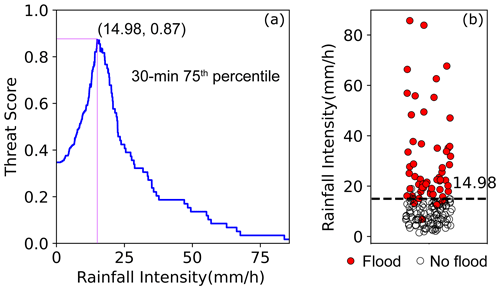
Figure 5Threat score (TS) of the peak 75th percentile of I30 in post-fire year 1. (a) Relationship between rainfall intensity and TS; (b) Scatter plots of positive (flood, red circle) and negative (no flood, hollow circle) with the rainfall intensity associated with the maximum TS.
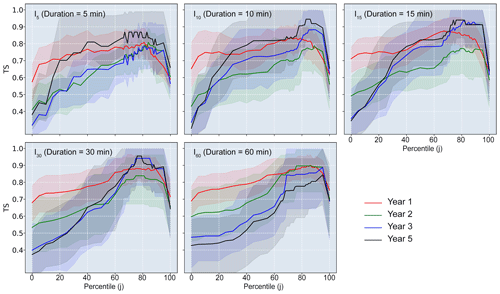
Figure 6The threat scores (TSmax) associated with flood occurrence and in post-fire years 1, 2, 3, and 5. Data used to analyze are from events with peak discharge greater than 2 m3 s−1.
4.1 Optimal summary metrics for defining rainfall ID thresholds
Linear regression analyses suggest that there is a stronger relationship between and peak discharge (Q) as j increases, with the exception of a rapid drop off in R2 for j>95 (Fig. 3). In post-fire year 1, the maximum R2 increases with duration (D) from a value of 0.72 associated with , to 0.75 associated with , to 0.80 associated with , to 0.87 associated with , to 0.89 associated with . In post-fire years 2–5, the R2 values associated with durations of 5, 10, and 15 min were maximized (0.79–0.86) within a window from the 60th–95th percentiles. The optimal rainfall threshold for flash floods (based on regressions of Q as a function of increased from 10.1 mm h−1 of (the 89th percentile of 60 min peak rainfall field) in year 1 to 44.6 mm h−1 of (the 90th percentile of 15 min peak rainfall field) in year 5 (Fig. 4; Table 2). More generally, averaging rainfall intensity over a duration of 15 min and choosing a percentile, j, of approximately 75–90 produced an R2 of approximately 0.80 or greater for all post-fire years (Fig. 3). None of the other rainfall summary metrics performed this well across all post-fire years.
Table 2The linear regression-based optimal rainfall ID metrics and corresponding rainfall thresholds for flash floods in post-fire years 1–5.
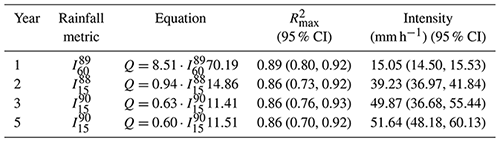
Note: we denote the peak jth percentile of ID (rainfall intensity over a duration D) as . For example, is the peak value of the 88th percentile of I15 (rainfall intensity over 15 min).
Thresholds derived using the ROC method yielded broadly similar trends. The maximum threat score, TSmax, generally increased with j up to a point (approximately j=90) and then began to decrease regardless of the choice of duration (D) (Fig. 6). The highest threat scores (TS), regardless of post-fire year or duration, were generally associated with the 70th–95th percentiles. For events in years 1–2, TSmax (0.90) occurs between and (the 76th–86th percentile of the peak I60 rainfall field); for events in years 3–5, the TSmax (0.94–0.96) occurs around (the 75th percentile of the peak I30 rainfall field). The optimal rainfall threshold for a flash flood increased from (the 86th percentile of 60 min peak rainfall field) in year 1 to (the 76th percentile of 30 min peak rainfall field) in year 5 (Table 3; Fig. 6). Averaging rainfall intensity over a duration of 30 min and choosing a percentile, j, of approximately 75–90 leads to threat scores of approximately 0.8 or greater for all post-fire years. Other metrics did not perform this well, on average, across all post-fire years.
4.2 Increases in rainfall intensity thresholds with time since fire
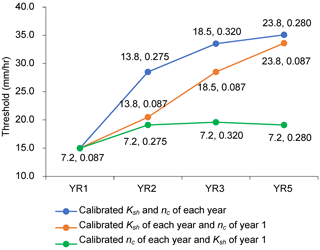
The rainfall intensity thresholds at each percentile increased substantially from post-fire year 1 to 5 (Figs. 4 and 7). However, the increase from year 1 to 2 is considerably larger than that from year 2 to 3 or from year 3 to 5. Taking the (the 75th percentile of the peak I30 rainfall field) as an example due to its strong performance as a threshold for all post-fire years, the thresholds based on linear regression analyses in years 1, 2, 3, and 5 are 16.8, 23.2, 26.9, and 27.6 mm h−1, respectively; the ROC-based thresholds in years 1, 2, 3, and 5 are 16.0, 26.9, 32.6, and 34.5 mm h−1, respectively (Fig. 7).
We are also able to use the model to assess the individual impacts of temporal changes in Ksh and nc on temporal variations in the flash flood threshold. If Ksh is allowed to vary from year to year (Table 1) and nc is held fixed at its calibrated value for year 1, then ROC analysis indicates that the optimal threshold of still increases with time since fire (Fig. 8). However, it increases slower than the case where both Ksh and nc are allowed to vary with time (Fig. 8). If nc is allowed to vary from year to year (Table 1) and Ksh is held fixed at its calibrated value for year 1, then ROC analysis indicates that the optimal threshold associated with increases from year 1 to year 2 but then stays roughly constant as time increases (Fig. 8). Therefore, changes in Ksh and nc both play important roles in determining the degree to which the flash flood threshold increases from year 1 to year 2, but further increases in the threshold in years 3 through 5 are driven mainly by increases in Ksh as a function of time since fire.
5.1 Optimal metrics of rainfall intensity and duration for flood warning
Rain gage records, which provide rainfall intensity data at a single point, are often used to define rainfall ID thresholds in debris-flow and flash-flood studies (e.g. Moody and Martin, 2001; Cannon et al., 2008, 2011; Guzzetti et al., 2008; Kean et al., 2011; Staley et al., 2013; Raymond et al., 2020; McGuire and Youberg, 2020). Using point source data to define thresholds for debris flows and flash floods is ideal when rainfall intensity does not vary substantially over the watershed, an assumption that is most appropriate for watershed areas less than several square kilometers. Radar-derived rainfall data has the advantage of providing spatially explicit information over an entire watershed at a high-temporal resolution (e.g. 5 min). However, one challenge in using radar-derived precipitation to define thresholds is the need to condense spatially and temporally variable rainfall intensity information down to a single rainfall intensity metric. Regardless of whether the approach to determining an ID threshold involves fitting empirical relationships (e.g., Moody and Martin, 2001; Cannon et al., 2008) or using ROC analysis (e.g., Staley et al., 2013), a single metric is required to represent the rainfall intensity for each duration.
We summarized spatially variable rainfall intensity data over the watershed by computing the peak value of , the jth percentile of ID(t) for each rainstorm. We used two different techniques, one based on a linear regression analysis and one based on ROC analysis (Fig. 2), to define thresholds for flash floods in post-fire years 1, 2, 3, and 5. Although the optimal metrics produced by the two approaches are not identical, they are generally similar in each post-fire year. In particular, high R2 and TSmax values are associated with metrics of the peak 75th–85th percentile of rainfall intensity averaged over 15–60 min ( for . In other words, a good indicator of the potential for a flash flood is the presence of intense pulses of rainfall over durations of 15–60 min that cover at least 15 %–25 % of the watershed (Fig. 9). This finding highlights the ability of rainstorms to produce flash floods even if they do not cover the majority of the watershed with intense rainfall. If rainfall over the majority of the watershed was required to produce flash floods, then we would expect that with j<50 would be a better predictor of flash floods.
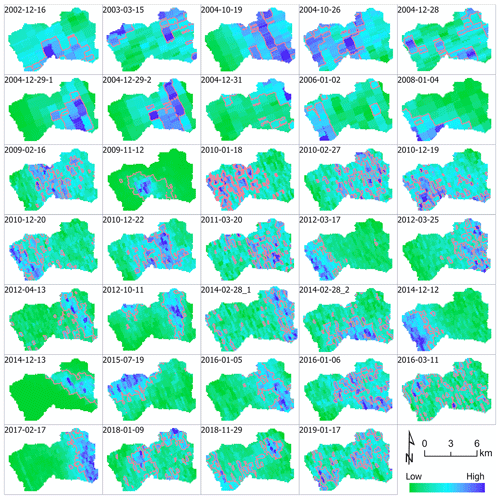
Figure 9Snapshots of the spatial patterns of of 34 unique storms. The peak jth percentile of ID (rainfall intensity over a duration D) is denoted as . is the peak value of the 75th percentile of I30 (rainfall intensity over 30 min). Red contours delineate the pixels with rainfall intensities larger than of each storm.
Previous work has also identified that 30 min rainfall intensity works well for predicting flash floods and debris flows (Moody and Martin, 2001; Kean et al., 2011; Staley et al., 2013). The finding that , , and work best as thresholds when could be helpful when issuing flash flood warnings based on radar-derived precipitation estimates or data from several real-time rain gages within a watershed. Current operational forecast models such as the High-Resolution Rapid Refresh model have a horizontal resolution of 3 km and minimum temporal resolution of 15 min (Benjamin et al., 2016; NOAA, 2021a), such that it is feasible to use either , , or in an operational forecast setting. Where sufficient operational NEXRAD weather radar coverage is present, radar-derived precipitation estimates such as the Multi-Radar/Multi-Sensor System (MRMS; Zhang et al., 2016) can provide near-real-time precipitation estimates at 1 km and as fine as 15 min temporal resolution (NOAA, 2021b). In the case of poor radar coverage, gap-filling radars may be temporarily deployed or installed (e.g., Jorgensen et al., 2011; Cifelli et al., 2018) to provide information necessary for accurate precipitation estimates. While the magnitude of rainfall thresholds estimated here may only work for similar, recently burned watersheds within the San Gabriel Mountains, this work provides a general methodology for exploring reliable predictors of post-fire flash floods for other watersheds and settings. Further testing is needed in watersheds with different watershed sizes, topographic characteristics, landscapes, and burn severity patterns.
Table 3The ROC-based optimal metrics of rainfall ID and corresponding rainfall thresholds for flash floods in post-fire year 1–5.
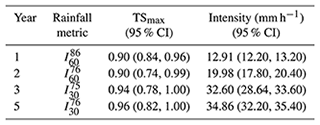
Note: we denote the peak jth percentile of ID (rainfall intensity over a duration D) as . For example, is the peak value of the 86th percentile of I60 (rainfall intensity over 60 min).
Several limitations are present in this work. First, we assess a small number of storm events (34) in the area as we are limited by the length of radar and gage records as well as the number of events that impact the indicator rain gages, though applying the five Z-R relationships provides us with 170 rainfall realizations to assess. We prefer the use of observed rainfall data (radar and gauges) over simulated products, such as output from a rainfall generator (e.g., Zhao et al., 2019; Evin et al., 2018), as the radar is able to capture the spatial and temporal patterns of rainfall intensity in the study area's complex terrain. Though rainfall generators have advanced to represent some synoptic-to-mesoscale features, such as frontal and convective precipitation (e.g., Zhao et al., 2019), they are fundamentally designed to represent statistical characteristics of rainfall in places with limited observations (Wilks and Wilby, 1999) and cannot be relied upon to replicate small-scale storm characteristics in complex terrain (e.g., Camera et al., 2017). Future work could compare results from this hydrological modeling experiment with observed versus simulated rainfall. Second, the challenges of using Z-R relationships to convert reflectivity into precipitation also present challenges in accurately representing precipitation values. This can be addressed in future work through studies to constrain Z-R relationships for storms producing intense rainfall in this region and through the deployment or installation of high-resolution gap-filling radars (e.g., Johnson et al., 2020).
5.2 The role of hydrological models in rainfall intensity threshold estimation
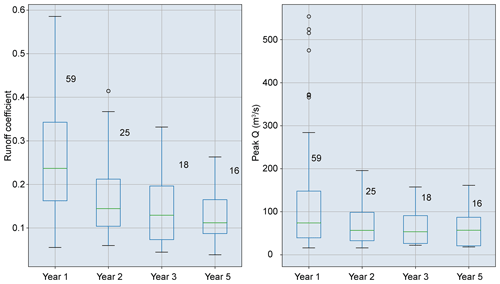
In this study we employed the K2 model calibrated by Liu et al. (2021) to parameterize hydrologic changes affecting Hortonian overland flow within a 5-year period following fires. Hillslope saturated hydraulic conductivity (Ksh=7.2 mm h−1) and hydraulic roughness in channels (nc=0.087 s m were lowest immediately after fire (Table 1), resulting in high runoff coefficients and low rainfall thresholds in post-fire year 1. In later years, with Ksh and nc gradually increasing (Table 1), more rainfall infiltrated into the soil and there was increased attenuation of flood peaks. Simulations indicate that the number of flash-flood-producing rainstorms decreased from 59 in year 1 to 25, 18, and 16 in years 2, 3, and 5, respectively. Runoff coefficients and peak discharge of simulated hydrographs also decreased with time since fire (Fig. 10). Given the same precipitation ensemble, the likelihood of flash floods significantly decreased with time. The peak discharge produced by the highest intensity rainfall event with of 51.8 mm h−1 was 554.0 m3 s−1 in the first year after the fire, which is 3 times greater than the peak discharges of 157.5 m3 s−1 in year 3 and 161.2 m3 s−1 in year 5 produced by the same rainstorm. From a flood hazard perspective, the downstream area may be exposed to a 1000-year flood under recently burned conditions (less than 1 year since the fire), whereas the discharge produced in years 3 and 5 amounts to roughly a 30- to 40-year flood (Fig. S3).
We were also able to perform numerical experiments to quantify the relative importance of temporal changes in Ksh and nc on temporal variations in the flash flood threshold (Fig. 8). Results suggest that changes in vegetation and grain roughness, which are likely to influence nc, throughout the recovery process are less important for determining flash flood potential in our study area relative to changes to saturated hydraulic conductivity on hillslopes. It is worth noting that temporal changes in other model parameters (e.g., hydraulic roughness on hillslopes, capillary drive) may play more of a role in driving changes in post-fire flash flood thresholds in other settings. In this study, however, we focus on changes in Ksh and nc because Liu et al. (2021) were able to detect temporal changes in nc and Ksh through time and were unable to detect similar temporal changes in other hydrologic parameters (e.g., hydraulic roughness on hillslopes, capillary drive) due to their relatively minor influence on runoff in the study watershed.
In this study, the optimal flash flood thresholds increased from 16.0–16.8 mm h−1 in post-fire year 1, to 23.2–26.9 mm h−1 in year 2, and 27.6–34.5 mm h−1 in post-fire year 5 (Figs. 4 and 7; Tables 2–3). In the San Gabriel Mountains and nearby San Bernardino and San Jacinto mountains, Cannon et al. (2008) estimated rainfall thresholds of I30=9.5 mm h−1 for flash floods and debris flows in the first winter rainy season following fires. They found that the thresholds for flash floods and debris flows increased to I30=19.8 mm h−1 in post-fire year 2. The thresholds that we infer from hydrological modeling are greater than those reported by Cannon et al. (2008), which may be partly due to differences in (1) the data and methods used and (2) the size of the studied watersheds. Our results are driven by a hydrological model, forced with a radar precipitation ensemble that consists of 170 rainstorms that contain a variety of storm types that impact southern California. The occurrence of a flash flood is based on exceedance of the maximum channel capacity and we summarize temporal changes in the rainfall ID threshold using since we find this to be a reliable metric for all post-fire years included in this study. In contrast, Cannon et al. (2008) established rainfall ID relations by using observations of rainstorms and hydrological responses in the 2 years following fires in 87 small watersheds (0.2–4.6 km2). They base their thresholds on rainfall characteristics that produced either flash floods or debris flows, whereas we focus solely on flash floods. In their dataset, flash floods and debris flows were identified by investigating flood and debris flow deposits at the outlet of those small watersheds in the field. Despite differences in the magnitude of the thresholds, the increase in the threshold from post-fire year 1 to year 2 in both studies are quite close. This agreement provides support for the use of simulation-based approaches to inform temporal shifts in rainfall ID thresholds.
During the recovery process, increasing thresholds for flash floods and debris flows have also been identified in other areas at different scales by either observation- or simulation-based studies, such as hillslopes in the Colorado Front Range (Ebel, 2020) and small watersheds in Australia (Noske et al., 2016). The consistent increase in rainfall ID thresholds with time since fire in different geographic and ecological zones implies that hydraulic and hydrological models may be useful tools for exploring how the transient effects of fires translate into changes in water-related hazards. The role of hydraulic and hydrological models becomes particularly more important when historic data are limited and traditional empirical methods are impractical for defining thresholds.
We used 250 m, 5 min radar-derived precipitation estimates over a 41.5 km2 watershed in combination with a calibrated hydrological model to estimate rainfall intensity–duration thresholds for post-fire flash floods as a function of time since fire. The main outcomes of this study are (1) identification of optimal radar-derived rainfall metrics for post-fire flash flood prediction in southern California, (2) estimates of temporal changes in rainfall ID thresholds for flash floods following disturbance in a chaparral-dominated ecosystem, and (3) a methodology for using a hydrological model to assess changes in post-fire flash flood thresholds.
Results indicate that thresholds based on the 75th–85th percentile of peak rainfall intensity averaged over 15–60 min perform best at predicting the occurrence of a flash flood in our study area. In other words, a flash flood tends to be produced when rainfall intensity over 15 %–25 % of the watershed area exceeds a critical value. A threshold based on performs consistently well for post-fire years 1, 2, 3, and 5, although the magnitude of the threshold increases with time since fire. For the watershed studied, the threshold increases from 16.0–16.8 mm h−1 for year 1 to 23.2–26.9, 26.9–32.6, and 27.6–34.5 mm h−1, for years 2, 3, and 5 respectively. Increases in the threshold value of can be primarily attributed to increases in Ksh rather than nc during the hydrological recovery process. The increase in the magnitude of the threshold from year 1 to year 2 is consistent with previous observations from nearby areas in southern California. Results provide a methodology for using radar-derived precipitation estimates and hydrological modeling to estimate flash flood thresholds for improved warning and mitigation of post-fire hydrologic hazards. Thresholds developed through these methods can then be built into operational tools that use incoming radar data to evaluate the flash flood hazard in near-real-time or precipitation forecasts to evaluate potential for flash flood hazard in burned watersheds.
The simulation data are available for research purposes at https://doi.org/10.17605/OSF.IO/62H3P (Liu, 2022). Model and parameters used in this work are available from Liu et al. (2021) at: https://doi.org/10.1002/hyp.14208.
The supplement related to this article is available online at: https://doi.org/10.5194/nhess-22-361-2022-supplement.
TL and LAM conceived the study. TL, LAM, NO, and FC contributed to the development and design of the methodology. TL analyzed and prepared the manuscript with review and analysis contributions from LAM, NO, and FC.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the special issue “Advances in flood forecasting and early warning”. It is not associated with a conference.
Haiyan Wei, Carl L. Unkrich, and David C. Goodrich, who are from the KINEROS2 development group in the USDA ARS Southwest Watershed Research Center in Tucson, helped with the setting up of the KINEROS2 model and ingestion of the RADAR precipitation data into the model. We are thankful for their great help.
This research has been supported by the National Oceanic and Atmospheric Administration (grant no. NA19NWS4680004) and by the National Integrated Drought Information System (NIDIS) (task order no. 1332KP20FNRMT0012).
This paper was edited by Jie Yin and reviewed by two anonymous referees.
Bartles, M., Brunner, G., Fleming, M., Faber, B., Karlovits, G., and Slaughter, J.: HEC-SSP Statistical Software Package Version 2.2, USACE [code], https://www.hec.usace.army.mil/software/hec-ssp/download.aspx (last access: 2 February 2022), 2019.
Benjamin, S. G., Weygandt, S. S., Brown, J. M., Hu, M., Alexander, C. R., Smirnova, T. G., Olson, J. B., James, E. P., Dowell, D. C., Grell, G. A., Lin, H., Peckham, S. E., Smith, T. L., Moninger, W. R., Kenyon, J. S., and Manikin, G. S.: A North American Hourly Assimilation and Model Forecast Cycle: The Rapid Refresh, Mon. Weather Rev., 144, 1669–1694, https://doi.org/10.1175/MWR-D-15-0242.1, 2016.
California Nevada River Forecast Center (CNRFC): NOAA / NWS News and Local CNRFC Information, https://www.cnrfc.noaa.gov/, last access: 2 February 2022.
Camera, C., Bruggeman, A., Hadjinicolaou, P., Michaelides, S., and Lange, M. A.: Evaluation of a spatial rainfall generator for generating high resolution precipitation projections over orographically complex terrain, Stoch. Env. Res. Risk A., 31, 757–773, https://doi.org/10.1007/s00477-016-1239-1, 2017.
Canfield, H. E., Goodrich, D. C., and Burns, I. S.: Selection of parameters values to model post-fire runoff and sediment transport at the watershed scale in southwestern forests, Proceedings of the 2005 Watershed Management Conference – Managing Watersheds for Human and Natural Impacts: Engineering, Ecological, and Economic Challenges, Williamsburg, Virginia, United States, 19–22 July 2005, 561–572, https://doi.org/10.1061/40763(178)48, 2005.
Cannon, F., Hecht, C. W., Cordeira, J. M., and Ralph, F. M.: Synoptic and mesoscale forcing of Southern California extreme precipitation, J. Geophys. Res.-Atmos., 123, 13714–13730, https://doi.org/10.1002/2017JD027355, 2018.
Cannon, F., Oakley, N. S., Hecht, C. W., Michaelis, A., Cordeira, J. M., Kawzenuk, B., Demirdjian, R., Weihs, R., Fish, M. A., Wilson, A. M., and Ralph, F. M.: Observations and Predictability of a High-Impact Narrow Cold-Frontal Rainband over Southern California on 2 February 2019, Weather Forecast., 35, 2083–2097, https://doi.org/10.1175/WAF-D-20-0012.1, 2020.
Cannon, S. H., Gartner, J. E., Wilson, R. C., Bowers, J. C., and Laber, J. L.: Storm rainfall conditions for floods and debris flows from recently burned areas in southwestern Colorado and southern California, Geomorphology, 96, 250–269, https://doi.org/10.1016/j.geomorph.2007.03.019, 2008.
Cannon, S. H., Boldt, E. M., Laber, J. L., Kean, J. W., and Staley, D. M.: Rainfall intensity-duration thresholds for postfire debris-flow emergency-response planning, Nat. Hazards, 59, 209–236, https://doi.org/10.1007/s11069-011-9747-2, 2011.
Cifelli, R., Chandrasekar, V., Chen, H., and Johnson, L. E.: High resolution radar quantitative precipitation estimation in the San Francisco Bay Area: Rainfall monitoring for the urban environment, J. Meteorol. Soc. Jpn., 96, 141–155, 2018.
Dyrness, C.: Effect of Wildfire on Soil Wettability in the High Cascades of Oregon, U.S. Department of Agriculture, Forest Service, Pacific Northwest forest and Range Experiment Station, Portland, Oregon, https://hdl.handle.net/2027/umn.31951d02995118i (last access: 7 February 2022), 1976.
Ebel, B. A.: Temporal evolution of measured and simulated infiltration following wildfire in the Colorado Front Range, USA: Shifting thresholds of runoff generation and hydrologic hazards, J. Hydrol., 585, 124765, https://doi.org/10.1016/j.jhydrol.2020.124765, 2020.
Ebel, B. A. and Martin, D. A.: Meta-analysis of field-saturated hydraulic conductivity recovery following wildland fire: Applications for hydrologic model parameterization and resilience assessment, Hydrol. Process., 31, 3682–3696, https://doi.org/10.1002/hyp.11288, 2017.
Ebel, B. A. and Moody, J. A.: Rethinking infiltration in wildfire-affected soils, Hydrol. Process., 27, 1510–1514, https://doi.org/10.1002/hyp.9696, 2013.
Ebel, B. A. and Moody, J. A.: Synthesis of soil-hydraulic properties and infiltration timescales in wildfire-affected soils, Hydrol. Process., 31, 324–340, https://doi.org/10.1002/hyp.10998, 2017.
Evin, G., Favre, A.-C., and Hingray, B.: Stochastic generation of multi-site daily precipitation focusing on extreme events, Hydrol. Earth Syst. Sci., 22, 655–672, https://doi.org/10.5194/hess-22-655-2018, 2018.
Gillett, N. P., Weaver, A. J., Zwiers, F. W., and Flannigan, M. D.: Detecting the effect of climate change on Canadian forest fires, Geophys. Res. Lett., 31, L18211, https://doi.org/10.1029/2004GL020876, 2004.
Goodrich, D. C., Burns, I. S., Unkrich, C. L., Semmens, D. J., Guertin, D. P., and Hernandez, M.: KINEROS2/AGWA: Model use, Calibration, and Validation, Transactions of the ASABE, 55, 1561–1574, https://doi.org/10.13031/2013.42264, 2012.
Guzzetti, F., Peruccacci, S., Rossi, M., and Stark, C. P.: The rainfall intensity-duration control of shallow landslides and debris flows: An update, Landslides, 5, 3–17, https://doi.org/10.1007/s10346-007-0112-1, 2012.
Hubbert, K. R. and Oriol, V.: Temporal fluctuations in soil water repellency following wildfire in chaparral steeplands, southern California, Int. J. Wildland Fire, 14, 439–447, https://doi.org/10.1071/WF05036, 2005.
Hubbert, K. R., Wohlgemuth, P. M., and Beyers, J. L.: Effects of hydromulch on post-fire erosion and plant recovery in chaparral shrublands of southern California, Int. J. Wildland Fire, 21, 155–167, https://doi.org/10.1071/WF10050, 2012.
Huffman, E. L., MacDonald, L. H., and Stednick, J. D.: Strength and persistence of fire-induced soil hydrophobicity under ponderosa and lodgepole pine, Colorado Front Range, Hydrol. Process., 15, 2877–2892, https://doi.org/10.1002/hyp.379, 2001.
Johnson, L. E., Cifelli, R., and White, A.: Benefits of an advanced quantitative precipitation information system, J. Flood Risk Manag., 13, e12573 https://doi.org/10.1111/jfr3.12573, 2020.
Jorgensen, D. P., Hanshaw, M. N., Schmidt, K. M., Laber, J. L., Staley, D. M., Kean, J. W., and Restrepo, P. J.: Value of a dual-polarized gap-filling radar in support of southern California post-fire debris-flow warnings, J. Hydrometeorol., 12, 1581–1595, https://doi.org/10.1175/JHM-D-11-05.1, 2011.
Kean, J. W., Staley, D. M., and Cannon, S. H.: In situ measurements of post-fire debris flows in southern California: Comparisons of the timing and magnitude of 24 debris-flow events with rainfall and soil moisture conditions, J. Geophys. Res.-Earth., 116, 1–21, https://doi.org/10.1029/2011JF002005, 2011.
Kitzberger, T., Falk, D. A., Westerling, A. L., and Swetnam, T. W.: Direct and indirect climate controls predict heterogeneous early-mid 21st century wildfire burned area across western and boreal North America, PLoS ONE, 12, 1–24, https://doi.org/10.1371/journal.pone.0188486, 2017.
Lamb, M. P., Scheingross, J. S., Amidon, W. H., Swanson, E., and Limaye, A.: A model for fire-induced sediment yield by dry ravel in steep landscapes, J. Geophys. Res.-Earth., 116, 1–13, https://doi.org/10.1029/2010JF001878, 2011.
Larson, I. J., MacDonald, L. H., Brown, E., Rough, D., Welsh, M. J., Pietraszek, J. H., Libohova, Z., de Dios Benavides-Solorio, J., and Schaffrath, K.: Causes of post-fire runoff and erosion: Water repellency, cover, or soil sealing?, Soil Sci. Soc. Am. J., 73, 1393–1407, https://doi.org/10.2136/sssaj2007.0432, 2009.
Leopold, L. B., Wolman, M. G., and Miller, J. P.: Fluvial Processes in Geomorphology, Publications Inc., New York, NY, ISBN 0-486-68588-8, 1964.
Liu, T.: NHESS-Temporal changes in rainfall intensity–duration thresholds, OSFHOME [data set], https://doi.org/10.17605/OSF.IO/62H3P, 2022.
Liu, T., McGurire, L. A., Wei, H. Y., Rengers, F. K., Gupta, H., Ji, L., and Goodrich, D. C.: The timing and magnitude of changes to Hortonian overland flow at the watershed scale during the post-fire recovery process, Hydrol. Process., 35, e14208, https://doi.org/10.1002/hyp.14208, 2021.
Marshall, J. S. and Palmer, W. M. K.: The distribution of raindrops with size, J. Meteor., 5, 165–166, https://doi.org/10.1175/1520-0469(1948)005<0165:TDORWS>2.0.CO;2, 1948.
McGuire, L. A. and Youberg, A. M.: What drives spatial variability in rainfall intensity-duration thresholds for post-wildfire debris flows?, Insights from the 2018 Buzzard Fire, NM, USA, Landslides, 17, 2385–2399, https://doi.org/10.1007/s10346-020-01470-y, 2020.
Meles, M. B., Goodrich, D. C., Gupta, H. V., Burns, S. I, Unkrich, C. L., Razavi, S., and Guertin, D. P.: Uncertainty and parameter sensitivity of the KINEROS2 physically-based distributed sediment and runoff model, in: Proceedings of SEDHYD 2019: Conferences on Sedimentation and Hydrologic Modeling, 24–28 June 2019, Reno, Nevada, USA, 2019.
Miller, S. N., Semmens, D. J., Goodrich, D. C., Hernandez, M., Miller, R. C., Kepner, W. G., and Guertin, D. P.: The automated geospatial watershed assessment tool, Environ. Modell. Softw., 22, 365–377, https://doi.org/10.1016/j.envsoft.2005.12.004, 2007.
Moody, J. A. and Ebel, B. A.: Hyper-dry conditions provide new insights into the cause of extreme floods after wildfire, Catena, 93, 58–63, https://doi.org/10.1016/J.CATENA.2012.01.006, 2012.
Moody, J. A. and Martin, D. A.: Post-fire, rainfall intensity–peak discharge relations for three mountainous watersheds in the western USA, Hydrol. Process., 15, 2981–2993, https://doi.org/10.1002/hyp.386, 2001.
Moreno, H. A., Gourley, J. J., Pham, T. G., and Spade, D. M.: Utility of satellite-derived burn severity to study short- and long-term effects of wildfire on streamflow at the basin scale, J. Hydrol., 580, 124244, https://doi.org/10.1016/j.jhydrol.2019.124244, 2020.
NOAA National Weather Service (NWS) Radar Operations Center: NOAA Next Generation Radar (NEXRAD) Level 2 Base Data, NOAA National Centers for Environmental Information [data set], https://doi.org/10.7289/V5W9574V, 1991.
NOAA: NOAA High-Resolution Rapid Refresh (HRRR) Model, NOAA [data set], available at: https://registry.opendata.aws/noaa-hrrr-pds/ (last access: 2 February 2022), 2021a.
NOAA: Multi-Radar/Multi-Sensor System (MRMS), NOAA [data set], available at: https://www.nssl.noaa.gov/projects/mrms/ (last access: 2 February 2022), 2021b.
Noske, P. J., Nyman, P., Lane, P. N. J., and Sheridan, G. J.: Effects of aridity in controlling the magnitude of runoff and erosion after wildfire, Water Resour. Res., 52, 4338–4357, https://doi.org/10.1002/2015WR017611, 2016.
Oakley, N. S., Lancaster, J. T., Kaplan, M. L., and Ralph, F. M.: Synoptic conditions associated with cool season post-fire debris flows in the Transverse Ranges of southern California, Nat. Hazards, 88, 327–354, https://doi.org/10.1007/s11069-017-2867-6, 2017.
Oakley, N. S., Lancaster, J. T., Hatchett, B. J., Stock, J., Ralph, F. M., Roj, S., and Lukashov, S.: A 22-Year climatology of cool season hourly precipitation thresholds conducive to shallow landslides in California, Earth Interact., 22, 1–35, https://doi.org/10.1175/EI-D-17-0029.1, 2018a.
Oakley, N. S., Cannon, F., Munroe, R., Lancaster, J. T., Gomberg, D., and Ralph, F. M.: Brief communication: Meteorological and climatological conditions associated with the 9 January 2018 post-fire debris flows in Montecito and Carpinteria, California, USA, Nat. Hazards Earth Syst. Sci., 18, 3037–3043, https://doi.org/10.5194/nhess-18-3037-2018, 2018b.
Parlange, J. Y., Lisle, I., Braddock, R. D., and Smith, R. E.: The three-parameter infiltration equation, Soil Sci., 133, 337–341, https://doi.org/10.1097/00010694-198206000-00001, 1982.
Raymond, C. A., McGuire, L. A., Youberg, A. M., Staley, D. M., and Kean, J. W.: Thresholds for post-wildfire debris flows: Insights from the Pinal Fire, Arizona, USA, Earth Surf. Proc. Land., 45, 1349–1360, https://doi.org/10.1002/esp.4805, 2020.
Rengers, F. K., McGuire, L. A., Kean, J. W., Staley, D. M., and Youberg, A. M.: Progress in simplifying hydrologic model parameterization for broad applications to post-wildfire flooding and debris-flow hazards, Earth Surf. Proc. Land., 44, 3078–3092, https://doi.org/10.1002/esp.4697, 2019.
Saksa, P. C., Bales, R. C., Tobin, B. W., Conklin, M. H., Tague, C. L., and Battles, J. J.: Fuels treatment and wildfire effects on runoff from Sierra Nevada mixed-conifer forests, Ecohydrology, 13, 1–16, https://doi.org/10.1002/eco.2151, 2020.
Schmidt, K. M., Hanshaw, M. N., Howle, J. F., Kean, J. W., Staley, D. M., Stock, J. D., and Bawden, G. W.: Hydrologic conditions and terrestrial laser scanning of post-fire debris flows in the San Gabriel Mountains, CA, U.S.A., in: Debris-Flow Hazards Mitigation, Mechanics, Prediction, and Assessment, edited by: Genevois, R., Hamilton, D. L., and Prestininzi, A., Casa Editrice Univ. La Sapienza, Rome, Italy, 583–593, 2011.
Smith, R. E., Goodrich, D. C., Woolhiser, D. A., and Unkrich, C. L.: KINEROS – A kinematic runoff and erosion model, in: Computer models of watershed hydrology, edited by: Singh, V. J., Water Resources Publications, Highlands Ranch, CO, USA, 697–732, 1995.
Staley, D. M., Kean, J. W., Cannon, S. H., Schmidt, K. M., and Laber, J. L.: Objective definition of rainfall intensity-duration thresholds for the initiation of post-fire debris flows in southern California, Landslides, 10, 547–562, https://doi.org/10.1007/s10346-012-0341-9, 2013.
Staley, D. M., Wasklewicz, T. A., and Kean, J. W.: Characterizing the primary material sources and dominant erosional processes for post-fire debris-flow initiation in a headwater basin using multi-temporal terrestrial laser scanning data, Geomorphology, 214, 324–338, 2014.
Staley, D. M., Negri, J. A., Kean, J. W., Laber, J. L., Tillery, A. C., and Youberg, A. M.: Prediction of spatially explicit rainfall intensity–duration thresholds for post-fire debris-flow generation in the western United States, Geomorphology, 278, 149–162, https://doi.org/10.1016/j.geomorph.2016.10.019, 2017.
Stoof, C. R., Vervoort, R. W., Iwema, J., van den Elsen, E., Ferreira, A. J. D., and Ritsema, C. J.: Hydrological response of a small catchment burned by experimental fire, Hydrol. Earth Syst. Sci., 16, 267–285, https://doi.org/10.5194/hess-16-267-2012, 2012.
Sweeney, T. L.: Modernized areal flash flood guidance, NOAA Technical Memorandum, NWS HYDRO, 44, 37 pp. 1992.
USDA Forest Service: Station fire BAER – Burned Area Report, USDA Forest Service, 22 pp., available at: https://www.fs.usda.gov/Internet/FSE_DOCUMENTS/stelprdb5245056.pdf (last access: 2 February 2022), 2009.
Watson, C. L. and Letey, J.: Indices for Characterizing Soil-Water Repellency Based upon Contact Angle-Surface Tension Relationships, Soil Sci. Soc. Am. J., 34, 841–844, https://doi.org/10.2136/sssaj1970.03615995003400060011x, 1970.
Westerling, A. L., Hidalgo, H. G., Cayan, D. R., and Swetnam, T. W.: Warming and earlier spring increase western US forest wildfire activity, Science, 313, 940–943, 2006.
Wilks, D. S. and Wilby, R. L.: The weather generation game: a review of stochastic weather models, Prog. Phys. Geog.-Earth Env., 23, 329–357, https://doi.org/10.1177/030913339902300302, 1999.
Wilson, C., Kampf, S. K., Wagenbrenner, J. W., and Macdonald, L. H.: Forest Ecology and Management Rainfall thresholds for post- fire runoff and sediment delivery from plot to watershed scales, Forest Ecol. Manag., 430, 346–356, https://doi.org/10.1016/j.foreco.2018.08.025, 2018.
Yatheendradas, S., Wagener, T., Gupta, H., Unkrich, C., Goodrich, D., Schaffner, M., and Stewart, A.: Understanding uncertainty in distributed flash flood forecasting for semiarid regions, Water Resour. Res., 44, 1–17, https://doi.org/10.1029/2007WR005940, 2008.
Zhang, J., Howard, K., Langston, C., Kaney, B., Qi, Y., Tang, L., Grams, H., Wang, Y., Cocks, S., Martinaitis, S., Arthur, A., Cooper, K., Brogden, J., and Kitzmiller, D.: Multi-Radar Multi-Sensor (MRMS) Quantitative Precipitation Estimation: Initial Operating Capabilities, B. Am. Meteorol. Soc., 97, 621–638, available at: https://journals.ametsoc.org/view/journals/bams/97/4/bams-d-14-00174.1.xml (last access: 2 February 2022), 2016.
Zhao, Y., Nearing, M. A., and Guertin, D. P.: A daily spatially explicit stochastic rainfall generator for a semi-arid climate, J. Hydrol., 574, 181–192, 2019.