Cost–benefit analysis of coastal flood defence measures in the North Adriatic Sea

The combined effect of global sea level rise and land subsidence phenomena poses a major threat to coastal settlements. Coastal flooding events are expected to grow in frequency and magnitude, increasing the potential economic losses and costs of adaptation. In Italy, a large share of the population and economic activities are located along the low-lying coastal plain of the North Adriatic coast, one of the most sensitive areas to relative sea level changes. Over the last half a century, this stretch of coast has experienced a significant rise in relative sea level, the main component of which was land subsidence; in the forthcoming decades, climate-induced sea level rise is expected to become the first driver of coastal inundation hazard. We propose an assessment of flood hazard and risk linked with extreme sea level scenarios, under both historical conditions and sea level rise projections in 2050 and 2100. We run a hydrodynamic inundation model on two pilot sites located along the North Adriatic coast of Emilia-Romagna: Rimini and Cesenatico. Here, we compare alternative extreme sea level scenarios accounting for the effect of planned and hypothetical seaside renovation projects against the historical baseline. We apply a flood damage model to estimate the potential economic damage linked to flood scenarios, and we calculate the change in expected annual damage according to changes in the relative sea level. Finally, damage reduction benefits are evaluated by means of cost–benefit analysis. Results suggest an overall profitability of the investigated projects over time, with increasing benefits due to increased probability of intense flooding in the near future.

1 Introduction

Globally, more than 700 million people live in low-lying coastal areas (McGranahan et al., 2007), and about 13 % of them are exposed to a 100-year-return-period flood event (Muis et al., 2016). Every year, on average, 1 million people located in coastal areas experience flooding (Hinkel et al., 2014). Coastal flood risk shows an increasing trend in many places due to socio-economic growth (Jongman et al., 2012b; Bouwer, 2011) and land subsidence (Nicholls and Cazenave, 2010; Syvitski et al., 2009), but in the near future sea level rise (SLR) will likely be the most important driver of increased coastal inundation risk (Hallegatte et al., 2013; Hinkel et al., 2014). Evidence shows that global sea level has risen at faster rates in the past century compared to the millennial trend (Church and White, 2011; Kemp et al., 2011), topping 3.6 mm yr⁻¹ in the last decade (2006–2015) mainly due to ocean thermal expansion and glacier melting processes (Meyssignac and Cazenave, 2012; Mitchum et al., 2010; Pötner et al., 2019). According to the IPCC projections, it is very likely that, by the end of the 21st century, the SLR rate will exceed that observed in the period 1971–2010 for all Representative Concentration Pathway (RCP) scenarios (Pötner et al., 2019); yet the local sea level can have strong regional variability, with some places experiencing significant deviations from the global mean change (Stocker et al., 2013). This is particularly worrisome in regions where small changes in the mean sea level (MSL) can drastically change the frequency of extreme sea level (ESL) events, leading to situations where a 100-year event may occur several times per year by 2100 (Vousdoukas et al., 2018, 2017; Carbognin et al., 2009, 2010; Kirezci et al., 2020). Changes in the frequency of extreme events are likely to make existing coastal protection inadequate in many places, causing a large part of European coasts to be exposed to flood hazard. Under these premises, coastal floods threaten to trigger devastating impacts on human settlements and activities (McInnes et al., 2003; Lowe et al., 2001; Vousdoukas et al., 2017). In this context, successful coastal risk mitigation and adaptation actions require accurate and detailed information about the characterization of coastal flood hazard and the performance of coastal defence options. Cost–benefit analysis (CBA) is widely used to evaluate the economic desirability of a disaster risk reduction (DRR) project (Jonkman et al., 2004; Price, 2018; Mechler, 2016), helping decision-makers in evaluating the efficacy of different adaptation options (Kind, 2014; Bos and Zwaneveld, 2017).

In this study, we estimate the benefits of coastal renovation projects along the coast of the Emilia-Romagna region (Italy) in terms of avoided economic losses from ESL inundation events under both current and future conditions. To do that, a range of hazard scenarios associated with ESL events are simulated over the two case study areas: (i) Rimini, a touristic hotspot that is currently implementing a seafront renovation project, and (ii) Cesenatico, a coastal city that could benefit from similar measures in addition to existing defence mechanisms. The scenarios are designed by combining probabilistic data from historical ESL events with the estimates of relative MSL change for those locations. Each scenario is evaluated in terms of direct economic impacts over residential areas using a flood damage model. The combination of different risk scenarios in a CBA framework allows the evaluation of the economic profitability brought by the project implementation in terms of avoided losses up to the end of the century.

2 Area of study

Located in the central Mediterranean Sea, the Italian peninsula has more than 8300 km of coastline, hosting around 18 % of the country's population, numerous towns and cities, industrial plants, commercial harbours, and touristic activities, as well as cultural and natural heritage sites. Existing country-scale estimates of SLR impacts up to the end of this century help to identify the most critically exposed coastal areas of Italy (Antonioli et al., 2017; Marsico et al., 2017; Bonaduce et al., 2016; Lambeck et al., 2011). About 40 % of the country's coastal perimeter consists of a flat profile (ISPRA, 2012), potentially more vulnerable to the impacts of ESL events. The North Adriatic coastal plain is the largest location and most vulnerable to extreme coastal events due to the shape, morphology and low bathymetry of the Adriatic Sea basin, which cause the water level to increase relatively fast during coastal storms (Perini et al., 2017; Ciavola and Coco, 2017; Carbognin et al., 2010). Here the ESL is driven mainly by the astronomical tide, ranging about 1 m in the northernmost sector, and by meteorological forcing, such as low pressure, seiches and prolonged rotational wind systems, which are the main trigger of storm surge (Vousdoukas et al., 2017; Umgiesser et al., 2020). In addition to that, the whole coastal profile of the Padan plain shows relatively fast subsiding rates, partially due to natural phenomena but in large part linked to human activities (Perini et al., 2017; Carbognin et al., 2009; Meli et al., 2020). As a contributing factor to coastal flood risk, the intensification of urbanization has led to increased exposure along the Adriatic coast during the last 50 years, with many regions building on over half of the available land within 300 m of the shoreline (ISPRA, 2012). Figure 1 shows the location of the two case study areas, Cesenatico and Rimini, along with land-cover maps showing the position of coastal defences accounted for in this study.

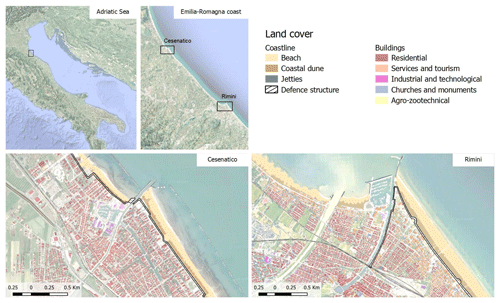
Figure 1 Case study locations along the Emilia-Romagna coast: Cesenatico and Rimini. The coastal defence structure assessed in this study are shown in black. Buildings' footprint data are from the Regional Environmental Protection Agency (ARPA) 2020. Basemap © Google Maps 2020.

The number of ESL events reported to cause impacts along the Emilia-Romagna coast has shown a steady increase since the second half of the past century (Perini et al., 2011); this is partially explained by socio-economic development, which has increased the extent of built-up assets potentially exposed to flood risk. The landscape along the 130 km regional coastline is almost completely flat, the only relief being old beach ridges, artificial embankments and a small number of dunes. The coastal perimeter is delineated by a wide sandy beach that is generally protected by offshore breakwaters, groins and jetties. The land elevation is often close to (or even below) the MSL, and the coastal corridor is heavily urbanized. Cesenatico has about 26 000 residents, while Rimini has 150 000. The towns are strongly touristic, hosting large beach resort and bathing facilities along the beach and with hundreds of hotels and rental housing located just behind the beach. Both places have been affected by coastal storms, resulting in flooding of buildings and facilities, beach erosion, and regression of the coastline. The most recent inundation events were observed in March 2010, November 2012 and February 2015. The 2015 event was one of the most severe ever recorded, with ESL values corresponding to a probability (return period) of once in 100 years. It caused severe damage along the whole regional coast and, in some locations, required the evacuation of people from their houses; many buildings and roads were covered by sand brought by the flood wave; touristic infrastructures near the shore were seriously damaged, and some port channels overflowed into the surrounding areas. The economic impact of the event was estimated to top EUR 7.5 million (Perini et al., 2015).

3 Methodology

3.1 Components of the analysis

Coastal inundation is caused by an increase in the total water level (TWL), most often associated with extreme sea level (ESL) events, which are often generated by a combination of high astronomical tide and meteorological drivers such as storm surge and wind waves (Fig. 2). Probabilistic flood risk assessments generally consider ESL the result of the combined effects of storm surge and tides (Muis et al., 2015; Vousdoukas et al., 2017). More recent studies also account for the effects of waves by either adding wave setup to the ESL or simulating the dynamics of breaking waves on the coast (Kirezci et al., 2020; Melet et al., 2020; Li et al., 2020; Wang et al., 2021; Muis et al., 2020; Lionello et al., 2021; McInnes et al., 2009; Idier et al., 2019). In our study, we consider the TWL nearshore the result of the combination of high tide, storm surge and action of waves, the latter combining wave setup (defined as the increase in mean sea level at the shore that is caused by the loss of wave momentum in the surf zone) with the wave periodicity of incoming breaking waves (which defines wave swash, i.e. the amplitude of the time-varying elevation due to breaking waves along the shore).

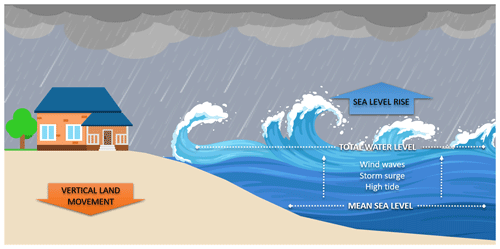
Figure 2 Components of the analysis for extreme sea level events: total water level is the sum of the maximum tide, storm surge and wind waves over mean sea level. Vertical land movement and sea level rise affect the mean sea level on the long run.

The identification of areas threatened by coastal flooding from ESL events is often done by means of flood maps, which are generated through hydrostatic or hydrodynamic modelling approaches. These approaches differ substantially in their complexity and their ability to represent environmental processes. The hydrostatic inundation approach (sometimes referred to as “bathtub”) is methodologically simple and computationally quick, as it does not consider dynamic processes such as flow mass conservation and the effect of land cover on the spread of floodwater, assuming flooded areas to be those with an elevation below a forcing water level (Hinkel et al., 2010, 2014; Jongman et al., 2012b; Ramirez et al., 2016; Vousdoukas et al., 2016; Muis et al., 2016). These assumptions and simplifications often result in substantial misestimation of flood extents compared to hydrodynamic flood modelling and observations (Bates et al., 2005; Vousdoukas et al., 2016; Breilh et al., 2013; Ramirez et al., 2016; Seenath et al., 2016; Kumbier et al., 2019; Anderson et al., 2018). To overcome these limitations, hydrodynamic flood modelling approaches capable of accounting for the effects of wind, waves, tide, current and river run-off can be used (Barnard et al., 2019). The most advanced models can simulate atmospheric–ocean–land interactions from the deep ocean to the coast with a satisfactory predictive skill (Bates et al., 2005; Seenath et al., 2016; Vousdoukas et al., 2016; Lewis et al., 2013), at the costs of a more complex model setup, extensive data requirements and significantly longer computational times (Teng et al., 2017). As an intermediate solution, simplified hydrodynamic flood models that focus on nearshore processes are capable of reducing the computational cost while taking into consideration water mass conservation (Breilh et al., 2013), aspects of flooding hydrodynamics (Dottori et al., 2018) and the presence of obstacles (Perini et al., 2016). They have proved to be reliable for coastal flooding applications, such as the simulation of coastal flooding due to storm tide events (Ramirez et al., 2016; Bates et al., 2005; Skinner et al., 2015; Smith et al., 2012).

In this study, estimates of ESL components (storm surge, tides and waves) are obtained for the North Adriatic up to the year 2100 by combining reference hazard scenarios derived from the analysis of historical records (Perini et al., 2011, 2016, 2017; Armaroli et al., 2012; Armaroli and Duo, 2018) with regionalized projections of SLR (Vousdoukas et al., 2017) and local vertical land movement (VLM) rates (Perini et al., 2017; Carbognin et al., 2009). On this basis, four hypothetical ESL scenarios are designed, ranging from low intensity–high frequency to high intensity–low frequency, under both current and future (2050 and 2100) conditions. The hydrodynamic model ANUGA (Roberts et al., 2015) is applied to simulate the inundation of land areas during periods of ESL, accounting for individual components. The land morphology and exposure of coastal settlements are described by high-resolution digital terrain model (DTM) (lidar) and bathymetry, in combination with land use and building footprints. The effect of hazard mitigation structures (both designed and under construction) are explicitly accounted for by the model in the “defended” scenario, in contrast to the baseline scenario, where only existing defence structures (groins, jetties, breakwaters and sand dunes) are considered.

3.2 Vertical land movement

Vertical land movements result from a combination of slow geological processes, such as tectonic activity and glacial isostatic adjustment (Peltier et al., 2015; Peltier, 2004), and medium-term phenomena, such as sediment loading and soil compaction (Carminati and Martinelli, 2002; Lambeck and Purcell, 2005). The latter can greatly exacerbate geological processes at a local scale (Wöppelmann and Marcos, 2012); in particular, faster subsidence occurs in the presence of intense anthropogenic activities such as water withdrawal and natural-gas extraction (Teatini et al., 2006; Polcari et al., 2018). Most of the peninsula shows a slow subsiding trend, although with some local variability. An estimate of VLM rates due to tectonic activity has been derived from studies conducted in Italy (Solari et al., 2018; Antonioli et al., 2017; Marsico et al., 2017; Lambeck et al., 2011). The North Adriatic coastal plain shows the most intense long-term geological subsidence rates (about 1 mm yr⁻¹), increasing north to south. Yet in the last few decades these rates have often been greatly exceeded by ground compaction rates observed by remote sensing (Gambolati et al., 1998; Antonioli et al., 2017; Polcari et al., 2018; Solari et al., 2018). Observed subsidence is about 1 order of magnitude faster where the aquifer system has been extensively exploited for agricultural, industrial and civil use since the post-war industrial boom. Since the 1970s, however, with the halt of groundwater withdrawals, anthropogenic drivers of subsidence have been strongly reduced or stopped (Carbognin et al., 2009). Nonetheless, subsidence still continues at much faster rates than expected from natural phenomena (Teatini et al., 2005). Geodetic surveys carried out from 1953 to 2003 along the Ravenna coast provide evidence of a cumulative land subsidence exceeding 1 m at some sites due to gas extraction activities. Average subsidence rates observed for 2006–2011 along the Emilia-Romagna coast are around 5 mm yr⁻¹, exceeding 10 mm yr⁻¹ on the backshore of the Cesenatico and Rimini areas and topping 20–50 mm yr⁻¹ in Ravenna (Perini et al., 2017; Carbognin et al., 2009). Based on these current rates, we assume an average fixed annual VLM of 5 mm in both Cesenatico and Rimini up to the end of the century. This remarkable difference between natural VLM rates and observations would produce a dramatic effect on the estimated SLR scenarios: at present rates, Rimini would see an increase in the MSL by 0.15 m in 2050 and more than 0.4 m in 2100 independently from eustatic SLR. Since these rates are connected with human activity, it is not possible to foresee how they will change in the longer run.

3.3 Sea level rise

The long-term availability of tide gauge data along the North Adriatic coast allows an assessment of the changes in MSL during the last century, estimated to be +1.3 mm yr⁻¹ (Scarascia and Lionello, 2013). This is consistent with published values for the Mediterranean Sea (Tsimplis et al., 2008; Tsimplis and Rixen, 2002) and the Adriatic Sea (Tsimplis et al., 2012; Carbognin et al., 2009). The projections of future MSL account for sea thermal expansions from four global circulation models, estimated contributions from ice sheets and glaciers (Hinkel et al., 2014), and long-term subsidence projections (Peltier, 2004). The ensemble mean is chosen to represent each RCP for different time slices. The increase in the central Mediterranean basin is projected to be approximately 0.2 m by 2050 and between 0.5 and 0.7 m by 2100, compared to the historical mean (1970–2004) (Vousdoukas et al., 2017). As agreed with local stakeholders (Comune di Rimini), our analysis considers the intermediate emission scenario RCP4.5, projecting an increase in the MSL of 0.53 m in 2100. It must be noted that these projections, although downscaled for the Adriatic basin, do not account for the peculiar continental characteristics of the shallow northern Adriatic sector, where the hydrodynamics and oceanographic parameters partially depend on the freshwater inflow (Zanchettin et al., 2007).

3.4 Tides and meteorological forcing

Storm surge and wind waves represent the largest contributions to the TWL during an ESL event. An estimation of these components is obtained for the two coastal sites from the analysis of tide gauge and buoy records and from the description of historical extreme events presented in local studies (Armaroli and Duo, 2018; Perini et al., 2012; Masina et al., 2015; Perini et al., 2011, 2017). This area is microtidal: the mean neap tidal range is 30–40 cm, and the mean spring tidal range is 80–90 cm. Most storm surge events have a duration of less than 24 h and a maximum significant wave height of about 2.5 m. During extreme cyclonic events, the sequence of SE wind (sirocco) piling the water north and ENE wind (bora) pushing waves towards the coast can generate severe inundation events, with the significant wave height ranging 3.3–4.7 m and exceptionally exceeding 5.5 m (Armaroli et al., 2012). Fifty significant events have been recorded from 1946 to 2010 on the Emilia-Romagna (ER) coast, with half of them causing severe impacts along the whole coast and 10 of them being associated with important flooding events (Perini et al., 2017). The most severe events are found when strong winds blow during exceptional tide peaks, most often happening in late autumn and winter. The event of November 1966 represents the highest ESL on record, causing significant impacts along the regional coast: the recorded water level was 1.20 m a.m.s.l., and wave heights offshore were estimated at around 6–7 m (Garnier et al., 2018; Perini et al., 2011). The whole coastline suffered from erosion and inundation, especially in the province of Rimini. Atmospheric forcing has shown significant variability for the period of 1960 onwards (Tsimplis et al., 2012), but there is no strong evidence supporting a significant change in marine storminess frequency or severity for the near future (Lionello, 2012; Zanchettin et al., 2020; Lionello et al., 2020, 2017). Thus, in our model we assume meteorological forcing to remain the same up to 2100.

3.5 Terrain morphology and coastal defence structures

Reliable bathymetry and topography are required in order to run the hydrodynamic modelling at the local scale. Bathymetric data for the Mediterranean Sea were obtained from the European Marine Observation and Data Network (EMODnet) at a 100 m resolution. The description of terrain morphology comes from the official high-resolution lidar DTM (MATTM, 2019). First, we combine the coastal dataset (2 m resolution and vertical accuracy of ±0.2 m) and the inland dataset (1 m resolution and vertical accuracy ±0.1 m) into one seamless layer. Then, the DTM is supplemented with geometries of existing coastal protection elements such as jetties, groins and breakwaters obtained from the digital regional technical map. In Rimini, the Parco del Mare (Fig. 3) is an urban renovation project which aims to improve the seafront promenade: the existing road and parking lots are converted into an urban green infrastructure consisting of a concrete barrier covered by vegetated sandy dunes with walking paths. This project also acts as a coastal defence system during extreme sea level events. The barrier rises 2.8 m along the southern section of the town, south of the marina; no barrier is planned on the northern coastal perimeter. The Parco del Mare project is expected to be completed by 2022 and has been taken into account in the evaluation of the defended scenarios by adding the barrier elevation to the DTM.

Figure 3 Prototype design of Parco del Mare project in Rimini. Adapted from JDS Architects.

In Cesenatico, the existing defence structures include a moving barrier system (Porte Vinciane) located in the port channel, coupled with a dewatering pump which discharges the meteoric waters into the sea. The barriers close automatically if the TWL surpasses 1 m over the mean sea level, preventing floods in the historical centre for up to 2.2 m of TWL. Additional defence structures include the winter dunes, which consist of a 2.2 m tall intermittent, non-reinforced sand barrier. In the defended scenario, we envisage a coastal defence structure similar to Rimini's Parco del Mare project, spanning both north and south of the port channel with a total length of 7.8 km. The DTM was manually edited based on additional reference data (i.e. on-site observations or aerial photography) in order to remove artefacts and to produce a more realistic representation of the land morphology. Bridges and tunnels are the most critical elements that required DTM correction in order to avoid misrepresentations of the water flow routing.

3.6 Scenario design

In order to design probabilistic nearshore scenarios associated with ESL of different intensities to use as boundary conditions in the hydrodynamic model, we rely on existing analysis of ESL events occurring on the regional coast (Perini et al., 2011, 2016, 2017), which have been adopted by the Regional Environmental Protection Agency to define the official coastal flood hazard zones and related protection standards (ARPA Emilia-Romagna, 2019). The probability of occurrence of these ESL scenarios is expressed in terms of the return period (RP), which is the estimated average time interval (in years) between events of similar intensity. Four scenarios of increasing intensity are designed, namely RP 1, 10, 100 and 250 years. For each of these hypothetical scenarios, the TWL nearshore is calculated as the sum of extreme values for the storm surge (SS) level, max tide (T_max) and wave contribution (W_c) at each time step (see Table 1). In particular, given the limitation of the considered 2D hydrodynamic model in not resolving vertical convection and wave breaking (i.e. swash), we include the wave contribution to the TWL by accounting for wave setup (W_s) with a periodicity equal to the incoming breaking waves (W_p), thus partially representing wave motion (Armaroli et al., 2012, 2009). We develop a set of trigonometric equations based on harmonic analysis concepts to characterize the amplitude and period of tidal, storm surge and wave levels as the harmonic constituents that describe the theoretical temporal evolution of the nearshore TWL during an ESL event (see Fig. 4). Harmonic constituents are the elements in a mathematical expression of a series of periodic terms and have been used in harmonic analysis for sea level prediction (Boon, 2011; Familkhalili et al., 2020; Fuhrmann et al., 2019; Annunziato and Probst, 2016). The set of equations used in the study is specified in Appendix A, together with sample applications and validation metrics of observed ESL events along the coast of ER. Additional variables to characterize the event dynamics are the storm surge duration (time, in hours) and the wave period (W_p, in seconds), both obtained from regional studies of ESL events (Armaroli et al., 2012; Armaroli and Duo, 2018). Projections of the TWL at 2050 and 2100 are calculated for the same set of RP scenarios by adding SLR and VLM contributions to the MSL, thus shifting the TWL curve up by 33 cm in 2050 and by 97 cm in 2100.

Table 1 Components of nearshore TWL for four ESL scenarios (RPs) designed according to analysis of historical ESL events and projected MSL change (2050 and 2100), accounting for both SLR (RCP4.5) and the average VLM rate.

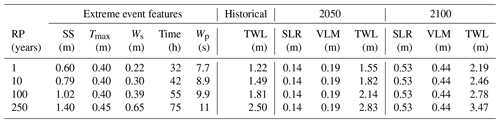
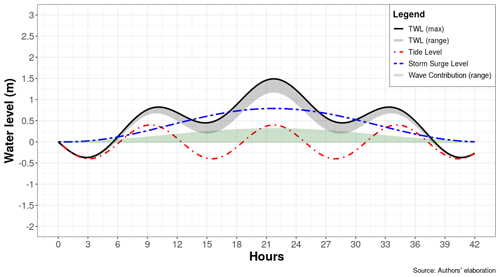
Figure 4 Design of dynamic ESL scenario corresponding to RP 10 years under historical MSL conditions. The maximum TWL is shown as the solid black line, while the TWL range at any given time is shown as the shaded grey area. The components of the nearshore TWL are the tide level (dashed red line), the storm surge level (dashed blue line) and the wave contribution (green-shaded area). Wave contribution is represented as a shaded area due to its high frequency (period of 8.9 s). In this scenario (RP 10) the maximum storm surge level is 0.79 m, the maximum high tide is 0.40 m and the wave contribution ranges from 0.00 to 0.30 m, with a wave period of 8.9 s. At the peak of the event, these conditions produce a maximum TWL of 1.49 m.

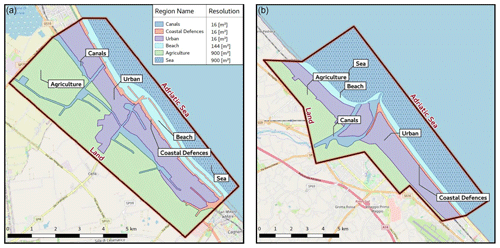
Figure 5 The definition of the simulation domain for the cities of Cesenatico (a) and Rimini (b). The legend shows the mesh resolution specific to each region simulated by the model.

Figure 5 shows how the nearshore TWL results at any given time from the combination of the storm surge, tide level and wave contribution in the scenario of RP 10 years (additional figures for all RP scenarios can be found in Appendix A). The individual contribution of SS and T_max levels are represented by coloured dashed lines in the figure. The W_c component is shown as a green-shaded area due to its high frequency (defined by the wave period, W_p, in seconds), thus representing the range of values assumed at any given time. The intensity of the wave contribution to the ESL is assumed to grow proportionally to the increase in the SS component. The shaded grey area represents the range of the TWL as a sum of these components, while the solid black line represents the maximum TWL at any given time. Our approach is precautionary as it provides worst-case TWL values: the SS peak is set to coincide with T_max and W_c at the middle of the event, thus resulting in the maximum TWL possible under each scenario.

3.7 Inundation modelling

The nearshore ESL scenarios specified in Table 1 and exemplified in Fig. 4 (and Appendix A) are used as forcing boundary conditions in ANUGA, a 2D hydrodynamic model suitable for the simulation of flooding resulting from riverine peak flows and storm surges (Roberts, 2020). The fluid dynamics simulation is based on a finite-volume method for solving the shallow-water wave equations, thus being based on continuity and a simplified momentum equation. Being a 2D hydrodynamic model, ANUGA does not resolve vertical convection, wave breaking or 3D turbulence (i.e. vorticity); thus it cannot account for the swash component of wave runup. The wave direction is set to be oriented perpendicularly to the coast. For each scenario, ANUGA computes the TWL on the coast, the resulting water depth of inundation and the horizontal momentum on an unstructured triangular grid (mesh) representing the two case study areas. The size of the triangles is variable within the mesh, thus allowing for a better representation in regions of particular interest, such as along the coastline, in urban areas and inside the canals. Six different regions are used in each case study to define different triangular mesh resolutions, varying from higher-resolution areas of 16 m² for canals and coastal defence structures to a lower resolution of 900 m² for sea areas. The output of the simulation consists of maps representing the flood extent, water depth and momentum at every time step (∼ 1 s), projected onto the high-resolution DTM grid (1 m). Figure 6 presents the two case study areas and the respective resolutions for each region. The resulting irregular mesh contains about 637 000 triangles for the Cesenatico domain and about 1.2 million triangles for the Rimini domain. The model includes an operator module that simulates the removal of sand associated with the overtopping of a sand dune by sea waves. The operator simulates the erosion, collapse, fluidization and removal of sand from the dune system (Kain et al., 2020). This option is enabled only in the undefended scenario for Cesenatico, where non-reinforced sand dunes are prone to erosion.

3.8 Risk modelling and expected annual damage

Direct damage to physical assets is estimated using a customary flood risk assessment approach originally developed for fluvial inundation, which is adapted to coastal flooding assuming that the dynamics of impact from long-setting floods depends on the same factors, namely (1) hazard magnitude and (2) the type, size and value of the exposed asset. Indirect economic losses due to secondary effects of damage (e.g. business interruption) are excluded from the computation. The hazard magnitude can be defined by a range of variables, but the most important predictors of damage are water depth and the extent of the flood event (Jongman et al., 2012a; Huizinga et al., 2017). The characterization of the exposed asset is built from a variety of sources, starting from land use and building footprints obtained from the regional environmental agencies' geodatabases and the OpenStreetMap database (Open Street Map data for Nord-Est Italy, 2019). Additional indicators about building characteristics are obtained from the database of the 2011 Italian Census (15^∘ censimento della populazione e delle abitazioni, 2019), while mean construction and restoration costs per building type are obtained from cadastral estimates (CRESME, 2019). The asset representation is static, thus not accounting for changes in land use or population density while allowing for the direct comparison of hazard mitigation options' results. A depth–damage function validated on empirical records (Amadio et al., 2019) is applied in order to translate each hazard scenario into an estimate of economic risk, measured as a share of the total exposed value. The damage function applies only to residential and mixed residential buildings, the area of which represents about 93 % of the total exposed footprints; other types (such as harbour infrastructures, industrial, commercial, historical monuments and natural sites) are excluded from risk computation. Abandoned or under-construction buildings are also excluded from the analysis. To avoid overcounting of marginally affected buildings, we set two threshold conditions for damage calculation: the flood extent must be greater than or equal to 10 m² and maximum water depth must be greater than or equal to 10 cm. The damage and probability scenarios are combined together as expected annual damage (EAD). EAD is the damage that would occur in any given year if damage from all flood probabilities were spread out evenly over time; mathematically, EAD is the integration of the flood risk density curve over all probabilities (Olsen et al., 2015), as in Eq. (1).

$$\begin{array}{}\text{(1)}& \text{EAD}=\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}D\left(p\right)dp\end{array}$$

The integration of the curve can be solved either analytically or numerically, depending on the complexity of the damage function D(p). Several different methods for numerical integration exist; we use an approach where EAD is the sum of the product of the fractions of exceedance probabilities and their corresponding damage (Fig. 7). We calculate D(p), which is the damage that occurs at the event with probability p, by using the depth–damage function for each hazard scenario. The exceedance probability of each event (p) is calculated based on an exponential function as shown in Eq. (2).

$$\begin{array}{}\text{(2)}& p=\mathrm{1}-e^{\left(\frac{-\mathrm{1}}{\text{RP}}\right)}\end{array}$$

Events with a high probability of occurrence and low intensity (below RP 1 year) are not simulated as they are assumed to not cause significant damage. This is consistent with the historical observations for the case study area, although this assumption could change with increasing MSL.

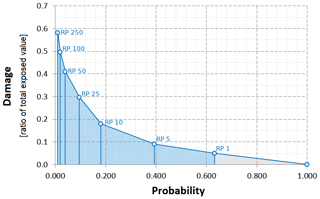
Figure 6 Schematic representation of the numerical integration of the damage function D(p) with respect to the exponential probability of the hazard events. Damage (y axis) represents the ratio of damage to the total exposed value estimated up to the most extreme scenario (RP 250 years). Events with a probability of occurrence higher than once in a year are expected to not cause damage (grey area).

Figure 7 Rimini: extent of land affected by flood according to the frequency of occurrence of ESL events up to 2100 for the baseline (a) and the defended (b) scenario. Basemap © Google Maps 2020.

3.9 Cost–benefit analysis

A CBA should include a complete assessment of the impacts brought by the implementation of the hazard mitigation option, i.e. direct and indirect and tangible and intangible impacts (Bos and Zwaneveld, 2017). The project we are considering, however, has not been primarily designed for a DRR purpose; instead, it is meant as an urban renovation project which aims to consolidate the touristic appeal of the area, to improve quality of life and the urban environment (Comune di Rimini, 2018). This implies some large indirect effects on the whole area, most of which are not strictly related to disaster risk management and, overall, are very difficult to estimate ex ante. Our evaluation focuses only on the benefits that are measurable in terms of direct flood loss reduction. Regarding the implementation costs, the CBA accounts for the initial investment required for setting up the adaptation measure and operational costs through time. According to the Parco del Mare project funding documentation (Comune di Rimini, 2019a, b, 2020, 2021a, b), the total cost of the project (to be completed during 2021) is EUR 33.3 million, corresponding to EUR 5.55 million per kilometre. No information is available about maintenance costs of the project, but given the nature of the project (static defence with low structural fragility), we assume they will be rather small compared to the initial investment. Ordinary annual maintenance costs (EAC) are accounted as 0.1 % of the total cost of the project. The same costs are assumed for the hypothetical barrier in Cesenatico, resulting in an initial investment cost of EUR 43.3 million. Costs and benefits occurring in the future periods need to be discounted, as people put higher value on the present (Rose et al., 2007). This is done by adjusting future costs and benefits using an annual discount rate (r). We chose a variable rate of r=3.5 for the first 50 years and r=3 from 2050 onwards (Lowe, 2008). A sensitivity analysis of the discount rate is included in Appendix B. The three main decision criteria used in CBA for project evaluation are the net present value (NPV), the benefit $/$ cost ratio (BCR) and the payback period. The NPV is the sum of expected annual benefits (B) up to the end of the time horizon, discounted, minus the total costs for the implementation of the defence measure, which takes into account initial investment plus discounted annual maintenance costs (C). In other words, the NPV of a project equals the present value of the net benefits (NB${}_i=B_i-C_i)$ over a period of time (Boardman et al., 2018), as in Eq. (3).

$$\begin{array}{}\text{(3)}& \text{NPV}=\mathrm{PV}\left(B\right)-\mathrm{PV}\left(C\right)=\sum _{t=\mathrm{0}}^n{\displaystyle \frac{{\text{NB}}_r}{(\mathrm{1}+r{)}^t}}\end{array}$$

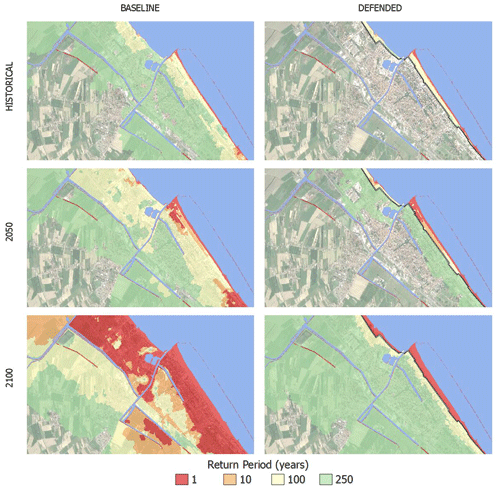
Figure 8 Cesenatico: extent of land affected by flood according to the frequency of occurrence of ESL events up to 2100 for the baseline (a) and the defended (b) scenario. Basemap © Google Maps 2020.

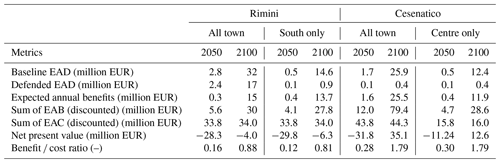
Table 2 Summary of CBA for planned or designed seaside defence project in Rimini (all town and south section only) and Cesenatico (all town and centre only) over a time horizon of 30 and 80 years (2021 to 2050 and 2021 to 2100).

A positive NPV means that the project is economically profitable. The BCR is instead the ratio between the benefits and the costs; a BCR larger than 1 means that the benefits of the project exceed the costs in the long term and the project is considered profitable. The payback period is the number of years required for the discounted benefits to equal the total costs.

4 Results

4.1 Inundation scenarios

Once the setup is completed, the hydrodynamic model performs relatively fast: each simulation is carried at half speed compared to real time, requiring about 24 h to simulate a 12 h event. Parallel simulations for the same area can run on a multicore processor, improving the efficiency of the process. The output of the hydrodynamic model consists of a set of inundation simulations that include several hazard intensity variables in relation to flood extent: water depth, flow velocity and duration of submersion. ESL scenarios are then summarized into static maps, each one representing the maximum value reached by hazard intensity variables during the simulated event at about a 1 m resolution. The flood extents corresponding to each RP scenario are shown for Rimini (Fig. 8) and Cesenatico (Fig. 9).

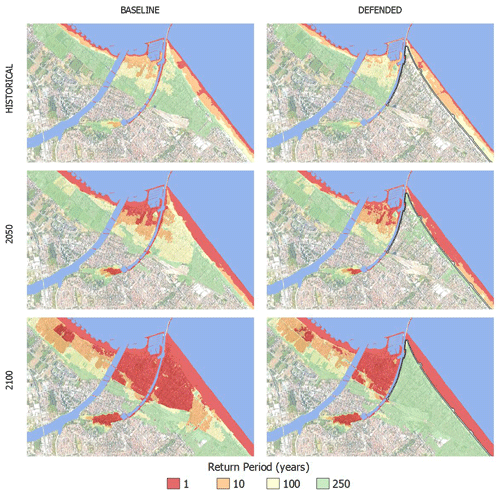
In Rimini, the Parco del Mare barrier produces benefits in terms of avoided flooding in the south-eastern part of the town (high-density area) for ESL events with a return period of 100 years or less. The north-western part and the marina are outside of the defended area; these areas are therefore subject to a similar amount of flooding across scenarios. In all the simulations, the buildings located behind the marina are the first to be flooded. In fact, the new and the old port channels located on both sides of the marina represent a hazard hotspot: as shown in the maps, the failure of the eastern channel, which has a relatively low elevation, is likely to cause the water to flood the eastern part of the town, even during inundation events that would not surpass the beach. In the defended scenarios, where both the coastal and the canal barriers are enabled, the flood extent in the south-eastern urban area becomes almost zero for ESL events with a probability of once in 100 years, even when accounting for SLR up to 2100. Under the most exceptional ESL conditions (RP 250 in 2100), the barrier is overtopped, generating a flood extent similar to the baseline scenario for the same occurrence probability.

In Cesenatico, a barrier designed similarly to Parco del Mare could provide significant reduction in flood extents under most hazard scenarios. Its effectiveness would be greater than in Rimini thanks to the complementary movable barrier system in use, which seals the port channel, allowing the walling off of the whole coastal perimeter and reducing the chance of water ingression in the urban area. In contrast, the erodible winter dune in the baseline defence scenario can only hold the heavy sea for shorter, less intense ESL events (RP 1–10 years) and becomes ineffective with more exceptional, long-lasting events; from 2050 on, the winter dune could be surmounted and dismantled by sea waves even during non-exceptional events (RP 1 year).

4.2 Expected annual damage

The expected annual damage is calculated as a function of the maximum exposed value and water depth. In Rimini, the EAD grows from around EUR 650 000 under historical conditions to EUR 2.8 million in 2050 and more than EUR 32.3 million in 2100. Under less severe ESL scenarios (RP below 100 years), the risk remains mostly confined to around the marina, which is located outside the defended area, producing expected damage below EUR 10 000. Under more extreme ESL scenarios, the benefits of the Parco del Mare project protecting the southern part of Rimini become more evident, avoiding about 65 % of the expected damage in the defended scenarios compared to the undefended ones. The damage avoided in the defended scenarios grows almost linearly with the increase in the baseline EAD under future projections of sea level rise: under the defended scenario, the EAD is reduced on average by 45 % in comparison with the undefended scenario (Fig. 10, left). The project produces benefits up to the scenario of RP 250 years in 2100, where a projected TWL of 3.5 m would cause the overtopping of the barrier, reducing the benefits to almost zero (Fig. 9, right).

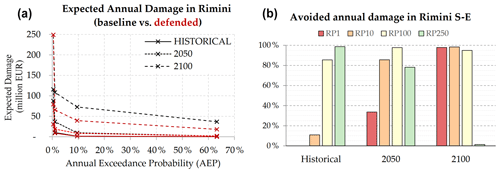
Figure 9 Rimini: expected annual damage (EAD) according to the undefended scenario up to 2100, all town considered (a); EAD reduction in the south-eastern part of the town thanks to hazard mitigation offered by the coastal barrier (b).

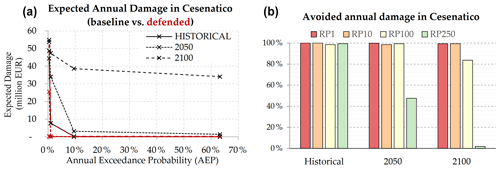
Figure 10 Cesenatico: expected annual damage (EAD) according to the undefended scenario up to 2100 (a); EAD reduction thanks to hazard mitigation offered by the coastal barrier (b).

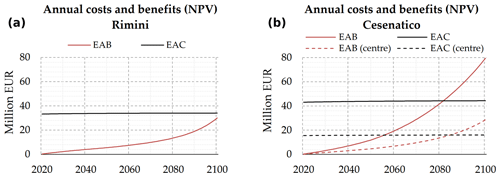
Figure 11 Cumulated flood defence costs and expected benefits at the net present value for Rimini (a) and Cesenatico (b).

In Cesenatico, the average EAD for the undefended scenario grows from around EUR 270 000 under historical conditions, to EUR 1.7 million in 2050 and almost EUR 26 million in 2100. In our simulations, the designed defence structure (a static barrier with a height of 2.8 m along 7.8 km of coast) is able to avoid most of the damage inflicted on residential buildings (Fig. 11, left). The measure becomes less efficient for the most extreme scenarios in 2050 and 2100, when the increase in TWL causes the surmounting of the barrier (Fig. 10, right). This assessment does not account for the impacts over those beach resorts and bathing facilities which are located along the barrier or between the barrier and the sea and thus are equally exposed in both the baseline and the defended scenario; they would likely represent an additional 7 %–25 % of the baseline damage.

4.3 Cost–benefit analysis

The estimates of avoided direct flood impacts are accounted for in a DRR-oriented CBA to evaluate the feasibility of mitigation measures in terms of the NPV, BCR and payback period for the two time horizons (for 2021–2050, 30 years; for 2021–2100, 80 years). The assessment does not measure the indirect benefits brought in terms of urban renovation, which are the primary focus of the Parco del Mare project, measuring, instead, only the direct benefits in terms of direct flood damage reduction. In Fig. 12, the expected annual benefit (EAB) brought by defence measures grows at a faster rate approaching 2100 in both sites because of the larger expected damage from increasing flood severity. The cost of defence implementation is repaid by avoided damage after about 40 years in Cesenatico and after 90 years in Rimini. In 2100, the BCR is 0.9 for Rimini and 1.8 for Cesenatico. These results clearly indicate an overall profitability of the defence structure implementation over the long term for Cesenatico. For the case of the municipality of Rimini, further investigation is required in order to account for the non-DRR benefits of the seafront renovation project. For instance, the potential reduction in indirect losses in terms of capital and labour productivity due to less frequent and less intense flooding events and the potential increase in tourism and well-being of citizens due to renewed urban landscape are factors that could be accounted for in a holistic CBA analysis and would likely return a shorter payback period.

In order to better understand the potential benefits of the mitigation measures over different areas of the two municipalities, we compare the results in terms of the CBR over a selection of exposed records corresponding to the towns' higher-density areas (i.e. Cesenatico historical centre, Rimini southern section). Table 2 summarizes the metrics of the assessment for different area extent selections. CBA results do not differ much when considering different extents. In Cesenatico benefits grow proportionally to costs, so the payback time does not change when considering a section of the town or the whole coastal perimeter.

5 Conclusions

In this study we addressed risk scenarios from coastal inundation over two coastal towns located along the North Adriatic coastal plain of Italy. This area is projected to become increasingly exposed to ESL events due to changes in MSL induced by SLR and local subsidence phenomena. Both locations are expected to suffer increasing economic losses from these events, unless effective coastal adaptation measures are put in place. In order to understand the upcoming impacts and the potential benefits of designed coastal projects, first we designed probabilistic ESL scenarios based on local historical observations; then, we projected these scenarios to 2050 and 2100, accounting for the combined effect of SLR and subsidence rates on the MSL. By using a high-resolution hydrodynamic model, we produced flood hazard maps associated with each ESL scenario under both the baseline scenario and the defended hypothesis. The defended scenario accounts for the effect of a coastal barrier based on the design of Parco del Mare, an urban renovation project under construction in Rimini. The same type of defence structure is envisaged along the coastal perimeter of the nearby town of Cesenatico. The hazard maps were fed to a locally calibrated damage model in order to calculate the expected annual damage for both baseline and defended scenarios.

We run a CBA comparing expected damage in terms of flood losses over residential buildings, which represent the largest share of exposed buildings' footprints (93 %). An increase in damage is expected for both urban areas from 2021 to 2100: in Cesenatico the EAD grows by a factor of 96 and in Rimini by a factor of 49. The results show that the profitability of present project investment grows over time in both locations due to the increase in expected damage triggered by intense ESL events: the EAD under the baseline hypothesis is expected to increase 3.5-fold in 2050 and up to 10-fold in 2100. The benefits brought by the coastal defence project become much larger in the second half of the century: the EAB grows 6.1-fold in Rimini and 6.5-fold in Cesenatico, from 2050 to 2100. Avoided losses are expected to match the project implementation costs after about 40 years in Cesenatico and 90 years in Rimini. Benefits are found to increase proportionally to costs; the payback period in Cesenatico is the same considering an investment in the protection of either the whole town or only part of it.

Further assessments of these renovation projects should look to measure the indirect and spillover effects on the local economy brought about by the project, possibly also accounting for the intangible benefits and scenarios of exposure change. The results are calculated in relation to emission scenario RCP4.5; compared to RCP8.5 in 2050, the difference in the SLR contribution is negligible (∼ 0.05 m), while in 2100, the difference between the two emission scenarios is larger (around 0.2 m); thus additional scenario analysis is suggested to better address risk by the end of the century. On the hazard modelling side, the particular consideration of combining wave setup and swash into a single wave contribution component can be considered theoretically questionable, as wave setup is defined as the increase in mean sea level at the shore that is caused by the loss of wave momentum in the surf zone, being often referred to as the static component of wave runup. For future works facing a similar challenge, we recommend accounting for the wave contribution to the TWL as individual dynamic (i.e. swash) and static (runup) components.

Appendix A

Here we present the equations and the graphical results of the theoretical ESL scenarios. The TWL results from the combination of storm surge, tide and wave components, each following a general functional form (i.e. harmonic component) describing the oscillation of the water level and following trigonometric functional forms for each component. The equations are given as follows.

$$\begin{array}{}\text{(A1)}& T_{\text{l}}=T_{\text{max}}\times \cos \left(\mathrm{2}\mathit{\pi }{\displaystyle \frac{\mathrm{1}}{T_{\text{p}}}}\left(t+T_{\text{d}}+T_{\text{p}}\right)\right),\end{array}$$

where T_l is the tide level in metres at any given time, T_max is the maximum tide level in metres, T_p is the tidal period in seconds, T_d is the tidal period shift in time in seconds (used to match the peaks of tides and storm surge events) and t is the time in seconds.

$$\begin{array}{}\text{(A2)}& \mathrm{\text{SS}}={\text{SS}}_{\text{max}}\times \mathrm{0.5}\times \left(\mathrm{1}+\cos \left(\mathrm{2}\mathit{\pi }{\displaystyle \frac{\mathrm{1}}{S_{\text{p}}}}\left(t+S_{\text{d}}+S_{\text{p}}\right)\right)\right),\end{array}$$

where SS is the storm surge level in metres at any given time, SS_max is the maximum storm surge level in metres, S_p is the storm surge duration in seconds, S_d is the storm surge shift in time in seconds (used to match the peaks of tides and storm surge events) and t is the time in seconds.

$$\begin{array}{}\text{(A3)}& {\displaystyle }{W}_{\text{c,int}}=\mathrm{0.5}\times \left(\mathrm{1}+\cos \left(\mathrm{2}\mathit{\pi }{\displaystyle \frac{\mathrm{1}}{S_{\text{p}}}}\left(t+S_{\text{d}}+S_{\text{p}}\right)\right)\right)\text{(A4)}& {\displaystyle }{W}_{\text{c}}=W_{\text{max}}\times \mathrm{0.5}\times \left(\mathrm{1}+\cos \left(\mathrm{2}\mathit{\pi }{\displaystyle \frac{\mathrm{1}}{W_{\text{p}}}}\left(t+{\displaystyle \frac{W_{\text{p}}}{\mathrm{4}}}\right)\right)\right)\times W_{\text{c,int}}\end{array}$$

Where W_c is the wave contribution in metres at any given time, W_max is the maximum wave setup level in metres, W_p is the wave period in seconds, W_c,int is the intensity factor (0–1) of the wave contribution event as a function of the storm surge intensity, S_p is the storm surge duration in seconds, S_d is the storm surge shift in time in seconds (used to match the peaks of tides and storm surge events), and t is the time in seconds.

We consider the wave contribution component nearshore as a function of the intensity of the storm surge level, as shown in Eqs. (A3) and (A4). As such, the action of waves is simulated as a composite function, where the maximum wave contribution level is designed to coincide in time with the maximum storm tide level and the directions of the waves are set to coincide with the direction of the storm surge event, in our case, perpendicular to the coastline. This is done first to follow the assumption of a worst-case scenario and second to incorporate the flood dynamics resulting from the momentum of waves directed inland. The composite function that combines Eqs. (A1) to (A4) and the effects of VLM and MSL (e.g. due to SLR) is shown in Eq. (A5). The results of each component in Eqs. (A1) to (A4) and for each probabilistic scenario are shown in Fig. A1.

$$\begin{array}{}\text{(A5)}& \text{TWL}=\text{MSL}+\text{VLM}+T_{\text{l}}+\text{SS}+W_{\text{s}}\end{array}$$

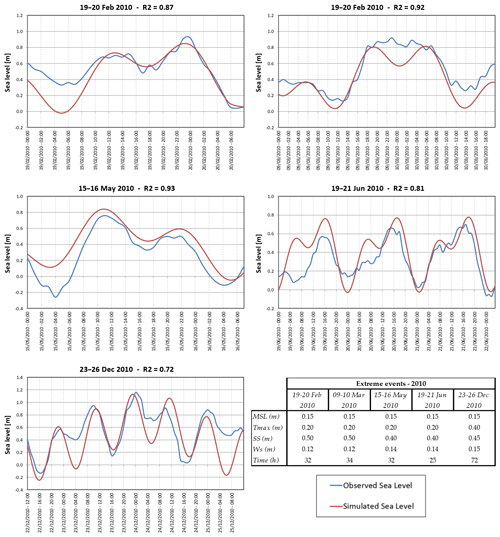
In order to verify the applicability of the aforementioned functions, we test the methods explained in this appendix for all five ESL events that were observed along the coastline of the ER region during the year 2010, as reported in Perini et al. (2011). Observed sea level data are obtained from ISPRA, for the station Ravenna – Porto Corsini (Rete Mareografica Nazionale, 2021). We evaluate the goodness of fit of the methods by means of the coefficient of determination (R²). The results of this analysis are shown in Fig. A2.

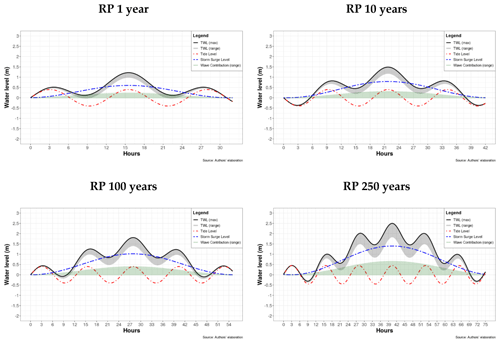
Figure A1 Dynamic boundary conditions for simulating theoretical extreme sea level events in ANUGA. The total water level is shown as the grey-shaded area, while the maximum total water level is shown by the black line at any given time. The tide (dashed red line), storm surge (dashed blue line) and wave contribution (green-shaded area) components define the total water level. Configurations are shown for the return periods of once in 1, 10, 100 and 250 years.

Figure A2 Comparison of the observed sea level (in blue) versus the simulated sea level using the harmonic components (in red).

Appendix B

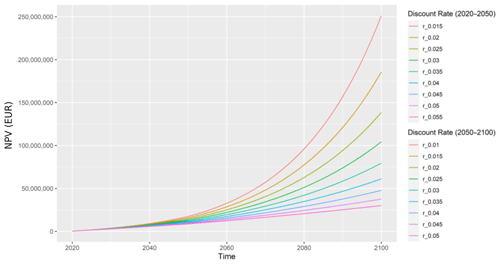
A sensitivity analysis is carried out on the discount rate. Figure B1 shows how the NPV changes with the discount rate r ranging from 1.5 % to 5.5 % (2020 to 2050) and 1 % to 5 % (2050–2100).

Figure B1 Sensitivity analysis of NPV using a variable discount rate.