the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Land subsidence due to groundwater pumping: hazard probability assessment through the combination of Bayesian model and fuzzy set theory
Huijun Li
Gaoxuan Guo
Yan Zhang
Zhenxue Dai
Xiaojuan Li
Linzhen Chang
Pietro Teatini
Land subsidence caused by groundwater overpumping threatens the sustainable development in Beijing. Hazard assessments of land subsidence can provide early warning information to improve prevention measures. However, uncertainty and fuzziness are the major issues during hazard assessments of land subsidence. We propose a method that integrates fuzzy set theory and weighted Bayesian model (FWBM) to evaluate the hazard probability of land subsidence measured by Interferometric Synthetic Aperture Radar (InSAR) technology. The model is structured as a directed acyclic graph. The hazard probability distribution of each factor triggering land subsidence is determined using Bayes' theorem. Fuzzification of the factor significance reduces the ambiguity of the relationship between the factors and subsidence. The probability of land subsidence hazard under multiple factors is then calculated with the FWBM. The subsidence time series obtained by InSAR is used to infer the updated posterior probability. The upper and middle parts of the Chaobai River alluvial fan are taken as a case-study site, which locates the first large-scale emergency groundwater resource region in the Beijing plain. The results show that rates of groundwater level decrease more than 1 m yr−1 in the confined and unconfined aquifers, with cumulative thicknesses of the compressible sediments between 160 and 170 m and Quaternary thicknesses between 400 and 500 m, yielding maximum hazard probabilities of 0.65, 0.68, 0.32, and 0.35, respectively. The overall hazard probability of land subsidence in the study area decreased from 51.3 % to 28.3 % between 2003 and 2017 due to lower rates of groundwater level decrease. This study provides useful insights for decision makers to select different approaches for land subsidence prevention.
- Article
(5152 KB) - Full-text XML
- BibTeX
- EndNote
The continuous overpumping of groundwater results in dramatic piezometric drawdown and induces regional land subsidence. Many countries such as China, Mexico, Italy, USA, Spain, and Iran (Teatini et al., 2005; Tomás et al., 2010; Galloway and Burbey, 2011; Chaussard et al., 2014; Zhu et al., 2015; Motagh et al., 2017) have reported land subsidence due to groundwater pumping. Land subsidence is a complex process influenced by the anthropogenic activities and geological environment. The anthropogenic extraction of groundwater from aquifer is the principal triggering factor because the rapid decline in the groundwater level leads to the compaction of the aquitard, and consequently the land surface subsides (Xue et al., 2005; Zhu et al., 2015; Gao et al., 2018). Although the drops of groundwater level in aquifers lead to land subsidence, this process is also controlled by the geological environment, which includes hydrologic and geomechanical conditions (Zhu et al., 2015, 2017; Gambolati and Teatini, 2015). Terzaghi's effective stress principle shows that a decrease in the pore pressure leads to an increase in the effective stress, which consequently induces land subsidence. The value of land subsidence is related to the soil mechanical properties (Bonì et al., 2020). Land subsidence threatens the environment and cause economic losses, such as municipal infrastructure damage, building fracture, and increasing flood risk (Wu et al., 2017; Peduto et al., 2017; Wang et al., 2018). Assessments of the subsidence hazard are necessary for risk prevention.
Recent studies have analyzed the hazards of land subsidence to buildings using field investigation and Interferometric Synthetic Aperture Radar (InSAR) (Julio-Miranda et al., 2012; Tomás et al., 2012; Bhattarai and Kondoh, 2017; Peduto et al., 2017). Some studies assessed the regional subsidence hazard and identified the areas with high risk using spatial modeling methods based on geographic information system (GIS; Huang et al., 2012; Bhattarai and Kondoh, 2017) and multi-objective decision-making (Jiang et al., 2012; Yang et al., 2013) or advanced methods along with fuzzy set theory (Mohebbi Tafreshi et al., 2019). The latter require expert score, which is subjective, and the produced risk level map is also qualitative. Mohebbi Tafreshi et al. (2019) adopted fuzzy functions to standardize parameters with different dimensions, which did not address the fuzziness of parameter importance. Land subsidence is a geological problem depending on various uncertain natural variables. Hazard assessments are associated with an inherent degree of uncertainty, which includes aleatoric aspects due to randomness and epistemic aspects related to insufficient information (Kiureghiana and Ditlevsen, 2009). Aleatoric uncertainty may come from the randomness of natural variables and data quality (Matthies, 2007). Epistemic uncertainty may be generated by inadequate expert knowledge, the selection of evaluation factors, and their quantitative effects on a hazard (Vilares and Kording, 2011). The methods mentioned above do not fully consider these uncertainties.
To avoid these disadvantages, some researchers have adopted more objective methods, such as evidence reasoning methods (Chen et al., 2014; Pradhan et al., 2014), physically based numerical models (Xu et al., 2015; Dai et al., 2016; Jia et al., 2018; Sundell et al., 2019), and machine learning (Park et al., 2012; Yi et al., 2017). However, numerical models require detailed geo-hydrological and geological parameters, which are generally difficult to collect (Smith and Knight, 2019). Evidence reasoning has strict combination rules and becomes exponentially intensive from the computational point of view as the number of elements increases, although it can handle both certain and uncertain information regardless of whether the information is complete or incomplete and precise or imprecise (Dai et al., 1999). Furthermore, current studies mainly focus on the identification and classification of hazard levels without any quantitative analysis of the subsidence hazard.
The main challenges in the field are to reduce the uncertainty of hazard assessments and to find an objective and effective method to assess hazard areas and risks. The mentioned uncertainty can be represented with probabilities. Bayesian models (BMs) are powerful probability approaches to deal with uncertainty (Vilares and Kording, 2011). BMs have been widely applied in disaster hazard assessments, such as flooding hazard and pipeline damage assessments (Liu et al., 2017; Zhang et al., 2016).
This paper proposes a fuzzy weighted Bayesian model (FWBM) that combines a weighted Bayesian model (WBM) and fuzzy set theory to evaluate the subsidence hazard probability and analyze the hazard probability for different rates of groundwater level change. The posterior probability is calculated using InSAR-derived land subsidence as model input to reduce the epistemic uncertainty. This new approach is applied in the Chaobai River alluvial fan in Beijing, China, where the first large-scale emergency groundwater resource region (EGRR) supplying water to Beijing is located. The hazard probability inferenced with the proposed relatively objective method can offer scientific support for the prediction of land subsidence hazard.
2.1 InSAR technology
InSAR is a microwave remote sensing technique that records the phase and amplitude of the electromagnetic waves of ground objects. The phase information is used to inversely determine the subsidence. Persistent scatterer InSAR (PS-InSAR) is the most popular method for detecting time series of land movements by calculating the differential interferometric phase on PS points with a millimetric accuracy (Sun et al., 2017). The density of PS points can reach 450 per km2 in urban areas (Ferretti et al., 2011). The differential interferometric phase Φ of each PS in the corresponding interferogram contains five components, including the deformation phase along the line of sight (LOS), the topographic phase, the phase component due to the atmospheric delay, the orbital error phase, and the phase noise (Teatini et al., 2007). The deformation phase along the LOS can be extracted by removing other phase information.
PS-InSAR processing includes four steps (Zhu et al., 2015):
-
master image selection,
-
construction of a series of interferograms,
-
PS point selection, and
-
unwrapping phase.
2.2 FWBM method
2.2.1 Basic principle of BM
BMs consider the probability distribution of random variables and can infer the posterior probability based on weakly informative prior probability to address uncertainty (Weise and Woger, 1993). A BM consists of a set of random variables with complex causalities that can be plotted using a directed acyclic graph (DAG), where random variables are represented as eigenvector nodes (Ren et al., 2009). In DAG (Fig. 1a), the hazard factors related to land subsidence are parent nodes (Yj), and the subsidence hazard is the child node (T). The arrows represent the probabilistic dependence between nodes (Korb and Nicholson, 2003).

Figure 1(a) DAG of the BM structure; (b) FWBM structure; (c) spatial features of the hazard factors (Yj, for example).
Bayes' theorem can be used to infer posterior probability distributions from weakly informative prior probability distributions through observed results (Verdin et al., 2019). The approach is formulated as follows:
where S represents the observed land subsidence; Y represents the hazard factor; P(Y|S) is the posterior probability of Y when S is observed; P(Y) is the prior probability independent of S; P(S|Y) is the likelihood function, representing the development of Y; and P(S) is the marginal probability.
For multiple factors in DAG, the jointly probability of multiple conditions can be expressed as
where Yj is the jth of the m factors that influence T.
2.2.2 FWBM construction
The conditional independence assumption must be met for BMs. This assumption generally can be strictly met in geological studies (Webb and Pazzan, 1998). WBMs use weighted assessment variables to relax the independence assumption and address the different contributions of parent nodes to child node (Webb and Pazzan, 1998). It has been widely used in hazard-related analyses (Tang et al., 2018). However, the weight of each factor, such as the piezometric decline, soil compressibility, or high static loads on the land surface, is determined by its importance to land subsidence and is usually qualitative and fuzzy (Chen et al., 2016; Li et al., 2017). The fuzziness of the factor contribution to land subsidence may cause ambiguity in weighting when their importance must be determined. These deviations can be modeled with fuzzy set theory, which expresses fuzziness through a membership function to objectively describe the relationship between land subsidence and the factors (Mentes and Helvacioglu, 2011). Therefore, the fuzzification of factor importance is applied to eliminate ambiguity.
We developed the FWBM by extending Eq. (2) with the introduction of a fuzzy-based weight. The probability of random variable T becomes
where is the fuzzy-based weight of Yj.
The structure of the FWBM is shown in Fig. 1b, which is an improvement of Fig. 1a. The eigenvector nodes are fuzzy weighted.
Referring to spatial variables, a BM is used to calculate the hazard probability of each factor through its spatial features. The spatial features of Yj are given by X, , Xj,2, …, , Xj,i, …, Xj,n}, where Xj,i is defined as the ith of the nth features of the jth factor, as shown in Fig. 1c. The value of n depends on the feature classification. Obviously, FWBM contains three parts including (i) probability of Yj, which consists of its n spatial features Xj,i; (ii) the fuzzy weight of Yj; and (iii) the probability of T.
The hazard probability of the spatial feature Xj,i at subsidence detection time k is calculated using the following equation, which is derived from Eq. (1):
where P(Xj,i, t=k) is the prior probability; P{S|Xj,i, t=k} is the conditional probability calculated with the ratio of the subsidence grid to the feature grid; and P(S) is the marginal probability, which is the sum of the probability of each Xj,i and is calculated by
2.2.3 FWBM implementation
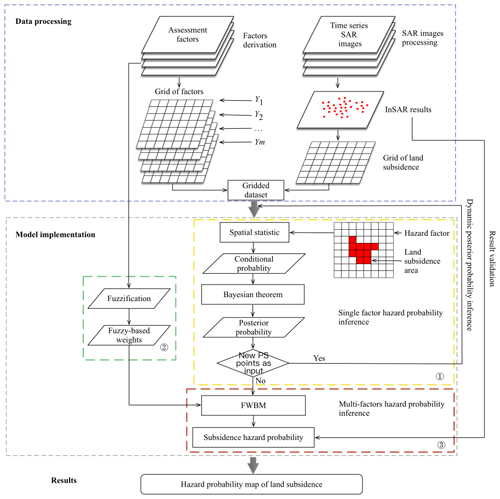
In the FWBM framework (Fig. 2), a BM is used to infer the hazard probability with the fuzzification of factor importance to reduce the ambiguity of the relationship between the hazard factors and land subsidence measured by InSAR.
The first part of the procedure consists of data (land subsidence measurements and hazard factors) gridding to obtain homogeneous datasets. The assessment hazard factors are derived first, which are parent nodes (Y1, Y2 …, Ym) in the model structure, from groundwater extraction and geological conditions. Additionally, the posterior probability in a BM can be adjusted using new observations to reduce the epistemic uncertainty (Weise and Woger, 1993). For the assessment of land subsidence hazard, InSAR is applied to obtain time series of land movements at the regional scale. A stack of SAR images is processed with PS-InSAR to obtain the time series of PS points. The PS points form a continuous input dataset to update the posterior probability of the FWBM, thus reducing the uncertainty in the assessment procedure. Simultaneously, the subsidence data are also used to validate the hazard assessment outcome. The various datasets are spatially connected using the spatial join tool in GIS for the statistical analysis of FWBM.
The second part is the model implementation. Three modules corresponding to the three variables that should be inferred in FWBM, i.e., probability of Yj and T and factor weight , are implemented.
-
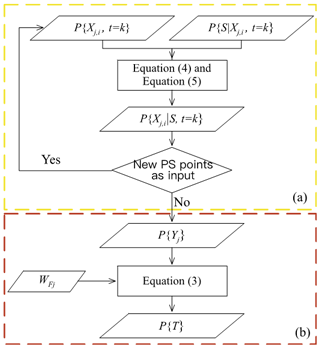
The first module infers the subsidence hazard probability of Yj, P(Yj). For a single factor, the posterior probability distribution of subsidence hazard is inferred through its spatial feature Xj,i using the Bayesian theorem. As shown in Fig. 3a, the hazard probability of Xj,i, P{Xj,i|S, t=k}, is calculated using Eqs. (4) and (5) with the calculated prior probability P(Xj,i, t=k) and conditional probability P{S|Xj,i, t=k} at subsidence detection time k. The prior probability and conditional probability are calculated through spatial statistical analysis with land subsidence records. This step is iterated when new subsidence events are observed (new PS points detected and used in input) to update the posterior probability.
-
The second module calculates the fuzzy-based weight . Fuzzification of the factor importance is processed by establishing fuzzy pairwise comparison matrices (f_PCM). According to the analytic hierarchy process (AHP) method, the pairwise comparison criteria is divided into five levels represented with odd numbers from 1–9 (Saaty, 1980). The five levels are regarded as fuzzy numbers, and the medium level is considered to be equally important. The value of each level is expressed as a triangular fuzzy number which is commonly used to express fuzziness (Mentes and Helvacioglu, 2011). Based on the constructed f_PCM, is calculated by the fuzzy extended AHP method (Van Laarhoven and Pedrycs, 1983).
-
The third module infers the probability of T, P(T). The hazard probability influenced by multiple factors is derived using the FWBM. As shown in Fig. 3b, with the probability density P(Yj) and factor weights, the gridded hazard probability of land subsidence P(T) is implemented using Eq. (3). The hazard probability map is reclassified using the natural breaks (Jenks) classification method, which is widely used in risk evaluation (Suh et al., 2016; Liu et al., 2017), and compared with the InSAR measurements to validate the assessed results.
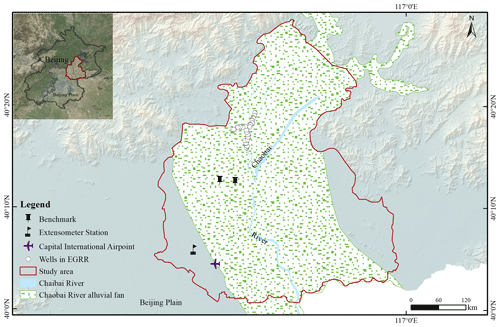
3.1 Description of the study area
The study area belongs to the upper-middle part of the Chaobai River alluvial fan in the northern Beijing plain and covers approximately 1350 km2 (Fig. 4). The Huairou EGRR is located in this area and designed to ensure the urban water supply in continuous dry or emergency conditions. Long-term groundwater overpumping has caused rapid decreases in the groundwater level, with a maximum value of approximately 40 m after the EGRR operation in 2003 (Zhu et al., 2015, 2016). This significant piezometric drop resulted in regional land subsidence. To relieve the situation, the South-to-North Water Transfer Project central route (SNWP-CR) was implemented at the end of 2014.
3.2 Datasets and processing
In this study, four hazard factors are considered: the rates of groundwater level change in confined (Y1 with the feature expressed as X1,i, i=1 … 4) and unconfined (Y2 with the feature expressed as X2,i, i=1 … 4) aquifers, which reflect the hydrologic conditions; the cumulative thicknesses of the compressible sediments (Y3 with the feature expressed as X3,i, i=1 … 17); and the thickness of the Quaternary unit (Y4 with the feature expressed as X4,i, i=1 … 14), which represent the geological setting.
The contour lines of compressible soil and Quaternary unit thickness were collected. The change in groundwater levels varied from −4 to 6 m between 2015 and 2017. The annual rates of groundwater level change were classified into four classes. The four factors are shown in Fig. 5.
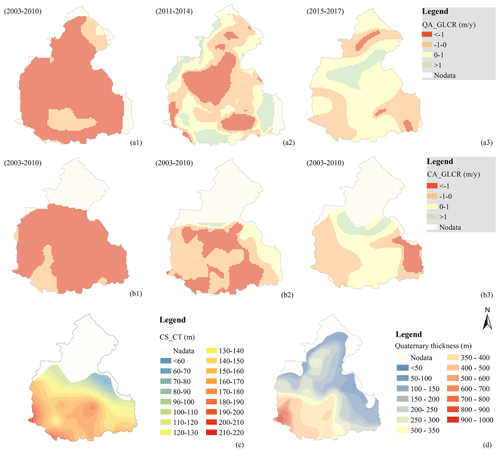
Figure 5Assessment factors: (a1–a3) annual rate of groundwater level change in the unconfined aquifer (QA_GLCR) over the three periods 2003–2010, 2011–2014, and 2015–2017, respectively. Negative values mean lowering; (b1–b3) annual rate of groundwater level change in the confined aquifer system (CA_GLCR) over the three periods 2003–2010, 2011–2014, and 2015–2017, respectively. Negative values mean lowering; (c) cumulative thickness of compressible sediments (CS_CT); (d) Quaternary thickness.
The distribution of the factors related to groundwater level change is split into three periods:
-
from January 2003 to December 2010, a period of massive groundwater exploitation after the EGRR establishment;
-
from January 2011 to December 2014, when the decline rate of the groundwater level slowed due to the long-term loss of groundwater which reduces the capacity of water supply and increased rainfall (Zhang et al., 2015); and
-
from January 2015 to December 2017, when the SNWP-CR operation partially relieved the groundwater exploitation.
A total of 125 SAR images were collected, including 37 ASAR images from June 2003 to January 2010, 38 RADARSAT-2 images from November 2010 to November 2014, and 50 Sentinel-1 images from December 2014 to December 2017. The subsidence results were validated and calibrated with an extensometer station and benchmark data (the location is shown in Fig. 4). The difference between the PS-InSAR solution and land-based land subsidence measurements amounted to ±7 mm (Zhu et al., 2015, 2020a). Note that the subsidence rate obtained by PS-InSAR is characterized by an uncertainty of 1–3 mm yr−1, depending on the number and quality of the processed images (Teatini et al., 2012). The PS points with a subsidence rate above 10 mm yr−1 were regarded as subsidence points.
All factors and subsidence datasets were gridded into 5664 cells, with a cell size of 500 m × 500 m. The outcomes on grid sizes of 200, 500, and 1000 m were initially compared. The results for the 200 and 500 m grid size were similar, with smoother edges but a higher computational cost for the former. The results obtained on the 1000 m grid size displayed too low a resolution. Each grid ID contains five features including four assessment factors and land subsidence.
3.3 Model implementation
3.3.1 Weight computation
The fuzzification of factor importance is expressed as a triangular fuzzy number considering the ambiguity between factors and subsidence. To compare the model performance when ambiguity was eliminated, we implemented the WBM with the non-fuzzy-based weight (Wj) calculated by the AHP method. The result of WBM was also reclassified and subtracted from FWBM to compare the levels of change when considering or not considering the ambiguity.
3.3.2 Probability of Yj inference
The hazard probability of feature Xj,i, P{Xj,i|S, t=k}, was calculated first. For example, X3,12 is the twelfth feature of the compressible soil thickness (Y3), indicating that the thickness ranges between 160 and 170 m. The prior probability P(X3,12) was calculated based on the feature grid number ratio between the number of grid cell with that feature and the total number of grid cells covering the study area. The conditional probability P{S|X3,12, from 2003 to 2010}, i.e., the percentage of grid cells for which land subsidence occurred in feature X3,12 from 2003 to 2010, was used as input for the FWBM. P{S} was the sum of P{S|X3,12, from 2003 to 2010} calculated based on Eq. (5). The posterior hazard probability P{X3,12|S, from 2003 to 2010} was calculated using Eq. (4).
The same procedure was applied to land subsidence data from 2011 to 2014 and from 2015 to 2017, and the posterior hazard probability at a previous time interval was set as the prior probability at the current one.
3.3.3 Probability of T inference
With the probability of the single factor and factor weights, the hazard probability of T, P(T), was then calculated. Since only a phreatic aquifer exists in the northern part of the study area and land subsidence was relatively low, the hazard probability in this portion of the study area was set to 0.01.
4.1 Validation of the results
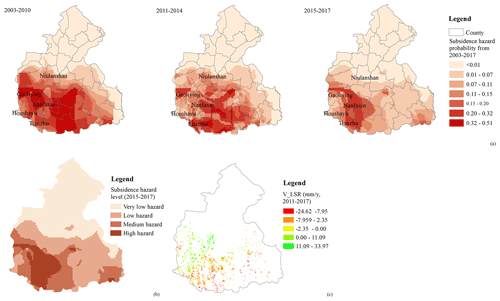
The proposed FWBM was applied to assess the subsidence hazard probability in the upper and middle part of the Chaobai River alluvial fans from 2003 to 2017. The hazard assessment distribution was reclassified into seven grades (Fig. 6a). A hazard probability less than 0.07 indicates a low-hazard area, and a hazard probability greater than 0.15 indicates a high-hazard area (Fig. 6b).
The changes in the land subsidence rate (Sr) detected by InSAR (Fig. 6c) between 2010–2014 and 2015–2017 were used to validate the assessment results. A positive value means the subsidence rate decreased (SrD) and a negative value means the subsidence rate increased (SrI). The total match ratio is 85 % (Table 2). Notably, Table 1 showed that some points with SrD are located in the high-hazard area. In fact, there are portions of the study plain where, because the piezometric level did not recover significantly, land subsidence rates remained larger than 50 mm yr−1 in 2017 (Zhu et al. 2020a, b) although smaller than the values observed in previous years.
Table 1Comparison of the match ratio (calculated by the ratio between the sum of the amount of SrI in the high-hazard area and SrD in the low-hazard area, and the total number of SrI and SrD) obtained with FWBM and WBM.
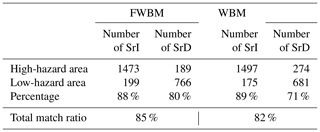
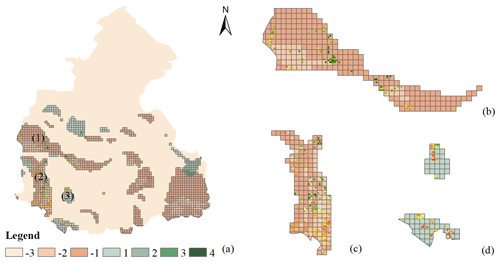
Figure 7(a) Variation of the subsidence hazard level between FWBM and WBM. Negative and positive values mean that WBM has a higher or a smaller hazard level than FWBM, respectively. An amplification of areas (1)–(3) highlighted in panel (a) is provided in panels (b)–(d), respectively. The colored dots represent the change in the land subsidence rate between 2010–2014 and 2015–2017 (the same as in Fig. 6c), with the green dots representing a lower hazard probability and the red dots a higher hazard probability.
4.2 Effect of fuzziness on model results
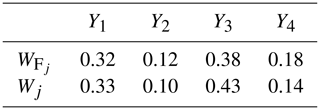
The FWBM results were compared with the results from a WBM that ignored the ambiguity in the hazard assessment framework. The fuzzy-based weights () and non-fuzzy-based weights (Wj) of the four considered factors are shown in Table 2. We found that the stronger the semantic fuzziness of the factor importance is, the greater the uncertainty of factor weights is, which may make the greater difference in hazard probability results.
The WBM results were also divided into seven levels. The degree of difference between WBM and FWBM outcomes is shown in Fig. 7a. Negative and positive values mean that WBM provides a higher or a lower hazard level than FWBM, respectively. In terms of the subsidence rate change (Fig. 6c), the WBM overestimates the subsidence hazard level for area 1 (Fig. 7b) and partially the level for area 2 (Fig. 7c), where the subsidence rate decreased in recent years. In addition, the WBM underestimates the hazard level for area 3 (Fig. 7d), where the subsidence rate increased. The FWBM performs better in regions with SrD and is characterized by a higher total match ratio than the WBM, as shown in Table 1.
4.3 Effect of assessment factors on hazard probability
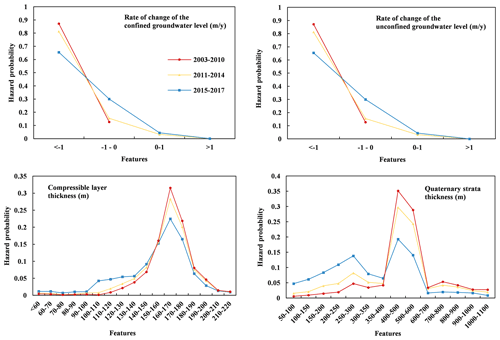
The hazard probability of factors addressed in the analysis is shown in Fig. 8. Using the period from 2015 to 2017 as an example, a rate reduction of the groundwater level in the confined aquifer greater than 1 m yr−1 has a maximum hazard probability of 0.65. The situation is the same for the groundwater change in the unconfined aquifer, with a 0.68 maximum hazard probability when the rate reduction exceeds 1 m yr−1. The results show that the higher the reduction rate of the groundwater levels is, the higher the hazard probability is, which is consistent with the general understanding and with the outcome of previous studies revealing that the rapid groundwater level decline leads to the subsidence of the land surface (Tomás et al., 2010; Galloway and Burbey, 2011; Zhu et al., 2015). Cumulative thicknesses of the compressible sediments between 160 and 170 m yield a maximum hazard probability of 0.32, and the Quaternary thickness between 400 and 500 m yields a maximum hazard probability of 0.35. This is also consistent with previous studies showing that land subsidence mainly occurred in the area where the cumulative thicknesses of the compressible sediments exceed 100 m (Lei et al., 2016). Note that an aquifer system with thick compressible sediments is more susceptible to causing large land subsidence, but this takes place only if a certain drawdown of the piezometric head, which is the triggering factor, occurs in that portion of the subsurface (Zhu et al., 2015). This can explain why the hazard probability decreases for the largest values of the compressible sediments and the Quaternary unit.
4.4 Temporal change in the subsidence hazard
Because land subsidence is negligible in the northern part of the study area (Zhu et al., 2015), the temporal change in the hazard probability of land subsidence is investigated only in the southern region, where the confined aquifer system is located.
As shown in Fig. 6a, the subsidence hazard probability in Niulanshan decreased from 2003 to 2017. Conversely, the southwestern portion of the study area, especially in Tianzhu and Nanfaxin where the groundwater level decrease exceeded 1 m yr−1 and the thickness of the cumulative compressible sediments exceeded 150 m, always maintains a high hazard probability.
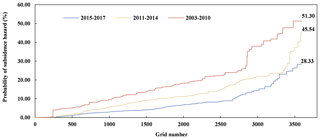
Figure 9 shows that the value of the subsidence hazard probability is between 0.01 % and 51.30 % from 2003 to 2010, between 0.01 % and 45.54 % from 2011 to 2014, and between 0.01 % and 28.33 % from 2015 to 2017.
Overall, the subsidence hazard decreased. This can be credited to the significant exploitation of groundwater resources and the following utilization policies. From 2003 to 2010, the operation of the EGRR led to a rapid drawdown of the groundwater levels. Between 2015 and 2017, the operation of the SNWP-CR conveyed a large amount of water to Beijing, reducing the pressure on the aquifer system and, consequently, slowing the rate of change in the groundwater level (Zhu et al., 2020b). Similarly, the California State Water Project, which is also a large water-transfer system, has been fundamental to controlling land subsidence in the Central Valley, California (Sneed et al., 2018).
4.5 Spatial distribution of subsidence hazard
Four subsidence hazard levels are classified from the probability map (Fig. 6b), consistent with previous studies (Yang et al., 2013; Zhu et al., 2015). The high hazard covers 10.7 % of the total area, and the medium hazard accounts for 17.5 % of the total area. The low and very low hazards represent 29.7 % and 42.1 % of the total area, respectively. As the thickness of the compressible sediments increases from north to south, the subsidence hazard probability increases accordingly. Tianzhu, Nanfaxin, Gaoliying, and Houshayu in the southwestern region experience medium–high hazards because the compressible strata in these areas are thick and the groundwater level dropped significantly. The InSAR results also revealed that the maximum subsidence rate in these regions increased to 84.9 mm yr−1 over the period from 2015 to 2017. Overall, the area of high subsidence hazard decreases versus time due to the reduction in the rate of groundwater level change.
Considering the ambiguity of the importance of various factors controlling land subsidence due to groundwater pumping and the uncertainty in the assessment process, a FWBM model was developed to assess the probability of land subsidence hazard at a regional scale. FWBM is based on a combination of BM and fuzzy set theory. The InSAR method was used to obtain land subsidence time series to adjust the posterior probability of the FWBM, thus reducing the model uncertainty.
The implementation of the FWBM in the Beijing area demonstrated the potentiality of this modeling approach and showed that it is superior when the ambiguity of the relationship between the factors and land subsidence is considered. The study is a first analysis of the hazard probability of land subsidence and the related hazard factors. From the case study, we found that subsidence probability decreased over time due to a change in water utilization, such as the operation of the SNWP-CR. A rate of groundwater level decline greater than 1 m yr−1 in the unconfined and confined aquifers yields the maximum hazard probabilities equal to 0.68 and 0.65, respectively. A compressible sediment thickness between 160 and 170 m yields a maximum hazard probability of 0.32. A Quaternary strata thickness between 400 and 500 m yields a maximum hazard probability of 0.35. The overall subsidence hazard probability in the study area decreased from 51.3 % to 28.3 % between 2003 and 2017 due to the decrease in the rate of groundwater level reduction.
The results of this study suggest that the proposed subsidence hazard assessment method significantly represents the uncertainty and ambiguity compared to traditional qualitative methods (Huang et al., 2012; Park et al., 2012; Yang et al., 2013; Chen et al., 2014; Tafreshi et al., 2019; Sundell et al., 2019). The hazard probability map of different time periods with different groundwater level conditions can offer scientific support for land subsidence prediction and help stakeholders and decision makers to develop more reliable water utilization strategies accounting for land subsidence hazard.
Improvements to the proposed methodology will be investigated in the future. The prior probability in this model is determined by the factor grid number ratio, which may have deviations. This ratio can be further improved by expert knowledge. Additionally, the impact of the selected assessment factors on the results will be investigated. Moreover, the cumulative land subsidence and not only the subsidence rate will be considered to assess the subsidence hazard with a more comprehensive perspective.
The calculations involved in this study are done using ArcGIS software.
The data used in this study are available from the corresponding author on reasonable request.
HL completed the experiment and paper, LZ and ZD provided rigorous guidance on the thesis and revised the manuscript, GG provided part of data and discussed the contents, YZ and LC revised the manuscript, and XL and PT provided guidance on the research conclusions and revised the manuscript.
The authors declare that they have no conflict of interest.
The authors are thankful to Tingbao Xu at the Australian National University and Yun Chen at CSIRO for their valuable comments and suggestions.
This research has been supported by the National Natural Science Foundation of China (grant nos. 41130744 and 41201420), the Natural Science Foundation of Beijing Municipality (grant no. 8202008), and the Capacity Building for Sci-Tech Innovation-Fundamental Scientific Research Funds (grant no. 025195305000/191).
This paper was edited by Olga Petrucci and reviewed by two anonymous referees.
Bhattarai, R. and Kondoh, A.: Risk Assessment of Land Subsidence in Kathmandu Valley, Nepal, Using Remote Sensing and GIS, Adv. Remote Sens., 6, 132–146, 2017.
Bonì, R., Meisina, C., Teatini, P., Zucca, F., Zoccarato, C., Franceschini, A., Ezquerro, P., Bejar, M., Fernandez-Merofo, J. A., Guardiola-Albert, C., Pastor Navarro, J., Tomás, R., and Herrera, G.: 3D groundwater flow and deformation modelling of Madrid aquifer, J. Hydrol., 585, 124773, https://doi.org/10.1016/j.jhydrol.2020.124773, 2020.
Chaussard, E., Wdowinski, S., Cabral-Cano, E., and Amelung, F.: Land subsidence in central Mexico detected by ALOS InSAR time-series, Remote Sens. Environ., 140, 94–106, 2014.
Chen, M., Tomás, R., Li, Z. H., Motagh, M., Li, T., Hu, L., Gong, H., Li, X., Yu, J., and Gong, X.: Imaging land subsidence induced by groundwater extraction in Beijing (China) using satellite radar interferometry, Remote Sens., 8, 468–489, 2016.
Chen, Y., Shu, L. C., and Burbey, T.: An Integrated Risk Assessment Model of Township-Scaled Land Subsidence Based on an Evidential Reasoning Algorithm and Fuzzy Set Theory, Risk Anal., 34, 656–669, 2014.
Dai, G., Pan, Q., Zhang, S., and Zhang, H.: The developments and problems in evidence reasoning, Contr. Theor. Appl., 16, 465–469, 1999.
Dai, Z., Viswanathan, H., Middleton, R., Middleton, R., Pan, F., Ampomah, W., Yang, C., Jia, W., Xiao, T., Lee, S. Y., Mcpherson, B., Balch, R., Grigg, R., and White, M.: CO2 Accounting and Risk Analysis for CO2 Sequestration at Enhanced Oil Recovery Sites, Environ. Sci. Technol., 50, 7546–7554, 2016.
Ferretti, A., Fumagalli, A., Novali, F., Prati, C., Rocca, F., and Rucci, A.: A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR, IEEE T. Geosci. Remote, 49, 3460–3470, 2011.
Galloway, D. L. and Burbey, T. J.: Review: Regional land subsidence accompanying groundwater extraction, Hydrogeol. J., 19, 1459–1486, 2011.
Gambolati, G. and Teatini, P.: Geomechanics of subsurface water withdrawal and injection, Water Resour. Res., 51, 3922–3955, 2015.
Gao, M. L., Gong, H. L., Chen, B. B., Li, X., Zhou, C., Shi, M., Si, Y., Chen, Z., and Duan, G.: Regional Land Subsidence Analysis in Eastern Beijing Plain by InSAR Time Series and Wavelet Transforms, Remote Sens., 10, 365–382, 2018.
Huang, B., Shu, L., and Yang, Y. S.: Groundwater overexploitation causing land subsidence: hazard risk assessment using field observation and spatial modelling, Water Resour. Manage., 26, 4225–4239, 2012.
Jia, W., McPherson, B., Pan, F., Dai, Z., and Xiao, T.: Uncertainty quantification of CO2 storage using Bayesian model averaging and polynomial chaos expansion, Int. J. Greenhouse Gas Contr., 71, 104–115, 2018.
Jiang, Y., Jia, S. M., and Wang, H. G.: Risk assessment and management of land subsidence in Beijing Plain, Chin. J. Geol. Hazard Contr., 23, 55–60, 2012.
Julio-Miranda, P., Ortíz-Rodríguez, A. J., Palacio-Aponte, A. G., López-Doncel, R., and Barboza-Gudiño, R.: Damage assessment associated with land subsidence in the San Luis Potosi-Soledad de Graciano Sanchez metropolitan area, Mexico, elements for risk management, Nat. Hazards, 64, 751–765, 2012.
Kiureghiana, A. D. and Ditlevsen, O.: Aleatory or epistemic? Does it matter?, Struct. Safe., 31, 105–112, 2009.
Korb, K. B. and Nicholson, A. E.: Bayesian Artificial Intelligence, CRC Press, Florida, 2003.
Lei, K. C., Luo, Y., Chen, B. B., and Guo, G. X., Zhou, Y.: Distribution characteristics and influence factors of land subsidence in Beijing area, Geol. China, 43, 2216–2225, 2016.
Li, Y. Y., Gong, H. L., Zhu, L., Li, X., Wang, R., and Guo, G.: Characterizing land displacement in complex hydrogeological and geological settings: a case study in the Beijing Plain, China, Nat. Hazards, 87, 323–343, 2017.
Liu, R., Chen, Y., Wu, J., Gao, L., Barrett, D., Xu, T., Li, X., Li, L., Huang, C., and Yu, J.: Integrating Entropy-Based Naïve Bayes and GIS for Spatial Evaluation of Flood Hazard, Risk Anal., 37, 756–773, 2017.
Matthies, H. G.: Quantifying uncertainty: modern computational representation of probability and applications, Extreme Man-Made and Natural Hazards in Dynamics of Structures, in: NATO Security through Science Series, Springer, Dordrecht, 105–135, 2007.
Mentes, A. and Helvacioglu, I. H.: An application of fuzzy fault tree analysis for spread mooring systems, Ocean Eng., 38, 285–294, 2011.
Mohebbi Tafreshi, G., Nakhaei, M., and Lak, R.: Land subsidence risk assessment using GIS fuzzy logic spatial modeling in Varamin aquifer, Iran, Geo J., 38, https://doi.org/10.1007/s10708-019-10129-8, 2019.
Motagh, M., Shamshiri, R., and Haghighi, M. H.: Quantifying groundwater exploitation induced subsidence in the Rafsanjan plain, southeastern Iran, using InSAR time-series and in situ measurements, Eng. Geol., 218, 134–151, 2017.
Park, I., Choi, J., Lee, M. J., and Lee, S.: Application of an adaptive neuro-fuzzy inference system to ground subsidence hazard mapping, Comput. Geosci., 48, 228–238, 2012.
Peduto, D., Nicodemo, G., Maccabiani, J., and Ferlisi, S.: Multi-scale analysis of settlement-induced building damage using damage surveys and DInSAR data: A case study in The Netherlands, Eng. Geol., 218, 117–133, 2017.
Pradhan, B., Abokharima, M. H., Jebur, M. N., and Tehrany, M. S.: Land subsidence susceptibility mapping at Kinta Valley (Malaysia) using the evidential belief function model in GIS, Nat. Hazards, 73, 1019–1042, 2014.
Ren, J., Jenkinson, I., Wang, J., Xu, D. L., and Yang, J. B.: An offshore risk analysis method using fuzzy Bayesian network, J. Offshore Mech. Arct. Eng., 131, 1–12, 2009.
Saaty, T. L.: The Analytic Hierarchy Process, McGraw-Hill Press, New York, 1980.
Smith, R. and Knight, R.: Modeling Land Subsidence Using InSAR and Airborne Electromagnetic Data, Water Resour. Res., 55, 2801–2819, 2019.
Sneed, M., Brandt, J., and Solt, M.: Land subsidence along the California aqueduct inWest-Central San Joaquin Valley, California, 2003–10, in: US Geological Survey Scientific Investigations Report 2018-5144, US Geological Survey, Reston, VA, https://doi.org/10.3133/sir20185144, 2018.
Suh, J., Choi, Y., and Park, H. D.: GIS-based evaluation of mining-induced subsidence susceptibility considering 3D multiple mine drifts and estimated mined panels, Environ. Earth Sci., 75, 1–19, 2016.
Sun, H., Zhang, Q., Zhao, C., Yang, C., Sun, Q., and Chen, W.: Monitoring land subsidence in the southern part of the lower Liaohe plain, China with a multi-track PS-InSAR technique, Remote Sens. Environ., 188, 73–84, 2017.
Sundell, J., Haaf, E., Tornborg, J., and Rosén, L.: Comprehensive risk assessment of groundwater drawdown induced subsidence, Stoch. Environ. Res. Risk A., 1, 427–449, 2019.
Tang, X., Shu, Y., Lian, Y., Zhao, Y., and Fu, Y.: A spatial assessment of urban waterlogging risk based on a Weighted Naive Bayes classifier, Sci. Total Environ., 630, 264–274, 2018.
Teatini, P., Ferronato, M., Gambolati, G., Bertoni, W., and Gonella, M.: A century of land subsidence in Ravenna, Italy, Environ. Geol., 47, 831–846, https://doi.org/10.1007/s00254-004-1215-9, 2005.
Teatini, P., Tosi, L., Strozzi, T., Carbognin, L., Cecconi, G., Rosselli, R., and Libardo, S.: Resolving land subsidence within the Venice Lagoon by persistent scatterer SAR interferometry, Phys. Chem. Earth., 40–41, 72–79, 2012.
Teatini, P., Strozzi, T., Tosi, L., Wegmüller, U., Werner, C., and Carbognin, L.: Assessing short and long-time displacements in the Venice coastland by synthetic aperture radar interferometric point target analysis, J. Geophys. Res., 112, F01012, https://doi.org/10.1029/2006JF000656, 2007.
Tomás, R., Herrera, G., Lopez-Sanchez, J. M., Vicente, F., Cuenca, A., and Mallorquí, J. J.: Study of the land subsidence in Orihuela City (SE Spain) using PSI data: Distribution, evolution and correlation with conditioning and triggering factors, Eng. Geol., 115, 105–121, 2010.
Tomás, R., García-Barba, J., Cano, M., Sanabria, M. P., Ivorra, S., Duro, J., and Herrera, G.: Subsidence damage assessment of a gothic church using Differential Interferometry and field data, Struct. Health Monit., 11, 751–762, 2012.
Van Laarhoven, P. J. M. and Pedrycs, W.: A fuzzy extension of Saaty's priority theory, Fuzzy Set. Syst., 11, 229–241, https://doi.org/10.1016/S0165-0114(83)80082-7, 1983.
Verdin, A., Rajagopalan, B., Kleiber, W., Podesta, G. P., and Bert, F.: BayGEN: A Bayesian Space-Time Stochastic Weather Generator, Water Resour. Res., 55, 2900–2915, 2019.
Vilares, I. and Kording, K.: Bayesian models: the structure of the world, uncertainty, behavior, and the brain, Ann. NY. Acad. Sci., 1224, 22–39, 2011.
Wang, J., Yi, S., Li, M., Wang, L., and Song, C.: Effects of sea level rise, land subsidence, bathymetric change and typhoon tracks on storm flooding in the coastal areas of Shanghai, Sci. Total Environ., 621, 228–234, 2018.
Webb, G. I. and Pazzan, J.: Adjusted probability Naive Bayesian induction, in: Proceedings of the 11th Australian Joint Conference on Artificial Intelligence, Springer Verlag, Berlin, 285–295, 1998.
Weise, K. and Woger, W.: A Bayesian theory of measurement uncertainty, Meas. Sci. Technol., 4, 1–11, 1993.
Wu, H. N., Shen, S. L., and Yang, J.: Identification of Tunnel Settlement Caused by Land Subsidence in Soft Deposit of Shanghai, J. Perform. Construct. Facil., 31, 04017092, https://doi.org/10.1061/(ASCE)CF.1943-5509.0001082, 2017.
Xu, Y. S., Yuan, Y., Shen, S. L., Yin, Z. Y., Wu, H. N., and Ma, L.: Investigation into subsidence hazards due to groundwater pumping from Aquifer II in Changzhou, China, Nat. Hazards, 78, 281–296, 2015.
Xue, Y. Q., Zhang, Y., Ye, S. J., Wu, J. C., and Li, Q. F.: Land subsidence in China, Environ. Geol., 48, 713–720, 2005.
Yang, Y., Zhang, F. D., Liu, L. C., Dou, Y. B., and Jia, S. M.: Susceptibility zoning and control measures on land subsidence caused by groundwater exploitation, Geol. China, 40, 653–658, 2013.
Yi, Y., Liu, H., Zhang, Y., Liu, X., and Qi, J.: Analysis of urban ground subsidence hazard induced by building load combined with weights of evidence model and deep learning, J. Catastrophol., 32, 50–59, 2017.
Zhang, J. H., Fan, J. D., and Li, S. J.: Research on the Groundwater Resources Conservation of Huairou Emergency Water Source after the South-to-north Water Transfer into Beijing, Urban Geol., 10, 17–20, 2015.
Zhang, L., Wu, X., Qin, Y., Skibniewski, M. J., and Liu, W.: Towards a Fuzzy Bayesian Network Based Approach for Safety Risk Analysis of Tunnel-Induced Pipeline Damage, Risk Anal., 36, 278–301, 2016.
Zhu, L., Gong, H. L., Li, X. J., Wang, R., Chen, B., Dai, Z., and Teatini, P.: Land subsidence due to groundwater withdrawal in the northern Beijing plain, China, Eng. Geol., 193, 243–255, 2015.
Zhu, L., Dai, Z. X., Gong, H., Gable, C., and Teatini, P.: Statistic inversion of multi-zone transition probability models for aquifer characterization in alluvial fans, Stoch. Environ. Res. Risk A., 30, 1005–1016, 2016.
Zhu, L., Gong, H., Dai, Z., Guo, G., and Teatini, P.: Modeling 3-D permeability distribution in alluvial fans using facies architecture and geophysical acquisitions, Hydrol. Earth Syst. Sci., 21, 721–733, https://doi.org/10.5194/hess-21-721-2017, 2017.
Zhu, L., Franceschini, A., Gong, H. L., Ferronato, M., Dai, Z., Ke, Y., Pan, Y., Li, X., Wang, R., and Teatini, P.: 3D facies and geomechanical modelling of land subsidence in the Chaobai plain, Beijing, Water Resour. Res., 54, e2019WR027026, https://doi.org/10.1029/2019WR027026, 2020a.
Zhu, L., Gong, H. L., Chen, Y., Wang, S., Ke, Y., Guo, G., Li, X., Chen, B., Wang, H., and Teatini, P.: Effects of Water Diversion Project on groundwater system and land subsidence in Beijing, China, Eng. Geol., 276, 105763, https://doi.org/10.1016/j.enggeo.2020.105763, 2020b.