The prediction of floods in Venice: methods, models and uncertainty (review article)

This paper reviews the state of the art in storm surge forecasting and its particular application in the northern Adriatic Sea. The city of Venice already depends on operational storm surge forecasting systems to warn the population and economy of imminent flood threats, as well as help to protect the extensive cultural heritage. This will be more important in the future, with the new mobile barriers called MOSE (MOdulo Sperimentale Elettromeccanico, Experimental Electromechanical Module) that will be completed by 2021. The barriers will depend on accurate storm surge forecasting to control their operation. In this paper, the physics behind the flooding of Venice is discussed, and the state of the art of storm surge forecasting in Europe is reviewed. The challenges for the surge forecasting systems are analyzed, especially in view of uncertainty. This includes consideration of selected historic extreme events that were particularly difficult to forecast. Four potential improvements are identified: (1) improve meteorological forecasts, (2) develop ensemble forecasting, (3) assimilation of water level measurements and (4) develop a multimodel approach.

1 Introduction

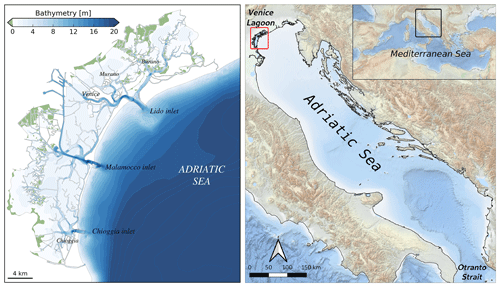
The city of Venice is situated inside the Venice Lagoon, which is connected to the Adriatic Sea by three inlets (Fig. 1). Due to its low elevation with respect to mean sea level, for centuries the city was subject to occasional floods due to storm surge events, called Acqua alta. During the last century the frequency of flooding has steadily increased (Ferla et al., 2007; Lionello et al., 2021a) due to local land subsidence and relative sea level rise driven mainly by climate change (Carbognin et al., 2004; Zanchettin et al., 2021).

Figure 1 Setting of the Venice Lagoon and the Adriatic Sea.

The last 3 years have seen some of the most devastating high water events that Venice has ever experienced. In October 2018 a storm produced a sea level 156 cm over datum (see Fig. 2 for a reference of the local datum and the flooding levels of Venice). In November and December 2019, a series of storms created five high tides with water levels exceeding 140 cm. These events are called exceptional because only 25 such events have been observed in the last 150 years. They flood nearly 60 % of the pedestrian walkways in the city and cover S. Mark's square with 60 cm of water. One of these high tides was the second highest water level ever measured in Venice at 189 cm which was only exceeded by the terrible flood in 1966 at 194 cm (Cavaleri et al., 2020).

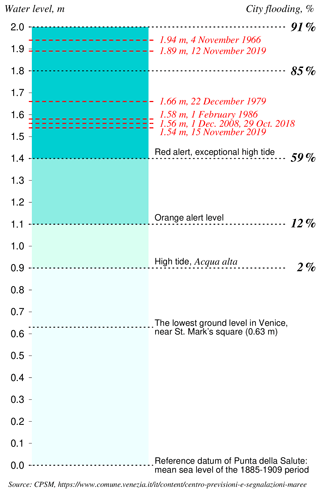
Figure 2 The local datum of Venice, the height of the lowest pavement level, the flooding percentages, definition of various alert levels and the height of important historic floods. Please note that the mean sea level of the last 10 years is approx. 32 cm above datum. Therefore, at spring tide the water level reaches values of over 80 cm without any meteorological contribution.

These flooding events pose a threat not only to the artistic, cultural and environmental heritage but also to the economic assets. To be able to face these events and to manage their occurrence, there have been investments in the safeguarding of Venice through the planning and building of flood barriers, many other structural measures, and forecasting operational systems, measurement networks and extreme event research activities (Barbano et al., 2012; Demarte et al., 2007).

Venice is tackling the problem of high water flooding by building mobile barriers (called MOSE, MOdulo Sperimentale Elettromeccanico, Experimental Electromechanical Module) at each inlet of the lagoon. These gates sit on the seabed, and compressed air is introduced into them to empty them of water, and they rise up until they emerge above the water to stop the tide from entering the lagoon. Construction has been underway since 2004 and has been criticized by many due to the elevated costs and the long timescale of construction. However, it is the only intervention that will be able to effectively defend Venice from flooding due to storm surges in the near and medium future (Consorzio Venezia Nuova, 1997). MOSE is presently being commissioned and is expected to be fully operational by the end of 2021.

The operation of the MOSE uses a complex protocol including water level measurements and atmospheric and oceanographic forecasting. In particular, the decision to close the MOSE will depend on the water level forecast. Once a decision to close the MOSE has been taken, the exact time of closure will be decided based on water level measurements inside the lagoon (Consorzio Venezia Nuova, 2005). Hence, water level forecasting is one of the fundamental aspects of the closing procedure of the mobile gates. Improving the reliability of these forecasts will contribute to avoid missing or false closures due to predictions that are too low or too high. This will save money as missing closures could result in flooding and damage to the city of Venice (shops, low lying apartments), while false closures will unnecessarily delay ship passage for its industrial and touristic ports (Vergano et al., 2010). Moreover, the forecast is essential to warn the population of imminent danger to life and goods and to prepare boat travel and walkways for pedestrians inside the city.

From a historical perspective, the need to alert the population, protect commercial activities and organize transport and pedestrian mobility during floods of the Venice city center was motivated by the development of surge prediction tools. Early studies were published in the 1970s in the wake of the initiatives motivated by the response to the dramatic flood in November 1966 (Finizio et al., 1972; Robinson et al., 1973; Tomasin, 1973; Tomasin and Frassetto, 1979). Development resumed in the 1990s, partially in association with the perspective of developing a system with the accuracy required for operating the MOSE system (Vieira et al., 1993; Lionello, 1995; Petaccia and Sallusti, 1995; Lionello et al., 1998; Bargagli et al., 2002).

This paper provides a state-of-the-art review of water level forecasting for the city of Venice. It presents the geographical setting of the city and the processes giving rise to the occurrence of high waters and flooding in Venice. It then reviews the forecasting capabilities across Europe where various institutions conduct operational forecasting, including for the Adriatic Sea and the Venice Lagoon. Different methodologies are presented that, in addition to the ones already operational, could significantly improve the forecasting system for Venice, including the operation of the MOSE barriers.

2 Geographic setting

2.1 The Adriatic Basin

The Adriatic Sea is an epicontinental basin within the eastern Mediterranean Sea extending southeastward from 46^∘ N, 12^∘ E to 40^∘ N, 19^∘ E, approximately 780 km long and 120–200 km wide (see Fig. 1 for reference).The bathymetry is characterized by a shallow northern shelf with water depths lower than 80 m, gently sloping in depth towards the middle part up to 250 m in the Jabuka Pit. The Palagruza Sill, 170 m deep, marks the beginning of the southern Adriatic, which extends up to Strait of Otranto separating the basin from the rest of the eastern Mediterranean Sea. In the southern Adriatic the bathymetry reaches 1200 m at the bottom of a wide depression known as the southern Adriatic Pit.

The general circulation of the basin is mainly cyclonic and primarily thermohaline, driven by a combination of surface buoyancy fluxes, river discharges and exchanges through the Strait of Otranto (Poulain and Cushman-Roisin, 2001). Along the eastern perimeter, the eastern Adriatic Current flows northward transporting saline Levantine Intermediate Water (Artegiani et al., 1989), while on the western border, the western Adriatic Current transports fresher surface water from the northern Adriatic toward the Straight of Otranto (Bignami et al., 1990a, b). Along this side of the basin, a deeper southward flow is also generated during the winter by the outflow of dense water masses generated in the northern part of the basin (Malanotte-Rizzoli, 1977; Artegiani et al., 1989, 1997a, b). The order of magnitude of the surface boundary currents (about 20 cm s⁻¹; Poulain, 2001) suggests that changes in sea surface elevation induced by geostrophic balance are negligible.

The tidal regime has been interpreted as co-oscillations with the Mediterranean Sea, forced through the Strait of Otranto and amplified by resonance phenomena along its longitudinal direction from south to north (Polli, 1961). The tidal dynamics are particularly evident in the northern Adriatic Sea, where the tidal range reaches values of more than 1 m at spring tide (see Sect. 3.1).

Over the Adriatic Sea, between October and March, meteorological disturbances are frequently and usually characterized by the passage of low-pressure systems or cyclones. These are often associated with strong southeasterly winds, the sirocco, as the cyclone approaches from the west, and with northeasterly katabatic winds, the bora, as the cyclone travels eastwards. These two winds represent the dominant wind regimes during the winter period (see Sect. 3.2).

2.2 The Venice Lagoon

The Venice Lagoon is situated at the northwestern end of the Adriatic Sea (Fig. 1). It is connected to the sea by three inlets with widths ranging from 500 to 1000 m. The depths of these inlets range from 7 to 13 m, depending on the inlet. The lagoon, during spring tide, has a peak exchange of around 20 000 m³ s⁻¹ with the Adriatic Sea, a very high amount considering that the average of the Po discharge is only around 1500 m³ s⁻¹ (Gačić et al., 2004).

The lagoon itself is quite shallow, on average around 1.5 m. Most areas are only 80 cm deep, but there are deep tidal channels that cut through the very shallow parts. Another particularity of the lagoon are the salt marshes that cover around 15 % of the total area (Umgiesser et al., 2004).

The tidal wave (tidal range 1 m) propagates mainly along the deep channels and then expands into the more shallow areas (Rinaldo, 2001). The delay between the signal at the beginning of the inlets and the city center is 40 min. What concerns the amplitude of the oscillation there is neither water level damping nor amplification, so the water level reaches the center of the lagoon nearly undisturbed (Ferrarin et al., 2015).

During the last 500 years major engineering works have been carried out inside the lagoon, including diversion of rivers, building of the inlet jetties, and dredging both existing and new artificial channels (Gambolati and Teatini, 2014). One of these channels, the Petroli channel, which runs from the central inlet across the lagoon to the industrial area, has been indicated to have worsened the phenomenon of Acqua alta inside the lagoon. This is, however, not the case because modeling studies show that the water level enhancement is limited to a few millimeters (Umgiesser, 1999). Much more influence (some centimeters of reduction) has resulted from the creation of reclaimed areas where fish farming is carried out inside the lagoon.

Apart from the local wind effect that can shift water masses inside the lagoon and can create water level differences of up to 50 cm between the north and south end, the level at the city of Venice is mostly determined by the water level just outside the inlets (Zecchetto et al., 1997). This means that the water level forecast can be divided into two different stages: the first one where the water level is determined at the lagoon inlets and the second one where the effects inside the lagoon are taken into account.

2.3 The city of Venice

The city of Venice is located in the central part of the lagoon and is situated on a group of 118 small islands that are separated by almost 160 canals (known as “rii”) having widths from a few to tens of meters and depths of 1–5 m. The average elevation of these islands is less than 1 m above the mean sea level (see Fig. 2 for reference). The Grand Canal is the main watercourse of this intricate network, in the shape of a large “S”. The overall length of the canal system is about 40 km and its surface corresponds to, approximately, 10 % of the total urban area (Zonta et al., 2005). The hydrodynamic regime in the canals is driven by tidal forcing as a consequence of phase lags and level gradients occurring at the city boundary. During the flood tide the flow is predominantly from southeast to northwest, while the direction is reversed during the ebb (Coraci et al., 2007). The current speed in the network is low, with average maximum values up to 25 cm s⁻¹ throughout the tidal cycle.

In the last century the city of Venice faced an increase in frequency and intensity of flooding events that periodically submerged parts of the old city center due to the combined effect of climate change and subsidence (Baldin and Crosato, 2017; Carbognin et al., 2004). The increasing frequency of inundations represent a serious problem for citizens, businesses and tourist activities. In October 2018 and November 2019, Venice and the northern Adriatic have been exposed to extreme marine conditions (sea level, waves; see also Fig. 2) in turn induced by extreme weather conditions (Morucci et al., 2020). A complete list of other extreme events can be found in Lionello et al. (2021b).

These flooding events pose a threat not only to the artistic, cultural and environmental heritage but also to the economic assets. To be able to face these events and to manage their occurrence, there have been investments in the safeguarding of Venice through the planning and building of flood barriers, many other structural measures, and forecasting operational systems, measurement networks and extreme event research activities (Barbano et al., 2012; Demarte et al., 2007).

3 The physics behind flooding in Venice

This section provides an overview of processes that influence and dominate the water level in front of and inside the Lagoon of Venice. The processes considered are tides, wind, atmospheric pressure and seiches.

3.1 Tides

Fluctuations of Adriatic Sea level and currents at tidal frequencies are among the largest in the entire Mediterranean Sea (Tsimplis et al., 1995). The tidal regime in the Adriatic Sea has been interpreted as co-oscillations with the Mediterranean Sea, forced through the Strait of Otranto and amplified by resonance phenomena along its longitudinal direction from south to north (Cushman-Roisin et al., 2001; Vilibić et al., 2017). Consequently, tidal dynamics are particularly evident in the northern Adriatic Sea, where the tidal range reaches values of more than 1 m at spring tide. For this reason, even without a meteorological contribution, during spring tide some parts of S. Mark's square are already flooded (Fig. 2). Only seven tidal constituents, four semidiurnal (M2, S2, N2 and K2) and three diurnal (K1, O1 and P1), give a significant contribution to the evolution of sea surface elevation in the northern Adriatic Sea, reaching a range of 1 m in the Trieste bay (Polli, 1961; Mosetti and Manca, 1972; Cushmain-Roisin et al., 2001; Orlić, 2001; Book et al., 2009) and resulting in a mixed, mainly semidiurnal tidal regime (Ferrarin et al., 2015, and references therein). The tidal form factor, consisting of the ratio of the amplitudes of the major diurnal and semidiurnal tidal constituents, reveals that the semidiurnal tidal regime (F<1) prevails in the Adriatic Sea, although the tide maintains a diurnal character (F>3) in the proximity of the semidiurnal amphidromic points located in the middle of central Adriatic Sea (Ursella and Gacic, 2001; Lovato et al., 2010; Ferrarin et al., 2017).

Tidal propagation in the shallow Venice Lagoon is controlled by many factors which define the relationship among the celerity of the tidal wave, the inertia of the water mass and dissipative forces due to friction. While propagating from the inlets to the lagoon, the tidal wave is deformed according to a relationship between local flow resistance and inertia and the characteristics of the incoming tidal wave. At present, the incoming tidal wave is amplified in the lagoon indicating that the driving and reflecting tides are close to the condition of resonance. As a consequence of natural and anthropogenic morphological changes that occurred in the lagoon in the last century, the amplitude of major tidal constituents grew, with a consequent increase in extreme high sea levels in Venice (Ferrarin et al., 2015).

3.2 Wind action

Due to the shape and the surrounding orography, the Adriatic Sea, and in particular the northern Adriatic, is mainly characterized by two wind regimes: the southeasterly sirocco and the northwesterly bora (Pasarić et al., 2009).

The sirocco is generally considered a basin response with large spatial scales (Signell et al., 2005). It is a warm and wet wind mainly associated with a minimum atmospheric pressure located in the northwestern Mediterranean or in the Tunisia–Sicily channel. It is channeled along the main axis of the Adriatic Sea by the bordering orography and blows often along the whole length of the basin, usually with a wind speed between 10 and 15 m s⁻¹ (Lionello et al., 2012). As a consequence it causes high waves and rain, and when a strong sirocco blows over the Adriatic, the water is piled-up in the northern part of the basin. In combination with tides it is the main driver of flooding in Venice and in general in the shallow coastal regions. It can also trigger resonance phenomena of water levels known as seiches (see Sect. 3.4).

While the sirocco is stronger and more frequent in the southern Adriatic, the bora blows more often in the northern Adriatic. With its northeasterly flow, it is a katabatic wind (Grisogono and Belušić, 2009) that, due to the complex orography of the Dinaric Alps on the eastern Adriatic coast, creates fine-structured jets and lee wakes with strong sub-basin-scale spatial gradients across the northern Adriatic, reaching gusts of about 100 km h⁻¹ and up to 200 km h⁻¹. Its strength is due to the gradient created by warm air over the sea surface and the cold area over the coastal mountains.

Two types of bora are known in the northern Adriatic: the bora scura, which is characterized by windy and rainy conditions caused by a cyclone centered over the south of Italy and an anticyclone over northern Europe, and bora chiara, which is a cold, violent, dry, gusty wind and is typically associated with a strong anticyclone over central and eastern Europe which conveys cold air falling on the Adriatic Sea surface through the various gaps and valleys of the Julian and Dinaric Alps. Both types of wind events can generate large waves and storm surges in the northern Adriatic, and especially in Venice, with different coastal impacts depending on the different morphology that characterizes the eastern Italian coast and the western Croatian one (Ferrarin et al., 2020).

3.3 Low-pressure systems

The passage of cyclones over the Mediterranean Sea produces positive and negative sea anomalies which reach their largest amplitude in the north Adriatic Sea and in the Gulf of Gabes (Lionello et al., 2019). The synoptic conditions leading to floods along the Adriatic coast (e.g., beside Venice, in Trieste and Dubrovnik) consist of a driving low-pressure center over central Europe and frequently of an associated cyclogenesis south of the Alps (Robinson et al., 1973; Trigo and Davies, 2002; Lionello, 2005; Lionello et al., 2019). In fact, a cyclone generated in the northwestern Mediterranean produces the largest storm surge events through a combination of inverse barometer effect and wind stress acting over shallow water (Lionello et al., 2012). The characteristics of the wind field and the cyclone track determine which location in the Mediterranean is most affected (Lionello et al., 2012; Meðugorac et al., 2018). The cyclogenesis in the western Mediterranean Sea is triggered by the interaction between the frontal layer of the primary cyclone and the Alps, and it evolves as a baroclinic instability perturbed by the orography (Buzzi and Tibaldi; 1978, Buzzi and Speranza, 1986; Speranza et al., 1985), which is further modified by the moist Mediterranean environment (Benzi et al., 1997; Krichak and Alpert, 1998). The presence of an area with frequent cyclogenesis in the northwestern Mediterranean Sea is evident in the climatological maps (e.g., Lionello et al., 2016).

3.4 Seiches

Seiches are standing waves that occur in enclosed water bodies – lakes, bays and channels. In the Adriatic Sea, a distinction could be made between basin-wide seiches, characterized by periods that are close to the inertial period and therefore considerably influenced by the Coriolis force, and local seiches, which have periods that are much smaller than the inertial period and thus marginally influenced by the rotation of the Earth.

Investigation of Adriatic-wide seiches was pioneered by Kesslitz (1910), who inspected de-tided sea level records in time domain, by Vercelli (1941), who performed filtering of tide-gauge records, and by Bozzi Zadro and Poretti (1971), who subjected sea level time series through spectral analysis. These analyses, and their numerous sequels, showed that the amplitudes of Adriatic-wide seiches could reach 50 cm and that the periods of two basic modes are close to 21.2 and 10.9 h. This seiche amplitude should be compared to the maximum spring amplitude of 50 cm (Fig. 2). The periods were verified by applying numerical modeling to the Adriatic Sea: one-dimensional (Sterneck, 1919) and two-dimensional (Accerboni and Manca, 1973) with nodal line imposed in the Straight of Otranto and two-dimensional (Schwab and Rao, 1983) with the Adriatic being considered as a part of a wider Mediterranean Sea. Numerical modeling expanded over the subsequent years, and, moreover, the question of generation and decay of the Adriatic seiches received some attention. Thus, Raicich et al. (1999) confirmed the sequence of events usually leading to the generation of basin-wide seiches: during the first phase, a storm surge develops in the Adriatic when a cyclone approaches the basin and thus exposes it to a combined action of low air pressure and sirocco wind; during the second phase, seiches are triggered in the Adriatic when the cyclone leaves the basin, and therefore air pressure rises, while sirocco wind slackens or veers to bora. It was also pointed out that the partition of energy between various normal modes depends on the spatial variability in sirocco wind and the Adriatic bathymetry. Cerovečki et al. (1997) considered 12 pronounced episodes of basin-wide seiches and obtained 3.2±0.5 d for the free decay time. It was concluded that the longevity of the Adriatic seiches could be ascribed to the weak influence of bottom friction and the small energy loss to the Mediterranean Sea. Due to their considerable amplitudes and persistence, the Adriatic-wide seiches could influence the flooding of the north Adriatic coastal area: if a cyclone approaches the Adriatic while the seiches related to the previous cyclone still last, a constructive or destructive superposition of the storm surge and the preexisting seiches may occur.

Local seiches were also found to be important in the Adriatic Sea. More specifically, the east Adriatic archipelago, with its numerous bays and channels, represents an ideal setting for the development of short-period seiches. An overview of these waves, and of their importance in the generation of meteotsunamis, is provided by Vilibić et al. (2017). Much less is known on local seiches along the west Adriatic coast. Thus, for example, seiches may be expected to occur in the Venice Lagoon with a period of 2–3 h defined by the length and depth of the basin. It appears, however, that the existence of such seiches and their possible influence on the flooding of Venice did not receive much attention. In a rare paper addressing the subject, the lack of interest was attributed to the small depth of the lagoon (the mean value being close to 1 m) and the consequent strong damping of local seiches (Zecchetto et al., 1997).

Mean sea level rise will affect Adriatic seiches and tides depending on the adopted strategy of coastal defense (Lionello et al., 2005; Haigh et al., 2020). If dams are built to preserve the current coastline, increased wave speed and reduced bottom friction will shorten the period of seiches and move it away from those of tides, whose amplitude would be consequently reduced. On the contrary, if the Adriatic Sea will be allowed to freely expand over coastal areas, the period of seiches will become closer to those of tides, whose amplitude would be, consequently, increased. Changes in amplitude will be on the order of 10 % for 1 m sea level rise, increasing substantially for larger values.

4 Storm surge modeling

In this section we describe existing storm surge modeling systems for Europe. It gives an overview of the capabilities and the peculiarities of the various areas and their forecast systems. Finally, the forecasting systems for the Adriatic Sea and the Venice Lagoon will be discussed.

Common for all regional storm surge models is the dependency on high-quality (a) meteorological forecast data and (b) basin geography. The error growth of the weather forecast with time is ported directly to the storm surge forecast and dominates the error growth of the latter from analysis time onwards. This is because the atmosphere behaves much more chaotic than the sea. The storm surge model error at analysis time may be brought down by data assimilation and may be considerable without it. Ideally, systematic model errors are identified and minimized by applying analyzed weather forcing in a calibration procedure prior to operationalization.

4.1 Storm surge modeling in Europe

4.1.1 The Atlantic coast

Storm surges increase northward along the European Atlantic coast (Vousdoukas et al., 2016; Fortunato et al., 2016) due to the northward growth of both the storm intensity and the width of the continental shelf, from tens of kilometers along the Iberian coast to a few hundred to the west of the British Isles. Devastating storm surges are therefore more common in the north. For instance, coastal inundation levels above 0.5 m occur about once a year in Ireland (O'Brien et al., 2018). Although less frequent, catastrophic events also occur on the French (Breilh et al., 2014) and Iberian (de Freitas and Dias, 2013) coasts.

These events have fueled the development of forecasts of tides and surges in the European Atlantic coasts (Fortunato et al., 2017; Sotillo et al., 2019; Oliveira et al., 2020), although the implementation details are often unavailable. The Portuguese Laboratório Nacional de Engenharia Civil produces 48 h forecasts of tides and surges using SCHISM (Zhang et al., 2016) in 2DH mode. The application is forced by the atmospheric global forecast system (GFS; NCEP, 2011) and the global tidal model FES2012 (Carrère et al., 2013) with a grid resolution of about 250 m along the Portuguese coast (Fortunato et al., 2017). In Spain, Puertos del Estado runs several forecasts, described in Sect. 4.4, while MeteoGalicia runs the Regional Ocean Modeling System (ROMS) at regional scales, with nested applications of MOHID (Mateus et al., 2012) at estuarine scales. In France, Météo-France applies Hybrid Coordinate Ocean Model (HYCOM; Bleck, 2002) in two dimensions, with a curvilinear grid of resolution down to 500 m along the coast and a spatially varying bottom friction. The British Met Office uses the Nucleus for European Modeling of the Ocean (NEMO) model (Madec and the NEMO team, 2016), with a spatial resolution of 7 km and a Charnock approach (Charnock, 1955) with a tuned Charnock parameter to compute surface stress. A refinement to 1.5 km and a wave-dependent approach to compute the surface stress are currently under development.

Simulations of tides and surges decoupled from waves are still the norm (Fortunato et al., 2017; Fernández-Montblanc et al., 2019), in particular in the routine predictions of official forecasts. However, the importance of waves on sea levels is well-established (Dodet el al., 2019). The increased roughness of the sea surface associated with steep young waves can significantly increase the wind stress, thereby enhancing wind-induced surge (Bertin et al., 2015). In addition, the wave-induced setup can contribute significantly to the overall surge along the coast, even in sheltered areas like estuaries (Lavaud et al., 2020). Hence, wave–current interactions will likely be increasingly included in forecast services. Also, the hazards associated with high river flows and storm surges are usually treated separately, but recent efforts target the simulation of flooding induced simultaneously by river discharges and storm surges (Ye et al., 2020).

4.1.2 The North Sea

The North Sea has a long history of coastal flooding with significant coastal flood events in 1099, 1421, 1446, 1530, 1570 and 1717 (Haigh et al., 2017). In the last century, the “Big Flood” of 31 January–1 February 1953 and the flood of 16–17 February 1962 provided a major incentive for establishing storm surge forecasting and warning services for North Sea countries and were the driving force for major improvements in sea defenses (Gilbert and Horner, 1986; Gerritsen, 2005).

Flather (2000) provided a review (now somewhat outdated) of the operational systems used for real-time prediction of storm tides and waves in northwest Europe. The Norwegian Meteorological Institute (DNMI) uses a 4 km resolution barotropic ROMS (Regional Ocean Modeling System) model, forced with ensemble weather predictions from the European Centre for Medium-Range Weather Forecasts (ECMWF) to forecast storm tides (Saetra et al., 2018). The Danish Meteorological Institute (DMI) runs two storm surge models covering the North Sea and Baltic Sea to provide storm tide forecasts for Danish Waters (Flather, 2000). In Germany, the Bundesamt für Seeschifffahrt und Hydrographie (BSH) uses a nested storm surge model, forced with meteorological predictions from global and local area models of the Deutscher Wetterdienst (DWD) to provide forecasts of water levels (Dick, 1997). In the Netherlands, water level forecasts are made by the Dutch storm surge warning service (SVSD) in close cooperation with the Royal Netherlands Meteorological Institute (KNMI) (Verlaan et al., 2005). These are based on the Dutch continental shelf model (DCSM) forced with forecasts from the meteorological high-resolution limited area model (HiRLAM). Since the early 1990s, a Kalman filter has been used to improve the accuracy of the forecasts by incorporating observations from tide gauges. In the United Kingdom, the Coastal Monitoring and Forecasting (UKCMF) service was established as a direct result of the 1953 floods (Flather, 2000). Presently, the operational system uses the CS3X hydrodynamic model (Flather, 1994), which has a resolution of ∼12 km, forced with the Met Office's Global and Regional Ensemble Prediction System (MOGREPS).

In the future the CS3X model will be replaced with a NEMO-surge tide model (O'Neil et al., 2016). Recently, Fernández-Montblanc et al. (2019) described efforts to create a pan-European storm surge forecasting system (EU-SSF). This uses the SCHISM (Semi-implicit Cross-scale Hydroscience Integrated System Model) unstructured grid model, forced with atmospheric fields from ERA-Interim, as well as by an ECMWF high-resolution forecast.

4.1.3 The Baltic Sea

The Baltic Sea is a large, elongated (∼1000 km), brackish, semi-enclosed estuary connected to the world ocean only via narrow and shallow straits. Baltic storm surges occur when the regional wind and atmospheric pressure conditions displace the water mass towards one far end of the basin (Samuelsson and Stigebrandt, 1996; The BACC II Author Team, 2015). Surges may reach 2–2.5 m, but at least one event in excess of 3 m has been reported and studied (Rosenhagen and Bork, 2009). While the Baltic Sea is (almost) devoid of tides, standing waves (seiches) may occur. The “preconditioning”, when a period of persistent North Sea westerlies may increase the Baltic mean sea level by up to $\mathrm{3}/\mathrm{4}$ m (Hupfer et al., 2003), plays a crucial role. During the relatively short course of a high wind event, the Baltic water volume stays almost constant. Infrequently “silent surges” occur when high winds over the central part of the basin may generate a storm surge at one basin end, under locally perfectly calm conditions. Under certain wind conditions, the peculiar shape of the far western Baltic leads to surges being built up from the north and the east simultaneously.

For operational purposes, hydrodynamic storm surge models of the Baltic often include part of or the entire North Sea. A closed-basin (or parameterized boundary) model may be chosen for theoretical studies. Some Baltic countries (Germany, Sweden and Denmark) have an extra-Baltic coastline as well, and they apply a connected-seas system with locally high resolution of the connecting straits, down to 1 km width. This may be accomplished, for example, by two-way nesting or by unstructured grids.

The inclusion of thermodynamics, sea ice modeling, fresh water discharge from a vast catchment area and high vertical resolution establishes a realistic estuarine circulation and further improves sea level and surge simulation.

High-resolution weather forcing from a limited area numerical weather prediction (NWP) model will generally produce an accurate sea level forecast a few days ahead, and it constitutes the basis for storm surge warnings in the region. Less detailed, medium-range global weather forcing may be used for pre-warning, when an alert is raised but no practical action taken just yet.

Operational Baltic storm surge model codes include, amongst others, the Baltic community model HBM (Berg and Poulsen, 2012) and the European NEMO model (Hordoir et al., 2019; Madec and the NEMO team, 2016), which constitute the model complex in the Copernicus Marine Service for the Baltic Sea and are also used for national storm surge warning systems, typically accurate within 20 cm for 1–20 year events (Nielsen, 2003). A BOOS concerted forecast exchange forms the basis for Baltic multimodel ensemble (MME) prediction (http://www.boos.org/multi-model-ensemble-of-forecast-products/, last access: June 2021).

4.1.4 The western Mediterranean

Forecasting sea level in this region is relevant to understand phenomena and support activities with an important socioeconomic impact, such as coastal erosion and inundation, infrastructure damage, harbor operations, and navigation. Existing operational services in the region are as follows:

Puertos del Estado storm surge system (Nivmar): operational since 1998 (Álvarez-Fanjul et al., 2001), it is based on a two-dimensional barotropic implementation of the HAMSOM model (Backhaus and Hainbucher, 1987). It is forced with ECMWF $\mathrm{1}/\mathrm{8}$^∘ atmospheric pressure and wind fields. Total sea level forecast is provided by adding the tidal signal derived from measurements. A nudging technique makes use of near-real-time tide gauge data to improve low frequency signals. More recently, a new multimodel ensemble forecast has been developed (Pérez-Gómez et al., 2012) combining the Copernicus Marine Environmental Service (CMEMS) operational models IBI-MFC (Sotillo et al., 2015) and MED-MFC (Clementi et al., 2019) (see description on Adriatic section) with the Nivmar solution (Pérez-González et al., 2017, 2019). The forecast is generated by means of a Bayesian model average technique. The new solution is statistically better than any of the individual members and includes a confidence band (Fig. 3).

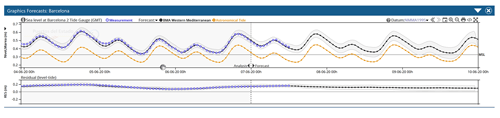
Figure 3 Sea level forecasted at Barcelona on 7 June 2020 (hourly time series): black: BMA solution (shaded area: 95 % uncertainty band based on the output of the different models); blue: tide gauge observations; orange: tide. The BMA solution is obtained by combining the sea level solutions from IBI-MFC, MED-MFC and Nivmar at Barcelona harbor (as displayed in PdE Portus system: https://portus.puertos.es, last access: June 2021).

Météo-France operational storm surge system: operational since 2014 and developed by SHOM and Météo-France, it is based on a barotropic version of the HYCOM code (Pasquet et al., 2014, 2017). The maximum resolution of the model is 1.5 km. Tides are not included. The system is launched 15 times per day with different atmospheric forcing, allowing the forecasters to assess the impact of each forcing on the sea level (Fig. 4). The model was validated with 22 storm events and 1 year of data to calibrate the wind drag coefficient (according to the Charnock formulation) (Casitas et al., 2018). Since 2016 an ensemble prediction system has been available, with 35 members of the Arpege Ensemble Forecasting System as forcing, running at 06:00 and 18:00 UTC, with forecast horizons of 90 and 108 h respectively.

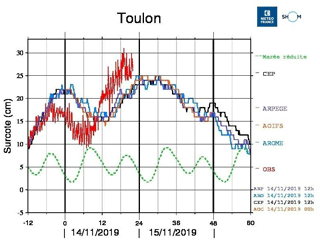
Figure 4 Temporal series (every 10 min) for the storm surge forecasted at Toulon (south of France) starting on 14 November 2019 at 12:00 UTC using the forcing provided by the global model IFS from ECMWF (named CEP, black), by the global model ARPEGE from Météo-France (purple), by the Météo-France LAM model AROME nested in ARPEGE (AROME) (blue) and by the Météo-France LAM model AROME-IFS nested in IFS (orange). Red: tide gauge observations; green: tide height (normalized).

4.2 The Adriatic Sea

Although scientific works on marine circulation in the Adriatic Sea are very numerous and analyze it in detail, papers presenting storm surge operational systems are few. Due to the importance of Venice, many systems were developed in several operational Italian institutions. Meteotsunamis are also an important concern in the Adriatic Sea, which has motivated the recent development of dedicated ocean–atmosphere modeling systems (Denamiel et al., 2019).

The sea level in Venice has been recorded for more than 100 years, and in this period there have been various extreme events, such as in 1966 (Cavaleri et al., 2010) and 1979 (Grazzini, 2006), but almost every year events of a certain intensity can happen (https://www.comune.venezia.it/node/6145, last access: June 2021), like in the last two years, 2018 and 2019 (Cavaleri et al., 2019, 2020). The following list contains the storm surge forecasting systems in the Adriatic Sea, divided according to the institution in which they operate:

The Institute of Marine Sciences (ISMAR) of Venice (Italy) is part of the National Research Council (CNR) and has been developing a hydrodynamic model called Shallow water HYdrodynamic Finite Element Model (SHYFEM) for over 30 years. SHYFEM is an open-source finite element model available on Github (https://github.com/SHYFEM-model/shyfem, last access: June 2021). This model has been used many times for storm surge prediction, and many of the following operational systems are based on it.

Kassandra: this system forecasts the total sea level and waves in the Mediterranean and the Black seas (Ferrarin et al., 2013). The system is based on the SHYFEM model, coupled to the wind wave model II (WWMII), and the forecast is available online (http://kassandra.ve.ismar.cnr.it:8080/kassandra, last access: June 2021). The resolution is variable but remains around 5 km throughout the Mediterranean and 1 km along the Italian coast. The model considers both the astronomical contribution to the sea level, with the calculation of the gravitational potential, and the wave setup, thanks to the two-way coupling with the wave model.

Tiresias: this system, based on the SHYFEM model, uses a baroclinic formulation of the shallow water equations and is therefore able to predict the temperature and salinity. The system extends to the whole Adriatic Sea and includes, in a single grid, the main lagoons (including the Venice Lagoon) and the Po delta (Ferrarin et al., 2019). This peculiarity allows for the reproduction of effects such as the saline wedge intrusion in the Po delta and the water circulation in three dimensions in the Adriatic.

Ismar Storm Surge Operational System (ISSOS): compared to the two previous systems, ISSOS, also based on the SHYFEM model, is focused on storm surge prediction. It operates with a computational grid, extended to the Mediterranean, with a lower resolution in order to reduce calculation times. Furthermore, the astronomical tide is not simulated but added locally where a total sea level forecast is needed. Although the simulation is barotropic and in two dimensions, the accuracy on the sea level is not affected. A second two-dimensional barotropic simulation is carried out in cascade to the first one to extend the forecast into the Venice Lagoon, using the forecast of the Mediterranean simulation with tide (Ferrarin et al., 2020). Finally, a slower three-dimensional baroclinic simulation is performed in the lagoon, using the same grid of the second simulation, in order to predict the temperature and salinity too. In this last simulation the temperature and salinity boundary conditions are retrieved by the Copernicus Marine Service.

The Centro Previsioni e Segnalazioni Maree (CPSM) is in charge of sea level forecasts and warning and is part of the municipality of Venice (Italy). This center has the task of issuing the official forecast, with updates sometimes hourly, and alerting the population using sirens scattered throughout the inhabited centers in the lagoon. An example of the daily forecast page is given in Fig. 5. Statistics of the operational forecast in CPSM have also been published (Zampato et al., 2016).

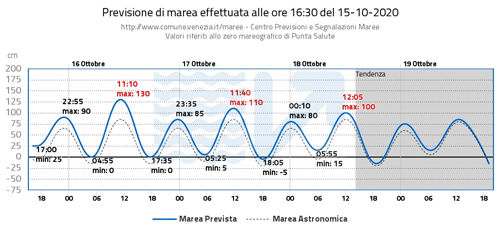
Figure 5 An example of the daily bulletin published on the official forecasts website of CPSM – Venice Municipality. The chart shows a 4 d forecast plus 1 d forecast trend. The water level refers to the Punta Salute datum, the historical zero of Venice defined in the year 1897. The blue line is the total expected sea level, and the dotted black line indicates the astronomical tide.

The operational model at CPSM is called SHYMED (SHYFEM on MEDiterranean). This system, based on the SHYFEM model, updates previous systems that are no longer operational (Bajo et al., 2007, Bajo and Umgiesser, 2010). Its structure is similar to ISSOS without the baroclinic simulation but uses different atmospheric forcing. In addition, there are three versions with various wind stress formulations and different corrections of the forecast wind. The forecast is emitted every 12 h, but every hour the forecast is updated by means of a one-dimensional Kalman filter, using the latest observations (Bajo, 2020).

Two other models were operational at CPSM. These were HYPSE, a two-dimensional finite difference model running over the Adriatic Sea with assimilation of one sea level station (Lionello et al., 2006), and a system based on Delft-3D. Both systems are not operational anymore and have been decommissioned.

The Italian National Institute for Environmental Protection and Research (ISPRA) is an institution under the umbrella of the Italian Ministry of Environment. The modeling system SIMM (Sistema Idro-Meteo-Mare) is a chain of operational systems that includes the atmosphere, waves and storm surge predictions (Speranza et al., 2007; Mariani et al., 2015). The storm surge forecasting system is based on the SHYFEM model, which is set to execute two-dimensional barotropic simulations. There are different versions that use different spatial resolutions, meteorological forcings and data assimilation (DA). The version with DA is based on the dual 4D-Var technique (Bajo et al., 2017) and assimilates sea level data from nine tide gauges along the Italian Adriatic coast.

Arpae is the Regional Agency for Prevention, Environment and Energy of Emilia-Romagna (Italy). The Hydro-Meteo-Climate Service of Arpae (Arpae-SIMC) actively works in numerical model forecasting, both deterministic and probabilistic, at different timescales from very short-range, in the case of extreme events, to seasonal scale. Arpae-SIMC is a center of competency for the Italian National Civil Protection system, as well as the support center for the Civil Protection Agency of Emilia-Romagna.

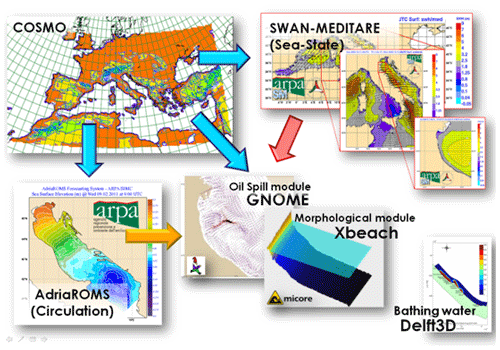
The integrated modeling system developed by Arpae-SIMC for its marine and coastal activities (Fig. 6) consists of a wave-forecasting operational chain called MEDITARE (Valentini et al., 2007) and AdriaROMS (Chiggiato and Oddo, 2008; Russo et al., 2013), which uses the ROMS model implemented in the Adriatic Sea (Shchepetkin and McWilliams, 2005). Both systems are forced by the non-hydrostatic limited-area COSMO-I meteorological model (Schättler et al., 2018).

Figure 6 The operational modeling system and the meteo-marine products provided by Arpae-SIMC.

Copernicus Marine Environmental Service (CMEMS) is the marine section of the European Copernicus program. This program provides remote sensing and modeling data freely available on the web (https://marine.copernicus.eu/, last access: June 2021). The modeling product for the Mediterranean Sea is called Med-MFC Analysis and Forecasting Physical System (MedFS). MedFS is a coupled hydrodynamic-wave (NEMO-WW3) system (Clementi et al., 2017a, b) with a data assimilation component (Storto et al., 2015). The horizontal grid resolution is $\mathrm{1}/\mathrm{24}$^∘ with 141 vertical levels. The model solves the three-dimensional baroclinic shallow water equations without the tidal component. Only the surge component is published at the web site.

Slovenian Environmental Agency (ARSO) is part of the Slovenian Ministry of the Environment and Spatial Planning. SMMO is a forecasting system based on the Aladin atmospheric model and originally on the Princeton Ocean Model (POM), with a regular resolution of $\mathrm{1}/\mathrm{30}$ of a degree. Its computational domain is limited to the Adriatic Sea (Ličer et al., 2016). The system has been recently upgraded to the NEMO ocean model with a resolution of $\mathrm{1}/\mathrm{216}$ of a degree (Matjaž Ličer, personal communication, 2020).

Consorzio Venezia Nuova (CVN) is the Italian consortium of companies responsible for building the Venice flood barrier system, named MOSE. They are also running a forecasting system for the operation of the mobile barriers. The storm surge model at CVN is developed by DHI and is based on Mike 21 (Vieira et al., 1993). Data from two atmospheric models are used (ECMWF and COSMO 5M). The modeling chain consists of a Mediterranean model that drives an Adriatic Sea model and in turn the Venice Lagoon model. The forecasting period varies between 18 h and 5 d (https://www.mosevenezia.eu/control-room/, last access: June 2021). The output of this forecasting system is not made public.

Many of the aforementioned models have been considered together in the I-STORMS multimodel system (Ferrarin et al., 2020), which provides ensemble forecasts for water levels and waves in the Adriatic and Ionian seas.

4.3 The Venice Lagoon

Forecasting of storm surge events is mainly done in the Adriatic Sea as described in the last section. In order to resolve also the tidal and storm surge propagation inside the lagoon high-resolution models have to be run inside the Venice Lagoon. This can be done either in a traditional way, in which the water levels computed outside the lagoon with models running on the Adriatic Sea are used to force a new model with a modeling domain resolving only the lagoon area, or a combined model with a domain including both the Adriatic Sea and the Venice Lagoon. Both types of approaches are used in Venice and are described below. Moreover, statistical models are also used for forecasting.

The CPSM has been running, for a long time (from 1981), statistical models that use the atmospheric pressure, wind and water level data from past events to forecast the new events in the future. Especially for the short time range (up to 12 h) this is quite effective. These models will be presented in the next section.

Concerning deterministic models that actually resolve the physics of the surge propagation, one of the first models that was implemented at the CPSM was a forecasting system based on the finite element model SHYFEM (Bajo et al., 2007). The system, named SHYMED (see Sect. 4.5), is implemented on the whole Mediterranean and uses atmospheric forcing from ECMWF and sea level boundary conditions from Copernicus. A second simulation inside the lagoon uses the forecast of the first simulation and the tide recorded at the oceanographic tower Acqua Alta, 8 nautical miles off the Venetian coast. In its actual implementation the model does not use assimilation techniques. However, the model results inside the lagoon were corrected with a neural network approach in the past (Bajo and Umgiesser, 2010) and now with a unidimensional Kalman filter (Bajo, 2020), which allows hourly updates of the forecast.

At ISPRA, another implementation of the SHYFEM model (SIMM) is running daily (Mariani et al., 2015). This application uses wind both from ECMWF and from another atmospheric model (BOLAM, Bologna Limited Area Model), produced by ISPRA in Rome. A version of this implementation uses a dual 4D-Var assimilation technique for which nine tide gauges in the Adriatic are used. Also in this case, a new model run propagates the water level inside the lagoon and publishes water levels for some important islands inside the lagoon, such as Venice, Burano and Chioggia.

At the CNR the ISSOS storm surge model is running. As the implementations of the models in CPSM and ISPRA, the model first resolves the Mediterranean Sea and then computes the water levels in a second run inside the lagoon. A lagoon run of this model is baroclinic, therefore taking also into account temperature and salinity (Ferrarin et al., 2020).

There is one model (Tiresias, Ferrarin et al., 2019) that is implemented on a numerical grid that comprises the whole Adriatic Sea and the Venice Lagoon. With this model, water levels are directly computed at the stations inside the lagoon, and there is no need to run a second model to propagate this information inside the lagoon.

5 Challenges in forecasting flooding for the Venice Lagoon

Here we stress the peculiarity of Venice for water level forecasting. We show what deterministic and statistical forecast models can do and how they complement themselves. We also discuss the importance of assimilation for improvement of the forecast and ensemble methods for the estimation of the uncertainty. We then also give some examples of past storm surge events.

5.1 Local effects

The Venice Lagoon has experienced significant subsidence effects (Baldin and Crosato, 2017; Carbognin et al., 2004) in the last century and is constantly exposed to the risk of flooding from storm surge, enhanced also through relative sea level rise (Frassetto, 2005). The semi-closed shape of the Adriatic Sea favors the occurrence of intense storm surge events, and the sea level rises to unusual values because of the local low-pressure system cyclogenesis (Genoa) and associated strong winds driven by orography. It is well-known that the hydrodynamics of the Venice Lagoon is strongly dependent upon both tides and prevalent local wind regimes (Berrelli et al., 2007).

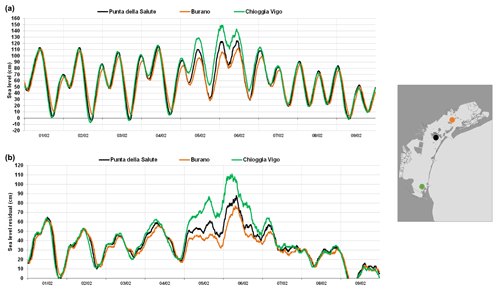
The level at the Punta della Salute tide gauge (Venice center) is not enough to widely represent the conditions of the lagoon basin during occurrences of storm surge (Ferla, 2005). Sea level observations have shown that the forcing action of the wind along the lagoon surface gives rise to considerable accumulations on the water against the southern or northern boundaries of the lagoon, depending on the wind direction. The maximum water levels are significantly different in Venice and in other larger inhabited centers, such as Chioggia in the southern section of the lagoon or Burano in the northern portion. Under these varying weather conditions, sea level differences between the various parts of the lagoon and especially between lagoon and sea can determine asymmetrical hydrodynamic conditions at the inlets.

Local surges, mainly due to wind setup, have a scale of a few kilometers inside the Venice Lagoon and can produce significant effects, especially near the lagoon borders; bora wind (northeasterly) has relevant effects in the southern lagoon, near Chioggia island, where fishing valleys and reclaimed areas are located, all situated below the mean sea level.

According to literature, an average difference of 50 cm has been estimated between the northern and southern part of the lagoon (Fig. 7) in different cases of bora wind of 5–7 m s⁻¹ (Pirazzoli, 1981; Berrelli et al., 2006) and higher difference in cases of extreme meteorological events (Cordella and Ferla, 2007). Such phenomena were observed mainly in February during the years 2012, 2014 and 2015 when a strong bora wind was blowing (ISPRA, 2012; Coraci and Crosato, 2014). As already mentioned in Sect. 3.2, sirocco winds (southeasterly) push water masses towards the Venice Lagoon. The combination of all these local effects and climate change (Rinaldo et al., 2008) could lead to severe and disastrous storm surge events, as has happened during the last 2 years (October 2018, November 2019; Morucci et al., 2020; AAVV, 2020).

Figure 7 Sea level (a) and residual level (b) at Venice–Punta della Salute (blue), Burano (red) and Chioggia (green) during a bora event (wind from northeast) on February 2015.

5.2 Deterministic forecast models

The deterministic operational models for predicting the sea level in Venice are typically storm surge models which solve shallow water equations in two or three dimensions. This simplified formulation is often used instead of more complex equations as it is extremely fast and has an accuracy comparable to more complex equations in storm surge resolution.

Many operational systems based on deterministic models use computational domains extended to the whole Mediterranean Sea even if some of them run only the Adriatic Sea. However, the extension to the Mediterranean Sea avoids problems in the reproduction of the seiches, which have a nodal point near the Strait of Otranto (Cerovečki et al., 1997). The lateral boundary conditions of sea level and, sometimes, water flux can be retrieved by other operational models, such as those of the European Copernicus Programme (https://marine.copernicus.eu/, last access: June 2021). The surface boundary conditions are the most important for a storm surge model and consist of wind and atmospheric pressure fields. Due to the orographic conformation around the Adriatic Sea, atmospheric models tend to have large errors, and local-scale models with high resolutions may be required.

Deterministic models can include the tidal potential in their equations and thus simulate the propagation of the astronomical tide. However, operational systems prefer to simulate only the storm surge component and locally add the astronomical tide, calculated through harmonic analysis, since the interactions between storm surge and tidal components are small in the northern Adriatic (see Lionello et al., 2021b, in this special issue for a short discussion).

Others possible problems in the Adriatic Sea concern the complexity of the coasts and the need to adequately represent them (for this purpose it is better to use models with unstructured grids), as well as the lack of high-resolution and accurate bathymetric datasets in the continental shelf border. Finally, forecast scores can further be improved through the estimation of the forecast thanks to data assimilation and ensemble forecast techniques, based on ensembles of different forcing perturbations (Mel and Lionello, 2014b) or a multimodel approach (Ferrarin et al., 2020).

5.3 Statistical forecast models

The statistical models represent a fundamental part of CPSM (Centro Previsione e Segnalazione Maree) tidal forecasting modeling system. The model structure has been designed and calibrated using a database of tide and atmospheric data over a period exceeding 50 years (from 1966 to 2016). The database contains the values of tide level, atmospheric pressure, baric gradients and wind in the Adriatic and Tyrrhenian seas. These values were used to obtain regression coefficients for different versions of the models inspired by the autoregressive scheme, with expert type, from the ARMAX family (Goldmann and Tomasin, 1971; Sguazzero et al., 1972; Tomasin, 1972)

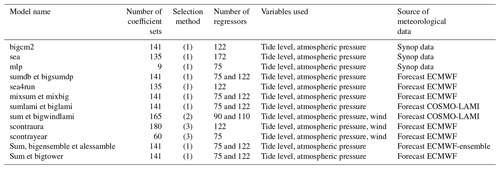
The actual operational structure of the system of statistical models is illustrated in Table 1. The engineering processes of the expert structure divided the database into subsets of similar cases, considering meteorological situation, seasonality and moment of forecast. With this process, many classes of coefficients have been created. Every single class corresponds to an appropriate set of coefficients used by the basic model for statistical interpretation of the evolution of sea level in the Venetian area (lagoon and sea).

Table 1 List of statistical models running at CPSM. The sets of coefficients are selected depending mainly on (1) maximum atmospheric pressure gradient between opposite coasts of the Adriatic Sea, seasonality; (2) classes of sirocco wind along the four region of Adriatic Sea, seasonality; and (3) classes of sirocco wind and bora wind along the multiple regions of Adriatic Sea, seasonality.

Another important development for the forecast of sea level with statistical models consists in using the expected atmospheric pressure and wind fields. CPSM is using the forecast fields issued by ECMWF and COSMO-I (Schättler et al., 2018). It allows us to make projections into the future, with an hourly step, using observations and predictions simultaneously (Canestrelli and Pastore, 2000; Tosoni and Canestrelli, 2011).

Since 2009, a multimodel ensemble system has been operational which is able to collect different information, making choices with reference to historical performance of single statistical models running in CPSM. Nowadays, two multimodel-ensemble (MME) families are operating in CPSM and are designed as follows:

1. For every step of forecast, models are selected which have historical minimal errors in similar meteorological conditions and in the same season, and a weighted average in relation to mean absolute error is calculated (Markowitz, 1952; Lintner, 1965).

2. For each forecast step, a linear regression is constructed with the historical set of all forecasts for a specified class. The coefficients obtained are applied to the expected values (Black, 1972; Mossin, 1966; Sharpe, 1964).

5.4 Data assimilation in flood forecasting

In the specific case of the Adriatic Sea, data assimilation has already been applied simulating the operational practice and using the 4D-Var technique (Lionello et al., 2006). Lionello et al. (2006) have shown that the prediction of the northern Adriatic storm surge can be improved by adopting a suitable data assimilation procedure. They used the hourly sea level observations available at the Acqua Alta platform 8 nautical miles offshore the lagoon inlet. The assimilation procedure is based on the adjoint model (Lewis and Derber, 1985; Talagrand and Courtier, 1987; Thacker and Long, 1988; Thacker, 1988). The procedure has been shown to be capable of compensating for the forecast errors (including those caused by inaccuracy of meteorological forcing and model shortcomings). The reliability of the storm surge forecast has been consistently improved simulating 1 month of operational prediction and reducing the error to 50 % of the original value in the 1 to 3 d forecast range. However, the availability of only one sea level station limited the capability of the method to correct any seiche oscillations extending along the entire Adriatic Basin.

A similar technique, the dual 4D-Var, has been used more recently in an operational system (SIMM; Sect. 4.5) to assimilate the residual level from nine stations along the Italian coast in order to improve the forecast of the storm surge. Furthermore, the same hydrodynamic model and data assimilation system were used to analyze the impact of the assimilation of altimeter data in two historical storm surge cases (Bajo et al., 2017). Although assimilation techniques based on 4D-Var are very advanced, the major problem is that of prescribing a good background error covariance matrix which, instead, is automatically calculated using assimilation techniques based on an ensemble of simulations. A technique belonging to this group, the ensemble Kalman filter (EnKF), was used more recently in Bajo et al. (2019), showing a significant improvement in the reproduction of the storm surge in two extreme events. In this case, the residual level from different coastal stations, both along the Italian and the Croatian coasts, was assimilated. The improvement was largely due to the presence of pre-existing seiches, which were better reproduced following the improvement of the initial state of the system.

The EnKF used in this paper and similar techniques exploit the variance of an ensemble of simulations to construct the background error covariance matrix (Carrassi et al., 2018). If the ensemble is well perturbed, the matrix is very realistic, and, moreover, it is variable over time. The ensemble can be calibrated so as to be “reliable”, that is, its width is able to represent the error that the forecast will actually commit (further discussed in the next section). In this way, data assimilation is able to exploit the correction of the observations to improve the whole state of the model in a physically coherent way (Bajo et al., 2019).

Finally, at the CPSM center “local” data assimilation techniques are used, which are much simpler to apply. These techniques are able to significantly improve the short-term forecast originally made by a deterministic model and to provide hourly updates of local forecast time series, as in the case of a statistical model (Bajo, 2020).

5.5 Dealing with uncertainty – ensemble forecast

A dynamic model generates a deterministic and single storm surge forecast time series at each individual grid point. If the model is validated against in situ tide gauges, the error or accuracy of the model at these specific locations can be assessed. However, uncertainty of the forecast and its dependence on the forcing, model characteristics or bathymetry is usually unknown and possibly underestimated, with the consequences this may have for risk managers and decision-makers who would preferably rely on probabilistic forecasts (forecast plus confidence interval).

The high sensitivity of the predicted weather evolution (which can be characterized as a chaotic system) makes weather deterministically unpredictable beyond a finite time range (practically beyond 10 d). In meteorological forecasts based on the combination of different model solutions, a so-called ensemble prediction system (hereafter EPS) has been used for years as the standard procedure for dealing with uncertainty (Leith, 1974; Hamill et al., 2000). EPS has been implemented at ECMWF since 1992 (Molteni et al., 1996). The technique is based on the combination of a set of forecasts that are different because of controlled changes. These can affect the initial conditions (including perturbations that mimic the uncertainty on the measurements or on the data assimilation method), the model physics (for example variations in the parameterization constants) or the open boundary conditions (Flowerdew et al., 2009). All these modifications are designed to represent the uncertainties in the knowledge of the state of the weather (Buizza and Palmer, 1995) and in our ability to forecast it with equations in which several processes, such as turbulence, are parameterized (Palmer and Hagedorn, 2006).

Now, using this technique is strongly recommended in oceanography. The deviation of wind and atmospheric pressure fields from their actual evolution will determine a corresponding deviation on the predicted sea level. If a set of different weather predictions are used to drive different sea level simulations, the probability distribution function of the forecast sea level values provides a practical tool for estimating the uncertainty of the sea level forecast and the probability of exceeding a given sea level threshold. Flowerdew et al. (2010, 2012) were the first to apply the EPS for operational surge prediction.

Another option is the combination of different operational models, with different characteristics, forcings and even physics, but providing sea level forecasts at the same area (multimodel forecast). A multimodel storm surge forecast was first implemented in the North Sea by combining the storm surge forecasts from different countries in the region in 2008. The system included the use of the Bayesian model average (BMA) statistical technique for the validation of the different members and generations of a combined improved prediction with a confidence interval (Beckers et al., 2008). This was the methodology tested first by Puertos del Estado in 2008, for the Spanish coast (Pérez-Gómez et al., 2012), combining in this case the output of an existing storm surge forecasting system (Nivmar; see Sect. 4.1.4) and circulation (baroclinic) models at that time already operating in the region. Today this multimodel forecast is operational at Puertos del Estado and combines Nivmar with the CMEMS regional operational models: IBI-MFC (Sotillo et al., 2015) and MED-MFC (Clementi et al., 2019). A first deterministic forecast is provided by the old Nivmar solution early in the morning every day. When later available, the CMEMS forecasts are integrated with the tide gauge data and, by means of the Bayesian model average (BMA) technique, a probabilistic forecast band is generated for each harbor (Pérez-González et al., 2017, 2019) (Fig. 3). A multimodel ensemble forecasting system has been recently developed for the Adriatic Sea combining 10 models predicting sea level height (either storm surge or total water level) and 9 predicting wave characteristics (Ferrarin et al., 2020). Other examples of this technique can be found for New York and the North Sea by Di Liberto et al. (2011) and Siek and Solomatine (2011), respectively. Recently, ensemble forecasting capabilities have also been recently explored for the prediction of meteotsunamis in the Balearic Islands (Mourre et al., 2021), showing an interesting potential to quantify the uncertainties associated with the predictions.

Storm surge ensemble prediction has been used to forecast sea level in Venice by Mel and Lionello (2014a). They used a 50 member ensemble to simulate 10 events showing that EPS slightly increases the accuracy of the prediction with respect to the deterministic forecast and that the probability distribution of maximum sea level produced by the EPS is acceptably realistic. They also showed that the storm surge peaks correspond to maxima of uncertainty and that the uncertainty of such maxima increases linearly with the forecast range. The same procedure was used for the simulation of the operational forecast practice for a 3 month long period (fall 2010) by Mel and Lionello (2014b).

Results have shown that uncertainty for short and long lead times of the forecast is mainly caused by the uncertainty of the initial condition and of the meteorological forcing, respectively. The probability forecast based on this ensemble technique has a clear skill in predicting the actual probability distribution of sea level. A computationally cheap alternative, called ensemble dressing method, has been proposed by Mel and Lionello (2016). It replaces the explicit computation of uncertainty by ensemble forecast with an empirical estimate. Instead of performing multiple forecasts, the procedure “dresses” the forecast of sea level with an error distribution form, which includes a dependence of the uncertainty on surge level and lead time, on the one hand, and of the uncertainty on the meteorological forcing, on the other hand. It is shown that this computationally cheap alternative provides acceptably realistic results.

5.6 Some examples of forecasting past storm surge events in Venice

Due to the crucial effect of climate changes, in the last century the city of Venice faced an increase in frequency and intensity of flooding events that periodically submerge parts of the old city center (Lionello et al., 2021a). The highest water level occurred in 1966 (194 cm over datum; see Fig. 2 for reference) followed by two more recent events in October 2018 (156 cm, Cavaleri et al., 2019) and in November 2019 (189 cm; Cavaleri et al., 2020), the latter much worse but the former potentially more dangerous (Morucci et al., 2020). Figure 2 shows the height of the floods and the datum the water levels refer to. According to Lionello et al. (2021b) the relative extreme sea level is composed of the contribution of various factors: astronomical tide, seiche, storm surge, long-lasting sea level anomalies due to planetary atmospheric waves (PAWs), meteotsunamis, wind setup within the lagoon, inter-decadal, interannual and seasonal (IDAS) sea level variability, and relative sea level rise. The combination of storm surge, meteotsunamis and PAW surge represents the direct action of the meteorological forcing on extreme sea levels, and it is collectively termed surge.

In 1966, the astronomical tide at the nominal time of the peak was at its minimum (−10 cm) and the peak sea level was due to an exceptional direct meteorological contribution (143 cm, Table 1 in Lionello et al., 2021b), mostly attributed to storm surge induced by a strong and persisting southerly wind over the whole Adriatic Sea. It was also extremely long in duration: for 22 h the level remained over 110 cm, and the surge was over 100 cm for more than 10 h and over 50 cm for about 40 h (De Zolt et al., 2006; Trincardi et al., 2016). The event of November 2019 represents the second higher storm surge, following the widespread flood event of 1966. De Zolt et al. (2006) and Roland et al. (2009) simulated the 1966 event with coupled wave–current models revealing the good accuracy of the model in the reproduction of the sea level in the northern Adriatic Sea and in Venice.

As for the 1966 case, the event of 29 October 2018 was due to a low-pressure system in the western Mediterranean Sea and an intense southeastern sirocco wind blowing for many hours along the Adriatic Sea. It showed a maximum surge contribution of 117 cm at 19:25 UTC (mostly due to storm surge and PAW surge) that happened during the minimum of astronomical tide. The development of the general meteorological pattern during the storm was forecasted well by the meteorological models (Fig. 8) with a resulting good predictability of the peak sea level in Venice some days ahead (Cavaleri et al., 2019; Ferrarin et al., 2020).

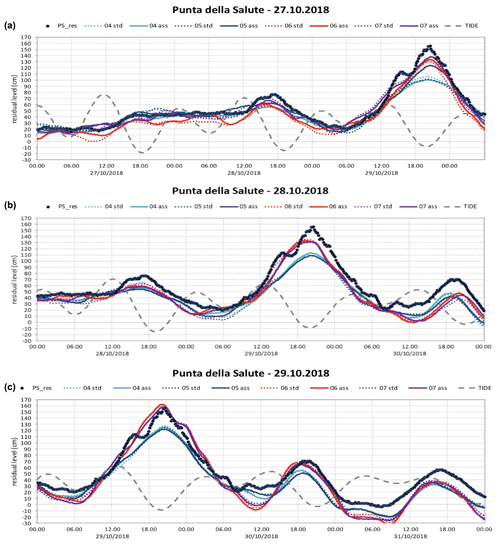
Figure 8 Forecast of the storm event – 29 October 2018 (“Vaia Storm”). Results are shown from various versions of the model running at ISPRA. The observed residual is given with black dots. (a) Forecast 3 d before the event, (b) 2 d and (c) 1 d.

The 12 November 2019 exceptional event was due to the combined effect of many meteorological forcings: the unusual high level of the Mediterranean Sea in November, reflecting an anomalous general atmospheric depression over the basin; a deep low-pressure system over the central-southern Tyrrhenian Sea that generated strong sirocco (southeasterly) winds along the main axis of the Adriatic Sea; a small-scale atmospheric pressure minimum developed over the northern Adriatic and moved rapidly northward along the Italian coast; and very strong winds over the Lagoon of Venice, which led to a rise in water levels and damage to the historic city (Cavaleri et al., 2020; Ferrarin et al., 2021). The peak of the meteorological contribution (100 cm) happened during the maximum of the astronomical tide with the disastrous effects of a total sea level of 189 cm. This event was strongly underestimated by all operational ocean forecasting systems. Such underestimation was mostly due to the uncertainties related to the reproduction of the intensity and path of the small-scale cyclone traveling in the northern Adriatic Sea generating the meteotsunami along the coast and local setup within the lagoon. Ferrarin et al. (2021) demonstrated that a relatively small error in the meteorological forecast (cyclone trajectory misplaced of about 10–20 km) may produce a relevant error in the sea level prediction in Venice which relies on accurate small-scale meteorological forcing.

The comparison between the mentioned events shows the important role played by the strength and timing of the different meteorological components of the sea level. The low-frequency meteorological components, i.e., interannual, seasonal and PAW oscillations, have minimal variations over a few days and can be easily considered in short-term sea level forecasts using near-real-time observations. The predictability of extreme high sea levels in Venice, therefore, resides in the model's capacity to reproduce storm surges, seiches and high-frequency oscillations (e.g., meteotsunamis). As discussed above for the 1966 and 2018 events, the large-scale synoptic framework associated with important storm surge events is predictable several days in advance. Seiche oscillations can be correctly simulated in the Adriatic Sea, especially when applying data assimilation (Bajo et al., 2019). Instead, beta mesoscale phenomena are still not reproduced well by the commonly used low-resolution (>2 km) mesoscale models, and therefore their contribution to the sea level remains underestimated (Denamiel et al., 2019).

6 Discussion and conclusions

Predictions of sea level variations to inform marine and coastal environment risk management have always been difficult to provide, This includes the northern Adriatic Sea and in the Venice Lagoon where the well-known Acqua alta phenomenon and relative sea level rise lead to growing threats of flooding. Even though forecasting models may provide important information on the evolution of sea level due to storm surges, they are still imperfect, and uncertainty in the future evolution of events plays an important role in decision making (Coccia, 2011). In order to better account for uncertainty, one of the viable possibilities is the use of ensemble forecasting using multiple models. Using this technique an improved indication of the uncertainty of a storm surge forecast is possible. Information of this kind is important to alert the population about risks concerning the flooding of the city. However, an indication of uncertainty is one step, and the next step is the communication of this uncertainty to the population, which is a difficult task. The I-STORMS project has also elaborated on risk communication under uncertainty (Ferrarin et al., 2020).

Data assimilation also offers an important tool to be exploited for simulations of the Venice Lagoon. This technique has been shown to be very successful, especially for a near-future forecast (up to 2 d). However, even if in forecasts of a few hours the error can be kept quite low, this effect seems to vanish if results of longer forecasts are examined. It has been shown (Lionello et al., 2006) that the prediction of the northern Adriatic storm surge can be improved by adopting a suitable data assimilation procedure. Bajo et al. (2019) have shown that assimilation of data from many sea level stations can improve the simulation of the timing of seiches in the Adriatic Basin and therefore correct the initial condition of this phenomenon. A further potential improvement could be assimilation of altimeter data, especially if in the future their temporal frequency and their resolution near coastal zones will improve (Bajo et al., 2017; De Biasio et al., 2016, 2017).

Another possibility is the combination of deterministic methods (that allows for forecasting periods of days) with statistical methods that are stronger in the short range forecasting. The idea is to statistically correct the results from deterministic models with statistical methods such as neural networks (Bajo and Umgiesser, 2010) or local Kalman filters (Bajo, 2020). Results have shown improvements in the quality of the forecasts except for those events that are outside the statistical samples and that are often wrongly interpreted by the method and show worse skills.

It is worth noting that the timing error (even of 1 h) of the meteorological forecasts may have dramatic impacts on the forecasted overall sea level because of the combination of surge and tide. Ensemble forecasts could be a solution providing the statistical distribution of the combined possibilities (Cavaleri et al., 2019).

Multimodel forecasts are another way to go forward. At CPSM a variety of models (deterministic and statistical) are running (Canestrelli and Pastore, 2000), and these model results can be used to provide a more reliable estimation of the future water level. This technique can be especially useful to give more weight to models that are better estimators under special conditions, where other models are less reliable.

The concept of predictive probability is crucial, and it is defined as the probability that an event will occur at a certain time in the future, conditional on prior observations and all the information available at the time of the forecast. Krzysztofowicz (1999) suggests that prior information can be encapsulated into one or more model forecasts. In other words, the decision-triggering threshold will not be based on different sea level thresholds (warning level, alert level, flooding level) but rather on different probabilities of a threshold being exceeded (Coccia, 2011).

In this framework, the model conditional processor (MCP-MT) has been implemented in its test configuration as hindcasting on Venice–Punta della Salute historical time series. It has been applied in a multimodel and multitemporal form to the Acqua alta forecast in the Venice Lagoon in order both to assess the predictive probability of threshold exceedance within a given time horizon and to estimate the expected time of occurrence of a given future event.

A quantitative comparison between all the storm surge models running in the Adriatic Sea is still lacking. The forecast error by the SHYFEM model running at CPSM was 5 cm for normal weather conditions (Zampato et al., 2016). This error clearly increased in situations of severe weather conditions and storm surge. The other study that used the input of more forecast models was the I-STORMS project that used multimodel analysis (Ferrarin et al., 2020). This application showed that the ensemble mean of the various models was a good indicator of the water level observations.

A good and reliable forecast is also required by the consortium that operates the mobile barriers (MOSE) at the inlets that are currently in a pre-operational phase. In October 2020, the barriers had already been closed three times, and in these cases they were able to protect the city from flooding. Complete operational functioning of the MOSE is estimated for the end of 2021. This analysis considers the preliminary results from these three closures. As can be seen (Fig. 2 in Lionello et al., 2021a), on 15 October 2020, a strong setup inside the lagoon happened, and the water level difference between the northern and southern lagoon exceeded 40 cm. A good forecast is needed for these situations in order to identify the best time for closing the barriers. Late closure may avoid flooding at Venice, but the city of Chioggia at the southern end of the lagoon could still experience flooding.

Once the MOSE is fully functional, a reliable forecast is needed in order to satisfy the various stakeholder needs. It is important to understand that the decision to close the lagoon is taken based on the forecast of the water level, wind and rain 4–6 h before the event (Consorzio Venezia Nuova, 2005). Once the decision has been made to close, a water level is identified that depends on the meteorological conditions (wind and rain). Once this level has been reached the barriers will be closed. It is therefore the forecast that in the end will decide if the MOSE will be operated or not. And this makes the operational forecasting of paramount importance for the lagoon and the city of Venice (Umgiesser, 2020).

The port wants to minimize closures to avoid interruption of ship passage and the maritime traffic and so wants to avoid forecasts that are too high. In contrast, shop keepers want to make absolutely sure that high water will not flood their shops and restaurants and want to avoid missed closures because a forecast was too low. A 10 cm forecast error matters here as a forecast 105 cm water level (for which the MOSE will not be activated) versus an actual 115 cm measured water level could lead to flooding in Venice. Hotel owners fear a water level forecast that is too high as reservations may be canceled due to these alarms.

Hence, reliable water level forecasting is essential in Venice. Operational systems are in place all around Europe that show the state of the art that Venice should strive to achieve in order to protect its inhabitants, warn them of adverse marine conditions, allow for safe operation of the MOSE mobile barriers and provide good service to all stakeholders. Only time will show if the scientific community is able to provide such a system that allows Venice to continue to remain one of the most beautiful and visited cities in the world.

As shown in the assessment above, there are many operational systems providing storm surge forecasts in Venice. Here we provide recommendations that could lead to significant improvements in the forecast systems and that should be tested and potentially implemented for Venice.

1. Improve meteorological forecasts. This is probably the most important action to improve water level forecasts. Wind fields from ECMWF are probably the most reliable source, but in some cases they are too coarse to resolve small-scale features both in time and space. Other models (COSMO-I, BOLAM, Moloch) provide higher spatial resolution and might resolve these small-scale processes, but assimilation is presently missing for these models. Satellites can correct wind fields with scatterometer data.

2. Develop ensemble forecasting. These are extremely useful as they allow for the quantification of uncertainty. Dealing with uncertainty is of paramount interest in the forecasting business because it allows us to alert the population of possible disaster and to make decisions based on this uncertainty in the operation of the MOSE.

3. Assimilation of water level measurements. This will improve initial conditions, which is especially important for forecasting seiches that are important contributors to high water levels in the Adriatic Sea. Continuous assimilation of tide gauge data will improve short-range forecasts, which is especially important for the operation of the MOSE, which needs a precise forecast some hours (4–6 h) ahead of the water level maximum.

4. Develop a multimodel approach. The availability of multiple (independent) models for Venice facilitates a multimodel approach. This would allow for a rating of the models and an identification of the most appropriate system for different weather conditions.

Implementing all these recommendations is feasible and would improve the art of storm surge forecasting and the control of the MOSE barriers, as well as facilitate better adaptation to floods in the Venice Lagoon over the coming decades.