Cascade effect of rock bridge failure in planar rock slides: numerical test with a distinct element code

Plane failure along inclined joints is a classical mechanism involved in rock slope movements. It is known that the number, size and position of rock bridges along the potential failure plane are of prime importance when assessing slope stability. However, the rock bridge failure phenomenology itself has not been comprehensively understood up to now. In this study, the propagation cascade effect of rock bridge failure leading to catastrophic block sliding is studied and the influence of rock bridge position in regard to the rockfall failure mode (shear or tension) is highlighted. Numerical modelling using the distinct element method (UDEC, Itasca) is undertaken in order to assess the stability of a 10 m³ rock block lying on an inclined joint with a dip angle of 40 or 80^∘. The progressive failure of rock bridges is simulated assuming a Mohr–Coulomb failure criterion and considering stress transfers from a failed bridge to the surrounding ones. Two phases of the failure process are described: (1) a stable propagation of the rock bridge failures along the joint and (2) an unstable propagation (cascade effect) of rock bridge failures until the block slides down. Additionally, the most critical position of rock bridges has been identified. It corresponds to the top of the rock block for a dip angle of 40^∘ and to its bottom for an angle of 80^∘.

1 Introduction

Rockfall hazard is defined as “the probability of occurrence of a potentially damaging rockfall within a given area and in a given period of time” (Varnes, 1984). The damaging phenomenon generally results from the failure of weakness planes and the fall of one or several rock blocks down to the target area (Corominas et al., 2005). In other words, the rockfall hazard can be defined as the failure probability multiplied by the probability of propagation. While different probabilistic methods exist to calculate the probability of propagation (Guzzetti et al., 2002; Jaboyedoff et al., 2005; Bourrier et al., 2009; Levy et al., 2018), the failure probability is more complex to assess. Methods mainly based on expert judgement (Delonca et al., 2016), empirical methods (Jaboyedoff et al., 2005; Mazzoccola and Hudson, 1996; Dussauge-Peisser et al., 2002) and kinematic analysis (Pappalardo and Mineo, 2015; Mineo et al., 2018; Kromer et al., 2018) have mostly been used to date, but they do not consider the failure mechanism leading to the triggering of an event. Statistical analysis (Chau et al., 2003; Coe et al., 2004; Delonca et al., 2014) can also be used to approach the temporality of the hazard but presents the same restriction as the other methods. However, the understanding of the failure process of weakness planes is a major issue for risk assessment as it is responsible for the generation of a rockfall and defines its time of occurrence.

The main parameter controlling the resistance of a rock joint, and therefore the failure mechanism, is rock bridges (Dershowitz and Einstein, 1988; Dershowitz and Herda, 1992), defined as areas of intact unfractured rock where discontinuities have yet to propagate (de Vilder et al., 2017). Therefore, intact rock bridges could be defined as portions of intact rock separating joint surfaces (Elmo et al., 2018). Along the rock joint, the following are accounted for: (1) rock bridge areas (intact rock), (2) open-crack areas, and (3) areas where rock bridges have already failed (“broken rock bridges”) and where the joint surfaces are in frictional contact. Figure 1a presents a diagram of a discontinuity along which these three elements can be observed. The photo (Fig. 1b) was taken after the fall of an unstable block. The open-crack areas as well as the broken rock bridges are visible. No rock bridges are observed in this photo; it is assumed that after the occurrence of the fall, there is no remaining rock bridge along the former joint. Before the fall of the unstable block, it can be expected that the broken rock bridge areas identified in the photo were in fact composed of intact rock and fresh intact rock rupture (broken rock bridges).

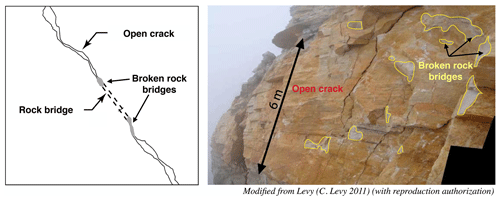
Figure 1 Left: definition of rock bridges; right: open-crack and failed-rock-bridge areas. Modified from Levy (2011) (with reproduction authorization).

Conceptually, the location and distribution of rock bridges along a scar is supposed to control the failure mode (Tuckey and Stead, 2016; Stock et al., 2011). For example, the presence of rock bridges over as little as just a few percent of the detachment surface is known to significantly increase the factor of safety by increasing apparent overall cohesion of a rock joint (Matasci et al., 2015; Tuckey and Stead, 2016). Moreover, the location of a rock bridge is important for understanding if rockfall fails in tension or shear, as it can form a pivot point about which the failing rock block is able to potentially rotate and fail in tension (Stock et al., 2012; Bonilla–Sierra et al., 2015).

Moreover, various authors (Frayssines and Hantz, 2009; Matasci et al., 2015; Tuckey and Stead, 2016) have shown the very low proportion of rock bridges existing before the fall (between only 0.2 % to 5 % of the detachment surface). In particular, Frayssines and Hantz (2009) have shown that rock blocks can remain stable for a long time thanks to rock bridges and that the rock bridge proportion in the failure surfaces in these rock blocks may be very small (less than 1 % of the joint surface).

Previous research has shown that failure occurs through progressive fracturing of intact rock bridges, in a process termed step-path failure (Kemeny, 2005; Eberhardt et al., 2004; Scavia, 1995; Brideau et al., 2009) that may in some cases be compared to a cascade-effect failure which can cause rock bridges to fail like dominoes along sloping channels (Bonilla–Sierra et al., 2015; Harthong et al., 2012; Zhou et al., 2015). The contribution of rock bridges has been implemented in numerical models of rock slope stability using apparent cohesion (Eberhardt et al., 2004; Fischer et al., 2010; Gischig et al., 2011) or areas of intact rock (Stead et al., 2006; Sturzenegger and Stead, 2009; Agliardi et al., 2013; Paronuzzi et al., 2016). These previous studies aimed to analyse the failure modes and evolution of the rock bridges. However, they do not analyse the phenomenology of the rock bridge failure's propagation.

This paper studies (1) the phenomenology of the rock bridge failure propagation and (2) the influence of the rock bridges' location, using a simple two-dimensional numerical model. The paper is structured as follows. In Sect. 2, the numerical modelling process considered in the study is presented: the geometry, characteristics and procedure of the models are defined. In Sect. 3, the results of our 2D simulations are shown: stress redistribution along the joint after reducing the proportion of rock bridges is observed leading to the highlighting of the rock bridge failure phenomenology. In Sect. 4, the results are discussed and the influence of the rock bridge location and the role of the tensile shear strength on the phenomenology is evaluated. Finally, the conclusions are presented in Sect. 5.

2 Numerical modelling of the rock bridge failure propagation

The simulations were undertaken with UDEC (Universal Distinct Element Code), a two-dimensional distinct element code developed by Cundall (Cundall, 1980) that can model the mechanical, hydraulic and thermal behaviour of a fractured rock mass. This code has successfully been used in past studies to model the behaviour of rock discontinuities (Gu and Ozbay, 2014; Jiang et al., 2006; He et al., 2018; Roslan et al., 2020). It has a scripting language embedded within it, FISH, that allows the user to create new model variables, customize functionality and interact with the model. This functionality has been decisive in the selection of the appropriate numerical tools, as it allows the rock bridge areas, open-crack areas and broken rock bridge areas to be defined.

UDEC models the rock medium as a collection of blocks separated by joints regarded as smooth planes. The blocks can be rigid or deformable. They can mechanically interact through discontinuities. A distinction is made between data relating to blocks – nodes and corners – and data relating to discontinuities – contacts and domains. The characteristics of the discontinuities are defined through the contacts.

In order to study the phenomenology of the failure, an idealized two-dimensional numerical model has been defined. Therefore, there is no consideration of water infiltration, thermal implication or icing impact on the discontinuity at this stage, even though these phenomena may act as preparatory or triggering factors.

2.1 Geometry and definition of the two models

Two numerical models were built. Both models describe a potential plane failure along a pre-existing joint. Model 1 presents a joint with an 80^∘ dip angle, while model 2 presents a dip angle of 40^∘. These two models have been proposed in agreement with the objective of this work: to study the phenomenology of the rock bridge failure. To do so, a steeply dipping rock wall and a gentle slope are considered. These two cases are defined in the function of the expected rockfall failure mode (shear or tension). It is expected that in the case of a steep slope, a tensile and/or shear failure mode will be observed. Indeed, authors (Stock et al., 2012; Bonilla–Sierra et al., 2015) have highlighted that the location of a rock bridge is important for understanding if rockfall fails in tension or shear, as they can form a pivot point about which the failing rock block is able to potentially rotate and fail in tension. In the case of a gentle slope, only a shear failure mode is expected. Therefore, it is possible to assess the influence of the location of the rock bridges as well as the initial morphology of the rock wall.

The geometry of the two models is presented in Fig. 2. The rock block presents a length of 6 m and a width of 1.5 m, leading to a total area of 9 m², which, considering an out-of-plane thickness of 1 m, is also the volume (in m³) defined as “particularly dangerous for linear infrastructures and private residence” (Effendiantz et al., 2004). The total height of the model is 12 m. In practice, the geometry of the two models is the same; only the inclination of gravity is changed (angle α in Fig. 2).

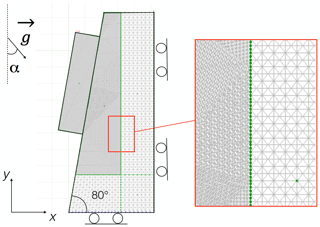
Figure 2 Geometry of both models. α is equal to 0^∘ for model 1 (slope angle 80^∘) and is equal to 40^∘ for model 2 (slope angle 40^∘).

During the meshing process, 128 contacts were created along the joint located between the block and the underlaying rock mass. Each contact can be defined by its coordinates in x and y (altitude). The behaviour of the rock joint is defined by the mechanical properties implemented for each individual contact (presented in Sect. 2.2). As only contacts belonging to regions can be modified in UDEC, the rock joint was then divided into 100 regions of the same length that can represent either “rock bridges” or “open-crack” areas. This division has been undertaken using the FISH language. Each region can therefore include one or two contacts. During the computation process, the local stress distribution along the joint can lead to the rupture of some rock bridge regions, then becoming a region of “failed rock bridges” that behaves as an open-crack area. This phenomenon progressively increases the number of open-crack regions along the joint.

Once the models are meshed, they are loaded only by gravity to evaluate the initial local state of stress along the joint.

Table 1 Mechanical properties of the rock mass based on Urgonian limestone.

Table 2 Elastic mechanical properties of typical rock joints in Urgonian limestone.

2.2 Mechanical parameters

An elastic model is assumed for the rock blocks, and a Mohr–Coulomb elasto-plastic model is assumed for the rock joint (contacts along the joint). A contact exhibits a shear failure mode when the local stress reaches the Mohr–Coulomb failure criterion and a tensile failure mode when its tensile normal stress becomes equal to the assigned tensile strength.

The mechanical properties of the rock blocks (Table 1) were defined based on a literature review of a common limestone in the French Alps (“Urgonian” limestone) (Frayssines, 2005). This limestone has been considered the reference in this study as it forms high cliffs in south-eastern France, where present traces of failed rock bridges are widely documented (Frayssines and Hantz, 2006).

Along the rock joint, three types of contact are considered:

1. rock bridge (RB) contacts which behave elastically with the same characteristics as the intact rock; to determine the normal and shear stiffness of the rock bridges, a centimetric opening of the joint has been considered;

2. open crack (OC) contacts which represent an absence of contact along the joint and behave in a perfectly plastic way;

3. rock bridge failed (RBF) contacts that failed due to stress transfers along the joint and behave in a perfectly plastic way after their rupture.

RB and RBF contacts have the same mechanical elastic parameters; the only difference between them comes from the fact that RB contacts present a purely elastic behaviour, while RBF contacts present an elasto-plastic behaviour.

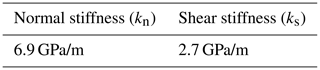
The normal and shear stiffnesses of RB and RBF contacts have been defined based on a literature review of Urgonian limestone fractures (Frayssines, 2005). They are presented in Table 2.

The failure envelope properties of RB and RBF contacts (cohesion, friction angle and tensile strength) were defined following a step-by-step procedure. As the objective of the numerical modelling is to study the phenomenology of the rock bridge failure propagation, the failure criterion has to be close enough to the initial stresses along the joint, when considering only RB contacts. Therefore, during a first step, the distribution of stresses has been evaluated and compared to “classical” failure criteria provided in the literature (Frayssines, 2005). Then, in a second step, the characteristics of the criteria have been decreased to fit the objective. The classical values and the ones defined with this procedure for the RB and RBF contacts are presented in Table 3. Even if the values considered in the study are much lower than those found in literature, it is assumed that the failure propagation phenomenology will be the same as in reality. In the case of OC contacts all the values are taken as equal to 0 (Table 3) to ensure the phenomenology is identified and not polluted by other behaviour.

Table 3 Shear strength characteristics of RB, RBF and OC areas along the joint for both model 1 and model 2.

2.3 Modelling protocol

The modelling protocol proposed to study the rock bridge failure phenomenology is based on the following steps. It is summarized in Fig. 3.

1. All the 100 regions and so the 128 contacts of the rock joint are initially considered rock bridge (RB). In other words, 100 % of the rock joint is defined as RB. The model is run to equilibrium under gravitational loading. This corresponds to the initial stage (Step 0).

2. Disturbances are introduced into the system. To do so, selected regions along the joint are transformed into open crack (OC) regions using FISH language (steps 1 to n, with n being the maximum number of steps before the block does not stabilize anymore). These regions can be selected randomly considering a uniform distribution or chosen intentionally by the user at specific locations. During these steps, X % of the rock joint is defined as OC and (100−X) % is defined as RB. At each of these calculating steps, the introduction of disturbance induces a stress redistribution along the joint, which leads to the failure of some rock bridges, then converted into RBF. This introduction of open-crack areas simulates a virtual time as it represents the aperture of a crack and the propagation of the discontinuity through the rock bridges. It simulates the joint alteration that can be caused by, for example, water, freeze–thaw, root growth or another external parameter.

3. New open cracks are introduced stepwise (Step n) until the block does not stabilize anymore.

At each step of the modelling process, the following data are recorded:

• the normal and shear stresses at each contact along the rock joint,

• the number of contacts considered open crack (OC),

• the number of considered failed contacts (open crack and rock bridges that failed due to the increased of the stresses, OC + RBF).

Considering this modelling protocol, different scenarios have been considered:

• Scenario 1. The propagation of an open fracture was simulated. A 60 cm long area of open crack (OC) (10 % of the rock joint length) was initially defined, located at the lower part of the rock joint (30 cm from point A) for both model 1 and model 2. Then, a progressive propagation of the open crack upwards was simulated (in this part of the study, contacts are not randomly modified from RB to OC.) At each step, the open-crack area is enlarged. For model 1, an increase of 2 % of the rock joint length is imposed (12 cm long area of open crack). For model 2, an increase of 10 % of the rock joint length is imposed (60 cm long area of open crack).

• Scenario 2. The influence of rock bridge location along the joint was studied. (1) Open cracks are introduced into the upper part of the rock joint (30 cm from point B), and (2) open cracks are introduced into the lower part of the joint (30 cm from point A). This protocol was followed for both dip angles – 40 and 80^∘. For model 1, an increase of 2 % in the rock joint length is imposed at each step (12 cm long area of open crack). For model 2, an increase of 10 % in the rock joint length is imposed at each step (60 cm long area of open crack).

• Scenario 3. A total of 40 simulations with a random introduction of new OC contacts were carried out to statistically compare results. For model 1, an increase of 2 % in the rock joint length is imposed at each step (12 cm long area of open crack). For model 2, an increase of 10 % in the rock joint length is imposed at each step (60 cm long area of open crack).

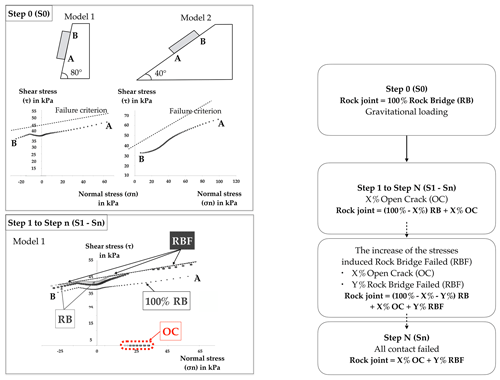
Figure 3 Modelling process. Step 0: 100 % of the rock joint is defined as rock bridge (RB). Step 1 to Step n: introduction of open crack (OC) contacts along the joint. From Step 2 to Step n, in the graph of model 1 the increase in shear stresses due to the introduction of OC contacts can be introduced.

It can be noted that the numerical model has been validated by comparing the stresses evaluated by a simple theoretical analytical calculation of a block laying on an inclined plane by numerical shear and normal stress values.

3 Results

3.1 Stress transfer and RB failure induced by the introduction of new OC contacts

To study the phenomenology of rock bridge failure (RB and RBF), the evolution of normal and shear stresses along the joint during the stepwise introduction of open-crack (OC) contacts has been analysed in detail. To do so, Scenario 1 was considered.

Figure 4 presents, for both model 1 and model 2, the distribution of the normal and shear stresses along the rock joint at different equilibrium steps 0 to n.

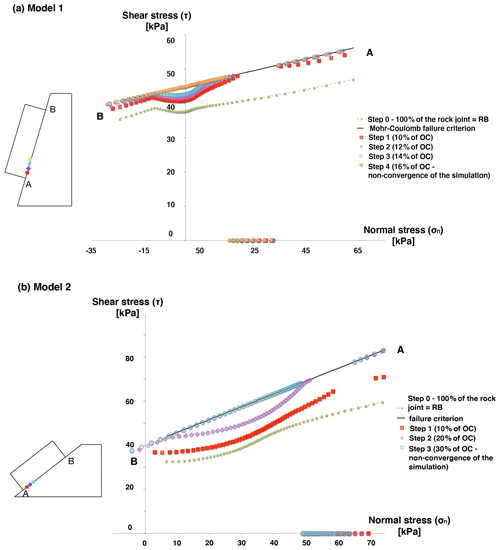
Figure 4 Distribution of the normal and shear stresses for models 1 and 2 considering Scenario 1. The different steps represent the introduction of new OC contacts until the model does not converge anymore. The points on the x axis have normal stress but no shear stress as if the friction angle were zero. Each colour between point A and point B in the model corresponds to the step presented in the graph.

First, the distribution of the stresses along the rock joint is presented at Step 0, considering that the joint is only composed of rock bridges. In the case of model 1 (slope of 80^∘), tension (σ_n<0) is observed at the upper part of the block (near point B in Fig. 4a). In model 2 (slope of 40^∘), no tension is observed.

For both models, at Step 1, 10 % of the rock joint is intentionally modified from RB to OC contacts. In both models, the introduction of OC contacts results in a general increase in the shear stresses along the rock joint, with a stronger increase in these shear stresses in the vicinity of the OC area. This increase in the shear stresses brings the joint closer to the failure criterion not only in the vicinity of the OC area but also elsewhere, in particular at contacts located in the upper part of the rock joint (point B in Fig. 4). The normal stresses slightly vary during this first stage.

During each subsequent Step 2 to n, 2 % of additional contacts are modified from RB to OC in model 1 and 10 % of additional contacts are modified from RB to OC in model 2. These modifications induce the failure of rock bridges directly near the OC contacts by increasing the shear stresses along the rock joint, but the model reaches a mechanical equilibrium at the end of each step. There is also an increase in the normal stresses along the rock joint. This phenomenon continues until no mechanical equilibrium is reached anymore, which is associated with the downward sliding of the block (simultaneous failure of all the contacts).

The non-convergence of the model occurs when 16 % of the contacts are converted to OC in the case of model 1 and 30 % for model 2.

These results highlighted two phases during the rock bridge failure: a first phase during which only the intentionally created open-crack contacts are observed and a second phase during which the stress transfers induce the additional failure of rock bridges. In other words, in a first phase, the crack enlarges without inducing rupture elsewhere, and in a second phase the open crack reaches a state where rupture self-propagation starts until the block slides along the joint.

3.2 Rock bridge cascading failure phenomenology

To study more specifically rock bridge cascading failure phenomenology, Scenario 2 was considered. Results are presented in Fig. 5 in terms of the proportion of so-called “failed contacts” (OC + RBF) versus the proportion of OC contacts along the joint. For both dip angles, there is a first linear phase during which the only failed contacts are the intentionally introduced OC ones. During this first phase, the block remains stable; i.e. a mechanical equilibrium is reached after each introduction of new OC contacts. Then, in a second phase, the redistribution of stresses caused by the introduction of new OC contacts induces the rupture of some RB contacts, which are converted into RBF contacts. During this second phase, even a small increase in the proportion of OC contacts leads to the rupture of additional rock bridges, which highlights the cascading failure phenomenology affecting the rock bridges. The slope of the linear regression in this second phase is around 10 in the case of model 1 and 5 in the case of model 2, meaning that the introduction of 1 OC contact leads to the failure of 10 RB contacts for model 1 and 5 RB contacts for model 2. This second phase starts for approximately 8 % of the rock joint defined as OC for model 1 and 23 % for model 2. The start of this phase differs slightly depending on the position of the RB and OC along the joint.

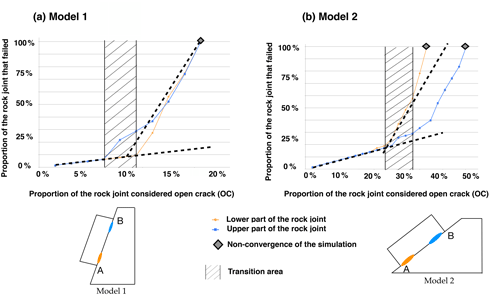
Figure 5 Propagation of rock bridge failure for models 1 and 2 considering Scenario 2. Intentionally introduced OC contacts are located in the upper part of the joint (blue curve) or in the lower part of the joint (orange curve). The proportion of the rock joint that failed is defined as a ratio between the number of failed contacts (OC + RBF) and the total number of contacts (OC + RB + RBF).

The non-convergence of the model starts when OC contacts represent 19 and 35 % of the joint for models 1 and 2 respectively.

Based on these preliminary results, Scenario 3 was considered. Results are shown in Fig. 6.

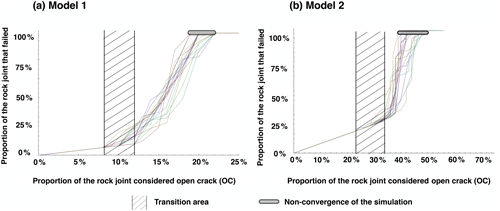
Figure 6 Propagation of rock bridge failure for models 1 and 2 considering Scenario 3 in the case of randomly introduced new OC contacts.

For both model 1 and model 2, two phases in the propagation of the rupture may be identified for all the simulations carried out. In the case of model 1, the second phase starts for an average of (10±2) % of the rock joint defined as OC, and the slide of the block (non-convergence of the simulation) occurs for an average proportion of (20±1.5) %. Regarding model 2, the second phase begins for an average of (29±5) % of the rock joint defined as OC, and the slide of the block occurs for an average proportion of (44±5) %. The transition area (Figs. 5–7) has first been identified in Fig. 6 and reported in Figs. 5–7. It corresponds to the transition between both phases in the propagation of the rock bridge failure and is due to the difference in the location of the RB.

Figure 7 Displacement of point C (in metres) with respect to the proportion of OC contacts along the joint, for models 1 and 2 considering Scenario 3. The transition zone presented here corresponds to the one defined previously (Sect. 3.2).

3.3 Block displacement with time

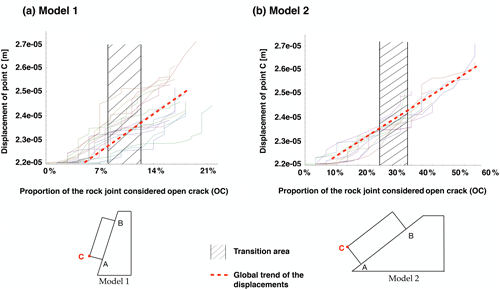
In order to check whether there is a correlation between the two phases of rock bridge failure and the displacement that can be monitored on a potentially unstable block, a tracking point (C), shown in Fig. 7, has been introduced. Such a point could easily be instrumented in the real case of motion tracking if displacements of the order of millimetres are observed before the failure of the block.

Scenario 3 was considered. The displacement of point C was studied versus the proportion of OC along the joint, which is a marker of “virtual time”. The movement is no longer recorded as soon as all the contacts have failed, because the computation does not converge anymore.

Figure 7 shows that there is only one phase when considering the displacement. Both phases identified previously cannot be observed through displacement. To be certain of this result, a smaller mesh has been defined, and the same results have been obtained.

4 Discussion

The results highlight that the rock bridge failure phenomenology presents two phases: a first phase during which only the intentionally created open-crack contacts are observed and a second phase during which stress transfers induce the additional failure of rock bridges. Based on these results, the influence of different parameters on this observed phenomenology was tested. The results are presented below.

4.1 Influence of OC location on the evolution of RBF with time

As highlighted by different authors (Tuckey and Stead, 2016; Stock et al., 2011), the location of the rock bridges has a strong impact on the stability of a potentially unstable block. To see whether our model leads to the same conclusion, the following protocol has been followed:

1. A number N of contacts is defined to be OC and randomly located along the joint. N is equal to 18 for model 1 (14 % of the joint) and to 46 for model 2 (36 % of the joint). These values were chosen for the model to be in the second phase, where the cascading failure phenomenology affecting the rock bridges is observed (Sect. 3.2). As seen previously, these proportions are sufficient to induce the additional RBF.

2. The number of considered failed contacts (OC + RBF) is determined.

3. The number of failed contacts is compared to the average altitude of the OC contact.

To maximize the number of data, Scenario 3 is run two times, and therefore 80 models are considered.

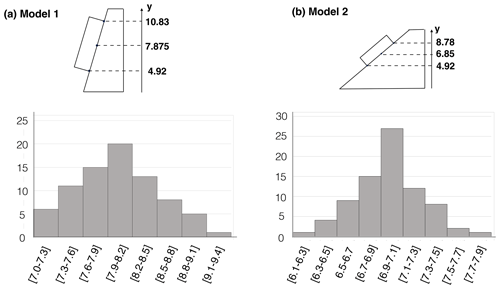
The results are presented in Fig. 8. The figure (top part) shows the values of the minimum, maximum and average contact altitude along the rock joint for both model 1 and model 2. It also shows (bottom part) the total number of considered failed contacts for a number N of contacts defined to be OC with respect to the average altitude of the OC contacts for both model 1 and model 2.

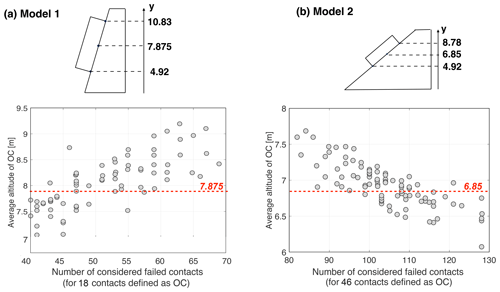
Figure 8 Number of considered failed contacts for a number N of contacts defined to be OC with respect to the average altitude (y coordinate) of the OC contacts, for models 1 and 2 considering Scenario 3 (run two times). N is equal to 18 and 46 for model 1 and 2 respectively.

Figure 8a presents the results of model 1. It highlights that there are a larger number of failed contacts (OC + RBF) when the OC contacts are localized on average in the upper part of the joint. Figure 8b shows that, for model 2, contrary to model 1, there are a larger number of failed contacts (OC + RBF) when the OC are localized on average in the lower part of the joint.

This difference highlighted between the two models can be explained by the distribution of the stresses along the joint.

1. In model 1, there is tension in the upper part of the rock joint (Fig. 4a) when considering 100 % of RB contacts. To the contrary, in model 2, there is no tension along the rock joint (Fig. 4b).

2. During the introduction of new OC contacts, the stresses increase along the entire rock joint and more specifically around the OC area. Therefore, the distance to the failure criterion must play an important role if it is assumed that the increase in stresses is made in a homogeneous way, which seems to be the case based on Fig. 4. For model 1, the distance to the criterion is the smallest in the upper part of the block and vice versa for model 2, which may explain the influence of the position of the open crack.

Figure 8 highlights the presence of the critical position of the OC area. Figure 9 presents the histogram of the average altitude of OC contacts. The critical position could be defined as the position where, for the same proportion of OC contacts, more RBF contacts will be generated than in any other position along the joint. In the case of model 1, the critical position of the open-crack area corresponds to the upper part of the joint (i.e. RB located preferentially in the lower part of the joint). To the contrary, for model 2, it is the OC area located in the lower part of the joint that corresponds to the critical position (RB located in the upper part of the joint). These results combined with geophysical-tool investigations (Stock et al., 2011; Matasci et al., 2015; Paronuzzi et al., 2016; Guerin et al., 2019; Frayssines and Hantz, 2006; Paronuzzi and Serafini, 2009; Spreafico et al., 2017) could allow the prioritization of the potentially unstable blocks.

Figure 9 Histogram of the average altitude (y coordinate) of the OC contacts, for models 1 and 2 considering Scenario 3 (run two times). N is equal to 18 and 46 for model 1 and 2 respectively.

4.2 Role of the tensile strength in the evolution of RBF with time

In the presented study, as the tensile strength is relatively high in comparison with the cohesion and the friction angle, only shear failure was observed, and no tensile failure was reported. Based on this observation, it is needed to study more specifically the role of tensile strength in the evolution of RBF with time. To do so, a new model 3 has been defined and run. It is based on model 1 (dip angle of 80^∘) as model 1 shows tension. In the new model, a tensile truncation was added to the Mohr–Coulomb failure criterion. The tensile strength (TS) has been taken as equal to the uniaxial compressive strength (UCS) value divided by 10 (UCS $/$ 10). The compressive strength is calculated according to Eq. (1).

$$\begin{array}{}\text{(1)}& \mathrm{UCS}={\displaystyle \frac{\mathrm{2}c\cos \mathit{\phi }}{\mathrm{1}-\sin \mathit{\phi }}},\end{array}$$

with c being the cohesion and ϕ the friction angle.

The mechanical characteristics of model 3 are listed in Table 4. The cohesion value has been increased in comparison to model 1 for numerical modelling requirements: when considering the same cohesion value, the model was not converging. The cohesion value has been increased until the model could be run.

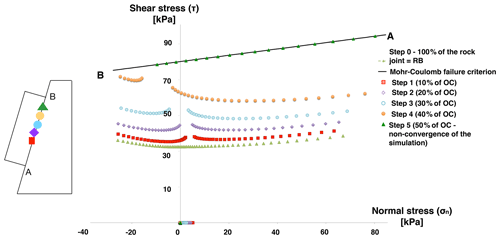
Figure 10 Distribution of the normal and tangential stresses in the plane of Mohr for model 3 considering Scenario 1. The various steps represent the introduction of 10 % of open-crack (OC) contacts each time, until the non-convergence of the model.

Table 4 Mechanical characteristics of rock bridges in model 3 used when studying the effect of tensile strength. The dip angle is equal to 80^∘.

^* As defined in model 1.

The results are presented in Fig. 10. The tensile truncation of the Mohr–Coulomb failure criterion results in tensile failure of 6 % of the joint at the initial Step 0 (eight contacts present a tensile normal stress that becomes equal to the assigned tensile strength). At each subsequent step, 10 % of additional OC contacts are introduced along the rock joint. Because the cohesion is 3 times higher than for model 1, the stresses along the joint are further away from the failure criterion of rupture than for model 1 (Fig. 10). As observed previously, the normal and shear stresses progressively increase. It can be noted, as for the previous models, there is a more significant increase in the shear stress in the vicinity of the OC area. Up to 40 % of the joint can be defined as OC area before the calculation does not converge anymore.

For model 3, the transition phase identified previously is comprised of between 40 % and 50 % of the rock joint defined as OC, while in model 1, it is comprised of between 10 % and 20 %. In other words, when increasing cohesion value, the proportion of open-crack area needs to be higher to reach the cascading failure affecting the rock bridges than when considering low cohesion values. It justifies that in reality, as the cohesion values of the rock bridges are 500 times higher than in the study presented in this paper, only a few portions of rock bridges allow a potentially instable block to be in place. The second phase observed in the paper occurs instants before the fall of the block.

This study shows that, when considering tensile failure through the tensile truncation of the Mohr–Coulomb failure criterion, a proportion of failed rock bridges comes from the tensile stresses along the joint. However, the same “bi-phase” propagation failure phenomenology was observed regardless of the comprehensive consideration of the tensile failure.

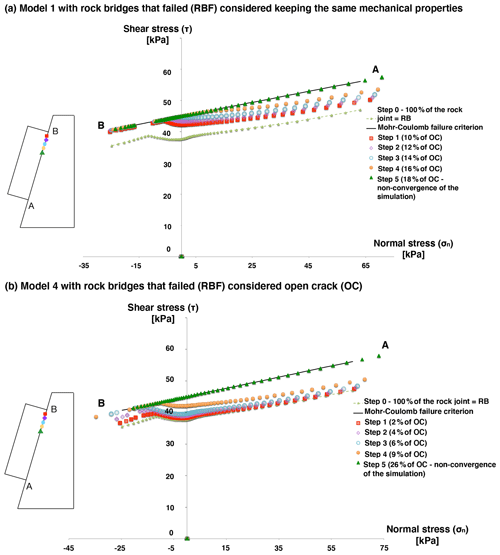
Figure 11 Normal and shear stress distribution for (a) model 1 in the case where three types of contact are considered (open crack (OC), rock bridge (RB), rock bridge that failed (RBF)) and (b) model 4 if the contacts defined as rock bridges that failed are automatically changed to open crack (OC) – Scenario 1.

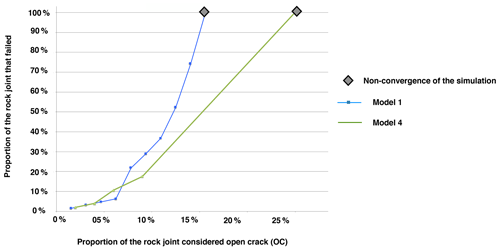
Figure 12 Propagation of rock bridge failure for (a) model 1 in the case where three types of contact are considered (open crack (OC), rock bridge (RB), rock bridge that failed (RBF)) and (b) model 4 if the contacts defined as rock bridges that failed are automatically changed to open crack (OC) – Scenario 2.

4.3 Influence of RBF shear strength on the results

In the modelling procedure presented in Sect. 2.3 and applied to models 1 to 3, the rock bridges that failed during the calculation (RBF) are considered to keep the same shear strength values as RB. This hypothesis has been made to consider asperity that can exist along areas of failed rock bridges. An alternate approach would be to consider that RBF contacts behave like OC contacts. This is discussed hereafter, by the mean of an additional model 4 comprising only two types of contact: RB and OC. RBF are considered to behave as OC. This model is based on model 1 (dip angle of 80^∘), to which it will be compared.

The new OC contacts will be introduced into the upper part of the joint as it has been highlighted that for model 1, there are a larger number of failed contacts (OC + RBF) when the OC contacts are localized on average in the upper part of the joint.

Figure 11 presents the distribution of stresses along the joint at different steps of computation for models 1 and 4. The first OC area is introduced into the upper part of the joint, 10 cm away from point B. It is observed, as previously, that there is a general increase in shear stresses and a very small increase in normal stresses. Model 1 stops converging when 18 % of the joint is defined as OC (Fig. 11a), which is in agreement with what was observed before. When considering 16 % of the joint defined as OC (last step before the model does not converge), there are 22 % failed contacts (OC + RBF). Model 4 stops converging for 26 % of OC (Fig. 11b). Therefore, considering two or three types of contact gives similar results. To test this theory, Fig. 12 presents the proportion of so-called failed contacts (OC + RBF) versus the proportion of OC contacts along the joint. It shows that the two phases highlighted previously are again identified. The main difference comes from the fact that considering only two types of contact, the first phase is smaller.

4.4 Influence of the rock bridges' mechanical properties

In this study, the choice has been made to consider much lower strength properties of the rock bridges than in reality (see Sect. 2.2), due to numerical restrictions. Indeed, it has been shown by various authors (Frayssines and Hantz, 2009; Matasci et al., 2015; Tuckey and Stead, 2016) that only a few percent of rock bridges along the detachment surface are enough to maintain a compartment in a stable state. This extremely low proportion of rock bridges brings modelling challenges, such as high stress concentration at rock bridges, that have yet to be overcome. From a numerical point of view, modelling less than 1 % of the joint as rock bridges would require an extremely dense meshing, due to the high stress concentration and stress gradients in the rock bridge areas. In order to answer the objective of this paper, which is to highlight the phenomenology of the rock bridge failure propagation and not to accurately represent rock bridge behaviour, the authors have considered that decreasing the mechanical properties of the rock bridges is an adequate way of answering the presented difficulty.

Despite the fact that low rock bridge mechanical properties are imposed by numerical modelling restrictions, it is essential to assess the influence of this choice. The authors feel confident in the proposed methodology as models have been realized with higher mechanical properties and have shown similar phenomenology. An example of this is model 3, which considers in particular a higher cohesion value (130 kPa for model 3 compared to 45 kPa for model 1). Moreover, as shown by previous research, the compartment instability occurs through progressive fracturing of intact rock bridges, in a process termed step-path failure (Kemeny, 2005; Eberhardt et al., 2004; Scavia, 1995; Brideau et al., 2009) that may in some cases be compared to a cascade-effect failure: they can fail like dominoes along sloping channels (Bonilla–Sierra, et al., 2015; Harthong et al., 2012; Zhou et al., 2015). The study presented in this paper corroborates the previously observed cascade-effect failure of rock bridges.

5 Conclusions

The work presented in this paper has allowed the phenomenology of rock bridge failure to be studied. It has shown that the rock bridge failure phenomenology can be associated with a cascade-effect failure (two phases in the failure propagation), which is consistent with previous research. This phenomenon can be explained by the increase in the shear stress in the vicinity of the open-crack areas, which can lead to the failure of the neighbouring rock bridges.

Moreover, it has been highlighted that the stress redistribution along the rock joint is directly related to the geometry and failure mode of the rock block: when considering a shear failure mode (sliding along a gentle slope), the increase in the shear stress is slower than when considering a tensile or shear failure mode along a steep slope. This observation can be directly related to the influence of the rock bridges' positions on the stability of the block. In the case of a steep slope, the critical position of the rock bridges corresponds to the lower part of the joint. To the contrary, for a gentle slope, it is the rock bridges located in the upper part of the joint that is critical. This result is consistent with previously published work (Tuckey and Stead, 2016; Stock et al., 2011).

These interesting results lead to a better understanding of the failure mechanism leading to the triggering of a rockfall. They help complement the current assessment methods of the failure probability of the rockfall hazard. In particular, they describe why it can be so challenging to assess the occurrence probability of such events and the temporal probability (Delonca et al., 2016).

Furthermore, the work presented in this paper has highlighted the importance of the rock bridge location and its assessment. Therefore, the use of geophysical investigations could allow the prioritization of the potentially unstable blocks. It is to be noted that the monitoring of displacements does not seem to be a good indicator to identify the two phases in the failure propagation and, therefore, to be able to anticipate or predict the acceleration of the rock bridge failure. Moreover, the monitored displacement in the models is of less than a hundredth of a millimetre, and this quantity is very difficult to monitor in the field.

Finally, while interesting results have been drawn and validated by previous work, additional work needs to be carried out and could be the topic of future studies:

• The choice of low rock bridges' shear strength characteristics, even if justified, does not allow a perfect comparison with real case conditions to be made. This means that more work has to be carried out to better model the cascade-effect failure of the rock bridges for realistic environments. From a numerical point of view, an extremely dense meshing could be realized to overcome the current limitations exposed in the presented work.

• Only shear and tension failure modes have been considered in the presented study, in order to focus on representative failure modes, that would allow clear conclusions about the phenomenon of failure and in particular the cascade effect of the failure to be drawn. To complete the analysis, more failures mode could be considered (for example transitional failure mode).

• The choice of discretizing the joint into regions and considering only a uniform distribution has allowed a first approximation of the process involved in the rock bridge failure to be observed. However, it would be interesting to test other random distribution (Bossi et al., 2016) and consider that every contact along the joint can be modified (not only the region). This should be considered in future work.

• A simplified planar open crack has been considered in the presented work. In reality, a discontinuity presents asperity, rugosity and defects that could affect the shear strength of the plane. This point could be integrated into future work.