Assessing the annual risk of vehicles being hit by a rainfall-induced landslide: a case study on Kennedy Road in Wan Chai, Hong Kong

Landslides threaten the safety of vehicles on highways. When analyzing the risk of a landslide hitting moving vehicles, the spacing between vehicles and the types of vehicles on the highway can be highly uncertain and have often been omitted in previous studies. Using a highway slope in Hong Kong as a case study, this paper presents a method for assessing the risk of moving vehicles being hit by a rainfall-induced landslide; this method also allows for the possible number of different types of vehicles hit by the landslide to be investigated. In this case study, the annual failure probability of the slope is analyzed based on historical slope failure data from Hong Kong. The spatial impact of the landslide is evaluated based on an empirical run-out prediction model. The consequences of the landslide are assessed using probabilistic modeling of the traffic, which can consider uncertainties in the vehicle spacing, vehicle types and slope failure time. Using the suggested method, the expected annual number of vehicles and people hit by the landslide can be conveniently calculated. This method can also be used to derive the cumulative frequency–number of fatalities curve for societal risk assessment. Using the suggested method, the effect of factors like the annual failure probability of the slope and the density of vehicles on the risk level of the slope can be conveniently assessed. The method described in this paper can provide a new guideline for highway slope design in terms of managing the risk of landslides hitting moving vehicles.

1 Introduction

Encompassing a total land area of about 1100 km², Hong Kong is one of the most densely populated regions in the world with a population of approximately 7.5 million people (GovHK, 2019). Throughout the territory of Hong Kong, there are more than 57 000 registered man-made slope features (Cheung and Tang, 2005). With an average annual rainfall of about 2400 mm, rainfall-induced landslides are one of the major natural hazards threatening public safety in the region (GEO, 2017). In particular, slope failures along highways have resulted in serious fatalities and vehicle damage. For example, in August 1994, a public light bus on Castle Peak Road was hit by landslide debris, causing three people to become trapped inside the bus and resulting in one fatality. In August 1995, due to intense rainfall, a landslide along Shum Wan Road resulted in two fatalities and five injuries, and a landslide along Fei Tsui Road resulted in one fatality and one injury (GEO, 2017). Similar phenomena have also been reported in many other parts of the world (Bíl et al., 2015), such as Italy (Donnini et al., 2017) and India (Negi et al., 2013).

There are many uncertainties in the assessment of the hazard posed by landslides to moving vehicles, such as the occurrence of the landslide, the spatial impact of the landslide, the number of vehicles hit by the landslide and the type of vehicles hit by the landslide. Risk assessment is a framework in which both the uncertainties and the consequences of a hazard can be addressed, and it has been increasingly used for landslide risk management (e.g., Lessing et al., 1983; Fell, 1994; Dai et al., 2002; Remondo et al., 2008; Erener, 2012; Vega and Hidalgo, 2016). Indeed, landslide risk assessment has been accepted as an effective tool for the planning of land use in Hong Kong. Nevertheless, risk assessment for moving vehicles affected by landslides is special because the elements at risk are highly mobile. In the past, many studies have been conducted on the individual risk associated with landslides, which is often measured by the annual probability that a person who frequently uses the highway is killed by a landslide (e.g., Bunce et al., 1997; Fell et al., 2005; Dorren et al., 2009; Michoud et al., 2012; Macciotta et al., 2015, 2017). Several studies have also examined the societal risk of vehicles being hit be landslides, in which the societal risk is measured in terms of the annual probability that at least one fatality occurs in 1 year (e.g., Budetta, 2004; Peila and Guardini, 2008; Pierson, 2012; Ferlisi et al., 2012; Corominas and Mavrouli, 2013; Macciotta et al., 2019). These studies have provided both useful insights and practical tools for the analysis and management of landslide/rockfall hazards. Nevertheless, it has commonly been assumed that traffic is uniformly distributed in time and space and that each vehicle is the same length (the mean length of all vehicles; e.g., Hungr et al., 1999; Nicolet et al., 2016). In reality, there is randomness associated with the spacing of vehicles on a highway. If such uncertainties are ignored, the resulting uncertainty associated with the number of vehicles hit by a landslide cannot be considered in the risk assessment process. Moreover, there might be various types of vehicles on a highway, and different types of vehicles may have different lengths and significantly different passenger capacities. If the difference between the different types of vehicles is ignored, it might be hard to estimate the number of people (passengers) hit by a landslide, which is also an important aspect of risk assessment.

Using Kennedy Road in Wan Chai, Hong Kong, as a case study, this paper aims to present a new method for assessing the risk of moving vehicles being hit by a rainfall-induced landslide; this method also allows for the possible number of different types of vehicles hit by the landslide to be investigated. In general, the quantitative analysis of vehicles endangered by landslides includes three scenarios: (1) a moving vehicle is impacted by falling material, (2) a moving vehicle impacts falling material on the highway, and (3) a line of stationary vehicles is impacted by falling material (Bunce et al., 1997). In this study, our focus is on the risk assessment of moving vehicles being impacted by a falling landslide. The structure of this paper is as follows. Firstly, the annual failure probability of the slope is calculated based on historical data from Hong Kong. Then, the spatial impact of the landslide is analyzed based on the run-out distance analysis. Thereafter, the consequences of the landslide are analyzed via a probabilistic model of traffic. Finally, the annual expected numbers of vehicles and people hit by the landslide are calculated, and the development of an F–N curve for societal risk assessment using this information is illustrated. Factors affecting the risk of vehicles being hit by a landslide are also discussed. The method suggested in this paper can support the establishment of new guidelines for highways design to improve roadway safety in terms of reducing the risk of landslides hitting vehicles and people.

2 Study slope and traffic information

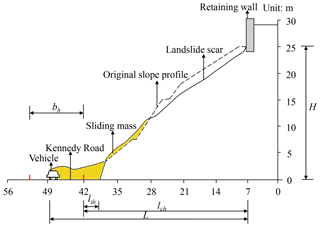
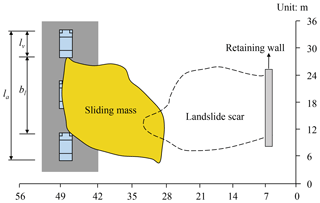
The study slope is located on Kennedy Road in the Wan Chai District of Hong Kong, as shown in Fig. 1. Wan Chai is one of the most traditional cultural areas in Hong Kong and attracts many international tourists every year. Kennedy Road is a major road in this area with three lanes, and it links with the Queen's Road in Wan Chai (TDHK, 2018). On 8 May 1992, the slope failed during intense rainfall and hit a car traveling along Kennedy Road, killing the driver (GEO, 1996). The slope is an old cut slope formed in 1967–1968 and was covered by trees before the landslide event occurred. Figure 2 shows a typical cross section of the slope and the landslide event. As shown in this figure, rainfall infiltration triggered the failure of the soil mass below the retaining wall, and the sliding mass hit the vehicle. The height of the slope (H) is 25 m, the horizontal distance from the crest of the landslide scar to the side of Kennedy Road closest to the slope (l_ch) is 35 m, and the horizontal distance from the slope toe to the side of Kennedy Road closest to the slope (l_th) is 3 m. The width of Kennedy Road (b_h) is 10 m. Figure 3 shows the plan view of the landslide event. The width of the slope is 18 m, and the volume of the landslide is 500 m³ (GEO, 1996).

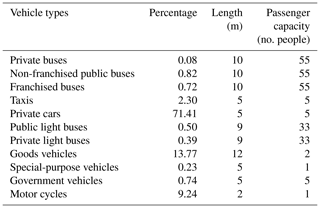
According to TDHK (2018), vehicle traffic in Hong Kong is composed of private buses, non-franchised public buses, franchised buses, taxis, private cars, public light buses, private light buses, goods vehicles, special-purpose vehicles, government vehicles and motor cycles. The percentage of each type of vehicle with respect to the total numbers of vehicles is shown in Table 1 along with the typical length of each type of vehicle and its passenger capacity. The purpose of this case study is to analyze the annual risk of different types of vehicles being hit by a landslide if the slope fails again due to rainfall.

Figure 1 Location of the landslide studied in this paper.

Figure 2 Typical cross section of the slope and the landslide studied in this paper.

Figure 3 Plan view of the landslide studied in this paper.

Table 1 Percentage contribution of the vehicle type to the total number of vehicles, and the length and passenger capacity of different vehicle types in Hong Kong.

3 Methodology

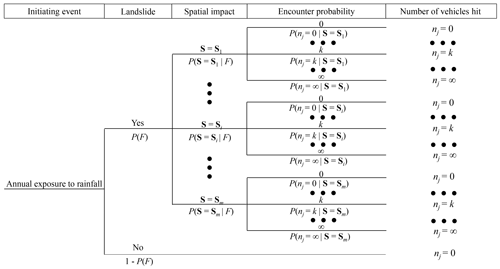
There are multiple types of vehicles on highways. In a landslide critical area of a road, the longer the vehicle, the greater the probability that it will be hit by a landslide. Figure 4 shows the event tree model employed in this study to assess the risk of a rainfall-induced landslide hitting type j vehicles. As can be seen from this figure, if the slope does not fail in a year, there is no spatial impact, and the number of type j vehicles hit is zero. Let P(F) denote the annual probability of slope failure. If the slope fails, its spatial impact, which can be characterized by the width of the landslide mass and the run-out distance of the landslide mass, is uncertain. In general, the spatial impact of a landslide depends on factors like the slope geometry, the soil profile, soil strength parameters, and the water content in the soil mass. The spatial impact can be evaluated using physically based methods or statistically based methods, and this will be discussed later in this paper. Suppose that there are m possible spatial impacts, and let $P(S=S_i|F)$ denote the probability that the spatial impact is S_i when the landslide occurs. For a given spatial impact, the number of type j vehicles hit is uncertain. Let n_j denote the number of type j vehicles hit by the landslide. Let $P(n_j=k|S=S_i)$ denote the encounter probability that k type j vehicles will be hit by a landslide when the spatial impact is S_i. If the landslide mass cannot reach the road for the case of S=S_i, the spatial impact is zero, which can be denoted as $P(n_j=\mathrm{0}|S=S_i)=\mathrm{1}$.

Figure 4 Event tree of the annual risk evaluation of type j vehicles being hit by a landslide.

Based on the event tree shown in Fig. 4, the annual probability of k type j vehicles being hit by the landslide is $P\left(F\right)\times P(S=S_i|F)\times P(n_j=k|S=S_i)$ when the spatial impact of the landslide is S_i, and the expected number of type j vehicles hit corresponding to such a scenario is $k\times P\left(F\right)\times P(S=S_i|F)\times P(n_j=k|S=S_i)$. As the pathways are mutually exclusive, the annual expected number of type j vehicles hit by the landslide (E_vj) is the summation of the expected numbers corresponding to all of the pathways in Fig. 4, which can be written as follows:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{E}_{\mathrm{v}j}& =P\left(F\right)\times \sum _{i=\mathrm{1}}^m[P\left(S=S_i\mathrm{|}F\right)\\ & \times \sum _{k=\mathrm{0}}^{\mathrm{\infty }}kP\left(n_j=k\mathrm{|}S=S_i\right)]\end{array}\end{array}$$

Let n denote all vehicle types. The total expected number of vehicles hit by the landslide considering all types of vehicles, i.e., E_v, can then be calculated as follows:

$$\begin{array}{}\text{(2)}& E_{\mathrm{v}}=\sum _{j=\mathrm{1}}^n{E}_{\mathrm{v}j}\end{array}$$

Let n_pj denote the passenger capacity of a type j vehicle. The expected number of people in type j vehicles hit by the landslide (E_pj) can then be calculated as follows:

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{E}_{\mathrm{p}j}& =P\left(F\right)\times \sum _{i=\mathrm{1}}^m[P\left(S=S_i\mathrm{|}F\right)\\ & \times \sum _{k=\mathrm{0}}^{\mathrm{\infty }}kP\left(n_j=k\mathrm{|}S=S_i\right)]\times n_{\mathrm{p}j}\end{array}\end{array}$$

The total expected number of people hit by the landslide considering all types of vehicles (E_p) can be calculated as follows:

$$\begin{array}{}\text{(4)}& E_{\mathrm{p}}=\sum _{j=\mathrm{1}}^n{E}_{\mathrm{p}j}\end{array}$$

Equation (2) can be extended to estimate the expected monetary losses with respect to vehicles hit by a landslide when information regarding the price of different types of vehicles is available. Nevertheless, during the analysis of the risk of vehicles hit by landslides, the social impact, which can be better measured by the number of vehicles than the cost of the vehicles, is often more important than the economic losses. Hence, the risk of vehicles being hit by landslides is not measured in terms of monetary losses in this study.

Previously, the individual risk has often been used to measure the threat of a landslide to a moving vehicle, which provides information about the probability of a frequent user of the highway being killed by a landslide. However, decision-makers may also be interested in the annual expected numbers of vehicles/people hit by landslides, which can be obtained using the method suggested in this paper. As will be shown later in the case study, the above framework can be easily extended to calculate the F–N curve for societal risk assessment, which is an important complement to previous methods on social risk assessment that rely solely on the probability of at least one fatality per year.

As indicated by Eq. (1), the key points for assessing the annual risk associated with type j vehicles are the evaluation of the following: (1) the annual failure probability of the landslide (P(F)), (2) the possible spatial impact of the landslide ($P(S=S_i|F)$) and (3) the encounter probability that expresses the possible number of the type j vehicle hit by a landslide for a given spatial impact ($P(n_j=k|S=S_i)$). How the above elements are assessed will be introduced in the following sections.

3.1 Evaluation of the annual probability of the landslide (P(F))

The estimation of the annual landslide probability or the landslide susceptibility is fundamental in landslide hazard assessment. As almost all slope failures in Hong Kong are caused by rainfall infiltration (e.g., Lumb, 1975; Brand, 1984; Finlay et al., 1999), assessing the annual probability of rainfall-induced landslides is important. In general, there are two types of methods for evaluating the likelihood of slope failure: physically based methods involving slope stability analysis (e.g., Christian et al., 1994; Fenton and Griffiths, 2005; Huang et al., 2010) and empirical methods involving the statistical analysis of historical slope failure data (e.g., Chau et al., 2004; Zang and Tang, 2009). Currently, landslide probability analyses via slope stability analyses mainly focus on the likelihood of slope failure for a given rainfall. In reality, the occurrence of landslides in a given year is highly uncertain. Currently, the method for calculating the annual failure probability of a landslide using physically based models considering rainfall uncertainty is still not well established; hence, statistical methods are adopted in this study to estimate the annual landslide probability.

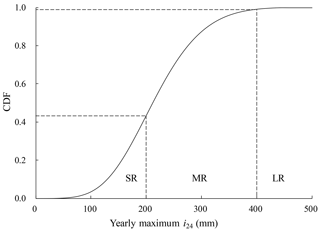
In Hong Kong, the failure of a slope is highly correlated with the 24 h rainfall, i₂₄ (Cheung and Tang, 2005). Based on i₂₄, rainstorms in Hong Kong can be divided into three categories: (1) i₂₄<200 mm d⁻¹, which refers to “small rainfall” and is denoted as SR; (2) 200 mm $<i_{\mathrm{24}}<\mathrm{400}$ mm d⁻¹, which refers to “medium rainfall” and is denoted as MR; and (3) i₂₄>400 mm d⁻¹, which refers to “large rainfall” and is denoted as LR (Zhang and Tang, 2009). Via statistical analysis of the slope failure data from 1984 to 2002 in Hong Kong, it is found that the failure probability of a slope in this region when subjected to small rainfall, medium rainfall and large rainfall is $\mathrm{1.09}\times {\mathrm{10}}^{-\mathrm{4}}$, $\mathrm{2.61}\times {\mathrm{10}}^{-\mathrm{3}}$ and $\mathrm{8.94}\times {\mathrm{10}}^{-\mathrm{3}}$, respectively, i.e., $P\left(F\right|\mathrm{SR})=\mathrm{1.09}\times {\mathrm{10}}^{-\mathrm{4}}$, $P\left(F\right|\mathrm{MR})=\mathrm{2.61}\times {\mathrm{10}}^{-\mathrm{3}}$ and $P\left(F\right|\mathrm{LR})=\mathrm{8.94}\times {\mathrm{10}}^{-\mathrm{3}}$, respectively (Zhang and Tang, 2009). In the statistical analysis, it is assumed that slopes in Hong Kong have the same failure probability when subjected to the same type of rainfall; hence, the failure probability obtained should be interpreted as the failure probability of an average slope. An assumption such as this is commonly adopted in the statistically based method for evaluating the failure probability of slopes in a region. As noticed by Dai et al. (2002), this type of method cannot consider the effect of the local geology and soil condition on the site-specific slope stability.

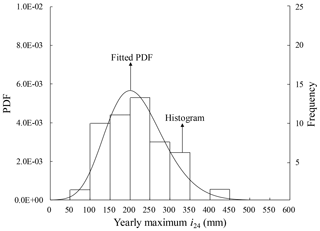
In Zhang and Tang (2009), the conditional failure probability of a slope for a given type of rainfall is provided. To calculate the annual failure probability of a slope, the uncertainty associated with the rainfall should be analyzed. In this study, the uncertainty associated with rainfall can be represented by the uncertainty associated with i₂₄. To characterize the uncertainty associated with i₂₄, we collected the yearly maximum i₂₄ values measured at the Hong Kong Observatory Headquarters from 1969 to 2018, as shown in Fig. 5 (HKO, 2018). As can be seen from Fig. 5, the maximum i₂₄ in a year in Hong Kong is mainly within the range of 100–350 mm. The generalized extreme value distribution (Hosking et al., 1985) with the following probability density function (PDF) seems to fit the histogram with reasonable accuracy:

$$\begin{array}{}\text{(5)}& \begin{array}{rl}f\left(i_{\mathrm{24}}\right)& ={\displaystyle \frac{\mathrm{1}}{\mathit{\beta }}}{\left[\mathrm{1}+\mathit{\gamma }\left({\displaystyle \frac{i_{\mathrm{24}}-\mathit{\mu }}{\mathit{\beta }}}\right)\right]}^{-\frac{\mathrm{1}}{\mathit{\gamma }}}\\ & \exp \left\{{\left[\mathrm{1}+\mathit{\gamma }\left({\displaystyle \frac{i_{\mathrm{24}}-\mathit{\mu }}{\mathit{\beta }}}\right)\right]}^{-\frac{\mathrm{1}}{\mathit{\gamma }}}\right\},\end{array}\end{array}$$

where β, μ and γ are the scale parameter, the location parameter and the shape parameter of the generalized extreme distribution, respectively. The values of β, μ and γ can be calculated based on the maximum likelihood method, and they are equal to −0.17, 66 and 188, respectively. Figure 6 shows the cumulative distribution function (CDF) of i₂₄ obtained based on the fitted generalized extreme value distribution. As can be seen from this figure, the probability that the rainfall with yearly maximum i₂₄ belongs to small rainfall, medium rainfall and large rainfall is 0.44, 0.55 and 0.01, respectively, i.e., P(SR)=0.44, P(MR)=0.55 and P(LR)=0.01, respectively. Based on the total probability theorem, the annual probability of a rainfall-induced slope failure can be computed as follows:

$$\begin{array}{}\text{(6)}& \begin{array}{rl}P\left(F\right)& =P\left(F\mathrm{|}\mathrm{SR}\right)P\left(\mathrm{SR}\right)+P\left(F\mathrm{|}\mathrm{MR}\right)P\left(\mathrm{MR}\right)\\ & +P\left(F\mathrm{|}\mathrm{LR}\right)P\left(\mathrm{LR}\right)\end{array}\end{array}$$

Using the above equation, the impact of the uncertainty of rainfall on the annual failure probability of the landslide is considered. The failure probability obtained is not conditional on the rainfall type and, hence, does not correspond to a certain return period of rainfall.

Figure 5 Histogram and fitted PDF of the yearly maximum i₂₄ in Hong Kong.

Figure 6 CDF of the yearly maximum i₂₄ in Hong Kong.

3.2  Evaluation of the spatial impact of the landslide ($P(S=S_i|F)$)

In this study, the spatial impact of the landslide is characterized by the landslide width and the run-out distance of the landslide. Let b_l denote the width of the landslide, and let L denote the run-out distance of the landslide, which is defined as the distance between the crest of the landslide scar and the toe of the slip; thus, $S=\left\{b_{\mathrm{l}},L\right\}$. For simplicity, the uncertainty of the landslide width is not considered. In a case such as this, the uncertainty associated with S is fully characterized by the uncertainty associated with the run-out distance. In principle, the run-out distance is a continuous random variable. For ease of computation, it can be discretized into a discrete variable. Let L_i denote the ith possible value of L. Then, $P(S=S_i|F)$ can be calculated by

$$\begin{array}{}\text{(7)}& P\left(S=S_i\mathrm{|}F\right)=P\left(L=L_i\right)\end{array}$$

In general, the run-out distance of a landslide depends on factors like the slope geometry, the soil profile, and geotechnical, hydraulic and rheological properties of sliding mass. The methods to investigate the run-out distance of a landslide can be divided into two categories (Hungr et al., 2005): (1) analytical or numerical methods based on the physical laws of solid and fluid dynamics (Scheidegger, 1973), which are usually solved numerically (e.g., Hungr and McDougall, 2009; Luo et al., 2019), and (2) empirical methods based on field observations and geometric correlations (e.g., Dai and Lee, 2002; Budetta and Riso, 2004). The use of the physically based methods requires detailed information on the ground condition as well as the geotechnical and hydraulic properties of the soils. In contrast, empirical methods based on geometry of the landslide are generally simple and relatively easy to use (e.g., Finlay et al., 1999; Dai et al., 2002). In this study, empirical methods are adopted due to the lack of information on the geotechnical and hydraulic conditions of the slope. In particular, the following empirical equation is used (Corominas, 1996):

$$\begin{array}{}\text{(8)}& \log L=\mathrm{0.085}\log V+\log H+\mathrm{0.047}+\mathit{\epsilon },\end{array}$$

where V is the volume of the sliding mass, and H is the height of the slope; ε is a random variable with a mean of zero and a standard deviation of σ=0.161. As shown in Finlay et al. (1999) and Gao et al. (2017), Eq. (8) can predict the run-out distance of cut and fill slopes in Hong Kong quite well. As mentioned previously, the slope studied in this paper is indeed a cut slope.

For the slope shown in Fig. 2, the height is 25 m, i.e., H=25 m. To apply Eq. (8), the landslide volume is needed. In general, the volume of a landslide can be estimated using methods based on surface area–volume relationship (e.g., Malamud et al., 2004; Imaizumi and Sidle, 2007; Guzzetti et al., 2008, 2009), slope stability analysis (e.g., Huang et al., 2013; Chen and Zhang, 2014) or morphology-based methods (e.g., Carter and Bentley, 1985; Jaboyedoff et al., 2012). A comprehensive review of such methods can be found in Jaboyedoff et al. (2020). Using these methods, the volume of a sliding mass can be estimated both for a slope that has not failed yet and for a landslide that has already occurred. In this study, the volume is estimated via the surface area–volume relationship. Let A_s denote the landslide scar area. The volume of the landslide in this case study is estimated with A_s using the following equation (Parker et al., 2011):

$$\begin{array}{}\text{(9)}& V=\mathrm{0.106}\times A_{\mathrm{s}}^{\mathrm{1.388}}\end{array}$$

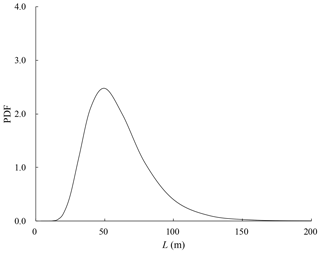
Based on Fig. 3, the landslide scar area is estimated to be 450 m². Based on Eq. (9), the volume is estimated to be about 510 m³, which is close to the volume of sliding mass (500 m³) reported in GEO (1996). Substituting the values of H and V into Eq. (8), it can be obtained that the travel distance of the landslide is lognormally distributed with a mean of 50.7 m and a standard deviation of 12.6 m. Figure 7 shows the PDF of the travel distance of the landslide. As can be seen from this figure, the travel distance of the landslide is mainly within the range of 20–150 m.

Figure 7 PDF of the run-out distance of the landslide studied in this paper.

3.3 Evaluation of the probability of encountering the landslide ($P(n_j=k|S=S_i)$)

As shown in Fig. 2, the horizontal distance from the crest of the landslide scar to the side of Kennedy Road closest to the slope (l_ch) is 35 m. The width of Kennedy Road (b_h) is 10 m. When L_i>l_ch, the landslide will reach Kennedy Road. When $L_i\ge l_{\mathrm{ch}}+b_{\mathrm{h}}$, Kennedy Road will be totally covered by the sliding mass. When $l_{\mathrm{ch}}<L_i<l_{\mathrm{ch}}+b_{\mathrm{h}}$, Kennedy Road will be partially affected. Thus, the percentage of vehicles within the affected length of the highway for a given spatial impact, which is denoted as α(S=S_i) here, can be calculated as follows:

$$\begin{array}{}\text{(10)}& \mathit{\alpha }\left(S=S_i\right)=\left\{\begin{array}{ll}\mathrm{0},& L_i\le l_{\mathrm{ch}}\\ \frac{L_i-l_{\mathrm{ch}}}{b_{\mathrm{h}}},& l_{\mathrm{ch}}<L_i<l_{\mathrm{ch}}+b_{\mathrm{h}}\\ \mathrm{1},& L_i\ge l_{\mathrm{ch}}+b_{\mathrm{h}}\end{array}\right.\end{array}$$

α(S=S_i) can also be interpreted as the degree to which the landslide impacts the area related to the run-out distance. As can be seen from Eq. (10), α(S=S_i) is between zero (the sliding mass does not reach the road) and one (the sliding mass totally covers the road). For a given run-out distance, the number of vehicles hit by the landslide highly depends on the length of road affected by the landslide as well as the density of vehicles. Let l_a denote the length of road affected by the landslide, and let l_v denote the length of vehicles. As shown in Fig. 3, when the head or the rear of a vehicle has contact with the landslide mass, the vehicle is considered to be hit by the landslide, i.e., the length of affected road (l_a) is equal to the sum of the width of the landslide (b_l) and the length of the vehicles (l_v) as follows:

$$\begin{array}{}\text{(11)}& l_{\mathrm{a}}=b_{\mathrm{l}}+\mathrm{2}{l}_{\mathrm{v}}\end{array}$$

In this study, the width of the landslide is assumed to be equal to the width of the slope, i.e., b_l=18 m (GEO, 1996). In transportation, the presence of the vehicles on a highway can be modeled as a Poisson process with a mean arrival rate of λ, which is equal to the density of vehicles on the highway (Paxson and Floyd, 1995). Let q denote the number of vehicles passing a given cross section of a road per unit time, and let v denote the average speed of the vehicles. Thus, the mean rate of occurrence of moving vehicles (λ) can be calculated as follows (Lighthill, 1955):

$$\begin{array}{}\text{(12)}& \mathit{\lambda }={\displaystyle \frac{q}{v}}\end{array}$$

Let w_j denote the proportion of type j vehicle in the traffic flow. The mean rate of occurrence of type j vehicles can be then written as follows:

$$\begin{array}{}\text{(13)}& {\mathit{\lambda }}_j=w_j\times {\displaystyle \frac{q}{v}}\end{array}$$

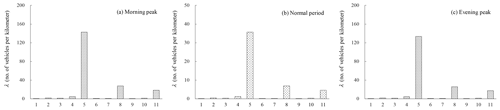
Figure 8 Mean rates of different types of vehicles during the (a) morning peak, (b) the normal period and (c) the evening peak. The numbers on the x axis refer to the following vehicle types: 1 – private buses, 2 – non-franchised public buses, 3 – franchised buses, 4 – taxis, 5 – private cars, 6 – public light buses, 7 – private light buses, 8 – goods vehicles, 9 – special-purpose vehicles, 10 – government vehicles, and 11 – motor cycles.

In general, the presence of vehicles also depends on the time of day. For example, Table 2 shows the q and v data for Kennedy road for the morning peak, the normal period and the evening peak, respectively (TDHK, 2018). The mean rate of occurrence of each type of vehicle is then obtained for the different periods the day as shown in Fig. 8a, b and c, respectively. It can be seen that the mean rate of occurrence of the vehicles during the morning and evening peaks is significantly higher than during the normal period. Among all vehicle types, the mean rate of occurrence of private cars on the affected road is the greatest, followed by goods vehicles, motor cycles and taxis.

Table 2 Number of vehicles passing a given cross section of the road per hour (q) and the average speed of vehicles on Kennedy Road (v) for different periods in a day.

Let T₁, T₂ and T₃ denote the morning peak, the normal period and the evening peak, respectively, and let l_aj denote the length of the road affected for type j vehicles. Based on the property of a Poisson process, if the spatial impact is S_i and the slope fails during period T_i, the encounter probability that k type j vehicles will be hit by the landslide can be computed as follows:

$$\begin{array}{}\text{(14)}& \begin{array}{rl}P\left(n_j=k\mathrm{|}t\in T_i,S=S_i\right)& ={\displaystyle \frac{{\left[{\mathit{\alpha }}_j\left(S=S_i\right){\mathit{\lambda }}_j{l}_{\mathrm{a}j}\right]}^k}{k\mathrm{!}}}\\ & \exp \left[-{\mathit{\alpha }}_j\left(S=S_i\right){\mathit{\lambda }}_j{l}_{\mathrm{a}j}\right]\end{array}\end{array}$$

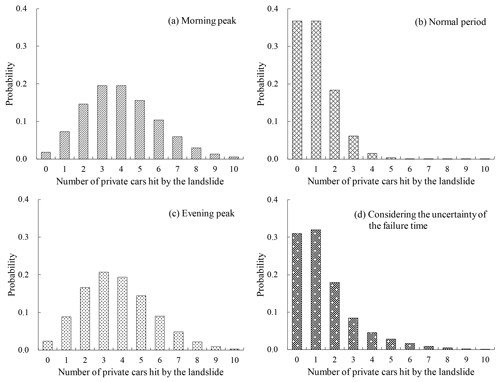
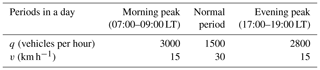
Figure 9 Probability distribution of the number of private cars hit by the landslide studied in this paper during different periods when the spatial impact is S_i and ${\mathit{\alpha }}_j(S=S_i)=\mathrm{1}$: (a) morning peak, (b) normal period, (c) evening peak and (d) considering the uncertainty of the failure time.

Equation (14) provides a probabilistic model of the number of vehicles hit by the landslide, which can consider the uncertainties of vehicle spacing, vehicle type and slope failure time. For example, Fig. 9a, b and c show the probability distributions of the number of private cars hit by the landslide during the morning peak, the normal period and the evening peak when the spatial impact is S_i and ${\mathit{\alpha }}_j(S=S_i)=\mathrm{1}$, respectively. As can be seen from these figures, the most probable number of private cars hit by the landslide during the respective morning and evening peaks is approximately three, and the probability is about 0.20 for both periods. The most probable number of private cars hit by the landslide during the normal period is approximately one, and the probability is about 0.37.

In reality, the slope can fail during any period of a day. Based on the total probability theorem, the probability that k type j vehicles will be hit for the case of S=S_i can be computed as follows:

$$\begin{array}{}\text{(15)}& \begin{array}{rl}P\left(n_j=k\mathrm{|}S=S_i\right)& =\sum _{i=\mathrm{1}}^{\mathrm{3}}P\left(n_j=k\mathrm{|}t\in T_i,S=S_i\right)\\ & P\left(t\in T_i\right)\end{array}\end{array}$$

As an example, Fig. 9d shows the probability distribution of the number of private cars hit by the landslide considering the uncertainty of the failure time when the spatial impact is S_i and ${\mathit{\alpha }}_j(S=S_i)=\mathrm{1}$. As can be seen from this figure, the most probable number of private cars hit by the landslide considering the uncertainty of the failure time is approximately one, and the probability is about 0.32.

3.4 Risk calculation and evaluation

In the above analyses, equations for evaluating P(F), $P(S=S_i|F)$ and $P(n_j=k|S=S_i)$ are introduced. Substituting these equations into Eq. (1), the expected number of each type of vehicles being hit by the landslide can then be calculated, as shown in Fig. 10a. As can be seen from this figure, the expected number of private cars hit by the landslide is highest with a value of $\mathrm{1.67}\times {\mathrm{10}}^{-\mathrm{3}}$ vehicles per year, followed by goods vehicles, motor cycles and taxis. The expected number of each type of vehicles hit by the landslide is highly correlated with the proportion of the vehicle type in the traffic flow. Private cars make up the greatest proportion of vehicles in the traffic flow; hence, it is natural to assume that they will be most impacted by landslides. In reality, the vehicle that was hit by the slope studied on 8 May 1992 was indeed a private car. Using Eq. (2), the total expected number of vehicles hit by the landslide considering all types of vehicles can be also calculated, which is about $\mathrm{2.48}\times {\mathrm{10}}^{-\mathrm{3}}$ vehicles per year.

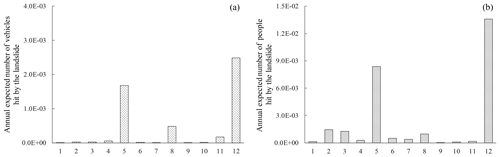
Figure 10 Annual expected number of elements, (a) vehicles and (b) people, hit by the landslide studied in this paper. The numbers on the x axis refer to the following vehicle types: 1 – private buses, 2 – non-franchised public buses, 3 – franchised buses, 4 – taxis, 5 – private cars, 6 – public light buses, 7 – private light buses, 8 – goods vehicles, 9 – special-purpose vehicles, 10 – government vehicles, 11 – motor cycles and 12 – all types of vehicles.

Introducing the passenger capacity of each type of vehicle into Eq. (3), the expected number of people hit by the landslide associated with each type of vehicle can be computed, and the results are shown in Fig. 10b. As can be seen from this figure, the expected number of people hit by the landslide in private cars is highest with a value of $\mathrm{8.37}\times {\mathrm{10}}^{-\mathrm{3}}$ people per year, followed by non-franchised public buses, franchised buses and goods vehicles. The expected number of people hit by the landslide in each type of vehicles highly depends on the proportion of vehicles in the traffic flow and the passenger capacity of the vehicles. Non-franchised public buses make up a higher proportion of the traffic flow and have the largest passenger capacity; hence, it is natural to assume that they will be associated with a greater expected number of passengers affected by landslides. Based on Eq. (4), the total expected number of people hit by the landslide considering all types of vehicles can be also calculated, which is about $\mathrm{1.36}\times {\mathrm{10}}^{-\mathrm{2}}$ people per year.

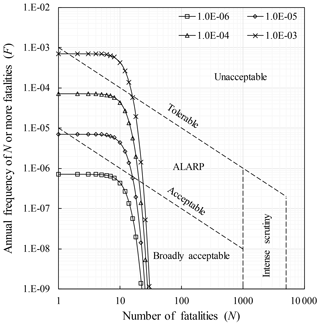
Society is less tolerant of events in which a large number of lives are lost in a single event compared with the same number of lives being lost over a large number of separate events – this can be measured via societal risk (Cascini et al., 2008). In Hong Kong, societal risk is measured using the F–N relationship (GEO, 1998; Fig. 11 in this paper). In Fig. 11, the x axis denotes the number of fatalities, and the y axis denotes cumulative annual frequency of the number of fatalities. There are four regions in this figure: the region in which the risk is unacceptable, the region in which the risk is broadly acceptable, the region in which the risk should be made as low as reasonably practicable (ALARP) and the intense scrutiny region. To assess the societal risk of the landslide, the relationship between the number of fatalities and the probability of such an event should be established. When the traffic flow is a Poisson process, the passengers in the traffic flow can also be modeled using a Poisson process. For example, the mean rate of occurrence of passengers in type j vehicles is λ_pj=n_pjλ_j, where n_pj is the passenger capacity of type j vehicles and λ_j is the mean rate of occurrence of type j vehicles. Let n_jp denote the number of people hit by the landslide. Using equations similar to Eqs. (14) and (15), the chance of k passengers in type j vehicles being hit by the landslide for a given spatial impact can also be calculated and is denoted as $P(n_{j\mathrm{p}}=k|S=S_i)$. The annual chance of k passengers in type j vehicles being hit by the landslide can be calculated as follows:

$$\begin{array}{}\text{(16)}& \begin{array}{rl}P\left(n_{j\mathrm{p}}=k\right)& =P\left(F\right)\sum _{i=\mathrm{1}}^m[P\left(n_{j\mathrm{p}}=k\mathrm{|}S=S_i\right)\\ & P\left(S=S_i\mathrm{|}F\right)]\end{array}\end{array}$$

Figure 11 Estimated annual frequency of N or more people being hit by the landslide studied in this paper (tolerable and acceptable F–N curves are those specified by the GEO, 1998). The numbers on the x axis refer to the following vehicle types: 1 – private buses, 2 – non-franchised public buses, 3 – franchised buses, 4 – taxis, 5 – private cars, 6 – public light buses, 7 – private light buses, 8 – goods vehicles, 9 – special-purpose vehicles, 10 – government vehicles, 11 – motor cycles and 12 – all types of vehicles.

Figure 11 shows the relationships between the number of people hit by the landslide and the annual probability that such an event occurs for different vehicle types. As can be seen from this figure, the risk associated with type 5 vehicles (private cars) is the greatest and is unacceptable; the risk associated with type 1 vehicles (private buses), type 9 vehicles (special-purpose vehicles) and type 10 vehicles (government vehicles) is in the acceptable region; and the risk associated with the rest of the vehicle types is in the ALARP region. Indeed, the person hit by the landslide on 8 May 1992 was in a private car.

As the flow of all vehicles on the highway is modeled as a Poisson process, the flow of people on the highway considering all vehicle type can also be modeled as Poisson process with a mean rate of ${\mathit{\lambda }}_{\mathrm{p}}=\mathit{\lambda }(w_{\mathrm{1}}{n}_{\mathrm{p}\mathrm{1}}+w_{\mathrm{2}}{n}_{\mathrm{p}\mathrm{2}}+\mathrm{\dots }{w}_n{n}_{\mathrm{p}n})$, where w is the proportion of each type of vehicle in the traffic flow, n is the number of vehicle types and λ is the mean rate of occurrence of all vehicles. Using an equation similar to Eq. (16), the annual probability of k people in the traffic flow considering all types of vehicles can also be calculated, and the F–N curve obtained considering all types of vehicles is shown in Fig. 11. As can be seen from this figure, the social risk considering all types of vehicles is greater than that of any individual type of vehicle and, hence, is also unacceptable.

4 Discussions

4.1 The effect of the annual failure probability of the slope

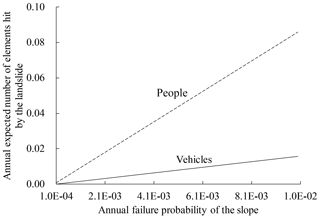
In the above analysis, the annual failure probability of the slope only represents the failure probability of an average slope in Hong Kong. To investigate the effect of the failure probability of the slope, Fig. 12 shows how the annual expected number of vehicles and people hit by the landslide for all types of vehicles changes with the annual failure probability of the slope. As can be seen from this figure, the expected number of vehicles hit by the landslide increases linearly as the annual failure probability of the slope increases. When the failure probability of the slope increase from $\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{4}}$ to $\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{2}}$, the expected number of vehicles hit increases from $\mathrm{1.57}\times {\mathrm{10}}^{-\mathrm{4}}$ vehicles per year to $\mathrm{1.57}\times {\mathrm{10}}^{-\mathrm{2}}$ vehicles per year. A similar observation can also be made for the annual expected number of people hit by the landslide. Figure 13 shows the how the societal risk for all types of vehicles changes as the annual failure probability of the slope changes. As can be seen from this figure, when the failure probability of the slope is smaller than $\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{4}}$, the societal risk is in the ALARP region. If the failure probability of the slope is further reduced to $\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{6}}$, the societal risk becomes acceptable. Hence, reducing the annual failure probability of a slope is an effective means to reduce the risk of the slope. In practice, the annual failure probability of a slope under rainfall can be reduced through the use of engineering measures such as structural reinforcement. To assess the effect of such measures on the failure probability of the slope, physically based methods will be used for hazard probability analysis.

Figure 12 Impact of the annual failure probability of the slope on the annual expected number of elements hit by the landslide.

Figure 13 Impact of the annual failure probability of the slope on the annual societal risk.

4.2 The effect of traffic density

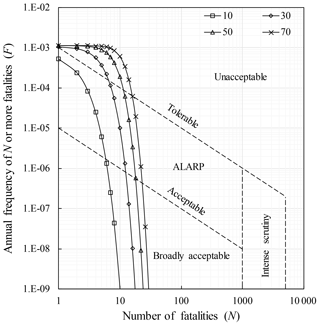
The density of vehicles may vary from one road to another. To investigate the effect of the density of vehicles, the annual expected number of vehicles and people hit by the landslide and the annual societal risk for all types of vehicles are investigated when the density of vehicles on the highway increases from 0 to 300 vehicles per kilometer, and the results are shown in Figs. 14 and 15, respectively. As can be seen from Fig. 14, there is a linear increasing trend in the expected number of vehicles and people impacted as the density of vehicles increases. When the density of vehicles is 300 vehicles per kilometer, the expected number of elements impacted can reach $\mathrm{1.01}\times {\mathrm{10}}^{-\mathrm{2}}$ vehicles hit per year and $\mathrm{5.52}\times {\mathrm{10}}^{-\mathrm{2}}$ people hit per year. As can be seen from Fig. 15, the societal risk also increases as the density of vehicles increases. When density of vehicles is less than 10 vehicles per kilometer, the societal risk is within the ALARP region. Therefore, depending on the density of the vehicles, the societal risk of a landslide may be acceptable when it is located near one highway but become unacceptable when it is located near another highway. Therefore, in the design of highway slopes, the failure probability of the slope should be decreased as the density of the vehicles increases.

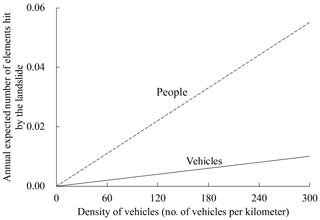
Figure 14 Impact of the density of vehicles on the annual expected number of elements hit by the landslide.

Figure 15 Impact of the density of vehicles on the annual societal risk. The numbers in the legend refer to the number of vehicles per kilometer.

5 The limitations and applicability of the method suggested in this study

Rainfall conditions may affect the failure probability of a slope as well as the traffic density and, hence, affect the risk. In this case study, the effect of rainfall conditions on the annual failure probability of the slope is considered using Eq. (6), which is based on both the chances of different types of rainfall and the failure probability of the slope under different rainfall conditions. Traffic conditions may also vary with rainfall conditions. However, data on the impact of rainfall conditions on the traffic density are rarely available. In this study, the impact of rainfall conditions on the traffic flow is not considered in the risk assessment.

The method used for the case study consists of three components: the hazard probability model, the spatial impact assessment model and the consequence assessment model. The annual failure probability of the slope is calculated based on the statistical analysis of past failure data in Hong Kong. It represents the failure probability of an average slope in Hong Kong, which is a common assumption adopted in empirical methods. When the method is applied in another region, the failure probability should be estimated using data from the region under study. Alternatively, to reflect the effects of factors like slope geometry and local ground conditions on the slope failure probability, the failure probability can also be estimated using physically based methods. As mentioned previously, current physically based methods mainly focus on the failure probability of a slope during a given rainfall event. It is important to also examine how to incorporate the uncertainty of the rainfall condition into the slope failure probability evaluation in future studies.

In this study, the spatial impact is estimated based on an empirical run-out distance prediction equation formulated using data from different types of landslides from several countries. When applying the method suggested in this paper in another region, the empirical equation should be tested to establish whether it can better fit landslides in the region under study or whether the run-out distance based on empirical relationships developed in the region under study should be estimated. The spatial impact of the landslide may also be estimated using physically based models. In recent years, large deformation analysis methods have been increasingly used for run-out distance analysis. It should be noted that, during the run-out distance analysis, the uncertainties in the geological condition and soil properties should be considered. Currently, large deformation analysis is often carried out in a deterministic way. It is highly desirable to combine large deformation analysis with the reliability theory such that the spatial impact of the landslide can also be predicted probabilistically.

The consequence assessment model is generally applicable and can be used to assess the impact of landslides on moving vehicles in other regions. Therefore, after the hazard probability model and the spatial impact model are replaced with models suitable for application in another region, the suggested method in this paper can also be used to assess the risk of moving vehicles being hit by a rainfall-induced landslide in another region.

There are multiple scenarios in which a landslide can impact vehicles on a highway. The focus of this paper is on the impact of falling materials on moving vehicles. In future studies, it would also be worthwhile developing methods to evaluate the effect of the uncertainty of the number and types of vehicles on the risk assessment of the impact of a landslide on vehicles in other scenarios.

6 Summary and conclusions

When assessing the risk of a landslide hitting moving vehicles, the number and types of vehicles hit can be highly uncertain. Using a case study in Hong Kong, this paper suggests a method for assessing the risk of vehicles being hit by a rainfall-induced landslide explicitly considering the above factors. The research findings from this study can be summarized as follows:

1. Using the method suggested in this paper, the expected annual number of vehicles/people hit by the landslide as well as the cumulative frequency–number of fatalities curve can be calculated. These results can complement existing results from previous studies on the risk assessment of landslides hitting moving vehicles, which mainly focus on the individual risk of a landslide or societal risk assessment relying on the probability of the occurrence of at least one fatality per year.

2. As the length, density and the passenger capacity of different vehicles are different, the annual number of vehicles/people hit by landslides varies for different types of vehicles. The societal risk associated with different types of vehicles is also variable. Thus, it is important to consider the different types of vehicles in the traffic flow.

3. The method suggested in this paper can be used to examine the effect of factors like the annual failure probability of the slope and the density of the vehicles on the road on the risk of a landslide hitting moving vehicles. The proposed method can be potentially useful in determining the target annual failure probability of a slope considering the traffic conditions on a highway, which can be used as a new guideline for highway landslide risk management.

In this case study, the annual failure probability of the slope is evaluated based on a statistical model, and the spatial impact of the landslide is analyzed using an empirical equation. While these methods are easy to use, they cannot consider the effect of local geology and soil condition on the failure and post-failure behavior of the slope. Further studies are needed to explore physically based methods to predict the annual failure probability and run-out distance with explicit consideration of the uncertainties involved.