Topographic uncertainty quantification for flow-like landslide models via stochastic simulations

Digital elevation models (DEMs) representing topography are an essential input for computational models capable of simulating the run-out of flow-like landslides. Yet, DEMs are often subject to error, a fact that is mostly overlooked in landslide modeling. We address this research gap and investigate the impact of topographic uncertainty on landslide run-out models. In particular, we will describe two different approaches to account for DEM uncertainty, namely unconditional and conditional stochastic simulation methods. We investigate and discuss their feasibility, as well as whether DEM uncertainty represented by stochastic simulations critically affects landslide run-out simulations. Based upon a historic flow-like landslide event in Hong Kong, we present a series of computational scenarios to compare both methods using our modular Python-based workflow. Our results show that DEM uncertainty can significantly affect simulation-based landslide run-out analyses, depending on how well the underlying flow path is captured by the DEM, as well as on further topographic characteristics and the DEM error's variability. We further find that, in the absence of systematic bias in the DEM, a performant root-mean-square-error-based unconditional stochastic simulation yields similar results to a computationally intensive conditional stochastic simulation that takes actual DEM error values at reference locations into account. In all other cases the unconditional stochastic simulation overestimates the variability in the DEM error, which leads to an increase in the potential hazard area as well as extreme values of dynamic flow properties.

1 Introduction

Landslides are natural hazards that occur frequently all around the world causing casualties, economic devastation, and environmental destruction. Most often, they are naturally driven, e.g., by means of long-lasting and/or intensive precipitation events or induced by earthquakes. Yet, landslides might also be triggered or an area's susceptibility to them increased as a result of human activities, e.g., deforestation and construction. According to the United Nations Office for Disaster Risk Reduction and the Centre for Research on the Epidemiology of Disasters, 378 recorded landslides from 1998 to 2017 affected 4.8 million people and caused 18 414 deaths as well as several billion US dollars of economic losses (Wallemacq et al., 2018). Froude and Petley (2018) reported that in total 55 997 people were killed during 4862 fatal nonseismic landslide events from January 2004 to December 2016. Still, it has to be assumed that the damage potential of landslides is underestimated as (1) events have been underreported for decades, especially in developing countries, and (2) losses caused by coseismic landslide events tend to be classified as secondary losses due to earthquakes.

Rapid flow-like landslides, such as rock avalanches and debris flows, show a particularly high hazard potential due to their high mobility, long travel distance, and fast propagation speed. In recent years, the geohazard community has put a lot of effort into developing computational run-out models in order to assess and predict risks associated with rapid landslides and to develop mitigation strategies. Most of the models in practical use are based on a (computationally efficient) “shallow-flow-type” process description and depth-averaging techniques (e.g., Pitman et al., 2003; Hungr, 2009; Pastor et al., 2009; Christen et al., 2010; Xia and Liang, 2018). In these, the flowing material is treated as an “equivalent fluid” and governed by idealized internal and basal rheologies (Hungr, 2009). Alternative (computationally demanding) models aim to directly describe fully three-dimensional flow behavior. They hence offer a higher process complexity level (e.g., Mast et al., 2014; Teufelsbauer et al., 2011) yet are typically not feasible for practical hazard mitigation purposes. Detailed reviews of computational run-out models for rapid, flow-like landslides have been published by McDougall (2017) and Pastor et al. (2018).

An indispensable input to any of these computational landslide run-out models is data that represent the terrain in which the slide is likely to occur. Pioneered by Miller and Laflamme (1958), digital elevation models (DEMs) have become the most popular form of representing topographies in the scientific community. Methods for generating DEMs have evolved rapidly over decades from conventional approaches, like field surveying and topographic-map digitizing, to passive and active remote sensing, such as stereoscopic photogrammetry, interferometric synthetic aperture radar (InSAR), and light detection and ranging (lidar); see Wilson (2012) for a comprehensive review. Differences between these methods exist in terms of their footprint, cost, resolution, and accuracy of the resulting DEM. Whatever method used, however, the resulting DEM will inevitably contain errors that are introduced either during source data acquisition or during data processing. The so-called DEM error hence refers to the difference between the true real-world elevations and their DEM representation. Typically, there is a lack of information on the DEM error, which has led to the notion of “DEM uncertainty”, which refers to what we do not know about the error; see Wechsler (2007).

Nowadays, several global DEM databases, e.g., SRTM (Rodriguez et al., 2006), AW3D30 (Courty et al., 2019), and TanDEM-X (Wessel et al., 2018), as well as some regional DEM databases (Pakoksung and Takagi, 2016) are publicly available. Commercial DEM databases that are associated with significant costs also exist (Hawker et al., 2018). Online initiatives such as OpenTopography facilitate community access and aim to democratize online availability of high-resolution topography data acquired with lidar and other technologies (Krishnan et al., 2011). Despite a broad variety of existing DEM sources, however, we are still facing (and will continue to face in the near future) a very limited availability of high-accuracy DEMs for some regions that are particularly prone to landslide hazards, e.g., in Asia (Froude and Petley, 2018). Whenever using DEM data for simulation-based landslide hazard analysis, it is hence important to be aware of DEM error and uncertainty and to consider their potential impact on computational run-out analyses and related computational risk assessments.

DEM error has had the attention of researchers for a long time. Many efforts have for instance been put into quantifying the error associated with specific DEM sources based on data of higher accuracy, e.g., acquired by satellite measurements (Berry et al., 2007; Mouratidis and Ampatzidis, 2019), medium-footprint lidar (Hofton et al., 2006), or GPS survey (Rodriguez et al., 2006; Bolkas et al., 2016; Patel et al., 2016; Wessel et al., 2018; Elkhrachy, 2018). Meanwhile, a variety of methods have been devised to classify DEM error into various categories (Oksanen, 2003; Hengl et al., 2004; Fisher and Tate, 2006). Due to the complexity of potential influencing factors (sensor technology, retrieval algorithms, data processing, land cover and surface morphology, terrain attributes; Wilson, 2012; Fisher and Tate, 2006; Gonga-Saholiariliva et al., 2011), these methods can only constrain the DEM error and will not deterministically correct for it at all grid points. Hence, DEM uncertainty remains and has to be accounted for in any subsequent analysis that relies on the DEM data.

In this circumstance, a stochastic simulation is an effective computational approach to deal with the situation (Holmes et al., 2000). Instead of considering a single (assumed as accurate) DEM, the fundamental idea of a stochastic simulation in the context of DEM uncertainty propagation is to separate the DEM into a known deterministic contribution and an unknown DEM error. DEM uncertainty is then accounted for by treating the DEM error as a random field consisting of a collection of random variables defined at selected grid points. An ensemble of equiprobable realizations of the random field is then generated based on certain assumptions and available information about DEM error. This could for instance be the so-called root mean square error (RMSE), a minimalist indicator for the overall error magnitude, or a semivariogram that provides information about the spatial autocorrelation of the DEM error. Adding the DEM error realizations to the known deterministic DEM contribution results in an ensemble of equiprobable DEM realizations, which can finally be used for a DEM uncertainty propagation analysis.

Stochastic simulation methods for DEM uncertainty propagation analyses have been developed since the 1990s and are by now widely applied in many fields, including terrain analysis (Holmes et al., 2000; Raaflaub and Collins, 2006; Moawad and EI Aziz, 2018), flood modeling (Watson et al., 2015; Hawker et al., 2018; Kiczko and Miroslaw-Swiatek, 2018), soil erosion modeling (Aziz et al., 2012), landslide susceptibility mapping (Qin et al., 2013), and dry-block-and-ash-flow modeling (Stefanescu et al., 2012). With respect to rapid, flow-like landslide run-out modeling, very little work has been done to assess the potential impact of DEM uncertainty, most likely due to the complexity, and hence level of sophistication, of the associated process models. Meanwhile, however, advances in computing technology have led to computationally feasible and well-developed landslide run-out simulation tools. As one of the most important inputs for these tools, a DEM determines the landslide's flow path. A natural next step is hence to consider the impact of DEM uncertainty in these models, as overlooking DEM uncertainty may lead to a bias in risk management decisions. The major aim of this study is therefore to describe two different approaches in order to incorporate DEM uncertainty into computational landslide run-out analyses and to investigate and discuss the feasibility of the approaches, as well as whether DEM uncertainty is critical to landslide run-out modeling and affects the modeling's results.

This paper is organized as follows: in Sect. 2, we briefly describe the landslide run-out model used in this study, which is a continuum-mechanical shallow-flow model based on the Voellmy–Salm rheology. In Sect. 3, we call on various methods to account for DEM uncertainty with a major focus on two approaches, namely an unconditional and a conditional stochastic simulation method. The rest of the paper is devoted to investigating DEM uncertainty propagation for rapid, flow-like landslides based on an integrated workflow that combines the aforementioned computational process model (Sect. 2) with the stochastic DEM simulations (Sect. 3). Note that, while in our particular study we chose to use a continuum-mechanical shallow-flow process model based on the Voellmy–Salm rheology, the workflow itself is modular and nonintrusive. It would hence also be possible to couple the stochastic DEM simulation with any other (DEM-based) computational landslide model. Section 4 describes the modular Python-based workflow that we developed in order to set up and manage the workflow and to interpret its simulation results. We present a series of computational scenarios based upon a historic landslide event in Sect. 5. All scenarios compare the unconditional and conditional stochastic DEM simulation. Finally, Sect. 6 is devoted to a discussion of our results. Important conclusions are drawn in Sect. 7.

2 Landslide process model

As detailed in the introduction, a variety of process-based computational landslide run-out models have been developed in recent decades. Among these is a family of depth-integrated shallow-flow-type landslide models that we chose as the basis for our work. Shallow-flow-type landslide models can be further classified based on their applied basal rheology, e.g., Voellmy, Bingham, and quadratic resistance model (Naef et al., 2006; Hungr and McDougall, 2009). Our study uses the Voellmy–Salm (VS) process model, which is a depth-averaged continuum-mechanical model incorporating the Voellmy basal rheology. Note that the stochastic workflow presented later is modular and does not depend on this choice. Hence, the Voellmy model can straightforwardly be substituted by other computational process models.

2.1 Reference frame and relation to topographic error

Let $\mathit{\{}X,Y,Z\mathit{\}}$ denote a fixed Cartesian coordinate system, in which X and Y are the horizontal axes and Z is the vertical axis. The coordinates of a point in the Cartesian coordinate system are denoted by $(X,Y,Z)$. A topography can then be expressed as a surface mapping of horizontal X and Y coordinates and represents the elevation at each point, namely Z(X,Y). The mapped topography induces a surface coordinate system $\mathit{\{}x,y,z\mathit{\}}$, in which x and y denote tangential directions and z points in the direction of the surface normal. Hence any vector that is constant with respect to the fixed Cartesian coordinates system, e.g., gravitational acceleration $\mathbf{g}=(g_X,g_Y,g_Z{)}^T=(\mathrm{0},\mathrm{0},-g{)}^T$, spatially varies when interpreted in terms of the surface-mapped coordinated system $\mathbf{g}=(g_x,g_y,g_z{)}^T$. Error or uncertainty in the topography representation Z(X,Y) hence directly translates into error and uncertainty in that vector representation.

2.2 Voellmy rheology computational process model

The Voellmy process model along with its computational implementation is described in Bartelt et al. (1999) and Christen et al. (2010). It assesses the slide's dynamics in terms of flow height $H(x,y,t)$ and depth-averaged velocity $\mathbf{U}(x,y,t):=\left(U_x\right(x,y,t),U_y(x,y,t){)}^T$, both of which depend on time t and spatial coordinates x and y. The governing system reads

$$\begin{array}{}\text{(1a)}& {\displaystyle }{\partial }_{t}H+{\partial }_x\left(H{U}_x\right)+{\partial }_y\left(H{U}_y\right)=\dot{Q}(x,y,t)\text{(1b)}& {\displaystyle }\begin{array}{rl}& {\partial }_t\left(H{U}_x\right)+{\partial }_x\left(H{U}_x^{\mathrm{2}}+g_z{\displaystyle \frac{H^{\mathrm{2}}}{\mathrm{2}}}\right)+{\partial }_y\left(H{U}_x{U}_y\right)\\ & =g_{x}H-n_x(\mathit{\mu }{g}_{z}H+g{∥\mathbf{U}∥}^{\mathrm{2}}/\mathit{\xi })\end{array}\text{(1c)}& {\displaystyle }\begin{array}{rl}& {\partial }_t\left(H{U}_y\right)+{\partial }_x\left(H{U}_x{U}_y\right)+{\partial }_y\left(H{U}_y^{\mathrm{2}}+g_z{\displaystyle \frac{H^{\mathrm{2}}}{\mathrm{2}}}\right)\\ & =g_{y}H-n_y(\mathit{\mu }{g}_{z}H+g{∥\mathbf{U}∥}^{\mathrm{2}}/\mathit{\xi }).\end{array}\end{array}$$

Here, Eq. (1a) denotes the mass balance, in which H, U_x, and U_y stand for height and surface tangential velocity components and $\dot{Q}(x,y,t)$ stands for a mass production source term that accounts for erosion of material along the way. Equations (1b) and (1c) denote the x and y momentum balance, in which g_x, g_y, and g_z are the three local components of gravitational acceleration vector g. Furthermore, n_x and n_y are x and y components of the unit vector n that opposes the local velocity, and μ and ξ are two friction parameters that stand for dry Coulomb and turbulent friction coefficients, respectively. The friction parameters are determined by back analysis based on historic events. Note that additional model parameters introduced in the original publications, such as velocity shape factors and nonhydrostatic pressure corrections, are not taken into account as they are hard to constrain and have been shown to not critically affect the slide's dynamics (e.g., Hungr et al., 2005; Christen et al., 2010).

The topographic surface Z(X,Y) enters the governing equations of the process model implicitly in terms of the spatially varying gravitational acceleration vector $\mathbf{g}=(g_x,g_y,g_z{)}^T$. Any error and uncertainty present in the topography representation hence also enters the landslide run-out simulation results.

The VS model was first proposed to model snow avalanche (Salm, 1993). Recently it has been widely applied to other types of gravity-driven rapid mass movements including flow-like landslides (Pastor et al., 2018; Frank et al., 2015; Hussin et al., 2012; Kumar et al., 2019). In this study, the proprietary mass flow simulation platform RAMMS (Christen et al., 2010) which provides a GIS-integrated implementation of the VS model is used for landslide run-out modeling. It is integrated as a module of our workflow (see Sect. 4) that is developed for the purpose of DEM uncertainty propagation analysis.

3 Methods to represent DEM uncertainty

Again, the topographic surface is expressed as a function Z(X,Y) parameterized in horizontal coordinates X and Y. In practice, the function Z(X,Y) is often constructed from discrete gridded raster data. We hence assume that a domain of interest D is discretized into the horizontal X and Y direction, which results in a spatial grid defined as

$$\begin{array}{}\text{(2)}& \begin{array}{rl}& {\mathbf{D}}_{\mathrm{mn}}=\mathit{\{}{D}_{ij}=(X_i,Y_j\left)\right|(X_i,Y_j)\in D;i=\mathrm{1},\mathrm{2},\\ & \mathrm{\dots },m;j=\mathrm{1},\mathrm{2},\mathrm{\dots },n\mathit{\}}.\end{array}\end{array}$$

The elevation data associated with each grid point D_ij are defined as

$$\begin{array}{}\text{(3)}& {\mathbf{Z}}_{\mathrm{mn}}=\mathit{\{}{Z}_{ij}=Z(X_i,Y_j\left)\right|\forall D_{ij}\in D_{\mathrm{mn}}\mathit{\}}.\end{array}$$

The elevation Z_mn of a common DEM data product might be erroneous with respect to the true values as discussed in the introduction. If we denote the true elevation as

$$\begin{array}{}\text{(4)}& {\mathbf{Z}}_{\mathrm{mn}}^{*}=\mathit{\{}{Z}_{ij}^{*}=Z^{*}(X_i,Y_j\left)\right|\forall D_{ij}\in D_{\mathrm{mn}}\mathit{\}},\end{array}$$

the DEM error can be expressed as

$$\begin{array}{}\text{(5)}& {\mathit{ϵ}}_{\mathrm{mn}}=\mathit{\{}{\mathit{ϵ}}_{ij}=Z_{ij}^{*}-Z_{ij}|\forall D_{ij}\in D_{\mathrm{mn}}\mathit{\}}.\end{array}$$

If we knew the error ϵ_mn, we would be able to recover the real-world topographic surface ${\mathbf{Z}}_{\mathrm{mn}}^{*}$. The fact, however, that the error is unknown or we only have limited information about it implies an uncertainty in the input to our landslide process simulation. Within this study, we will refer to the uncertainty associated with the unknown DEM error as DEM uncertainty. In this circumstance, each ϵ_ij is treated as a random variable and ϵ_mn is accordingly treated as a random field, which consists of a collection of random variables ϵ_ij. By generating multiple realizations of the random field ϵ_mn, DEM uncertainty can be represented. This process is widely known as stochastic simulation. It requires a suitable model to describe the jointed uncertainty in all ϵ_ij based on limited available information about DEM error. The task can be further divided into determining (1) the probability distribution function (pdf) of each ϵ_ij which quantifies local uncertainty at each grid point and (2) the correlation between different ϵ_ij which is usually termed spatial autocorrelation of DEM error.

According to available information on the DEM error, existing approaches that could be used to solve the two issues can be generally classified into two groups:

• a.

  unconditional stochastic simulation (USS),

• b.

  conditional stochastic simulation (CSS).

More specifically, USS is only informed of properties of DEM error, e.g., the RMSE, and thus does not honor any actual DEM error values. CSS is informed of a certain number of actual DEM error values at reference locations within the DEM, e.g., obtained from higher-accuracy reference data, and thus could directly honor the actual DEM error values at reference locations (Fisher and Tate, 2006).

3.1 Unconditional stochastic simulation (USS) based on the RMSE

Typically available information about the DEM error provided by DEM vendors is the root mean square error (RMSE). For a set of K reference locations, it is defined as

$$\begin{array}{}\text{(6)}& \mathrm{RMSE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{K}}\sum _{k=\mathrm{1}}^K(Z_{kk}^{*}-Z_{kk}{)}^{\mathrm{2}}}.\end{array}$$

Here, ${\mathbf{Z}}_{KK}^{*}=\mathit{\{}{Z}_{kk}^{*}=Z^{*}(X_k,Y_k\left)\right|(X_k,Y_k)\in D;k=\mathrm{1},\mathrm{2},\mathrm{\dots },K\mathit{\}}$ denotes higher-accuracy elevation values measured at the reference locations and ${\mathbf{Z}}_{KK}=\mathit{\{}{Z}_{kk}=Z(X_k,Y_k\left)\right|(X_k,Y_k)\in D;k=\mathrm{1},\mathrm{2},\mathrm{\dots },K\mathit{\}}$ denotes corresponding elevation values based on the DEM.

It should be noted that, while the RMSE is typically available, this is not true for the reference elevation values ${\mathbf{Z}}_{KK}^{*}$ themselves. As stated numerous times in the literature, it is critical that the RMSE only provides a global indication of DEM error magnitude without any information about its spatial autocorrelation. Still, it is by far the most widely used DEM error indicator for many DEM databases and mostly the only available information that are included with DEM products. In this circumstance, USS could be used to represent DEM uncertainty and study its propagation into landslide run-out analyses.

Modeling DEM uncertainty based on USS assumes that all local error values ϵ_ij are independent and fulfill the same univariate Gaussian distribution with a mean (μ) of zero and a standard deviation (σ) equivalent to the given RMSE. Under this assumption, an ensemble of spatially uncorrelated realizations of the random field ϵ_mn can be generated by randomly assigning error values to each ϵ_ij according to its local Gaussian probability distribution.

In the next step, we have to account for the (unknown) spatial autocorrelation of ϵ_mn. Potential methods that could be applied are simulated annealing, spatial autoregressive modeling, spatial moving averages, etc.; see Wechsler (2007). Simulated annealing is generally computationally intensive, and spatial autoregressive modeling becomes impractical for the simulation of large areas (Oksanen, 2006). In this study, we use the spatial moving-averages method that increases the spatial autocorrelation by filtering spatially uncorrelated realizations with a distance-weighted filter proposed by Wechsler and Kroll (2006). For ϵ_ij at one grid point of an uncorrelated realization, its value is replaced by the weighted average of ϵ_ij at all grid points within the filter kernel. The weight decreases with increasing distance to the grid point, which is similar to semivariogram trends (Wechsler and Kroll, 2006). The size of the filter denoted as d depends on the maximum autocorrelation length of ϵ_mn which again is unknown if the RMSE is the only available information. In practice, d is often determined based on the maximum autocorrelation length of the original DEM (Wechsler, 2007; Aziz et al., 2012).

Though it relies on some assumptions, such as an appropriate choice of correlation length d, the sketched approach is generally applicable if the RMSE is the only available information. It may become critical if a DEM contains a systematic bias which means that the mean of ${\mathbf{Z}}_{kk}^{*}-{\mathbf{Z}}_{kk}$ deviates largely from zero. More specifically, if we follow Fisher and Tate (2006) and Wessel et al. (2018) in defining mean μ and standard deviation σ as

$$\begin{array}{}\text{(7)}& \begin{array}{rl}& \mathit{\mu }={\displaystyle \frac{\mathrm{1}}{K}}\sum _{k=\mathrm{1}}^K(Z_{kk}^{*}-Z_{kk})\mathrm{and}\\ & \mathit{\sigma }=\sqrt{{\displaystyle \frac{\mathrm{1}}{K-\mathrm{1}}}\sum _{k=\mathrm{1}}^K\left(\right(Z_{kk}^{*}-Z_{kk})-\mathit{\mu }{)}^{\mathrm{2}}},\end{array}\end{array}$$

we can express the RMSE in terms of μ and σ as

$$\begin{array}{}\text{(8)}& \mathrm{RMSE}=\sqrt{{\mathit{\mu }}^{\mathrm{2}}+{\displaystyle \frac{K-\mathrm{1}}{K}}{\mathit{\sigma }}^{\mathrm{2}}}.\end{array}$$

If the number of reference points K is relatively large, $\sqrt{(K-\mathrm{1})/K}$ is close to 1. Equation (8) then indicates that the RMSE is larger than the standard deviation σ if the mean μ deviates from zero. The difference between the RMSE and σ increases with increasing μ. For example, the μ, σ, and RMSE of the global TanDEM-X DEM based on about 3 million reference points are 0.17, 1.28, and 1.29 m (Wessel et al., 2018). Those of the EU-DEM of Central Macedonia based on 12 943 reference points are 1.8, 3.6, and 4.0 m, while those of the ASTER GDEM of the same area based on the same reference points are 6.8, 7.6, and 10.2 m (Mouratidis and Ampatzidis, 2019). This means that assuming the standard deviation of the DEM error to be given as the RMSE consequently overestimates the variability in the DEM error if the mean deviates largely from zero.

The implications of both issues, namely the fact that the filter size d is unknown and has to be subjectively chosen and that the RMSE provides an insufficient representation of the DEM error, are investigated in the following study. For convenience, the two issues are referred to as

• unrepresentative RMSE and

• subjective d.

3.2 Conditional stochastic simulation (CSS) based on higher-accuracy reference data

This approach requires the availability of higher-accuracy reference data at certain reference locations, e.g., from higher-accuracy DEM products or GPS surveys. Note that, although these data might be subject to error themselves, it is fair to assume this error to be much smaller. This justifies the use of the higher-accuracy reference data as true elevation values ${\mathbf{Z}}_{KK}^{*}$. Based on ${\mathbf{Z}}_{KK}^{*}$, we could determine the statistics of the DEM error, e.g., the RMSE, the μ, and the σ as discussed in Sect. 3.1. Likewise, we can assess the spatial autocorrelation of the DEM error, e.g., in the form of a semivariogram model (see Sect. 5.2.1). In addition, we know the DEM error at the reference locations exactly, denoted as ${\mathit{ϵ}}_{KK}^{*}=\mathit{\left\{}{\mathit{ϵ}}_{kk}^{*}\right|k=\mathrm{1},\mathrm{2},\mathrm{\dots },K\mathit{\}}$. Yet, we still lack knowledge about the DEM error away from the K reference locations, hence the complete random field ϵ_mn.

In that situation, conditional stochastic simulation (CSS) can be used to simulate, i.e., generate, realizations of the random field ϵ_mn. Many geostatistical methods of conditional simulation could be applied, including sequential simulation algorithms, the p-field approach, and simulated annealing (Goovaerts, 1997). In this study, we apply a sequential Gaussian simulation. It is the most attractive technique for stochastic spatial simulation according to Temme et al. (2009) and has been widely utilized in DEM uncertainty propagation analysis (Holmes et al., 2000; Aziz et al., 2012).

The sequential Gaussian simulation sequentially samples each local error ϵ_ij along a random path that consists of all grid points D_ij under the multi-Gaussian assumption. This means that, assuming the random field ϵ_mn satisfies a multivariate Gaussian distribution, each ϵ_ij fulfills a univariate Gaussian distribution denoted as N(μ_ij,σ_ij). The essential idea now is that the mean μ_ij and standard deviation σ_ij are determined sequentially by means of simple kriging based on the semivariogram model of DEM error that provides covariances in simple kriging equations and the conditioning information including ${\mathit{ϵ}}_{KK}^{*}$ and previously sampled ϵ_ij. By making each univariate Gaussian distribution conditional not only on ${\mathit{ϵ}}_{KK}^{*}$ but also on all previously sampled ϵ_ij, the semivariogram model of DEM error is reproduced in realizations of ϵ_mn (Goovaerts, 1997). The process to generate one realization of ϵ_mn is as follows:

1. Determine a semivariogram model to represent the spatial autocorrelation of DEM error based on normal score transformed ${\mathit{ϵ}}_{KK}^{*}$.

2. Define a random path visiting each D_ij once.

3. At each D_ij, determine N(μ_ij,σ_ij) using simple kriging based on the semivariogram model and normal score transformed ${\mathit{ϵ}}_{KK}^{*}$.

4. Sample a value from N(μ_ij,σ_ij), assign it to ϵ_ij, and add ϵ_ij into normal score transformed ${\mathit{ϵ}}_{KK}^{*}$.

5. Repeat steps (3) and (4) until all D_ij along the path are visited.

6. Back-transform all sampled ϵ_ij to the original distribution of ${\mathit{ϵ}}_{KK}^{*}$.

Multiple realizations can be generated by defining different random paths.

4 Implementation

Studying the impact of DEM uncertainty on landslide run-out modeling is computationally intensive and technically demanding. It includes representing DEM uncertainty in terms of a large number of DEM realizations, conducting numerous landslide run-out modeling based on the DEM realizations, and postprocessing extensive output data. In addition, understanding how DEM uncertainty affects terrain attributes may facilitate us in interpreting its impact on landslide run-out modeling. This requires the ability to calculate terrain attributes, e.g., slope and roughness, of the original DEM as well as of the generated DEM realizations.

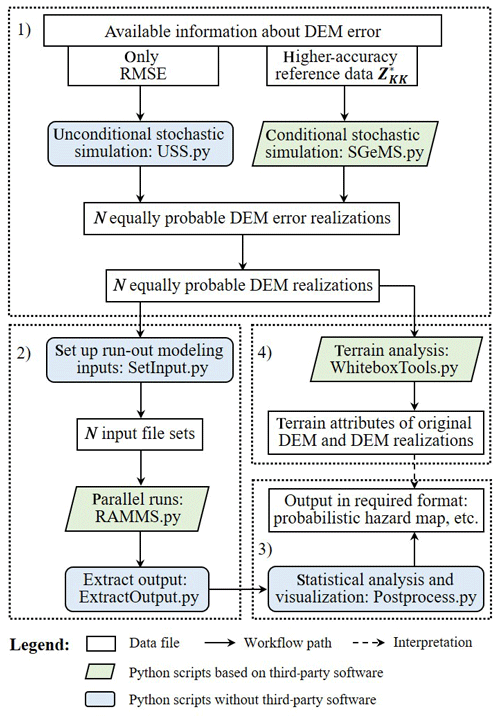
Figure 1 Computational workflow of DEM uncertainty propagation in landslide run-out simulation. It is part of our PSI-slide package in development that is designed for the purpose of systematically investigating the impact of various sources of uncertainty on simulating gravity-driven mass movements (Kowalski et al., 2018; Zhao and Kowalski, 2018). The workflow consists of four modules: (1) DEM uncertainty representation, (2) landslide run-out modeling, (3) statistical analysis and visualization, and (4) terrain analysis.

In this study, we propose a workflow that integrates our own Python implementation of selected aspects of the workflow and existing software as well as toolboxes to solve the above-mentioned tasks. It is part of our PSI-slide (Predictive Simulation of Slides) package in development that is designed for the purpose of systematically investigating the impact of the various sources of uncertainty on simulating gravity-driven mass movements (Kowalski et al., 2018; Zhao and Kowalski, 2018). Herein, we focus on DEM uncertainty. Figure 1 illustrates the workflow. It consists of four modules:

1. DEM uncertainty representation. In this module, we generate an ensemble of N equally probable DEM realizations to represent DEM uncertainty based on available information about DEM error. USS as introduced in Sect. 3.1 is implemented without third-party software (USS.py) for cases in which only the RMSE is available. For cases in which higher-accuracy reference data are provided, CSS as introduced in Sect. 3.2 is implemented by integrating the sequential Gaussian simulation algorithm of the Stanford Geostatistical Modeling Software (SGeMS; Remy et al., 2009) into our workflow (SGeMS.py).

2. Landslide run-out modeling. This module is used to conduct N landslide run-out simulations based on the N DEM realizations generated in module (1). In this study we employ the proprietary mass flow simulation platform RAMMS (Christen et al., 2010) which provides a GIS-integrated implementation of the VS model. First, a Python script named SetInput.py is called to set up required inputs for each simulation run. Then a Python script named RAMMS.py starts parallel runs of RAMMS using the Python SCOOP module. In the end, a Python script named ExtractOutput.py is called to extract user-specified outputs.

3. Statistical analysis and visualization. This module is used to conduct statistical analysis on the user-specified outputs from module (2) and visualize results. It is mainly based on the Python NumPy and Matplotlib modules. For example, a probabilistic hazard map can be produced to indicate potential hazard area.

4. Terrain analysis. This module is used to analyze terrain characteristics of the original DEM and DEM realizations from module (1), which may help us to interpret outputs from module (3). This is achieved by integrating several terrain analysis tools from WhiteboxTools (Lindsay, 2018) like calculating slope, aspect, roughness index, etc. into our workflow (WhiteboxTools.py).

5 Case study

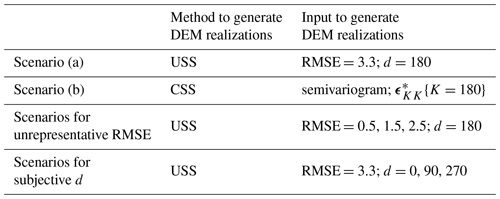
This study is based upon a historic landslide and two DEM sources. For the purpose of DEM uncertainty propagation analysis, we assume one DEM source to be more accurate than the other and then obtain higher-accuracy reference data from the more accurate DEM source to assess elevation error in the less accurate DEM source. We design a series of computational scenarios based on the higher-accuracy reference data to study the impact of DEM uncertainty on landslide process simulation for both the case where only the RMSE is available and the case where higher-accuracy reference data are available. Additional computational scenarios are designed to study the unrepresentative RMSE and subjective d issues as detailed in Sect. 3.1 in the form of a sensitivity analysis.

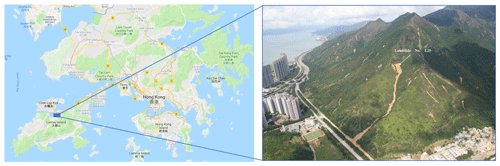
Figure 2 The 2008 Yu Tung Road landslide. Left: Google map of Hong Kong (map data © 2019). Right: aerial photograph of Yu Tung Road site after the 2008 landslide. It corresponds to the No. L25 landslide in the GEO Report (AECOM Asia Company Limited, 2012).

5.1 Scenario background and DEM sources

A historic landslide happened on 7 June 2008 on the hillside above Yu Tung Road in Hong Kong due to an intense rainfall event; see Fig. 2. It was the largest flow-like landslide out of 19 landslides during that event. Around 3400 m³ of material was mobilized and traveled about 600 m until it was deposited. The landslide event had a severe infrastructural impact, as it led to closure of the westbound lanes of Yu Tung Road for more than 2 months (AECOM Asia Company Limited, 2012). The Yu Tung Road landslide also served as a benchmark case for predictive landslide run-out analysis at the second Joint Technical Committee on Natural Slopes and Landslides (JTC1) workshop on Triggering and Propagation of Rapid Flow-like Landslides in Hong Kong 2018 (Pastor et al., 2018). Two types of DEM data of the Yu Tung Road area were the basis for this study:

• A public 5 m resolution digital terrain model covering the whole area of Hong Kong (HK-DTM). It can be downloaded from the website of the Survey and Mapping Office of Hong Kong. The HK-DTM is generated from a series of digital orthophotos, which are derived from aerial photographs taken in 2014 and 2015. The reported accuracy is ±5 m at a 90 % confidence level. (DATA.GOV.HK, 2020)

• A 2 m resolution DEM (2m-DEM) covering the main area of the Yu Tung Road landslide event. Its boundary is shown in Fig. 3a. It was provided for the benchmark exercise during the second JTC1 workshop. It is produced based on the field mapping after the 2008 Yu Tung Road landslide event and a pre-event DEM. According to the “note to participants” of the second JTC1 workshop (which can be found under the link http://www.hkges.org/JTC1_2nd/be.html, last access: 18 May 2020), the 2m-DEM represents the rupture surface in the release zone area and the pre-event slope surface in other areas. The rupture surface is obtained based on the field mapping (AECOM Asia Company Limited, 2012).

In this study, we assume the 2m-DEM to be more accurate than the 5 m resolution HK-DTM. Similar to our consideration at the beginning of Sect. 3.2, the 2m-DEM and 5 m resolution HK-DTM correspond to Z^* and Z as defined in Sect. 3. A set of higher-accuracy reference data ${\mathbf{Z}}_{KK}^{*}$ can hence be determined to provide information to represent uncertainty in the 5 m resolution HK-DTM. At the channel base, information on vegetation in the 2m-DEM is not available. The 5 m resolution HK-DTM includes vegetation. In this study, any vegetation present in the channel base in the 5 m resolution HK-DTM is not explicitly accounted for in the sense of a modeled DTM correction. Rather, it is subsumed as part of the DEM error.

It should be noted that, due to a different time of DEM data acquisition, there are infrastructural factors present in the 5 m resolution HK-DTM but not in the 2m-DEM. After the time of data acquisition of the 2m-DEM, debris-resisting barriers and a road were built in the area within the red ellipse and blue rectangle, respectively, in Fig. 3a. They are reflected in the HK-DTM but not in the 2m-DEM, which leads to large inconsistency between the two DEMs in that area. Therefore, to avoid an unrealistically large error in the HK-DTM, data from the 2m-DEM in that area are excluded from higher-accuracy reference data ${\mathbf{Z}}_{KK}^{*}$.

5.2 DEM realizations

5.2.1 Information on DEM error

As shown in Fig. 3a, we pick 180 evenly spaced reference locations from the HK-DTM grid points within the boundary of the 2m-DEM. Higher-accuracy reference data at these locations are obtained from the 2m-DEM using bilinear interpolation, denoted as ${\mathbf{Z}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$. Subtracting the corresponding elevation values of the HK-DTM Z_KK{K=180} from ${\mathbf{Z}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$, we obtain elevation error values of the HK-DTM at the 180 reference locations, denoted as ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$.

Figure 3b shows the histogram of ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$. Of the elevation error values, 90 % are within −5.84 m and −1.04 m, which is close to the reported accuracy (see Sect. 5.1). The μ, σ, and RMSE according to Eqs. (7) and (6) are −3.0, 1.5, and 3.3 m, respectively. Here, it should be noted that the RMSE is larger than the σ since the μ is not zero, which indicates a systematic bias. As discussed in Sect. 3.1, this also indicates that assuming the standard deviation of the HK-DTM error to be equivalent to the RMSE in USS would overestimate the variability in the HK-DTM error.

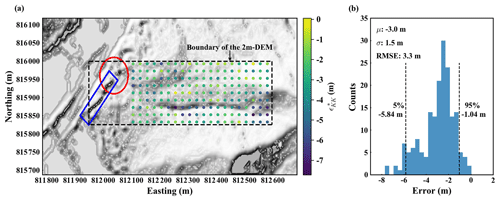
Figure 3 (a) Elevation error ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$ of the HK-DTM at 180 reference locations. The background is the hillshade plot of the HK-DTM. Debris-resisting barriers and a road in the area indicated by the red ellipse and blue rectangle constructed after the 2008 landslide event are represented in the HK-DTM but not in the 2m-DEM. It causes inconsistency between the two DEMs in that area. To avoid an unrealistically large error in the HK-DTM, data from the 2m-DEM in that area are excluded from higher-accuracy reference data. (b) Histogram of ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$. The RMSE is larger than the standard deviation (σ) since the mean (μ) is not zero. As discussed in Sect. 3.1, this indicates that assuming the standard deviation of the HK-DTM error to be equivalent to the RMSE in USS would overestimate the variability in the HK-DTM error.

Figure 4 Experimental semivariances based on ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$ and fitted parameterized semivariogram model given by Eq. (9). The range of the semivariogram model is 180 m. It indicates the maximum autocorrelation length of DEM error, on which the size of the spatial moving filter d depends (see Sect. 3.1).

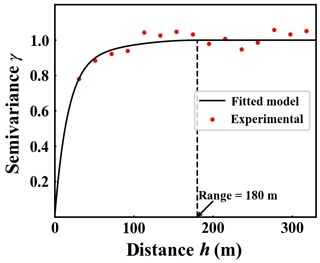
Based on ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$, we can determine an isotropic semivariogram model which describes the spatial autocorrelation of the HK-DTM error. It results in

$$\begin{array}{}\text{(9)}& \mathit{\gamma }\left(h\right)=\mathrm{0.1}\times \mathrm{Sph}\left({\displaystyle \frac{h}{\mathrm{180}}}\right)+\mathrm{0.9}\times \mathrm{Exp}\left({\displaystyle \frac{h}{\mathrm{50}}}\right).\end{array}$$

Here, Sph(⋅) and Exp(⋅) denote the basic spherical and exponential semivariogram models (Goovaerts, 1997) and h denotes the horizontal distance between any two locations. A comparison between the experimental semivariance values based on ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$ and the parameterized semivariogram model given by Eq. (9) can be seen in Fig. 4. Semivariance is a measure of spatial dependence between DEM error values at two different locations. The continuous semivariogram model is fitted to the experimental semivariance values so as to deduce semivariance values for any possible distance h required by simple kriging (Goovaerts, 1997). The range of the semivariogram model is 180 m. It indicates the maximum autocorrelation length of the HK-DTM error, on which the size of the spatial moving filter d depends (see Sect. 3.1).

5.2.2 DEM uncertainty scenarios

As mentioned in Sect. 3, DEM users are often restricted to DEM error information in the form of a single RMSE value per data product. Rarely, they have higher-accuracy reference data. In order to account for both situations, two corresponding information levels are considered in the following study.

• a.

  Rudimentary error information – the RMSE only. In this situation, the RMSE is assumed to be the only available error information for the 5 m resolution HK-DTM. In order to compare results to (b), we employ the RMSE 3.3 m as generated based on ${\mathbf{Z}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$ as well as the size of the spatial moving filter d of 180 m to match the range of the fitted semivariogram model in Fig. 4. USS introduced in Sect. 3.1 is used to generate N realizations of the HK-DTM, denoted as USS_N{RMSE =3.3, d=180}.

• b.

  Highly informed – higher-accuracy reference data. In this situation, ${\mathbf{Z}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$ is assumed to be available. That means we know the error ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$ at the reference locations exactly and the fitted semivariogram model based on ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$. CSS introduced in Sect. 3.2 is used to generate N realizations of the HK-DTM, denoted as CSS_N.

Following the two nominal scenarios (a) and (b) that are based on specific error ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$ at reference locations determined from the available data sources, we also want to analyze the impact of unrepresentative RMSE and subjective d issues of USS as introduced in Sect. 3.1 in the form of a sensitivity analysis. Hence, to what extent can we trust the results of USS if only a single RMSE value per data product is available. Three additional values of the RMSE that are 0.5, 1.5, and 2.5 m with a fixed d of 180 m are used as inputs for USS to study the unrepresentative RMSE issue. It should be noted that the RMSE 1.5 m corresponds to the true standard deviation σ based on ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$; see Fig. 3b. Another three additional values of d that are 0, 90, and 270 m with a fixed RMSE of 3.3 m are used to consider the subjective d issue. The corresponding realizations of the HK-DTM are denoted as USS_N{RMSE =0.5, 1.5, 2.5, d=180} and USS_N{RMSE =3.3, d=0, 90, 270}. To sum up, all the scenarios for stochastic simulation are listed in Table 1.

Table 1 Scenarios for stochastic simulation.

Note that, in scenario (a) and (b), the inputs to generate DEM realizations are obtained from higher-accuracy reference data at the 180 reference locations.

5.2.3 Number of DEM realizations

The integrity of a stochastic simulation requires a large number of DEM realizations, and more realizations naturally require many computational resources. Thus one has to find a reasonable compromise. Typically, this can be found through a representative convergence study. Since in our study we address the impact of topographic uncertainty on landslide run-out simulation, we analyze the relative change in topographic attributes with an increasing number of HK-DTM realizations in a preliminary study. In this study, 1000 HK-DTM realizations are generated for the two information levels (a) and (b) as introduced in Sect. 5.2.2, namely USS_N=1000{RMSE =3.3, d=180} and CSS_N=1000, respectively. Topographic attributes including slope, aspect, and roughness at all HK-DTM grid points are calculated for each realization.

We define an indicator of the relative change similarly to Raaflaub and Collins (2006) to investigate the converging behavior. Taking slope as an example, for a given number n of HK-DTM realizations, we first calculate the standard deviation of slope at each HK-DTM grid point over the n realizations. The calculated standard deviation values at all grid points constitute a grid of standard deviation values. Then we calculate the standard deviation of the grid of standard deviation values, which leads to a single standard deviation value for the given number n. For each n from 1 to 1000, we can correspondingly calculate a standard deviation value. The same procedure is applied to aspect, roughness, and elevation.

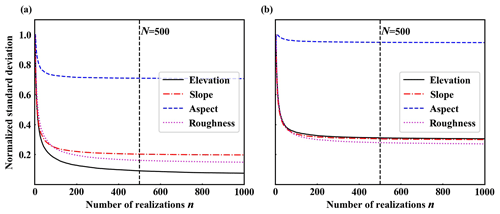
Figure 5 The relative change in topographic attributes with respect to the number of HK-DTM realizations. The realizations are generated with (a) USS_N{RMSE =3.3, d=180}; (b) CSS_N. Beyond N=500, adding more realizations has little impact on topographic attributes. Therefore, we set N=500 for all computational scenarios in Table 1.

Figure 5 shows plots of normalized standard deviation of the grid of standard deviation values with respect to the number of HK-DTM realizations for the two situations (a) and (b). It can be seen that for situation (a), aspect levels out first, followed by slope, roughness, and elevation. Beyond 500 realizations, there is little change in normalized standard deviations. This indicates that adding more realizations has little impact on topographic attributes. For situation (b), aspect also levels out first while the other three attributes show less difference. Compared to (a), (b) converges faster, which indicates CSS requires fewer DEM realizations than USS does. Nevertheless, we set N=500 for the remainder of this study both for USS and CSS. Namely, we generate 500 HK-DTM realizations for each scenario input set as listed in Table 1.

5.2.4 Statistics of DEM error realizations

In order to conduct a further quality check of our implementation of both USS and CSS, we investigate the corresponding DEM error realizations of the USS_N=500{RMSE =3.3, d=180} and CSS_N=500 scenarios, denoted as ${\mathrm{USS}}_{N=\mathrm{500}}^{\mathrm{Error}}$ {RMSE =3.3, d=180} and ${\mathrm{CSS}}_{N=\mathrm{500}}^{\mathrm{Error}}$, respectively. Ideally, the local mean μ_ij and standard deviation σ_ij of DEM error realizations at each grid point D_ij should match the underlying assumptions as introduced in Sect. 3 if the number of DEM error realizations is sufficiently large.

Figure 6a and c show the mean and standard deviation grid of the ${\mathrm{USS}}_{N=\mathrm{500}}^{\mathrm{Error}}${RMSE =3.3, d=180}. It can be seen that the mean values at all grid points are centered around 0 m. The standard deviation values are centered around 3.3 m. This corresponds to the assumption underlying USS that all ϵ_ij fulfill the same univariate Gaussian distribution with a mean (μ) of zero and a standard deviation (σ) given by the RMSE (see Sect. 3.1).

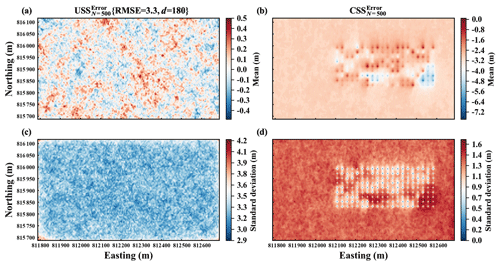
Figure 6 Statistics of HK-DTM error realizations. (a) Mean and (c) standard deviation grid of ${\mathrm{USS}}_{N=\mathrm{500}}^{\mathrm{Error}}${RMSE =3.3, d=180}. The mean and standard deviation values are centered around 0 and 3.3 m. (b) Mean and (d) standard deviation grid of ${\mathrm{CSS}}_{N=\mathrm{500}}^{\mathrm{Error}}$. The mean values at grid points away from the reference locations are centered around the mean (μ) −3.0 m of ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$ and are equal to ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$ at the reference locations. The standard deviation values at grid points away from the reference locations are centered around the standard deviation (σ) 1.5 m of ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$ and vanish at the reference locations. This matches the assumptions underlying USS and CSS as introduced in Sect. 3.

Figure 6b and d show the mean and standard deviation grid of the ${\mathrm{CSS}}_{N=\mathrm{500}}^{\mathrm{Error}}$. The mean values at grid points away from the reference locations are centered around the mean (μ) −3.0 m based on ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$. They become close to ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$ with the decrease in distance between grid points and the reference locations and are equal to ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$ at the reference locations. Similarly, the standard deviation values at grid points away from the reference locations are centered around the standard deviation (σ) 1.5 m based on ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$. They vanish at the reference locations. This also corresponds to the assumption underlying CSS that each ϵ_ij fulfills a univariate Gaussian distribution with a mean μ_ij and standard deviation σ_ij given by the simple kriging estimate and simple kriging standard deviation at D_ij (see Sect. 3.2).

5.3 Landslide process simulation setup

With the DEM realizations generated in Sect. 5.2, we can study the impact of DEM uncertainty on landslide process simulation. Here, we introduce the key inputs and our setup for the process simulation.

5.3.1 Model input

Release zone area and fracture height, friction parameters, and a DEM are three key inputs for performing a deterministic landslide process simulation based on the VS model and utilizing the mass movement simulation platform RAMMS (Christen et al., 2010). For all scenarios, we consistently use the release zone area as provided for the benchmark exercise during the second JTC1 workshop, which matches that of the 2008 Yu Tung Road landslide (Pastor et al., 2018) as shown in Fig. 7b. The fracture height is assumed to be 1.2 m, leading to a release volume of around 2900 m³, based on the 5 m resolution HK-DTM. The friction parameters μ and ξ used in this study are 0.105 and 300 m s⁻², respectively. They are suggested in the GEO Report issued by the Civil Engineering and Development Department of Hong Kong and are obtained using back analysis with information from a video capturing the lower portion of the landslide and detailed field mapping after the landslide (AECOM Asia Company Limited, 2012). The HK-DTM and all HK-DTM realizations generated in Sect. 5.2 are used as DEM inputs. Entrainment is not considered in this study.

It should be noted that release zone area and fracture height, as well as friction parameters, may also be subject to uncertainty in landslide modeling practice. In this study we keep them fixed and focus only on the DEM uncertainty which is mostly overlooked in landslide run-out modeling. Future work should therefore continue to focus on systematically quantifying all the uncertainty factors and evaluating their relative importance and interaction. Researchers carrying out this work should notice that increasing the dimension of uncertainty factors instantly requires a much larger number of simulation runs for stochastic simulation and computational-resource consumption may become prohibitively expensive. One promising solution to this challenge is to employ emulator techniques.

5.3.2 Simulation ensembles

We denote a deterministic landslide process simulation based on a DEM as a simulation run and N deterministic landslide process simulations based on N DEM realizations as a simulation ensemble. The following deterministic simulation and simulation ensembles are conducted based on the original HK-DTM and the aforementioned computational scenarios; see Table 1. They are named after the corresponding DEM and DEM realizations.

1. Deterministic simulation HK-DTM. One landslide process simulation run is conducted based on the original HK-DTM. This one time simulation corresponds to what is traditionally performed in a simulation-based hazard assessment study. The results serve as the basis to assess the impact of DEM uncertainty.

2. USS_N=500{RMSE =3.3, d=180} ensemble. A total of 500 landslide process simulations are conducted based on the USS_N=500{RMSE =3.3, d=180} DEM realizations as introduced in Sect. 5.2. Each of them is referred to as ${\mathrm{USS}}_{N=\mathrm{500}}^n${RMSE =3.3, d=180}, with $n=\mathrm{1},\mathrm{2},\mathrm{\dots },\mathrm{500}$. This ensemble allows us to access the impact of DEM uncertainty if only the RMSE is available.

3. CSS_N=500 ensemble. A total of 500 landslide process simulations are conducted based on the CSS_N=500 DEM realizations. Similar to (2), each of them is referred to as ${\mathrm{CSS}}_{N=\mathrm{500}}^n$, with $n=\mathrm{1},\mathrm{2},\mathrm{\dots },\mathrm{500}$. This ensemble allows us to assess the impact of DEM uncertainty if higher-accuracy reference data are available.

4. USS_N=500{RMSE =0.5, 1.5, 2.5, d=180} ensembles. For each of the three different RMSE values, 500 landslide process simulations are conducted, while keeping the maximum autocorrelation length d constant. They lead to 1500 process simulations. The results allow us to discuss the unrepresentative RMSE issue as detailed in Sect. 3.1. They can be also used to discuss the relationship between the degree of DEM uncertainty and its impact.

5. USS_N=500{RMSE =3.3, d=0, 90, 270} ensembles. For each of the three maximum autocorrelation length values, 500 landslide process simulations are conducted, while keeping the RMSE constant. They lead to 1500 process simulations. The results allow us to discuss the subjective d issue as detailed in Sect. 3.1.

All in all this adds up to one deterministic simulation run HK-DTM, as well as to simulation ensembles of 500 process simulations of both the USS_N=500 {RMSE =3.3, d=180} ensemble and the CSS_N=500 ensemble, which is constructed from higher-accuracy reference data based on the 2m-DEM, and 3000 additional process simulations to result in six ensembles of USS_N=500{RMSE =0.5, 1.5, 2.5, d=180} and USS_N=500{RMSE =3.3, d=0, 90, 270} to test sensitivities. Each process simulation takes around 1 min on a laptop with Intel Core i7-9750H CPU, adding up to around 67 h of simulation time.

6 Results and discussions

This section is organized according to the simulation ensembles introduced in Sect. 5.3.2. Section 6.1 presents the results of the deterministic simulation HK-DTM which serves as the basis for all following discussions. Section 6.2 is devoted to analyzing the impact of DEM uncertainty on landslide process simulation in the cases of only the RMSE being available (USS_N=500{RMSE =3.3, d=180} ensemble) and higher-accuracy reference data being available (CSS_N=500 ensemble). In Sect. 6.3, the unrepresentative RMSE and subjective d issues are discussed based on the ensembles described in Sect. 5.3.2 (labeled 4 and 5).

6.1 Deterministic simulation HK-DTM

In a continuum-mechanical landslide process model such as that used for this study and introduced in Sect. 2, the landslide flow behavior is characterized by its spatially varying height and velocity distribution over time, denoted as $H(x,y,t)$ and $\mathbf{U}(x,y,t)$. Hence, for the purpose of landslide hazard assessment and mitigation measure development, maximum height and velocity data over the duration of the landslide are most informative. Thus, we focus on the maximum values of $H(x,y,t)$ and $\mathbf{U}(x,y,t)$ over the whole time, denoted as H_max(x,y) and ∥U_max(x,y)∥.

Figure 7a and b show H_max(x,y) and ∥U_max(x,y)∥ as given by the deterministic simulation HK-DTM. It should be noted that there is a relatively high elevation area at the end part of the channel in the HK-DTM as denoted within the red circle in Fig. 7b. It corresponds to the construction of debris-resisting barriers after the 2008 Yu Tung Road landslide as introduced in Sect. 5.1. The flow material is decelerated and held back here. We will come back to this point later in Sect. 6.2.1.

Landslide run-out distance is often characterized in terms of its apparent friction angle. The tangent of the apparent friction angle is equal to the ratio of the landslide fall height and the run-out distance (DeBlasio and Elverhoi, 2008). The apparent friction angle evaluated from the deterministic simulation is 16.80^∘. This result is used as a reference to assess the impact of DEM uncertainty in the following discussions.

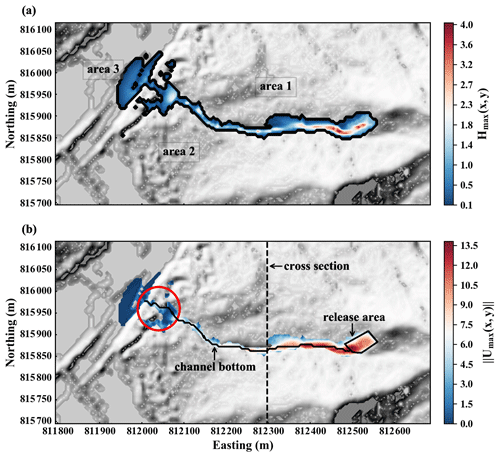
Figure 7 Results of the deterministic simulation HK-DTM. (a) H_max(x,y) above a cutoff threshold of 0.1 m. The black outline is the 0.1 m contour of H_max(x,y). The area within this outline is regarded as the hazard area. Area 1–3 are denoted for later discussions (see Sect. 6.2.1). (b) ∥U_max(x,y)∥ above a cutoff threshold of 0.01 m s⁻¹. The relatively high elevation area within the red circle decelerates and holds back the flow material. The channel bottom and cross section are denoted for later discussions (see Sect. 6.2.2).

6.2 USS_N=500{RMSE =3.3, d=180} ensemble and CSS_N=500 ensemble

While it is straightforward to present the results of a deterministic simulation run as shown in Sect. 6.1, a stochastic simulation-based ensemble of N simulation runs calls for tailored statistics to manage and interpret the extensive output data. First, we define the hazard probability $P_{(x_l,y_l)}$ at one location (x_l,y_l) as the frequency of H_max(x_l,y_l) exceeding a certain predefined height threshold value; hence

$$\begin{array}{}\text{(10)}& \begin{array}{rl}{P}_{(x_l,y_l)}& ={\displaystyle \frac{{\sum }_{n=\mathrm{1}}^N{P}_{(x_l,y_l)}^n}{N}},P_{(x_l,y_l)}^n\\ & =\left\{\begin{array}{ll}\mathrm{1},& \mathrm{if}{H}_{\max }^n(x_l,y_l)\ge \mathrm{threshold}\\ \mathrm{0},& \mathrm{otherwise},\end{array}\right.\end{array}\end{array}$$

where $H_{\max }^n(x_l,y_l)$ denotes the maximum flow height at location (x_l,y_l) for the nth simulation run of the corresponding ensemble. Hence $P_{(x_l,y_l)}^n$ indicates whether location (x_l,y_l) is within the hazard area of the nth simulation run for a given threshold, and $P_{(x_l,y_l)}$ indicates the resulting hazard probability at location (x_l,y_l) considering the complete ensemble. Here, the threshold is set as 0.1 m, which matches the cutoff threshold of the deterministic simulation HK-DTM in Fig. 7a. Evaluation of hazard probabilities at all locations then gives rise to a probabilistic hazard map (Stefanescu et al., 2012), which provides an overall view of the DEM uncertainty impact.

Besides assessing the overall impact of DEM uncertainty in terms of the probabilistic hazard map, we will also discuss the local impact of DEM uncertainty on dynamic flow properties, focusing on H_max(x,y) and ∥U_max(x,y)∥ at locations along the channel bottom and the channel cross section denoted in Fig. 7b.

6.2.1 Probabilistic hazard maps

Figure 8a and c show the probabilistic hazard map for both the USS_N=500 {RMSE =3.3, d=180} ensemble and the CSS_N=500 ensemble. It can be seen that the potential hazard area is much larger than the deterministic hazard area for both ensembles. The difference between the deterministic and the ensemble-based hazard area is most pronounced in area 1–3 for the USS_N=500 {RMSE =3.3, d=180} ensemble and in area 3 for the CSS_N=500 ensemble. Fig. 8b and d show boxplots of the apparent friction angle distribution for both ensembles. It is evident that the apparent friction angle of both ensembles varies largely with respect to the apparent friction angle of the deterministic simulation (16.80^∘). The CSS_N=500 ensemble-based apparent friction angle (mean 15.39^∘) is smaller than the USS_N=500 {RMSE =3.3, d=180} ensemble-based apparent friction angle (mean 16.76^∘).

As stated in Sect. 4, analyzing terrain characteristics of the original DEM and DEM realizations may help us to interpret simulation results. By a preliminary analysis, we did not find obvious relationships between landslide run-out simulation results and terrain characteristics at a specific location (on the cell level). One obvious reason for this is that a simulation result at one location is affected not only by terrain characteristics at the specific location but also by the complete upstream and surrounding terrain. Instead of discussing the effects of terrain characteristics at the cell level, we therefore focus on several compound terrain characteristics that help us to understand how DEM uncertainty may affect simulation results. The compound terrain characteristics include banks of the channel, especially the north bank near area 1 and south bank near area 2; the relatively high elevation area at the end part of the channel that holds back flow material as shown in Fig. 7b; topographic roughness; and the relatively flat area of area 3 (namely area with a relatively small slope).

Due to DEM uncertainty, topographic characteristics represented in DEM realizations vary from those represented in the original DEM. Specifically, firstly, topographic details of the deterministic channel tend to be dampened out in DEM realizations. The topographic details include banks of the channel as well as the relatively high elevation area at the end part of the channel that holds back flow material. Secondly, topographic roughness tends to increase.

Whether, where, and to what extent the topographic characteristics in DEM realizations would differ from the original DEM depend on (1) variability in DEM error – intuitively, the larger the variability, the more likely that topographic details of the deterministic channel would be dampened out and the larger the topographic roughness in DEM realizations – and (2) topographic details of the original DEM. If subject to the same DEM error, less well defined topographic characteristics in the original DEM are more likely to be changed in DEM realizations. For example, along the channel of the HK-DTM, the north bank of the channel near area 1, and the south bank of the channel near area 2, characteristics are less well defined compared to other parts of the channel banks. Flow material could be more easily diverted to area 1 and area 2 where elevations are relatively low and some local small channels exist. Area 3 could also be regarded as less well defined since it is relatively flat and thus is sensitive to DEM uncertainty (Temme et al., 2009).

The change in each topographic characteristic has a corresponding impact on landslide run-out behavior. Specifically (1) if banks of the deterministic channel are dampened out in DEM realizations, flow material tends to spread out along the channel cross-section direction and travel distance is shorter; (2) if the relatively high elevation area that holds back flow material is dampened out, flow material tends to travel further; and (3) increasing topographic roughness leads to higher simulated momentum losses and shorter travel distance as pointed out by McDougall (2017).

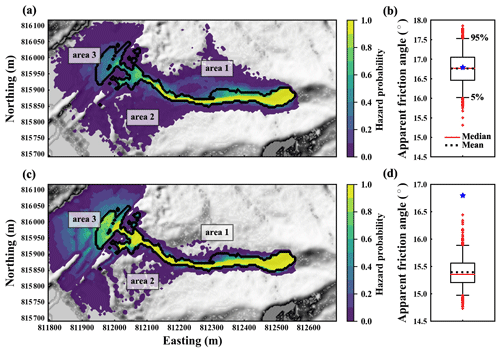
Figure 8 (a) Probabilistic hazard map and (b) corresponding apparent friction angle distribution of the USS_N=500 {RMSE =3.3, d=180} ensemble; (c) probabilistic hazard map and (d) corresponding apparent friction angle distribution of the CSS_N=500 ensemble. The black outline plotted on the hazard maps represents the deterministic hazard area (see Fig. 7a). In the boxplots, the blue star denotes the apparent friction angle of the deterministic simulation HK-DTM (see Sect. 6.1). The difference between the deterministic and the ensemble-based hazard area is most pronounced in area 1–3 for the USS_N=500 {RMSE =3.3, d=180} ensemble and in area 3 for the CSS_N=500 ensemble.

For the USS_N=500 {RMSE =3.3, d=180} ensemble, the variability in DEM error is relatively large, i.e., around 3.3 m governed by the non-bias-corrected RMSE based on ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$ (see Fig. 6c). In this situation, both the north bank near area 1 and south bank near area 2 as well as the relatively high elevation area at the end part of the channel can be dampened out in HK-DTM realizations. For the CSS_N=500 ensemble, the variability in DEM error is relatively small, i.e., around 1.5 m governed by the standard deviation (σ) based on ${\mathit{ϵ}}_{KK}^{*}\mathit{\{}K=\mathrm{180}\mathit{\}}$ (see Fig. 6d). In this situation, the banks tend to remain well defined, while the relatively high elevation area can be dampened out in HK-DTM realizations. Thus, area 1 and area 2 are possibly subject to hazard in the USS_N=500 {RMSE =3.3, d=180} ensemble but less likely to be so in the CSS_N=500 ensemble. As mentioned above, area 3 is a flat area which is sensitive to DEM uncertainty. Furthermore, it is located near the deposition, around which the impact of upstream DEM uncertainty seems to accumulate. Thus, it is highly affected in both ensembles.

The apparent friction angle distribution is determined by a combined effect of change in channel banks, change in the relatively high elevation area at the end part of the channel, and increasing topographic roughness. For the USS_N=500 {RMSE =3.3, d=180} ensemble, a deteriorated channel bank representation and increasing topographic roughness make flow material travel a shorter distance, i.e., larger apparent friction angle, while a deteriorated relatively high elevation area representation allows flow material to travel further, i.e., smaller apparent friction angle. For the CSS_N=500 ensemble, channel banks are likely to remain well defined and the degree of topographic roughness increase is lower due to its relatively small variability in DEM error compared to the USS_N=500 {RMSE =3.3, d=180} ensemble. Thus, flow material in the CSS_N=500 ensemble tends to travel a longer distance, i.e., smaller apparent friction angle, compared to the flow material in the USS_N=500 {RMSE =3.3, d=180} ensemble.

In summary, we can conclude from the probabilistic hazard maps and boxplots of apparent friction angle distribution that (1) accounting for DEM uncertainty may significantly increase the potential hazard area, (2) the potential hazard area is highly related to the variability in DEM error and topographic characteristics of the original DEM, and (3) USS based on the RMSE only may overestimate the spread of potential hazard area and underestimate travel distance due to a non-bias-corrected RMSE that overestimates the variability in DEM error.

It should be noted that the probabilistic hazard map here is constructed based on maximum height and a predefined threshold. In simulation-based hazard assessment practice, one may indicate potential hazard using other indicators, e.g., the maximum momentum that reflects the impact pressure, and correspondingly modify the threshold value. In this case, our workflow is easily extendible to account for other indicators.

6.2.2 Dynamic flow properties

Figure 9a, c, and e show elevation, maximum height, and maximum velocity at locations along the channel bottom based on the USS_N=500 {RMSE =3.3, d=180} ensemble. It is evident that both maximum height and maximum velocity at these locations largely vary from those of the deterministic simulation. Specifically, the mean of maximum height (maximum velocity) values at all the locations based on the deterministic simulation is 1.28 m (7.17 m s⁻¹). The mean of the ensemble-based 90 % confidence interval of maximum height (maximum velocity) is [0.18 m, 2.17 m] ([0.99 m s⁻¹, 7.89 m s⁻¹]; the range between the mean of the ensemble-based 5th percentile and the mean of the ensemble-based 95th percentile). Another observation is that the ensemble-based mean of flow dynamic properties is generally smaller than the mean of flow dynamic properties of the deterministic simulation (as seen by the dashed red line being generally under the black line in both Fig. 9c and e). The mean of the ensemble-based mean of maximum height (maximum velocity) is 0.85 m (4.57 m s⁻¹), around 66 % (64 %) of the mean of the deterministic simulation at 1.28 m (7.17 m s⁻¹; see Fig. 9c and e).

Figure 9b, d, and f show corresponding results based on the CSS_N=500 ensemble. Similar trends to those in the USS_N=500 {RMSE =3.3, d=180} ensemble can also be observed. Namely, both maximum height and maximum velocity at these locations largely vary from those of the deterministic simulation, and the ensemble-based mean of flow dynamic properties is generally smaller than that of the deterministic results. The main differences are that the variation range of CSS_N=500 ensemble-based flow dynamic properties is smaller and the CSS_N=500 ensemble-based mean of flow dynamic properties is larger compared to those of the USS_N=500 {RMSE =3.3, d=180} ensemble. More specifically, the mean of the CSS_N=500 ensemble-based 90 % confidence interval of maximum height (maximum velocity) is [0.5 m, 2.03 m] ([3.56 m s⁻¹, 7.99 m s⁻¹]). The mean of the CSS_N=500 ensemble-based mean of maximum height (maximum velocity) is 1.1 m (6.01 m s⁻¹), around 86 % (84 %) of the mean of the deterministic simulation 1.28 m (7.17 m s⁻¹; see Fig. 9d and f).

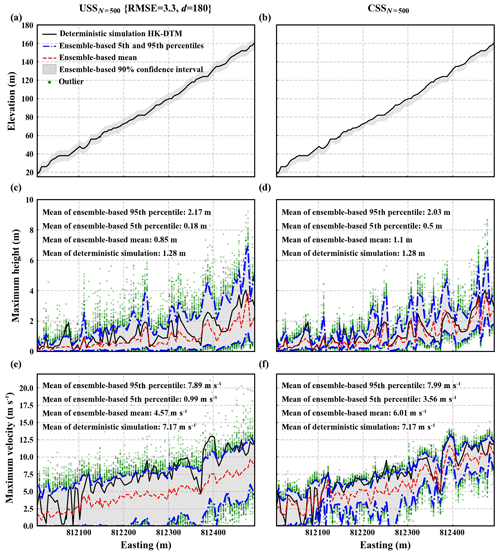
Figure 9 Elevation, maximum height, and maximum velocity at locations along the channel bottom (see Fig. 7b). Panels (a), (c), and (e) correspond to the USS_N=500 {RMSE =3.3, d=180} ensemble and panels (b), (d), and (f) to the CSS_N=500 ensemble. In each panel, dash-dotted blue lines represent the ensemble-based 5th and 95th percentiles of the quantity. The dashed red line represents the ensemble-based mean of the quantity. The black line denotes corresponding results of the deterministic simulation. Annotated mean values are an average of all the locations. Ensemble-based flow dynamic properties largely vary from deterministic simulation results. The variation range of the USS_N=500 {RMSE =3.3, d=180} ensemble is larger, while its ensemble-based mean is smaller, compared to counterparts of the CSS_N=500 ensemble.

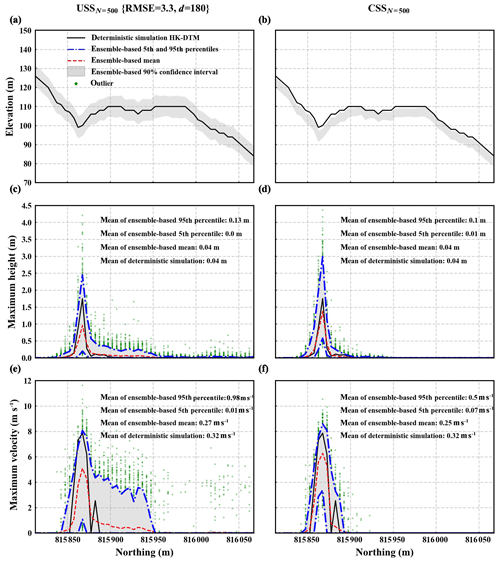
Figure 10 Elevation, maximum height, and maximum velocity at locations along the channel cross section (see Fig. 7b). Panels (a), (c), and (e) correspond to the USS_N=500 {RMSE =3.3, d=180} ensemble and panels (b), (d), and (f) to the CSS_N=500 ensemble. In each panel, dash-dotted blue lines represent ensemble-based 5th and 95th percentiles of the quantity. The dashed red line represents the ensemble-based mean of the quantity. The black line denotes corresponding results of the deterministic simulation. Annotated mean values are an average of all the locations. Due to DEM uncertainty, flow material of both ensembles tends to spread out along the channel cross-section direction. The ensemble-based mean of flow dynamic properties at the channel bottom location is smaller than flow dynamic properties at the channel bottom location of the deterministic simulation (compare peak value of dashed red line with peak value of black line). The more the flow material spreads out, the smaller the ensemble-based mean of flow dynamic properties at the channel bottom location (compare results of the USS_N=500 {RMSE =3.3, d=180} ensemble with those of the CSS_N=500 ensemble).

The above observations result from similar factors to those discussed in Sect. 6.2.1. Due to DEM uncertainty, the following statements can be made:

• Ensemble-based flow dynamic properties are likely to vary from those of the deterministic simulation. Larger variability in DEM error is likely to result in more extreme results. As discussed in Sect. 6.2.1, the variability in DEM error for the USS_N=500 {RMSE =3.3, d=180} ensemble is larger than that for the CSS_N=500 ensemble due to the unrepresentative RMSE issue. Thus the variation range of USS_N=500 {RMSE =3.3, d=180} ensemble-based flow dynamic properties is generally larger than that of CSS_N=500 ensemble-based flow dynamic properties, giving a larger mean of the ensemble-based 90 % confidence interval (the trend would be more clear if we also consider outliers outside the 90 % confidence interval).

• Banks of the deterministic channel may be dampened out in DEM realizations. Deteriorated channel bank representation makes flow material more spread out along the channel cross-section direction. This could lead to a smaller ensemble-based mean of flow dynamic properties at channel bottom locations compared to flow dynamic properties of the deterministic simulation. This can be directly seen in Fig. 10, which displays results of one channel cross section. Also, due to larger variability in DEM error, flow material in the USS_N=500 {RMSE =3.3, d=180} ensemble is more spread along the channel cross-section direction, resulting in a smaller ensemble-based mean of flow dynamic properties at channel bottom locations compared to that of the CSS_N=500 ensemble. This can also be seen in Fig. 10.

• Topographic roughness in DEM realizations tends to increase. As pointed out in Sect. 6.2.1, increasing topographic roughness results in higher simulated momentum losses and thus smaller flow dynamic properties on average. The higher the degree of topographic roughness increase, the higher the simulated momentum losses and the smaller the flow dynamic properties. This also contributes to a smaller ensemble-based mean of flow dynamic properties at channel bottom locations compared to flow dynamic properties of the deterministic simulation, as well as to a smaller USS_N=500 {RMSE =3.3, d=180} ensemble-based mean of flow dynamic properties at channel bottom locations compared to the CSS_N=500 ensemble.

Based on the ensembles' dynamic flow properties we can conclude that (1) accounting for DEM uncertainty may significantly affect dynamic flow properties, e.g., maximum height and maximum velocity, and hence any hazard assessment that is based on landslide dynamics and (2) USS based only on the RMSE may overestimate the range of dynamic flow properties and underestimate the ensemble-based mean of dynamic flow properties due to an unrepresentative RMSE that overestimates the variability in DEM error.

6.3 Additional ensembles to investigate USS sensitivities in RMSE and d

Here, we discuss the unrepresentative RMSE and subjective d issues as introduced in Sect. 3.1 based on six additional ensembles, USS_N=500 {RMSE =0.5, 1.5, 2.5, d=180} and {RMSE =3.3, d=0, 90, 270} (refer to Sect. 5.3.2), as well as the USS_N=500 {RMSE =3.3, d=180} ensemble. Results of the CSS_N=500 ensemble are used as a reference since CSS_N=500 incorporated more information on the DEM error. It is thus reasonable to assume that its results reflect the reality better.

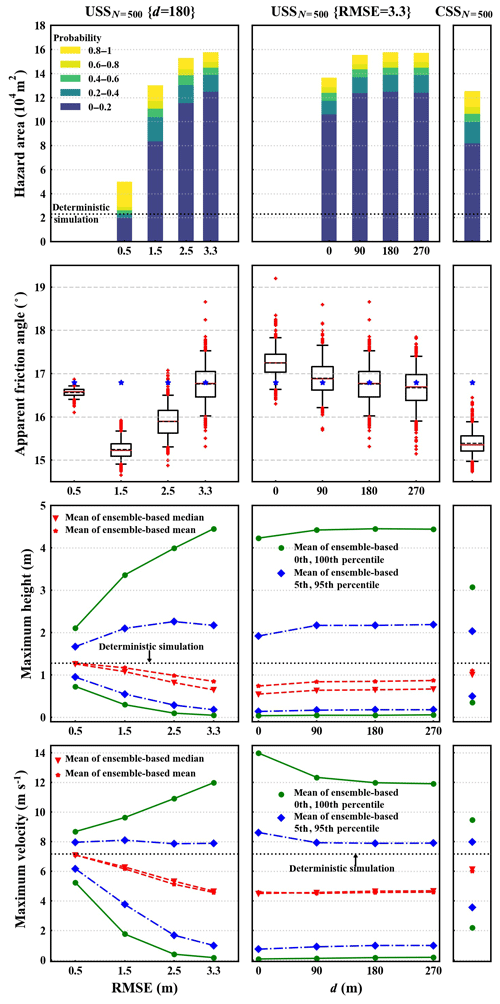
Figure 11 Consolidated results of all ensembles. The left, middle, and right columns correspond to the set of USS_N=500 {RMSE =0.5, 1.5, 2.5, 3.3, d=180} ensembles, set of USS_N=500 {RMSE =3.3, d=0, 90, 180, 270} ensembles, and CSS_N=500 ensemble, respectively. The first row shows stacked bar plots of the potential hazard area's magnitude based on the probabilistic hazard map for each ensemble (see Fig. 8a and c). The second row shows apparent friction angle distribution. The last two rows show statistics of maximum height and maximum velocity at channel bottom locations (see Fig. 9c–f).

Figure 11 shows the consolidated results of the ensembles. The left, middle, and right column correspond to the set of USS_N=500 {RMSE =0.5, 1.5, 2.5, 3.3, d=180} ensembles, set of USS_N=500 {RMSE =3.3, d=0, 90, 180, 270} ensembles, and CSS_N=500 ensemble, respectively. The first row shows stacked bar plots of the potential hazard area's magnitude based on the probabilistic hazard map for each ensemble (see Fig. 8a and c). The second row shows the apparent friction angle distribution. The last two rows show statistics of maximum height and maximum velocity at channel bottom locations (see Fig. 9c–f). Also, deterministic simulation results are included.

Focusing on the left column, it can be seen that with increasing RMSE (1) low-probability (0–0.2) hazard area significantly increases and high-probability (0.8–1) hazard area gradually decreases, leading to increase in overall potential hazard area if we keep the same threshold value; (2) except for the RMSE =0.5 m ensemble, the apparent friction angle steadily increases; and (3) the range of extreme values of maximum height (maximum velocity) at channel bottom locations increases while the average of maximum height (maximum velocity) at channel bottom locations decreases.

For purely RMSE-based USS, the standard deviation of DEM error is assumed to be determined by the RMSE. Hence larger RMSE indicates larger variability in DEM error in DEM realizations. The larger the variability in DEM error, the more likely topographic details of the deterministic channel would be dampened out and the larger the topographic roughness in DEM realizations. As discussed in Sect. 6.2.1, this would make flow material more spread out along the channel cross-section direction (namely larger potential hazard area) and travel a shorter distance (namely larger apparent friction angle). As discussed in Sect. 6.2.2, larger variability in DEM error is likely to result in more extreme values of flow dynamic properties (namely larger range of extreme values), while spreading of flow material along the channel cross-section direction and larger topographic roughness lead to a smaller ensemble-based mean of flow dynamic properties at channel bottom locations.

As discussed in Sect. 6.2.1, the apparent friction angle distribution is determined by a combined effect of change in channel banks, change in the relatively high elevation area at the end part of the channel, and increasing topographic roughness. It naturally follows that for a small variability in DEM error (here RMSE =0.5 m), all the changes are less significant in DEM realizations, and thus the apparent friction angle of the USS_N=500{RMSE =0.5, d=180} ensemble closely matches the deterministic simulation result. For an intermediate variability in DEM error (here RMSE = 1.5 m), the relatively high elevation area at the end part of the channel is subject to change, while channel banks tend to remain well defined in DEM realizations. This leads to a longer travel distance of the USS_N=500{RMSE=1.5, d=180} ensemble (namely smaller apparent friction angle) in comparison to that of the deterministic simulation result.

From the middle column of Fig. 11, we find that the results for a USS ensemble of vanishing spatial autocorrelation USS_N=500 {RMSE =3.3, d=0} consistently differ significantly from USS ensembles that include spatial autocorrelation, namely USS_N=500{RMSE =3.3, d=90, 180, 270} ensembles. This indicates that whether spatial autocorrelation is considered or not may make a difference but the extent of spatial autocorrelation has less influence on simulation results. As we know spatial autocorrelation to be present in topographic data but often lack information on its exact autocorrelation length, this is actually good news for practical hazard assessment studies.

Comparing the left column of Fig. 11 with the right column, it can furthermore be seen that the results of the USS_N=500 {RMSE =1.5, d=180} ensemble are quite close to the results of the CSS_N=500 ensemble. The USS_N=500 {RMSE =1.5, d=180} ensemble is informed of the bias-corrected RMSE (namely the true standard deviation, in our case 1.5 m; see Fig. 3b). It indicates that if a bias-corrected RMSE is given, USS is able to provide reasonable results considering that the extent of spatial autocorrelation has less influence on simulation results.

All in all, we find that (1) the results of USS are in general more sensitive to values of the RMSE and less sensitive to values of d; (2) an unrepresentative RMSE that overestimates the variability in DEM error may overestimate the potential hazard area and extreme values of dynamic flow properties; (3) whether or not spatial autocorrelation of DEM error is considered can make a difference in ensemble-based simulation results; and (4) if a bias-corrected RMSE is given, it is possible to obtain reasonable ensemble-based simulation results using USS.

7 Conclusions

In this paper, we investigated different approaches to studying the impact of topographic uncertainty on simulation-based flow-like landslide run-out analyses. Based upon a historic landslide event for which two DEM data sets of different accuracy were available, we presented a series of computational scenarios. Unconditional and conditional stochastic simulation are conducted to generate DEM realizations, both for the case in which only the RMSE is available and for the case in which reference data of higher accuracy are available. The computational workflow including the stochastic simulation to generate the DEM realizations and the landslide run-out simulation is implemented as a modular Python-based package. How topographic uncertainty propagates in the results of landslide run-out analysis is discussed in detail. In addition, we addressed the two major issues of purely RMSE-based unconditional stochastic simulation, i.e., the fact that non-bias-corrected RMSE overestimates the variability in DEM error (referred to as unrepresentative RMSE in our study) and the fact that determining the size of the spatially moving filter in the absence of further information on the spatial DEM error structure is often subjective (referred to as subjective d in our study). Our main conclusions are as follows:

• DEM uncertainty significantly affects simulation-based landslide run-out modeling depending on how well the underlying flow path is represented, which is determined by topographic characteristics of the original DEM and the variability in DEM error. For the same degree of variability in DEM error, the less well defined parts of the flow path in the original DEM are more likely to be affected and thus lead to change in flow behavior at these parts. Also, an increasing variability in DEM error leads to an increased impact. More specifically, with increasing variability in the DEM error, the potential hazard area and extreme values of dynamic flow properties are likely to increase. This shows the importance of considering topography-induced uncertainty for simulation-based landslide hazard assessment rather than simply trusting the results of a deterministic simulation if a high accuracy of the DEM source is not guaranteed. Also, a preliminary terrain analysis may give some hints on areas that will potentially be affected by a topographic uncertainty study.

• Both unconditional and conditional stochastic simulation methods can be applied to study DEM uncertainty propagation in landslide run-out modeling. Their main difference is that the computationally performant unconditional stochastic simulation can be conducted based on RMSE information only, while the computationally costly conditional stochastic simulation requires the availability of higher-accuracy reference data and is thus more accurate. The higher-accuracy reference data provide additional information on the DEM error structure, i.e., its spatial autocorrelation. If the DEM does not contain systematic bias or alternatively a bias-corrected RMSE is provided, the unconditional stochastic simulation yields reasonable results. Otherwise, the assumptions underlying the unconditional stochastic simulation lead to an overestimation of the DEM error variability, which leads to an increased potential impact of DEM uncertainty on the potential hazard area and to extreme values of dynamic flow properties. In particular, our study shows that if no higher-accuracy reference data are available or if computational costs of a conditional stochastic simulation are too large, the results of a RMSE-based unconditional stochastic simulation can still be used to provide an upper bound on the potential hazard area as well as extreme values of flow dynamic properties for a hazard assessment to take topographic uncertainties into account.

• Results of an unconditional stochastic simulation are in general sensitive to the RMSE value as well as sensitive to whether or not the DEM error's spatial autocorrelation is considered. If the latter is taken into account, results are less sensitive to the actual value of the DEM error's maximum autocorrelation length. This indicates that determining a representative RMSE may be more important than finding a correct maximum autocorrelation length, while the DEM error's spatial autocorrelation should not be ignored for simulation-based landslide hazard assessment.