the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Economic assessment of precautionary measures against floods: insights from a non-contextual approach
Claire Richert
Hélène Boisgontier
Frédéric Grelot
To limit the losses due to floods, public authorities can try to foster the adoption of private measures aimed at reducing the vulnerability of dwellings. However, the efficacy and cost-efficiency of such measures to reduce material losses are not well-known. In particular, the influence of building and flood characteristics on these variables has not been thoroughly studied. A better understanding of this topic would help identify the measures that are relevant to implement in specific contexts. To address this gap, we examined the effect of building and flood characteristics on the cost, efficacy, and cost-efficiency of three groups of measures taken for existing dwellings: one consists of elevating the dwelling, one of dry proofing it, and one of using construction materials that are resistant to water or cheap to repair or replace. We combined expert judgement and computer modelling to assess their cost, efficacy, and cost-efficiency for a wide range of flood depths and durations, building characteristics, and levels of exposure. We found that the value of the building components has a positive effect on the efficacy of dry proofing and elevating a dwelling. Both the efficacy and cost of these two groups of measures increase with the size of the dwelling. Moreover, according to our results, dry proofing and elevating a dwelling are unlikely to be cost-efficient for dwellings that are not exposed to floods with a return period lower than 100 and 30 years, respectively. Our findings also highlight that it is often less expensive to use the adapted than the original materials when rebuilding a damaged dwelling. Moreover, adapting the materials of an intact dwelling is unlikely to be cost-efficient for dwellings that are not exposed to floods with a return period lower than 20 years. Our results apply to France because the damage and the installation costs of the measures are specific to France and the geometry of the dwellings considered to perform our analyses is based on French dwellings.
- Article
(1906 KB) - Full-text XML
- BibTeX
- EndNote
A flood risk can be defined as the combination of a hazard, exposed assets and populations, and their vulnerability to the hazard (e.g. Apel et al., 2009). Thus, mitigating such a phenomenon boils down to reducing at least one of these three components. Throughout the 20th century, it was largely preferred in several countries to only target the hazard component of flood risks through the building of physical defence (e.g. in the Netherlands – Vis et al., 2003; in the UK – Werritty, 2006; or in the US – Tobin, 1995). Nowadays, several authors report that flood risk management policies are increasingly combining flood defences with measures aimed at reducing the vulnerability of people and assets (Klijn and Samuels, 2008; Merz et al., 2010). This tendency is driven by the awareness that physical defences can harm ecosystems and that levee failures can have catastrophic consequences (Klijn and Samuels, 2008) and by the increasing uncertainty regarding the risks of floods due to climate change (Merz et al., 2010). Thus, in countries such as England, France, Hungary, or Germany, recent policies were designed to limit development in flood-prone areas, provide more efficient insurance schemes, raise human awareness of the risk, or foster the adoption of measures aimed at reducing the vulnerability of dwellings (Klijn and Samuels, 2008). Policymakers need to be able to compare these different means of reducing the vulnerability to floods in order to efficiently allocate public funds among them in terms of subsidies and communication.
We focused on measures aimed at reducing the vulnerability of existing dwellings to floods, which we call “precautionary measures”, and analysed their efficacy, cost, and cost-efficiency. We define the cost-efficiency of a measure as the discounted sum of the difference between its annual expected efficacy and its annual cost over its lifespan. The efficacy of a precautionary measure indicates the extent to which it reduces the level of damage to a dwelling. It depends on the flood intensity. The annual expected efficacy is thus the probability-weighted average of the values of efficacy computed for all possible flood intensities.
So far, the efficacy of precautionary measures has been examined at the household level using mainly empirical approaches and expert judgement (see Kreibich et al., 2015, for a review). For instance, the International Commission for the Protection of the Rhine relied on expert judgement to assess the efficacy of flood-proofing measures (ICPR, 2002). On the other hand, Kreibich et al. (2005) surveyed people who were affected by the flood that took place in 2002 in the Elbe River basin. They compared the damage to the building and contents of dwellings with and without different types of precautionary measures. Their results suggest that installing flood barriers and adapting the building structure, use, and layout to floods were effective measures to reduce material damage in their case study. The same conclusion was reached by Kreibich and Thieken (2009) after comparing the levels of damage due to different floods that occurred in a given area in Germany and between which the proportion of inhabitants who took measures had increased. Using a similar approach in another case study in Germany, Bubeck et al. (2012) also suggest that precautionary measures significantly reduced material damage.
All these studies assessed the efficacy of precautionary measures for particular flood events. However, the comparison of the cost and efficacy of a measure requires estimating its annual expected efficacy. Kreibich et al. (2011), Poussin et al. (2015), and Xian et al. (2017) proposed various methods for assessing the annual expected efficacy of some measures. Kreibich et al. (2011) surveyed people who were affected by floods in Germany. They assumed that the mean efficacy of a measure is the difference between the mean amount of damage suffered by those who lived in houses where the measure was not implemented and the mean amount of damage suffered by the others. They multiplied the estimated mean efficacies by several frequencies to obtain annual expected efficacies that relate to various flood return periods. Poussin et al. (2015) conducted a survey in France to assess the cost-efficiency of some precautionary measures. They used ordinary least-squares regression models to explain the relationship between the amount of damage and several independent variables, such as the presence of some precautionary measures and the flood depth. They assumed that the mean efficacy of a measure is the difference between the estimated levels of damage suffered by an average home without and with this measure. To assess the annual expected efficacy, they proceeded in the same way as Kreibich et al. (2011). Xian et al. (2017) assumed that the annual expected efficacy of elevating a dwelling is the reduction in the risk-based annual insurance premium due to this measure, which they computed following the guidelines of the Federal Emergency Management Agency (FEMA, 2014, 2018). As explained in a report of the National Research Council (2015), the risk-based annual insurance premium takes into account the average annual expected damage, which is obtained across classes of buildings which are in the same flood zone and share some characteristics, including their elevation. The values of average annual expected damage are computed using two types of depth–damage functions: some were obtained by using claims data and others come from the US Army Corps of Engineers, but the method used to obtain them is not well-documented, according to the National Research Council (2015). Thus, Xian et al. (2017) ultimately relied partly on empirical data and partly on data of an unknown nature to assess the annual expected efficacy of elevating a dwelling.
While empirical studies analyse precautionary measures in realistic settings, the results they provide are largely context-dependent, as reported by Poussin et al. (2015) and Kreibich et al. (2015). Moreover, since they do not control for all the parameters that influence the amount of damage, they cannot be used to anticipate the efficacy or cost-efficiency of precautionary measures in other contexts. In particular, they do not take into account the influence of the materials used for the components of the buildings on the vulnerability to floods, which could partly explain the variance in the amount of damage (National Research Council, 2015). As for the reports based on expert judgement, since they contain little methodological information, it is difficult to evaluate their reliability in specific contexts.
In brief, the existing literature focuses on assessing the efficacy or cost-efficiency of precautionary measures rather than on explaining their variability. The aim of our study was to address this gap. We combined data based on expert judgement and computer modelling to analyse three types of measures (elevation, dry proofing, and component adaptations) for a wide range of flood intensities and dwellings characteristics, including the materials used for their components. More specifically, we assessed ranges of cost and efficacy of the measures and examined the influence of building and flood characteristics on these variables. For each type of measure, we also found a range of exposure level for which it is unlikely that the measure could be cost-efficient independently of the building characteristics.
In the following section, we present the measures that we focus on. We describe the method used to assess their efficacy, cost, and cost-efficiency in Sect. 3. Then, we present the results in Sect. 4. We discuss them in Sect. 5 and conclude in Sect. 6.
We reviewed the measures recommended to reduce the vulnerability of dwellings to floods in a joint report of the French ministries in charge of environment and housing (Ministère de l'égalité des Territoires et du Logement – Ministère de l'écologie, du Développement durable, et de l'énergie, 2012), a report of the European Center for Flood Risk Prevention (CEPRI, 2010), and a report of the Doubs and Saône catchment management agency (EPTB Saône et Doubs, 2015).
The measures described in these reports can be classified into three categories: some aim at avoiding damage by elevating the house, storing valuables upstairs, or elevating heating and electrical utilities, for example; some at preventing the water from entering into the dwelling; and some at limiting the costs of repair and replacement of building components.
We analysed the measure that consists of elevating the house and the measures that aim at preventing the water from entering into the dwelling or at limiting the costs of repair and replacement of the building components. We refer to the first measure as the elevation strategy, to the second group of measures as the dry-proofing strategy, and to the third group of measures as the component adaptation strategy.
2.1 Elevation
To avoid damage up to a given flood depth, dwellings can sometimes be elevated. According to a report of the FEMA (2009), if a dwelling is built on a basement, a crawl space, or on open foundations, the first step for elevating it consists generally of separating it from its foundations and raising it on hydraulic jacks while it is held by a temporary support. Then, the existing foundations can be extended or new ones can be built. If the dwelling has slab-on-grade foundations, they are lifted together and new foundations are constructed below the slab1. In both cases, an external staircase must be built to access the dwelling and utility lines must be extended.
We analysed the efficacy, cost, and cost-efficiency of elevating dwellings by 50, 100, and 250 cm. We assumed that only single-storey houses can be elevated because other types of dwellings are too large.
2.2 Dry proofing
Measures can be taken to prevent the water from entering into a dwelling if the flood depth stays below 1 m and the flood lasts less than 48 h. For higher flood depths or longer flood durations, the pressure on the vertical elements of the building structure can cause severe damage.
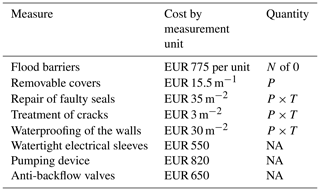
For a dwelling without a basement, the following measures must be taken together and dimensioned consistently to prevent the water from entering up to a chosen threshold: installing flood barriers, repairing faulty seals in the external walls, waterproofing the external walls, treating cracks in the external walls, installing removable covers on small openings that are below the chosen threshold, installing anti-backflow valves, ensuring that the electrical cable sleeves are watertight, and buying a pumping device2. Following Poussin et al. (2012), we call “dry proofing” the combination of these measures. We assessed the efficacy, cost, and cost-efficiency of dry proofing a dwelling without a basement in the cases where it prevents the water from entering up to flood depths of 50 cm and 1 m.
2.3 Component adaptations
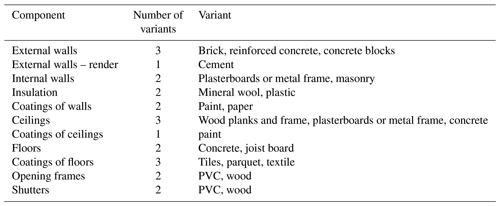
We define “component adaptation” as a measure which consists of using building materials that are resistant to water or cheap to repair or replace. We studied component adaptations which pertain to the ceilings, the walls, the floors, and the openings. We detail in Table 1 the component adaptations that pertain to each of these building components.
3.1 Overview
We used a computer tool called floodam (Grelot and Richert, 2019) and developed in R language (R Core Team, 2017) to assess the efficacy of the strategies aimed at reducing the vulnerability of existing dwellings. floodam requires, as input, a numerical model of a building and produces a function which associates a level of damage with several combinations of flood depth and duration. We call this type of output a damage function. floodam has been developed to produce national damage functions that are recommended by the French state in its cost–benefit analysis methodology (Rouchon et al., 2018).
The efficacy and the cost of the strategies were assessed for several numerical models of dwellings. The cost of each strategy depends on the geometry of the dwellings and, in some cases, on whether the strategy is taken for an intact or damaged building and for the building materials. The efficacy is assessed by comparing the damage functions of the dwellings obtained with and without a strategy. It depends on the flood depth and duration, on the geometry of the dwellings, and on the building materials.
In this section, we describe the numerical models used as inputs, we provide an overview of how floodam works, we present the advantages of floodam to assess the strategies compared to other flood damage models, and we describe how we modelled the strategies. We then explain how we assessed the cost, the efficacy, and the cost-efficiency of each strategy.
3.2 Numerical models of dwellings
The numerical model of a dwelling is made up of an XML file and a CSV file. The former indicates the ground floor height above ground level, the layout and size of the rooms, and the construction materials used for the building. Figure 1 provides a graphical interpretation of the XML file of a numerical model. The CSV file indicates the pieces of furniture that are present in each room and their height above the floor. For instance, Table 2 shows the information that pertains to a bedroom contained in the CSV file of a numerical model.
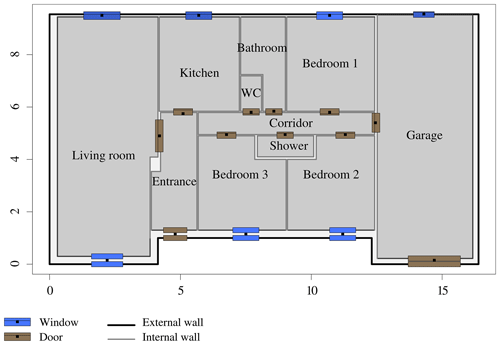
Figure 1Top view of the single-storey house. The external walls are in black, the internal walls in grey, the doors in brown, and the windows in blue.
Table 2Pieces of furniture contained in Bedroom 1 of the single-storey house (see Fig. 1).

Originally, we had three numerical models which represent real dwellings: we visited an apartment to establish its plan and make an inventory of its furniture, the European Center for Flood Risk Prevention did the same with a single-storey house (CEPRI, 2014) and gave us access to their data, and we used the architectural plan of a double-storey house. Since we had no real data regarding the furniture of the double-storey house, we first allocated the pieces of furniture of the single-storey house to the corresponding rooms of the double-storey house. Then, we added pieces of furniture to one room which had no correspondence in the single-storey house (a home office) and to two dressing rooms. More specifically, we assumed that the home office contained a desk, a chair, and a cupboard in chipboard and that the dressing rooms each contained a variety of small items.
In order to be able to generalise our results, we developed several versions of these three numerical models of dwellings by modifying the combination of the building components listed in Table 3. These components were chosen because they are widely used in French buildings, according to a report of the agency of building quality (Agence Qualité Construction, 2009). Each version contains only one variant of each component listed in Table 3. Since there are 1728 possible combinations of all components, we developed the same number of versions for each of the three original numerical models of dwellings. In total, we thus have 5184 numerical models of dwellings.
3.3 Overview of floodam
We define the damage suffered by a good as the expected cost of the actions that must be performed after a flood in order to bring it back to its pre-flood state. Using this definition, floodam relies on two main assumptions: (1) the damage suffered by a building is the sum of the levels of damage suffered by its components, and (2) the levels of damage of the components are independent.
floodam relies on a database of 431 elementary damage functions. An elementary damage function associates a level of damage suffered by an elementary component with several combinations of flood depth and duration. A partition wall in plaster and a washing machine are examples of elementary components. The elementary damage functions come from interviews with insurance and construction experts. We used elementary damage functions with data points at immersion depth values from 0 to 500 cm (included) in 10 cm increments and immersion duration values from 0 to 144 h (included)3 in 12 h increments.
For a given numerical model, floodam computes the height above the ground of all elementary components and the size or quantity of the elementary components of the building. Then, for each combination of depth and duration of immersion, it (1) computes the depth of immersion of each elementary component, (2) retrieves the corresponding levels of damage by measurement unit for the duration of immersion considered, (3) multiplies each level of damage by the size or quantity of the corresponding elementary component, and (4) sums the obtained values to obtain the level of damage at the scale of the dwelling. The damage function of the numerical model considered is made up of the levels of damage computed for each combination of immersion depth and duration.
floodam is used to estimate the damage due to floods that do not cause failure of walls and that do not involve salt water.
A more detailed description of floodam can be found in Grelot and Richert (2019).
3.4 Suitability of floodam for assessing the precautionary measures
Numerous empirical and synthetic flood loss models exist. floodam belongs to the latter category. Empirical models are based on observed flood loss data, whereas synthetic models rely on a description of flood damage mechanisms (Gerl et al., 2016).
Some empirical flood damage models include precautionary measures as explanatory variables (see for example Kreibich et al., 2017) and can be used to estimate their mean efficacy (Sairam et al., 2019). These models account for the mean effect on flood damage of all the measures observed in the case studies used to produce them. Thus, they cannot be used to estimate the efficacy of specific precautionary measures. Moreover, the influence of the flood parameters and building characteristics on the efficacy of precautionary measures cannot be deduced from these models.
The damage mechanisms are more explicit in synthetic models (see for example Custer and Nishijima, 2015; Dottori et al., 2016; Nadal et al., 2010; Zevenbergen et al., 2007). They can be altered to depict the effect of specific precautionary measures.
To our knowledge, floodam is the synthetic model based on the most detailed database of elementary damage functions. This characteristic enabled us to examine the influence of a wide variety of building materials on the efficacy of specific precautionary measures.
3.5 Modelling of the strategies
3.5.1 Elevation
Modelling the elevation of a dwelling consists of choosing a threshold of flood depth below which damage should be avoided. The cost and efficacy of the strategy are deduced from this threshold.
3.5.2 Dry proofing
To model the dry proofing of a dwelling, a threshold below which the water should be prevented from entering must first be chosen. The number of openings that are below the threshold is the number of flood barriers that must be installed. Then, the perimeter of the dwelling, from which the quantity of removable covers that must be installed is deduced, is computed. The perimeter is multiplied by the threshold to obtain the area on which faulty seals and cracks in the external walls must be repaired and on which the external walls must be waterproofed.
3.5.3 Component adaptations
Adapting a given component of the numerical model of a dwelling boils down to replacing its original variant by the recommended one (see Table 1) if the latter is different from the former.
3.6 Analysis
3.6.1 Assessment of the cost
Elevation
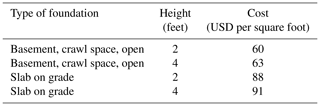
To assess the cost of elevating a dwelling, we relied on the estimates provided by the FEMA (2009) and reported in Table 4. We first converted each of these estimates into 2017 euros per square foot. To do so, we multiplied them by the ratio between the construction prices in France and the United States (0.97; see https://www.fgould.com/americas/articles/construction-intelligence-prospects-global/, last access: May 2019), the exchange rate between the US dollar and the euro in 2009 (0.72), and an index that gives the construction price development in France between 2009 and December 2017 (; see https://www.insee.fr/fr/statistiques/serie/000008630, last access: May 2019).
Table 5Costs of elevating a masonry dwelling used in our study.
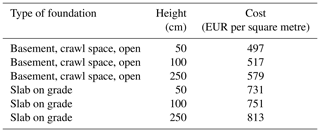
The costs per square metre are in EUR 2017.
Once the costs were in euros per square foot, we converted them into euros per square metre by dividing them by 0.30482 ft2 m−2 (1 ft = 0.3048 m). After that, we computed the cost for elevations of 50, 100, and 250 cm by assuming that the cost increases linearly between 50 and 250 cm. Finally, we used the costs indicated in Table 5.
Dry proofing
The cost of each measure that must be implemented to dry proof a dwelling was assessed by a construction expert for the single-storey house. Knowing the characteristics of this dwelling, we estimated the cost of each measure by measurement unit. For each numerical model of a dwelling, they were multiplied by the quantities on which the measures must be applied. Table 6 indicates the cost of each measure and its measurement unit.
Component adaptations
A given component can be destroyed or intact when the adaptation takes place. At the level of a dwelling, we consider two situations: either all the components are destroyed or they are all intact when the adaptation takes place. In the first case, which we call the repair context, the adaptation cost is the difference between the costs of installing the recommended and the original variants of the components. In the second case, which we call the prevention context, the adaptation cost is the sum of the costs of installing the recommended variant of the components (if they are different from the original ones) and of reinstalling the original coatings (of the walls, floors, and ceilings).
3.6.2 Assessment of the efficacy
We define the efficacy of a strategy for a given numerical model of a dwelling as the difference between the damage functions computed without and with the strategy.
Elevation
When a dwelling is elevated by x centimetres, its damage function (f), which depends on the flood depth (de) and duration (du), becomes g(de, du) such as
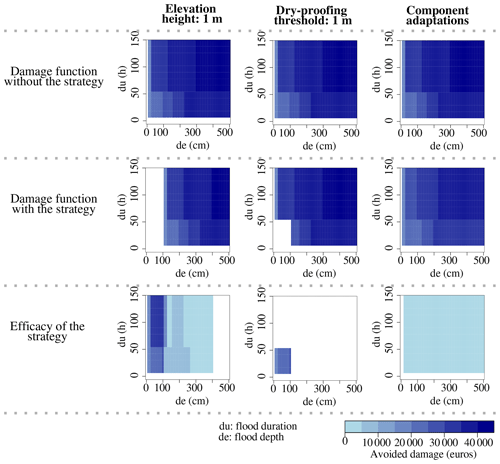
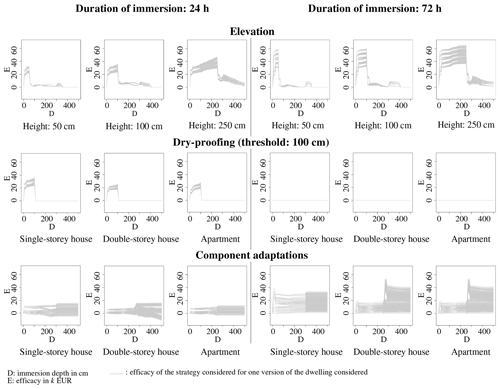
Therefore, the efficacy of elevating a given numerical model depends on the immersion depth and duration. For example, elevating the original version of the single-storey house by 1 m can reduce the damage by up to EUR 30 000 approximately, as shown in Fig. 2.
Dry proofing
The damage function of the numerical model of a dwelling where the dry-proofing strategy is installed is equal to zero for combinations of immersion depths below or equal to the threshold and immersion durations below or equal to 48 h. For all other combinations of immersion depth and duration, dry proofing has no effect on the damage function. For example, Fig. 2 shows the damage functions of the original version of the single-storey house without and with the dry-proofing strategy with a threshold of 1 m and the resulting efficacy. For this dwelling, the maximum avoided damage due to dry proofing is approximately EUR 25 000.
Component adaptations
The efficacy of a component adaptation to reduce the vulnerability of a dwelling is the difference between the damage functions computed with the original and recommended variants of the component. Hence, the efficacy depends on the immersion depth and duration. For instance, Fig. 2 shows that the maximum avoided damage due to the component adaptation strategy in the original single-storey house is lower than EUR 5000.
3.6.3 Assessment of the maximum cost-efficiency
The maximum cost-efficiency of a strategy for a given type of dwelling (single-storey house, double-storey house, or apartment) is defined as a supremum of the cost-efficiency computed for the version for which the strategy is the most cost-efficient. It is thus a supremum of the cost-efficiency for the type of dwelling considered. In other words, for a given strategy and a given type of dwelling, the cost-efficiency of the strategy is always lower than the maximum cost-efficiency regardless of the building materials or the relationship between the flood intensity and frequency.
In this section, we mathematically define the cost-efficiency and maximum cost-efficiency of a strategy.
The cost-efficiency (CE) of a strategy is defined for a contextualised dwelling, which is a dwelling that has a given location and thus a given exposure to floods depending on their frequency. The cost-efficiency is the discounted sum of the difference between the annual expected efficacy (AEE) and the cost of the strategy over a defined time horizon (H):
where r is the discount rate, AEC the annual expected maintenance cost of the strategy, and IC its installation cost. We assume that AEE and AEC are constant over the time horizon considered. A strategy is cost-efficient for a given contextualised dwelling if CE > 0, that is to say, if
Moreover, the annual expected efficiency of a strategy for a given dwelling is equal to
with f being the flood frequency, “de” the immersion depth, “du” the immersion duration, and E the efficacy.
What we call maximum cost-efficiency is in fact an upper boundary of the cost-efficiency. We first computed it for each version of a given type of dwelling.
To compute the maximum cost-efficiency of a strategy s for a given dwelling d, we use a lower boundary of the cost by taking only the installation cost into account. We also define the following upper boundary of annual expected efficiency
with fmax being the frequency of the flood that affects d the most often, Tmin the return period of the flood that affects d the most often, and the highest value of efficacy of s for d over all possible combinations of immersion depth and duration.
Thus, we define the maximum cost-efficiency of s for d as follows:
The maximum cost-efficiency of a strategy s for a given type of dwelling is then the cost-efficiency computed for the version of the dwelling for which the ratio is the lowest.
We used a discount rate of 2.5 %, which is the value recommended to assess public investments in France (Commissariat général à la stratégie et à la prospective, 2013).
For each type of dwelling, we computed the maximum cost-efficiency for values of H from 1 to 50 (for dry proofing and component adaptations) or 100 years (for elevation) in 1-year increments and T from 1 to 120 years in 1-year increments. H can be considered to be the lifespan of the strategy.
For each strategy and type of dwelling, we searched for the combinations of the time horizon and return period for which the maximum cost-efficiency is negative. In these contexts, our results suggest that the strategy is unlikely to be cost-efficient. Indeed, unlike the cost-efficiency, the maximum cost-efficiency for a given type of dwelling does not depend on the building materials and on the relationship between the flood intensity (immersion depth and duration) and frequency. It only depends on the time horizon and return period. Thus, for the combinations of the time horizon and return period associated with a negative maximum cost-efficiency, the strategy is always cost-inefficient regardless of the building materials and of the relationship between the flood intensity and frequency.
We present the ranges of cost and efficacy and the maximum cost-efficiency of the elevation, dry proofing, and component adaptation strategies.
4.1 Range of cost
As shown in Table 7, the cost of a given strategy does not depend on the immersion depth and duration. It always varies with the type of dwelling and the characteristic of the strategy (the height of elevation, the threshold, or the adaptation context). In the specific case of the component adaptation strategy, it also depends on the original variant used for the building components.
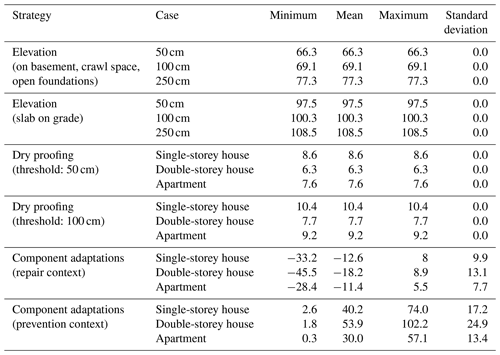
The cost of elevating a single-storey house lies between EUR 66 000 and EUR 109 000. Thus, it is always higher that the highest value of efficacy for this strategy. It increases with the elevation and is always the highest for dwellings that have slab-on-grade foundations.
The cost of dry proofing a dwelling ranges from EUR 6000 to EUR 10 000. For a given threshold, the cost of dry proofing is always maximum for the single-storey house and minimum for the double-storey house. This is due to the fact that the single-storey house has the greatest perimeter (54 m) and the double-storey house the smallest (40 m). The area on which some measures must be applied increases with the threshold. Thus, the cost of dry proofing is greater when the threshold is 100 cm than when it is 50 cm.
Regarding the adaptation of all building components, if it takes place on a damaged building (repair context), it is often less expensive to adapt the dwelling than to install the original variants of the components again. More precisely, it is the case for 91 % of the 5184 numerical models of dwellings. On the contrary, if the dwelling is intact when the adaptation takes place (prevention context), the mean cost of adapting all components is approximately 4 times higher than the cost of dry proofing. In the prevention context, the minimum costs relate to versions of the dwellings for which the original variants of the components are highly similar to the recommended ones. Note that we did not compute numerical models of dwellings that were made up of all the recommended variants of the components. The cost and efficacy of adapting all building components of such dwellings would be null. The highest adaptation costs relate to versions of the dwellings for which almost all components must be adapted.
4.2 Range of efficacy
Figure 3 shows the range of efficacy obtained for each strategy. The efficacy of a strategy depends on the type and components of the dwelling, on the immersion depth and duration, and sometimes on some characteristics of the strategy.
More specifically, the efficacy of elevating a dwelling increases with the value of elevation and with the value of the components of the dwelling. For this strategy, the highest efficacy is obtained for numerical models of dwellings which contain a lot of wooden components (joist boards, parquet, and opening frames and shutters in wood). The highest efficacy is observed for an immersion depth equal to the elevation value.
As for dry proofing, its efficacy increases with the threshold, the value of the components of the dwelling, and the floor area. The highest maximum efficacies relate to the single-storey house and the lowest to the double-storey house because the former has the largest floor area (133.5 m2) and the latter the smallest (98 m2). For a given numerical model of a dwelling, the efficacy of dry proofing increases up to an immersion depth equal to the threshold and an immersion duration of 48 h. In keeping with the assumptions used when modelling dry proofing, the efficacy is equal to zero for higher immersion depths and longer immersion durations.
Adapting all components can sometimes generate the same or a higher level of damage than keeping all the original components. This is the case for the 576 versions of each type of dwelling, which originally have masonry internal walls and tiles or textiles as coatings of floors. There is indeed a probability greater than zero that the adapted walls in plaster must be replaced for immersion depths greater than or equal to 30 cm, no matter the immersion duration. On the contrary, the probability that masonry walls must be replaced for immersion durations lower than 72 h is equal to zero. This type of wall needs only to be repaired in such cases. As a consequence, for some immersion depths, the elementary damage function of an internal wall in plaster is above the one of a masonry internal wall for immersion durations lower than 72 h. Negative levels of efficacy are observed only for dwellings which originally have tiles or textile as coatings of floors because the high efficacy of replacing parquet floors by sealed tiling floors compensates the negative efficacy of replacing masonry walls by walls in plaster. The efficacy of adapting all components is always positive for immersion durations higher than or equal to 72 h. The variance in the efficacy increases with the quantity of building components to adapt.
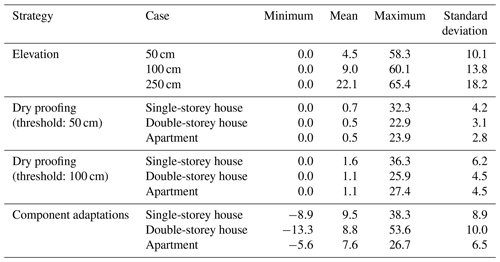
Table 8 shows the distribution of the efficacy of each strategy. The efficacy of elevating a dwelling lies between EUR 0 and EUR 65 000. Dry proofing a dwelling leads to a reduction of damage ranging between EUR 0 and EUR 36 000, and the efficacy of adapting all the components of the building is between EUR −14 000 and EUR 54 000. These results highlight the high variability of the efficacy of each strategy.
4.3 Maximum cost-efficiency
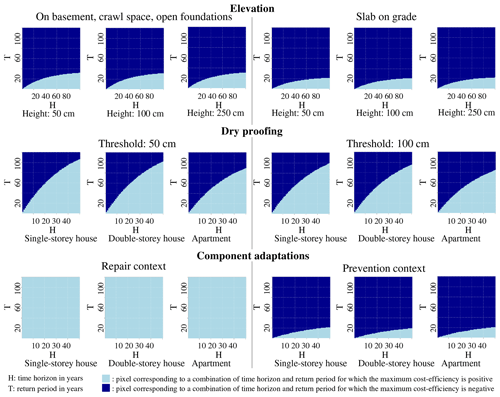
Figure 4 indicates the maximum cost-efficiency of each strategy, depending on the type of dwelling and on some characteristics of the strategy (the elevation, the threshold, or the adaptation context) and for several combinations of the time horizon and return period.
For the analysed values of the time horizon, it is never cost-efficient to elevate a single-storey house which is only exposed to floods with a return period higher than 30 years. If the dwelling has slab-on-grade foundations, the minimum return period for which it could be cost-efficient to elevate a dwelling is 20 years approximately.
Similarly, according to our results, adapting all building components is never cost-efficient for intact dwellings that are not exposed to floods that have a return period of less than 20 years. However, when component adaptations take place on a damaged dwelling, our results do not indicate ranges of the time horizon and return period for which this strategy is never cost-efficient.
Regarding dry proofing, the results are similar for the three types of dwellings and are not affected by the threshold. They suggest that dry proofing is never cost-efficient for dwellings that are not exposed to floods with a return period of 100 years or less.
Except in the case of adapting all the building components of a damaged building, we observe that the maximum return period for which a strategy is cost-efficient increases with the time horizon. For instance, for a dwelling that must be entirely dry proofed again after 20 years and that is not exposed to floods with a return period of less than 60 years, this strategy will never be cost-efficient.
We assessed the cost and efficacy of some precautionary measures by taking into account some characteristics of the dwellings (their building components and size), parameters of the measures, grouped in strategies (their dimension or implementation context), and flood characteristics (immersion depth and duration). Then, we computed the maximum cost-efficiency of each strategy for several combinations of the time horizon and return period. We could thus identify exposure levels for which it is unlikely that the strategies could be cost-efficient.
5.1 Main results
The value of the building components by square metre has a positive effect on the efficacy of dry proofing and elevating a dwelling, while it does not affect the cost of these strategies. Hence, the more expensive the components of a dwelling, the more relevant it can be to elevate or dry proof it. By contrast, both the efficacy and the cost of dry proofing and elevation increase with the flood depth below which damage must be avoided and with the size of the dwelling. Consequently, these parameters do not affect the maximum cost-efficiency of dry proofing and elevation. According to our results, these strategies are unlikely to be cost-efficient for dwellings only exposed to floods with a return period higher than 100 and 30 years, respectively.
The efficacy of adapting the building components strongly depends on their original materials. It can even be negative for floods that last less than 72 h if the internal walls are originally in masonry. The cost of adapting the building components is influenced by the adaptation context and by the original materials. If the adaptation takes place on an already-damaged building, it is most of the time less expensive to adapt it than to reinstall the original variants of the components. However, it costs approximately EUR 40 000 on average to adapt an intact building. Since the cost and efficacy both increase with the quantity of components to adapt, the maximum cost-efficiency does not depend on the size of the dwelling. Adapting an intact dwelling that is not exposed to floods with a return period lower than 20 years is unlikely to be cost-efficient. In a repair context, we could not identify exposure levels for which it is never cost-efficient to adapt all building components.
Note that the cost-efficiency of all strategies increases with their lifespan and with the level of exposure in terms of frequency of floods.
5.2 Comparison with previous studies
5.2.1 Elevation
According to Poussin et al. (2015), the mean efficacy of elevating the ground floor is EUR 8000 approximately, and the cost of this strategy for existing buildings lies between EUR 25 000 and 69 000. The range of cost comes from an article written by Aerts et al. (2013). These authors also used the data from the report of the FEMA (2009) to estimate the costs of elevating dwellings. Thus, our estimates of the cost of elevation are of the same order of magnitude as those reported by Poussin et al. (2015), even if they are higher on average (EUR 87 000). Moreover, the mean efficacy estimated by these authors lies in the range of efficacy that we found (between EUR 0 and 65 000). Poussin et al. (2015) also found that elevating an existing building is only cost-efficient for dwellings exposed to floods with a return period lower than 10 years. These results are compatible with our study.
Similarly to our results, those of Xian et al. (2017) indicate that the cost-efficiency of elevating a dwelling is positively affected by the value by square metre of the latter, the frequency of floods, and the lifespan of the strategy.
5.2.2 Dry proofing
Zevenbergen et al. (2007) investigated the cost-efficiency of dry proofing a dwelling until 0.9 m. They found that it would cost EUR 8000 to implement this strategy on a typical Dutch single-family dwelling. These results lie within the range of cost we found for this strategy. In the two case studies examined by Zevenbergen et al. (2007), dry proofing was cost-efficient until a return period of 30 years. This is in line with our results.
Kreibich et al. (2011) and Poussin et al. (2015) studied the efficacy, cost, and cost-efficiency of installing flood barriers. The average efficacy of flood barriers estimated by Kreibich et al. (2011) is EUR 23 491, and the estimated cost of this measure is EUR 6100 for an average house. As explained in Sect. 3, flood barriers must be complemented by other measures to dry proof a dwelling. Since Kreibich et al. (2011) only asked whether flood barriers were installed, it is likely that the average efficacy they found is lower than the one that would have been observed for completely dry-proofed dwellings. Moreover, since the flood depth which affected the dwellings of the respondents is not known, we cannot precisely compare our results with this average efficacy. However, it lies in the range of efficacy that we found for the dry-proofing strategy. Moreover, we found an average cost for the installation of flood barriers only of EUR 3100, which is 2 times lower than the one used by Kreibich et al. (2011) but stays within the same order of magnitude. According to the results of Kreibich et al. (2011), flood barriers are only cost-efficient for dwellings affected by floods with a return period lower than 40 years approximately. These results are compatible with those of our study, since we found that it is unlikely that dry proofing could be cost-efficient for dwellings only exposed to floods with a return period higher than 100 years.
Poussin et al. (2015) found that flood barriers did not significantly reduce material damage in their whole sample. However, they highlight that this result may not be reliable because of multi-collinearity issues.
5.2.3 Component adaptations
We did not find studies which analyse specifically the efficacy, cost, or cost-efficiency of adapting all the building components. However, Kreibich et al. (2005) studied the efficacy of the combination of using waterproof building materials and having mostly movable pieces of furniture on the ground floor. They found that this strategy reduced the total damage by EUR 39 000 on average. In line with this result, our estimates of the efficacy of adapting all building components are between EUR −14 000 and 54 000.
According to Poussin et al. (2015), adapting the walls and equipment increases the damage by EUR 2000 on average. This result is compatible with our finding that adapting the walls can lead to negative levels of efficacy. These authors did not estimate the cost of this measure. They also found that adapting the floors could reduce the damage by EUR 400 to 10 000. They used a cost for this measure that lies between EUR 800 and 7250. They do not specify the adaptation context for which this cost was estimated, but given that it is always positive, we assume that it was assessed for an intact building. To adapt only the floors, we found costs in a prevention context that amounted to between EUR 10 000 and 23 000. These values are higher than those used by Poussin et al. (2015). As for the efficacy of adapting only the floors, we estimate that it lies between EUR 0 and 16 000, depending on the flood depth and duration. These values are in line with those found by Poussin et al. (2015).
5.3 Recommendations based on our results
Our results seem reliable, since they are mostly in line with previous studies. They suggest that elevating or adapting the building components of intact dwellings that are not exposed to frequent floods (i.e. with a return period lower than 30 years) should not be fostered by policymakers who wish to limit material damage due to floods. However, after a flood, it could be efficient to take advantage of the reconstruction phase to adapt the building components, since it is often less expensive to install the recommended components than to rebuild dwellings as they were before the event. Given that the post-disaster recovery often occurs in a climate of urgency, it could be useful to design in advance policy tools to help people adapt their dwelling during this phase.
Moreover, policymakers should not promote the installation of dry-proofing measures in dwellings that are not exposed to floods with a return period lower than 100 years.
Besides the level of exposure, the building components should be taken into account to assess the vulnerability of the dwellings and thus the relevance of implementing precautionary measures that sometimes generate higher costs than benefits.
5.4 Limits
Decisions regarding the allocation of public funds to communicate about the strategies considered here or to subsidise their installation cannot be based solely on the present study because of several limits relating either to its perimeter or to the method on which it relies. Several limits due to the method are linked to the assumptions and data used in floodam.
5.4.1 Limits linked to the study perimeter
We only took into account the damage in terms of monetary losses and did not consider the impact of the strategies on the damage related to human health. While the latter is unlikely to be influenced by component adaptations, it could be reduced by dry proofing and even more by elevating the dwelling.
Moreover, our results cannot be used to identify a range of exposures for which it is likely that the studied precautionary measures would efficiently reduce monetary losses. Contextualised studies are required to finely relate the efficiency of precautionary measures to the characteristics of a dwelling and its level of exposure to floods.
5.4.2 Limits linked to the method
Our results are mainly relevant for relatively slow riverine floods. Indeed, floodam assumes that the pieces of furniture are never moved by the water during a flood and that the salinity level of the water is negligible.
Moreover, our results apply to France because we used French data to estimate the costs of the measures, the database of elementary damage functions of floodam relies on French costs, and we used French dwellings to develop the numerical models. These elements should be adapted to conduct our study in another country.
We only studied the efficacy and cost-efficiency of the strategies for dwellings that are exposed to floods that do not last more than 144 h because the experts interviewed to develop the elementary damage functions of floodam did not have information about the consequences of longer floods. The efficacy of dry proofing for such floods is null because it is recommended to let the water enter the building after 48 h. As for the elevation strategy, its efficacy in the case of floods that last more than 144 h depends on the propensity of such floods to generate foundations' failure. If the foundations fail, the fact that the building is elevated does not reduce the damage. The efficacy of the component adaptation strategy for floods longer than 144 h depends on the vulnerability of the recommended components when they are in contact with water for more than 144 h.
Our results also depend on the geometry of the dwellings used to develop the numerical models. For instance, dry proofing was only analysed for dwellings that do not contain a basement.
floodam is the tool used by the French state to produce currently recommended national flood damage functions to be used in cost–benefit analyses. The comparison of these damage functions to formerly recommended empirical flood damage functions and to empirical data collected in the south of France (CEPRI, 2014) led to this recommendation. The national damage functions were also used in a case study in the south of France, and the estimates obtained were compared with empirical flood damage data (Richert and Grelot, 2018): the mean damage estimate amounted to 70 % (99 %) of the mean empirical damage to houses (apartments). Nevertheless, in the present article, we used floodam for a wide range of configurations for which validation against empirical data has not been done. To perform such a validation, we would need to have access to detailed data about a given flood. These data should indicate precisely the location and characteristics (in terms of building materials, furniture, and geometry) of the dwellings of the flooded area, the flood depth and duration outside and inside these dwellings, and the flood damage suffered by each dwelling. At the present moment, this data type is not available.
We analysed three types of precautionary measures in a non-contextualised setting. This novel approach enabled us to explore the influence of several building and flood characteristics on the cost and efficacy of the precautionary measures and to find ranges of exposure for which they are unlikely to be cost-efficient. In particular, we found that adapting all the building components or elevating an existing dwelling is unlikely to be cost-efficient if the probability of occurrence of floods is lower than 1∕30 per year. As for dry proofing, this measure is unlikely to be cost-efficient for dwellings exposed only to floods with a return period higher than 100 years. Our results apply to the whole country of France. Decision-makers could rely on them to recommend precautionary measures only to inhabitants that live in dwellings for which they could be advantageous.
floodam is developed as an R library. floodam and data at building levels are available upon request through a Git repository maintained by Irstea and under certain conditions.
CR modelled the elevation strategy, analysed the data, and wrote the article. HB modelled the other strategies. FG developed floodam, supervised the project, and proofread the article.
The authors declare that they have no conflict of interest.
This research has been supported by the Ministère de la Transition écologique et Solidaire (grant no. 2102049246).
This paper was edited by Kai Schröter and reviewed by two anonymous referees.
Aerts, J. C., Botzen, W. W., de Moel, H., and Bowman, M.: Cost estimates for flood resilience and protection strategies in New York City, Ann. NY. Acad. Sc., 1294, 1–104, https://doi.org/10.1111/nyas.12200, 2013. a
Agence Qualité Construction: Résidentiel neuf, l'évolution des parts de marché des produits et matériaux de la construction, Tech. rep., Paris, 2009. a
Apel, H., Aronica, G. T., Kreibich, H., and Thieken, A. H.: Flood risk analyses – how detailed do we need to be?, Nat. Hazards, 49, 79–98, https://doi.org/10.1007/s11069-008-9277-8, 2009. a
Bubeck, P., Botzen, W. J. W., Kreibich, H., and Aerts, J. C. J.: Long-term development and effectiveness of private flood mitigation measures: An analysis for the German part of the river Rhine, Nat. Hazards Earth Syst. Sci., 12, 3507–3518, https://doi.org/10.5194/nhess-12-3507-2012, 2012. a
CEPRI: Le bâtiment face à l'inondation, diagnostiquer et réduire sa vulnérabilité, Tech. rep., CEPRI, Orléans, France, 2010. a
CEPRI: Évaluation des dommages liés aux inondations sur les logements, Tech. rep., CEPRI, Orléans, France, 2014. a, b
Commissariat général à la stratégie et à la prospective: L'évaluation socioéconomique des investissements publics, Tech. rep., Commissariat général à la stratégie et à la prospective, Paris, 2013. a
Custer, R. and Nishijima, K.: Flood vulnerability assessment of residential buildings by explicit damage process modelling, Nat. Hazards, 78, 461–496, https://doi.org/10.1007/s11069-015-1725-7, 2015. a
Dottori, F., Figueiredo, R., Martina, M. L. V., Molinari, D., and Scorzini, A. R.: INSYDE: a synthetic, probabilistic flood damage model based on explicit cost analysis, Nat. Hazards Earth Syst. Sci., 16, 2577–2591, https://doi.org/10.5194/nhess-16-2577-2016, 2016. a
EPTB Saône et Doubs: Réduction de la vulnérabilité – Préconisation d'aménagement de l'habitat face aux inondations, Tech. rep., EPTB Saône et Doubs, Mâcon, France, 2015. a
FEMA: Homeowner's Guide to Retrofitting, available at: http://www.fema.gov/floodproofing (last access: May 2019), 2009. a, b, c, d
FEMA: Flood Insurance Manual – Section 5: Rating, Tech. rep., FEMA, Washington, D.C., 2014. a
FEMA: NFIP rating and the community rating system, available at: https://www.fema.gov/national-flood-insurance-program-community-rating-system (last access: May 2019), 2018. a
Gerl, T., Kreibich, H., Franco, G., Marechal, D., and Schröter, K.: A Review of Flood Loss Models as Basis for Harmonization and Benchmarking, PLoS ONE, 11, 1–22, https://doi.org/10.1371/journal.pone.0159791, 2016. a
Grelot, F. and Richert, C.: floodam – Modelling Flood Damage functions of buildings – Manual for floodam v1.0.0, Tech. rep., IRSTEA, available at: https://irsteadoc.irstea.fr/cemoa/PUB00061355, last access: May 2019. a, b
ICPR – International Commission for the Protection of the Rhine: Non Structural Flood Plain Management: Measures and Their Effectiveness, Tech. rep., Koblenz, 2002. a
Klijn, F. and Samuels, P. G.: Towards flood risk management in the EU: State of affairs with examples from various European countries, Int. J. River Basin Manage., 6, 307–321, https://doi.org/10.1080/15715124.2008.9635358, 2008. a, b, c
Kreibich, H. and Thieken, A. H.: Coping with floods in the city of Dresden, Germany, Nat. Hazards, 51, 423–436, https://doi.org/10.1007/s11069-007-9200-8, 2009. a
Kreibich, H., Thieken, A. H., Petrow, T., Müller, M., and Merz, B.: Flood loss reduction of private households due to building precautionary measures – lessons learned from the Elbe flood in August 2002, Nat. Hazards Earth Syst. Sci., 5, 117–126, https://doi.org/10.5194/nhess-5-117-2005, 2005. a, b
Kreibich, H., Christenberger, S., and Schwarze, R.: Economic motivation of households to undertake private precautionary measures against floods, Nat. Hazards Earth Syst. Sci., 11, 309–321, https://doi.org/10.5194/nhess-11-309-2011, 2011. a, b, c, d, e, f, g, h
Kreibich, H., Bubeck, P., Van Vliet, M., and De Moel, H.: A review of damage-reducing measures to manage fluvial flood risks in a changing climate, Mitig. Adapt. Strat. Global Change, 20, 967–989, https://doi.org/10.1007/s11027-014-9629-5, 2015. a, b
Kreibich, H., Botto, A., Merz, B., and Schr, K.: Probabilistic , Multivariable Flood Loss Modeling on the Mesoscale with BT-FLEMO, Risk Analysis, 37, 774–787, https://doi.org/10.1111/risa.12650, 2017. a
Merz, B., Hall, J., Disse, M., and Schumann, A.: Fluvial flood risk management in a changing world, Nat. Hazards Earth Syst. Sci., 10, 509–527, https://doi.org/10.5194/nhess-10-509-2010, 2010. a, b
Ministère de l'égalité des Territoires et du Logement – Ministère de l'écologie, du Développement durable, et de l'énergie: Référentiel de travaux de prévention du risque d'inondation dans l'habitat existant, Tech. rep., Ministère de l'écologie, du Développement durable et de l,Énergie, Paris, France, 2012. a
Nadal, N. C., Zapata, R. E., Pagán, I., López, R., and Agudelo, J.: Building Damage due to Riverine and Coastal Floods, J. Water Resour. Pl. Manage., 136, 327–336, https://doi.org/10.1061/(ASCE)WR.1943-5452.0000036, 2010. a
National Research Council: Tying Flood Insurance to Flood Risk for Low-Lying Structures in the Floodplain, Washington, https://doi.org/10.17226/21720, 2015. a, b, c
Poussin, J. K., Bubeck, P., Aerts, J. C., and Ward, P. J.: Potential of semi-structural and non-structural adaptation strategies to reduce future flood risk: Case study for the Meuse, Nat. Hazards Earth Syst. Sci., 12, 3455–3471, https://doi.org/10.5194/nhess-12-3455-2012, 2012. a
Poussin, J. K., Botzen, W. J. W., and Aerts, J. C. J. H.: Effectiveness of flood damage mitigation measures: Empirical evidence from French flood disasters, Global Environ. Change, 31, 74–84, https://doi.org/10.1016/j.gloenvcha.2014.12.007, 2015. a, b, c, d, e, f, g, h, i, j, k
R Core Team: R: A Language en Environment for Statistical Computing, Tech. rep., R Foundation for Statistical Computing, Vienna, Austria, available at: https://www.r-project.org/ (last access: May 2019), 2017. a
Richert, C. and Grelot, F.: Comparaison des modèles de dommages nationaux avec les données de sinistralité, Tech. rep., IRSTEA, Montpellier, France, 2018. a
Rouchon, D., Christin, N., Peinturier, C., and Nicklaus, D.: Analyse multicritères des projets de prévention des inondations. Guide méthodologique 2018, Théma – balises, Ministère de la Transition Écologique et Solidaire, Commissariat général au développement durable, Paris, France, 2018. a
Sairam, N., Schröter, K., Lüdtke, S., Merz, B., and Kreibich, H.: Quantifying Flood Vulnerability Reduction via Private Precaution, Earth's Future, 7, 235–249, https://doi.org/10.1029/2018EF000994, 2019. a
Tobin, G. A.: The levee love affaire: a stormy relationship?, J. Am. Water Resour. Assoc., 31, 359–367, 1995. a
Vis, M., Klijn, F., Bruijn, K. M., and Buuren, M. V.: Resilience strategies for flood risk management in the Netherlands, Int. J. River Basin Manage., 1, 33–40, https://doi.org/10.1080/15715124.2003.9635190, 2003. a
Werritty, A.: Sustainable flood management: oxymoron or new paradigm?, Area, 38, 16–23, https://doi.org/10.1111/j.1475-4762.2006.00658.x, 2006. a
Xian, S., Lin, N., and Kunreuther, H.: Optimal house elevation for reducing flood-related losses, J. Hydrology, 548, 63–74, https://doi.org/10.1016/j.jhydrol.2017.02.057, 2017. a, b, c, d
Zevenbergen, C., Gersonius, B., Puyan, N., and Van Herk, S.: Economic Feasibility Study of Flood Proofing Domestic Dwellings, in: Advances in urban flood management, chap. 13, edited by: Ashley, R., Garvin, S. L., Pasche, E., Vassipoulos, A., and Zevenbergen, C., Taylor & Francis, London, UK, 299–319, https://doi.org/10.1201/9780203945988, 2007. a, b, c
It is also possible to leave the slab on the ground and to construct a new floor after lifting the house.
For dwellings with a basement, additional measures must be taken. We only analysed the measures which aim to prevent the water from entering into a dwelling without a basement.
Some floods can last more than 144 h. The experts interviewed did not provide data regarding the vulnerability of the elementary components to such floods. Thus, we did not study the efficacy of precautionary measures for floods longer than 144 h.