the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Mapping the susceptibility of rain-triggered lahars at Vulcano island (Italy) combining field characterization, geotechnical analysis, and numerical modelling
Valérie Baumann
Costanza Bonadonna
Sabatino Cuomo
Mariagiovanna Moscariello
Sebastien Biass
Marco Pistolesi
Alessandro Gattuso
The characterization of triggering dynamics and remobilized volumes is crucial to the assessment of associated lahar hazards. We propose an innovative treatment of the cascading effect between tephra fallout and lahar hazards based on probabilistic modelling that also accounts for a detailed description of source sediments. As an example, we have estimated the volumes of tephra fallout deposit that could be remobilized by rainfall-triggered lahars in association with two eruptive scenarios that have characterized the activity of the La Fossa cone (Vulcano, Italy) in the last 1000 years: a long-lasting Vulcanian cycle and a subplinian eruption. The spatial distribution and volume of deposits that could potentially trigger lahars were analysed based on a combination of tephra fallout probabilistic modelling (with TEPHRA2), slope-stability modelling (with TRIGRS), field observations, and geotechnical tests. Model input data were obtained from both geotechnical tests and field measurements (e.g. hydraulic conductivity, friction angle, cohesion, total unit weight of the soil, and saturated and residual water content). TRIGRS simulations show how shallow landsliding is an effective process for eroding pyroclastic deposits on Vulcano. Nonetheless, the remobilized volumes and the deposit thickness threshold for lahar initiation strongly depend on slope angle, rainfall intensity, grain size, friction angle, hydraulic conductivity, and the cohesion of the source deposit.
- Article
(13149 KB) - Full-text XML
-
Supplement
(387 KB) - BibTeX
- EndNote
Lahars, an Indonesian term to indicate volcanic debris flows and hyper-concentrated flows with various amounts of volcanic solid content, can cause loss of life and damage to infrastructure and cultivated lands; they represent one of the most devastating hazards for people living in volcanic areas (Pierson et al., 1990, 1992; Janda et al., 1996; Scott et al., 1996, 2005; Lavigne et al., 2000; Witham, 2005; De Bélizal et al., 2013). The most destructive lahars are caused by the breakout of crater lakes or volcano dammed lakes (e.g. Mt. Kelud in Indonesia; Thouret et al., 1998) and by the interaction of hot pyroclastic density currents (PDCs) with glacial ice and snow at ice-capped volcanoes (e.g. Nevado del Ruiz in Colombia; Pierson et al., 1990). However, the most common lahars are those generated by heavy rainfall on tephra fallout and PDC deposits emplaced on volcano slopes (e.g. Casita Volcano, Nicaragua; Scott et al., 2005; Panabaj, Guatemala; Charbonnier et al., 2018). For example, torrential rainstorms on loose pyroclastic deposits produced by the 1991 eruption of Pinatubo (Philippines) have generated hundreds of secondary lahars for years after the end of the eruption (e.g. Janda et al., 1996; Newhall and Punongbayan, 1996). Despite their relatively small volumes, over 6 years, these lahars have remobilized 2.5 km3 of the 5.5 km3 of primary pyroclastic material, inundated 400 km2 of villages and fields, and caused the evacuation of more than 50 000 people (Vallance and Iverson, 2015).
Many studies exist that make use of various analytical and numerical models to describe the potential inundation area of lahars (e.g. Procter et al., 2012; Córdoba et al., 2015; Caballero et al., 2016; Mead and Magill, 2017; Charbonnier et al., 2018). The associated outcomes are fundamental to the development of risk reduction strategies; nonetheless, all inundation models require the determination of the volume of potentially remobilized material that is often approximated due to the lack of information. In fact, the identification of lahar source areas and lahar initiation mechanisms is crucial to the evaluation of lahar recurrence and magnitude. With “lahar source areas” we refer to areas with pyroclastic material that can be remobilized to form lahars; these areas are normally located on steep slopes (> 20∘) and at the head of channels draining the volcano flanks. The generation of rain-triggered lahars may be influenced by several factors such as the amount of rainfall, deposit stratigraphy, slope gradient, vegetation cover, and the physical characteristics of pyroclastic deposits (e.g. thickness, permeability, pore pressure, and grain size distribution). Two main mechanisms have been identified for the triggering of lahars by rainfall on pyroclastic material: sheet and rill erosion due to Hortonian overland flow caused by deposit saturation (e.g. Collins and Dunne, 1986; Cuomo et al., 2015) and the infiltration of slope surface by rainfall that can generate shallow landslides (e.g. Iverson and Lahusen, 1989; Manville et al., 2000; Crosta and Dal Negro, 2003; Zanchetta et al., 2004; Volentik et al., 2009; Cascini et al., 2010). Infiltration occurs when the rainfall intensity is lower than the hydraulic conductivity, while overland runoff occurs when rainfall intensity is greater than infiltration capacity, which is also related to capillary suction for unsaturated soils (Cuomo and Della Sala, 2013). Overland runoff is enhanced by the emplacement of very fine ash layers (< 0.125 mm) that reduce the infiltration capacity (Collins and Dunne, 1986; Leavesley et al., 1989; Pierson et al., 2013; Cuomo et al., 2016). Poor infiltration capacities of fresh pyroclastic deposits have been measured, for example at Mount St. Helens in 1980, USA (Collins and Dunne, 1986; Leavesley et al., 1989; Major et al., 2000; Major and Yamakoshi, 2005), Mt. Unzen in 1990–1995, Japan (Yamakoshi and Suwa, 2000; Yamamoto, 1984), and Chaitén in 2008, Chile (Pierson et al., 2013). The combination of a large supply of loose pyroclastic deposits and intense rainfall episodes therefore increases the likelihood of lahars. This is the case on Vulcano island (Italy; Fig. 1), where the deposits of the 1888–1890 eruption, the last eruption of the La Fossa volcano, are still remobilized during the rainy season (e.g. Frazzetta et al., 1984; Dellino and La Volpe, 1997; De Astis et al., 2013; Di Traglia et al., 2013). The initiation mechanism of recent lahars has been studied in detail by Ferrucci et al. (2005), but the initiation mechanism during and just after long-lasting eruptions and in association with short sustained eruptions (such as the eruptions that have characterized the activity of the volcano in the last 1000 years; Di Traglia et al., 2013) has not yet been characterized.
In order to determine the volume of potentially remobilized material, Volentik et al. (2009) and Galderisi et al. (2013) have already combined lahar-triggering modelling with probabilistic assessment of tephra deposition based on a static hydrological model (Iverson, 2000) and assuming total saturation of the deposit. In addition, Tierz et al. (2017) have compiled a probabilistic lahar hazard assessment through the Bayesian belief network “Multihaz” based on a combination of probabilistic hazard assessment of both tephra fallout and PDCs with a dynamic physical model for lahar propagation. Even though these three examples were pioneering in assessing the effect of cascading hazards, the associated description of lahar triggering was overly simplified (i.e. fundamental aspects such as hydraulic conductivity and friction angle were not taken into account) and the soil characteristics as well as the intensity and duration of the rainfall were not considered. In our paper we build on these first studies to show the importance of the application of physically based models in combination with the characterization of pyroclastic material for the determination of deposit instability. Our goal is to accurately predict the volume of tephra fallout that could be remobilized by a rainfall-triggered shallow landslide in association with various eruptive conditions at the La Fossa cone in order to compile a rain-triggered lahar susceptibility map. To achieve this task, we combine the shallow landslide model TRIGRS (Baum et al., 2002) with both probabilistic modelling of tephra fallout (for eruptions of different duration and magnitude) and field and geotechnical characterizations of tephra fallout deposits (i.e. grain size, hydraulic conductivity, soil suction, deposit density).
First, we describe the physical characteristics (e.g. grain size, hydraulic conductivity, angle of friction) of selected tephra fallout deposits associated with both a long-lasting Vulcanian eruption (i.e. the 1888–1890 eruption) and a subplinian eruption (PAL-D eruption of the Palizzi sequence; Di Traglia et al., 2013). Second, we characterize the lahar deposits associated with the 1888–1890 eruption, which provide insights into lahar source areas, flow emplacement mechanisms, and inundation areas of future lahars. The physical characteristics of tephra fallout deposits are used in combination with a probabilistic modelling of tephra fallout (Biass et al., 2016a) to estimate the unstable areas based on the shallow landslide model TRIGRS (Baum et al., 2002). This approach provides the first integrated attempt to quantify the source volume of lahars as a function of probabilistic hazard assessment for tephra fallout (with TEPHRA2), numerical modelling of lahar triggering (with TRIGRS), field observations (including primary tephra fallout deposits, geology, geomorphology, and precipitation), and geotechnical tests of source deposits. Finally, we propose a new strategy to map syn-eruptive lahar susceptibility as a critical tephra fallout deposit thickness resulting in unstable conditions, which could represent a valuable tool for contingency plans. Here the term syn-eruptive is used in the sense of Sulpizio et al. (2006) to indicate lahars that originated during volcanic eruptions or shortly after, while post-eruptive lahar events are generated long (i.e. a few to several years) after an eruption. This is also in agreement with the current definition of primary (syn-eruptive) and secondary lahars (post-eruptive or unrelated to eruptions) provided by Vallance and Iverson (2015) and Gudmunsson (2015). To sum up, this study explores new strategies for volcanic multi-hazard assessment and offers an innovative treatment of the cascading effects between tephra fallout and lahar susceptibility.
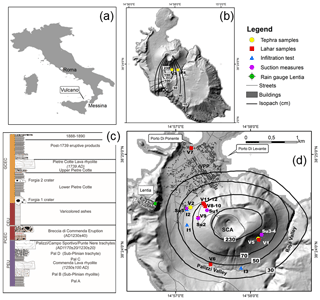
Figure 1Overview of the study area. (a) location of the island of Vulcano in Italy. (b) Isopach map on a shaded relief of Vulcano island of the cumulative tephra fallout PAL-D deposit (after Di Traglia, 2011). (c) Simplified stratigraphy of the last 1000 years of the La Fossa volcano based on Di Traglia et al. (2013) and De Astis et al. (1997, 2013) (see Table 1 for more details). (d) Isopach map of the cumulative 1888–1890 tephra fallout deposit (after Di Traglia, 2011) and sample locations. Sample names refer to V samples of tephra fallout (yellow circles) and lahars (red squares), I to infiltration measures (blue triangle), and Su to suction measurements (pink diamond). SCA: summit cone area. VPP: Vulcano Porto Plain. The rain gauge of Lentia is also shown (green circle).
Table 1Number of observed eruptions for the different types of activity in the last 1000 years on Vulcano island. Values of frequencies and the detailed events for each type are also reported. In bold are the selected scenarios used in Sect. 3.3; based on data from Di Traglia et al. (2013) and De Astis et al. (1997, 2013).

2.1 Eruptive history
The island of Vulcano, the southernmost island of the Aeolian archipelago, consists of several volcanic edifices whose formation overlapped in time and space beginning 120 kyr ago. The most recently active volcano is the La Fossa cone, a 391 m high active composite cone that began to erupt 5.5 kyr ago (Frazzetta et al., 1984) and whose erupted products vary in composition from latitic to rhyolitic, with minor shoshonites (Keller, 1980; De Astis et al., 1997; Gioncada et al., 2003). The stratigraphy of the La Fossa cone has been described in detail in several studies (Keller, 1980; Frazzetta et al., 1983; Di Traglia et al., 2013; De Astis et al., 2013). The last period of eruptive activity (younger than 1 ka) has been recently divided into two main eruptive clusters, further separated into eruptive units (Di Traglia et al., 2013; Fig. 1). The activity of the Palizzi and Commenda eruptive units (PEU and CEU, respectively) is grouped into a single eruptive period (Palizzi–Commenda eruptive cluster, PCEC) lasting approximately 200 years (11th to 13th century). The following Pietre Cotte cycle, with the post-1739 CE and 1888–1890 CE activity form the Gran Cratere eruptive cluster (GCEC, 1444–1890 CE; Di Traglia et al., 2013). The stratigraphic sequence of PEU displays a large variety of eruptive products and a wide spectrum of magma compositions, including cross-stratified and parallel-bedded ash layers (e.g. PAL-A and PAL-C in Di Traglia et al., 2013), pumiceous tephra fallout layers of rhyolitic (PAL-B) and trachytic composition (PAL-D), several lava flows intercalated in the sequence (e.g. the rhyolitic obsidian of Commenda and the trachytic lava flows of Palizzi, Campo Sportivo, and Punte Nere), and, finally, several ash layers and widely dispersed PDC deposits (CEU) associated with the hydrothermal eruption of the Breccia di Commenda eruptive unit (Gurioli et al., 2012; Rosi et al., 2018), which closes the PCEC. The GCEC includes the recent products of the Pietre Cotte eruptive unit (ash and lapilli layers from Vulcanian activity), rhyolitic pumiceous tephra fallout layers, and the rhyolitic 1739 CE Pietre Cotte lava flow. The uppermost part of the GCEC is represented by the products of the 1888–1890 CE eruption, consisting of latitic spatters, trachytic and rhyolitic ash, lapilli layers, and the characteristic bread-crust bombs. Historical chronicles (Mercalli and Silvestri, 1891; De Fiore, 1922), archaeomagnetic data (Arrighi et al., 2006; Zanella et al., 1999; Lanza and Zanella, 2003), and stratigraphic investigations (Di Traglia et al., 2013; De Astis et al., 1997, 2013) concur in indicating that in the past 1000 years at least 20 effusive and explosive eruptions have occurred. Among the explosive eruptions, the Vulcanian cycles represent the most important events in terms of recurrence (at least five long-lasting episodes corresponding to annual frequencies of year−1) and erupted volumes, followed by rarer short-lived, higher-intensity events, strombolian explosions, and phreatic eruptions (Table 1). In this work, we will focus on the tephra fallout associated with two main eruptive styles of the past 1000 years: a long-lasting Vulcanian eruption such as that of 1888–1890 (e.g. Di Traglia et al., 2013; Biass et al., 2016a) and a subplinian eruption, which emplaced deposits such as the Palizzi-D subunit. For simplicity, we refer to the deposits of the last 1888–1890 long-lasting Vulcanian event as the “1888–1890 eruption” and to the fallout deposit of the subplinian Palizzi-D eruption as “PAL-D” primary deposits.
2.2 Climate
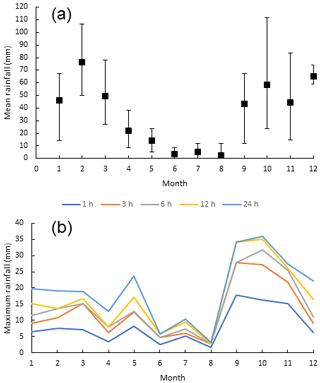
Vulcano island has a typical semi-arid Mediterranean climate (De Martonne, 1926) with annual rainfall between 326 and 505 mm, falling mostly during autumn and winter seasons (Fig. 2a). Based on Arnone et al. (2013), rainfall trends in Sicily island can be classified in three intensity-based categories: light precipitation (0.1–4 mm d−1), moderate precipitation (4–20 mm d−1), and heavy–torrential precipitation (> 20 mm d−1). Heavy–torrential precipitation occurred three times in 2010 and 2011, two times in 2012, and one time in 2013 and 2014 (INGV Palermo); the associated rainfall duration can last 2–3 h to 3 d and occurs normally in September, October, November, December, and, more rarely, in May (Fig. 2b). Such an observation agrees with the observations of De Fiore (1922) for the period just following the 1888–1890 eruption, indicating that the weather pattern in the region has been pretty constant. These meteorological conditions associated with poor vegetation coverage (Valentine et al., 1998), steep slopes (Fig. 1d), and the presence of layered, fine-grained tephra (lapilli and ash) favour the remobilization of volcanic deposits (Ferrucci et al., 2005; Di Traglia, 2011). Wind patterns inferred from the ECMWF ERA-Interim dataset (Dee et al., 2011) for the period 1980–2010 show a preferential dispersal towards SE at altitudes lower than 10 km above sea level (a.s.l.), which above shift towards E (Biass et al., 2016a).
2.3 Recent lahars
Both syn-eruptive and post-eruptive lahar events induced the progressive erosion of the tephra deposits that cover the La Fossa cone. The tephra fallout deposit associated with the most recent Vulcanian eruption (1888–1890) has been almost completely removed from the upper slopes and accumulated at the foot of the cone, where the stratigraphic sections show a succession of lahar deposits with thicknesses between 0.1 and 1 m (Ferrucci et al., 2005). The entire tephra sequence of the Gran Cratere eruptive cluster (including the 1888–1890 Vulcanian eruption) lies on top of thinly stratified, reddish, impermeable ash layers (varicoloured tuffs or “tufi varicolori”; Frazzetta et al., 1983; Capaccioni and Coniglio, 1995; Dellino et al., 2011), which concluded the Breccia di Commenda phase. In most parts of the cone, the dark grey tephra of the Vulcanian cycles is almost completely eroded and the tufi varicolori are exposed. A rill network developed on the impermeable fine-grained tuffs that conveys water to a funnel-shaped area, where a main gully defines a drainage basin (Ferrucci et al., 2005). The main gullies start where the loose grey interdigitated tephra fallout and lahar deposits crop out (Fig. 1). Lahar volumes and travel distance strongly depend on both the availability of pyroclastic material in the source area and on the characteristics of the rainfall events (intensity and duration). Ferrucci et al. (2005) estimated volumes between 20 and 50 m3 for three recent lahars based on levees and terminal-lobe deposit geometry on the NW sector of the La Fossa cone. We describe, as an additional example, a small lahar that occurred on September 2017 (just before our main field survey) on the NW cone flank covering part of the La Fossa crater trail (the Supplement). However, the occurrence of larger syn-eruptive lahars (103–104 m3) reaching the Porto di Levante and Porto di Ponente areas have also been reported (Di Traglia, 2011). Much of the material of the La Fossa ring plain has been transported by lahars during the post-1000 CE period; in fact, the Porto di Levante and Porto di Ponente plains were progressively filled up with 2–3 m of reworked tephra fallout deposits during this time interval (Di Traglia et al., 2013). In 1921 the loose grey 1888–1890 tephra fallout deposit was already largely eroded and the tufi varicolori were already exposed (De Fiore, 1922). Di Traglia et al. (2013) also reported post-eruptive lahar deposits on the flank of the volcano with increasing thickness towards the base. Deposit thickness then decreases on the ring plain in the Porto area where they also show finer grain size and lamination. The study of recent lahars located on the NW flank of the La Fossa cone indicated that the deposits were emplaced by saturated slurries in which grain interaction dominated the flow dynamics (Ferrucci et al., 2005). The use of the empirical ratio clay ∕ (sand + silt + clay) (Vallance and Scott, 1997) and the physically based calculation of Nmass (Iverson and Vallance, 2001) suggest non-cohesive debris flows and transport dominated by granular flows (Ferrucci et al., 2005).
3.1 Field sampling
The field characterization of both tephra fallout primary deposits in the lahar initiation zones and lahar deposits was carried out during two field campaigns in 2017 and 2018. Eight undisturbed samples of tephra fallout primary deposit were collected for geotechnical tests from four outcrops on the La Fossa cone and Palizzi valley for the 1888–1890 and the PAL-D units (yellow circles in Fig. 1b and d). In particular, PAL-D tephra fallout primary deposit was sampled at locations V3 (one sample) and V4 (one sample) (Fig. 1b), while the 1888–1890 tephra fallout primary deposit was sampled at locations V1 (four samples) and V2 (two samples) (Fig. 1d). In addition, five samples for grain size analysis were collected vertically every 6 cm at two 1888–1890 tephra fallout primary deposit outcrops (yellow circles V1 and V2 in Fig. 1d). We consider the tephra fallout primary deposit of V1 and V2 as representative of the lahar initiation zone on the S and NW flanks of the La Fossa cone, respectively. In contrast, the lahar source area associated with the PAL-D primary deposit is either covered by new eruptive products or eroded. As a result, PAL-D had to be sampled at the base of the cone (V3 and V4 in Fig. 1b). Deposit sampling for geotechnical tests was performed by inserting a steel tube with a height of 30 cm and a diameter of 10 cm into the ground (see Appendix A, Fig. A1). A basal support was then inserted, and the tube was extracted from the deposit with minimum disturbance of the internal stratigraphy. The tube was then covered on both ends to preserve the deposit for further laboratory analysis (see Sect. 3.2). Due to the sampling apparatus, most geotechnical tests could only be carried out on the top 30 cm of each deposit location. As a comparison, in V1 the 30 cm tube was inserted after having eliminated the top 30 cm of deposit to analyse the central part of the outcrop. Given the characteristics of the deposit, we consider 30 cm of sampling to be representative for the main characteristics of both the 1888–1890 (which is thinly laminated across the entire section) and the PAL-D (which is mostly massive) deposits. Soil suction measurements were carried out in situ on the 1888–1890 tephra fallout deposit with a soil moisture probe (“Quick Draw” model 2900FI) (Fig. 1 and Appendix A). The saturated hydraulic conductivity was estimated in the field with a single-ring permeameter on PAL-D primary deposits (V3 and I3 in Fig. 1) and on 1888–1890 primary deposits (I1 and I2, near the V2 location in Fig. 1) (see Appendix A, Fig. A3). The field description and sampling of syn-eruptive lahar deposits associated with the 1888–1890 eruption were performed on the NW volcano flanks, in the Palizzi valley, and in the Porto Plain (red squares in Fig. 1; V5 to V12). At total of 11 samples of lahar matrices were sampled on the S cone flank (V5), on the NW cone flank (V8–V12), in the Palizzi valley (V6), and in the Porto Plain (four samples in V7).
3.2 Laboratory analyses
Grain size analyses were carried out at the University of Geneva for three tephra fallout sections (11 samples) and for 11 lahar deposit matrix samples (fractions between −6 and 10Φ). The phi (Φ) scale is a sediment particle size scale diameter calculated as the negative logarithm to the base 2 of the particle diameter (in millimetres) (Krumbein, 1938). Samples were mechanically dry-sieved at half-Φ intervals for the coarser fraction between 16 and 0.25 mm. The laser granulometry technique (CILAS 1180 instrument) was used for fractions smaller than 0.25 mm. The deposit density of five samples of the 1888–1890 primary deposits and one sample of the PAL-D tephra fallout deposit was also determined at the University of Geneva by weighing a given volume of sample material measured with a graduated cylinder.
Natural water content and shear strength were measured on undisturbed samples at the University of Salerno. The natural water content (wn) was evaluated at several depths (from 0.06 to 0.3 m) for six samples of the 1888–1890 primary deposits and for four samples of the PAL-D primary deposit. The shear strength of primary deposits was measured through direct shear tests performed with a conventional direct shear apparatus in the Laboratory of Geotechnics at the University of Salerno. Tests on undisturbed specimens of the 1888–1890 primary deposit were performed at both natural water content and in fully saturated conditions. The natural water content (wn) and the degree of saturation were evaluated before and after the tests. The modified Kovács (1981) model of Aubertin et al. (2003) was used to obtain the soil water retention curve (SWRC) from the grain size data of the source area (i.e. D10 and D60, the diameter corresponding to 10 % and 60 % of the grain size distribution; see the Supplement, Table S2) and the liquid limit. SWRC relates the water content to soil suction. The tests were interpreted in terms of shear stress and the vertical effective stress as defined by Bishop (1959), referring to the “effective saturation degree” (Sre) following Eq. (1):
where σij (kPa) is the total stress tensor, ua (kPa) is the pore air pressure, uw (kPa) is the pore water pressure, ua−uw is the matric suction, and Sr (%) is the degree of saturation.
The saturated hydraulic conductivity Ks (m s−1) for the 1888–1890 primary deposit was measured through laboratory tests at the University of Salerno. The test was carried out on a reconstructed specimen with a height of 140 mm and a diameter of 39.4 mm obtained through a water pluviation technique, ensuring specimen saturation. A constant water volume (5 mL) was forced to go through the specimens by applying a difference of pore pressure between the top and bottom, while the time was measured. The test was repeated five times and each time Ks was evaluated.
The saturated soil diffusivity D0 (m2 s−1) was evaluated for both deposits using the soil water retention relationship of Rossi et al. (2013) as a function of the saturated hydraulic conductivity and the parameters (hb, λ) of Brooks and Corey (1964, 1966) following Eq. (2):
where θs (%) is the soil water content at saturation, hb (kPa) the bubbling pressure, and λ (m2 g−1) the pore size index distribution. The parameters hb and λ were estimated by interpolating the data of SWRC.
3.3 Probabilistic tephra fallout modelling
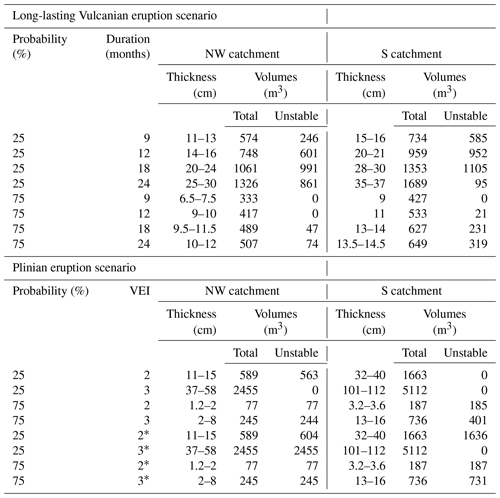
In order to best describe the cascading effect between tephra deposition and lahar triggering susceptibility in the context of multi-hazard assessments, the tephra fallout deposits considered in our analysis are those probabilistically modelled by Biass et al. (2016a). Based on the stratigraphy of the last 1000 years of La Fossa (Di Traglia et al., 2013), Biass et al. (2016a) defined three eruption scenarios for tephra fallout including the following: (i) a long-lasting Vulcanian eruption scenario (plume heights: 1–10 km a.s.l.; total mass: 1.9–140×109 kg; duration: 30 d–3 years); (ii) a VEI 2 (Volcanic Explosivity Index; Newhall and Self, 1982) subplinian eruption scenario (plume heights: 5–12 km a.s.l.; mass: 0.6–6×109 kg; duration: 0.5–6 h); and (iii) a VEI 3 subplinian eruption scenario (plume heights: 8–17 km a.s.l.; mass: 6–60×109 kg; duration: 0.5–6 h). Note that although no VEI 3 eruption is observed in the stratigraphy of the last 1000 years of activity, evidence of VEI 3 eruptions is found in the older history of La Fossa. All three scenarios were simulated probabilistically using the TEPHRA2 model (Bonadonna et al., 2005) with the TephraProb software (Biass et al., 2016b). Probabilistic isomass maps were computed for various probability thresholds, which express the distribution of tephra load for a fixed probability of occurrence within a given eruption scenario (Biass et al., 2016b). For the long-lasting Vulcanian scenario, various probabilistic isomass maps were computed to express the cumulative tephra fallout at a given time after eruption onset. Note that these cumulative maps ignore remobilization of the primary deposit between single Vulcanian explosions. These probabilistic isomass maps were converted into probabilistic isopach maps using deposit densities of 1200 and 600 kg m−3 for the Vulcanian and subplinian scenarios, respectively (Biass et al., 2016a).
3.4 TRIGRS model
Based on the physical characteristics of the tephra fallout deposits (high permeability) and on the high intensity of rainfall events, we assume that the most probable rain-triggered lahar initiation mechanism on the La Fossa cone is shallow landsliding. Shallow landsliding is produced by an increase in water pore pressure due to rainfall infiltration on tephra deposits, which causes a slope failure. Several slope-stability models have been used to predict lahar initiation processes as shallow landslides in volcanic areas (e.g. Cascini et al., 2010; Frattini et al., 2004; Crosta and Dal Negro, 2003; Sorbino et al., 2007, 2010; Cascini et al., 2011; Cuomo and Iervolino, 2016; Cuomo and Della Sala, 2016; Mead et al., 2016, Baumann et al., 2018). Among those, the Fortran programme TRIGRS (Baum et al., 2002) can be used for computing transient pore pressure and the related changes in the factor of safety due to rainfall infiltration. Here, TRIGRS is used to investigate the timing and location of shallow landslides in response to rainfall in large areas (e.g. Baumann et al., 2018). Baum et al. (2002) extended the method of Iverson (2000) by implementing the solutions for a complex time sequence of rainfall intensity, an impermeable basal boundary at infinite depth, and an optional unsaturated zone above the water table. TRIGRS is applicable for unsaturated initial conditions, with a two-layer system consisting of a saturated zone with a capillary fringe above the water table overlain by an unsaturated zone that extends to the ground surface. The unsaturated zone acts like a filter that smooths and delays the surface infiltration signal at depth. The model uses the soil water characteristic curve for wetting of the unsaturated soil proposed by Gardner (1958) and approximates the infiltration process as a one-dimensional vertical flow (Srivastava and Yeh, 1991; Savage et al., 2004). The reader is referred to the vast literature published on the application of this model for more details (e.g. Baum et al., 2002, 2008; Savage et al., 2003; Salciarini et al., 2006; Cuomo and Iervolino, 2016). Briefly, the infiltration models in TRIGRS for wet initial conditions are based on Iverson's (2000) linearized solution of the Richards equation and its extension to that solution (Baum et al., 2002; Savage et al., 2003, 2004). The solution is valid only where the transient infiltration is vertically downward and the transient lateral flow is relatively small.
Following Iverson (2000), slope stability is calculated using an infinite slope-stability analysis. Incipient failure of infinite slopes is described by an equation that balances the downslope component of gravitational driving stress against the resisting stress due to basal Coulomb soil friction and the influence of groundwater (Iverson, 2000). The factor of safety (FS) is calculated at a depth Z by Eq. (3):
where c′ (kPa) is the effective soil cohesion, ϕ′ (deg) is the effective friction angle, ψ(Z,t) is the ground water pressure head ψ (kPa) as a function of depth Z (m) and time t (s), β (deg) is the slope angle, Υw (kN m−3) is the unit weight of groundwater, and Υs (kN m−3) is the unit weight of soil. The pressure head ψ(Z,t) in Eq. (3) is obtained from various formulas depending on the particular condition modelled. FS is calculated for pressure heads at multiple depths (Z). The slope is predicted to be instable where FS < 1, in a state of limiting equilibrium where FS =1, and stable where FS > 1. Thus, the depth Z of landslide initiation is where FS first drops below 1.
TRIGRS for unsaturated initial conditions was applied on the probabilistic isopach maps described in Sect. 3.3 for the long-lasting Vulcanian, the subplinian VEI 2, and the subplinian VEI 3 eruption scenarios. For each eruption scenario, probabilistic isopach maps are computed for probabilities of occurrence of 25 % and 75 % (Biass et al., 2016a). The eruption associated with the subplinian scenario is considered to be short lived (< 6 h), and therefore one single deposit is analysed. Instead, for the long-lasting Vulcanian scenario, deposits are computed for durations of 3, 6, 9, 12, 18, and 24 months. A 5 m resolution digital elevation model (DEM) of Vulcano island was used in our susceptibility analysis that was computed from contour lines and spot heights reconstructed from stereo-photograms at a scale of 1:35 000 collected during an aerophotogrammetric flight in 1994–1995 (Bisson et al., 2003). The maximum planimetric error of the contour lines reconstructed from stereo models is less than 3.5 m. The vertical error of the DEM is lower than 0.5 m in the area of the La Fossa cone and < 1 m in the flat area of Vulcano Porto (Bisson et al., 2003).
4.1 Field characterization of tephra fallout and lahar deposits
4.1.1 PAL-D tephra fallout deposit
We logged two sections of the PAL-D tephra fallout deposit at outcrops located in the Palizzi valley (point V3 and V4; Fig. 1b). The isopach map of Di Traglia (2011) shows the associated southward dispersal (Fig. 1b). The PAL-D section at V3 is a 1 m thick, massive, grain-supported, and well-sorted pumice deposit between two subunits of the Palizzi cycle (Fig. 3a): PAL-C deposit at the base (alternation of black lapilli and ash) and the rhyolitic white ash of the Rocche Rosse eruption from Lipari and the Breccia di Commenda at the top (Di Traglia et al., 2013; Rosi et al., 2018). The mean saturated hydraulic conductivity of the PAL-D deposit measured in the field at V3 (Fig. 1b) is m s−1.
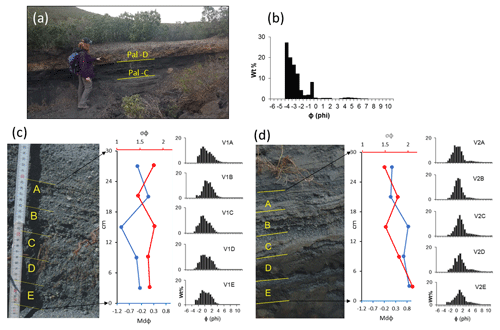
Figure 3(a) PAL-D subplinian tephra fallout deposit outcrop (V3; Fig.1). (b) Grain size distribution of PAL-D subplinian tephra fallout deposit. (c, d) MdΦ, σΦ, and grain size distribution of the first 30 cm of the tephra fallout deposit associated with the 1888–1890 Vulcanian eruption for stratigraphic sections V1 and V2 (Fig. 1). Thickness of the layers analysed: A (24–30 cm); B (24–18 cm); C (18–12 cm); D (12–6 cm); E (6–0 cm).
4.1.2 1888–1890 tephra fallout deposit
Two stratigraphic sections of the 1888–1890 tephra fallout deposit were logged in the upper part of the La Fossa cone S flank (V1 in Fig. 1d; Fig. 3c) and at the base of the NW flank (V2 in Fig. 1d; Fig. 3d). The isopach map for the 1888–1890 primary tephra fallout deposit shows an almost circular dispersal (Fig. 1d). The V1 section overlies several older tephra fallout and lahar units. It is a 1 m thick deposit consisting of an alternation of thin ash and lapilli layers overtopped by 0.2 m of reworked tephra. The whole sequence shows an inclination of 30∘. The second section (V2) is a 0.5 m thick deposit laying on the Commenda tephra sequence and is overlaid by 0.3 m of reworked tephra. Seven soil suction measurements on the 1888–1890 deposits located on the La Fossa cone in the upper catchment and lower part of the cone are comprised between 15 and 27 kPa (Fig. 1d and Table S1). The mean saturated hydraulic conductivity measured in the field varies between 6.0 and m s−1 (Fig. 1d; I1 and I2).
4.1.3 1888–1890 lahar deposits
Stratigraphic sections in gullies and small channels on the NW flank of the La Fossa cone show several massive to laminated, remobilized deposits covering the 1888–1890 primary tephra fallout deposit. Unfortunately, no map exists that describes the distribution of lahars on Vulcano, mostly due to the difficulty of correlating the exposed deposits across the different gullies. The thickness of each lahar layer, representing different flow pulses, varies between ∼0.20 and 1 m. The lahar deposits are massive to thinly laminated and matrix supported, with boulders immersed in a coarse ash and lapilli matrix. The observed boulders have a diameter between 5 and 15 cm. Although the distinction among debris flow and hyper-concentrated flow emplacement mechanisms from direct observations in the field was not possible due to the lack of information related to original water content, we speculate that most of the well-sorted, massive deposits were related to hyper-concentrated flows based on the definition of Pierson (2005).
4.2 Laboratory characterization of tephra fallout and lahar deposits
4.2.1 Grain size analyses
The MdΦ of the majority of tephra fallout and lahar samples is in the range of 2Φ and −1Φ, and most deposits are well sorted (σΦ mostly between 1 and 2) (Fig. 5; associated grain size distributions are shown in the Supplement, Fig. S3). An exception is represented by the grain size distribution of the top 30 cm of the PAL-D primary tephra fallout deposit at section V3 that shows an MdΦ and σΦ of −3.42 and 1.55, respectively (Fig. 5). Grain size distributions of the top 30 cm of the 1888–1890 tephra fallout deposit on the S flank of the La Fossa cone (V1) show MdΦ between −0.88 and 0.08 and σΦ between 1.46 and 1.80, respectively (Fig. 5). At the base of the cone on the NW sector (V2), grain size distributions of the 1888–1890 tephra fallout deposit are slightly finer (MdΦ of 0.09 to 0.9) and with a poorer sorting (σΦ of 1.49 to 2.1). The grain size distributions of the top 30 cm of the 1888–1890 tephra fallout deposit at V1 and V2 show a predominance of coarse ash (Fig. 3). All lahar matrix samples have a low content of fine ash (i.e. 2.4 %–16 %) and contain 60 %–83 % coarse ash and 2 %–36 % lapilli. The MdΦ vs. σΦ diagram shows a finer grain size distribution for lahar matrices located in the Palizzi valley and Porto di Ponente harbour (V6 and V7 samples, respectively; Fig. 5) than for those located on the La Fossa cone (V5 sample; Fig. 5). In general, the grain size distributions of the 1888–1890 primary tephra fallout deposits is similar to their remobilized counterparts (Fig. 5 and Fig. S3). Only three primary tephra fallout deposits are coarser than lahar matrices (V1C, V1D, and V3; Fig. 5)

Figure 4(a) Lahar levee deposit (sample V5 in Fig. 1) above the 1888–1890 tephra fallout, located in a channel cut on the S of the La Fossa cone. (b) Lahar deposit (sample V6) above the 1888–1890 tephra fallout in the Palizzi valley. (c) The profile observed at the beachside in Porto di Ponente (1) is a 14 cm bed of coarse ash, with a 1 cm thick grey fine ash grey layer; this is the primary 1888–1890 CE tephra fallout. Layer V7-1 is a 26 cm lahar deposit of coarse ash to fine lapilli inversely graded. Layer V7-2 is an 11 cm fine lapilli lahar deposit with 1 cm of soil on the top. V7-3 is a 10 cm lahar deposit of coarse to fine ash with soil on the top and a 6 cm lahar deposit (V7-4) of coarse to fine ash with recent soil on the top. (d) Several lahar deposits located in a channel on the NW of the La Fossa cone: the first deposit above 1888–1890 was sampled (V9 in Fig. 1). (e) Lahar deposits located in a channel on the NW of the La Fossa cone on the top of the 1888–1890 tephra fallout deposit.
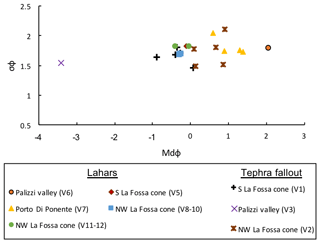
Figure 5MdΦ vs. σΦ diagram for the lahar matrix and tephra fallout deposits. Porto Di Ponente (orange triangle) corresponds to the following samples: V7-1, V7-2, V7-3, V7-4 S (Fig. 4c). The La Fossa cone V1 (black cross): V1A, V1B, V1C, V1D, V1E (Fig. 3c). NW La Fossa cone V2 (brown star): V2A, V2B, V2C, V2D, V2E (Fig. 3d).
4.2.2 Natural water content
The natural water content (wn) of the 1888–1890 tephra fallout deposit varies from 2.64 % to 3.65 %, while the PAL-D tephra fallout deposit exhibits higher wn (10.80 %–30.63 %). The specific gravity (Gs) for the solid fraction was measured for both deposits and shows values of 2.57 and 2.42 for the 1888–1890 and PAL-D tephra fallout deposits, respectively.
Table 2Geotechnical parameters for the subplinian tephra fallout deposit (PAL-D) and the Vulcanian tephra fallout deposit associated with the 1888–1890 eruption (Vulc).

c′: cohesion; Φ′: friction angle; γs: total unit weight of the soil; Ks: saturated conductivity; D0: saturated diffusivity; θs: saturated water content; θr: residual water content; α: Gardner parameter; Gs: specific gravity; n: porosity; e: void ratio. ∗ Diffusivity was evaluated using the procedure proposed in Rossi et al. (2013).
4.2.3 Shear strength
Although the four specimens of the 1888–1890 primary tephra fallout deposit are consolidated at three different total stresses, all specimens exhibit a slight hardening associated with a dilative behaviour. The shear stress envelope exhibits high friction angle (ϕ=42∘) and zero cohesion (Table 2). For PAL-D tephra fallout deposits, direct shear tests are performed on reconstructed specimens constituted only by the size fraction smaller than 20 mm (i.e. lapilli and ash). In order to maintain the in situ characteristics, the specimen is reconstructed using an air pluviation method into the shear box, i.e. pouring the dry deposit material with a spoon from zero drop height. The specimens exhibit high porosity (n equals about 0.72). The tests are performed in dry conditions and all specimens exhibit a dilative behaviour. The friction angle at the peak is high and typical of lapilli clasts (ϕ=54∘), while the cohesion is null (Table 2). The angle of dilatation (Ψ) is also evaluated and is about 13∘. Thus, according to Taylor (1948) the friction angle is about 41∘, but it will be reached at large deformation.
4.2.4 Hydraulic conductivity
The mean saturated hydraulic conductivity of the 1888–1890 tephra fallout deposit measured in the laboratory ( m s−1) is similar to that obtained during field measurements (6.0 and m s−1). The mean hydraulic saturated conductivity of the PAL-D tephra fallout deposit could not be measured in the laboratory because the deposit grain size (Md) is too coarse for the apparatus. As a result, we use two values for the modelling: one from the literature derived for coarse-grained volcanic soils and one obtained from field measurements. A value of m s−1 (Table 2) is inferred from the hydraulic conductivity measured in the field for the 2011 Cordón Caulle (Chile) eruption lapilli deposits (Baumann et al., 2018) and from the lower pumice deposit from Vesuvius (Crosta and Dal Negro, 2003). These values are significantly higher with respect to our field measurements of m s−1. These two endmembers are hereafter referred to as high (i.e. m s−1) and low (i.e. m s−1) hydraulic conductivities and will be used to explore a variety of deposit conditions.
4.2.5 Soil water retention curve
The SWRC of the 1888–1890 primary tephra fallout deposit exhibits an air entry value equal to 1 kPa, while the water content at saturation (θs) is 0.47 and the residual water content (θr) is 0.04. The SWRC of the PAL-D deposit exhibits an air entry value lower than 1 kPa, slightly high water content at saturation (θs=0.72), and low residual water content (θr=0.03) (Table 2). The data are interpolated using the equations from both Gardner (1958) and Brooks and Corey (1964, 1966).
4.2.6 Saturated soil diffusivity
The saturated soil diffusivity of the 1888–1890 and PAL-D tephra fallout deposits are 1 order of magnitude higher than their saturated soil conductivity (Table 2). The 1888–1890 tephra fallout deposit shows a value of m2 s−1, while the PAL-D primary tephra fallout deposit has a value of m2 s−1.
4.3 Modelling
Based on the local weather pattern (Sect. 2.2), TRIGRS simulations were run using one high-intensity rainfall scenario of 6.4 mm h−1 over 5 h (i.e. total of 32 mm). As mentioned in Sect. 2.2, such heavy–torrential precipitation occurred twice in 2011, causing widespread floods in the Porto floodplain, and can be considered amongst the most intense scenarios to occur on Vulcano based on available data (Fig. 2). Following Arnone et al. (2013), we consider this scenario to be a heavy–torrential scenario and we used it to investigate the maximum unstable tephra fallout volume. For the PAL-D tephra fallout deposit, we used two different hydraulic conductivities in order to consider both endmembers as described in laboratory analyses (Table 3).
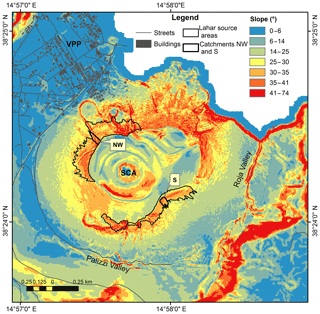
Figure 6Slope map for the La Fossa cone and surrounding areas. Northwestern and southern lahar source areas are indicated with a black contour. The NW and S upper catchments are indicated with a black contour. SCA: summit cone area; VPP: Vulcano Porto Plain.
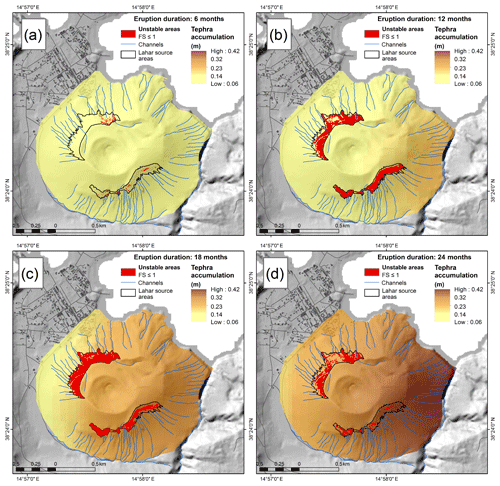
Figure 7Probabilistic isopach maps (converted from the probabilistic isomass maps of Biass et al., 2016a, based on deposit density) and corresponding instability maps compiled with TRIGRS for a Vulcanian eruption with the following: (a) an eruption duration of 6 months and a probability of occurrence of 25 %; (b) an eruption duration of 12 months and a probability of occurrence of 25 %; (c) an eruption duration of 18 months and a probability of occurrence of 25 %; (d) an eruption duration of 24 months and a probability of occurrence of 25 %. The rainfall intensity is 6.4 mm h−1 with a duration of 5 h for all the scenarios, and the parameters for the 1888–1890 Vulcanian deposits are listed in Table 3.
Table 3Input parameters for the subplinian (Ks from the literature), subplinian∗ (Ks measured in the field), and 1888–1890 Vulcanian eruption scenarios used for simulation with TRIGRS.

c′: cohesion; Φ′: friction angle; γs: total unit weight of the soil; Ks: saturated conductivity; D0: saturated diffusivity; θs: saturated water content; θr: residual water content; α: Gardner parameter.
Table 4Unstable areas (FS ≤1) for long-lasting Vulcanian and subplinian eruptions (VEI: Ks from the literature; VEI∗: Ks measured in the field) calculated with TRIGRS for NW and S source areas (Fig. 6). Rainfall intensity 6.4 mm h−1 with a duration of 5 h. Thickness: tephra fallout deposit thickness from probabilistic isopach maps considered in the model. Input parameters used for the simulation are described in Table 3. VEI: Volcanic explosivity index.
TRIGRS simulations assume the following: (i) a water table is located at the bottom of the tephra fallout sequence (lower boundary); and (ii) the tephra fallout sequence lies on an impermeable layer. These assumptions are supported by the exposure of the consolidated and impermeable tufi varicolori unit on the upper part of the La Fossa cone (Frazzetta et al., 1983; Capaccioni and Coniglio, 1995; Dellino et al., 2011). Although lahars have been initiated all around the La Fossa cone in the past, here we analyse the slope and the stability condition of the tephra deposits in two selected potential lahar source areas (Fig. 6, black lines). The first NW source area represents a direct threat to the populated Porto village, while the second S source area is downwind of the prevailing wind and presents the highest probabilities of tephra accumulation (Sect. 1.2; Biass et al., 2016a). The percentage of slope angle ranges (Fig. 6) for the NW and S lahars source area are the following: 18 % and 22 % for a slope angle between 6∘ and 30∘; 38 % and 46 % for a slope angle between 30∘ and 35∘; 31 % and 24 % for slope angles between 35∘ and 41∘; and 12 % and 7 % for slope angles bigger than 41∘. Comparing the slope angle distribution for both areas, we observe that the percentage of steep slopes is higher in the NW area. Finally, we selected two upper catchments with similar surface area and reshaped the S upper catchment to have the same size of 4665 m2 in order to facilitate the comparison of remobilized volumes associated with different eruptive conditions (Fig. 6). The catchment boundaries were defined with a semiautomatic tool in ArcGIS using the flow direction raster and defining a pour point for the catchment; then we obtained the contributing area above the pour point, which was defined as the lahar source area.
4.3.1 Deposition and remobilization scenarios
Vulcanian eruption scenarios
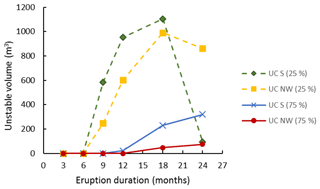
Figure 7 shows the probabilistic isopach maps (for a probability of occurrence of 25 %) and the instability maps for eruption durations of 6, 12, 18, and 24 months. For an eruption duration of 6 months, only 4.8 % percent of the NW and 6 % of the S lahar source areas, respectively, are unstable due to the small tephra fallout deposit thickness (between 6 and 12 cm) (Fig. 7a). For an eruption duration of 12 months, the unstable areas are significantly higher: 69 % for the NW and 81 % for the S lahar source areas, respectively (tephra fallout deposit thickness between 14 and 22 cm; Fig. 7b and Table 4). For an eruption duration of 18 months the percentage of unstable areas for the NW is also very high (89 %) and reached a value of 66 % for the S area (Fig. 7c). The percentage of unstable area decreases for an eruption duration of 24 months, with 52 % for the NW and 22 % for the S; the tephra fallout deposit accumulation is more than 35 cm in the case of the S source area (Fig. 7d, Table 4). Figure 8 shows the unstable volumes as a function of the eruption durations described above calculated for the two single upper catchments with the same area (4665 m2) located in the NW source area (NW catchment) and in the S source area (S catchment; Fig. 6). The largest unstable volume is reached for an eruption duration of 18 months, with a volume of 1105 m3 for the S upper catchment and 990 m3 for the NW upper catchment in the case of the 25 % probability of occurrence scenario (Table 5, Fig. 8).
Subplinian eruption scenarios
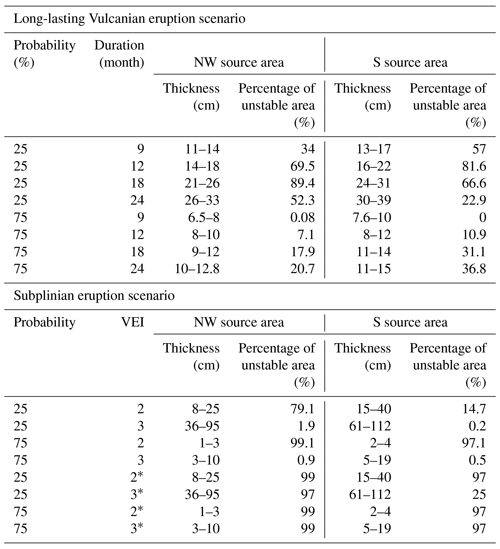
The same two lahar source areas were used for investigating the instability of the subplinian deposits. Four probabilistic isopach maps were considered (VEI 2 and VEI 3 with a 25 % and 75 % probability of occurrence) and combined with hydraulic conductivities measured in the field and derived from the literature (i.e. m s−1 and m s−1). Using the highest hydraulic conductivity, a VEI 2 eruption with a 25 % probability of occurrence results in 79 % and 14 % of unstable areas in the NW and S flank, respectively (Table 4). A 75 % probability of occurrence increases the unstable areas to 99 % and 97 %. In contrast, considering a VEI 3 eruption with a 25 % probability of occurrence, only the tephra fallout deposit located on slope > 48∘ is unstable (2 % and 0.02 %). A 75 % probability shows 99 % unstable area in the NW and 58 % in the S area. Using the lowest hydraulic conductivity, almost the entire deposit resulting from VEI 2 is unstable (99 % of the NW source area and 97 % of the S source area) regardless of the probability of occurrence (Table 4). In the case of a VEI 3 scenario with a 25 % probability of occurrence, a high percentage of the NW source area is unstable (97 %), whereas only 25 % of the S source area is unstable (Table 4). The unstable tephra fallout volumes calculated for the subplinian scenarios for the two single upper catchments NW and S show that the largest volume (2455 m3) resulted for the NW upper catchment and the subplinian VEI 3 (25 %) scenario with (i.e. hydraulic conductivity measured in the field) (Table 5, Fig. 9).
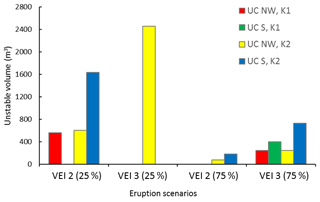
Figure 9Unstable tephra fallout volume for the S and NW upper catchments obtained with TRIGRS for the subplinian scenarios VEI 2 and VEI 3 with m s−1 (from the literature) and for VEI2 and VEI3 with m s−1 (as measured in the field) for probabilities of occurrence of 25 % and 75 %.
Table 5Total and unstable volumes of primary tephra deposits for long-lasting Vulcanian and subplinian eruptions (VEI: Ks from the literature; VEI∗: Ks measured in the field) calculated with TRIGRS for the NW and S upper catchments. The NW and S upper catchments have the same area (4665 m2), with a mean slope of 43.5 and 40.1∘, respectively. Rainfall intensity is 6.4 mm h−1 with a duration of 5 h. Thickness: tephra fallout deposit thickness from probabilistic isopach maps considered in the model.
4.3.2 Parameterization of unstable area based on variable tephra fallout thickness
In order to characterize the minimum tephra fallout deposit thickness necessary to trigger lahars on Vulcano during or just after either a Vulcanian cycle or a subplinian eruption, we carried out TRIGRS simulations using the characteristics of the 1888–1890 and PAL-D tephra fallout deposits, with increasing deposit thicknesses from 0.1 to 1.1 m and an interval of 0.05 m. In these simulations, the deposit thickness was considered constant over the whole NW and SE source areas. The same rainfall scenario was applied. The percentage of unstable areas for the NW and S source areas (Fig. 10) shows that the tephra fallout deposit thickness generating the largest instability for the 1888–1890 eruption tephra fallout deposit is between 20 and 30 cm. For PAL-D tephra fallout deposits using the lowest hydraulic conductivity, the unstable percentage area decreases rapidly with an increase in deposit thickness, with virtually the entire deposit being stable beyond a 45 cm thickness. In contrast, when the PAL-D tephra fallout deposit is simulated with high hydraulic conductivity, almost all of the lahar source area is unstable (98 %) for deposit thickness between 10 and 65 cm, after which the fraction of unstable area decreases with increasing deposit thickness.
Table 6Summary description of outcomes of Figs. 11 and 12 showing the relation between tephra fallout deposit thickness and the factor of safety (FS) based on various key parameters (i.e. tephra fallout properties, slope angle, rainfall intensities). Unstable deposit thickness is shown in bold. The ratio between rainfall intensity and hydraulic conductivity (I∕Ks) is also shown as an indication of the time for the rainfall water to reach the bottom of the deposit.
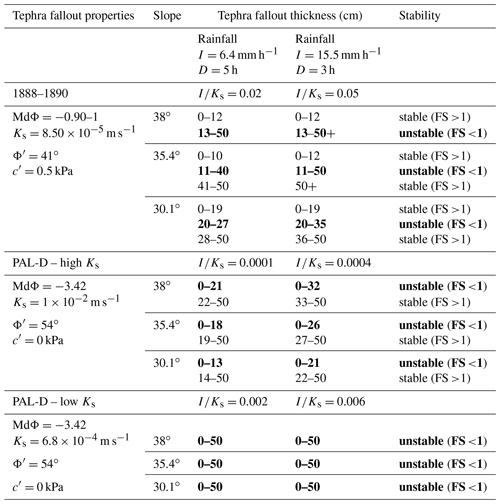
In order to investigate the combination of multiple parameters (FS, deposit thickness, pore pressure, slope, rainfall intensity), we have carried out dedicated simulations for a smaller area (100 pixels only on the NW source area) (Fig. 11 for the 1888–1890 eruption and Fig. 12 for PAL-D). Three slope angles (38, 35.4, and 30.1∘) and two rainfall intensities have been considered (6.4 mm h−1 with a duration of 5 h and 15.5 mm h−1 with a duration of 3 h). In particular, the rainfall intensity of 15.5 mm h−1 represents the worst rainfall scenario for 2017 (rainfall event recorded at Lentia station on 11 November 2017, with a total of 46.5 mm). In summary, Table 6 shows how a lapilli-rich tephra fallout deposit with a low hydraulic conductivity is unstable for slopes >30∘ regardless of the associated thickness (deposit features of the PAL-D eruption); nonetheless, Fig. 10 shows that the deposit becomes stable for thickness values >65 cm. In fact, a constant FS (dashed lines in Fig. 12b, d) is the result of the upper boundary of the pressure head, which is physically limited at the beta line (Iverson, 2000; Baum et al., 2008). The total pore pressure cannot be above the values denoted by a water table at the ground surface (beta line) and the model calculates FS with this value, which is the worst condition for instability. In contrast, the same lapilli-rich tephra fallout deposit is unstable at all observed slopes only for thickness values <10–20 cm in the case of high hydraulic conductivity. Finally, a tephra fallout deposit dominated by coarse ash is unstable at slopes <35.4∘, mostly for thickness values between about 10 and 40 cm (deposit features of the 1888–1890 eruption); for a slope >38∘ the same tephra fallout deposit is unstable for thickness values larger than 13 cm. For the same tephra fallout deposit the ratio of rainfall intensity and hydraulic conductivity (I∕Ks) determines the time to reach the water table (located at the bottom of the deposit in our case study); the rate of rise of the water table increases with an increase in the I∕Ks ratio (Li et al., 2013). In the case of the 1888–1890 tephra fallout deposit, the upper critical thickness for instabilities increases with the increase in rainfall intensity and total rainfall. It is also important to note how the maximum value of total pore pressure, and therefore the potential for triggering lahars, is shifted toward larger values of tephra fallout deposit thickness when rainfall intensity is increased. As an example, the maximum value of pore pressure for a 38∘ slope angle (blue solid line in Fig. 12a, c) is reached at 15 and 30 cm for a rainfall intensity of 6.4 and 15.5 mm h−1, respectively.
Table 7Median grain size, hydraulic conductivity, and infiltration capacity on tephra fallout (TF) and PDC deposits measured near volcanic vents and the lahar volumes of selected examples.
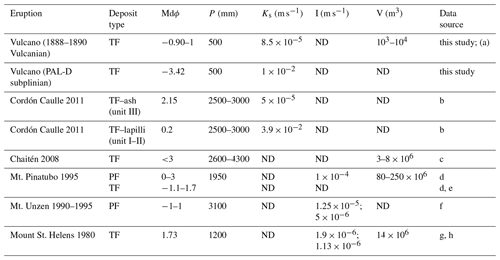
MdΦ: median grain size of deposit; P: annual precipitation; Ks: hydraulic conductivity; I: post-eruption infiltration capacity: V: lahar volume; ND: no data. References: (a) Di Traglia et al. (2013); (b) Baumann et al. (2018); (c) Pierson et al. (2013); (d) Daag (2003); (e) Janda et al. (1996); (f) Yamakoshi and Suwa (2000); (g) Leavesley et al. (1989); (h) Pierson (1985).
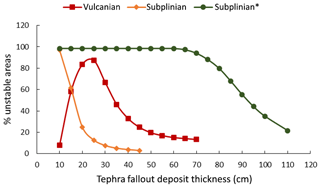
Figure 10Percentage of unstable area for the NW and S lahar source areas simulated with TRIGRS for tephra fallout deposit thicknesses of 0.1–1.1 m and a rainfall intensity of 6.4 mm h−1 with a duration of 5 h, as well as parameters for the following: Vulcanian tephra fallout deposits (red squares); subplinian tephra fallout deposits with m s−1 (value from the literature; orange diamonds); and subplinian tephra fallout deposits with m s−1 (value measured in the field; green circles).
5.1 Characteristics of lahar source deposits
Rain-triggered lahars associated with both tephra fallout and PDC deposits are associated with a variety of precipitation, grain size, hydraulic conductivity, and infiltration capacity (Table 7). It is important to note that infiltration capacity and hydraulic conductivity can be considered similar parameters for the sake of this comparison. In fact, the infiltration capacity is a measure of the rate at which soil is able to absorb water (Horton, 1945), while the hydraulic conductivity measures the ease with which water will pass through a porous medium (Darcy, 1856). Infiltration capacity typically decreases through time and converges to a constant value, which is the hydraulic conductivity. Infiltration capacity is more easily measured in the field, while hydraulic conductivity is more easily measured in the laboratory. Examples of lahar generation enhanced by fine-grained deposits include Mount St. Helens in 1980 (Leavesley et al., 1989), Chaitén in 2008 (Pierson et al., 2013), and Cordón Caulle in 2011 (Pistolesi et al., 2015) (Table 7). In contrast, the grain size of the Vulcano 1888–1890 tephra fallout deposit is closer to Mt. Unzen PDCs and the Pinatubo tephra fallout deposit. Hydraulic conductivity associated with the Vulcano 1888–1890 tephra fallout deposit is 44 times higher than the infiltration capacity of the PDC in Shultz Creek (Mount St. Helens). Infiltration capacity is also low in the case of Mt. Unzen but is higher for the PDCs of Mt. Pinatubo. If we also compare the lahar volumes of Mount St. Helens in 1980, Pinatubo in 1990, Chaitén in 2008, and Vulcano in 1888–1890, we observe that the volumes are in the range of millions of cubic metres for the first three volcanoes, while in the case of Vulcano the larger events were only in the range of thousands of cubic metres. An important difference between the deposits studied in this paper and the other deposits is the climatic conditions (Table 7). In fact, Vulcano is characterized by semi-arid, poorly vegetated regions with nonpermanent streams and limited annual rainfall (500 mm), while all other cases are characterized by forested area with permanent streams draining the volcano flanks and annual precipitation between 1000 mm and 4300 mm.
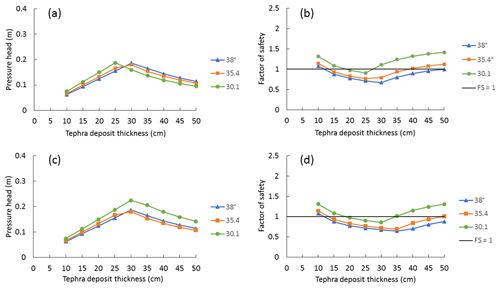
Figure 11Total pressure head and factor of safety versus tephra fallout deposit thicknesses between 0.1 and 0.55 m for Vulcanian tephra fallout deposits (Table 3) and a rainfall intensity of the following: (a, b) 6.4 mm h−1 with a duration of 5 h (); (c, d) 15.5 mm h−1 with a duration of 3 h () (see also Table 6).
Lahar triggering is clearly influenced by the hydraulic conductivity and infiltration capacity of the primary deposits, which in turn are strongly related to deposit grain size. The highest hydraulic conductivities () are associated with MdΦ<−1Φ (lapilli), while the lowest hydraulic conductivities and infiltration capacities (between and ) result for MdΦ>1 (coarse and fine ash), except for the PDCs at Mt. Unzen where MdΦ is between −1 and 1Φ (Table 6). Nonetheless, in the case of Mt. Unzen, the poor infiltration capacity is not due to fine grain size but to the development of an impermeable crust on the top of the deposit (Yamakoshi et al., 2000). The combination of hydraulic conductivity (or infiltration capacity) and rainfall intensity influences the lahar triggering mechanism either in terms of slope failure or erosion (Cuomo and Della Sala, 2013). If hydraulic conductivity exceeds rainfall intensity only infiltration occurs, but if rainfall intensity exceeds hydraulic conductivity runoff (overland flow) occurs (Cuomo and Della Sala, 2013; Pierson et al., 2014).
The effect of grain size on runoff has also been investigated based on laboratory experiments. As an example, Jones et al. (2017) investigated the behaviour of two tephra fallout samples with contrasting grain size (a fine-grained sample from the Chaitén 2008 eruption (D50=4.2Φ, fine ash) and a coarse-grained sample from the Mt. Kelud 2014 eruption (D50=0.9Φ, coarse ash)) in relation to one rainfall intensity (150 mm h−1). Experiments showed that surface sealing occurred within minutes of rainfall on dry fine-grained tephra but was not evident on coarser material. The surface sealing on fine-grained tephra reduces infiltration and enhances overland flow, generating downslope sediment transportation. Additionally, antecedent rainfall, and thus increased moisture content, increased runoff rates and reduced runoff lag time; low rainfall intensities with short durations could therefore still trigger lahars when the tephra residual moisture content is high (Jones et al., 2017). More experimental investigations should be carried out considering a range of rainfall intensities and more directly relating grain size with hydraulic conductivity. Nonetheless, these outcomes confirm that the lahar triggering mechanism is strongly influenced by grain size and therefore by hydraulic conductivity and rainfall intensity; it could be complicated by the deposit local grain size, composition, and weather patterns. It is interesting to note that on Vulcano some specific material formed a solid crust that made it impermeable, forming an ideal surface for shallow landsliding (e.g. tufi varicolori), while some other material remains unconsolidated over the years (e.g. the 1888–1890 deposit); this is probably related to the grain size and composition of the pyroclastic material and to the variable fumarolic activity at the time of deposition (De Fiore 1922; Fulignati et al., 2002).
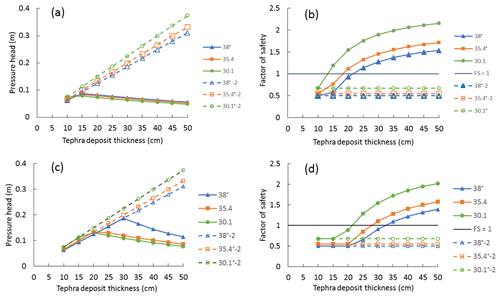
Figure 12Total pressure head and factor of safety versus tephra fallout deposit thicknesses between 0.1 and 0.55 m for subplinian tephra fallout deposits with m s−1 and m s−1 (dashed lines) for two different rainfall intensities and durations: (a, b) 6.4 mm h−1 with a duration of 5 h; (c, d) 15.5 mm h−1 with a duration of 3 h (see also Table 6).
5.2 Short versus long-lasting eruptions
The duration of a long-lasting eruption plays an important role in the pattern of remobilization of tephra fallout deposits. Different unstable volumes calculated with TRIGRS were obtained for durations of Vulcanian eruptive cycles between 3 and 24 months without considering remobilization between the eruptive cycles. The results show that for an eruption time of 18 months and a probability of occurrence of 25 % (corresponding to a tephra fallout deposit thickness between 17 and 33 cm) the unstable areas, and therefore the remobilized volumes from the lahar source areas, reached a maximum (1105 m3 for the S upper catchment and 990 m3 for the NW upper catchment). For the eruption duration of 24 months, the increase in tephra fallout deposit thickness (between 21 and 42 cm) produced a decrease in the unstable areas (95 m3 for the S upper catchment and 861 m3 for the NW upper catchment). It is worth noting that the thickness of the deposit also affects both the driving and resisting forces along the slip surface at the bedrock contact. In addition, a higher soil thickness also increases the time for rainfall to produce significant changes in pore water pressure at the bedrock contact. Thus, a lower volume of remobilized material may occur despite a thicker deposit. The results obtained with TRIGRS showed that there is an unstable window of tephra fallout deposit thickness, which depends on amount and duration of rainfall, slope angle, and geotechnical characteristics of the deposit (Table 6). These results are in agreement with the window of potentially unstable soil thickness found by Dietrich et al. (2007) for a range of non-volcanic case studies. In their work, Dietrich et al. (2007) adopted a slope-stability model that includes shear resistance due to lateral and basal boundaries as a result of the combination of cohesion (soil and root cohesion) and friction.
The morphology of the middle and the upper part of the La Fossa cone shows a strong remobilization of the 1888–1890 eruption tephra fallout deposit. The coarse ash grain size range and medium permeability of the 1888–1890 tephra fallout deposits in combination with the impermeable deposits at the base of the sequence (i.e. tufi varicolori) make this deposit easily remobilized by rainfall through a shallow landslide initiation mechanism. Deep channels due to the continuous remobilization of this deposit can be observed on the cone (Fig. 1). Because of the short transport distance (200–400 m) the lahar deposits on the La Fossa cone have almost the same grain size as the 1888–1890 tephra fallout deposits (Fig. 5). The same relation between the primary pyroclastic deposits and the lahars has been described for the la Cuesta succession (Valentine et al., 1998).
Field evidence for post-PAL-D remobilization and lahar deposits is not recorded in the stratigraphic record (Di Traglia, 2011). This is consistent with our modelling results with m s−1 that show the low potential for remobilization associated with thick lapilli deposits. In this case, a high hydraulic conductivity allows the water to rapidly migrate down to the water table with low transient pressure. Therefore, the water table rarely rises sufficiently to induce instability, which explains why thicker deposits are relatively less unstable. In fact, the thick lapilli deposits associated with both VEI 2 and VEI 3 as well as a high permeability are stable even for the largest rainfall event occurring on Vulcano, e.g. VEI 3 and a 25 % probability of occurrence (Table 4). Studies on rainfall lahar generation at the Mayon volcano, Philippines, also demonstrated that coarse and high-permeability pyroclastic deposits on volcano slopes remain stable in most cases (Rodolfo and Arguden, 1991). A similar case occurred at Mount St. Helens, where rainfall-induced lahar drastically dropped when the erosion of fine ash exposed coarser and more permeable material (Collins and Dunne, 1986).
5.3 Initiation mechanisms of rain-triggered lahars
The tephra remobilization model used in our study assumes rainfall-induced shallow landslides caused by the infiltration of rain on the slope surface. These shallow landslides can eventually transform into lahars depending on the availability of water, slope morphology, and characteristics of tephra deposits. In particular, we studied cases in which rainfall intensity (I) is lower than hydraulic conductivity (Ks) and infiltration occurs before runoff (Cuomo and Della Sala, 2013). At Vulcano, both the 1888–1890 and the PAL-D tephra fallout deposits have high permeability compared to the cases of the Mount St. Helens (1980) and Chaitén (2008) fine-grained tephra fallout deposits (Table 3). The fine-grained tephra fallout deposits reduce infiltration capacity on basin slopes, enhancing runoff and producing larger peak flows. However, we cannot discard the mechanism of sheet and rill erosion in Vulcano, which was not simulated in this study. The physical characteristics of primary tephra fallout deposits (e.g. high hydraulic conductivity) and the rainfall characteristics on Vulcano indicate that the main lahar initiation mechanism is most likely shallow landsliding.
The relationship between unstable areas and deposit thicknesses suggests a significant influence of the hydraulic conductivity on the model outcomes and on the resulting estimation of unstable volumes (Fig. 7 and Tables 4 and 5). Our results better explain the parameter values affecting slope instability (Fig. 10 and Tables 4 and 5). In fact, the tephra fallout deposit thickness of 21–33 cm, associated with the largest unstable volumes for the Vulcanian scenarios (18- and 24-month durations), correlates well with the thickness of 20–30 cm shown in Fig. 10. Similarly, the tephra fallout deposit thickness associated with the largest unstable volumes for the VEI 2 and 3 scenarios (with Ks derived from the literature, i.e. m s−1), i.e. 8–25 cm, also shows how a higher hydraulic conductivity generates lahars for a lower deposit thickness. These values of tephra fallout deposit thickness are in good agreement with the critical threshold for lahar generation found by Sulpizio et al. (2006) for syn-eruptive lahars in the Vesuvian area (i.e. 10 cm).
For the 1888–1890 tephra fallout deposit, results suggest that cohesion leads to a critical minimum landslide depth size (lower-limit deposit thickness for instability) dependent on the slope angle (Fig. 11b, d; Table 6). Using a model for natural slopes, Milledge et al. (2014) found a critical depth in cohesive soil, resulting in a minimum size for failure. For cohesionless material, such as the primary PAL-D, the lower thickness limit is not defined as most small deposit thicknesses are unstable and become progressively stable with a deposit thickness increase depending on rainfall intensity, duration, and slope angle (Fig. 12b, d; Table 6). The different behaviour shown by the different tephra fallout deposits modelled in our study could relate to the fact that rainfall-induced slope failure can occur by two mechanisms (Li et al., 2013): (1) rainfall infiltration that produces a rise in groundwater, generating positive pore pressure and adding weight on the slope (Cho and Lee, 2002; Crosta and Frattini, 2003; Soddu et al., 2003); and (2) rainfall that results in the propagation of a wetting front, causing an increase in water content and pore pressure (loss in matric suction) (Ng et al., 2001; Collins and Znidarcic, 2004; Rahardjo et al., 2007). First, in the case of subplinian tephra fallout deposit with m s−1 (low conductivity), the wetting front mechanism moves from the ground surface toward the bedrock, which means that the time for the perturbation to reach the bedrock contact increases with deposit thickness. As a result, for the same rainfall, the higher the thickness the more stable the slope (Fig. 10, green curve). Second, in the case of subplinian tephra fallout deposit with m s−1 (high conductivity), the water moves fast down to the water table with low transient pressure (a sort of drained condition). This means that the water table should be the same provided by the same rainfall, independently from the total deposit thickness. The slope is very sensitive to the ratio of water table to total thickness and becomes stable with the increase in deposit thickness. Finally, in the case of the 1888–1890 tephra fallout deposit, the increase in deposit stability (right side of the red curve in Fig. 10) could be explained by both mechanisms described above, but the first decrease in stability (left side of the red curve) indicates that for small deposit thicknesses the pore pressure reached at the end of the rainfall is not enough to neutralize the effect of cohesion (0.5 kPa).
The results obtained with the TRIGRS model show the potential for the evaluation of transient pore water pressure stability conditions and lahar (landslide) source areas during rainfall (Godt et al., 2008), even though the role of suction in unsaturated conditions, which plays a fundamental role for the pore pressure regime, is not included in the model (Sorbino et al., 2010). Matrix suction between 24 and 27 kPa was measured in 1888–1890 primary tephra deposits in May 2018 (at the beginning of the dry season), but further seasonal matrix suction variation needs to be performed to evaluate the role of suction in potentially unstable areas and the most critical period for slope stability (Pirone et al., 2016). Finally, our deposit-stability analysis could be largely strengthened by validation with the volume of observed lahar deposits, which is unfortunately difficult to obtain for the 1888–1890 eruption due to complex deposit correlation.
5.4 Impact and risk implications
Remobilized tephra fallout volume was calculated with TRIGRS for two different catchments with same area, one located on the NW flank and the other on S flank of La Fossa volcano; different values were obtained for the same eruption scenarios (Figs. 8 and 9). Two main factors are responsible for these differences in volume. The first factor is that the tephra deposit is thicker for the S flank due to the prevailing wind direction to the SE, and therefore it inhibits the formation of lahars as it requires more water to be remobilized (which is not frequently available in the Vulcano area). In fact, there is a thickness threshold for instability depending on rainfall intensity and tephra fallout deposit properties (Figs. 11 and 12). An additional factor influencing the deposit stability is the slope morphology. Steep slopes (>35∘) are more frequent on the NW flank, with 42 % for the NW basin and 32 % for the S basin, which explains the higher percentage of unstable area for the NW part. As a result, due to both the lower deposit thickness and the steeper slopes, the NW flank is more likely to generate lahars than the S flank, even though lahars from the S flank can also be significant (Figs. 8 and 9). It is important to consider that one of the most populated parts of the island, which is also where the key infrastructures are located (i.e. Porto village; Galderisi et al., 2013), is directly exposed to the lahars potentially generated on the NW flank of the volcano. In contrast, the residential area of Piano located on the S of the island is protected by a caldera rim that could easily block all lahars forming on the S flank. It is also important to highlight the importance of assessing the effect of compounding hazards in the case of multi-hazard environments such as volcanic eruptions. In fact, volcanic hazards are often assessed individually, and an investigation of the associated cascading effects such as tephra sedimentation and lahars should be considered (e.g. Volentik et al., 2009; Tierz et al., 2017). Our results demonstrate the effectiveness and strength of combining probabilistic tephra hazard modelling with both physically based lahar-triggering modelling and physical and geotechnical characterization of the pyroclastic material. The next step necessary to assess the impact of the combination between tephra sedimentation and lahar generation is lahar inundation modelling. Clearly, each step requires dedicated studies and investigations and has some intrinsic value on its own; however, the combination of all aspects has tremendous potential for the impact assessment of communities located in volcanic areas.
We presented a detailed analysis of the volume of tephra fallout deposit that could be potentially remobilized by rainfall as a result of two likely eruptive scenarios of the La Fossa volcano, the main volcanic system on Vulcano island: a long-lasting Vulcanian eruption (i.e. using the 1888–1890 eruption as the reference event) and a short-lived eruption (VEI 2 and VEI 3; using the PAL-D eruption as the reference event) (Fig. 1 and Table 1). The great novelty of this work is the assessment of compounding hazards (tephra fallout deposits and lahar triggering) based on both numerical modelling and field and geotechnical characterization of the source deposit. In fact, volumes of tephra fallout deposit that could be remobilized by rain-triggered lahars were analysed by combining a tephra sedimentation model (TEPHRA2) and slope-stability model (TRIGRS) along with field observations and geotechnical tests.
We have considered 12 probabilistic isopach maps with different eruption durations and probabilities of occurrence of 25 % and 75 % in the case of the Vulcanian eruptive scenario. We have also considered four probabilistic isopach maps for two short-lived eruptions of VEI 2 and 3 and the same probabilities of occurrence as in the case of the Vulcanian eruptive scenario. In addition, a parametric analysis was performed with TRIGRS to determine the tephra fallout thickness thresholds required to trigger lahars for a given rainfall event. Two basins of same area were identified on the NW and S flank of the volcano to analyse the effect of different morphology and different accumulation related to the prevailing wind direction. The results of unstable volumes for the two basins show the following:
-
for the Vulcanian scenario, the largest unstable volume is reached for an eruption duration of 18 months and a 25 % probability of occurrence scenario, with a volume of 1105 m3 for the S basin and 990 m3 for the NW basin (Fig. 8);
-
for the subplinian scenario, the largest unstable volume (2455 m3) resulted for the VEI 3 (25 % probability of occurrence) with m s−1 (i.e. hydraulic conductivity measured in the field) in the case of the NW basin (Fig. 9); and
-
for the subplinian scenario with m s−1 (i.e. hydraulic conductivity estimated from the literature) the largest unstable volume (563 m3) was found for the NW basin with scenario VEI 2 (25 % probability of occurrence) (Fig. 9).
For a tephra fallout deposit with features associated with a Vulcanian eruption we observe an unstable window of deposit thickness, suggesting that particle cohesion leads to a critical minimum landslide depth, which is dependent on the slope angle; an increase in rainfall intensity enlarges the windows of thickness instability (Table 6). In contrast, for cohesionless material such as the primary PAL-D, a low thickness limit of instability is not reached, and the deposit becomes stable with thickness increase depending on rainfall intensity and slope angle (Table 6). In particular, the parametric analysis with variable tephra fallout thickness and slope, with two rainfall intensities of 6.4 mm h−1 for 5 h and 15.5 mm h−1 for 3 h, shows the following:
-
for a tephra fallout deposit with features associated with a Vulcanian eruption, the thickness generating the largest instability is between 20 and 27 cm for a rainfall intensity of 6.4 mm h−1 and between 20 and 35 cm for 15.5 mm h−1 (Fig. 11 and Table 6);
-
for a tephra fallout deposit with features associated with a subplinian eruption with m s−1, the unstable area decreases rapidly with an increase in deposit thickness, with all area almost stable beyond a thickness of 32 cm (Fig. 12 and Table 6); and
-
for a tephra fallout deposit with features associated with a subplinian eruption with m s−1, almost all the lahar source area is unstable (98 %) for deposit thickness <65 cm (Figs. 10, 12 and Table 6).
The results modelled with TRIGRS show that shallow landsliding is an effective process for eroding both Vulcanian-type and subplinian-type (with m s−1) tephra fallout deposits in combination with high-intensity rainfall events with short durations, such as those occurring in Vulcano every year. Nonetheless, the occurrence of shallow landsliding is a complex process (e.g. Table 4 and Fig. 10) and the tephra fallout deposit thickness threshold strongly depends on rainfall intensity, tephra fallout deposit characteristics, and geomorphology features. Both eruptive scenarios (e.g. plume height, erupted mass, eruption duration) and prevailing wind direction are therefore crucial to the generation of rain-triggered lahars, having a 1st-order control on tephra fallout deposit thickness. The physical characteristics of tephra fallout deposits (e.g. hydraulic conductivity, grain size, friction angle, and cohesion), geomorphological features (e.g. flank slopes), the characteristics of soil at the base of the deposits, and vegetation are also important parameters to consider as they have a 1st-order control on slope instability. We can conclude that deposit thickness and rainfall intensity alone are not sufficient to derive thresholds for lahar triggering; a comprehensive assessment of unstable volumes that could potentially trigger lahars, in fact, requires dedicated numerical simulations combined with detailed field observations and geotechnical analysis as we have shown in this study.
Most of the relevant data are made available in the main tables and the Supplement. Additional data are available upon request based on a collaborative agreement.
A1 Sampling of undisturbed deposit for geotechnical tests
Undisturbed tephra fallout deposit is sampled for testing the properties in the laboratory without disturbing structure texture, density, natural water content, and stress condition (Figs. A1a and b). Sampling was performed by inserting a steel tube 3 mm thick with a height of 30 cm and a diameter of 10 cm into the ground (Fig. A1a). After that, we cleaned the entire deposit around the tube to extract it with minimum disturbance. Then, a support was inserted at the base of the cylinder, and the tube was extracted from the deposit. Finally, the tube was covered on both ends with a plastic cover and plastic tape to preserve the deposit during transport (Fig. A1b).
A2 Soil suction measurement
Soil suction measurements were carried out in situ on the 1888–1890 tephra fallout deposit with a soil moisture probe (“Quick Draw” model 2900FI) (Fig. A2b). The first step in taking a reading with the probe is to core a hole by pushing the coring tool into the soil (Fig. A2a). After removing the coring tool, we have a proper sized hole to insert the probe. The second step is to insert the probe in the soil and wait approximately 1 min (equalization time assessed for such soils). Finally, the suction can be read on the dial gauge (Fig. A2b). The soil suction is created by water capillary pressure that each soil particle applies to the soil. The moisture probe has a porous ceramic sensing tip at the end of the tube. The soil suction reading is obtained when a small amount of water transfers between the sensing tip of the probe and the soil.
A3 Saturated hydraulic conductivity measurement
The saturated hydraulic conductivity was estimated in the field with a single-ring permeameter for both deposits (Figs. A3a and b). The apparatus for the measurements consists of a steel ring with a diameter of 21 cm and height of 12 cm, as well as a plastic cover with a hole to insert a Mariotte bottle (Fig. A3b). In the field, we put the ring on a horizontal plane surface on the tephra fallout deposit. Then, the first 6 cm was pushed into the ground. Finally, we filled the Mariotte bottle with water and inserted it on the tape turned upside down. The water first formed a 1 cm layer on the tephra fallout deposit and then started to infiltrate the deposit. For the infiltration rate measurements, the readings were done every minute in the case of the 1888–1890 eruption deposit and every 30 s in the case of the PAL-D deposit. The duration of the measurements was 40 min for the 1888–1890 deposit and 3.2 min for the PAL-D deposit.

Figure A1(a) Sampling the 1888–1890 tephra fallout deposit with a 30 cm steel tube. We cleaned the entire deposit around the tube to extract it with minimum disturbance. (b) Sampling the PAL-D tephra fallout deposit with a 30 cm steel tube. The tube is covered with a plastic cover and plastic tape before extracting it from the deposit with a basal support.

Figure A2(a) Coring tool into the deposit before soil suction measurement. (b) Soil suction measurement on the 1888–1890 primary tephra fallout deposit on the NW volcano flank.
The supplement related to this article is available online at: https://doi.org/10.5194/nhess-19-2421-2019-supplement.
VB, CB, and SC conceived the study. VB, CB, SB, MP, and AG were involved in the fieldwork. VB carried out sample characterization both in the field and in the laboratory. SB carried out the tephra fallout modelling. SC and MM carried out the geotechnical tests in the laboratory. VB, SC, and MM carried out the slope-stability modelling. VB analysed the results and compiled the figures with input from the other authors. VB and CB prepared the paper with contributions from all co-authors. All the authors read, reviewed, and approved all versions of the paper.
The authors declare that they have no conflict of interest.
The authors are grateful to Irene Manzella, Michel Jaboyedoff, and Mario Sartori for valuable discussion and thank the NHESS editor, Jenni Barclay, and an anonymous reviewer for detailed and constructive comments.
This research has been supported by the Swiss National Science Foundation (grant no. 200021_163152) and the project Progetti di Ricerca di Ateneo (grant no. PRA 2018-19).
This paper was edited by Giovanni Macedonio and reviewed by Jenni Barclay and one anonymous referee.
Arnone, E., Pumo, D., Viola, F., Noto, L. V., and La Loggia, G.: Rainfall statistics changes in Sicily, Hydrol. Earth Syst. Sci., 17, 2449–2458, https://doi.org/10.5194/hess-17-2449-2013, 2013.
Arrighi, S., Tanguy, J. C., and Rosi, M.: Eruptions of the last 2200 years at Vulcano and Vulcanello (Aeolian Islands, Italy) dated by high-accuracy archeomagnetism, Phys. Earth Planet. In., 159, 225–233, 2006.
Aubertin, M., Mbonimpa, M., Bussière, B., and Chapuis, R. P.: A model to predict the water retention curve from basic geotechnical properties, Can. Geotech. J., 40, 1104–1122, https://doi.org/10.1139/t03-054, 2003.
Baum, R. L., Savage, W. Z., and Godt, J. W.: TRIGRS – a Fortran Program for Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability Analysis, US geological survey open-file report, 424, 38, 2002.
Baum, R. L., Savage, W. Z., and Godt, J. W.: TRIGRS – A Fortran Program for Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability Analysis, Version 2.0, U.S. Geological Survey Open-File Report, No 02-0424, Open-file Report, p. 35, 75 pp., 2008.
Baumann, V., Bonadonna, C., Cuomo, S., Moscariello, M., and Manzella, I.: Slope stability models for rainfall-induced lahars during long-lasting eruptions, J. Volcanol. Geoth. Res., 359, 78–94, https://doi.org/10.1016/j.jvolgeores.2018.06.018, 2018.
Biass, S., Bonadonna, C., Di Traglia, F., Pistolesi, M., Rosi, M., and Lestuzzi, P.: Probabilistic evaluation of the physical impact of future tephra fallout events for the Island of Vulcano, Italy, Bull. Volcanol., 78, 1–22, https://doi.org/10.1007/s00445-016-1028-1, 2016a.
Biass, S., Bonadonna, C., Connor, L., and Connor, C.: TephraProb: a Matlab package for probabilistic hazard assessments of tephra fallout, Journal of Applied Volcanology, 5, 10, https://doi.org/10.1186/s13617-016-0050-5, 2016b.
Bishop A. W.: The principle of effective stress, Teknik Ukeblad., 39, 859–863, 1959.
Bisson, M., Favalli, M., Mazzarini, F., Mori, A., Pareschi, M. T., and Sinapi, L.: A morphometric model of the Aeolian Islands (Italy), Editrice Compositori Bologna, Bologna, Italy, NUOVO CIMENTO-SOCIETA ITALIANA DI FISICA SEZIONE C, 26, 417–436, 2003.
Bonadonna, C., Connor, C. B., Houghton, B. F., Connor, L., Byrne, M., Laing, A., and Hincks, T.: Probabilistic modeling of tephra dispersion: hazard assessment of a multi-phase eruption at Tarawera, New Zealand, J. Geophys. Res., 110, B03203, https://doi.org/10.1029/2003JB002896, 2005.
Brooks, R. H. and Corey, A. T.: Hydraulic properties of porous media, Hydrology paper No. 3, Colorado State Univ., Fort Collins, 1964.
Brooks, R. H. and Corey, A. T.: Properties of porous media affecting fluid flow, J. Irr. Drain. Div.-ASCE, 92, 61–90, 1966.
Caballero, L., Capra, L., and Vázquez, R.: Evaluating the Performance of FLO2D for Simulating Past Lahar Events at the Most Active Mexican Volcanoes: Popocatépetl and Volcán de Colima, Natural Hazard Uncertainty Assessment: Modeling and Decision Support, Geophysical Monograph Book Series, 223, 179–189, 2016.
Capaccioni, B. and Coniglio, S.: Varicolored and vesiculated tuffs from La Fossa volcano, Vulcano Island (Aeolian Archipelago, Italy): evidence of syndepositional alteration processes, B. Volcanol., 57, 61–70, 1995.
Cascini, L., Cuomo, S., Pastor, M., and Sorbino, G.: Modeling of Rainfall-Induced Shallow Landslides of the Flow-Type, J. Geotech. Geoenviron., 136, 85–98, https://doi.org/10.1061/(ASCE)GT.1943-5606.0000182, 2010.
Cascini, L., Cuomo, S., and Della Sala, M.: Spatial and temporal occurrence of rainfall-induced shallow landslides of flow type: A case of Sarno-Quindici, Italy, Geomorphology, 126, 148–158, https://doi.org/10.1016/j.geomorph.2010.10.038, 2011.
Charbonnier, S. J., Connor, C. B., Connor, L. J., Sheridan, M. F., Oliva Hernández, J. P., and Richardson, J. A.: Modeling the October 2005 lahars at Panabaj (Guatemala), B. Volcanol., 80, https://doi.org/10.1007/s00445-017-1169-x, 2018.
Cho, S. E. and Lee, S. R.: Evaluation of surficial stability for homogeneous slopes considering rainfall characteristics, J. Geotech. Geoenviron., 128, 756–763, 2002.
Collins, B. D. and Dunne, T.: Erosion of tephra from the 1980 eruption of Mount St. Helens, Geol. Soc. Am. Bull., 97, 896–905, 1986.
Collins, B. D. and Znidarcic, D.: Stability analyses of rainfall induced landslides, J. Geotech. Geoenviron., 130, 362–372, 2004.
Córdoba, G., Villarosa, G., Sheridan, M. F., Viramonte, J. G., Beigt, D., and Salmuni, G.: Secondary lahar hazard assessment for Villa la Angostura, Argentina, using Two-Phase-Titan modelling code during 2011 Cordón Caulle eruption, Nat. Hazards Earth Syst. Sci., 15, 757–766, https://doi.org/10.5194/nhess-15-757-2015, 2015.
Crosta, G. B. and Dal Negro, P.: Observations and modelling of soil slip-debris flow initiation processes in pyroclastic deposits: the Sarno 1998 event, Nat. Hazards Earth Syst. Sci., 3, 53–69, https://doi.org/10.5194/nhess-3-53-2003, 2003.
Crosta, G. B. and Frattini, P.: Distributed modelling of shallow landslides triggered by intense rainfall, Nat. Hazards Earth Syst. Sci., 3, 81–93, https://doi.org/10.5194/nhess-3-81-2003, 2003.
Cuomo, S. and Della Sala, M.: Rainfall-induced infiltration, runoff and failure in steep unsaturated shallow soil deposits, Eng. Geol., 162, 118–127, https://doi.org/10.1016/j.enggeo.2013.05.010, 2013.
Cuomo, S. and Iervolino, A.: Investigating the role of stratigraphy in large-area physically-based analysis of December 1999 Cervinara shallow landslides, J. Mt. Sci., 13, 104–115, 2016.
Cuomo, S., Della Sala, M., and Novità, A.: Physically based modelling of soil erosion induced by rainfall in small mountain basins, Geomorphology, 243, 106–115, https://doi.org/10.1016/j.geomorph.2015.04.019, 2015.
Cuomo, S., Chareyre, B., d'Arista, P., Della Sala, M., and Cascini, L.: Micromechanical modelling of rainsplash erosion in unsaturated soils by Discrete Element Method, Catena, 147, 146–152, 2016.
Daag, A. S.: Modelling the erosion of pyroclastic flow deposits and the occurrences of lahars at Mt. Pinatubo, Philippines. Unpublished PhD thesis, ITC Dissertation number 104, Utrecht, Univesity of Utrecht, 2003.
Darcy, H.: Les fontaines publiques de la ville de Dijon : exposition et application des principes à suivre et des formules à employer dans les questions de distribution d'eau, Victor Dalmont, Paris, 1856.
De Astis, G., La Volpe, L., Peccerillo, A., and Civetta, L.: Volcanological and petrologicalevolution of Vulcano Island (Aeolian Arc, Southern Tyrrenian Sea), J. Geophys. Res., 102, 8021–8050, 1997.
De Astis, G., Lucchi, F., Dellino, P., La Volpe, L., Tranne, C. A., Frezzotti, M. L., and Peccerillo, A.: Chapter 11 Geology, volcanic history and petrology of Vulcano (central Aeolian archipelago), Geological Society, London, Memoirs 37, 281–349, https://doi.org/10.1144/M37.11, 2013.
De Bélizal, E., Lavigne, F., Hadmoko, D. S., Degeai, J. P., Dipayana, G. A., Wahyo Mutaqin, B., Aris Marfai, M., Coquet, M., Le Mauff, B., Robin, A.-K., Vidal, C., Cholik, N., and Aisyah, N.: Rain-triggered lahars following the 2010 eruption of Merapi volcano, Indonesia: A major risk, J. Volcanol. Geoth. Res., 261, 330–347, 2013.
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R. , Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kallberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, 2011.
De Fiore, O.: Vulcano (isole eolie), in: Revisita vulcanologica (suppl. 3), edited by: Friedlaender, I., Reimer, D., and Vohsen, E., Berlin, Germany, 1–393, 1922.
Dellino, P. and La Volpe, L.: Stratigrafia, dinamiche eruttive e deposizionali, scenario eruttivo evalutazioni di pericolosit`a a La Fossa di Vulcano, Tech. rep., CNR-gruppo Nazionale per la Vulcanologia, Volume speciale Vulcano-Progetto triennale, 1992–1995, 1997.
Dellino, P., De Astis, G., La Volpe, L., Mele, D., and Sulpizio, R.: Quantitative hazard assessment of phreatomagmatic eruptions at Vulcano (Aeolian Islands, Southern Italy) as obtained by combining stratigraphy, event statistics and physical modelling, J. Volcanol. Geoth. Res., 201, 364–384, 2011.
De Martonne, E.: Une nouvelle fonction climatologique: l'indice d'aridité, La Météorologie, 2, 449–458, 1926.
Di Traglia, F.: The last 1000 years of eruptive activity at the Fossa Cone (Island of Vulcano, Southern Italy), PhD thesis, Dipartimento di Scienze della Terra, Scuola di Dottorato di Ricerca in Scienze di Base Galileo Galilei, Programma di Scienze della Terra, Università degli Studi di Pisa, 2011.
Di Traglia, F., Pistolesi, M., Rosi, M., Bonadonna, C., Fusillo, R., and Roverato, M.: Geomorphology Growth and erosion: The volcanic geology and morphological evolution of La Fossa (Island of Vulcano, Southern Italy) in the last 1000 years, Geomorphology, 194, 94–107, https://doi.org/10.1016/j.geomorph.2013.04.018, 2013.
Dietrich, W., McKean, J., Bellugi, D., and Perron, T.: The prediction of shallow landslide location and size using a multidimensional landslide analysis in a digital terrain model, 4th International Conference on Debris-Flow Hazards Mitigation – Mechanics, Prediction and Assessment, Chengdu, China, 12, 2007.
Ferrucci, M., Pertusati, S., Sulpizio, R., Zanchetta, G., Pareschi, M. T., and Santacroce, R.: Volcaniclastic debris flows at La Fossa Volcano (Vulcano Island, southern Italy): Insights for erosion behaviour of loose pyroclastic material on steep slopes, J. Volcanol. Geoth. Res., 145, 173–191, 2005.
Frattini, P., Crosta, G. B., Fusi, N., and Dal Negro, P.: Shallow landslides in pyroclastic soils: A distributed modelling approach for hazard assessment, Eng. Geol., 73, 277–295, https://doi.org/10.1016/j.enggeo.2004.01.009, 2004.
Frazzetta, G., La Volpe, L., and Sheridan, M. F.: Evolution of the Fossa cone, Vulcano, J. Volcanol. Geoth. Res., 17, 329–360, 1983.
Frazzetta, G., Gillot, P. Y., La Volpe, L., and Sheridan, M. F.: Volcanic hazards at Fossa of Vulcano: Data from the last 6,000 years, Bulletin Volcanologique, 47, 105–124, https://doi.org/10.1007/BF01960543, 1984.
Fulignati, P., Sbrana, A., Luperini, W., and Greco, V.: Formation of rock coatings induced by the acid fumarole plume of the passively degassing volcano of La Fossa (Vulcano Island, Italy), J. Volcanol. Geoth. Res., 115, 397–41, 2002.
Galderisi, A., Bonadonna, C., Delmonaco, G., Ferrara, F. F., Menoni, S., Ceudech, A., Biass, S., Frischknecht, C., Manzella, I., Minucci, G., and Gregg C.: Vulnerability assessment and risk mitigation: the case of Vulcano Island, Italy, Proceedings of the Second World Landslide Forum, 3–7 October 2011, Rome, 2013.
Gardner, W. R.: Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table, Soil Sci., 85, 228–232, 1958.
Gioncada, A., Mazzuoli, R., Bisson, M., and Pareschi, M. T.: Petrology of volcanic products younger than 42 ka on the Lipari-Vulcano complex (Aeolian Islands, Italy): An example of volcanism controlled by tectonics, J. Volcanol. Geotherm. Res., 122, 191–220, https://doi.org/10.1016/S0377-0273(02)00502-4, 2003.
Godt, J. W., Baum, R. L., Savage, W. Z., Salciarini, D., Schulz, W. H., and Harp, E. L.: Transient deterministic shallow landslide modeling: Requirements for susceptibility and hazard assessments in a GIS framework, Eng. Geol., 102, 214–226, https://doi.org/10.1016/j.enggeo.2008.03.019, 2008.
Gudmundsson, M. T.: Hazards from Lahars and Jökulhlaups, The Encyclopedia of volcanoes, Academis, San Diego, 971–984, 2015.
Gurioli, L., Zanella, E., Gioncada, A., and Sbrana, A.: The historic magmatic–hydrothermal eruption of the breccia di Commenda, Vulcano, Italy, Bull. Volcanol., 74, 1235–1254, 2012.
Horton, R. E.: Erosional development of streams and their drainage basins; hydrophysical approach to quantitative morphology, Geol. Soc. Am. Bull., 56, 275–370, 1945.
INGV (Istituto Nazionale de Geofisica e Vulcanologia): Palermo, available at: https://www.pa.ingv.it/, last access: 7 March 2019.
Iverson, R. M.: Landslide triggering by rain infiltration, Water Resour. Res., 36, 1897–1910, https://doi.org/10.1029/2000WR900090, 2000.
Iverson, R. M. and Lahusen, R. G.: Dynamic Pore-Pressure Fluctuations in Rapidly Shearing Granular Materials, Am. Assoc. Adv. Sci., 246, 796–799, 1989.
Iverson, R. M. and Vallance, J.: New views of granular mass flows, Geology, 29, 115–118, https://doi.org/10.1130/0091-7613(2001)029<0115:NVOGMF>2.0.CO;2, 2001.
Janda, R., Daag, A., Delos Reyes, P., Newhall, C., Pierson, T., Punongbayan, R., and Rodolfo, K.: Assessment and Response to Lahar Hazard around Mount Pinatubo, 1991 to 1993, Fire Mud, Eruptions Lahars Mt. Pinatubo, Philipp, 107–139, 1996.
Jones, R., Thomas, R. E., Peakall, J., and Manville, V.: Rainfall-runoff properties of tephra: Simulated effects of grain-size and antecedent rainfall, Geomorphology, 282, 39–51, https://doi.org/10.1016/j.geomorph.2016.12.023, 2017.
Keller, J.: The island of Vulcano, Rend. Soc. Italian Miner. Petrol., 36, 369–414, 1980.
Kovács, G.: Seepage hydraulics, Elsevier Science Publishers, Amsterdam, 1981.
Krumbein, W. C.: Size frequency distributions of sediments and the normal phi curve, J. Sediment. Petrol., 8, 84–90, 1938.
Lanza, R. and Zanella, E.: Paleomagnetic secular variation at Vulcano (Aeolian islands) during the last 135 kyr, Earth Planet. Sci. Lett., 213, 321–336, 2003.
Lavigne, F., Thouret, J.-C., Voight, B., Young, K., LaHusen, R., Marso, J., Suwa, H., Sumaryono, A., Sayudi, D., and Dejean, M.: Instrumental lahar monitoring at Merapi Volcano, Central Java, Indonesia, J. Volcanol. Geotherm. Res., 100, 457–478, https://doi.org/10.1016/S0377-0273(00)00151-7, 2000.
Leavesley, G. H., Lusby, G. C., and Lichty, R. W.: Infiltration and erosion characteristics of selected tephra deposits from the 1980 eruption of Mount St. Helens, Washington, USA, Hydrolog. Sci. J., 34, 339–353, 1989.
Li, W. C., Lee, L. M., Cai, H., Li, H. J., Dai, F. C., and Wang, M. L.: Combined roles of saturated permeability and rainfall characteristics on surficial failure of homogeneous soil slope, Eng. Geol., 153, 105–113, https://doi.org/10.1016/j.enggeo.2012.11.017, 2013.
Major, J. J. and Yamakoshi, T.: Decadal-scale change of infiltration characteristics of a tephra-mantled hillslope at Mount St Helens, Washington, Hydrol. Process., 19, 3621–3630, https://doi.org/10.1002/hyp.5863, 2005.
Major, J. J., Pierson, T. C., Dinehart, R. L., and Costa, J. E.: Sediment yield following severe volcanic disturbance – A two-decade perspective from Mount St. Helens, Geology, 28, 819–822, https://doi.org/10.1130/0091-7613(2000)28<819:SYFSVD>2.0.CO;2, 2000.
Manville, V., White, J. D. L., and Hodgson, K. A.: Dynamic interactions between lahars and stream flow: A case study from Ruapehu volcano, New Zealand: Discussion and reply: Discussion, Geol. Soc. Am. Bull., 112, 1149–1151, 2000.
Mead, S., Magill, C., and Hilton, J.: Rain-triggered lahar susceptibility using a shallow landslide and surface erosion model, Geomorphology, 273, 168–177, https://doi.org/10.1016/j.geomorph.2016.08.022, 2016.
Mead, S. and Magill, C.: Probabilistic hazard modelling of rain-triggered lahars, Journal of Applied Volcanology, 273, 168–177, https://doi.org/10.1016/j.geomorph.2016.08.022, 2017.
Mercalli, G. and Silvestri, O.: Le eruzioni dell'isola di Vulcano, incominciate il 3 Augusto 1888 e terminate il 22 Marzo 1880, Ann. Uffic. Cent. Meteorol. Geodin., 10, 213 pp., 1891.
Milledge, D. G., Bellugi, D., Mckean, J. A., Densmore, A. L., and Dietrich, W. E.: A multidimensional stability model for predicting shallow landslide size and shape across landscapes, J. Geophys. Res.-Earth, 119, 2481–2504, https://doi.org/10.1002/2014JF003135, 2014.
Ng, C. W., Wang, B., and Tung, Y. K.: Three-dimensional numerical investigations of groundwater responses in an unsaturated slope subjected to various rainfall patterns, Can. Geotech. J., 38, 1049–1062, 2001.
Newhall, C. G. and Punongbayan, R. (Eds.): Fire and mud: eruptions and lahars of Mount Pinatubo, Philippines, p. 1126, Quezon City, Philippine Institute of Volcanology and Seismology, 1996.
Newhall C. G. and Self S.: The volcanic explosivity index (VEI) – an estimate of explosive magnitude for historical volcanism, J. Geophys. Res., 87, 1231–1238, 1982.
Pierson, T. C.: Initiation and flow behavior of the 1980 Pine Creek and Muddy river lahars, Mount St. Helens, Washington, Geol. Soc. Am. Bull., 96, 1056–1069, 1985.
Pierson, T. C.: Hyperconcentrated flow–transitional process between water flow and debris flow, in: Debris-flow hazards and related phenomena, edited by: Jakob, M. and Hungr, O., Springer-Praxis, Chichester, 159–202, 2005.
Pierson, T. C. and Major, J. J.: Hydrogeomorphic Effects of Explosive Volcanic Eruptions on Drainage Basins, Annu. Rev. Earth Pl. Sc., 42, 469–507, https://doi.org/10.1146/annurev-earth-060313-054913, 2014.
Pierson, T. C., Janda, R. J., Thouret, J. C., and Borrero, C. A.: Perturbation and melting of snow and ice by the 13 November 1985 eruption of Nevado del Ruiz, Colombia, and consequent mobilization, flow and deposition of lahars, J. Volcanol. Geoth. Res., 41, 17–66, 1990.
Pierson, T. C., Janda, R. J., Umbal, J. V., and Daag, A. S.: Immediate and long-term hazards from lahars and excess sedimentation in rivers draining Mount Pinatubo, Philippines, U.S. Geol. Surv. Water-Resour. Invest. Rep., 92-4039, 1–35, 1992.
Pierson, T. C., Major, J. J., Amigo, Á., and Moreno, H.: Acute sedimentation response to rainfall following the explosive phase of the 2008–2009 eruption of Chaitén volcano, Chile, B. Volcanol., 75, 1–17, https://doi.org/10.1007/s00445-013-0723-4, 2013.
Pirone, M., Papa, R., Nicotera, M. V., and Urciuoli, G.: Analysis of safety factor in unsaturated pyroclastic slope, Landslides and Engineered Slopes, Experience, Theory and Practice, 1647–1654, CRC Press, 2016.
Pistolesi, M., Cioni, R., Bonadonna, C., Elissondo, M., Baumann, V., Bertagnini, A., Chiari, L., Gonzales, R., Rosi, M., and Francalanci, L.: Complex dynamics of small-moderate volcanic events: the example of the 2011 rhyolitic Cordón Caulle eruption, Chile, Bull. Volcanol., 77, https://doi.org/10.1007/s00445-014-0898-3, 2015.
Procter, J. N., Cronin, S. J., and Sheridan, M. F.: Evaluation of Titan2D modelling forecasts for the 2007 Crater Lake break-out lahar, Mt. Ruapehu, New Zealand, Geomorphology, 136, 95–105, 2012.
Rahardjo, H., Ong, T. H., Rezaur, R. B., and Leong, E. C.: Factors controlling instability of homogeneous soil slopes under rainfall, J. Geotech. Geoenviron., 133, 1532–1543, 2007.
Rodolfo, K. S. and Arguden, A. T.: Rain-lahar generation and sediment delivery systems at Mayon Volcano, Philippines, Society for Sedimentary Geology (SEPM), 71–87, 1991.
Rosi, M., Di Traglia, F., Pistolesi, M., Esposti Ongaro, T., de' Michieli Vitturi, M., and Bonadonna, C.: Dynamics of shallow hydrothermal eruptions: new insights from Vulcano's Breccia di Commenda eruption, Bull Volcanol., 80, 1–28, https://doi.org/10.1007/s00445-018-1252-y, 2018.
Rossi, G., Catani, F., Leoni, L., Segoni, S., and Tofani, V.: HIRESSS: a physically based slope stability simulator for HPC applications, Nat. Hazards Earth Syst. Sci., 13, 151–166, https://doi.org/10.5194/nhess-13-151-2013, 2013.
Salciarini, D., Godt, J. W., Savage, W. Z., Conversini, P., Baum, R. L., and Michael, J. A.: Modeling regional initiation of rainfall-induced shallow landslides in the eastern Umbria Region of central Italy, Landslides, 3, 181–194, https://doi.org/10.1007/s10346-006-0037-0, 2006.
Savage, W. Z., Godt, J. W., and Baum, R. L.: A model for spatially and temporally distributed shallow landslide initiation by rainfall infiltration, 3rd International Conference on Debris-Flow Hazards Mitigation: Mechanics, Prediction, and Assessment, 10–12 September 2003, Davos, Switzerland, Vol. 1, 179–187, 2003.
Savage, W. Z., Godt, J. W., and Baum, R. L.: Modeling time-dependent areal slope stability, Landslides: evaluation and stabilization, Balkema, Taylor & Francis Group, London, 23–38, 2004.
Scott, W. E., Hoblitt, R. P., Torres, R. C., Self, S., Martinez, M. L., and Nillos, T.: Pyroclastic flows of the June 15, 1991, climactic eruption of Mount Pinatubo, Fire and Mud: eruptions and lahars of Mount Pinatubo, Philippines, edited by: Newhall, C. G. and Punongbayan, R. S., 545–570, 1996.
Scott, K. M., Vallance, J. W., Kerle, N., Macías, J. L., Strauch, W., and Devoli, G.: Catastrophic precipitation-triggered lahar at Casita volcano, Nicaragua: Occurrence, bulking and transformation, Earth Surf. Proc. Land., 30, 59–79, https://doi.org/10.1002/esp.1127, 2005.
Soddu, S., Delitala, G., Sciabica, M., and Barrocu, G.: Modelling groundwater effects on slope stability, Materials and Geoenvironment, 50, 349–352, 2003.
Sorbino, G., Sica, C., Cascini, L., and Cuomo, S.: On the forecasting of flowslides triggering areas using physically based models, Proceedings of 1st North American landslides conference AEG Special Publication, 3–8 June 2007, Colorado, Vol. 1, 305–315, 2007.
Sorbino, G., Sica, C., and Cascini, L.: Susceptibility analysis of shallow landslides source areas using physically based models, Nat. Hazards, 53, 313–332, https://doi.org/10.1007/s11069-009-9431-y, 2010.
Srivastava, R. and Yeh, T. C. J.: Analytical solutions for one-dimensional, transient infiltration toward the water table in homogeneous and layered soils, Water Resour. Res., 27, 753–762, 1991.
Sulpizio, R., Zanchetta, G., Demi, F., Di Vito, M. A., Pareschi, M. T., and Santacroce, R.: The Holocene syneruptive volcaniclastic debris flows in the Vesuvian area: Geological data as a guide for hazard assessment, in: Neogene-Quaternary continental margin volcanism: A Perspective from México: Geological Society of America Special paper, edited by: Siebe, C., Macias, J. L., and Aguirre-Díaz, J., 402, 203–221, https://doi.org/10.1130/2006.2402(10), 2006.
Taylor, D.: Fundamentals of soil mechanics, Chapman and Hall, Limited, New York, 1948.
Thouret, J. C., Abdurachman, K. E., Bourdier, J. L., and Bronto, S.: Origin, characteristics, and behaviour of lahars following the 1990 eruption of Kelud volcano, eastern Java (Indonesia), B. Volcanol., 59, 460–480, 1998.
Tierz, P., Woodhouse, M. J., Phillips, J. C., Sandri, L., Selva, J., Marzocchi, W., and Odbert, H. M.: A Framework for Probabilistic Multi-Hazard Assessment of Rain-Triggered Lahars Using Bayesian Belief Networks, 5, 1–23, https://doi.org/10.3389/feart.2017.00073, 2017.
Valentine, G. A., Palladino, D. M., Agosta, E., Teddeucci, J., and Triglia, R.: Volcaniclastic aggradation in a semiarid environment, northwestern Vulcano Island, Italy, Geol. Soc. Amer. Bull., 110, 630–643, 1998.
Vallance, J. W. and Iverson, R. M.: Lahars and their Deposits, The Encyclopedia of volcanoes, Academis, San Diego, 649–664, 2015.
Vallance, J. W. and Scott, K. M.: The Osceola Mudflow from Mount Rainier: Sedimentology and hazard implications of a huge clay-rich debris flow, Geol. Soc. Am. Bull., 109, 143–163, 1997.
Witham, C. S.: Volcanic disasters and incidents: a new database, J. Volcanol. Geotherm. Res., 148, 191–233, 2005.
Volentik, A. C. M., Connor, C. B., Connor, L. J., and Bonadonna, C.: Aspects of volcanic hazard assessment for the Bataan nuclear power plant, Luzon Peninsula, Philippines, Volcan. Tecton. Hazard Assess. Nucl. Facil., 9, 229–256, https://doi.org/10.1017/CBO9780511635380.010, 2009.
Yamakoshi T. and Suwa H.: Post eruption characteristics of surface runoff and sediment discharge on the slopes of pyroclastic-flow deposits, Mount Unzen, Japan, Transactions, Japanese Geomorphological Union, 21-4, 469–497, 2000.
Yamamoto, H.: Erosion of the 1977–1978 tephra layers on a slope of Usu Volcano, Hokkaido, EOS, Transactions, American Geophysical Union, 5, 111–124, 1984.
Zanchetta, G., Sulpizio, R., Pareschi, M. T., Leoni, F. M., and Santacroce, R.: Characteristics of May 5–6, 1998 volcaniclastic debris flows in the Sarno area (Campania, southern Italy): Relationships to structural damage and hazard zonation, J. Volcanol. Geotherm. Res., 133, 377–393, https://doi.org/10.1016/S0377-0273(03)00409-8, 2004.
Zanella, E., De Astis, G., Dellino, P., Lanza, R., and La Volpe, L.: Magnetic fabric and remanent magnetization of pyroclastic surge deposits from Vulcano (Aeolian Islands, Italy), J. Volcanol. Geoth. Res., 93, 217–236, 1999.