Stochastic downscaling of precipitation in complex orography: a simple method to reproduce a realistic fine-scale climatology

Stochastic rainfall downscaling methods usually do not take into account orographic effects or local precipitation features at spatial scales finer than those resolved by the large-scale input field. For this reason they may be less reliable in areas with complex topography or with sub-grid surface heterogeneities. Here we test a simple method to introduce realistic fine-scale precipitation patterns into the downscaled fields, with the objective of producing downscaled data more suitable for climatological and hydrological applications as well as for extreme event studies. The proposed method relies on the availability of a reference fine-scale precipitation climatology from which corrective weights for the downscaled fields are derived. We demonstrate the method by applying it to the Rainfall Filtered Autoregressive Model (RainFARM) stochastic rainfall downscaling algorithm.

The modified RainFARM method is tested focusing on an area of complex topography encompassing the Swiss Alps, first, in a “perfect-model experiment” in which high-resolution (4 km) simulations performed with the Weather Research and Forecasting (WRF) regional model are aggregated to a coarser resolution (64 km) and then downscaled back to 4 km and compared with the original data. Second, the modified RainFARM is applied to the E-OBS gridded precipitation data (0.25^∘ spatial resolution) over Switzerland, where high-quality gridded precipitation climatologies and accurate in situ observations are available for comparison with the downscaled data for the period 1981–2010.

The results of the perfect-model experiment confirm a clear improvement in the description of the precipitation distribution when the RainFARM stochastic downscaling is applied, either with or without the implemented orographic adjustment. When we separately analyze grid points with precipitation climatology higher or lower than the median calculated over the neighboring grid points, we find that the probability density function (PDF) of the real precipitation is better reproduced using the modified RainFARM rather than the standard RainFARM method. In fact, the modified method successfully assigns more precipitation to areas where precipitation is on average more abundant according to a reference long-term climatology.

The results of the E-OBS downscaling show that the modified RainFARM introduces improvements in the representation of precipitation amplitudes. While for low-precipitation areas the downscaled and the observed PDFs are in good agreement, for high-precipitation areas residual differences persist, mainly related to known E-OBS deficiencies in properly representing the correct range of precipitation values in the Alpine region. The downscaling method discussed is not intended to correct the bias which may be present in the coarse-scale data, so possible biases should be adjusted before applying the downscaling procedure.

1 Introduction

Assessing the impacts of climate change on extreme precipitation events and hydrometeorological hazards requires reliable precipitation data at fine spatial and temporal resolution. A wide range of downscaling methods have been developed to obtain fine-scale precipitation fields from coarse-scale data (see Maraun et al., 2010, for a review): in addition to physically based dynamical downscaling approaches, in which high-resolution regional climate models are nested in global datasets, an effective approach is provided by statistical and stochastic downscaling. While statistical downscaling is based on mapping large-scale predictors for precipitation at small scales to produce the expected small-scale rainfall field (e.g., Maraun et al., 2010; Chiew et al., 2010), stochastic rainfall downscaling, a type of weather generator, uses information directly from the large-scale precipitation to generate an ensemble of possible stochastic realizations of precipitation fields with a realistic spatial and temporal correlation structure and preserving the large-scale properties of the original field (see e.g., Ferraris et al., 2003).

Stochastic approaches are attractive owing to their computational efficiency, which allows us to perform ensemble simulations to evaluate the uncertainties in the small-scale precipitation fields, and owing to their flexibility, as most of them can be applied to a range of temporal scales (Bordoy and Burlando, 2014). Several stochastic downscaling methods have been proposed for precipitation, some of them devised for generating time series at single stations or at a set of stations (Vrac and Naveau, 2007; Mehrotra and Sharma, 2006; Charles et al., 1999; Wilks, 1999, 1998). Here we focus on full-field generators, which have the characteristic of simulating fields of precipitation, thus providing continuous spatial information usable as input to distributed hydrological models. Detailed discussions on these models are offered by Bordoy and Burlando (2014) and Ferraris et al. (2003). Full-field weather generators are generally based upon simple autoregressive models, so-called meta-Gaussian models (Rebora et al., 2006), or point process models simulating individual rain cells (Rodriguez-Iturbe et al., 1988, 1987), or spatiotemporal implementation of multifractal cascade models (Lovejoy and Schertzer, 2006; Deidda, 2000, 1999; Lovejoy and Mandelbrot, 1985).

Among the meta-Gaussian models, an example is provided by the Rainfall Filtered Autoregressive Model (RainFARM) procedure, a stochastic rainfall downscaling method based on the extrapolation of the coarse-scale Fourier power spectrum to small scales. This method was originally developed for spatiotemporal downscaling of rainfall predictions on meteorological timescales (Rebora et al., 2006) and then extended to climatic timescales (D'Onofrio et al., 2014). An advantage of stochastic downscaling methods like RainFARM is that they have few free parameters, they do not require further fields in addition to the original precipitation to downscale, and the small-scale correlation structure is estimated from the large-scale field. This makes such methods also directly applicable to model outputs in areas where further fine-scale information is not available. Still, the main limitation of most stochastic downscaling methods is that they do not take into account orographic effects at scales smaller than those resolved by the original precipitation field to downscale. Orographic precipitation mechanisms, such as orographic lifting, play an important role in determining patterns of small-scale precipitation in areas with complex orography (Roe, 2005; Smith, 2006). Thus, when the fine-scale distribution of precipitation in the downscaled fields is not conditioned on orography, the long-term climatology at individual grid points may differ significantly from observations. This may make such downscaling methods not suitable for applications in which the small-scale hydrological balance is of importance, such as studies involving changes in snow cover or water resources in small mountain basins.

The addition of an orographic component to rainfall downscaling models over land has been investigated, among others, by Harris et al. (1996), Jothityangkoon et al. (2000), Purdy et al. (2001), Pathirana and Herath (2002), and Badas et al. (2005, 2006). In particular Harris et al. (1996) and Purdy et al. (2001) were among the first studies using a cascade-based approach to analyze the multiscale statistical properties of orographic rainfall. Badas et al. (2005, 2006) studied the scaling behavior of orographic rainfall using a high-temporal-resolution rain gauge network in Sardinia, Italy, and developed a modified cascade-based rainfall downscaling model conditioned on local average precipitation and on terrain elevation. These methods require detailed calibration for each study area and the availability of an extensive dataset of local measurements at high temporal frequencies, detailed data which may not be readily available for several regions. Nonetheless, for many areas, information on the spatial distribution of precipitation, at least as a long-term climatological average, may be available from different sources, such as gridded reconstructions based on rain gauge observations (e.g., the EURO4M dataset for the greater Alpine region, http://www.euro4m.eu/datasets.html, last access: 1 October 2018) or from dynamical downscaling simulations with regional climate models (RCMs). In particular non-hydrostatic RCMs, when applied at very fine scales (1 to 5 km resolution), can capture the main physical mechanisms for orographic precipitation and may lead to a realistic spatial distribution of precipitation amounts on average, also over complex topography, albeit often with significant biases in amplitude (Kotlarski et al., 2014; Viterbo et al., 2016).

In this paper we present a very simple approach, described and tested for the specific case of the RainFARM method, which allows the integration into a stochastic downscaling method of information on the fine-scale spatial distribution of precipitation, available from high-resolution gridded observations or from dynamical downscaling. This information is used to locally modulate the distribution of precipitation inside each large-scale grid element of the field to downscale or in the neighborhood of each point. The precipitation amplitudes on the fine grid are first determined by the stochastic downscaling procedure, then the downscaled precipitation is modulated using the realistic pattern derived from a fine-scale reference precipitation climatology. This last step, consisting in the application of correction factors (or weights), allows us to take into account the heterogeneity at the fine scales, including topographic effects. Finally, the overall precipitation amounts at the resolution of the precipitation fields to downscale are adjusted to ensure the conservation of the total precipitation at the large scale, a requirement already present in the standard RainFARM procedure.

We demonstrate the application of the method in two cases. First, in a perfect-model experiment, in which a high-resolution precipitation dataset is first upscaled by aggregating it to a coarser resolution and then downscaled with RainFARM to its initial resolution to check the agreement with the original high-resolution field. To this end, a 30-year-long simulation with the Weather Research and Forecasting (WRF) model over Europe (Pieri et al., 2015) is used, providing the reference fine-scale (4 km) precipitation dataset, which is first aggregated to derive the coarse-scale field to be downscaled and then used for validating the downscaled field. Second, we demonstrate the method in a more realistic setup, by applying it to the E-OBS observational dataset (version 17; Haylock et al., 2008) at about 25 km resolution and by validating the statistics of the downscaled precipitation fields against surface observations from a dense network of rain gauge stations in Switzerland. Since a high-quality precipitation climatology to be used for calculating correction factors is not always available for many regions of the world, we test the impact of different reference climatologies on the downscaled fields, considering three different datasets with different degrees of accuracy.

The paper is organized as follows: Sect. 2 describes the datasets used in this study; Sect. 3 presents the modifications included in RainFARM to better describe the precipitation at fine scales; Sect. 4 shows the application and the evaluation of the method, first in a “perfect-model experiment” and then in a more realistic case in which E-OBS precipitation is downscaled and the results are compared to surface station measurements; Sects. 5 and 6 provide a discussion of the results and the main conclusions of the paper.

2 Datasets

In order to present and validate the method, we employ different precipitation datasets, described briefly in the following.

2.1 WRF simulation outputs

The perfect-model experiment, described further on in Sect. 4.1, is performed using precipitation data from a very high-resolution climate simulation with the regional climate Weather Research and Forecasting (WRF v3.4.1) model, described in Pieri et al. (2015). WRF was forced in the period 1979–2008 with boundary conditions from the ERA-Interim reanalysis (Dee et al., 2011) and run over the European domain with a double nesting, with a resolution for the inner domain of about 0.037^∘ (∼4 km in the meridional direction). This dataset has been validated through comparison with a range of observation-based and reanalysis datasets (Pieri et al., 2015). In agreement with the general behavior of several regional (as well as global) climate models, which are known to exhibit wet biases over mountainous areas especially in winter (e.g., Kotlarski et al., 2014; Palazzi et al., 2015), this WRF simulation also overestimates precipitation and localized precipitation extremes over the Alps (Pieri et al., 2015).

To perform a perfect-model experiment we aggregate WRF precipitation data originally available at ∼4 km resolution to a coarser resolution of 64 km by box averaging. The upscaled field is then downscaled back to 4 km with RainFARM and finally its statistics are compared with those of the original 4 km WRF precipitation. By construction, the results obtained with this approach are not affected by possible biases in the considered datasets; i.e., the total average precipitation flux is the same in the large-scale fields and in the validation dataset.

2.2 E-OBS

A more realistic application is provided by a comparison between precipitation downscaled from the European daily observation-based gridded dataset E-OBS (version 17; Haylock et al., 2008) and station data. E-OBS provides daily precipitation over land areas from 25 to 75^∘ N in latitude and 40^∘ W to 75^∘ E in longitude, based on the interpolation of in situ station data. For the present study we analyze E-OBS precipitation data at 0.25^∘ lat–long resolution corresponding to about 25 km grid size in the meridional direction. Being based on the interpolation of in situ stations, E-OBS has potential inaccuracies coming from the interpolation algorithms that are employed and from sampling error related to the capability of estimating reliable grid point values from the nearest few available stations. This type of uncertainty is largest in areas with sparse and uneven station coverage, in particular in high-elevation regions where the station distribution is biased towards the lower elevations. It is also worth stressing that, in general, rain gauges tend to underestimate total precipitation in mountain areas since they do not properly account for snowfall, which represents an important contribution in high-elevation regions especially in the cold season.

We use the E-OBS gridded dataset as a sample large-scale precipitation field to be downscaled with RainFARM. The E-OBS data downscaled at 1 km resolution are then compared with MeteoSwiss station data (described in the following) to check the performances of RainFARM and for validation purposes. It is worth noting that in this, as well as in other, “real-case” experiments, average precipitation in the fields to downscale (E-OBS in this case) is generally expected to differ from that of the validation dataset and this is a bias that our downscaling method does not address. This source of uncertainty should be considered when evaluating the downscaling performances.

2.3 WorldClim

WorldClim 1.4 (Hijmans et al., 2005) is used here as an example of globally available precipitation climatology that could also be used in regions where no high-quality local gridded data are available. WorldClim consists in a set of global gridded climatologies based on observations with a nominal spatial resolution of about 1 km × 1 km. It is a popular choice for ecosystem studies (Bedia et al., 2013; Warren and Seifert, 2011; Peterson and Nakazawa, 2008; Townsend Peterson et al., 2007; Waltari et al., 2007). WorldClim provides 30-year monthly averages of the minimum, mean, and maximum temperature and of precipitation, as well as of other bioclimatic variables, for a reference historical period (1960–1990, labeled as current climate) and for a future period (2050–2080) for four Representative Concentration Pathways (RCPs). Monthly climatologies were obtained from various data sources through spline interpolation methods, which use the latitude, longitude, and elevation as independent variables. Assessment of uncertainties in the gridded products were made, highlighting that the most uncertain estimates correspond to mountainous and other poorly sampled areas. In fact, Hijmans et al. (2005) compared WorldClim data to two high-resolution datasets in the US and found significant differences, particularly in high-elevation regions.

2.4 MeteoSwiss station and gridded data

To validate the RainFARM downscaling algorithm we consider precipitation observations registered by 160 automatic stations of the MeteoSwiss network. These data are preprocessed by MeteoSwiss, which performs temporal aggregation, gap filling, and quality control to correct wrong or implausible measurement values according to agreed protocols (https://www.meteoswiss.admin.ch/home/measurement-and-forecasting-systems/datenmanagement/data-preparation.html, last access: 1 October 2018). We focus our analysis on the period 1981–2010 and retain only the stations providing at least 80 % of daily data over this period, leading to a reduced set of 59 stations, shown in Fig. 1.

We also employ the MeteoSwiss climatology RnormM (Begert et al., 2013) to calculate the corrective weights for the RainFARM downscaling. RnormM provides the average monthly accumulated precipitation over the standard period 1981–2010, calculated from the data of all automatic and manual stations in Switzerland, achieving high accuracy and detailed spatial resolution. RnormM provides precipitation with nominal spatial resolution of 2.2 km in WGS-84 long–lat coordinates, while the effective resolution, i.e., the average distance between individual weather stations, is 15–20 km. The accuracy of the RnormM analysis depends on the accuracy of the underlying measuring stations and on the ability of the interpolation method that is employed.

3 The RainFARM stochastic downscaling method and its modification

3.1 RainFARM

The RainFARM procedure is described in detail in Rebora et al. (2006) and D'Onofrio et al. (2014), and in the present paper we refer to the spatial-only downscaling method described in the latter. The RainFARM method downscales a large-scale spatiotemporal precipitation field P(X, Y, t), which is considered reliable at scales larger than a reliability scale L_o (which often may coincide with the spatial resolution of the field). Here and in the following we use uppercase coordinates (X, Y) and lowercase coordinates (x, y) to indicate that a field is defined on a coarse or fine grid, respectively.

From the large-scale field to downscale, the method generates a fine-scale field $\stackrel{\mathrm{̃}}{r}(x$, y, t) at a desired fine-scale resolution by extrapolation of its large-scale power spectrum to the unresolved smaller scales, using the same spectral slope in a log–log plot as the large-scale field, choosing random Fourier phases at small scales and finally using an inverse Fourier transform to return to physical space. Since this procedure by itself would create intermediate fields g(x, y, t) with an unrealistic, almost Gaussian amplitude distribution, a final nonlinear (exponential) transformation is applied to the resulting field in physical space: $\stackrel{\mathrm{̃}}{r}(x$, y, t)=exp (γg). The parameter γ represents an additional free parameter of the procedure, but, as discussed in D'Onofrio et al. (2014), γ=1 is commonly used when there is no adequate information to tune it.

In the final step of the procedure, $\stackrel{\mathrm{̃}}{r}(x$, y, t) is further adjusted to guarantee that when upscaled (aggregated) at the large reliability scale, it reproduces exactly the original field to downscale P(X, Y, t):

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }r(x,y,t)={\displaystyle \frac{\stackrel{\mathrm{̃}}{r}(x,y,t)\langle P(x,y,t){\rangle }_{L_{\mathrm{o}}}}{\langle \stackrel{\mathrm{̃}}{r}(x,y,t){\rangle }_{L_{\mathrm{o}}}}},\end{array}$$

where the operator $\langle \cdot {\rangle }_{L_{\mathrm{o}}}$ indicates aggregation (averaging) at scale L_o using simple averaging over boxes of side L_o, followed by interpolation using nearest neighbors to the fine-scale grid (x, y).

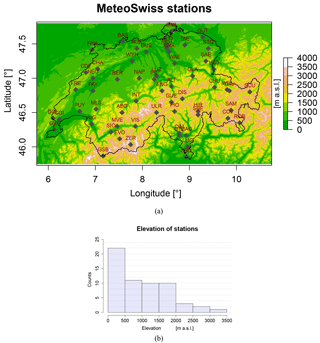
Figure 1 (a) Orography of the study area including the Swiss Alps, according to a 500 m resolution digital elevation model. Automatic meteorological stations of the MeteoSwiss network providing at least 80 % of valid daily total precipitation data over the period 1981–2010 are labeled with gray diamonds. (b) Distribution of the elevations of the MeteoSwiss stations grouped in 500 m elevation bins.

In this work we additionally apply a smoothing operator S to both numerator and denominator of Eq. (1), averaging the box-averaged fields a(x, y) over a moving Gaussian window with size $\mathit{\sigma }=L_{\mathrm{o}}/\mathrm{2}$:

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle }S\left[a\right(x,y){]}_{L_{\mathrm{o}}}=\underset{\mathrm{\Omega }}{\int }K(x-x^{\prime },y-y^{\prime }\left)a\right(x^{\prime },y^{\prime })\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime },\end{array}$$

where Ω is the entire domain of interest and $K(x-x^{\prime }$, $y-y^{\prime })=\exp \mathit{\{}-\left[\right(x-x^{\prime }{)}^{\mathrm{2}}+(y-y^{\prime }{)}^{\mathrm{2}}]/{\mathit{\sigma }}^{\mathrm{2}}\mathit{\}}$ is a kernel representing an isotropic distribution of Gaussian weights. The resulting transformation in this case is

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }r(x,y,t)={\displaystyle \frac{\stackrel{\mathrm{̃}}{r}(x,y,t)S{\left[\langle P(x,y,t){\rangle }_{L_{\mathrm{o}}}\right]}_{L_{\mathrm{o}}}}{S{\left[\langle \stackrel{\mathrm{̃}}{r}(x,y,t){\rangle }_{L_{\mathrm{o}}}\right]}_{L_{\mathrm{o}}}}}.\end{array}$$

Using this improved approach allows us to conserve average precipitation at scale L_o, avoiding box-shaped artifacts in the resulting fields. We verified that all qualitative results discussed in this paper do not change whether the final smoothing step is applied or not.

3.2 Reproducing fine-scale precipitation climatology in RainFARM

We assume that a reference precipitation climatology c(x, y) at fine spatial scales is available. This could be obtained from long-term time averages of gridded observational precipitation datasets, radar or satellite observations, or from numerical simulations with high-resolution models. This reference climatology is used only to derive local weights used to modify the spatial distribution of precipitation, but the absolute value of precipitation itself is not taken into account, so that possible large-scale biases in the reference climatology are not introduced in the downscaling chain and do not affect the results.

The spatial pattern of precipitation is translated into a map of weights that is used to correct the spatial pattern of the downscaled precipitation fields as follows:

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle }w(x,y)=c(x,y)/S\left[c\right(x,y){]}_{L_{\mathrm{o}}}.\end{array}$$

That is, we divide each value of c(x, y) by its local smooth average at scale L_o. When the spatial average of c(x, y) is 0 (as may happen in arid areas), the weights are all set to 1. The resulting weight field reflects the distribution in space, inside each cell of size L_o, of the climatological precipitation in the reference dataset. Notice that this provides a map of weights with both positive and negative values and that, on average, precipitation at scale L_o is conserved using this approach.

In general, if the climatology needs to be reproduced at a monthly time-scale, this method can be applied separately for each month, computing monthly weights w_i(x, y) from Eq. (4), where c_i(x, y) is the long-term monthly average of the reference precipitation dataset for month i, with $i=\mathrm{1},\mathrm{\dots },\mathrm{12}$.

The weights are then applied to the fine-scale field produced by the RainFARM procedure:

$$\begin{array}{}\text{(5)}& {\displaystyle }{\displaystyle }\stackrel{\mathrm{̃}}{r}(x,y,t)\to \stackrel{\mathrm{̃}}{r}(x,y,t)\cdot w(x,y),\end{array}$$

generating a new field in which precipitation is reduced or intensified according to the weights obtained from the long-term climatology. As a last step, the final amplitude adjustment to conserve average precipitation at scale L_o, i.e., Eq. (3), is again applied to $\stackrel{\mathrm{̃}}{r}(x$, y, t).

The resulting fine-scale field r(x, y, t) still coincides exactly with the large-scale field P(X, Y, t) when both are aggregated at the confidence scale L_o, but its long-term time-averaged climatology will reflect the small-scale spatial distribution of the reference dataset c(x, y). Notice that the weights in Eq. (4) only use the local distribution of precipitation so they are not sensitive to possible large-scale biases in the precipitation climatology.

4 Results

4.1 Application of RainFARM in a perfect-model experiment

We demonstrate the method using daily precipitation data from long-term simulations (1980–2008) performed with the WRF model over the European domain, at 4 km spatial resolution, forced with ERA-Interim reanalysis data (Dee et al., 2011). We focus on the Alpine region, choosing an area encompassing northwestern Italy and Switzerland (see Fig. 2a). The area comprises 128×128 grid elements of the WRF precipitation field, p(x, y, t).

The dataset p(x, y, t) is used for the perfect-model experiment

• i.

  to create the coarse-scale field P(X, Y, t) to be downscaled, obtained by aggregating the fine-scale field at scale L_o=64 km, corresponding to 16×16 fine-scale grid points, using a box-averaging aggregation.

• ii.

  to calculate the reference fine-scale climatology, which is necessary for the modified RainFARM algorithm to estimate the weights.

• iii.

  to validate the fine-scale fields produced by the downscaling method.

In our example we consider separately monthly climatologies in order to show a general case in which the variability in precipitation at seasonal and subseasonal scales is non-negligible.

The coarse-scale field, P(X, Y, t), resulting from the aggregation of p(x, y, t), has 8×8 spatial grid elements. After applying RainFARM to P(X, Y, t), the fine-scale output r(x, y, t) should reproduce, as close as possible, the statistical properties of the original field p(x, y, t). To this end, we tune the value of the parameter γ, described in Sect. 3.1, so that the amplitude distributions of the downscaled fields r(x, y, t) include that of the original field p(x, y, t) (shown in Fig. 3a). A suitable value for the γ parameter is found to be γ=0.75. The spatial spectral slope for the RainFARM procedure is estimated separately for each month of the year from the original coarse precipitation data P(X, Y, t), starting at wave number k=2, corresponding to a change of slope in the spatial power spectra of precipitation in the WRF dataset.

Figure 2a shows the long-term time average (1980–2008) of the WRF 4 km resolution precipitation dataset p(x, y, t). The field presents small-scale details that reflect the underlying topography, and several features can be easily identified, such as the Apennine Mountains in the Italian regions of Liguria and Tuscany (lower corner) or features connected to individual river basins in the Alps. From the small-scale field p(x, y, t) we calculate the monthly climatologies, used as a reference to derive the corresponding fine-scale maps of weights, according to Eq. (4).

Figure 2b shows the long-term time average of the coarse 64 km spatial resolution dataset to be downscaled, P(X, Y, t), obtained by box-averaging aggregation of the fine-scale WRF data p(x, y, t). The RainFARM downscaling procedure estimates the large-scale spectral slopes, month by month, directly from the large-scale field P(X, Y, t).

Figure 2c shows the long-term average of the fine-scale fields obtained using the standard RainFARM procedure and using a smooth moving Gaussian window with an averaging operator of size $\mathit{\sigma }=L_{\mathrm{o}}/\mathrm{2}$ (Eq. 2). Since RainFARM alone does not take into account orography at scales smaller than the reliability scale L_o, the climatology of the downscaled field matches the reference climatology only if coarse-scale averages of the downscaled climatology are considered. Inside each grid element of size L_o, the RainFARM field presents a distribution that has no correspondence with the actual reference precipitation climatology. Actually, the fine-scale distribution introduced by RainFARM in each large-scale grid element of size L_o is statistically almost homogeneous, as reflected in the smooth distributions found in the long-term average (Fig. 2c). Indeed if a box-averaging operator had been used (Eq. 1 instead of Eq. 3), the resulting climatology of the RainFARM downscaled field would be very similar to Fig. 2b.

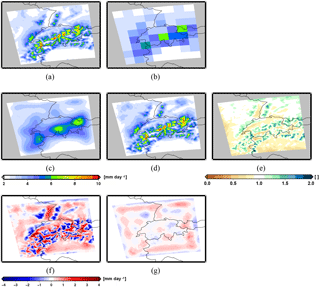
Figure 2 The “perfect-model” experiment. Average daily precipitation climatology (1980–2008) derived from (a) high-resolution WRF daily fields at 4 km, here considered to be the“truth”; (b) WRF daily fields aggregated at 64 km, i.e., the fields, P(X, Y, t), to be downscaled; (c) P(X, Y, t) downscaled at 4 km using the standard RainFARM method; (d) P(X, Y, t) downscaled at 4 km using the modified RainFARM method; (e) an example of a map of weights obtained in this case for the month of June; (f, g) anomalies of the downscaled climatologies in (c) and (d) with respect to the reference precipitation field (a).

Figure 2d shows the same as Fig. 2c but using the modified RainFARM algorithm, i.e., applying the weights w_i(x, y) computed from the WRF monthly climatologies. An example of a weights map is provided in Fig. 2e, which refers to the month of June. In this case the weights correspond to correction factors ranging between 0.4 and 2.3, but similar ranges are found for the other months. Compared to Fig. 2c, in Fig. 2d individual orographic features are now clearly recognizable and there is a significantly improved correspondence with the reference climatology. The improvement gained by the modified RainFARM procedure is better highlighted in Fig. 2f and g, which report the anomalies of the climatologies obtained with the different downscaling procedures (Fig. 2c and d) compared to the reference climatology (Fig. 2a). These figures show that the modified RainFARM algorithm allows us to remarkably reduce the bias with respect to the reference climatology in both the valleys and the mountain ridges. Furthermore, when we compare the climatologies of the standard RainFARM downscaled fields with the reference, we find a pattern correlation of 0.79 and a root-mean-square error (RMSE) of 0.86 mm day⁻¹, while the modified method improves these to a correlation of 0.98 and a RMSE of 0.27 mm day⁻¹.

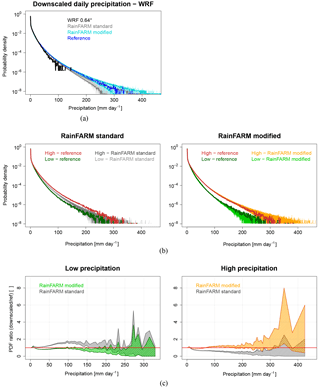
Figure 3 The “perfect-model” experiment: (a) probability density function (PDF) of WRF daily precipitation at coarse resolution (64 km, black) of the downscaled WRF precipitation (from 64 to 4 km) obtained using the standard (gray) and modified (light blue) RainFARM methods compared to the original fine-resolution (4 km) WRF precipitation (blue). Gray and light-blue bands and lines represent the spread of the ensemble and the fifth and 95th percentile ranges, respectively, calculated from 80 realizations of the stochastic downscaled field; (b) same as (a) but separating high- and low-precipitation grid points as specified in the text; (c) ratio between the PDF of WRF downscaled precipitation and the PDF of the reference, for low- and high-precipitation grid points, with the standard and the modified RainFARM methods.

We proceed investigating the extent to which the two RainFARM methods correct the amplitude distributions of the coarse-scale daily precipitation with respect to the reference fine-scale data. Figure 3 shows the PDFs of the WRF daily precipitation before and after application of the downscaling methods. The PDFs are calculated including all the grid points of the previously described precipitation datasets, i.e., $\mathrm{8}\times \mathrm{8}\times N$ grid points in the coarse-scale dataset and $\mathrm{128}\times \mathrm{128}\times N$ grid points in both the downscaled and the validation datasets, N being the number of (daily) time steps in the period 1980–2008. For each downscaling method (standard and modified RainFARM) we generate an ensemble of 80 stochastic realizations of the downscaled rainfall fields in order to provide an estimate of the uncertainty associated with the small-scale precipitation. The different realizations are characterized by the same spectral slope and different sets of random Fourier phases. In Fig. 3a we report as light blue and gray the spread of the PDF ensembles and as thick light blue and gray lines the fifth and 95th percentiles of the range of the PDFs obtained with the modified and the standard RainFARM, respectively.

The coarse-scale precipitation fields provide precipitation values mainly below 100–120 mm day⁻¹ and, in any case, they never exceed 150 mm day⁻¹. However, the range of precipitation values simulated at high resolution (∼4 km) by WRF extends up to 400 mm day⁻¹. The aggregation has clearly smoothed out the precipitation extremes, which appear insufficiently represented in the coarse-scale dataset. Both RainFARM downscaling methods reintroduce high-precipitation values in the range of 150–400 mm day⁻¹ with a probability of occurrence that is comparable to that seen in the original WRF dataset. The PDF of the real reference precipitation is included in the range of PDFs obtained via stochastic downscaling: this result confirms the strength of the RainFARM method as a way to effectively represent the upper tails of the precipitation distribution, also when the new modified procedure described in this work is used. In fact, using the modified RainFARM procedure we obtain a PDF distribution similar to in the case of the standard RainFARM, just slightly shifted towards higher precipitation values. The modified procedure, while better reproducing the long-term climatology of precipitation at each point, does not affect the overall capability of the RainFARM method of reproducing extreme precipitation values.

In Fig. 3a all grid points in the study area have been considered together. Since the modified RainFARM procedure leads to an overall better representation of the downscaled precipitation climatology (Fig. 2d and g), it is interesting to analyze more in detail the effects of the downscaling procedure when we separately consider grid points characterized by long-term average precipitation, which is higher and lower with respect to the median over the neighboring grid points. To this end, in each large-scale box of size L_o we separate grid points into two groups with the same numerosity, using the local median of the long-term climatology (Fig. 2a) as a threshold. Grid points with average precipitation climatology above or equal to the local median are classified as “high-precipitation” grid points, while those with average precipitation below the threshold are labeled as “low-precipitation” grid points. For each of the two groups we calculate the PDF of the downscaled daily precipitation and we compare it to the PDF of the original 4 km WRF data in the same group. This exercise is performed using both the standard and the modified RainFARM outputs.

Figure 3b shows the results when the standard (left) and the modified (right) RainFARM methods are applied. When using the standard RainFARM the PDFs of the high- and low-precipitation grid points are not clearly separated from each other, and for given precipitation ranges the reference PDF lies outside the range of variability in the PDFs of the downscaled data. Instead, the modified RainFARM is able to capture the reference rainfall PDF, better separating the high- from the low-precipitation grid points, and the reference PDFs are included in the range of PDFs of the downscaled datasets.

In order to better compare the performance of the modified versus the standard RainFARM, we show the ratio between the PDFs of the downscaled datasets with respect to the PDF of the reference data: the closer the ratio is to 1, the better the model performance is. The results are reported in Fig. 3c in which low- and high-precipitation grid points are shown in the left and right panels, respectively. Also in this case we use the full 80-member ensemble, and the bands in the plot represent the range of variability in the ensemble. The standard RainFARM shows good skill in representing very rare events with precipitation above 200 mm day⁻¹ in low-precipitation grid points. Apart from this, the standard RainFARM overestimates the frequency of precipitation below 200 mm day⁻¹ in low-precipitation grid points and underestimates the frequency of precipitation below 300 mm day⁻¹ in high-precipitation grid points. These results show that the standard RainFARM method is, by construction, not sensitive to the differences between low- and high-precipitation grid points at the fine scale, so precipitation is generally overestimated in low-precipitation grid points and underestimated in high-precipitation grid points (Fig. 3b).

This problem is corrected when the modified RainFARM is used. The modified RainFARM provides precipitation distributions that are closer to the real one, for almost the full range of precipitation values, for both low- and high-precipitation grid points. The only exception is for very rare events with daily precipitation above 300 mm day⁻¹, occurring in high-precipitation grid points only, where the standard RainFARM already showed a good agreement: the frequency of these events is now overestimated with respect to the reference. Apart from this feature, the modified RainFARM outperforms the standard method and allows redistribution of coarse-scale precipitation among the corresponding small-scale grid points in a more realistic way based only on their average climatology.

4.2 A more realistic test case

In this section we demonstrate an application in which the large-scale precipitation field, the reference climatology, and the verification data are not derived from the same high-resolution dataset but from different sources. We downscale the E-OBS dataset, one of the most extensively used gridded observational precipitation datasets over Europe, and we compare downscaled data directly with daily station measurements from MeteoSwiss. The domain of study is again the Swiss Alps, for which a high-quality dataset from surface stations is available (Fig. 1). The reference precipitation climatology used to derive the corrective weights is the MeteoSwiss RnormM monthly climatology (see Sect. 2.4), possibly the best available gridded product for the study region. Notice that the MeteoSwiss station data used for verification are included among the stations used to construct this gridded climatology, so the climatology is not independent, but we discuss in Sect. 4.3 the impact of different precipitation climatologies.

Also, in this case we estimate spectral slopes at a monthly scale from the coarse E-OBS fields, starting from wave number k=2. A comparison between the downscaled E-OBS precipitation and MeteoSwiss observations suggested choosing γ=1.35 in this case.

We analyze the PDFs of the E-OBS original dataset at 25 km, including only grid points containing at least one surface station. If one grid point includes more than one station the E-OBS time series is repeated in order to have the same number of time series from the surface stations and from E-OBS. As a second step, we separate points characterized by “high” and “low” long-term average precipitation. To this end we use the station data and we calculate the long-term average daily precipitation climatology at each station. The stations are then split into two groups based on the median of the distribution of the precipitation climatologies, so that low-precipitation stations have below-median long-term daily precipitation climatologies and high-precipitation stations have above-median long-term daily precipitation climatologies. The corresponding E-OBS grid points containing the stations are grouped based on the classification of the station which they contain. Notice that this separation is different from that carried out in the previous section for the perfect-model case in which each grid point was compared with its immediate neighbors since in this case our reference dataset is an ensemble of sparse stations instead of a continuous gridded field. Instead of selecting grid points with high or low precipitation compared only to their neighbors, we select stations with high- or low-precipitation compared to all available stations.

Figure 4a shows the PDFs of E-OBS at its original resolution, of E-OBS downscaled with the standard and the modified RainFARM methods (80 realizations for each experiment) and the PDF of the observations from the 59 stations. The displayed results refer to the case with no distinction between low- and high-precipitation grid points, so all the grid points are considered part of the same sample. In this case the two RainFARM methods provide very similar results, with almost no difference in the fifth and the 95th percentiles of the two PDF distributions. Both downscaling methods introduce variability at small spatial scales, increasing the probability of precipitation events above 100 mm day⁻¹ with respect to the original coarse-scale data. The PDF of the original E-OBS data lies around the lower fifth percentile of the PDF distribution of the downscaled data. The downscaling clearly improves the agreement with observations and allows us to fully capture the observed PDF.

To further investigate this result we separate high- and low-precipitation grid points as previously explained and we evaluate (i) the ratio between the PDF of E-OBS data and that of observations in order to better characterize the E-OBS dataset and (ii) the ratio between the PDF of each downscaling realization (80 realizations for each of the two ensembles) and the observed PDF in order to characterize the performances of the two downscaling methods (Fig. 4b and c). The closer the PDF ratio to 1, the better the agreement with the observations. Please note that the displayed precipitation range corresponds to the full observed precipitation range by construction.

When considering low-precipitation grid points (Fig. 4b), E-OBS at the original spatial resolution shows a clear tendency to overestimate the frequency of precipitation events from a few millimeters per day up to about 80 mm day⁻¹. Above this precipitation threshold the events become rare, with no events above 150 mm day⁻¹. The small-scale fields obtained with the standard RainFARM downscaling method inherit the overestimation errors in the range between a few millimeters per day and about 80 mm day⁻¹. The standard method acts mainly on the tails of the distribution by amplifying the frequency of heavy precipitation events. Their frequency becomes remarkably higher with respect to observations above 100 mm day⁻¹. If the modified RainFARM algorithm is applied, the PDF ratios get closer to 1 throughout the range, showing a clear improvement in the representation of the precipitation distribution with respect to the standard RainFARM method.

When considering high-precipitation grid points (Fig. 4c), E-OBS at the original spatial resolution shows important deficiencies and limited capability to reproduce the observed PDF. The agreement between the E-OBS PDF and the observed PDF drops for values higher than about 20 mm day⁻¹ and gets close to zero in the range between 100 and 300 mm day⁻¹. Such inadequacy found for the E-OBS dataset is expected to also be reflected to some extent in the downscaled data. In fact, we find that, with respect to E-OBS at its original spatial resolution, both downscaling methods correctly increase the frequency of high-precipitation events and they contribute to reducing the discrepancy with respect to the reference dataset. In short, both downscaling methods improve the description of the tail of the precipitation distribution but the discrepancy between the original coarse-scale dataset and the observations is too large to be entirely canceled out by the downscaling method only.

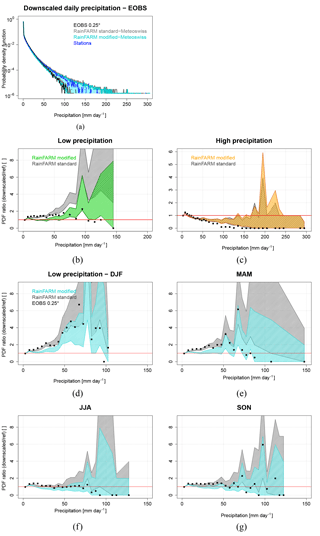
Figure 4 (a) The “real-case” experiment. Probability density function (PDF) of E-OBS daily precipitation at the original resolution of 0.25^∘ (black), E-OBS precipitation downscaled using the standard (gray) and the modified (light blue) RainFARM with the MeteoSwiss weights, and the observations from 59 stations in Switzerland (dark blue). Gray and light-blue bands and lines represent the spread of the ensemble and the fifth and 95th percentile ranges, respectively, calculated from 80 realizations of the stochastic downscaled field. (b, c) The ratio between the PDFs of (i) E-OBS at its original resolution (black squares), (ii) 80 E-OBS downscaling realizations with the standard (gray) and the modified (colors) RainFARM, and the PDF of the observations, for low-precipitation (b) and high-precipitation (c) grid points. (d–g) Same as (b) but for different seasons (DJF, MAM, JJA, SON) and for low-precipitation grid points.

To further investigate and better characterize the performances of the downscaling methods, we compare the skills of the standard and of the modified RainFARM in different seasons. Figure 4d–g report the results for low-precipitation stations. The overestimation of the observed PDF from E-OBS at its original resolution (0.25^∘) at low-precipitation stations (see Fig. 4b) occurs mainly in winter and, to a lesser extent, in spring and autumn. When considering the downscaled E-OBS precipitation, a clear difference emerges between the standard and the modified RainFARM methods. The standard RainFARM reproduces and amplifies the E-OBS overestimation, showing large discrepancies with respect to the observed PDF, especially for precipitation above 50 mm day⁻¹ (winter and spring). The modified RainFARM, instead, reduces the original E-OBS overestimation, leading to a closer agreement with observations. In spring and autumn, in particular, the observed PDFs are reproduced very well. In summer, E-OBS at its original resolution is able to correctly reproduce the observed PDF up to about 70 mm day⁻¹. In this case, a clear improvement of the modified RainFARM with respect to the standard RainFARM is registered only for precipitation events above 50 mm day⁻¹. Below this threshold the modified RainFARM still gives PDF ratios close to 1.

For high-precipitation stations (not shown), the performances of the standard and the modified RainFARM methods are similar to each other and they show little variability across different seasons. In fact, for all seasons, the performances of both downscaling methods reflect the behavior found at an annual timescale (Fig. 4c).

4.3 Sensitivity of the method to the reference precipitation climatology

The results described in the previous section have been obtained employing a high-quality reference precipitation climatology for the calculation of the corrective weights. The availability of such a high-quality dataset is quite rare in mountain regions, allowed here by the fact that the Alps are among the most instrumented mountain regions of the world. Such high-quality data could be unavailable for other regions in the world. For this reason we explore the sensitivity of the modified RainFARM algorithm to the accuracy of the reference precipitation climatology and we show possible alternatives if a high-quality gridded precipitation climatology is not available. In these cases, one possibility is to use, for example, a high-resolution global precipitation gridded climatology such as WorldClim, already described in Sect. 2.3, which nominally provides monthly climatologies at 1 km resolution, based on more than 47 000 stations distributed around the globe. Clearly, the distribution of the stations is uneven and reflects the level of economic development and the population density of a country, as well as the national data access policies, so the uncertainty in areas with low station density can be remarkable (Hijmans et al., 2005). Even in a station-dense area such as the Swiss Alps the station database used for WorldClim v1.4 counts only 22 stations (Hijmans et al., 2010), so it is sparser than that used to compile the regional-scale MeteoSwiss RnormM climatology (Begert et al., 2013), and consequently likely characterized by lower accuracy. Apart from WorldClim, a second possible option in absence of a trusted, high-resolution gridded precipitation climatology over the domain of interest could be to use a reference climatology derived from very high-resolution regional climate model simulations. To address this possibility in the following test, we use the WRF climatology at 4 km resolution already exploited in the perfect case experiment, this time applied only to derive the weights for the correction in Eq. (5).

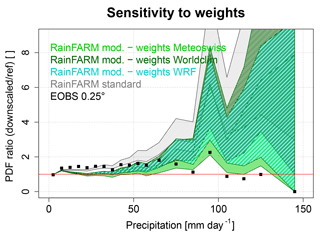
Figure 5 Sensitivity of the modified RainFARM downscaling method to different weights, derived from MeteoSwiss (light green), WorldClim (dark green), and WRF (cyan) climatologies for low-precipitation grid points. The performances of the standard RainFARM method (gray) are shown for comparison. The bands show the range of variability in the PDF ratios between each of the 80 downscaling realizations and the PDF of observations, while black squares represent the ratio between the PDF of E-OBS at its original spatial resolution and the PDF of observations.

Figure 5 compares the results of the downscaling performed using weights derived from three different climatologies, i.e., MeteoSwiss, WorldClim, and WRF 4 km resolution climate simulations. For each of the three experiments we use ensembles of 80 realizations. Keeping in mind the issues of E-OBS (see Sect. 4.2) regarding its limited capability of describing the observed precipitation range for high-precipitation grid points and the consequent difficulties in disentangling the limitations of E-OBS from the limitations of the downscaling method, here we focus the analysis on the low-precipitation grid points that are not affected by these problems. While, not surprisingly, the MeteoSwiss climatology provides the best results, the WorldClim and the WRF climatologies also improve the agreement with the observed PDF, leading to significantly better results than using the original RainFARM method. Up to about 60 mm day⁻¹ all three methods provide PDFs that stay very close to the observed PDF, while at higher values the ensembles of PDFs of the downscaled fields tend to overestimate the verification PDF. It is important to notice that at very high precipitation levels (around 150 mm day⁻¹) all the three ensembles obtained with the different climatologies tend to again contain the verification PDF.

Both the WRF and the WorldClim climatologies tend to slightly overestimate the observed PDF compared to the use of the MeteoSwiss climatology, particularly at higher precipitation levels, with the WRF climatology performing slightly better than the WorldClim climatology. The limitations of the WRF climatology might be due to well-known difficulties of regional models in accurately reproducing precipitation over topography, with significant biases, also dependent on the specific parameterizations used, as also discussed in Pieri et al. (2015). The performance of the WorldClim climatology is probably affected by its sparser station density compared to the MeteoSwiss dataset.

5 Discussion

A simple modification to take into account precipitation variability at scales of the order of 1 km into stochastic precipitation downscaling methods has been proposed, applied to RainFARM, and tested in the Swiss Alps in two different cases. First, in the perfect-model framework, high-resolution WRF simulations (0.037^∘, ∼4 km) have been upscaled to 64 km resolution in such a way that the amount of precipitation in a grid point at the coarse scale is, on average, the same as the precipitation fallen in the corresponding 16×16 grid points in the original fine-scale field. The downscaling procedure applied to this coarse-scale dataset shows a very good agreement with the true precipitation data in terms of their amplitude distribution. When separately analyzing grid points with low- and high-precipitation climatology (low and high with respect to the median of the fine-scale daily average precipitation climatology in each coarse-scale grid point), the added value of the new RainFARM version over the standard RainFARM is evident. The new version allows reproduction of the distribution of precipitation in low- and high-precipitation grid points with very high accuracy, remarkably better than the standard RainFARM.

Second, we have considered a more realistic application in which E-OBS gridded precipitation data are downscaled over Switzerland at about 1 km spatial resolution and then compared to in situ observations from the MeteoSwiss network. In this case a preliminary evaluation of the E-OBS dataset has revealed important discrepancies compared to the observations, especially in high-precipitation grid points. In fact, in high-precipitation grid points the frequency of precipitation events is increasingly underestimated from a few millimeters per day up to 100 mm day⁻¹, and events with precipitation above about 140 mm day⁻¹ are simply not represented. In this context, both downscaling methods remarkably improve the agreement with the observations, also reproducing extreme precipitation values, so that downscaled precipitation values cover the full observed precipitation range. Although the downscaling does not fully compensate for the original E-OBS underestimation in high-precipitation grid points, both the standard and the modified RainFARM remarkably improve the agreement with the observations. In particular, in low-precipitation grid points, only the modified downscaling method allows the reconstruction of the observed PDF. The modified RainFARM outperforms the standard RainFARM method by leading to a better agreement of the amplitude distributions compared to observations.

The two experiments discussed in this paper, in a perfect-model and a realistic case framework provide complementary information regarding the skills of the presented downscaling method, and they clearly show what we can expect (or not) when it is used in practical applications. In the perfect-model experiment there is exact conservation of the water flux between the coarse-scale dataset to downscale and the validation dataset, as the former has been derived by aggregation of the latter. This implies that the error associated with the validation dataset is zero and the degree of agreement between the downscaled and the validation data is an exact measure of the skills of the downscaling method. This experiment shows the very good performance of the modified RainFARM in adjusting the PDF of the downscaled data in such a way that they are not distinguishable from the reference PDF. Conversely, in the real-case experiment, the flux conservation between the coarse-scale and validation datasets is not to be expected owing to their very different nature and characteristics. In fact, E-OBS (version 17) is a 25 km resolution dataset generated by interpolating measurements from a subset of all the Swiss surface stations, precisely 36 stations active in the considered period 1981–2010, with elevation ranging between 200 and 2500 m a.s.l. (source E-OBS documentation, http://www.ecad.eu/, last access: 28 August 2018). On the contrary, the validation dataset consists of 59 stations representative of elevations up to 3302 m a.s.l., 50 % of these stations lying above 600 m, with 25 % in the range of 600–1600 m, 10 % in the range of 1600–2000 m, 10 % in the range of 2000–2500 m, and 5 % above 2500 m. Clearly, the reduced number of underlying stations in E-OBS, together with the stations biased toward low elevations, contribute to uncertainties and discrepancies with respect to the station data, especially in areas prone to high precipitation (Fig. 4c).

Among the other sources of errors affecting the downscaled fields in the real-case experiments, the fine-scale climatology used to derive the correction factors (weights) has to be considered. In our case the MeteoSwiss RnormM climatology is probably affected by sources of uncertainty similar to the E-OBS dataset, but to a smaller extent owing to the higher density of stations included and their better altitude representativeness. In detail, RnormM is also derived by interpolation of data from surface stations whose average distance is 15–20 km. The interpolation tends to smooth out peaks and troughs in a surface, so we can expect that the interpolation product provides lower precipitation extremes than the original point measurements. As a consequence, the resulting RnormM climatology, as well as the maps of weights, are smoothed out with respect to the single surface station climatology, with evident impacts on the agreement between the downscaled fields and the validation (surface station) reference.

Despite the fact that experiments in real cases are generally characterized by errors and/or biases in the coarse-scale datasets to downscale, in the climatology used to derive the weights, and in the validation datasets, we show that the RainFARM downscaling method is still effective in improving the agreement between the amplitude distributions of the observed precipitation and of the downscaled fields.

The modified RainFARM algorithm has been shown to also provide robust results in absence of an accurate regional fine-scale precipitation climatology tailored to the area of study. In fact, a fine-scale global monthly precipitation product such as WorldClim (at nominally 1 km spatial resolution, but obtained from a limited number of measurement stations) provides sufficient information for the weight calculation so that the outputs of the downscaling are close to those derived in the optimal case using the regional and more accurate MeteoSwiss climatology. Alternatively, we have also shown that using a climatology from a high-resolution regional climate model simulation to derive weights also provides good results. This suggests that the modified RainFARM method could also be applied in regions of the globe where only limited climatological information is available, such as that provided by the WorldClim dataset or by a regional climate model simulation. Since RainFARM does not require providing or tuning additional parameters it could then be applied directly to the coarse-scale dataset to be downscaled.

In the simple method that we presented, downscaled precipitation data in each grid point and for each month have been corrected by a constant factor each time precipitation occurs. This is of course an approximation that only modifies the amplitude of precipitation events at that point and not their frequency. The same climatological average precipitation at a point could be obtained modifying either the event frequencies or their intensities. Nonetheless, we have seen that the RainFARM method allows reconstruction of plausible fine-scale precipitation values with a frequency of occurrence in agreement with observations, when statistics over 30 years are considered. This makes the new RainFARM approach suitable for downscaling climate model data when we need to describe the statistics of precipitation over long (climatic) timescales, and we are not interested in temporal correlations with the observed fields at finer temporal scales. Further work should be carried out to assess if the new RainFARM algorithm provides added value when the temporal correlation between the downscaled data and the observations is of importance.

The proposed method has been developed and tested in a mountain environment but it could also be used, in principle, in other areas of the globe. In such an extended framework, the more general added value brought by the new RainFARM algorithm is the reproduction of an observed precipitation pattern, no matter if it originates from topography or other surface heterogeneities. When the reference fine-scale precipitation climatology is almost constant over a portion of the domain, or zero as for example in very arid or desert areas in dry months, the resulting weights are all 1 and the modified RainFARM method provides results identical to those of the standard RainFARM method.

6 Conclusions

Stochastic precipitation downscaling methods generally do not take into account local precipitation patterns at spatial scales below those explicitly resolved in the coarse-scale dataset. We propose a simple technique that can be applied to stochastic precipitation downscaling methods to improve the representation of the fine-scale daily precipitation in complex and spatially heterogeneous regions, such as mountain areas. The application of this method requires exclusively fine-scale information on the precipitation climatology from an external reference dataset.

This technique, here applied to the RainFARM stochastic downscaling algorithm, adjusts the fine-scale daily precipitation values calculated by the standard RainFARM method by using monthly sub-grid weights derived by a reference monthly fine-scale climatology before imposing the conservation of the average water flux at the coarse grid scale between the coarse-scale dataset and the downscaled dataset. In our perfect-model experiment, compared to the standard RainFARM, the modified RainFARM allowed reduction of the root-mean-square error on the long-term precipitation climatology from 0.86 to 0.27 mm day⁻¹, thus introducing clear improvements in the downscaling performance. The modified RainFARM has been shown to assign precipitation values to the small-scale grid in such a way that when grid points with low or high average climatological precipitation are considered separately, the distributions (PDFs) of the downscaled precipitation are closer to the PDFs of the corresponding reference dataset. Given its ability to reconstruct the overall precipitation distribution, the modified RainFARM downscaling method can be employed in a number of applications, including the analysis of extreme events and their statistics and of hydrometeorological hazards.

Like the standard RainFARM, the new RainFARM downscaling method is not intended to correct the biases affecting the coarse-scale dataset. Prior to applying the downscaling, it is recommended to evaluate the degree of agreement between the coarse-scale and possible verification datasets. If the coarse-scale dataset presents clear deficiencies or its long-term climatology is substantially different from the observed climatology, bias adjustment of the coarse-scale dataset could be applied before downscaling.

The proposed method can be useful in particular for downscaling climate model data and for any application for which a correlation over fine temporal scales between the downscaled and the observed data is not required. Further work should aim to investigate if this method employing fixed correction factors also improves the downscaling performance when the spatial structures of precipitation have to be reproduced at fine (daily or sub-daily) temporal scales such as applications of downscaling at weather timescales.

In absence of a high-quality fine-scale observed precipitation climatology at regional scales, global datasets, such as WorldClim or a high-resolution regional climate simulation, could also be successfully employed and they provided good performance in our study area.

In conclusion, in spite of its simplicity, the proposed method is found to introduce realistic small-scale variability in the downscaled precipitation fields using only a fine-scale monthly precipitation climatology, and it could be applied in different regions of the world, not only mountain areas, to provide a more realistic representation of the distribution and the climatology of precipitation.