the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Formation, breaching and flood consequences of a landslide dam near Bujumbura, Burundi
Léonidas Nibigira
Hans-Balder Havenith
Pierre Archambeau
Benjamin Dewals
This paper investigates the possible formation of a landslide dam on the Kanyosha River near Bujumbura, the capital of Burundi, as well as the interplay between the breaching of this landslide dam and the flooding along the river. We present an end-to-end analysis, ranging from the origin of the landslide up to the computation of flood waves induced by the dam breaching. The study includes three main steps. First, the mass movement site was investigated with various geophysical methods that allowed us to build a general 3-D model and detailed 2-D sections of the landslide. Second, this model was used for dynamic landslide process modelling with the Universal Distinct Element Code. The results showed that a 15 m high landslide dam may form on the river. Finally, a 2-D hydraulic model was set up to find out the consequences of the breaching of the landslide dam on flooding along the river, especially in an urban area located downstream. Based on 2-D maps of maximum water depth, flow velocity and wave propagation time, the results highlight that neglecting the influence of such landslide dams leads to substantial underestimation of flood intensity in the downstream area.
- Article
(10190 KB) - Full-text XML
-
Supplement
(1121 KB) - BibTeX
- EndNote
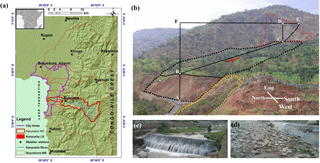
Figure 1(a) Bujumbura region with indication of watersheds of the main rivers, the limits of the city and Lake Tanganyika. The watershed of the Kanyosha River is highlighted in the central part, with the river network inside. The weather stations in and around Bujumbura, the Kanyosha landslide (in the text called “Banana Tree Landslide”, also referred to as BTL, in red contours) and the Congo–Nile crest are also shown. “LS” and “WS” stand for “landslide” and “watershed”, respectively. (b) View of BTL (black dotted contour) and the main scarp (red dotted contour) as well as its lateral local instabilities (orange and light blue dotted contours). The landslide sliding direction and the river flow direction are indicated by the red and the black arrows, respectively. AB indicates the height (26 m) of the landslide frontal part near the river; BC outlines the BTL length in the sliding direction (∼ 750 m); CD shows the height of the main scarp (∼ 75 m) along profile points B–C–E. The blue line indicates the river channel axis. (c) Waterfall over a former flood control structure (located 270 m downstream of cross section 3 shown in Fig. 3). (d) View of the riverbed during the dry season with presence of cobbles and fine boulders that are deposited after floods during the wet season.
The city of Bujumbura, the capital of Burundi, faces serious problems related to natural hazards. Floods are the most important natural challenge in terms of induced losses. This is aggravated by heavy tropical rains. It also becomes clear that geohazards strongly contribute to the risk of flooding. In February 2014, floods resulting from a failure of a temporarily created landslide dam caused 64 casualties. Over 940 houses were destroyed and this resulted in over 12 500 homeless people (UNITAR/UNOSAT, 2014; Reliefweb, 2014). This indicates that a complete assessment of flood risk should take into account landslides which may be considered as some of the most important natural hazards in the region. They interact with the hydrographic network by forming natural dams. The formation of landslide dams is caused by the combination of several factors. Many spectacular cases were reported in which earthquakes were a major trigger (Adams, 1981; Cui et al., 2012). For example, the Wenchuan earthquake in 2008 caused up to 828 landslide dams (Fan et al., 2012, 2017). In addition to earthquakes, long and heavy rainfall (Li et al., 2011) as well as other local parameters can lead to slope instability and to landslide dam formation. Losses related to natural dams can occur both during and after the formation of the dam. Losses that occurred during the formation are exemplified by the case of the village of Xiaolin that had been entirely buried in 2011 under a massive debris flow and landslide in southern Taiwan (Li et al., 2011), or by the sweeping of the Attabad and Sarat villages in northern Pakistan in 2010 (Butt et al., 2013). In many other cases, losses are mainly linked to the dam failure and associated downstream floods. Related studies (Cui et al., 2006; Wells et al., 2007; Downs et al., 2009; Wang et al., 2016; Costa and Schuster, 1988; Li et al., 2002; Chen et al., 2004) show that the effects of dam failure can be many times greater than those caused by the sliding during the formation of the dam. Although different methods have been proposed and applied to understand their formation and/or breaching mechanisms (Korup, 2004; Corominas and Moya, 2008; Crosta and Clague, 2009; Dong et al., 2009; Nandi and Shakoor, 2009; Shrestha and Nakagawa, 2016), each of the natural dam cases has its own specificities related to the local context. Therefore, case studies are very important. Unfortunately, there is a lack of both case studies and data required for the analyses, especially in Africa. Consequently, statistical studies based on past events are missing, and that is a challenge when the risk of dam formation or the breaching of an existing dam has to be assessed. This underlines the importance of scenario simulations supported by the use of modern modelling tools. In central Africa (including Burundi), despite existing studies in the field of environmental hazard analysis (Ilunga, 2006; Moeyersons et al., 2010; Nibigira et al., 2015; Michellier et al., 2016; Jacobs et al., 2016), quantified landslide multi-hazard scenario analyses are still rare. This lack of multi-hazard studies in equatorial Africa was highlighted recently by Jacobs et al. (2016). For the city of Bujumbura, there is a need to develop a multi-risk study, on one hand, analysing the hazard related to landslide activation and natural dam formation, and, on the other hand, assessing the potential impacts of the dam failure on the hydrographic network.

Figure 2Field observations highlighting the critical stability state of BTL. (a) Pond on the landslide with an oil palm designated by the white arrow. This shows that these ponds are recent (oil palm trees do not grow in water; its particular foliage compared to others shows that its growth was stopped recently). (b) View of the rock structures at the foot of the landslide, generally dipping towards the north (left side), parallel to the sliding direction (red arrow). The blue arrow indicates the river flow direction. (c) View of a crack on the sliding interface in a clay layer. The red arrow shows the direction of sliding of the right part along the clay layer. (d) A crack found on the landslide surface.
We performed such a study to the existing mass movement called “Banana Tree Landslide” (called BTL below). This landslide was selected for its size (it is one of the largest active landslides in the vicinity of Bujumbura with a volume of more than 4 × 106 m3) and its position along the Kanyosha River, upstream of the city (Fig. 1a and b) making it a potential danger for people and infrastructures in the area.
Since the gorge of the valley is relatively narrow in the landslide area, a displacement of the BTL of a few tens of metres would be enough to form a natural dam and a reservoir lake, which could later break with all the risks that such an event represents for the part of the city located downstream. The lifespan of natural dams cannot be known accurately and can be relatively short: it is less than 1 h for 34 % of the known cases investigated by Peng and Zang (2012) and 27 % of all cases according to Costa and Schuster (1988). Moreover, considering the tropical climate context of the target area, it can be assumed that the reservoir behind a new dam can be quickly filled after very intense rainfall that occurs on a regular basis during the wet season. All those parameters reduce considerably the time between the dam formation and the possible dam breaching, highlighting the necessity to know in advance the consequences corresponding to different scenarios, particularly for such areas where warning systems are not very effective or just missing.
Our recent observations show that the western part of the landslide (in the foreground of Fig. 1b), with relatively soft slopes, is marked by very local slope instabilities (yellow and light blue dotted contours) that do not contribute to the general movement. However, the eastern part (black dot outlines in Fig. 1b) presents steep slopes near the river; this active zone is 250 m wide and could soon move to form a landslide dam. The presence of water ponds in this eastern part (Fig. 2a) is likely to contribute to future instability that could develop along the main sliding BC axis (shown in Fig. 1b).
In order to understand the landslide mechanisms in terms of triggering factors, evolution and effects, numerical modelling has been carried out to analyse its stability, also under dynamic (seismic) conditions. The effects of the dam and its breaching on the flood potential along the river and the consequences especially downstream in the urban area were studied through an additional hydraulic model. Simulated flood scenarios are discussed with respect to parameters such as the water depth, the flow velocity and the floodplain delineation.
2.1 Channel description
The Kanyosha River is one of the most important rivers in Bujumbura. Most of its watershed is located in the Congo–Nile crest, on the east side of the city. The upstream parts consist of a V-shaped valley, while the north and south flanks are made up of wooded areas and steep agricultural areas subject to the erosive action of the runoff descending the shoulders of the rift. The grain size of the riverbed deposits is variable. Based on the extended Udden–Wentworth grain-size scale nomenclature (Terry and Goff, 2014), the riverbed material can be classified into three main groups.
-
The first consists of cobbles of around 10 cm in diameter or more (Fig. 1d). The coarse part of this category consists of fine boulders, with a diameter generally under 40 cm.
-
The second group is made up of isolated medium boulders that are often prone to the action of humans, carving them into building materials (mainly paving plates). This category is difficult to take into account due to its strong irregularity.
-
The third group consists of silt and clay zones, generally near former hydraulic structures in the downstream part of the river. In this category, we can mention small herbaceous islets, often located near the river overbanks. As in the second group, this category is found only in small isolated and scattered areas, subject to strong seasonal variations.
Details on the Udden–Wentworth grain-size scale nomenclature are provided in the Supplement (Table S1). Globally, the first group is hydraulically predominant. Here, the variability of the grain size was accounted for by means of sensitivity analysis (Sect. 3.3). In 2006, hydraulic structures were constructed to regulate the river, but they were quickly damaged by floods during the following rainy seasons. Nonetheless, isolated coarse materials resulting from the destruction of these structures are observed. They join the second group described above. The accumulation of material upstream of the remains of the structures often forms horizontal platforms, generating small waterfalls (Fig. 1c).
2.2 Topographic and geophysical data
We used a 10 m resolution digital elevation model (DEM) of the river valley, provided in the coordinate system UTM35S and in raster format (Fig. 3). It was produced in 2012 by the Bureau de Centralisation Geomatique du Burundi. The DEM was resampled at a resolution of 2 m × 2 m, which is the resolution used for hydraulic modelling. For the second part of the analysis, the geometry of the dam was incorporated, taking into account the results provided by the first part related to the landslide process analysis.
Given that no data were available for defining the river bathymetry and the overbank topography, the flow was computed based on the DEM. The average width of the river is about 20 m for a discharge of 3 m3 s−1, 32 m for 60 m3 s−1 (20-year flood) and 40 m for 120 m3 s−1 (50-year flood). Hence, a computational spacing of 2 m (obtained after resampling) is certainly fine enough to represent the flow field over the width of the river, since the number of computational cells over the width of the river is between 10 and 20.
While resampling the DEM is important for computational reasons, only the topographic details already present in the initial DEM (10 m × 10 m) are captured. Ideally, the hydraulic analysis should use a higher-resolution DEM such as light detection and ranging (lidar) elevation data. However, in the data-scarce environment of the study area which is commonplace in many parts of Africa, a 10 m resolution is among the best in the region, especially when compared to Shuttle Radar Topography Mission (SRTM) and Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) Global Digital Elevation Model (GDEM) provided by the US Geological Survey (USGS). The example of some recent work (Jacobs et al., 2016; Alvarez et al., 2017) showed that using medium- or low-resolution products remains a valuable intermediate step to advance the understanding of flood risk in data-scarce areas in Africa, provided that the results are interpreted in light of the uncertainties affecting the input data.
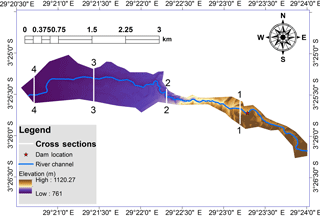
Figure 3Digital elevation model (m) used for hydraulic modelling within the computational domain, with cross sections where hydrographs were extracted and dam location. The river main channel is also highlighted.
Moreover, to assess the DEM used for hydraulic modelling, we also considered a field survey that was conducted in the study area during the dry seasons (June–September) in 2014 and in 2015. The field measurements covered the main riverbed and part of the floodplains (band of 10–20 m) of the Kanyosha River, from 500 m upstream of the dam down to Lake Tanganyika. As shown in Fig. 4, the differences between the DEM used in our hydraulic simulations and data from the field survey remain moderate, as they range mostly between −0.5 and +0.5 m. The median and mean differences are both −7 cm. The rms error between the 10 m × 10 m DEM and field measurements is 65 cm, which seems reasonable. Most significant differences are obtained near the riverbanks. This may result from discretization errors and/or from the instability of the banks due to planform evolution of the riverbed over the period from 2012 (when the 10 m × 10 m DEM was produced) to 2014 (field survey in the main riverbed).
In the upper part of the valley, showing a distinctive V-shape with relatively steep lateral slopes, the flow tends to concentrate in the central main channel and its vicinity. Therefore, the hydraulic modelling results should be less affected by small inaccuracies in the DEM than further downstream. A sensitivity analysis of the simulation results with respect to the inaccuracy in the topographic data is presented in Sect. 4.3.2.
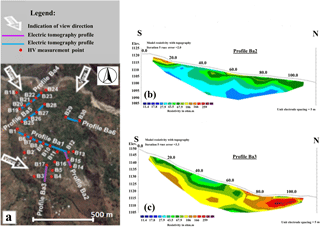
For the landslide stability analysis, the surface data provided by the DEM were combined with subsurface information obtained by local geophysical field measurements completed in summer 2013. They consist in electrical resistivity tomography (ERT) and ambient noise horizontal (H) and vertical (V) components (HV) measurements. Figure 5 provides an overview of the measurements and two examples of ERT profiles. From these investigations, the thickness of the landslide mass and some of its geophysical properties (notably, the elastic properties) could be determined.
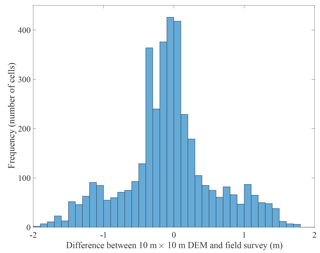
Figure 4Elevation difference between the topography from field measurement and the resampled 2 m × 2 m DEM used for hydraulic modelling.
2.3 Landslide analysis with Universal Distinct Element Code (UDEC): model construction
From the field measurements, a model of the landslide was established. Figure 6 corresponds to a 2-D section along the main axis of the mass movement and shows the present (actual) topography of the landslide (plain line) and the reconstructed (estimated) initial topography (before first instabilities appeared, marked by a dashed line) as well as the main sliding surface (dotted line). The initial situation is characterized by an average slope of about 15∘, while the current profile (plain line) is marked by a clear scarp in the upper part, below which the landslide material has a thickness of about 15 m and by more massive landslide deposits (thickness of about 50 m) in the middle and the lower part towards the river.
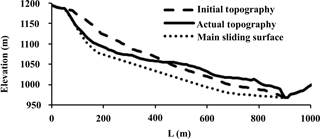
Figure 6Initial and present BTL profiles. The larger thickness of the present profile in the downstream part of the model is a result of the relative lift-up after a trans-rotational sliding and material accumulation from the upper parts of the initial profile.
On the basis of this cross section of the landslide a slope stability analysis (both a back analysis starting from the reconstructed pre-landslide model and a “predictive” analysis starting from the present-day situation) as well as mass movement modelling were carried out in 2-D using the Universal Distinct Element Code (UDEC). UDEC was developed by Cundall (1971) to evaluate the response of materials (discretized as blocks) to a given loading in static and dynamic (e.g. seismic) conditions. The distinct element method has been used in various studies and it is particularly suitable for rock slope stability analyses (Kveldsvik et al., 2009; Kainthola et al., 2012; Bhasin and Kaynia, 2004; Esaki et al., 1999; Chuhan et al., 1997).
For the modelling with UDEC, the landslide was subdivided into three main blocks (see numerical measurement points 12, 13 and 15 in Fig. 7, which are located on the upper, middle and lower blocks, respectively). Cracks (joints) included between the blocks (that represent also main geomorphic and geophysical units observed in the field) allow for the simulation of a more flexible movement of the mass. The same material (material 1 in Table 1) was attributed to all landslide blocks. It corresponds to the average type of the material found within the landslide. The original material of BTL is a gneiss which, by weathering, is partially transformed into a clay on the surface. The depth of the weathered layer is about 20 m. The study area experiences alternations between dry and rainy seasons. The long dry season (from June to September) is followed by the small rainy season (from October to December), then by the small dry season (during the months of January and February). The cycle ends with the strong rainy season from March to May, just before the return of the dry season. Since the photos in Fig. 2 were taken in October, the ground was relatively wet but not as wet as is usually the case in December and during the strong rainy season. Especially for the lower parts of the landslide, the humidity is never very low due to the recharge of the water table by the ponds of water located on the landslide. On the other hand, the groundwater recharge follows the dynamics of the seasons. In the context mentioned above, the action of the rainy season in the body of the landslide is quickly remarkable, due to the higher amounts of infiltrating water. Material 2 was attributed to the stable bedrock (Table 1 and Fig. 7).
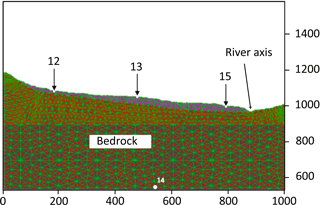
Figure 7Materialization of blocks, joints and materials for the actual model. History (measurement) points 12, 13 and 15 (white dots) located, respectively, on the upper, middle and lower blocks correspond to the surface area where parameters were monitored (e.g. the x acceleration). Point 14 is located at the base of the model, within the bedrock. The axis of the Kanyosha River is located to the right of history point 15.
The block materials were considered as purely elastic; therefore, the plastic deformation was only computed along joints. For the block materials, the following properties were defined: dry density (ρ), Young's modulus (E), bulk modulus (K) and shear modulus (G), Poisson's ratio (ν) (elastic properties determined on the basis of the estimated and locally measured P-wave velocity Vp and S-wave velocity Vs). To allow for plastic deformation along the joints, it is necessary to define the cohesion and the friction angle for the joint/contact material between the blocks. The contact properties are summarized in Table 2. Plastic contact materials were used along the sliding surface and between the blocks (joint material 1); for other (auxiliary) contacts, joint material 2 was used, which only allows for elastic deformation.
Table 2Contact properties: applied values for normal stiffness (jkn), tangential stiffness (jks), range of used cohesion values (jcoh), range of used friction angle values (jfric) and permeability (jperm).

Scenarios were prepared based on the knowledge of the landslide-triggering and evolution factors. Those scenarios were preceded by a back analysis as the pre-slide topography was used as starting point. Calculations first targeted the reproduction of the present situation of the mass movement before simulating future possible evolution of the landslide, including the formation of a dam. Variable factors are related to slope geometry, slope material strength, hydrogeological conditions, structural discontinuity, weathering, development of weak zones, lithology and earthquakes (those variables were selected according to those used by published works, such as by Bhasin and Kaynia, 2004; Umrao et al., 2011; Singh et al., 2013; Kainthola et al., 2012; Sharma et al., 2017). As a major triggering factor, the variable groundwater level was modelled. Further, to test the possible seismic influence on initial slope stability and the possible future evolution of the landslide, a synthetic earthquake signal was used as input for some models.
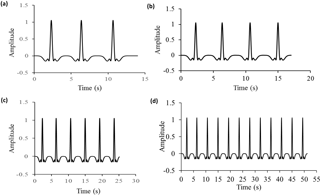
Actually, a partial contribution of earthquake shaking to the destabilization of the slope is highly probable as the site is located in a seismically active area (see last seismic hazard maps of the western branch of the East African Rift by Delvaux et al., 2016). Data availability helps to refer to an existing database and case studies within the study area. Unfortunately, in the context of data scarcity in the region (for instance, there are no strong motion records available for the target area), it is not easy to fix suitable unique values for predictions. This was handled by the use of four shaking duration values to well illustrate the behaviour of the model corresponding to different scenarios. The seismic context was analysed on the basis of earthquake data from the Global Seismographic Network stations of the Incorporated Research Institutions for Seismology (IRIS) on the Lake Tanganyika region. Therefore, based on that situation, we applied a Ricker wavelet with maximum amplitude of 0.105 g (about 1.05 m s−2) and central frequencies of 0.5 and 1.4 Hz. The loading was varied in terms of changing shaking duration. Four different values were considered: 14, 17, 25 and 51 s. Figure 8 provides the corresponding signals.
The effects of groundwater level were studied considering five different cases: no groundwater (dry scenario), saturation of the whole profile (GWT4), groundwater level at a depth of 15 m in the upper block and the saturation of the middle and lower blocks (GWT5), and finally the groundwater at a regular depth of 7 m below the surface (GWT6). Results discussed in this paper are derived from a set of 52 scenarios given in Fig. S1 in the Supplement.
2.4 Hydraulic modelling
For the hydraulic analysis, we used the academic model WOLF 2-D, which solves the shallow-water equations by means of a stable and conservative finite volume scheme. This model has been extensively validated and applied for simulating flow induced by dam and dike breaching (Dewals et al., 2011; Roger et al., 2009) as well as for conducting flood risk analysis (Arrault et al., 2016; Beckers et al., 2013; Bruwier et al., 2015; Detrembleur et al., 2015; Ernst et al., 2010).
We only included water in the flood wave computation, while the actual breaching of the landslide dam would release a substantial amount of solid material. The real flow would have an intermediate behaviour between clear-water flow and debris or granular flow. As shown in Table S2, some recent studies neglected sediment transport in the analysis of floods induced by the breaching of landslide dams (Fan et al., 2012; Yang et al., 2013), while others did take sediment transport into account (Li et al., 2011; Shrestha and Nakagawa, 2016) since it may have considerable implications on the volume of mobilized material as well as on morphological evolution of the valley bottom (e.g. sediment deposition). Nonetheless, we believe that, in the context of the present study, going for more complexity in the modelling framework (i.e. including sediment transport) would mainly produce more speculative results because validation data are neither available for our case study nor for any similar one in the region, which remains largely understudied. Table S2 shows that previous studies which considered sediment transport benefited all from available validation data, such as observed flood discharges or depths of sediment deposits. The implications of this assumption are further discussed in Sect. 4.3.3.
We detail below how friction was parameterized in the hydraulic model, as well as the prescribed boundary conditions and the modelling procedure, including the parameterized breaching mechanism included in the flow simulations.
2.4.1 Parameterization of friction
In the hydraulic model, flow resistance was parameterized using the formulation developed by Machiels et al. (2011). Compared to more standard friction formulae (e.g. Manning, Chezy), it offers two main advantages: (i) being truly physically based, it reduces substantially the need for recalibrating the model when the range of flow rate is varied; (ii) the only parameter to be set is the characteristic size of bottom irregularities, which can be estimated from field observations. This parameterization is hence particularly suitable for applications for which only scarce flow monitoring data are available, such as in the present case.
Here, we tested three values for the roughness height: 0.1, 0.2 and 0.3 m, corresponding to the prevalent class of grain size in the riverbed material (as described in Sect. 2.1). In the following, to show the effects of the roughness of the riverbed, we present the results for the two extreme values of the roughness height (ks= 0.1 m and ks=0.3 m).
2.4.2 Hydraulic boundary conditions and computed scenarios
The upstream boundary condition is a prescribed flow hydrograph, representing either a flood wave coming from the upstream catchment or a steady inflow. As detailed in Sects. 2.4.3 and S1 in the Supplement, we used only steady inflows, corresponding, respectively, to a base flow (3 m3 s−1), a 20-year flood (peak discharge of 60 m3 s−1) and a 50-year flood (peak discharge of 120 m3 s−1).
At the downstream end of the computational domain, the river mouth in Lake Tanganyika was not included explicitly because only limited information was available on bathymetric and hydraulic data at this location. Consequently, the hydraulic behaviour of the river mouth is lumped into the boundary condition prescribed at the downstream end of the computational domain.
The proposed boundary condition is based on a Weir equation, relating the outflow discharge Qo to the averaged water level ho close to the simulation downstream boundary:
with g being the gravity acceleration (m s−2), CD a non-dimensional discharge coefficient (taken equal to 0.75), L an equivalent crest length (m) and w an equivalent crest height (m). Equation (1) enables simulating different configurations (e.g. loosely vs. strongly varying downstream water level when the flow rate changes), and we performed a sensitivity analysis by varying L and w. For very high values of L, ho remains virtually constant whatever Qo; otherwise, it varies with Qo. However, as shown in Sect. S2 and S3, this boundary condition has actually an influence only over a very limited distance upstream of the domain boundary: in all the conducted tests, this influence zone did not extend over more than 300 m. This very limited influence results from the relatively steep slope of the river (around 1.5 % in the downstream area; 6 % in the upstream reach). Consequently, the particular formulation of the downstream boundary condition (Eq. 1) can be safely disregarded when analysing the modelling results over virtually the whole computational domain (except the most downstream 300 m) since they remain independent of L and w.
2.4.3 Modelling procedure
The hydraulic simulations aim at evaluating the impact of the dam failure as a result of the water impoundment behind it and the river overflowing the dam crest. Thus, the initial step of hydraulic modelling considers a filled reservoir and a steady flow of water over the crest of the dam before failure. In line with Dewals et al. (2011), the modelling procedure involves two steps (Table 3):
-
Step 1: a pre-failure steady flow is computed in the river, under three different hydrological scenarios (steady flow corresponding to the mean discharge in the river or to a 20-year flood, or a 50-year flood).
-
Step 2: using the result of Step 1 as the initial condition, the flow induced by the breaching of the dam is computed.
In Step 1, the dam geometry is incorporated in the topographic data used for flow computation. This means that the dynamics of material sliding into the river is not explicitly reproduced in the hydraulic modelling. As it is not possible to anticipate when the landslide dam breaching might occur, we consider three different pre-failure flow conditions: base flow, 20-year flood and 50-year flood. In Step 2, using a parametric description of the breaching, the dam is gradually removed from the topography, so that the water impounded behind the dam is released. The model computes the unsteady propagation of the induced flood wave in the downstream valley.
Examples of results of Step 1 and Step 2 are displayed, respectively, in Figs. S2 and S3–S6 in Sect. S3.
2.4.4 Modelling of the breaching mechanism
The mechanisms of breaching of natural dams are complex, highly variable and incompletely understood. Hence, the modelling of the dam breaching may be a substantial source of uncertainty. In the present study, process-oriented modelling of the breaching was not considered as a viable option, mainly due to the lack of detailed information on the dam material (graded, non-homogeneous material), the complexity of the breaching of natural dams and the absence of validation data from similar case studies in the region. Instead, we opted for a simpler parametric description of the dam breaching which appears more consistent with the quality of available data and the overall level of uncertainty affecting the present study.
Among the various possible failure modes, we chose to represent dam “overtopping”, which is the most frequent failure mode for landslide dams. Failure induced by dam overtopping was reported for over 90 % of all landslide dams reviewed by Costa and Schuster (1988) and for 131 out of 144 cases reviewed by Peng and Zhang (2012).
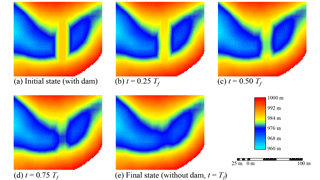
As sketched in Fig. 9, the parametric breach model was implemented in the 2-D flow model by means of a time-varying topography. The breach outflow is thus explicitly computed by the flow model, enabling the representation of the hydraulic coupling between reservoir depletion, flow through the breach and possible backwater effects. This procedure requires a user-defined initial dam geometry (Fig. 9a) and a user-defined final geometry corresponding to the breached dam (Fig. 9e). In between these two geometries, the algorithm performs a linear interpolation in time (Dewals et al., 2011). The breaching duration also needs to be prescribed by the user.
Several prediction formulae have been tested for estimating the breaching duration (Froehlich, 2008; Peng and Zhang, 2012; BREACH model). They lead to scattered values, ranging between 10 min and 1 or 2 h. Such discrepancies result from the limited number of real-world case studies for which information on breaching duration is available. For instance, out of a total of 1239 cases reported by Peng and Zhang (2012), only 52 contain detailed information on the breaching and only 14 cases have records of breaching duration. Moreover, inconsistencies exist in these records, so that the regression results for breaching duration are generally less satisfactory (in terms of R2) than for other breach parameters. These are the reasons why we considered a range of plausible assumptions on the breaching duration, between 10 min and 1 h. We also tested one extreme assumption (instantaneous dam failure) to characterize the envelope of possible results. The latter scenario could also correspond to an almost instantaneous breaching as a result of an earthquake.
2.5 Flood intensity mapping
The results of the hydraulic computations were processed to display the inundation extent as well as information on water depth and flow velocity in the floodplains. The method used by Alvarez et al. (2017) was considered for the classification of flood intensity in high, medium and low categories. To be classified in the high category, the location must have a water depth higher than 1 m, a water velocity greater than 1 m s−1 or a product of the velocity and the water depth greater than 0.5 m2 s−1. Conditions to be classified in the category of low flood intensity are a water height below 0.5 m, a flood velocity below 0.5 m s−1 and a product of the velocity and the water depth below 0.25 m2 s−1. The medium intensity category corresponds to all intermediate situations.
3.1 Landslide triggering: back analysis
The results obtained from the elastic model with initial topography (scenarios 1 and 2 in Fig. S1a) were first measured in terms of peak ground acceleration (PGA) and Arias intensity (Ia; see Arias, 1970) in different parts of the profile. This was calculated from the acceleration recorded in x direction for specific history points chosen within the model profile. Figure 10 and Table 4 provide x acceleration, PGA and Ia for the upper and lower blocks considering 14 and 25 s. As we were interested in finding how the landslide was triggered and evolved, we tracked the upper block displacement and its detachment from the later scarp, while the lower block movements needed to be analysed in detail to assess the damming potential (also in comparison with the present situation).
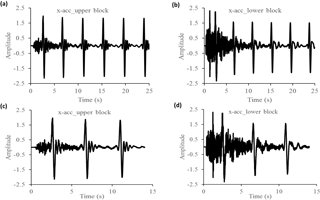
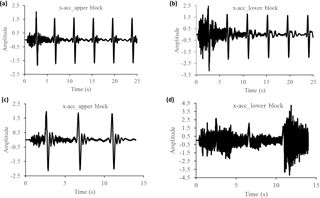
Figure 10x acceleration for 25 s (a, b) and 14 s (c, d) computational time. Accelerations labelled as “x-acc_lower block” and “x-acc_upper block” correspond, respectively, to history points 15 and 12 mentioned in Fig. 7.
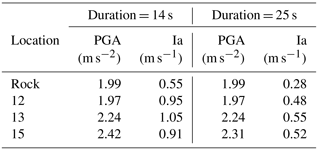
Table 4PGA and Ia measured along the profile for the 14 and 25 s in the bedrock, in the upper block (point 12), in the middle block (point 13) and in the lower block (point 15).
Regarding the main landslide-triggering factors, this was assessed by analysing the calculated safety factor. Scenarios were simulated to highlight the intrinsic behaviour of the model under different loading conditions. First, this was fulfilled in the absence of water and seismic loads. Then, groundwater was added to the model and a seismic input was used. The groundwater data were recorded along the sliding surface with an x increment of 10 m. Results of the safety analysis was completed for different hydrogeological conditions.
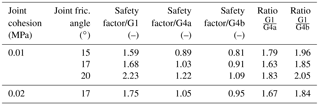
Dry and non-seismic models are assumed to be much more stable. Therefore, scenarios have been made to track the limits from which instability begins. Our discussion is based on the results of the safety factor obtained for a cohesion of 0.01 and 0.02 MPa and for friction angles of 15, 17 and 20∘ as summarized in Table 5.
As expected, those results in Table 5 show a strong dependence of the factor of safety (FoS) of the slope on the friction angle of the slope material. Furthermore, we notice that the FoS of the slope for dry and non-seismic scenarios is almost 2 times larger than the safety factor corresponding to saturated and seismic conditions. Actually, in the absence of water and seismic vibration, the initial slope of the Banana Tree Landslide site would have been stable unless very (and unrealistically) low values of cohesion and friction angle are considered (e.g. friction angle of less than 10∘). This confirms our first estimates of the important role of groundwater pressures and seismic vibrations with respect to the slope destabilization. Based on the local and regional context, other environmental and anthropogenic parameters were identified as factors that have contributed to the increase of field stresses, forcing the landslide triggering and evolution. These factors are earthquakes, erosion at the slope toe (fluvial erosion and quarrying) and upper slope overloading due to the installation of the inhabitants. The last factor also causes other effects like the vegetation removal and galleries due to some cultural techniques which can evolve to a favourable situation for landslide triggering under heavy rain context. This is in line with steps of the process leading to slope instability and landslide triggering as described by Terzaghi (1950), Varnes (1978), Popescu and Yamagami (1994) and Popescu (2002). Moreover, the general north–south direction of the layers could have contributed much to the process amplification. As illustrated in Fig. 2b, the layers are parallel to the direction of the sliding; this allows easy movements downwards in the case of even small slope destabilization.
Table 5Safety factor obtained for a cohesion of 0.01 and 0.02 MPa for different friction angles (G1 is dry and non-seismic; G4 is seismic and saturated). Scenarios involving groundwater and seismic shaking considered a complete saturation of the sliding layers (additional GWT5 scenario) and a wavelet of 25 s shaking time. G4a and G4b correspond to partial and complete saturation.
3.2 Analysis of the actual state of stability and potential x displacement
After the back analysis, simulations of the current situation of the landslide were computed to study the present landslide state of stability. In this section, we have focused on a displacement-oriented analysis, as the main purpose is the study of the conditions under which the landslide could form a dam. The results given in Fig. 11 and Table 6 constitute the basis for this analysis. Large PGA and Ia are observed at the lower (and thicker) block of the landslide. This difference is also observed for the values and the distribution of the x accelerations during the shaking time, again with high values for the downstream block. This difference will also affect the disproportionate horizontal x displacements of the blocks, creating extension and compression zones. Extension zones can lead to the opening of large cracks.
Table 6PGA and Ia in the profile for the 14 and 25 s. Locations 12, 13 and 15 refer to the upper, the middle and the lower blocks, as mentioned in Fig. 7.
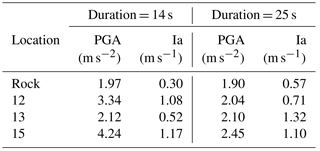
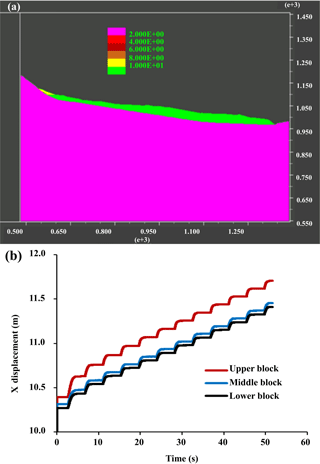
Figure 12Plots of blocks (a) and displacements (b) as given in the UDEC output for run 13 (see Fig. S1b: using a cohesion of 0.01 MPa and a seismic shaking of 51 s).
Figure 12 describes the landslide situation after scenario 13 (detailed in Fig. S1b), showing that increasing the shaking duration would result in a displacement increase over 12 m. The model sometimes provided disproportionate displacements between the three main blocks (Fig. 12b). This leads to compression and shear zones between the blocks and could even probably be the main cause of the spurts of groundwater to form the small lakes hanging up the Kanyosha River.
Table 7The role of water in the model behaviour. Values are based on recorded displacements under scenarios 9, 10, 11, 14, 16 and 17.

The results of this Table 7 show the effects of water on the dynamics of the BTL. Under certain conditions of cohesion and shaking duration, the presence of water increases the x displacement by 2.4 to 14 times. Kainthola et al. (2012) found a change of 79.1 %, corresponding to an increase of approximately a factor of 1.8. This explains why many cases of reactivation or acceleration of landslides occur during rainy periods. These results are discussed with more detail in Sect. 4.1. A full river blockage is possible. Actually, it is likely that the displacements would have been larger for stronger shaking and if we had also modelled plasticity within the blocks. Furthermore, we must consider that some destabilisation mechanisms cannot be computed with UDEC, such as fluidisation or liquefaction of the clayey landslide material, which would produce much larger displacements.
3.3 Effects of the dam breaching on flood intensity
3.3.1 Water depth
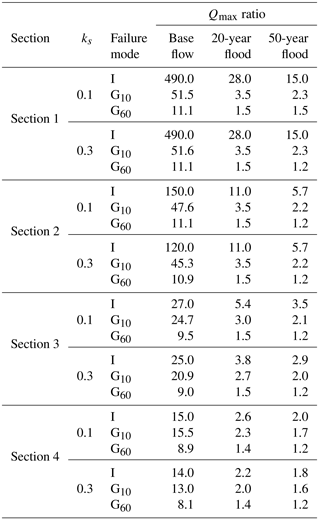
In this section, we examine to which extent the water depths are affected by the occurrence of a landslide dam breaching. The computed water depths are discussed here for four cross sections, labelled sections 1 to 4 (Fig. 3). Figure 13 displays the computed water depths for the pre-failure flow and for the breach-induced flow, for sections 1 to 4, considering a roughness height of 0.1 m (Fig. 13a) and 0.3 m (Fig. 13b), as well as three pre-failure flow scenarios (base flow, 20-year flood and 50-year flood).
The results strongly depend on the assumed breaching time, pre-failure flow scenario and distance to the dam, whereas the value of ks has a more limited influence on the results.
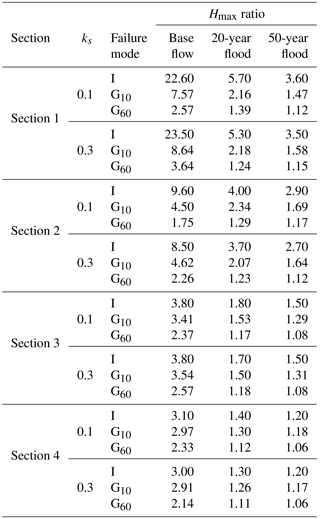
In the extreme case of an instantaneous failure, the computed water depth in section 1 is about 24 times higher when instantaneous dam breaching is assumed compared to a base flow situation without dam breaching. This value is reduced to about 5 and 4, respectively, for pre-failure flow conditions corresponding to a 20- and a 50-year flood. Similarly, the increase in water depths induced by the instantaneous dam breaching becomes more moderate for sections 2, 3 and 4 which are located, respectively, at about 2, 4 and 6 km downstream of the dam. In the case of a 20-year flood or a 50-year flood, the maximum water depth is less than doubled in sections 3 (+50–70 %) and 4 (+20–30 %).
In the case of a gradual dam failure in 10 min, dramatic increases in water depths are obtained only in the case of a base flow as pre-failure flow scenario. In such a case, the computed water depths are multiplied by approximately 9, 5, 4 and 3 in sections 1, 2, 3 and 4, respectively. In contrast, in the cases of a 20- or 50-year flood as the initial flow conditions, the computed water depths are, at maximum, about doubled. In section 4, the increases are limited to 20–30 %. Hence, the severity of the amplification of water depths as a result of dam breaching is, in relative terms, significantly influenced by the assumed pre-failure flow.
Finally, in the case of a gradual breaching in 60 min, the computed water depths are affected by a factor of 3.6 in section 1 and 2.1–2.6 in sections 2 to 4 if a base flow is assumed as the initial condition. In contrast, if a 20- or 50-year flood is assumed initially, the growth in the computed water depths as a result of dam breaching is generally no more than about 20 %.
Nonetheless, in all cases, the increases in water depth as a result of dam breaching remain highly significant from the perspective of flood risk. These results show that dam breaching exacerbates considerably the flood conditions in the downstream river. This conclusion remains robust despite the high uncertainties on the roughness parameter. Indeed, as shown in Table 8, changing the roughness has little influence on the relative effect of dam breaching on the water depths. This is also confirmed by the high similarity between Fig. 13a and b.
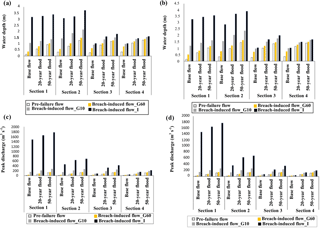
Figure 13Computed maximum water depths (a, b) and peak discharges (c, d) in cross sections 1 to 4, for various pre-failure flow conditions (base flow, 20- and 50-year floods) and for roughness heights ks=0.1 m (a, c) or 0.3 m (b, d). “Breach-induced flow_G60”, “breach-induced flow_G10” and “breach-induced flow_I” stand for “flow induced by the failure of the landslide dam” with, respectively, a breaching time of 60 min, a breaching time of 10 min and an instantaneous failure.
Table 8Ratio between the maximum water depth (Hmax) following dam breaching and the water depth in the pre-failure flow conditions in sections 1 to 4, considering two different roughness heights (ks= 0.1 m and ks= 0.3 m) and various pre-failure flows (base flow, 20-year flood and 50-year flood). I and G10 and G60 stand for instantaneous, 10 min gradual breaching and 60 min gradual breaching, respectively.
3.3.2 Peak discharge
The peak discharge of the flood waves induced by instantaneous dam breaching are in the ranges 1500–1700, 460–570, 77–300 and 41–110 m3 s−1 in sections 1, 2, 3 and 4, respectively (Fig. 13c and d). In the uppermost section (section 1), which is located close to the toe of the dam, the roughness height has virtually no influence on the computed peak discharge, as the flow in this area is predominantly controlled by the dam failure. In contrast, the peak discharge is gradually more influenced by the roughness height as the flood wave propagates towards the more downstream cross sections (sections 2, 3 and 4). Similarly to the results for the water depths, the peak discharges decrease significantly in the case of gradual failure; e.g. for a 1 h breaching scenario, these peak flow value ranges become 33.4–149, 33.3–148.4, 28.5–147.2 and 26.6–134.6 m3 s−1 in sections 1, 2, 3 and 4, respectively. Intermediate results are obtained for a breaching time of 10 min.
In cross section 1, the peak discharge of the instantaneous dam-breaching flood wave is roughly 500 times higher than the base flow, 30 times larger than a 20-year flood and 15 times larger than a 50-year flood (Table 9). In the more downstream cross sections, these numbers become smaller, but the peak flow after dam breaching remains at least 2–10 times larger than typical flood discharges (20- or 50-year floods) and can be 100 times larger than the base flow in the river. These results are only slightly affected by a change in the roughness height.
We find again that neglecting dam failure would result in a strong underestimation of the downstream flood intensity. This underestimation is particularly severe in the cross sections located close to the dam, whereas in the more downstream area, this effect is mediated by peak flow attenuation during wave propagation.
3.3.3 Wave propagation time
Figure 14 displays the wave propagation time in sections 1 to 4, i.e. the time elapsed between the dam failure and the moment the flood wave reaches the corresponding section of the river. The time to peak, i.e. the time between the dam breaching and the arrival of the peak discharge in the corresponding river sections, is also displayed. Results are shown for two roughness heights, ks= 0.1 m and ks= 0.3 m.
In the upper part of the river, the wave propagation time remains mostly independent of the pre-failure flow. The flood wave takes between 2.5 and 3 min to reach section 2, which corresponds to a wave velocity of the order of 10 to 12 m s−1. Further downstream (in the urbanized area), the pre-failure flow has a strong influence on the wave propagation velocity. When the pre-failure conditions in the river correspond to base flow, the wave takes roughly 12 min to reach section 3 and 25 min to reach section 4. These values drop to 7–8 and 12–14 min if the instantaneous dam breaching takes place during a river flood, corresponding to a rise in the mean wave velocity from 4 to 6 m s−1 in base flow conditions up to 7–9 m s−1. In the case of a 10 min gradual breaching, the wave propagation time to get to sections 3 and 4 becomes 9–10 and 14–16 min, respectively. From a 10 min to a 60 min breaching scenarios, the wave travel time is moderately increased by 26 % in section 3 and 33 % in section 4 when a river flood is considered, but here again, these values remain lower than the corresponding travel time in the case of base flow scenarios.
Hence, the higher the pre-failure discharge in the river, the shorter the wave propagation time and time to peak. Compared to a dam failure occurring when the river discharge is low (base flow), the wave propagation time and time to peak are approximately reduced by a factor of 2 if the failure occurs during a flood, which corresponds incidentally to the most likely scenario. Although dam breaching has a relatively weaker influence on maximum water depth and peak discharge when the pre-failure flow corresponds to flood conditions (Sect. 3.3.1 and 3.3.2), the results obtained here demonstrate that even in flood situations, dam breaching is particularly dangerous because of the shorter time between the occurrence of failure and the wave arrival. Overall, the velocity of the flood wave gives little chance for the population to take precautionary measures such as evacuation, unless the population is very well prepared and some early-warning system can be put in place.
Figure 14 shows also the diffusion of the flood wave as it propagates in the valley. While the difference between the wave arrival time and the time to peak is low in sections 1 and 2 (generally below 0.5 min), it reaches 1 to 2 min in section 3 and 2.5 to 4.5 min in section 4. This shows that the flood wave is considerably steeper in the upper part of the valley (sections 1 and 2). Also, the wave remains steeper when dam breaching occurs during a river flood than when it occurs during base flow.
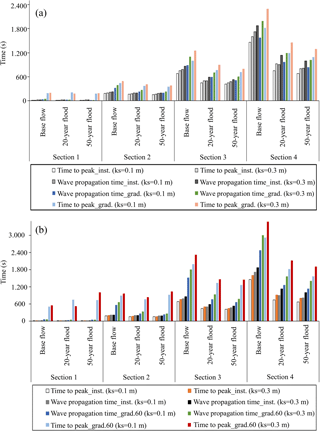
Figure 14(a) Computed wave propagation time and time to peak in sections 1 to 4, for various pre-failure flow conditions (base flow, 20- and 50-year flood) and for two different roughness heights (ks= 0.1 m and ks= 0.3 m). The gradual failure time is 10 min. (b) Computed wave propagation time and time to peak in sections 1 to 4, for various pre-failure flow conditions (base flow, 20- and 50-year flood) and for two different roughness heights (ks= 0.1 m and ks= 0.3 m). The gradual failure time is 60 min.
The value chosen for the roughness height has virtually no influence on the computational results in sections 1 and 2, which are relatively close to the dam, whereas it has more influence in sections 3 and 4. Nonetheless, the main observations detailed above remain valid for both values of the roughness height (ks= 0.1 m and ks= 0.3 m).
3.4 Floodplain delineation and flood intensity mapping
The spatial extent of floodplains, expressed in terms of surface and its variation for different return periods, is analysed here. For each case, as given in Table 10, values are given for both failure and non-failure scenarios. Changes induced by the instantaneous as well as the 10 and 60 min gradual dam failures are also quantified and discussed. Under the same roughness height, both in a failure or a non-failure situation, the flood extent remains greatly linked to the steady flow discharge. For example, from the base flow to the 50-year flood, the average flood area increase is 25 %, using a roughness height of 0.1 m. This increase is approximately 16 % from the base flow to the 20-year steady flow. These ratios remain almost constant both in the failure and non-failure scenarios.
The floodplain extent variations are also linked to the roughness changes. For pre-failure scenarios, from a height of 0.1 to 0.3 m, the surface of the floodplain increases by 10, 14 and 34 % for the base flow, 20 years and 50 years of the return period. These increases are 4, 8 and 29 %, 4, 9 and 21 %, and 6, 7 and 19 % in the cases of a 60 min dam breaching, a 10 min dam breaching and an instantaneous dam breaching.
The maps in Fig. 15a and b show the spatial distribution of the flood intensity. Values are calculated on the basis of the water depth and velocity. Then, they are classified according to the methodology described in Sect. 2.5. The maps show the impact of the dam failure on the flood intensity. These maps relate to the lower parts of the watershed, between sections 3 and 4 of Fig. 3, in the city of Bujumbura. For both Fig. 15a and b, maps in the first column (left column) represent the scenarios without dam breaching while those in the third column relate to the corresponding instantaneous failure scenarios. The maps in the second column correspond to the intermediate situation: gradual failure in 10 min for Fig. 15a and 60 min for Fig. 15b. Subfigures (a), (b) and (c) relate to pre-failure flow conditions corresponding to base flow, while the subfigures (d) to (f) are related to a pre-failure 50-year flood with a roughness height of 0.1 m. Subfigures (g), (h) and (i) differ from those in the second rows by the fact that a roughness of 0.3 m is applied instead of 0.1 m. The comparison of maps of the first and second rows helps to analyse changes related to the initial flow, while the differences between the second and the third rows are the result of the change in roughness within the bottom of the river. Each time, the maps in the second and third columns highlight changes due to the dam breaching.
The maps in the first row correspond to the base flow case. Their comparison allows to realize a significant change especially downstream with a lateral extension of the flooded area. Thus, notable changes are observed and consist of a change in the flood intensity level. According to subfigures (a), (b) and (d), almost all zones classified in the low-level flood intensity category in the non-failure case migrated directly into the high flood intensity category in the case of a failure scenario (subfigures a and b). This is also the case from the base flow to a 50-year flood (subfigures a and d), but here, the change due to the increase of pre-failure flow is more important than that resulting from the dam breaching. The vertical comparison of the first two rows highlights the variations of the flood intensity depending on the initial flow rate, as well as in a failure and in a non-failure case, under a roughness height of 0.1 m. Unlike the previous ones (subfigures a and b), the no-breach scenario (Fig. 15, subfigure d) already includes zones under the high-category flood intensity. However, the lateral extension of flooding is much more obvious than previously, especially near cross section 3. The corresponding failure scenario (map, subfigure e) shows significant increases in flood intensity both on the south and north riverbanks. Comparison of subfigures (d), (e) and (f) to (g), (h) and (i) reveals that a higher roughness height increases substantially the estimated flood intensity, due to the corresponding increase in water depth. These observations apply to both Fig. 15a and b. The main difference observed between Fig. 15a and b relates to subfigures (b), (e) and (h) corresponding to the gradual failure. The flood intensity is higher for a breaching time of 10 min (Fig. 15a) than for a breaching time of 60 min (Fig. 15b). Overall, the flood intensity increases as the pre-failure flow increases and as breaching time becomes shorter.
Table 10Predicted changes in terms of flooded area due to the landslide-induced dam breaching for roughness are equal to 0.1 and 0.3 m.
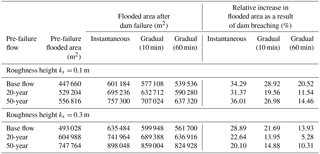
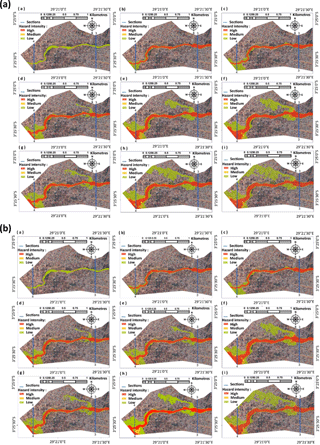
Figure 15Flood intensity maps for various initial steady discharges and roughness: the first column (subfigures a, d, g) corresponds to the pre-failure scenarios, while the second (subfigures b, e, h) and third (subfigures c, f, i) columns relate to the gradual (a 10 min and b 60 min as breaching time) and instantaneous breaching. The first line (subfigures a, b, c) is based on the base flow and a roughness height of 0.1 m. The scenarios of the second line (subfigures d, e, f) are simulated using a 50-year flood and a roughness of 0.1 m. The third line (subfigures g, h, i) is similar to the second one but considers a roughness height of 0.3 m.
4.1 Comments on the landslide analysis
The main question about the present state of the BTL has already been introduced above: under certain conditions BTL is likely to be destabilized, but is a full blockage of the river possible?
In addition to the above modelling results, we present here some direct proofs of the likely future massive activation of the landslide – under certain conditions (similar to the simulated worst-case scenarios). First, the scenario of future formation of a landslide dam is supported by observations indicating that the landslide had already formed a dam in the past. Actually, directly upstream from the landslide the valley widens and it is filled both by coarse and by fine deposits. In particular, the latter indicate that a lake has existed upstream from the landslide, probably due to the damming of the river that must have lasted a certain amount of time (probably months or years). Second, many ground cracks as well as rock structures favouring sliding along the slope (Fig. 2b and d) were found on the landslide surface and at its foot, respectively. Apart from the fact that these cracks and layers constitute zones of weakness, they contribute to the landslide destabilization by diverting large quantities of the runoff water to the inner part of the landslide and to the main sliding surface. This water can contribute to the lubrication of the clay that may then form “soap layers” (see such “soap layer” surface in Fig. 2c), or by the recharge of the aquifer whose rise leads to the slope instability as shown in the sections above. Due to the landslide surface morphology, water could accumulate at its surface and form some ponds (see view of main pond in Fig. 2a). Those ponds do not only contribute to the saturation of the soil, but they also constitute an additional active load for sliding. One scenario that could not be simulated includes the opening of fractures below those ponds that would drastically increase the groundwater pressures at depth. All these elements allow us to validate the simulated scenarios considering worst-case conditions (high groundwater pressure, seismic activation) and indicate that even much larger movements could occur than those that were modelled: seismic vibrations could contribute to fracture opening, which in turn would allow rapid inflow of surface (and runoff) water, which could result in massive movements of materials. At least a 15 m high landslide dam could form; our simulations resulted in such a 15 m high dam along the river axis, but it did not fully block the river section as the 12 m horizontal displacement would still allow the river to flow around the landslide. Larger horizontal displacements such as those expected after pouring of all existing pond water into the landslide, down to the sliding surface, would probably result in a full river blockage. Behind this dam, a water impoundment of about 60 × 103 m3 or more could develop. For the evaluation of this volume, we consider the extension of past lakes that had been dammed by the same landslide as proved by the presence of lake sediments directly upstream from the landslide (covering a surface area of about 12 000 m2).
4.2 Key findings from the hydraulic modelling
One of the key elements highlighted by our flood scenario analysis is the influence of the surface roughness on the dynamics of the Kanyosha River. The studied dam failure scenarios complete the findings of the stationary analysis by providing a better understanding of the hydrological behaviour of the Kanyosha River. Most importantly, we found that, according to the worst-case scenarios, a large flow discharge is expected to arrive very quickly near the inhabited regions, which might not allow the inhabitants to escape. This result is strongly dependent on the riverbed roughness change, potentially due to previous floods and/or anthropogenic disturbances. These findings are of great interest, as they can help decision makers to promote non-risky city management near the Kanyosha River and other rivers in similar conditions, by controlling all activities that can alter the roughness of the rivers, knowing their effects on the severity of flooding. Flood intensity maps are valuable tools showing the areas that can be affected under different scenarios and helping to take adequate measures to avoid losses due to floods. The effects of dam failure on the flood intensity are well highlighted. Significant changes in failure scenarios computed only with base flow constitute the most important element in risk prevention. Indeed, warning systems are based on data provided by meteorological services analysing the likelihood of heavy rainfall. However, dam failures can produce floods that are several times more severe than those caused by concentrated surface runoff. This shows that dam failure can distort flood forecasts, creating surprises through unexpected circumstances. Hence, multi-hazard analyses remain of great interest in high geological risk environments such as those found along the East African Rift system.
4.3 Uncertainties and limitations
4.3.1 Influence of general assumptions and parameterization
The characteristic size of the bottom irregularities was observed to vary along the river channel. Therefore, although we tested different values of the friction coefficient in our simulations, uncertainties remain regarding the effect of the spatial variability on bottom roughness.
In our simulations, we also assume that the reservoir behind the dam is completely filled when the failure starts. The actual situation could be different, as the breaching may occur before the complete filling of the reservoir. However, in such a case, the severity of the induced flooding would be lower, so our assumption makes sense from the perspective of risk management. Filling of the reservoir takes about 5.5 h, 17 min and 9 min in, respectively, the base flow scenario, the 20-year flood scenario and the 50-year flood scenario. This remains of the same order as the typical lifespan of a landslide dam.
Figure 16Water depth and peak discharge obtained from simulations based on the 10 m × 10 m DEM and from a topographic field survey. The breaching duration is 60 min.
Moreover, the dam breaching mechanism and dynamics depend on a series of factors related to the resistance of the natural dam. Although it may considerably affect the actual breaching and the induced flood wave, the detailed prediction of this resistance is out of the scope of the present study and was handled by reasonable and discussed assumptions of the breach formation time.
4.3.2 Influence of the topographic and bathymetric data on the water depth and on the peak discharge
To assess the sensitivity of water depth and peak discharge to the DEM, we compared the results of simulations based on the initial 10 m × 10 m DEM and those based on the topographic field survey (Sect. 2.2). The results given in Fig. 16 allow the comparison of computed water depths and peak discharges in both cases, for various initial flow in the river and roughness heights of 10 or 30 cm.
Some significant deviations are found for the computed water depths, indicating that the values of water depths are strongly influenced by local details in the topographic data. These influences are highly variable in space. This is an expected result and, for instance, the water level would show a more limited sensitivity to the topographic details than the water depths do. The differences may result from the limited accuracy of the topographic datasets, from planform variations of the river channel since the riverbanks are not stabilized and frequently undergo changes due to erosion and anthropogenic disturbances. Changes may have occurred between the production of the 10 m × 10 m DEM (2012) and the field survey (2014–2015).
In contrast, the differences in the peak discharges remain very limited, since they are equal to 3 % on average and they never exceed 10 % (this value is obtained for an initial base flow and a relatively high roughness height). The higher the initial flow in the river, the lower the sensitivity of the peak discharge. This suggests a reduced influence of the topographic details on the peak discharge, as also confirmed in Table S4.
To quantify the sensitivity of the flood extent to the topographic data used, an indicator was calculated based on the pixels included in the flooded area computed based on the two topographic datasets. This indicator is the ratio between the number of pixels in the intersection and the number of pixels of the union of the two computed flood extents. Its value ranges between 0 (no overlap) and 1 (perfect agreement). For ks= 0.1 m, the results show an indicator of 0.82, 0.85 and 0.77 for a base flow, a 20-year flood and a 50-year flood, respectively. For ks= 0.3 m, the corresponding computed indicators are equal to 0.83, 0.85 and 0.86, respectively. These results reveal a moderate sensitivity of the flood extent with respect to the two tested topographic datasets. The details of the results are provided in Table S5, considering a breaching duration of 60 min.
4.3.3 Impact of solid transport on the flow
To appreciate the effect of the mobilized solid material, we used the volume of the landslide dam as a proxy for the volume of released solid material. The volume Vd of the landslide dam is about 16 000 m3, while the volume Vl of water impounded behind the landslide dam prior to dam breaching is roughly 55 000 m3. Table 11 provides an estimate of the ratio between the volume of dam material and the total volume of water contributing to dam erosion in the various considered scenarios. Table 11 suggests that only in the case of a 20- or a 50-year flood and a slow erosion of the dam (in hours), the volume of dam material could reasonably be neglected compared to the volume of water, as in this case, the volume of water contributing to the dam erosion is approximately 20–30 times larger than the volume of the dam material. In all other cases, the volume of dam material ranges between 12 and 30 % of the water volume and is therefore not negligible.
Table 11Estimated volume of water released at the dam over the breaching duration, evaluated as Vl + Tc × Qr. Notation Vl refers to the volume of water initially impounded behind the landslide dam, Qr, to the river discharge before dam breaching, and Tc is a characteristic time, taken equal to 60 s for the extreme scenario of instantaneous dam breaching and equal to Tf (breaching duration) in the other cases. Notation Vd designates the volume of the dam.

In addition, we may appreciate the plausible consequences of morphodynamic evolution (erosion, deposition) based on the results of the sensitivity analysis conducted with respect to a change in the DEM (Sect. 4.3.2). The differences between the two considered DEMs are of course not correlated with locations of preferential erosion or deposition in the valley, but the overall order of magnitude of these differences is in agreement with a plausible amount of deposits resulting from the volume of solid material released during the breaching. Indeed, given the volume of the landslide dam (Vd= 16 000 m3), if we assume an average flow width of 30 m and a sediment spread over only 1500 m, the thickness of the deposits is of the order of 35 cm. This thickness remains in the same range as the differences between the 10 m × 10 m DEM and the field measurements (Sect. 2.2). Therefore, we speculate that the changes in the computed flow characteristics as a result of a change of the DEM (Sect. 4.3.2) might be of the same order as those which would result from erosion and deposition of solid materials (higher sensitivity of the water depths compared to flood discharge). This requires obviously a thorough verification by means of the more sophisticated flow and morphodynamic models than used here.
The processes of the triggering and evolution of the Banana Tree Landslide along the slope south of the Kanyosha River near Bujumbura were analysed. A large set of simulations was computed to understand how the landslide evolved from its initial situation to the current state by back analysis. Results showed that the sliding must have been initially triggered under extreme conditions, involving high groundwater pressures and most likely also quite strong seismic shaking. Furthermore, we showed that the Banana Tree Landslide in its present state can still lead to disasters in the future, as the combination of earthquakes and increased groundwater pressures could result in massive downslope movements.
It should be highlighted that the landslide is still active, especially within the downstream block where the river erosion at the foot of the slope and the ground saturation are accelerating sliding processes. Enhancement of those processes (by higher groundwater pressures, possibly also due to seismic shaking and/or due to ground cracks allowing for rapid surface water infiltration, etc.) will inevitably lead to larger movements and the formation of a landslide dam, behind which a large lake could develop.
A hydraulic model provided valuable quantitative information on the flood wave characteristics and propagation resulting from a possible landslide dam breach. Here, we primarily considered the precondition of a total dam formation and a later (more or less) sudden and full collapse leading to a rapid release of (possibly all) the water stored behind the dam. It enabled us to assess quantitatively different failure scenarios as well as the influence of various parameters. One of the most important conclusions of this work is that some areas assumed to be in security with respect to regular floods related to simple concentrated surface water runoff might become exposed to extreme flooding in the case of an upstream dam failure. Hence, it is important to take these realities into account in a sustainable spatial management planning and especially in areas marked by high population densities. Flood intensity mapping is still a valuable tool and can be used as a guide, helping decision makers in urban planning. Since some hydraulic parameters (e.g. the water depth) are sensitive to topographic data, efforts have to be made to gather suitable topographic data with high resolution, in order to minimize uncertainties in flood forecasting.
As emphasized in Sect. 4.3.3, the present study should be pursued by taking into account the volume of released solid material and applying a sediment transport and morphodynamic model, as included in more advanced debris flow/granular flow modelling tools such as presented by Mergili et al. (2012a, b, 2017) or others, and adapted to channelized debris flow.
Our underlying research datasets consist essentially of topographic, climatic and geophysical data. They were received in the context of either an ongoing project or an institution that defines the conditions for data acquisition. Thus, the topographic data (as well as the orthophoto used in the background of Fig. 15) obtained from the Bureau de Centralisation Geomatique du Burundi were accessed on the basis of a specified and conditional request. This is also the case for climate data for the intensity–frequency–duration law of Bujumbura provided by the Geographic Institute of Burundi (IGEBU), as mentioned in the Supplement. The backup and access to these data are therefore rights strictly reserved to this institution. Moreover, geophysical data were obtained in the frame of the GeoRisCA project. The data resulting from field surveys both on the BTL site and on other sites covered by the project can be accessed by personalized and motivated request to the project managers. For that reason, we would like to apologize for not having created a particular repository thereto. However, we provide hereafter the useful contacts for whoever would be interested in any formal request:
-
Bureau de Centralisation Géomatique du Burundi (BCG), http://www.sp-bcg.gov.bi, info@sp-bcg.gov.bi
-
Geo-Risk in Central Africa (GeoRisCA): integrating multi-hazards and vulnerability to support risk management, http://georisca.africamuseum.be/
-
Institut Géographique du Burundi (IGEBU), http://www.igebu.gov.bi
The supplement related to this article is available online at: https://doi.org/10.5194/nhess-18-1867-2018-supplement.
Field surveys and landslide analysis with UDEC have been carried out by LN and HBH. Hydraulic modeling has been done by LN, BD and PA. Final formatting and manuscript revisions have been performed by all authors.
The authors declare that they have no conflict of interest.
Results presented in this paper were obtained in the frame of research funded
by the Burundi government who supported the PhD studies of Leonidas Nibigira,
and by the Belspo (Belgian Federal Science Policy) project GeoRisCA
(2012–2016): Geo-Risk in Central Africa: integrating multi-hazards and
vulnerability to support risk management. Elevation and meteorological data
were provided by the Geographic Institute of Burundi (IGEBU) and the
Bureau de Centralisation Geomatique du Burundi. Therefore, the
authors are grateful to both financial supporters and data providers.
Edited by: Thomas Glade
Reviewed by: Olivier Dewitte and Martin Mergili
Adams, J. E.: Earthquake-dammed lakes in New Zealand, Geology, 9, 215–219, 1981.
Alvarez, M., Puertas, J., Peña, E., and Bermúdez, M.: Two-Dimensional Dam-Break Flood Analysis in Data-Scarce Regions: The Case Study of Chipembe Dam, Mozambique, Water, 9, 432, https://doi.org/10.3390/w9060432, 2017.
Arias, A.: A measure of earthquake intensity, in: Seismic design for Nuclear Powerplants, edited by: Hansen, R. J., MIT Press, Cambridge, Massachusetts, 438–483, 1970.
Arrault, A., Finaud-Guyot, P., Archambeau, P., Bruwier, M., Erpicum, S., Pirotton, M., and Dewals, B.: Hydrodynamics of long-duration urban floods: experiments and numerical modelling, Nat. Hazards Earth Syst. Sci., 16, 1413–1429, https://doi.org/10.5194/nhess-16-1413-2016, 2016.
Beckers, A., Dewals, B., Erpicum, S., Dujardin, S., Detrembleur, S., Teller, J., Pirotton, M., and Archambeau, P.: Contribution of land use changes to future flood damage along the river Meuse in the Walloon region, Nat. Hazards Earth Syst. Sci., 13, 2301–2318, https://doi.org/10.5194/nhess-13-2301-2013, 2013.
Bhasin, R. and Kaynia, A. M.: Static and dynamic simulation of a 700-m high rock slope in western Norway, Eng. Geol., 71, 213–226, 2004.
Bruwier, M., Erpicum, S., Pirotton, M., Archambeau, P., and Dewals, B. J.: Assessing the operation rules of a reservoir system based on a detailed modelling chain, Nat. Hazards Earth Syst. Sci., 15, 365–379, https://doi.org/10.5194/nhess-15-365-2015, 2015.
Butt, M., Umar, M., and Qamar, M.: Landslide dam and subsequent dam-break flood estimation using HEC-RAS model in Northern Pakistan, Nat. Hazard, 65, 241–254, 2013.
Chen, C. Y., Chen, T. C., Yu, F. C., and Hung, F. Y.: A landslide dam breach induced debris flow – A case study on downstream hazard areas delineation, Environ. Geol., 47, 91–101, 2004.
Chuhan, Z., Pekau, O. A., Feng, J., and Guanglun, W.: Application of distinct element method in dynamic analysis of high rock slopes and blocky structures, Soil Dyn. Earthq. Eng., 16, 385–394, 1997.
Corominas, J. and Moya, J.: A review of assessing landslide frequency for hazard zoning purposes, Eng. Geol., 102, 193–213, 2008.
Costa, J. E. and Schuster, R. L.: Formation and failure of natural dams, Bull. Geol. Soc. Am., 100, 1054–1068, 1988.
Crosta, G. B. and Clague, J. J.: Dating, triggering, modelling, and hazard assessment of large landslides, Geomorphology, 103, 1–4, 2009.
Cui, Y., Parker, G., Braudrick, C., Dietrich, W. E., and Cluer, B.: Dam removal Express Assessment Models (DREAM), Part 1: Model development and validation, J. Hydraul. Res., 44, 291–307, 2006.
Cui, P., Dang, C., Zhuang, J. Q., You, Y., Chen, X. Q., and Scott, K. M.: Landslide-dammed lake at Tangjiashan, Sichuan province, China (Triggered by the Wenchuan Earthquake, May 12, 2008): risk assessment, mitigation strategy, and lessons learned, Environ. Earth Sci., 65, 1055–1065, 2012.
Cundall, P. A.: A computer model for simulating progressive large scale movement in blocky rock system, Symposium of the International Society for Rock Mechanics (ISRM) on Rock Fracture, Nancy, France, 4–6 October, 1971.
Delvaux, D., Mulumba, J. L., Sebagenzi Mwene Ntabwoba, S., Bondo, S. F., Kervyn, F., and Havenith, H. B.: Seismic hazard of the Kivu rift (western branch, East African Rift system): new neotectonic map and seismotectonic zonation model, J. Afr. Earth Sci., 134, 831–855, https://doi.org/10.1016/j.jafrearsci.2016.10.004, 2016.
Detrembleur, S., Stilmant, F., Dewals, B., Erpicum, S., Archambeau, P., and Pirotton, M.: Impacts of climate change on future flood damage on the river Meuse, with a distributed uncertainty analysis, Nat. Hazards, 77, 1533–1549, 2015.
Dewals, B., Erpicum, S., Detrembleur, S., Archambeau, P., and Pirotton, M.: Failure of dams arranged in series or in complex, Nat. Hazards, 56, 917–939, 2011.
Dong, J. J., Tung, Y. H., Chen, C. C., Liao, J. J., and Pan, Y. W.: Discriminant analysis of the geomorphic characteristics and stability of landslide dams, Geomorphology, 110, 162–171, 2009.
Downs, P. W., Cui, Y., Wooster, J. K., Dusterhoff, S. R., Booth, D. K., Dietrich, W. E., and Sklar, L. S.: Managing reservoir sediment realease in dam removal projects: An approach informed by physical and numerical modelling of non-cohesive sediment, Int. J. River Basin Manage., 7, 433–452, 2009.
Ernst, J., Dewals, B. J., Detrembleur, S., Archambeau, P., Erpicum, S., and Pirotton, M.: Micro-scale flood risk analysis based on detailed 2D hydraulic modelling and high resolution geographic data, Nat. Hazards, 55, 181–209, 2010.
Esaki, T., Jiang, Y., Bhattarai, T. N., Maeda, T., Nozaki, A., and Mizokami, T.: Modelling jointed rock masses and prediction of slope stabilities by DEM, in: Vail Rocks 1999, The 37th US Symposium on Rock Mechanics (USRMS), American Rock Mechanics Association, Vail, CO, 7–9 June, 1999.
Fan, X. M., Westen, C. J., Xu, Q., Gorum, T., and Dai, F. C.: Analysis of landslide dams induced by the 2008 Wenchuan earthquake, J. Asian Earth Sci., 57, 25–37, 2012.
Fan, X. M., Xu, Q., Van Westen, C. J., Huang, R., and Tang, R.: Characteristics and classification of landslide dams associated with the 2008 Wenchuan earthquake, Geoenviron. Disasters, 4, 12, https://doi.org/10.1186/s40677-017-0079-8, 2017.
Froehlich, D. C.: Embankment dam breach parameters and their uncertainties, J. Hydraul. Eng., 134, 1708–1721, 2008.
Ilunga, L.: Etude des sites majeurs d'érosion à Uvira (R.D. Congo), Geo-Eco-Trop, 30, 1–12, 2006.
Jacobs, L., Maes, J., Mertens, K., Sekajugo, J., Thiery, W., Van Lipzig, N., Poesen, J., Kervyn, M., and Dewitte, O.: Reconstruction of a flash flood event through a multi-hazard approach: Focus on the Rwenzori Mountains, Uganda, Nat. Hazards, 84, 851–876, https://doi.org/10.1007/s11069-016-2458-y, 2016.
Kainthola, A., Singh, P. K., Wasnik, A. B., Sazid, M., and Singh, T. N.: Distinct element modelling of Mahabaleshwar road cut hill slope, Int. J. Geomaterials, 2, 105–113, 2012.
Korup, O.: Geomorphometric characteristics of New Zealand landslide dams, Eng. Geol., 73, 13–35, 2004.
Kveldsvik, V., Kaynia, A. M., Nadim, F., Bhasin, R., Nilsen, B., and Einstein, H. H.: Dynamic distinct-element analysis of the 800 m high Åknes rock slope, Int. J. Rock Mech. Min., 46, 686–698, 2009.
Li, M. H., Hsu, M. H., Hsieh, L. S., and Teng, W. H.: Inundation potentials analysis for Tsao-Ling landslide lake formed by Chi-Chi earthquake in Taiwan, Nat. Hazards, 25, 289–303, 2002.
Li, M.-H., Sung, R.-T., Dong, J.-J., Lee, C.-T., and Chen, C.-C.: The formation and breaching of a short-lived landslide dam at Hsiaolin Village, Taiwan – Part II: Simulation of debris flow with landslide dam breach, Eng. Geol., 123, 60–71, 2011.
Machiels, O., Erpicum, S., Archambeau, P., Dewals, B., and Pirotton, M.: Theoretical and numerical analysis of the influence of the bottom friction formulation in free surface flow modelling, Water, 37, 221–228, 2011.
Mergili, M., Schratz, K., Ostermann, A., and Fellin, W.: Physically-based modelling of granular flows with Open Source GIS, Nat. Hazards Earth Syst. Sci., 12, 187–200, https://doi.org/10.5194/nhess-12-187-2012, 2012a.
Mergili, M., Fellin, W., Moreiras, S. M., and Stötter, J.: Simulation of debris flows in the Central Andes based on Open Source GIS: Possibilities, limitations, and parameter sensitivity, Nat. Hazard, 61, 1051–1081, 2012b.
Mergili, M., Fischer, J.-T., Krenn, J., and Pudasaini, S. P.: r.avaflow v1, an advanced open-source computational framework for the propagation and interaction of two-phase mass flows, Geosci. Model Dev., 10, 553–569, https://doi.org/10.5194/gmd-10-553-2017, 2017.
Michellier, C., Pigeon, P., and Kervyn, F.: Contextualizing vulnerability assessment: a support to geo-risk management in central Africa, Nat. Hazards, 82, 27–42, 2016.
Moeyersons, J., Trefois, P., Nahimana, L., Ilunga, L., Vandecasteele, I., Byizigiro, V., and Sadiki, S.: River and landslide dynamics on the western Tanganyika rift border, Uvira, DR Congo: diachronic observations and a GIS inventory of traces of extreme geomorphologic activity, Nat. Hazards, 53, 291–311, 2010.
Nandi, A. and Shakoor, A.: A GIS-based landslide susceptibility evaluation using bivariate and multivariate statistical analyses, Eng. Geol., 110, 11–20, 2009.
Nibigira, L., Draidia, S., and Havenith, H.-B.: GIS-based landslide susceptibility mapping in the Great Lakes region of Africa, Case study of Bujumbura Burundi, Eng. Geol. Soc. Terr., 2, 985–988, 2015.
Peng, M. and Zhang, L. M.: Breaching parameters of landslide dams, Landslides, 9, 13–31, 2012.
Popescu, M. E.: Landslide causal factors and landslide remedial options, Proc. 3rd Int. Conf. Landslides Slope Stability and Safety of Infra-Structures, Conference Secretariat, CI-Premier, Singapore, 61–81, 2002.
Popescu, M. E. and Yamagami, T.: Back Analysis Of Slope Failures – A Possibility Or A Challenge?, Proc. 7th Intern. IAEG Congress, Lisbon, A. A. Balkema, Rotterdam, 4737–3744, 1994.
Reliefweb: Burundi: Floods and Landslides – Feb 2014, available at: http://reliefweb.int/disaster/fl-2014-000019-bdi (last access: 21 November 2016), 2014.
Roger, S., Dewals, B. J., Erpicum, S., Schwanenberg, D., Schuttrumpf, H., Kongeter, J., and Pirotton, M.: Experimental and numerical investigations of dike-break induced flows, J. Hydraul. Res., 47, 349–359, 2009.
Sharma, L. K., Umrao, R. K., Singh, R., Ahmad, M., and Singh, T. N.: Stability Investigation of Hill Cut Soil Slopes along National Highway 222 at Malshej Ghat, Maharashtra, J. Geol. Soc. India, 89, 165–174, 2017.
Shrestha, B. and Nakagawa, H.: Hazard assessment of the formation and failure of the Sunkoshi landslide dam in Nepal, Nat. Hazards, 82, 2029–2049, 2016.
Singh, P. K., Wasnik, A. B., Kainthola, A., Sazid, M., and Singh, T. N.: The stability of road cut cliff face along SH-121: a case study, Nat. Hazards, 68, 497–507, 2013.
Terry, J. P. and Goff, J.: Mega clasts: proposed revised nomenclature at the coarse end of the Udden-Wentworth grain-size scale for sedimentary particles, J. Sediment. Res., 84, 192–197, 2014.
Terzaghi, K.: Mechanisms Of Landslides, Geological Society of America, Berkley, 83–123, 1950.
Umrao, R. K., Singh, R., Ahmad, M., and Singh, T. N.: Stability analysis of cut slopes using continuous slope mass rating and kinematic analysis in Rudraprayag district, Uttarakhand, Geomaterials, 1, 79–87, 2011.
UNITAR/UNOSAT: Storm damage, Kinama/Kamenge, Areas of Bujumbura, Burundi, available at: http://reliefweb.int/map/burundi/storm-damage-kinamakamenge-areas-bujumbura-burundi-17-february-2014 (last access: 21 November 2016), 2014.
Varnes, D. J.: Slope movement types and processes, in: Landslides, Analysis and Control, Special report 176, edited by: Schuster, R. L. and Krizek, R. J., Transportation Research Board, National Academy of Sciences, Washington, DC, 11–33, 1978.
Wang, H.-W., Tullos, D., and Kuo, W.-H.: Simulating bed evolution following the Barlin Dam (Taiwan, China), failure with implications for sediment dynamics modeling of dam removal, Int. J. Sediment Res., 31, 299–310, 2016.
Wells, R. R., Langendoen, E., and Simon, A.: Modeling pre and post removal sediment dynamics: The Kalamazoo River, Michigan, J. Am. Water Ressour. Assoc., 43, 773–785, 2007.
Yang, S. H., Pan, Y. W., Dong, J. J., Yeh, K. C., and Liao, J. J.: A systematic approach for the assessment of flooding hazard and risk associated with a landslide dam, Nat. Hazards, 65, 41–62, 2013.