Impacts from cascading multi-hazards using hypergraphs: a case study from the 2015 Gorkha earthquake in Nepal

This study introduces a new approach to multi-hazard risk assessment, leveraging hypergraph theory to model the interconnected risks posed by cascading natural hazards. Traditional single-hazard risk models fail to account for the complex interrelationships and compounding effects of multiple simultaneous or sequential hazards. By conceptualising risks within a hypergraph framework, our model overcomes these limitations, enabling efficient simulation of multi-hazard interactions and their impacts on infrastructure. We apply this model to the 2015 M_w 7.8 Gorkha earthquake in Nepal as a case study, demonstrating its ability to simulate the primary and secondary effects of the earthquake on buildings and roads across the whole earthquake-affected area. The model predicts the overall pattern of earthquake-induced building damage and landslide impacts, albeit with a tendency towards over-prediction. Our findings underscore the potential of the hypergraph approach for multi-hazard risk assessment, offering advances in rapid computation and scenario exploration for cascading geo-hazards. This approach could provide valuable insights for disaster risk reduction and humanitarian contingency planning, where the anticipation of large-scale trends is often more important than the prediction of detailed impacts.

1 Introduction

There has been a growing recognition over the last 15 years that natural hazards can interact and occur in conjunction with each other, leading to a potential compounding effect that is greater than the sum of the single-hazard impacts (Kappes et al., 2012; Arosio et al., 2020; Terzi et al., 2019). While the global prevalence of cascading hazards specifically is difficult to quantify reliably, there are increasing calls for effective multi-hazard risk assessments (e.g. Ward et al., 2022). Multi-hazards are defined by the UNISDR (2016) as “events [that] may occur simultaneously, cascadingly or cumulatively over time, and taking into account the potential interrelated effects”. Multi-hazard approaches seek to overcome the limitations of a narrower focus on single-hazard models, which are unable to account for the observed interrelationships between different hazards as well as potential compounding or cascading effects (e.g. Gill and Malamud, 2014; Tilloy et al., 2019; Dunant, 2021; Ming et al., 2022). Multi-hazard approaches to risk are now widely encouraged (e.g. UNISDR, 2005; Government Office for Science, 2012) and are increasingly integrated into risk assessment (see recent reviews by Gill et al., 2022; Ward et al., 2022).

There remain, however, some important challenges and limitations with multi-hazard risk assessment. Because of the difficulties in recognising, understanding, and defining the interrelationships between hazards, as well as the lack of data on their co-dependence (Tilloy et al., 2019; Hochrainer-Stigler et al., 2023), most “multi-hazard risk” models simply overlay single hazards without considering their interactions – an approach that Gill and Malamud (2014) termed “multi-layer single hazard”. Even when hazard–hazard interactions are considered in risk models, there is still a lack of comprehensive approaches that capture the intricate interplay among hazards, exposure, and vulnerability beyond simple spatial overlaps (Mignan et al., 2014; De Ruiter et al., 2020). These interactions are critical because of the possibility that risks may be clustered in space and time or may amplify each other, as demonstrated by Mignan et al. (2014). Zschau (2017) extended the ideas of Gill and Malamud (2014) to risk assessment, distinguishing between risk from single hazards, risk from multi-layer single hazards, and risk from multi-hazards – the latter allowing for dynamic hazard interactions but no dynamic interactions between hazard and exposure or vulnerability. Hochrainer-Stigler et al. (2023) noted that hazard–exposure relationships and changes in exposure over time, as well as vulnerability, are also critical to fully characterise multi-risks. This complexity means that multi-hazard risk modelling can be both computationally expensive and extremely demanding of quality input data (e.g. Kappes et al., 2012). Multi-hazard risk models may also be limited by the diversity of hazard types that can be incorporated, mismatches in the appropriate spatial and temporal scale of analyses, and complex data requirements (e.g. Kappes et al., 2012; Tilloy et al., 2019; Dunant, 2021).

A further complication is the growing need for national, regional, or even global-scale risk assessments in order to understand potential patterns of impacts, provide science-based evidence for disaster risk reduction and advocacy, and allow coordinated planning (see review by Ward et al., 2020). At the same time, data are available at ever-increasing spatial and temporal resolution, including information on populations, building stock, and topography, as well as datasets on hazard drivers such as rainfall forecasts or observed precipitation. While these are welcome developments, the combination of demands for increasing scale and increasingly fine-spatial- and fine-temporal-resolution data leads to a much higher computational burden. Addressing the need for both larger spatial scales and finer spatio-temporal resolutions is a growing challenge for the assessment of multi-hazard risks. The distribution of risk may also be highly spatially imbalanced if exposed elements are concentrated in specific areas, meaning that grid-based or GIS-based approaches to risk modelling may expend a lot of computational effort on areas where risk is low or negligible.

To address these concerns, Dunant et al. (2021a) proposed a novel approach to multi-hazard risk modelling using graph theory. In this framework, both the hazards and the elements at risk are modelled as a set of interconnections between nodes. For example, a house can be linked to ground accelerations in an earthquake or a hillslope to rainfall in a storm. This framework can then be used to generate many disaster scenarios by cascading from node to node according to a set of rules (e.g. a threshold earthquake shaking value for slope failure). The resulting network model is highly computationally efficient, and the network structure is a natural fit to the simulation of coincident or cascading events and their propagation through exposure networks (Dunant et al., 2021a) because network structures are purposefully designed to capture the interdependencies and feedbacks among different elements. The framework is agnostic to the types of objects that can be included, so it can be easily adapted to include hazard–hazard, hazard–exposure, and hazard–vulnerability relationships. It is also highly flexible so that the links between objects can be represented via different interactions depending on the level of understanding and data availability, including threshold values, empirical functions, fuzzy distributions, process models, or other approaches (e.g. Tilloy et al., 2019).

Despite its advantages, however, the network model suffers from some important limitations. Most critically, because the interactions in a network model are modelled as pairs, the computational burden grows substantially as the number of components (nodes and edges) of the model increases. Prior applications focused on the epicentral area of the 2016 M_w 7.8 Kaikōura earthquake (Dunant et al., 2021a) and the area around Franz Josef township (Dunant et al., 2021b), both in New Zealand and containing on the order of hundreds of nodes. Expanding the network model to a national scale at a similar resolution would increase the model size by several orders of magnitude. Similarly, increasing the number of hazards that are considered would lead to a combinatorial increase in interactions and rapid growth in computation time.

Here we propose a new approach to modelling the impacts of multi-hazards using hypergraphs – two-dimensional surface equivalents of the pairwise links found in the graph-theory network model of Dunant et al. (2021a). The hypergraph model retains the advantages of the network approach while simultaneously reducing the model complexity. Below, we first present a brief review of graphs and hypergraphs and outline the benefits of using hypergraphs in a multi-hazard risk modelling framework. We describe the structure of the multi-hazard impact model, including its components and the interactions between nodes. We illustrate its application by simulating the impacts from the 2015 M_w 7.8 Gorkha earthquake in Nepal, as an exemplar of a large-scale event that had cascading effects on people and infrastructure due to both primary and secondary hazards. We close by considering wider potential applications of the hypergraph model, including national- or regional-scale disaster scenario ensembles and how they might be used to support humanitarian contingency planning (e.g. Robinson et al., 2018).

2 Summary of graph and hypergraph approaches

A graph is essentially a mathematical representation of a network. The term was originally introduced by Sylvester (1878), but graph theory had been used more than a hundred years before by Euler (1741) to solve the “Seven Bridges of Königsberg” problem. Since then, graph theory has been used in a wide variety of fields such as geography, computer science, social science, and biology (e.g. Buzna et al., 2006; Chorley and Kennedy, 1971; Dezső and Barabási, 2002; Dorogovtsev and Mendes, 2003).

A graph comprises a set of nodes connected by edges. In the context of risks posed by environmental hazards, such nodes may represent a geographical location (spatially explicit; e.g. a fault segment or a house) or a nominal property (spatially implicit; e.g. the occurrence of an earthquake), and the edges represent the relations between the nodes (e.g. earthquake shaking affecting exposed houses) (Fig. 1a).

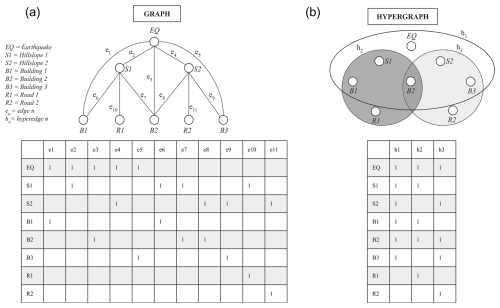
Figure 1 Graph (a) and hypergraph (b) representations of a hypothetical set of hazard and exposure interactions. The same set of elements are represented in both graphical form (top panels) and tabular form as incidence matrices (bottom panels). In the tables, a blank cell means no interaction between the nodes, and a value of 1 means that interactions are possible between the nodes.

A defining characteristic of graphs is the set of pairwise connections or edges between nodes that define the relationships between these nodes. For example, we would represent earthquake shaking on a set of hillslopes as edges between the earthquake and each hillslope that is affected. In tabular form, each edge is represented by a row in a relational database, called an incidence matrix (Fig. 1a). The edges are directional, so a two-way relationship – for example, a hillslope potentially affecting a road via landslides and a road potentially affecting a hillslope via excavation and steepening – would be represented by two separate rows.

As summarised by Dunant et al. (2021a), here we consider relationships between nodes that are observed or felt – that is, via shaking, mass movement, or water flow. We also consider that nodes are connected if (1) the geographical effect of one node overlaps that of another and (2) that effect is relevant to considering impacts from hazards. For example, earthquake ground shaking might affect a hillslope and trigger a new landslide or the mobilisation of loose material in a debris flow; to allow for these effects, we would represent the relationship between earthquake and the hillslope as an edge and the relationship between the hillslope and any houses or road segments on it as a series of additional edges (Fig. 1a). If we were to assume that the earthquake ground motion can potentially cause direct impacts on houses but not roads, then the earthquake would be connected to the houses by edges but not to the road segments (Fig. 1a).

In contrast, a hypergraph is a special type of graph where the edges, called hyperedges, can link one or more nodes (Fig. 1b). This allows us to represent interactions that extend beyond a single pair of nodes (Wolf et al., 2016). Compared to pairwise edges, which only connect two nodes, hyperedges can connect multiple nodes and provide a more natural representation for the spatial overlap between exposed elements, like houses, and geographical hazard footprints. Hyperedges can thus represent nested information between the nodes of the system, such as their properties or locations, with far fewer tabular entries (Fig. 1b). The hypergraph uses fewer edges to represent the same number of interactions for a given number of nodes; this size difference (e.g. for the example in Fig. 1, $\mathrm{11}\times \mathrm{8}=\mathrm{88}$ entries for the graph framework and $\mathrm{3}\times \mathrm{8}=\mathrm{24}$ for the hypergraph framework) highlights the efficiency of the hypergraph approach.

The increased efficiency enabled by hypergraphs becomes more apparent when dealing with large, interconnected datasets and when iterative data manipulation is required. For example, we can run hundreds or thousands of separate simulations on the same hypergraph, choosing different events or altering input parameters within a Monte Carlo framework (e.g. Dunant et al., 2021a) to generate ensemble distributions of scenario outcomes (Robinson et al., 2018). The improvement in computation time allows the hypergraph framework to be applied to multi-hazards risk assessment over larger extents, over longer time periods, and with more complex interactions than would be feasible using a GIS-based approach or standard graph framework.

3 Methodology

Below we describe the set-up and operation of the multi-hazard hypergraph model and describe its application to the 2015 Gorkha earthquake.

3.1 Model overview and set-up

The model is based around a set of interactions between elements in Nepal that are drawn from experience in both the annual monsoon (Kincey et al., 2022; Jimee et al., 2019; Goda et al., 2015; Rosser et al., 2021; Kargel et al., 2016) and recent earthquakes, including the 2015 Gorkha event (e.g. Roback et al., 2018; Milledge et al., 2019; Kincey et al., 2021). For the simulations in this paper, the model is driven only by earthquakes (Fig. 2) and seeks to assess the risk to buildings and roads at a national scale. Earthquake shaking is simulated as a spatial distribution of peak ground acceleration (PGA) values; these could be derived from measurements or generated for a potential scenario earthquake via a shaking model. For the experiments shown here, we use empirical PGA values estimated by the US Geological Survey ShakeMap for the 2015 Gorkha earthquake (https://earthquake.usgs.gov/earthquakes/eventpage/us20002926/shakemap/pga, last access: 1 March 2022). Earthquake shaking can affect infrastructure either directly (described via a set of fragility functions) or by triggering landslides. Landslides, in turn, may affect both buildings and roads. In this version of the model, other hazards such as rainfall and floods are not considered, but they could be added via additional sets of hyperedges and interactions.

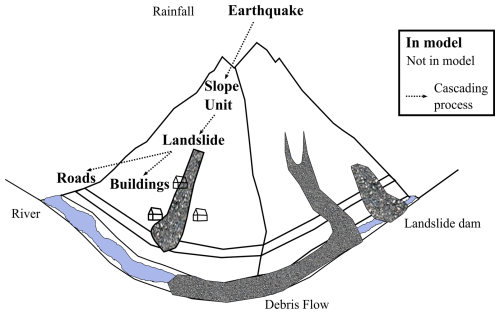
Figure 2 Driving stimuli and important process interactions for the area affected by the 2015 Gorkha earthquake in Nepal. The elements that are included in the multi-hazard impact experiments documented here are shown in bold text.

To model coseismic landslides, we subdivide the landscape into discrete units and consider the characteristics of the topography as well as the driving mechanisms within those subdivisions. Here we divide the landscape into slope units that are bounded by drainages and divide lines (Alvioli et al., 2016; Woodard et al., 2024) (see Supplement and Fig. S1). Woodard et al. (2024) demonstrated that slope units are preferable to gridded topography when representing landslide susceptibility, especially for input landslide data that are imprecise or highly spatially variable in quality. The slope units were generated following the procedure from Kincey et al. (2021) where a DEM is used to segment the landscape into distinct terrain units defined by hydrological and geomorphological boundaries.

The hyperedges are constructed based on the interactions in Fig. 2. A hyperedge connects the earthquake node with all of the slope units and buildings within the “footprint” of the earthquake, defined by the extent of a minimum PGA (X in g) contour. Similarly, hyperedges connect each slope unit with the buildings and roads (divided into 100 m segments) within it; we therefore assume that landslides from one slope unit cannot impact elements in another. Attributes for each building, road segment, and slope unit, such as location, PGA, building type, and landslide susceptibility, are stored on the hyperedges and can be displayed as continuous values in a tabular form. We describe each of these attributes below.

We use building locations and roads taken from the Humanitarian OpenStreetMap Team, covering the whole of Nepal and available at https://data.humdata.org/dataset/hotosm_npl_buildings (last access: 1 January 2022) and https://data.humdata.org/dataset/hotosm_npl_roads (last access: 1 January 2021), respectively. The datasets contain ca. 7.1 million building polygons and ca. 3 million road segments. Because we lack specific information on the construction type of each building to assess its fragility, we instead use exposure data from the Modeling Exposure Through Earth Observation Routines (METEOR) project (https://maps.meteor-project.org/map/building-exposure-map-of-nepal, last access: 1 January 2021) (version 2020-02-15), which includes a list of building types and the number and value of each type within each cell of a 90×90 m grid across Nepal. The METEOR project used a combination of Earth observation (EO) data, such as satellite imagery, and ground-based sampling to classify homogeneous development regions and assess vulnerability of building structures in countries like Nepal and the United States. The development patterns are then associated with typologies observed on the ground (https://nora.nerc.ac.uk/id/eprint/533439/, last access: 1 January 2021) to create a national-scale vulnerability layer. The PGA value of the 2015 Gorkha earthquake is extracted at the centroid of each METEOR grid cell. To account for variability in construction detail and quality within these broad types, we adopt low, middle, and high fragility functions for the “complete damage” state for typical building types in Nepal from the METEOR dataset (Fig. 3). We take the definition of “complete damage” from the Hazus framework of the US Federal Emergency Management Agency (FEMA, 2020). We generate a weighted-average fragility function for the buildings within each 90×90 m grid cell based on the proportion of different building types; thus, in the absence of any national-scale building-specific information, all buildings within that cell are assumed to have the same average fragility. We assess the likelihood of complete damage because this implies loss of usability or habitability, with consequences for displacement and disruption to life and livelihoods, and is typically used to estimate fatality and injury rates (FEMA, 2020).

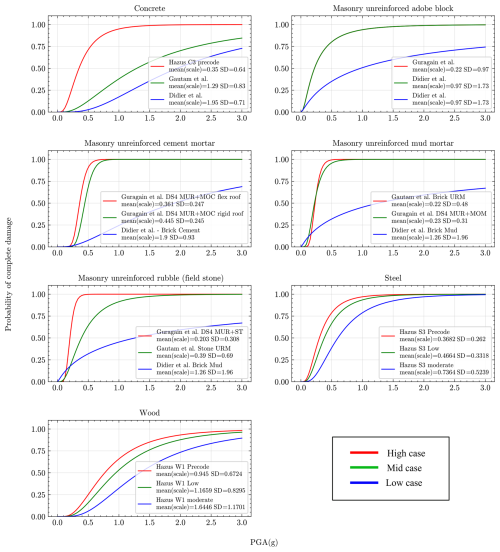
Figure 3 Fragility functions used in the hypergraph network modelling. Each panel shows fragility curves for a different building type in the METEOR dataset which relate the peak ground acceleration (PGA, in g) to the probability of being reduced to a complete damage state. Note that each sigmoidal fragility curve is defined by two parameters: a mean or scale parameter that sets the PGA value for a 50 % probability of complete damage and a standard deviation (SD) that defines the spread of the curve. Parameter values and sources for the fragility curves are included in the plots.

We estimate landslide susceptibility based on topographic factors alone, using a seven-parameter static susceptibility model that incorporates elevation, hillslope aspect, distance to rivers, plan-view curvature, regional relief, local hillslope gradient, and a terrain ruggedness index. These factors are derived from a 10 m digital elevation model (DEM) that was downsampled from the 5 m Advanced Land Observing Satellite World 3D DEM (https://www.aw3d.jp/en/products/standard/, last access: 1 January 2021). We generate the susceptibility model using a gradient-boosting machine learning approach, XGBoost, implemented in Python. For the experiments shown here, the susceptibility model is trained on the locations of coseismic landslides triggered by the 2015 Gorkha earthquake as mapped by Kincey et al. (2021), yielding an area under the receiver operating characteristic (ROC) curve of 0.75 (Fig. S2). We stress that this susceptibility layer is used simply as an exemplar which is optimised for the 2015 Gorkha earthquake; for other model applications, susceptibility data generated with other approaches (see review in Reichenbach et al., 2018) or trained on different inventories could be substituted. Because landslide susceptibility is modelled on a 10×10 m grid, each slope unit contains a unique distribution of cell-wise susceptibility values in the range [0, 1], and each building polygon or road segment overlaps with one or more cell-wise susceptibility values. Importantly, because the multi-hazard model is intended to simulate dynamic cascading scenarios, we choose not to include earthquake shaking as a determining factor in the static landslide susceptibility model. This choice preserves independence between shaking, landslide triggering, and the propagation of hazards along the hyperedges within the model.

We extract the mean and standard deviation of susceptibility for each slope unit, building, and road segment, although other measures of the distribution could also be used. Because we lack general building or road fragility functions for landslides that are comparable to those for earthquakes and that encompass the wide range of possible landslide types and sizes (see Luo et al., 2023, for a recent review), we adopt a simplified binary vulnerability model such that any building or road that is affected by a landslide is considered “impacted”.

3.2 Simulation steps

In each simulation, the model works iteratively through the hyperedges that connect the driving stimulus of earthquake shaking to the other elements in the model, checking against a condition to see whether that hyperedge of the network is “activated” – i.e. a building is damaged by earthquake shaking or a slope unit is affected by one or more landslides. Activation of that hyperedge then allows the stimulus to propagate and potentially to cascade along other hyperedges if further conditions are met (Fig. 4). The simulation continues until all cascades stop and no further impacts are possible.

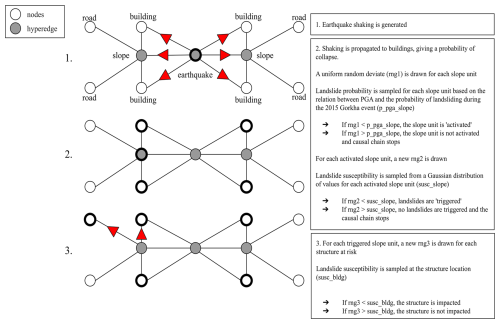
Figure 4 Step-by-step overview of the hypergraph framework for modelling cascading multi-hazard impacts. The hypergraph is represented in a simplified example on the left, and the algorithm steps are specified on the right. The simplified hypergraph assumes a landscape with two slope units, each of which contains two buildings and two road segments. The causal cascades of the algorithm are represented in three steps: from top to bottom, these are (1) earthquake shaking, (2) tests for “activation” of a hillslope and “triggering” of landslides, and (3) tests for impacts on structures by landslides. In the simplified hypergraph, black outlines show the hyperedges where hazards occur (e.g. landslides are triggered by the earthquake) and the nodes that are damaged by either shaking (step 2) or landsliding (step 3). The process is embedded in an iterative Monte Carlo simulation to determine the uncertainty associated with each step, creating a series of disaster scenarios that can be queried for further analysis.

In the experiments shown here, the first step is to work through the hyperedge that connects the earthquake to the individual buildings to assess their damage state. For each building, we assign the PGA value at the centroid of its 90×90 m METEOR grid cell. We use the high, middle, and low weighted mean fragility functions for that grid cell to determine the likelihood of that building being completely damaged – which is equivalent to the proportion of buildings within that 90×90 m grid cell in the METEOR dataset that is completely damaged. This likelihood of complete damage [0, 1] reproduces the weighted mean fragility when applied over the METEOR grid cell. The low, middle, and high cases provide a range of outcomes for an individual building at a specific PGA value. The per-building likelihoods of complete damage under the three cases can then be summed by slope unit or administrative area to give the total predicted number of completely damaged buildings in each area.

Next, we assess which slope units are “activated” by ground shaking (Fig. 4). Activation of a slope unit means that the ground accelerations are high enough to potentially trigger one or more landslides if this is permitted by the topographic conditions as represented by the landslide susceptibility. Again, this allows the stimulus to propagate within the earthquake hyperedge to the slope unit and potentially to cascade within that slope unit (and affect buildings or road segments within it). In these experiments, we conduct a logistic regression between PGA and the locations of landslides in the inventory of coseismic landslides triggered by the 2015 Gorkha earthquake (Kincey et al., 2021) to define the regional-scale probability of landslide occurrence as a lognormal function of PGA (see Supplement and Fig. S3).

We begin by calculating the mean PGA value for each slope unit. This mean PGA value is then used to determine the probability of a landslide occurring within that slope unit, based on the lognormal distribution previously mentioned. To simulate whether a landslide may actually occurs, we compare this calculated probability to a randomly generated number from a uniform distribution. The value sample is coming uniformly distributed over the half-open interval [0, 1). In other words, any value within the given interval is equally likely to be drawn. If the probability exceeds the random number, the slope unit is considered “activated”, indicating that the conditions are sufficient for a potential landslide.

Over many simulations, slope units with a higher frequency of observed coseismic landslides will generally be activated more often, reflecting their greater susceptibility to landsliding. However, because the activation in each simulation depends on the random number generated, the specific pattern of activated slope units will differ from one simulation to the next. As a result, different portions of the hypergraph network are sampled in each individual simulation, providing a varied assessment of potential cascading scenarios.

Once a slope unit is activated, the model advances to assess the potential impact on subsequent components of the network, specifically focusing on whether buildings or road segments within the slope unit are directly affected by a landslide (as illustrated in Fig. 4). This assessment is conducted through a two-step process in the experiments presented here. First, the model checks whether a landslide actually occurred within the activated slope unit. Even if the shaking was intense enough to “activate” the slope unit, the slope might still not experience a landslide due to its low susceptibility. In other words, an activated slope unit does not always result in a “triggered” landslide.

Triggering in the slope unit is determined by drawing a value (A) from a Gaussian distribution of landslide susceptibility with the same mean and standard deviation as the distribution of susceptibility values in that slope unit and comparing that value with a uniform random deviate (B). We employ a Gaussian distribution for efficiency, as this can be calculated in advance of the simulation, and note that it provides a reasonable fit to the actual distribution across a wide range of slope units (Supplement, Fig. S4). If the susceptibility value A is smaller than B, then no landslide has occurred in that slope unit, and propagation along that hyperedge stops. If A is larger than B, then one or more landslides have occurred in that slope unit. We then check if each building and road segment within the slope unit is affected by this landsliding by comparing the landslide susceptibility value at the infrastructure location with another uniform random deviate. If the random deviate exceeds the landslide susceptibility value, then the building or road segment remains unaffected by the landslide (in other words, even if a landslide happens in the slope unit, it does not affect the building or road). Then, the simulation continues to evaluate other buildings or roads within the same slope unit and then moves on to other slope units activated by the earthquake. If the random deviate is less than the susceptibility value, then the building or road segment is impacted by landsliding. In this case, we add it to the pool of affected elements for this simulation and move to the next building or road. We continue this process to search iteratively through all slope units in the network to generate a single cascading impact scenario.

3.3 Outputs and evaluation

The iterative simulation process outlined above is repeated within a Monte Carlo framework to create an ensemble of scenarios, each of which explores a different set of outcomes within the same set of hyperedges. In the experiments shown here, we generate 10 000 scenarios from the initial stimulus of the 2015 Gorkha earthquake. Hence, all scenarios in these experiments use the same spatial distribution of PGA values, and thus the probability of an individual building suffering complete damage by shaking stays the same. What differs between scenarios are the details of which slope units are activated, which slope units experience landsliding, and which buildings or road segments are impacted by those landslides. Thus, we take the likelihood of a structure being affected by landsliding over the whole ensemble as the proportion of the 10 000 scenarios in which the structure is impacted. This leads to a shaking impact likelihood and a landslide impact likelihood, both in the range [0, 1], for each of the buildings and road segments in our combined dataset.

To explore the trade-off between spatial resolution and model performance, we aggregate the structure-level results over successively larger administrative units. Nepal is divided, from smallest unit to largest, into 6743 wards, 753 urban and rural municipalities, 77 districts, and 7 provinces. Aggregation across these units allows us to evaluate the performance of the model against independent measures of earthquake impacts from the 2015 Gorkha earthquake at different spatial resolutions. For buildings damaged by earthquake shaking, we evaluate the model in two ways. First, we sum up the per-building likelihoods of complete damage in each district for the low, middle, and high fragility estimates – which yields the number of completely damaged buildings in each case – and compare those sums to incident reports summarising the number of “fully damaged” buildings per district and published on the Government of Nepal's Bipad Portal (http://drrportal.gov.np/, last access: 1 January 2022; see also Chaulagain et al., 2018) based on the Post-Disaster Needs Assessment (PDNA) (Government of Nepal – National Planning Commission, 2015). This assesses the ability of the model to estimate the absolute number of damaged buildings. While these data remain the most extensive for validation purposes, the PDNA was done urgently after the disaster with limited systematic gathering; hence it relies on judgement by the PDNA participants and, therefore, carries significant uncertainty (Lallemant et al., 2017). Note that wards and municipalities were defined in the federal restructuring of Nepal in 2017, and so data on damaged buildings from the 2015 earthquake are not available at the ward or municipality level. Second, we take the mean likelihood of complete damage in each district, in the range [0, 1], and compare that with the presence or absence of damaged buildings in each of the 77 districts. This second measure is independent of the absolute number of buildings and gives information instead on the ability of the model to anticipate the occurrence of one or more completely damaged buildings in an area.

For structures impacted by landslides, we derive similar statistical measures for model evaluation. First, we sum up the per-structure likelihoods of landslide impact over successively larger areas of aggregation – ward, municipality, district, and province. Because there are no systematic published data on observed landslide impacts on buildings and roads in the 2015 earthquake, we generate an estimate of affected structures by overlaying the coseismic landslide polygons from Kincey et al. (2021) on our building and road dataset; all structures that intersect with a mapped landslide polygon are assumed to have been impacted by landsliding in the earthquake. Note that this measure of landslide impacts does not consider the significant post-earthquake changes in landslide footprint and debris runout (e.g. Tian et al., 2020; Kincey et al., 2022). Also, the coseismic landslides were mapped on medium-resolution satellite imagery (ca. 10 m, equivalent to our DEM and derived topographic metrics) and so will have omitted small landslides or rockfalls, especially in areas of dense vegetation or steep topography (e.g. Williams et al., 2018); this error and the inherent uncertainty in mapped landslide outlines (Kincey et al., 2021) mean that our estimate of the number of landslide-affected structures is likely to represent a lower bound. We then sum the observed number of impacted buildings and road segments by administrative area to compare with our modelled totals. We also compare the mean likelihood of landslide impact, averaged by administrative area and ranging from [0, 1], with the presence or absence of landslide impacts in that area. We evaluate the relationship between these parameters with the area under the ROC curve and the F₁ score.

4 Results

4.1 Impacts from earthquake shaking

We first consider modelled impacts from earthquake shaking alone. Unsurprisingly, the probability of complete damage per building, or equivalently the proportion of completely damaged buildings within each 90×90 m exposure grid cell, closely matches the estimated PGA contours from the Gorkha earthquake (Fig. 5a). There are particularly high probabilities in the hill and mountain districts, especially to the east and northeast of Kathmandu, where the values exceed 0.7. Notably, these values generally increase to the north, and this increase is cut off only by the lack of buildings above elevations of around 3500 m in northern Nepal (visible as the white areas in Fig. 5a). The Kathmandu Valley itself yields a low proportion of completely damaged buildings, despite moderately high PGA values, due to the preponderance of less-fragile building types.

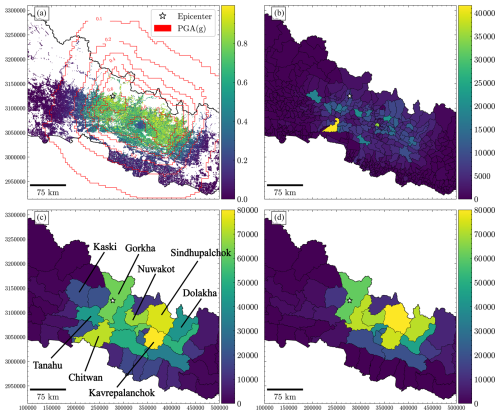
Figure 5 Modelled building impacts from shaking in the 2015 Gorkha earthquake. In all panels, the red contours show the estimated PGA values from the earthquake (in g). Note that these results are derived from the middle-case fragility functions in Fig. 4. (a) Modelled probability of complete damage for individual buildings across the country. This is equivalent to the proportion of completely damaged buildings in each 90×90 m grid cell in the METEOR exposure dataset. (b) Modelled sum total of completely damaged buildings aggregated by municipality. (c) Modelled sum total of completely damaged buildings aggregated by district. (d) Actual sum of reported “fully damaged” buildings aggregated by district. Note similar colour scales in panels (c) and (d).

We convert the proportion of completely damaged buildings per grid cell into a sum total aggregated over municipalities (Fig. 5b) and districts (Fig. 5c). These totals reflect the PGA pattern and the weighted mean fragility functions but importantly also the number of buildings within each administrative area. When aggregated by municipality, the largest modelled totals tend to occur in the more densely populated Middle Hills in the vicinity of Kathmandu rather than the more sparsely populated north. There are some notable exceptions to this pattern, such as Bharatpur to the south of the earthquake epicentre (Fig. 5b), which combines a large stock of fragile building types with moderately high PGA values. When aggregated by district, the largest modelled totals are again dominated by areas with both large numbers of buildings and moderate to high PGA values (Fig. 5c). With the exception of Chitwan to the south of the epicentre, the largest totals are found in districts where PGA exceeded 0.4 g. It is instructive to compare the aggregated pattern by district to the actual numbers of completely damaged buildings (Fig. 5d). There are broad similarities between modelled and observed totals, especially in the hill and mountain districts of Sindhupalchok, Nuwakot, and Kavrepalanchok. Notably, the model over-predicts the impacts in districts close to the epicentre, including Gorkha and Chitwan, and under-predicts the impacts at the eastern margin of the rupture in Dolakha (Fig. 5d).

To better visualise the agreement between modelled and observed totals of completely damaged buildings, we compare the observed totals for all 77 districts in Nepal with model results using the high, middle, and low fragility cases (Fig. 6a). For most districts with non-zero impacts, the observed totals fall within the range of model results using the different fragility curves, with a slight bias toward model over-prediction (Fig. 6b). Among the top 15 districts in terms of modelled impacts, observed impacts fall below that range in 3 districts (Chitwan, Tanahu, and Kaski; see Fig. 5c for locations), within that range in 11, and above that range in only 1 (Dolakha). Alternatively, out of the “14 worst-affected districts” identified by the Government of Nepal, observed impacts fall within the range of model results in 13 districts, with Dolakha being the only outlier. The model thus appears to be somewhat conservative in that it slightly over-predicts building impacts due to shaking in the 2015 earthquake. The mismatch between modelled and observed totals is not clearly related to building typologies (Fig. 6c). There may be a weak correlation with shaking; districts with significant over-prediction tend to be those with lower mean PGA values (typically <0.44 g), while Dolakha has a larger mean PGA (0.59 g), and we explore this point in the Discussion.

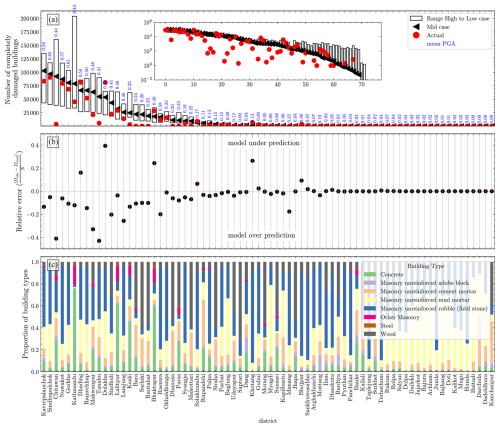
Figure 6 (a) Comparison of modelled and observed numbers of completely damaged buildings per district in the 2015 Gorkha earthquake. Bars show the range of modelled results for each district using high and low fragility cases (see Fig. 4), with the middle case shown by the black arrow. Red dots show the reported numbers of “fully damaged” buildings. Blue numbers show the mean PGA for each district (in g). The inset shows the same quantities with a logarithmic y-axis scale. (b) Mismatch between observed (D_obs) and modelled (D_mod) numbers for each district, normalised by the total number of buildings in that district (N). Negative values indicate model over-prediction, while positive values indicate model under-prediction. Note that impacts in most of the districts with non-zero damage values are slightly under-predicted. (c) Proportion of different building types in each district from the METEOR exposure dataset. There is no clear correlation between the residuals in panel (b) and the dominant building types.

4.2 Impacts from coseismic landslides

As with shaking damage, the modelled probability of a building (Fig. 7a) or road segment (Fig. 7d) being impacted by a coseismic landslide scales with PGA; this is simply a consequence of the assumed relationship between PGA and landslide triggering (Fig. S3). Higher probability values are found in northern areas of Nepal, where landslide susceptibility is elevated (Fig. S2). We aggregate these probabilities to estimate the number of impacted buildings and road segments at the municipality (Fig. 7b and e) and district (Fig. 7c and f) levels. The regions experiencing the highest predicted impacts closely align with those observed, notably concentrated in Sindhupalchok district, where both modelled and observed landslide impacts are most prevalent (Fig. 7c and f). Again, these areas predominantly lie in northern Nepal where susceptibility to landslides is greatest, contrasting somewhat with the distribution of modelled shaking damage. This disparity may stem from the higher and more widely dispersed density of buildings in the southern regions. Consequently, while shaking-related damage appears diffuse, landslide-related damage is more focused in specific regions due to localised exposure. Importantly, the model anticipates fewer building impacts from landslides by approximately an order of magnitude as compared to those damaged by shaking (note the scale difference between Figs. 5 and 7). We also note that, while the overall spatial patterns of modelled building and road impacts are similar, the model predicts somewhat higher numbers of road impacts (by about 50 %) and that this generally matches the observed differences in intersections between these infrastructure types and coseismic landslides (Fig. 7). Roads are typically sited along or near valley floors, thus increasing their exposure to landslides. Additionally, there is a significant association between roads and landslides (e.g. Hearn and Shakya, 2017; McAdoo et al., 2018), suggesting that the interaction between landslides and roads may cover a broader spatial extent compared to the relationship between landslides and buildings.

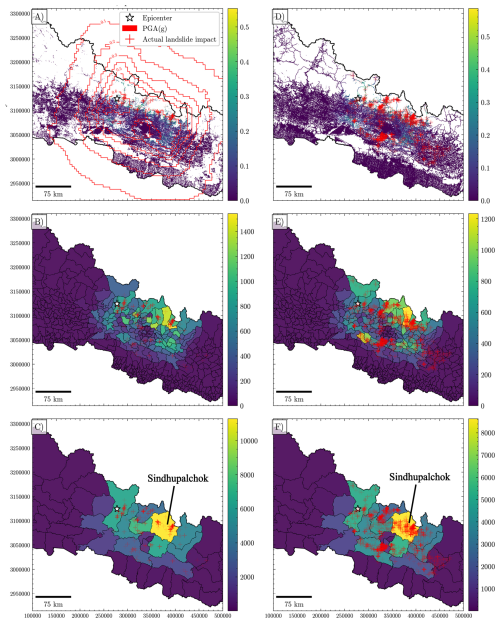
Figure 7 Modelled structural impacts from coseismic landslides in the 2015 Gorkha earthquake. In all panels, the red contours show the estimated PGA values from the earthquake (in g). The red crosses show observed landslide impacts on buildings (a–c) and road segments (d–f), derived by mapping the intersections between those structure locations and the coseismic landslide inventory of Kincey et al. (2021). (a) Modelled probability of impact for individual buildings across the country. (b) Sum of per-building probabilities aggregated by municipality, of which there are 753 in Nepal. (c) Sum of per-building probabilities aggregated by district, of which there are 77 in Nepal. (d) Modelled probability of impact for individual 100 m road segments across the country. (e) Sum of per-road segment probabilities aggregated by municipality. (f) Sum of per-road segment probabilities aggregated by district.

The correlation between the modelled and observed numbers of buildings impacted by landslides depends upon the area over which they are aggregated (Fig. 8). At province (n=7) and district (n=77) levels, there is an approximately linear relationship between modelled and observed numbers of buildings, with a Pearson's correlation coefficient > 0.80 (Fig. 8). At municipality and ward levels, however, the correlation is much weaker. Notably, modelled numbers of buildings over-predict the observed totals by a factor of about 0–100, irrespective of the administrative area. Similar results are seen for road segments: good linear correlations for province- and district-level aggregation, much weaker performance for municipalities and wards, and over-prediction of impacts by a factor of about 20–25 (Fig. 8).

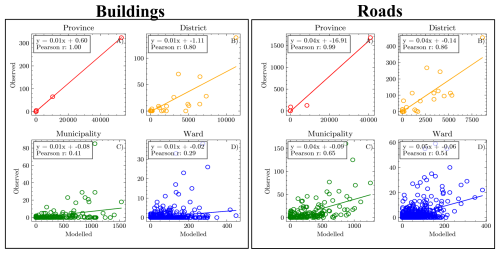
Figure 8 Comparison of modelled (x axis) and observed (y axis) numbers of building and road impacts from coseismic landslides in the 2015 Gorkha earthquake, summed over different administrative areas. Straight lines show best-fit linear regression results. Note differences in axis limits depending on the area of aggregation by province (red), district (orange), municipality (green), or ward (blue).

As a more permissive test of the model's ability to anticipate landslide impacts, we also compare the mean likelihood of landslide impacts, averaged by administrative area, with the presence or absence of impacts in those areas. While the area under the ROC curves is high for all aggregation levels (Fig. 9), this is likely due to the strong imbalance between prediction categories (i.e. there are many more non-impacted buildings than impacted buildings, so the ROC curve is dominated by the large number of true negative model results). In contrast, precision–recall curves show a progressive decrease in model performance at progressively smaller levels of aggregation, from province to ward, and very low precision at the scale of an individual building or road segment (Fig. 9). Because F₁ scores combine precision and recall, they show a similar pattern (Fig. 9); across the full range of thresholds, F₁ scores for both buildings and roads (Fig. 9) are highest for province- and district-level aggregation and lowest for ward-level aggregation. For an optimal model threshold, province-level aggregation achieves maximum F₁ scores of ca. 0.8 for buildings and ca. 0.65 for roads. The maximum F₁ scores for buildings are also around 0.8 for districts and diminish progressively to 0.55 for municipalities and 0.4 for wards. For roads, the maximum F₁ scores are 0.8 for districts and municipalities and 0.55 for wards. In sum, these results indicate that, while the model can reproduce the spatial pattern of landslide impacts at the provincial or district scale, its predictive capability is much weaker when assessing impacts within smaller administrative units like municipalities and wards, and it should not be used to predict impacts on individual buildings or road segments.

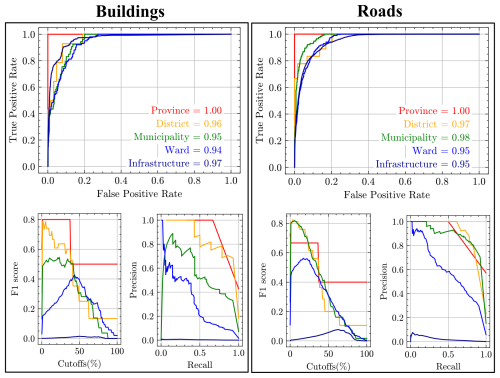
Figure 9 ROC (top panels), F₁ (lower left panels), and precision–recall (lower right panels) curves for coseismic landslide impacts of buildings and road segments aggregated over province, district, municipality, ward, and individual infrastructure scales. Numbers in the top panels show the area under the ROC curves. Line colours match the symbol colours in Fig. 8.

5 Discussion

5.1 General observations

Overall, the hyperedge model is able to reproduce the overall spatial pattern of the impacts from the Gorkha earthquake. This lends some confidence that the model framework could be adapted to estimate the potential impacts from a future event, such as a large earthquake or rainstorm. While the computational efficiency of the hyperedge approach is a notable strength – enabling rapid simulations involving extensive elements, such as the approximately 7.1 million individual buildings and 3 million road segments in our case – its significance extends beyond speed and flexibility because it fosters the generation of multi-hazard scenario ensembles, diverging from the limitation of focusing solely on deterministic impact scenarios. Robinson et al. (2018) demonstrated the advantages of scenario ensembles over the more common approach of single deterministic scenarios, especially as a tool for facilitating awareness of what could be possible in a future event. While the creation of multi-hazard scenario ensembles is our wider goal, the experiments shown here focus on multiple realisations of the same past event for the purpose of evaluation.

A key finding of the experiments is the trade-off between model performance, in terms of the ability to anticipate both the spatial pattern and number of impacts, and the resolution of the model outputs. Because of the probabilistic nature of the model and limitations in our understanding of exposure, earthquake shaking, and landslide susceptibilities, we cannot say with confidence which buildings were impacted by hazards related to the 2015 earthquake. As we aggregate the model results over increasingly large areas, however, our ability to rank those areas in terms of impact and to estimate the number of structures affected increases monotonically. While our results can therefore not be used to anticipate the risk to individual households, they could be used by organisations working at a larger scale to identify areas that are more or less prone to different types of hazards and provide a relative ranking in terms of the number and scale of expected impacts. Thus, the value and potential usefulness of the hypergraph approach as implemented here lies more in informing planning over larger spatial scales, at which the model performs best, as opposed to rapid response to a particular event where detailed spatial information would be required. There is some indication that absolute numbers of affected structures could be generated for larger administrative units by extrapolating the scaling by our analysis of the 2015 earthquake (see, for example, Fig. 8), but we hesitate to draw conclusions from a single earthquake without further testing.

5.2 Over-prediction and relative impacts between hazards

We note that the model over-predicts the number of impacts at all levels of aggregation and is therefore conservative in terms of anticipating the scale of impacts for the 2015 earthquake. The possible reasons for this over-prediction are likely to differ for shaking and landslide impacts. The mismatch in the number of buildings damaged by shaking is especially notable for districts with moderate mean PGA values (typically <0.5 g; Fig. 6a). The sigmoidal fragility functions used in the model are steepest at moderate PGA values (Fig. 3); for the middle case, this corresponds to PGA values of ∼0.2–0.5 g for the most common building types in Nepal. Thus, small uncertainties in PGA will yield large differences in the likelihood of complete damage and thus in the numbers of completely damaged buildings in our model experiments. This issue is compounded by the highly uncertain values of ground motion of the Gorkha earthquake stemming from the paucity of strong-motion recordings, as noted by Goda et al. (2015). We also note that our experiments do not account for aftershocks, including the M_w 7.3 earthquake that occurred on 12 May and that ruptured the eastern end of the 25 April slip patch under Dolakha district (Avouac et al., 2015). This event likely led to additional building damage which was included in the observations but is not simulated here, perhaps leading to under-prediction in Dolakha in particular.

Over-prediction of observed landslide impacts, in contrast, may result from a range of different factors. As noted above, in the absence of an independent dataset of landslide impacts on buildings or roads for the 2015 earthquake, we have generated these data by intersecting those elements at risk with the coseismic landslide inventory of Kincey et al. (2021). This is likely to under-predict the actual number of impacts due to errors and limitations in landslide mapping as well as the potential for buildings to be omitted from the Humanitarian OpenStreetMap Team database. It is also important to note that our approach relies on a probabilistic sampling of an underlying landslide susceptibility dataset in order to anticipate (1) the slope units in which a landslide is most likely to be triggered and (2) the buildings and road segments that were most likely to be affected. Our results are thus highly dependent upon the quality of the underlying susceptibility information. In the experiments described here, susceptibility is a static quantity that depends only upon local topography. Because we are focused on a single event, there is no direct provision for dynamic variation in susceptibility over time or for other factors that may affect landslide occurrence, such as the presence or absence of antecedent rainfall, soil moisture or other measures of ground condition, or land cover. Further applications of the model could incorporate susceptibility estimates that are trained on other landslide inventories – for example, time-varying susceptibility that captures the evolution of landslide hazard over time (e.g. Tian et al., 2020; Kincey et al., 2021, 2022) or that depends upon other causative factors (e.g. Reichenbach et al., 2018).

Our model result that the number of buildings damaged by ground shaking is approximately an order of magnitude greater than that impacted by landslides is difficult to test directly because of the lack of a systematic description of the sources of building damage in the 2015 Gorkha earthquake. It is broadly consistent, however, with previous work on the relative importance of secondary hazards – including landslides – and ground shaking in determining earthquake losses. Bird and Bommer (2004) assessed the relative impacts of ground shaking and ground failure on direct and indirect losses from earthquakes. They found that fatal landslides occurred in 10 of their 50 studied earthquakes and that landslides could be the primary cause of building damage in affected areas, locally overshadowing ground shaking. Overall, however, ground shaking was the primary cause of building damage in 88 % of their studied earthquakes and landslides in only 6 %. They also found that landslide-induced disruption of road or transport networks was much more common than building damage, which matches our model results for the Gorkha earthquake. Daniell et al. (2017) argued that ground shaking has caused 62 % of total economic costs in earthquakes over the period 1900–2016, with landslides responsible for 5 % of total costs. Marano et al. (2010) found that 21.5 % of the fatal earthquakes in the PAGER-CAT database had deaths due to secondary hazards but that these were rarely the main cause of death. Landslides were the leading cause of non-shaking-related deaths if the great 2004 Sumatra earthquake was excluded, although they accounted for about an-order-of-magnitude fewer deaths than ground shaking. In contrast, Budimir et al. (2014) demonstrated that earthquakes with landslides typically cause more fatalities than those without, independent of other factors such as earthquake size or affected population. Their results demonstrate the need to account for the full multi-hazard cascade in anticipating losses at anything other than a simplified regional scale (e.g. Bird and Bommer, 2004; Daniell et al., 2017).

5.3 Limitations

While the model operates on a hyperedge that connects every structure within the dataset, there are a number of factors that cannot be resolved at a building scale. Notably, PGA values were gridded at a spatial resolution of 100 m by 100 m, meaning that we have no information on the actual accelerations experienced by individual buildings or road segments. Similarly, while landslide susceptibility was estimated using a comparatively fine-scale DEM with a grid size of 10×10 m, each individual building or road segment occupies at most a few grid cells and the susceptibility values are thus highly location-dependent. It is also important to note that we do not simulate the triggering, occurrence, and runout of individual landslides, nor do we “place” landslides in the landscape as would be done for example in a landscape evolution model (e.g. Croissant et al., 2017, 2019). Such a calculation would dramatically increase the model complexity, making it infeasible to construct a multi-hazard scenario ensemble at a national scale. Because of this limitation, we cannot directly evaluate which elements at risk are directly impacted by landslides, nor can we anticipate which elements may be affected by the remobilisation and runout of landslide debris (e.g. Kincey et al., 2022). By sampling the landslide susceptibility distribution for each slope unit and the landslide susceptibility values for each building, we are (over enough iterations) recovering those distributions, but we cannot overcome the inherent uncertainty in susceptibility at those locations. Finally, the METEOR exposure dataset contains information on the building types and numbers within each 90×90 m grid cell, but we have no information on the type and fragility of individual buildings. Therefore, while impact likelihood is calculated at the scale of individual structures, we stress that this estimate is only meaningful across the whole scenario ensemble and should never be interpreted as a statement that “building X will be affected by this earthquake”.

5.4 Other applications

Because of its efficiency, the framework allows exploration of other elements of model performance, including the distinction between false positive and false negative errors. While performance measures such as the area under an ROC or precision–recall curve can be used to define an “optimum” model outcome, the model application and users may determine which type of error is more important to minimise. For example, a humanitarian organisation may view false positives as more acceptable than false negatives; the former may lead at worst to unnecessary preparations, whereas the latter means that impacts are not anticipated and may delay relief and recovery efforts. By quickly generating numerous multi-hazard scenarios, the framework can be run with users to explore these different outcomes and to examine the specificity of model results to the details of a particular scenario (e.g. Robinson et al., 2018). The model could also be used to explore “what if” questions with users to examine the effects of particular interventions or remediation measures. In addition, the efficiency of the framework could be used to explore the evolution of risk over time, where increased simulation length or time resolution would lead to an increase in computational cost. Thus, the effects of policy decisions, climate change and consequent changes in hazard occurrence, or demographic shifts on the pattern of anticipated impacts could be explored (Zschau, 2017).

The flexibility of the hyperedge framework also lends itself to other types of simulation. Other elements of the multi-hazard chain shown in Fig. 2 could be included; for example, susceptibility to landslide debris remobilisation and runout could be included and sampled for each element at risk, allowing the model to anticipate both the direct impacts within an event and the potential longer-term impacts arising from later secondary hazards (e.g. Fan et al., 2019; Kincey et al., 2022). Impacts from other types of driving events, such as monsoon rainfall, could also be explored. It would be feasible, for example, to generate an ensemble of scenarios around different rainfall patterns associated with a seasonal monsoon outlook or with different iterations of shorter-term weather forecasts to look at the pattern and specificity of impacts. Such an application would be subject to the comparatively low spatial resolution of both observational (e.g. Hou et al., 2014) and forecast rainfall data products so that – just as with the earthquake scenarios developed here – the impact results at the scale of an individual structure would not be meaningful. The hyperedge framework would, however, allow exploration of the trade-offs between aggregation and model performance, as demonstrated here, and could be useful for informing humanitarian contingency planning for annual rainfall-related impacts in Nepal and other monsoon-affected countries.

6 Conclusions

Accounting for the multi-hazard aspects of risk is crucial for disaster risk reduction and humanitarian planning. Traditional approaches to risk modelling tend to omit the interactions between hazards and, even when these interactions are accounted for, may struggle to meet the computational demands posed by such complex scenarios. Here, we demonstrate that a new model based on hypergraph theory, a type of network modelling approach, is able to efficiently simulate multi-hazard risk. The model framework accounts for the interactions between a driving stimulus such as an earthquake or rainstorm with processes on the landscape (such as landslides) and exposed infrastructure. Beyond overcoming computational challenges, this framework can facilitate multi-hazard risk assessments by enabling the generation of ensembles to explore the importance of different geophysical hazards, larger areas, longer time frames, and diverse counterfactual scenarios. This versatility enhances our understanding of complex risk landscapes and empowers decision-makers with valuable insights for proactive disaster preparedness and response strategies.

We explore the capabilities of the model through a case study of the 2015 M_w 7.8 Gorkha earthquake in Nepal, which caused widespread damage due to both primary shaking and secondary landslides. We find that the model can reproduce the overall spatial pattern of earthquake impacts. The observed numbers of completely damaged buildings in most districts, including 13 out of the 14 worst-affected districts, fall within the range of model predictions, which depends primarily on the assumed fragility functions for the typical building types found in Nepal. The model also broadly reproduces the spatial patterns of structures that were damaged by coseismic landslides in the earthquake, although it overestimates the absolute number of impacts. This may be due to limitations in the data used by the model to determine impacts. Importantly, there is an increase in model performance when the results are aggregated over larger administrative areas; the model does a reasonable job of anticipating the relative impacts at a province or district scale but performs much less well at the smaller scales of municipalities or wards. This result suggests that the hypergraph framework could be usefully applied to rank administrative areas by expected impacts, for example due to a future earthquake or rainstorm, to underpin pre-disaster contingency planning efforts where large-scale trends are more important than detailed impact predictions. The computational efficiency of the hypergraph framework, even at the scale of an entire country such as Nepal, lends itself to the generation of multiple impact scenarios and raises the possibility of using an ensemble of potential scenario results rather than depending upon single-event scenarios for disaster preparedness and planning.