Comparative analysis of μ(I) and Voellmy-type grain flow rheologies in geophysical mass flows: insights from theoretical and real case studies

The experimentally based μ(I) rheology is now prevalent in describing the movement of gravitational mass flows. We reinterpret the μ(I) rheology as a Voellmy-type relationship to highlight its connection to grain flow theory and demonstrate its practical applications. Using one-dimensional block modeling and two real-world case studies – the 2017 Piz Cengalo rock–ice avalanche and an experimental snow avalanche at the Swiss Vallée de la Sionne test site – we demonstrate the relationship between the dimensionless number I and the granular temperature R, establishing the equivalence between μ(I) and widely used Voellmy-type grain flow rheologies μ(R). Results indicate that μ(I) rheology utilizes the dimensionless inertial number I to mimic contributions of granular temperature/fluctuation energy to flow behavior. In terms of Voellmy, the μ(I) rheology contains a velocity-dependent turbulent friction coefficient that models shear-thinning behavior. This turbulent friction assumes the production and decay of fluctuation energy are in balance, exhibiting no difference during accelerative and depositional phases of avalanche flow. The constant Coulomb friction coefficient prevents μ(I) rheology from accurately modeling the dispositional characteristics of actual mass flows. The modeled evolution of the snow avalanche using the μ(I) rheology is too slow, lagging 5 s behind the measured values. More importantly, the calculated runout extends approximately 200 m beyond the observed limits, with significant deposit anomalies in the valley. By incorporating non-steady production and decay of fluctuation energy in the μ(R) framework, it becomes possible to achieve a good match with both the measured velocities and the observed runout. Our results highlight the strengths and limitations of both μ(I) and Voellmy μ(R) rheologies, bolstering the theoretical foundation of mass flow modeling while revealing practical engineering challenges.

1 Introduction

Creating dependable methods to forecast the runout and deposition characteristics of geophysical mass flows stands as a fundamental challenge in natural hazard research. Long-runout mass flows, like debris flows, rock–ice avalanches, and snow slides, occur in complex mountain terrain and exhibit an array of complex outcomes depending on their initial material composition and dynamic interactions with the substrate. These mass movements of granular composition exhibit significant mobility, vast energy, and diverse flow patterns, posing challenges for prediction using numerical models (Crosta et al., 2007; Hürlimann et al., 2015; Iverson et al., 2015; Frigo et al., 2021; Shugar et al., 2021). A crucial element for precise modeling of their various behaviors is the development of a universal rheology capable of accurately capturing their granular motion, including long-distance travel, transitions between flow regimes, and eventual deposition.

Presently, two primary types of numerical models dominate in engineering practice: discrete element methodologies (Scaringi et al., 2018; Zhao and Crosta, 2018) and continuum approaches, often employing depth-averaged techniques (Hungr and McDougall, 2009; Christen et al., 2010). Discrete approaches simulate particle interactions, incorporating fragmentation processes and thus adeptly portraying the complex behavior of flowing granular materials (Katz et al., 2014; Zhao et al., 2017; Zhuang et al., 2023a). Nonetheless, accurately replicating the sheer volume of particles within real geophysical mass flows remains a formidable challenge, constraining the utility of discrete approaches for solving large-scale problems due to computational constraints. Conversely, the continuum approaches treat the mass flow as a “granular fluid” consisting of particle ensembles. They utilize a series of differential equations to calculate the flow process, offering high computational efficiency (McDougall and Hungr, 2004; Christen et al., 2010; Mergili et al., 2017). Because existing continuum approaches account for the essential process of ground entrainment (Sovilla and Bartelt, 2002; Bartelt et al., 2018a), frictional heating, and phase changes (Valero et al., 2015; Bartelt et al., 2018b), they are somewhat more advanced than discrete element approaches and thus have been widely used to assess mass flow hazard.

The Voellmy rheology (Voellmy, 1955) has a long tradition in the hazard mitigation community and is applied to predict the velocity and runout of avalanches and debris flows (Hungr, 1995; Schraml et al., 2015; Aaron et al., 2019; Zhuang et al., 2020). It defines the relationship $\mathit{\mu }\left(V\right)=S/N$ as follows:

$$\begin{array}{}\text{(1)}& \mathit{\mu }\left(V\right)={\displaystyle \frac{S}{N}}={\mathit{\mu }}_{\mathrm{s}}+{\displaystyle \frac{v^{\mathrm{2}}}{{\mathit{\xi }}_{\mathrm{0}}h}},\end{array}$$

where μ_s considers the Coulomb friction at “stopping”, v is the flowing velocity, ξ₀ is the “turbulent” friction parameter, and h is the flowing height. Voellmy considers μ_s to describe the “solid” behavior of the flowing mass, whereas ξ₀ represents the “fluid”-like behavior. Because the Voellmy model is grounded in clear physical principles and involves only two parameters, it is frequently used in hazard mitigation. However, a major issue with the Voellmy model is that the travel resistance of mass flows varies significantly with the flow regime (Gruber and Bartelt, 1998). In the Voellmy model, each flow regime requires a distinct set of calibrated flow parameters; there is no universal parameter set available, rendering the Voellmy approach somewhat makeshift. To address this issue, multiple researchers have suggested incorporating the concept of granular temperature (fluctuation energy R) to accurately model the flow of granular materials across both dense and fluidized flow regimes (Haff, 1983; Jenkins and Savage, 1983; Jenkins and Mancini, 1987; Gubler, 1987; Buser and Bartelt, 2009). The term granular temperature (fluctuation energy R) originates from thermodynamics and represents the kinetic energy associated with random particle motions in the granular ensemble; it is defined based on the velocity fluctuations of individual grains (Campbell, 2006). This approach involves adding an extra differential equation to account for the generation and dissipation of kinetic energy due to random particle movements (Bartelt et al., 2006). The fluctuation energy arises from the shear-work rate ${\dot{W}}_{\mathrm{f}}$ and decays by dissipative granular interactions (Haff, 1983):

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}}=\mathit{\alpha }{\dot{W}}_{\mathrm{f}}\left(t\right)-\mathit{\beta }\left(qR\right)R\left(t\right),\end{array}$$

where α governs the production and β governs the decay of the fluctuation energy. It is possible to express the friction parameters (μ_s, ξ) as a function of the fluctuation energy, named μ(R) rheology. Within the Voellmy framework, the μ(R) rheology has the following form (Christen et al., 2010; Zhuang et al., 2024):

$$\begin{array}{}\text{(3)}& \mathit{\mu }\left(R\right)={\mathit{\mu }}_{\mathrm{s}}\left(R\right)+{\displaystyle \frac{v^{\mathrm{2}}}{\mathit{\xi }\left(R\right)h}},\end{array}$$

where ${\mathit{\mu }}_{\mathrm{s}}\left(R\right)={\mathit{\mu }}_{\mathrm{s}}{e}^{-\frac{R\left(t\right)}{R_{\mathrm{0}}}}$ and $\mathit{\xi }\left(R\right)={\mathit{\xi }}_{\mathrm{0}}{e}^{\frac{R\left(t\right)}{R_{\mathrm{0}}}}$; the parameter R₀ scales the fluctuation energy. This μ(R) rheology has the advantage of modeling shear thinning in avalanche flows, showing better agreement with observed front velocities and mapped deposition patterns of avalanches than the classic Voellmy approach (Preuth et al., 2010; Bartelt et al., 2012).

Recently, is has been proposed that the μ(I) rheology describes the motion of geophysical flows. This arose directly from the study of small-scale granular experiments (GDR MIDI, 2004; Jop et al., 2006):

$$\begin{array}{}\text{(4)}& \mathit{\mu }\left(I\right)={\displaystyle \frac{S}{N}}={\mathit{\mu }}_{\mathrm{s}}+{\displaystyle \frac{({\mathit{\mu }}_{\mathrm{2}}-{\mathit{\mu }}_{\mathrm{s}})}{\frac{I_{\mathrm{0}}}{I_n}+\mathrm{1}}}.\end{array}$$

Similarly to Voellmy's approach, the model consists of two parts. The first part consists of the stopping friction μ_s. The second term is controlled by the inertial number I_n, which describes the ratio of inertial forces of grains to imposed forces and is defined as (GDR MIDI, 2004)

$$\begin{array}{}\text{(5)}& I_{\mathrm{n}}={\displaystyle \frac{\mathrm{5}}{\mathrm{2}h}}{\displaystyle \frac{vd}{\sqrt{g_{\mathrm{z}}h}}},\end{array}$$

where d is the granule diameter and g_z the slope-perpendicular component of gravity. The model contains two additional constant parameters, I₀ and μ₂, which can be considered the friction at large values of I_n. Because of its well-established experimental foundation, the μ(I) model has become popular in the granular mechanics community and is applied in hazard practice (e.g., Longo et al., 2019; Liu et al., 2022). Although there is broad interest and advocacy for its use, the physical implications of the μ(I) rheology are not completely understood, which restricts its widespread adoption.

In this study, we reformulate the μ(I) rheology as a Voellmy-type relationship. Through one-dimensional block modeling, we investigate the equivalence and difference between the μ(I) and Voellmy-type grain flow rheologies. Two historical cases – the 2017 Piz Cengalo rock–ice avalanche and a snow avalanche at the Vallée de la Sionne test site in Switzerland – are further analyzed to demonstrate the performance of the μ(I) rheology. The primary objective of this study is to establish the μ(I) rheology within a more robust theoretical framework, critically enhancing our understanding of its utility in predicting the dynamics of geophysical mass flows. This endeavor is essential to establish a comparative understanding of different models presently used in natural hazard practice.

2 Method and data

2.1 Reformulation of the μ(I) rheology

The rheological model describes the relationship between the shear stress S and the normal stress N of the flowing mass. Comparison between the μ(V) and μ(I) rheologies is, for practical applications, intuitively made in S vs. N space. Here, we vary the flow height (normal stress) and fix the velocity at a specific value to make the comparison, as presented in Fig. 1a. The quantitative and qualitative similarity between the μ(V) and μ(I) approaches in S vs. N space suggests a mathematical relationship between the two models. In light of this, we have reformulated the μ(I) rheology using a Voellmy sum:

$$\begin{array}{}\text{(6)}& \mathit{\mu }\left(I\right)={\mathit{\mu }}_{\mathrm{s}}+{\displaystyle \frac{v^{\mathrm{2}}}{\mathit{\xi }\left(I\right)h}},\end{array}$$

where ξ(I) characterizes the “turbulent friction” of the μ(I) model. We find

$$\begin{array}{}\text{(7)}& \mathit{\xi }\left(I\right)={\displaystyle \frac{v\left[\mathrm{2}{I}_{o}h\sqrt{g_{\mathrm{z}}h}+\mathrm{5}vd\right]}{\mathrm{5}({\mathit{\mu }}_{\mathrm{2}}-{\mathit{\mu }}_{\mathrm{s}})d}}.\end{array}$$

Differently from the constant ξ₀ value in the Voellmy approach, ξ(I) is changing during the flowing process and is dependent on the flowing velocity and height (Fig. 1b).

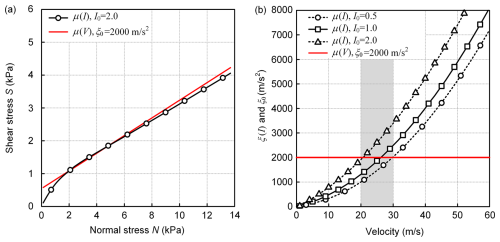
Figure 1 μ(I) vs. μ(V) rheology for typical snow avalanche conditions, v = 20 m s⁻¹ and ρ = 300 kg m⁻³. For this example, we take μ_s = 0.2679 = tan (15°) and μ₂ = 0.8391 = tan (40°). (a) The curve I₀ = 2.0 plotted against μ(V) with ξ₀ = 2000 m s⁻². Note the strong similarity between the μ(I) and μ(V) approaches in S vs. N space. (b) Comparison of the μ(I) vs. μ(V) rheologies in velocity space. ξ(I) increases with velocity; ξ(V)=ξ₀ is constant. In the shaded region 20 m s⁻¹ ≤ v ≤ 30 m s⁻¹, the ξ(I) and ξ(V) values are similar.

2.2 One-dimensional block modeling analysis

The turbulent friction coefficient ξ(I) is velocity-dependent. According to Fig. 1, the primary reason for the similarity of the two results is the selected velocity for the comparison v = 20 m s⁻¹. For velocities outside this range, the ξ(I) and ξ(V)=ξ₀ = constant values differ (Fig. 1b). Therefore, to investigate the difference between μ(I) and μ(V,R), we must study the models over a wide range of velocities typical of a specific geophysical flow from initiation to runout.

For this purpose, we construct a one-dimensional block model. A block of height h and mass m starts from rest on a steep slope of 35° (release zone). After 30 s, the block enters a transition zone of 20°, where it begins to decelerate. After 90 s, the block enters a flat runout zone and stops. We calculate the speed and location of the block's center of mass; friction is given by μ(I), μ(V), and μ(R). The governing ordinary differential equations for this model are

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}}=v\left(t\right),\text{(9)}& {\displaystyle \frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}}=g_x\left(t\right)-\mathit{\mu }(I,V,R)g_z\left(t\right),\end{array}$$

where x(t) is the flowing distance, v(t) is the flowing velocity, and (g_x, g_z) are the components of gravity acceleration.

We consider the motion of the center of mass to represent the motion of a granular, geophysical flow. Such simple, one-dimensional sliding-block models of avalanche flow have been used extensively to calculate hazard maps (Perla et al., 1980). This approach allows us to compare the μ(I) and μ(V,R) rheologies in velocity space.

2.3 Case study of historical avalanches

According to the reformulation of the μ(I) rheology, the ξ(I) parameter is a function of both flowing height and flowing velocity (Eq. 7), which are heavily dependent on the flowing regime and entrainment process. The one-dimensional block model ignores the essential features and processes mentioned above. Therefore, we conduct an analysis of two historical avalanche cases: the 2017 Piz Cengalo rock–ice avalanche (Mergili et al., 2020) and a snow avalanche (no. 20163017) that occurred at the Vallée de la Sionne test site, Switzerland (Sovilla et al., 2018). The Piz Cengalo avalanche occurred on 23 August 2017 with a released rock volume of ∼ 3 × 10⁶ m³. The sliding mass entrained the glacier of 6 × 10⁵ m³ and formed a rock–ice avalanche. This avalanche is well documented with laser scans of release and deposits, providing natural materials to confirm the numerical model (Mergili et al., 2020; Walter et al., 2020). The snow avalanche (no. 20163017) was artificially triggered on 18 January 2016. The avalanche involved an initial volume of 86 560 m³ and a runout of ∼ 2500 m. The difference between DEMs before and after the event indicated the deposit structure, and cameras recorded the evolution of the snow avalanche. Detailed information about this particular snow avalanche is presented in Sovilla et al. (2018).

We implement the Voellmy μ(V), μ(I), and μ(R) rheologies in a continuum-approach-based model RAMMS (Christen et al., 2010; Bartelt et al., 2018b; Zhuang et al., 2024) to elucidate the performance and limitations of the μ(I) rheology in calculating the evolution of geophysical mass flows. Detailed information about the well-established RAMMS model can be found in Christen et al. (2010), Bartelt et al. (2016, 2018b), and Zhuang et al. (2024).

3 Results

3.1 Rheology comparison using the one-dimensional block model

3.1.1 The μ(I) and μ(V) rheologies in velocity space

The direct comparison of μ(I) and μ(V) reveals that both models can produce similar runout levels (Fig. 2a) and velocity (Fig. 2b). However, the μ(V) approach reaches a smaller peak velocity at the end of the release zone and decelerates less strongly in the transition zone (Fig. 2b). Ultimately, the velocity at the beginning of the runout zone is higher. This result can also be visualized in the depiction of location through time (Fig. 2a). The Voellmy flow reaches the same runout distance but lags the μ(I) model along the intermediate transition segment. Of interest is a direct comparison of μ(I) and μ(V) through time (Fig. 2c). The μ(V) with constant ξ₀ reaches larger values (lower velocities) but decreases rapidly during the transition to the flatter 20° slope, falling to values smaller than μ(I). Both models predict the same μ values as the block enters the flat runout zone. According to Eq. (7), ξ(I) increases with the flowing velocity, indicating a shear-thinning type of behavior and therefore a smaller resistance in the acceleration stage. The general model behavior over the three slope segments can be explained by the fact that the constant ξ₀ value characterizes a mean value within the domain of possible ξ(I) values. Model parameters can be selected such that similar results are obtained; experiments are required to determine which accelerative/decelerative behavior represents the best fit to observations. However, there is a method to bring the two model approaches into equivalence.

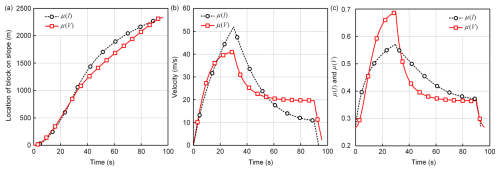
Figure 2 The μ(I) vs. μ(V) rheologies in velocity space. (a) Location of center of mass over time. In the transition zone, the Voellmy model with a constant ξ₀ lags the μ(I) model. (b) Velocity over time. With a constant ξ₀, the Voellmy model tends towards a steady velocity, albeit a lower velocity than that of μ(I). At the end of the transition zone, the Voellmy model predicts a higher (steady-state) velocity. (c) $S/N$ for μ(I) and μ(V). The Voellmy model predicts higher friction before entering the transition zone.

3.1.2 The Voellmy grain flow equivalent to μ(I): the μ(R) grain flow rheology

The Voellmy-type μ(R) rheology is a function of granular temperature/fluctuation energy, which arises from shearing work and decays by dissipative granular interactions. To better compare the μ(I) and μ(R) rheologies, we made the Coulomb friction parameter μ_s(R) a constant but the turbulent friction parameter ξ(R) a function of fluctuation energy so that the two rheologies are in the same Voellmy type. When we re-solve the ordinary differential equations (Eqs. 8 and 9) with the additional production–decay equation (Eq. 2) and the parameters α = 0.05, β = 0.95, ξ₀ = 500 m s⁻², and R₀ = 6 kJ, we find remarkable duplication of the μ(I) results with regard to the calculated location (Fig. 3a), velocity (Fig. 3b), and calculated μ(I) and μ(R) (Fig. 3c). In this comparison, the μ(I) model employed the following parameters: I₀ = 1.0, d = 0.07 m, μ₂ = tan (40°), and μ_s = tan (15°).

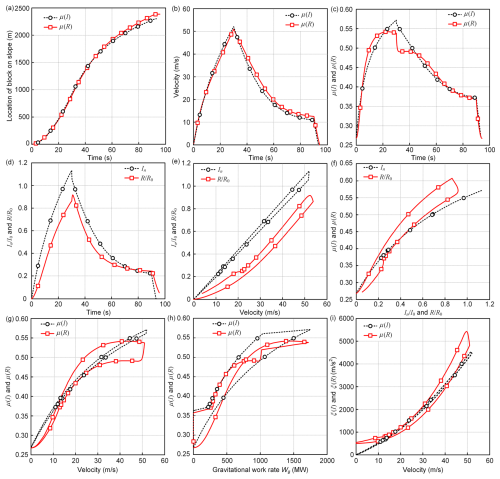
Figure 3 Comparison between the μ(I) vs. μ(R) rheologies. (a–c) The calculated location of the center of mass, velocity, and friction of the two rheologies. (d, e) Comparison between $I_{\mathrm{n}}/I_{\mathrm{0}}$ and $R/R_{\mathrm{0}}$ over time and flow velocity. (f) Calculated friction μ(I) vs. μ(R) as a function of $I_{\mathrm{n}}/I_{\mathrm{0}}$ and $R/R_{\mathrm{0}}$. (g, h) Calculated μ(I) vs. μ(R) as a function of the velocity and gravitational work rate. (i) Comparison between ξ(I) (Eq. 7) and ξ(R).

These results suggest that the empirical I_n function mimics the production and decay of the granular temperature R. Indeed, there is a strong qualitative similarity between the calculated I_n and R functions. When the two dimensionless parameters $I_{\mathrm{n}}/I_{\mathrm{0}}$ and $R/R_{\mathrm{0}}$ are plotted over time (Fig. 3d) or as a function of the calculated velocity (Fig. 3e), there is both strong qualitative and strong quantitative agreement. Because I_n is a pure function of velocity (for a constant height), the calculated friction μ(I) exhibits no change during the accelerative and decelerative phases of the flow: it ascends and descends on the same path (Fig. 3f). In contrast, because R is a result of a production–decay equation, it exhibits a hysteresis (the friction does not follow the same path in the accelerative and decelerative phases of the flow).

Hysteresis effects have been observed in experiments with granular materials (Platzer et al., 2004; Bartelt et al., 2007) and grain flows of snow (Platzer et al., 2007; Bartelt et al., 2015). They indicate a process-dependent flow rheology that cannot be described by rheologies with constant flow parameters (e.g., μ(V)). They suggest that the friction must change as the state of the flow changes, for example as the grain flow continuum changes velocity. The correspondence between μ(I) and μ(R) models underscores the importance of embracing randomness and temporal evolution in the modeling of granular flows.

Both μ(I) and μ(R) rheologies exhibit hysteresis in terms of velocity (Fig. 3g) or the gravitational work rate (Fig. 3h). Although the μ(I) friction expressed in terms of $I_{\mathrm{n}}/I_{\mathrm{0}}$ exhibits no hysteresis (Fig. 3f), the μ(I) rheology in terms of velocity and gravitational work rate does. However, this dependency is much more prominent in the μ(R)-type rheologies because it is governed by two processes – both the production of fluctuation energy and its eventual decay. The μ(I) approach models the net production, always assuming that the two are in balance. During slope transitions, or other flow states in which production and decay are out of balance, this might not be the appropriate description. This is why the most apparent differences between μ(I) and μ(R) arise during slope transitions. Despite these differences, there is a strong correlation between μ(I) and μ(R). For example, when we depict the calculated ξ(I) and ξ(R) function in terms of velocity, there is almost 1 : 1 agreement in the numerical values (Fig. 3i). The only significant difference is that the μ(I) rheology predicts infinite friction (ξ(I)=0) at the velocity of zero, whereas the μ(R) approach predicts some finite value (in this case when R=0, ξ(R)=ξ₀).

3.2 Rheology comparison using real case studies

3.2.1 Piz Cengalo rock–ice avalanche

We apply the μ(I), μ(V), and μ(R) rheologies to calculate the dynamics of the Piz Cengalo rock–ice avalanche and the Vallée de la Sionne snow avalanche (Sovilla et al., 2018). Modeling parameters and results for the Piz Cengalo avalanche are presented in Fig. 4. The μ(R) parameters are empirical values, which arise from numerous practical experiences and have been widely used in rock–ice avalanche research (Munch et al., 2024; Zhuang et al., 2024). The input parameters (μ_s,rock, μ_s,ice, ξ_s,rock, ξ_s,ice) represent the frictional parameters for a dense, granular packing of a rock–ice mixture. Here, the Coulomb and turbulent friction coefficients 〈μ_s(R),ξ(R)〉 are both functions of the fluctuation energy. In the μ(I) rheology, I₀ = 0.3 is a typical value from Pouliquen and Forterre (2002), Forterre and Pouliquen (2003), and Jop et al. (2006); d = 1.0 m and μ₂ = tan (40°) = 0.839 arise from field investigations of particle size and deposit distribution. The μ_s value and parameters in the μ(V) rheology are determined from inversion analysis indicating that the calculated avalanche runout matches the actual conditions. For ease of comparison, the same Coulomb friction coefficients are applied in the μ(I) and μ(V) rheologies. Sensitivity analyses of parameters in the μ(I) and μ(V) rheologies have been well presented (Iannacone et al., 2013; Argentin et al., 2022; Zhao et al., 2024; Zhuang et al., 2023c) and are not performed here.

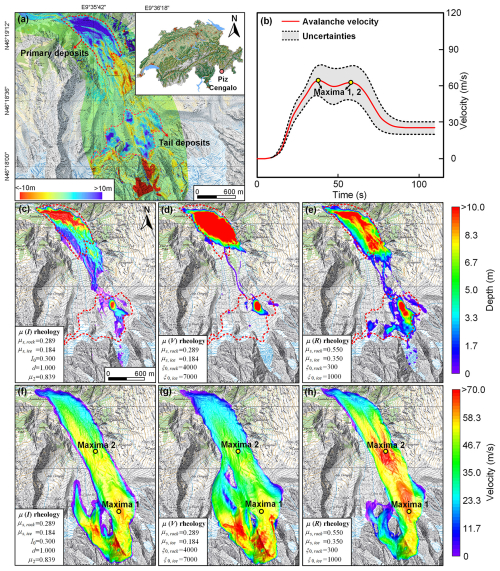
Figure 4 Rheology comparison with the Piz Cengalo rock–ice avalanche. (a) Deposit structure arises from the laser scans. The grid represents the longitude and latitude of the study area. (b) Seismic signal analysis of the avalanche velocity, derived by Walter et al. (2020). (c–e) Modeled avalanche deposits with different rheologies. (f–h) Modeled avalanche velocity with different rheologies. Two maxima represent the locations derived by seismic signal analysis.

Modeling results of all three rheologies exhibit a satisfactory runout distance, but there are deviations in the calculated deposit structure and avalanche velocity. Laser scans indicate two deposit areas of the Piz Cengalo avalanche (Fig. 4a): a primary deposit area of ∼ 2 × 10⁵ m² at the mountain toe (1350–1450 $\mathrm{m}\mathrm{a}.\mathrm{s}.\mathrm{l}.$) and tail deposits spread on the steep slope (2000–2250 $\mathrm{m}\mathrm{a}.\mathrm{s}.\mathrm{l}.$). Both μ(I) and μ(V) models make a deposit anomaly at the mountain toe (Fig. 4c and d), exceeding the measurements considerably. Very few deposits remained on the steep slope, resulting in a significantly smaller accumulation area and thickness compared to the actual conditions. Conversely, modeling deposits of the μ(R) model exhibits a reasonable deposit structure, whether in the primary deposit area or on the steep slope (Fig. 4e). To align the calculated avalanche runout with the actual conditions, small Coulomb friction μ_s, which is dominant when the avalanche comes close to stopping, is applied in the μ(I) and μ(V) models. This modification dictates the final runout accumulation, leading to deposits primarily concentrated on areas with gentle slopes and smaller deposits being left on steeper inclines. According to seismic signal analysis (Fig. 4b; Walter et al., 2020), the Piz Cengalo avalanche has a duration of ∼ 100 s and a maximum velocity of 64 m s⁻¹. There are two avalanche velocity maxima: the first is reached when the avalanche leaves the steep glacier portion, and the second occurs behind the steep terrain step in the central runout area. The mean velocity between the two maxima is 40–60 m s⁻¹. Analysis comparing modeled avalanche velocities and seismic signals indicates that the μ(R) rheology outperforms other rheologies in terms of peak values and velocity evolution, as shown in Fig. 4h. Seismic signal analysis, representing the average velocity of the mass center, explains why a slightly higher peak velocity is observed in the modeling results. In contrast, the μ(I) and μ(V) rheologies display higher velocities downstream of the source area but show reduced velocities in the transition and deposition areas, deviating from actual conditions as depicted in Fig. 4f and g. The small Coulomb friction μ_s and high ξ₀ value impart the avalanche with high mobility in the initial stage. This result is also visualized in the modeled deposit distribution, with very few materials being deposited on the steep slope.

3.2.2 Vallée de la Sionne snow avalanche (no. 20163017)

For the analyzed snow avalanche, the modeling parameters were calibrated to align the simulated avalanche evolution and velocity with the measured values. The progression of the avalanche front was recorded at fixed time intervals of 5 s, providing a basis for comparison. The modeling parameters and results for the μ(I) and μ(R) rheologies are illustrated in Fig. 5.

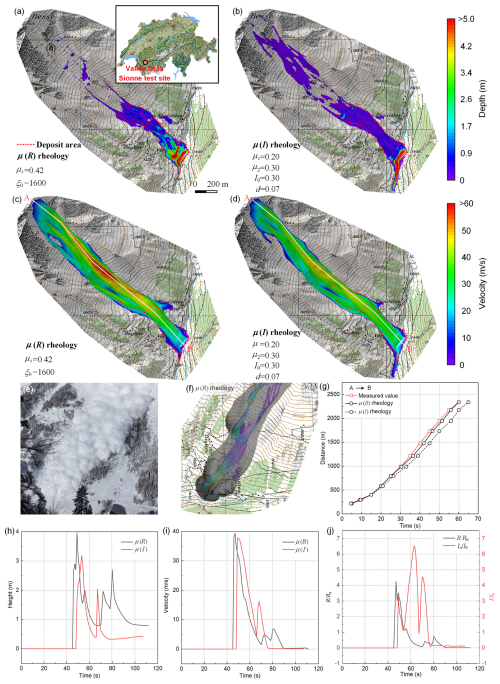
Figure 5 Modeling results of the Vallée de la Sionne snow avalanche (no. 20163017). Panels (a)–(d) show the simulated avalanche deposits and velocity with the two rheologies. The grid represents the longitude and latitude of the study area. Panels (e) and (f) show a comparison between recorded videos and modeling results of the μ(R) rheology. (g) Comparison between measured avalanche evolution and modeling results. The profile AB is presented in panels (c) and (d). (h, i) The simulated height and velocity of the mass center with the two rheologies. (j) Comparison between $R/R_{\mathrm{0}}$ and $I_{\mathrm{n}}/I_{\mathrm{0}}$.

Both rheological models capture the avalanche's evolution and velocity satisfactorily, though the rheology underestimates the timing by approximately 5 s compared to the actual conditions (Fig. 5c, d, and g). Yet, profound differences regarding μ(I) emerge when examining the simulated runout distance and deposit structure. In the μ(R) rheology, the avalanche achieves a runout distance of approximately 2500 m. The deposits are concentrated at the mountain's toe, where the slope transitions to a gentler incline, closely mirroring field observations (Fig. 5a, e, and f).

In contrast, the μ(I) rheology exhibits significantly different behavior. The avalanche does not stop at the mountain's toe but continues moving into the valley, showing excessive mobility (Fig. 5b). The sliding mass bulks unnaturally in the valley, and the deposit depth greatly exceeds observed conditions. This divergence arises from the Coulomb friction coefficient μ_s used in the μ(I) rheology. To match the measured velocity, a smaller μ_s value was applied, resulting in an extended runout and deposition in the flatter terrain of the valley.

Further insight emerges when contrasting $R/R_{\mathrm{0}}$ with and $I_{\mathrm{n}}/I_{\mathrm{0}}$, as shown in Fig. 5j. The scaling factors R₀ and I₀ encapsulate the influence of sliding materials. While R₀ = 2 kJ m⁻³ represents a typical value for snow avalanches (Buser and Bartelt, 2015), I₀ is derived from laboratory experiments using glass beads (Forterre and Pouliquen, 2003; Jop et al., 2006). This disparity in scaling reflects the intrinsic differences in material behavior and introduces a subtle, yet significant, divergence in rheological interpretation.

Through this analysis, we observe that the μ(R) rheology, with its non-steady production and dissipation of fluctuation energy, achieves a more faithful reproduction of both the avalanche's dynamics and its deposition patterns, underscoring the nuanced interplay of microscopic and macroscopic principles in granular flow systems.

4 Discussion and implications

With this contribution, we strengthen the theoretical foundation of the μ(I) rheology. It has an equivalence with the Voellmy-type grain flow rheologies, which are composed of Coulomb stopping friction and turbulent friction that control the flow velocity. Compared with the classic μ(V) rheology of constant friction parameters, an advantage of the μ(I) rheology is to define the turbulent friction parameter ξ(I) as a function of flowing velocity and height (using inertial number I_n). This modification incorporates the shear-thinning behavior (Hu et al., 2022) and the impact of volume (where increased normal stress results in a reduced friction coefficient; see Heim, 1932, and Wang et al., 2018), capturing key characteristics of these phenomena. With the help of grain flow theory (Haff, 1983; Jenkins and Savage, 1983; Buser and Bartelt, 2009), we find the contribution of I_n can be attributed to its empirical representation of the granular temperature/fluctuation energy R. However, the inertial number I_n is just a function of flowing velocity, assuming the production and decay of the fluctuation energy are in balance. The μ(I) rheology, therefore, exhibits no change during the acceleration and deceleration process, leading to the deviation of calculated velocity for real case studies.

Though the μ(I) rheology demonstrates an improvement over the classic μ(V) rheology, it has a critical flaw in ignoring the contribution of fluctuation energy to the Coulomb friction coefficient μ_s. In the μ(I) rheology, the constant μ_s value makes the sliding mass stop at a single slope angle (arctan(μ_s)). Consequently, the modeled deposits of the Piz Cengalo avalanche and Vallée de la Sionne snow avalanche become concentrated at the mountain toe, with very few materials deposited on the slope. Considering that avalanche deposits in real-world scenarios often cover a broad area with varying thicknesses, using a constant μ_s value is unlikely to yield an accurate representation of the deposit structure.

A significant challenge in landslide risk assessment is to establish reliable numerical parameters, highlighting a limitation in both the μ(I) and the classic μ(V) rheologies: the reliance on input parameters derived from inversion analysis (Zhao et al., 2024). Although the μ(I) rheology is based on experimental data, relevant experiments are limited, and the test materials used are predominantly glass beads (Forterre and Pouliquen, 2003; Jop et al., 2006). To date, no large-scale experiments have been conducted on geophysical mass flows to our knowledge. Considering the substantial differences in properties among materials in the flowing mass, such as rock, ice, snow, and water, it proves highly challenging to accurately characterize avalanche motion using a uniform surrogate material with different properties, such as glass. Additionally, the dynamics of avalanches are greatly influenced by the flow regime and topography, indicating that avalanches composed of the same material can display varied runout lengths and deposit patterns under different conditions.

This phenomenon further complicates the task of selecting appropriate model parameters. In this study, to achieve a satisfactory runout of the Piz Cengalo avalanche and a reasonable velocity of the Vallée de la Sionne snow avalanche, small μ_s values that arise from inversion analysis are applied for the calculation of μ(I) and μ(V) models. We admit that model parameters can be calibrated such that realistic runout or velocity is obtained, but these parameters calibrated by site limit the engineering application of the model, particularly when conducting risk assessments of potential avalanches. The existing μ(R) model offers a possible solution (Christen et al., 2010; Bartelt et al., 2011; Zhuang et al., 2023c). By defining the Coulomb stopping friction and turbulent friction parameters as functions of fluctuation energy, we can characterize the effects of flow regime and topography changes on the friction of landslides (Preuth et al., 2010). Using a group of empirical parameters, which represent the material properties of rock, ice, and snow, realistic deposit structure and velocity evolution can be obtained. Because R represents the energy associated with random particle motions, it introduces an element of stochasticity into avalanche modeling. Clearly, it is impossible to precisely determine the position of every individual particle in an avalanche, contrary to what discrete element modeling (DEM) might imply. Nonetheless, the behavior of the granular ensemble seems to be directed by a production–decay equation, which, even when estimated approximately, can impart a discernible trajectory to the avalanche process and deposition dynamic, thereby enhancing the predictive accuracy of numerical models.

Further case studies on various types of geophysical mass flows, such as rock avalanches, ice avalanches, and snow avalanches, will help quantify the modeling parameters of μ(R) rheology (production and decay of fluctuation energy) with less uncertainty. The remaining challenge is to formulate a comprehensive rheology that incorporates the critical physical processes involved in mass flows, including water lubrication, fluidization, sliding materials, and ground roughness.

5 Conclusion

In this paper, we describe the equivalence and difference between three widely used rheologies to model geophysical mass flows: (1) the classic Voellmy rheology, (2) μ(I) rheology, and (3) μ(R) rheology. The μ(I) rheology can be reformulated as a Voellmy-type rheology that is composed of a Coulomb and a turbulent friction term. Differently from the classic Voellmy rheology (constant ξ value), μ(I) rheology involves a velocity-dependent ξ parameter, modeling a shear-thinning behavior. It utilizes a dimensionless inertial number I_n to mimic contributions of fluctuation energy to the runout behavior of mass flows, building an equivalence with the μ(R) rheology. Though both μ(I) and μ(R) models indicate that friction is a process, changing in time and space, the μ(I) rheology assumes that the production and decay of fluctuation energy are in balance, exhibiting the same friction behavior during the accelerative and depositional phases. More importantly, a critical flaw of the μ(I) rheology is it implying constant Coulomb friction, ignoring the impacts of fluctuation energy on the Coulomb stopping friction. Modeled avalanche deposits of the Piz Cengalo rock–ice avalanche and the Vallée de la Sionne snow avalanche are both concentrated in areas with gentle slopes. The existing μ(R) rheology makes up for shortcomings, exhibiting good performance in predicting the deposit patterns of geophysical mass flows. These insights have practical implications for improving geophysical flow models, offering a more comprehensive understanding of flow behavior and its dependence on factors such as velocity, terrain features, and material properties. As we continue to refine our models, we move closer to more accurate assessments and better mitigation of geophysical hazards.