the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Estimating soil moisture conditions for drought monitoring with random forests and a simple soil moisture accounting scheme
Pere Quintana Seguí
Soil moisture is a key variable for drought monitoring, but soil moisture measurements networks are very scarce. Land-surface models can provide a valuable alternative for simulating soil moisture dynamics, but only a few countries have such modelling schemes implemented for monitoring soil moisture at high spatial resolution. In this study, a soil moisture accounting model (SMA) was regionalized over the Iberian Peninsula, taking as a reference the soil moisture simulated by a high-resolution land-surface model. To estimate the soil water holding capacity, the sole parameter required to run the SMA model, two approaches were compared: the direct estimation from European soil maps using pedotransfer functions or an indirect estimation by a machine learning approach, random forests, using as predictors altitude, temperature, precipitation, potential evapotranspiration and land use. Results showed that the random forest model estimates are more robust, especially for estimating low soil moisture levels. Consequently, the proposed approach can provide an efficient way to simulate daily soil moisture and therefore monitor soil moisture droughts, in contexts where high-resolution soil maps are not available, as it relies on a set of covariates that can be reliably estimated from global databases.
- Article
(4712 KB) - Full-text XML
- BibTeX
- EndNote
Soil moisture droughts have strong impacts on vegetation and agricultural production (Raymond et al., 2019; Tramblay et al., 2020; Vicente-Serrano et al., 2014; Pena-Gallardo et al., 2019). There is a growing interest in simple indicators to monitor drought events at short timescales that could be related to impacts (Li et al., 2020; Noguera et al., 2021). In particular, soil moisture indicators could be more relevant than climatic ones to monitor potential impacts of droughts on agriculture and natural vegetation (Piedallu et al., 2013). Since actual soil moisture measurements remain very scarce, soil moisture simulated from land-surface models is an interesting proxy to develop simplified methodologies that could be applied on data-sparse regions. Land-surface models (LSMs) are valuable tools for a fine-scale monitoring of drought events; however, their implementation requires accurate forcing data and computational resources (Almendra-Martín et al., 2021; Quintana-Seguí et al., 2019; Barella-Ortiz and Quintana-Seguí, 2019). Global implementation also exists but with a coarser resolution and driven by reanalysis data (Rodell et al., 2004; Muñoz Sabater, 2020) that may not be adequate for local-scale applications. Only very few countries have land-surface schemes implemented at the national level to monitor droughts (Habets et al., 2008).
Remote sensing is another option which allows for monitoring soil moisture (Dorigo et al., 2017; Brocca et al., 2019). Microwave sensors allow for the monitoring of surface soil moisture (first 5 cm for L-band-based products and skin for C-band-based products), without the interference of clouds. However, surface soil moisture is not enough for most applications, which require root zone soil moisture, which is the water resource in the soil available to plants. Furthermore, passive L-band products, such as SMOS (Soil Moisture and Ocean Salinity; Martínez-Fernández et al., 2016) or SMAP (Soil Moisture Active Passive; Mishra et al., 2017), have a low resolution, and active C-band products, such as Sentinel-1 (Bauer-Marschallinger et al., 2019), which have a higher resolution, suffer from higher noise and are more sensitive to vegetation. Thus, even though remote sensing is very useful, it still has problems to be surmounted. The resolution of passive L-band products can be increased using optical data (NDVI, normalized difference vegetation index; LST, land-surface temperature), by means of downscaling algorithms (Merlin et al., 2013; Fang et al., 2021), but then the resulting product is sensitive to cloud cover. Also, some progress has been made in deriving root zone soil moisture from surface soil moisture estimations using an exponential filter (Stefan et al., 2021) calibrated using the SURFEX LSM (Surface Externalisée; Masson et al., 2013), but these products are in their early stages and are not operational yet.
Simplified methodologies to estimate and monitor the status of soil moisture are needed in contexts where LSM data are not available and where remote sensing products fall short, such as areas and time periods with dense vegetation or high soil roughness which may affect their accuracy (Escorihuela and Quintana-Seguí, 2016). Different modelling approaches have been proposed, either with conceptual soil moisture accounting models or computational variants of the antecedent precipitation index (Willgoose and Perera, 2001; Javelle et al., 2010; Brocca et al., 2014; Zhao et al., 2019; Li et al., 2020). The general availability of spatial estimates of soil moisture content would help introduce soil moisture into drought monitoring systems, improving their scope and usefulness. Furthermore, this would also facilitate the creation of long-term reanalysis, based on meteorological forcing data, and future climate change studies, without the need for running LSMs. However, to apply this model type at a regional or national scale, there is a need to estimate their parameters over the area of interest. For that purpose, regionalization methods have been employed in hydrology for decades to estimate the parameters of hydrological models in ungauged basins (Blöschl and Sivapalan, 1995; He et al., 2011; Hrachowitz et al., 2013). Several methods exist, based on either catchment similarity or the direct estimation of model parameters using regression techniques with physiographic attributes. For soil moisture modelling, up to now only very few studies have considered these approaches to apply soil moisture accounting models at ungauged locations (Grillakis et al., 2021) or estimate root zone soil moisture using machine learning methods (Carranza et al., 2021).
The goal of the present study is to regionalize a simple soil moisture accounting (SMA) scheme that could be used to monitor soil moisture droughts. The SMA model considered in the present study requires a single parameter, the maximum soil water holding capacity. Two different approaches are compared to estimate this parameter regionally: direct estimation with soil maps or with a machine learning technique, namely random forests.
The study area of this work is the Iberian Peninsula, which is located between the Mediterranean Sea and the Atlantic Ocean and thus is influenced by both synoptic-scale systems, which often come from the Atlantic side, and mesoscale heavy-precipitation events, which often come from the Mediterranean side. The Iberian Peninsula presents a marked relief, with a large and high central plateau and different mountain ranges, which heavily influence the spatial patterns of precipitation, enhancing it windward and decreasing it leeward, generating areas of high precipitation in the west, northwest and north and very dry areas on the central plains and, especially, in the southeast. As a consequence the Iberian Peninsula has a heterogeneous distribution of average annual rainfall, with values ranging from 2000 mm yr−1 to less than 100 mm yr−1. All this has a strong influence on the spatial and temporal variability of soil moisture and soil moisture regimes, having wet regimes in the west and north, where the soil is hardly stressed, and semi-arid areas elsewhere, with a wet (energy-limited) and a dry (water-limited) season, with a dry down that might be interrupted by convective events. All this makes the modelling of soil moisture in Iberia a rather challenging task.
Daily precipitation, temperature and potential evapotranspiration (PET) were retrieved from the SAFRAN-Spain database (Quintana-Seguí et al., 2017). SAFRAN (Durand et al., 1993) is a meteorological reanalysis that produces gridded datasets by combining the outputs of a meteorological model and all available observations using an optimal interpolation algorithm. It has been implemented over France (Quintana-Seguí et al., 2008) and recently over the Iberian Peninsula (Quintana-Seguí et al., 2017) with a 5 km × 5 km spatial resolution. The SAFRAN dataset used in this study includes not only observations from the Spanish part of the Iberian Peninsula but also ingested data from Portugal. The SURFEX LSM (Masson et al., 2013) has been run using SAFRAN-Spain as the meteorological forcing dataset and on the same grid, as was done in Quintana-Seguí et al. (2019). SURFEX uses the ECOCLIMAP2 (Faroux et al., 2013) physiographic database, and it uses the ISBA (Interaction Sol-Biosphère-Atmosphère) scheme (Noilhan and Mahfouf, 1996) for natural surfaces. ISBA has different options; we have used ISBA-DIF, the multi-layer diffusion version (Boone, 2000; Habets et al., 2003). From this simulation, we have extracted the soil moisture of the first 60 cm of the soil by calculating the weighted average of the soil layers that fall within this range. This simulated soil moisture over the Iberian Peninsula is considered herein as the observed reference, in the absence of dense monitoring networks of soil moisture (Martínez-Fernández et al., 2016). From the ECOCLIMAP2 database, elevation and land cover data have also been retrieved and aggregated into the following nine categories: water, bare, ice/snow, urban, forest, grass, dry crops, irrigated crops and wetlands.
We also use the European Soil Database (ESDB) produced by the European Soil Data Centre (Panagos et al., 2012). The ESDB contains information on soil characteristics, including soil depth and texture for topsoil (0–30 cm) and subsoil (30–70 cm) layers at a grid resolution of 1 km. The total available water content (TAWC) is a volumetric parameter describing the water content between the field capacity and permanent wilting point, as a function of the available water content, presence of coarse fragments and depth (Reynolds et al., 2000). In the ESDB, water content at the field capacity and permanent wilting point were determined following the equation from van Genuchten (1980) to estimate the soil water retention curve (Hiederer, 2013). The parameters of the equation are provided by a pedotransfer function (Wösten et al., 1999) for the volumetric soil water content computed from the soil water retention curve. The pedotransfer function uses soil texture, organic carbon content and bulk density to determine the parameters of the soil water retention curve (Hiederer, 2013).
3.1 Soil moisture accounting model
The soil moisture model considered here has been previously applied in several studies for applications related to soil moisture monitoring (Anctil et al., 2004; Javelle et al., 2010; Tramblay et al., 2012, 2014). It consists in the SMA part of the GR4J model (Génie Rural à 4 paramètres Journalier; Perrin et al., 2003), driven by precipitation and PET, which represents a conceptual formulation of the impact of precipitation and PET on the soil water balance, using a soil reservoir of fixed depth A. This parameter represents the maximum capacity of that reservoir, which can be assumed to be equivalent to the soil water holding capacity (Perrin et al., 2003; Javelle et al., 2010; Tramblay et al., 2014).
The soil reservoir has a net outflow when PET exceed rainfall.
If Pt≤PETt,
In all the other cases it has a net inflow.
If Pt≤PETt,
where S* can never exceed the maximum reservoir capacity. Finally, the outflow from the storage reservoir due to percolation is taken into account using
The level of the soil reservoir is given by , ranging between 0 and 1, which provides a soil wetness index (SWI) for the catchment. The outputs of SURFEX soil moisture are first normalized with the maximum and minimum values to obtain an SWI consistent with the SMA model output. Then, the SMA model parameter A is calibrated using this normalized SURFEX soil moisture as a reference. The SMA model is calibrated for each grid cell independently using soil moisture simulated with SURFEX covering the full Iberian Peninsula domain. The Nelder–Mead simplex algorithm is used for the calibration with the Nash efficiency criterion. To regionally estimate the values of A, two different methods are compared: the direct estimation of A with TAWC from ESDB soil maps or its indirect estimation with machine learning methods, namely random forests using 5 km × 5 km grid physiographic and climatic properties.
3.2 Regionalization with soil maps
The first approach consists in using the total available water content from the ESDB to estimate the A parameter for each grid cell. In the present work, the TAWC of subsoil and topsoil layers have been added and averaged at the scale of 5 km × 5 km, matching the spatial resolution of the SAFRAN grid. Then, these estimates have been used to set the A parameter of the SMA model. Thus, this regionalization approach is based on the a priori estimation of the A parameter from soil maps solely.
3.3 Regionalization with random forests
Random forests (RFs; Breiman, 2001) belong to the class of machine learning techniques. RFs are based on a bootstrap aggregation (Breiman, 1996) of classification and regression trees (Breiman et al., 2017). They generate a bootstrap sample from the original data and trains a tree model using this sample. The procedure is repeated many times, and the bagging's prediction is the average of the predictions. Among the many advantages of RFs, they are fast, non-parametric, robust to noise in the predictor variables, able to capture nonlinear dependencies between predictors and dependent variables, and can simultaneously incorporate continuous and categorical variables (Tyralis et al., 2019). The drawbacks are that they are complex to interpret and cannot extrapolate outside the training range. Given their advantages, this algorithm is particularly suited for the estimation of spatial variables such as soil properties (Booker and Woods, 2014; Hengl et al., 2018; Gagkas and Lilly, 2019; Stein et al., 2021). In the present work, an RF model is generated to estimate the values of the A parameter of the SMA model, representing the soil water holding capacity, with the properties of the 5×5 km grid cells, namely altitude, land cover, mean annual precipitation, temperature and PET, using random forests.
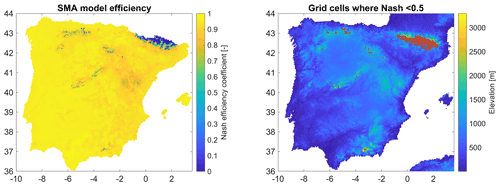
Figure 1Efficiency of the SMA model to reproduce the soil wetness index obtained from simulated SURFEX soil moisture.
To estimate the reliability of the method, the 5 km × 5 km grid cells covering the Iberian Peninsula have been split randomly into a training sample containing 70 % of the cells (15 636 data points) and a testing sample with the remaining 30 % cells (6701 data points). The random selection of the training and testing sets have been performed using a Latin hypercube sampling (McKay et al., 1979) to ensure homogeneous sampling over the Iberian Peninsula. Given that the RF trees cannot be interpreted directly, as for example the weights in a linear regression, we additionally implemented an out-of-bag predictor importance estimation by permutation (Loh and Shih, 1997) to measure how influential the predictor variables in the model are at predicting the response. The influence of a predictor increases with the value of this measure. If a predictor is influential in prediction, then permuting its values should affect the model error. If a predictor is not influential, then permuting its values should have little to no effect on the model error.
3.4 Validation on the ability to detect dry soil moisture conditions
To compare the efficiency of the two methods compared to estimate the A parameter of the SMA model, the SMA model was run using the two methods, and all daily values of soil moisture below the 10th percentile were extracted, corresponding to dry soil conditions. Only the grid cells in the testing sample were considered for this validation. We computed different verification scores to assess the relative efficiency of the two methods to reproduce daily soil moisture below the 10th percentile using the ISBA simulated soil moisture as a benchmark: the probability of detection (POD), the false-alarm ratio (FAR) and the Heidke skill score (HSS) summarizing the global efficiency to detect dry periods (Jolliffe and Stephenson, 2011). These scores are based on the contingency table between forecasts (or simulated values in the case of the present study) and observations (Table 1).
Table 1Contingency table of the comparison between forecasts and observations or any two analyses. The symbols a–d are the different numbers of cases observed to occur in each category.

POD is the probability of detection (Eq. 1); FAR is the number of false alarms per the total number of warnings or alarms (Eq. 2); and HSS is a skill score ranging from −∞ to 1 (Eq. 3), for categorical forecasts where the proportion of correct measure is scaled with the reference value from correct forecasts due to chance.
4.1 Calibration of the SMA model
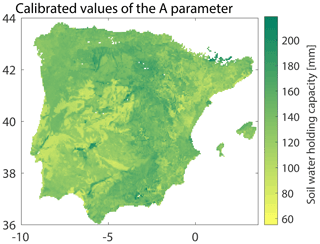
The calibration results of the SMA model against SURFEX soil moisture provide very good model performance, with a mean Nash coefficient equal to 0.94, indicating its ability to reproduce the soil moisture dynamics as simulated by SURFEX. Nash values below 0.5 are found for 1.21 % of grid cells (n=273); these are only for areas located in the mountainous range affected by snow processes above 1500 m a.s.l. (Fig. 1). This outcome is expected; since the SMA model does not include a snow module, it cannot reproduce snow dynamics in these areas. However, high-elevation areas with seasonal snow cover are not the areas most at risk of soil moisture droughts for agricultural activities in Spain. The calibrated values of the A parameter of the SMA model range from 60 to 250 mm, depending on the location (Fig. 2). There is no significant correlation between A and the mean annual precipitation or the aridity index (). This highlights the interplays between soil properties and climate to explain the spatial variability of the soil water holding capacity.
4.2 Regional estimation of the A parameter
The values of the calibrated A parameter are related to the properties of the 5 km × 5 km grid cells using random forests. First, an out-of-bag predictor importance estimation by permutation is applied to compute the overall performance of RFs and estimate the relative influence of each predictor. When using the A out-of-bag estimates to run the SMA model, the loss of performance is very small; the decrease in Nash values in validation is on average equal to −0.0019 (with a maximum decrease of −0.04). This is due to the low sensitivity of the SMA model to the value of A, given that the error in the estimation of A is in the range of 10 mm (RMSE of 13.18 mm). This type of validation mimics the case when the estimation at one single location is required, yet since all the remaining points are used for the estimation, it makes the approach in that case very robust. The relative importance for each predictor is plotted in Fig. 3, indicating that precipitation and potential evapotranspiration are the two most important predictors, followed by altitude. On the contrary, the land cover attributes for each grid cell are the least important predictors, and removing them from the RF model does not significantly change the results. This shows the relative importance of climatic variables in the spatial variability of the soil moisture holding capacity.
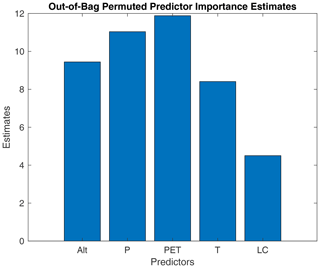
Figure 3Relative importance of each predictor (Alt: altitude, P: precipitation, PET: potential evapotranspiration, T: temperature and LC: land cover class) in the random forest method.
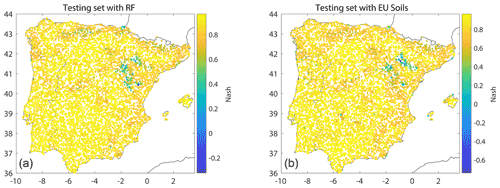
To estimate the robustness of the method, we applied a split-sample validation into a testing and a training sample. The results are presented for the testing set (Fig. 4). The performance in terms of Nash for the SMA model with A estimated by random forests or soil map is very similar, with a mean Nash value equal to 0.86 (median of 0.89) with RFs and 0.81 (median of 0.85) with soil maps. The Nash values in validation (testing set) are low, or even negative, only for mountainous ranges, as expected. Overall, the spatial patterns of the Nash coefficients obtained with RFs or the ESDB are very similar too. There are no significant relationships between model efficiency and the aridity index or the presence of irrigated areas, as identified in the ECOCLIMAP2 land cover database.
4.3 Estimation of dry soil conditions
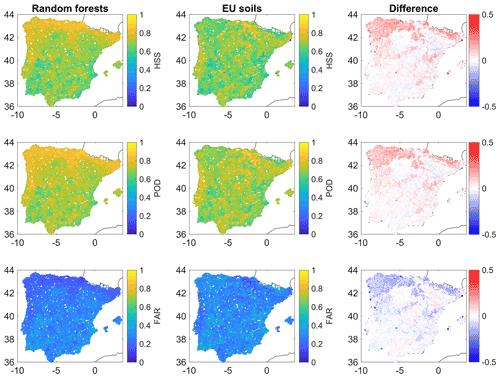
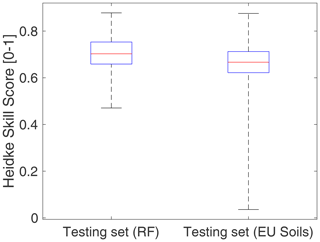
A further validation is made for daily soil moisture below the 10th percentile corresponding to dry soil conditions. We computed the probability of detection (POD), the false-alarm ratio (FAR) and the Heidke skill score (HSS) summarizing the global efficiency to detect dry periods. For both approaches to estimate A, the mean POD is very high, close to 97 %, while FAR is close to 3 %. But these average results hide some discrepancy in the different regions (Fig. 5): the efficiency is the highest for the northwestern region, the wettest areas of Spain, with the most important increase of HSS and POD, associated with a decrease in FAR, using random forests, while in the southern and central parts of Spain, the performance is lower on average and very similar to the two regionalization approaches. For the wettest parts of the Iberian Peninsula, POD remains higher than 94 %, and FAR is lower than 6 %; it is the region where the main improvements with RFs are observed. As shown in Fig. 5, the results with random forests mostly follow the climate conditions, with improved estimations in the wettest regions of the northern and northwestern parts of Spain. For the estimation with EU soil maps, the results seem related to soil depth and, to a lesser extent, land cover. Indeed, higher scores are found in regions with shallow soils, such as those of plutonic (Galicia, western parts of the Extremaduran mountainous ranges and Douro basin) or metamorphic origins (western Cantabrian Range, northern Iberian Range, eastern-central regions and Sierra Morena in Andalucia) and also sedimentary regions with shallow limestones (eastern Cantabrian mountains, Basque Country and southern Iberian Range). On the other hand, lower scores are found in regions with the deepest soils (Guadalquivir floodplains, mid Tagus River, upper Douro, piedmonts of the Cantabrian Mountains in Leon and Palencia, and most of middle Navarre). The exception is regions such as Biscay or coastal Portugal, with a dense forest cover (mostly Pinus radiata or P. pinaster), where soil depth is probably overestimated. On average, the RF estimation method outperforms the approach based on the ESDB (Fig. 6), with more stable results in terms of HSS, since all values obtained with RFs are above 0.4, while with the ESDB for the grid cells, the HSS scores drops to values close to zero.
In this study, a simple model allowing for the monitoring of soil moisture conditions was regionalized over the entire Iberian Peninsula, taking as a reference the soil moisture simulated by a high-resolution land-surface model. Two different regionalization methods have been compared, either by the direct estimation of the soil water holding capacity from European soil maps or by random forests, using covariates such as altitude, temperature, precipitation, potential evapotranspiration and land cover. Results have shown that the estimation by random forests is more robust notably to estimate low soil moisture levels. Despite similar average performance between the two methods, the use of soil maps to set the water holding capacity reveals less stable results in some cases, most probably related to the uncertainties in the pedotransfer functions used. While these pedotransfer functions are process-based predictive functions of certain soil properties, random forests are not based on physical processes and are tailored to provide the best estimates in a statistical sense. Therefore, they provide a valuable alternative in contexts where high-resolution soil maps are not available, since they rely on a set of covariates that can be reliably estimated from global databases, such as satellite or reanalysis products (Funk et al., 2015; Hersbach et al., 2020; Muñoz Sabater, 2020).
It should be noted that the results presented herein are highly dependent on the quality of land-surface simulations, in the absence of dense monitoring networks of in situ soil moisture data; thus these results suffer from the same limitations as LSMs, notably, the lack of human process representation in these models (notably irrigation). However, new remote sensing irrigation estimates are being developed (Massari et al., 2021); as a consequence, once the RF model is trained, irrigation estimates could be added to the precipitation forcing data in order to include the human impacts on soil moisture estimations. The results show that this approach could allow for cheaply extending the value of high-resolution LSM simulations to areas where no LSM is implemented (i.e. northern Africa), as long as the climate conditions belong to the range of values used to train the model, mostly in terms of precipitation and potential evapotranspiration ranges. Thus, the model train over the Iberian Peninsula could be applied to other similar areas such as northern Africa, Italy or Greece. As a perspective, other simulations from countries where high-resolution LSM simulations are available, such as France or the USA, could be added to the database in order to expand the coverage over different physiographic and climate contexts (Ma et al., 2021). Consequently, the benefits of LSM simulations of soil moisture could be expanded to other areas, provided those suitable forcing datasets are available. Furthermore, if public meteorological and hydrological organizations were to create soil moisture observation networks, cleverly designed to cover the most relevant climates of their countries, this approach could be used to train the model using these observations and then regionalize the results to the rest of the territory, thus, converting an in situ observation dataset into a gridded dataset with a much greater spatial coverage.
Codes (such as MATLAB scripts and functions) are available upon request.
The SAFRAN dataset is available in the HyMeX database, published under https://doi.org/10.14768/MISTRALS-HYMEX.1388 (Quintana Seguí, 2015). The European Soil Database is available at https://esdac.jrc.ec.europa.eu/content/european-soil-database-v20-vector-and-attribute-data (ESDAC, 2022).
YT and PQS designed the study. YT carried out the data processing, analyses and visualization and wrote the initial draft of the paper. PQS extracted all the required data, performed the SURFEX simulations and reviewed the initial draft of the paper.
The contact author has declared that neither they nor their co-author has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the special issue “Hydrological cycle in the Mediterranean (ACP/AMT/GMD/HESS/NHESS/OS inter-journal SI)”. It is not associated with a conference.
This work is a contribution to the HyMeX programme through the HUMID (grant no. CGL2017-85687-R, AEI/FEDER, UE) and ANR HILIAISE projects. We thank Jaime Gaona (Instituto de Investigación en Agrobiotecnología – CIALE, Universidad de Salamanca, Villamayor, Salamanca, Spain) for his comments on some aspects of the manuscript and two anonymous reviewers for their suggestions to improve the manuscript.
This research has been supported by the Ministerio de Ciencia, Innovación y Universidades (HUMID project; grant no. CGL2017-85687-R, AEI/FEDER, UE).
This paper was edited by Christian Barthlott and reviewed by two anonymous referees.
Almendra-Martín, L., Martínez-Fernández, J., González-Zamora, Á., Benito-Verdugo, P., and Herrero-Jiménez, C. M.: Agricultural Drought Trends on the Iberian Peninsula: An Analysis Using Modeled and Reanalysis Soil Moisture Products, Atmosphere, 12, 236, https://doi.org/10.3390/atmos12020236, 2021.
Anctil, F., Michel, C., Perrin, C., and Andréassian, V.: A soil moisture index as an auxiliary ANN input for stream flow forecasting, J. Hydrol., 286, 155–167, https://doi.org/10.1016/j.jhydrol.2003.09.006, 2004.
Barella-Ortiz, A. and Quintana-Seguí, P.: Evaluation of drought representation and propagation in regional climate model simulations across Spain, Hydrol. Earth Syst. Sci., 23, 5111–5131, https://doi.org/10.5194/hess-23-5111-2019, 2019.
Bauer-Marschallinger, B., Freeman, V., Cao, S., Paulik, C., Schaufler, S., Stachl, T., Modanesi, S., Massari, C., Ciabatta, L., Brocca, L., and Wagner, W.: Toward Global Soil Moisture Monitoring With Sentinel-1: Harnessing Assets and Overcoming Obstacles, IEEE T. Geosci. Remote, 57, 520–539, https://doi.org/10.1109/TGRS.2018.2858004, 2019.
Blöschl, G. and Sivapalan, M.: Scale issues in hydrological modelling: A review, Hydrol. Process., 9, 251–290, https://doi.org/10.1002/hyp.3360090305, 1995.
Booker, D. J. and Woods, R. A.: Comparing and combining physically-based and empirically-based approaches for estimating the hydrology of ungauged catchments, J. Hydrol., 508, 227–239, https://doi.org/10.1016/j.jhydrol.2013.11.007, 2014.
Boone, A.: Modélisation des processus hydrologiques dans le schéma de surface ISBA: Inclusion d'un réservoir hydrologique, du gel et modélisation de la neige PhD thesis, Université Paul Sabatier, Toulouse III, https://www.umr-cnrm.fr/IMG/pdf/boone_thesis_2000.pdf (last access: 10 April 2022), 2000.
Breiman, L.: Bagging predictors, Mach. Learn., 24, 123–140, https://doi.org/10.1007/BF00058655, 1996.
Breiman, L.: Random Forests, Mach. Learn., 45, 5–32, https://doi.org/10.1023/A:1010933404324, 2001.
Breiman, L., Friedman, J. H., Olshen, R. A., and Stone, C. J.: Classification And Regression Trees, 1st Edn., Routledge, https://doi.org/10.1201/9781315139470, 2017.
Brocca, L., Camici, S., Melone, F., Moramarco, T., Martínez-Fernández, J., Didon-Lescot, J.-F., and Morbidelli, R.: Improving the representation of soil moisture by using a semi-analytical infiltration model, Hydrol. Process., 28, 2103–2115, https://doi.org/10.1002/hyp.9766, 2014.
Brocca, L., Filippucci, P., Hahn, S., Ciabatta, L., Massari, C., Camici, S., Schüller, L., Bojkov, B., and Wagner, W.: SM2RAIN–ASCAT (2007–2018): global daily satellite rainfall data from ASCAT soil moisture observations, Earth Syst. Sci. Data, 11, 1583–1601, https://doi.org/10.5194/essd-11-1583-2019, 2019.
Carranza, C., Nolet, C., Pezij, M., and van der Ploeg, M.: Root zone soil moisture estimation with Random Forest, J. Hydrol., 593, 125840, https://doi.org/10.1016/j.jhydrol.2020.125840, 2021.
Dorigo, W., Wagner, W., Albergel, C., Albrecht, F., Balsamo, G., Brocca, L., Chung, D., Ertl, M., Forkel, M., Gruber, A., Haas, E., Hamer, P. D., Hirschi, M., Ikonen, J., de Jeu, R., Kidd, R., Lahoz, W., Liu, Y. Y., Miralles, D., Mistelbauer, T., Nicolai-Shaw, N., Parinussa, R., Pratola, C., Reimer, C., van der Schalie, R., Seneviratne, S. I., Smolander, T., and Lecomte, P.: ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions, Remote Sens. Environ., 203, 185–215, https://doi.org/10.1016/j.rse.2017.07.001, 2017.
Durand, Y., Brun, E., Merindol, L., Guyomarc'h, G., Lesaffre, B., and Martin, E.: A meteorological estimation of relevant parameters for snow models, Ann. Glaciol., 18, 65–71, https://doi.org/10.1017/S0260305500011277, 1993.
Escorihuela, M. J. and Quintana-Seguí, P.: Comparison of remote sensing and simulated soil moisture datasets in Mediterranean landscapes, Remote Sens. Environ., 180, 99–114, https://doi.org/10.1016/j.rse.2016.02.046, 2016.
ESDAC: European Soil Database v2.0 (vector and attribute data), ESDAC [data set], https://esdac.jrc.ec.europa.eu/content/european-soil-database-v20-vector-and-attribute-data, last access: 10 April 2022.
Fang, B., Kansara, P., Dandridge, C., and Lakshmi, V.: Drought monitoring using high spatial resolution soil moisture data over Australia in 2015–2019, J. Hydrol., 594, 125960, https://doi.org/10.1016/j.jhydrol.2021.125960, 2021.
Faroux, S., Kaptué Tchuenté, A. T., Roujean, J.-L., Masson, V., Martin, E., and Le Moigne, P.: ECOCLIMAP-II/Europe: a twofold database of ecosystems and surface parameters at 1 km resolution based on satellite information for use in land surface, meteorological and climate models, Geosci. Model Dev., 6, 563–582, https://doi.org/10.5194/gmd-6-563-2013, 2013.
Funk, C., Peterson, P., Landsfeld, M., Pedreros, D., Verdin, J., Shukla, S., Husak, G., Rowland, J., Harrison, L., Hoell, A., and Michaelsen, J.: The climate hazards infrared precipitation with stations – a new environmental record for monitoring extremes, Sci. Data, 2, 150066, https://doi.org/10.1038/sdata.2015.66, 2015.
Gagkas, Z. and Lilly, A.: Downscaling soil hydrological mapping used to predict catchment hydrological response with random forests, Geoderma, 341, 216–235, https://doi.org/10.1016/j.geoderma.2019.01.048, 2019.
Grillakis, M. G., Koutroulis, A. G., Alexakis, D. D., Polykretis, C., and Daliakopoulos, I. N.: Regionalizing root-zone soil moisture estimates from ESA CCI Soil Water Index using machine learning and information on soil, vegetation, and climate, Water Resour. Res., 57, e2020WR029249. https://doi.org/10.1029/2020WR029249, 2021.
Habets F., Boone A., and Noilhan J.: Simulation of a Scandinavian basin using the diffusion transfer version of ISBA, Global Planet. Change, 38, 137–149, 2003.
Habets, F., Boone, A., Champeaux, J. L., Etchevers, P., Franchistéguy, L., Leblois, E., Ledoux, E., Le Moigne, P., Martin, E., Morel, S., Noilhan, J., Quintana Seguí, P., Rousset-Regimbeau, F., and Viennot, P.: The SAFRAN-ISBA-MODCOU hydrometeorological model applied over France, J. Geophys. Res., 113, D06113, https://doi.org/10.1029/2007JD008548, 2008.
He, Y., Bárdossy, A., and Zehe, E.: A review of regionalisation for continuous streamflow simulation, Hydrol. Earth Syst. Sci., 15, 3539–3553, https://doi.org/10.5194/hess-15-3539-2011, 2011.
Hengl, T., Nussbaum, M., Wright, M. N., Heuvelink, G. B. M., and Gräler, B.: Random forest as a generic framework for predictive modeling of spatial and spatio-temporal variables, Peer J., 6, e5518, https://doi.org/10.7717/peerj.5518, 2018.
Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muñoz-Sabater, J., Nicolas, J., Peubey, C., Radu, R., Schepers, D., Simmons, A., Soci, C., Abdalla, S., Abellan, X., Balsamo, G., Bechtold, P., Biavati, G., Bidlot, J., Bonavita, M., Chiara, G., Dahlgren, P., Dee, D., Diamantakis, M., Dragani, R., Flemming, J., Forbes, R., Fuentes, M., Geer, A., Haimberger, L., Healy, S., Hogan, R. J., Hólm, E., Janisková, M., Keeley, S., Laloyaux, P., Lopez, P., Lupu, C., Radnoti, G., Rosnay, P., Rozum, I., Vamborg, F., Villaume, S., and Thépaut, J.: The ERA5 global reanalysis, Q. J. Roy. Meteorol. Soc., 146, 1999–2049, https://doi.org/10.1002/qj.3803, 2020.
Hiederer R. Mapping Soil Properties for Europe – Spatial Representation of Soil Database Attributes, EUR 26082, JRC83425 , Publications Office of the European Union, Luxembourg, https://publications.jrc.ec.europa.eu/repository/handle/JRC83425 (last access: 10 April 2022) 2013.
Hrachowitz, M., Savenije, H. H. G., Blöschl, G., McDonnell, J. J., Sivapalan, M., Pomeroy, J. W., Arheimer, B., Blume, T., Clark, M. P., Ehret, U., Fenicia, F., Freer, J. E., Gelfan, A., Gupta, H. V., Hughes, D. A., Hut, R. W., Montanari, A., Pande, S., Tetzlaff, D., Troch, P. A., Uhlenbrook, S., Wagener, T., Winsemius, H. C., Woods, R. A., Zehe, E., and Cudennec, C.: A decade of Predictions in Ungauged Basins (PUB) – a review, Hydrolog. Sci. J., 58, 1198–1255, https://doi.org/10.1080/02626667.2013.803183, 2013.
Javelle, P., Fouchier, C., Arnaud, P., and Lavabre, J.: Flash flood warning at ungauged locations using radar rainfall and antecedent soil moisture estimations, J. Hydrol., 394, 267–274, https://doi.org/10.1016/j.jhydrol.2010.03.032, 2010.
Jolliffe, I. T. and Stephenson, D. B. (Eds.): Forecast Verification: A Practitioner's Guide in Atmospheric Science, John Wiley & Sons, Ltd, Chichester, UK, https://doi.org/10.1002/9781119960003, 2011.
Li, J., Wang, Z., Wu, X., Xu, C.-Y., Guo, S., and Chen, X.: Toward Monitoring Short-Term Droughts Using a Novel Daily Scale, Standardized Antecedent Precipitation Evapotranspiration Index, J. Hydrometeorol., 21, 891–908, https://doi.org/10.1175/JHM-D-19-0298.1, 2020.
Loh, W. Y. and Shih, Y. S.: Split Selection Methods for Classification Trees, Statist. Sinica, 7, 815–840, 1997.
Ma, K., Feng, D., Lawson, K., Tsai, W.-P., Liang, C., Huang, X., Sharma, A., Shen, C.: Transferring hydrologic data across continents – leveraging data-rich regions to improve hydrologic prediction in data-sparse regions, Water Resour. Res., 57, e2020WR028600, https://doi.org/10.1029/2020WR028600, 2021.
Martínez-Fernández, J., González-Zamora, A., Sánchez, N., and Gumuzzio, A.: A soil water based index as a suitable agricultural drought indicator, J. Hydrol., 522, 265–273, https://doi.org/10.1016/j.jhydrol.2014.12.051, 2015.
Martínez-Fernández, J., González-Zamora, A., Sánchez, N., Gumuzzio, A., and Herrero-Jiménez, C. M.: Satellite soil moisture for agricultural drought monitoring: Assessment of the SMOS derived Soil Water Deficit Index, Remote Sens. Environ., 177, 277–286, https://doi.org/10.1016/j.rse.2016.02.064, 2016.
Massari, C., Modanesi, S., Dari, J., Gruber, A., De Lannoy, G. J. M., Girotto, M., Quintana-Seguí, P., Le Page, M., Jarlan, L., Zribi, M., Ouaadi, N., Vreugdenhil, M., Zappa, L., Dorigo, W., Wagner, W., Brombacher, J., Pelgrum, H., Jaquot, P., Freeman, V., Volden, E., Fernandez Prieto, D., Tarpanelli, A., Barbetta, S., and Brocca, L.: A Review of Irrigation Information Retrievals from Space and Their Utility for Users, Remote Sens., 13, 4112, https://doi.org/10.3390/rs13204112, 2021.
Masson, V., Le Moigne, P., Martin, E., Faroux, S., Alias, A., Alkama, R., Belamari, S., Barbu, A., Boone, A., Bouyssel, F., Brousseau, P., Brun, E., Calvet, J.-C., Carrer, D., Decharme, B., Delire, C., Donier, S., Essaouini, K., Gibelin, A.-L., Giordani, H., Habets, F., Jidane, M., Kerdraon, G., Kourzeneva, E., Lafaysse, M., Lafont, S., Lebeaupin Brossier, C., Lemonsu, A., Mahfouf, J.-F., Marguinaud, P., Mokhtari, M., Morin, S., Pigeon, G., Salgado, R., Seity, Y., Taillefer, F., Tanguy, G., Tulet, P., Vincendon, B., Vionnet, V., and Voldoire, A.: The SURFEXv7.2 land and ocean surface platform for coupled or offline simulation of earth surface variables and fluxes, Geosci. Model Dev., 6, 929–960, https://doi.org/10.5194/gmd-6-929-2013, 2013.
McKay, M. D., Beckman, R. J., and Conover, W. J.: Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code, Technometrics, 21, 239–245, https://doi.org/10.1080/00401706.1979.10489755, 1979.
Merlin, O., Escorihuela, M. J., Mayoral, M. A., Hagolle, O., Al Bitar, A., and Kerr, Y.: Self-calibrated evaporation-based disaggregation of SMOS soil moisture: An evaluation study at 3 km and 100 m resolution in Catalunya, Spain, Remote Sens. Environ., 130, 25–38, https://doi.org/10.1016/j.rse.2012.11.008, 2013.
Mishra, A., Vu, T., Veettil, A. V., and Entekhabi, D.: Drought monitoring with soil moisture active passive (SMAP) measurements, J. Hydrol., 552, 620–632, https://doi.org/10.1016/j.jhydrol.2017.07.033, 2017.
Muñoz Sabater, J.: ERA5-Land hourly data from 1981 to present, Copernicus Climate Change Service (C3S) Climate Data Store (CDS), https://doi.org/10.24381/cds.e2161bac, 2020.
Noguera, I., Domínguez-Castro, F., and Vicente-Serrano, S. M.: Flash Drought Response to Precipitation and Atmospheric Evaporative Demand in Spain, Atmosphere, 12, 165, https://doi.org/10.3390/atmos12020165, 2021.
Noilhan, J. and Mahfouf, J.-F.: The ISBA land surface parameterisation scheme, Global Planet. Change, 13, 145–159, https://doi.org/10.1016/0921-8181(95)00043-7, 1996.
Panagos, P., Van Liedekerke, M., Jones, A., and Montanarella, L.: European Soil Data Centre: Response to European policy support and public data requirements, Land Use Policy, 29, 329–338, https://doi.org/10.1016/j.landusepol.2011.07.003, 2012.
Pena-Gallardo, M., Vicente-Serrano, S. M., Domínguez-Castro, F., and Beguería, S.: The impact of drought on the productivity of two rainfed crops in Spain, Nat. Hazards Earth Syst. Sci., 19, 1215–1234, https://doi.org/10.5194/nhess-19-1215-2019, 2019.
Perrin, C., Michel, C., and Andréassian, V.: Improvement of a parsimonious model for streamflow simulation, J. Hydrol., 279, 275–289, https://doi.org/10.1016/S0022-1694(03)00225-7, 2003.
Piedallu, C., Gégout, J.-C., Perez, V., and Lebourgeois, F.: Soil water balance performs better than climatic water variables in tree species distribution modelling: Soil water balance improves tree species distribution models, Global Ecol. Biogeogr., 22, 470–482, https://doi.org/10.1111/geb.12012, 2013.
Quintana Seguí, P.: SAFRAN analysis over Spain, ESPRI/IPSL [data set], https://doi.org/10.14768/MISTRALS-HYMEX.1388, 2015.
Quintana-Seguí, P., Le Moigne, P., Durand, Y., Martin, E., Habets, F., Baillon, M., Canellas, C., Franchisteguy, L., and Morel, S.: Analysis of Near-Surface Atmospheric Variables: Validation of the SAFRAN Analysis over France, J. Appl. Meteorol. Clim., 47, 92–107, https://doi.org/10.1175/2007JAMC1636.1, 2008.
Quintana-Seguí, P., Turco, M., Herrera, S., and Miguez-Macho, G.: Validation of a new SAFRAN-based gridded precipitation product for Spain and comparisons to Spain02 and ERA-Interim, Hydrol. Earth Syst. Sci., 21, 2187–2201, https://doi.org/10.5194/hess-21-2187-2017, 2017.
Quintana-Seguí, P., Barella-Ortiz, A., Regueiro-Sanfiz, S., and Miguez-Macho, G.: The Utility of Land-Surface Model Simulations to Provide Drought Information in a Water Management Context Using Global and Local Forcing Datasets, Water Resour. Manage., 34, 2135–2156, https://doi.org/10.1007/s11269-018-2160-9, 2019.
Raymond, F., Ullmann, A., Tramblay, Y., Drobinski, P., and Camberlin, P.: Evolution of Mediterranean extreme dry spells during the wet season under climate change, Reg. Environ. Change, 19, 2339–2351, https://doi.org/10.1007/s10113-019-01526-3, 2019.
Reynolds, C. A., Jackson, T. J., and Rawls, W. J.: Estimating soil water-holding capacities by linking the Food and Agriculture Organization Soil map of the world with global pedon databases and continuous pedotransfer functions, Water Resour. Res., 36, 3653–3662, https://doi.org/10.1029/2000WR900130, 2000.
Rodell, M., Houser, P. R., Jambor, U., Gottschalck, J., Mitchell, K., Meng, C.-J., Arsenault, K., Cosgrove, B., Radakovich, J., Bosilovich, M., Entin, J. K., Walker, J. P., Lohmann, D., and Toll, D.: The Global Land Data Assimilation System, B. Am. Meteorol. Soc., 85, 381–394, https://doi.org/10.1175/BAMS-85-3-381, 2004.
Stefan, V. G., Indrio, G., Escorihuela, M. J., Quintana-Seguí, P., and Villar, J. M.: High-Resolution SMAP-Derived Root-Zone Soil Moisture Using an Exponential Filter Model Calibrated per Land Cover Type, Remote Sens., 13, 1112, https://doi.org/10.3390/rs13061112, 2021.
Stein, L., Clark, M. P., Knoben, W. J. M., Pianosi, F., and Woods, R. A.: How Do Climate and Catchment Attributes Influence Flood Generating Processes? A Large-Sample Study for 671 Catchments Across the Contiguous USA, Water Resour. Res., 57, e2020WR028300, https://doi.org/10.1029/2020WR028300, 2021.
Tramblay, Y., Bouaicha, R., Brocca, L., Dorigo, W., Bouvier, C., Camici, S., and Servat, E.: Estimation of antecedent wetness conditions for flood modelling in northern Morocco, Hydrol. Earth Syst. Sci., 16, 4375–4386, https://doi.org/10.5194/hess-16-4375-2012, 2012.
Tramblay, Y., Amoussou, E., Dorigo, W., and Mahé, G.: Flood risk under future climate in data sparse regions: Linking extreme value models and flood generating processes, J. Hydrol., 519, 549–558, https://doi.org/10.1016/j.jhydrol.2014.07.052, 2014.
Tramblay, Y., Koutroulis, A., Samaniego, L., Vicente-Serrano, S. M., Volaire, F., Boone, A., Le Page, M., Llasat, M. C., Albergel, C., Burak, S., Cailleret, M., Kalin, K. C., Davi, H., Dupuy, J.-L., Greve, P., Grillakis, M., Hanich, L., Jarlan, L., Martin-StPaul, N., Martínez-Vilalta, J., Mouillot, F., Pulido-Velazquez, D., Quintana-Seguí, P., Renard, D., Turco, M., Türkeş, M., Trigo, R., Vidal, J.-P., Vilagrosa, A., Zribi, M., and Polcher, J.: Challenges for drought assessment in the Mediterranean region under future climate scenarios, Earth-Sci. Rev., 210, 103348, https://doi.org/10.1016/j.earscirev.2020.103348, 2020.
Tyralis, H., Papacharalampous, G., and Langousis, A.: A Brief Review of Random Forests for Water Scientists and Practitioners and Their Recent History in Water Resources, Water, 11, 910, https://doi.org/10.3390/w11050910, 2019.
van Genuchten, M. T.: A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils, Soil Sci. Soc. Am. J., 44, 892–898, https://doi.org/10.2136/sssaj1980.03615995004400050002x, 1980.
Vicente-Serrano, S. M., Lopez-Moreno, J.-I., Beguería, S., Lorenzo-Lacruz, J., Sanchez-Lorenzo, A., García-Ruiz, J. M., Azorin-Molina, C., Morán-Tejeda, E., Revuelto, J., Trigo, R., Coelho, F., and Espejo, F.: Evidence of increasing drought severity caused by temperature rise in southern Europe, Environ. Res. Lett., 9, 044001, https://doi.org/10.1088/1748-9326/9/4/044001, 2014.
Willgoose, G. and Perera, H.: A simple model of saturation excess runoff generation based on geomorphology, steady state soil moisture, Water Resour. Res., 37, 147–155, https://doi.org/10.1029/2000WR900265, 2001.
Wösten, J. H. M., Lilly, A., Nemes, A., and Le Bas, C.: Development and use of a database of hydraulic properties of European soils, Geoderma, 90, 169–185, https://doi.org/10.1016/S0016-7061(98)00132-3, 1999.
Zhao, B., Dai, Q., Han, D., Dai, H., Mao, J., Zhuo, L., and Rong, G.: Estimation of soil moisture using modified antecedent precipitation index with application in landslide predictions, Landslides, 16, 2381–2393, https://doi.org/10.1007/s10346-019-01255-y, 2019.