Reliability-based strength modification factor for seismic design spectra considering structural degradation

For earthquake-resistant design, structural degradation is considered using traditional strength modification factors, which are obtained via the ratio of the nonlinear seismic response of degrading and non-degrading structural single-degree-of-freedom (SDOF) systems. In this paper, with the aim to avoid the nonlinear seismic response to compute strength modification factors, a methodology based on probabilistic seismic hazard analyses (PSHAs), is proposed in order to obtain strength modification factors of design spectra which consider structural degradation through the spectral-shape intensity measure $I_{N_{\mathrm{p}}}$. PSHAs using $I_{N_{\mathrm{p}}}$ to account for structural degradation and Sa(T₁), which represents the spectral acceleration associated with the fundamental period and does not consider such degradation, are performed. The ratio of the uniform hazard spectra in terms of $I_{N_{\mathrm{p}}}$ and Sa(T₁), which represent the response of degrading and non-degrading systems, provides new strength modification factors without the need to develop nonlinear time history analysis. A mathematical expression is fitted to the ratios that correspond to systems located in different soil types. The expression is validated by comparing the results with those derived from nonlinear time history analyses of structural systems.

1 Introduction

Structures subjected to cyclic loading induced by intense ground motions can exhibit stiffness and/or strength degradation due to the inelastic nonlinear behavior of their structural elements, which can give place to lengthening of the structural fundamental vibration period T₁. The effect of such lengthening can be beneficial for structures whose fundamental period is in the descendant branch of the acceleration response spectrum, and their higher vibration modes have little influence on the structural response. Conversely, the effect can be detrimental for structures whose vibration period is in the ascendant branch of the response spectrum. In the latter case, the effect of “structural softening” can have severe consequences because the structure undergoes seismic loading greater than that assumed for its design (Akkar et al., 2004; Chenouda and Ashraf, 2008; Chopra and Chintanapakdee, 2004; Terán-Gilmore and Espinosa Johnson, 2008). For example, during the Guerrero-Michoacán 19 September 1985 Mexican earthquake, many mid-rise buildings (5- to 10-story buildings) with T₁=0.7–1.2 s approximately, located in soft soil of Mexico City, which has a vibration period around 2 s, suffered severe structural damage (including collapse) because of the degrading structural effect (Montiel and Ruiz, 2007).

Seismic design guidelines for building structures recommend modifying the response-spectra ordinates by a series of factors in order to include relevant structural behavior that affects the structural response. Those factors are related, for example, to seismic behavior, structural over-strength, structural irregularity, degrading behavior, etc. A common practice to derive those modification factors is by means of the ratio between specific response spectra of single-degree-of-freedom (SDOF) systems. Indeed, most current seismic code provisions implement simplified analyses based on these ratios. For example, the Federal Emergency Management Agency (FEMA) introduced the so-called coefficient method (FEMA-273, 1997; FEMA-356, 2000), which consists of multiplying the elastic design spectrum by several coefficients. One of them takes into account the hysteretic structure-degrading behavior. More recently, FEMA-440 (2005) presented some improvements to current nonlinear analysis procedures. Accordingly, the coefficient method suffered slight adjustments, where the coefficient that incorporates the effect of degrading structural behavior was updated. At present, the simplified nonlinear approach is available in FEMA P-58 (2012) methodology. Another example is the Manual for Civil Structures Design (MCSD, 2015), developed by the Federal Commission of Electricity of Mexico, which specifies a degrading factor that increases or decreases the design spectral ordinates, due to structural deterioration.

The hysteretic degrading behavior is particularly severe for structures located in soft soil, like that in the lake bed zone of Mexico City, where there is a high-density population, and the site effects make it susceptible to severe earthquake damage (Singh et al., 1988, 2018). In spite of that, the current Mexico City Building Code (MCBC, 2017) does not specify any structure-degrading factor.

This study is aiming to propose a methodology for obtaining a mathematical expression corresponding to a structure-degrading factor for seismic design of buildings that exhibit period lengthening. The expression is a function of both the structural period and the dominant period of the soil. The methodology can be applied to any high-seismic-hazard region of the world. Finally, notice that the variation in the vibration periods of a structure from the undamaged to the damaged state strongly depends of several parameters, and this is crucial to consider different design limit states. Although the procedure is not affected by these parameters, the variation in the structural period could be taken into account considering different values of T_N (see definition of N_p below); however, the assessment of this value accounts for the design limit state, structural type, interaction of the structural elements with the nonstructural ones requiring the study of specific structural systems such as reinforced concrete, moment-resisting steel frames, masonry, structures with eccentrically buckling restrained braces, and posttensioned based isolators, which are out of the scope of the present study. On the other hand, soil–structure interaction (SSI) was not taken into account to compute the structure-degrading modification factors for seismic design spectra; nevertheless, notice that the effect of SSI is more important for stiff structures located on soft soil, in such a way that for this type of structure, the ordinates of the response spectra tend to increase while the opposite occurs for flexible structures (Avilés and Pérez-Rocha, 2007). The results obtained in the present study could be modified to include the effect of SSI via the current Mexico City Building Code (MCBC, 2017) which provides recommendations about this issue.

2 Methodology proposed

First, it is necessary to perform probabilistic seismic hazard analyses (PSHAs) corresponding to a firm-ground site and then soft-soil sites located in the seismic area of interest. PSHAs are associated with Sa(T₁) and alternatively with $I_{N_{\mathrm{p}}}$ intensity measures, where Sa(T₁) represents the spectral acceleration at the fundamental period of a structure, and I_Npis an intensity measure that accounts for the period lengthening due to structure-degrading behavior ($I_{N_{\mathrm{p}}}$ is defined below). Although Sa(T₁) is the most used ground motion intensity measure (IM) around the world for PSHAs, it has some limitations. For example, it does not consider the effect of period lengthening of the structure due to its nonlinear behavior and mechanical property degradation (Baker and Cornell, 2005; Bojórquez et al., 2008, 2017a; Bojórquez and Iervolino, 2011; Kostinakis et al., 2018; Cordova et al., 2001; Shome et al., 1998; Tothong and Luco, 2007).

Second, uniform hazard spectra (UHS) of $I_{N_{\mathrm{p}}}$ and Sa(T₁), which represent the response of degrading and non-degrading systems, respectively, are obtained. The UHS are computed for several seismic recording stations located in different soil conditions. Subsequently, the effect of the structural degradation on the response of SDOF systems is characterized by the ratio between the uniform hazard spectra: $I_{N_{\mathrm{p}}}/\mathrm{Sa}\left(T_{\mathrm{1}}\right)$.

Finally, a mathematical expression is adjusted to the spectral ratios. In order to verify that the mathematical expression leads to reasonable results, it is convenient to compare these with those obtained with other expressions found in the literature.

Figure 1 Block diagram of the proposed methodology.

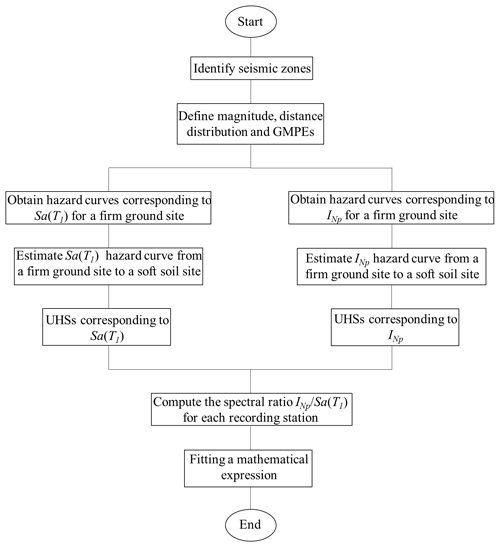
In what follows, a description of the methodology is presented (see Fig. 1).

• First, PSHAs are carried out for the firm-ground site of interest, corresponding to Sa(T₁) and, alternatively, to $I_{N_{\mathrm{p}}}$. With the purpose of performing the analyses, the seismic tectonic zones that contribute to the seismic hazard of the site are identified.

• Then, the probability distribution for earthquake magnitude and source-to-site distance are assumed. Additionally, it is necessary to define adequate ground motion prediction equations (GMPEs).

• With the total probability theorem and the information previously defined, the mean annual rates of exceedance (seismic hazard curves) corresponding to the site located in firm ground are obtained.

• Once the hazard curves for firm ground are available, the mean annual rates of exceedance of seismic recording stations located in different soil types of the seismic area of interest are estimated (using a technique described in the following sections). The stations are grouped in different zones, which depend on the dominant period of the soil, T_s.

• For each recording station site, UHS associated with a given return period are computed for Sa(T₁), and alternatively, for $I_{N_{\mathrm{p}}}$.

• Next, the spectral ratio $I_{N_{\mathrm{p}}}/\mathrm{Sa}\left(T_{\mathrm{1}}\right)$ is estimated for each site. $I_{N_{\mathrm{p}}}/\mathrm{Sa}\left(T_{\mathrm{1}}\right)$ represents the ratio of strength demands between systems with degrading and systems with non-degrading structural behavior.

• Finally, a simplified mathematical expression is adjusted to the spectral ratio $I_{N_{\mathrm{p}}}/\mathrm{Sa}\left(T_{\mathrm{1}}\right)$. The expression contains parameters that depend on the zone of interest.

• The results of the expression proposed are compared with those obtained from other expressions found in the literature, which were obtained from time history analyses.

For illustrative purposes, in the following sections, the methodology proposed above is applied in order to find mathematical expressions of structure-degrading factors of the design spectra specified in MCBC; however, the approach can be applied to any seismic region in the world.

Figure 2 (a) Interplate seismicity regions, (b) intraslab seismicity regions and (c) characteristic seismicity regions.

3 Probabilistic seismic hazard analysis (PSHA)

3.1 Earthquake sources

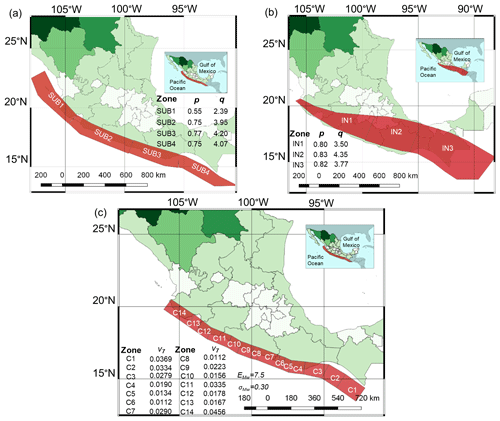
The evaluation of a probabilistic seismic hazard analysis for a particular site requires identification of all possible earthquake sources capable of producing a significant seismic event. For this purpose, Zúñiga et al. (2017) proposed a seismic regionalization for Mexico, which is used in the present study. Figure 2a shows the shallow-depth seismic zones where interplate earthquakes occur due to the subduction of the Rivera and Cocos plates (SUB1–SUB4). Figure 2b illustrates the intermediate-depth seismic zones. This region corresponds to intraslab events that take place inside the subducted Rivera and Cocos plates below south-central Mexico (IN1 to IN3). Additionally, Fig. 2c displays the seismic zones for characteristic seismic events (C1 to C14) proposed by Ordaz and Reyes (1999). Seismic zones in Fig. 2c are also included in the present study to compute PSHA.

3.2 Magnitude probability distribution

Seismic sources are capable of producing different earthquake sizes. Therefore, it is crucial to define the probability distribution of the earthquake magnitudes and corresponding rates of occurrence for each source. In this regard, the distribution of earthquake sizes is commonly described by the bounded Gutenberg–Richter recurrence law (Eq. 1).

$$\begin{array}{}\text{(1)}& {\mathit{\lambda }}_{\mathrm{m}}=\mathit{\nu }{\displaystyle \frac{\exp \left[-\mathit{\beta }\left(M_{\mathrm{w}}-M_{\min }\right)\right]-\exp \left[-\mathit{\beta }\left(M_{\max }-M_{\min }\right)\right]}{\mathrm{1}-\exp \left[-\mathit{\beta }\left(M_{\max }-M_{\min }\right)\right]}},\end{array}$$

where λ_m is the mean annual rate of exceedance for earthquakes between a minimum magnitude M_min and a maximum magnitude M_max, and $\mathit{\nu }=\exp (\mathit{\alpha }-\mathit{\beta }{M}_{\min })$ is the mean annual number of earthquakes of magnitude M_w≥M_min, where α=2.303p and β=2.303q. The values of p and q are indicated in Fig. 2a and b, according to Zúñiga et al. (2017).

For the seismic sources related to characteristic earthquakes (Fig. 2c), the bounded Gutenberg–Richter recurrence law does not accurately describe the magnitude exceedance rates. Accordingly, for M_w>7, we employ a Gaussian probability distribution function (pdf) of magnitudes to account for the characteristic events in the Mexican subduction zones (see Eq. 2) (Ordaz and Reyes, 1999).

$$\begin{array}{}\text{(2)}& {\mathit{\lambda }}_{\mathrm{m}}={\mathit{\nu }}_{\mathrm{7}}\left[\mathrm{1}-\mathrm{\Phi }\left({\displaystyle \frac{M_{\mathrm{w}}-E_{M_{\mathrm{w}}}}{{\mathit{\sigma }}_{M_{\mathrm{w}}}}}\right)\right],\end{array}$$

where ν₇ is the mean annual number of earthquakes of magnitude M_w>7; $E_{M_{\mathrm{w}}}$ and ${\mathit{\sigma }}_{M_{\mathrm{w}}}$ are the mean and standard deviation of the magnitude, respectively, and Φ (.) is the normal distribution function. The corresponding parameters to evaluate the distribution are shown in Fig. 2c.

The present study assumes M_min=4.5 and M_max=6.9 for the interplate shallow-depth seismic zones SUB1–SUB3 (see Fig. 2a). In contrast, M_min=4.5 and M_max=7.2, 7.8 and 7.9 are assumed for IN1–IN3, respectively (intermediate-depth seismic zones, Fig. 2b). Finally, M_min=7.0 and M_max=8.1 are assumed for the 14 earthquake sources shown in Fig. 2c.

3.3 Source-to-distance distribution

Once the earthquake magnitude distribution is established, the pdf of distances from the earthquake location to the site of interest must be characterized. A uniform pdf is generally assigned to any point in the seismic zone (McGuire, 1995; Kramer, 1996). Since the area sources, where earthquakes can occur, are well-delimited (Fig. 2a–c), it is straightforward to determine the source-to-distance distribution.

3.4 Ground motion prediction equations

Attenuation relationships are fundamental for PSHA. They are commonly developed to predict the peak ground acceleration, PGA, or the spectral acceleration, Sa(T₁). Unfortunately, attenuation models have not yet been devised to provide $I_{N_{\mathrm{p}}}$ as a function of the vibration period (as is done with existing GMPEs); however, with GMPEs for Sa(T₁) currently available, it is possible to perform PSHA using $I_{N_{\mathrm{p}}}$. Here we employ the GMPEs proposed by Reyes et al. (2002) and Jaimes et al. (2015) for interplate and intraslab events, respectively. They were developed using accelerometric data recorded at Ciudad Universitaria station (CU), which is located at the hill zone (firm ground) of Mexico City, basically conformed by a surface layer of lava flows and volcanic tuffs with a shear wave velocity in the upper 30 m of 750 m s⁻¹ (Ordaz and Singh, 1992; Singh et al., 2018).

3.5 Seismic hazard curves

The final product of a PSHA can be expressed in different forms. Seismic hazard curves are used frequently to represent the seismic hazard. They indicate the annual rate of exceeding a variety of intensity levels of a ground motion parameter at a site of interest. The procedure to compute a ground motion hazard curve is based on the total probability theorem (Baker, 2013; Cornell, 1968; Esteva, 1968; McGuire, 1995; Kramer, 1996).

4 $I_{N_{\mathrm{p}}}$ intensity measure

In order to overcome the limitations of traditional IMs (e.g., PGA, Sa(T₁)), advanced seismic IMs have been proposed. Some researchers suggest using vector-valued ground motion IMs. By including two or more representative parameters of the ground motion, accurate evaluations of seismic performance can be achieved (Baker and Cornell, 2005; Bojórquez et al., 2008, 2017a; Bojórquez and Iervolino, 2011; Kostinakis et al., 2018; Cordova et al., 2001; Tothong and Luco, 2007). Accordingly, Bojórquez et al. (2008) developed the vector-valued intensity measure <Sa(T₁), N_p>, where N_p is a parameter proxy for the spectral shape. This IM is an advancement in predicting the seismic response in comparison with other IMs. However, the evaluation of PSHA using vector-valued IMs is a complicated and impractical task; therefore, Bojórquez and Iervolino (2011) introduced a scalar IM based on Sa(T₁) and N_p, called $I_{N_{\mathrm{p}}}$; both N_p scalar and vector-valued intensity measures have been effectively used (Bojórquez et al., 2012, 2017b).

Accordingly, Buratti (2012) made an exhaustive comparison of the most influential scalar IMs available in the literature with respect to efficiency and sufficiency. The study concluded that the most effective intensity measure was $I_{N_{\mathrm{p}}}$. Additionally, De Biasio et al. (2014), based on a comparative study of structures with nonlinear behavior, showed the good performance of $I_{N_{\mathrm{p}}}$ to predict maximum interstory drift and maximum ductility demands. Moreover, Modica and Stafford (2014) using <Sa(T₁) and N_p>, estimated the fragility and performance of buildings with higher efficiency with respect to different IMs. In this context, Minas and Galasso (2019) showed the advantages of $I_{N_{\mathrm{p}}}$ comparing Sa(T₁) fragility curves, for different damage states. Additionally, Yakhchalian et al. (2015) demonstrated the efficiency of the parameter N_p. They showed that the parameter N_p works appropriately, particularly in performance levels related to moderate levels of nonlinearity. Similarly, Kostinakis and Athanatopoulou (2016) proved the adequate efficiency of $I_{N_{\mathrm{p}}}$ to reduce the uncertainty in the prediction of the response of reinforced concrete buildings. In addition, Jamshidiha et al. (2018) examined the ability of different IMs to predict the seismic collapse capacity of steel moment-resisting frames with fluid viscous dampers. They concluded that the scalar IM that resulted from the combination with the parameter N_p was most efficient.

Based on the literature mentioned above, the authors of the present study concluded that $I_{N_{\mathrm{p}}}$ is a promising tool to perform PSHA.

4.1 Methodology to perform a PSHA using $I_{N_{\mathrm{p}}}$

In this section a methodology to perform PSHA using $I_{N_{\mathrm{p}}}$ is proposed. First, $I_{N_{\mathrm{p}}}$ is defined as follows (Bojórquez and Iervolino, 2011):

$$\begin{array}{}\text{(3)}& {\displaystyle }& {\displaystyle }{I}_{N_{\mathrm{p}}}=\mathrm{Sa}\left(T_{\mathrm{1}}\right)\cdot N_{\mathrm{P}}^{\mathit{\alpha }},\text{(4)}& {\displaystyle }& {\displaystyle }{N}_{\mathrm{P}}={\displaystyle \frac{{\mathrm{Sa}}_{\mathrm{avg}}\left(T_{\mathrm{1}}\mathrm{\dots }{T}_N\right)}{\mathrm{Sa}\left(T_{\mathrm{1}}\right)}},\end{array}$$

where $I_{N_{\mathrm{p}}}$ is the scalar intensity measure, α is a parameter that should be calibrated according to the structure and the earthquake demand parameter selected (in this study α=0.5 is adopted, as recommended in Bojórquez and Iervolino, 2011), and Sa_avg(T₁ … T_N) is the geometric mean of the spectral acceleration at N numbers of structural vibration periods considered. Sa_avg(T₁ …T_N) takes into account the vibration period lengthening due to structural damage and is expressed as

$$\begin{array}{}\text{(5)}& {\mathrm{Sa}}_{\mathrm{avg}}\left(T_{\mathrm{1}}\mathrm{\dots }{T}_N\right)={\left(\prod _{i=\mathrm{1}}^N\mathrm{Sa}\left(T_i\right)\right)}^{\mathrm{1}/N}.\end{array}$$

Substituting Eqs. (4) and (5) into Eq. (3), applying the natural logarithm, results in

$$\begin{array}{}\text{(6)}& \ln \left(I_{N_{\mathrm{p}}}\right)=(\mathrm{1}-\mathit{\alpha })\ln \left[\mathrm{Sa}\left(T_{\mathrm{1}}\right)\right]+{\displaystyle \frac{\mathit{\alpha }}{N}}\sum _{i=\mathrm{1}}^N\ln \left[\mathrm{Sa}\left(T_i\right)\right].\end{array}$$

Then, the expected value and the variance of $\ln \left(I_{N_{\mathrm{p}}}\right)$ can be expressed as in Eqs. (7) and (8), respectively.

$$\begin{array}{}\text{(7)}& {\displaystyle }\begin{array}{rl}E\left[\ln \left(I_{N_{\mathrm{p}}}\right)\right]& =(\mathrm{1}-\mathit{\alpha })E\left\{\ln \left[\mathrm{Sa}\left(T_{\mathrm{1}}\right)\right]\right\}\\ & +{\displaystyle \frac{\mathit{\alpha }}{N}}\sum _{i=\mathrm{1}}^{N}E\left\{\ln \left[\mathrm{Sa}\left(T_i\right)\right]\right\}\end{array}\text{(8)}& {\displaystyle }\begin{array}{rl}\mathrm{Var}\left[\ln \left(I_{N_{\mathrm{p}}}\right)\right]& ={\mathit{\alpha }}^{\mathrm{2}}\mathrm{Var}\left\{\ln \left[{\mathrm{Sa}}_{\mathrm{avg}}\left(T_{\mathrm{1}}\mathrm{\dots }{T}_N\right)\right]\right\}\\ & +(\mathrm{1}-\mathit{\alpha }{)}^{\mathrm{2}}\mathrm{Var}\left\{\ln \left[\mathrm{Sa}\left(T_{\mathrm{1}}\right)\right]\right\}\\ & +\mathrm{2}\mathit{\alpha }(\mathrm{1}-\mathit{\alpha }){\mathit{\rho }}_{\ln \left[{\mathrm{Sa}}_{\mathrm{avg}}\left(T_{\mathrm{1}}\mathrm{\dots }{T}_N\right)\right],\ln \left[\mathrm{Sa}\left(T_{\mathrm{1}}\right)\right]}\\ & {\mathit{\sigma }}_{\ln \left[{\mathrm{Sa}}_{\mathrm{avg}}\left(T_{\mathrm{1}}\mathrm{\dots }{T}_N\right)\right]}{\mathit{\sigma }}_{\ln \left[\mathrm{Sa}\left(T_{\mathrm{1}}\right)\right]}\end{array}\end{array}$$

The values of ln [Sa(T_i)] are obtained from existing attenuation models (e.g., the GMPEs described in Sect. 3.4). On the other hand, ln [Sa(T_i)] terms are commonly assumed to have a joint Gaussian pdf; consequently, the summation also has Gaussian distribution. Therefore, the variance Var{ln [Sa_avg(T₁ … T_N)]} and the correlation coefficient ρln [Sa_avg(T₁ … T_N)]ln [Sa(T_i)] can be obtained by Eqs. (9) and (10), respectively:

$$\begin{array}{}\text{(9)}& {\displaystyle }\begin{array}{rl}\mathrm{Var}& \left\{\ln \left[{\mathrm{Sa}}_{\mathrm{avg}}\left(T_{\mathrm{1}}\mathrm{\dots }{T}_N\right)\right]\right\}={\displaystyle \frac{\mathrm{1}}{N^{\mathrm{2}}}}\sum _{i=\mathrm{1}}^N\sum _{j=\mathrm{1}}^N\\ & \left[{\mathit{\rho }}_{\ln \left[\mathrm{Sa}\left(T_i\right)\right],\ln \left[\mathrm{Sa}\left(T_j\right)\right]}{\mathit{\sigma }}_{\ln \left[\mathrm{Sa}\left(T_i\right)\right]}{\mathit{\sigma }}_{\ln \left[\mathrm{Sa}\left(T_j\right)\right]}\right],\end{array}\text{(10)}& {\displaystyle }\begin{array}{rl}& {\mathit{\rho }}_{\ln \left[{\mathrm{Sa}}_{\mathrm{avg}}\left(T_{\mathrm{1}}\mathrm{\dots }{T}_N\right)\right],\ln \left[\mathrm{Sa}\left(T_{\mathrm{1}}\right)\right]}\\ & ={\displaystyle \frac{{\sum }_{i=\mathrm{1}}^N{\mathit{\rho }}_{\ln \left[\mathrm{Sa}\left(T_i\right)\right],\ln \left[\mathrm{Sa}\left(T_{\mathrm{1}}\right)\right]}{\mathit{\sigma }}_{\ln \left[\mathrm{Sa}\left(T_i\right)\right]}}{\sqrt{{\sum }_{i=\mathrm{1}}^N{\sum }_{j=\mathrm{1}}^N\left[{\mathit{\rho }}_{\ln \left[\mathrm{Sa}\left(T_i\right)\right],\ln \left[\mathrm{Sa}\left(T_j\right)\right]}{\mathit{\sigma }}_{\ln \left[\mathrm{Sa}\left(T_i\right)\right]}{\mathit{\sigma }}_{\ln \left[\mathrm{Sa}\left(T_j\right)\right]}\right]}}},\end{array}\end{array}$$

where the term ρln [Sa(T_i)], ln [Sa(T_j)] represents the correlation between spectral acceleration values at periods T_i and T_j. The correlation coefficients have been obtained by the authors of the present study (Rodríguez-Castellanos et al., 2019, 2020).

4.2 Values of T_N

Among the parameters that define the intensity measure $I_{N_{\mathrm{p}}}$, the geometric mean, Sa_avg(T₁ … T_N), has a crucial role when computing the uniform hazard spectra (UHS). The T_N value (Nth structural vibration period) takes into account the level of nonlinearity developed by the structure. Bojórquez et al. (2008) and Bojórquez and Iervolino (2011) recommend using T_N=2.0T1. Nevertheless, we consider that there is no optimal period range for Sa_avg(T₁ … T_N) that meets the entire range of structural vibration periods; therefore, here we propose that T_N should depend on the structural vibration period, which is in agreement with Tsantaki et al. (2012, 2017).

It has been pointed out that the stiffer the structure, the larger the period lengthening. Accordingly, for structures with short vibration periods, we adopt T_N=2.0T₁, which agrees with recommendations made by Bianchini et al. (2009), Katsanos and Sextos (2015), and Tsantaki et al. (2017), for relatively stiff structures, and assuming a ductility demand between 2 and 3.

At short to moderate vibration periods, the structural period lengthening diminishes somewhat linearly until it reaches a semi-constant behavior (which is independent of the level of nonlinearity developed by the structure) (Katsanos and Sextos, 2015). In this regard, Di Sarno and Amiri (2019) quantified the fundamental period lengthening of structures by the ratio of response spectra corresponding to the lengthened and the elastic structural vibration period ($T_{\mathrm{in}}/T_{\mathrm{el}}$). They suggested dividing the response spectra into two main regions: the first associated with short to moderate period structures, whose period shift ratio $T_{\mathrm{in}}/T_{\mathrm{el}}$ decreases with increasing the elastic period, and the second region related to long-period structures, where the ratio period $T_{\mathrm{in}}/T_{\mathrm{el}}$ behaves practically constant. Consequently, there must be a certain bound where the period shift ratio switches to remain constant; therefore, we propose T_N=T_s as that bound from which the lengthening of the structural vibration period remains almost constant. In this context, Miranda and Ruiz-Garcia (2002), Ruiz-Garcia and Miranda (2003), and independently Terán-Gilmore and Espinosa Johnson (2008), found that strength demands between degrading and non-degrading systems are similar when the structural period and dominant soil period are comparable, which means that the mean ratio value should be approximate to one when T_n≈T_s.

For vibration periods longer than the dominant soil period, it is assumed T_N=1.25T₁, which is, on average, the period shift ratio value for structures with a short to moderate nonlinearity level, that is, with a ductility ratio around 2 to 3 (Katsanos and Sextos, 2015; Di Sarno and Amiri, 2019).

Summarizing, we used T_N=2.0T₁ in this study for structural systems with a short fundamental period; T_N=T_s for those with an intermediate period and T_N=1.25T₁ for systems with a long fundamental period. It is possible to get a better approximation of T_N bounds, by means of a parametric study of the ratios of the equivalent period of SDOF degraded systems and that of the elastic systems ($T_{\mathrm{in}}/T_{\mathrm{el}}$), as a function of T_el, for a given ductility. Such a study can consider both ground motion characteristics and structural properties (such as degrading stiffness ratio, pinching factor, accumulated damage factor, etc.), as was done by Di Sarno and Amiri (2019). They proposed a mathematical expression for estimating the lengthening of the fundamental period as a function of the structural elastic period and the significant structural parameters, which is applicable to systems in site classes D and C according to ASCE 7–10 (2010), with shear wave velocities $\mathrm{182.88}<V_{{\mathrm{s}}_{\mathrm{30}}}<\mathrm{365.76}$ and $\mathrm{365.76}<V_{{\mathrm{S}}_{\mathrm{30}}}<\mathrm{762}$ m s⁻¹, respectively. However, the T_N bounds used here lead to reasonable results, as is verified below.

Figure 3 (a) Uniform hazard spectra for CU and (b) uniform hazard spectra of Sa(T₁) and $I_{N_{\mathrm{p}}}$ for CU (250-year return period).

5 Probabilistic seismic hazard analysis using $I_{N_{\mathrm{p}}}$

5.1 Uniform hazard spectra corresponding to firm ground

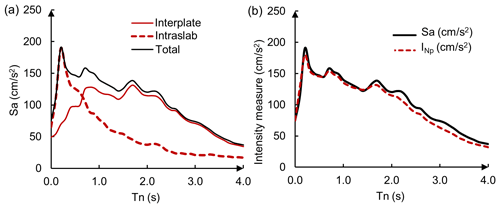
The uniform hazard spectra are computed, first, for the CU site, which is in firm ground. Figure 3a shows the UHS if only interplate, or alternatively intraslab, earthquakes occur. It also displays when both types of events are considered simultaneously (Total). Figure 3b shows the total UHS of Sa(T₁) and $I_{N_{\mathrm{p}}}$, both associated with a 250-year return period. It can be seen that the spectra are quite similar; practically, they reach the same acceleration levels, and slight differences occur at long periods.

Table 1 Zones of Mexico City grouped in accordance with the dominant soil period.

5.2 Uniform hazard spectra corresponding to soft-soil sites

Estimating the seismic hazard at firm ground allows us to proceed with a technique to assess the seismic hazard at soft-soil sites. In this regard, Esteva (1970) presented a formulation in which through a known hazard curve at a reference site it is feasible to estimate a hazard curve at a recipient site. In this study, we used CU station as the reference site because, since 1964, it has recorded all the significant ground motions that have struck Mexico City. In addition, different studies have taken CU as a reference site (Ordaz et al., 1988; Reinoso and Ordaz, 1999; Singh et al., 1988). Therefore, it is viable to perform a hazard analysis for CU station and then to compute the annual rate of exceedance at other sites located in soft or medium soils, as follows:

$$\begin{array}{}\text{(11)}& {\mathit{\nu }}_Y\left(y\right)=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\mathit{\nu }}_X\left({\displaystyle \frac{y}{\mathit{\tau }}}\right)f_{\mathit{\tau }}\left(\mathit{\tau }\right)d\mathit{\tau }=E_{\mathit{\tau }}\left({\mathit{\nu }}_x\left({\displaystyle \frac{y}{z}}\right)\right),\end{array}$$

where ν_Y(y) is the mean annual rate of exceedance of a seismic IM, for the recipient site. ${\mathit{\nu }}_x(y/\mathit{\tau })$ is the mean annual rate of exceedance of a seismic IM for the reference site, divided by the variable τ. τ represents the response spectral ratios between the response spectra corresponding to the recipient site and the reference site ($Y/X$). fτ(τ) is the pdf of τ.

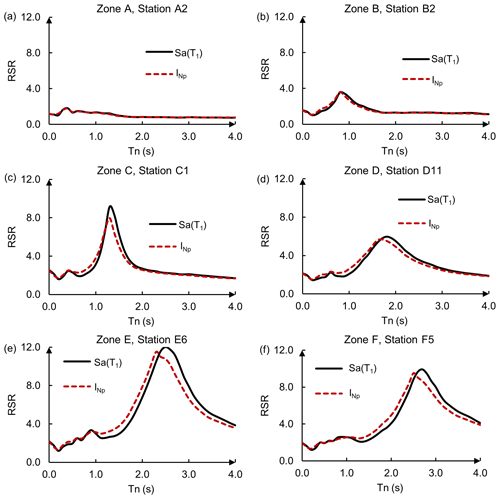
Figure 4 Mean response spectral ratios for Sa(T₁) and $I_{N_{\mathrm{p}}}$ corresponding to one representative station of each zone listed in Table 1.

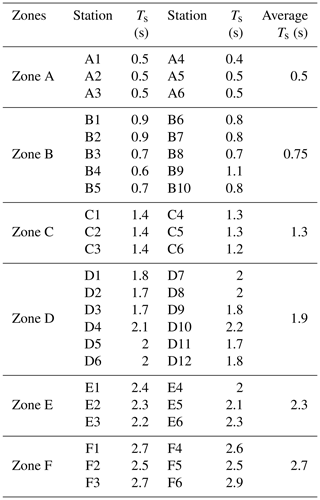
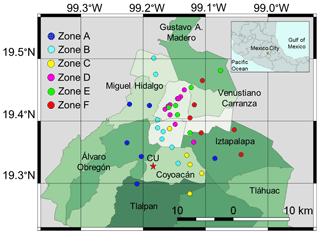
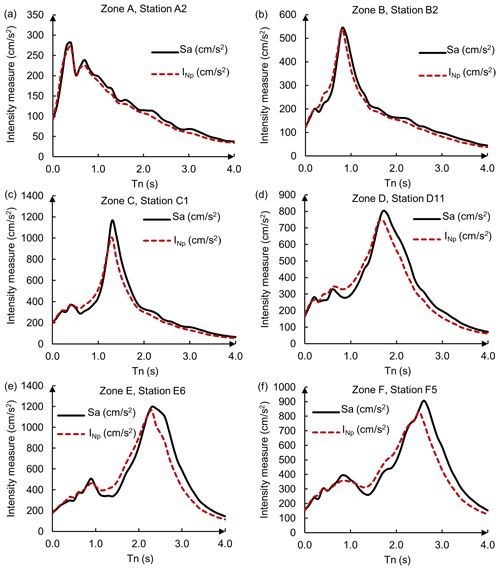
Therefore, to evaluate the previous function, firstly, the spectral ratios are estimated, and then they are coupled with the seismic hazard curves via Eq. (11). In this respect, Fig. 4a–f show the mean response of the spectral ratios for Sa(T₁) (solid line) and $I_{N_{\mathrm{p}}}$ (dashed line) for one representative station located in each of the zones listed in Table 1. In this sense, the spectral ratios roughly represent the spectral amplification of soft soil with respect to firm ground. It is observed how the peak values shift towards increasingly longer periods, which, approximately, match with the dominant soil period (see Table 1). For this analysis, more than 1100 ground motion records corresponding to the different recording stations were used. The stations are grouped depending on the dominant soil period where these are located, as follows: zone A: T_s<0.5 s; zone B: 0.5 s < T_s < 1.0 s; zone C: 1.0 s < T_s < 1.5 s; zone D: 1.5 s < T_s < 2.0 s; zone E: 2.0 s < T_s < 2.5 s; and zone F: 2.5 s < T_s < 3.0 s. Additionally, Fig. 5 shows the location of the recording stations in Mexico City, which are represented with circles of different colors associated with each of the proposed zones (see Table 1).

Figure 5 Locations of seismic recording stations in Mexico City (see Table 1).

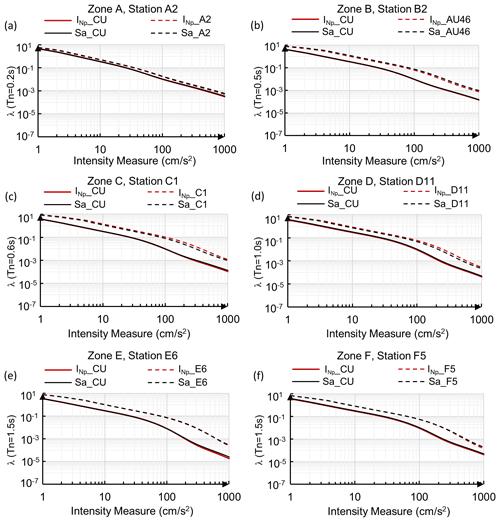
Figure 6 Mean annual rate of exceedance (λ) of Sa(T₁) and $I_{N_{\mathrm{p}}}$, for different vibration periods, corresponding to one representative station of each zone listed in Table 1.

Next, in order to compute the mean annual rate of exceedance of Sa(T₁) and $I_{N_{\mathrm{p}}}$, the seismic hazard curves corresponding to CU station are coupled with the response spectral ratios, using Eq. (11). Figure 6a to f show the hazard curves (λ) of Sa(T₁) and $I_{N_{\mathrm{p}}}$, associated with different vibration periods, corresponding to CU and the same recording stations of Fig. 4a to f. First, as expected, the rates of exceedance for all the recording stations analyzed are higher than the corresponding ones of CU (up and down). Additionally, concerning the CU site, the hazard curves for both intensity measures $I_{N_{\mathrm{p}}}$ and Sa(T₁) are very similar, and differences are barely visible at long return periods. Now, for the rest of the recording stations, Fig. 4c and d show noticeable variations between exceedance rates of Sa(T₁) and $I_{N_{\mathrm{p}}}$; nevertheless, Fig. 4e and f display almost no contrast between the rates of exceedance of the two intensity measures. The previous is relative, because to fully characterize the variations between exceedance rates of Sa(T₁) and $I_{N_{\mathrm{p}}}$, a wide range of periods need to be covered; for this reason, we estimate the UHS in the following.

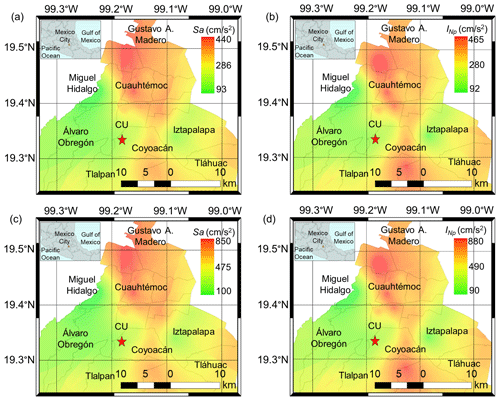
Then, having the mean rates of exceedance for each recording station site (see Table 1), the UHS are estimated for a given return interval. Figure 7a to f show the UHS of Sa(T₁) and I_Np for the same stations of Fig. 6a to f, for a 250-year return period. It is observed that, at vibration periods shorter than the dominant soil period, the spectral ordinates corresponding to firm ground (zones A–C) are comparable for both IMs. However, at soft soil (zones D–F), the spectral ordinates of $I_{N_{\mathrm{p}}}$ are notably higher than those of Sa(T₁) (up to 30 %). In contrast, at vibration periods longer than T_s, they are smaller than those corresponding to Sa(T₁) (5 % to 20 %, depending on the soil type). The same can be appreciated for different sites of the city in the maps shown in Fig. 8a to d, which corresponds to Sa(T₁) (left side) and $I_{N_{\mathrm{p}}}$ (right side), for T₁=0.5 s (up side) and T₁=1.0 s (down side), for a return interval of T_r=250 years.

Figure 7 Uniform hazard spectra of Sa(T₁) and $I_{N_{\mathrm{p}}}$, corresponding to one representative station of each zone listed in Table 1, considering 250-year return interval.

Figure 8 Intensity maps corresponding to Sa(T₁) (a, c) and $I_{N_{\mathrm{p}}}$ (b, d), for T₁=0.5 s (a, b) and T₁=1.0 s (c, d), for a 250-year return interval.

6 Degrading structural behavior effect

Once the uniform hazard spectra of Sa(T₁) and $I_{N_{\mathrm{p}}}$ were estimated, the degrading structural behavior effect is evaluated by means of the ratio $I_{N_{\mathrm{p}}}/\mathrm{Sa}\left(T_{\mathrm{1}}\right)$. It represents the ratio of strength demands between a system with degrading and the same system with non-degrading structural behavior. The ratios are obtained for each station of the zones listed in Table 1. Figure 9a to f show the $I_{N_{\mathrm{p}}}/\mathrm{Sa}\left(T_{\mathrm{1}}\right)$ ratios (thin gray lines) as a function of the normalized periods $T_n/T_{\mathrm{s}}$, for zones A to F, respectively.

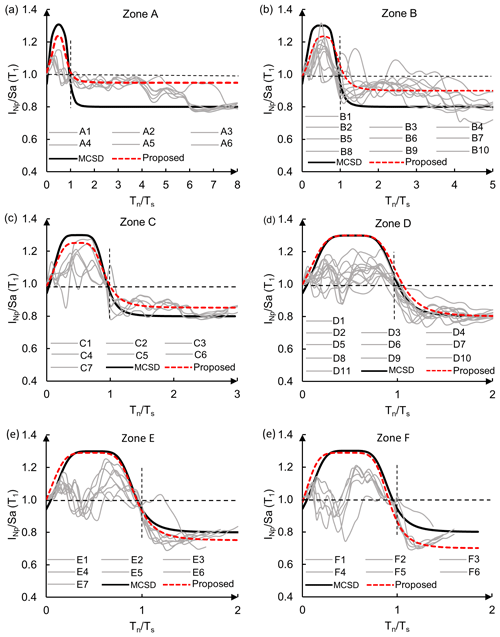
Figure 9 Spectral ratios between the uniform hazard spectra of $I_{N_{\mathrm{p}}}$ and Sa(T₁) ($I_{N_{\mathrm{p}}}/\mathrm{Sa}\left(T_{\mathrm{1}}\right)$), for the recording stations, corresponding to six zones in Mexico City (see Table 1).

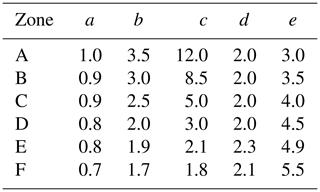
Based on these ratios, the following spectral modification function (SMF) was proposed, which is a variation of that specified by MCSD (2015):

$$\begin{array}{}\text{(12)}& \mathrm{SMF}=a+{\displaystyle \frac{\mathrm{1}}{b+c{\left|d\frac{T_n}{T_{\mathrm{s}}}-\mathrm{1}\right|}^e}},\end{array}$$

where the values of a–e are shown in Table 2. It is noticed that the values of the parameters depend on the type of soil where the structure is located; conversely, those in the MCSD function are constant values. In addition, such a function is restricted only to soft soils.

Table 2 Numerical coefficients for SMF expression (Eq. 12).

Figure 9a to f show the equation proposed here (Eq. 12) (thick dashed line), as well as the MCSD (2015) function (thick solid line). In the figures, the horizontal and vertical dotted lines, aligned at $I_{N_{\mathrm{p}}}/\mathrm{Sa}\left(T_{\mathrm{1}}\right)=\mathrm{1}$ and $T_n/T_{\mathrm{s}}=\mathrm{1}$, approximately delimitate the increase or decrease in the spectral amplification.

The figures show the following.

• a.

  The highest $I_{N_{\mathrm{p}}}/\mathrm{Sa}\left(T_{\mathrm{1}}\right)$ ratios are reached for structures with vibration periods shorter than the dominant soil period (approximately $T_s/\mathrm{2}$), which indicates that the lateral strength demand for degrading systems is higher than the strength demand for non-degrading systems.

• b.

  When the vibration period of the system is close to the dominant soil period ($T_n/T_{\mathrm{s}}\approx \mathrm{1}$), the strength demands for degrading and non-degrading systems are similar.

• c.

  When $T_n/T_{\mathrm{s}}>\mathrm{1}$, the demands of the degrading systems decrease with respect to those of the non-degrading systems. This means that for structural vibration periods longer than T_s, the degrading behavior provides a beneficial effect.

• d.

  It is noticed that for zone D (Fig. 9d), the MCSD function predicts spectral modification values which are similar to the function proposed in the present study (Eq. 12). This happens because the MCSD function was calibrated using ground motion data recorded at a station located in that zone (SCT station in zone D); however, it does not happen the same for other soil conditions, especially for $T_n/T_{\mathrm{s}}>\mathrm{1}$.

• e.

  Equation (12) predicts values closer to unity at sites in zones A–C (firm ground and transition soil) than at zones D–F, which means that the structural softening is not as significant as it is for zones D–F. In this respect, several studies have observed that the degradation of the stiffness has little effect on the strength demands for structures located on firm sites (Akkar et al., 2004; Chenouda and Ashraf, 2008; Chopra and Chintanapakdee, 2004). Moreover, it is noticed that at very short vibration period systems ($T_n/T_{\mathrm{s}}<\mathrm{0.1}$), the SMF proposed here predicts amplification values very close to unity, which is consistent for extremely stiff structures.

• f.

  Finally, the reduction of strength demand according to Eq. (12) fits the observed data (thin gray lines) better for each type of soil (zones A to F) than that recommended by MCSD guidelines.

With the aim of verifying the validity of the proposed expression, Fig. 10a and b compare the results of Eq. (12) with those obtained from time history analysis of SDOF systems. The figures show the mean ratio of strength demands of degrading and of non-degrading systems (elasto-plastic behavior) corresponding to a ductility value, μ_u (thin gray lines), using firm-ground and soft-soil records, respectively (Miranda and Ruiz-Garcia, 2002; Terán-Gilmore and Espinosa Johnson, 2008). The ground motions at firm ground (Fig.10a) correspond to synthetic accelerograms (T_s=1.0 s) (Terán-Gilmore and Espinosa Johnson, 2008) and ground motions recorded in the San Francisco Bay area during the 1989 the Loma Prieta earthquake (T_s≈1.1 s) (Miranda and Ruiz-Garcia, 2002). In contrast, the ground motions in soft soil were recorded in the lake bed zone of Mexico City (T_s≈2.0 s) (Fig. 10b).

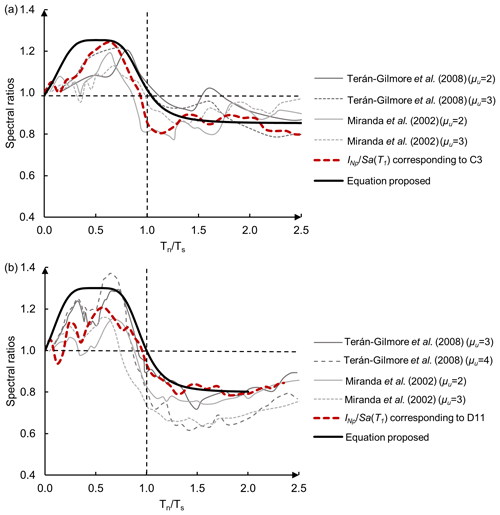
Figure 10 Mean ratios of strength demands of degrading and of non-degrading systems corresponding to (a) firm ground (zone C) and (b) soft soil (zone D) of Mexico City.

Figure 10a and b also include the $I_{N_{\mathrm{p}}}/\mathrm{Sa}\left(T_{\mathrm{1}}\right)$ ratios, corresponding to the stations D11 and C3, estimated from the uniform hazard spectra normalization (thick red dotted lines). It can be observed that the $I_{N_{\mathrm{p}}}/\mathrm{Sa}\left(T_{\mathrm{1}}\right)$ ratio agrees with the results of Miranda and Ruiz-Garcia (2002), and of Terán-Gilmore and Espinosa Johnson (2008). The figures also show that the function given by Eq. (12) is in agreement with both the observed data obtained from the time history analyses and the $I_{N_{\mathrm{p}}}/\mathrm{Sa}\left(T_{\mathrm{1}}\right)$ ratio calculated from the study based on seismic hazard analyses.

7 Conclusions

A methodology based on probabilistic seismic hazard analysis is proposed to evaluate the effect of degrading behavior on the strength demands of SDOF systems. For this aim, uniform hazard spectra are obtained for two alternative intensity measures: $I_{N_{\mathrm{p}}}$ and Sa(T₁), which represent the response of degrading and non-degrading systems, respectively. Thus, the ratio of the hazard spectra $I_{N_{\mathrm{p}}}/\mathrm{Sa}\left(T_{\mathrm{1}}\right)$ characterizes the strength demands of systems with degrading behavior to those of systems with non-degrading behavior. Based on the $I_{N_{\mathrm{p}}}/\mathrm{Sa}\left(T_{\mathrm{1}}\right)$ ratios, which correspond to systems located at different sites, grouped in different seismic zones (depending on the type of soil where the structures are located), a mathematical expression is proposed. The methodology is applied here to structural systems located in Mexico City, but it can be applied to any seismic region of the world.

From the study the following is concluded.

1. For structures with vibration periods shorter than the dominant soil period ($T_n/T_{\mathrm{s}}<\mathrm{1}$), degrading systems exhibit strength demands up to 30 % higher than systems with non-degrading behavior.

2. For structures with vibration periods close to the dominant soil period ($T_n/T_{\mathrm{s}}\approx \mathrm{1}$), the strength demands for degrading and non-degrading systems are similar.

3. For systems with vibration periods longer than the dominant soil period ($T_n/T_{\mathrm{s}}>\mathrm{1}$), the strength demands for structures with degrading behavior are lower, approximately 5 % to 20 %, than structures with non-degrading behavior. That reduction highly depends on the dominant soil period at the site, and it is larger for systems with longer dominant soil periods. For these cases, the structure-degrading behavior produces a beneficial effect, reducing the lateral strength requirement of the structures.

4. A strength modification factor was proposed (Eq. 12). The expression was fitted according to the spectral ratios $I_{N_{\mathrm{p}}}/\mathrm{Sa}\left(T_{\mathrm{1}}\right)$ corresponding to different soil conditions. The value of the parameters included in the equation depends on the type of soil where the structure is located.

5. The expression proposed (Eq. 12) is a useful tool for simplified nonlinear modal analyses, to explicitly incorporate the effect of degrading behavior according to the type of soil where the structure is located. It was verified that the mathematical expression proposed leads to results that are comparable to those obtained from time history analyses of SDOF systems located in soft soil.

6. In addition, the study presents a methodology to elaborate seismic hazard maps in terms of the intensity measure $I_{N_{\mathrm{p}}}$. Based on that methodology, the first seismic hazard map of Mexico City is presented, in terms of $I_{N_{\mathrm{p}}}$.