Drought propagation and construction of a comprehensive drought index based on the Soil and Water Assessment Tool (SWAT) and empirical Kendall distribution function (K_C′): a case study for the Jinta River basin in northwestern China

Monitoring drought and mastering the laws of drought propagation are the basis for regional drought prevention and resistance. Multivariate drought indicators considering meteorological, agricultural and hydrological information may fully describe drought conditions. However, series of hydrological variables in cold and arid regions that are too short or missing make it difficult to monitor drought. This paper proposed a method combining Soil and Water Assessment Tool (SWAT) and empirical Kendall distribution function ($K_{{\mathrm{C}}^{\prime }}$) for drought monitoring. The SWAT model, based on the principle of runoff formation, was used to simulate the hydrological variables of the drought evolution process. Three univariate drought indexes, namely meteorological drought (standardized precipitation evapotranspiration index; SPEI), agricultural drought (standardized soil moisture index; SSI) and hydrological drought (standardized streamflow drought index; SDI), were constructed using a parametric or non-parametric method to analyze the propagation time from meteorological drought to agricultural drought and hydrological drought. The $K_{{\mathrm{C}}^{\prime }}$ was used to build a multivariable comprehensive meteorology–agriculture–hydrology drought index (MAHDI) that integrated meteorological, agricultural and hydrological drought to analyze the characteristics of a comprehensive drought evolution. The Jinta River in the inland basin of northwestern China was used as the study area. The results showed that agricultural and hydrological drought had a seasonal lag time from meteorological drought. The degree of drought in this basin was high in the northern and low in the southern regions. MAHDI proved to be acceptable in that it was consistent with historical drought records, could catch drought conditions characterized by univariate drought indexes, and capture the occurrence and end of droughts. Nevertheless, its ability to characterize mild and moderate droughts was stronger than severe droughts. In addition, the comprehensive drought conditions showed insignificant aggravating trends in spring and summer and showed insignificant alleviating trends in autumn and winter and at annual scales. The results provided theoretical support for the drought monitoring in the Jinta River basin. This method provided the possibility for drought monitoring in other watersheds lacking measured data.

1 Introduction

According to the fifth evaluation report of the Intergovernmental Panel on Climate Change (IPCC), climate change characterized by temperature rise is the main concern of the global change in the past half-century with the most rapid warming in the mid-latitudes of the Northern Hemisphere (IPCC, 2018; Ji et al., 2014). The arid inland river basins of China are mainly located in the hinterland of the Eurasian continent in the mid-latitudes and are very sensitive to global climate change. Therefore, it is particularly important to study the drought conditions of the inland river basins of China under the prevailing climate change scenario.

Drought is a dynamic creeping phenomenon (Oikonomou et al., 2019; Ahmadi and Moradkhani, 2019); however, there is no precise definition for the differences in hydro-meteorological variables and socioeconomic elements (Mishra and Singh, 2010). Generally, the droughts are divided into four categories (Heim, 2002): (i) meteorological drought, referring to a period of time with a lack of precipitation (Mishra and Singh, 2010; Dai, 2011), (ii) agricultural drought, referring to a period with low soil water hindering crop growth and reducing grain yield (Crow et al., 2012; Panu and Sharma, 2002), (iii) hydrological drought, referring to a deficit in streamflow or groundwater resources (Cammalleri et al., 2016), and (iv) socioeconomic drought, referring to a phenomenon that water shortage affects production, consumption and other socioeconomic activities. There is a close relationship among the various droughts. Insufficient precipitation for a long time leads to meteorological drought. When this situation lasts for a long period of time, the soil water content decreases, which leads to a reduction in crop yield, resulting in agricultural drought. Insufficient precipitation for a long period of time also causes a significant drop in surface water and groundwater, resulting in hydrological drought. When all these three types of drought adversely affect social production and economic development, socioeconomic drought occurs.

Drought index is an important indicator to characterize and measure the degree of drought, and it can be used to monitor, evaluate and study the development of drought. For example, the standardized precipitation index (SPI) (McKee et al., 1993) and the standardized precipitation evapotranspiration index (SPEI) (Vicente-Serrano et al., 2010) are commonly used as meteorological drought indexes (Vicente-Serrano et al., 2012). The hydrological drought indexes are usually generated using streamflow, such as the streamflow drought index (SDI; Nalbantis and Tsakiris, 2008) and the standardized runoff index (SRI; Shukla and Wood, 2008). The soil water content is the main variable to calculate the agricultural drought index, for instance, the crop water stress index (Jackson et al., 1988) and the standardized soil moisture index (Mishra et al., 2015). Calculation of the drought index requires a long time series of drought variables. However, the scarcity of measured data is a major problem in the process of drought index construction. Therefore, to derive hydrological datasets, indirect means have been attempted, such as the watershed hydrological model. A recent study carried out by Dash et al. (2019) apply the Soil and Water Assessment Tool (SWAT) hydrological model to simulate the soil moisture data and develop a soil moisture stress index (SMSI) for agricultural drought analysis. Further, Zhang et al. (2017a) adopt the variable infiltration capacity (VIC) hydrological model to monitor soil moisture drought and construct a seasonal forecasting framework subsequently.

With the deepening of drought research, the insufficiency of univariate drought indexes has gradually emerged. Because drought characteristics are usually interrelated, traditional drought research based on univariate frequency analysis can hardly reflect the multi-dimensional effects of drought on society. Therefore, it is necessary to develop a comprehensive drought index integrating multiple variables related to drought. Keyantash and Dracup (2004) use principal component analysis (PCA) to extract dominant drought variables to develop an aggregate drought index (ADI) for comprehensive drought features (Rajsekhar et al., 2015). However, this method is a linear combination of related variables which could not reveal its nonlinear structural characteristics. The copula function can connect different marginal distributions and consider the correlation between them. It is one of the most commonly used connection methods at present and has been widely used in the field of hydrometeorology (Hao and AghaKouchak, 2013). For example, the joint drought index (JDI) is constructed by copula using joint accumulated distribution of the runoff and precipitation (Kao and Govindaraju, 2010). Guo et al. (2019) use copula to propose an improved multivariate standardized reliability and resilience index (IMARRI) to fully appraise the dynamic risk of socioeconomic drought. Wang et al. (2020) construct a standardized precipitation evapotranspiration streamflow index (SPESI) based on copula to comprehensively display characteristics of meteorological and hydrological drought. Nevertheless, the limitation of the copula function is reflected when connecting three or more drought indicators (Hao and Singh, 2013; Kao and Govindaraju, 2008, 2010), and this phenomenon is generally called “curse of dimensionality” (Hao and Singh, 2013). To overcome this limitation, this study applied empirical Kendall distribution function ($K_{{\mathrm{C}}^{\prime }}$) to construct a new comprehensive drought indicator by combining precipitation, evapotranspiration, soil water and streamflow. The $K_{{\mathrm{C}}^{\prime }}$ is obtained by Nelsen (2006), which is based on the generation function of the Archimedean copula function family. It is a probability integral transformation method and can transform multidimensional variable information into single-dimensional variable information (Hao et al., 2017).

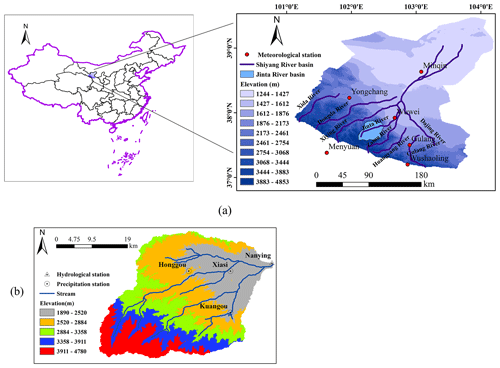
Figure 1 Basic information about the Jinta River basin. (a) The geographic location of the Jinta River in northwestern China; (b) precipitation and hydrological stations in the Jinta River basin.

The Jinta River basin (JRB) is a tributary basin of the Shiyang River basin (SRB) located in a climate-sensitive area (Wei et al., 2020). Therefore, it is important to study further drought conditions in the basin under the influence of climate change. The description of drought conditions is based on the construction of a drought index, which is limited by the shortage of measured data. In addition, the construction of a comprehensive drought index should reflect the drought situation comprehensively. In this paper, the univariate drought indexes (SDI, SSI and SPEI) established by measuring precipitation, streamflow, soil water and evapotranspiration simulated by the SWAT model (Arnold et al., 1998; Zhang et al., 2010) explored the propagation time from meteorological drought to hydrological and agricultural drought. A new meteorology–agriculture–hydrology drought index (MAHDI) was developed using the empirical Kendall distribution function based on the differences between precipitation and evapotranspiration, streamflow, and soil water. MAHDI was also used to estimate the spatial distribution of the temporal tendency in different seasons. The specific objectives are (i) to investigate the propagation time characteristics from meteorological drought to hydrological and agricultural drought; (ii) to validate the applicability of MAHDI by comparing it with historical drought events and univariate drought indexes (SDI, SSI and SPEI); and (iii) to estimate the spatial distribution of MAHDI's temporal tendency in different seasons.

2 Materials and methods

2.1 Study area

The Jinta River basin (JRB) with an area of 841 km² originates in the Qilian Mountains and is a tributary of the Shiyang River basin located in Gansu Province, China (see Fig. 1). It is bounded between 37^∘02^′ and 39^∘17^′ N and 100^∘57^′ and 104^∘12^′ E. The JRB is located in the middle of the eight subbasins, adjacent to the Zamu River in the east and to the Xiying River in the west, as shown in Fig. 1a. The terrain of the JRB is higher in the south and lower in the north, sloping from southwest to northeast. The altitude ranges from 1890 to 4780 m, with an average altitude of 3000 m (Fig. 1b). The annual precipitation in the basin ranges from 200 to 500 mm, and the annual evaporation is about 700–1200 mm.

2.2 Data sources

A digital elevation model (DEM) with a spatial resolution of 30 m provided by the Geospatial Data Cloud site, Computer Network Information Center, Chinese Academy of Sciences (http://www.gscloud.cn, last access: 15 June 2020), was used for watershed delineation. The digital soil map was obtained from the Harmonized World Soil Database (HWSD, version 1.1) developed by the Food and Agricultural Organization of the United Nations (FAO–UN). The map provided data for 5000 soil types containing two soil layers' worth of information (0–30 and 30–100 cm depth). The land-use data (30 m × 30 m) were derived from the satellite remote sensing image data of Landsat Thematic Mapper (TM) provided by the Geographical Information Monitoring Cloud Platform (http://www.dsac.cn/DataProduct, last access: 18 June 2020). The observed climatic information of precipitation, maximum air temperature, minimum air temperature, wind speed and relative humidity was obtained from six meteorological stations shown in Fig. 1a and three precipitation stations shown in Fig. 1b. The monthly river discharge data for the model calibration and validation were obtained from the Nanying hydrological station at the Hydrology and Water Resources Bureau of Gansu Province for the period of 1986–2012.

2.3 SWAT model

The SWAT model developed by the Agricultural Research Service of the United States Department of Agriculture (USDA-ARS) is a continuous-time, semi-distributed and physics-based water quality model (Arnold et al., 1998; Gassman et al., 2014; Romagnoli et al., 2017) for simulating hydrological cycle, plant growth cycle and transportation of sediments (Arnold et al., 1998; Pyo et al., 2019; Stefanidis et al., 2018; Wu et al., 2011). The SWAT model delineates a catchment into subbasins based on the stream network and topography and subsequently into hydrological response units (HRUs) representing different combinations of soil types, land use and slope. The simulation calculation of soil effective moisture content, surface runoff, nitrogen content and sediment yield are carried out for each of the HRUs. The hydrological part of the model is based on the water balance equation in the soil profile with processes, including precipitation, surface runoff, infiltration, evapotranspiration, lateral flow, percolation and groundwater flow (Arnold et al., 1998; Kiniry et al., 2005).

$$\begin{array}{}\text{(1)}& {\mathrm{SW}}_t={\mathrm{SW}}_{\mathrm{0}}+\sum _{i=\mathrm{1}}^t\left(R_{\mathrm{day},i}-Q_{\mathrm{surf},i}-E_{\mathit{\alpha },i}-w_{\mathrm{seep},i}-Q_{\mathrm{gw},i}\right),\end{array}$$

where SW_t is the final soil water content at time period t (mm), SW₀ is the initial soil water content (mm), t is the time (number of days), R_days,i is the amount of rainfall on ith day (mm), Q_surf,i is the amount of surface runoff on ith day (mm), E_α,i is the amount of evapotranspiration on ith day (mm), w_seep,i is the amount of water giving recharge to groundwater from the soil profile on ith day (mm), and Q_gw,i is the amount of return flow on ith day (mm).

The runoff simulation of the watershed mainly consists of evapotranspiration, surface runoff, soil water and groundwater. The SWAT model has two main methods for estimating surface runoff, which are predicted by the Soil Conservation Service (SCS) curve (Bouraoui et al., 2005). The channel routing uses the Muskingum method or the variable storage coefficient model, including the migration of water, sediment, nutrients and pesticides in the river network. The simultaneous calculation of reservoir confluence is also required. Evapotranspiration in the SWAT model refers to the process of surface water transforming into water vapor, including water evaporation, transpiration and sublimation retained by tree crowns, as well as soil water evaporation. A part of the soil water is absorbed by plants or lost by transpiration, a part of it supplies the groundwater, and the other part forms runoff on the surface. Groundwater runoff exists in the form of base flow calculated by groundwater storage and continuous runoff in the dry season.

2.4 Univariate drought index

A drought index contains a clear physical mechanism (Keyantash and Dracup, 2002) and is the main tool for the quantitative analysis of drought characteristics. In addition, it can monitor the situation of the start time, the end time, duration, intensity and spatial range of drought. Therefore, the construction of the drought index is the basis of drought research. The differences of precipitation and evapotranspiration (P–ET), soil moisture (SM) and streamflow (D) simulated by the SWAT model were used to construct a meteorological drought index (SPEI), agricultural drought index (SSI) and hydrological drought index (SDI) for different timescales (1, 3 and 12 months) using parametric or non-parametric methods.

2.4.1 Parametric methods

The monthly sequence for each drought variable was fitted one by one by selecting an appropriate distribution function. The maximum likelihood method was applied to estimate the relevant parameters of the distribution function, the Kolmogorov–Smirnov (K–S) test was used to test the fitting priority, and the Akaike's information criterion (AIC) was used to select the optimal fitting function. The cumulative probability distribution for each drought variable was then transformed into the standard normal distribution. Finally, the inverse function of the normal distribution was used to calculate the drought index.

• i.

  The distributions selected in this study include gamma distribution, log-normal distribution, Weibull distribution, normal distribution and logistic distribution. Assuming that each distribution was suitable for the related drought variable series of each timescale, the maximum likelihood method was used to fit the parameter estimation. For a probability density function f(x,θ), θ is the parameter to be estimated, and X₁, X₂, X₃, …, X_n is a sample from the population. If x₁, x₂, x₃, …, x_n is the sample value, the steps of the maximum likelihood method are as follows.

  • a.

    Construct the likelihood function of the sample.

    $$\begin{array}{}\text{(2)}& L\left(\mathit{\theta }\right)=L\left(x_{\mathrm{1}},x_{\mathrm{2}},\mathrm{\dots },x_n;\mathit{\theta }\right)=\prod _{i=\mathrm{1}}^{n}f\left(x_i,\mathit{\theta }\right)\end{array}$$
  • b.

    The log-likelihood function is given as follows:

    $$\begin{array}{}\text{(3)}& \ln L\left(\mathit{\theta }\right)=\sum _{i=\mathrm{1}}^{n}f\left(x_i,\mathit{\theta }\right).\end{array}$$
  • c.

    Take the derivative of the parameter θ in Eq. (3) and make the derivative value 0:

    $$\begin{array}{}\text{(4)}& {\displaystyle \frac{\mathrm{d}\ln L\left(\mathit{\theta }\right)}{\mathrm{d}\mathit{\theta }}}=\mathrm{0}.\end{array}$$
  • d.

    Solve the likelihood equation to get the maximum likelihood estimate $\widehat{\mathit{\theta }}$ for the parameter θ.

• ii.

  The Kolmogorov–Smirnov (K–S) test is suitable for testing the goodness-of-fit of a dataset for most of the probability distributions regardless of the sample size by comparing the cumulative sample distribution with the cumulative distribution function specified by the null hypothesis. If the absolute value of the difference is within the specified range, the sample obeys the assumed theoretical distribution. We made H₀ the sample obeying the theoretical distribution, and H₁ indicated that the sample did not follow the theoretical distribution. The statistic D is constructed as follows:

  $$\begin{array}{}\text{(5)}& D=\max \left|F_{\mathrm{1}}\left(x\right)-F_{\mathrm{2}}\left(x\right)\right|,\end{array}$$

  where F₁(x) represents the cumulative distribution of samples, and F₂(x) represents the theoretical distribution. At the selected significance level of α (α=0.05), if $D>D(n,\mathit{\alpha })$ (n is the sample size), the H₀ is rejected, and H₁ is accepted; otherwise, H₀ is accepted, and H₁ is rejected.

• iii.

  Akaike's information criterion (AIC) is a standard to measure the goodness-of-fit of the statistical model founded and developed by Japanese statistician Akaike. It weighs the complexity of the estimated model and the goodness of the model fitting data and is given as follows:

  $$\begin{array}{}\text{(6)}& \mathrm{AIC}=\mathrm{2}m-\ln L,\end{array}$$

  where m is the number of parameters estimated by the distribution function, and L is the maximum likelihood function value. As increasing the number of free parameters improves the goodness of fitting, AIC encourages the goodness of data fitting but tries to avoid overfitting. Therefore, the priority model should be the one with the lowest AIC value. A lower AIC value indicates a better fit.

  According to the AIC, the optimal theoretical distribution was selected. The inverse standardized value of the theoretical distribution value corresponding to each drought variable was taken as the parametric drought index:

  $$\begin{array}{}\text{(7)}& {\mathrm{DI}}_{\mathrm{p}}={\mathrm{\varnothing }}^{-\mathrm{1}}\left(P\right),\end{array}$$

  where DI_p is the parametric drought index value, ∅ is the standard normal distribution function, and P is the theoretical cumulative probability.

2.4.2 Non-parametric method

If the four theoretical distributions for a certain drought variable could not pass the K–S test in the process of building a parametric drought index, the non-parametric method was used to build the drought index.

$$\begin{array}{}\text{(8)}& P_{\mathrm{nonp}}\left(x_i\right)={\displaystyle \frac{i-\mathrm{0.44}}{n+\mathrm{0.12}}},\end{array}$$

where n is the length of the sequence, i is the order when the sequence of variables is ascending, and P_nonp is the empirical cumulative probability. The inverse standardization of the empirical cumulative probability is the non-parametric drought index expressed as follows:

$$\begin{array}{}\text{(9)}& {\mathrm{DI}}_{\mathrm{nonp}}={\mathrm{\varnothing }}^{-\mathrm{1}}\left(P_{\mathrm{nonp}}\right),\end{array}$$

where DI_nonp is the non-parametric drought index value.

2.5 Trivariate drought index

The Kendall distribution function is obtained from the generation function of the Archimedean copula function family. It is a probability integral transformation method (Nelsen, 2006) and can convert multidimensional variable information into one-dimensional variable information. As some copula functions may not have the analytic expression of the Kendall distribution function, this study used a non-parametric method to construct the empirical Kendall distribution function (Nelsen et al., 2003; Hao et al., 2017) expressed as follows:

$$\begin{array}{}\text{(10)}& K_{{\mathrm{C}}^{\prime }}=P_{\mathrm{tri}}={\displaystyle \frac{n_{\mathrm{2}}}{n}},\end{array}$$

where n₂ is the number of samples satisfying $C^{\prime }(i/n$, $j/n$, $k/n)\le p$ (C^′ is the empirical copula function), n is the total number of samples, and P_tri is the three-dimensional cumulative probability. The express of empirical copula is given as follows (Hao et al., 2017):

$$\begin{array}{}\text{(11)}& C^{\prime }\left({\displaystyle \frac{i}{n}},{\displaystyle \frac{j}{n}},{\displaystyle \frac{k}{n}}\right)={\displaystyle \frac{n_{\mathrm{1}}}{n}},\end{array}$$

where n₁ is the number of the samples (x_m, y_m, z_m) satisfying (x_m≤x_(i) and y_m≤y_(j) and z_m≤z_(k)) and $\mathrm{1}\le m\le n$.

The empirical Kendall distribution function was used to join the three drought-related variables to obtain a trivariate drought indicator by inverse standardization:

$$\begin{array}{}\text{(12)}& \mathrm{MAHDI}={\mathrm{\varnothing }}^{-\mathrm{1}}\left(P_{\mathrm{tri}}\right),\end{array}$$

where MAHDI is the trivariate drought index value.

3 Results and discussion

3.1 SWAT model calibration and validation

In order to calibrate and validate the runoff-related parameters, we applied the SWAT calibration and uncertainty programs (SWAT-CUPs). The calibration period was taken as 1986–2000, and the validation period was taken as 2001–2012. In addition, a warm-up period of 1984–1986 was considered to minimize the uncertainty caused by the initial environment of the model (Zhang et al., 2019). In the SWAT-CUPs, the sequential uncertainty fitting version 2 (SUFI-2) algorithm (Abbaspour et al., 2007) was chosen for parameter sensitivity and model uncertainty analysis (Abbaspour et al., 2015).

Table 1 Sensitivity analysis and final value range of parameters in Jinta River basin.

Note that as the CN2 of different land-use types was calibrated separately, a range of the optimal CN2 values was provided.

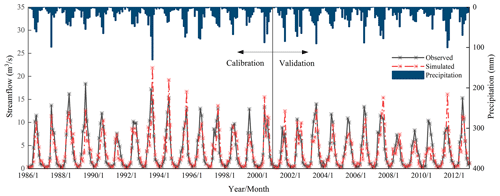
Figure 2 Simulated and observed monthly streamflow series relative to precipitation (P) during the calibration and validation periods in the JRB.

Table 1 shows the top four sensitivity parameters of the JRB and their initial and fitted values. The CN2, the comprehensive response of the underlying surface characteristics, was the most sensitive parameter in the hydrological process. The value of CN2 was calibrated to 70.51–95.03 for different land-use types. In order, the next sensitivity parameters were SOL_AWC, TLAPS and SOL_K. Among them, SOL_AWC and SOL_K are soil-related sensitivity parameters, and their fitted values were 0.008 and 99.65, respectively. The TLAPS is a parameter related to temperature, and its optimal value was 2.83.

Uncertainty of the model was adjudged on the basis of P-factor and R-factor indicators (Abbaspour et al., 2007). When the P factor > 0.7 and R factor < 1.5, the uncertainty of the model was considered as acceptable, and the parameter ranges were taken as the calibrated parameters. Table 2 shows that two indicators are in the acceptable range, with a P factor of 0.72 and an R factor of 0.65. To measure the model performance, we selected the coefficient of determination (R²) and the Nash–Sutcliffe simulation efficiency (E_NS) (Table 2). The simulation results showed that the R² and E_NS in the JRB were 0.76 and 0.75, respectively, for the calibration period and 0.73 and 0.72, respectively, for the validation period. Figure 2 shows the plots for the simulated monthly streamflow against the observations. The figure indicated that the simulated and observed monthly streamflow were in good agreement with the period considered, and their changes followed the precipitation. Overall, the model performance was satisfactory for subsequent analysis.

Table 2 Model performance in monthly streamflow in JRB.

3.2 Drought characterization

The SPEI, SSI, SDI and MAHDI were applied to all subbasins for different timescales. For calculating the four indexes, precipitation, evapotranspiration, soil moisture and streamflow, data from 1986 to 2012 were adopted in this study. Thresholds of the indexes were divided according to the SPI (McKee et al., 1993).

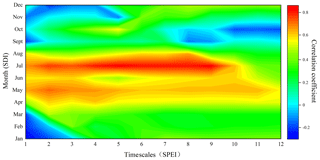
Figure 3 The correlation coefficients between monthly SDI and SPEI with different timescales at subbasin no. 6.

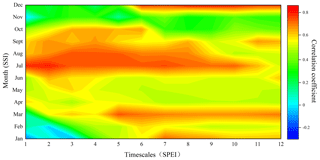
Figure 4 The correlation coefficients between monthly SSI and SPEI with different timescales at subbasin no. 6.

3.2.1 The propagation time from meteorological drought to hydrological and agricultural drought

To study the propagation time from meteorological drought to hydrological drought, the relationships between the SDI and the SPEI with various timescales were explored. Similarly, the relationship between SSI and SPEI on different timescales also reflected the propagation time from meteorological drought to agricultural drought. We can mention subbasin no. 6 where the hydrological station is located as an example.

Figure 3 shows the correlation coefficients between monthly SDI and SPEI with various timescales at subbasin no. 6. High correlation coefficients (>0.7) of SDI and SPEI were observed for spring and summer with the timescales from 2 to 9 months. Low correlation coefficients (>0.4) were observed for autumn and winter with about a 6–9 month scale. The lag time in spring and summer was more obvious, showing certain seasonal characteristics, whereas the lag time in autumn and winter had inconspicuous seasonal characteristics. A reasonable explanation for this phenomenon might be more sources of recharge (rainfall and iceberg snowmelt) in spring and summer, while groundwater was the only source of recharging the river in autumn and winter, which was related to the water stored during spring and summer.

Similarly, Fig. 4 depicts the propagation time from meteorological drought to agricultural drought at subbasin no. 6, which also shows an obvious seasonal characteristic. In summer, the lag time was approximately concentrated over 2 months with a correlation coefficient value higher than 0.8, while the response time in other seasons was longer. The propagation time from meteorological drought to agricultural drought was, therefore, the shortest in summer. This may be the result of high soil moisture due to high rainfall during the season. The propagation time in spring was 3 months longer than that in summer, which may be because of the potential influence of snowmelt. In the autumn and winter, there was a longer lag time (6–12 months) in responding to the meteorological drought, possibly due to the infiltration of soil water during the preceding months. Compared with spring and summer, the evaporation rate of soil water in autumn and winter was slower than that in spring and summer, which prolonged the time when the soil water content reduced to that of the threshold for agricultural drought. This made the agricultural drought lag behind the meteorological drought for a long time.

Compared to Fig. 3, Fig. 4 is more precise in showing that the propagation time from meteorological drought to agricultural drought increases with a decrease in temperature and precipitation, and there is a clear gap between different seasons. However, the time of hydrological drought lagging behind the meteorological drought was not obvious. The distribution of glaciers in the upper reaches of the Jinta River and the significantly longer time of soil water infiltration than that of confluence formation might made the propagation time from meteorological drought to agricultural drought more obvious in different seasons compared to the propagation time from meteorological drought to hydrological drought. Studying the lag time of different types of droughts from meteorological droughts was helpful in predicting other droughts using meteorological drought in the absence of measured data and may provide a theoretical basis for drought prevention.

Both drought propagation and the construction of a comprehensive drought index were based on the data output by the SWAT hydrological model. Drought propagation described the response relationship between different types of drought based on the lag time from agricultural drought and hydrological drought to meteorological drought. The goal in the construction of the comprehensive drought index was to combine different types of drought indexes and include the lag time from agricultural drought and hydrological drought to meteorological drought. It reflected the drought state when only one or two kinds of drought occur and could be used to describe the characteristics of drought.

3.2.2 Applicability analysis of MAHDI

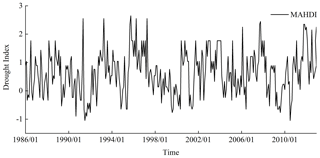
Using the empirical Kendall function to combine the univariate drought indexes, a comprehensive drought index, MAHDI, that can simultaneously characterize meteorological, agricultural and hydrological drought was obtained. The monthly change in MAHDI series in sub-watershed no. 6 from 1986 to 2012 was plotted, as shown in Fig. 5. It can be seen from the figure that 1991, July 1999–May 2000, November 1994–January 1995, 2009 and July 2010 were the drought months. According to the China Meteorological Disaster Dictionary: Gansu Volume, the area was hot and less rainy in 1991, and continuous drought occurred in summer and autumn; in 1994–1995, the region suffered from continuous drought in winter and spring; and in 1999, the region suffered from severe drought in autumn and winter, which were consistent with the drought events described by MAHDI. According to the “Water Resources Bulletin of Gansu Province in 2009”, the area had slightly less annual precipitation and higher temperatures. MAHDI also captured the drought in this year. Above all, MAHDI can be used to detect the occurrence and development of drought.

Figure 5 Monthly scale MAHDI sequence at subbasin no. 6.

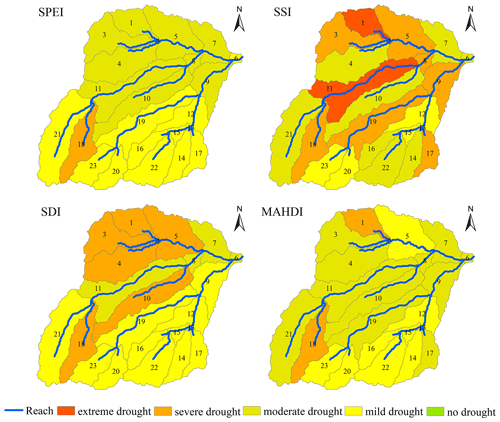
To analyze the distribution of different droughts and the applicability of MAHDI, the year 1999 was selected for analysis. The spatial distribution of SDI, SSI, SPEI and MAHDI for the year 1999 is shown in Fig. 6. For SDI, severe drought was distributed in subbasin nos. 1–5, 10 and 18. Moderate drought was observed in subbasin nos. 6–8 and 11, and mild drought was observed in the rest of the subbasins. For SSI, extreme drought was distributed in subbasin nos. 1, 2 and 11, severe drought was located in subbasin nos. 3, 5, 8, 9 and 17–19, moderate drought was observed in subbasin nos. 4, 6, 7, 10, 14, 16 and 21–22, and mild drought was distributed in subbasin nos. 12, 13, 15, 20 and 23. For SPEI, severe drought was observed in subbasin no. 18, moderate drought was located in subbasin nos. 1–5 and 7–11, and mild drought was observed in the rest of the subbasins. For MAHDI, severe drought was located in subbasin nos. 1, 2 and 18, mild drought was distributed in subbasin nos. 5, 12–16, 20 and 22–23, and moderate drought was located in the rest of the subbasins. In conclusion, the drought in the northern part of the basin was stronger than that in the southern part of the basin.

Figure 6 Distribution of SDI, SSI, SPEI and MAHDI at a 12-month scale in JRB in 1999.

Different drought indexes showed different degrees of drought severity. For univariate drought indexes, SSI showed the highest degree of drought, followed by SDI, and SPEI showed the lowest degree of drought. SPEI reflected the lowest degree of meteorological drought, which was similar to that described by the Thornthwaite aridity index (AI) constructed by Zhang et al. (2017b) using rainfall and potential evapotranspiration. As rainfall and temperature were the core elements of SPEI, the meteorological drought was alleviated (Guo et al., 2016). The highest degree of drought shown by SSI might be for topographic factors. There are many glaciers in the JRB, and the river confluence speed was faster than the soil infiltration speed resulting in low soil water storage capacity. Besides, the calibrated value of SOL_AWC by the SWAT model was only 0.008 (Table 1), showing that the water storage in the soil layer in the basin was very small. MAHDI captured all the mild and moderate droughts shown by SDI, SSI and SPEI, as well as the severe drought in some subbasins. However, it could not capture the extreme drought shown by SSI in subbasin nos. 1 and 11. Therefore, it may be concluded that MAHDI's ability to capture mild and moderate droughts is stronger than its ability to capture severe and extreme droughts.

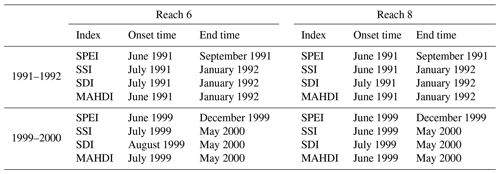
Drought events in the periods of 1991–1992 and 1999–2000 in subbasin nos. 6 and 8 were selected to verify MAHDI's ability to capture the onset and end time of drought events (Table 3 shows the capture time of various drought indexes for these drought events). Among the univariate drought indexes, the SPEI captured the drought earlier than any other index, and it also captured the earliest end time of drought. The starting and ending time of drought represented by SSI and SDI was later than that of SPEI, which made the drought have a longer duration. This was because the rate of change in precipitation and temperature was the fastest, whereas runoff generation and soil water infiltration required a certain time, making meteorological drought the most sensitive to environmental changes. Compared with univariate drought indexes, MAHDI characterized drought at the same time as that of the SPEI and was consistent with SSI and SDI's characterization of the drought end time. It may be concluded that MAHDI combined the advantages of SDI, SSI and SPEI and was a comprehensive function of streamflow, soil water, precipitation and temperature. Overall, the three-dimensional drought index, MAHDI, constructed in this paper was acceptable.

Table 3 The capture time of various drought indexes for the drought events that occurred in the periods 1991–1992 and 1999–2000 in subbasin no. 6 and subbasin no. 8.

3.2.3 Drought temporal characterization

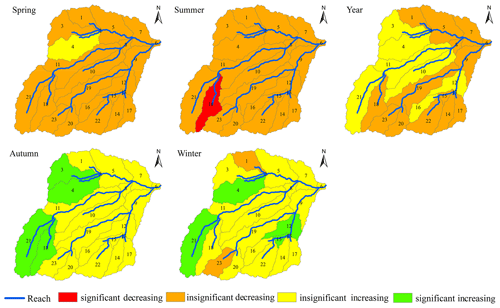
To assess the spatial characteristics of comprehensive drought temporal tendency in the JRB, we calculated the Man–Kendall (M–K) statistics. The M–K statistics with a significant level in MAHDI were represented for different seasons and a 12-month scale (Fig. 7). A positive M–K statistic indicated an increasing tendency in the drought index and vice versa. Besides, the M–K statistic values also included a test of significance (significance level was α=0.05 and the threshold values were ±1.96).

Figure 7 M–K trend test of MAHDI at 3- and 12-month scales in JRB.

Figure 7 shows different spatial characteristics of drought temporal trends for various seasons. In spring, MAHDI of most of the subbasins showed a nonsignificant decreasing trend, and only subbasin no. 4 showed an insignificant increasing trend. In summer, MAHDI for most of the subbasins also showed an insignificant decreasing trend; subbasin no. 18 showed a significant decreasing trend. In autumn, the drought index in subbasin nos. 3, 4, 21 and 18 showed a significant increasing trend, and the rest of the subbasins showed an insignificant upward trend. In winter, the drought index in subbasin nos. 1 and 23 showed an insignificant decreasing trend, and the changes in subbasin nos. 4, 12, 13, 15 and 21 showed a significant increasing tendency; the rest of the subbasins showed an insignificant increasing trend. For a 12-month scale, MAHDI's tendency was mainly composed of an insignificant upward trend and an insignificant downward trend. The subbasins with a drought index showing an insignificant decreasing trend were subbasin nos. 3, 4, 10–12, 16 and 21, and the rest of the subbasins with a drought index showed an insignificant increasing trend. Therefore, it might be concluded that the temporal trend of drought had spatial differences that were influenced by seasonal characteristics and geographical conditions in the JRB during the study period.

Drought temporal tendency analysis can help people predict drought and take measures in advance to reduce the drought damage. Our results found that an insignificant decreasing trend of MAHDI mainly occurred in spring and summer, and autumn and winter showed an insignificant increasing trend. About one-third of the subbasins showed an insignificant decreasing trend, and about two-thirds of the subbasins showed an insignificant increasing trend at a 12-month scale. A possible explanation for this may be that global warming made the climate in the upper reaches of the Shiyang River warmer and more humid (Guo et al., 2016). The trend of warming and humidification in autumn and winter was more obvious, which is consistent with the conclusions put forward by previous researchers (Zhou et al., 2012).

4 Conclusion

In this paper, the SWAT hydrological model was used as an indirect way to obtain hydrometeorological data, to simulate the missing data to construct SDI, SSI and SPEI at different timescales, and to analyze the transfer relationship between different droughts. In addition, for the “dimensional disaster” phenomenon that occurred when the copula function was used to connect multidimensional variables, this study used $K_{{\mathrm{C}}^{\prime }}$ to combine multiple hydrometeorological variables to construct a comprehensive drought index, MAHDI, that can simultaneously characterize meteorological, agricultural and hydrological drought, and it analyzed the features of drought changes in the JRB. The following conclusions were derived from the research.

• i.

  Agricultural and hydrological drought had a certain lag to meteorological drought, and the lag time had seasonal characteristics. The shortest lag time of about 2 months was observed in summer, followed by spring. The lag time in autumn and winter was the longest, mostly exceeding 6 months. The lag time of agricultural drought was more obvious than that of hydrological drought, which may be the reason that soil water infiltration time was longer than runoff concentration time.

• ii.

  The degree of drought in the north of the basin was stronger than that in the south. The degree of agricultural drought was the strongest, followed by hydrological drought, and that of meteorological drought was the weakest. This was due to the low water storage capacity of the soil (the calibrated value of SOL_AWC by the SWAT model is only 0.008).

• iii.

  The drought represented by MAHDI was consistent with historical drought events, and it could catch the drought events captured by univariate drought indexes (SDI, SSI and SPEI); however, its description ability of mild and moderate drought was better than that of severe drought. This may be due to the fact that the empirical Kendall function uses a nonparametric method to connect three-dimensional sequences, weakening the influence of extrema in the sequence. In addition, it can timely catch the occurrence and end of drought events. In general, MAHDI was an acceptable comprehensive drought index.

• iv.

  MAHDI showed an insignificant downward trend in spring and summer and an insignificant upward trend in autumn and winter. For a 12-month scale, for about one-third of the subbasins, MAHDI showed an insignificant downward trend, and for about two-thirds of the subbasins it showed an insignificant upward trend. The drought situation in the JRB had been alleviated under the influence of climate change.

The methods utilized in the present study to construct a comprehensive drought index (MAHDI) combining SWAT and copula can be carried out in any other area with deficient observed data. These results are emblematic of the drought phenomenon in the JRB. However, the ability of MAHDI to characterize severe drought is relatively low, and further research is required to improve its ability to monitor severe drought.