A joint probabilistic index for objective drought identification: the case study of Haiti

Since drought is a multifaceted phenomenon, more than one variable should be considered for a proper understanding of such an extreme event in order to implement adequate risk mitigation strategies such as weather or agricultural indices insurance programmes or disaster risk financing tools. This paper proposes a new composite drought index that accounts for both meteorological and agricultural drought conditions by combining in a probabilistic framework two consolidated drought indices: the standardized precipitation index (SPI) and the vegetation health index (VHI). The new index, called the probabilistic precipitation vegetation index (PPVI), is scalable, transferable all over the globe and can be updated in near real time. Furthermore, it is a remote-sensing product, since precipitation is retrieved from satellite data and the VHI is a remote-sensing index. In addition, a set of rules to objectively identify drought events is developed and implemented. Both the index and the set of rules have been applied to Haiti. The performance of the PPVI has been evaluated by means of a receiver operating characteristic curve and compared to that of the SPI and VHI considered separately. The new index outperformed SPI and VHI both in drought identification and characterization, thus revealing potential for an effective implementation within drought early-warning systems.

1 Introduction

Every year droughts affect an increasing number of people. In the years from 2014 to 2018, more than 70 drought events were reported all over the world and about 450 million people suffered because of drought-related impacts (CRED, 2017). Due to its complexity, various definitions of the phenomenon have been proposed by different institutions, such as the World Meteorological Organization (WMO), the Food and Agriculture Organization (FAO), and the United Nations Convention to Combat Desertification (UNCCD). All the institutions focus their attention on a specific aspect of drought: the WMO on the lack of precipitation, the FAO on the decline in crop productivity and the UNCCD on the loss of arable land.

In addition, the quantification of drought effects is a complicated task, since drought impacts are non-structural, widespread over large areas, and of different types and magnitudes within the drought-affected area; they also depend on economic, social and environmental system vulnerabilities (Wilhite, 2000).

Drought identification through an objective and automatic determination of drought onset, termination and severity allows for the timely adoption of appropriate risk management strategies, such as weather index insurance programmes (Barnett and Mahul, 2007), agricultural index insurance programmes (Jensen and Barrett, 2017), disaster financing (Guimarães Nobre et al., 2019; Linnerooth-Bayer and Hochrainer-Stigler, 2015) and early action planning (Drechsler and Soe, 2016).

Drought features are usually determined through the use of two instruments: indicators, which are variables and parameters used to assess drought conditions (such as precipitation, temperature and others), and indices, which are numerically computed values from meteorological or hydrological inputs (World Meteorological Organization and Global Water Partnership, 2016). More than 100 indices have been developed by the scientific community (Zargar et al., 2011), each one focusing on a specific aspect of drought (meteorological, hydrological, agricultural and so on). Meteorological drought is related to precipitation shortages; hydrological drought refers to periods of precipitation shortfall affecting surface water supply (Sheffield and Wood, 2011), while agricultural drought is conventionally linked to soil moisture deficit. Insufficient soil moisture leads to crop failure and consequent yield reduction; therefore the first economic sector that suffers because of drought is agriculture, particularly in those areas where it relies on rainfall. A deeper understanding of agricultural drought dynamics can promote the adoption of risk reduction strategies, such as crop insurance programmes.

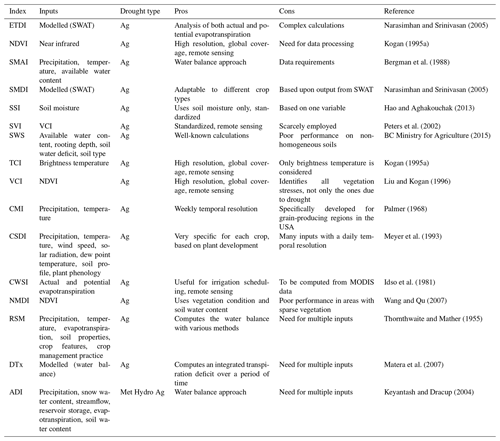
In recent years various remote-sensing indices have been developed and can be employed in agricultural drought monitoring. The most widespread is the normalized difference vegetation index (NDVI), which uses NOAA AVHRR satellite data to monitor vegetation greenness (Kogan, 1995a). The main advantages of the NDVI are the very high spatial resolution and the global coverage. The NDVI has already been applied in drought monitoring, such as in Gu et al. (2008). Many products were derived from the NDVI, such as the vegetation condition index (VCI), which compares the current NDVI to the range of values observed in the same period in previous years (Liu and Kogan, 1996; Kogan, 1995b), and the standardized vegetation index (SVI), which describes the probability of vegetation condition deviation from normal (Peters et al., 2002). A suite of agricultural drought indices is presented in Table 1.

Narasimhan and Srinivasan (2005)Kogan (1995a)Bergman et al. (1988)Narasimhan and Srinivasan (2005)Hao and Aghakouchak (2013)Peters et al. (2002)BC Ministry for Agriculture (2015)Kogan (1995a)Liu and Kogan (1996)Palmer (1968)Meyer et al. (1993)Idso et al. (1981)Wang and Qu (2007)Thornthwaite and Mather (1955)Matera et al. (2007)Keyantash and Dracup (2004)

Table 1 An overview of indices used in agricultural drought monitoring; Met is meteorological, Hydro is hydrological, Ag is agricultural.

Since drought is a complex phenomenon, a single index or indicator can be insufficient to fully characterize drought severity and extent. The combination of more than one indicator can be invaluable in the evaluation of all the variables involved in drought monitoring, such as precipitation, soil moisture and streamflow. Over the past 20 years many composite indicators, relying on two or more drought indices or indicators, have been proposed to overcome the issues related to the use of a single variable. Table 2 shows a list of selected composite indices that can be used in agricultural drought monitoring since, in their formulation, soil moisture, vegetation condition or variables related to water availability for plants are included.

Brown et al. (2008)Kogan (1990)Hao and Aghakouchak (2013)Sepulcre-Canto et al. (2012)Bijaber et al. (2018)Karamouz et al. (2009)Tadesse and Wardlow (2007)Dieker et al. (2010)Svoboda et al. (2002)Lambin and Ehrlich (1995)Wang et al. (2001)Bateni et al. (2018)

Table 2 An overview of aggregate and composite drought indices useful for agricultural drought monitoring; Met is meteorological, Hydro is hydrological, Ag is agricultural. Input abbreviations not defined in the text are as follows: fraction of absorbed photosynthetically active radiation (fAPAR), soil moisture anomaly (SMA), evapotranspiration (ET) and land surface temperature (LST).

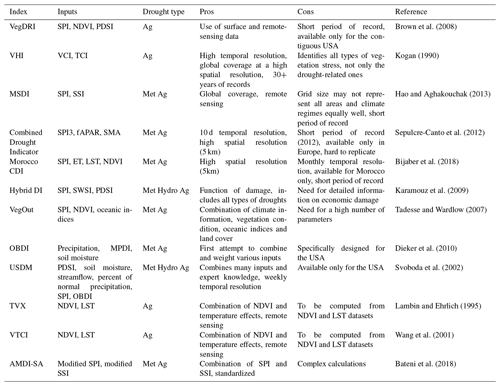
Multiple methods for taking into account the multivariate behaviour of drought have been explored (Hao and Singh, 2015, 2016). The vegetation drought response index (VegDRI), for example, uses a data mining approach to combine multiple inputs such as the SPI, the NDVI and the Palmer drought severity index (PDSI). A weighted linear combination of the inputs is quite common; it is applied to construct the composite drought indicator (CDI) for Morocco, the vegetation health index (VHI) and the objective blend of drought indicators (OBDI). The United States Drought Monitor (USDM) also applies a weighted linear combination of the inputs but adds an expert judgement to define the drought class.

In the last few years multiple studies have focused the attention on modelling the joint behaviour of two drought characteristics or indices applying bivariate or multivariate statistical approaches. In various cases bivariate distributions are developed by means of copulas as in Serinaldi et al. (2009) and Bonaccorso et al. (2012), where the joint behaviour of various drought properties is investigated, or in Shiau (2006), where two-dimensional copulas are employed to study the joint behaviour of drought duration and severity in Taiwan. Shiau et al. (2007) also investigate the hydrological droughts of the Yellow River in China using a bivariate distribution to model drought duration and severity jointly. A trivariate Plackett copula is used in Songbai and Singh (2010) to model drought duration, severity and inter-arrival time jointly.

The use of copulas to quantify the joint behaviour of drought indices is gaining popularity too. Many drought indices derived by multivariate distributions have been proposed. For example the multivariate standardized drought index (MSDI; Hao and Aghakouchak, 2013), which combines the SPI and the standardized soil moisture index (SSI), uses copulas to form joint probabilities of precipitation and soil moisture content, while the joint drought index (JDI; Kao and Govindaraju, 2010) does the same for obtaining the joint probabilities while considering precipitation and streamflow. The composite agrometeorological drought index accounting for seasonality and autocorrelation (AMDI-SA) combines two drought indices, the modified SPI and the modified SSI, employing both the copula concept and the Kendall function (Bateni et al., 2018). The use of copulas seems promising and is highly effective when dealing with two or more variables. An advantage of copula functions is the fact that the index derived from this approach has a probabilistic form.

Both single and composite indices for agricultural drought monitoring showed some limitations, highlighted in Tables 1 and 2. Single indices often rely on multiple inputs, are available only for some locations or identify all types of vegetation stresses. In any case single indices do not account for the multivariate nature of drought. Composite indices often rely on relatively new datasets; in many cases a short period of record is available (for example the VegDRI records start in 2009) or the index is not available in near real time; some of them are specifically designed for a well-identified region (the OBDI and the USDM are available only for the USA, the Combined Drought Indicator only for Europe); other indices do not consider the meteorological aspect of drought (temperature vegetation index, TVX, and vegetation temperature condition index, VTCI, are based on the NDVI and the land surface temperature); other ones do not have a sufficiently refined spatial resolution (MSDI). Most of them, with the exception of the AMDI-SA and MSDI, are not expressed in probabilistic terms; therefore uncertainty quantification and evaluation is not an easy task.

In this paper, we propose the following:

1. a new drought index, the probabilistic precipitation vegetation index (PPVI), that takes advantage of well-consolidated indices, the standardized precipitation index (SPI; Mckee et al., 1993) and the vegetation health index (VHI; Kogan, 1997), and tries to overcome their individual limitations by coupling them in a probabilistic framework through the use of a bivariate normal distribution function;

2. a framework to identify a drought event using the new index, i.e. a set of rules for the definition of a drought event; when the set of conditions is verified, a drought event is identified based on the new index; otherwise, no drought event is identified.

With respect to the indices already available in the literature, we will show in this paper that the new index has some interesting features:

• It is able to identify drought-driven events of vegetation stress.

• It is parsimonious in terms of number of inputs required.

• It is a remote-sensing product with high spatial and temporal resolution.

• It is based on quasi-near-real-time datasets, with a relatively short latency time (less than 1 week).

• More than 30 years of records are available at global scale for its calibration.

The paper is structured as follows: Sect. 2 describes the datasets employed in the development of the new index and presents the methodology used to combine the SPI and the VHI; Sect. 3 illustrates the application to the case study, shows the validation process of the new index, and compares the performance of the new index to those of the SPI and the VHI considered separately; in addition the advantages related to the adoption of the index and the possible applications in agricultural drought risk management are summarized.

2 Datasets and methods

2.1 Datasets

Two remote-sensing datasets were used: one for precipitation and the other for the VHI. Precipitation was retrieved from the satellite-only Climate Hazards Group Infrared Precipitation (CHIRP) dataset. CHIRP has a quasi-global coverage (50^∘ S–50^∘ N); high spatial resolution (0.05^∘); and daily, pentadal and monthly temporal resolution. Records start from 1 January 1981. CHIRP was chosen because it has been specifically developed to monitor agricultural drought. The use of CHIRP instead of CHIRPS (the Climate Hazards Group Infrared Precipitation with Stations) is related to the data latency time. Since the aim of the work is the development of an index for near-real-time drought monitoring, the product with the shortest latency time was selected. CHIRPS data have a latency time of about 3 weeks (Funk et al., 2015), while CHIRP's latency is about 2 d, as can be checked on the dataset's website (Climate Hazard Group, 2015). The development and the main characteristics of the dataset are described in Funk et al. (2015). In the present study CHIRP with a daily temporal resolution was used to have the possibility of computing weekly precipitation. Data are available on the project website (Climate Hazard Group, 1999).

The vegetation health index was retrieved from the global vegetation health products (global VHP) of the National Oceanic and Atmospheric Administration (NOAA) Center for Satellite Applications and Research (Kogan, 1997). Data can be retrieved from the NOAA website (NOAA, 2011). The dataset contains blended VHP derived from VIIRS (2013–present) and AVHRR (1981–2012) GAC data. The dataset has 4 km spatial resolution, weekly temporal resolution and global coverage. Both the selected datasets are freely available.

2.2 Methods

2.2.1 The standardized precipitation index

As previously mentioned, two consolidate drought indices were combined: the SPI and the VHI. The SPI was selected because it is a commonly used index to detect meteorological drought; it is standardized, and therefore SPI values can be compared even in different climate regimes; and it is recommended by the WMO (World Meteorological Organization, 2009).

SPI computation is based on a long-term precipitation record for a desired period. The precipitation record is then fitted to a probability distribution (in this work a gamma distribution was used), which is then transformed into a normal distribution. Traditionally monthly precipitation records are employed, and the SPI is computed aggregating precipitation at a predefined time step (for example 1, 3, 6, 9 and 12 months are the aggregation periods suggested by the WMO; World Meteorological Organization, 2009).

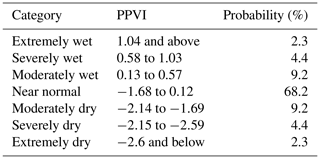
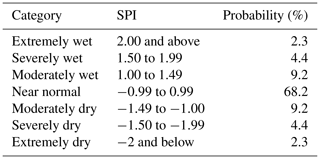
In the present work, weekly precipitation records were used. The SPI aggregation period was then selected, and the index, computed over one of the traditional aggregation periods, was updated every week. The SPI is normally distributed by definition. Conventionally drought starts when the SPI is lower than −1 and ends when the SPI comes back to the value of 0 (Mckee et al., 1993). Drought classification according to the SPI, as proposed in Mckee et al. (1993), is reported in Table 3. The percentages reported in the third column of Table 3 indicate the probability of SPI values falling within the range reported in the second column of the same table.

Table 3 Drought classification based on SPI according to Mckee et al. (1993).

2.2.2 The vegetation health index

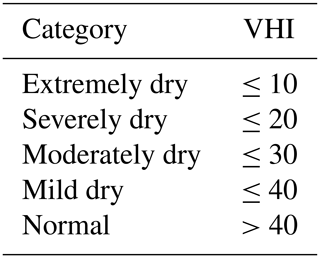
The VHI is a remote-sensing index developed to include the effects of temperature on vegetation; in fact, it combines the VCI with the temperature condition index (TCI; Kogan, 1995a), which is another remote-sensing index used to determine vegetation stress caused by temperature and excessive wetness. The VHI is based on a linear combination of VCI and TCI: $\text{VHI}=\mathit{\alpha }\text{VCI}+(\mathrm{1}-\mathit{\alpha })\text{TCI}$. As suggested by Kogan et al. (2016), when VCI and TCI contributions are not known, α=0.5. One drawback of the VHI is the impossibility of identifying the cause of the vegetation stress; in fact, vegetation can suffer because of various events: excessive wetness, pests, fires, droughts or other factors. The VCI is a biophysical indicator of a lack of precipitation but can also be seen as representing drought impacts on the ground (Bachmair et al., 2016). It goes from 0, which stands for vegetation in very bad conditions, to 100, meaning perfectly healthy vegetation. The classification scheme of the VHI, as proposed in Dalezios et al. (2017), is presented in Table 4.

Table 4 Drought classification based on VHI according to Dalezios et al. (2017).

The VHI is standardized to make comparisons with the SPI easier. As mentioned by Peters et al. (2002), all remote-sensing indices can be expressed as deviations from the mean; therefore, the standardized variable, VHI_st, is computed according to the following equation:

$$\begin{array}{}\text{(1)}& {\text{VHI}}_{\text{st}}={\displaystyle \frac{\text{VHI}-\stackrel{\mathrm{‾}}{\text{VHI}}}{\mathit{\sigma }}},\end{array}$$

where $\stackrel{\mathrm{‾}}{\text{VHI}}$ is the mean of the distribution and σ its standard deviation. Thus, the same procedure proposed in Peters et al. (2002) in the case of the NDVI has been applied to the VHI. The standardized variable, VHI_st, has a distribution with 0 mean and 1 as standard deviation.

2.2.3 The probabilistic precipitation vegetation index (PPVI)

The probabilistic precipitation vegetation index (PPVI) is a composite index that takes into account both meteorological drought through the SPI and agricultural drought conditions by including the VHI.

In order to combine the two consolidated indices, the following preparatory steps are performed:

1. extraction of the area under study from both the datasets;

2. regridding of both precipitation and the VHI to bring them to the same spatial resolution (0.05^∘);

3. aggregation of precipitation at a weekly timescale (CHIRP has daily temporal resolution);

4. computation and weekly update of the SPI according to the methodology proposed in USDA Risk Management Agency et al. (2006), where precipitation is fitted to a gamma distribution; the goodness of fit to the gamma distribution has been verified by means of probability plot;

5. standardization of the VHI, as previously described.

The combination of the SPI and VHI is performed using a bivariate normal distribution function, as defined by Kotz et al. (2000). The normality of the SPI and VHI_st distributions has been verified as will be shown in Sect. 3.2. Therefore it is acceptable to assume that the joint probability of the two considered distributions takes the form of the bivariate normal for correlated variables:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }f(s,v)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }{\mathit{\sigma }}_s{\mathit{\sigma }}_v\sqrt{\mathrm{1}-{\mathit{\rho }}^{\mathrm{2}}}}}\exp (-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}(\mathrm{1}-{\mathit{\rho }}^{\mathrm{2}})}}\\ \text{(2)}& {\displaystyle }& {\displaystyle }\cdot \left[{\displaystyle \frac{(s-{\mathit{\mu }}_s{)}^{\mathrm{2}}}{{\mathit{\sigma }}_s}}+{\displaystyle \frac{(v-{\mathit{\mu }}_v{)}^{\mathrm{2}}}{{\mathit{\sigma }}_v}}+{\displaystyle \frac{\mathrm{2}\mathit{\rho }(s-{\mathit{\mu }}_s)(v-{\mathit{\mu }}_v)}{{\mathit{\sigma }}_s{\mathit{\sigma }}_v}}\right]),\end{array}$$

where the following notation is adopted. The SPI is identified as s, and the VHI_st is identified as v. The mean and the standard deviation of the SPI distribution f(s) are respectively, by construction, μ_s=0 and σ_s=1, and the mean and standard deviation of the VHI_st distribution f(v) are respectively μ_v=0 and σ_v=1. The covariance matrix Σ and the correlation coefficient ρ are defined according to Eqs. (3) and (4) respectively, where σ_sv is the covariance between s and v.

$$\begin{array}{}\text{(3)}& {\displaystyle }& {\displaystyle }\mathbf{\Sigma }=\left[\begin{array}{cc}{\mathit{\sigma }}_s^{\mathrm{2}}& \mathit{\rho }{\mathit{\sigma }}_s{\mathit{\sigma }}_v\\ \mathit{\rho }{\mathit{\sigma }}_s{\mathit{\sigma }}_v& {\mathit{\sigma }}_v^{\mathrm{2}}\end{array}\right]\text{(4)}& {\displaystyle }& {\displaystyle }\mathit{\rho }={\displaystyle \frac{{\mathit{\sigma }}_{sv}}{{\mathit{\sigma }}_s{\mathit{\sigma }}_v}}\end{array}$$

To check the assumption of normality for the joint distribution, the joint probability values, retrieved from Eq. (2), are plotted against the bivariate empirical cumulative distribution values (Fig. 1), as performed in Kao and Govindaraju (2010). The bivariate empirical copula for the random variables s and v has been evaluated according to Nelsen (2006) using the following equation:

$$\begin{array}{}\text{(5)}& C\left({\displaystyle \frac{i}{m}},{\displaystyle \frac{j}{m}}\right)={\displaystyle \frac{\mathit{\#}(s\le s_{\left(i\right)},v\le v_{\left(j\right)})}{m}}={\displaystyle \frac{m_{\mathrm{1}}}{m}},\end{array}$$

where s_(i) and v_(j) $(\mathrm{1}\le i,j\le m)$ are ordered statistics of the SPI sample of size m and m₁ is the number of samples (s_(k),v_(k)) satisfying $(s_{\left(k\right)}\le s_{\left(i\right)}and{v}_{\left(k\right)}\le v_{\left(j\right)})$ with $\mathrm{1}\le k\le m$. The resulting plot is shown in Fig. 1.

Figure 1 PPVI validation: empirical copula versus bivariate joint probability function. The red line corresponds to the 45^∘ line. Joint probability values have been computed from Eq. (2), while empirical copula values according to Eq. (5).

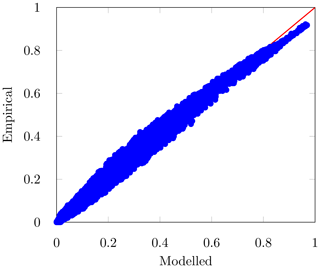
Since the data lie on the 45^∘ line, it is fair to assume that the joint probability f(s,v) is normal. Therefore, a normalization of the index is performed through normal quantile transformation.

By keeping the same probability intervals of the SPI, we can compute the PPVI values for the drought classification as shown in Table 5.

Table 5 Drought classification according to PPVI.

2.2.4 Identification of drought events

Once the index is defined, the set of rules to establish when a grid cell is in a drought should be identified. In particular, two parameters have to be identified:

1. a threshold Z of the index that marks the beginning of a drought in a grid cell

2. a threshold z that marks the end of a drought in the same grid cell.

According to the model proposed here, a drought in a grid cell starts when the index is lower than Z and ends when the index is above z. Then regional drought events are defined. Again, two parameters are identified: N and n. A drought events starts if more than N grid cells are in drought conditions and ends if less than n grid cells are in drought conditions.

2.2.5 Skill assessment

Observations of drought are compared with the model outputs for various combinations of thresholds Z, z, N and n. The receiver operating characteristic (ROC) curve is used for this comparison. The ROC curve was at first used in signal detection; its use in meteorological applications is documented and well described in Joliffe and Stephenson (2012). The ROC curve is employed to classify instances, as in the present case. The ROC curve was already employed in various studies to compare the performance of a model versus observations with varying thresholds (Zhu et al., 2016; Khadr, 2016). The contingency matrix (shown in Table 6) is a 2-by-2 matrix to visualize the disposition of a set of instances. True positives or hits are represented by the weeks that are reported to be in drought conditions in the observations and are correctly identified as drought weeks by the model. True negatives (correct rejections) are represented by those weeks that are not in drought according to both the observations and the model. Those weeks that are recorded as drought according to the observations but are not identified as drought weeks by the model are considered as false negatives (missing events), while false positives (false alarms) are represented by the weeks that are not in drought conditions according to the observations but are identified as drought weeks by the model. In this paper for each combination of thresholds Z, z, N and n, probability of detection (POD), or hit rate, and probability of false detection (POFD), or false alarm rate, are computed according to Joliffe and Stephenson (2012) with the following equations:

$$\begin{array}{}\text{(6)}& {\displaystyle }& {\displaystyle }\text{POD}={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}},\text{(7)}& {\displaystyle }& {\displaystyle }\text{POFD}={\displaystyle \frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FP}}},\end{array}$$

where TP, TN, FP and FN are defined as in Table 6.

Table 6 Contingency table for the deterministic estimates of a series of binary events (Joliffe and Stephenson, 2012).

The optimal threshold for a ROC curve is the one for which the distance from the 45^∘ line is maximal (Zhu et al., 2016). The performances of the model based on the PPVI in identifying drought events have been evaluated on the case study described in the next section.

2.2.6 Case study

The case study region is Haiti. The country, which has an extent of 27 750 km², is located in the Caribbean's Greater Antilles and shares the island of Hispaniola with the Dominican Republic. The climate is predominantly tropical, with daily temperatures ranging between 19 and 28 ^∘C during winter and between 23 and 33 ^∘C during summer. The island topography is varied; the central region is mainly mountainous, while the northern and western regions are near the coastline. Annual precipitation in the central region averages 1200 mm, while in the lowlands it is about 550 mm (GFDRR, 2011). Haiti is subject to the variability associated with El Niño and La Niña phenomena, with El Niño bringing drier and hotter conditions and La Niña a colder and wetter climate. Haiti experiences a first rainy season from April to July and a second, and most important, rainy season from August to the end of November. The dry season starts in December and goes on until the end of March (FEWSNET, 2019).

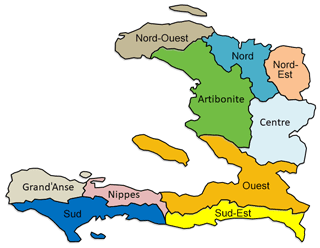
Haiti is divided administratively into 10 departments (Fig. 2), with people living mainly in Ouest, where the capital Port-au-Prince is located, and in Artibonite. The total population in 2017 was about 11 million people (World Bank, 2017). Haiti is the poorest country in the Western Hemisphere; the economy is mainly agricultural. Of the country's total area, 67 % is devoted to agriculture, but only 4.35 % of the agricultural area is irrigated (Trading Economics, 2013), posing a major threat to local production.

Figure 2 Map of Haiti departments.

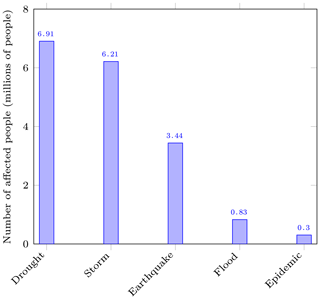
Haiti produces over half of the world's vetiver oil (used in cosmetics), and mangos and cocoa are the most important export crops. Two-fifths of all Haitians depend on the agriculture sector, mainly small-scale subsistence farming. The country is prone to all types of natural hazards. Earthquakes, storms, hurricanes, landslides and droughts have caused huge damage and losses in recent years. Haiti was ranked as the third country most affected by extreme weather events in terms of lives lost and economic damage in the period from 1994 to 2013 (GFDRR, 2011). More than 96 % of the population lives in areas at risk of two or more hazards. The most frequent disasters are floods and storms, but droughts are the disasters involving the highest number of persons (Fig. 3).

Figure 3 Number of people affected by natural disasters in Haiti (1900–2018). Source: CRED (2017).

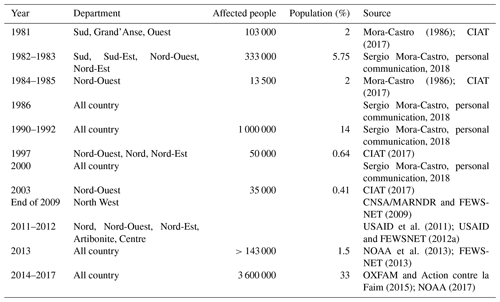
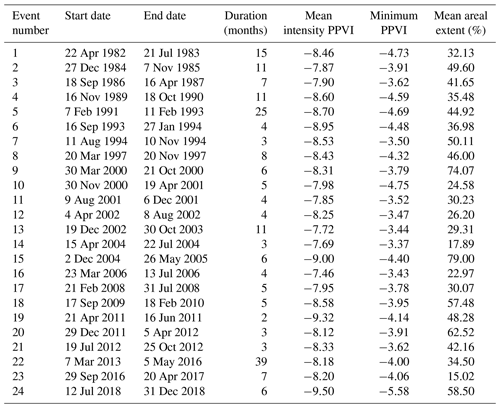
Droughts threaten the livelihoods of Haitians in many different ways. The scarcity of crops production means a rise in food prices that brings widespread food insecurity since the majority of people cannot afford the increase. Unavailability of drinking water leads to cholera outbreaks among the population. Water is also an issue for breeders, who lose livestock on which they rely for milk production and meat consumption. In the period from 1980 to the present, more than 10 drought events have been reported by the government or the humanitarian organizations working in Haiti (Table 7). The worst drought was the one of 2014–2017, affecting more than 3 million inhabitants (about one-third of Haiti's population).

Mora-Castro (1986); CIAT (2017)Mora-Castro (1986); CIAT (2017)CIAT (2017)CIAT (2017)CNSA/MARNDR and FEWSNET (2009)USAID et al. (2011); USAID and FEWSNET (2012a)NOAA et al. (2013); FEWSNET (2013)OXFAM and Action contre la Faim (2015); NOAA (2017)

Table 7 Reported drought events in Haiti from 1980 to the present.

Effective drought management is crucial for Haiti, but at present, a reliable early-warning system for drought is still lacking. Weather stations on the ground are few and data records are often very short and therefore not useful for drought monitoring of the entire country. Satellite images can be an effective and inexpensive tool to improve drought management and preparedness in the country.

3 Results and discussion

3.1 Correlation analysis

Haiti has been divided into 987 grid cells, accounting for 90 % of the country's area. A total of 1941 weeks were considered, starting from week 35 of 1981 and ending with week 52 of 2018. The release date of a new VHI image was considered as the starting date of a week. In the present study, four precipitation aggregation periods were considered (1, 2, 3 and 6 months), and the corresponding values of SPI (SPI1, SPI2, SPI3 and SPI6) were computed in order to select the SPI aggregation timescale to be used to create the PPVI.

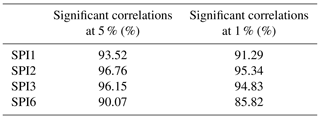
To evaluate the strength of the statistical relationship between the SPI at various timescales and the VHI, a correlation analysis was then performed. Various studies have already evaluated the correlation among drought indices or between drought indices and exogenous variables; for example Bonaccorso et al. (2015) investigated the correlation between the SPI and North Atlantic oscillation (NAO), while Hongshuo et al. (2014) investigated the correlation between the SPI (various aggregation periods) and the VHI. The Pearson correlation coefficient was employed in the present study as a measure of the statistical relationship between the indices. The number of significant correlations at 5 % and 1 % was evaluated for four SPI aggregation timescales (Table 8). The highest number of significant correlations was found in the cases of the SPI2 and SPI3, which exhibit very similar performances at a 1 % significant level. This finding is in agreement with previous studies such as those of Hongshuo et al. (2014), which found that the VHI and SPI3 have the highest correlation with croplands, whereas the VHI and 6-month SPI have the highest correlation with forest in the southwest of China, and Ma'rufah et al. (2017), which found that significant correlation coefficient values of the SPI3 and VHI are common in the southern part of Indonesia. Since the SPI3 has been used in the literature and the percentage of significant correlation at the 1 % level is relevant, it has been decided to aggregate the SPI over a 3-month period and use SPI3 in the following discussion.

Table 8 Number of significant correlations (Pearson correlation coefficient) between VHI and various SPI aggregation timescales. Values are expressed as percentages evaluated with respect to the total number of grid cells (987).

3.2 Normality of SPI and VHI distributions

Before computing PPVI as described in the previous sections, a test on the normality of the SPI3 and VHI_st distributions was performed. The goodness of fit of the SPI3 and the VHI_st distributions was verified through the histograms in Fig. 4 (panels a and b respectively), where the boxplots represent the relative frequencies of the SPI3 and VHI_st values. Both the SPI3 and the VHI_st data can therefore be considered normally distributed.

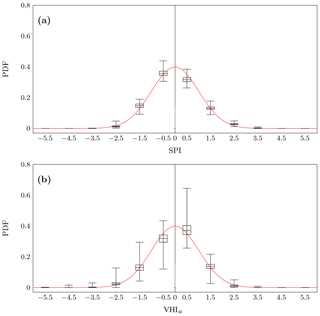
Figure 4 (a) Distribution of SPI values and (b) distribution of VHI_st values. The red lines represent the PDFs of the standard normal distributions; boxplots represent the percentage of values lying within the range; 12 ranges were considered, starting from −6 and ending with 6 with a step equal to 1.

3.3 Selection of threshold values

The PPVI was computed as described in Sect. 2.2, and its performance in identifying past drought events in Haiti when used in combination with the set of rules described in Sect. 2.2.4 was evaluated. To this end, the ROC curve classification methodology was applied. The set of rules meant that, at first, cells in drought conditions were identified: drought started in a specific grid cell at week W when the PPVI was lower than the threshold Z and ended when the PPVI was up to the threshold z in the same grid cell at a week w (with w coming after W). Then a regional drought event was identified: the drought event started when more than N cells at a specific week W₁ were in drought conditions and ended at a week W₂ when fewer than n grid cells were in drought conditions. The comparison was performed on a weekly basis, with observations derived from the reported events described in Table 7.

The ROC curves were computed according to the following methodology: at first a combination of the thresholds Z, z, N and n was selected. On the basis of the set of rules established in Sect. 2.2.4, the ability of the selected combination of thresholds in reproducing the observations was assessed by computing TP, TN, FP and FN as defined in Table 6, together with POD and POFD. A couple (POFD, POD) represents a point in a ROC graph. Then one threshold among Z, z, N and n was selected. The selected threshold was variable during the analysis, while the other three were kept constant. The step of variation was identified according to the threshold maximum and minimum values. For each combination of the four thresholds (the varying one and the three fixed), TP, TN, FP, FN, and POD and POFD were computed. The resulting set of couples (POFD, POD) represented the ROC curve for the considered set of thresholds.

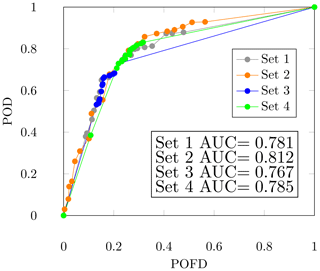
The analysis was repeated by varying another threshold among Z, z, N and n. As an example, Fig. 5 shows four ROC curves for the thresholds in Table 9. Thresholds N and n in Table 9 are expressed as the percentage of the country's area instead of as the number of grid cells. For each of the curves the best-performing set of thresholds (Z, z, N and n) was selected by identifying the point farthest from the 45^∘ line, as performed by Zhu et al. (2016). The area under the curve (AUC) was used as a criterion to establish which of the ROC curves should be preferred (as was performed by Dutra et al., 2014; Mason and Graham, 2002; Zhu et al., 2012). An AUC near to 1 indicates good performance, while an AUC of 0.5 indicates the model has no predictive skills. From Fig. 5 it is clear that the curve corresponding to the parameters defined as Set 2 in Table 9 should be preferred, since the AUC is the closest to 1.

Figure 5 ROC curves for the set of thresholds reported in Table 9.

Table 9 Example of set of thresholds used to draw ROC curves for model calibration. Thresholds N and n are expressed as the percentage of the country's area instead of as the number of grid cells.

3.4 Comparison of drought indices with observed drought events

The aim of this section is not to validate in absolute terms the proposed methodology since the data record is too short to serve both for calibration and for validation. In the present section, instead, we provide a validation by comparing the performance of the PPVI in identifying observed drought events with those of widely recognized and used indices such as the SPI and VHI.

The performance of the PPVI was then compared to those of the SPI3 and VHI considered separately. Thresholds analogous to Z and z were defined for the SPI3 and VHI. Thresholds Z_S and z_S mark respectively the beginning and the end of drought conditions in a grid cell according to the SPI3, and thresholds Z_V and z_V do the same in the case of the VHI. Again the four thresholds Z, z, N, and n were varied in order to identify the optimal values. As an example, Fig. 6 shows a comparison among the ROC curves for the three indices. In each panel of Fig. 6, n and z and z_S and z_V (for PPVI, SPI3 and VHI) remained constant, while Z, Z_S and Z_V were varying; N was fixed in each panel but varied between the panels. Z varied from −4 to −1.1 with a step equal to 0.1; Z_S varied from −3 to 0 with a step equal to 0.1, and Z_V varied from 10 to 40 with a step equal to 5.

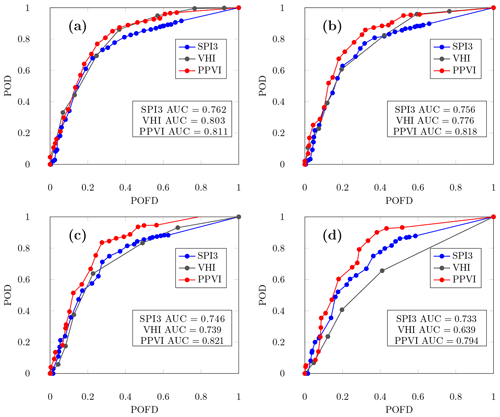
Figure 6 Comparison between the performances of the SPI3, VHI and PPVI in identifying reported drought events; thresholds Z, Z_S and Z_V are varying; $z=-\mathrm{1.1}$; z_S=0, and z_V=40; n=80, and four cases for N are shown. (a) N=10 %; (b) N=20 %; (c) N=30 %; and (d) N=50 %.

It is clear from Fig. 6 that the red curve, representing the PPVI, is the furthest from the diagonal line in all the panels of the figure. The area under the curve (AUC) was used as a criterion to establish which index gave the best performances. AUC values are shown in Fig. 6 for each index and various configurations of the model. The AUC value of the PPVI was in line with similar results reported in the literature (Mwangi et al., 2014). As can be seen from Fig. 6, the new index provided better results with respect to the ones obtained with the SPI3 or VHI considered separately. In all the four configurations shown in Fig. 6, the AUC for the curve constructed with the PPVI was larger than the ones for the SPI3 and VHI. The AUC values are in line with the ones considered good in the literature for drought predictive skills (see Khadr, 2016). The optimal thresholds to configure the model when applied with each of the three considered indices were then determined by selecting the point farthest from the 45^∘ line, as performed by Zhu et al. (2016). The best configuration parameters are shown in Table 10. The drought events were therefore identified using the optimal parameters (Table 10). A graphical representation of the performance of the model in reproducing observed drought events is given in Fig. 7. Only the period from 2000 to 2018 is shown.

Table 10 Best configuration parameters for the model when applied with the PPVI, SPI3 and VHI.

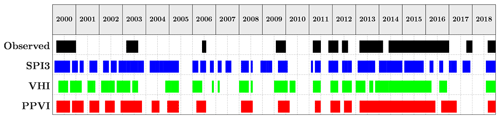
Figure 7 Comparison between observed drought events and drought events identified by the PPVI, SPI3 and VHI when calibrated with the best-performing parameters shown in Table 10. The comparison is shown for the period from 2000 to 2018.

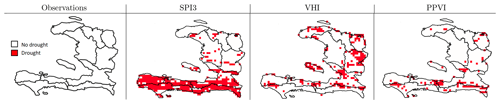
Figure 8 Comparison of the performance of the SPI3, VHI, and PPVI in identifying the areas hit by drought in week 45 of 1995. Departments highlighted in red are the ones in drought according to observations (Table 7); red cells are the ones in drought conditions according to the various indices.

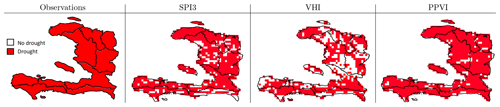
Figure 9 Same as Fig. 8 but for week 33 of 2015. Departments highlighted in red are the ones in drought according to observations; red cells are the ones in drought conditions according to the various indices.

The ability of the model in identifying the country area hit by the drought was also assessed. A visual comparison of the areas under drought identified by the three indices was performed, as was performed by Dutta et al. (2015).

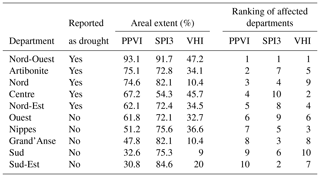
Here some significant weeks are shown. At first, week 45 of 1995 was considered. No drought events were reported in that period according to the information available in the analysed documents (see Table 7). Figure 8 shows that, while the SPI3 identified the whole southern part of the country as dry areas and the VHI showed vegetation suffering in two departments (Centre and Ouest), the PPVI did not show signs of drought, except for in a minor number of grid cells. Figure 9 shows that in 2015, when the whole country was reported to be in severe drought conditions (see Table 7 and NOAA, 2017; OXFAM and Action contre la Faim, 2015), the PPVI captured the pattern well; only a few grid cells were not in drought conditions. The SPI3 was also able to capture the situation, while for the VHI only 58 % of the county was in drought. During week 8 of 2012, only the northern part of the country was in drought (Fig. 10), as highlighted by USAID and FEWSNET (2012b) (see Table 7). Five departments were reported to be stressed (Nord, Nord-Ouest, Nord-Est, Artibonite, Centre; see Table 7). All the three indices showed the Nord-Ouest as the department most affected by drought when considering the percentage of the department area hit by the drought. The PPVI then classified Artibonite, Nord, Centre and Nord Est as the next most affected, while the SPI3 identified Sud and Grand'Anse as the second- and third-most-affected departments and the VHI identified Centre and Nippes (Table 11).

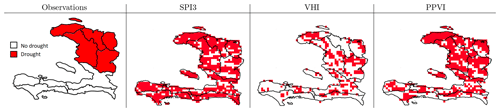
Figure 10 Same as Fig. 8 but for week 8 of 2012. Departments highlighted in red are the ones in drought according to observations; red cells are the ones in drought conditions according to the various indices.

Table 11 Performance of the PPVI, SPI3 and VHI in identifying departments hit by drought during week 8 of 2012 and comparison with observations. Observations are retrieved from the text-based documents reported in Table 7.

Severity, duration and mean areal extent of the drought events identified by the PPVI were computed. Severity was computed as the sum of all the values identified by the condition that a grid cell is in a drought condition when the PPVI is lower than −1.8 and exits from drought when the PPVI is up to −1.1. Duration is expressed in months, and the mean areal extent is the average percentage of the area in drought during a specific event. Results are presented in Table 12.

Table 12 Drought events in Haiti according to the PPVI, duration, severity and mean areal extent.

The PPVI showed overall a better capacity in identifying drought events with respect to the SPI3 and VHI considered separately. However, some false alarms still remain. This can be linked to the uncertainty in information on past drought events for the analysed area. Short-term droughts are often not reported in text-based documents, and information on drought start and end dates was retrieved from documents that mainly described the impacts related to drought. The PPVI showed a good agreement with reported information in identifying the areas of the country hit by droughts.

4 Conclusions

The timely identification of drought events is of great importance in agricultural areas, especially when rainfed agriculture is practised. At the same time, the evaluation of the damage caused by drought is a key point to select appropriate risk management strategies, such as weather index insurance programmes, agricultural index insurance, disaster financing and early action planning. The new composite index proposed in this paper, the probabilistic precipitation vegetation index, PPVI, is a powerful tool since it can identify events of vegetation stress and, at the same time, select from among those the ones actually due to drought, thanks to the use of both the VHI and the SPI. As such it can be helpful in agricultural drought monitoring and can be used to identify drought events affecting a region, their severity and their duration as was shown in the case of Haiti. In particular, the PPVI can be invaluable in those areas where rainfed agriculture is of vital importance since people rely on it for food production for personal consumption.

Among the interesting aspects of the PPVI, there is the fact that few data are required for its computation: only precipitation and the VHI. This aspect is crucial, since many composite indicators able to identify agricultural droughts already exist, but large quantities of data are required to compute them. For example, the United States Drought Monitor combines more than 40–50 inputs, while other indices specific to agricultural drought monitoring, such as the VegDRI and the VegOut, require the use of temperature and oceanic indices. The number of parameters required to compute the PPVI is low even with respect to the OBDI, SWS, CDI or CDSI.

A second important advantage is that, since the SPI was computed starting from satellite precipitation (CHIRP dataset) and that the VHI is a remote-sensing drought index, the PPVI is also a remote-sensing product. The use of datasets with global coverage means that the PPVI is easily transferable and scalable over the entire globe. In addition, the PPVI can be a very useful tool in areas with scarce gauge coverage such as the Caribbean islands. Both precipitation and the VHI have a very high spatial and temporal resolution, thus allowing drought monitoring via satellite even in small areas. The PPVI can be computed even in those regions with short data records, since the VHI has more than 30 years of records (data collection began in August 1981) and CHIRP precipitation is available from January 1981.

Both the SPI and the VHI are updated with a weekly time step since every week a new VHI image is released, and the CHIRP precipitation dataset has a daily temporal resolution; therefore the PPVI can be updated more frequently than other composite indices, such as the CDI, which is updated every 10 d. In addition, due to the relatively short latency time (less than 1 week) of both the datasets employed to create the PPVI, the index is available in near real time, therefore allowing for the timely implementation of drought mitigation strategies. This last feature is of particular interest when the PPVI is used to implement measures to reduce drought risk in agriculture, where a timely identification of drought is crucial to prevent damage to the sector.

Many advantages are also related to the adoption of the set of rules here proposed to identify drought events. First of all, these rules enable an objective and standardized identification of drought events from the mathematical point of view. Additionally, they can be adjusted according to the needs and the objectives of various possible end users of the model, such as farmers, governments or insurance companies.

The performances of the PPVI in identifying drought events were tested in a specific case study (Haiti) and compared to the ones of the SPI and VHI considered separately. The PPVI performed better than the single indices considered separately in reproducing past drought events. The PPVI identified drought areas in Haiti better than the SPI and VHI even from the spatial point of view; thus it is more reliable than a single index. A comparison of PPVI performances with respect to the ones of other composite indices was not performed in the present study due to the unavailability of composite indices with the same characteristics of the PPVI. In fact previous composite indices do not include both the meteorological and the agricultural aspect of drought, are not available globally, or cannot be computed with only remote-sensing datasets.