A statistical analysis of rogue waves in the southern North Sea

A new wave data set from the southern North Sea covering the period 2011–2016 and composed of wave buoy and radar measurements sampling the sea surface height at frequencies between 1.28 and 4 Hz was quality controlled and scanned for the presence of rogue waves. Here, rogue waves refer to waves whose height exceeds twice the significant wave height. Rogue wave frequencies were analyzed and compared to Rayleigh and Forristall distributions, and spatial, seasonal, and long-term variability was assessed. Rogue wave frequency appeared to be relatively constant over the course of the year and uncorrelated among the different measurement sites. While data from buoys basically correspond with expectations from the Forristall distribution, radar measurement showed some deviations in the upper tail pointing towards higher rogue wave frequencies. The amount of data available in the upper tail is, however, still too limited to allow a robust assessment. Some indications were found that the distribution of waves in samples with and without rogue waves was different in a statistical sense. However, differences were small and deemed not to be relevant as attempts to use them as a criterion for rogue wave detection were not successful in Monte Carlo experiments based on the available data.

1 Introduction

Waves that are exceptionally higher than expected for a given sea state are commonly referred to as rogue waves (Bitner-Gregersen and Gramstad, 2016). What exactly “expected” and “exceptionally” mean is a matter of definition which is not addressed consistently throughout the literature (e.g., Dysthe et al., 2008). A common approach is to define a rogue wave as a wave whose height exceeds twice the significant wave height of the surrounding seas. Here, significant wave height refers to the average height of the highest third of the waves in a record and is intended to correspond to the height estimated by a “trained observer”.

The above definition of a rogue wave is based on a criterion developed by Haver and Andersen (2000). As rogue waves are often associated with incidents and damages to ships and offshore platforms (Haver and Andersen, 2000), these authors were primarily interested in whether or not such waves represent rare realizations of typical distributions of waves in a sea state. Based on 20 min wave samples, Haver (2000) called a wave a rogue wave when it represented an outlier in reference to the second-order model commonly used in engineering design processes. He concluded that “… the ratio of wave height to significant wave height that is likely to be exceeded in 1 out of 100 cases [in a second-order process] is about 2.0” (Haver, 2000).

Since the late 1990s, there has been an increasing number of studies analyzing observed rogue waves or studying potential mechanisms for rogue wave generation. Such studies comprise the description and analysis of measurements of individual rogue wave events (e.g., Skourup et al., 1997; Haver, 2004; Magnusson and Donelan, 2013) or the description of rogue wave statistics from longer records (e.g., Chien et al., 2002; Mori et al., 2002; Stansell, 2004; Baschek and Imai, 2011; Christou and Ewans, 2014). Several studies contain attempts to identify potential physical mechanisms of rogue wave formation, such as second-order nonlinearities (Fedele et al., 2016), modulational instability (Benjamin, 1967) caused by nonlinear wave focusing (Janssen, 2003), or the directionality of the wave spectrum (Onorato et al., 2002). Soares et al. (2003) analyzed laser records from the Draupner and North Alwyn platforms in the North Sea and found that rogue waves in stormy conditions here showed higher skewness coefficients and a lower steepness than waves simulated from second-order theory. They concluded that rogue waves must result from higher than second-order models. Based on an analysis of waves from two locations in the North Sea and the North Atlantic, Olagnon and van Iseghem (2000) reported that in high sea states, extreme waves occurred more frequently in seas steeper than on average. From the analysis of a large data set, mostly from radars and lasers in the North Sea complemented with some data from other regions, Christou and Ewans (2014), on the other hand, concluded that rogue wave frequencies were not governed by steepness and other parameters describing the overall sea state. Based on analyses of laser altimeter data, Stansell (2004) described rogue wave frequencies to be only weakly dependent on significant wave height, significant wave steepness, and spectral bandwidth. Cattrell et al. (2018) emphasized that predictors for rogue wave probability can probably not be derived for an entire data set but argued that location-specific forecasts might be possible. In general, Kharif et al. (2009) concluded that the complexity of processes in the ocean makes it difficult to link the probability of rogue wave occurrences to typical sea state characteristics.

So far, there is still no generally accepted picture, and the overarching question raised by Haver and Andersen (2000) on whether rogue waves can be considered “rare realizations of a typical population” or “typical realizations of a rare population” is still being debated. To address this question, a definition of what is “typical” for a given sea state and/or location is needed. In deep water and under the assumption that the sea surface represents a stationary Gaussian process, wave heights of waves with a narrow spectrum can be shown to be Rayleigh distributed (Holthuijsen, 2007). The Rayleigh distribution represents a special form of a Weibull distribution,

$$\begin{array}{}\text{(1)}& P\left(H>c{H}_{\mathrm{s}}\right)=\exp \left(-{\displaystyle \frac{c^{\mathit{\alpha }}}{\mathit{\beta }}}\right),\end{array}$$

with parameters α=2 and β=0.5. Here, P denotes the probability that the height H of an individual wave exceeds the significant wave height H_s by a factor c. Forristall (1978) analyzed the frequency of large waves from 116 h with hurricane wind speeds in the Gulf of Mexico. He found that for these cases the Rayleigh distribution substantially overestimated the frequency of large wave heights. From his data and analyses, he estimated that a Weibull distribution with parameters α=2.126 and β=0.5263 provided a better fit to the observed data. Note that in this fit, the significant wave height used for normalization was estimated as being 4 times the standard deviation of the sea surface elevation, which, especially in very shallow water, leads to lower estimates compared to the traditional definition of H_s as the average of the highest third of waves in a record. In the ocean wave literature, a Weibull distribution with these parameters is commonly referred to as the Forristall distribution. Compared to the Rayleigh distribution, it is characterized by smaller probabilities for large wave heights, the differences increasing with wave height. More complex models and distributions accounting for the effects of spectral bandwidth were developed by, e.g., Tayfun (1990) or Naess (1985).

To address the question of whether or not rogue waves represent typical realizations of such distributions, several studies compared them with data from observations. For stormy seas, Waseda et al. (2011) found that radar measurements were in agreement with expectations from a Weibull distribution with parameters close to those found by Forristall. Including both stormy and fair weather conditions, de Pinho et al. (2004) found rogue waves in the Campos Basin, Brazil, to occur more often than expected, while for coastal rogue waves, the occurrence probability was found to remain below the expectations of a Rayleigh distribution (Chien et al., 2002). Mori et al. (2002) considered the distribution of wave heights, crests, and troughs independently in the same sample. They found that wave heights closely followed the Rayleigh distribution, while the distributions of crests and troughs substantially deviated. Data from different types of instruments and different kinds of sea states were found to be located in-between Gaussian and second-order statistics (Christou and Ewans, 2014). Magnusson et al. (2003) found an agreement in the majority of their laser and buoy measurement data with Rayleigh and Weibull distributions but reported deviations from the known distributions in the upper tail. They were, however, undetermined about the significance of those deviations. Similar deviations from the Forristall distribution were reported by Forristall (2005) in which individual 30 min wave records were analyzed. When the records were combined, the data were again found to fit the Forristall distribution. These results suggest that larger samples including rogue waves might be needed to derive robust results.

In the present study, we analyze new data that have not been available for analysis before. Compared to previous studies, the data set is large, comprising 6 common years of nearly uninterrupted measurements from 11 radar stations and wave buoys located in the southern North Sea. From these data, observed wave heights were compared with Rayleigh and Forristall distributions, and seasonality, trends, and spatial correlation were assessed. Whether or not information from the background field may be derived that points towards increased rogue wave probability for given sea states was further tested.

2 Data and methods

2.1 Data

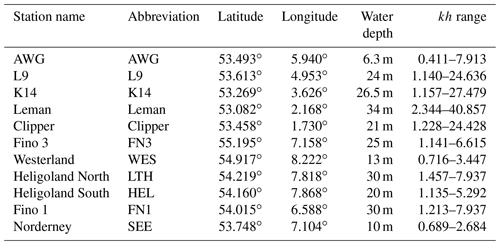
The 6 common consecutive years of sea surface elevation data from 2011 to 2016 were available from 11 measurement stations in the southern North Sea (Fig. 1). At the five stations represented by red circles, radar devices are installed that measure the air gap to the water surface with a frequency of 2 or 4 Hz. The six blue boxes mark surface-following Datawell Directional Waverider buoys of type MkIII that measures at a frequency of 1.28 Hz. The buoy stations are located in the German Bight, while the radar stations are situated in the southern part of the North Sea off the Dutch coast and towards Great Britain. Table 1 provides an overview of the positions of the measurement stations and the water depth at each position.

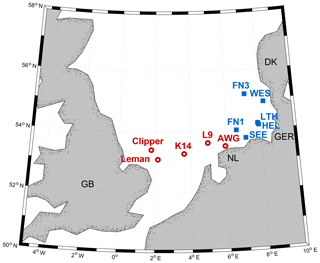
Figure 1 Wave measurement sites in the southern North Sea considered in this study. Blue squares: wave buoys; red circles: radar stations.

Table 1 Position and water depth h at the measurement sites. In addition, typical ratios between water depth and wavelength L are shown as $kh=\mathrm{2}\mathit{\pi }{L}^{-\mathrm{1}}h$.

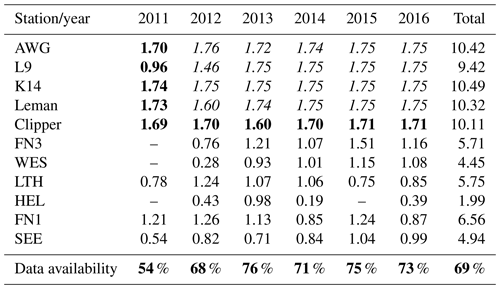
The buoys delivered their data in the form of surface elevation samples, each of which had a length of 30 min (1800 s). Radar data were available as continuous time series. For comparison, they were also split into half-hour samples. In total, the procedure yielded approximately 797 000 half-hour samples from 6 years of observations at the 11 stations (Table 2). Subsequently, all buoy and radar samples were treated equally.

Table 2 Number of available half-hour samples (×10⁴) in 2011–2016 at each station after quality control (see Sect. 2.2). Measurement frequencies are indicated by font style: 1.28 Hz (normal text), 2 Hz (bold), 4 Hz (italic). The bottom row indicates data availability per year (in %).

In the following, a wave was defined as the course of the sea surface elevation in the time interval between two successive zero upcrossings. This way, a total of approximately 329 million individual waves were derived from the 797 000 samples. Parameters describing the distribution of waves are found to be unaffected by the choice of upcrossing or downcrossing approaches (Goda, 1986).

2.2 Quality control and rogue wave identification

Both buoy and radar data were delivered in the form of raw surface elevation data. To identify and to eliminate spikes and erroneous data, each time series was checked and tested according to a number of quality criteria. These criteria were selected such that unreasonable spikes and data should be flagged and removed, while at the same time extreme peaks that may qualify as rogue waves should be maintained. In detail, the following procedure was applied to the raw samples.

1. Data within a 30 min sample should be as complete as possible to allow for the robust estimation of sea state parameters and individual waves. Samples missing more than three data points were discarded.

2. Since data were obtained not only during stormy but also in moderate and calm weather conditions, some samples contained a very large number of small waves. It was presumed that each wave in a record should be described by at least five measurement points to be reliably counted. When n_p denotes the minimum number of measurement points per wave, the maximum number of waves n_max in a 30 min (1800 s) sample is given by n_max=1800 s $f_{\mathrm{s}}{n}_{\mathrm{p}}^{-\mathrm{1}}$, where f_s denotes the sampling frequency. For data from wave buoys sampled at a frequency of 1.28 Hz, 30 min records containing more than 460 waves were thus discarded. For the radar stations recording with sampling frequencies of 2 and 4 Hz, samples containing more than 720 and 1440 waves, respectively, were excluded.

3. To eliminate influences from tides, the mean of each sample was subtracted. Subsequently, for each record, statistics such as significant wave height H_s, zero upcrossing period T_z, and standard deviation σ were calculated using the zero upcrossing method. Significant wave height was computed as the average of the highest third of the waves in a 30 min record.

4. Subsequently and based on physical reasoning, a set of error indicators (EIs) adopted from Christou and Ewans (2014) (EI 1–EI 5) and from Baschek and Imai (2011) (EI 6–EI 8) was applied. Time series were discarded if any of the error indicators were true.

   • EI 1. A 30 min sample included 10 or more consecutive points of equal value.

   • EI 2. A 30 min sample included a wave with a zero upcrossing period longer than T_z=25 s. For such waves to be wind generated, extreme wind speeds exceeding hurricane strength over a fetch of more than 4000 km for several hours would be required (WMO, 1998, p. 44), which appears unrealistic over the North Sea.

   • EI 3. The limit rate of change S_y of the water surface was exceeded. According to Christou and Ewans (2014), the limit rate is given by $S_y=\mathrm{2}\mathit{\pi }\mathit{\sigma }{\stackrel{\mathrm{‾}}{T_z}}^{-\mathrm{1}}\sqrt{\mathrm{2}\ln N_z}$, where σ represents the standard deviation of the surface elevation in the 30 min sample and $\stackrel{\mathrm{‾}}{T_z}=N(f_{\mathrm{s}}{N}_z{)}^{-\mathrm{1}}$ denotes the mean zero upcrossing period. In the latter, N denotes the number of elevation points, f_s again the sampling rate, and N_z  the number of zero upcrossings in the sample. The criteria were applied for both the surface elevation and its acceleration.

   • EI 4. The energy in the wave spectrum at frequencies below 0.04 Hz (periods larger than 25 s) exceeded 5 % of the total wave energy.

   • EI 5. The energy in the wave spectrum at frequencies above 0.60 Hz exceeded 5 %. These waves are too short to be captured by five or more measurements at sampling frequencies of 1.28 or 2 Hz.

   • EI 6. The sample included at least one data spike for which the vertical velocity of the surface exceeded 6 m s⁻¹.

   • EI 7. The ratio between the magnitudes of vertical and horizontal displacements exceeded a factor of 1.5 which, in deep water, is indicative of unexpected deviations from the orbital motions of the water particles.

   • EI 8. At least one wave height in the sample exceeded the water depth.

5. The remaining samples were tested for the presence of rogue waves. They were considered to contain rogue waves if at least one of the waves in the sample fulfilled the criteria of Haver and Andersen (2000):

   $$\begin{array}{}\text{(2)}& {\displaystyle \frac{H}{H_{\mathrm{s}}}}\ge \mathrm{2}\mathrm{and}/\mathrm{or}{\displaystyle \frac{C}{H_{\mathrm{s}}}}\ge \mathrm{1.25},\end{array}$$

   where H and C denote the individual wave and crest height, respectively.

6. The detected rogue wave should again be described by at least five measurement points in order to be considered further.

7. Eventually, all remaining rogues underwent a subjective visual check to ensure that all spurious extremes were removed.

Applying these criteria, in total approximately 28 % of the buoy samples and 15 % of the radar samples were eliminated and discarded from further analyses.

3 Results

Rogue waves refer to exceptionally high waves within a given sea state in which the state of the sea is commonly characterized by the significant wave height H_s. Whether or not a wave qualifies as a rogue under the definition of Haver and Andersen (2000) thus does not directly depend on its height but on its height relative to the height of the prevailing waves characterized by H_s. Rogue waves may hence occur in heavy seas but also during moderate or relatively calm conditions. Because the largest waves have the largest impact, many studies have focused on the analysis of extreme cases only, which is the analysis of rogue waves for large H_s (e.g., Forristall, 1978; Soares et al., 2003; Stansell, 2004; Waseda et al., 2011). Unlike these studies, in the following, we use all available data from all sea states, which is to say also cases with rogue waves from small or moderate sea states. In some cases, when only rogue waves during high sea states are considered, this is explicitly mentioned. We generally analyzed the number of rogue waves in relation to the total number of individual waves, which in the following is referred to as rogue wave frequency.

3.1 Spatial distribution of rogue wave frequencies

Rogue wave frequency observed at the different stations within the period 2011–2016 varied between $\mathrm{1.24}\times {\mathrm{10}}^{-\mathrm{4}}$ at WES and $\mathrm{1.95}\times {\mathrm{10}}^{-\mathrm{4}}$ at AWG (Fig. 2). This corresponds on average to about 1.24 and 1.95 rogue waves in every 10 000 waves. Generally, rogue waves were detected more frequently in the radar than in the buoy samples. At all radar stations, rogue wave frequency exceeded the values expected from a Forristall distribution (Fig. 2), while, with the exception of SEE, values at buoy locations were below expectations from a Forristall distribution. Rogue wave frequencies are larger in the western part of our analysis domain, but as all radar/buoy stations are located in western/eastern part of the domain, we cannot infer whether this is a result of the different measurement techniques or spatial location. When water depth is considered in addition (Table 1), no clear relation between rogue wave frequency and depth could be inferred.

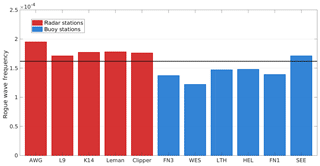
Figure 2 Rogue wave frequency in 2011–2016 at the 11 radar (red) and buoy (blue) locations. The solid black line indicates the rogue wave frequency ($\mathrm{1.62}\times {\mathrm{10}}^{-\mathrm{4}}$) derived from the Forristall distribution (Forristall, 1978).

Table 3 Correlations between monthly rogue wave frequencies in 2012–2016 at the 11 measurement sites.

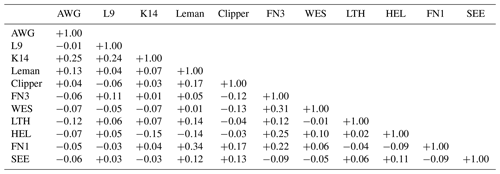
Spatial coherence between rogue wave frequencies at the different sites was analyzed based on monthly values. Correlations were computed to test for the likelihood of joint occurrences of increased or decreased frequencies at the different stations for a given month. Only data from 2012 to 2016 were used because of larger gaps in 2011. Correlations between monthly rogue wave frequencies at the different stations varied between −0.15 for K14 and HEL and +0.34 for Leman and FN1 (Table 3). For the given sample size of N=60 monthly values, these correlations are not significantly different from zero at the 95 % confidence level. This indicates that monthly frequencies of rogue waves vary independently at the different stations.

3.2 Temporal distribution of rogue wave frequencies

3.2.1 Seasonality

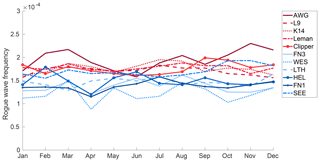
Rogue wave frequency, which is to say the number of rogue waves per number of observed waves, was found to be relatively constant and to vary only little in the course of the year (Fig. 3). Even so, a considerably higher number of rogue waves were observed during late summer and early fall. In absolute numbers, these waves are not necessarily high as significant wave heights in summer and early fall are generally small. In winter, there are fewer rogue waves, but they generally occur during higher sea states and may thus have larger impacts. Moreover, wave periods are shorter in summer than in winter. Therefore, on average a 30 min sample from the winter seasons contains fewer waves than a corresponding sample from summer (Fig. 3). In total, both effects cancel each other out, and rogue wave frequency was found to be remarkably stable in the course of the year. Similar conclusions hold when the different measurement sites are analyzed individually (Fig. 4).

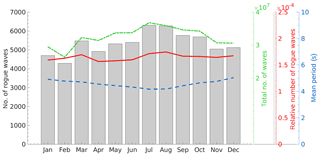
Figure 3 Seasonal distribution of rogue wave frequency (red), total number of waves (green), and rogues waves (gray bars) in the period 2011–2016 and of monthly mean zero upcrossing wave periods (blue) based on data from all measurement sites. Note the different scales and y axis for the different parameters.

Figure 4 Seasonal distribution of rogue wave frequency in 2011–2016 at the 11 measurement sites. Red colors: radar stations; blue colors: wave buoys.

3.2.2 Interannual variability

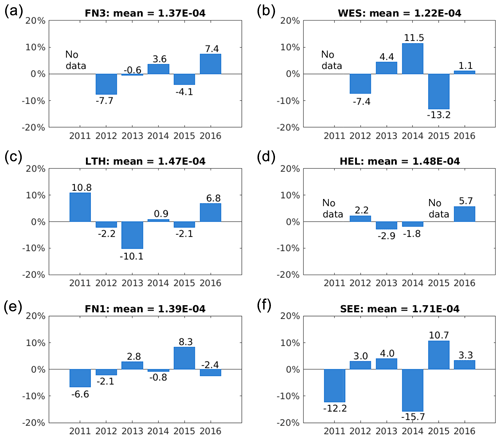
There was pronounced interannual variability in rogue wave frequency around its long-term mean at each measurement site (Figs. 5 and 6). Variability was found to be somewhat larger at the radar stations in the western part of our domain. The largest fluctuation where found at AWG where rogue wave frequency varied between −27 % and 16.5 % around the 2011–2016 mean. Variability derived from the wave buoy data was somewhat smaller with the exception of the two buoys WES and SEE, both located in relatively shallow water (Table 1). Again, there is hardly any correlation between the values at the different stations. While, for example, most stations suggest a minimum in rogue wave frequency for the year 2011, it was above average at LTH. While LTH in turn showed very small frequencies in 2013, most other stations had values close to their long-term means. Whereas AWG had a maximum in rogue wave frequency in 2014, other stations showed only small anomalies, and SEE even had low values in 2014. Although rogue wave frequency in 2016 was enhanced at most stations, this was not supported by L9, Clipper, and FN1. This further supports the results from the correlation analysis of monthly rogue wave frequencies (Table 3). Despite the small distances between the measurement stations, rogue wave frequencies seem to vary independently. This suggests that mechanisms driving rogue wave variability on larger scales might be difficult to identify.

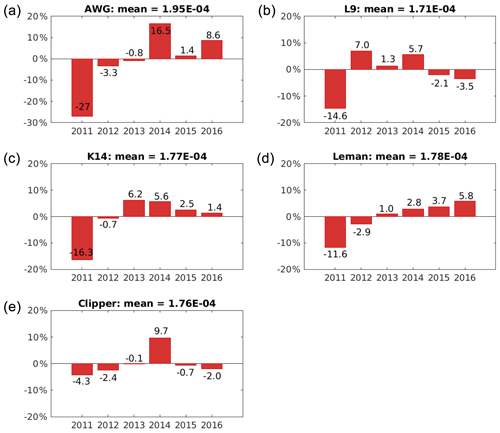
Figure 5 Anomalies in percent of annual rogue wave frequency relative to the corresponding long-term mean at each site for the five radar stations: AWG, L9, K14, Leman, and Clipper (from a to d).

Figure 6 Anomalies in percent of annual rogue wave frequency relative to the corresponding long-term mean at each site for the six wave buoys: FN3, WES, LTH, HEL, FN1, and SEE (from a to f).

3.3 Comparison of observations with Rayleigh and Forristall distributions

The cumulative frequencies of occurrences of wave heights relative to the significant wave height derived from the measurements were compared to corresponding exceedance probabilities given by Weibull distributions with both Rayleigh and Forristall parameters (Fig. 7). For wave heights up to twice the significant wave height, which corresponds to the threshold used to identify rogue waves, the measurement data are well described by the Forristall distribution. At a height of H≈2H_s, the data begin to deviate from the Forristall distribution. Both distributions increasingly diverge for larger relative wave heights, $H{H}_{\mathrm{s}}^{-\mathrm{1}}$. This suggests that in our data, rogue waves occurred more frequently than could be expected from the Forristall distribution. The frequency of rogue waves much larger than twice the significant wave height also exceeded expectations given by the Rayleigh distribution. The figure further illustrates that for increasing relative wave heights, these findings are based on increasingly smaller samples.

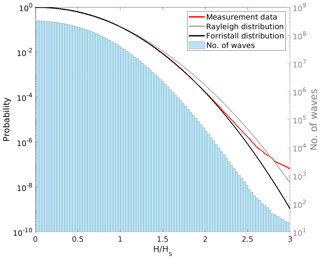
Figure 7 Comparison of the exceedance frequency of relative wave heights derived from observations (red) and corresponding exceedance probabilities derived from the Rayleigh (gray) and Forristall (black) distributions, together with a histogram (100 bins) of the number of available relative wave height observations (blue bars). Note the different y axes for exceedance probability (left) and the number of waves (right) and that the x axis shows relative wave height, which is to say the height of each wave relative to the significant wave height of its 30 min sample.

To assess whether these deviations reflect a common behavior or originate from a few measurement sites only, the analysis was repeated for each station individually (Fig. 8). Substantial differences between the various sites were found. At AWG and Clipper, the frequency of waves higher than about 2 times the significant wave height increasingly deviated from the Forristall distribution, and for waves larger than about 2.7 times the significant wave height, the frequency reached or even exceeded that estimated from a Rayleigh distribution. This behavior was found to be typical for the radar sites. On the other hand and with the exception of SEE, observations from the wave buoys generally followed (e.g., LTH) or underestimated (e.g. WES) frequencies from the Forristall distribution. Thus the radar stations were mostly responsible for the strong deviation of the overall data set from the Forristall distribution for extreme waves. This again may indicate differences arising from the different measurement techniques or the region.

Table 4 Long-term 95th percentile of significant wave height at each site.

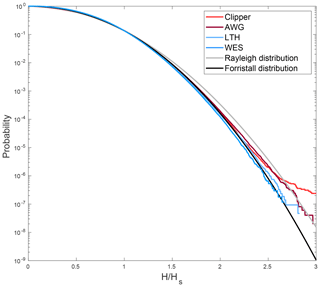
Figure 8 Comparison of the distributions of relative wave height at different stations to Rayleigh and Forristall distributions. On the x axis, the height of each individual wave in relation to the significant wave height of its half-hour sample is given. The y axis shows the probability of relative wave heights being exceeded.

So far the analyses were carried out for all sea states. For design purposes and navigation or other marine operations, rogue waves in high sea states that may cause the greatest damage are generally the most interesting ones. To assess whether a similar behavior is found also for these waves, the analysis was repeated including only cases in which the significant wave height exceeded the long-term 95th percentile at each site (Fig. 9 and Table 4). Again a similar behavior for all waves was found. For smaller waves, the frequency follows a Forristall distribution. The frequency of larger waves is substantially increased, in particular for rogue waves exceeding about 2.2 times the significant wave height. Again, the data from the radar stations accounted for most of the deviation, while data from the buoys followed the Forristall distribution more closely.

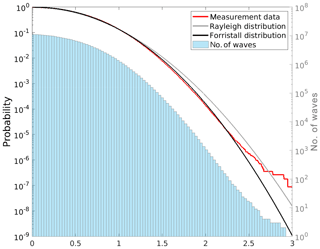
Figure 9 As in Fig. 7 but only including samples in which the significant wave height exceeded the corresponding long-term 95th percentile at the different sites.

In summary, while results from the buoys (with the exception of SEE) suggest that rogue waves did not occur more frequently than could be expected from a Forristall distribution and thus could be considered typical rare realizations within a given sea state, results from the radar measurements pointed towards enhanced rogue wave probability which might be indicative of mechanisms not described by second-order statistics. This holds for rogue waves both in all sea states and in high sea states only.

3.4 Analysis of the background wave field

Data from some sites, especially the radar stations, suggested that differences between the frequency distributions derived from observations and the Forristall distribution may exist for higher relative wave heights and in particular for those qualifying as rogue waves. In the following, we distinguish between rogue waves and all other waves in 30 min samples. The latter will be referred to as the background field. The aim was to investigate whether or not in samples with and without rogue waves differences in the distribution of waves in the background field might be identified that may potentially predict rogue waves.

More specifically, the measurement data were divided into two groups of samples: Group 1 comprised all samples including at least one rogue wave exceeding twice the significant wave height, and Group 2 included all other samples. Subsequently, a third group was built from Group 1 by removing the individual rogue waves but retaining all other waves, which is to say the background field. In the following, to what extent differences in the background fields in groups 2 and 3 can be identified is assessed.

3.4.1 Wave height distribution in the background field

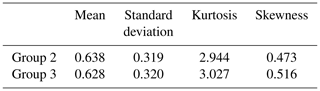
The frequency distributions of wave heights in the background field in samples with and without rogue waves were compared (Fig. 10). Visually, both distributions appear to be quite similar, and also the curve representing samples from Group 2 (normal samples not containing rogue waves) is systematically below that of Group 3 (background field of samples containing rogue waves). This is supported by comparing the moments of the distributions, with Group 2 having a slightly larger mean and being marginally more flat-topped than Group 3 (Table 5). Additionally, the skewness of both distributions is positive, with the skewness of Group 3 slightly deviating more from that of a normal distribution than Group 2.

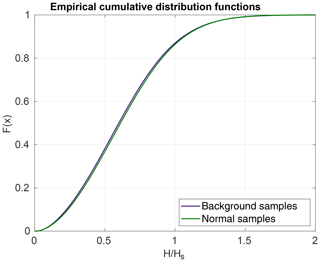
Figure 10 Empirical cumulative frequency distributions of relative wave heights in groups 2 (green) and 3 (purple).

Table 5 Moments of the relative wave height distribution shown in Fig. 10. Note that the relative wave height is nondimensional.

To test whether the differences between the two groups were significant, a Kolmogorov–Smirnov (KS) test (von Storch and Zwiers, 1999) was applied. More specifically, the KS test is a nonparametric test that compares two empirical distributions and tests whether or not the null hypothesis that both distributions represent data from the same population can be rejected. The test is based on the distance D between the two empirical distribution functions F_1,n and F_2,m (Fig.  10) such that

$$\begin{array}{}\text{(3)}& D_{n,m}=\underset{x}{sup}\left|F_{\mathrm{1},n}\right(x)-F_{\mathrm{2},m}(x\left)\right|,\end{array}$$

where sup denotes the supremum function and n and m denote the corresponding sample sizes. For large samples, the null hypothesis is rejected at level α when

$$\begin{array}{}\text{(4)}& D_{n,m}>K_{\mathit{\alpha }}\sqrt{{\displaystyle \frac{n+m}{nm}}},\end{array}$$

where

$$\begin{array}{}\text{(5)}& K_{\mathit{\alpha }}=\sqrt{\mathrm{0.5}\ln {\displaystyle \frac{\mathrm{2}}{\mathit{\alpha }}}}.\end{array}$$

For sample sizes of n=306 282 148 waves in Group 2 and m=23 073 717 waves in Group 3, the null hypothesis is to be rejected at α=0.05 when D_n,m is greater than $\mathrm{2.93}\times {\mathrm{10}}^{-\mathrm{4}}$. From the data, $D_{n,m}=\mathrm{1.42}\times {\mathrm{10}}^{-\mathrm{2}}$ was estimated, suggesting that the null hypothesis that both samples originate from the same population should be rejected at the 95 % confidence level. This indicates that although differences appear to be small, the test identified statistically significant differences between the background wave field from samples with and without rogue waves.

We suppose that this might be a consequence of the large sample sizes in which the test renders even very small differences as being significant at a given significance level. We argue that for the differences to be relevant, they should further bear the potential for rogue wave prediction or detection. To test this, a simple prediction/detection scheme was applied and tested for potential efficacy.

1. We split the data from groups 2 and 3 into two halves and recomputed the cumulative distribution function (cdf) of the first half.

2. From the second half, we randomly selected a 30 min sample 10 000 times. In the case of a sample containing a rogue wave, it was removed to only retain the background field. Subsequently, the empirical cdf of these data was computed.

3. Subsequently, the distances between the empirical cdf and those of Group 2 and Group 3 (step 1) were computed.

4. Based on the smaller of these distances, we predicted that a rogue wave was likely or unlikely to occur within the given sample.

5. We assessed whether or not the prediction would have been correct and marked the result accordingly.

The results and the skill of this simple exercise are shown in Fig. 11. It can be inferred that the probability of detecting a rogue wave correctly, given only the knowledge about the distribution of waves in the background field, is only about 55 % ($\mathrm{POD}=a(a+c{)}^{-\mathrm{1}}$; Wilks, 2011). The probability of false detection, $b(b+d{)}^{-\mathrm{1}}$ (often referred to as false alarm rate; Barnes et al., 2009), indicating how often a rogue wave would have been detected incorrectly, is about 41 %. While this would still imply some limited skill, the probability of a false alarm, $b(a+b{)}^{-\mathrm{1}}$ (often called the false alarm ratio; Barnes et al., 2009), is extremely large and exceeds 90 %. In total, the overall critical success index, $a(a+b+c{)}^{-\mathrm{1}}$ (Wilks, 2011), which refers to the number of correct yes forecasts divided by the total number of occasions on which the event was forecast and/or observed, is only about 0.08. For a perfect forecast, the critical success index would be unity. This suggests that although the KS test identified statistically significant differences between the distributions of wave heights in the background field of samples with and without rogue waves, these differences appear not to be relevant as they hardly bear any potential for rogue wave detection or prediction. For an extended discussion about statistical significance and relevance, see, e.g., Frost (2017). To test whether analyses done separately for the individual stations yield different results, the exercise was repeated only for stations that showed deviations from the Forristall distributions in the upper tail. In principle, the same results were obtained. For example, the analysis of data from Clipper only yields a probability of detection of about 49 %, a probability of false detection of about 46 %, and a probability of false alarm of 93 %, which are very close to the values derived from the entire data set.

Figure 11 Contingency table of forecast/event pairs: a is hits, b is false alarms, c is misses, and d is correct negatives.

3.4.2 Wave steepness distribution in the background field

Mean steepness

Rogue waves are often described as exceptionally steep waves, which is to say waves whose height is large compared to their length or period (Christou and Ewans, 2014; Donelan and Magnusson, 2017). In the following, we investigate whether wave steepness differs in samples with and without rogue waves. Following the approach taken in Christou and Ewans (2014), the mean wave steepness S for each sample was derived from $S=H_{\mathrm{s}}{L}^{-\mathrm{1}}$, where L denotes the mean wavelength in the sample. As both wave buoys and radar devices provide point measurements, L is not directly available but was estimated from the wave period and the water depth by iteratively solving the wave dispersion relation. Similar to Christou and Ewans (2014), the maximum crest height in each sample was plotted as a function of mean wave steepness for samples both with and without rogue waves (Fig. 12). The analysis was performed separately for stations with a water depth of less than and more than 15 m, as well as for radar and buoy stations. Generally, the shape of the scatter plots is in agreement with the findings of Paprota et al. (2003), who showed that for increasingly higher waves, the steepness approaches values of approximately 0.06. Also, in all cases, rogue wave samples appear to be a subset of the samples without rogue waves. In other words, from the analysis, it could not be inferred that the mean steepness in a rogue wave sample exceeds that in samples without rogue waves. This holds for both wave buoys and radar stations. For the most shallow radar station, it is even inferred that while there exists a considerable number of samples with very high wave heights and steepnesses, none of those contained a rogue wave (Fig. 12a). This is consistent with the findings of Christou and Ewans (2014) and Paprota et al. (2003), who, for their data sets, concluded that the steepness in wave records containing a rogue wave is not significantly different from that of other records. The same results as for the entire data set were obtained when only stations that showed deviations from the Forristall distribution in the upper tail were taken into account.

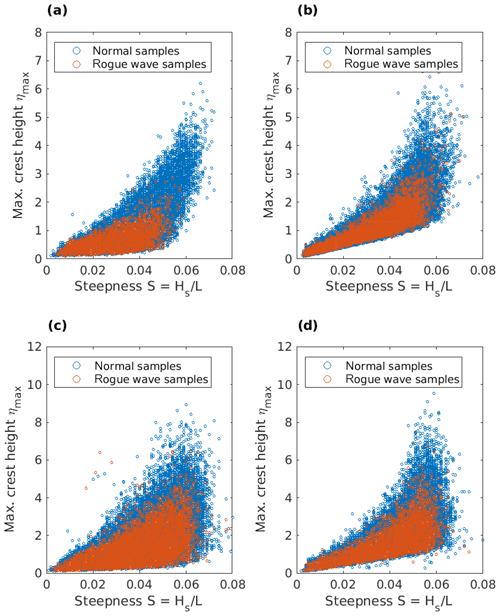
Figure 12 Scatter plot between mean wave steepness and maximum crest height in samples with (red) and without (blue) rogue waves. (a, c) Data from radar stations. (b, d) Data from wave buoys. (a, b) Data from stations with a water depth of less than 15 m. (c, d) Data from stations with a water depth of more than 15 m.

Steepness in the vicinity of a rogue wave

While mean wave steepness was not found to systematically deviate between samples with or without rogue waves, such differences might still be limited to waves in the immediate vicinity of the rogue wave. Wilms (2017) investigated breaking waves in a hydrodynamic wave tank and observed increases in wave steepness five to six waves ahead of a breaking wave. To elaborate whether such behavior can also be found ahead of observed rogue waves in the real ocean, 1234 rogue wave samples from radar devices and 716 rogue wave samples from wave buoys were used to derive a distribution of wave steepness of individual waves ahead of the rogue wave (Fig. 13). Only severe sea states were considered; that is, only samples for which the significant wave height exceeded the corresponding long-term 95th percentile at each station were regarded . This was done as determining the shape and steepness of individual waves was more robust and reliable for high waves with large periods.

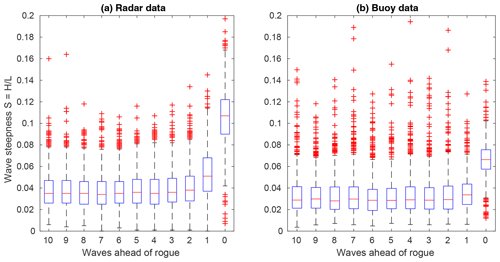
Figure 13 Distribution of wave steepness of the 10 individual waves preceding a rogue wave (wave 0) for radar (a) and wave buoy (b) locations. Distributions were obtained from 1234 (716) rogue wave samples at radar (buoy) locations for which the significant wave height exceeded the corresponding long-term 95th percentile. Distributions are shown as box-and-whisker plots (median: red line; box: interquartile range; whiskers: 1.5 times the interquartile range; red crosses: data outside the whiskers).

For both radar and wave stations, the rogue waves themselves stick out as waves of strongly increased wave steepness on the order of about twice that of the preceding waves. The distributions of the 2–10 waves ahead of the rogue wave were not peculiarly noticeable. All of them were characterized by almost constant median steepnesses ranging between about 0.037 and 0.041 at radar and between about 0.032 and 0.034 at wave buoy locations. Only the waves directly ahead of the rogue wave showed a tendency towards increased wave steepness (0.054 and 0.036 for radar and buoy stations, respectively). However, the latter strongly depends on the choice of the method used to define the waves. In our analyses, a zero upcrossing approach was used. In this case, the trough preceding a rogue wave is considered to be part of the wave ahead. If zero downcrossings would have been used instead, the wave trough preceding the rogue wave would have been treated as part of the rogue wave itself. Since the wave trough ahead of a rogue wave is usually not as deep as the one following it, this would have led, in most cases, to a decrease in the steepness of the rogue wave and its preceding wave. Consequently, such a definition would have supported the conclusion that also the steepness of the wave immediately ahead of the rogue wave is not outstanding compared to the others.

3.4.3 Asymmetry of waves preceding rogue waves

For steep waves such as rogue waves, due to nonlinear wave–wave interactions, higher wave crests are expected compared to second-order theory (Forristall, 2005; Christou and Ewans, 2014). This results in asymmetric waves in which the asymmetry μ can be described as the ratio between crest height C and wave height H. For linear sine waves, the asymmetry is μ=0.5; for second-order Stokes waves in deep water, it is μ=0.61 (Wilms, 2017). The parameter μ is commonly used for the description of the geometry of breaking waves (Kjeldsen and Myrhaug, 1980). According to Kjeldsen and Myrhaug (1980), the asymmetry of breaking waves may reach values of up to μ=0.84–0.95. For rogue waves, Magnusson and Donelan (2000) stated that they are characterized by pronounced crest-to-trough asymmetries similar to breaking waves. From wave tank experiments, Wilms (2017) concluded that increased asymmetries may occur five to six waves ahead of breaking waves.

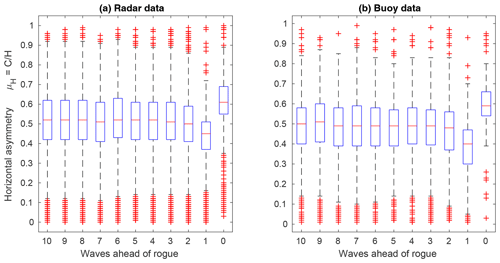
Figure 14 Distribution of asymmetry of individual waves ahead of rogue waves (wave 0) for radar (a) and wave buoy (b) locations. Distributions were obtained from 1234 (716) rogue wave samples at radar (buoy) locations for which the significant wave height exceeded the corresponding long-term 95th percentile. Distributions are shown as box-and-whisker plots (median: red line; box: interquartile range; whiskers: 1.5 times the interquartile range; red crosses: data outside the whiskers).

Using the same rogue wave samples of 1234 radar and 716 buoy data as above for which the significant wave height exceeded the long-term 95th percentile, the distributions of wave asymmetries of the waves preceding the rogue waves were computed (Fig. 14). Generally and on average, for both radar and wave buoy stations, asymmetries of the 2–10 waves preceding the rogue wave were close to the value of μ=0.5 expected from linear theory. The waves immediately ahead of the rogue waves on average showed a strong decrease in asymmetry, while the asymmetry of the rogue waves themselves was increased, indicating higher crests than troughs. Again, this result strongly depends on how the individual waves were defined. The reduced asymmetry of the wave immediately ahead of the rogue wave is due to the assignment of the relatively deep trough ahead of the rogue to the preceding wave. Using a zero downcrossing analysis, this trough is assigned to the rogue wave, and the mean asymmetry remains constant at approximately 0.5 with the exception of the rogue wave itself. Additionally, it is interesting to note that the average asymmetry of waves ahead of rogue waves in our data set was usually close to μ=0.5, which represents a typical value for regular first-order waves. Furthermore, it can be inferred that the radar devices measured slightly more asymmetric and steep waves than the wave buoys. The tendency of buoys to underestimate wave crests is recognized in the literature (Allender et al., 1989; Forristall, 2000).

4 Discussion

The comparison of rogue wave frequencies in our data set revealed that the radar stations usually identified more rogue waves during the measurement period than the wave buoys. Generally, all radar stations were located in the western part and all wave buoys in the eastern part of our analysis domain. By means of the available data set, it is therefore not possible to unambiguously assign these differences to either the use of different measurement devices or to the location of measurements in different regions. Generally, it is known that different wave measurement devices yield different results. Compared to other instruments, wave buoys tend to underestimate the statistics of the amplitude (Allender et al., 1989) and yield statistics below the Gaussian curve (Baschek and Imai, 2011). Possible explanations for these effects were given by Forristall (2000), who concluded that wave buoys may, on the one hand, be dragged through or slide away from (short) wave crests, which might result in missing the maximum amplitudes. On the other hand, these devices tend to cancel the second-order nonlinearities by their own Lagrangian movement and thus overestimate the mean water level, which in turn leads to an underestimation of crest heights (Forristall, 2000). Especially for steep waves which are strongly nonlinear, this leads to significant differences compared to fixed Eulerian sensors (Longuet-Higgins, 1986). In addition, it must be taken into account that wave buoys are moored and as such represent a part of a damped mechanical system. The influence of the anchoring is not clear to identify (Forristall, 2000). Radar systems looking down at the water surface, on the other hand, may overestimate crests by misinterpreting spray, breaking waves, or even fog (Grønlie, 2006). Forristall (2005) noted that there is no standard way to calibrate measurement instruments and that it is not possible to decide which instrument yields the “most correct” results. Moreover, differences may arise from different sampling frequencies. It is conceivable that wave buoys which measure at a lower sampling frequency than radar devices miss some of the wave maxima and minima. To test this, we subsampled the radar time series that were originally measured at 4 Hz with a frequency of 1 Hz, which is close to the buoy sampling frequency of 1.28 Hz. In this way, fewer rogue waves were detected than in the original time series. This was especially true for lower significant wave heights (and shorter periods) for which waves are described by fewer measurement points. This indicates that the differences in sampling frequencies can account for differences in the statistics obtained from wave buoys and radars. Because of these obvious differences that may arise from different sensors, we assume that at least large parts of the observed differences were likely caused by the different measurement techniques used. We can, however, not fully rule out that some differences in rogue wave frequencies between the different regions do exist. To address this issue, joint installations of wave buoys and radar devices at a location would be desirable.

While we assume that large parts of the observed differences in rogue wave frequencies might be attributed to the use of different sensors, there are some examples in the literature which indicate that rogue wave statistics may differ regionally, for example, due to different fetch, bathymetry, or proximity to the coast. Baschek and Imai (2011) found that rogue wave frequencies were not significantly different in deep and shallow water but were reduced in sheltered coastal oceans. Cattrell et al. (2018), on the other hand, reported that rogue wave frequencies were not spatially uniform and increased in coastal seas. In our case, there was one buoy (SEE) at which more rogue waves than expected from the Forristall distribution were identified. There are several options that may explain this behavior. These options need to be explored further. At first, the buoy is deployed at a rather shallow average water depth. This may lead to measurement issues as described above, in particular in the presence of breaking waves. Furthermore, the region is characterized by a strongly structured bathymetry with strong gradients and by strong tidal currents, both of which may contribute to a focusing of wave energy. In fact, SEE reveals very particular bathymetry conditions. Located close to the island of Norderney, the measurement buoy is placed directly above a sudden change in water depth. This stimulates shoaling and refraction leading to an increase in wave height (Goda, 2010). Trulsen et al. (2012) have shown experimentally that the propagation of waves over a slope from deep to shallow water may provoke a maximum in kurtosis and skewness. According to Trulsen et al. (2020), the behavior of waves propagating over a shoal is different in various depth regimes. Based on their findings, they anticipate a local maximum of rogue wave probability which would be in accordance with observations at SEE but would need further investigation to be fully confirmed.

We compared the relative wave height distribution in our data set to the Rayleigh and Forristall distributions. Waseda et al. (2011) found that the Forristall distribution fits well with storm wave records from the northern North Sea (190 m water depth) both when regarding the entire data set of 2723 records and when forming subsets along different significant wave heights. Over a range of sea states and from a large data set of 122 million waves in water depths between about 7 and 1311 m, Christou and Ewans (2014) found that the waves possess statistical characteristics in between linear and second-order theory. In our data, which were gathered in comparably shallow water, the distribution of wave heights in the total data set showed a fair agreement with the Forristall distribution up to a relative wave height $H{H}_{\mathrm{s}}^{-\mathrm{1}}\sim \mathrm{2}$. Rogue waves, and especially rogue waves with a very large relative wave height, occurred more often than expected from the Forristall distribution. Deviations from this distribution, however, varied across stations and between buoys and radar stations.

Our results may to some extent be affected by the choice to define a wave as the course of the sea surface elevation between two successive upcrossings or downcrossings. For rogue waves of moderate relative wave heights and wave steepness, numerical studies indicate no fundamental differences between rogue wave frequencies when upcrossing or downcrossing approaches were taken (e.g., Sergeeva and Slunyaev, 2013). However, for extreme rogue waves whose heights exceed 8σ in very steep wave conditions, numerical simulations suggested differences in frequencies when upcrossing or downcrossing definitions were used (Slunyaev et al., 2016). For in situ measurements, de Pinho et al. (2004) reported increased rogue wave frequencies when zero upcrossing approaches were taken.

Magnusson et al. (2003) reported deviations in the upper tail of the relative wave height distribution similar to the present study, although they find the statistics of their analyzed individual wave heights from buoy and laser data at 70 m water depth to be in agreement with Rayleigh and Weibull distributions. Forristall (2005) confirmed an underestimation of large individual wave heights by his distribution when single records were considered but could not find such behavior for larger amounts of data. He concluded that “a large wave which stands out as unusual in a short record may be expected if we look long enough. […] If we wait a long time, Gaussian statistics can produce a very large wave” (Forristall, 2005). In fact, Haver and Andersen (2000), who brought up the question of whether or not rogue waves can be considered part of a typical distribution, stated that a statistical approach based on empirical data may not be sufficient to address this question as empirical records typically contain too few rogue waves. Even in our large data set, there is only the small number of 21 cases in which relative wave heights exceeded a factor of $H{H}_{\mathrm{s}}^{-\mathrm{1}}\mathit{\gtrsim }\mathrm{3}$.

5 Conclusions

The 6 years of wave measurements from 11 measurement sites in the southern North Sea were quality controlled and analyzed for rogue wave occurrences and frequency. We found that rogue wave frequencies were relatively constant over seasons and uncorrelated between stations. We found that on average, the distribution of wave heights followed the Forristall distribution with some deviations in the upper tail, in particular for radar sites. However, deviations are based on estimates from a relatively small number of cases. While there appeared to be some differences in the wave height distribution in samples with and without rogue waves, differences were too small to be usable in rogue wave detection. Other properties such as wave steepness or wave asymmetry did not show substantial differences between samples containing a rogue wave or not. From the analyses of their data, Christou and Ewans (2014) suggested that rogue waves may simply represent rare realizations from typical distributions caused by dispersive focusing. Using a different data set, this conclusion is in principle supported by our analyses.