Extremeness of recent drought events in Switzerland: dependence on variable and return period choice

The 2018 drought event had severe ecological, economic, and social impacts. How extreme was it in Switzerland? We addressed this question by looking at different types of drought, including meteorological, hydrological, agricultural, and groundwater drought, and at the two characteristics deficit and deficit duration. The analysis consisted of three main steps: (1) event identification using a threshold-level approach, (2) drought frequency analysis, and (3) comparison of the 2018 event to the severe 2003 and 2015 events. In Step 2 the variables precipitation, discharge, soil moisture, and low-flow storage were first considered separately in a univariate frequency analysis; pairs of variables were then investigated jointly in a bivariate frequency analysis using a copula model for expressing the dependence between the two variables under consideration. Our results show that the 2018 event was especially severe in north-eastern Switzerland in terms of soil moisture, with return periods locally exceeding 100 years. Slightly longer return periods were estimated when discharge and soil moisture deficits were considered together. The return period estimates depended on the region, variable, and return period considered. A single answer to the question of how extreme the 2018 drought event was in Switzerland is therefore not possible – rather, it depends on the processes one is interested in.

1 Introduction

Drought events can have negative economic impacts on agriculture, energy production, river-borne transportation, and public water supply in addition to severe ecological and social impacts (Van Loon, 2015; Freire-González et al., 2017). Europe has experienced a number of hot and dry summers since the beginning of the 21st century (Hanel et al., 2018), including the years 2003, 2010, 2013, 2015, and 2018. Among these, the 2003, 2015, and 2018 events were especially severe in terms of precipitation deficits during the vegetation period (Hanel et al., 2018). In 2003, Europe was affected by a series of persistent heatwaves during summer. Even though this summer was not the driest on record, its impacts were considerable in vast areas of Europe with large losses in crop yield because of high evapotranspiration rates (Fink et al., 2004) and extremely low discharge levels. Similarly, the summer of 2015 was characterized by very high temperatures and a lack of precipitation in many parts of central and eastern Europe, resulting in high evapotranspiration rates and low river flows. In contrast to the 2003 event, the 2015 drought was more centred over eastern Europe (Ionita et al., 2017; Laaha et al., 2017).

The summer of 2018 was again hot and dry and had severe negative impacts. But how extreme was this recent event compared to the 2003 and 2015 events? This question is not straightforward to answer because drought events affect different parts of natural systems, which results in a diverse set of possible drought definitions (Yevjevich, 1967) ranging from meteorological and hydrological droughts to groundwater, agricultural, and socio-economic droughts (Mishra and Singh, 2010). Meteorological droughts are defined by a lack of precipitation over a period of time, while hydrological droughts are related to lower than normal discharge levels. Groundwater droughts are characterized by below-normal groundwater recharge levels, and agricultural droughts refer to periods with soil moisture deficits and associated losses in crop yield. Socio-economic droughts, finally, are associated with situations where water demand can not be fully met (Mishra and Singh, 2010). The primary cause of a drought is usually a lack of precipitation, which can lead to an agricultural drought, due to a depletion in soil moisture and/or to surface water deficits, and eventually to the development of a groundwater drought (Hisdal and Tallaksen, 2000). Haslinger et al. (2014) showed that there is a significant link between meteorological and hydrological droughts, except in catchments where groundwater storage and snow and glacier processes are important.

Drought assessments traditionally focused on one specific type of drought (Hannaford et al., 2010; Sen, 1998), expressed by rainfall or streamflow deficits, even though these different variables provide complementary information and different types of drought can deviate significantly in their statistical characteristics (Laaha et al., 2017). Therefore, studies started being designed to consider the joint occurrence of different types of drought. These more recent studies often included various standardized indices, such as the Palmer drought severity index (PDSI) (Palmer, 1965; Soulé, 1992), the standardized precipitation index (SPI) (McKee et al., 1993; Lloyd-Hughes and Saunders, 2002), the standardized precipitation evapotranspiration index (SPEI) (Vicente-Serrano et al., 2010), the standardized streamflow index (Peña-Gallardo et al., 2019), or the standardized snowmelt and rain index (SMRI) (Staudinger et al., 2014). An alternative to the use of standardized indices is the threshold approach where the start of an event is defined as the time when a time series falls below a certain threshold and the end of an event as the time the values exceed this threshold again (Yevjevich, 1967). This approach characterizes a drought by its duration, the interval during which the discharge is below a fixed threshold, and its severity, defined as the cumulative volume deficit below the given threshold. The advantage of this threshold level method compared to the indices mentioned above is that it can be applied to any drought type and the start and end of an event are explicitly defined, which means that the deficit volume and duration can be determined. These two characteristics, deficit and deficit duration, are important in terms of drought impacts. For aquatic ecosystems, the duration of a drought in streamflow is crucial, whereas for hydropower production the deficit volume is more relevant (Van Loon and Laaha, 2015).

Few studies have assessed drought severity in terms of both different variables, i.e. precipitation and discharge, and different characteristics, i.e. deficit and deficit duration. Wong et al. (2011) looked at the four variables precipitation, discharge, soil moisture, and groundwater, but only in terms of deficit duration using a simulated dataset for 121 catchments in Norway. Wong et al. (2013) investigated the dependence between meteorological and hydrological drought duration and severity, and they showed that areas which have a slower responding subsurface system give rise to stronger correlations between meteorological and hydrological characteristics. Vidal et al. (2010) looked at different drought characteristics (duration, magnitude, and severity) derived from standardized indices of precipitation, discharge, and soil moisture. They showed that the drought patterns identified depend on both the variable and the characteristic considered. However, they did not make any attempt to quantify the extremeness of events in terms of return periods. Van Loon et al. (2014) went in this direction by assessing the bivariate distribution of drought duration and standardized deficit for the variables precipitation, soil moisture, and discharge, which are often strongly correlated (Forzieri et al., 2014; Salvadori and Michele, 2015). However, they did not use these distributions to determine the rareness/extremeness of individual events. Such a frequency analysis requires, besides the determination of the distributions of the variables under consideration, the definition of a specific type of return period.

A first option to define return periods is to look at the drought in a univariate manner. Each of the variables under study, e.g. discharge deficit or precipitation deficit duration, is then considered individually in a univariate frequency analysis using the classical definition of a return period ($T=\mathrm{1}/p$, where p is the non-exceedance probability). A second option is the use of multivariate return periods, where different variables are jointly considered in a multivariate probabilistic framework (Salvadori and Michele, 2015; Brunner et al., 2016). Serinaldi (2016) highlighted that the return period computed for a certain event strongly depends on the choice of the type of return period chosen for the analysis. Univariate frequency analysis provides different information than multivariate analysis, which hinders the formation of a single set of conclusions on the rarity of an event. The choice of one type of frequency analysis over another should be made based on the problem at hand, which is not always straightforward to define because there is no consensus on which drought variable/characteristic best represents drought impacts for a given sector (Bachmair et al., 2016). For some sectors, a univariate analysis might be sufficient; e.g. discharge deficit is the main variable of interest for hydropower because it determines reservoir inflow. For other sectors, e.g. agriculture, where discharge is sometimes used for irrigation once soil water storage has been depleted, a bivariate assessment might be more informative. A univariate analysis enables the comparison of event extremeness in terms of individual variables, while the aim of a multivariate analysis is to provide a more comprehensive assessment of extremeness. If one chooses to work in a bi- or multivariate framework, one needs to understand and model the interdependence between individual variables, as well as their marginal distributions (Serinaldi, 2015).

In this study, the question “how extreme was the 2018 drought event in Switzerland compared to the 2003 and 2015 events?” was addressed, by looking at the four variables precipitation, discharge, soil moisture, and low-flow storage. For each of these variables, the two characteristics deficit and deficit duration were considered. This resulted in a set of eight drought variables considered in the analyses: (i) precipitation deficit duration, (ii) precipitation deficit, (iii) discharge deficit duration, (iv) discharge deficit, (v) soil moisture deficit duration, (vi) soil moisture deficit, (vii) low-flow storage deficit duration, and (viii) low-flow storage deficit. On the one hand, each variable was investigated individually to identify the variables most affected by the 2018 event. On the other hand, pairs of variables, which jointly affect certain sectors, were considered to get a more comprehensive estimate of the severity of the event. This combination of univariate and bivariate frequency analyses facilitated an integrative assessment of the severity of the 2018 event and how it compared to past events.

2 Study area

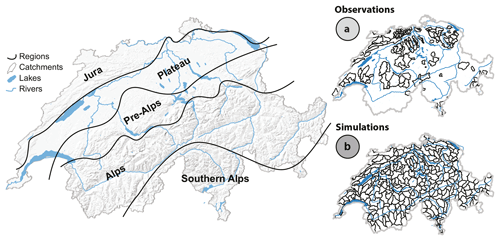
Switzerland is characterized by variable topography, with high elevations in the Alps and the Jura but low elevations in the Swiss Plateau region (Fig. 1), which is associated with diverse hydro-meteorological conditions. The Alps region is characterized by comparably high precipitation rates and therefore high discharge, while precipitation and discharge are lower in the Swiss Plateau region. Discharge varies not only spatially but also temporally depending on the hydrological regime type (Brunner et al., 2019b). The Alps have a melt-dominated regime with a winter low-flow season and a summer high-flow season. The Swiss Plateau, the Jura, and southern Switzerland have rainfall-dominated regimes with high flow in winter and low flow in summer. The Alps region is therefore mostly affected by winter droughts, while the remaining regions are affected by summer droughts.

Figure 1 Switzerland and its topographical regions: Jura, Swiss Plateau, Swiss Prealps, Alps, and southern Switzerland. (a) Dataset consisting of catchments with observed hydro-meteorological variables. (b) Dataset consisting of catchments with simulated hydro-meteorological variables.

3 Materials and methods

To assess the drought severity for the past three drought events (2003, 2015, and 2018) we used two datasets: (1) a dataset consisting of 137 catchments (Fig. 1a) for which observed precipitation and discharge time series were available and (2) a dataset consisting of 307 medium-sized catchments (Fig. 1b) for which discharge, soil moisture, and low-flow storage time series were simulated. The observed dataset was reliable because it was based on real time series. However, it was only available for precipitation and discharge and for a limited number of catchments without full spatial coverage. The simulated dataset extended the observed one with respect to the number of variables that could be considered and with respect to its spatial coverage. The analysis for each of the datasets consisted of three steps: (1) event identification using a threshold-level approach, (2) drought frequency analysis, and (3) comparison of the three events 2003, 2015, and 2018 (Fig. 2). The two datasets and the three steps of the analysis are described in Sect. 3.1–3.3.

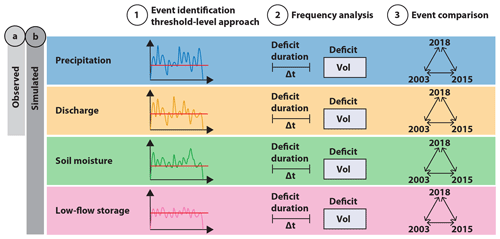
Figure 2 Drought severity assessment framework employed in this study. The severity of the 2003, 2015, and 2018 drought events was assessed in terms of precipitation and discharge using (a) observed and (b) simulated data and in terms of soil moisture and low-flow storage using only simulated data. The assessment consisted of three steps: (1) event identification using a threshold-level approach, (2) drought frequency analysis, and (3) comparison of the three events in 2003, 2015, and 2018.

3.1 Datasets

3.1.1 Observations

Observed daily discharge time series for the period 1989–2018 were available for 137 catchments in Switzerland that are only minimally influenced by humans (Fig. 1a). The dataset consisted of 78 stations operated by the Swiss Federal Office for the Environment (Federal Office for the Environment FOEN, 2009) and 59 stations operated by the cantons Aargau, Baselland, Bern, St. Gallen, and Zürich. The catchment selection covered a wide range of catchment characteristics and hydrological regime types. The catchments are small to medium-sized and situated between 400 and 2600 m a.s.l. The selection corresponds to a subset of the dataset used by Brunner et al. (2018a), where catchments with records of only 20 years were used (see Fig. 1 and Table 5 in Brunner et al., 2018a). The corresponding time series of areal precipitation were derived from the gridded precipitation product RhiresD provided by MeteoSwiss (2013).

Soil moisture and groundwater level data were not available for the same locations as discharge and precipitation data. An additional, simulated dataset was therefore considered.

3.1.2 Simulations

Discharge, soil moisture, and low-flow storage time series were simulated using the hydrological model PREVAH for 307 medium-sized catchments in Switzerland for the period 1981–2018 (Zappa and Brunner, 2019). This dataset extended the observed one in space and time and added the variables soil moisture and low-flow storage.

PREVAH is a conceptual process-based model consisting of several sub-models, which represent different parts of the hydrological system (Viviroli et al., 2009). These include interception storage, soil water storage and depletion by evapotranspiration, snow accumulation and melt, glacier melt, groundwater, discharge and baseflow generation, discharge concentration, and flow routing. PREVAH was chosen because it has been shown to reliably simulate the water balance of Switzerland (Zappa and Pfaundler, 2009; Speich et al., 2015). We used the same model setup as Brunner et al. (2019a), i.e. a gridded version of PREVAH at a spatial resolution of 500 m (Speich et al., 2015). The model was calibrated on runoff time series from 140 mesoscale catchments covering the different runoff regimes in Switzerland resulting in Nash–Sutcliffe efficiency values >0.7 for most catchments in both the calibration and validation periods (Köplin et al., 2010).

Table 1 Median of the observed (obs) and simulated (sim) distributions for precipitation deficit duration, precipitation deficit, discharge deficit duration, and discharge deficit for the catchments Massa–Blatten, Emme–Eggiwil, Schächen–Bürglen, Sitter–Appenzell, Ova dal Fuorn–Zernez, and Sorne–Delémont.

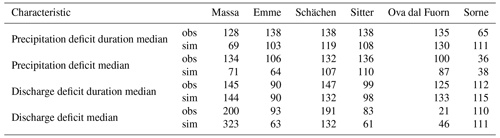
The calibrated and validated model was run with daily meteorological data including precipitation, temperature, relative humidity, shortwave radiation, and wind speed for the period 1981–2018, as interpolated from local station data using the tools presented in Viviroli et al. (2009). The model was evaluated regarding the reproduction of observed drought statistics for 6 of the 307 catchments distributed over the regions of Switzerland for which observed discharge time series were available: Massa–Blatten, Emme–Eggiwil, Schächen–Bürglen, Sitter–Appenzell, Ova dal Fuorn–Zernez, and Sorne–Delémont. The simulated time series were evaluated in terms of the drought characteristics deficit and deficit duration for meteorological and hydrological droughts (see Table 1 for the median of the distributions), and the return periods were estimated for the hydrological drought events in 2003, 2015, and 2018.

The correspondence between the return periods derived from the simulations and those derived from the observations was – with a mean absolute error of fewer than three events over all years and variables – satisfactory for the six catchments considered in the evaluation.

3.2 Event identification

We used the threshold-level approach (Yevjevich, 1967) on each of the variables considered with a fixed threshold at the 0.5 flow percentile of the variable of interest, to identify drought events within the observed and simulated time series. A fixed threshold was favoured over a variable threshold because we were interested in detecting the major summer drought events. The threshold for individual variables was set at the 0.5 percentile because this enabled the selection of one event per year on average, while lower percentiles identified too few events for a statistical analysis. The time series were smoothed over a window of 60 d prior to event extraction to limit the selection of dependent events and minor events (Tallaksen and Hisdal, 1997; Van Loon and Laaha, 2015). Independence of events was further ensured by prescribing a minimum event duration of 20 d. After the identification of events in the individual time series, joint events, i.e. events affecting all variables of interest, were identified (see Fig. 3 for an example). To do so, only the main events in years for which all variables fell below a threshold were retained; i.e. different events were detected in different catchments. This extraction procedure resulted in roughly 30 joint events per catchment. For each of the events, the drought deficit and deficit duration were determined as indices characterizing a drought event.

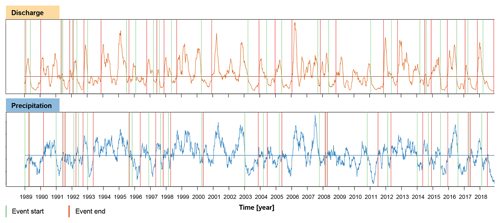
Figure 3 Extracted joint precipitation–discharge deficit events for the catchment Dünnern–Olten based on observed time series. The start of each joint event is indicated with a green line, and the end of each event with a red line. The thresholds (0.5 flow percentile) of the individual variables are indicated by horizontal lines.

3.3 Frequency analysis

The frequency analysis was performed on each of the variables individually and on pairs of variables jointly. The comparison of estimates derived by the univariate analysis on individual variables enabled a comparison of event severity in terms of different variables, while the bivariate analysis on two variables facilitated a joint assessment of the events' frequencies. A univariate analysis is relevant in the energy sector where discharge deficit is the main variable of interest because it determines reservoir inflow. In addition, such an analysis can be relevant in the transport sector where discharge deficit duration determines for how long river-borne transportation is inhibited. The univariate distributions of the drought deficits and deficit durations of the individual drought variables were heavily tailed. We therefore fitted the generalized extreme value (GEV) distribution using maximum likelihood estimation (Coles, 2001), which was not rejected at α=0.05 for most catchments according to the Anderson–Darling goodness-of-fit test (Chernobai et al., 2015).

To model the joint frequency for several variables, we focused on bivariate frequency analysis because our dataset was too small to allow for a multivariate (e.g. 4-D) analysis (Brunner et al., 2018b; Jiang et al., 2019). When conducting bivariate drought frequency analysis, a clear problem definition is essential because different definitions of bivariate return periods exist (Serinaldi, 2015). We applied the AND return period (Eq. 2), which uses the probability that two variables jointly exceed a threshold in a given event, e.g. where event deficit and deficit duration are both above a threshold (Brunner et al., 2016).

We focused on specific variable pairs which could be of interest in practice. First, we looked at the pair discharge deficit and discharge deficit duration, which are relevant for river ecology because both of these variables can affect ecosystem functioning. Second, we considered the pair discharge deficit and soil moisture deficit, which are relevant in agriculture because water for irrigation is sometimes extracted from rivers once water for plant growth is no longer available in the soil.

The bivariate frequencies of these variables were modelled using a copula model combined with the univariate marginals mentioned above. The copula approach to dependence modelling is rooted in a representation theorem proposed by Sklar (1959). He stated that the value of the joint cumulative distribution function F_XY of any pair (X,Y) of continuous random variables at (x,y) may be written in the form of

$$\begin{array}{}\text{(1)}& F_{XY}(x,y)=C\left[F_X\left(x\right),F_Y\left(y\right)\right]=C(u,v),x,y\mathit{ϵ}\mathbb{R},\end{array}$$

where F_X(x) denoted by u and F_Y(y) denoted by v are realizations of the marginal distributions of X and Y, whose dependence is modelled by a copula C. For a more detailed overview on copula theory, the reader is referred to Joe et al. (2015) and Genest and Favre (2007).

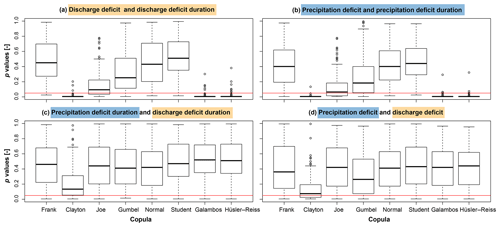
Figure 4 The p values determined by the bootstrap goodness-of-fit test for the eight copulas Frank, Clayton, Joe, Gumbel, Normal, Student's t, Galambos, and Hüsler–Reiss for the variable pairs (a) discharge deficit and discharge deficit duration, (b) precipitation deficit and precipitation deficit duration, (c) precipitation deficit duration and discharge deficit duration, and (d) precipitation deficit and discharge deficit. The red line indicates the 0.05 significance level.

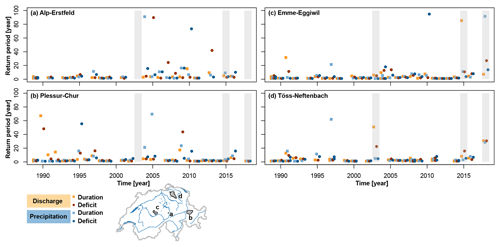
Figure 5 Univariate return periods of the extracted events within the period 1989–2018 for the alpine catchments Alp–Erstfeld (a) and Plessur–Chur (b) and for the catchments Emme–Eggiwil (c) in the Swiss Prealps, and Töss–Neftenbach (d) in the Swiss Plateau region, in terms of discharge deficit duration (orange squares), discharge deficit (red circles), precipitation deficit duration (blue squares), and precipitation deficit (blue circles). The grey polygons indicate the events in 2003, 2015, and 2018.

To choose an appropriate copula model, we looked at the dependence structure between the variable pairs available for the observed time series: (a) discharge deficit and discharge deficit duration, (b) precipitation deficit and precipitation deficit duration, (c) precipitation and discharge deficit duration, and (d) precipitation and discharge deficit. We tested several copulas from the Archimedean, elliptical, and extreme value families: Clayton, Joe, Frank, and Gumbel; normal and Student's t; Galambos and Hüsler–Reiss. The analysis of the dependence structure for the variable pairs mentioned above showed a strong general dependence and both upper and lower tail dependence. The correlation was strongest for the pairs (a) discharge deficit and discharge deficit duration and (b) precipitation deficit and precipitation deficit duration (Kendall's tau around 0.8) and was still visible for the pairs (c) precipitation and discharge deficit duration and (d) precipitation and discharge deficit (Kendall's tau around 0.2). The goodness-of-fit test (Fig. 4), which was based on a bootstrap procedure (Genest et al., 2009), rejected the Clayton, Galambos, and Hüsler–Reiss copulas in most catchments and the Joe copula in several catchments for the variable pairs discharge deficit and discharge deficit duration and precipitation deficit and precipitation deficit duration. In contrast, the Frank, Gumbel, Normal, and Student's t copulas were not rejected in most catchments at α=0.05. Due to the rather small sample size, the test could not make a further distinction between suitable and non-suitable copulas. According to the analysis of the dependence structure, however, the selected copula should be able to model both upper and lower tail dependence. We therefore selected the Student's t copula for modelling dependence because it was the only non-rejected copula that met this criterion. It is important to note, however, that it is only possible to model symmetric tail dependence with this copula (Favre et al., 2018).

The Student's t copula was used in combination with the GEV marginals to determine the bivariate distributions of the variable pairs of interest. These distributions were then used to compute the bivariate AND return periods T_AND for all joint events sampled. The AND return period is given by

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{T}_{\mathrm{AND}}(x,y)& ={\displaystyle \frac{\mathit{\mu }}{\mathrm{Pr}[X>x\wedge Y>y]}}\\ & ={\displaystyle \frac{\mathit{\mu }}{\mathrm{1}-F_X\left(x\right)-F_Y\left(y\right)+C(u,v)}},\end{array}\end{array}$$

where μ is the mean inter-arrival time between sampled drought events. The univariate and bivariate return periods derived for the events in 2003, 2015, and 2018 were compared in terms of their severity at individual stations and in terms of their spatial severity patterns.

4 Results

4.1 Observed time series

The univariate frequency analysis for discharge deficit and discharge deficit duration and precipitation deficit and precipitation deficit duration showed that the events in 2003, 2015, and 2018 differed in severity depending on the variable and on the catchment considered (see Fig. 5 for four example catchments). All three events were triggered by high temperatures and a precipitation deficit in summer. In the alpine catchments, e.g. Alp–Erstfeld (a) and Plessur–Chur (b), only the 2015 drought was identified as a joint event (discharge and precipitation). These catchments are characterized by melt-dominated discharge regimes, with a discharge deficit in winter rather than summer. In contrast, all three events were identified as joint events, e.g. for the Swiss Prealpine catchments Emme–Eggiwil (c) and Töss–Neftenbach, located in the Swiss Plateau region (d). In the catchment Emme–Eggiwil (c), the 2015 event was found to be most severe in terms of discharge deficit duration, while the 2018 event was most severe in terms of precipitation deficit duration and less so in terms of discharge due to large snowmelt contributions (Liechti et al., 2019). In the catchment Töss–Neftenbach (d), the 2003 event was severe in terms of discharge deficit duration, while the 2018 event showed similar return periods for all four variables considered.

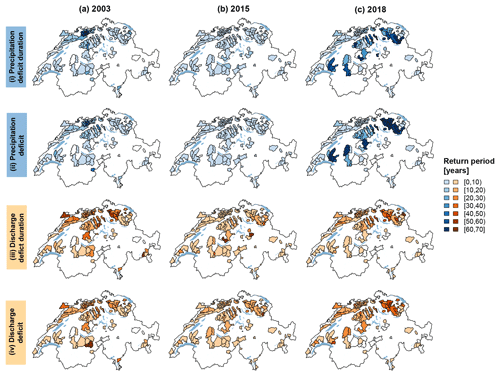
Figure 6 Univariate return periods for the three drought events in (a) 2003, (b) 2015, and (c) 2018 for the 137 catchments in the observed dataset for the variables (i) precipitation deficit duration, (ii) precipitation deficit, (iii) discharge deficit duration, and (iv) discharge deficit. Darker colours indicate longer estimated return periods. For catchments displayed in white, no joint events were extracted.

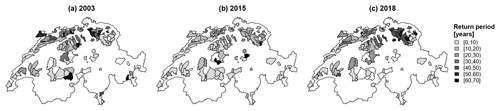
Figure 7 Bivariate AND return periods estimated for the drought events in (a) 2003, (b) 2015, and (c) 2018 for the 137 catchments in the observed dataset for the variable pair discharge deficit and discharge deficit duration. Darker shading indicates a longer return period. For catchments displayed in white, no joint events were extracted.

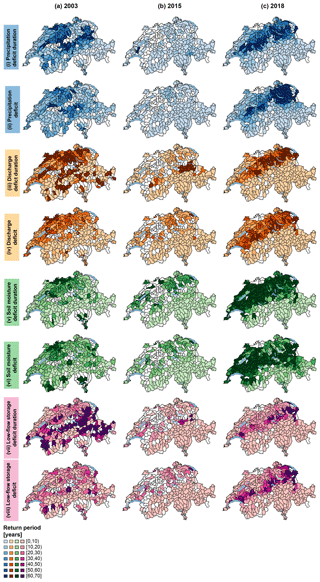
Figure 8 Univariate return periods estimated for the drought events in (a) 2003, (b) 2015, and (c) 2018 for the 307 catchments in the simulated dataset for the eight variables (i) precipitation deficit duration, (ii) precipitation deficit, (iii) discharge deficit duration, (iv) discharge deficit, (v) soil moisture deficit duration, (vi) soil moisture deficit, (vii) low-flow storage deficit duration, and (viii) low-flow storage deficit. For catchments displayed in white, no joint event for all variables was identified.

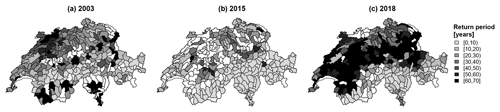
Figure 9 Estimated bivariate AND return periods in terms of discharge deficit and soil moisture deficits for the events in (a) 2003, (b) 2015, and (c) 2018 for the 307 catchments in the simulated dataset. For catchments displayed in white, no joint event for all variables was identified.

A comparison of the return period of the three events revealed spatial patterns in the severity of the four variables discharge deficit duration, discharge deficit, precipitation deficit duration, and precipitation deficit (Fig. 6). The 2003 event was most severe in northern Switzerland in terms of all four variables (return periods between 20 and 50 years), while the 2018 event was most severe in north-eastern Switzerland (return periods exceeding 70 years in some cases). In terms of precipitation deficit and precipitation deficit duration, the 2018 event was also severe in the Swiss Prealps, but not so much in terms of discharge because of the moderating effect of snowmelt. The 2015 event was estimated to be the least severe of the three events, with no specific region standing out as the most severely affected one (return periods around 10 years).

The same regions stood out when looking at the bivariate return periods estimated for the variable pair discharge deficit and discharge deficit duration (Fig. 7). Northern Switzerland was most affected by the 2003 event (return periods between 20 and 50 years), while north-eastern Switzerland was most affected by the 2018 event (return periods between 20 and 50 years). All catchments were similarly affected by the 2015 event (return periods around 10 years).

4.2 Simulated time series

The spatial patterns detected for the severity of the 2003, 2015, and 2018 events in the observed time series became even more apparent when the return periods derived using the simulated time series were considered (Fig. 8). As for the observations, the 2015 event was clearly the least severe in terms of all variables considered. Regarding precipitation deficit duration, the 2003 event was most severe in northern and central Switzerland and the 2018 event was most severe in the Swiss Prealps (return periods around 50–70 years). In terms of precipitation deficit, the 2003 event was slightly less severe than in terms of precipitation deficit duration and the 2018 event was most severe in north-eastern Switzerland with return periods of up to 80 years. The severity of the 2015 event was estimated to be much lower than that of the other two events, with no region affected more than the others. The discharge variables revealed similar severity patterns as the precipitation variables, with northern Switzerland most affected during the 2003 event and the Swiss Prealps and north-eastern Switzerland most affected by the 2018 event. Differences between the 2003 and 2018 events were even more apparent regarding the soil moisture conditions. The 2018 event led to very severe soil moisture deficits over a long period with return periods regionally exceeding 100 years, while the 2003 event hardly exceeded return periods of 30 years. In contrast, the 2003 event was estimated to have been more severe in terms of low-flow storage deficit duration, with return periods of up to 60 years compared to return periods hardly exceeding 15 years in 2015 and 2018. In short, the main area affected during the 2003 event was northern Switzerland, while the main areas affected during the 2018 event were north-eastern Switzerland and the Swiss Prealps. The variables most affected in 2003 were discharge and low-flow storage deficit duration, while soil moisture was most affected in 2018.

Spatial patterns found for the bivariate return periods computed for the variable pair discharge deficit and soil moisture deficit were similar to those found for the individual variables, which is important regarding agricultural water needs (Fig. 9). The 2003 event was rather severe in the Jura and southern Switzerland (return periods of up to 60 years) in terms of discharge deficit and soil moisture deficit, while large parts of the Swiss Plateau region and the Swiss Prealps were severely affected by the 2018 event (return periods of up to 100 years).

5 Discussion and conclusions

The analysis presented here combined the strengths of an observed and a simulated dataset, providing a comprehensive picture of the extremeness of past drought events across both space and variables. Our results showed that the extremeness of the 2003 and 2018 events differed between regions and between variables. This is not surprising, as meteorological and hydrological events have been shown to develop differently in space and time and in terms of extent and severity (Soulé, 1992; Laaha et al., 2017). Not all drought events were identified in melt-dominated regions because hardly any summer discharge deficits develop there, owing to sufficient melt contributions. Our findings further demonstrate that the use of univariate and bivariate analyses can lead to different severity estimates for individual catchments and divergent conclusions on the extremeness of individual events. This is not surprising since univariate and bivariate return periods provide different pieces of information (Serinaldi, 2016). The spatial patterns identified, however, were similar for different variables and return periods.

The results of the frequency analyses should be interpreted cautiously for several reasons. First, the record length only spans 30 to 40 years, which means that the number of drought events observed was limited. Second, the choice and fitting of the statistical models are associated with uncertainty (Brunner et al., 2018b). We used only univariate and bivariate analyses in order to reduce the negative effects of these uncertainty sources compared to an analysis in more dimensions, which would require the estimation of more parameters. For an analysis to be reliable considering all four variables jointly, a larger record period would be necessary (Jiang et al., 2019). Even if such a long record were available, the question would remain whether a multivariate return period covering the variables precipitation, discharge, soil moisture, and low-flow storage is relevant in practice. From a sectoral perspective, a univariate or bivariate analysis is probably sufficient in most cases. More research is needed to define relevant variables and variable combinations of interest for different sectors and stakeholders.

We conclude that the 2003 event was most severe in northern Switzerland, especially in terms of discharge, while the 2018 event was most extreme in north-eastern Switzerland in terms of soil moisture, with return periods of up to 100 years. The 2015 event was the least severe among the considered events for all the variables analysed and did not show distinct spatial patterns in severity. Our results demonstrate that the extremeness of an event is spatially variable and depends on the variable and the type of return period chosen. This means that the answer to the question “how extreme was the 2018 drought event?” depends on location, variable(s), and problem under consideration.