the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Evaluating the impact of model complexity on flood wave propagation and inundation extent with a hydrologic–hydrodynamic model coupling framework
Dirk Eilander
Hiroaki Ikeuchi
Fedor Baart
Hessel C. Winsemius
Fluvial flood events are a major threat to people and infrastructure. Typically, flood hazard is driven by hydrologic or river routing and floodplain flow processes. Since they are often simulated by different models, coupling these models may be a viable way to increase the integration of different physical drivers of simulated inundation estimates. To facilitate coupling different models and integrating across flood hazard processes, we here present GLOFRIM 2.0, a globally applicable framework for integrated hydrologic–hydrodynamic modelling. We then tested the hypothesis that smart model coupling can advance inundation modelling in the Amazon and Ganges basins. By means of GLOFRIM, we coupled the global hydrologic model PCR-GLOBWB with the hydrodynamic models CaMa-Flood and LISFLOOD-FP. Results show that replacing the kinematic wave approximation of the hydrologic model with the local inertia equation of CaMa-Flood greatly enhances accuracy of peak discharge simulations as expressed by an increase in the Nash–Sutcliffe efficiency (NSE) from 0.48 to 0.71. Flood maps obtained with LISFLOOD-FP improved representation of observed flood extent (critical success index C=0.46), compared to downscaled products of PCR-GLOBWB and CaMa-Flood (C=0.30 and C=0.25, respectively). Results confirm that model coupling can indeed be a viable way forward towards more integrated flood simulations. However, results also suggest that the accuracy of coupled models still largely depends on the model forcing. Hence, further efforts must be undertaken to improve the magnitude and timing of simulated runoff. In addition, flood risk is, particularly in delta areas, driven by coastal processes. A more holistic representation of flood processes in delta areas, for example by incorporating a tide and surge model, must therefore be a next development step of GLOFRIM, making even more physically robust estimates possible for adequate flood risk management practices.
- Article
(5619 KB) - Full-text XML
-
Supplement
(211 KB) - BibTeX
- EndNote
Globally, the number of exposed population and assets as well as casualties and economic damage due to flooding increased greatly in recent decades (Hirabayashi et al., 2013; Jongman et al., 2012; Ward et al., 2013; Winsemius et al., 2016). To better predict and understand current and future flood hazard as well as to plan mitigation and adaption measures, several numerical models, so-called global flood models (Trigg et al., 2016; Ward et al., 2015) were developed to provide current and future estimates.
Current global flood models, however, are tailor-made for certain applications and excel at, for instance, their representation of hydrologic processes, computationally efficient routing, or hydrodynamic surface flow processes. Depending on model structure and workflow, each model therefore has specific advantages and shortcomings. Also, there are marked differences between the spatial resolutions, affecting both the range of physical processes to be simulated and the applicability of model output maps (Beven et al., 2015; Bierkens et al., 2015).
Additionally, different physical processes may be governing at different spatial scales. For instance, 1-D hydrodynamics may be appropriate for large-scale or even global applications, explicitly modelling floodplain flow with 1-D and 2-D models can be vital for more local assessments. Depending on the envisaged application, modelling set-ups must thus be able to reflect the importance of various flood triggers by integrating across the relevant physical processes and spatial scales. Answering the question of how much complexity is needed can have benefits in avoiding not only under-fitting but also over-fitting of the problem (Neal et al., 2012b). For instance, applying higher-order approximations of the shallow water equations may be disproportionate for high-gradient regions where channel flow is the main physical process to consider while it is very much needed if inundation patterns in flat delta areas are simulated.
For simulating physical processes and hazards across spatial scales without adding just another new model, flexible computational frameworks are viable means as they can be designed depending on envisaged application. One example is the “plug-and-play” model coupling tool pyMT (Python Modeling Tool; https://csdms.colorado.edu/wiki/PyMT, last access: 23 July 2019) developed by the CSDMS (Community Surface Dynamics Modelling System; Syvitski et al., 2014), which, however, focusses on the whole range of Earth-surface models. By providing the flexibility to couple models depending on the application, fit-for-purpose coupled models can be created. For instance, one can address different processes that govern at different spatial (and temporal) resolutions by nesting local high-resolution 2-D models in large-scale 1-D models only where these processes are relevant. This is in contrast to other approaches aiming at combining floodplain runoff with river channel routing via predefined lateral inflows (Biancamaria et al., 2009; Felder et al., 2017; Lian et al., 2007).
To our knowledge, the development and application of flexible model coupling frameworks specifically designed for large-scale coupled hydrologic and hydrodynamic modelling is very limited. For example, GLOFRIM, a framework for integrated hydrologic–hydrodynamic modelling, was developed and applied recently (Hoch et al., 2017b, 2018). Both studies coupled the coarse-resolution global hydrologic model PCR-GLOBWB (Sutanudjaja et al., 2018) with the fine-resolution hydrodynamic models Delft3D Flexible Mesh (Kernkamp et al., 2011) and LISFLOOD-FP (Bates et al., 2010) set up for a fraction of the studied basin only. These studies showed that coupling hydrologic processes with more advanced hydrodynamic processes improves both representation of inundation along reaches as well as the simulation of flood wave propagation.
As the coupling framework was, however, still limited to large-scale hydrologic models and local 1-D–2-D hydrodynamic models covering the floodplains, flood-triggering processes outside the domain of the hydrodynamic models might be hampered because of the simplified routing still executed by the hydrologic models.
Adding a river routing component to the model coupling framework allows for potentially improved flood wave propagation throughout the entire domain (Zhao et al., 2017) and makes it possible to focus the computationally heavy 2-D hydrodynamics on even smaller domains. Consequently, it would be possible to create various coupled models with different levels of complexity depending which model and model types are combined for which fraction of the study area.
To assess whether and under which circumstances model coupling is beneficial for yielding improved discharge and inundation extent and how additional layers of complexity may benefit output accuracy, we tested different coupling designs of different complexity. Hence, the overarching research objectives of this study are to gain insights into the opportunities as well as challenges of (a) establishing a modular and flexible model coupling framework and (b) applying coupling configurations of different complexity to two case studies.
To this end, GLOFRIM was evolved by creating a more modular framework, extending the models contained, providing a plug-and-play tool allowing for spatially explicit coupling of hydrologic and hydrodynamic models. To enhance process and scale integration, we added the global river routing model CaMa-Flood (Yamazaki et al., 2011) to improve runoff routing over entire catchments. In addition, we added the wflow hydrologic modelling platform (Schellekens et al., 2019) to give the end-user a greater choice which hydrologic model to use and at which spatial resolution.
With its revised concept, we envisage two applications as the core of the new GLOFRIM 2.0 framework: (a) fast routing of runoff over large domains and (b) detailed local inundation modelling for smaller “spatially nested” areas such as river deltas. In addition, GLOFRIM can also be applied for benchmarking hydrologic and hydrodynamic models.
In the remainder of this article, we will first describe GLOFRIM and the models contained briefly. The benefit of applying a flexible model coupling framework for large-scale inundation modelling is then tested by two applications in the Amazon and Ganges–Brahmaputra basins. We conclude with recommendations and an outlook for future applications in integrated flood hazard modelling and assessment.
2.1 GLOFRIM 2.0
GLOFRIM 2.0 continues and extends the online and spatially explicit model coupling approach of the previously published framework GLOFRIM 1.0 (Hoch et al., 2017b). With GLOFRIM 1.0 it was possible to couple the global hydrologic model PCR-GLOBWB (Sutanudjaja et al., 2018) with the hydrodynamic models Delft3D Flexible Mesh (Kernkamp et al., 2011) and LISFLOOD-FP (Bates et al., 2010) by employing the Basic Model Interface (BMI; Peckham et al., 2013). In the new GLOFRIM version, the models CaMa-Flood (CMF; Yamazaki et al., 2011) and wflow (WFL; Schellekens et al., 2019) have been added. In its current version, GLOFRIM has been tested for one-way coupling only; that is, model output can be exchanged from one model to another but not interchangeably. While this is entirely sufficient for the presented showcases documenting the advances of GLOFRIM, the full potential of online coupling will only be tapped if two-way coupling is also fully supported.
For further information on the motivation, design, and technical implementation of the BMI itself and within GLOFRIM, we refer to the mentioned articles as well as the online documentations of the BMI (https://csdms.colorado.edu/wiki/BMI_Description, last access: 23 July 2019) and GLOFRIM (https://glofrim.readthedocs.io, last access: 23 July 2019).
We decided to employ the BMI concept since it is non-invasive, avoiding entanglement of code from different models. In addition, the coupling workflow and design can be designed flexibly and altered easily. Flexible coupling via interfaces allows for other models to be added to GLOFRIM once the BMI is implemented and homogenised with CSDSM BMI standards (https://bmi-spec.readthedocs.io/en/latest/, last access: 23 July 2019). The BMI standard was expanded by adding a step to the initialisation of the models. In this step, prior to the actual model initialisation, only the configuration is initialised, which allows for changing parameters of the individual models. Furthermore, a common time definition between all models was adopted. In addition to the BMI, a submodule was added which interprets the model grid type and spatial domain. Using this sub-module, a spatial index of the 2-D domain (and 1-D network if present) is constructed, which allows for straightforward spatially explicit coupling of models.
2.2 The supported models
Hereafter, the three models used for the two test cases are briefly outlined. For a complete overview of all five available models currently included in GLOFRIM as well as for a more detailed description of the models, we refer to the Supplement “GLOFRIM 2.0 and description of supported models”, the GLOFRIM online documentation, and the model-specific description papers.
2.2.1 PCR-GLOBWB
PCR-GLOBWB (PCR; Sutanudjaja et al., 2018) is a global hydrologic model solving the water balance for the entire global terrestrial surface at a daily time step. It is forced with meteorological data such as precipitation, evaporation, and temperature, which drive hydrologic processes in two vertically stacked soil layers as well as a bucket-type groundwater module. For all applications, we employed PCR at 30 arcmin spatial resolution, which is equivalent to around 50 km × 50 km at the Equator.
By default, resulting surface runoff can be routed solving the kinematic wave approximation. To allow for a fair comparison and at least minimum simplistic interaction between channel and floodplain volumes, the “DynRout” extension of PCR was used.
2.2.2 CaMa-Flood
CaMa-Flood (CMF; Yamazaki et al., 2011) simulates the floodplain hydrodynamics of continental-scale rivers globally employing an adaptive time stepping scheme. Since it solves the 1-D local inertial equation (Bates et al., 2010; Yamazaki et al., 2013) and only changes in water storage are prognosticated, simulations are computationally efficient. Another advantage is that CMF is a global model and therefore model data exist for the entire terrestrial surface, reducing the need to manually set up the model. Yet, this possibility is also provided in case more accurate local data are available. Output is provided at 0.25∘ spatial resolution, but inundation depth can be downscaled to 0.005∘ for more accurate assessments.
2.2.3 LISFLOOD-FP
LISFLOOD-FP (LFP; Bates et al., 2010) solves the local inertia equations for both channels and floodplains using a sub-grid channel scheme (Neal et al., 2012a) and adaptive time stepping, allowing for simulating flow not only in longitudinal but also lateral directions. By explicitly simulating floodplain flow, inundation dynamics such as velocity and duration as well as channel–floodplain interactions such as return flows can be captured.
LFP can be discretised at any spatial resolution but is typically employed for fine-resolution assessment of inundation dynamics. The required input data can be produced using common GIS programmes and do not require extensive pre-processing.
2.3 Possible coupling realisations
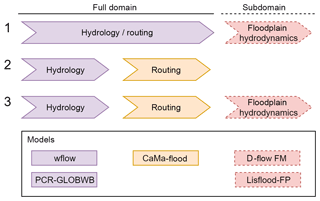
We envision GLOFRIM as a plug-and-play tool where the user can design the coupled model depending on required model complexity. With the increased number of models contained by GLOFRIM 2.0, the number of possible combinations increased too; see Fig. 1. We define three categories of models: (i) hydrologic models computing runoff from meteorological data (PCR and WFL; purple in Fig. 1); (ii) routing models focussing on simulating water transport along a 1-D river network (CMF; yellow in Fig. 1); and (iii) hydrodynamic models determining discharge for both 1-D river networks and 2-D floodplain areas (DFM and LFP; red in Fig. 1).
While combination (1) in Fig. 1 was already applied and assessed in previous work (see Hoch et al., 2017a, b), we merely focus on possibilities (2) and (3) in this study. To test the combinations, we designed two separate test cases to achieve the research objectives: while in test A we assess the opportunities and challenges for advancing the simulation of flood wave propagation by coupling large-scale hydrology with a routing model, test B aims at investigating the benefit of nesting a high-resolution 1-D–2-D hydrodynamic model into large-scale models for improved local inundation mapping.
3.1 Test A: improving large-scale routing and benchmarking hydrology
3.1.1 Model set-up
One possible application of GLOFRIM is routing hydrologic output over large distances, using more sophisticated flow solvers than implemented in global hydrologic models. To assess the value added, the routing scheme of CMF replaced the kinematic wave approximation as implemented in PCR-DynRout with the local inertia equations in the Amazon River basin. In addition to the more advanced solver, the channel network of CMF is resolved at a finer spatial resolution than PCR (Fig. 2).
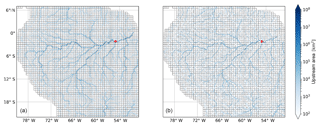
Figure 2The PCR drainage network (LDD) of the Amazon River basin at 30 arcmin spatial resolution (a) as well as the 1-D channel network of CMF (b). The upstream area of the drainage network is shown in shades of blue and the location of the Óbidos gauge in red.
Both CMF and PCR are models with global extent. Consequently, we did not have to create basin-specific discretisations but could use the already existing default model set-up after clipping to the needed extent. PCR contains only a Manning's roughness coefficient for channels which was set to 0.03 s m. The channel roughness coefficient of CMF was aligned with PCR, and the floodplain roughness coefficient was set to 0.10 s m. No a priori calibration was performed but roughness coefficients were selected merely based on previous model applications. For spatially explicit model coupling, simulated surface runoff per PCR cell was provided to CMF using BMI functions and subsequently interpolated within CMF using model-internal routines.
3.1.2 Model validation
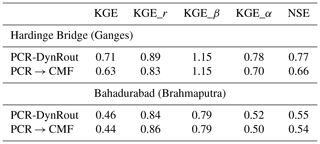
We separately ran PCR-DynRout and CMF coupled to PCR (PCR → CMF hereafter) for the period 2007 until 2009, preceded by 2 years of spin-up for both models. As a test basin we focussed on the Amazon River basin as it is characterised by pronounced flood wave propagation and long travel distance. To validate our runs and obtain information on a wide range of time series properties, we used observed discharge from ORE-HYBAM (http://www.ore-hybam.org/index.php/eng, last access: 23 July 2019) at Óbidos and calculated the total Kling–Gupta efficiency (KGE) and its individual components (linear correlation KGE_r, bias ratio KGE_β, and variability KGE_α) as well as the Nash–Sutcliffe Efficiency (NSE) for extra emphasis on peak flow simulations. For all time series analyses we used the hydroGOF package for R (Zambrano-Bigiarini, 2017). Also, we compared the average time difference between observed and simulated peak discharge (τ) by averaging the annual time gap between observed and simulated peak discharge.
3.1.3 Results and discussion
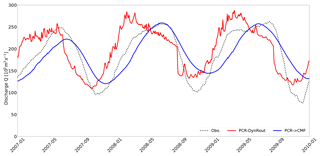
Results show that, although the identical runoff volumes are routed, obtained discharge estimates vary greatly, particularly with respect to the timing of peak discharge (Table 1) and the hydrograph smoothness (Fig. 3). In general, both set-ups have skill as expressed by both KGEs being greater than 0.7. While differences in total KGE are marginal, PCR-DynRout only shows better performance when assessing KGE_α, indicating that simulated variability represents observations better. PCR → CMF, in turn, is less biased (it is in fact not biased at all as indicated by a KGE_β of 1) compared to PCR-DynRout. The difference in KGE_β, indicating a difference in simulated flood volume of 6 % between the models, is to some extent caused by the coarse model resolution of PCR, which results in an overestimation of 1 % of the catchment area compared to CMF, which determines the catchment boundary at a sub-grid level. As a result, a greater volume is routed with PCR-DynRout than with the coupled CMF model. Quantifying the effect of other factors such as the role of evaporation and groundwater infiltration as simulated by PCR-DynRout but not PCR → CMF was outside the scope of this study, yet previous work indicates that these hydrologic processes may impact both discharge volume and flood extent (Hoch et al., 2018).
Table 1Assessment of performance of PCR-DynRout and PCR → CMF runs at Óbidos; the bold values indicate better performance.

Also, the correlation KGE_r of PCR → CMF with observation is better than with PCR-DynRout, most likely due to the ruggedness of the hydrograph simulated by PCR-DynRout. This ruggedness, we suspect, stems from the faster response of the kinematic wave approximation in combination with the derived river slopes of PCR-DynRout compared to the local inertia approximation of CMF. In addition, the first-order routing and volume distribution scheme of PCR-DynRout may have impacted model results.
It is particularly the difference in NSE that is of interest for flood hazard modelling as this measure is most sensitive towards bias of peak discharge. Here, we see that the coupled model PCR → CMF greatly outperforms PCR-DynRout. This finding is in line with previous research showing that the kinematic wave approximation applied by most GHMs (global hydrologic models) is not suitable for peak flow simulations (Hoch et al., 2017a, b; Yamazaki et al., 2011; Zhao et al., 2017). Particularly for catchments with low gradients such as the Amazon River basin, the absence of local acceleration and advection terms results in lower peak discharge accuracy.
Related to this finding is that a marked difference can be found in the average time difference between simulated and observed peak discharge. While PCR-DynRout, on average, predicts peak discharge more than 2 months earlier than observed, adding the CMF routing reduces this to 4 d. As it is particularly the correct timing of peak discharge that is important for operational flood forecasting, results show that the higher model complexity of CMF with respect to river routing may be beneficial for more actionable model results.
3.2 Test B: the benefit of local floodplain hydrodynamics
Employing explicit floodplain flow solvers may be particularly essential for low-lying and flat delta areas, but not throughout the entire basin as runtimes would increase greatly. Thus, GLOFRIM allows for spatially nested modelling; that is, the local hydrodynamic model is embedded in the basin-wide hydrologic and routing models.
3.2.1 Model set-up
In test B, we assess the impact of adding hydrodynamic models for both the river routing as well as floodplain inundation processes. We compared three model coupling configurations with increasing complexity: PCR-DynRout, PCR → CMF (see configuration 2 in Fig. 1), and PCR → CMF → LFP (see configuration 3 in Fig. 1) for the Ganges–Brahmaputra basin. While PCR still provides the runoff forcing for CMF for the entire catchment, various boundary conditions apply for the hydrodynamic model; that is, upstream discharge from CMF, local runoff from CMF, and downstream water level dynamics as prescribed within LFP itself (in this case 0 m).
Similar to test A, we used the global default model set-ups of PCR and CMF and clipped them to the extent of the Ganges–Brahmaputra basin. What is different to test A is, however, that we had to perform a calibration of CMF floodplain roughness coefficients and channel depth due to initially insufficient accuracy of discharge by PCR → CMF. Therefore, we applied a Manning's coefficient of 0.03 s m for PCR as well as for both river and floodplains in CMF. Channel depth was also increased by changing the first factor from its default value 0.14 to 0.20 in the subsequent equation:
where B is channel depth (m) and Rup is the annual maximum of 30 d moving average of upstream runoff (m3 s−1).
For the LFP model, we made use of the underlying surface elevation and channel dimension raster data of CMF at 18 arcsec and created a LFP discretisation for a small domain at the river delta at identical spatial resolution (Fig. 4).
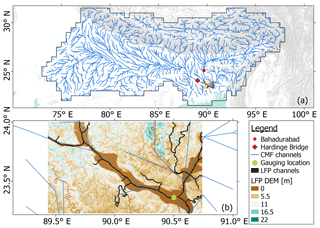
Figure 4(a) CMF channel network in the Ganges–Brahmaputra basin as well as locations of observation stations Hardinge Bridge and Bahadurabad for validating model output from both PCR and CMF; (b) zoom to LFP extent showing LFP DEM and channel network as well as gauging stations where output from PCR, CMF, and LFP is compared.
3.2.2 Model validation
To assess the quality of discharge simulations, we calculated the KGE and its components as well as the NSE based on simulated and observed values for two locations: Hardinge Bridge in the Ganges River and Bahadurabad in the Brahmaputra River (see Fig. 4). Observed values were kindly provided by the Institute of Water Modeling, Bangladesh, and the Bangladesh Water Development Board. As both locations lie outside the LFP domain, we could only validate the PCR-DynRout and PCR → CMF at those two locations and therefore had to perform a separate analysis of the PCR → CMF → LFP run. For this, we qualitatively compared the model results from all three model settings at a (arbitrarily chosen) location close to the river mouth (see Fig. 4), setting simulated discharge from all three set-ups into relation. In contrast to test A, we desisted from determining τ as there is more than one peak per flood season, which complicates an unambiguous analysis.
Additionally, the simulated inundation maps were compared with observed imagery. Therefore, PCR and CMF maps were first downscaled to a resolution of 1 km and 500 m, respectively, making use of their model-specific downscaling routines. As validation data, 8 d composite MODIS imagery of 2007 was used (see Kotera et al., 2016) as this year was characterised by strong monsoon-induced inundations (Islam et al., 2010).
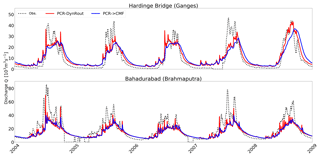
Figure 5Simulated discharge by PCR-DynRout and PCR → CMF as well as observed discharge at both Hardinge Bridge (Ganges) and Bahadurabad (Brahmaputra).
We compared simulated results from 18 August 2007, the day of maximum total flood extent in the CMF model, of all models with the corresponding 8 d composite MODIS image. The motivation for this approach was threefold: first, to not use LFP output as its output validation should be unaffected by previous decisions, second, because downscaled CMF output has a higher resolution than PCR, and third, to be able to assess differences in both timing and magnitude of simulated inundation extent. To guarantee comparability, maps of both observed and simulated flood extent were clipped to the LFP model domain and resampled to 500 m spatial resolution applying the nearest neighbour approach.
Inundation extent was validated for all set-ups following the approach of Fewtrell et al. (2008). Thereby, the hit rate H, the false alarm ratio F, and the critical success index C were determined for each inundation map with respect to observed MODIS extent. H, F, and C were computed with the subsequent equations where Nobs and Nsim indicate the number of inundated cells according to observations and the simulation result under consideration, respectively.
All parameters can vary between 0 and 1. While H=1 shows that all inundated cells in the benchmark data are also inundated in the comparison data, F=1 indicates that the inundated cells in the comparison are entirely false alarms with respect to the benchmark. The critical success rate C, in turn, should be 1 for perfect agreement, thereby penalising for both under- and overestimation.
3.2.3 Results and discussion
Simulated discharge
Validating discharge simulated by PCR-DynRout and PCR → CMF at Hardinge Bridge (Ganges River) and Bahadurabad (Brahmaputra River) shows slightly opposite behaviour than the previous test A. For both the Ganges and the Brahmaputra, PCR unexpectedly outperforms the coupled set-up, with results generally being more accurate for the Ganges River (Fig. 5, Table 2).
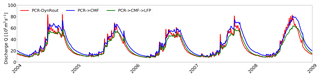
Figure 6Simulated discharge from PCR-DynRout, PCR → CMF, and PCR → CMF → LFP at the common observation point as depicted in Fig. 4.

Figure 7(a) Observed flood extent by MODIS; overlay of observed and modelled flood extent for (b) downscaled PCR, (c) downscaled PCR → CMF, and (d) PCR → CMF → LFP where blue indicates model only, red indicates observation only, and green indicates agreement between model and observations.
Table 2Assessment of performance of PCR, PCR → CMF, and PCR → CMF → LFP runs at both Hardinge Bridge (Ganges) and Bahadurabad (Brahmaputra); the coloured boxes indicate best performance compared to other set-ups.
These results show that added models with higher complexity do not always yield actually better results, as in this case the local inertia equations solved by CMF did not outperform the kinematic wave approximation of PCR. The local inertial equation is derived by neglecting only the advection term in the shallow water equations as advection is insignificant for many natural river and floodplain flow conditions with low gradients (de Almeida and Bates, 2013; Hunter et al., 2007; Yamazaki et al., 2013). The kinematic wave approximation, however, only accounts for channel and friction slope. While the reduced physics are less impacting for high-gradient areas, such as mountainous areas, or areas with clearly incised river channels, the Ganges–Brahmaputra basin is characterised by its large and flat floodplains. From a theoretical point of view, models applying the local inertia equations should therefore outperform simpler routing schemes in this study area. Yet, this is not the case and thus points to one of the key structural challenges with such cascading one-directional model coupling: while the most advanced hydrodynamic schemes can be added, the overall model accuracy still depends greatly on model data and parameter uncertainties, calibration, and both the meteorological and hydrologic forcing. Recent research showed, for instance, that the meteorological data set used can be a key control of discharge accuracy (Towner et al., 2019). Note also that PCR-DynRout and CMF use different topography and river bathymetry data as well as different river network concepts (i.e. flexible location of waterways (FLOW; Yamazaki et al., 2009) in CMF compared to eight directions toward neighbouring cells (D8) in PCR DynRout) to derive the routing schematisation. The differences in modelled discharge can therefore not only be attributed to the difference in approximation of the shallow water equations.
Benchmarking simulated discharge from PCR, PCR → CMF, and PCR → CMF → LFP corroborates that including 2-D floodplain flow processes reduced the volume routed along the main river channel whereas the timing of peak discharge does not deviate markedly between the coupled set-ups (Fig. 6). In combination with the simulated flood extent of PCR → CMF → LFP (Fig. 7d), the difference in discharge rate in the main channel can be attributed to the additional flow through a smaller side channel, which is only possible if 2-D flow is explicitly modelled. Even though no validation is possible due to the lack of observed data within the LFP domain, the already prevailing underestimation of discharge by PCR → CMF lets one speculate that PCR → CMF → LFP is less accurate in resembling discharge magnitude. Since CMF and LFP use the same underlying data for deriving river geometry and floodplain topography, we assume that model-internal input-data-independent factors result in the deviations between the CMF and LFP. At the current stage, unfortunately, an unambiguous explanation cannot be made yet as a further investigation exceeds the scope of this study.
Inundation extent
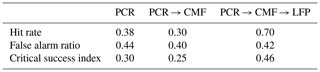
Simulating inundation maps can benefit greatly from adding 2-D hydrodynamic floodplain flow computations. Validating the downscaled inundation maps from PCR and PCR → CMF with the modelled results of PCR → CMF → LFP shows significant deviations between model set-ups (Fig. 7). In fact, results insinuate that acceptable representation of inundation patterns as expressed by the critical success index C can only be achieved by also accounting for floodplain flow and discharge through side channels (Table 3).
Table 3 furthermore shows that, despite having comparable false alarm ratios, the hit rate H is much higher for PCR → CMF → LFP and, in turn, so is the critical success index C. The differences in hit rate largely result from simulated inundations along smaller water bodies, especially compared to PCR → CMF, and from simulating the extent across the entire river floodplain, which is particularly not the case for PCR (Fig. 7). It is for those areas, which may not necessarily be directly adjacent to the main river stem, that downscaling procedures based on volume or water depth distribution curves may not suffice to represent the actual locally relevant flood-triggering processes, leading to a low hit rate.
It is interesting to see that PCR → CMF does not show any inundation for a part of the main river reach of the Ganges–Brahmaputra. This is the result of the combination of the unit catchment scheme used in CMF where different river reaches may have different geometry and the static downscaling approach. The deviations to PCR → CMF → LFP are hence a function of model-internal specifications as the underlying input data are identical. Consequently, this comparison hints at a positive impact of models with higher complexity explicitly modelling floodplain flow instead of downscaling, and that the threshold for LFP to predict excess channel volume may be lower than for CMF.
Despite all efforts to make the validation as fair as possible, there are still some limitations that must be kept in mind. For example, inundation patterns of the Ganges-Brahmaputra delta are largely affected by tide and surge dynamics (Ikeuchi et al., 2015). Since we discretised all models with a steady 0 m water level boundary, it must be acknowledged that a perfect fit between observations and simulations would not be possible. In addition, the downscaling routines of PCR and PCR → CMF employ different approaches and data, resulting in locally marked differences in results. Aligning the routines was, however, outside of the scope of this study. The arising issues of different inundation extent due to different model routines and data was already discussed by other studies and remains subject to ongoing debate on how to minimise the gap between models (Bernhofen et al., 2018; Hoch and Trigg, 2019; Trigg et al., 2016). Last, it is important to state that no calibration of the models with respect to simulated flood extent was performed. While this gives a fair picture of what a model is capable of under genuine conditions, the values presented here do not reflect that actual potential of each model.
We developed GLOFRIM 2.0, a globally applicable framework for integrated hydrologic–hydrodynamic modelling, to evaluate the added value of model coupling and applying models with varying complexity for discharge and flood extent simulations, testing it in two case studies. By combining hydrology and hydrodynamics in a plug-and-play way, it is possible to integrate across a suite of flood hazard drivers and design different coupled models, each having another level of varying complexity while maintaining identical spatially varying model forcing.
In this context, the main conclusions are as follows.
-
For discharge simulations, applying models with higher complexity is beneficial. By replacing the kinematic wave approximation with the local inertia equations, obtained results can be improved given the model schematisation and runoff forcing itself are accurate. Including more complex 1-D and 2-D hydrodynamic processes does not further improve discharge simulations compared to 1-D simulations.
-
For inundation extent simulations, employing a model capable of explicitly simulating floodplain flow and channel–floodplain interactions at a fine spatial resolution outperforms less complex models, particularly those using a downscaling approach. Using a 1-D or 2-D model can be of added value for those areas where no river network is present.
Results therefore suggest that including additional layers of complexity can indeed benefit model accuracy, yet this depends on the output variable under consideration. This means that for some applications opting for less complex model compositions suffices to obtain accurate results, possibly even at shorter runtimes.
In addition, the findings lead to several important conclusions concerning wider implications of coupling different models and model components.
-
(Re-)calibration of coupled model may be needed when replacing a native process from one model, for instance the kinematic wave routing in PCR, with the same process in another model, for instance routing based on the local inertia equations. While we did calibrate the Manning coefficient and channel depth parameters of CMF in the present study, new strategies for the calibration of coupled models might be required before yielding improved results.
-
Before full use can be made of adding models with higher complexity, it should be ensured that the model forcing (here runoff) is accurate. Wrongly timed runoff routed with simplistic routing schemes can still yield the right results for the wrong reasons; runoff simulated by hydrologic models needs to be validated before employing in a modelling cascade.
Our evaluation furthermore shows that including floodplain flow and discharge through secondary channels is paramount for accurately simulated inundation maps. Notwithstanding the best performance of this set-up, a critical success index of 0.46 indicates that only around half of the actual extent is correctly captured by the model, leaving much room for improvement. For example, a thorough analysis of the used DEM may help to reveal whether water is trapped in local depressions, hampering return flows and therefore increasing the flood extent unnecessarily. Possible problems could be solved by hydraulic conditioning (Yamazaki et al., 2012) or by updating the model data with the newly developed MERIT-DEM (Yamazaki et al., 2017). It is hence worth noting that in this study, we did not optimise the schematisations of the models involved for the sake of an untarnished evaluation of the impact of their complexity. Yet, GLOFRIM 2.0 can also be applied for more bespoke studies where optimised schematisations may be used, and thus overall evaluation scores will most likely increase strongly. Furthermore, as the river networks for CMF and PCR-DynRout are set up following a different conceptualisation, it was not possible to eliminate the effect of river schematisation from the shallow water equation approximation.
Despite the progress made in integrating various drivers of flood hazard, this is still limited to fluvial processes. Despite the predicted increase in fluvial flood hazard, most low-lying delta regions are under even greater threat from coastal flood events (Tessler et al., 2015; Visser et al., 2012). Additionally, compound events of simultaneous high discharge and high sea level will have to be included in future flood hazard estimates in many delta regions (Ikeuchi et al., 2017; Ward et al., 2018). Thus, it will be necessary to integrate fluvial and coastal flood hazard too. One avenue would be to use dynamic sea level boundaries. Another, more advanced, option would be to include surge and tide models into GLOFRIM such as the Global Tide and Surge Reanalysis product (Muis et al., 2016) once they are equipped with a Basic Model Interface. In addition to increasing the number of representable processes, future work will also focus on testing and further developing a two-way coupling scheme which would allow for more complex integrations and a mutual update of prognostic variables between models. By linking hydrologic, routing, and hydrodynamic models, we can establish a model cascade which can simulate the inundation-driving processes from the mountains to the coast. As such, GLOFRIM 2.0 can be a key tool for more holistic future modelling studies researching the effect of the interplay of meteorology and hydrology, river routing, and floodplain dynamics on flood hazard and risk. Being designed as a plug-and-play tool, flexible coupling frameworks could thus provide scientific evidence supporting decision-making and risk management for a wide range of conditions.
GLOFRIM 2.0 code is stored online and free to use, spread, and modify under the GNU GPL 3.0 license at https://doi.org/10.5281/zenodo.3364388 (Hoch et al., 2019). The model input data as well as schematisations and scripts used for the analysis can be found at https://doi.org/10.5281/zenodo.3346803 (Eilander and Hoch, 2019) under the MIT license. For further information regarding GLOFRIM v2.0 and the currently supported models, we refer to the relevant papers as well as to the supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/nhess-19-1723-2019-supplement.
We would like to acknowledge that this work has profited from equal contributions of JMH, DE, and HI. Thus, JMH, DE, and HI were all responsible for restructuring and adding code, performing test runs, and validating model results. FB and HI implemented the BMI adapters into CaMa-Flood while FB and JMH implemented them into LISFLOOD-FP. JMH and DE designed the updated workflow of GLOFRIM 2.0. All authors contributed to the paper.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Advances in computational modelling of natural hazards and geohazards”. It is a result of Geoprocesses, geohazards – CSDMS 2018, Boulder, USA, 22–24 May 2018.
We want to thank Willem van Verseveld and Mark Hegnauer (both Deltares) for the help with WFLOW as well as Rens van Beek and Edwin Sutanudjaja (both Utrecht University) for the help with PCR-GLOBWB. Observed river discharge data for the Ganges and Brahmaputra rivers were kindly provided by the Institute of Water Modeling, Bangladesh, and the Bangladesh Water Development Board.
Jannis M. Hoch was financed by the EIT Climate-KIC programme under project title “Global high-resolution database of current and future river flood hazard to support planning, adaption and re-insurance”. Dirk Eilander received funding from NWO VIDI (grant no. 016.161.324). Hiroaki Ikeuchi was financially supported by Japan Society for the Promotion of Science (JSPS) KAKENHI (grant no. JP16J07523.)
This paper was edited by Albert J. Kettner and reviewed by Guy J.-P. Schumann and one anonymous referee.
Bates, P. D., Horritt, M. S., and Fewtrell, T. J.: A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling, J. Hydrol., 387, 33–45, https://doi.org/10.1016/j.jhydrol.2010.03.027, 2010.
Bernhofen, M., Whyman, C., Trigg, M. A., Sleigh, P. A., Smith, A. M., Sampson, C. C., Yamazaki, D., Ward, P. J., Rudari, R., Pappenberger, F., Dottori, F., Salamon, P., and Winsemius, H. C.: A first collective validation of global fluvial flood models for major floods in Nigeria and Mozambique, Environ. Res. Lett., 13, 104007, https://doi.org/10.1088/1748-9326/aae014, 2018.
Beven, K., Cloke, H., Pappenberger, F., Lamb, R., and Hunter, N.: Hyperresolution information and hyperresolution ignorance in modelling the hydrology of the land surface, Sci. China Earth Sci., 58, 25–35, https://doi.org/10.1007/s11430-014-5003-4, 2015.
Biancamaria, S., Bates, P. D., Boone, A., and Mognard, N. M.: Large-scale coupled hydrologic and hydraulic modelling of the Ob river in Siberia, J. Hydrol., 379, 136–150, https://doi.org/10.1016/j.jhydrol.2009.09.054, 2009.
Bierkens, M. F. P., Bell, V. A., Burek, P., Chaney, N., Condon, L. E., David, C. H., de Roo, A., Döll, P., Drost, N., Famiglietti, J. S., M., Gochis, D. J., Houser, P., Hut, R., Keune, J., Kollet, S., Maxwell, R. M., Reager, J. T., Samaniego, L., Sudicky, E., Sutanudjaja, E. H., van de Giesen, N., Winsemius, H., and Wood, E. F.: Hyper-resolution global hydrological modelling: what is next: “Everywhere and locally relevant,” Hydrol. Process., 29, 310–320, https://doi.org/10.1002/hyp.10391, 2015.
de Almeida, G. A. M. and Bates, P.: Applicability of the local inertial approximation of the shallow water equations to flood modeling, Water Resour. Res., 49, 4833–4844, https://doi.org/10.1002/wrcr.20366, 2013.
Eilander, D. and Hoch, J.: DirkEilander/glofrim_v2.0-experiments: nhess publication release, https://doi.org/10.5281/zenodo.3346803, 2019.
Felder, G., Zischg, A., and Weingartner, R.: The effect of coupling hydrologic and hydrodynamic models on probable maximum flood estimation, J. Hydrol., 550, 157–165, https://doi.org/10.1016/j.jhydrol.2017.04.052, 2017.
Fewtrell, T. J., Bates, P. D., Horritt, M. S., and Hunter, N. M.: Evaluating the effect of scale in flood inundation modelling in urban environments, Hydrol. Process., 22, 5107–5118, https://doi.org/10.1002/hyp.7148, 2008.
Hirabayashi, Y., Mahendran, R., Koirala, S., Konoshima, L., Yamazaki, D., Watanabe, S., Kim, H., and Kanae, S.: Global flood risk under climate change, Nat. Clim. Change, 3, 816–821, https://doi.org/10.1038/nclimate1911, 2013.
Hoch, J. M. and Trigg, M. A.: Advancing global flood hazard simulations by improving comparability, benchmarking, and integration of global flood models, Environ. Res. Lett., 14, 034001, https://doi.org/10.1088/1748-9326/aaf3d3, 2019.
Hoch, J. M., Haag, A. V., van Dam, A., Winsemius, H. C., van Beek, L. P. H., and Bierkens, M. F. P.: Assessing the impact of hydrodynamics on large-scale flood wave propagation – a case study for the Amazon Basin, Hydrol. Earth Syst. Sci., 21, 117–132, https://doi.org/10.5194/hess-21-117-2017, 2017a.
Hoch, J. M., Neal, J. C., Baart, F., van Beek, R., Winsemius, H. C., Bates, P. D., and Bierkens, M. F. P.: GLOFRIM v1.0 – A globally applicable computational framework for integrated hydrological–hydrodynamic modelling, Geosci. Model Dev., 10, 3913–3929, https://doi.org/10.5194/gmd-10-3913-2017, 2017b.
Hoch, J. M., Van Beek, L. P. H., Winsemius, H. C., and Bierkens, M. F. P.: Benchmarking flexible meshes and regular grids for large-scale fluvial inundation modelling, Adv. Water Resour., 121, 350–360, https://doi.org/10.1016/j.advwatres.2018.09.003, 2018.
Hoch, J. M., Eilander, D., Ikeuchi, H., and Baart, F.: openearth/glofrim: NHESS article release, https://doi.org/10.5281/zenodo.3364388, 2019.
Hunter, N. M., Bates, P. D., Horritt, M. S., and Wilson, M. D.: Simple spatially-distributed models for predicting flood inundation: A review, Geomorphology, 90, 208–225, https://doi.org/10.1016/j.geomorph.2006.10.021, 2007.
Ikeuchi, H., Hirabayashi, Y., Yamazaki, D., Kiguchi, M., Koirala, S.,Nagano, T., Kotera, A., and Kanae, S.: Modeling complex flow dynamics of fluvial floods exacerbated by sea level rise in the Ganges–Brahmaputra–Meghna Delta, Environ. Res. Lett., 10, 124011, https://doi.org/10.1088/1748-9326/10/12/124011, 2015.
Ikeuchi, H., Hirabayashi, Y., Yamazaki, D., Muis, S., Ward, P. J., Winsemius, H. C., Verlaan, M., and Kanae, S.: Compound simulation of fluvial floods and storm surges in a global coupled river-coast flood model: Model development and its application to 2007 Cyclone Sidr in Bangladesh, J. Adv. Modeling Earth Syst., 9, 1847–1862, https://doi.org/10.1002/2017MS000943, 2017.
Islam, A. S., Haque, A., and Bala, S. K.: Hydrologic characteristics of floods in Ganges–Brahmaputra–Meghna (GBM) delta, Nat. Hazards, 54, 797–811, https://doi.org/10.1007/s11069-010-9504-y, 2010.
Jongman, B., Ward, P. J., and Aerts, J. C. J. H.: Global exposure to river and coastal flooding: Long term trends and changes, Global Environ. Change, 22, 823–835, https://doi.org/10.1016/j.gloenvcha.2012.07.004, 2012.
Kernkamp, H. W. J., Van Dam, A., Stelling, G. S., and de Goede, E. D.: Efficient scheme for the shallow water equations on unstructured grids with application to the Continental Shelf, Ocean Dynam., 61, 1175–1188, https://doi.org/10.1007/s10236-011-0423-6, 2011.
Kotera, A., Nagano, T., Hanittinan, P., and Koontanakulvong, S.: Assessing the degree of flood damage to rice crops in the Chao Phraya delta, Thailand, using MODIS satellite imaging, Paddy Water Environ., 14, 271–280, 2016.
Lian, Y., Chan, I.-C., Singh, J., Demissie, M., Knapp, V., and Xie, H.: Coupling of hydrologic and hydraulic models for the Illinois River Basin, J. Hydrol., 344, 210–222, https://doi.org/10.1016/j.jhydrol.2007.08.004, 2007.
Muis, S., Verlaan, M., Winsemius, H. C., Aerts, J. C. J. H., and Ward, P. J.: A global reanalysis of storm surges and extreme sea levels, Nat. Commun., 7, 11969, https://doi.org/10.1038/ncomms11969, 2016.
Neal, J., Schumann, G., and Bates, P.: A subgrid channel model for simulating river hydraulics and floodplain inundation over large and data sparse areas: Floodplain Inundation Over Large Areas, Water Resour. Res., 48, W11506, https://doi.org/10.1029/2012WR012514, 2012a.
Neal, J., Villanueva, I., Wright, N., Willis, T., Fewtrell, T., and Bates, P.: How much physical complexity is needed to model flood inundation?, Hydrol. Process., 26, 2264–2282, https://doi.org/10.1002/hyp.8339, 2012b.
Peckham, S. D., Hutton, E. W. H., and Norris, B.: A component-based approach to integrated modeling in the geosciences: The design of CSDMS, Comput. Geosci., 53, 3–12, https://doi.org/10.1016/j.cageo.2012.04.002, 2013.
Schellekens, J., Van Verseveld, W., Euser, T., Winsemius, H. C., Thiange, C., Bouaziz, L., Tollenaar, D., and De Vries, S.: openstreams/wflow: master-unstable, available at: https://github.com/openstreams/wflow, last access: 9 August 2019.
Sutanudjaja, E. H., van Beek, R., Wanders, N., Wada, Y., Bosmans, J. H. C., Drost, N., van der Ent, R. J., de Graaf, I. E. M., Hoch, J. M., de Jong, K., Karssenberg, D., López López, P., Peßenteiner, S., Schmitz, O., Straatsma, M. W., Vannametee, E., Wisser, D., and Bierkens, M. F. P.: PCR-GLOBWB 2: a 5 arcmin global hydrological and water resources model, Geosci. Model Dev., 11, 2429–2453, https://doi.org/10.5194/gmd-11-2429-2018, 2018.
Syvitski, J. P. M., Hutton, E. H., Piper, M., Overeem, I., Kettner, A., and Peckham, S. D.: Plug and play component modeling – the CSDMS 2.0 approach, in: Proceedings of the 7th Intl. Congress on Env. Modelling and Software, International Environmental Modelling and Software Society, San Diego, 2014.
Tessler, Z. D., Vörösmarty, C. J., Grossberg, M., Gladkova, I., Aizenman, H., Syvitski, J. P. M., and Foufoula-Georgiou, E.: Profiling risk and sustainability in coastal deltas of the world, Science, 349, 638–643, 2015.
Towner, J., Cloke, H. L., Zsoter, E., Flamig, Z., Hoch, J. M., Bazo, J., Coughlan de Perez, E., and Stephens, E. M.: Assessing the performance of global hydrological models for capturing peak river flows in the Amazon basin, Hydrol. Earth Syst. Sci., 23, 3057–3080, https://doi.org/10.5194/hess-23-3057-2019, 2019.
Trigg, M. A., Birch, C. E., Neal, J. C., Bates, P. D., Smith, A., Sampson, C. C., Yamazaki, D., Hirabayashi, Y., Pappenberger, F., Dutra, E., Ward, P. J., Winsemius, H. C., Salamon, P., Dottori, F., Rudari, R., Kappes, M. S., Simpson, A. L., Hadzilacos, G., and Fewtrell, T. J.: The credibility challenge for global fluvial flood risk analysis, Environ. Res. Lett., 11, 094014, https://doi.org/10.1088/1748-9326/11/9/094014, 2016.
Visser, H., Bouwman, A., Ligtvoet, W., and Petersen, A.: A statistical study of weather-related disasters: past, present and future, PBL Netherlands Environmental Assessment Agency, the Hague/Bilthoven, the Netherlands, 2012.
Ward, P. J., Jongman, B., Weiland, F. S., Bouwman, A., van Beek, R., Bierkens, M. F. P., Ligtvoet, W., and Winsemius, H. C.: Assessing flood risk at the global scale: model setup, results, and sensitivity, Environ. Res. Lett., 8, 044019, https://doi.org/10.1088/1748-9326/8/4/044019, 2013.
Ward, P. J., Jongman, B., Salamon, P., Simpson, A., Bates, P., De Groeve, T., Muis, S., de Perez, E. C., Rudari, R., Trigg, M. A., and Winsemius, H. C.: Usefulness and limitations of global flood risk models, Nat. Clim. Change, 5, 712–715, https://doi.org/10.1038/nclimate2742, 2015.
Ward, P. J., Couasnon, A., Eilander, D., Haigh, I. D., Hendry, A., Muis, S., Veldkamp, T. I. E., Winsemius, H. C., and Wahl, T.: Dependence between high sea-level and high river discharge increases flood hazard in global deltas and estuaries, Environ. Res. Lett., 13, 084012, https://doi.org/10.1088/1748-9326/aad400, 2018.
Winsemius, H. C., Aerts, J. C. J. H., van Beek, L. P. H., Bierkens, M. F. P., Bouwman, A., Jongman, B., Kwadijk, J. C. J., Ligtvoet, W., Lucas, P. L., van Vuuren, D. P., and Ward, P. J.: Global drivers of future river flood risk, Nat. Clim. Change, 6, 381–385, https://doi.org/10.1038/nclimate2893, 2016.
Yamazaki, D., Oki, T., and Kanae, S.: Deriving a global river network map and its sub-grid topographic characteristics from a fine-resolution flow direction map, Hydrol. Earth Syst. Sci., 13, 2241–2251, https://doi.org/10.5194/hess-13-2241-2009, 2009.
Yamazaki, D., Kanae, S., Kim, H., and Oki, T.: A physically based description of floodplain inundation dynamics in a global river routing model, Water Resour. Res., 47, W04501, https://doi.org/10.1029/2010WR009726, 2011.
Yamazaki, D., Baugh, C. A., Bates, P. D., Kanae, S., Alsdorf, D. E., and Oki, T.: Adjustment of a spaceborne DEM for use in floodplain hydrodynamic modeling, J. Hydrol., 436–437, 81–91, https://doi.org/10.1016/j.jhydrol.2012.02.045, 2012.
Yamazaki, D., de Almeida, G. A. M., and Bates, P. D.: Improving computational efficiency in global river models by implementing the local inertial flow equation and a vector-based river network map: Speeding Up Global River Model Simulations, Water Resour. Res., 49, 7221–7235, https://doi.org/10.1002/wrcr.20552, 2013.
Yamazaki, D., Ikeshima, D., Tawatari, R., Yamaguchi, T., O'Loughlin, F., Neal, J. C., Sampson, C. C., Kanae, S., and Bates, P. D.: A high-accuracy map of global terrain elevations: Accurate Global Terrain Elevation map, Geophys. Res. Lett., 44, 5844–5853, https://doi.org/10.1002/2017GL072874, 2017.
Zambrano-Bigiarini, M.: hydroGOF: Goodness-of-fit functions for comparison of simulated and observed hydrological time series, available at: https://github.com/hzambran/hydroGOF (last access: 9 August 2019), 2017.
Zhao, F., Veldkamp, T. I. E., Frieler, K., Schewe, J., Ostberg, S., Willner, S., Schauberger, B., Gosling, S. N., Schmied, H. M., Portmann, F. T., Leng, G., Huang, M., Liu, X., Tang, Q., Hanasaki, N., Biemans, H., Gerten, D., Satoh, Y., Pokhrel, Y., Stacke, T., Ciais, P., Chang, J., Ducharne, A., Guimberteau, M., Wada, Y., Kim, H., and Yamazaki, D.: The critical role of the routing scheme in simulating peak river discharge in global hydrological models, Environ. Res. Lett., 12, 075003, https://doi.org/10.1088/1748-9326/aa7250, 2017.