the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A review and upgrade of the lithospheric dynamics in context of the seismo-electromagnetic theory
Patricio Venegas-Aravena
Enrique G. Cordaro
David Laroze
This publication highlights theoretical work that could explain five different empirical observations indicating a direct relationship between magnetic fields and earthquakes, which would allow the description of a causal mechanism prior to and during the occurrence of earthquakes. These theoretical calculations seek to elucidate the role of the magnetic field in different aspects of solid Earth dynamics, with an interest in the study and comprehension of the physics that could generate earthquakes accompanied by simultaneous magnetic signals within the lithosphere. The motion of charged edge dislocations (MCD) model and its correlation with the magnetic field have been used in order to include the generation of electric currents. The electric currents resulting from stress variation in the lithosphere help us to analyze the lithosphere as a critical system, before and after the occurrence of earthquakes, by using the concept of earthquake entropy. Where it is found that the nonexistence of seismic and magnetic precursors could be interpreted as a violation of the second law of thermodynamics. In addition, the seismic moment and the moment magnitude of some great earthquakes are quite accurately calculated using the coseismic magnetic field. The distance-dependent coseismic magnetic field has been theorized for some of the largest recorded earthquakes. The frequency of oscillation of the Earth's magnetic field that could be associated with earthquakes is calculated and is consistent with the ultra-low-frequency (ULF) signals that some authors propose in the so-called “LAIC effect” (lithosphere–atmosphere–ionosphere coupling). Finally, the location and dimensions of the microcracks that explain some anomalous magnetic measurements are shown.
- Article
(4118 KB) - Full-text XML
- BibTeX
- EndNote
A number of investigations attempting to relate the magnetic field to seismic events have emerged over the past few years, (e.g., Park, 1996; Surkov et al., 2003; Johnston et al., 2006; Balasis and Mandea, 2007; Sgrigna et al., 2007; Saradjian and Akhoondzadeh, 2011; Varotsos et al., 2011; De Santis, 2014, 2017; Donner et al., 2015; Schekotov and Hayakawa, 2015; Daneshvar and Freund, 2017; Cordaro et al., 2018, 2019; Marchetti and Akhoondzadeh, 2018; Pulinets et al., 2018; among others). However, there is still no unified causal mechanism that is widely accepted and that may account for the physics of all these observations prior to or during the occurrence of an earthquake (Hough, 2010), although the laboratory evidence shows the possibility of an increase in the conductivity of rocks when subjected to stress changes, through either microcracks or chemical imperfections (Freund, 2003; Anastasiadis et al., 2004; Cartwright-Taylor et al., 2014). Therefore, this paper will attempt to explain the physics of magnetic observations recorded by different researchers accurately, organizing them in five categories.
-
Since the lithosphere can be considered a nonequilibrium system (De Santis et al., 2011), it is necessary to study any change in stress on rocks. The generation of current and magnetic field resulting from stress changes in rocks and their relationship with earthquakes has been shown empirically and theoretically by Vallianatos and Tzanis (2003), Anastasiadis et al. (2004), and Scoville et al. (2015), among others. This information is relevant, as any mechanism to be related to earthquakes should provide some connection with stress changes in the lithosphere. Many explanations have been offered about the generation of currents through stress changes in rocks, including the piezoelectric effect (Tuck et al., 1977), the presence of fluids in rocks through the so-called electrokinetic effect (Morgan et al., 1989) or chemical processes in rocks (Paudel et al., 2018). However, the generation of transient currents occurs in rocks either with or without the presence of water or liquids (Yoshida et al., 1998), in non-piezoelectric materials (Freund and Borucki, 1999), and in materials under nonelastic conditions (Triantis et al., 2012). Thus, a simple model for the study of current generation by stress changes is the so-called motion of charged edge dislocations (MCD), which consists of the movement of charges due to the generation of microcracks within a brittle and semi-brittle material similar to the crust that has undergone a stress change (Triantis et al., 2012). Once the physical mechanism that generates magnetism by stress changes has been found, it is essential to study the temporal evolution of the lithospheric system, which is referred to in group 2.
-
According to De Santis et al. (2011, 2014), the measurement of the temporal evolution of stress is achieved by measuring the “earthquake entropy” since the occurrence of an earthquake is an irreversible process comparable to a “critical system”, due to the irreversible change in the state of such a system, i.e., from a high-stress to a lower-stress lithosphere during an earthquake (De Santis et al., 2017). However, in order to correctly apply the stress configuration in an area of the lithosphere, it is necessary to know the “b-value” of Gutenberg–Richter's empirical law since according to Schorlemmer et al. (2005), this value can be interpreted as a type of inverse measure of stress and therefore the temporal evolution of the b-value could be related to the temporal evolution of stress and magnetic field through group 1.
-
Once the evolution of the stress has been determined according to the magnetic field, the calculation of the seismic moment and the moment magnitude of earthquakes will be carried out by using the coseismic magnetic field since, as stated by Utada et al. (2011), a possible coseismic magnetic variation of 0.8 nT was recorded at about 100 km from the Tohoku 2011 Mw 9.0 earthquake rupture area while Johnston et al. (2006) also reported changes in the magnetic field close to earthquake fault during the Parkfield 2004 M 6.0 earthquake. Furthermore, during the Loma Prieta 1989 Mw 7.1 earthquake coseismic changes in magnetic field were also reported possible (Karakeliana et al., 2002).
-
One of the most important groups of measurements corresponds to the recording of ultra-low-frequency (ULF) magnetic signals, i.e., frequencies below 1 Hz, as many researchers have found such anomalous frequencies prior to or during earthquakes, mainly close to millihertz and microhertz (Fenoglio et al., 1995; Sorokin and Pokhotelov, 2010; Schekotov and Hayakawa, 2015; De Santis et al., 2017; Cordaro et al., 2018, 2019; Marchetti and Akhoondzadeh, 2018; among others), although according to Vallianatos and Tzanis (2003) the magnetic field oscillation frequencies that could be related to earthquakes have a range of at least 3 orders of magnitude, so that kilohertz variations measured by other groups could also be included (Rozhnoi et al., 2008; Büyüksaraç et al., 2015; Potirakis et al., 2018a; among others).
-
A final aspect to consider is the origin of the possible magnetic variations studied. The great problem of the LAIC effect is the lack of certainty about the mechanism that generates currents towards the atmosphere and ionosphere. Some authors consider the currents to be of external origin to the lithosphere (e.g., Marchetti and Akhoondzadeh, 2018), while others suggest internal origin (e.g., Vallianatos and Tzanis, 2003). To avoid this lack of consensus, it is essential to be able to define the approximate place where the currents are created and to explain the measurements of all the research groups during non-coseismic times.
After the general description of each of these five topics, each theoretical framework is developed in Sects. 2, 3, 4, 5 and 6, maintaining the same order set out in this introduction. Finally, Sect. 7 summarizes the calculations and results obtained, and where the conclusions reached are presented.
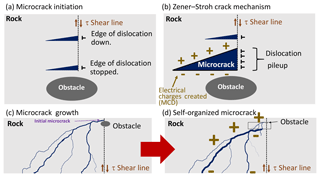
Figure 1Schematic description of the generation of microcracks and currents due to mechanical stresses on rocks. (a) A moving edge dislocation meets a barrier or obstacle. (b) A set of edge dislocations are piled up generating a microcrack (blue triangle). The microcracks generate the breaking of ionic bonds, which allows polarization of the microcracks. (c) Microcracks can propagate through different paths (blue lines). (d) An avalanche of microcracks can cause larger-scale cracks.
The Zener–Stroh mechanism explains the generation and propagation of microcracks within a solid as the pileup of edge dislocations at a certain location due to critical external mechanical stress or load (e.g., Stroh, 1955; Ma et al., 2011, and references therein). The movement of an edge dislocation stops when it encounters an obstacle or barrier within the solid (a scheme is shown in Fig. 1a). Other edge dislocations may also reach the obstacle and will begin to pile up if they cannot overcome that obstacle (Fig. 1b). This stacking will create a shear stress τ, which will create a microcrack (blue triangle in Fig. 1b) (e.g., Fan, 1994, and references therein). The microcracks can continue the propagation through different paths within the material (e.g., Xie and Sanderson, 1995) (blue lines in Fig. 1c). This will generate avalanches of cracks due to the nucleation of neighboring cracks, which will allow large-scale cracks (blue lines in Fig. 1d) (e.g., Main et al., 1993; Wang et al., 2015, and references therein).
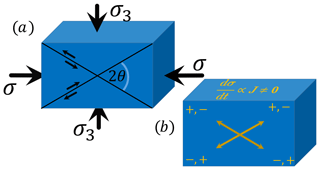
Figure 2Outline of the experiments carried out with rocks during compressive modes. (a) The change of effort σ generates one failure of the rock at an angle 2θ. The black arrows indicate the relative slip within the rock. (b) Electrification of the rock in microcracks zones close to the fault. The yellow arrows indicate the direction of the generated currents.
Conversely, the edge dislocations are electrically neutral in thermal equilibrium (Whitworth, 1975). However, the generation of microcracks is a dynamic process that breaks the ionic bonds that hold the solid together, so the microcracks will be accompanied by polarization and current density (e.g., Vallianatos and Tzanis, 1998). This phenomena is known as the motion of charged edge dislocations model (MCD model) (a scheme of polarization by the MCD model is shown in Fig. 1b, d). Several authors have shown that it is possible to detect electrification when a rock sample is compressed (pressure stimulating currents) uniaxially as shown in Fig. 2a (e.g., Stavrakas et al., 2004, and references therein). It is thought that the electrification is due to the MCD model and it can scale with the rock fracture (Fig. 1d) (e.g., Vallianatos and Triantis, 2008). According to Tzanis and Vallianatos (2002) the generation of a current density J within rocks can be represented as the temporal change in plastic deformation that rocks undergo under compressional stress changes with time (dσ∕dt) by
where ql is the linear charge density of edge dislocation, b is the Burgers vector module, and β varies between 1 and 1.5 and corresponds to the ratio (. Λ+ and Λ− represent dislocation number created by compression and uniaxial tension within a rock (Whitworth, 1975; Vaillianatos and Tzanis, 1998), and Yeff is the Young's effective module (Turcotte et al., 2003). Figure 2b is a schematic showing the direction of main currents J when the stress σ changes with time. The currents would tend to be parallel to the axes of fracture; however, the electrification of rocks can also propagate in other directions within the rock samples (Saltas et al., 2018) (Fig. 1d).
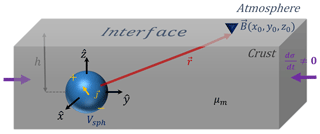
Figure 3Schematic magnetic field measured in an interface due to a polarized sphere of volume V embedded in a medium with magnetic permeability μm.
Conversely, Vallianatos and Tzanis (2003) model the magnetic field on the lithosphere surface as the magnetic field measured at the interface (with r and θ coordinates) of a conductive half-space (since the rocks could become (semi)conductive when they undergo stress changes Freund, 2003; Anastasiadis et al., 2004). Then, the magnetic field could be created by a polarized sphere embedded in this conductive medium (Griffiths, 1996; Vallianatos and Tzanis, 2003). A scheme can be seen in Fig. 3. According to Vallianatos and Tzanis (2003), the magnetic field on the surface of the lithosphere is determined by
where μm is the magnetic permeability of the medium (half-space), is the horizontal current density, r the distance to the sphere, and V the volume of the polarized sphere embedded in a medium. Equation (2) is valid for any source that generates polarization changes in the medium. According to Vallianatos and Tzanis (2003) if electric current is generated by microcracks then it has a volume lower than V. This can be seen from the scheme of Fig. 1d, where microcracks are represented by blue lines and do not cover the entire volume. The paths of these microcracks and their distribution are fractal in nature (e.g., Xie and Sanderson, 1995; Uritsky et al., 2004). According to Turcotte (1997), the fractal volume of all the microcracks within the medium can be represented by
where lmax is the radius of the largest microcracks, D is the rock fractal dimension, and SR is a factor defined by , where lmin is the radius of the smallest microcrack. It is assumed that the ratio is small, so SR≈1. The factor appears from the fractal integration of the microcrack. Where S is the largest fracture area. Therefore, the maximum magnetic field () is reached by replacing Eq. (3) in (2):
If J2 corresponds to the total current density J present in the half-space, then Eq. (1) may be replaced in Eq. (6):
The only amounts that are explicitly time-dependent are B and so that at the end, the temporal evolution of stress is proportional to the temporal integral of the magnetic field:
with , where k is in units of amperes per meter per second, or magnetization per seconds. Equation (6) shows that it is possible to use the magnetic field to measure the evolution of stress in laboratory rocks while k represents the geometric and mechanical properties of the source of electrification in laboratory rocks. If these experiments are correct, it would be expected that the magnetic field could reveal changes of stress on a geodynamic scale.
The seismicity of an area is statistically determined by Gutenberg–Richter's law on a geodynamic scale (Gutenberg and Richter, 1944). This law shows the number of earthquakes N with magnitude equal to or greater than M under the logarithmic relation: and where parameters a and b depend on each study area. Each earthquake is generated by a sudden release of energy that is not recovered, so the Gutenberg–Richter's law describes the occurrence of a set of irreversible events (e.g., Stein and Wysession, 2003). Since parameters a and b give information about the stress conditions in which these irreversible events occur, De Santis et al. (2011) developed the concept of earthquake entropy H based on Shannon entropy. Shannon's entropy measures the information of a system and its changes; however, the information of this system corresponds to the stress states of the lithosphere. In this way, the concept of earthquake entropy can be understood as the measure of the transition between different states of stress in the lithosphere. Using this, De Santis et al. (2011) found that the temporal variation in the b-value of Gutenberg–Richter's law is related to earthquake entropy H(t) through
where bmax=elog 10e, which is constant. As H(t) can be understood as the measure of lithospheric stress (De Santis et al., 2011), the earthquake entropy can be directly related to stress through H(t)≡k0σ(t), where k0 is in units of inverse stress. If the result shown by Eq. (6) is self-similar and is also applicable at geodynamic scale, it implies that the b-value of Gutenberg–Richter's law (Eq. 7) can be temporarily related to the magnetic field (Eq. 6) by means of
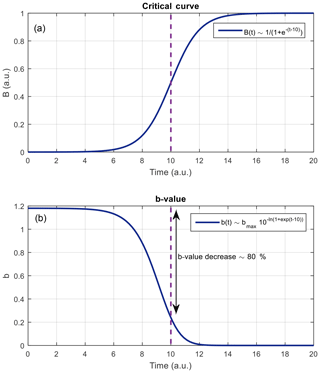
Conversely, De Santis et al. (2017) and Marchetti and Akhoondzadeh (2018) found that the daily accumulation of magnetic field anomalies before and after the Nepal 2015 Mw 7.8 and Mexico 2018 Mw 8.2 earthquakes had a behavior similar to that of a critical system so the shape of the magnetic field can be approximated to a sigmoid function: (Fig. 4a). The integral of the sigmoid is shaped , so by choosing k(Yeff)=1 and t0=10 in Eq. (8), it may show the b-value temporal evolution (Fig. 4b). In it, the b-value decreases before an earthquake, suggesting that there must be a change in the lithospheric regime (to an imminent collapse) because of increased seismicity prior to the occurrence of an earthquake, i.e., the existence of seismic or foreshock swarms (Schorlemmer et al., 2005; Ruiz and Madariaga, 2018). This is consistent with other research that suggests that a b-value decrease may serve as an earthquake predictor since a decreasing b-value means that earthquakes of higher magnitudes are required in order to satisfy the Gutenberg–Richter's law (Imoto, 1991; Kulhanek et al., 2018).
The area S that is implicit in the factor A in Eq. (4) is considered to calculate the coseismic magnetic relation Bcs with earthquakes since it may correspond to the rupture area (Turcotte, 1997):
By replacing Eq. (9) in the scalar seismic moment equation M0 (, where μ is the shear modulus and d the average slip) there is (Aki, 1966)
With the scalar seismic moment it is possible to calculate the moment magnitude scale Mw (, for M0 in newton meters, and where 107 is in reciprocal newton meters; Hanks and Kanamori, 1979). Then, according to the coseismic magnetic field the moment magnitude is
If we consider the fractal dimension of granite (D=2.6) (Turcotte, 1997) we have a more compact version of Eq. (11a):
Utada el al. (2011) reported a variation in Bcs=0.8 nT at a distance r of the order of 100 km from the fault plane during the 2011 Tohoku earthquake Mw 9.0 (Table 1). If we consider a minimum fracture of m (Shah, 2011), for granite N A−2 (Scott, 1983) and A m−2 (Tzanis and Vallianatos, 2002). In addition to the data provided by the USGS, km2, d=5.27 m and μ=57 GPa, where the moment magnitude calculated with the magnetic field must be
Conversely, Johnston et al. (2006) reported changes in the magnetic field at several stations fairly close to the Parkfield 2004 M 6.0 earthquake (Table 1). For instance, the station GDM (latitude: 35.8420; longitude: −120.3380) measured a variation in Bcs=0.3 nT at a distance r≈2.5 km from the fault. Using the general values μm, J2 and lmin and the earthquake information μ=30 GPa (Barbot et al., 2009), km2 (Kim and Dreger, 2008) and m, with Nm (Kim and Dreger, 2008). Moment magnitude calculated with the magnetic field is
The last example corresponds to the Loma Prieta 1989 M 7.1 earthquake (Table 1). During the earthquake, at a distance of r≈7 km (Corralitos station) a peak of 0.9 nT that excelled the intense (non-seismic) magnetic noise was measured (Fenoglio et al., 1995; Karakeliana et al., 2002; Thomas et al., 2009). Using the same values of this section μm, J2 and lmin and for this earthquake Bcs=0.9 nT, r≈7 km (Karakeliana et al., 2002), μ=30 GPa and km2 (Wallace and Wallace, 1993), and d=1.2 (Berkeley Seismology Lab), the moment magnitude calculated is
The results of Eqs. (12a), (12b) and (12c) are similar to the real one; therefore Eq. (11) is valid for the following analyses. The expected coseismic magnetic field can be obtained from Eq. (11b) in accordance with distance:
The factor is in newton meters. Keeping the same values of μm, J2 and lmin used so far, plus the data for the Tohoku 2011, Maule 2010, Sumatra 2004, Illapel 2015, Parkfield and Loma Prieta earthquakes (Table 1), the expected coseismic magnetic variation for these events can be observed in Fig. 5. This figure also shows that coseismic magnetic variations can reach hundreds of kilometers of radial distance from the rupture area. Even these variations can reach the ionosphere (48 km high from Earth's surface; https://www.nasa.gov/mission_pages/sunearth/science/atmosphere-layers2.html, last access: 29 July 2019), which could disturb the electron density within the ionosphere (Astafyeva et al., 2013; Kelley, 2017; Marchetti and Akhoondzadeh, 2018; Potirakis et al., 2018b). According to Kelley et al. (2017), it is possible to propagate a disturbance in the ionosphere if there is an electric field of the order of ∼0.5 mV m−1 at ∼90 km from the Earth's surface. This is nT in magnetic terms if we consider E=cB, with m s−1, the speed of light. Kelley et al. (2017) also claim that the electrical disturbance required at Earth's surface should be close to ∼0.2 V m−1 or ∼0.5 nT. Figure 5 shows that the conditions of nT at ∼90 km from the Earth's surface and ∼0.5 nT at Earth's surface (∼10–20 km from epicenter) are reached for all earthquakes studied with moment magnitude greater than ∼Mw 7. Therefore, ionospheric disturbances would not be expected for earthquakes with moment magnitudes less than ∼Mw 7.
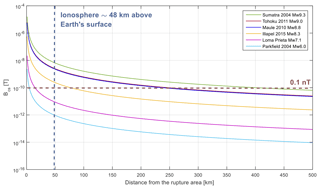
Figure 5Expected coseismic magnetic field as a function of distance for the Tohoku 2011, Maule 2010, Sumatra 2004, Illapel 2015 and Parkfield 2004 earthquakes (see Table 1 for earthquake information).
Table 1Earthquake data from Tohoku 2009 (USGS), Maule 2010 (Vigny et al., 2011; Yue et al., 2014), Sumatra 2004 (Menke et al., 2006), Illapel 2015 (Tilmann et al., 2016; Shrivastava et al., 2016), Parkfield 2004 (Kim and Dreger, 2008; Barbot et al., 2009) and Loma Prieta 1989 (Berkeley Seismology Lab; Wallace and Wallace, 1993).

After establishing the magnitude of the expected coseismic magnetic field, it is necessary to determine the order of magnitude of the oscillations present in the magnetic field. With this purpose, we consider that the current density is oscillating and can be expressed as a function of the polarization density as ; so using the above in Eq. (13) the following result is obtained:
where (Vallianatos and Tzanis, 1998), where the displacement of the fracture dx is normally comparable to the Burgers vector and has a typical value of m (Slifkin, 1993), a minimum excess dislocation m−2 in semiconductor materials (JAMS-CS, 1999) and the electrical charge line C m−1 (Slifkin, 1993). Considering m (Shah, 2011), N A−2 (Scott, 1983) and A m−2 (Tzanis and Vallianatos, 2002). Also, the data for the 2010 Tohoku earthquake from Table 1 and Bcs=0.8 nT and r=100 km (Utada el al., 2011), the frequency of the magnetic field oscillation associated with the 2011 Tohoku earthquake is of the order of 106 Hz; however, the coseismic displacement dx is not comparable to the Burgers vector but to the average displacement d; i.e., d m, so the magnetic field oscillation frequency is
Oscillations of the order of millihertz have been detected by De Santis et al. (2017), which is consistent with Eq. (15), although frequencies of the order of microhertz have been detected by Cordaro el at. (2018). However, according to Vallianatos and Tzanis (2003), the frequency of magnetic field oscillation associated with earthquakes is manifested in a range of at least 3 orders of magnitude, and this coincides with the measurements of Cordaro el at. (2018) (µHz) and De Santis et al. (2017) (mHz). The above information implies that in order to generate oscillation frequencies of the magnetic field in the pre-seismic stage similar to the coseismic frequencies, polarizations P0 and current densities J within the lithosphere should be similar to those found in the coseismic stage ( C m−2 and A m−2) and even these electrical conditions should be in some places of the lithosphere away from the fracture zone (main fault) (Scoville et al., 2015). Conversely, if the polarization is similar and the current density is lower, frequencies lower than those presented in Eq. (15) are obtained. For example, if the lithosphere polarization is maintained in the pre-earthquake stage and the current density decreases by 2 orders of magnitude (i.e., A m−2), it is possible to obtain frequencies of the order of the microhertz ( Hz), which means that according to Eq. (1), to create lower magnetic frequencies there must be a lower stress change.
However, Eq. (14) depends on lmax and corresponds to the maximum radius of the rupture area of an earthquake. This implies that at other times there will be a lower lmax and therefore higher frequencies. In addition, we must remember that lmax was calculated using the microcrack fractality. This means that lmax can have a large range of orders of magnitude. Therefore, the oscillation frequency of the magnetic field associated with earthquakes must also have a fractal nature. This fractal property in magnetic measurements had already been found by other researchers prior to the occurrence of earthquakes (e.g., Potirakis et al., 2017, and references therein).
Kelley et al. (2017) show that it is necessary to have close to 0.5 nT at Earth's surface in order to propagate a disturbance in the ionosphere. If we consider that Marchetti and Akhoondzadeh (2018) found anomalous behaviors in the magnetic field using satellites, it can be suggested that ∼0.1–0.5 nT is the magnetic variation created in the lithosphere prior to the occurrence of an earthquake. However, it is necessary to estimate the place in the lithosphere where these cracks might be occurring. It is also necessary to determine the order of magnitude of the microcrack dimensions within the lithosphere.
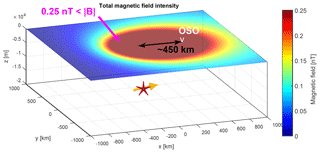
Figure 6Total magnetic field intensity at the Earth's surface using parameters of Table 2 and lmax≈300 m in Eqs. (3) and (16). The domain is km3. Values greater than 0.2 nT can be observed at the OSO station (close to 450 km from the future Maule earthquake). The red star shows the hypocenter of the future earthquake and the yellow arrow is the direction of the electric current J.
Cordaro et al. (2018) show disturbances in the magnetic field prior to the 2010 Maule earthquake (36∘17′24.0′′ S 73∘14′20.4′′ W). If we consider the OSO station (40∘20′24′′ S, 73∘05′24.0′′ W), we can note that it is ∼450 km from the epicenter of the 2010 Maule earthquake (the closest magnetic station to earthquake). As in this case we only want to calculate the orders of magnitude of the microcracks and their location, we will consider the general version of Eq. (2), which is shown in Eq. (16) (Griffiths, 1996; Vallianatos and Tazanis, 2003).
where V is the fractal volume defined in Eq. (3), x0 and y0 are the points near the surface of the lithosphere where the station is located, and h is the depth of the microcrack. This depth h corresponds to the semi-brittle–ductile transition and is between 10 and 20 km deep (Scholz, 2002; Sun, 2011). For these calculations we will consider that km. If we consider that the microcracks are occurring in the future earthquake rupture zone, in addition to the data in Table 2, it would imply that the microcracks would have dimensions of the order of ∼300 m to obtain more than ∼0.2 nT at ∼450 km. The result of using this microcrack length (300 m) and the data in Table 2 is shown in Fig. 6. Using the same values, we find that greater magnetic variations exist closer to the future seismic rupture zone. For example, within a radius of 100 km there are magnetic variations of 10 nT (white circle in Fig. 7), while within a radius of 10 km there would be variations of the order of 160 nT (magenta circle in Fig. 7). These variations have never been recorded; therefore microcracks cannot be of the order of hundreds of meters, but must be smaller. Neither can they come from the future seismic source.
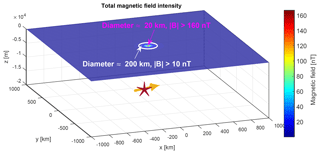
Figure 7Total magnetic field intensity at the Earth's surface using the same parameters of Fig. 6. However, in this figure we indicate the places where it is possible to find magnetic variations of 10 nT (white circle) and 160 nT (magenta circle). These variations have never been recorded.
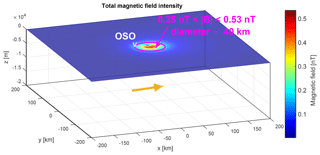
Figure 8Total magnetic field intensity at the Earth's surface using parameters of Table 2 and lmax≈30 m in Eqs. (3) and (16). The domain is km3. Values greater than 0.2 nT can be observed at the OSO station. The yellow arrow is the direction of the electric current J. This size of microcracks could be the one that allows us to explain the measurements of magnetic variations of Cordaro et al. (2018) and Marchetti and Akhoondzadeh (2018) and the suggestion of Kelley et al. (2017).
However, if we consider that microcracks are occurring near the stations, it is enough to take a ∼30 m to obtain magnetic variations similar to those suggested by Kelley et al. (2017) at Earth's surface. Figure 8 shows that with this configuration the measurements can be replicated. However, it is necessary that microcracks with lmax of the order of tens of meters occur in different places of the lithosphere.
This work studied the role of the magnetic field in the lithospheric dynamics, specifically, the physics that could be associated with various measurements that relate magnetic fields and earthquakes in a complete cycle, i.e., from a stress disturbance to the magnetic frequencies correlated with the occurrence of an earthquake. The results of each section are below.
Since a change in stress could trigger an earthquake, Sect. 2 discussed the way a change in stress causes fractures within the rocks, the flow of electrical currents and the generation of magnetic fields. Therefore, the goal of this section was to achieve a relationship (Eq. 6) between the temporal evolution of stress with the integral over time of the magnetic field through a constant k. It was also possible to store all the electrical and mechanical information of the rocks in the constant k, which represents the magnetization per second of the rocks.
The goal of Sect. 3 is of great relevance since it established a relationship between the behavior of the magnetic field (critical system) and a b-value decrease in the Gutenberg–Richter law before and after the occurrence of earthquakes through the earthquake entropy concept (Eq. 8 and Fig. 4). This was possible by assuming that the behavior of laboratory samples would exhibit the same physics as lithospheric rocks. Another goal of this section was to obtain a more physical interpretation about the entropy of earthquakes, their relation with magnetism and the impending earthquakes: as entropy can be considered as the energy diffusion of a system, the accumulation of stress (energy) in the lithosphere (open system) must be diffused. This means that the increment in the number of magnetic anomalies and their relationship with an increase in seismicity (earthquake swarms and/or seismic precursors) prior to the occurrence of large earthquakes are part of the energy diffusion mechanisms. However, this may also be interpreted inversely: the nonexistence of seismic and magnetic precursors could violate the second law of thermodynamics. However, more studies are needed to corroborate whether the emission of magnetic signals really has any relationship with the entropy of earthquakes.
The great goal of Sect. 4 was to find and corroborate an analytical relationship between coseismic magnetic measurements and the magnitude of earthquakes (Eqs. 11a, 11b). It was possible to obtain Eqs. (11a) and (11b) by considering the area of rupture of the earthquake as a crack of the MCD model. Another goal of this section was to find an analytical relationship that would allow us to determine the magnitude of coseismic magnetic signals as a function of the epicentral distance (Eq. 13). Figure 5 shows the intensity of the expected coseismic magnetic variation for several earthquakes as a function of the distance to the area of rupture. It is observed that magnetic variations can easily reach the ionosphere for earthquakes of magnitudes greater than Mw 8.3 (dashed blue line). Many magnetometers have the resolution of 0.1 nT (dashed red line) so magnetic variations produced by large earthquakes (∼Mw 9) could be detectable by magnetometers several hundred kilometers from the area of rupture. However, it is not expected that the magnetometers can detect magnetic variations related to small earthquakes, i.e., magnitudes much lower than Mw 8.0 and tens of kilometers from the source. For instance, during the L'Aquila 2009 M 6.1 earthquake (central Italy), large magnetic variations were reported associated with displacements of the instruments due to seismic waves (0.8 nT) at 6.7 km away from the source of the earthquake (Nenovski, 2015; Masci and Thomas, 2016). However, using r≈6.7 km (Nenovski, 2015), Mw=6.1, Pa , d=0.4 m, and km2 (Walters et al., 2009) and the same values of μm, J2 and lmin used in Sect. 5 in Eq. (13) the expected coseismic magnetic field is Bcs≈0.04 nT, which is quite close to the instrumental noise of the L'Aquila station (0.02 nT) (Villante et al., 2010), making these magnetic coseismic variations almost undetectable.
The goal of Sect. 5 was to theoretically find the oscillation frequencies of the magnetic field that may be related to the occurrence of earthquakes. They were found to have frequencies of the order of millihertz. The existence of frequencies of different orders of magnitude and the fractal nature of oscillations prior to earthquakes were also analyzed. It is concluded that for there to be magnetic variations in the lithosphere prior to earthquakes it is necessary that the conditions of polarization and density of currents are similar to those that can be found in the coseismic stage. All these magnetic variations are part of the ULF reported by several authors.
Section 6 looked for the location of the microcracks and their size. It was found that microcracks are unlikely to be created in the future seismic rupture zone. However, if microcracks of the order of 30 m exist at depths of 10–20 km, it is possible to explain the expected magnetic variations (∼0.2 nT). This implies that microcracks must be occurring throughout the lithosphere due to a change in the stress field.
Conversely, the physics of the coseismic stage (Sect. 4) and the stage prior to earthquakes (Sect. 6) could be the same: microcracks, where the only difference comes from the size of lmax. This is relevant since in the future it will be necessary to investigate microcracks as a factor that allows propagation of seismic fractures. In addition, it will also be necessary to study the distribution of microcracks throughout the lithosphere. This would allow estimation of the places where it is more likely to find magnetic variations as well as possible future earthquakes.
Finally, it can be concluded that the controversial magnetic phenomena registered by different research groups, behavior of cumulative daily number of magnetic anomalies, coseismic magnetic field and oscillation frequencies of the magnetic field can all have the same and unique physical origin: the cracking of brittle and semi-brittle materials of the crust due to stress changes. However, there is still no clarity about how these stress changes can generate the nucleation of earthquakes. Therefore, future studies should focus on interpreting magnetic records as a tool to measure stress changes in the lithosphere, especially when there are no appreciable deformations of the lithosphere. This could provide new information to seismic source studies.
All the data are open source and can be found using the references that are listed in the text. The numerical data can be easily generated by everyone using the equations and indications of the text. If you have any problems, do not hesitate to write and ask the authors.
PVA conceived the theoretical derivation and numerical implementation. PVA also performed the initial paper writing and created the figures. EGC and DL carried out the writing corrections and generated the scientific view, background and support.
The authors declare that they have no conflict of interest.
Patricio Venegas-Aravena acknowledges Patricia Aravena, Alejandro Venegas, Patricia Venegas and Richard Sandoval for outstanding support to carry out this work, and Valeria Becerra-Carreño for her scientific support.
This research has been partially supported by Centers of Excellence with BASAL/CONICYT (grant no. FB0807, CEDENNA).
This paper was edited by Filippos Vallianatos and reviewed by Angelo De Santis and Michael E. Contadakis.
Aki, K.: Generation and propagation of G waves from the Niigata earthquake of June 14, 1964. Part 2. Estimation of earthquake moment, released energy and stress-strain drop from G wave spectrum, Bulletin of the Earthquake Research Institute, 44, 73–88, 1966.
Anastasiadis, C., Triantis, D., Stavrakas, I., and Vallianatos, F.: Pressure Stimulated Currents (PSC) in marble samples, Ann. Geophys., 47, 21–28, 2004.
Astafyeva, E., Shalimov, S., Olshanskaya, E., and Lognonné, P.: Ionospheric response to earthquakes of different magnitudes: Larger quakes perturb the ionosphere stronger and longer, Geophys. Res. Lett., 40, 1675–1681, https://doi.org/10.1002/grl.50398, 2013.
Balasis, G. and Mandea, M.: Can electromagnetic disturbances related to the recent great earthquakes be detected by satellite magnetometers?, Tectonophysics, 431, 173–195, 2007.
Barbot, S., Fialko, Y., and Bock, Y.: Postseismic deformation due to the Mw 6.0 2004 Parkfield earthquake: Stress-driven creep on a fault with spatially variable rate-and-state friction parameters, J. Geophys. Res., 114, B07405, https://doi.org/10.1029/2008JB005748, 2009.
Büyüksaraç, A., Pınar, A., and Koşaroğlu, S.: Precursory Anomaly in VLF/LF Recordings Prior to the Çaglayan (Erzincan-Turkey) Earthquake on July 30th, 2009, Bitlis Eren Univ. J. Sci. & Technol., 5, 18–23, 2015.
Cartwright-Taylor, A., Vallianatos, F., and Sammonds, P.: Superstatistical view of stress-induced electric current fluctuations in rocks, Physica A, 414, 368–377, 2014.
Cordaro, E. G., Venegas, P., and Laroze, D.: Latitudinal variation rate of geomagnetic cutoff rigidity in the active Chilean convergent margin, Ann. Geophys., 36, 275–285, https://doi.org/10.5194/angeo-36-275-2018, 2018.
Cordaro, E. G., Venegas-Aravena, P., and Laroze, D.: Variations of geomagnetic cutoff rigidity in the southern hemisphere close to 70∘ W (South-Atlantic Anomaly and Antarctic zones) in the period 1975–2010, Adv. Space Res., 63, 2290–2299, https://doi.org/10.1016/j.asr.2018.12.019, 2019.
Daneshvar, M. R. M. and Freund, F. T.: Remote Sensing of Atmospheric and Ionospheric Signals Prior to the Mw 8.3 Illapel Earthquake, Chile 2015, Pure Appl. Geophys., 174, 11–45, https://doi.org/10.1007/s00024-016-1366-0, 2017.
De Santis, A.: Geosystemics, Entropy and Criticality of Earthquakes: A Vision of Our Planet and a Key of Access, in: Nonlinear Phenomena in Complex Systems: From Nano to Macro Scale, edited by: Matrasulov, D. and Stanley, H., NATO Science for Peace and Security Series C: Environmental Security, Springer, Dordrecht, https://doi.org/10.1007/978-94-017-8704-8_1, 2014.
De Santis, A., Cianchini, G., Favali, P., Beranzoli, L., and Boschi, E.: The Gutenberg–Richter Law and Entropy of Earthquakes: Two Case Studies in Central Italy, B. Seismol. Soc. Am., 101, 1386–1395, https://doi.org/10.1785/0120090390, 2011.
De Santis, A., Balasis, G., Pavón-Carrasco, F. J., Cianchini, G., and Mandea, M.: Potential earthquake precursory pattern from space: The 2015 Nepal event as seen by magnetic Swarm satellites, Earth Planet. Sc. Lett., 461, 119–126, https://doi.org/10.1016/j.epsl.2016.12.037, 2017.
Donner, R. V., Potirakis, S. M., Balasis, G., Eftaxias, K., and Kurths, J.: Temporal correlation patterns in pre-seismic electromagnetic emissions reveal distinct complexity profiles prior to major earthquakes, Phys. Chem. Earth, 85–86, 44–55, 2015.
Fan, H.: Interfacial Zener-Stroh Crack, J. Appl. Mech., 61, 829–834, https://doi.org/10.1115/1.2901564, 1994.
Fenoglio, M. A., Johnston, M. J. S., and Byedee, J.: Magnetic and electric fields associated with changes in high pore pressure in fault zones: application to the Loma Prieta ULF emissions, J. Geophys. Res., 100, 12951–12958, 1995.
Freund, F.: Rocks That Crackle and Sparkle and Glow: Strange Pre-Earthquake Phenomena, Journal of Scientic Exploration, 17, 37–71, 2003.
Freund, F. and Borucki, J. G.: Charge carrier generation and charge cloud propagation following 100 m/sec impacts on igneous rocks, in: Atmospheric and Ionospheric Electromagnetic Phenomena Associated with Earthquakes, edited by: Hayakawa, M., Terra Scientific Publishing Co., Tokyo, 839–857, 1999.
Griffiths, D. J.: Electrodynamics, 2nd Edition, Prentice Hall, 218–223, 1996.
Gutenberg, B. and Richter, C. F.: Frequency of earthquakes in California, B. Seismol. Soc. Am., 34, 185–188, 1944.
Hanks, T. C. and Kanamori, H.: A moment magnitude scale, J. Geophys. Res., 84, 2348–2350, https://doi.org/10.1029/JB084iB05p02348, 1979.
Hough, S.: Predicting the unpredictable, the tumultuous science of earthquake prediction, Published by Princeton University Press, 41 William Street, Princeton, New Jersey 08540, ISBN 978-0-691-13816-9, 2010.
Imoto, M.: Changes in the magnitude–frequency b-value prior to large (M ≥6.0) earthquakes in Japan, Tectonophysics, 193, 311–325, 1991.
JAMS-CS (Japan Manufacturer's Society of Compound Semiconductor Materials): EPD measurements for low dislocation density GaAs and InP substrates, III-Vs Review, 12, 32–37, https://doi.org/10.1016/S0961-1290(00)86710-1, 1999.
Johnston, M. J. S., Sasai, Y., Egbert, G. D., and Mueller, R. J.: Seismomagnetic Effects from the Long-Awaited 28 September 2004 M 6.0 Parkfield Earthquake, B. Seismol. Soc. Am., 96, S206–S220, https://doi.org/10.1785/0120050810, 2006.
Karakeliana, D., Klemperera, S. L., Fraser-Smith, A. C., and Thompson, G. A.: Ultra-low frequency electromagnetic measurements associated with the 1998 Mw 5.1 San Juan Bautista, California earthquake and implications for mechanisms of electromagnetic earthquake precursors, Tectonophysics, 359, 65–79, 2002.
Kelley, M. C., Swartz, W. E., and Heki, K.: Apparent ionospheric total electron content variations prior to major earthquakes due to electric fields created by tectonic stresses, J. Geophys. Res.-Space, 122, 6689–6695, https://doi.org/10.1002/2016ja023601, 2017.
Kim, A. and Dreger, D. S.: Rupture process of the 2004 Parkfield earthquake from near-fault seismic waveform and geodetic records, J. Geophys. Res., 113, B07308, https://doi.org/10.1029/2007JB005115, 2008.
Kulhanek, O., Persson, L., and Nuannin, P.: Variations of b-values preceding large earthquakes in the shallow subduction zones of Cocos and Nazca plates, J. S. Am. Earth Sci., 82, 207–214, 2018.
Ma, L., Zhao, J., and Ni, B.: A Zener-Stroh crack interacting with an edge dislocation, Theoretical and Applied Mechanics Letters, 2, 021003, https://doi.org/10.1063/2.1102103, 2011.
Main, I. G., Sammonds, P. R., and Meredith, P. G.: Application of a modified Griffith criterion to the evolution of fractal damage during compressional rock failure, Geophys. J. Int., 115, 367–380, 1993.
Marchetti, D. and Akhoondzadeh, M.: Analysis of Swarm satellites data showing seismo-ionospheric anomalies around the time of the strong Mexico (Mw=8.2) earthquake of 08 September 2017, Adv. Space Res., 62, 614–623, https://doi.org/10.1016/j.asr.2018.04.043, 2018.
Masci, F. and Thomas, J. N.: Evidence of underground electric current generation during the 2009 L'Aquila earthquake: Real or instrumental?, Geophys. Res. Lett., 43, 6153–6161, https://doi.org/10.1002/2016GL069759, 2016.
Menke, W., Abend, H., Bach, D., Newman, K., and Levin, V.: Review of the source characteristics of the Great Sumatra–Andaman Islands earthquake of 2004, Surv. Geophys., 27, 603–613, 2006.
Morgan, F. D., Williams, E. R., and Madden, T. R.: Streaming potential properties of Westerly granite with applications, J. Geophys. Res., 94, 12449–12461, 1989.
Nenovski, P.: Experimental evidence of electrification processes during the 2009 L'Aquila earthquake main shock, Geophys. Res. Lett., 42, 7476–7482, https://doi.org/10.1002/2015GL065126, 2015.
Park, S. K.: Precursors to earthquakes: Seismoelectromagnetic signals, Surv. Geophys., 17, 493–516, 1996.
Paudel, S. R., Banjara, S. P., Wagle, A., and Freund, F. T.: Earthquake chemical precursors in groundwater: a review, J. Seismol., 22, 1293–1314, https://doi.org/10.1007/s10950-018-9739-8, 2018.
Potirakis, S. M., Hayakawa, M., and Schekotov, A.: Fractal analysis of the ground-recorded ULF magnetic fields prior to the 11 March 2011 Tohoku earthquake (MW=9): discriminating possible earthquake precursors from space-sourced disturbances, Nat. Hazards, 85, 59–86, https://doi.org/10.1007/s11069-016-2558-8, 2017.
Potirakis, S. M., Contoyiannis, Y., Asano, T., and Hayakawa, M.: Intermittency-induced criticality in the lower ionosphere prior to the 2016 Kumamoto earthquakes as embedded in the VLF propagation data observed at multiple stations, Tectonophysics, 722, 422–431, 2018a.
Potirakis, S. M., Asano, T., and Hayakawa, M.: Criticality Analysis of the Lower Ionosphere Perturbations Prior to the 2016 Kumamoto (Japan) Earthquakes as Based on VLF Electromagnetic Wave Propagation Data Observed at Multiple Stations, Entropy, 20, 199, https://doi.org/10.3390/e20030199, 2018b.
Pulinets, S., Ouzounov, D., and Davidenko, D.: The possibility of earthquake forecasting: learning from nature, Geophysical Research Abstracts, Vol. 20, EGU2018-9191, EGU General Assembly, 2018.
Rozhnoi, A., Solovieva, M., Molchanov, O., Akentieva, O., Berthelier, J. J., Parrot, M., Biagi, P. F., and Hayakawa, M.: Statistical correlation of spectral broadening in VLF transmitter signal and low-frequency ionospheric turbulence from observation on DEMETER satellite, Nat. Hazards Earth Syst. Sci., 8, 1105–1111, https://doi.org/10.5194/nhess-8-1105-2008, 2008.
Ruiz, S. and Madariaga, R.: Historical and recent large megathrust earthquakes in Chile, Tectonophysics, 733, 37–56, 2018.
Saltas, V., Vallianatos, F., Triantis, D., and Stavrakas, I.: Complexity in Laboratory Seismology, Complexity of Seismic Time Series, 239–273, 2018.
Saradjian, M. R. and Akhoondzadeh, M.: Prediction of the date, magnitude and affected area of impending strong earthquakes using integration of multi precursors earthquake parameters, Nat. Hazards Earth Syst. Sci., 11, 1109–1119, https://doi.org/10.5194/nhess-11-1109-2011, 2011.
Schekotov, A. and Hayakawa, M.: Seismo-meteo-electromagnetic phenomena observed during a 5-year interval around the 2011 Tohoku earthquake, Phys. Chem. Earth, 85–86, 167–173, https://doi.org/10.1016/j.pce.2015.01.010, 2015.
Scholz, C. H.: The Mechanics of Earthquakes and Faulting, 2nd edition, Cambridge University Press, ISBN 978-0-521-65540-8, 2002.
Schorlemmer, D., Wiemer, S., and Wyss, M.: Variations in earthquake size distribution across different stress regimes, Nature, 437, 539–542, 2005.
Scott, J. H.: Electrical and Magnetic properties of rock and soil. UNITED STATES DEPARTMENT OF THE INTERIOR GEOLOGICAL SURVEY, USGS Open-File Report, 83–915, 1983.
Scoville, J., Heraud, J., and Freund, F.: Pre-earthquake magnetic pulses, Nat. Hazards Earth Syst. Sci., 15, 1873–1880, https://doi.org/10.5194/nhess-15-1873-2015, 2015.
Sgrigna, V., Buzzi, A., Conti, L., Picozza, P., Stagni, C., and Zilpimiani, D.: Seismo-induced effects in the near-earth space: Combined ground and space investigations as a contribution to earthquake prediction, Tectonophysics, 431, 153–171, 2007.
Shah, K. P.: The Hand Book on Mechanical Maintenance, Practical Maintenance, compiled by: K. P. Shah, available at: http://practicalmaintenance.net/?p=1135 (last access: 29 July 2019), 2011.
Shrivastava, M. N., González, G., Moreno, M., Chlieh, M., Salazar, P., Reddy, C. D., Báez, J. C., Yáñez, G., González, J., and de la Llera, J. C.: Coseismic slip and afterslip of the 2015 Mw 8.3 Illapel (Chile) earthquake determined from continuous GPS data, Geophys. Res. Lett., 43, 10710–10719, https://doi.org/10.1002/2016GL070684, 2016.
Slifkin, L.: Seismic electric signals from displacement of charged dislocations, Tectonophysics, 224, 149–152, 1993.
Sorokin, V. M. and Pokhotelov, O. A.: Generation of ULF geomagnetic pulsations during early stage of earthquake preparation, J. Atmos. Sol.-Terr. Phys., 72, 763–766, 2010.
Stavrakas, I., Triantis, D., Agioutantis, Z., Maurigiannakis, S., Saltas, V., Vallianatos, F., and Clarke, M.: Pressure stimulated currents in rocks and their correlation with mechanical properties, Nat. Hazards Earth Syst. Sci., 4, 563–567, https://doi.org/10.5194/nhess-4-563-2004, 2004.
Stein, S. and Wysession, M.: An introduction to seismology, earthquakes, and earth structure. Malden, MA, Blackwell Pub, 2003.
Stroh, A. N.: The Formation of Cracks in Plastic Flow II, Philos. T. R. Soc. Lond., A232, 548–560, 1955.
Sun, S.: Seismic velocities, anisotropy and elastic properties of crystalline rocks and implications for interpretation of seismic data (PhD thesis, École Polytechnique de Montréal), available at: https://publications.polymtl.ca/725/ (last access: 29 July 2019), 2011.
Surkov, V. V., Molchanov, O. A., and Hayakawa, M.: Pre-earthquake ULF electromagnetic perturbations as a result of inductive seismomagnetic phenomena during microfracturing, J. Atmos. Sol.-Terr. Phy., 65, 31–46, 2003.
Thomas, J. N., Love, J. J., and Johnston, M. J. S.: On the reported magnetic precursor of the 1989 Loma Prieta earthquake, Phys. Earth Planet. In., 173, 207–215, 2009.
Tilmann, F., Zhang, Y., Moreno, M., Saul, J., Eckelmann, F., Palo, M., Deng, Z., Babeyko, A., Chen, K., Baez, J. C., Schurr, B., Wang, R., and Dahm, T.: The 2015 Illapel earthquake, central Chile: A type case for a characteristic earthquake?, Geophys. Res. Lett., 43, 574–583, https://doi.org/10.1002/2015GL066963, 2016.
Triantis, D., Vallianatos, F., Stavrakas, I., and Hloupis, G.: Relaxation phenomena of electrical signal emissions from rock following application of abrupt mechanical stress, Ann. Geophy., 55, https://doi.org/10.4401/ag-5316, 2012.
Tuck, B. T., Stacey, F. D., and Starkey, J.: A search for the piezoelectric effect in quartz-bearing rock, Tectonophysics, 39, 7–11, 1977.
Turcotte, D. L.: Fractals and Chaos in Geology and Geophysics, Cambridge University Press, Second edition, 397 pp., 1997.
Turcotte, D. L., Newman, W. I., and Shcherbakov, R.: Micro and macroscopic models of rock fracture, Geophys. J. Int., 152, 718–728, 2003.
Tzanis A. and Vallianatos, F.: A physical model of electrical earthquake precursors due to crack propagation and the motion of charged edge dislocations, in: Seismo Electromagnetics (Lithosphere–Atmosphere–Ionosphere-Coupling), TerraPub, 2002, 117–130, 2002.
Uritsky, V., Smirnova, N., Troyan, V., and Vallianatos, F.: Critical dynamics of fractal fault systems and its role in the generation of pre-seismic electromagnetic emissions, Phys. Chem. Earth, 29, 473–480, 2004.
Utada, H., Shimizu, H., Ogawa, T., Maeda, T., Furumura, T., Yamamoto, T., Yamazaki, N., Yoshitake, Y., and Nagamachi, S.: Geomagnetic field changes in response to the 2011 off the Pacific Coast of Tohoku earthquake and tsunami, Earth Planet. Sc. Lett., 311, 11–27, https://doi.org/10.1016/j.epsl.2011.09.036, 2011.
Vallianatos, F. and Tzanis, A.: Electric Current Generation Associated with the Deformation Rate of a Solid: Preseismic and Coseismic Signals, Phys. Chem. Earth, 23, 933–938, 1998.
Vallianatos, F. and Tzanis, A.: On the nature, scaling and spectral properties of pre-seismic ULF signals, Nat. Hazards Earth Syst. Sci., 3, 237–242, https://doi.org/10.5194/nhess-3-237-2003, 2003.
Vallianatos, F. and Triantis, D.: Scaling in Pressure Stimulated Currents related with rock fracture, Physica A, 387, 4940–4946, https://doi.org/10.1016/j.physa.2008.03.028, 2008.
Varotsos, P., Sarlis, N., and Skordas, E. S.: Natural Time Analysis: The New View of Time, Springer, Berlin, 2011.
Vigny, C., Socquet, A., Peyrat, S., Ruegg, J.-C., Metois, M., Madariaga, R., Morvan, S.,Lancieri, M., Lacassin, R., Campos, J., Carrizo, D., Bejar-Pizarro, M., Barrientos, S., Armijo, R., Aranda, C., Valderas-Bermejo, M.-C., Ortega, I., Bondoux, F., Baize, S.,Lyon-Caen, H., Pavez, A., Vilotte, J. P., Bevis, M., Brooks, B., Smalley, R., Parra, H., Baez, J.-C., Blanco, M., Cimbaro, S., and Kendrick, E.: The 2010 Mw 8.8 Maule Megathrust Earthquake of Central Chile, monitored by GPS, Science, 332, 1417–1421, 2011.
Villante, U., De Lauretis, M., De Paulis, C., Francia, P., Piancatelli, A., Pietropaolo, E., Vellante, M., Meloni, A., Palangio, P., Schwingenschuh, K., Prattes, G., Magnes, W., and Nenovski, P.: The 6 April 2009 earthquake at L'Aquila: a preliminary analysis of magnetic field measurements, Nat. Hazards Earth Syst. Sci., 10, 203–214, https://doi.org/10.5194/nhess-10-203-2010, 2010.
Wallace, M. H. and Wallace, T. C.: The paradox of the Loma Prieta Earthquake: Why did rupture terminate at depth?, J. Geophys. Res., 98, 19859–19867, 1993.
Walters, R. J., Elliott, J. R., D'Agostino, N., England, P. C., Hunstad, I., Jackson, J. A., Parsons, B., Phillips, R. J., and Roberts, G.: The 2009 L'Aquila earthquake (central Italy): A source mechanism and implications for seismic hazard, Geophys. Res. Lett., 36, L17312, https://doi.org/10.1029/2009GL039337, 2009.
Wang, Z., Li, J., Zhang, W., Qiao, J., and Wang, B.: The Self-Organized Critical Behavior in Pd-based Bulk Metallic Glass, Metals, 2015, 1188–1196; https://doi.org/10.3390/met5031188, 2015.
Whitworth, R. W.: Charged dislocations in ionic crystals, Adv. Phys., 24, 203–304, 1975.
Xie, H. and Sanderson, D. J.: Fractal kinematics of crack propagation in geomaterials, Eng. Fract. Mech., 50, 529–536, 1995.
Yin, D., Chen, S., Liu, X., and Ma, H.: Simulation Study on Strength and Failure Characteristics for Granite with a Set of Cross-Joints of Different Lengths, Advances in Civil Engineering, 2018, 2384579, https://doi.org/10.1155/2018/2384579, 2018.
Yoshida, S., Oswald, C. C., and Sammonds, P. R.: Electric potential changes prior to shear fracture in dry and saturated rocks, Geophys. Res. Lett., 25, 1557–1580, 1998.
Yue, H., Lay, T., Rivera, L., An, C., Vigny, C., Tong, X., and Báez Soto, J. C.: Localized fault slip to the trench in the 2010 Maule, Chile Mw=8.8 earthquake from joint inversion of high-rate GPS, teleseismic body waves, InSAR, campaign GPS, and tsunami observations, J. Geophys. Res.-Sol. Ea, 119, 7786–7804, https://doi.org/10.1002/2014JB011340, 2014.
- Abstract
- Introduction
- Rock physics, stress change, current generation and magnetic field
- b-value, earthquake entropy, magnetic field and critical system
- Seismic moment, moment magnitude and coseismic magnetic field
- Ultra-low-frequency magnetic signals
- Location of microcracks
- Summary and conclusions
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Rock physics, stress change, current generation and magnetic field
- b-value, earthquake entropy, magnetic field and critical system
- Seismic moment, moment magnitude and coseismic magnetic field
- Ultra-low-frequency magnetic signals
- Location of microcracks
- Summary and conclusions
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References