Simultaneous state–parameter estimation of rainfall-induced landslide displacement using data assimilation

Landslide displacement prediction has great practical engineering significance to landslide stability evaluation and early warning. The evolution of landslide is a complex dynamic process, and applying a classical prediction method will result in significant error. The data assimilation method offers a new way to merge multisource data with the model. However, data assimilation is still deficient in the ability to meet the demand of dynamic landslide systems. In this paper, simultaneous state and parameter estimation (SSPE) using particle-filter-based data assimilation is applied to predict displacement of the landslide. A landslide SSPE assimilation strategy can make use of time-series displacements and hydrological information for the joint estimation of landslide displacement and model parameters, which can improve the performance considerably. We select Xishan Village, Sichuan Province, China, as the experiment site to test the SSPE assimilation strategy. Based on the comparison of actual monitoring data with prediction values, results strongly suggest the effectiveness and feasibility of the SSPE assimilation strategy in short-term landslide displacement estimation.

1 Introduction

Landslide is a common geological hazard which greatly endangers the security of property and lives of the people (Huang et al., 2017; Froude and Petley, 2018; Zhang and Huang, 2018; Pham et al., 2018). The landslide in Sri Lanka in May 2017 resulted in more than 200 casualties and injured 698 289 people. (Kumarasiri, 2018). In China alone, landslide hazards account for about 72.6 % of the total geological disasters from 2005 to 2014 (Xue et al., 2016). Therefore, landslides are important to study, lending themselves for prevention studies like early warning systems and deformation predictions (Liu et al., 2014; Jiang et al., 2016; Michoud et al., 2016).

Landslide prediction and forecast methods have been developed and improved continually (Crosta et al., 2013; Li et al., 2018). Chaussard et al. (2014) used the time-series analysis method applied to ALOS (Advanced Land Observing Satellite) data to resolve land displacement in the Mexico region. Dong and Li (2012) proposed a model that coupled the Gray method and general regression neural networks (GM-GRNN) and applied it to the prediction of sliding deformation of the Dahu landslide. Li and Kong (2014) carried out a genetic algorithm and support vector machine (GA-SVM) method to establish a mathematical function prediction model. Although the above methods have certain practicability in the prediction of landslides, it is still problematic to carry out forecasts of rainfall-induced landslides in real time (Yin et al., 2010) – for the reason that surveillance photographs or optical remote-sensing satellites are not immediately available (Lee et al., 2019). It may take days, even months, to obtain field data and establish a process model of the study area. Moreover, most of the current model-based predictions cannot use the newest observation data effectively and therefore most likely deviate from the actual observations. The data assimilation method is a new technology that can help to overcome these challenges. By combining surface observational data with the process model, data assimilation provides an optimal true value that is continuously distributed over time and space (Xue et al., 2018). Data assimilation has been widely tested and used in geoscience fields like hydrologic and atmospheric sciences (Reichle et al., 2002; Abbaszadeh et al., 2017; Wikle, 2002). And although very promising, there have been only a few preliminary studies using data assimilation techniques that involve studying landslides.

Data assimilation can be divided into two types: the sequential-based method and the continuous-based method (Qin et al., 2009). The sequential-based method is an online approach that updates the prediction each time (Nakano et al., 2007), so it is more suitable for landslide systems than the continuous-based method. A particle filter (PF) is a typical sequential data assimilation algorithm which was initially put forward by Gordon (Gordon et al., 2002). Because the PF is nonlinear filtering based on Bayesian estimation, it can solve nonlinear and non-Gaussian problems (Moradkhani and Weihermüller, 2011). Landslides and parameters that describe landslides are typically nonlinear (Leeuwen, 2010), so we choose PF as the algorithm to integrate multisource data with the model.

The evolution of a landslide is a time-varying process, so the model parameters are required to be adjusted over time. However, primal sequential data assimilation only updates state vectors, and the model parameters are generally given by known information, which will result in discrepancies between state and model parameters under a particular model relationship (Nearing et al., 2012). To meet the requirements of updating state values and model parameters simultaneously, we apply the simultaneous state and parameter estimation (SSPE) here. The SSPE method can continuously renew the output by sequentially merging new measurements. Moradkhani et al. (2005) optimized this process in the hydrological field. Vrugt et al. (2006) combined the simultaneous optimization with data assimilation. Joint estimation of the state parameter has proven to be a useful strategy to improve prediction performance (Qin et al., 2009; Lü et al., 2011).

In this paper, we applied the SSPE assimilation strategy to predict landslide displacement. In landslide SSPE assimilation, an external factor, hydrological data, has been integrated into the dynamic model of landslide deformation data, which can adjust model parameters and the state vector simultaneously according to the hydrologic information. During the process, internal factors of a landslide are combined with external observation factors, reducing the simulation error.

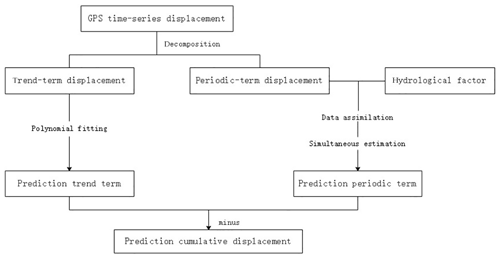
First, we will present the applied research method by describing the time-series decomposition and how we established the model and landslide SSPE assimilation strategy applying the PF algorithm. The Xishan Village landslide is used here as the study area to examine the SSPE assimilation strategy. The prediction of deformation will be optimized by coupling GPS observation data with a hydrological factor. Finally, we will present and discuss the results.

2 Method

2.1 Time-series displacement decomposition

Landslide deformation is the interaction between internal geological conditions and the external environment (Desai et al., 1995). Therefore the displacement can be divided into (a) a trend-term displacement generated by internal factors, (b) a periodic-term displacement caused by external factors (such as rainfall and reservoir water level) and (c) a stochastic-term displacement (human impacted, snowpack, etc.) (Zhou et al., 2016). However, after noise filtering, the stochastic term is too small and can be neglected. So the time-series displacement decomposition is as follows:

$$\begin{array}{}\text{(1)}& S\left(i\right)=\mathit{\phi }\left(i\right)+x\left(i\right),\end{array}$$

where S(i) is the cumulative displacement of landslides, φ(i) denotes the trend term and x(i) denotes the periodic term.

The trend term of time series is extracted with the moving average method because it can remove the disturbance effectively and leave long-term signals for research (Seng, 2013).

$$\begin{array}{}\text{(2)}& {\mathit{\phi }}_i={\displaystyle \frac{S_{i-\mathrm{1}}+S_{i-\mathrm{2}}+\mathrm{\cdots }{S}_{i-n}}{n}},\end{array}$$

where φ_i is the periodic term of step i, S_i−1 is the cumulative displacement of step i−1 and n is the moving average period.

So the periodic-term displacement can be calculated by subtracting the trend term from the total displacement.

2.2 Landslide periodic displacement modeling

For rainfall-induced landslides, atmospheric rainfall is one of the most susceptible disaster-causing factors and directly affects the periodic displacement of a landslide (Lian et al., 2015; Ren et al., 2015). So the periodic term can be regarded as a function of time and rainfall. The numerical function method is adopted here to establish a periodic displacement model. The periodic displacement variation is minimal for short periods of time. Therefore, the model can be derived through expanding periodic displacement value using a Taylor-series expansion method:

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{\displaystyle }x\left(t_{i+\mathrm{1}},r_{i+\mathrm{1}}\right)& {\displaystyle }=x\left(t_i,r_i\right)+{\left({\displaystyle \frac{\partial x}{\partial t}}\right)}_{t_i}\left(t_{i+\mathrm{1}}-t_i\right)\\ {\displaystyle }& {\displaystyle }+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial t^{\mathrm{2}}}}\right)}_{t_i}{\left(t_{i+\mathrm{1}}-t_i\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{\partial x}{\partial r}}\right)}_{r_i}\left(r_{i+\mathrm{1}}-r_i\right)\\ {\displaystyle }& {\displaystyle }+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial r^{\mathrm{2}}}}\right)}_{r_i}{\left(r_{i+\mathrm{1}}-r_i\right)}^{\mathrm{2}}+g_i,\end{array}\end{array}$$

where x denotes displacement of the landslide, r_i+1 is the rainfall of time i+1, $\frac{\partial x}{\partial t}$ and $\frac{\partial x}{\partial r}$ are the first-order partial derivative of displacement, $\frac{{\partial }^{\mathrm{2}}x}{\partial t^{\mathrm{2}}}$ and $\frac{{\partial }^{\mathrm{2}}x}{\partial r^{\mathrm{2}}}$ are the second-order partial derivative, and g_i is the remainder of Taylor's expansion.

2.3 Landslide SSPE assimilation strategy using PF

2.3.1 State estimation

The general state-space model for a nonlinear dynamic system is defined to be

$$\begin{array}{}\text{(4)}& {\displaystyle }& {\displaystyle }\mathrm{State}\mathrm{model}:{\mathit{x}}_{i+\mathrm{1}}=f\left({\mathit{x}}_i,u_i\right)+v_{i+\mathrm{1}},\text{(5)}& {\displaystyle }& {\displaystyle }\mathrm{Observation}\mathrm{model}:{\mathit{y}}_{i+\mathrm{1}}=g\left({\mathit{x}}_{i+\mathrm{1}}\right)+w_{i+\mathrm{1}},\end{array}$$

where x is the state vector and y is the observation vector, i is a time step, f and g are nonlinear functions forecasting the state and observation, u represents the model parameters, v is the model error and w is observation noise.

2.3.2 Landslide SSPE method

In sequential data assimilation, the SSPE algorithm can be applied through the state augmentation method (Chen et al., 2005). Considering the model in Eq. (4), the original state vector x_i is now augmented with the parameters u(t) to be

$$\begin{array}{}\text{(6)}& {\mathit{X}}_i=\left[\begin{array}{c}{x}_i\\ u_i\end{array}\right].\end{array}$$

By incorporating the simultaneous state–parameter estimation method into the practical landslide state model Eq. (3), the extended state vector can be expressed as

$$\begin{array}{}\text{(7)}& {\mathit{X}}_i={\left[x\left(t_i,r_i\right){\left({\displaystyle \frac{\partial x}{\partial t}}\right)}_{t_i}{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial t^{\mathrm{2}}}}\right)}_{t_i}{\left({\displaystyle \frac{\partial x}{\partial r}}\right)}_{r_i}{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial r^{\mathrm{2}}}}\right)}_{r_i}\right]}^T.\end{array}$$

And we set

$$\begin{array}{}\text{(8)}& {\displaystyle }& {\displaystyle }{\left({\displaystyle \frac{\partial x}{\partial t}}\right)}_{t_{i+\mathrm{1}}}={\left({\displaystyle \frac{\partial x}{\partial t}}\right)}_{t_i}+{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial t^{\mathrm{2}}}}\right)}_{t_i}\left(t_{i+\mathrm{1}}-t_i\right)+m_i,\text{(9)}& {\displaystyle }& {\displaystyle }{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial t^{\mathrm{2}}}}\right)}_{t_{i+\mathrm{1}}}={\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial t^{\mathrm{2}}}}\right)}_{t_i}+n_i,\text{(10)}& {\displaystyle }& {\displaystyle }{\left({\displaystyle \frac{\partial x}{\partial r}}\right)}_{r_{i+\mathrm{1}}}={\left({\displaystyle \frac{\partial x}{\partial r}}\right)}_{r_i}+{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial r^{\mathrm{2}}}}\right)}_{r_i}\left(r_{i+\mathrm{1}}-r_i\right)+u_i,\text{(11)}& {\displaystyle }& {\displaystyle }{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial r^{\mathrm{2}}}}\right)}_{r_{i+\mathrm{1}}}={\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial r^{\mathrm{2}}}}\right)}_{r_i}+v_i,\end{array}$$

where m_i, n_i, u_i and v_i are noise.

So the next moment X_i+1 is

$$\begin{array}{}\text{(12)}& \begin{array}{rl}{\displaystyle }& {\displaystyle }{X}_{i+\mathrm{1}}=\left[\begin{array}{l}x\left(t_{i+\mathrm{1},r_{i+\mathrm{1}}}\right)\\ {\left({\displaystyle \frac{\partial x}{\partial t}}\right)}_{t_{i+\mathrm{1}}}\\ {\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial t^{\mathrm{2}}}}\right)}_{t_{i+\mathrm{1}}}\\ {\left({\displaystyle \frac{\partial x}{\partial r}}\right)}_{r_{i+\mathrm{1}}}\\ {\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial r^{\mathrm{2}}}}\right)}_{r_{i+\mathrm{1}}}\end{array}\right]\\ {\displaystyle }& {\displaystyle }=\left[\begin{array}{l}x\left(t_i,r_i\right)+{\left({\displaystyle \frac{\partial x}{\partial t}}\right)}_{t_i}\left(t_{i+\mathrm{1}}-t_i\right)+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial t^{\mathrm{2}}}}\right)}_{t_i}{\left(t_{i+\mathrm{1}}-t_i\right)}^{\mathrm{2}}\\ +{\left({\displaystyle \frac{\partial x}{\partial r}}\right)}_{r_i}\left(r_{i+\mathrm{1}}-r_i\right)+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial r^{\mathrm{2}}}}\right)}_{r_i}{\left(r_{i+\mathrm{1}}-r_i\right)}^{\mathrm{2}}+g_i\\ {\left({\displaystyle \frac{\partial x}{\partial t}}\right)}_{t_i}+{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial t^{\mathrm{2}}}}\right)}_{t_i}\left(t_{i+\mathrm{1}}-t_i\right)+m_i\\ {\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial t^{\mathrm{2}}}}\right)}_{t_i}+n_i\\ {\left({\displaystyle \frac{\partial x}{\partial r}}\right)}_{r_i}+{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial r^{\mathrm{2}}}}\right)}_{r_i}\left(r_{i+\mathrm{1}}-r_i\right)+u_i\\ {\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial r^{\mathrm{2}}}}\right)}_{r_i}+v_i\end{array}\right]\\ {\displaystyle }& {\displaystyle }=\left[\begin{array}{lllll}\mathrm{1}& t_{i+\mathrm{1}}-t_i& {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left(t_{i+\mathrm{1}}-t_i\right)}^{\mathrm{2}}& r_{i+\mathrm{1}}-r_i& {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left(r_{i+\mathrm{1}}-r_i\right)}^{\mathrm{2}}\\ \mathrm{0}& \mathrm{1}& t_{i+\mathrm{1}}-t_i& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& r_{i+\mathrm{1}}-r_i\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right]\cdot \\ {\displaystyle }& {\displaystyle }\left[\begin{array}{l}x\left(t_i,r_i\right)\\ {\left({\displaystyle \frac{\partial x}{\partial t}}\right)}_{t_i}\\ {\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial t^{\mathrm{2}}}}\right)}_{t_i}\\ {\left({\displaystyle \frac{\partial x}{\partial r}}\right)}_{r_i}\\ {\left({\displaystyle \frac{{\partial }^{\mathrm{2}}x}{\partial r^{\mathrm{2}}}}\right)}_{r_i}\end{array}\right]+\left[\begin{array}{l}{g}_i\\ m_i\\ n_i\\ u_i\\ v_i\end{array}\right]\\ {\displaystyle }& {\displaystyle }=\left[\begin{array}{lllll}\mathrm{1}& t_{i+\mathrm{1}}-t_i& {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left(t_{i+\mathrm{1}}-t_i\right)}^{\mathrm{2}}& r_{i+\mathrm{1}}-r_i& {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left(r_{i+\mathrm{1}}-r_i\right)}^{\mathrm{2}}\\ \mathrm{0}& \mathrm{1}& t_{i+\mathrm{1}}-t_i& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& r_{i+\mathrm{1}}-r_i\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right]\\ {\displaystyle }& {\displaystyle }\cdot X_i+\left[\begin{array}{c}{g}_i\\ m_i\\ n_i\\ u_i\\ v_i\end{array}\right].\end{array}\end{array}$$

In Eq. (12) we make

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\left[\begin{array}{lllll}\mathrm{1}& t_{i+\mathrm{1}}-t_i& {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left(t_{i+\mathrm{1}}-t_i\right)}^{\mathrm{2}}& r_{i+\mathrm{1}}-r_i& {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left(r_{i+\mathrm{1}}-r_i\right)}^{\mathrm{2}}\\ \mathrm{0}& \mathrm{1}& t_{i+\mathrm{1}}-t_i& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& r_{i+\mathrm{1}}-r_i\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right]\\ {\displaystyle }& {\displaystyle }={\mathit{\omega }}_{i+\mathrm{1}},\left[\begin{array}{c}{g}_i\\ m_i\\ n_i\\ u_i\\ v_i\end{array}\right]={\mathit{\epsilon }}_{i+\mathrm{1}},\end{array}$$

so Eq. (12) can be expressed as

$$\begin{array}{}\text{(13)}& X_{i+\mathrm{1}}={\mathit{\omega }}_{i+\mathrm{1}}\cdot X_i+{\mathit{\epsilon }}_{i+\mathrm{1}}.\end{array}$$

The observation of landslide deformation can be expressed as

$$\begin{array}{}\text{(14)}& y_{i+\mathrm{1}}={\mathit{x}}_i+w_{i+\mathrm{1}}.\end{array}$$

Combining the two expressions, Eqs. (13) and (14), we can build the landslide SSPE state-space model to jointly estimate the landslide periodic displacement and the model parameters.

2.3.3 PF algorithm

However, some parameters in the landslide state-space model, Eqs. (13) and (14), are difficult to obtain (e.g., ${\left(\frac{\partial x}{\partial t}\right)}_{t_i}$, ${\left(\frac{{\partial }^{\mathrm{2}}x}{\partial t^{\mathrm{2}}}\right)}_{t_i}$). By applying Monte Carlo simulations, the PF can be adjusted to solve this. Instead of calculating the partial derivative directly, PF generates a large number of samples (particles) to approximate the posterior probability of the states, thus obtaining an optimal result (Maskell and Gordon, 2002).

From the Bayesian theorem, the posterior probability of the states can be inferred through

1. forecast,

   $$\begin{array}{}\text{(15)}& p\left(x_i\mathrm{|}{y}_{\mathrm{1}:i-\mathrm{1}}\right)=\int p\left(x_i\mathrm{|}{x}_{i-\mathrm{1}}\right)p\left(x_{i-\mathrm{1}}\mathrm{|}{y}_{\mathrm{1}:i-\mathrm{1}}\right)\mathrm{d}{x}_{i-\mathrm{1}},\end{array}$$

2. and update,

   $$\begin{array}{}\text{(16)}& p\left({\mathit{x}}_i\mathrm{|}{y}_{\mathrm{1}:i}\right)={\displaystyle \frac{p\left({\mathit{y}}_i\mathrm{|}{\mathit{x}}_i\right)p\left({\mathit{x}}_i\mathrm{|}{y}_{\mathrm{1}:i-\mathrm{1}}\right)}{p\left({\mathit{y}}_i\mathrm{|}{y}_{\mathrm{1}:i-\mathrm{1}}\right)}},\end{array}$$

   where i is time, x_i is the state vector, y_i is the observation vector, $y_{\mathrm{1}:i}=\mathit{\{}{y}_{\mathrm{1}},y_{\mathrm{2}},\mathrm{\cdots },{\mathit{y}}_i\mathit{\}}$, $p\left({\mathit{x}}_{i-\mathrm{1}}\mathrm{|}{y}_{\mathrm{1}:i-\mathrm{1}}\right)$ is the posterior distribution function (PDF) for time step i−1, $p\left({\mathit{x}}_i\mathrm{|}{y}_{\mathrm{1}:i-\mathrm{1}}\right)$ is the prior distribution for time step i and p(x_i|x_i−1) can be derived from the model.

In PF, the posterior probability of the states is approximated by discrete random measures defined by particles and a set of weights associated with particles:

$$\begin{array}{}\text{(17)}& \widehat{p}\left({\mathit{x}}_i\mathrm{|}{y}_{\mathrm{1}:i}\right)\approx \sum _{k=\mathrm{1}}^N{w}_i^k\mathit{\delta }\left(x_{\mathrm{0}:i}-x_{\mathrm{0}:i}^k\right),\end{array}$$

where $\widehat{p}\left(x_i\mathrm{|}{y}_{\mathrm{1}:i}\right)$ is the approximate value of p(x_i|y_1:i), $x_{\mathrm{0}:i}^k$ and $w_i^k$ are particles and associated weight, $\sum _{i=\mathrm{1}}^N{w}_i^k=\mathrm{1}$ and δ denotes the Dirac delta function.

Direct sampling of target p(x_i|y_1:i) can be problematic, so sequential importance sampling (SIS) is considered here to overcome this. The SIS gathers particles from a known density function and updates the importance weights by using an iterative method (Doucet et al., 2000). Meanwhile, the sampling importance resampling (SIR) is used to avoid particles deviates away from the true value (Gordon et al., 2002). The SIR algorithm gathers particles by their importance weight. So the estimates of the state vector can be described as

$$\begin{array}{}\text{(18)}& \widehat{{\mathit{x}}_i}=\sum _{k=\mathrm{1}}^N{\mathit{x}}_i^k{w}_i^k.\end{array}$$

The procedure of the landslide SSPE assimilation strategy is shown in Fig. 1.

Figure 1 The flow chart of the landslide SSPE assimilation strategy.

3 Study area and data

3.1 Study area

Our study area is located in Xishan Village, Li County, Sichuan Province, China (Fig. 2), in the upper part of the northern bank slope of the Zagunao River. The slope of this landslide is about 25–45^∘. The length is about 4200 m, and the width is around 1700 m. The altitude of the leading edge is 1500 m, and the trailing edge is 3400 m. Thus the elevation is 1900 m. This landslide can be best described as a massive accumulative landslide. It can be divided into three parts according to geomorphogenesis: (i) erosional with a dip direction of about 178^∘, (ii) erosional and denudational with a dip direction of about 200^∘, and (iii) glacial and periglacial with a dip direction of about 208^∘. The distribution of the three parts is shown in Fig. 3. The Xishan landslide is a soft rock, layered structure slope. Exposed strata in the study area resemble mainly blue grey phyllite. The upper deposit is formed due to the collapse of slope and ice water accumulation and is mainly composed of silt and gravel soil.

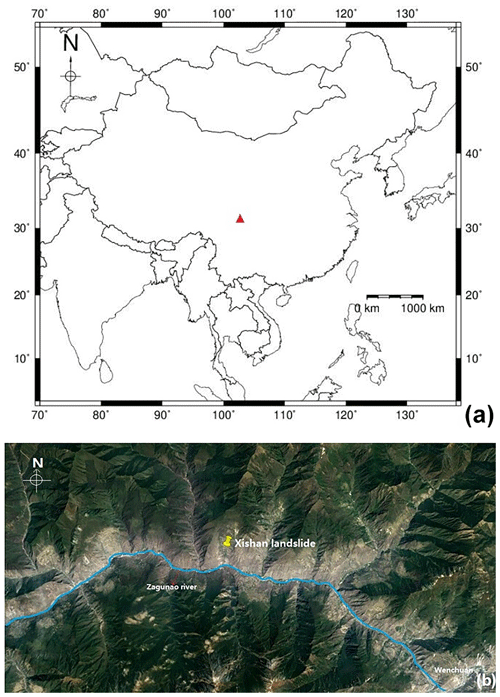
Figure 2 Location of the Xishan landslide in China (a); the Xishan landslides in the west of Wenchuan County associated with landform. Map obtained from Google Earth (b).

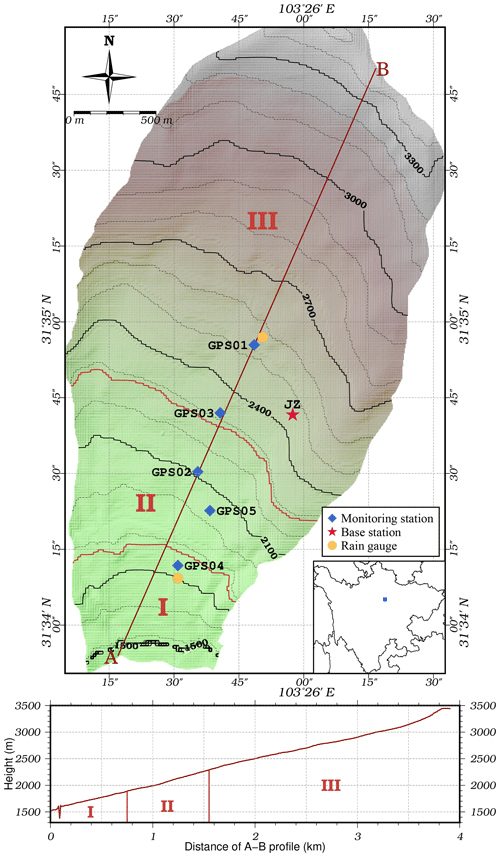
Figure 3 The distribution of the three parts (I–III), GPS stations and rain gauges at the Xishan landslide.

Landform undulation leads to apparent local variations. The Xishan Village landslide has a 52 m thick active sliding layer which can lead to the movement of about 85 million cubic meters. Before 2008, many cracks appeared in the front and middle of this landslide, causing a direct economic loss of Yuan 0.5 million and affecting 189 people. The creep deformation intensified after the Wenchuan earthquake (May 2008), which threatened the security of residents' lives and properties. The estimated potential economic loss was about Yuan 50 million. For the purpose of reducing damage by providing early warning, this study was used to forecast the deformation of this landslide.

3.2 Data introduction

3.2.1 GPS-derived time-series displacement

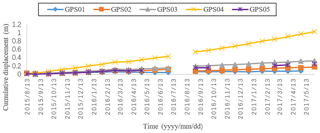
Five continuous GPS observation stations have been set up for the Xishan Village landslide to obtain any deformation observations. The GPS receivers were connected to a network so the observations could be transferred in real time. At the same time, a GPS reference station was placed in a stable area and used for reference. Figure 3 shows the distribution of all stations. After the GPS baseline calculation, we calculated the deformation of every observation station from August 2015 to June 2017. Figure 4 shows the final results. Due to transmission problems, there are several gaps in the data. An interpolation method was applied to overcome these data gaps (Velicer and Colby, 2005; Lenda et al., 2016).

3.2.2 Rainfall data

There are two rain gauges on the landslide, which can transmit rainfall data in real time. Figure 3 shows the location of the rain gauges. Both are near GPS stations. The daily rainfall data are illustrated in Fig. 6. Since the rain gauges are located near the GPS station, the mean values of the two gauges are taken as the rainfall of the Xishan landslide.

4 Results and analysis

In this experiment, the performance of the proposed SSPE using the particle-filter-based data assimilation strategy is benchmarked with the SSPE method. The SSPE method only applied the SSPE strategy and updated the state value with Eq. (13), without using data assimilation to optimize model and state parameters. All the experimental data were obtained at the Xishan Village landslide between August 2015 and June 2017. We only present our findings for two stations, GPS03 and GPS04, because the deformation is more evident there. Due to the complex terrain and insufficient power supply of Xishan Village, the monitoring GPS sequence contained significant noise or errors. In order to reduce the influence of this, we need to modify the time step. After experiment and evaluation among different time steps, a 5 d time step gives the best correlation with rainfall data. Therefore the time step is set to 5 d. The predicted displacement can be separated by a trend term, a period term and a cumulative term. Then the error analysis is taken to validate the efficiency of our method.

4.1 Prediction of trend-term displacement

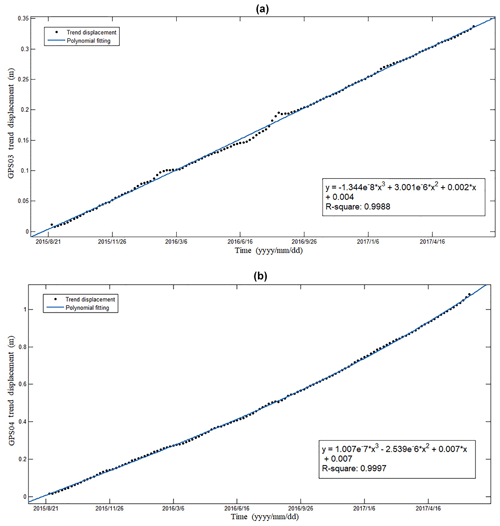
The trend-term displacement is a time monotone function so that it can be fitted to a polynomial. The most optimal results of the trend-term prediction and the fitting formula are shown in Fig. 5.

Figure 4 The GPS-derived time-series displacement of the Xishan landslide.

Figure 5 The trend-term displacement prediction of (a) station GPS03 and (b) station GPS04.

4.2 Prediction of period-term displacement

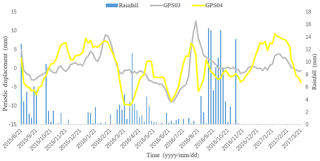
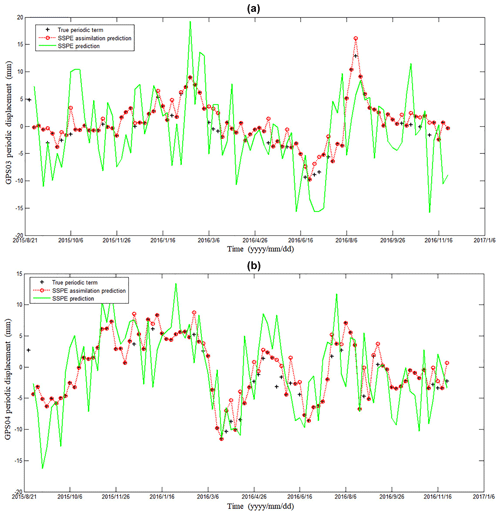
The periodic-term displacement can be calculated using the difference between the total displacement and the trend term. Figure 6 shows the periodic displacement in station GPS03 and GPS04 and the rainfall data. It can be seen clearly that the period term is a complex nonlinear sequence series. Besides, fluctuation of the period term of the two stations shows relatively the same changing tendency for both, which lags behind that of rainfall. However, there are small differences in fluctuation like time step 40 to 50 and 70 to 76. This could be attributed to the impact of geology. The GPS04 stations monitor the first part of the landslide. There are a large number of people living here. The combined contribution of surface water, domestic water and ground water reduces the friction of the sliding belt, thus leading to drastic distortion. Station GPS03 monitors part III, the upper part of the landslide (Fig. 3). This part with rare plant cover is susceptible to heavy rainfall season.

Figure 6 The periodic-term displacement combined with rainfall data in GPS03 and GPS04.

We applied the SSPE assimilation method to predict periodic displacement. The prediction results are as shown in Fig. 7. It can be seen that the SSPE assimilation method gets closer to the measured value than the SSPE method without assimilation.

Figure 7 The periodic-term displacement prediction of (a) station GPS03 and (b) station GPS04.

4.3 Prediction of cumulative displacement

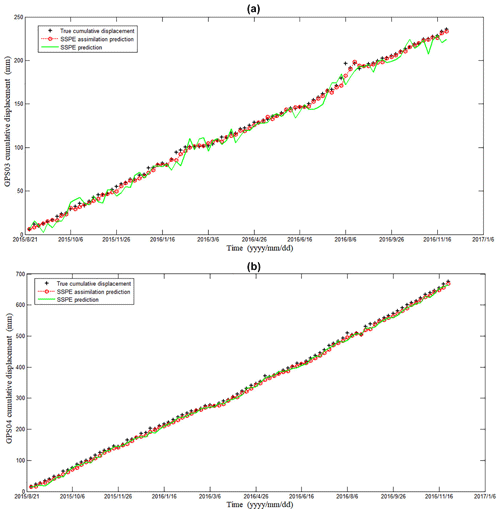
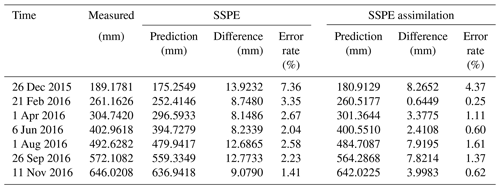
The predicted values of cumulative displacement can be obtained by summation of the predicted values of trend and periodic displacement. The prediction results for each station are shown in Fig. 8. Additionally, some detailed prediction data, differences between predicted and measured displacement, and the error rates are enumerated in Tables 1 and 2. Experimental results verify the feasibility of the SSPE assimilation method.

Figure 8 The cumulative displacement prediction of (a) station GPS03 and (b) station GPS04.

Table 1 Comparison between the predicted values of cumulative displacement and measured displacement using different methods in station GPS03.

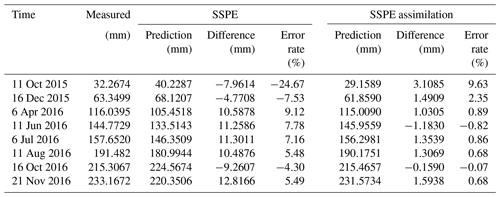
Table 2 Comparison between the predicted values of cumulative displacement and measured displacement using different methods in station GPS04.

Table 3 Comparison of mean absolute error (MAE), mean squared error (MSE) and root mean square error (RMSE) performance and needed time using different methods in two stations.

4.4 Relative error analysis

In this section, a more quantitative analysis is carried out to assess the performance of each method. Three criteria – mean absolute error (MAE), mean squared error (MSE) and root mean square error (RMSE) – were used to evaluate the prediction effect. They can measure the deviation between the predicted value and the measured value and are calculated by

$$\begin{array}{}\text{(19)}& {\displaystyle }{\displaystyle }\mathrm{MAE}={\displaystyle \frac{\mathrm{1}}{N}}\cdot \sum _{i=\mathrm{1}}^N\left|x_i-{\widehat{x}}_i\right|,\end{array}$$

$$\begin{array}{}\text{(20)}& {\displaystyle }& {\displaystyle }\mathrm{MSE}={\displaystyle \frac{\mathrm{1}}{N}}\cdot \sum _{i=\mathrm{1}}^N{\left(x_i-{\widehat{x}}_i\right)}^{\mathrm{2}},\text{(21)}& {\displaystyle }& {\displaystyle }\mathrm{RMSE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{N}}\cdot \sum _{i=\mathrm{1}}^N{\left(x_i-{\widehat{x}}_i\right)}^{\mathrm{2}}},\end{array}$$

where x_i is the measured value and ${\widehat{x}}_i$ is the prediction value.

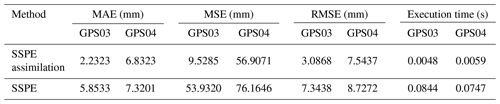
The results are shown in Table 3. According to the prediction evaluation indexes, the SSPE assimilation method offers a better forecast effect than the SSPE method. The MAE, MSE and RMSE values of the SSPE assimilation method were 64.85 %, 82.33 % and 57.97 % lower than those of the SSPE method in GPS03 station, respectively, and 6.66 %, 25.28 % and 13.56 % lower in GPS04 station, respectively. The result suggests that the SSPE assimilation method has achieved great performance in landslide displacement prediction. Besides, the total execution time of the two methods is calculated. Building the SSPE model for landslide displacement prediction only takes 0.0048 and 0.0059 s for the two stations, while the SSPE assimilation strategy takes 0.0844 and 0.0747 s. It can therefore be considered as a near-real-time solution to make a displacement prediction simultaneously.

5 Conclusion

This paper presents a practical strategy for accurately predicting landslide displacement by coupling landslide deformation with external factors. For this, the PF data assimilation algorithm was integrated with the SSPE method. For the real data experiment, first the landslide deformation from GPS measurements was decomposed into a trend term and a period term. The period term was predicted with the hydrological factor in simultaneous estimation data assimilation, while the trend term was computed by polynomial fitting.

Our results show that the SSPE assimilation strategy has an excellent ability to predict landslide displacement and can provide assistance in early risk assessment and landslide forecasting.