Automatic detection of snow avalanches in continuous seismic data using hidden Markov models

Snow avalanches generate seismic signals as many other mass movements. Detection of avalanches by seismic monitoring is highly relevant to assess avalanche danger. In contrast to other seismic events, signals generated by avalanches do not have a characteristic first arrival nor is it possible to detect different wave phases. In addition, the moving source character of avalanches increases the intricacy of the signals. Although it is possible to visually detect seismic signals produced by avalanches, reliable automatic detection methods for all types of avalanches do not exist yet. We therefore evaluate whether hidden Markov models (HMMs) are suitable for the automatic detection of avalanches in continuous seismic data. We analyzed data recorded during the winter season 2010 by a seismic array deployed in an avalanche starting zone above Davos, Switzerland. We re-evaluated a reference catalogue containing 385 events by grouping the events in seven probability classes. Since most of the data consist of noise, we first applied a simple amplitude threshold to reduce the amount of data. As first classification results were unsatisfying, we analyzed the temporal behavior of the seismic signals for the whole data set and found that there is a high variability in the seismic signals. We therefore applied further post-processing steps to reduce the number of false alarms by defining a minimal duration for the detected event, implementing a voting-based approach and analyzing the coherence of the detected events. We obtained the best classification results for events detected by at least five sensors and with a minimal duration of 12 s. These processing steps allowed identifying two periods of high avalanche activity, suggesting that HMMs are suitable for the automatic detection of avalanches in seismic data. However, our results also showed that more sensitive sensors and more appropriate sensor locations are needed to improve the signal-to-noise ratio of the signals and therefore the classification.

1 Introduction

During the winter season, snow avalanches may threaten people and infrastructure in mountainous regions throughout the world. Avalanche forecasting services therefore regularly issue avalanche bulletins to inform the public about the avalanche conditions. Such an avalanche forecast requires meteorological data, information about the snowpack and avalanche activity data. The latter are mostly obtained through visual observations requiring good visibility. Avalanche activity data are therefore often lacking during periods of intense snowfall, which are typically the periods when they are most important for forecasting. A possible alternative approach to determine the avalanche activity is to use a seismic monitoring system (e.g., van Herwijnen and Schweizer, 2011a).

Seismic monitoring systems are well suited to detect mass movements such as rockfalls, pyroclastic flows and snow and ice avalanches (Faillettaz et al., 2015; Podolskiy and Walter, 2016; Caplan-Auerbach and Huggel, 2007; Suriñach et al., 2005; Zobin et al., 2009). The ability to detect snow avalanches through seismic methods was first demonstrated in the 1970s. St. Lawrence and Williams (1976) and Harrison (1976) deployed geophones near avalanche paths and manually identified signals generated by avalanches in the seismogram. They showed that the seismic signature of avalanches differs from other seismic events such as earthquakes or nearby blasts. A more in-depth analysis of seismic signals generated by avalanches was performed 20 years later, identifying typical characteristics in both the time and time–frequency domain (Kishimura and Izumi, 1997; Sabot et al., 1998). Using automatic cameras to film avalanches, Sabot et al. (1998) showed that specific features in the seismic signals were related directly to changes in the flow of the avalanche; these findings were confirmed by Suriñach et al. (2000) and Suriñach et al. (2001). Since then, seismic signal characteristics were used to estimate specific properties of single avalanches such as the flow velocity (Vilajosana et al., 2007a), the total energy of the avalanche (Vilajosana et al., 2007b) or the runout distance (Pérez-Guillén et al., 2016; van Herwijnen et al., 2013).

While many studies focused on using seismic signals to better understand the properties of single avalanches, continuous monitoring of avalanche starting zones to obtain more accurate avalanche activity data is of particular interest for avalanche forecasting (e.g., van Herwijnen et al., 2016). Leprettre et al. (1996) deployed three-component seismic sensors at two different field sites and compared seismic signal characteristics to a database including avalanches, helicopters, thunder rolls and earthquakes. Lacroix et al. (2012) improved the seismic monitoring system used by Leprettre et al. (1996) by deploying a seismic array between two known avalanche paths. The array consisted of six vertical component geophones arranged in a circle around a three component geophone in the center. Using array techniques, Lacroix et al. (2012) determined the release area and the path of manually identified avalanches and estimated their speed. These studies mainly monitored medium and large avalanches. Van Herwijnen and Schweizer (2011) however, deployed seismic sensors near an avalanche starting zone above Davos in the eastern Swiss Alps to also detect small avalanches. They manually identified several hundred avalanche events in the continuous seismic data during 4 winter months.

While these studies have highlighted the usefulness of seismic monitoring to obtain more accurate and complete avalanche activity data, using machine learning algorithms to automatically detect snow avalanches has thus far remained relatively unsuccessful. Nevertheless, the interest in these techniques has been evident for several decades (Leprettre et al., 1998; Bessason et al., 2007; Rubin et al., 2012). The first attempt to automatically detect avalanches focused on using fuzzy logic rules and credibility factors derived from features of the seismic signal in the time and time–frequency domain (Leprettre et al., 1996, 1998). In a first step, the features of unambiguously identified seismic events were analyzed including avalanches, blast and teleseismic events. They then formulated several fuzzy logic rules for each type of event to train a classifier used to identify the type of a new unknown seismic event. While the probability of detection (POD), i.e., the number of detected avalanches divided by the total number of observed avalanches, was high (≈ 90 %), one of the main drawbacks of this method is the subjective expert knowledge used to derive the fuzzy logic rules and the need to adapt these rules to each individual field site.

Bessason et al. (2007) deployed seismic sensors in several known avalanche paths along an exposed road in Iceland. They used a nearest-neighbor method to automatically identify avalanche events. The method consists of comparing new events with those in a database. Although a 10-year database was used, the identification performed rather poorly. Seismic signals generated by rockfalls and debris flows were wrongly classified as avalanches and vice versa, resulting in a POD of about 65 %.

In an attempt to improve the automatic detection of avalanches, Rubin et al. (2012) used a seismic avalanche catalogue presented by van Herwijnen and Schweizer (2011b) and compared the performance of 12 different machine learning algorithms. The PODs of all classifiers were high (between 84 and 93 %). However, the main drawback were the high false alarm rates, much too high for operational tasks.

The methods described above are generally difficult to apply at new sites since they require time to build a training data set and/or expert knowledge to define thresholds and rules. To overcome these drawbacks, we investigate using a hidden Markov model (HMM). A HMM is a statistical pattern recognition tool commonly used for speech recognition (Rabiner, 1989) and was first introduced for the classification of seismic traces by Ohrnberger (2001). The advantage of HMMs compared to other classification algorithms is that the time dependency of the data is explicitly taken into account. First studies using HMMs for the classification of seismic data relied on large training data sets (Ohrnberger, 2001). Using this approach, Beyreuther et al. (2012) created an earthquake detector.

More recently, Hammer et al. (2012) developed a new approach which only requires one training event. This approach was applied for a volcano fast response system (Hammer et al., 2012) and the detection of rockfalls, earthquakes and quarry blasts on seismic broadband stations of the Swiss Seismological Service (SED; Hammer et al., 2013; Dammeier et al., 2016. Furthermore, Hammer et al. (2017) also detected snow avalanches using data from a seismic broadband station of the SED. During a period with high avalanche activity in February 1999, 43 very large confirmed avalanches were detected over a 5-day period with only four presumable false alarms. While these detection rates are very encouraging, the investigated avalanche period was exceptional. Furthermore, due to the location of the broadband station at valley bottom, they could not detect small or medium-sized avalanches.

For avalanche forecasting information on smaller avalanches is also required. To resolve this issue, we investigate a method to obtain local (i.e., scale of a small valley) avalanche activity data using a seismic monitoring system (van Herwijnen and Schweizer, 2011a). We therefore implement the approach outlined by Hammer et al. (2017) to detect avalanches in the continuous seismic data obtained with the sensors deployed near avalanche starting zones (van Herwijnen and Schweizer, 2011b).

Based on the duration of the seismic signals, the majority of these avalanches were likely rather small (van Herwijnen et al., 2016). We therefore used this avalanche catalogue to train and evaluate the performance of a HMM model and discuss limitations and possible improvements.

2 Field site and instrumentation

We analyzed data obtained from a seismic array deployed above Davos, Switzerland. The field site is located at 2500 m a.s.l. and is surrounded by several avalanche starting zones. The site is easily accessible during the entire year and is also equipped with various automatic weather stations and automatic cameras observing the adjacent slopes.

The array consisted of seven vertical geophones with an eigenfrequency of 14 Hz. The maximum distance between the sensors was 12 m. Six of the geophones were inserted in a styrofoam housing and placed within the snow, whereas the seventh geophone (Sensor 7) was inserted in the ground with a spike (see Figs. 3 and 4 in van Herwijnen and Schweizer, 2011a). Sensors 1 and 4 are the ones nearest to the ridge and most deeply covered (see Fig. 2 in van Herwijnen and Schweizer, 2011b). The seismic sensors were deployed at the field site from early December until the snow had melted.

The instrumentation was originally designed to record higher frequency signals in order to detect precursor signals of avalanche release (van Herwijnen and Schweizer, 2011b). A 24 bit data acquisition system (Seismic Instruments) was used to continuously acquire data from the sensors at a sampling rate of 500 Hz. The data were stored locally on a low power computer and manually retrieved approximately every 10 days. A more detailed description of the field site and the instrumentation can be found in van Herwijnen and Schweizer (2011a) and van Herwijnen and Schweizer (2011b).

3 Data

Continuous seismic data were recorded from 12 January to 30 April 2010. These data were previously used by van Herwijnen and Schweizer (2011b), Rubin et al. (2012) and van Herwijnen et al. (2016). The recorded seismic data contain various types of events (van Herwijnen and Schweizer, 2011a), including aeroplanes, helicopters and of course avalanches (Fig. 1).

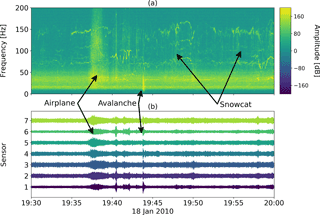
Figure 1 (a) Spectrogram of an unfiltered 30 min time series. (b) Corresponding time series. An airplane and an avalanche are visible. Furthermore, noise produced by a snowcat can be seen in the second half of the time series.

3.1 Pre-processing of the seismic data

While during the 107-day period several hundred avalanches were identified, the vast majority of the data consist of noise or seismic events produced by other sources. To reduce the amount of data to process, we applied a simple threshold-based event detection method. It consisted of dividing the continuous seismic data stream in non-overlapping windows of 1024 samples. For each window, a mean absolute amplitude A_i was determined. When $A_i\ge \mathrm{5}\stackrel{\mathrm{‾}}{A}$, with $\stackrel{\mathrm{‾}}{A}$ the daily mean amplitude, the data were used. Furthermore, a data section of Δt=60 s before and after each event was also included to ensure that the onset and coda of each event were incorporated. The amount of data to process was thus reduced by 80 % (Fig. 2).

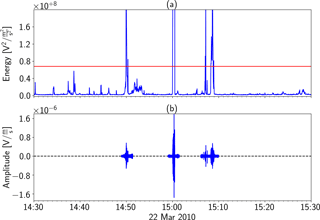
Figure 2 Example of the pre-processing: (a) the mean energy values of each window shown as the blue line and the threshold value indicated by the red line; (b) the remaining data cut by the pre-processing step.

Finally, before we used the data for the detection, we applied a bandpass filter. Previous studies showed that seismic signals generated by avalanches typically have a frequency below 50 Hz (e.g., Harrison, 1976; Schaerer and Salway, 1980). We therefore applied a fourth-order Butterworth bandpass filter to our data between 1 and 50 Hz.

3.2 Reference avalanche catalogue

Van Herwijnen and Schweizer (2011) visually analyzed the unprocessed seismic time series and the corresponding spectrogram of one sensor and identified N=385 avalanches between 12 January and 30 April 2010. They thus obtained an avalanche catalogue consisting of the release time t_i and duration T_i for each avalanche. The onset was defined as the first appearance of energetic low frequency signals (i.e., between 15 and 25 Hz), while the end of the signal was defined as the time when low frequency signals reverted back to background levels. However, only 25 of these avalanches were confirmed by visual observations, i.e., on images obtained from automatic cameras. Hence there remains substantial uncertainty about the nature of the identified events.

To reduce the uncertainty, three of the authors therefore independently re-evaluated this avalanche catalogue. From the 385 avalanches in the original avalanche catalogue only N_pre=283 remained after pre-processing (see Sect. 3.1); none of the 25 confirmed avalanches were dismissed. By visually inspecting the seismic time series of the seven sensors and the stacked spectrogram for each event, they then assigned a subjective probability p_e to each of these possible avalanche events. Three probabilities were assigned: 1 when it was certain that the observed event was an avalanche, 0 when it was certain that the observed event was not an avalanche and 0.5 when it was uncertain whether the event was an avalanche or not. The probabilities were then combined into seven probability classes depending on the mean probability of each event:

$$\begin{array}{}\text{(1)}& P_{\mathrm{ava}}={\displaystyle \frac{\mathrm{1}}{\mathrm{3}}}\sum _{e=\mathrm{1}}^{\mathrm{3}}{p}_e,\end{array}$$

with p_e the subjective probability that each assigned to a specific event. In Table 1 the number of events in each probability class is listed. In the reclassified data set, only 20 avalanches were considered as certain avalanche by all three evaluators and 58 events were marked as certainly not an avalanche. Furthermore 18 of the 25 visually confirmed avalanches were within the two highest probability classes.

Table 1 Number of events per probability class P_ava after re-evaluation and the corresponding number of confirmed events for each class. The first row shows the possible combinations of subjective probability (p_e): when p_e=1 it was certain that the event was an avalanche; when p_e=0.5 it was uncertain; and when p_e=0 it was certain that the event was not an avalanche.

The avalanche activity of the season 2010 is shown in Fig. 3.

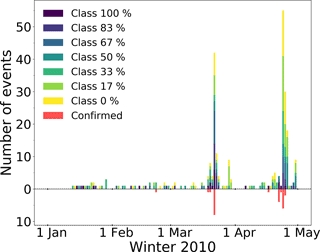
Figure 3 Avalanche activity for the winter season of 2010. The different colors above the zero line indicate the different probability classes derived from the manual detection. The red bars below the zero line indicate the visually confirmed events.

Overall, most avalanches were detected in the second half of the investigated period, with two distinct peaks in the avalanche activity around 22 March and 24 April.

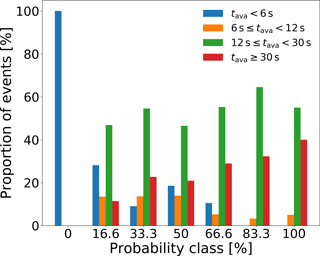
The distribution of the event duration changed as the probability class increased (Fig. 4). All events in the lowest probability class had a duration <6 s. More than 90 % of the events had durations ≥12 s for the three highest probability classes.

Figure 4 Event duration distribution per probability class.

4 Methods

4.1 Hidden Markov model

To automatically detect avalanches in our continuous seismic data we used HMMs. This statistical classifier models observations (i.e., the seismic time series or its features) by a sequence of multivariate Gaussian probability distributions. The characteristics of the distributions (i.e., mean and covariance) are derived from training sets of known events, so-called pre-labeled training sets. Several classes describing different types of events can be implemented in the classifier but each class needs its own training set to determine its unique distribution characteristics. Therefore, the actual classifier consists of several HMMs, one for each class. This classical approach, as used for the classification of seismic time series by, e.g., Ohrnberger (2001) and Beyreuther et al. (2012), relies on well-known pre-labeled training sets. In our case, however, avalanches are rare events and it is nearly impossible or too time consuming to obtain an adequate training set. To circumvent the problem of obtaining sufficiently large training sets, we used a new approach developed by Hammer et al. (2012). This classification approach exploits the abundance of data containing mainly background signals to obtain general wave-field properties. Using these properties, a widespread background model can be learned from the general properties. A new event class is then implemented by using the background model to adjust the event model description by using only one training event. The so-obtained classifier therefore consists of the background model and one model for each implemented event class. The classification process itself calculates the likelihood that an unknown data stream has been generated by a specific class for each individual class HMM. More detailed information can be found in Hammer et al. (2012, 2013).

4.2 Feature calculation

Although it is possible to use the raw seismic data as input for the hidden Markov model, we used a compressed form of it, so-called features. Several features can be calculated representing different aspects of the time series such as spectral, temporal or polarization characteristics. The representation of the seismic signals by features is more adequate to highlight differences between diverse event types. Since we used single component geophones, we only used spectral and temporal features. Based on preliminary analysis, we used the following features:

• central frequency

• dominant frequency

• instantaneous bandwidth

• instantaneous frequency

• cepstral coefficients

• half-octave bands.

A detailed list of the functions used to calculate these features can be found in Hammer et al. (2012).

To calculate the features, we used a sliding window with width, w of 1024 samples. The sliding window is then moved forward with a step of 0.05 s or 25 samples, resulting in an overlap of 97 %.

For the half-octave bands we used a central frequency of f_c=1.3 Hz for the first band and a total number of nine bands. Since the geophones have an eigenfrequency of 14 Hz, only signals with a higher frequency are recorded without any loss of information. However, preliminary results showed that half-octave bands with a central frequency higher than f_min=5 Hz are adequate.

4.3 Post-processing

The HMM classification resulted in several hundred events in the avalanche class. Many of these events were, however, of very short duration or only identified at one sensor and did not necessarily coincide with avalanches in the reference catalogue; i.e., these events were likely false alarms. We therefore investigated three post-processing methods to reduce the number of false alarms, namely

1. applying a duration threshold for the detected events;

2. analyzing the results of all sensors by introducing a voting-based classification;

3. analyzing the coherence between all sensors for each detected event.

First, we used an event duration threshold. The duration T_j of any automatically detected event j was determined by the HMM. Based on the analysis of van Herwijnen et al. (2013) and van Herwijnen et al. (2016), we can assume that event duration correlates with avalanche size. The first post-processing method therefore consisted of using a minimal duration T_min for the events as described below in Sect. 5.3.1. Any automatically detected event j with T_j≤T_min was thus removed. Similarly, any avalanche i in the reference catalogue with a duration T_i≤T_min was also removed.

Second, we used a voting-based threshold by tallying the classified events of each sensor. Rubin et al. (2012) used a similar approach and found that with increasing votes the false alarm rate decreased. The overall idea is that although an avalanche event might not be recorded by one sensor, for instance due to poor coupling of the sensor, it is unlikely that an avalanche is missed by all sensors, especially larger avalanches (Faillettaz et al., 2016). Any automatically detected event with V_j≤V_min with V the number of votes was removed.

Third, we used a threshold based on the cross-correlation coefficient between the seven sensors. Wave fields generated by avalanches should be relatively coherent, while wave fields generated by noise (e.g., wind) are expected to be incoherent. We therefore divided the seismic data in non-overlapping windows of 1024 samples and for each window we defined a mean normalized correlation coefficient as

$$\begin{array}{}\text{(2)}& R\left(t_{\mathrm{win}}\right)={\displaystyle \frac{\mathrm{1}}{N_{\mathrm{pairs}}}}\sum _{k=\mathrm{1}}^{N_{\mathrm{pairs}}}{r}_{kl}\left(t_{\mathrm{win}}\right),\end{array}$$

with N_pairs=21 the number of sensor pairs, r_kl(t_win) the maximum in the normalized cross correlation between sensor k and l and t_win the time of the sliding window. The normalized cross correlation is defined as

$$\begin{array}{}\text{(3)}& {\stackrel{\mathrm{‾}}{\mathit{\varphi }}}_{kl}\left(t\right)={\displaystyle \frac{{\mathit{\varphi }}_{kl}\left(t\right)}{\sqrt{{\mathit{\varphi }}_{kk}\left(\mathrm{0}\right){\mathit{\varphi }}_{ll}\left(\mathrm{0}\right)}}},\end{array}$$

with ϕ_kk(0) and ϕ_ll(0) the zero lag autocorrelation of each sensor, which is equal to the energy of each single time window. The maximum of the normalized correlation is picked for a maximum lag of t_max=0.05 s, which is the time a sonic wave field at a speed of 330 m s⁻¹ needs to travel the maximum distance between the most distant receiver pair (≈15 m):

$$\begin{array}{}\text{(4)}& r_{kl}\left(t_{\mathrm{win}}\right)=max{\stackrel{\mathrm{‾}}{\mathit{\varphi }}}_{kl}\left(t\right),\mathrm{|}t\mathrm{|}\le \mathrm{0.05}\mathrm{s}.\end{array}$$

The normalized cross correlation only yields values between −1 (perfectly anticorrelated) and 1 (perfectly correlated). A value of 0 means that the signals are completely uncorrelated. Finally, the coherence of each automatically detected event was defined as

$$\begin{array}{}\text{(5)}& C_j=maxR\left(t_{\mathrm{win}}\right),\mathrm{0}\le t_{\mathrm{win}}\le T_j.\end{array}$$

Any automatically detected event with C_j≤C_min was removed.

4.4 Model performance evaluation

To evaluate the performance of the HMM classification, we compared the automatic picks with the reference data set described in Sect. 3.2. To assign an event classified by the HMM as a positive detection we defined a tolerance interval d: the time $t_j^{\mathrm{HMM}}$ of an event had to be within the interval $t_i-d\le t_j^{\mathrm{HMM}}\le t_i+d$, with t_i the release time of the ith avalanche in the reference data set and d=60 s. The tolerance interval d was necessary, since the release times t_i of the avalanches were picked manually and may contain some uncertainties. In addition, the releases times $t_j^{\mathrm{HMM}}$ do not necessarily coincide with the reference data since the classifier is not an onset picker.

To describe the performance of the classifier we used three values: N_hit, N_unassigned and N_miss. The first value N_hit describes the total number of avalanches which were correctly detected by the classifier, i.e., events identified by the classifier which corresponded to avalanches in the reference data set. The second value N_unassigned describes the number of events identified by the classifier which did not correspond to an avalanche in the reference data set. We do not call these events false alarms as during the manual detection some avalanche events might have been missed that are therefore not present in the reference data set. Avalanche events may still be found in the unassigned detections. Finally, the third value N_miss describes the number of avalanches in the reference data that were not identified by the HMM classifier. The three values were used to evaluate the overall model performance in terms of POD and false alarm ratio (FAR), defined as POD $=N_{\mathrm{hit}}/(N_{\mathrm{hit}}+N_{\mathrm{miss}})$ and FAR $=N_{\mathrm{unassigned}}/(N_{\mathrm{hit}}+N_{\mathrm{unassigned}})$ (Wilks, 2011).

To determine the best threshold values for the post-processing steps (Sect. 4.3), we plotted POD against FAR values for all probability classes and for different values of T_min, v_min and C_min. One curve therefore illustrates the POD and FAR with respect to the probability classes for a fixed threshold value. Ideally, when only considering the 100 % probability class, the POD value should be 1 while the FAR value should also be relatively high since all detections of the lower classes are counted as false alarms. By taking more probability classes into account, the FAR will decrease while the POD value should stay close to 1. A perfect model should therefore result in constant POD values of 1 whereas the FAR values should decrease to 0. For realistic models, however, POD and FAR values are expected to decrease when accounting for more probability classes. By plotting POD against FAR values for different threshold values, the optimal threshold value can be found by searching for the largest area under the curve (AUC). A perfect model would result in an AUC value of 1, while an AUC value of 0.5 corresponds to a model with a 50–50 chance. Threshold values obtained for models with an AUC value lower than 0.5 are therefore not reliable and any random threshold value can be chosen. In our case, the POD–FAR curves did not span from 0 to 1 on the x axis. To determine the AUC value we therefore calculated the ratio between the area under the POD–FAR curve and the area under the bisector with the same x-axis limits:

$$\begin{array}{}\text{(6)}& \mathrm{AUC}={\displaystyle \frac{{\mathrm{AUC}}_{\mathrm{HMM}}}{{\mathrm{AUC}}_{\mathrm{bisector}}}}\cdot \mathrm{0.5}.\end{array}$$

5 Results

5.1 Temporal feature distribution

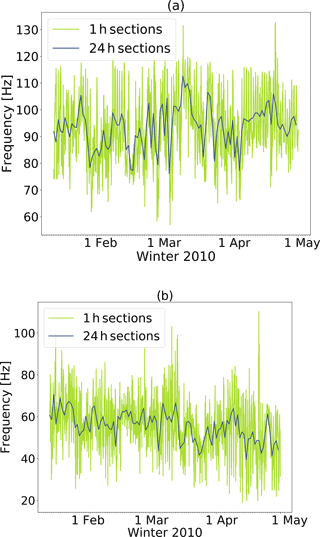
To investigate changes in feature distribution over time, for instance due to diurnal changes in environmental noise levels or seasonal changes in snow cover properties, we calculated hourly and daily mean values for all features (see Fig. 5 for the central frequency and dominant frequency). Throughout the season there were large variations in the feature distribution at various timescales. First, there were strong diurnal variations (yellow lines in Fig. 5). These were observed in all features (not shown). Second, there were also large variations at longer timescales (blue lines in Fig. 5). While for some features there were significant seasonal trends, for instance for the dominant frequency (Pearson $r=-\mathrm{0.56}$, p<0.001; Fig. 5b), for others there were no clear trends, for instance for the central frequency (Pearson r=0.23, p=0.02; Fig. 5a). Building a single background model to classify the entire season would therefore likely not result in a reliable classification. The background model thus has to be regularly recalculated. We therefore decided to recalculate the background model each day to classify the events within the same day.

Figure 5 (a) Temporal variations in the central frequency hourly average (yellow) and daily average (blue). (b) Temporal variations in the dominant frequency.

5.2 Training event

While building a representative background model is important, choosing an appropriate training event is of utmost importance for the classifier. As outlined in van Herwijnen et al. (2016), the avalanche catalogue consists of various avalanches of different size and type. At the beginning of the season the avalanches are most likely dry-snow avalanches, while at the end of the season there a mostly wet-snow avalanches. Our avalanche catalogue only consists of the release time and little information is available on the type of the avalanches. We therefore compared the feature distribution of four different avalanche events, on 21 January, 27 February, 22 March and 24 April 2010, to investigate whether substantial differences related to avalanche type existed (Fig. 6).

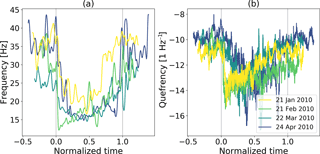
Figure 6 (a) Central frequency with normalized time for four different avalanche events (colors) from 4 different months. For comparison, the time was normalized by the event duration, with 0 indicating the start of the avalanche and 1 the end of the event. (b) Second cepstral coefficient.

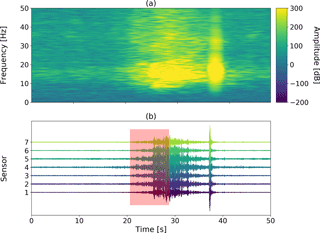
While there were some subtle differences in the feature distribution for the four avalanches (e.g., between the avalanches on 21 January and 22 March 2010 in Fig. 6a), overall the four avalanches exhibited very similar behavior. Thus, when viewing avalanches in the feature space, wet- and dry-snow avalanches appear to be very similar. We therefore used one single avalanche class for the HMM classifier and used one training event to learn the model. Specifically, we used an avalanche with P_ava=100 % recorded on 22 March 2010 (Fig. 7) with a duration of 30 s. However, as seen in Fig. 6, the most rapid changes in feature values occurred at the beginning of the events. In the coda changes in feature values were rather slow, providing limited relevant information for the classifier. We therefore only used the first 8 s of the training event (marked by the red rectangle in Fig. 7).

Figure 7 The event used for training the HMM. (a) Stacked spectrogram of all seven sensors. (b) Seismic waveform for each individual sensor (colors). The red area highlights the part of the signal used as the training event for the HMM.

5.3 Automatic avalanche classification

5.3.1 Single sensor classification

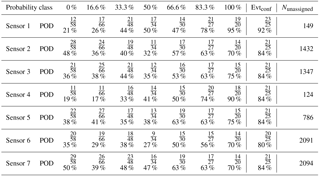
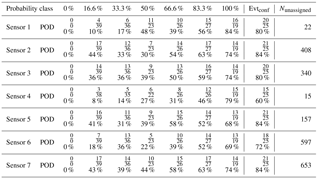
We used the entire reference data set containing 283 avalanche events to evaluate model performance as function of probability class. The first model was built for each individual sensor and without any post-processing. For each sensor a separate model was built containing only the data of the specific sensor. In Table 2 the number of detections for each probability class is listed. For the highest probability class the POD values were relatively high, ranging from 70 to 95 % and the values generally decreased with decreasing probability class. For the confirmed avalanches, the POD ranged between 80 and 92 %. Nevertheless, even for the lowest probability class events were still detected. Furthermore, numerous events, between 124 and 2091 events, were detected for each sensor which were not listed in the reference data set. Clearly without any post-processing the number of unassigned events was high.

Table 2 Number of detections (N_hit) and probability of detection (POD) for each sensor and each probability class as well as the POD for confirmed events Evt_conf and number of events that were not in the reference data set (N_unassigned).

To reduce the number of unassigned events we applied a minimum duration T_min to remove events. To obtain a reasonable threshold value, we determined the area under the POD–FAR curve for different T_min values (Fig. 8).

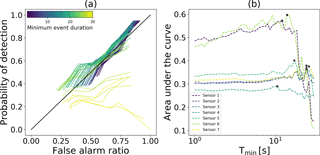
Figure 8 (a) POD–FAR curves for sensor 1 for different minimum event durations T_min (colors). (b) Area under the POD–FAR curve with T_min for all sensors (colors). The stars show the T_min value with the largest area under the curve for each sensor.

Due to the large number of unassigned events (see Table 2) AUC values were generally below 0.5 and using a minimum duration threshold did not result in much improvement. However, for sensors 1 and 6 the number of unassigned events was much lower and there was an optimum T_min threshold value around 12 s (Fig. 8 b). In the following, we therefore used the same minimal duration T_min=12 s for all sensors. While with this T_min threshold the POD values for the highest probability class somewhat decreased, they still remained high (between 68 and 84 %; Table 3). Furthermore, the POD for the confirmed avalanches also remained relatively high, ranging from 60 to 84 %. Note that the duration threshold was also applied to remove events from the reference data set. For a threshold value of T_min=12 s, the number of events in the reference data set reduced from 283 to 170 while the number of confirmed avalanches was not affected.

Table 3 Number of detections (N_hit) and probability of detection (POD) for each sensor and each probability class as well as the POD for confirmed events Evt_conf and number of events that were not in the reference data set (N_unassigned) using a minimal event duration of T_min=12 s.

Overall the number of unassigned events substantially decreased (compare Tables 2 and 3), especially for sensors 1 and 6. For these two sensors the POD values also substantially decreased for the lower probability classes but the two main avalanche periods in March and April are clearly visible in the detections (see Fig. 9a for sensor 1). However, for the other sensors, the POD values remained relatively high for the lower probability classes and there were still many unassigned events and the two main avalanche periods were less evident (see Fig. 9b for sensor 7). Clearly, for some of the sensors the number of unassigned events remained very high.

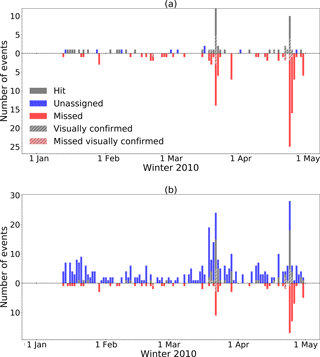
Figure 9 Classification results using a minimal event duration length of 12 s for (a) sensor 1 and (b) sensor 7. Grey bars show the number of matching detections (hit), blue bars show the unassigned events and the red bars show the events that were not detected as an avalanche (missed). The hatched bars indicate the number of hits (grey) or misses (red) for the confirmed events.

5.3.2 Array-based classification

To further reduce the number of unassigned events (potential false alarms), we applied two array-based post-processing methods to eliminate events, namely a minimum number of votes and coherence threshold (see Sect. 4.3). To define an optimal number of votes or coherence threshold we used the same procedure as for the determination of a minimal duration threshold (Fig. 8). Since for these array-based methods the detections from all sensors were pooled, the number of unassigned events was very high. This resulted in much higher FAR values and thus poor model performance with low AUC values, all below 0.5. Arbitrary values for v_min or C_min could therefore be chosen. However, the overall goal of these post-processing steps was to reduce the number of unassigned events, while still retaining a reasonable POD. We therefore analyzed the effect of different threshold values on FAR values as well as on POD values for the probability classes.

Overall, for both processing steps the number of unassigned events decreased with increasing threshold values (Figs. 10 and 11). By using a minimal number of five votes the POD stayed relatively high with a low number of unassigned events. Following the same procedure we selected a coherence value of 0.6. Using this value, the POD was relatively high and the number of unassigned events could be reduced to less than 100 events.

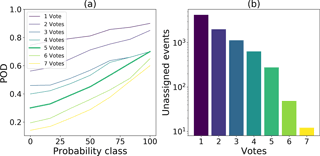
Figure 10 (a) POD for each probability class depending on the minimum number of votes (colors). (b) Number of unassigned events for different number of votes (colors).

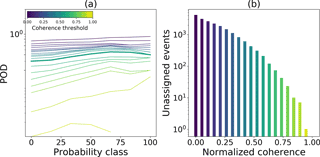
Figure 11 (a) POD for each probability class depending on the minimal coherence (colors). (b) Number of unassigned events for different coherence threshold values (colors).

In total, we thus have three different post-processing steps which can be applied to the data: a minimal event duration T_min=12 s, a minimum number of votes v_min=5 and a coherence threshold C_min=0.6. By combining these three steps, six array-based post-processing workflows were implemented:

• $v:v_j\ge v_{\min }$

• $c:C_j\ge C_{\min }$

• $vc:v_j\ge v_{\min }$ and C_j≥C_min

• $tv:T_j\ge T_{\min }$ and v_j≥v_min

• $tc:T_j\ge T_{\min }$ and C_j≥C_min

• $tvc:T_j\ge T_{\min }$, v_j≥v_min and C_j≥C_min.

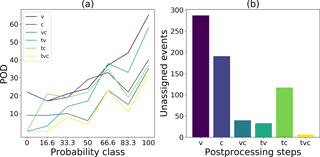
Figure 12 (a) POD for each probability class for different post-processing workflows (colors). v is minimal number of votes used, t is minimal event duration and c is minimal coherence. (b) Number of unassigned events remaining after the post-processing for each workflow.

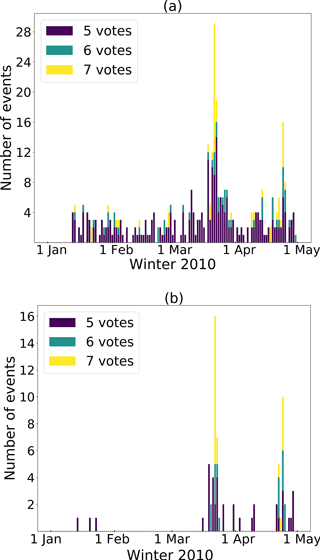
Figure 13 All events detected by at least five sensors. The different colors indicate the number of votes. (a) The results without any limitation of the duration of the events are plotted. (b) Only events with a minimum duration as mentioned before are taken into account. On the right the two main avalanche periods are more clearly visible.

The number of unassigned events decreased most with a combined approach always including the number of votes (vc, tv, or tvc in Fig. 12). When using only one array-based post-processing step, the number of unassigned events remained high (v and c in Fig. 12b). While the lowest number of unassigned events was achieved when combining all three post-processing steps, this model also resulted in low POD values for all probability classes (tvc Fig. 12a). Overall, the highest POD values and the steepest decrease for the lowest probability classes were obtained for the voting-based processing with and without a minimal duration of the events (v and tv in Fig. 12a). For both these post-processing workflows the two periods of high avalanche activity are visible (Fig. 13). However, by also applying the duration threshold, the total number of detections decreased and the two periods in March and April became more clearly visible (Fig. 13b).

5.3.3 Unassigned events

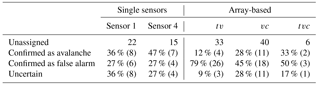
We compared the automatic detections with the reference avalanche catalogue and obtained a large number of unassigned events. It remains unclear whether the unassigned events are all false alarms or partly correspond to avalanches that were not identified in the reference data. We therefore visually inspected the unassigned events. In order to keep this reanalysis manageable, we only focused on the post-processing steps which resulted in less than 50 unassigned events. Thus, we individually investigated single sensor results from sensor 1 and 4 with T_min=12 s and array-based results for tv, vc and tvc. The visual inspection showed that for the single sensor results between 36 and 47 % of the unassigned events were likely unidentified avalanches and less than one-third were false alarms (Table 4). For the array-based results, however, most of the unassigned events (between 45 and 79 %) were false alarms while fewer events were likely associated with avalanches that were missed by van Herwijnen and Schweizer (2011a).

Table 4 Results of the reanalysis of the detections not covered by the test data set. Left side of the table shows the results of the reanalysis of two single sensors, while the right side shows the results of the array-based classification. For the single sensors a minimum duration for the events of t_min=12 s was taken into account. The voting-based processing steps analyzed are minimum number of votes (v), minimum duration (t) and coherence (c).

6 Discussion and summary

We trained HMMs, a machine learning algorithm, to automatically detect avalanches in continuous seismic data recorded near an avalanche starting zone above Davos, Switzerland, for the winter season of 2010. To reduce the amount of data to process, we pre-processed the continuous data using an amplitude threshold (Fig. 2). We then implemented single sensor and array-based post-processing steps and the performance of the models was evaluated using a previously published reference avalanche catalogue obtained from the same seismic data (van Herwijnen and Schweizer, 2011a; van Herwijnen et al., 2016).

After pre-processing the data, the reference avalanche catalogue contained 283 avalanches between 12 January and 30 April 2010, events that were identified by visual inspection of the waveform and spectrogram of a single sensor (van Herwijnen and Schweizer, 2011a). Since only 25 of these events were independently confirmed avalanches, considerable uncertainty remained about the identified events. To reduce the uncertainty in the reference catalogue, three of the authors therefore re-evaluated the data. This allowed us to assign seven subjective probability classes between 0 and 100 % to each event. Overall, only 20 events were marked as certain avalanche (Table 1) and hence the performance of the classifiers can only be evaluated for these particular events. For the remaining events, there are still uncertainties and hence the performance of the classifier can only be estimated. Furthermore, this reanalysis highlighted the difficulty in obtaining an objective and reliable reference avalanche catalogue. It also showed that expert decisions are biased and there is a need for a reliable automatic classifier to identify avalanches in continuous seismic data.

Recent work by Hammer et al. (2017) showed very promising results for applying a HMM to automatically detect avalanches in continuous seismic data. While they only focused on a 5-day period during an exceptional avalanche cycle in 1999, our goal was to classify continuous seismic data spanning more than 100 days. This prevented us from building a single background model to classify the entire season since temporal variations in feature distributions at various timescales were present (Fig. 5). Indeed, when using a single background model to classify the entire season for sensor 1 only two-thirds of the events were detected by having almost 6 times the number of unassigned events. One possible reason for these variations in feature distribution was likely the setup of the sensor array. The geophones were packed in a Styrofoam housing and inserted within the snowpack. As such, less snow covered the sensors than if they had been inserted in the ground, making them more susceptible to environmental noise. Furthermore, it is also likely that the snow cover introduced additional noise in spring due to the rapid settlement and water infiltration. We therefore recalculated the background model for each day and for each sensor to classify the data from the same day. However, for the operational implementation this would be impractical, since there would always be a 24 h delay in the detections. Other strategies for regularly updating the background model should therefore be investigated (e.g., Riggelsen and Ohrnberger, 2014).

We performed the automatic classification over the entire season by recalculating the classifier for each day and for each sensor. Overall, POD values decreased with decreasing probability class and the highest POD values were associated with the highest probability class for all sensors (Table 2). Indeed, between 70 and 95 % of all avalanches in the highest probability class were detected, which is comparable to the results presented by Bessason et al. (2007) and Leprettre et al. (1996), who reported POD values of approximately 65 and 90 %. Nevertheless, without any post-processing, the number of unassigned events was high, questioning the reliability of the models as many of these events were likely false alarms. Post-processing of the results was therefore required. Applying a minimal signal duration drastically reduced the number of unassigned events while still retaining reasonable POD values, in particular for sensor 1 and sensor 4 (Table 3). However, there were large differences in model performance between the sensors (Figs. 8 and 9). The reason for these performance differences is very likely the deployment of the sensors. Indeed, sensors 1 and 4 were deployed at the top of the slope closest to a cornice where the snow was the deepest (van Herwijnen and Schweizer, 2011a). The other five sensors were covered by less snow due to local inhomogeneities, leaving these sensors more sensitive to environmental noise. For future deployments it will thus be important to deploy the sensors below a homogeneous snow cover and not within the snow cover. This should reduce the amount of environmental noise and consequently the number of false alarms.

To further reduce the number of false alarms, we implemented two array-based post-processing steps, namely a voting-based approach and a signal coherence threshold. In combination with the minimal event duration, we thus investigated six array-based post-processing workflows. Results showed that these array-based methods were effective in reducing the number of unassigned events (Fig. 12). However, the POD values generally also decreased, resulting in overall fewer detections. Combined post-processing methods which included the voting-based approach resulted in better model performance, in line with results presented by Rubin et al. (2012). The best model performance was obtained by combining the event duration threshold for events with at least five votes. The number of unassigned events reduced to about 30 and POD values were highest (∼ 55 %) for the highest probability class and decreased for the lower classes. Despite the large differences in model performance for the individual sensors, the model still performed marginally better when pooling the data from the entire array. These results are promising as with an improved sensor deployment strategy array-based post-processing is likely to further improve.

Comparing our model performance to previously published studies is not straightforward. We assigned subjective probability classes to our reference avalanche catalogue rather than using a yes or no approach. Furthermore, we used geophones deployed in an avalanche starting zone, while Bessason et al. (2007), Leprettre et al. (1996) and Hammer et al. (2017) used sensitive broadband seismometers deployed at valley bottom. Therefore, it is very likely that there was more environmental noise in our data and many of the detected avalanches in our reference data set were rather small (van Herwijnen et al., 2016). Given these differences in instrumentation and deployment, our detection results are encouraging and highlight the advantage of using HMMs for the automatic identification of avalanches in continuous seismic data.

The main advantages of the proposed approach is that only one training event (Fig. 7) is needed to classify the entire season. As shown by Hammer et al. (2017), for large avalanches it is possible to build a HMM with a high POD and very low FAR with one training event. Even though we used less-sensitive sensors in this work, we were also able to identify periods of high avalanche activity (compare Fig. 3 with Figs. 9 and 13). Furthermore, when only considering the visually confirmed avalanches, the POD was typically around 80 % (see Tables 2 and 3). This suggests that HMMs can easily be implemented at new sites. In contrast, the model used by Bessason et al. (2007) relied on a 10-year database, and Leprettre et al. (1996) used a set of fuzzy logic rules derived by the experts. Note that the post-processing steps we investigated are likely site dependent, in particular the event duration threshold. However, such a threshold value is intuitive, has a linear influence on model outcome and is thus easily tunable.

For operational use, the model should be able to automatically detect avalanches in near real time. The main disadvantage of the proposed approach is its computational cost. The feature calculation for 1 day takes ≈ 1 h for the pre-processed data and ≈ 7 h for the unprocessed data. Replacing the used features with computationally less expensive attributes would decrease the processing time drastically and encourage real-time applications.

In this work, we classified the data from each sensor individually, requiring a separate background model for each sensor. The results from the different sensors were then combined using post-processing rules either on a voting-based approach or taking the coherence into account. Strictly speaking, the coherence could have been added to the model as an additional feature. However, calculating the coherence for 21 receiver pairs, even after applying the amplitude threshold during pre-processing, was still very time consuming (≈ 200 % real time).

Overall, our results suggest that HMMs may be well suited for the automatic detection of avalanches in continuous seismic data. The variable model performance between the different sensors highlighted problems which can likely be overcome by improving the sensor deployment strategy. Specifically, we suggest that the sensors should be deployed 30 to 50 cm underground at a site with a homogeneous and preferably thick snow cover and to increase the distance between the sensors to apply array processing techniques for source localization (Lacroix et al., 2012). In addition, further avalanche events may be used for training to improve model performance. Finally, incorporating localization parameters as new features in the HMM could open the door for further model improvement, as is done for the automatic detection of avalanches in continuous infrasound data (Marchetti et al., 2015; Thüring et al., 2015). These features can then either be implemented directly into the HMM or be used in additional post-processing steps.