Probabilistic landslide ensemble prediction systems: lessons to be learned from hydrology

Landslide forecasting and early warning has a long tradition in landslide research and is primarily carried out based on empirical and statistical approaches, e.g., landslide-triggering rainfall thresholds. In the last decade, flood forecasting started the operational mode of so-called ensemble prediction systems following the success of the use of ensembles for weather forecasting. These probabilistic approaches acknowledge the presence of unavoidable variability and uncertainty when larger areas are considered and explicitly introduce them into the model results. Now that highly detailed numerical weather predictions and high-performance computing are becoming more common, physically based landslide forecasting for larger areas is becoming feasible, and the landslide research community could benefit from the experiences that have been reported from flood forecasting using ensemble predictions. This paper reviews and summarizes concepts of ensemble prediction in hydrology and discusses how these could facilitate improved landslide forecasting. In addition, a prototype landslide forecasting system utilizing the physically based TRIGRS (Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability) model is presented to highlight how such forecasting systems could be implemented. The paper concludes with a discussion of challenges related to parameter variability and uncertainty, calibration and validation, and computational concerns.

1 Introduction

Landslide prediction at the regional scale is a hot topic within the scientific community as the time-varying aspects of landslide susceptibilities, hazards, and even risks are crucial for emergency response planning and protecting public safety (Baum et al., 2010; Glade and Crozier, 2015). Further, the number of landslides is assumed to increase due to global change (Crozier, 2010; Gariano et al., 2017; Papathoma-Köhle and Glade, 2013). This calls for increased efforts for the development of early warning procedures with the aim of issuing timely warnings of an upcoming hazardous event to temporarily reduce the exposure of vulnerable persons or infrastructure (Thiebes and Glade, 2016). In this paper, we explicitly distinguish between prediction or forecasting systems and early warning systems although the terms are frequently used synonymously within the landslide community. We regard landslide forecasts as predictions of landslide occurrences for a specific time and space, e.g., the likely slope failure locations for an expected rainfall event. Landslide early warnings expand the predictions of forecasting systems and must also cover dissemination and response strategies (UNEP, 2012). Warnings can be considered calls for the public to take protective action, and the timescale of a warning depends on the associated weather event (Stensrud et al., 2009).

The forecasting of rainfall-triggered natural hazards with a rapid onset such as landslides and flash floods greatly benefits from numerical weather predictions (NWPs), in particular from rainfall nowcasting and short-term rainfall forecasting that offer rainfall predictions several hours ahead. While it is evident that processes with a potentially very short response time require more efforts for timely early warning than just real-time measurement of rainfall, real forecasting initiatives are scarce, especially in the landslide community (Devoli et al., 2018). At present, only a few countries operate nationwide landslide early warning systems, and Italy (Rossi et al., 2012) and Norway (Devoli et al., 2015, 2018) are probably the most prominent examples.

The reasons for the few large-area applications of landslide early warning systems are manifold. One important reason might be that losses from landslides are perceived as mainly private and localized economic losses and thus only a few public resources have been allocated to develop sound spatial landslide early warning systems (Baum and Godt, 2010). Consequently, long monitoring time series, which are indispensable for sound and reliable early warning systems (such as those available for floods, storms, etc.), are commonly not available. Another reason might be the complexity of single landslide detachments: the same landslide-triggering event does not necessarily cause other landslides as the time between propagation stage and the collapse phase may vary significantly based on differences in local conditions (Greco and Pagano, 2017).

Present regional landslide forecasting and early warning systems are primarily based on empirical–statistical relationships between landslide occurrences and their associated rainfall events. Guzzetti et al. (2007) and Segoni et al. (2018a) give an overview of rainfall and climate variables used in the literature for the definition of rainfall thresholds for the initiation of landslides; however, such empirical–statistical approaches disregard the physical relationship between rainfall occurrence and the mechanisms leading to landslides, neglecting local environmental conditions and the role of the hydrological processes occurring along slopes (Reichenbach et al., 1998; Bogaard and Greco, 2018). Attempts to relate landslide-triggering thresholds to weather and other physically based characteristics can be very challenging given the quality of currently available data (Peres et al., 2018).

Physically based forecasting approaches put a strong focus on modeling the actual landslide initiation; however, such approaches are not commonly used for landslide forecasting and early warning systems. A reason for the negligence of such process-based models might be related to concerns about data quality and parameter uncertainties when dealing with large areas. However, recently reported methodological advances with respect to the treatment of uncertainties for operational flash flood forecasting systems (Hapuarachchi et al., 2011; Liu et al., 2012; Yu et al., 2015) could also facilitate the implementation of physically based landslide forecasting and early warning systems.

With this paper, we want to identify a gap in the prevalent landslide forecasting methods. Although ensemble predictions and the explicit integration of uncertainties in forecasts are now widely used in the fields of meteorology and hydrology, such activities are not yet common for landslide forecasting. We therefore think that the landslide community could benefit from the experiences of the neighboring disciplines and that our paper can provide a starting point for increased efforts in this direction. The overall aim of this paper is to form a basis for discussion on how probabilistic landslide forecasting and early warning systems could be implemented. To this end, we provide a review on how probabilistic modeling methods and in particular ensemble predictions are applied for hydrological forecasts and how these deal with uncertainties. Moreover, we highlight challenges and limitations for the calibration of models focusing on extreme events such as landslides. An important novelty of our paper consists in the presentation of a landslide ensemble forecasting framework utilizing the physically based landslide model Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability (TRIGRS), which we implemented within an open-source environment. In our case study, the geotechnical parameters are treated probabilistically to highlight how ensemble prediction for landslides could be implemented as operational systems. In addition, we present suggestions on how probabilistic landslide forecasts can be visualized in a way on which stakeholders can base their decisions. We conclude the paper with a discussion of concerns about and challenges of probabilistic landslide forecasting approaches utilizing physically based models that we hope will ultimately lead to increased efforts in this research direction.

1.1 Probabilistic forecasting in hydrology and ties to landslide research

When considering ensemble prediction systems (EPSs), one should clarify what is expressed with the term ensemble and why EPS should be used at all since it is virtually unused in the landslide community. In the Guidelines on Ensemble Prediction Systems and Forecasting issued by the World Meteorological Organization (WMO, 2012), EPSs are defined as

NWP systems that allow us to estimate the uncertainty in a weather forecast as well as the most likely outcome. Instead of running the NWP model once (i.e., a deterministic forecast), the model is run many times from very slightly different initial conditions. Often the model physics is also slightly perturbed, and some ensembles use more than one model within the ensemble (multi-model EPS) or the same model but with different combinations of physical parameterization schemes (multi-physics EPS). […] The range of different solutions in the forecast allows us to assess the uncertainty in the forecast, and how confident we should be in a deterministic forecast. […] The EPS is designed to sample the probability distribution function (pdf) of the forecast, and is often used to produce probability forecasts – to assess the probability that certain outcomes will occur (WMO, 2012).

Krzysztofowicz (2001) argues that forecasts should be stated in probabilistic, rather than deterministic, terms and that this “has been argued from common sense and decision-theoretic perspectives for almost a century” (Krzysztofowicz, 2001). But still, by the new millennium, most operational hydrological forecasting systems relied on deterministic forecasts and there was a strong emphasis on finding the best estimates rather than quantifying the predictive uncertainty (Krzysztofowicz, 2001). However, those times have been overcome a decade later (Cloke and Pappenberger, 2009). From a scientific and historical perspective, landslide prediction has strong roots in empirical–statistical threshold-based approaches (Wieczorek and Glade, 2005; Guzzetti et al., 2007). This has been valid until today since most operational landslide forecasting and early warning systems rely on the relationship between rainfall and landslide occurrence, thus representing only a simplification of the underlying physical processes. Bogaard and Greco (2018) critically analyze the role of rainfall thresholds for shallow landslides and debris flows from a hydrometeorological point of view. It is beyond the scope of this paper to provide a review of past and present landslide early warning systems, which can be found elsewhere (e.g., Baum and Godt, 2010; Alfieri et al., 2012a; Thiebes, 2012; Thiebes and Glade, 2016; Piciullo et al., 2018). Guidelines on how landslide early warning systems can be implemented have been put forward by Intrieri et al. (2013), for example.

One reason why landslide forecasting is seemingly more challenging than flood forecasting can be attributed to the spatial and temporal predictability of landslide processes. The spatial occurrence of floods is topographically foreseeable and controllable but is more difficult to assess for landslides in distributed modeling due to their localized nature (Alfieri et al., 2012a; Canli et al., 2017). Despite considerable measurement uncertainties in phases of high flow, the prediction domain in flooding, which is usually streamflow, is more straightforward and can be measured more or less accurately over a long time.

In the past 15 years, a mind-set of adapting probabilistic concepts to account for inherent uncertainties has taken over in the hydrologic community and the move towards EPS in flood forecasting represents the state of the art in forecasting science, following the success of the use of ensembles for weather forecasting (Cloke and Pappenberger, 2009). Unfortunately, initiatives such as the Hydrological Ensemble Prediction Experiment (HEPEX) have not been fostered in the landslide community to date. The general aims of this ongoing bottom-up initiative are to investigate how to produce, communicate, and use hydrologic ensemble forecasts in a multidisciplinary approach (Schaake et al., 2007). One reason for the absence of such cooperative efforts might be the political, and therefore also financial, situation that led to the advancement of ensemble predictions in hydrology. Many international bodies demonstrated their interest in EPS, which led to this superior position of hydrological prediction. This is even more so the case when taking into account transboundary floods that are typically more severe in their magnitude, affect larger areas, and cause more damage and overall losses (Thielen et al., 2009).

1.2 Benefits and types of probabilistic approaches

Generally speaking, in an ensemble forecast small changes (perturbations) are made to the model parameters and then the model is rerun with these slightly perturbed starting conditions. If the different model realizations (ensemble members) are similar to each other, the forecasting confidence is rather high. Conversely, if they all develop differently, the confidence is much lower (WMO, 2012). By considering the proportion of the ensemble members that predict an event, e.g., a storm or a landslide, we can make an estimate of how likely the event is.

The term ensemble prediction for environmental applications was coined in the field of meteorology, thus describing the application of NWP systems, but it is used in different ways in neighboring disciplines. The atmospheric component is consistently described as weather ensemble input, yet the same applies to how observations of the land surface are incorporated into distributed forecasting models. In the data assimilation stage, ensembles of plausible land surface state observations (e.g., initial streamflow, soil moisture, snowpack) are created. Using multiple feasible parameter sets for each model or for each model run will realistically increase the spread of possible outcomes, yet it is more objective in terms of considered input parameters that were not directly observed (Schaake et al., 2007). Thus, the term ensemble prediction may be used in any instance of multi-parametric or multi-model data input that is used for forecasting the target variable.

In landslide research, a number of attempts have been reported that explicitly address ensemble techniques as a means of overcoming limitations from purely deterministic approaches or by increasing the predictive performance of statistically based landslide susceptibility mapping (e.g., Arnone et al., 2014; Cho, 2007; Haneberg, 2004; Melchiorre and Frattini, 2012; Rubio et al., 2004). None of them, however, incorporate ensemble techniques in real-time applications. Pradhan et al. (2017) used an ensemble approach to evaluate the output of a physically based model for a statistical machine learning model in varying hydrological conditions. Their ensemble model is based on a maximum entropy model that creates and combines multiple models to improve modeling results. However, their distributed output does not predict when or exactly where landsliding will occur but yields a classified map with information on where landslide occurrence can be expected over the long-term. Thus, their presented ensemble approach indicates landslide susceptibility that may be applicable for spatial planning. While the term ensemble is by no means used a lot in landslide studies, it seems that it is predominantly used by the statistical landslide susceptibility modeling community (e.g., Lee and Oh, 2012; Althuwaynee et al., 2014a, b). It is, however, not used in a way to address uncertainties in a forecasting model (Bartholmes and Todini, 2005; Vincendon et al., 2011). In a very promising approach, Chen et al. (2016) coupled a deterministic model with probabilistically treated geotechnical parameters with rainfall input from an operational multi-scale and multi-member NWP system (GRAPES) to forecast spatial landslide occurrences with their ensemble prediction model (GRAPES-Landslide).

While there are not many landslide studies using or addressing ensemble techniques, there has been a lot of work done on probabilistic landslide hazard analysis in the recent past. Lari et al. (2014) proposed a probabilistic approach expressing hazard as a function of landslide destructive power in which landslide intensity (in terms of displacement rate) is considered rather than the magnitude. Haneberg (2004), Park et al. (2013), Raia et al. (2014), Lee and Park (2016), and Zhang et al. (2018) treat soil properties in regional-scale applications in a probabilistic way by randomly selecting variables from a given probability density function (pdf), mostly by means of Monte Carlo (MC) simulation. Salciarini et al. (2017) tried to enhance those approaches by considering geostatistical methods to provide the spatial distribution of soil properties and by using the point estimate method (PEM) as a computationally more efficient method compared to MC simulation. But still, none of those probabilistic approaches were explicitly aimed at spatial real-time early warning systems. The research of Schmidt et al. (2008) represents a remarkable exception: they proposed a coupled regional forecasting system in New Zealand based on multiple process-based models (NWP, soil hydrology, slope stability). Unfortunately, a continuation of this research was not further pursued.

1.3 The hydrological equivalent of rainfall-induced shallow landslides: the case of flash floods

One major difference between flood and landslide early warning is the available lead time. While the lead time in larger river basins is sufficiently long to provide warnings for potentially hazardous situations from river flooding, shallow landslides, in the case of first-time failures, generally occur suddenly and are spatially unforeseeable in a specific area susceptible to landsliding. As opposed to regular floods, however, flash floods can indeed be considered an appropriate counterpart to rainfall-induced shallow landslide occurrence. Flash floods are, similar to shallow landslides, characterized by the superior importance of small-scale extreme precipitation events and their rapid onset, which leaves only little response time. It is therefore appropriate to examine how flash flood forecasting is performed and how it is applicable to landslide forecasting. What makes landslide forecasting particularly challenging is the evolutionary sequence of the process.

Greco and Pagano (2017) distinguish among three stages of a typical predictive system's architecture: (i) the predisposing stage, (ii) the triggering and propagation stage, and (iii) the collapse stage. While in flood forecasting applications stages (ii) and (iii) are hardly distinguishable from each other, for rainfall-induced landslides this is not necessarily the case. While the predisposing stage (i) is determined by increasing pore water pressure due to a varying length of rainfall input that worsens the slope stability conditions, the triggering and propagation stage (ii) spans from first local slope failures until the formation of associated slip surfaces. The collapse phase (iii) ultimately consists of the mobilization of the entire mass, leading to the actual failure. However, the time between stages (ii) and (iii) may vary significantly based on differences in landslide types, local geomorphology, soil, vegetation, etc. and spans from a couple of minutes (e.g., flow slides in slopes covered with shallow coarsely grained soils) to years (e.g., earth flows in slopes of finely grained soils) (Greco and Pagano, 2017). Even when spatially distributed process-based landslide predictions are performed in relatively homogeneous regions, this time offset still prevails and makes landslide modeling in any context a challenging task. Therefore, warnings should generally be issued during indications of stage (ii) since the lead time of stage (iii) might be too short given the rapid kinematic characterization of the post-failure behavior, as recent disastrous examples in Italy have shown (Greco and Pagano, 2017).

Flood forecasting systems relying only on rainfall observations do not allow for a sufficiently long lead time for warnings. Extending this forecasting lead time further than the watershed response times requires the use of quantitative precipitation forecasts (QPFs) from NWP (Vincendon et al., 2011). Additionally, models to represent hydrologic and hydraulic processes within a catchment to determine how rainfall–runoff accumulates are required (Hapuarachchi et al., 2011). With regard to producing quantitative precipitation estimates (QPEs) in real time, research has gone into blending multiple sources of information (radar, satellite, and gauged data) to increase the accuracy of QPEs. This process is generally referred to as data assimilation and is considered to be increasingly important for improving hydrological predictions (Reichle, 2008). For predicting flash floods, however, lead times of several hours are desirable and thus high-resolution QPFs with 1–6 h lead times are generated. In recent years, the spatial (<5 km) and temporal (<1 h) resolutions of NWP model rainfall forecasts have significantly improved, while the combination of such NWP model forecasts with input from recent radar, satellite, and gauged rainfall data additionally increased the accuracy of nowcasting products (Hapuarachchi et al., 2011). Based on such high-resolution NWP model forecasts, probabilistic EPSs have aided in exploring and quantifying uncertainties. Numerous studies have used those probabilistic precipitation forecasts to drive hydrological models (Vincendon et al., 2011; Bartholmes and Todini, 2005; Siccardi et al., 2005; Thielen et al., 2009). The application of such convective-permitting ensemble NWPs is computationally very demanding and still in its infancy with respect to flash flood prediction (Alfieri et al., 2012b). However, a further reduction of the spatial uncertainties of high-resolution rainfall fields is highly desirable, given the fact that rainfall is still considered to be the most uncertain parameter in hydrological forecasting systems (Hapuarachchi et al., 2011; Alfieri et al., 2012b).

1.4 Many sizes fit all: the concept of equifinality

The concept of equifinality is deeply rooted in the hydrological community. It expresses an acceptance that many sets of parameters may provide equally acceptable forecasts (Beven, 1996; Beven and Freer, 2001; Collier, 2007). The concept of equifinality revolves around the rejection of the concept of the optimal model in favor of multiple possibilities for producing acceptable simulations (Beven and Freer, 2001). This concept is based on the understanding of physical theory and relates to the plethora of interactions among the components of a system whose resulting representations may be equally acceptable. Research generally follows a working paradigm that should lead to realistic representations of the real processes and characteristics. This idea of identifying a single optimal representation of reality is very distinct in environmental sciences. A major problem arises from the scale discrepancy between sampling and distributed modeling in which the use of global parameters undoubtedly leads to errors in predicting local responses at points with unique characteristics (Beven and Freer, 2001).

Geomorphological systems can be considered transient, inheriting remnants of past and present processes. Environmental systems can exhibit certain degrees of chaotic behavior, which results in an inability to express the trajectory of their development based on present-day evidence alone. Therefore, equifinality should not be considered an indication of a poorly developed methodology but as something inherent in geomorphological systems (Beven, 1996). However, it should most certainly not serve as a loophole for an inadequate methodology or model setup. A practical consequence of this equifinality may lead to a more robust approach to testing the viability of different model setups with the aim to reject some but to retain many of the offered solutions (Beven, 1996). Similarities and differences in model results should ultimately lead to an improved process understanding and hence predictive models with a higher sensitivity and specificity.

1.5 Calibration and validation

A model is an abstraction and a simplification of reality, hence the need for assessing its validity. Model validation provides legitimacy in terms of arguments and methods (Oreskes et al., 1994). However, model validation is difficult when the most interesting events are rare, which is generally the case for flash floods or landslides. Also, calibration might be difficult for certain variables, or where suitable observations are not available. The WMO (2012) suggests that direct model output (DMO) from ensembles, although not ideal, still provides valuable information (WMO, 2012). The probabilistic forecasts with a DMO might not be as sharp (e.g., larger ensemble spread), but they still offer an estimate of the uncertainties and thus pose an advantage over purely deterministic forecasts. But even where measurements of modeling parameters are available, it has often shown that those parameters cannot be assumed constant in space or time, which makes calibration even more difficult. Additionally, the scale of measurement generally differs significantly from the scale at which the applied model requires “effective” parameter values to be specified (Beven, 1996).

Deterministic models for landslide prediction synthesize the interaction among hydrology, topography, vegetation, and soil mechanics in order to physically understand and predict the location and timing of landslide triggering. These models usually contain a hydraulic and a slope stability component with different degrees of simplification (Formetta et al., 2016). In most cases, the target variable is the slope safety factor (FoS), which is useful as it enables decision makers to take actions when it falls short of a certain threshold (the slope is unstable with FoS < 1.0, but higher thresholds are used in practice). In contrast to the FoS, which at least in theory has a clear physical meaning, the definition of thresholds still poses a challenge when it comes to probabilities of events. When talking about the probability of events occurring, these events must be defined:

• the threshold value to be exceeded.

• the exact time or time period to which the forecast refers.

• the exact location or area to which the forecast applies.

• uncertainties and their role in the modeling process.

With regard to those questions and as a starting point, the FoS is a suitable variable for probabilistic forecasting. Yet it has two major flaws: (a) it represents the ratio of resisting forces to driving forces that is commonly not directly measured in the field and cannot be directly monitored, and (b) landslide events are rare and their future location of occurrence remains unknown until they occur. This makes landslide calibration a challenging task. And there are limitations of model calibration in the case of rare events. Commonly, calibration will improve the reliability of forecasts (i.e., the match of the target variable or forecast probabilities to frequency of observations of the event) but reduce the resolution of the forecast (the ability to discriminate whether an event will occur or not). Consequently, calibration will improve forecasts of common events but will also lead to the underprediction of more extreme events (WMO, 2012). The WMO (2012) argues that this is the case for rare events since the statistical distributions are trained to the more common occurrences. Hence, for rare events calibration cannot be expected to provide significant improvement over the raw forecasts. Considering the issue of equifinality, changing the calibration period or the goodness-of-fit measure results in an altered ranking of parameter sets to fit the observations. Consequently, there is no single parameter set (or model structure) that serves as the characteristic parameter input for any given area, but there is a certain degree of model equifinality involved when reproducing observations with model predictions (Beven, 1996). Therefore, given the issues with multiple (interacting) parameter values, measurement scales, spatial and temporal heterogeneity, or the model structure, there can never be a single set of parameter values for the calibration process that represents an optimum for the study area, but calibration can contribute to the reduction of range in the possible parameter space.

Before being used for predictions, calibrated parameter sets have to be exposed to independent event data in order to further evaluate the validity – or, more appropriately, the empirical adequacy – of the results obtained with the calibrated set of parameters. In practice, few (if any) models are entirely confirmed by observational data, and few are completely refuted (Oreskes et al., 1994).

As a result, this is a field in which probabilistic model output really shines, as it expresses the entire model spread with its inherent uncertainties not in absolute terms but shows the relative performance of a model with respect to observational data. Many decision makers and practitioners in all kind of Earth science-related fields still favor absolute model output, especially in areas in which public policy and public safety are at stake. Unfortunately, certainty is an illusion due to the lack of full access, either in time or space, to the phenomena of interest (Oreskes et al., 1994).

2 Case study

With a case study application to a larger study area in Austria (approx. 1366 km²) we put forward a physically based landslide forecasting framework using an ensemble prediction approach. As this case study is intended as a proof of concept and not as an operational forecasting system, we chose a simplified ensemble modeling approach in which only the geotechnical parameters are treated probabilistically; notably the precipitation input is considered a fixed input and consists of a historic rainfall event. However, from a technical point of view, real rainfall forecasts could easily be integrated. In addition, we present how probabilistic landslide forecasts could be visualized in order to support the decision-making process and early warning.

2.1 Study area

The Rhenodanubian Flysch zone (RDF) in the federal state of Lower Austria stretches over approximately 130 km in a SW–NE-striking direction. The study area is limited to this geological zone in order to keep the subsurface as homogeneous as possible (Fig. 1). The Cretaceous–early Tertiary RDF is located in the northern foothills of the East Alps, in between the Molasse basin to the north and the northern Calcareous Alps to the south. The RDF is a paleogeographic–tectonic unit as part of the oceanic Penninic zone that was to a large degree part eliminated in the subduction process involved in the Alpine orogeny (Hesse, 2011). Flysch materials in the RDF are typically deeply weathered and mainly consist of alterations of pelitic layers (clayey shales, silty shales, marls) and sandstones. Physiographically, the RDF can be characterized as a low mountain region with a highly undulating terrain. It is exceptionally prone to landsliding, exhibiting around five landslides per square kilometer (Petschko et al., 2014). Heavy rainfall events (exceeding 100 mm per day) as well as rapid snowmelt are considered to be the main triggering factors for slope failures in the region (Schwenk, 1992; Schweigl and Hervás, 2009).

Figure 1 (a) Location of Lower Austria in Austria. (b) Location of the Rhenodanubian Flysch zone in Lower Austria (DTM: CC BY 3.0 AT–federal state of Lower Austria). (c) Typical earth slide in Lower Austria after a heavy rainfall event in May 2014 (Photograph by K. Gokesch).

2.2 TRIGRS model

Physically based models used to be attributed to local-scale applications (e.g., Corominas et al., 2014; van Westen et al., 2008) because of their computational requirements and data constraints. This has clearly shifted in the last years and by now physically based models can be quite commonly found to evaluate rainfall-induced landslide susceptibility at the regional scale (Ciurleo et al., 2017; Park et al., 2017; Thiebes et al., 2017). The majority are based on the infinite-slope model, which only requires a few input parameters to be suitable at a regional scale. Increasing the number of physical parameters in a model comes at the cost of an increased demand for data and model parameterization, while the available data for calibration do not increase at the same time and could lead to problematic over-parameterization (Beven, 1996). Even the simplest infinite-slope stability models generally require a higher level of parameterization than can be justified by available data. However, there are some general features of hillslope hydrology that are relevant to slope instability that can be considered to a certain degree by infinite-slope models: vertical infiltration, dependence of infiltration on initial soil moisture conditions, varying timescales for infiltration, and lateral flow (Baum et al., 2010). As a result, TRIGRS (transient rainfall infiltration and grid-based regional slope-stability analysis; refer to Baum et al. (2008) for details), which we use in this case study, offers a good trade-off between model complexity and flexibility while we acknowledge the availability of other dynamic, physically based models that were applied at a regional scale, such as STARWARS/PROBSTAB (Kuriakose et al., 2009) or r.slope.stability (Mergili et al., 2014a). Raia et al. (2014) with their TRIGRS_P model and Salciarini et al. (2017) with their PG_TRIGRS model have already attempted a probabilistic TRIGRS derivative in the recent past that gave us the confidence to use TRIGRS in an automated probabilistic approach.

TRIGRS was specifically developed for modeling the potential occurrences of shallow landslides by incorporating transient pressure response to rainfall and downward infiltration processes (Baum et al., 2008). It uses the classical infinite-slope stability approach, based on the Mohr–Coulomb model with effective cohesion c^′ (N m⁻²), effective angle of internal friction φ^′ (^∘), and specific weight of the soil γ (N m⁻³) as geotechnical parameters. Initial soil conditions are assumed either saturated or tension-saturated. TRIGRS computes transient pore-pressure changes to find analytical solutions to partial differential equations, representing one-dimensional vertical flow in isotropic, homogeneous materials due to infiltration from rainfall events with durations ranging from hours to a few days. It uses a generalized version of the infiltration model solution of Iverson (2000) to the boundary problem posed by Richard's equation. This solution assesses the effects of transient rainfall on the timing and location of landslides by modeling the pore water pressure of a steady component and a transient component (Liao et al., 2011). However, the model is limited by its distributed one-dimensional modeling approach with noninteracting grid cells and its simplified soil–water characteristic curve (Baum et al., 2010). However, recently Tran et al. (2018) presented a case study in which TRIGRS is combined with other models to be able to analyze slope stability in 3-D. The entire theoretical basis together with all model-related assumptions and equations can be found in Baum et al. (2008, 2010). TRIGRS computes a FoS for each grid cell based on an infinite-slope model. It allows for the implementation of spatially varying raster input (e.g., rainfall, soil depth, infiltration) to account for horizontal heterogeneity. The FoS can generally be referred to as the ratio of resisting forces (the resisting basal Coulomb friction) over driving forces (the gravitationally induced downslope basal driving stress) on the potential failure surface, with a FoS < 1.0 indicating slope instability and a FoS ≥ 1 slope stability.

2.3 Model setup

The probabilistic modeling setup is realized entirely in an open-source framework. This was carried out not only to make it as easily reproducible as possible, but also because it offered the largest flexibility. TRIGRS, which itself is open source, is operated by providing input text files. These input files are used to specify the numerical values of the input parameters, the location of the input raster files in the file system, and all other relevant grids to be considered (e.g., spatially distributed rainfall maps, different property zones to subdivide the study area in homogenous regions, spatially distributed soil depth maps). We used the Python programming language in a script for all string formatting procedures that receives its data from an initialization file. That Python script is also used for parsing the raw input into variables usable for TRIGRS. User-provided arguments in this initialization file hold the number of property zones needed, the rainfall duration pattern, number of time steps, and all variables that are used for the probabilistic treatment of parameters, such as minimum and maximum values for soil depth, effective cohesion and effective friction angle, and the number of model runs. The most recent rainfall input can be automatically imported by predefined naming conventions.

We used the GDAL package (GDAL Development Team, 2017) for reading and writing raster files and the NumPy package (van der Walt et al., 2011) for all raster calculations in the Python script. Based on the number of predefined model runs, for each run a single deterministic output is generated based on the selected input parameters derived randomly from a normal distribution. We computed 25 model runs for each hour, which resulted in 25 equally probable model results based on the different input parameters. After the first of the 25 model runs, a file is created and updated after each iteration. This probability of failure (PoF) grid file tracks the number of model runs that resulted in a FoS < 1.0 (unstable cell) for any given raster cell. Thus, the PoF represents the number of simulations that resulted in instability in relation to the total number of simulations.

All used variables, deterministic model outputs (i.e., the FoS maps), and the probabilistic model output (i.e., the PoF map) are parsed through to R (R Core Team, 2017). In R, all piped arguments from the Python script are used for producing ready-to-use maps (packages: rgdal, Bivand et al., 2017; sp, Pebesma and Bivand, 2005) or to visualize performance measures such as ROC plots (package: ROCR; Sing et al., 2005). The entire procedure from importing raw data to producing usable maps is fully automated within an executable file that may be initiated every hour. This open code structure is flexible enough to enable the direct implementation of the most recent available data (rainfall data, soil moisture data, etc.) with minimal effort and thus makes it a useful tool in considering data assimilation techniques.

2.4 Data and model parameterization

The main data used in this case study consist of a digital terrain model (DTM), geotechnical parameter and soil depth ranges, and rainfall data. In addition, landslide inventory data were used for a qualitative validation of the simulation results. Information on infrastructure from the OpenStreetMap (OSM) database was used for the calculation of building exposures. Table 1 lists the utilized data and their properties.

Table 1 Data used in the case study.

We used a bare-earth lidar-based DTM, i.e., the vegetation and most infrastructure features such as houses are filtered. The raster cell size of the DTM to derive all model-relevant topographical parameters used in this case study was 10 m. This cell size allows for a sufficiently high representation of surface topography without losing too much information through surface aggregation and smoothing.

As rainfall input, a historic 3 h long rainfall event was used. This specific rainfall event occurred in June 2009 and was a period of strong precipitation within an approximately 10 h long rainfall that covered the study area in its entirety. Precipitation was the strongest in the central and western parts of the study area and reached a total of up to 59 mm while hourly intensities reached maximum values of 25 mm. The historic rainfall event was used to facilitate our proof of concept; for an operational landslide forecasting and early warning service it would be necessary to replace the file with actual rainfall forecasts by meteorological services. The spatially distributed rainfall raster maps representing hourly rainfall are based on an automated geostatistical interpolation (the methodology is described in detail in Canli et al., 2017). The selection of hourly rainfall input as well as the decision to choose a 3 h timeframe was made arbitrarily as for the study area there is no published information available on the hydrological response of landslides to rainfall. The spatial resolution of 1 km for the rainfall input was resampled to match the cell size of the DTM, which is a prerequisite of TRIGRS.

Information on the spatial distribution of landslides was used for a qualitative validation of the modeling results for the following reasons: (a) for Lower Austria a very comprehensive and spatially accurate landslide inventory based on high-resolution airborne lidar-based DTM mapping exists (Petschko et al., 2015); however, it does not contain any temporal information; (b) the Building Ground Registry (BGR) is the most comprehensive source of reported damage-causing landslides in Austria; however, its spatial and temporal accuracy is insufficient for physically based model calibration and validation. As a result, it is not directly possible to quantitatively validate the model outputs.

For the visualization of our probabilistic results and for the calculation of building exposures, the OSM database was used. OSM covers almost the entirety of existing buildings in Austria and is based on official Austrian administrative data, which are under an open government data (OGD) license. Building exposure was computed by a simple spatial join that assigned each building the highest PoF value within 25 m. This value, while arbitrarily chosen, further accounts for spatial uncertainties since TRIGRS models only the location of landslide initiation.

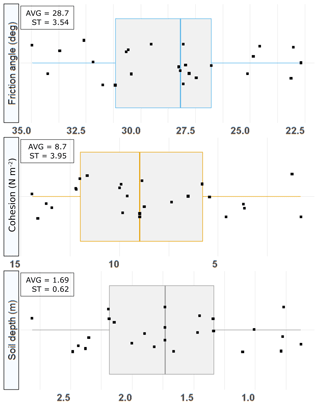
Model parameterization over large areas is a difficult task given the poor spatial comprehension of the spatial organization of involved geotechnical and hydraulic input parameters. Tofani et al. (2017) performed 59 site investigations to parameterize their distributed slope stability model; this number of in situ soil samplings with associated lab measurements is exceptional and a solid foundation for determining the pdf's. Although Tofani et al. (2017) ultimately used the median value for each lithological class, the box plots suggested normal to lognormal parameter distributions. This is a common observation and might be a result of the central limit theorem, which indicates that lumping data from many different sources (i.e., different in situ soil sampling sites in this case) tends to result in a normal or lognormal distribution (Wang et al., 2015). Based on these findings, plausible geotechnical parameter ranges in this study were selected from published sources and a normal distribution was assumed. We used a simple MC simulation of multiple randomly chosen parameter sets within a predefined parameter range and within a single model structure as the basis for incorporating the inherent parameter uncertainties.

Parameters that were considered in a probabilistic way are soil depth, c^′, and φ^′ (Fig. 2); rainfall and elevation data (i.e., the DTM) were utilized as fixed input. We assumed fully saturated conditions (volumetric water content θ=40 %) and slope-parallel groundwater flow for the sake of simplicity and given the absence of appropriate initial water conditions. Using all this information, it was possible to conduct a spatially distributed probabilistic assessment of the FoS, expressed as the PoF. As TRIGRS is capable of calculating the increase in pore water pressure within the soil, the result is a distributed representation of the decrease in shear strength until slope failure (FoS < 1.0) is reached at a certain depth.

Figure 2 Probabilistically derived modeling parameters based on random sampling from a normally distributed function. Jittering dots (to prevent overplotting) indicate individual samples within a plausible parameter range.

3 Results

Figure 3 shows the results for a selection of four model iterations out of the total of 25 based on a spatially distributed hourly rainfall input over 3 h. Each ensemble member was initialized with probabilistically derived geotechnical parameters that are displayed on each map. EPS representations that show a range of individual ensemble members are referred to as postage stamp maps by the WMO (2012) and allow forecasters to view the scenarios in each member forecast. The results for our specific rainfall event indicate quite significant changes across individual members but also partly high similarities, although parameters change drastically among some of the members. For example, a depth of 2.5 m, an effective cohesion of 13.4 Nm⁻², and an effective friction angle of 35^∘ in one of the deterministic outputs reveal the almost identical FoS distribution compared to a depth of 2.0 m, an effective cohesion of 5.4 Nm⁻², and an effective friction angle of 22.7^∘.

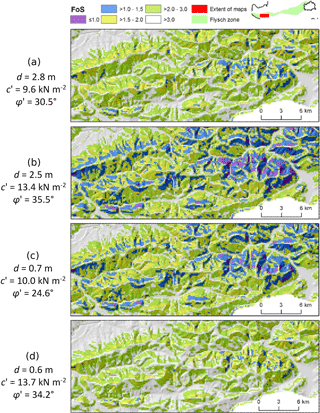
Figure 3 Selection of individual model iterations (postage stamp map). Each ensemble member was initialized with altered geotechnical parameters within a plausible range to account for variability and spatial uncertainty and for a specific rainfall event. FoS values <1 indicate slope instability.

By using a probabilistic representation, this variability and uncertainty of model outputs is accounted for. Here, the probability is estimated as a proportion of the ensemble members that predict an event to occur (FoS < 1.0) at a specific raster cell. For example, a probability between 0.75 and 1.0 means that a specific raster cell, under varying input parameter settings, was modeled as unstable in 75 % to 100 % of all model runs. To provide additional information and to support different actors responsible for managing landslide hazards, the PoF is underlain with building polygons and roads for a direct exposure visualization of the elements at risk of landslides (Fig. 4). High building exposure along the river is a modeling artifact introduced by the steep retaining wall and the associated sudden and steep decline in slope angle. For operational landslide forecasting, these areas would need to be excluded to avoid false alarms. The results of the PoF map suggest quite a narrow ensemble spread, which could be an expression of equifinality. The narrow ensemble spread can be considered to be some kind of spatial confidence buffer that gives some reliance that under varying input data the location of possible slope failure is modeled quite consistently at the more or less same location.

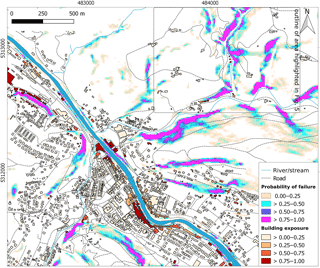
Figure 4 Probability of failure depicted as a proportion of the ensemble members that predict an event to occur (FoS < 1.0). Building exposure to current slope failure predictions adds an additional information layer for decision makers. Buildings and roads are imported from the OSM database (© OpenStreetMap contributors).

In this case study, only a qualitative validation could be performed due to landslide inventory data insufficiencies. Qualitative validation by visual comparison (Fig. 5) indicates, for this specific time and under the given rainfall input, that there is an agreement between some of the landslide initiation points and areas of high failure probability. It must, however, be noted that the triggering conditions of the mapped landslides are unknown and therefore no complete agreement with the model results for our specific rainfall event can be expected.

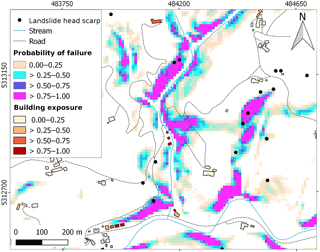
Figure 5 Probability of failure map detail for a specific rainfall event. Known historic landslide initiation points (black dots) partly overlap with current slope stability conditions. However, high spatial resolution, and therefore a high degree of spatial discontinuity, poses a risk for missing many real landslide events in an early warning situation.

4 Discussion

The presented probabilistic framework for landslide forecasting does not eliminate uncertainty, but it explicitly introduces it into the model results. Introducing uncertainties may seem detrimental to the ultimate goal of predictive modeling: to be a positionally and temporally accurate mitigation tool. However, we argue that a probabilistic approach is a viable alternative to deterministic landslide forecasting models as they allow forecasters to make informed decisions based on the uncertainties and limitations involved with model predictions. In contrast, a purely deterministic model output, in particular highly detailed map representations of slope failure probability, could suggest a certainty that simply is not achievable in landslide modeling. Although a probabilistic approach depicts spatial parameter variability and uncertainty much better than any purely deterministic result, there are still unaccounted for uncertainties involved with respect to actual slope failure prediction, e.g., related to limitations of the modeling approach, quality and uncertainties of data treated in a non-probabilistic way, or the limited number of model iterations that might not be sufficient to fully explore the parameter space.

The narrow ensemble spread highlighted in our PoF maps (i.e., Figs. 3 and 5) underlines the important impact of slope angle, and thus DTM quality, on model outputs. Neves Seefelder et al. (2016) and Zieher et al. (2017) identified slope angle as one of the most sensitive modeling parameters in TRIGRS, which is not surprising since slope failures are in general associated with higher slope angles (Liao et al., 2011). Even under greatly varying geotechnical or hydraulic input parameter settings, the same slope segments experience the highest likelihood of slope failure. As a consequence, slope failure probability will ultimately vary spatially based on slope and temporally based on rainfall input unless the study area includes different geological units with greatly varying geotechnical parameters appropriately reflected in the available data.

The great variability among the ensemble members (Fig. 4) raises the question of whether extensive model calibration for deriving a single model output is the ideal solution. Purely deterministic forecasts suppress information and limit the possibility to judge uncertainty. They generally pretend to be based on an optimal set of input parameter settings. Only recently have empirical approaches, such as the commonly used rainfall thresholds in landslide forecasting and early warning applications, started to incorporate estimates of uncertainty by defining rainfall thresholds at different exceedance probabilities (e.g., Melillo et al., 2016; Piciullo et al., 2017). Yet, they rely on very good landslide event catalogues and knowledge of the triggering conditions. However, reported landslides and their triggering conditions are often affected by large errors (Peres et al., 2018). Gariano et al. (2015) found that an underestimation of only 1 % in the number of considered landslides can result in a significant decrease in the performance of a threshold-based landslide prediction system. Additionally, rainfall thresholds represent a simplification of the underlying physical processes by establishing no more than a statistical relationship between rainfall and landslide occurrence (Bogaard and Greco, 2018). Both deterministic and empirical approaches may create the illusion of certainty in a user's mind, which could easily lead to wrong conclusions and poor decision-making.

We argue that hiding the predictive uncertainty behind the façade of a precise estimate is wrong and careless. Concerns about the acceptance of probabilities in decision-making turned out to be unwarranted (Krzysztofowicz, 2001). Based on our observations we found that many published landslide studies dealing with physically based hindcasting applications rely too strongly on purely number-based validation outputs. Deterministic results are taken as given when the modelers achieve satisfactory results based on the model validation, without defining what the criteria are for this satisfaction or when this state of satisfaction is reached. Beven (1996) argues that this is generally owed to relativism, when there is a need to adopt less stringent criteria of acceptability or to acknowledge that it is not possible to predict all the observations all the time (with common arguments ranging from scale issues, spatial heterogeneity, uncertainty in model structure, to process understanding, etc.). In general, probabilistic approaches should be prioritized since they not only allow for the incorporation of parametric uncertainties but also facilitate the geomorphic plausibility control in the absence of proper data for model calibration and validation. Also, for ensemble predictions narrowing down uncertainties is a good first step, but the ultimate goal should be to determine and explore the differences among model predictions (Challinor et al., 2014). In any case, high-quality data are necessary but are often scarce in landslide research. The potential of local-scale studies to draw conclusions for larger-area applications (e.g., Bordoni et al., 2015) remains a very important field of study in the near future. In this regard, data assimilation might be a key factor for producing accurate model predictions while reducing those inherent uncertainties. Liu et al. (2012) give an in-depth review on the current state of data assimilation applications in both hydrologic research and operational practices that are in many parts valid for landslide prediction too. While there are a few adaptive systems in landslide early warning based on empirical thresholds, such as the SIGMA early warning system in Italy (Martelloni et al., 2012; Segoni et al., 2018b), there are not yet any that use physically based predictions with blends of the most recent QPEs or other independent observations. For extreme events, this might be key if the probability of extreme floods or landslides occurring is continuously and objectively evaluated and updated in real time, especially when it comes to assimilating new observations from multiple sources across a range of spatiotemporal scales (Liu et al., 2012).

While we explicitly acknowledge the achievements and the success of deterministic or empiric landslide now- and forecasting approaches, we argue that the implementation of EPS approaches utilizing physically based landslide prediction models could facilitate future landslide early warning systems. In particular, highly detailed convection-permitting NWP would be ideal to run a physically based landslide forecasting service. Such high-resolution (<3 km) NWP services are presently available for Germany (COSMO-DE; Baldauf et al., 2011; Gebhardt et al., 2011), France (AROME; Seity et al., 2011), the UK (MOGREPS-UK; Golding et al., 2016), and the US (HRRR; Ikeda et al., 2013). However, there might be concerns whether the operation of physically based EPS modeling approaches is feasible for large areas, in particular related to concerns regarding parameter uncertainties and variability, model calibration, and the computational burden. In the following, we want to provide a discussion of these issues.

An important limiting factor for the application of physically based landslide models to large areas is related to parameter variability and uncertainty and issues with the parameterization of the respective models. Current practices for geotechnical parameterization in physically based landslide modeling include the application of averaged values from in situ measurements (e.g., Thiebes et al., 2014; Tofani et al., 2017; Zieher et al., 2017) or using values from existing databases, lookup tables, or other published/unpublished sources (e.g., Schmidt et al., 2008; Kuriakose et al., 2009; Mergili et al., 2014b). In the landslide research community, probabilistic treatment of input parameters for regional model application has seen a rise only in the last couple of years (e.g., Mergili et al., 2014a; Raia et al., 2013; Neves Seefelder et al., 2017). Probabilistic approaches allow for a more thorough consideration of uncertainties and inherent variability in model-specific parameters. Spatially varying parameters (both geotechnical and hydraulic) are usually represented as univariate distributions of random variables based on an underlying pdf and statistical characteristics (Fan et al., 2016). Friction angle and cohesion are commonly considered to be such varying variables that are treated in a probabilistic way for model parameterization (e.g., Park et al., 2013; Chen and Zhang, 2014; Raia et al., 2014; Salciarini et al., 2017). Interestingly, in hydrological streamflow prediction the parameter uncertainty of the hydraulic model is often neglected in favor of a deterministic parameter input. This is explained by the superior proportion of total estimation uncertainty introduced by the weather predictions alone, which blurs the streamflow variability that the meteorological input data cannot explain (Alfieri et al., 2012b). Measuring geotechnical and hydrological parameters for large areas is difficult, time-consuming, and expensive. Therefore, applying spatially distributed physically based models with spatially variable geotechnical parameters is not straightforward and it is impossible to find an approach that is universally accepted (Tofani et al., 2017). Even if there is a sufficiently large number of measured values available for one, some, or even all parameter values in a model up to the point at which it is possible to specify distributions and covariances for the parameter values, there remain some methodological obstacles. For example, there is no guarantee that values measured at one scale will reflect the actual values required in the model to achieve satisfactory predictions of observed variables (Beven and Freer, 2001). For larger areas (e.g., scales > 1 : 25 000), there are several factors that cause spatial variation in, for example, soil water content; topography; differences in soil depth, soil type, and soil texture; vegetation characteristics; and rainfall patterns. Additionally, spatially varying soil and hydraulic properties are influenced by interrelated soil formation processes (such as weathering processes, biological perturbations, atmospheric interactions) (Fan et al., 2016), and thus making selective in situ soil sampling a tricky task when performed at a larger scale. Small-area (e.g., scales < 1 : 10 000) variability usually lacks a spatial organization, hence its representation as a stochastic process. The larger the area, however, the more soil forming processes manifest a persistent deterministic signature due to the predetermined geology, topography, climate, etc. (Seyfried and Wilcox, 1995; Fan et al., 2016). Neves Seefelder et al. (2016) suggest applying rather broad ranges of parameters for physically based approaches to be on the “safe side” as they yield results comparable in quality to those derived with best-fit narrow ranges. By acknowledging the fact that geotechnical and hydrological parameters – when working on larger areas – are highly variable, uncertain, and often poorly known, narrow parameter ranges or even singular combinations of parameters come with the risk of being off target (Neves Seefelder et al., 2016). This basically implies that, when working on a regional scale and beyond, an actual parameterization with in situ measured samples might not be purposeful. The use of literature values could mean enormous savings in time and money spent, yet this clearly needs further research to evaluate whether there is and to what degree the benefits of actual sampled in situ data are compared to just utilizing literature values in broad ranges when modeling for larger areas.

Like flood events, landslide types with a rapid onset can be considered extreme events. Thus, extreme does not necessarily refer to the size of the displaced landslide volumes – also, small landslides might be considered extreme in terms of potential consequences. While it is possible to continuously monitor and forecast regular streamflow, extreme events are scarce, which makes model calibration and consequently forecasting a real challenge. We argue that this is even more so the case for landslides as there are no directly observable target variables to be monitored at a regional scale. Landslide models can only be calibrated on a case-by-case basis. Shallow landslides are one of the most common landslide types (van Asch et al., 1999). While they occur in abundance when looking at their spatial distribution, they are typically low-frequency events. And most of them do occur in so called “low-risk” environments as defined by Klimeš et al. (2017): low annual frequency of landslides; the majority of the landslides are of small size and are low-impact events. Due to the scarcity of such extreme events, Collier (2007) argues that such events may lie outside of what model calibration is capable of providing for forecasting approaches. Therefore, it is very difficult to calibrate a model for future use, as it can only be continually evaluated in light of the most recent data (Oreskes et al., 1994; Challinor et al., 2014). It is beyond the scope of the present paper to propose new approaches for the calibration and validation of regional landslide forecasting models. However, we think that, at least to some extent, the experiences of continuous local-scale monitoring systems might be able to facilitate the calibration process for regional-scale applications; however, additional research is required.

Landslides are per se extreme events with no common events attributed to them as they only occur under exceptional circumstances given the environmental interactions involved. This raises the question of whether any averaged model output, and that is by definition every model output based on model calibration from past events, will ever be able to precisely forecast extreme events at the regional scale. The sensitivity of the model must be lowered in a way that much larger areas of slope failure need to be forecasted to catch a few real extreme events at the cost of significantly raising the number of false alerts. In addition, it has been reported that it is not always possible to develop sensitive models due to data constraints (e.g., Gioia et al., 2015; Alvioli and Baum, 2016). Creating sensitive models that are able to forecast all events is especially difficult when engineering conservatism comes into play in decision-making, thus leaving probabilistic forecasting attempts in an inferior state over purely deterministic approaches. This is a known issue (e.g., Baum et al., 2010) in a way that FoS computations are usually more likely to identify areas prone to slope failure during a given rainfall event rather than predicting exact locations of specific landslides. A term such as landslide susceptibility forecasting seems more appropriate in that case. Our results in the Flysch zone of Lower Austria seem to point in that direction so far. This is definitely an issue that needs far more in-depth research in the future. In addition, the technical specifications of the modeling approach for slope stability analysis at a regional scale have to be kept in mind. The most commonly applied modeling approach relies on the infinite-slope stability model, which reduces the landslide geometry to a slope-parallel layer of infinite length and width. This leads to very pronounced patterns of the factor of safety, whereas modeling approaches that introduce more complex landslide geometries produce smoother results since the effects of neighboring pixels are averaged out. Whether complex approaches such as r.slope.stability (Mergili et al., 2014a), Scoops3d (Reid et al., 2015), or approaches based on slip circles or ellipsoids (Xie et al., 2003, 2004, 2006) are able to outperform the infinite-slope stability model depends on the settings, notably the landslide geometries. In theory, the infinite-slope stability model is suitable for shallow landslides with length-to-depth ratios above 18–25 (Griffiths et al., 2011; Milledge et al., 2012). Consequently, parameters representing the landslide geometry assumed by the model (i.e., slope angle and depth) are highly sensitive (Zieher et al., 2017). This means that the underlying model itself already performs some sort of averaging too since the precise landslide geometry cannot be adequately resolved in the infinite-slope stability model.

Traditionally, physically based approaches for modeling rainfall-induced shallow landslides were suggested to be applied to small study areas while statistically based approaches were recommended for regional susceptibility assessments (e.g., van Westen et al., 2006; Corominas et al., 2014). One reason usually mentioned is the poor comprehension of the spatial organization of the geotechnical and hydraulic input parameters (e.g., Tofani et al., 2017; Park et al., 2013). However, as outlined above, it does not make too much of a difference whether the underlying study area is 50 or 5000 km² investigated at a scale of 1 : 1000 or 1 : 25 000 – the model is still influenced by errors or uncertainties from the input parameters given how input parameters are derived, and one should not believe that uncertainties disappear (or even decrease) with more data and more measurements.

Another major limitation used to be the computational costs involved when carrying out physically based modeling at a regional scale. However, in recent years computational power has become available at reasonable costs, and the area size, associated with a high-resolution DTM, steadily increased over time for physically based applications and today exceeds thousands of square kilometers (e.g., Tofani et al., 2017; Alvioli and Baum, 2016). Recent landslide model development aims towards featuring multithreading and parallelization, and significant reductions of simulation durations of almost 90 % have been reported (Rossi et al., 2013). Since high-resolution DTMs are available in many parts of the world, the computational demands increased significantly, especially when applied in a dynamic and time-dependent modeling framework. Parallelization has great potential in grid-based landslide modeling, especially for the time-consuming hydraulic model components, for several reasons: in the case of TRIGRS, for example, which is a coupled slope stability and hydraulic model, only excess water from infiltration is directed to the neighboring cells, which makes it the only variable that relies on explicit neighborhood relations. This needs to be performed only once, however. Vertical groundwater flow and one-dimensional slope stability in a two-dimensional array of noninteracting columns can subsequently be computed independently for each cell, which is a prime example for parallelization purposes (Baum et al., 2010; Alvioli and Baum, 2016). In addition to TRIGRS v2.1, which received its parallel implementation from Alvioli and Baum (2016) only recently, other models for physically based landslide applications use a parallelized module: NewAge-JGrass (Formetta et al., 2016) or r.slope.stability (Mergili et al., 2014a). In our case study, the computational time for one model iteration is about 45 min, which is far too long for computing a large set of different ensemble members in an operational real-time application. We did not yet use the parallel implementation of TRIGRS on our regular commodity machine (3.40 GHz quad-processor equipped with 32 GB RAM), but Alvioli and Baum (2016) reported that parallel computation on a multi-core node already led to a significant speedup compared to a single-node local machine. When applied to a HPC (high-performance computing) cluster, they were even able to reduce running time from 1 day to 1 h. This allows the exploration of new possibilities in how landslide forecasting can be approached in the future. While HPC applications are common in meteorological (Bauer et al., 2015) and flood forecasting (Shi et al., 2015), there are only a few landslide-related studies (Mulligan and Take, 2017; Shute et al., 2017; Song et al., 2017); however, there are none aiming specifically at landslide forecasting. This opens up possibilities to encompass fine-tuning of input parameters by means of multiple model runs, probabilistic applications, and, first and foremost, real-time applications with a continuous consideration of antecedent and forecasted rainfall information (Alvioli and Baum, 2016).

5 Conclusions

The adoption of EPS approaches in meteorological and hydrological modeling has led to the implementation of the operational forecasting system over the last years. Therein, parameter uncertainties are explicitly integrated in the forecasts and the results are made available to decision makers. However, similar approaches have not yet been reported from the landslide research community. By identifying this gap, i.e., the lack of landslide EPS forecasting systems, this paper aims to foster the discussion on this topic, which hopefully facilitates additional research activities in this direction.

Our case study implementation of a landslide forecasting system, although simplified due to the limited number of parameters treated in a probabilistic way, highlights how a physically based model could be operated for larger areas, and how uncertainties can be dealt with. Still, there are concerns regarding such large-area model applications, in particular related to parameter variability and uncertainty, model calibration and validation, and the feasibility with respect to the computational burden. We argue that these concerns are to some extent unwarranted and can be overcome with probabilistic approaches and additional model development. However, the calibration of forecasting models focusing on extreme events such as landslides remains a major challenge and needs further research and high-quality data.