the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Limit analysis of earthquake-induced landslides considering two strength envelopes
Yuke Wang
Xin Chen
Stability analysis of soil slopes undergoing earthquake remains an important research aspect. The earthquake may have some different effects on slope stabilities associated with nonlinear and linear criteria, which need to be further investigated. For homogeneous soil slopes undergoing earthquakes, this paper established the three-dimensional (3D) failure mechanisms with the power-law strength envelope. The quasi-static method was employed to derive the work rate done by the earthquake in limit analysis theory. The critical heights and critical slip surfaces associated with nonlinear and linear criteria were obtained for four slope examples undergoing different seismic loads. Comparisons of the nonlinear and linear results illustrated that two critical inclinations (resulting from the overlap of nonlinear and linear results) both decrease as the seismic force increases, but their difference is almost constant. For steep slopes, the use of linear strength envelope can lead to the non-negligible overestimation of slope critical height. This overestimation will become significant with the increase in seismic force, especially for the steeper slope with a narrow width. Since the seismic force has a positive influence on equivalent internal friction angle, the critical slip surface for the slope-obeying nonlinear envelope tends to be slightly deeper as the earthquake becomes stronger. For steep soil slopes undergoing the earthquake, the development of 3D stability analysis with a nonlinear yield criterion is necessary and significant. These findings can provide some references for the risk assessment and landslide disaster reduction of soil slopes.
- Article
(4224 KB) - Full-text XML
- BibTeX
- EndNote
Landslide is the classical problem, but it remains to be a hot topic in geotechnical engineering and mining engineering fields. The linear Mohr–Coulomb (MC) failure envelope has universal applications in slope design standards and landside analyses. However, the assumption of a linear strength envelope is less rigorous, and the curvature of geomaterial strength has been explored by many experimental studies (e.g., Penman, 1953; Bishop et al., 1965; Hoek and Brown, 1980; Maksimovic, 1989; Baker, 2004a). To consider the nonlinear strength behavior of soils, various nonlinear strength criteria have been presented by many researchers (e.g., De Mello, 1977; Zhang and Chen, 1987; Baker, 2004a; Anyaegbunam, 2015; Wang et al., 2023). Meanwhile, a number of scholars have successively conducted research on slope stability analysis using nonlinear strength criteria. Based on the assumptions of slip surfaces and stress distributions, limit equilibrium methods have been widely used to evaluate the slope safety with nonlinear criteria (Charles and Soares, 1984; Srbulov, 1997; Jiang et al., 2003; Baker, 2004b; Eid, 2010; Deng and Li, 2019; Wan et al., 2023). Besides, some limit analysis approaches with nonlinear strength criteria were conducted to solve slope stability problems by using the tangential method (Drescher and Christopoulos, 1988; Yang and Yin, 2004; Gao et al., 2015; Li and Yang, 2019; Wu et al., 2023). Moreover, several authors employed numerical methods to analyze the safety of slopes obeying nonlinear criteria (Popescu et al., 2000; Li, 2007; Li and Yang, 2018; Chen and Lin, 2019).
The early work of Charles and Soares (1984) illustrated that the slope safety derived by the linear envelope would be higher than that derived by the nonlinear envelope. Afterwards, numerous authors have paid attention to the distinctions between slope stabilities derived by nonlinear and linear strength envelopes (Srbulov, 1997; Popescu et al., 2000; Jiang et al., 2003; Baker, 2004b; Gao et al., 2015; Li and Yang, 2019). Among them, Baker (2004b) and Gao et al. (2015) compared slope critical heights associated with nonlinear and linear envelopes and found that using a linear envelope could underestimate the stability of slopes in a certain range of inclinations. Gao et al. (2015) further revealed that the linear criterion would derive more significant overestimation or underestimation of slope stability in three-dimensional (3D) conditions. Meanwhile, some attempts have been made to discuss the effects of nonlinear strengths on slip surfaces of two-dimensional (2D) slopes and 3D slopes (Charles and Soares, 1984; Jiang et al., 2003; Wu et al., 2021a). It is known that the error caused by using the linear criterion is not negligible in the assessment of slope safety. The negligible difference between the nonlinear and linear solutions may change for slopes subject to different external influences, such as water pressure and earthquakes. Wu et al. (2021b, 2024) have made some investigations into the effects of pore-water pressure and outside water pressure on the nonlinear and linear solutions. As to the influence of seismic action on the linear and nonlinear solutions for soil slope stability, researchers have paid a lot of attention to this issue.
In the field of slope engineering, earthquakes are one of the main factors inducing landslide accidents, and numerous investigations have been made to reveal effects of seismic action on the safety of 2D and 3D slopes satisfying the linear MC yield criterion. It has been generally accepted that the slope safety will reduce as the seismic action becomes stronger (e.g., Yang et al., 2004; Li et al., 2009; Huang and Ji, 2022). With regard to the influence of earthquakes on the rock slope safety, Yang et al. (2004) used the quasi-static method to conduct a limit analysis for seismic stability of 2D slopes with the Hoek–Brown yield envelope. The limit analysis approach was then carried out by Zhao et al. (2017b) and Pang and Gu (2019) to address seismic stability and seismic displacement of fissured slopes obeying the Hoek–Brown criterion, respectively. Zhong and Yang (2022) presented a modified pseudo-dynamic method to assess seismic stability of 2D slopes by using the Hoek–Brown criterion. Allowing for the 3D character of slope geometry, Gao et al. (2016) and Wu et al. (2023) analyzed the seismic stability and the equivalent Mohr–Coulomb parameters for rock slopes with the Hoek–Brown envelope in a 3D limit analysis framework, respectively. Besides, Li et al. (2009) and Shen and Karakus (2013) performed numerical methods to assess the slope stability considering the nonlinear Hoek–Brown envelope and seismic action in 2D and 3D conditions, respectively. For slopes in soils governed by the nonlinear criterion, Zhao et al. (2017a) focused on the effect of vertical earthquakes on the seismic displacement of 2D slopes by using the limit analysis method. Considering the 3D geometry of soil slopes, only the studies of Xu and Yang (2019) and Li and Yang (2019) carried out the limit analysis of seismic stability and seismic displacement of reinforced slopes, respectively. From a general survey of relevant studies, there is a lack of research on seismic stability of 3D homogeneous soil slopes with nonlinear criteria. Especially for soil slopes in 3D conditions, few attempts have been made to illustrate the effect of seismic action on the difference between nonlinear and linear solutions for slope stability.
This paper focuses on the influences of earthquake action on 3D soil slope stabilities (in the forms of critical height and critical slip surface) derived by nonlinear and linear strength envelopes. Firstly, the 3D failure mechanisms with the power-law strength envelope were developed for soil slopes. Then the quasi-static method was employed to obtain the work rate done by the earthquake, and the energy balance equation was established. Afterwards, the optimal upper-bound solutions, in the forms of critical height and slip surface, were derived by using an optimization procedure. For several slope examples, the critical heights and slip surfaces associated with nonlinear and linear envelopes were calculated with respect to different slope geometries and seismic actions. The effects of earthquakes on nonlinear and linear solutions were discussed on the basis of presented comparison charts.
2.1 Equivalent MC parameters for nonlinear failure envelope
Among these presented nonlinear strength envelopes, a power-law (PL) failure envelope has been applied by many studies to assess slope safety (e.g., Zhang and Chen, 1987; Yang and Yin, 2004; Deng and Yang, 2021; Wu et al., 2023). The PL failure function is presented in the coordinate system of shear stress τ and normal stress σn, which is written in the following equation:
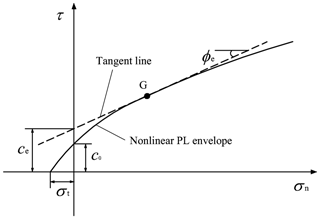
where c0, σt, and m are nonlinear strength parameters determined by test data. Figure 1 gives the schematic diagram of the PL strength envelope. Parameter σt denotes the tensile strength when τ= 0, c0 is named as the initial cohesion, and m relates to the nonlinearity coefficient with its value bigger than 1.0. When m is equal to 1.0, the PL strength function will be reduced to the MC yield criterion. Hence, the following slope stability analysis combined with a nonlinear strength envelope will contain the solutions for slopes using the linear MC criterion.
As presented in Eq. (1), the friction angle φ and the cohesion c will be not constant when the normal stress σn is different. This character will result in a big difficulty in applying the nonlinear PL failure envelope into the slope stability assessment. Drescher and Christopoulos (1988) firstly addressed such a problem by proposing a tangential technique to simplify the nonlinear strength envelope to an instantaneous linear criterion. This tangential technique was then adopted by some researchers to solve slope safety problems with nonlinear yield criteria (e.g., Yang and Yin, 2004; Zhao et al., 2017a; Pang and Gu, 2019; Deng and Yang, 2021; Wu et al., 2023). These studies gained a certain confidence in the application of the tangential technique. A brief description of the tangential technique is presented in Fig. 1. The tangent line function for this curve strength envelope can be presented as follows:
Here, φe and ce are the instantaneous strength parameters of the tangent line. In this study, they are named as the equivalent friction angle and equivalent cohesion, respectively. Combining the tangent line function and the differential equation tan φe= d, the equivalent cohesion ce can be derived as a function of φe, which is written as follows:
In the tangential technique, the tangent line in the form of equivalent shear strengths will be used instead of the PL strength envelope. Hence, the equal or bigger shear strengths will be derived by the tangent line for the curve PL envelope in the same σn range. Note that the equivalent friction angle φe will be an optimization variable in the establishment of following the limit analysis approach.
2.2 3D failure mechanisms of slopes
For soil slopes obeying the MC strength criterion, the 3D failure mechanism presented by Michalowski and Drescher (2009) has been widely applied and further developed in the limit analysis approach (e.g., Gao et al., 2013; Xu and Yang, 2018; Michalowski and Park, 2021; Pan et al., 2023). Considering nonlinear strength behavior of slope soils, Gao et al. (2015) utilized the tangential technique to employ the PL envelope into the modified 3D failure mechanisms of Gao et al. (2013). The 3D kinematic approach was then carried out to further illustrate the effects of soil strength nonlinearity on stability assessment of slopes (Gao et al., 2015; Wu et al., 2021a). In this study, the 3D failure mechanisms combined with the nonlinear PL envelope will be similarly adopted to evaluate the stability of homogeneous dry slopes considering seismic actions.
As presented by Gao et al. (2015), the 3D failure mechanisms with the nonlinear PL failure envelope should consist of two conditions: the slip surface above slope toe (face failure) and the slip surface below slope toe (base failure). As illustrated in the original figures of Gao et al. (2015), these 3D failure mechanisms are separated by two parts: a curvilinear cone and a plane insertosome. The widths of the two parts are 2b′ and b, and the total slope width is marked by B. The slope height is marked by H. The apex angles for these failure mechanisms are marked by an added variable φe, which also represents the tangential line position for the PL envelope. It should be noted that these 3D mechanisms can degrade into the plane-strain 2D mechanism once the relative width becomes infinite. More comprehensive descriptions of these 3D mechanisms can be found in Gao et al. (2013).
2.3 Work rates done by seismic action
To consider earthquakes in the evaluation of slope safety, the quasi-static method is widely applied in the slope stability analysis (e.g., Yang et al., 2004; Li et al., 2009; Pang and Gu, 2019; Huang and Ji, 2022; Wu et al., 2023). In the limit analysis theory, Wu et al. (2023) used the quasi-static method to conduct the seismic stability analysis for rock slopes with a 3D toe failure mechanism. Hence, this paper similarly adopted the quasi-static method to evaluate the seismic load on the modified 3D failure mechanisms of soil slopes. The seismic action can be represented by a constant seismic acceleration, which is uniformly distributed in the whole sliding body. The seismic load is calculated by multiplying the soil self-weight with the seismic acceleration coefficient. Because of the limitation of the quasi-static method, the nonlinear character of seismic load can be hardly overall elaborated. In the subsequent study, other approaches will be tried to explore the influences of the nonlinear effects of seismic load on slope stability.
Some previous studies have suggested that vertical acceleration significantly affects the seismic performance and the permanent displacement of slopes when the horizontal acceleration is high and the slope is steep (Ling et al., 1997; Ling and Leshchinsky, 1998; Ingles et al., 2006). But in the quasi-static method adopted in this study, vertical acceleration can be reflected in the increase in gravitational acceleration. The results for the dynamic stability of slopes by using vertical acceleration will be a linear proportional relation to those for the static stability of slopes. Hence, horizontal seismic acceleration will have more significant effects on slope stability, and vertical acceleration was ignored in this study. The seismic load is calculated by multiplying the soil self-weight with the horizontal seismic acceleration coefficient kh. For the value of seismic acceleration coefficient kh, this study adopted the range of 0.0–0.3.
In the work energy equation of limit analysis theory, the external work rates consist of two types: self-weight work rate Wγ and horizontal seismic work rate Ws. The work energy function is established by making these two kinds of external work rates equal to the internal energy dissipation rate D, which has the following expression:
where the superscripts “c” and “p” are used to distinguish the energy rates for the curvilinear cone and the plane insertosome, respectively. For self-weight work rate and internal energy dissipation rate Dc of the curvilinear cone part, see specific expressions in the references of Gao et al. (2013, 2015). The expressions for and Dp of the insertosome part can be found in the study of Chen (1975). Due to the application of the tangential method, the parameters c and φ in these equations need be changed to the equivalent-strength parameters ce and φe, which have the specific relational expression of Eq. (3). The horizontal seismic work rates Ws are similarly divided into two parts: for the curvilinear cone and for the plane insertosome.
For the 3D face failure mechanism, the horizontal seismic work rates and for the curvilinear cone and the plane insertosome are derived by the following expressions:
The expressions for the variables a, d1, and θB and the functions of fs1, fs2, and fs3 are listed as follows:
where ω relates to the angular velocity, γ is the soil unit weight, and β represents the slope inclination. The other parameters r0, , a, d1, θ0, θB, θh, R, and rm have been marked in the original figures of Gao et al. (2015).
For the 3D base failure mechanism, the seismic work rate done by the slide body below the toe should be added on the base of these formulas for the 3D face failure mechanism. Hence, these horizontal seismic work rates and for the curvilinear cone and the plane insertosome are calculated as the following expressions:
The relations for the parameters d2, e, and θC and the functions of fs1, fs2, fs3, and fs4 can be calculated from the following equations:
where the definitions of the notations d2, e, θC, and β′ can be found in the original figures of Gao et al. (2015).
2.4 Determination of upper-bound solution
For a given slope with seismic load, the upper bounds of slope stability will be derived by substituting the equations of work rates and internal energy dissipation rates into the work energy equation. In this study, the upper-bound solutions consist of the slope critical height Hcr and the slip surface. The critical height Hcr is the optimized least slope height with the safety factor Fs= 1.0. The expression of Hcr can be formulated as follows:
As shown in Eq. (27), the critical height Hcr for the face failure mechanism will be calculated in regard to six variables: θ0, θh, φe, , , and . Similarly, the critical height Hcr for the base failure mechanism will be determined in regard to the following variables: θ0, θh, φe, , , and β′. The definitions of variables θ0, θh, β′, and H′ can be seen in the original figures of Gao et al. (2015). The variable φe denotes the apex angle of the 3D failure mechanism, which will also determine the location of the tangent point on the nonlinear PL envelope.
To find out the least upper-bound solutions in the limit analysis theorem, the optimization procedure of Chen (1992) written in the computer codes of the MATLAB software was applied in this study. Given the nonlinear and geometric parameters for a slope with a certain seismic load, the least values of Hcr and corresponding slip surfaces for two failure mechanisms will both be derived by using the optimization procedure. The optimal least upper bound on Hcr is the minimum value of the two least upper bounds for the two failure mechanisms. Meanwhile, the optimal values of the variables (θ0, θh, , , n or β′, and φe) will be also determined with respect to the optimal critical height Hcr.
For 3D soil slopes obeying the linear MC criterion, seismic stability solutions can be obtained by using the conversion relationships of φe= arctan() and ce= c0, which are addressed in Sect. 2.1. In the optimization procedure for least upper-bound solutions, the internal friction angle φe will be a fixed value, and it should be removed from the optimization variables.
To further validate the rigor of the research method and the accuracy of the presented results, this section compares the presented results with other studies for two slope examples obeying the linear criterion and the nonlinear criterion, respectively. To facilitate a comparison in the form of the safety factor F, the shear strength of the nonlinear criterion needs to be divided by F. The reduced shear strength will be used in the presented limit analysis method, and the minimum of F can be derived with respect to the least upper bound.
3.1 Comparisons with other linear solutions
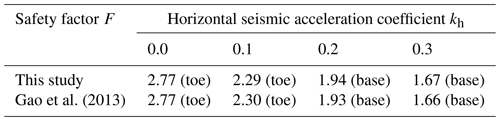
For the validation of the accurate linear results derived by this study, the slope example of Gao et al. (2013) was adopted here. For the homogeneous slope, the geometry parameters are given as B= 20 m, H= 10 m, and β= 30°. The slope soil has the properties of c= 40 kPa, φ= 15°, and γ= 18 kN m−3. The slope undergoes both static and seismic actions with kh= 0.0, 0.1, 0.2, and 0.3. Based on the presented limit analysis method, the minimum safety factor F and the corresponding failure mechanism for this slope example are presented in Table 1. The solutions of Gao et al. (2013) were easily obtained from their given stability charts. Table 1 illustrates that the linear solutions derived by this study are in good agreement with the results of Gao et al. (2013). Besides, the failure mechanisms for the slope example under different seismic conditions are also the same for the two studies.
Note that the result marked by “toe” in brackets denotes that the corresponding slope failure surface passes the toe, and the result marked by “base” denotes that the critical failure surface passes the base.
3.2 Comparisons with other nonlinear solutions
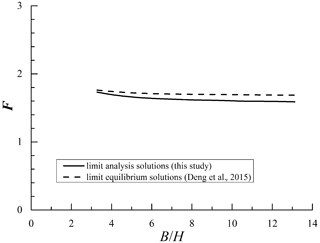
The slope problem obeying the nonlinear criterion was adopted from the study of Deng et al. (2015). The nonlinear strength parameters of slope soil are given as follows: c0= 29.3 kPa, σt= 80.5 kPa, and m= 1.5. The soil unit weight γ is 19.2 kN m−3. The slope has a height H of 12.2 m, and the slope has an inclination β of 26.6°. The slope width is in the range of 40–160 m. For this slope example under static conditions, the minimum values of F for slopes with various were calculated and are presented in Fig. 2. Meanwhile, the limit equilibrium solutions of Deng et al. (2015) are also given in this figure. It can be found that the upper-bound solutions obtained in this study are slightly less than the limit equilibrium solutions of Deng et al. (2015), and the maximum difference between them is no more than 5 %. Since the slope failure mechanism of Deng et al. (2015) was assumed to be ellipsoid, which seems to be less reasonable than the failure mechanism of this study, the limit analysis method will derive a slightly smaller safety factor for slopes than the limit equilibrium method. This comparison can further verify the validity of the research method and the accuracy of the presented nonlinear results in this study.
4.1 Slope examples
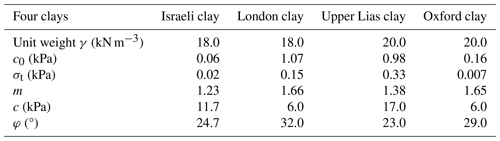
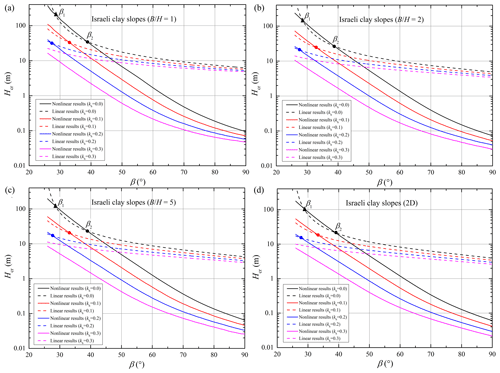
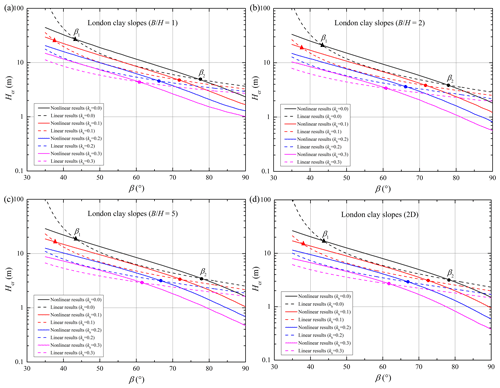
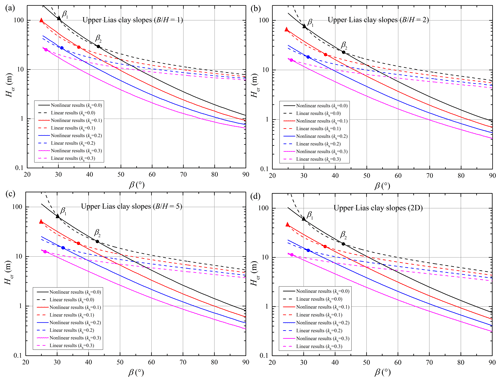
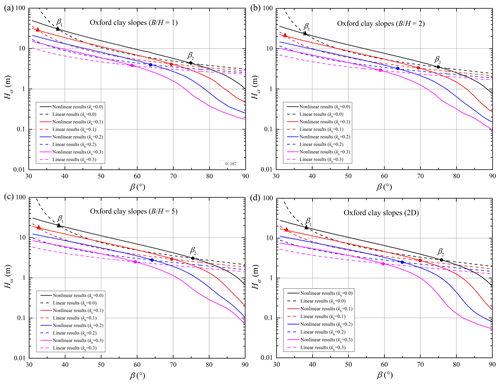
To account for the earthquake effect on landslide evaluations using nonlinear and linear strength envelopes, slope examples in four homogenous dry clays were considered in this study. Israeli clay, London clay, Upper Lias clay, and Oxford clay were selected as the slope bodies of four slope examples. The detailed values of the nonlinear and linear strength parameters for these four clays are shown in Table 2 for previous studies (Gao et al., 2015; Wu et al., 2021a). It should be noted that the drainage conditions for these four clays were not consistent in the shear strength tests. Though the total strength parameters derived by unconsolidated–undrained strength tests will be appropriate for water-bearing slopes undergoing earthquake actions, the effective or total strength parameters are both valid for clays in dry conditions. Hence, the nonlinear and linear strength parameters for the four clays can be selected for slope examples in this study.
4.2 Critical heights of slopes undergoing seismic action
The critical heights for the four slopes obeying the nonlinear and linear envelopes are presented in Figs. 3–6 with respect to various width constraints and seismic loads. The subgraphs (a–d) in each figure relate to the four conditions of slope examples with different width constraints 1.0, 2.0, 5.0, and ∞ (2D). In these subgraphs, the critical heights associated with the nonlinear criterion (abbreviated as the nonlinear results) are represented by the solid curves, and the critical heights associated with the linear criterion (abbreviated as the linear results) are represented by the dotted curves. Besides, different color curves represent the critical heights undergoing different seismic loads with kh= 0.0, 0.1, 0.2, and 0.3.
As illustrated in Figs. 3–6, the two critical slope inclinations β1 (marked by a solid triangle) and β2 (marked by a solid circle) appear as a result of the overlap between nonlinear and linear solutions. For slopes with β1 < β < β2, the linear solution appears to be higher than the nonlinear one. But for slopes with β < β1 or β > β2, using the linear criterion will overestimate the slope critical height, and the overestimation cannot be neglected. As illustrated in previous studies (Baker, 2004b; Gao et al., 2015), the two critical slope inclinations are closely related to the overlap of the two strength envelopes. For example, when the stability analysis for particular slopes with β1 < β < β2 is presented by using the nonlinear criterion, the average shear strengths along the critical slip surface will be larger than those derived by using the linear criterion. Correspondingly, the nonlinear solution in the form of critical height is larger than the linear one.
The locations of β1 and β2 for each slope example will change with the increasing seismic force coefficient kh. For specific performances, the critical inclination β1 gradually decreases, and the critical inclination β2 also becomes smaller or vanishes as kh increases. However, the difference between the two critical inclinations β1 and β2 seemed to be constant for slopes with different seismic forces. This finding reveals that the linear solution is a little smaller than the nonlinear solution for gentle slopes undergoing a strong earthquake. For steep slopes obeying the nonlinear PL envelope, the linear MC criterion will derive a bigger critical height, and the overestimation will be more significant with the increase in slope inclination. Besides, Figs. 3–6 show that these distinctions between nonlinear and linear results for slopes with β > β2 become bigger with an increase in kh. This may illustrate that using the linear MC criterion will more obviously overestimate the critical height of steeper slopes following the nonlinear PL envelope, especially in the case of strong seismic force. This phenomenon will be further investigated by analyzing the slope slip surface in the next section, which will provide some guidelines for the necessary consideration of soil strength nonlinearity for steep slopes undergoing strong seismic force.
Meanwhile, Figs. 3–6 also reveal the 3D effects on nonlinear and linear results for the four slopes undergoing different seismic loads. It can be observed that the positions of the two critical inclinations (β1 and β2) tend to be nearly unchanged with an increase in width constraint . But the differences between nonlinear and linear results seem to be smaller as gets bigger. For steeper slopes with stronger seismic loads, the ratio of has a more obvious effect on the nonlinear result, and then the differences between nonlinear and linear results become significant. This indicates that the application of the 3D stability analysis for slopes obeying nonlinear yield criteria is quite necessary, especially for steep slopes with seismic loads.
4.3 Slip surfaces of slopes undergoing seismic action
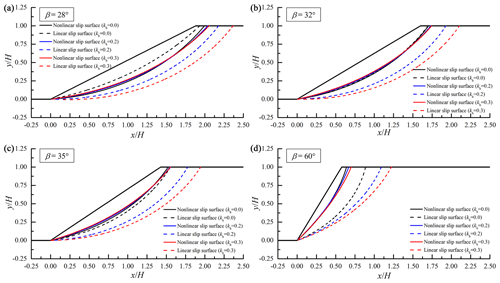
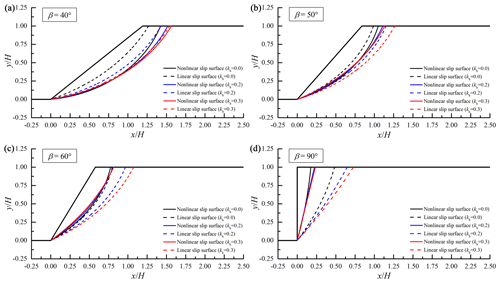
Since 3D effects on slope critical slip surfaces derived by nonlinear and linear envelopes have been well investigated in our foregoing study of Wu et al. (2021a), this section chooses 2D slopes in Israeli clay and London clay as examples. The influences of seismic load on critical slip surfaces derived by the two strength criteria are presented in Figs. 7 and 8 for 2D Israeli clay slopes and 2D London clay slopes. The critical slip surface derived by the nonlinear PL envelope (abbreviated as nonlinear slip surface) is represented by the solid line, and the critical slip surface derived by the linear MC envelope (abbreviated as linear slip surface) is represented by the dotted line. The critical slip surfaces with various seismic forces are also described by lines in different colors. The four inclinations in subgraphs a–d are chosen from the ranges of β < β1, β1 < β < β2, and β > β2 for two slopes without seismic load.
As shown in Figs. 7 and 8, for gentle slopes (β < β1), the linear envelope could derive shallower critical slip surfaces than the nonlinear envelope when the linear average shear strengths are smaller than the nonlinear ones. For slopes with β > β2, the slope slip surface derived by the linear envelope appeared to be deeper than that derived by the nonlinear envelope. These findings are similar to the discoveries in the study of Wu et al. (2021a), which can be referred to for the specific illustration of the above phenomenon.
From Figs. 7 and 8, it can be observed that the influence of seismic load on the critical slip surface with the nonlinear envelope is different from that on the critical slip surface with the linear envelope. For slopes with the linear envelope, it has been widely accepted that the critical slip surfaces become obviously deeper with an increase in seismic force coefficient kh. In contrast, the effect of seismic load on critical slip surfaces with the nonlinear envelope seemed to be less significant. As the seismic force coefficient kh becomes bigger, the whole slip surface derived by the nonlinear envelope appears to slightly deepen with its starting point farther away from the slope shoulder. Moreover, the effect of seismic force on the critical slip surface associated with the nonlinear envelope will become less significant for slopes with bigger inclinations. When the slope inclination is large, the slope slip surface is relatively shallow with a small normal stress distribution. In this case, the shear strength associated with the linear criterion is obviously higher than that associated with the nonlinear criterion. Especially for steep slopes undergoing strong earthquakes, the slope safety is low and its slip surface is shallow. Hence, the differences between the linear solution and the nonlinear solution (slope critical heights and critical slip surfaces) will become outstanding for steep slopes in the case of a strong earthquake. This is consistent with the results and findings in the previous section.
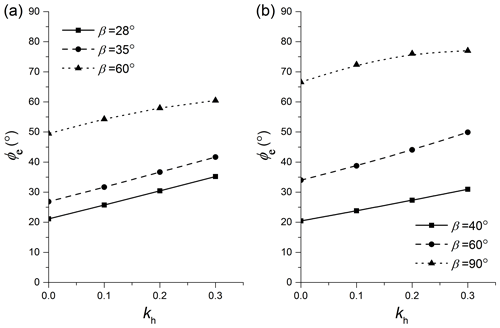
The above phenomenon may be related to the fact that the equivalent internal friction angle φe has a variable value affected by the changing seismic load. As illustrated in Fig. 9, the equivalent internal friction angle φe will get bigger as the seismic force coefficient kh increases. Many previous studies have revealed that the effects of the seismic force coefficient kh and the internal friction angle φ on the slope slip surface location are opposite; namely, the slope slip surface becomes deeper as kh increases or as φ decreases. Hence, considering the influence of φe on the critical slip surface, the slope tends to have a slightly deeper slip surface with increasing kh. It may reveal that kh has a more significant influence than φe on critical slip surfaces. Besides, it can be observed from Fig. 9 that the effect of kh on φe seems to be less obvious for steep slopes. As a consequence, the seismic load appears to have a less obvious effect on the critical slip surfaces of steeper slopes.
In the limit analysis framework, this paper extended an analytic method to assess the stability of 3D soil slopes considering strength nonlinearity and seismic action. The tangential method was used to establish the 3D face failure and 3D base failure mechanisms with the nonlinear PL envelope. The earthquake action was treated as an external seismic force on the failure mechanisms. For a soil slope undergoing an earthquake, the upper-bound solutions in the forms of critical height and critical slip surface were derived by using an optimization scheme. The validity of this study was verified by comparisons with other research. For the four clay slope examples, the comparisons of critical heights and slip surfaces associated with nonlinear and linear criteria were presented to illustrate the effects of seismic action on the slope stability evaluations. These results and discussions drew the following conclusions:
-
As the seismic force increases, the two critical inclinations β1 and β2 (resulting from the overlap of nonlinear and linear solutions) become smaller or vanish with a constant difference. For gentle slopes undergoing a strong seismic force, using the linear MC envelope will lead to a small underestimation of the slope critical height. For steep slopes undergoing an earthquake, the use of the linear MC envelope can pronouncedly overestimate the critical height. Using the nonlinear strength criterion in slope stability analysis is more necessary and significant for steep slopes under earthquake loads.
-
The slope width has a slight effect on the positions of the two critical inclinations β1 and β2 for slopes under seismic action. But the distinctions between nonlinear and linear results become bigger as the slope width becomes smaller. For steeper soil slopes with stronger seismic loads, the 3D effect on the slope stability with the nonlinear criterion is more obvious.
-
Compared to the effect of seismic action on linear slip surfaces, seismic action has a less significant influence on slope slip surfaces derived by the nonlinear envelope. When the seismic force becomes bigger, the whole slip surface derived by the nonlinear envelope will be a little deeper with its starting point farther away from the slope shoulder. This is related to the fact that equivalent internal friction angle φe will get bigger with an increase in seismic force.
Under earthquake conditions, the actual slope failure may result in cracks at the top of the slope. This problem can hardly be considered in the failure mechanism adopted in this study. The establishment of a three-dimensional failure mechanism with a crack may be attempted in subsequent studies. Besides, this study considered a simple homogeneous three-dimensional slope, while many actual slopes are heterogeneous or multi-layered and have complex geometric shapes. The stability analysis of heterogeneous slopes with complex shapes is a problem worth studying by using the limit analysis method proposed in this paper.
The data used to support the findings of this study are available in Figs. 2–9 and Tables 1–2 in this article. The data sets can be accessed through the following link: https://pan.baidu.com/s/1-F0ItOekGVtYxGReQzDR-A?pwd=4uxx (wudi9172, 2024).
DW designed the study with contributions from YW. DW and XC performed the data analysis and interpretation. All authors discussed the results. DW prepared the manuscript with contributions from all co-authors.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
This research has been supported by the National Natural Science Foundation of China (grant nos. 52178369, 52109140, and 52208361), the Natural Science Research of Jiangsu Higher Education Institutions of China (grant no. 23KJB410001), and the Natural Science Foundation of Jiangsu Province (grant no. BK20220638).
This paper was edited by Daniele Giordan and reviewed by four anonymous referees.
Anyaegbunam, A.: Nonlinear power-type failure laws for geomaterials: Synthesis from triaxial data, properties, and applications, Int. J. Geomech., 15, 04014036, https://doi.org/10.1061/(ASCE)GM.1943-5622.0000348, 2015.
Baker, R.: Nonlinear Mohr envelopes based on triaxial data, J. Geotech. Geoenviron., 130, 498–506, https://doi.org/10.1061/(ASCE)1090-0241(2004)130:5(498), 2004a.
Baker, R.: Stability charts for zero tensile strength Hoek-Brown materials-The variational solution and its engineering implications, Soils Found., 44, 125–132, https://doi.org/10.1061/(ASCE)1090-0241(2004)130:5(498), 2004b.
Bishop, A. W., Webb, D. L., and Lewin, P. I.: Undisturbed samples of London clay from the Ashford common shaft: strength–effective stress relationships, Geotechnique, 15, 1–31, https://doi.org/10.1680/geot.1965.15.1.1, 1965.
Charles, J. A. and Soares, M.: The stability of slopes in soils with nonlinear failure envelopes, Can. Geotech. J., 21, 397–406, https://doi.org/10.1139/t84-044, 1984.
Chen, W. F.: Limit analysis and soil plasticity, Amsterdam: Elsevier, ISBN 9781932159738, 1975.
Chen, Y. and Lin, H.: Consistency analysis of Hoek–Brown and equivalent Mohr–coulomb parameters in calculating slope safety factor, B. Eng. Geol. Environ., 78, 4349–4361, https://doi.org/10.1007/s10064-018-1418-z, 2019.
Chen, Z. Y.: Random trials used in determining global minimum factors of safety of slopes, Can. Geotech. J., 29, 225–233, https://doi.org/10.1139/t92-026, 1992.
De Mello, V. B. F.: Reflections on design decisions of practical significance to embankment dams: 17th rankine lecture, Geotechnique, 27, 281–354, https://doi.org/10.1680/geot.1977.27.3.281, 1977.
Deng, B. and Yang, M.: Bearing capacity analysis of submerged slopes subjected to water drawdown based on a nonassociated flow rule and nonlinear failure criteria, B. Eng. Geol. Environ., 80, 835–850, https://doi.org/10.1007/s10064-020-01975-9, 2021.
Deng, D., Zhao, L., and Li, L.: Limit equilibrium slope stability analysis using the nonlinear strength failure criterion, Can. Geotech. J., 5, 563–576, https://doi.org/10.1139/cgj-2014-0111, 2015.
Deng, D. P. and Li, L.: Limit equilibrium analysis of slope stability with coupling nonlinear strength criterion and double-strength reduction technique, Int. J. Geomech., 19, 04019052, https://doi.org/10.1061/(ASCE)GM.1943-5622.0001431, 2019.
Drescher, A. and Christopoulos, C.: Limit analysis slope stability with nonlinear yield condition, Int. J. Numer. Anal. Met., 12, 341–345, https://doi.org/10.1002/nag.1610120307, 1988.
Eid, H. T.: Two- and three-dimensional analyses of translational slides in soils with nonlinear failure envelopes, Can. Geotech. J., 47, 388–399, https://doi.org/10.1016/j.enggeo.2013.10.021, 2010.
Gao, Y., Zhang, F., Lei, G.H., Li, D., Wu, Y., and Zhang, N.: Stability charts for 3D failures of homogeneous slopes, J. Geotech. Geoenviron., 139, 1528–1538, https://doi.org/10.1061/(ASCE)GT.1943-5606.0000866, 2013.
Gao, Y., Wu, D., and Zhang, F.: Effects of nonlinear failure criterion on the three-dimensional stability analysis of uniform slopes, Eng. Geol., 198, 87–93, https://doi.org/10.1016/j.enggeo.2015.09.010, 2015.
Gao, Y., Wu, D., Zhang, F., Lei, G.H., Qin, H., and Qiu, Y.: Limit analysis of 3D rock slope stability with non-linear failure criterion, Geomech. Eng., 10, 59–76, https://doi.org/10.12989/gae.2016.10.1.059, 2016.
Hoek, E. and Brown, E. T.: Empirical strength criterion for rock masses, J. Geotech. Eng. Division, 106, 1013–1035, https://doi.org/10.1016/0022-1694(80)90029-3, 1980.
Huang, W. and Ji, J.: Closed-form solutions for regional earthquake–induced landslide prediction: rotational failure mechanism, Landslides, 19, 2671–2684, https://doi.org/10.1007/s10346-022-01916-5, 2022.
Ingles, J., Darrozes, J., and Soula, J. C.: Effects of the vertical component of ground shaking on earthquake-induced landslide displacements using generalized Newmark analysis, Eng. Geol., 86, 134–147, https://doi.org/10.1016/j.enggeo.2006.02.018, 2006.
Jiang, J. C., Baker, R., and Yamagami, T.: The effect of strength envelope nonlinearity on slope stability computations, Can. Geotech. J., 40, 308–325, https://doi.org/10.1139/t02-111, 2003.
Li, A. J., Lyamin, A. V., and Merifield, R. S.: Seismic rock slope stability charts based on limit analysis methods, Comput. Geotech., 36, 135–148, https://doi.org/10.1016/j.compgeo.2008.01.004, 2009.
Li, X.: Finite element analysis of slope stability using a nonlinear failure criterion, Comput. Geotech., 34, 127–136, https://doi.org/10.1016/j.compgeo.2006.11.005, 2007.
Li, Y. and Yang, X.: Seismic displacement of 3D slope reinforced by piles with nonlinear failure criterion, Int. J. Geomech., 19, 04019042, https://doi.org/10.1061/(ASCE)GM.1943-5622.0001411, 2019.
Li, Y. X. and Yang, X. L.: Soil-slope stability considering effect of soil-strength nonlinearity, Int. J. Geomech., 19, 04018201, https://doi.org/10.1061/(ASCE)GM.1943-5622.0001355, 2018.
Ling, H. I. and Leshchinsky, D.: Effects of vertical acceleration on seismic design of geosynthetic-reinforced soil structures, Geotechnique, 48, 347–373, https://doi.org/10.1680/geot.1998.48.3.347, 1998.
Ling, H. I., Leshchinsky, D., and Yoshiyuki, M.: Soil slopes under combined horizontal and vertical seismic accelerations, Earthq. Eng. Struct. D., 26, 1231–1241, https://doi.org/10.1002/(SICI)1096-9845(199712)26:12<1231::AID-EQE707>3.0.CO;2-Z, 1997.
Maksimovic, M.: Nonlinear failure envelope for soils, J. Geotech. Eng., 115, 581–586, https://doi.org/10.1061/(ASCE)0733-9410(1989)115:4(581), 1989.
Michalowski, R. L. and Drescher, A.: Three-dimensional stability of slopes and excavations, Geotechnique, 59, 839–850, https://doi.org/10.1680/geot.8.P.136, 2009.
Michalowski, R. L. and Park, D.: Three-dimensional ridge collapse mechanism for narrow soil slopes, Int. J. Numer. Anal. Met., 45, 1972–1987, https://doi.org/10.1029/JC084iC01p00338, 2021.
Pan, Q., Zhang, R., Wang, S., Chen, J., Zhang, B., Zou, J., and Yang, X.: Three-dimensional stability of slopes under water drawdown conditions, Int. J. Geomech., 23, 04022254, https://doi.org/10.1061/(ASCE)GM.1943-5622.0002614, 2023.
Pang, Z. and Gu, D.: Seismic stability of a fissured slope based on nonlinear failure criterion, Geotech. Geol. Eng., 37, 3487–3496, https://doi.org/10.1007/s10706-019-00806-3, 2019.
Penman, A.: Shear characteristics of saturated silt measured in triaxial compression, Geotechnique, 3, 312–328, https://doi.org/10.1680/geot.1953.3.8.312, 1953.
Popescu, M., Ugai, K., and Trandafir, A.: Linear versus nonlinear failure envelopes in LEM and FEM slope stability analysis, Proc. 8th Int. Symp. on Landslides, Cardiff, UK, 3, 1227–1234, 2000.
Shen, J. and Karakus, M.: Three-dimensional numerical analysis for rock slope stability using shear strength reduction method, Can. Geotech. J., 51, 164–172, https://doi.org/10.1139/cgj-2013-0191, 2013.
Srbulov, M.: On the influence of soil strength brittleness and nonlinearity on slope stability, Comput. Geotech., 20, 95–104, https://doi.org/10.1016/S0266-352X(96)00014-6, 1997.
Wan, Y., Gao, X., Wu, D., and Zhu, L.: Reliability of spatially variable soil slope based on nonlinear failure criterion, Nat. Hazards, 117, 1179–1189, https://doi.org/10.1007/s11069-023-05868-4, 2023.
Wang, Z., Pan, P., Zuo, J., and Gao, Y.: A generalized nonlinear three-dimensional failure criterion based on fracture mechanics, J. Rock Mech. Geotech. Eng., 15, 630–640, https://doi.org/10.1016/j.jrmge.2022.05.006, 2023.
wudi9172: Data and charts for Limit analysis of earthquake-induced landslides considering two strength envelopes, Baidu Netdisk [data set], https://pan.baidu.com/s/1-F0ItOekGVtYxGReQzDR-A?pwd=4uxx, last access: 11 December 2024.
Wu, D., Gao, Y., Chen, X., and Wang, Y.: Effects of soil strength nonlinearity on slip surfaces of homogeneous slopes, Int. J. Geomech., 21, 06020035, https://doi.org/10.1061/(ASCE)GM.1943-5622.0001896, 2021a.
Wu, D., Wang, Y., Zhang, F., and Qiu, Yue.: Influences of pore-water pressure on slope stability considering strength nonlinearity, Adv. Civ. Eng., 2021, 1–16, https://doi.org/10.1155/2021/8823899, 2021b.
Wu, D., Chen, X., Tao, Y., and Meng, X.: Estimating Mohr–Coulomb strength parameters from the Hoek–Brown criterion for rock slopes undergoing earthquake, Sustainability, 15, 5405, https://doi.org/10.3390/su15065405, 2023.
Wu, D., Chen, X., and Zhang J.: Effect of sea level drawdown on coastal clay slope stability considering two strength criteria, Mar. Georesour. Geotec., 2024, 1–19, https://doi.org/10.1080/1064119X.2024.2311780, 2024.
Xu, J. and Yang, X.: Seismic stability of 3D soil slope reinforced by geosynthetic with nonlinear failure criterion, Soil Dyn. Earthq. Eng., 118, 86–97, https://doi.org/10.1016/j.soildyn.2018.12.019, 2019.
Xu, J. S. and Yang, X. L.: Three-dimensional stability analysis of slope in unsaturated soils considering strength nonlinearity under water drawdown, Eng. Geol., 237, 102–115, https://doi.org/10.1016/j.enggeo.2018.02.010, 2018.
Yang, X. L. and Yin, J. H.: Slope stability analysis with nonlinear failure criterion, J. Eng. Mech., 130, 267–273, https://doi.org/10.1061/(ASCE)0733-9399(2004)130:3(267), 2004.
Yang, X. L., Li, L., and Yin, J. H.: Seismic and static stability analysis for rock slopes by a kinematical approach, Geotechnique, 54, 543–550, https://doi.org/10.1680/geot.2004.54.8.543, 2004.
Zhang, X. J. and Chen, W. F.: Stability analysis of slopes with general nonlinear failure criterion, Int. J. Numer. Anal. Met., 11, 33–50, https://doi.org/10.1002/nag.1610110104, 1987.
Zhao, L., Cheng, X., Dan, H., Tang, Z., and Zhang, Y.: Effect of the vertical earthquake component on permanent seismic displacement of soil slopes based on the nonlinear Mohr–Coulomb failure criterion, Soils Found., 57, 237–251, https://doi.org/10.1016/j.sandf.2016.12.002, 2017a.
Zhao, L., Cheng, X., Li, L., Chen, J., and Zhang, Y.: Seismic displacement along a log-spiral failure surface with crack using rock Hoek–Brown failure criterion, Soil. Dyn. Earthq. Eng., 99, 74–85, https://doi.org/10.1016/j.sandf.2016.12.002, 2017b.
Zhong, J. H. and Yang, X. L.: Pseudo-dynamic stability of rock slope considering Hoek–Brown strength criterion, Acta Geotech., 17, 2481–2494, https://doi.org/10.1007/s11440-021-01425-0, 2022.