Probabilistic seismic hazard assessment of Sweden

Assessing seismic hazard in stable continental regions such as Sweden poses unique challenges compared to active seismic regions. With diffuse seismicity, low seismicity rate, few large-magnitude earthquakes and little strong-motion data, estimating recurrence parameters and determining appropriate attenuation relationships is challenging. This study presents a probabilistic seismic hazard assessment of Sweden based on a recent earthquake catalogue, which includes a high number of events with magnitudes ranging from M_w −1.4 to M_w 5.9, enabling recurrence parameters to be calculated for smaller source zones than in previous studies and with less uncertainty. Recent ground motion models developed specifically for stable continental regions, including Fennoscandia, are used in the logic tree accounting for their uncertainty, and the hazard is calculated using the OpenQuake engine. The results are presented in the form of mean peak ground acceleration (PGA) maps at 475- and 2500-year return periods and hazard curves for four seismically active areas in Sweden. We find the highest hazard in Sweden in the northernmost part of the country, in the post-glacial fault province. This is in contrast to previous studies, which have not considered the relatively high seismic activity on the post-glacial faults. We also find hazard to be relatively high along the northeast coast and in southwestern Sweden, whereas the southeast of Sweden and the mountain region to the northwest have low hazard. For a 475-year return period we estimate the highest PGA values to be 0.04–0.06 g in the far north, and for a 2500-year return period it is 0.1–0.15 g in the same area. Much remains to be addressed in regards to the intraplate seismicity in Sweden, including the homogenization of small local magnitudes with large moment magnitudes, the occurrence of large events in areas with little prior seismicity and the uncertainties surrounding the potential for large earthquakes on the post-glacial faults in northern Fennoscandia.

1 Introduction

Earthquakes are known to cause some of the most fatal natural disasters. As short-term prediction of where and when large earthquakes occur is currently not routinely possible, and as earthquakes can rapidly evolve into disasters, earthquake risk reduction strategies must focus on the mitigation and preparation phases of the disaster cycle (Elliott, 2020). One key component of this is producing an accurate seismic hazard assessment in terms of probable ground motions, which can help identify areas of high hazard and allow for designing appropriate risk reduction strategies.

At plate boundaries, earthquake activity is high, and large events can often be associated with identified fault zones. Conversely, stable continental regions, such as Sweden, tend to show a more diffuse geographically distributed pattern of seismicity (Schulte and Mooney, 2005; England and Jackson, 2011), occurrence rates are low (e.g. Lund et al., 2021) and areas of high hazard can be difficult to define (e.g. Calais et al., 2016). However, as England and Jackson (2011) show, the risk posed by earthquakes in such intraplate areas is far from negligible. They showed that of the 130 earthquakes with 1000 or more casualties occurring over a 120-year period prior to 2012, about 100 took place in continental interiors. These intraplate earthquakes also caused approximately 75 % more total deaths than the plate boundary events.

Based on their analysis of historical and instrumental data before 2005, Bödvarsson et al. (2006) suggest that Sweden can expect on the order of one magnitude 5 earthquake every century and a magnitude 6 earthquake every millennium. As the rate of occurrence of these higher-magnitude earthquakes is low, the national authority in charge of building codes (Swedish National Board of Housing, Building and Planning – Boverket) has no current plans to implement Eurocode 8 in Sweden (Boverket, personal communication, 2020), and there is no official national seismic hazard map. The general increase in risk awareness in society, especially after particularly disastrous earthquakes (Tan and Maharjan, 2018), has, however, led to an increased number of requests for seismic hazard information from building companies and corporate site planning projects. For sensitive infrastructure sites such as nuclear power plants, repositories of spent nuclear fuel, dams and mines, seismic hazard estimates are required, and there is therefore a need to better define the hazard spatially, estimate potential ground motions and investigate associated uncertainties.

In this paper, we review earlier estimates of seismic hazard in Sweden, with a special emphasis on the recent release of the European Seismic Hazard Model 2020 (Danciu et al., 2021). We then discuss the development of a new probabilistic seismic hazard model for Sweden, which will take into account the large number of smaller earthquakes recorded by the Fennoscandian seismic networks in the last 2 decades (e.g. Lund et al., 2021; Veikkolainen et al., 2021; Ottemöller et al., 2018) as well as recent developments in ground motion models (Fülöp et al., 2020; Weatherill and Cotton, 2020). We use the OpenQuake engine (Pagani et al., 2014) to develop hazard maps with mean estimates for peak ground acceleration (PGA) corresponding to return periods of 475 and 2500 years, as well as hazard curves for Sweden's most seismically active areas. Finally, we discuss the uncertainties inherent in the models and the potential need for additional approaches to seismic hazard assessments in Sweden.

2 Earthquake activity in Sweden

Sweden is located in a stable continental region (SCR) with very few damaging earthquakes (Bödvarsson et al., 2006; Lund et al., 2021). Most of the country is part of the Fennoscandian Shield of the East European Craton (see Fig. 1), with Archean and early Paleoproterozoic rocks in the north that were, to a large extent, reworked during the Paleoproterozoic Svecokarelian orogeny (Stephens and Bergman-Weihed, 2020). The eastern part of the country is dominated by Svecokarelian rocks, whereas the southwest contains Mesoproterozoic and Neoproterozoic rock of the Sveconorwegian orogeny (Stephens and Bergman-Weihed, 2020). The Gulf of Bothnia in the east and the Baltic Sea further southeast comprise Mesoproterozoic to Ediacaran and lower Paleozoic sedimentary platformal cover rocks of varying thickness. Onshore Finland comprises Archean, Svecokarelian and Mesoproterozoic rocks, whereas further south, the Baltic countries are covered by sedimentary rocks deposited on the East European Craton (Bogdanova et al., 2008). In western Sweden, older basement and Paleozoic cover rocks are affected by the Caledonian orogeny, which created the present-day Swedish mountain chain (Stephens and Bergman-Weihed, 2020). Further west, Norway is composed mostly of rocks from the Caledonian and Sveconorwegian orogens onshore and passive margin deposits offshore (e.g. Corfu et al., 2014; Bingen et al., 2021). To the south, the craton is separated from Phanerozoic Europe by deformation zones through southernmost Sweden (the Sorgenfrei-Tornquist Zone) and Denmark (the Trans-European Suture Zone), over which major changes in lithospheric, crustal and sediment cover thicknesses occur (e.g. Sandersen et al., 2021). The opening of the Atlantic some 60 Myr ago is the latest large-scale tectonic event to significantly affect Fennoscandia (Stephens and Bergman-Weihed, 2020).

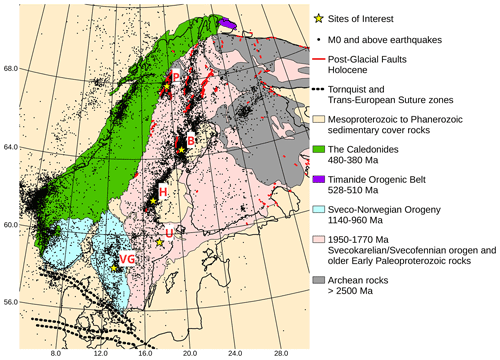
Figure 1 Seismicity, geology, and tectonic map of Fennoscandia. Black dots indicate earthquakes in the declustered catalogue in this study. Yellow stars indicate locations referred to in the text, from north: “P”, the Pärvie fault; “B”, the Burträsk fault; “H”, the Hälsingland region; “U”, Uppsala; and “VG”, Västergötland, south of Lake Vänern. The Sorgenfrei-Tornquist Zone and Trans-European Suture Zone are marked with dashed black lines. Post-glacial faults (red) from Munier et al. (2020). Map modified after Gregersen et al. (2021).

Fennoscandia has been subject to repeated glaciations during the Quaternary. The latest, the Weichselian ice sheet, reached its maximum approximately 20 000 yr BP (before present) (Svendsen et al., 2004), before retreating and disappearing around 10 kyr BP. Large fault scarps in northern Fennoscandia (see Fig. 1) have been dated to the final deglaciation phase (Lagerbäck and Sundh, 2008; Smith et al., 2021) and are inferred to have resulted from earthquakes with moment magnitudes up to M_w 8 (e.g. Lindblom et al., 2015). Glacial isostatic adjustment is still ongoing in Fennoscandia, and GNSS measurements show that all of Sweden is rebounding, with a maximum uplift velocity of 10.3 mm yr⁻¹ on the northeast coast, decreasing to about 1 mm yr⁻¹ in southernmost Sweden (Vestøl et al., 2019).

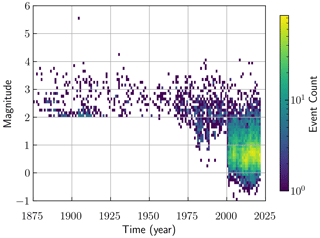
The seismicity in Fennoscandia has been the subject of many studies; Gregersen et al. (2021) provide a recent review of the whole region, whereas Lund et al. (2021) focus on recent observations of earthquakes in Sweden, which we briefly review here. The expansion of the Swedish National Seismic Network (SNSN) from 6 to 65 stations during the first decade of the 21st century has provided a wealth of new earthquake observations, increasing the total number of recorded events from about 1600 prior to the year 2000 to about 12 500 in 2021 (see Figs. 1 and 2). Most of the events are small, with the magnitude of completeness estimated at local magnitude M_L 0.5 within the network. Earthquakes in Sweden are mostly strike-slip, and focal depths vary between near-surface and 35 km depth. Areas of relatively high seismic activity within Sweden include the southwest across Lake Vänern, the northeast along the coast and in the far north along the post-glacial faults (see Fig. 2). The southwest and the northeast coast seismicity agrees well with what was known already from the pre-instrumental period (e.g. Kjellén, 1910); the new data have, however, revealed that activity locally clusters along specific zones and is less diffuse than previously thought. The new observations have significantly changed how seismic activity in the north is viewed. We now know that seismicity is strongly correlated with the mapped post-glacial fault (PGF) scarps, indicating that the faults are still very active, although event magnitudes are generally low (M_L −1 to 3.5, Lindblom et al., 2015). One reason for the lack of early observations along the PGFs is the low population density inland. On the Pärvie fault (Fig. 1), for example, there is only one event in the catalogue prior to 1967 – a M_L 2.6 event in 1927. The largest recorded Pärvie event had M_L 3.7 in 1967 (Ahjos and Uski, 1992). Conversely, the Burträsk PGF (Fig. 1), on the northeast coast, has earthquake reports going back to the 18th century, with the largest events having magnitudes around M_L 4–4.5 (Ahjos and Uski, 1992), and the recent data show that it is the most seismically active region in Sweden.

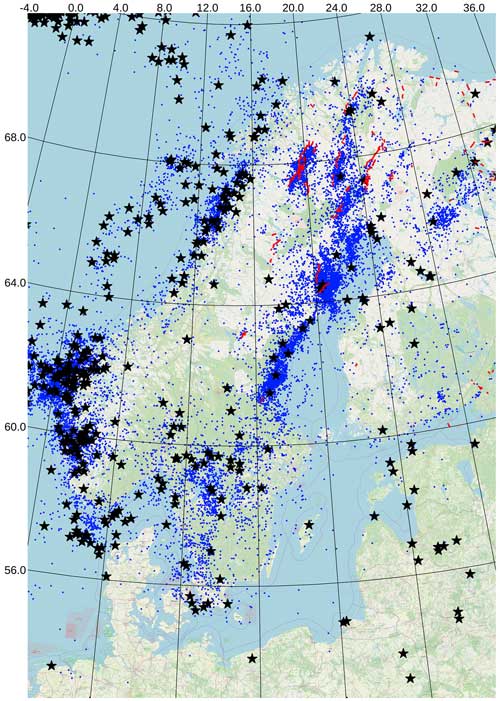
Figure 2 Earthquakes in the Fennoscandian region from our catalogue between 1875 and 2022 (blue dots) and the ESHM20 catalogue for 1497–2014, where M_w≥3.5 (black stars). Red lines: post-glacial faults from Munier et al. (2020). Basemap from © OpenStreetMap contributors 2024. Distributed under the Open Data Commons Open Database License (ODbL) v1.0 by the OpenStreetMap Foundation (OSMF).

The largest historically recorded earthquake on land in Fennoscandia was the 1819 Lurøy M_w 5.9 event in Nordland, Norway, located about 80 km from the Swedish border (Mäntyniemi et al., 2020). In 1759, an event with a surface-wave magnitude of 5.6 occurred in the waters between Sweden and Denmark (Muir Wood, 1989), and in 1904 a M_w 5.4 event took place just off the Swedish west coast close to the Norwegian border (Bungum et al., 2016). Additional M_w 5+ events have occurred in the regions around Sweden, such as the 2004 Kaliningrad earthquake doublet (Gregersen et al., 2007), the 1892 M_w 5.2 western and the 1834 M_w 5.0 southern Norway events (Ahjos and Uski, 1992). Recently, Olesen et al. (2021) trenched the post-glacial Stuoragurra fault in northern Norway and found evidence of an event with a magnitude of about 7 occurring as recently as 700 years ago. This indicates that the PGFs may still be capable of generating very large earthquakes.

The driving forces of Fennoscandian seismicity have been a debated subject (see Gregersen et al., 2021, for a recent review). As glacial rebound dominates the deformation rates of the Fennoscandian crust, both vertically and horizontally, GNSS measurements cannot resolve any tectonic-driven deformation (Vestøl et al., 2019). However, evidence such as focal mechanisms and in situ stress measurements points to ridge push from the opening of the Atlantic as the main driving force for seismicity, potentially moderated by glacially induced stress, sediment load or other regional to local stresses (Gregersen et al., 2021).

3 Previous seismic hazard assessments for Sweden

Here we review earlier seismic hazard assessments for Sweden. We will refer to the intercept and slope of the earthquake frequency–magnitude distribution as the a and b values (Gutenberg and Richter, 1944), M_c as the magnitude of completeness of a frequency–magnitude distribution, and M_max as the maximum possible magnitude for an area.

The studies by Båth (1979) and Slunga (1979) were the first to estimate seismic hazard in Sweden. They only had access to some 25 years of instrumental data and thus relied to a large extent on macroseismic data, which are limited in parts of Sweden due to the low population density. Båth (1979) estimated recurrence rates for earthquakes of varying magnitudes in a 2° by 2° grid across Fennoscandia and calculated earthquake risk according to the formula put forward by Lomnitz (1974), describing earthquake risk as “the probability $R(D/T)$ that a shock of mean return period T occurs during a design period D”. He found the highest hazard on the Norwegian west coast and, for Sweden, estimated a 5 % probability in 10 years (a return period of 195 years) of an event of M_L 5 and above on both the southwest and northeast coasts. Slunga (1979), investigating the seismic hazard at sites of the then four Swedish nuclear power plants, estimated accelerations of 0.05–0.20 g for an annual probability of 10⁻⁵. The development of the FENCAT catalogue (Ahjos and Uski, 1992), a continuously updated joint regional catalogue of earthquakes in northern Europe since 1375, enabled later studies to use a larger, more homogeneous data set for Fennoscandia.

FENCAT data until 1987 were used for the first Swedish probabilistic seismic hazard assessment (PSHA), directed at site-specific assessments for Sweden's four nuclear power plants (SKI, 1992). The study included Fennoscandian earthquakes south of latitude 61° to estimate the seismicity rate. The lack of strong-motion data from Fennoscandia prompted SKI (1992) to turn to existing Japanese “standard response spectra for rock sites” for ground motion models. The Japanese spectra were modified to fit Swedish earthquake source properties and crustal attenuation properties. The envelope ground response spectra resulting from the SKI (1992) study are still in use in the Swedish nuclear industry today, and the estimated PGA is 0.11 g for a hard rock site at an annual probability of 10⁻⁵ and a damping of 5 % (SKI, 1992; Larsson and Larsson, 2018). In a review, Lund et al. (2017) found that SKI (1992) may underestimate the rate of events larger than approximately M_w 5.2 and recommended an update with modern data and methodologies.

Kijko et al. (1993) used FENCAT and a model that accounts for varying magnitudes of completeness through time in order to quantify probabilistic seismic hazard in Sweden by estimating the recurrence rates of earthquakes. They found that Sweden can expect 5.5 earthquakes per year with magnitudes equal to or greater than 2.4, with the maximum expected earthquake magnitude in southern Sweden being 4.9 for a 615-year time span and a maximum magnitude of 4.3 in northern Sweden over 331 years. Mäntyniemi et al. (1993) expanded the Kijko et al. (1993) study to all of Fennoscandia and also included probabilities for non-exceedance of various magnitudes in 1 and 50 years in defined subregions. The results for Sweden were similar to that of Kijko et al. (1993).

The Wahlström and Grünthal (2000, 2001) studies perform full probabilistic seismic hazard assessments for Fennoscandia using the FENCAT catalogue. Wahlström and Grünthal (2001) apply two different magnitude homogenization schemes. They used two large regions for magnitude completeness estimates and six different regional and non-regionalized seismic source zones. Combining the recurrence parameters with two different ground motion models in a logic tree, Wahlström and Grünthal (2001) produce a hazard map for Fennoscandia, with 90 % probability of non-exceedance of median horizontal PGA in 50 years, and hazard curves and hazard deaggregations for Sweden, Norway, Denmark and Finland. Their results indicate that the Norwegian west and northwest coasts have the highest hazard in Fennoscandia. The highest hazard in Sweden was found in the southwest, close to the Norwegian border, with an estimated PGA of 0.03 g for a 475-year return period and 0.08 g for a 4745-year return period.

Mäntyniemi et al. (2001) produced a seismic hazard map of Fennoscandia by using the site-specific technique of Kijko and Graham (1998, 1999) and applying it to a grid of Fennoscandian locations, similar to a smoothed seismicity approach (e.g. Danciu et al., 2021). They estimate a, b and M_max values from the data in a specific area around a grid point and use those with a ground motion model to calculate the hazard in terms of ground motion probabilities. Mäntyniemi et al. (2001) used a 0.5° by 0.5° grid with a constant b value of 0.84±0.01 and an M_max of 5.8 over the entire region, while the a value varied with the seismicity included at each grid point. Ground motion models by Uski and Tuppurainen (1996) and EMSC (1999) were used, and the resulting hazard map shows PGA for a 475-year return period, where the highest hazard was obtained at the northwestern coast of Norway with 0.038 g (note that western Norway around Bergen was not included in the analysis). The highest PGA in Sweden reached 0.022 g both in southwestern Sweden and on the northeast coast.

Bodare and Kulhánek (2006) used the results in Kijko et al. (1993) and Mäntyniemi et al. (1993) together with a relationship between M_L and the acceleration at the epicentre (Båth, 1980) to infer that seismic hazard at hydropower dams in northern Sweden is unlikely to exceed 0.04 g in the next 50–100 years. In two large PSHA projects for the nuclear industry in Finland, analysis of seismicity and definition of seismic source zones was undertaken for Sweden and Finland. The first, the Fennovoima project, assembled seismologists and geologists from Finland and Sweden to perform a full site-specific PSHA for a proposed new nuclear power plant in northern Finland (Korja and Kosonen, 2015; Saari et al., 2015). Using a similar methodology, a PSHA revision was later performed for the sites of the existing nuclear power plants in Finland (Korja and Kihlman, 2016). The hazard results of these studies have not been made public. On a larger scale, the Global Seismic Hazard Assessment Program (GSHAP, Grünthal and Group, 1999) and the European Seismic Hazard Models 2013 and 2020 (ESHM13 and ESHM20; Woessner et al., 2015; Danciu et al., 2021, respectively) have estimated seismic hazard in Sweden. ESHM20 is described in some detail in Sect. 3.1 below.

3.1 Sweden in the European Seismic Hazard Model 2020

The most recent evaluation of seismic hazard in Sweden comes from the 2020 European Seismic Hazard Model (ESHM20) (Danciu et al., 2021), which assesses earthquake hazard in the Euro-Mediterranean region and builds on the 2013 version of the model (ESHM13; Woessner et al., 2015). ESHM20 applies a fully probabilistic framework homogeneously across the entire pan-European region, while accounting for cross-country-border issues. The earthquake data come from the European PreInstrumental Earthquake CAtalogue (EPICA, Rovida and Antonucci, 2021), which spans the years 1000 to 1899, and from an extension of the European-Mediterranean Earthquake Catalogue (EMEC, Grünthal et al., 2013), such that it spans the time from 1900 to the end of 2014. Magnitudes are harmonized to the moment magnitude M_w, the catalogue is declustered and only events with M_w≥3.5 are included in the magnitude–frequency analysis. For Sweden and the surrounding region within 300 km of Sweden's borders and economic zone, the unified ESHM20 earthquake catalogue contains 212 events, from 1497 to 2014, with magnitudes $\mathrm{3.5}\le M_{\mathrm{w}}\le \mathrm{5.8}$ (see Fig. 2).

In order to estimate the recurrence parameters of the magnitude–frequency distribution at the most appropriate spatial distribution, ESHM20 uses a hierarchy of seismic source zones. Fennoscandia is assigned to a single maximum magnitude zone, within which M_max is uniform. It is divided into two completeness zones where reporting is assumed to be homogeneous through time such that the temporal variation in M_c is the same all through the zone. At the next levels, Fennoscandia is divided into four tectonic source zones, TSZs, and about 20 smaller area source zones, ASZs, based on geology, seismicity and an assumption of homogeneous seismicity rate. In these zones, a- and b-vales are calculated using a doubly truncated Gutenberg–Richter distribution, using an automatic maximum likelihood method based on the earthquakes within the zone (Danciu et al., 2017), for zones with more than 30 earthquakes. For ASZs with less than 30 events, the b value from the TSZ is re-used, and the a value is re-scaled from the TSZ with the ratio of the number of complete events in the ASZ and TSZ. If the ASZ does not contain any events above the magnitude of completeness, an a value is assigned by re-scaling the TSZ value with the area ratio of ASZ to TSZ. Uncertainties are estimated using random sampling and discrete approximation of probability distribution methods, giving 16th, 50th and 84th percentile estimates of the median a and b values. A tapered Pareto distribution is also defined to describe the recurrence parameters, primarily to provide a faster decaying alternative closer to M_max. For Sweden and a 300 km border region, only two ASZs have enough events for separate estimates of the recurrence parameters; all other use the TSZ b values and re-scaled a values. All seismogenic source models are implemented through a logic tree, with the median, 5th percentile and 95th percentile describing the branches of individual area source Gutenberg–Richter parameters, with 0.6, 0.2 and 0.2 as the respective branch weights. M_max in Fennoscandia has three branches, where M_max is 6.3, 6.6 and 6.9, with weights 0.5, 0.4 and 0.1, respectively.

ESHM20 uses a scaled backbone approach for implementing ground motion models (GMMs). This is done by selecting a relevant GMM from the literature and modifying it based on the observations and knowledge of the region's crustal properties to account for the uncertainty in the expected ground motions. The scaled backbone GMM for the cratonic region is obtained by generating median ground motions on hard rock for various magnitude ($\mathrm{4.0}\le M_{\mathrm{w}}\le \mathrm{8.0}$) and distance ranges ($\mathrm{1.0}\le R_{\mathrm{rup}}\le \mathrm{500}$ km), starting with equally weighing 21 Central and Eastern United States (CEUS) GMMs and fitting to a parametric GMM of the same form as Kotha et al. (2020) (defined for active shallow crustal regions in ESHM20), mapped into a scaled backbone logic tree (Weatherill and Cotton, 2020). These ground motions are defined for very hard rock conditions ($V_{\mathrm{S},\mathrm{30}}=\mathrm{3000}$ m s⁻¹) and re-scaled to reference $V_{\mathrm{S},\mathrm{30}}=\mathrm{800}$ m s⁻¹ rock conditions using the CEUS site amplification models of Stewart et al. (2020) and Hashash et al. (2020). Weatherill and Cotton (2020) calibrate the model's epistemic uncertainties and propose a logic tree for the application of the model to cratonic regions where one branch is the new parametric craton model and one branch an adaption of the shallow crustal seismicity model used for central Europe (Kotha et al., 2020), only retaining the mid and upper (i.e. higher velocity) twigs of that branch. This GMM logic tree combination is used for most of Sweden, Finland and the Baltic region, while the shallow crustal logic tree is used for most of Norway and Denmark.

The final hazard map shows that for Fennoscandia, the seismic hazard is highest along the Norwegian west coast. The Swedish northeast coast and the coast of the Baltic countries also have relatively high hazard, whereas most of Denmark, the interior of north and central Sweden, and south-central Finland have the lowest hazard. The highest estimated mean PGA for Sweden is 0.025 g for a return period of 475 years and 0.11 g for a return period of 2500 years.

4 Methods

Probabilistic seismic hazard assessment (PSHA) is a widely used technique to estimate seismic hazard, which we utilize in this study. It quantifies the rate at which ground motions are expected for all possible earthquake scenarios (Cornell, 1968), based on earthquake recurrence data and crustal attenuation properties. Here we detail how our study implements the steps involved: (1) preparing earthquake data, which involves merging data from different catalogues, removing dependent events and homogenizing the earthquake magnitude; (2) defining seismic source zones and associating earthquakes to them; (3) calculating recurrence parameters for each seismic source zone; (4) defining the seismic source model logic tree; (5) selecting appropriate ground motion models that represent the attenuation of seismic waves and defining the ground motion model logic tree; and (6) estimating hazard probabilistically by accounting for the epistemic uncertainties through a logic tree.

4.1 Data preparation

A number of seismic networks in Fennoscandia collect seismic data and report to FENCAT and other international compilations: the Swedish National Seismic Network (SNSN, Lund et al., 2021), the Norwegian National Seismic Network (NNSN, Ottemöller et al., 2018) and NORSAR (Norsar, 1971), the Finnish National Seismic Network (FNSN, Veikkolainen et al., 2021; Ahjos and Uski, 1992) and Oulu University (Sodankylä Geophysical Observatory/University of Oulu, 1980), the Geological Survey of Denmark and Greenland (GEUS, 2023), and the Geological Survey of Estonia (Soosalu et al., 2022). Location and magnitude uncertainties for the recorded earthquakes have decreased through time, with increased population density in the pre-instrumental period and with improved network configurations in later times. There are no uncertainties associated with location and magnitude estimates in the FENCAT, but since around 2010 the SNSN has average uncertainties of about 2–3 km in the epicentres and 0.1–0.2 in the magnitudes. Since the rate of recorded non-tectonic seismic events such as mine, quarry, construction, and military blasts and mining-induced events exceeds the earthquake rate by up to a factor of 10 or more in much of Fennoscandia, the Fennoscandian seismic network analysts have a high focus on classification, nowadays aided by machine learning algorithms (Kortström et al., 2016; Eggertsson et al., 2024). During FENCAT data merging, additional checks for non-tectonic events are carried out, such that the final catalogue is as free as possible from such events. In the older data, there are, however, probably still both human-made and frost-related events present that are difficult to identify (Uski et al., 2015). The earthquake data are processed with the methodologies developed in Uski et al. (2015), comprising (i) data merging and cleaning, (ii) declustering, and (iii) magnitude homogenization. We briefly describe these steps below.

4.1.1 Data merging and cleaning

The version of the FENCAT catalogue at our disposal spans the year 1375 until the end of 2014 (Korja and Kihlman, 2016). We added the semi-reviewed FENCAT between 1 January 2015 and 30 September 2020 (Finnish National Seismic Network, 2023). Both these catalogues contain earthquakes from all over Fennoscandia and some other areas in northern Europe. The SNSN does not report all small microearthquakes to FENCAT, so we also added the entire 15 August 2000 to 28 February 2022 SNSN catalogue to the data set. As we need data from a zone surrounding Sweden out to 300 km distance, we also extracted eight events from the unified ESHM20 catalogue (Danciu et al., 2021) that were not present in our version of FENCAT. Duplicates were removed from the resulting list of events, and remaining non-tectonic events that could be identified were removed from the data. As FENCAT contains events far from Sweden, such as along the Mid-Atlantic Ridge, we removed these together with events in Britain, central Poland, Russia east of 40^∘ longitude and Svalbard prior to further processing. The joint earthquake catalogue comprises 24 215 events within the tectonic source zones (Sect. 4.2) of the hazard assessment, with earthquake magnitudes between M_w −1.4 and M_w 6.1.

4.1.2 Declustering

Probabilistic seismic hazard assessment generally assumes that the earthquakes included in the assessment occur independently of each other, following a Poisson process (Baker et al., 2021). In reality, many events occur as a consequence of other events, such as foreshocks, aftershocks and swarm events. Separating the catalogue into dependent and independent events is referred to as declustering, and numerous techniques exist for this purpose; see review in van Stiphout et al. (e.g. 2012). As discussed in detail in Uski et al. (2015), most declustering methods are designed for plate boundary seismicity, with large events and significant Omori-type aftershock activity. In intraplate Fennoscandia, on the contrary, events are generally small, and even moderately large events can have few and small aftershocks, inconsistent with both the Omori and Båth aftershock relationships. Following Uski et al. (2015), we implemented a declustering scheme using a Gardner and Knopoff (1974) windowing procedure based on conservative estimates of location error and manual inspection of clusters. We set the spatial (radius) and temporal distances between an event and its potential aftershock or swarm member to 10 km and 30 d for events with magnitude larger than 1.5 and to 5 km and 15 d for smaller events. We did not consider the magnitude of completeness or the relative size of events in the clustering. The largest event in each cluster was considered the independent event and forwarded to the declustered catalogue.

The results were checked manually and also by comparing the inter-event times of subsets of the declustered catalogue to those from synthetic Poissonian catalogues (produced using the observed average rates and an average of 1000 simulated inter-event time sequences). The subsets were defined in time intervals where the average yearly rate is approximately similar and visual inspection of the subset inter-event time distributions (Fig. A1) shows that the declustering process to a large degree removes the non-Poissonian short-inter-event-time events in the original catalogue.

In agreement with Mäntyniemi (1996) and Uski et al. (2015), we find that the fraction of dependent events in Fennoscandia is low. Our catalogue retains 19 943 independent events (Fig. 2), implying approximately 18 % dependent events. The results show that clustering in Sweden is highest along the very active post-glacial faults in the north, especially the Pärvie and Burträsk faults, and is also significant along the northeast coast and in some areas south of Lake Vänern (Fig. A2). The largest cluster contains 199 events and occurred in the Kouvola area in southern Finland, known for its shallow swarm activity. In their study of a 500 km radius area around Pyhäjoki on the northeast coast of Finland, Uski et al. (2015) found a smaller fraction of dependent events (11 %) than we find here. Although their area of interest included most of the seismicity of Finland and Sweden north of Uppsala (Fig. 1), the difference is probably due to it not including the highly active west coast and Nordland regions in Norway, where swarm activity is frequently observed (e.g. Shiddiqi et al., 2022). Comparing to ESHM20, we note that the ESHM20 earthquake catalogue only contains a total of 360 events, all with M_w≥3.5, for the area covered by our declustered catalogue.

4.1.3 Magnitude homogenization

Seismic hazard assessments should be based on homogeneous earthquake size estimates, as commonly represented by the moment magnitude, M_w, scale (Hanks and Kanamori, 1979), which does not saturate at large magnitudes. Most earthquakes in the FENCAT catalogue, however, have magnitude estimates either from macroseismic observations or from local magnitude scales from the various network operators, with scales varying slightly over time and institute. Uski et al. (2015) constructed a consistent moment-based magnitude scale, M_w(HEL), based on the local Helsinki magnitude scale, M_L(HEL), earthquakes in SNSN after 15 August 2000, which all have estimates of the scalar seismic moment (Rögnvaldsson and Slunga, 1993) and other moment estimates from individual studies. They provided relationships between the various magnitude scales, M_L(HEL) and M_w(HEL), and related M_w(HEL) to the scalar seismic moment M₀ as

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{M}_{\mathrm{w}}\left(\mathrm{HEL}\right)=\mathrm{0.83}{\log }_{\mathrm{10}}\left(M_{\mathrm{0}}\right)-\mathrm{7.98}\mathrm{for}{\log }_{\mathrm{10}}\left(M_{\mathrm{0}}\right)\le \mathrm{13.5},\\ {\displaystyle }& {\displaystyle }{M}_{\mathrm{w}}\left(\mathrm{HEL}\right)=\mathrm{0.59}{\log }_{\mathrm{10}}\left(M_{\mathrm{0}}\right)-\mathrm{4.73}\mathrm{for}{\log }_{\mathrm{10}}\left(M_{\mathrm{0}}\right)>\mathrm{13.5}.\end{array}$$

We will use the M_w(HEL) magnitude homogenization scheme for all events in this study and for brevity denote M_w(HEL) as M_w. Uski et al. (2015) points out that the relation is only defined by observations to log ₁₀(M₀)≈17.5 (M_w≈5.6) but that it agrees well with the original (Hanks and Kanamori, 1979) to approximately log ₁₀(M₀)=19, or M_w=6.6.

The final declustered and magnitude homogenized catalogue has 19 943 events, with magnitudes ranging between $-\mathrm{1.4}\le M_{\mathrm{w}}\le \mathrm{5.9}$. There are 341 events with M_w≥3.5 and 182 events with M_w≥4.0 in the tectonic source zones, indicating that our magnitude homogenization scheme produces slightly lower magnitudes than the one used by ESHM20 for Fennoscandia, which has 360 events with M_w≥3.5 in the same area. We will only use events recorded from the year 1875 onwards, which is approximately when the Swedish Geological Society started more systematic investigations of earthquake reports (Kjellén, 1910). Figure 3 shows earthquake magnitude density plotted as a function of time for Sweden and the Swedish economic zone and highlights the significant improvement in completeness after the year 2000. We also note the lack of reported M_w≥3.2 events between 1936 and 1962, the reason for which we do not know, and the very few recorded events with M_w≥4. Prior to 1950 the data stem almost entirely from macroseismic observations; Fig. 3 shows that this has produced a lower magnitude threshold at approximately M_w 2, which was the lowest magnitude given to macroseismically observed events.

Figure 3 Magnitude–time density plot of earthquakes from the declustered and magnitude homogenized catalogue since 1875. These earthquakes lie within a zone that is 300 km from the Swedish national border or economic zone boundaries (blue dots within the red zone in Fig. 4a).

4.2 Seismic source zones

Seismic source zones (SSZs) are defined based on geological and tectonic features, the clustering of seismicity and homogeneity of the seismicity rate; i.e. variations in M_c are the same within each zone. The source zones form the basis upon which recurrence parameters, maximum magnitude and ground motion models are calculated and assigned. During the Finnish nuclear industry projects (Korja and Kosonen, 2015; Korja and Kihlman, 2016), Fennoscandian seismologists and geologists came together to define appropriate cross-border SSZs for these site-specific PSHAs. Work on harmonized Fennoscandian SSZs was continued as part of the review for ESHM20 and further developed in workshops in 2022 and 2023 for this study and ongoing studies in Finland and Norway.

As this study focuses on Sweden, we use earthquakes in the area of Sweden and a 300 km wide area surrounding the national boundaries and, in the sea, the Swedish economic zone. Following the concept of super zones in ESHM20, we define large-scale tectonic source zones (TSZs) and area source zones (ASZs) (see Fig. 4). The TSZs capture large-scale aspects of the crust, such as the regional orogenies and deformation structures, while attempting to ensure homogeneous seismicity patterns. Given the relatively large number of earthquakes in the TSZs, they provide large-scale recurrence parameters which we use for ASZs with insufficient number of events. We define four TSZs: tectonic source zone T1 comprises the Archean and Svecokarelian rocks of eastern and northeastern Sweden and northern Finland, including the seismicity along the Swedish northeast coast, most of the Fennoscandian post-glacial faults, the Kuusamo seismicity in Finland and the scattered seismicity in southeastern Sweden. Zone T2 spans the Sveconorwegian rocks in southwestern Sweden and southern Norway plus the Oslo graben, which are all areas of relatively high seismicity. Western and northern Norway with the Caledonides and the adjacent ocean areas make up zone T3, including the intense seismicity along the west coast and in the Nordland region. T4 is the least seismically active area, with the Svecokarelian and Archean rocks of central and southern Finland and the Baltic countries on the sediment-covered East European Platform.

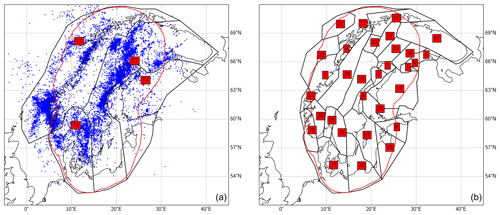
Figure 4 (a) Tectonic source zonation scheme with the fully declustered earthquake catalogue used in this study (blue dots). (b) Area source zonation scheme. The red line indicates a zone encompassing Sweden that is 300 km from the Swedish border or economic zone boundaries. Numbers detail the zone numbers.

The smaller zones, ASZs, are delineated based on active deformational features, such as post-glacial faults, smaller-scale geological and tectonic features, and distinct seismicity patterns (see Fig. 4). For zones that extend outside the 300 km limit, we include all events in the zones in the calculations in order to increase the significance of the results. Uncertainty in the location of earthquakes are on the order of a few kilometres for the post-2000 data, which will have a minimal effect on the allocation of events to ASZs. For the pre-instrumental data the location uncertainties can be much larger, especially for event in the sea areas, but as most zones are large the problem is likely small, and we do not attempt to consider these uncertainties in the allocation to ASZs.

4.3 Maximum magnitude

An estimate of the maximum possible earthquake magnitude, M_max, in each seismic zone is used both when calculating the recurrence parameters, using a doubly truncated Gutenberg–Richter distribution (e.g. Weichert, 1980), and when performing the actual hazard calculation. In stable continental regions like Fennoscandia, estimation of M_max is complicated by low seismicity rates and short observation times; lack of well-defined active fault zones; and general uncertainty about the length, or existence, of an earthquake cycle (e.g. Wheeler, 2016; Calais et al., 2016). A number of different approaches have therefore been taken in assessing M_max for PSHA. Two frequently used methods are extreme value type statistics (EVTS) based on observational data (e.g. Kijko and Graham, 1998; Kijko and Singh, 2011; Beirlant et al., 2019; Zöller, 2022) and the so-called EPRI method of combining global tectonically analogous data sets with local observations (Johnston et al., 1994; Wheeler, 2016).

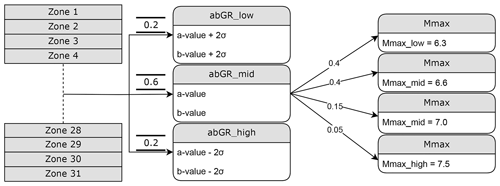
The largest observed earthquake in Fennoscandia is the Lurøy, Norway, event of 1819, with M_w 5.9 (Mäntyniemi et al., 2020). Using two varieties of EVTS, Mäntyniemi et al. (2001) found Fennoscandian M_max of 5.84±0.50 and 5.94±0.52, close to the observed maximum magnitude (excluding the post-glacial faults). As noted by Kijko and Singh (2011), the EVTS methods often underestimate M_max. Wahlström and Grünthal (2001) used the EPRI approach and found a five-point probability distribution of M_max for onshore Fennoscandia, from M_max 5.85 to 7.70, with equal probabilities of 0.2. ESHM13 and ESHM20 both use the same EPRI-based approach to M_max for Fennoscandia, with a resulting distribution of M_max of 6.3, 6.6 and 6.9, with probabilities of 0.5, 0.4 and 0.1, respectively.

The post-glacial faults of northern Fennoscandia are still seismically active (e.g. Lindblom et al., 2015), although the main ruptures are inferred to have occurred at the end of the latest deglaciation some 10 000 years ago (e.g. Smith et al., 2021). They have surface lengths of 40–150 km (Smith et al., 2021), indicating potential magnitudes of up to M_w 8 (Lindblom et al., 2015). Such large events have been inferred to be triggered by the glacial isostatic stress contribution from the late deglacial phase (e.g. Lund, 2015), but as the recent trenching of the Stuoragurra fault in northern Norway indicates ruptures of magnitude 7 as late as 700 years ago (Olesen et al., 2021), the potential for very large earthquakes in the current stress field needs to be considered.

Here we combine the EPRI approach of ESHM20 with the post-glacial fault information and use an M_max distribution of 6.3, 6.6, 7.0 and 7.5, with probabilities of 0.4, 0.4, 0.15 and 0.05, respectively. The large magnitudes mostly affect the hazard on long timescales, as discussed further in Sect. 6.

4.4 Calculating recurrence parameters

Recurrence parameters for each source zone are calculated assuming that the mainshocks in the catalogue follow a Poisson distribution that can be represented by the Gutenberg–Richter (Gutenberg and Richter, 1944) relationship

$$\begin{array}{}\text{(1)}& {\log }_{\mathrm{10}}N\left(M\right)=a-bM,\end{array}$$

where N(M) is the cumulative number of earthquakes per year with (moment) magnitude greater than, or equal to, M; a is the activity rate; and b represents the ratio of low-magnitude events to high-magnitude events. The relationship breaks down for events with magnitudes smaller than some completeness magnitude M_c, where not all events are recorded. Estimating recurrence parameters is challenging in a low seismicity area like Fennoscandia, where larger earthquakes are rare and population density low. Very few events have been recorded prior to the installation of more sensitive seismic networks in the 1960s and 1970s. The completeness magnitude of the national earthquake catalogue has varied during most the 20th century between about M 3 to about M 2. As Fig. 3 shows, due to the rapid expansion of the seismic network in the early 2000, the completeness magnitude for Sweden within the seismic network has dropped to below M 1. However, once the catalogue is subdivided into tectonic or area source zones, the number of earthquakes and M_c vary significantly with time, and we estimate M_cseparately for each zone. A time-varying completeness algorithm (Weichert, 1980), as implemented by the OpenQuake (OQ) engine (Pagani et al., 2014), was used to estimate the recurrence parameters. For quality control, we also used Aki's 1965 maximum likelihood method, as modified by Tinti and Mulargia (1987) in certain time intervals. We do not take into account uncertainties in individual magnitudes in the recurrence calculations but consider these to be accounted for by the uncertainties in the recurrence parameters themselves. Recurrence parameters, with associated uncertainties, are estimated for the four tectonic source zones and for area source zones with sufficient data.

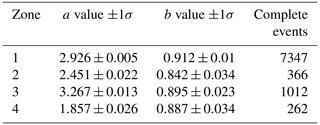
As is well established, calculation of a and b values with small sample sizes or a small magnitude range may lead to significant bias in the estimates, outside the formal uncertainty limits (e.g. Geffers et al., 2022). We therefore require that a zone contains more than 200 events for a recurrence parameter calculation. For area source zones sparse in data we follow the ESHM20 methodology and assign them the b value from the corresponding tectonic source zone, while an a value is calculated by re-scaling the tectonic zone a value by the ratio of the number of events with magnitude above M_c in the two zones, $N_{\mathrm{ASZ}}/N_{\mathrm{TSZ}}$. If there are no events in the zone, the tectonic a value is scaled by the areal ratio of the two zones.

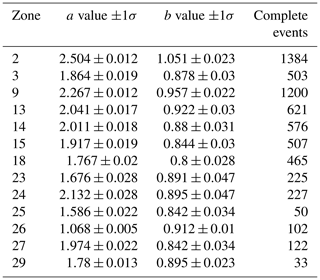
In most zones we use data from the late 1800 or early 1900 onward. In the far north, however, where there is very little macroseismic data, our records start with the increase in station density in the 1960s. The number of complete events in each tectonic source zone range from 262 in T4 to 7347 in T1. The a values range from 1.857 in T4 to 3.267 in T3, and the b values from 0.842 in T2 to 0.912 in T1 (see Table 1). In the ASZs, recurrence parameters could only be calculated for 12 out of the 31 zones (zones 2, 3, 4, 9, 13, 14, 15, 18, 23, 24, 30 and 31) due to the sparsity of data in most zones. For zones within 300 km of Sweden, the a values for the ASZs range between 0.041 for zone 20 in T4 to 2.504 for zone 2 in T1. The b values range between 0.8 for zone 18 in T1 and 1.051 in ASZ 2 (see Table 2, where we list the ASZs in Sweden). Uncertainties are calculated using the OQ implementation of the Weichert algorithm. Zone 23 has the largest b-value uncertainty of about 5 %, followed by zone 4 at around 4 %. Due to the large number of events with magnitude above M_c in tectonic zone T1, the b-value uncertainty is only ±0.007, which we find unreasonably small compared to how the b-value changes when M_c is varied. We therefore set the minimum b-value uncertainty to ±0.01. In zones with too few events for a separate calculation of recurrence parameters, we assign the same uncertainty as what we find for the tectonic zone calculations to the a and b values. As the a value is scaled by the number of complete events, this implies that the a-value uncertainty becomes relatively large in some ASZs.

Table 1 Recurrence parameters for tectonic source zonation schemes.

Table 2 Recurrence parameters for area source zones in Sweden.

4.5 Source model logic tree

The source model logic tree is based on the earthquake catalogue, the zonation, the derived recurrence parameters for each zone and their uncertainties, and the maximum magnitude information (see Fig. 5). The first branching level represents each individual area source zone, followed by three branches representing the maximum likelihood estimate of the doubly truncated Gutenberg–Richter distribution and 2 standard deviations, representing the 5th and 95th percentiles. Four further branching levels are applied to each model for the M_max values of 6.3, 6.6, 7.0 and 7.5, each with 0.4, 0.4, 0.15 and 0.05 as their respective weights. The overall structure of the source model logic tree is as implemented in the ESHM20 calculations for the region (Danciu et al., 2021). With 3 branches each for the a and b values and 4 for M_max, a total of 12 branches are defined for each ASZ (Fig. 5).

Figure 5 Source model logic tree. The numbers indicate the weights of the different branches.

4.6 Ground motion models

The attenuation characteristics of the crust are of utmost importance for a seismic hazard assessment as they determine how the ground motions from an earthquake decay with distance. In stable continental regions like Fennoscandia, such ground motion models are difficult to construct as the low seismicity rate of the region, the region's size and the relatively sparse seismic networks imply that there is usually very little strong-motion data available. Notwithstanding, Fülöp et al. (2020) used weak-motion data from events in Finland and Sweden between 2006 and 2018, with magnitudes $\mathrm{1.5}\le M_{\mathrm{L}}\le \mathrm{4.2}$, in the development of a Fennoscandian ground motion model, Fenno-G16. In order to make up for the lack of large events, they added data from an eastern Canadian subset of the NGA-East data (Goulet et al., 2014), with the largest magnitude of M_w 6.76, and implemented Fenno-G16 based on an adjustment of the backbone curves of the G16 equation developed by Graizer (2016) for Central and Eastern North America (CENA). The released version of Fenno-G16 contains only one branch in the logic tree and uses a V_S,30 for very hard rock of 2800 m s⁻¹.

The recently developed scaled backbone GMM for cratonic regions in ESHM20 (Weatherill and Cotton, 2020), described in Sect. 3.1, also partly incorporated NGA-East data and models (Goulet et al., 2021) and used the Fülöp et al. (2020) data set to aid in deciding the weights for the two main branches, cratonic (0.8) and shallow crustal (0.2), in the logic tree.

In this study, we use the two recently developed cratonic GMMs, Fenno-G16 (Fülöp et al., 2020) and ESHM20 cratonic, (Weatherill and Cotton, 2020) together with the shallow crustal seismicity model used for much of Europe in ESHM20 (Kotha et al., 2020). In order to study the effects of the different GMMs on the hazard estimates, we use our earthquake data set and seismic source zones and calculate hazard at a specific site for each of the following logic tree combinations:

1. The native ESHM20 logic trees for shallow-default and cratonic regions, for a $V_{\mathrm{S},\mathrm{30}}=\mathrm{800}$ m s⁻¹, which is the ESHM20 default.

2. The native ESHM20 logic tree for shallow-default regions and the ESHM20 cratonic logic tree with V_S,30 set to 3 km s⁻¹.

3. The ESHM20 logic tree for the shallow-default regions and the single-branch Fenno-G16 GMM for the cratonic regions. ($V_{\mathrm{S},\mathrm{30}}=\mathrm{3}$ km s⁻¹ for basement sites and $V_{\mathrm{S},\mathrm{30}}=\mathrm{800}$ m s⁻¹ for the sedimentary rocks in Skåne, Öland and Gotland.)

4. The ESHM20 logic tree for the shallow-default regions and for the cratonic regions' two branches – one with a modified ESHM20 cratonic logic tree, weight 0.6, where the 20 % branch with the shallow crustal GMM has been removed, and one with the single-branch Fenno-G16, weight 0.4 (see Fig. 6). $V_{\mathrm{S},\mathrm{30}}=\mathrm{3}$ km s⁻¹ for the cratonic regions. Figure 6 shows the ESHM20 five-branch implementation for epistemic uncertainty of the GMM, σ_μ (Weatherill and Cotton, 2020), where the ϵ_ii and weights assigned to each branch are determined by a discrete approximation of the Gaussian distribution depending on the number of standard deviations to include (Danciu et al., 2021; Miller and Rice, 1983). The epistemic uncertainty of the site amplification factor, σ_μ,S, is similarly included with three branches, however, as we do not adjust the site amplification to $V_{\mathrm{S},\mathrm{30}}=\mathrm{800}$ m s⁻¹ for cratonic areas these branches cancel.

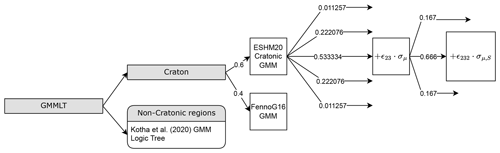
Figure 6 Ground motion model logic tree. The numbers indicate the weights of the different branches. The logic tree is further detailed in Sect. 4.6.

Figure 7 shows how the hazard curves at the location of Uppsala (Fig. 1) vary with the different GMM combinations. The mean hazard estimates are rather similar; we see that the Fenno-G16 model consistently produces slightly higher PGAs at the same probability of exceedance (PoE) compared to the ESHM20 models and that using a V_S,30 of 3 km s⁻¹ consistently lowers the hazard compared to a V_S,30 of 800 m s⁻¹, as expected. The uncertainty distribution for Fenno-G16 is generally narrower than those for the ESHM20 models, for which the lower 0.16 fractile limit extends to significantly lower PGA for the same PoE. Model 4, with the combination of Fenno-G16 and ESHM20, has a mean hazard similar to Fenno-G16 at higher PoE but moves toward the midway point between the two at higher PoE. The 0.16 and 0.84 fractile distributions behave similarly.

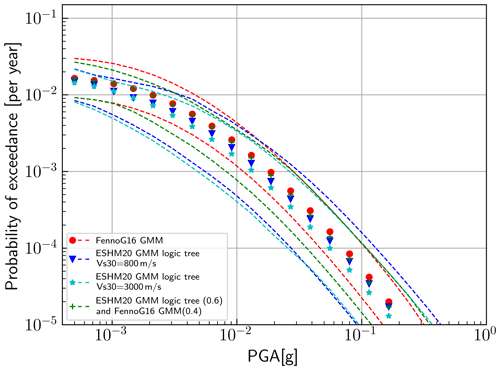
Figure 7 Mean hazard curves for Uppsala, Sweden, for different GMM implementations (see Sect. 4.6 for details). Yearly probability of exceedance versus PGA (in g). Solid symbols show the mean, while the upper and lower dashed lines show the 0.84 and 0.16 fractile limits.

We choose model 4 as our preferred ground motion model for cratonic areas in this study, as it combines the two most recent cratonic GMMs, incorporates data and models from eastern North America, and takes into account seismic observations in Fennoscandia. The weights between Fenno-G16 and the ESHM20 GMMs were determined such that we obtain a larger epistemic uncertainty distribution than Fenno-G16 while somewhat reducing the ESHM20 distribution to lower hazard.

Referring to the zone numbers in Fig. 4, we use our cratonic model 4 ground motion logic tree for tectonic zones T1 and T4, encompassing much of Sweden, Finland and the Baltic countries. In tectonic zones T2 and T3 we use the ESHM20 shallow-default logic tree, except for in area source zones 24, 28 and 30, which all use the cratonic combination. As described in Sect. 2, Swedish surface rock mostly consists of Proterozoic bedrock which in places is covered by a few metres to tens of metres of glacial sediments. There have been no large-scale studies of V_S,30 in Sweden, but, generally speaking, many single houses and larger constructions are built on bedrock or using piling to bedrock. We therefore use a V_S,30 of 3 km s⁻¹ for all cratonic zones, similar to the 2800 m s⁻¹ used by Fülöp et al. (2020) and corroborated by, for example, Sadeghisorkhani et al. (2020). The two Baltic islands of Öland and Gotland are covered in sandstone and limestone (Rosberg and Erlström, 2019); for these areas we use the ESHM20 default of $V_{\mathrm{S},\mathrm{30}}=\mathrm{800}$ m s⁻¹. In all zones with the shallow-default GMM we also use the default ESHM20 $V_{\mathrm{S},\mathrm{30}}=\mathrm{800}$ m s⁻¹.

4.7 Definition of OpenQuake parameters

We use the OpenQuake (OQ) engine (v3.12) (Pagani et al., 2014) to estimate the annual probability of exceedance of peak ground acceleration at the 0.0021 and 0.0004 levels, corresponding to return periods of 475 and 2500 years. The OQ engine uses the classical PSHA approach based on the methodology proposed by Cornell (1968) and McGuire (1976). The engine allows for flexibility in modelling seismic sources, using predefined GMMs or implementing new GMMs, and characterizes epistemic uncertainty through a logic tree. The engine incorporates the OpenSHA (Field et al., 2003) calculation structures and workflows, which we use on an equally spaced 5 km calculation grid. Area sources were defined as per the OQ NRML schema for each ASZ (Schorlemmer et al., 2011).

The minimum magnitude, M_min, used for the hazard computation is taken as the magnitude where damages may start to appear. ESHM20 uses a M_min of 4.5, but we follow Mosca et al. (2022) and use M_min 4.0 in order to account for the impulsive nature and high-frequency content of smaller events in a slowly attenuating crust, such as that of Sweden. The damage potential of a M_w 4.0 earthquake was demonstrated in the Folkestone 2007 M_w 4.0 event, which cased significant non-structural but also some structural damage (Sargeant et al., 2008).

We define a depth distribution where ruptures take place, using 5, 10, 20 and 30 km depth weighted as 0.15, 0.35, 0.35 and 0.15. This accounts for the fact that although most events occur down to about 20 km depth, some areas have significantly deeper earthquakes (e.g. Veikkolainen et al., 2017). Point ruptures are used as we do not include specific faults in the model. Truncated Gutenberg–Richter distributions are defined by the lower and upper magnitude bounds M_min and M_max, and the previously calculated a and b values with their uncertainties are used in different branches of the logic tree. Each seismic source area requires the definition of orientations and faulting styles of ruptures, quantified by the strike, dip and rake of nodal planes. We use the strike and dip values adopted by ESHM20 in their calculations and choose a strike of 0° and a dip of 90°. We define two rake values of 0 or 180°, each with a weight of 0.5 in the probability distribution.

The calculation parameters for the OQ engine are summarized as follows: 12 end branches for area source models of the shallow crust and cratonic regions; 18 072 equally spaced grid points (5 km spacing) defined on land within Swedish land borders; a $V_{\mathrm{S},\mathrm{30}}=\mathrm{3}$ km s⁻¹; point ruptures; a weighted depth distribution; predefined nodal plane orientations, with vertical planes striking north with a rake of 0 or 180; 25 intensity measures that cover PGA ground motion discretization levels between 0.005 and 3 g; and calculations for the complete enumerated logic tree.

5 Results

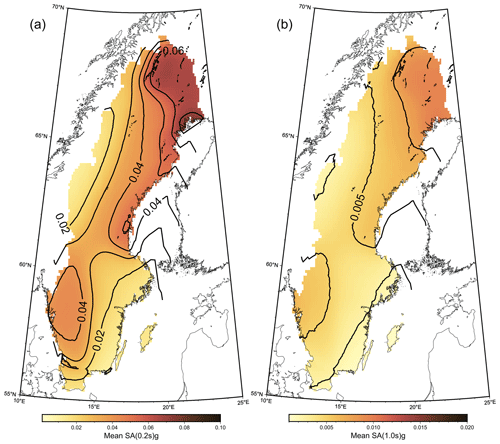
We present ground motion exceedance levels for mainshock earthquakes in terms of peak ground acceleration (PGA), using our source and ground motion model logic tree implementations as discussed in Sect. 4.5 and 4.6. PSHA results are commonly presented as hazard maps showing PGA with a 10 % probability of exceedance (PoE) in 50 years, as that level is used for building codes, e.g. in Eurocode 8. A 10 % exceedance level in 50 years is equivalent to a statistical (Poissonian) return period of 475 years. ESHM20 uses annual PoEs, where $\mathrm{2.1}\times {\mathrm{10}}^{-\mathrm{3}}$ is equivalent to 10 % in 50 years and $\mathrm{4}\times {\mathrm{10}}^{-\mathrm{4}}$ is equivalent to the previously used 2 % in 50 years, slightly altering the return period from 2475 to 2500 years. We follow ESHM20 and present our results as hazard maps for return periods of 475 and 2500 years and as hazard curves for four seismically active regions in Sweden. Ground motion exceedance levels for spectral acceleration periods of 0.2 and 1 s for a return period of 475 years are presented in the Appendix.

5.1 Seismic hazard maps for Sweden

Seismic hazard maps for Sweden with 475- and 2500-year return times are shown in Fig. 8. As usual in probabilistic seismic hazard assessment, hazard closely follows the observed earthquake distribution. The maps show the mean horizontal PGA, and we see that for a 475-year return period the highest hazard is estimated in the northernmost part of Sweden, in the area of the post-glacial faults and at the northern shores of the Bay of Bothnia, where hazard reaches 0.06 g. Much of the northeastern coast of Sweden shows a mean PGA of 0.03–0.04 g, and the southwest of Sweden shows a mean PGA of 0.02–0.03 g. The southeast and northwest of Sweden have an estimated mean hazard of less than 0.02 g. For the 2500-year hazard map, hazard is similarly distributed, but the highest mean PGA is now 0.15 g in the northeast of Sweden, followed by the northeast coast at about 0.1–0.125 g and the southwest of Sweden between 0.075–0.1 g. As before, the southeastern and the northwestern regions show the lowest hazard of less than 0.05 g. The spectral acceleration (SA) maps, in Fig. A3, show similar results to the PGA map for the spatial distribution of hazard. We find, however, that the mean hazard at SA (0.2 s) is generally higher than the mean PGA by about 0.01 g in all of the country. At SA (1.0 s) the mean hazard is everywhere below 0.01 g.

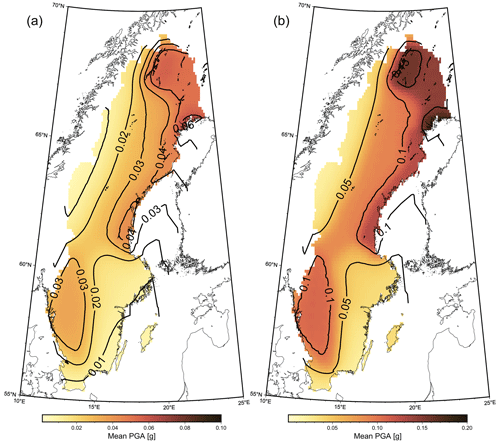
Figure 8 Seismic hazard maps for return periods of 475 years (a) and 2500 years (b). Contour lines represent 0.01 g for the 475-year map and 0.05 g for the 2500-year map. Post-glacial faults indicated by black lines.

We note that the earthquake activity in the Oslo graben in Norway (ASZ 25) and even the activity on the Norwegian west coast affect the hazard levels in southwestern Sweden to some degree. Interestingly, we do not see the same influence from the Nordland region in Norway (ASZ 4) into Sweden, although seismic activity there is high and it is the region where the largest known earthquake in Fennoscandia occurred in 1819. This is likely due to the relatively high b value we estimate for ASZ 4 (b=0.933) and the fact that many of the events occur in swarms which are removed in the declustering.

We complement our maps with a disaggregation analysis for the location in the northeast with the highest hazard in our study and the location in the southwest where Wahlström and Grünthal (2001) found the highest hazard in Sweden. Figure 9 shows that the main contribution to the hazard is primarily from small earthquakes at 10–50 km distance, which is similar for both locations. We note that our study predicts a higher hazard contribution from larger earthquakes than does the Wahlström and Grünthal (2001) analysis.

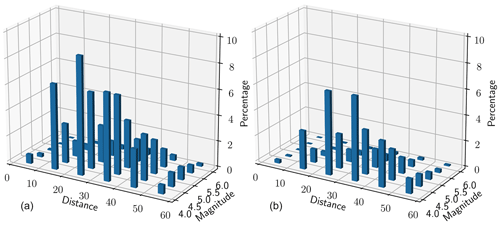
Figure 9 Disaggregation analysis showing the contribution of earthquakes with different magnitudes at different distances to the seismic hazard. The analysis is carried out for the site with the highest hazard estimate in our study (65.7° N, 22.97° E) (a) and the site in Sweden used by Wahlström and Grünthal (2001) in their study (59.5° N, 12.0° E) (b), both for a return period of 475 years.

5.2 Hazard curves for seismogenic areas

The regions in Sweden with the highest seismic activity can broadly be defined as the southwest around Lake Vänern, the northeast coast and the post-glacial fault province in the north. In Fig. 10 we illustrate the seismic hazard at four locations in these regions, using hazard curves with the annual probability of exceedance versus PGA: the post-glacial Pärvie and Burträsk faults, the Hälsingland area around Hudiksvall, and Västergötland south of Lake Vänern (see stars in Fig. 1). We see that the hazard curves are similar for all four regions, with the Pärvie and Burträsk faults having slightly higher short-term PGA estimates and Västergötland the lowest hazard overall, although all four are within the uncertainty limits of each other. We restrict our curves to a lower limit of an annual PoE of 10⁻⁵, with the 0.16 and 0.84 fractile estimates ranging between 0.3 and 0.9 g at this limit. Comparing to the Uppsala curves in Fig. 7, we note that the short-term hazard is similar in Uppsala and Västergötland but that the longer-term hazard is significantly lower in Uppsala.

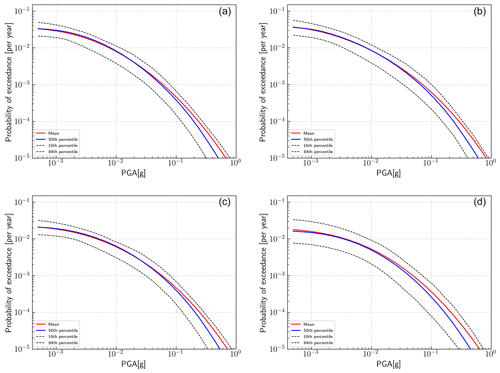
Figure 10 Seismic hazard curves for areas of relatively high seismicity in Sweden (yellow stars in Fig. 1). (a) Pärvie, (b) Burträsk, (c) Hälsingland, and (d) Västergötland. Annual probability of exceedance versus peak ground acceleration (in g). Mean (red lines), 50 % (blue), and 0.16 and 0.84 fractile limits (dashed).

6 Discussion

The result of our seismic hazard assessment, as illustrated in the maps in Fig. 8, differ from many of the previous assessments for Sweden in that the estimated hazard is largest in the far north. This is due to the new emerging understanding of the seismic activity on the post-glacial faults (PGFs) in northernmost Fennoscandia (Lindblom et al., 2015). The expansion of the Swedish National Seismic Network in the early 2000s, from 2 to 22 stations north of 63.5° latitude (Lund et al., 2021), has enabled observations of previously unknown seismic activity rates on these faults (Lindblom et al., 2015). Almost 3700 earthquakes have been observed in the region in the last 2 decades (Fig. 2), and all but two have magnitudes below 3, which is consistent with the few observations prior to the network expansion. The very low population density and limited reporting possibilities in earlier times probably explains the almost complete lack of observations in, for example, the Pärvie area prior to 1967. Unfortunately, there are no conclusive data on current slip rates on the PGFs. For example, the InSAR study by Mantovani and Scherneck (2013) inferred vertical displacements at a few segments along the Pärvie fault but did not conclude any slip rates. This complicates the inclusion of the post-glacial faults explicitly in a PSHA.

The inference that the last 20 years of earthquake data in northern Sweden indicate that the area has a relatively high seismic hazard is interesting in the light of recent work on the PGFs in the region. Smith et al. (2021) found repeated ruptures on the Lainio PGF, with the latest recurring after deglaciation, and Olesen et al. (2021) identified ruptures of magnitude 7 as recently as 700 years ago on the Stuoragurra fault in northern Norway. Taken together, all observations suggest that seismic hazard should be taken into careful consideration in the region, especially since the region is home to major mining operations, large hydroelectric power dams and an increasing number of wind energy installations.

6.1 Estimation of recurrence parameters

With Fennoscandia being a low-seismicity region, estimating the recurrence parameters is a major challenge in the seismic hazard assessment process. The problem is multifaceted and involves the low seismicity rate, the few large events and the magnitude homogenization process. As the rate of earthquakes large enough to be felt is low (Lund et al., 2021), there is little data prior to the installation of an improved seismic network in the 1960s. That network consisted of only six analogue stations, so the more significant increase in earthquake observations came with the modern SNSN, from the year 2000 onward, when the completeness magnitude fell below M 1 (Fig. 3) for a large part of the country (Lund et al., 2021). Many of the observed larger events occurred in earlier times and therefore have macroseismic magnitudes with significant uncertainty. Later events have a variety of local magnitudes, which complicates the magnitude homogenization procedure (Uski et al., 2015). In addition, the magnitude estimation for the many small events in our data set comes with appreciable uncertainty, e.g. due to low station density, which further complicates the magnitude homogenization procedure.

As discussed in Sect. 4.4, we use the Weichert (1980) method, as implemented by OpenQuake, to calculate the recurrence parameters, using data reaching back to 1875. We also use Aki's method (Aki, 1965), as revised by Tinti and Mulargia (1987), with the post-2000 data to add confidence in the results. We found that varying M_max during parameter estimation has no significant effect on the results. However, the results are sensitive to variations in the magnitude of completeness, and a change in M_c by 0.2 can lead to a significant change in a or b value, beyond the formal uncertainties of the original results. The magnitude of completeness is non-trivial to estimate, manually or using some curvature method, especially for the very sparse historical data. It is thus likely that uncertainties in a and b values are sometimes larger than the formal estimates, which led us to set a minimum b-value uncertainty to 0.01. This was needed for tectonic zone T1, which contains 7347 events above M_c and therefore produces a very small formal uncertainty.

We note that in their investigation of the sensitivity of site-specific PSHA in Finland to variations in the input parameters, Fülöp et al. (2023) found that M_max variations do not affect the PGA results significantly but are more important at low ground motion frequencies at an annual frequency of exceedance of 10⁻⁵. They also point out that a- and b-value variations have a large effect on the results, in agreement with our conclusions.

6.2 Comparisons with previous seismic hazard studies

As discussed above, the most significant difference between our seismic hazard model and previous studies is the spatial distribution of hazard in northern Sweden. The Wahlström and Grünthal (2001) study found the largest hazard in Sweden focused in the area surrounding the 1904 M_w 5.4 earthquake on the west coast, with a median PGA of 0.03–0.035 g for a 475-year return period. This is slightly higher than our estimate of about 0.025 g in that area. Similar to us, they found that southeastern and northwestern Sweden, east of the mountain range, has the lowest hazard, below 0.015 g. Along the northeast coast they estimate a PGA of 0.015–0.02 g, lower than our approximately 0.03 g, and in the northernmost region of Sweden their 475-year PGA estimates vary between 0.01–0.02 g, significantly lower than our 0.03–0.06 g. We note that Wahlström and Grünthal (2001) use the median hazard for their estimates. As we use mean estimates, our hazard values are likely to be generally somewhat higher than theirs.

The Mäntyniemi et al. (2001) hazard map is similar to the one from Wahlström and Grünthal (2001). They find high hazard in the southwest and along the northeast coast, with the 475-year PGA reaching 0.02–0.025 g in both regions, similar to our results. In the north, their hazard estimate is lower than ours, at 0.01–0.015 g. We note that both Wahlström and Grünthal (2001) and Mäntyniemi et al. (2001) estimate a higher hazard in the northern Swedish mountain region than us, indicating that their area source zone definition is such that the high seismicity in Norwegian Nordland produces significant hazard in Sweden in their model or that they estimate lower b values than we do in that region.

The 2013 European Seismic Hazard Model (ESHM13, Woessner et al., 2015) found the highest hazard in Sweden to be focused in a narrow region across the southernmost part of the country and up along the west coast, with a maximum PGA for a 475-year return period at approximately 0.025 g in the south. This is significantly more than our estimate of less than 0.01 g in that area. Along the southwest coast of Sweden the hazard in ESHM13 is about 0.02 g, similar to ours, while the rest of the country has a hazard between 0.001–0.02 g, with again significantly less hazard in the north than in our model.

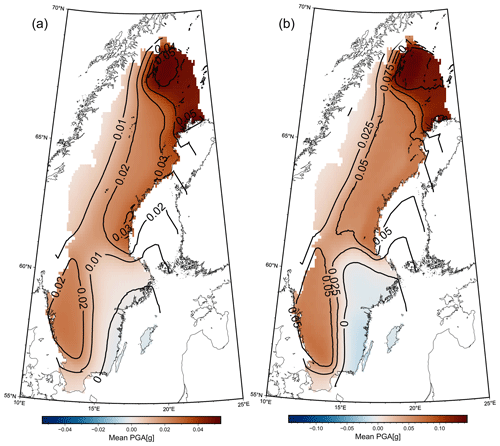
Figure 11 Seismic hazard maps showing the difference between our results and ESHM20 (this study minus ESHM20) results for return periods of 475 years (a) and 2500 years (b). Contour lines represent 0.01 g for the 475-year map and 0.025 g for the 2500-year map. Post-glacial faults are indicated by black lines. Brown colours indicate that our hazard estimate is higher, and blue colours indicate that the ESHM20 hazard estimate is higher.

The most recent iteration of the European Seismic Hazard Model (ESHM20, Danciu et al., 2021) changed the distribution of hazard in Sweden significantly as compared to ESHM13 (see Lund et al., 2024, for an in-depth comparison). Hazard estimates in ESHM20 are lower in the southern and southwestern parts of the country and higher in the south-central part of the country and up along the northeastern coast, following the coastline around the northern Bay of Bothnia. This agrees with the distribution of hazard in our model, except that in our model the hazard is lower in the southeast. We illustrate the differences between our model and ESHM20 for 475- and 2500-year return periods in Fig. 11, which shows that our model produces higher hazard than ESHM20 for both return periods in most of the country. Again, the most notable difference is in the north, where ESHM20 uses the recurrence parameters from the large tectonic zones but where we have much more data (Fig. 2), such that we can better constrain the a and b values. Comparing recurrence parameters we note that the ESHM20 area source zone NOAS376 in northern Fennoscandia, encompassing many of the PGFs, is approximately 30 % larger in size than our ASZs 13, 14 and 15 combined. The ESHM20 b value is 0.91±0.032 in that area, which is within the 1σ uncertainties of the b values in our ASZ 13 and 14 and just above the uncertainty limits of ASZ 15 (see Table 2). The ESHM20 a value 1.584±0.0059 is re-scaled from the tectonic zone and significantly lower, considering the much larger area, than our a values around 1.9–2.0 (Table 2) for the individual zones 13, 14 and 15. We see in Fig. 11 that our PGA is more than 0.04 g higher for a 475-year return period than the ESHM20 estimate in some areas in the north. For a 2500-year return period the difference is 0.125 g. Further south along the northeast coast our hazard is still higher by some 0.02 g, a difference which decreases towards the southeast, and along the southeast coast the hazard in our model is smaller than in ESHM20. In the southwest, our model estimates higher hazard than ESHM20 by about 0.015 g. We note that ESHM20 and our model agree well along the northwestern border, where none of the models see much influence of the Norwegian coastal seismicity.

6.3 Seismic hazard and risk in Sweden

Comparing to surrounding regions, the seismic hazard we find in northern Sweden is only surpassed by the hazard in western Norway around Bergen and in the Nordland region in northwestern Norway. Our new results for northern Sweden will be compared to results obtained in neighbouring countries in order to calibrate the hazard along the borders. Probabilistic seismic hazard projects are ongoing in both Norway and Finland, and we aim to further the work on a joint homogenized Fennoscandian seismic hazard model in the near future.

Our results show that the hazard correlates well with the observed seismicity. We note, however, that most of the seismic activity is of low magnitude and that there is not a clear correlation between the observed larger events, above e.g. M_w 4, and more intense microearthquake activity. The Tornquist zone in southern Sweden, for example, has experienced five events with M_w≥3.7 in the last century but has a low seismicity rate, whereas the Burträsk fault, the most seismically active area in Sweden, has only seen two such events during that time. There was a M_w 3.9 event in west-central Sweden in 2014 in an area with only a few prior small events (Lund et al., 2014), and the large magnitude 5 events in Kaliningrad in 2004 (Gregersen et al., 2007) occurred in an area with very few previously observed events. These surprise events, and the sometimes poor correlation between the rate of small events to large events, point to the difficulty of PSHA in stable continental regions. Adding to the problem is the largely unknown level of temporal and spatial stationarity of earthquakes in these regions.

The large post-glacial faults of northern Fennoscandia pose an interesting problem to seismic hazard assessment. Previously inferred to have ruptured only once, at the time of final deglaciation of the region (e.g. Lagerbäck and Sundh, 2008), the main question has been whether or not the faults could rupture again without an intervening major glaciation. Glacial isostatic adjustment modelling (see review in Lund, 2015) shows that glacially induced stresses combine with the tectonic stress state and bring the PGFs towards instability at deglaciation. Due to the slow strain accumulation in the Fennoscandian Shield, repeated large ruptures on the same faults segments have been considered unlikely, with repeat times of less than 100 000 years (Korja and Kosonen, 2015). However, as alluded to above, more recent investigations have found that the PGF systems have seen multiple ruptures along the faults and also multiple ruptures at the same location (see reviews for Fennoscandia in Steffen et al., 2021). Including the PGFs in a PSHA is currently only possible as an increase in M_max for area source zones including PGFs since it has not been possible to detect any ongoing surface slip on the faults. The weight on such a high M_max branch in the logic tree is difficult to assess due to the current lack of data. We have seen that a high M_max branch does not have a large effect on the estimated PGA but is more likely to affect the longer periods of ground motion (Fülöp et al., 2023).

A more appropriate mechanism, at this time, to take the PGFs into account is through deterministic seismic hazard assessment (DSHA). The faults are mapped in high resolution (e.g. Smith et al., 2021), and the depth extent of current seismicity is known for some PGFs (e.g. Lindblom et al., 2015), making it possible to use scaling relations to estimate potential rupture magnitudes. While a deterministic scenario may have a very low probability of occurrence, a DSHA will provide additional insights from a risk reduction perspective and potentially highlight events that may dominate the seismic risk in a certain area or for a specific site and therefore must be considered (McGuire, 2001). An approach that combines the probabilistic and deterministic seismic hazard assessments may be the most appropriate to evaluate the site-specific seismic hazard, and risk, in the postglacial fault province in northern Fennoscandia, especially for critical infrastructure sites, such as dams, where low annual exceedance probabilities must be considered.

7 Summary

This study provides a probabilistic seismic hazard model of Sweden based on updated earthquake catalogues from the Swedish National Seismic Network (Lund et al., 2021) and neighbouring networks, as well as recent results and methods from the European Seismic Hazard Model ESHM20 (Danciu et al., 2021). The hazard is calculated using the OpenQuake engine (Pagani et al., 2014), using earthquakes since 1875 represented through 31 area sources zones, and recently developed ground motion models (Fülöp et al., 2020; Weatherill and Cotton, 2020; Kotha et al., 2020). A weighted logic tree approach is used to represent the uncertainties in the recurrence parameter estimates, M_max and the ground motion models. The resulting hazard estimates are calculated as peak ground acceleration (PGA) values and mapped in Fig. 8 for 475- and 2500-year return periods.

The updated earthquake data allow us to use a large number of smaller events that have not previously been available, or used, in seismic hazard assessment. This makes it possible to better constrain the recurrence parameters (a and b values) in much of the country, especially for the post-glacial fault province in northern Sweden.

We find a seismic hazard distribution in Sweden which is significantly different to that of earlier studies. The new data from the north indicates that hazard in northernmost Sweden is higher than elsewhere in country, both at 475- and 2500-year return periods. For a return period of 475 years, mean PGA along the post-glacial faults and the northern coastal tip of the Bay of Bothnia is estimated to be about 0.04 to 0.06 g. For the rest of the northeastern coast, mean PGA is estimated to be 0.02–0.03 g. The lowest PGA estimates in the country, 0.02 g and lower, are found in the southeast and northwest. Similar trends are seen for the 2500-year PGA estimates, with the highest mean PGA of 0.15 g seen in the northeast, 0.1–0.125 g for the post-glacial faults and the northeastern coast, 0.075–0.1 g for the southwest, and less than 0.05 g for the southeast and the northwest. Hazard curves for four locations in some the most active areas of the country, the Pärvie and Burträsk faults, the Hälsingland area, and south of Lake Vänern, show similar hazard in these areas, with slightly higher hazard along the post-glacial faults.

Compared to ESHM20 (Danciu et al., 2021), our model shows somewhat higher hazard in the more seismically active areas of Sweden but slightly lower hazard in the less active areas. The main difference is in the north, where we find significantly higher hazard. We note that our declustered, homogenized earthquake catalogue contains 19 943 events, with magnitudes down to just below zero, compared to 360 events in the same area for ESHM20, all with M_w≥3.5.

Challenges remain in seismic hazard estimation for Fennoscandia. There are significant uncertainties in magnitude homogenization, for the smaller-magnitude events compared to the larger ones, in the estimate of recurrence parameters, as larger events occur infrequently, and in the estimation of ground motions models for the Fennoscandian Shield, as sparse to non-existing data for larger events and short distances imply that both epistemic and aleatory uncertainties are difficult to estimate. On a larger scale, the occurrence of large events in areas with little prior seismicity and the uncertainties surrounding the potential for large earthquakes on the post-glacial faults in northern Fennoscandia pose problems for seismic hazard and risk assessment and require continued studies.

Appendix A: Figures

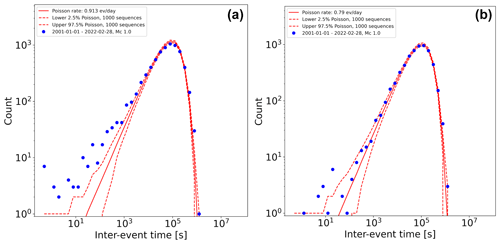
Figure A1 Inter-event time distributions for the Fennoscandia earthquake data set from 1 January 2001 until 28 February 2022 and a magnitude of completeness of 1.0. (a) Full catalogue; (b) declustered catalogue. Data, blue dots. Average Poisson inter-event times, red line. Lower 2.5 % and upper 97.5 % confidence limits, dashed red lines.

Figure A2 Map of Fennoscandia with events belonging to clusters resulting from the declustering algorithm. Cluster sizes indicated by the colours of the dots: 2 events, grey; 3–5 events, blue; 6–10, green; 11–20, red; above 20, orange. Larger clusters plotted on top of smaller clusters. Basemap from GMT (Wessel et al., 2019).

Figure A3 Seismic hazard maps showing the mean spectral acceleration (0.2 s, a; 1.0 s, b) for a return period of 475 years. Contour lines at 0.01 g (a) and 0.0025 g (b). Post-glacial faults indicated by black lines.