New insights into combined surfzone, embayment, and estuarine bathing hazards

Rip currents are the single largest cause of beach safety incidents globally, but where an estuary mouth intersects a beach, additional flows are created that can exceed the speed of a typical rip current, significantly increasing the hazard level for bathers. However, there is a paucity of observations of surfzone currents at estuary mouth beaches, and our understanding and ability to predict how the bathing hazard varies under different wave and tide conditions are therefore limited. Using field observations and process-based XBeach modelling at an embayed, estuary mouth beach, we demonstrate how surfzone currents can be driven by combinations of estuary discharge and wave-driven bathymetric and boundary rip currents under various combinations of wave and tide forcing. While previous studies have demonstrated the high hazard that rip currents pose, typically during lower stages of the tide, here we demonstrate that an estuary mouth beach can exhibit flows reaching 1.5 m s⁻¹ – up to 50 % stronger than typical rip current flows – with a high proportion (> 60 %) of simulated bathers exiting the surfzone during the upper half of the tidal cycle. The three-dimensional ebb shoal delta was found to strongly control surfzone currents by (1) providing a conduit for estuary flows that connect to headland boundary rips and (2) acting as a nearshore bar system to generate wave-driven “river channel bathymetric rips”. Despite significant spatio-temporal variability in the position of the river channels on the beach face, it was possible to hindcast the timing and severity of past bathing incidents from model simulations, providing a means to forewarn bathers of hazardous flows.

1 Introduction

Estuary mouth beaches are energetic environments where dynamic exchanges between marine and estuarine processes take place, resulting in complex hydrodynamics and a high degree of morphologic variability (Barnard and Warrick, 2010). For the present study we define them as wave-dominated beaches which feature an estuary that exits across the beach face, and we distinguish them from estuarine beaches, which sit within enclosed estuary environments and where only fetch-limited, locally generated waves are important (Nordstrom, 1992). Estuary mouth beaches are ubiquitous across the globe (Fig. 1), with examples in meso- to macro-tidal environments in New Zealand (Hume and Herdendorf, 1988; Hume et al., 2007) and the UK (Pye and Blott, 2014), as well as micro-tidal environments such as South Africa (Cooper, 2001) and Australia (Roy, 1984; Kench, 1999). Hume and Herdendorf (1988) class these environments as a barrier (beach) enclosed estuary, which are typically small estuaries with low fluvial inflow, where the inlet is restricted by the barrier beach and direct exchange with the ocean only occurs near high tide (Hume and Herdendorf, 1988; Hume et al., 2007). In the United Kingdom, 25 % of designated bathing beaches feature a river or estuary. Of these 159 beaches, 29, including the present study site, are embayed with an alongshore distance between headlands of less than 3 km, concentrating the dynamic estuarine flows and sediment exchanges over a relatively short length of coast.

Figure 1 Examples of estuary mouth beaches from around the world: (a) Mtentu, Eastern Cape, South Africa; (b) Tuross Head, New South Wales, Australia; (c) Crantock, Cornwall, United Kingdom – the study site for this research; (d) Waikawau, Coromandel, New Zealand. © Google Earth Pro.

Along the world's open coasts, rip currents have been identified as the largest cause of surfzone rescues and fatalities where incident records exist (Scott et al., 2008; MacMahan et al., 2011; Scott et al., 2011; Brighton et al., 2013), causing hundreds of drownings and tens of thousands of rescues globally each year (Castelle et al., 2016). A rip current occurs when water set-up by wave breaking in the surfzone returns back out to sea in a concentrated and often fast-moving offshore flow (Brander, 1999; MacMahan et al., 2006) and has the potential to carry water users from the shallows out into deeper water. Previous research has demonstrated various forcing mechanisms for rip currents (Castelle et al., 2016), including hydrodynamic instabilities in the surfzone (“shear instability rips” and “flash rips”), bathymetric control of wave breaking and return flows (“channel rips” and “focus rips”), and control of wave-driven flows by headlands or other boundaries (“deflection rips”, “shadow rips”, and “cellular circulation”). When rips occur, a combination of factors, including circulation pattern, speed, and surfzone retention, influence the bathing hazard. Surfzone circulation typically varies between “alongshore” flow at the shore, which poses a low level of bathing hazard; “rotational” flow, where offshore and onshore currents circulate within the surfzone, posing an intermediate level of bathing hazard; and “exiting” behaviour, where rip currents flow directly or obliquely seaward beyond the breaker zone to deeper water, representing the highest hazard to bathers (Scott et al., 2014).

However, while studies across these rip types from various countries have observed rip velocities to average 0.4–1 m s⁻¹ (Scott et al., 2014; Austin et al., 2010; MacMahan et al., 2010; McCarroll et al., 2017, 2018; Mouragues et al., 2020; Moulton et al., 2017a; Castelle et al., 2014), flows within estuary channels on beaches have been observed to average 1–1.5 m s⁻¹ and exceed 2 m s⁻¹ during ebbing stages of the tide (Allen, 1971; Lessa and Masselink, 1995; Jiang et al., 2013; Kastner et al., 2019), with strong seaward-flowing circulation. It is therefore surprising that, despite posing an equal or potentially even higher bathing hazard than rip currents, surfzone currents on estuary mouth beaches have received little attention in the scientific literature. While several studies have investigated surfzone retention of river plumes in the context of larva, contaminant, and freshwater dispersal (Rodriguez et al., 2018; Kastner et al., 2019; Olabarrieta et al., 2014), the effect of river or estuary discharges on surfzone bathing hazard remains unstudied.

Beach morphology classification schemes identify that intermediate beach states – those featuring three-dimensional nearshore bars and channels – are key locations for rip current activity and bathing hazard (Wright and Short, 1984; Lippmann and Holman, 1990; Masselink and Short, 1993; Scott et al., 2011). While beach classification schemes form the basis of our understanding of surfzone hazards and underpin lifeguard risk assessments in many nations (for example, the UK, Australia, and New Zealand), they ignore the presence of estuary mouths. Where an estuary mouth occurs on a beach, its channel and ebb-tide delta form an integral part of the beach morphology (Hume et al., 2007) and strongly influence the local flow velocities and nearshore circulation pattern, often promoting offshore flows during the ebb-tide phase (Cooper, 2001; Pye and Blott, 2014; Hume et al., 2007). A better understanding of nearshore circulation patterns and flow velocities at estuary mouth beaches is therefore required to fully understand combined surfzone and estuarine environments and the hazard they pose to bathers.

This contribution aims to investigate the interaction between estuarine flows and surfzone currents at an embayed, macro-tidal, high-energy beach on the north coast of Cornwall in southwest England and evaluate the contribution of the various interacting processes on surfzone circulation and bathing hazard. A further aim is to develop a predictive system capable of forecasting the level of bathing hazard to forewarn bathers prior to entering the beach. The study site is described in Sect. 2. In Sect. 3, a field experiment yielding Eulerian and Lagrangian flow measurements is described, leading to the development of a calibrated and validated hydrodynamic model of the estuary mouth beach system. In Sect. 4, the model is used to explore surfzone circulation under various combinations of wave and tide forcing, and their influence on bathing hazard. In Sect. 5, a bathing hazard forecast system is described that represents the first operational forecast model for bathing hazards on an estuary mouth beach. Discussion, limitations, and conclusions are provided in Sects. 6–8.

2 Study site

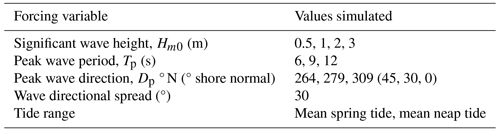
Crantock Beach (Fig. 1c) is located in southwest England on the energetic and macro-tidal north coast of Cornwall (Fig. 2a). The beach is flanked on either side by the East Pentire and West Pentire headlands, resulting in an embaymentisation ratio (alongshore length / headland length) of 0.4 (Masselink et al., 2022). Because of the size of the headlands and angle of the beach (310°) relative to the dominant wave approach (280°), the north end of the bay is exposed to more wave energy than the south, resulting in a strong gradient in wave height along the shore – a known precursor for headland boundary circulation (Castelle and Coco, 2012). Crantock experiences a mean spring tidal range of 6.3 m and is exposed to a mean and 1-year return period significant wave height H_s of 1.5 and 6.5 m, respectively.

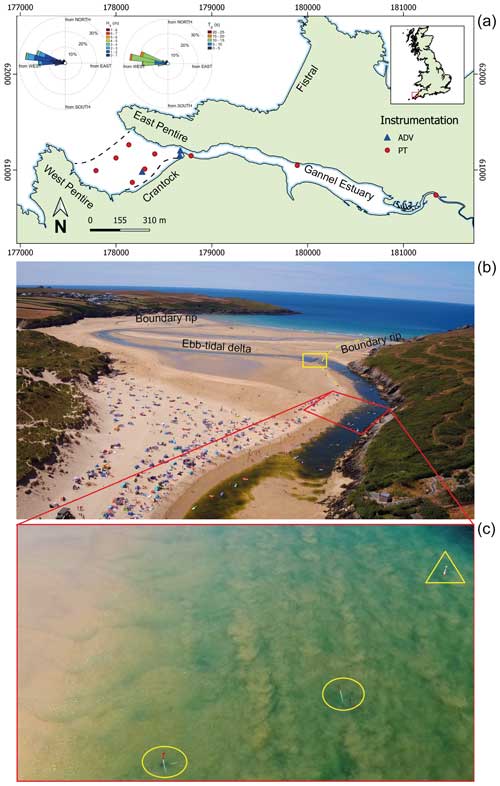
Figure 2 (a) Crantock Beach and Gannel Estuary, field instrument locations, wave roses, and location in southwest England (OSGB36 eastings and northings). Mean low- and high-water lines are shown as dashed lines. (b) Aerial image showing the river channel across the intertidal beach, relic training wall (yellow rectangle), and former river channel position (dashed yellow line). (c) Aerial view of river flow during a high ebbing tide, with fixed ADV instrument rigs (yellow circles) and a Lagrangian GNSS drifter (yellow triangle). Note the high level of sediment suspension due to the strong flows.

Crantock is classed as an intermediate low-tide bar–rip beach following the classification scheme of Scott et al. (2011), but it features distinctly different low-tide and high-tide morphology. At low tide, the beach face is relatively planar, aside from pronounced boundary rip channels along each headland. At mid- to high tide, the morphology is dominated by the ebb-tide delta and the channel system associated with the Gannel Estuary. This results in complex three-dimensional features across the upper-beach face, comprising often more than one river channel and multiple shoals (Fig. 2b).

The Gannel Estuary has a catchment of 41 km² and flows onto Crantock Beach at its northeast corner (Fig. 2a) with mean and 5 % exceedance riverine flow rates of 0.7 and 2 m³ s⁻¹, as measured by a monitoring weir 2 km upstream of the tidal limit of the estuary (https://check-for-flooding.service.gov.uk/station/3135, last access: 10 June 2022). Tidal discharges into and out of the estuary, however, are an order of magnitude larger than the riverine input (Sect. 2). For a number of decades, the river channel was artificially pinned against the northern headland by a small rock training wall (Fig. 2b) to maintain a navigation channel across the beach for boats. However, following significant redistribution of the beach sediment during the unprecedented storms of the 2013–2014 winter (Hird et al., 2021; Masselink et al., 2016), the river channel avulsed and now meanders laterally across the beach towards the south before discharging seaward through a channel that migrates between the south and north of the bay.

Royal National Lifeboat Institution (RNLI) lifeguards, who provide a lifeguard service at more than 250 UK beaches and have been present at Crantock Beach since 2001, have reported a rapid increase in both beach-user numbers and lifeguard rescues in the years since the river avulsed. For example, lifeguard assistance and rescue numbers have increased from < 40 yr⁻¹ in 2014 to > 190 yr⁻¹ in 2018, including two fatalities when lifeguards were not present on the beach. The increase in rescues is likely to be driven in part by the increase in water users at the beach, but lifeguards also report that the river's new position has increased the level of bathing hazard. There is a particular concern that immediately before and after lifeguard patrol hours (10:00–18:00 LST) estuary flows are at their strongest due to the coincidence of high spring tides at these times in the region. Bathers are therefore often exposed to strong ebb-tide flows (Fig. 2c) without any lifeguard supervision. The new river course has carved deep troughs in the beach face which are submerged between mid- and high tide, creating steep seabed gradients and spatially and temporally varying flows that are not visible to beach users.

3 Methodology

3.1 Methodological approach

This study uses a combination of field data and numerical model simulations to investigate surfzone circulation patterns and bathing hazard. The field experiment allowed collection of both Eulerian and Lagrangian flow characteristics under average wave conditions combined with spring tides (Sect. 3.2) but was limited to the range of wave and tide conditions experienced over the 3 d deployment. The numerical model provides the means to understand flow characteristics and bathing hazard under a much wider range of wave and tide conditions (Sect. 4.3.1) and with different realisations of the beach morphology (Sect. 4.3.2). Furthermore, the model provides the ability to “switch off” the estuarine flows (Sect. 4.3.3), enabling us to disentangle the contribution of wave- and estuary-driven hydrodynamics on the surfzone circulation.

3.2 Field data

The field experiment (11–14 May 2021) focussed on the collection of topographic and bathymetric survey data, Eulerian wave and current measurements, and Lagrangian flow observations. Topographic data were collected using high-resolution aerial imagery captured with a DJI Phantom 4 RTK uncrewed aerial vehicle (UAV), equipped with an accurate global navigation satellite system (GNSS) positioning system, flown across the site collecting multiple aerial images with an 80 % overlap. The images were processed using photogrammetric techniques (structure-from-motion and multiview stereo) to create a digital elevation model (DEM) of the site. The DEM achieves a vertical root mean square error (RMSE) of 0.03 m compared to independent spot checks against ground control points not used to geolocate the DEM during processing. The UAV flights were conducted around low water to maximise the coverage and visibility of the river channels. Once the data were captured, they were processed and translated onto a regular grid for further analysis.

For the full model domain to be mapped, a bathymetric survey was conducted at high tide to map the subtidal region, as well as overlap with the intertidal areas covered by the UAV. Multiple cross-shore transects ∼ 25 m apart were recorded using a Valeport MIDAS Surveyor echosounder (acoustic frequency 210 kHz; sample rate 6 Hz), pole-mounted on an inflatable surf rescue vessel, with external Trimble RTK-GNSS positioning (Trimble 5800; sample rate 1 Hz). The bathymetric survey achieves a vertical RMSE of 0.1 m in the intertidal region when compared to the previously mentioned ground control points. By merging the echosounder and UAV datasets (Sect. 3.4), the full survey region was extended down to ∼ 10 m water depth, covering the full embayment (Fig. 1).

Figure 3 Field instrumentation. (a) Frame supporting the ADV logger, batteries, and sensor head ∼ 0.1 m above the bed; (b) pressure transducer sensor installed at bed level using a sand screw; and (c) a Lagrangian “GNSS drifter” designed to map surface currents.

Eulerian measurements were collected by three Nortek acoustic Doppler velocimeters (ADVs) deployed on a rigid frame to allow current measurements to be logged ∼ 0.1 m above the beach (Figs. 2 and 3), measuring alongshore, cross-shore, and vertical flow velocities. Wave and tidal signals were logged using an array of nine pressure transducers (PTs) installed at bed level across the survey domain, three of which were co-located with ADVs (Fig. 2). All sensors were programmed to log at 4 Hz continuously. Outliers and spikes in the datasets were removed as part of quality control checks.

Lagrangian measurements were collected using GNSS-tracked surfzone drifters (Fig. 3), which are designed to mimic a bather being carried by the surface flows (submerged approximately 0.5 m beneath the surface) and avoid surfing landward on waves. These were telemetered in real time, allowing shore-based logging using the QPS Qinsy software package (following Mouragues et al., 2020). Six drifters were deployed at numerous locations multiple times across the survey area throughout the tidal cycle and were retrieved from the shallows before they ran aground. The raw data were then processed to remove time periods when the drifters were stationary on the beach, were being deployed by hand, or were being recovered by the inshore survey boat. The cleaned data provide an $x,y,t$ dataset, where t = time.

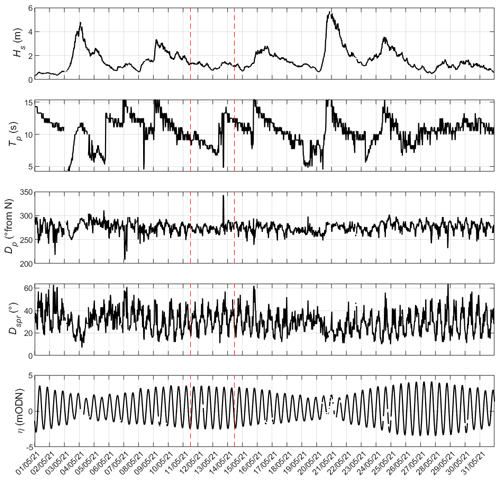
Figure 4 Hydrodynamic conditions during the field deployment period (dashed red lines) measured at a waverider buoy 7 km south of Crantock and a tide gauge 29 km north of Crantock (https://coastalmonitoring.org/cco/, last access: 23 September 2021). From top to bottom: significant wave height H_s, peak wave period T_p, direction of wave approach D_p, wave directional spread D_spr, and tidal water level η.

3.3 Numerical model

The process-based numerical model XBeach (https://download.deltares.nl/xbeach, Deltares, Delft University of Technology, Rijkswaterstaat, UNESCO-IHE, University of Miami, and US Army Corps of Engineers, 2021) was used to simulate rip current and estuary-driven flows across Crantock Beach. The model solves for the time-dependent short-wave action-balance equations, roller energy equations, the non-linear shallow water equations of mass and momentum, sediment transport formulations, and morphological updating (Roelvink et al., 2010). Wave group dissipation is modelled (Roelvink, 1993; Daly et al., 2012), and a roller model (Svendsen, 1984; Nairn et al., 1990; Roelvink and Reniers, 2011) is used to represent the momentum carried after wave breaking. Radiation stress gradients (Longuet-Higgins and Stewart, 1962, 1964) then drive infragravity motion and unsteady currents in the model, which are solved with the non-linear shallow water equations (Phillips, 1977). In the “surfbeat” mode of operation used in this study, XBeach solves the variation of the short-wave envelope on the scale of individual wave groups (Roelvink et al., 2018), which has previously been found to reproduce measured hydrodynamics at dissipative and intermediate beaches favourably, including channel and boundary rip current behaviour (Austin et al., 2013; Scott et al., 2016; McCarroll et al., 2015; Dudkowska et al., 2020; Mouragues et al., 2021). In the present study, morphological updating was switched off.

3.4 Model domain

A 2D-H (two horizontal dimensions, depth averaged) model was developed covering the full extent of Crantock Beach (Fig. 5), from the supratidal down to a seaward depth of 20 m below Ordnance Datum Newlyn (ODN). The domain was developed using the survey data described in Sect. 3.2 to cover the intertidal (−1 to +5 m ODN) and subtidal (−10 to +1 m ODN) regions. Repeat surveys were conducted in May 2021, August 2021, May 2022, and July 2022, providing four different realisations of the beach and estuary mouth morphology (Sect. 4.3.3). These data were complemented by open-source aerial lidar data, surveyed in February 2019, and single-beam bathymetry data, surveyed in 2007 by the regional coastal monitoring programme (https://coastalmonitoring.org/, last access: 19 September 2022), to cover the estuary and supratidal areas, as well as the offshore subtidal (−10 to −20 m ODN) region, respectively. Prior to developing the model domain, the various spatial data types were merged into a single 1 m × 1 m gridded spatial dataset using two-dimensional linear interpolation while ensuring that smooth elevation transitions were achieved between the different data types.

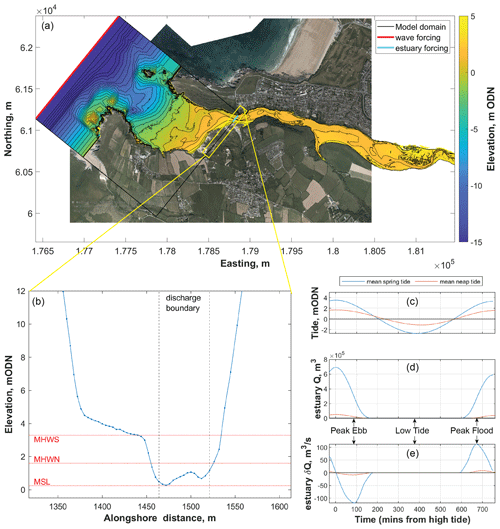
Figure 5 (a) Model domain (black box) overlaid onto aerial imagery of Crantock Beach and the surrounding area. The coloured topography shows the elevation of beach and estuary morphology. (b) Alongshore cross section of the model DEM (dotted blue line) in the area where the Gannel enters Crantock Beach, showing the location (dashed black lines) and resolution (blue dots) of the discharge forcing boundary. Tidal elevations are shown for mean high water spring (MHWS), mean high water neap (MHWN), and mean sea level (MSL). (c–e) Hypsometry of the Gannel Estuary, including mean spring and neap tidal excursion in metres above Ordnance Datum Newlyn (c), submerged volume Q (d), and change in volume δQ (e) of the estuary. Aerial imagery courtesy of National Network of Regional Coastal Monitoring Programmes of England, © 2024 NNRCMP.

To optimise computational effort, the model grid was developed with a variable resolution. Within the embayment, the cross-shore and alongshore resolution was fixed at 4 m, while outside the bay the cross-shore resolution was gradually decreased from 10 m depth using the Courant condition to optimise resolution based on water depth, giving a cross-shore resolution of 34 m at the offshore model boundary. On both sides of the bounding headlands, the alongshore resolution was decreased from 4 m to a maximum of 20 m at the lateral boundaries. The model extends linearly 200 m to the northeast and 400 m to the southwest of the bounding headlands to ensure that any wave shadowing from the lateral boundaries does not impact conditions within the bay, and a linear transition was implemented at the offshore boundary to remove any near-boundary gradients (Fig. 5a).

3.5 Boundary forcing conditions

The XBeach model was forced with waves uniformly along the seaward boundary, while tidal variation was imposed uniformly across the modal domain. For calibration and validation, wave forcing (time-varying wave height, period, direction, and directional spread) was obtained from a nearby directional waverider buoy located 7.5 km southwest of Crantock Beach at 10 m water depth at mid-tide (https://coastalmonitoring.org/, last access: 23 September 2021), with waves reverse shoaled to the boundary depth of 20 m using linear wave theory. Tidal variation was obtained from admiralty tide charts. Once the model was calibrated (Sect. 3.7), 72 combinations of wave and tide conditions were selected to run in the model covering the full range of summer wave conditions (Table 1), with each set of wave conditions run over a mean neap tidal cycle and a mean spring tidal cycle (with 30 min spin-up time). The most energetic conditions are approximately 3.5 times higher than the summer (June, July, August) average wave power, equivalent to approximately the one in 1-year return period wave height, which would be conditions under which the lifeguards would close the beach to bathers. Each 12 h simulation was then divided into 1 h tidal segments at 30 min increments, providing 1728 unique combinations of wave and tide forcing from which to evaluate circulation patterns and bathing hazard from the simulated flow fields.

Table 1 Summary of XBeach forcing variables used to populate the hazard look-up table.

The XBeach model itself does not include the Gannel Estuary, as, while it is possible to compute estuary flows within XBeach (Hartanto et al., 2011), this would add considerable computational effort given the spatial extent of the estuary. Instead, the ebbing and flooding flows from the Gannel were imposed using a discharge boundary. This forces a flow of water into the model domain (positive discharge) or out of the model domain (negative discharge) to describe the ebbing and flooding of the tide, respectively, through the relatively narrow estuary mouth at the northeastern side of the beach. Discharges were applied to the model across a 60 m section of the landward model boundary, covering the deepest part of the river channel (Fig. 5b).

The submerged volume of the Gannel Estuary (Q; Fig. 5d) was quantified landward of the model boundary beneath a range of tidal elevations (Fig. 5c) through interrogation of the Gannel Estuary DEM (Fig. 5a). The difference in volume between two elevation plains (dQ) and the time frame over which the tide changes between those elevations (dt) were then used to estimate the tidal discharge into or out of the estuary at different stages of the tide ($\mathrm{d}Q/\mathrm{d}t$). This analysis indicates peak discharges are 8 and 110 m³ s⁻¹ during average neap and spring tides, respectively (Fig. 5e). For the scenario simulations, the discharge applied at the boundary was computed from the estimated spring and neap tidal discharge rate at a given point in time, plus an additional 2 m³ s⁻¹ to conservatively account for fluvial flow (5 % exceedance river discharge), which is rare during the summer bathing season. However, initial tests with only fluvial discharge applied showed that this fluvial discharge rate has a negligible effect on surfzone flows.

3.6 Quantification of flow behaviour and bathing hazard

To assess surfzone circulation and quantify bathing hazard, generalised Lagrangian mean flow velocity (Groeneweg and Klopman, 1998) fields from XBeach were used to advect virtual drifters within the model and the drifter tracks were then analysed to provide bathing hazard proxies. The drifters were seeded within the surfzone randomly in time and space, seeding across a depth range representing safe-depth limits for children to adults (0.7–1.2 m, respectively), informed by previous studies (McCarroll et al., 2014b; McCarroll et al., 2015). Depths shallower than 0.7 m are deemed “safe” as bathers can stand up without being swept off their feet by typical surfzone currents. A total of 1500 drifters were seeded during each simulated period, with 500 of these seeded along the bank of the River Gannel where the estuary enters the beach and the rest seeded along the shoreline of the beach. Each virtual drifter was advected for 20 min or until they had returned to a safe water depth (< 0.7 m). The 20 min time frame was chosen to represent a typical timescale of a bathing incident – it is likely that a person in a strong current would be either rescued or in a critical state within 20 min. Furthermore, as we simulate with non-stationary tides, leaving drifters to circulate for longer blurs the effects of different tidal stages.

Seaward Lagrangian flow speed U_off and the percentage of drifters exiting beyond the extent of the surfzone E have previously been shown to provide good predictors of bathing hazard (Austin et al., 2013; Scott et al., 2014). We applied these parameters to the virtual drifter data from XBeach to quantify when and where peak bathing hazard occurs. Defining and determining a single value of U_off and E for each simulation is not trivial (Castelle et al., 2010; Austin et al., 2013), as surfzone velocities and circulation vary spatially and temporally. In rip current studies, U_off (often termed U_rip) is usually quantified at a pre-defined location such as the rip channel neck under study (Austin et al., 2013; Castelle et al., 2010), and E similarly requires a specific cross-shore threshold to be crossed in order to count surfzone exits. In the present study we define U_off following the approach of Austin et al. (2013) using hourly averaged Lagrangian velocities from independent drifter passes through 10 m spatial bins:

$$\begin{array}{}\text{(1)}& U_{\text{off}}=\sqrt{\stackrel{\mathrm{‾}}{u_{\text{off}}^{\mathrm{2}}}+\stackrel{\mathrm{‾}}{v^{\mathrm{2}}}},\end{array}$$

where u_off is the offshore-directed flow velocity, v is the alongshore-directed velocity, and the overbar signifies time averaging. The reader is referred to Castelle et al. (2010) for the method of determining independent drifter passes. Only spatial bins with at least five independent drifter passes were included, and the spatial bin with the maximum U_off value defines U_off for the entire beach. The U_off values presented herein therefore represent a spatial maximum, akin to U_rip values from previous rip current studies.

To quantify the proportion of surfzone exits E occurring during each 1 h simulated period, we determine the percentage of virtual drifters that travel seaward at least the same distance as the alongshore-averaged surfzone width. For comparability with previous studies, we define the seaward extent of the surfzone as the location where the cross-shore roller energy exceeds 10 % of its cross-shore maximum (Reniers et al., 2009), determining the average width of the surfzone across the length of the embayment. To forecast bathing hazard (Sect. 5), U_off and E were quantified at each time step across three different sections of the beach (northern half, southern half, and estuary mouth) to acknowledge the fact that offshore flow velocity varies in different places along the shore and to differentiate the hazard a bather might experience in one part of the beach from another. However, given the large range of forcing and bathymetric combinations tested, the results presented in Sect. 4 summarise the variables as a single value across the entire beach.

3.7 Model calibration and validation

The developed XBeach model was calibrated against the first tidal cycle of Eulerian field data (Figs. 6 and 7), with measured and modelled wave height compared at each of the surfzone PTs and flow velocity compared at each of the three ADV locations. Six hydrodynamic tuning parameters were adjusted in the model during calibration: the wave breaking formulation, the breaker slope coefficient, the wave dissipation coefficient, the wave breaker parameter, the bed friction formulation, and the bed friction coefficient. The wave and flow comparison was found to be insensitive to the breaker formulation, breaker slope coefficient, and wave dissipation coefficient, so these parameters were left at their default values. The wave breaker parameter γ, which controls the break point and surfzone width, and the bed friction formulation and coefficient C, which influence the current velocities, had a greater effect on the hydrodynamic performance of the model. Optimal settings for these parameters were found to be a breaker coefficient of γ = 0.50 and a Chezy bed friction coefficient of C = 45 ${\mathrm{m}}^{\mathrm{1}/\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$. These same settings were previously found to provide optimal tuning for headland rip modelling by Mouragues et al. (2021).

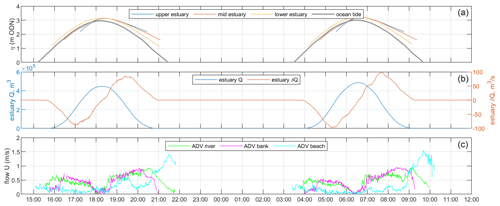
Figure 6 Eulerian field data collected in the vicinity of the Gannel Estuary over the first two high tides of the field experiment. (a) Water level signal as measured by PTs at different locations in the Gannel Estuary and ocean tide level from admiralty tide charts. (b) Gannel Estuary volume, Q, and change in volume, dQ, estimated from the mid-estuary PT data, as per Sect. 3.5. (c) Velocity magnitude measured by ADVs in the estuary mouth (“ADV river”), ebb shoal riverbank (“ADV bank”), and within the beach face channel (“ADV beach”). See Fig. 2 for instrument locations. Note that the estuary is dry for 3 h on either side of low tide.

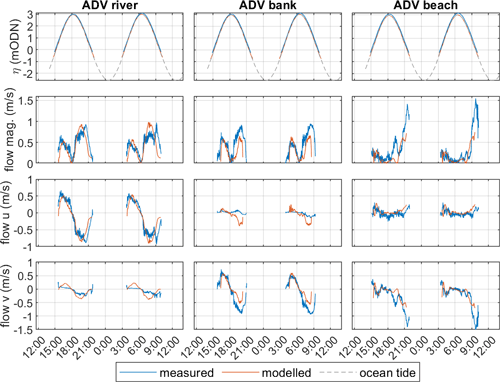
Figure 7 Comparison between measured and modelled flow velocity at the three acoustic Doppler velocimeters (ADVs) during the first two tidal cycles of the field experiment used for model calibration. The location of each ADV is shown in Fig. 2. Positive (negative) u velocities represent landward (seaward) flows, while positive (negative) v velocities represent northward (southward) flows.

Another important calibration for the present study is the weighting of the discharge during the flooding and ebbing stages of the tide, applied at the estuarine boundary. Initially it was assumed that $\mathrm{d}Q/\mathrm{d}t$ could be applied directly from the hypsometric analysis (Sect. 3.5); while this was found to replicate flow velocities on the ebbing tide well, it overpredicted landward flow velocities on the flooding tide. Peak ebb-tide velocities have been observed at other sites to occur in the deepest morphological channels, while peak flood-tide velocities are generally weaker and do not necessarily occur in the deepest channels (Allen, 1971; Lessa and Masselink, 1995). A weighting coefficient is therefore required to account for the fact that, while the ebb tide exits directly through the river channel (here used as the discharge boundary), the flood tide enters the estuary through both the channel and the surrounding shoal and beach areas. Applying $\mathrm{d}Q/\mathrm{d}t$ across our fixed discharge boundary location (Fig. 5) is therefore a reasonable representation during the ebbing phase of the tide but not during the flood phase. To account for this, we use separate discharge coefficients, α, for the flood-tide (α_flood) and ebb-tide (α_ebb) periods, applied to the hypsometric discharges as

$$\begin{array}{}\text{(2)}& {\displaystyle }& {\displaystyle }(\mathrm{d}Q/\mathrm{d}t){\mathit{\alpha }}_{\text{flood}}\text{ for }{\displaystyle \frac{\mathrm{d}Q}{\mathrm{d}t}}\ge \mathrm{0},\text{(3)}& {\displaystyle }& {\displaystyle }(\mathrm{d}Q/\mathrm{d}t){\mathit{\alpha }}_{\text{ebb}}\text{ for }{\displaystyle \frac{\mathrm{d}Q}{\mathrm{d}t}}<\mathrm{0}.\end{array}$$

Optimal values to replicate the estuary flow velocities were found to be α_flood = 0.5 and α_ebb = 1. However, this may not be generalisable and would need to be calibrated for other study sites.

Using these calibration settings, the model was validated against the Eulerian data from the entire field deployment period (three tidal cycles). Model skill was quantified using the root mean square error (RMSE), defined as

$$\begin{array}{}\text{(4)}& \text{RMSE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^n(X_{\text{XB}\left(i\right)}-X_{M\left(i\right)}{)}^{\mathrm{2}}},\end{array}$$

where X refers to the hydrodynamic variable being assessed and subscripts XB and M refer to the modelled and measured values, respectively. The RMSE values were also normalised (NRMSE) by the mean H_s value or maximum U value at each instrument location across the periods under comparison to assess the relative magnitude of the error (Mouragues et al., 2021).

4 Results

4.1 Eulerian and Lagrangian field measurements

The field experiment was conducted during approximately average summer wave and tide conditions (H_s = 0.7–1.4 m, T_p = 7–14 s, D_p = 260–290°, tide range = 5.6 m; Fig. 4). Water level data from the mid-estuary PT show that the estuary began to fill as the tide increased above ∼ 1 m ODN, with the volume peaking at approximately 500 000 m³ at high tide (Fig. 6). Estuary flow, however, peaked just over an hour before high tide (landward discharge) and after high tide (seaward discharge), with fluxes of up to 100 m³ s⁻¹ estimated from the water levels measured during the experiment (Sect. 3.2).

The estuary discharge generated strong surfzone flows, which can be seen in the observed field data. Figure 6 demonstrates Eulerian velocities from the ADVs located on the intertidal ebb shoal bank adjacent to the estuary mouth and within the estuary mouth itself. Each of the measured tidal cycles showed a similar hydrodynamic signature: peak velocities in the estuary mouth occurred 1–2 h before and after high tide and diminished to zero at high tide. Comparable velocities were measured on the ebb shoal bank 30 min after (before) the estuary mouth on the rising (falling) tide. The seaward flow out of the estuary measured on the falling tide was 1.5–2 times faster than the landward flow on the rising stage of the tide, with seaward velocities at the ADV peaking at 0.75–1 m s⁻¹ and landward velocities at 0.5 m s⁻¹ for these two example tides. However, as the ADV in the estuary mouth was not in the deepest part of the channel, it is expected that peak flows exceeded 1 m s⁻¹ elsewhere.

The intertidal beach face ADV shows velocities remained notably low on the rising and high stages of the tide but increased rapidly up to 1.5 m s⁻¹ on the falling tide especially once the water level had dropped below 1.5 m ODN, concentrating the flow within the submerged beach face river channels. This ADV was located in the centre of the channel, so this represents a realistic estimate of the peak ebb-tide velocity. The u and v velocity components (Fig. 7) indicate that cross-shore flows dominated within the seaward-facing estuary mouth, while alongshore flows dominated on the ebb shoal bank and within the alongshore-oriented beach face river channel.

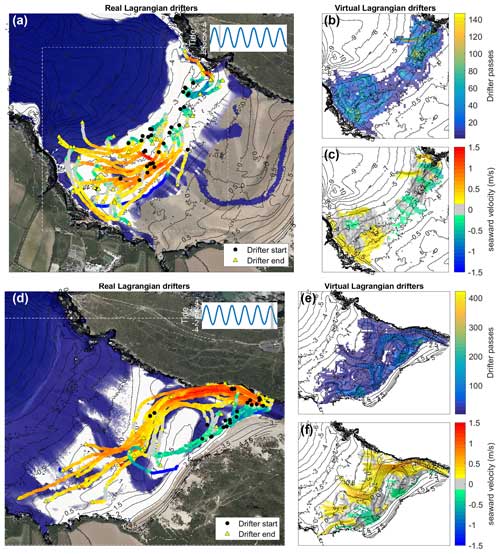
Figure 8 Comparison of measured and modelled circulation patterns using Lagrangian velocities from real GNSS drifters (a, d) and virtual drifters seeded in the XBeach model (b, c, e, f). Panels (a–c) show low-tide drifter data from 12 May 2021, and panels (d–f) show high-ebb-tide drifter data from 14 May 2021. Dashed white boxes in the left panels indicate the zoom extents of the right panels. Circles in the right panels show example virtual drifter tracks, while colours represent drifter velocities averaged onto 10 m spatial bins. Blue and white areas in the left panels show average water level and predicted wave dissipation > 1 W m⁻² during the field experiment for reference. Aerial imagery courtesy of National Network of Regional Coastal Monitoring Programmes of England, © 2024 NNRCMP.

The Lagrangian GNSS drifter tracks reveal that various circulation behaviours occurred simultaneously across the beach, including alongshore, rotational, and exiting flows, creating a complex flow field (Fig. 8). The observed circulation patterns evolved from low to high tide due to differences in the underlying beach morphology, as well as the activation and de-activation of the estuary at mid-tide. The GNSS drifters show a strong estuarine current flowing seaward during the ebbing high tide (Fig. 8d), which diverts laterally across the beach through various submerged river channels. Median Lagrangian velocity observed during this phase of the tide was 0.5 m s⁻¹, but drifter velocities exceeding 1 m s⁻¹ occurred where the river channel bends sharply away from the northern headland. Although many of the GNSS drifters exited the surfzone during the ebbing phase of the high tide, rotational flow also returned some drifters shoreward and back along the shore towards the main river channel (Fig. 8). Conversely, at low tide the GNSS drifters show weaker onshore and alongshore flows, leading to boundary rips at either headland which exit seaward or circulate back towards shore (Fig. 8a). The spatially averaged Lagrangian velocity during this phase of the tide was 0.3 m s⁻¹, with peak velocities exceeding 0.6 m s⁻¹ within the surfzone and in the neck of the boundary rip channels. Apart from a shallow (< 1 m), fast-flowing fluvial component, the estuary was inactive at tide levels below ∼ 0 m ODN.

4.2 Comparison of modelled and measured flows

Comparing the measured and modelled Eulerian flows (Fig. 7), the XBeach model reproduces the flow magnitude and phase from the ADVs well, albeit with some underprediction of flow during the ebbing tide on the ebb shoal bank and within the alongshore-oriented beach face river channel. The model reproduced the direction of the Eulerian flows well, with cross-shore velocities dominating in the river channel and alongshore velocities dominating on the ebb shoal riverbank and in the alongshore-oriented beach face river channel. Overall, the calibrated model achieved RMSE (NRMSE) of 0.2 m (20 %) for H_s, 0.16 m s⁻¹ (20 %) for u velocity, and 0.22 m s⁻¹ (21 %) for v velocity. Bias (mean absolute error) in the flow magnitude was −0.07 m s⁻¹, indicating the model tends to slightly underpredict the flow velocities.

Compared to the Lagrangian circulation patterns measured in the field during the low-tide period (Fig. 8a–c), the bin-averaged velocities from the virtual drifters (Sect. 3.6) reproduce the measured boundary rip velocities at the north and south headlands (∼ 0.5 and ∼ 0.7 m s⁻¹ at the southern and northern headlands, respectively). The virtual drifters also capture the net onshore flow in the middle of the bay and net seaward flows in the southern half of the bay and adjacent to the north headland. During the high-ebb-tide period (Fig. 8d–f), both the measured and modelled drifters coherently follow the river channels in the beach face, with seaward flows diverting away from the north headland across the beach before either exiting seaward through the beach face river channel or circulating back towards the estuary along the shore. Interestingly, large numbers of virtual drifters are predicted to pass through certain points in the inner surfzone (Fig. 8e), which are interpreted as stagnation points where quiescent circulation between onshore and offshore flow is occurring. These features are not present in the real GNSS drifter tracks because of the statistical limitations of deploying a small fleet of drifters, but the velocity patterns in these areas are reproduced. The model reproduces the strong seaward ebb-tide flow entering the beach from the estuary, where median Lagrangian velocities exceeding 1 m s⁻¹ were both modelled and observed. The circulation patterns show that the ebb-tide flows convey water rapidly through the main river channel before they connect to channel rips and boundary rips hundreds of metres away from the estuary mouth.

Overall, the calibrated model reproduces the measured Eulerian and Lagrangian flows from the 3 d field deployment well, especially considering the complexity of the flow field, and is therefore deemed suitable to assess surfzone circulation under a wider range of conditions.

4.3 Simulated Lagrangian circulation

In the following sections, the calibrated XBeach model is used to explore circulation patterns under a wider range of wave and tide conditions than was achieved in the field, as well as quantifying the exit potential and flow velocities under different forcing scenarios.

4.3.1 Influence of tidal stage and wave conditions

The XBeach simulations demonstrate that tidal translation across the beach significantly alters the surfzone circulation. Different circulation patterns and associated bathing hazards are seen at high, mid-, and low tide, and, furthermore, circulation is predicted to be distinctly different under a rising tide or a falling tide. For example, during an ebbing high spring tide with average waves (Fig. 9a), the virtual Lagrangian drifters are carried alongshore by littoral currents before exiting seaward in a narrow and fast-flowing estuarine current (U_off = 1.1 m s⁻¹; E = 56 %). At mid- to high-tide stages (Fig. 9b, c, f, and g), the surfzone is wider and the flows become channel-constrained under average waves. The flows follow the path of the submerged river channels alongshore and seaward towards channel rips and headland boundary rips, which are enhanced when the tide is ebbing (U_off = 1.2 m s⁻¹; E = 25 %) and diminished but still present when the estuary is flooding (U_off = 0.52 m s⁻¹; E = 0 %). Below mid-tide (Fig. 9d and e), the river channels and estuary discharge no longer influence surfzone circulation, and seaward flows predominantly occur within headland boundary rips at either side of the beach under average waves (U_off = 0.59 m s⁻¹; E = 13 %).

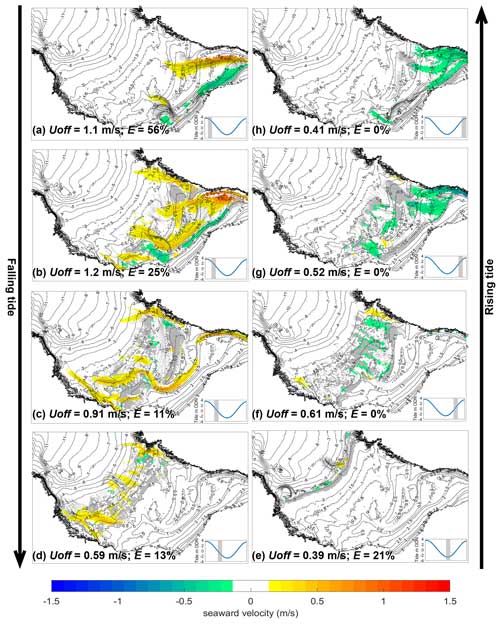
Figure 9 Simulated Lagrangian surfzone circulation from XBeach during a spring tidal cycle with average wave conditions (H_s = 1 m, T_p = 12 s, D_p = 279°, W_F = 1). Circles show example virtual drifter tracks, while colours represent drifter velocities averaged over 1 h onto 10 m spatial bins. The bin with the maximum seaward-directed flow velocity defines U_off for the entire beach, while E is computed from the proportion of virtual drifters that exit the surfzone (Sect. 3.6). Contours indicate beach morphology (m ODN), while grey areas show where breaker dissipation exceeds 10 % of the surfzone maxima. Tidal stage is shown in the inset panels.

Tide range influences the hazard signature in two distinct ways. Firstly, it determines how much water is flushed from the estuary during the ebbing high-tide phase, with an order of magnitude more estuary discharge (Fig. 5) during a spring tide (Q≈ 700 m³) than during a neap tide (Q≈ 50 m³), which substantially increases the estuary-driven flows in the hour following high spring tide (U_off = 1.1 m s⁻¹; E = 56 %) compared to those following high neap tide (U_off = 0.63 m s⁻¹; E = 15 %). However, at equivalent tide elevations, the circulation patterns are almost identical during a neap and spring tide (not shown here) because the ebb shoal channels dictate the circulation. Secondly, during high (Fig. 9a) and low (Fig. 9e) spring tides, the beach gradient is steeper and the surfzone is narrower than at any stage of a neap tide. This controls the ability of estuary and rip current flows to exit the surfzone, with a far wider, more saturated surfzone, and subsequently fewer exits, occurring during a neap tide than under high or low spring tides.

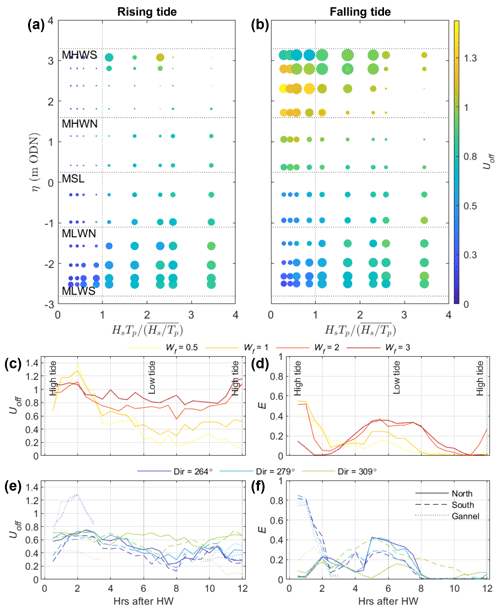
Figure 10 (a, b) Proportion of surfzone exits (E, bubble size) and offshore-directed drifter velocity (U_off m s⁻¹, bubble colour) from XBeach simulations with a mean spring tide and mean angle of wave approach (D_p = 279°). Bubble size range represents 0 $\le E\le$ 58 %. Results are plotted as a function of water level η and wave factor W_f = $H_{\mathrm{s}}{T}_{\mathrm{P}}/\left(\stackrel{\mathrm{‾}}{H_{\mathrm{s}}{T}_{\mathrm{P}}}\right)$. The vertical dashed line indicates average wave power ($\stackrel{\mathrm{‾}}{H_{\mathrm{s}}{T}_{\mathrm{P}}}$), while the horizontal lines represent mean high water spring (MHWS), mean high water neap (MHWN), mean sea level (MSL), mean low water neap (MLWN), and mean low water spring (MLWS) water levels. (c, d) Variation in U_off and E over a tidal cycle for four different W_f values, with a fixed wave period and direction of T_p = 12 s and D_p = 279°. (e, f) Variation in U_off and E over a tidal cycle for three different wave directions, with a fixed wave height and period of H_s = 1 m and T_p = 12 s (W_f = 1). Solid and dashed lines compare results for drifters released from the northern and southern half of Crantock Beach, while dotted lines show drifters released along the Gannel Estuary mouth (only for tide > 1 m ODN).

Figure 10a and b summarise the predicted flow velocity and exit potential under various combinations of wave and tide conditions. Wave power is parameterised relative to the time series mean using a “wave factor” parameter (Scott et al., 2014) W_f = $H_{\mathrm{s}}{T}_{\mathrm{P}}/(\stackrel{\mathrm{‾}}{H_{\mathrm{s}}{T}_{\mathrm{P}})}$, which describes the ratio between the associated H_sT_P (proportionally representing wave power) and the 16-year summer (June, July, August) mean ($\stackrel{\mathrm{‾}}{H_{\mathrm{s}}{T}_{\mathrm{P}}}$). This analysis shows that below mid-tide, tidal direction (falling or rising) becomes relatively unimportant, but seaward flow and exit potential are predicted to increase with increasing wave power, from U_off = 0.3–0.5 m s⁻¹ and E = 5 %–15 % when W_f < 0.5 to U_off = 0.7–1.0 m s⁻¹ and E = 20 %–40 % when W_f = 3–4. However, above mid-tide there are significant differences predicted in flow velocity and exit potential under rising or falling stages of the tide. The least hazardous conditions are predicted to occur during a rising mid- to high tide (Fig. 10a) with wave power below average, when seaward flows are almost entirely absent (U_off < 0.5 m s⁻¹; E = 0 %). Conversely, the most hazardous flows are predicted to occur during ebbing high spring tides (Fig. 10b) with wave power below average (U_off = 1.5 m s⁻¹; E = 58 %), when the estuary discharge can flow seaward completely unhindered by the surfzone. As wave power increases above average (W_f > 1), these ebbing flow velocities are predicted to remain high, but exit potential decreases significantly, as estuary flow is hindered by a wider, more saturated surfzone. This is further summarised in Fig. 10c and d, which compare variation in U_off and E over a mean spring tide for four different W_f values, with a fixed wave period and direction of T_p = 12 s and D_p = 279°. This demonstrates that during high ebbing tides, the highest exit potential and offshore flow speeds occur when wave power is low, while during all other stages of the tide, high wave power leads to increased exit potential and flow speeds.

Wave direction also appears to play a role in controlling the hazard signature at Crantock. Considerably more surfzone exits were predicted at the southern “downstream” headland of Crantock (max E = 90 %) or at the northern “upstream” headland (max E = 72 %) depending on the angle of wave approach. Below mid-tide, wave direction varied U_off by only 0.008 m s⁻¹ on average, but E increased by 12 % when wave direction was varied from the most oblique wave approach simulated (45°) to a shore-normal wave approach (0°). Figure 10e and f compare variation in U_off and E over a mean spring tide for three different wave approaches, with a fixed wave height and period of H_s = 1 m and T_p = 12 s (W_F = 1). This shows that drifters released in the north of the bay had a much lower exit potential than drifters released in the south of the bay during oblique wave approaches due to the southern drifters being released near the shadow boundary rip that occurs under oblique waves. Despite starting in the northern half of the beach, drifters released in the Gannel Estuary mouth had a high exit potential even during oblique waves, as the estuary flows transported drifters rapidly south towards the southern headland boundary rip. The ebbing estuary flows are predicted to be hindered during shore-normal waves with average wave power, with exit potential and seaward flow speed predicted to be reduced by approximately half compared to during oblique wave approaches.

Overall, the simulations suggest that, while wave power and direction strongly influence the hazard signature, tidal stage plays the most important role in controlling both surfzone exits and the velocity of surfzone currents at an embayed, estuary mouth beach like Crantock, with U_off and E varying by up to 0.44 m s⁻¹ and 70 %, respectively, when averaged at each tidal level.

4.3.2 Influence of estuary discharge

The estuary has been shown to drive extremely strong seaward flows through the surfzone in the hours following a high spring tide, with flow velocities up to 1.5 m s⁻¹. However, the estuary influences the flow dynamics in two distinct ways: (1) water flushing into and out of the estuary drives increasingly strong surfzone currents as tide range increases and (2) the river channel morphology acts to constrain surfzone flows in the same way that rip channels funnel wave-driven flows. In fact, ignoring estuary flows, the ebb shoal delta acts very much like a bar–rip system found on an intermediate morphology beach, providing shallow areas that induce wave breaking and deeper areas where wave-driven flows can return seaward. To demonstrate this, XBeach simulations were compared with and without estuary discharge activated in the model to disentangle the effect of the river channel morphology from the strong estuary flows (Fig. 11).

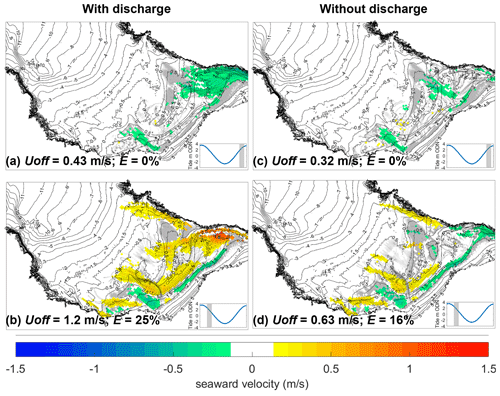
Figure 11 Simulated Lagrangian surfzone circulation from XBeach with (a, b) and without (c, d) estuary discharge activated in the model. The simulated conditions are 1.5–2.5 h before (a, c) and after (b, d) a high spring tide with average wave conditions (H_s = 1 m, T_p = 12 s, D_p = 279°). Circles show example virtual drifter tracks, while colours represent drifter velocities averaged over 1 h onto 10 m spatial bins. The bin with the maximum seaward-directed flow velocity defines U_off for the entire beach, while E is computed from the proportion of virtual drifters that exit the surfzone (Sect. 3.6). Contours indicate beach morphology (m ODN), while grey areas show where breaker dissipation exceeds 10 % of the surfzone maxima. Tidal stage is shown in the inset panels.

In the hours immediately prior to a high spring tide a significant flow of water floods the estuary (Fig. 11a), with strong landward flows occurring near the shore adjacent to the estuary. With estuary discharge switched off in the model (Fig. 11c), onshore flows are still predicted to occur near the shore due to wave breaking over the shallow ebb shoal bathymetry, but the strong landward flows in the estuary mouth no longer occur. However, wave breaking on the ebb shoal delta is predicted to drive weak seaward-flowing rips in the river channel away from the estuary, especially when estuary discharge is switched off, indicating that the river channel morphology induces channel rip behaviour independently of the estuary flows.

Immediately following a high spring tide there is a strong seaward flow driven by the estuary (Fig. 11b). Switching the estuary discharge off in the model (Fig. 11d) unsurprisingly has a strong effect on the flows immediately adjacent to the estuary mouth, but in the river channels more than 300 m from the estuary mouth the predicted circulation patterns are very similar whether estuary discharge is applied in the model or not. The river morphology is predicted to induce channel rip behaviour and contributes to bathing hazard independently of the estuary flows. Seaward flows in the main river channel in the middle of the beach are predicted to be similar in magnitude (0.6 m s⁻¹) in the absence of estuary flows to those with estuary flows activated (0.8 m s⁻¹), as are the boundary rip current velocities (0.8 m s⁻¹).

4.3.3 Influence of beach morphology

Four different surveys of the sub- and intertidal bathymetry of the beach were conducted during May 2021, August 2021, May 2022, and July 2022 (Sect. 3.4). As Fig. 12 shows, the morphology of the upper intertidal beach is dominated by the main river channel, which carves troughs > 1 m deep in the beach face and evolves noticeably over the four surveys. In contrast, the lower-beach contours remain relatively stable over this period, aside from slight variations in the ∼ 1 m deep headland boundary rip channels at either side of the beach, as well as the appearance and disappearance of smaller rip channels away from the headlands. The main river channel enters the beach with a constant position along the northern headland before deflecting away from the headland towards the middle of the beach. Initially, this channel exits approximately through the middle of the beach face (May 2021; Fig. 12a), but in subsequent surveys the river channel is seen to shift periodically a few hundred metres southward (August 2021; Fig. 12b) and northward (May 2022; Fig. 12c). Less-defined channels are also exhibited at various points in time, revealing relic positions of the main river channel.

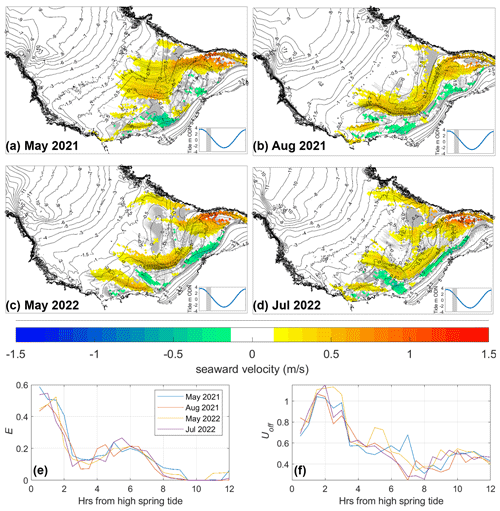
Figure 12 (a–d) Lagrangian surfzone circulation from XBeach run with four different measured bathymetries. The simulated conditions are 1.5–2.5 h after a high spring tide with average wave conditions (H_s = 1 m, T_p = 12 s, D_p = 279°). Circles show example virtual drifter tracks, while colours represent drifter velocities averaged over 1 h onto 10 m spatial bins. Contours indicate beach morphology (m ODN), while grey areas show where breaker dissipation exceeds 10 % of the surfzone maxima. Tidal stage is shown in the inset panels. (e) Proportion of surfzone exits E and (f) seaward flow velocity U_off predicted by XBeach (Sect. 3.6) over a spring tidal cycle with average wave conditions over the four different bathymetries.

XBeach simulations performed on the four different realisations of the morphology show that the variation in the spatial flow patterns over the four surveys is quite substantial (Fig. 12a–d), with the direction of the flows through the main river channel varying by more than 45° across the middle of the beach. Furthermore, the precise position of those strong channelised flows shifts over a distance of a few hundred metres. However, the hazard signature, here represented by U_off and E, is altered surprisingly little by the variations in the morphology (Fig. 12e and f). Over an average spring tide with average wave forcing (H_s = 1 m, T_p = 12 s, D_p = 279°), analysis of the virtual drifters suggests that the hazard signature is consistent across the four bathymetries, with seaward flows and surfzone exits maximised within 2 h of high tide (1 < U_off < 1.4 m s⁻¹; 30 % < E< 60 %) and reduced seaward flows (0.3 < U_off < 0.6 m s⁻¹) predicted for the remainder of the tidal cycle, albeit with a second peak in exits occurring at low tide (E≈ 20 %). For a given tide level, the standard deviation in E and U_off across the four bathymetries is ≤ 8 % and ≤ 0.22 m s⁻¹, respectively, with maximum differences of up to 18 % and 0.53 m s⁻¹, respectively. In comparison, the variation in E and U_off due to the tide moving over a single bathymetry is 60 % and 1.2 m s⁻¹.

This suggests that temporal variation in the position and flow direction of the river channels due to the shifting morphology does not significantly impact the overall hazard characteristics and that for a given set of forcing conditions the variation in morphology plays a secondary role in the hazard level compared to the effect of varying the forcing conditions themselves. This relative insensitivity of the hazard level to beach morphology facilitates the development of a beach hazard prediction tool (Sect. 5), as frequent morphological updating is not required.

5 Forecasting bathing hazard

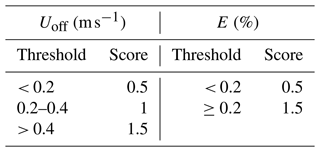
A site-specific bathing hazard forecast was developed for Crantock Beach in collaboration with the local landowners and the RNLI, with the intention of informing beach users of hazardous currents prior to accessing the beach. The calibrated XBeach model was used in the forecast system by running a suite of offline simulations (described in Sect. 3.5 and Table 1) and storing U_off and E values alongside their associated forcing conditions from each hourly segment of model output in a look-up table. The simulations used to populate the database were carefully designed to cover the full range of summer wave and tide conditions while also optimising the computational effort required to initially populate the database (Sect. 3.5). Forecasted ocean wave and tide conditions at the boundary of the XBeach model are gathered each day from the UK Met Office AMM15 wave and tide models. These are compared using a nearest-neighbour search to the forcing conditions in the look-up table to find the nearest simulated conditions to those forecasted in the coming days, resulting in a time series of predicted U_off and E values. A “hazard score” (HS1, HS2, or HS3) is then applied to each forecast time step by comparing the predicted U_off and E values for that time step to pre-determined thresholds calibrated below (Table 2). Low values of both U_off and E represent the lowest bathing hazard (HS1), as bathers would be advected slowly and retained in shallow water, while high values of U_off and E represent the highest hazard (HS3), as bathers would be transported quickly towards deep water. Other combinations represent a medium hazard level (HS2).

Table 2 Hazard thresholds applied to seaward flow velocity U_off and proportion of exits E from each model simulation to calculate bathing hazard score.

To calibrate the hazard thresholds, hazards must first be quantified in some way using records of past bathing incidents. Applying the approach endorsed by the World Health Organisation (WHO) for emergency and disaster risk management (Saulnier et al., 2020), it can be said that the total number of bathing incidents (or in WHO terms, the “life risk”) that occur over a given period is the product of three key factors: exposure, hazard, and vulnerability (Kennedy et al., 2013). For example, a high number of bathing incidents can occur at a beach even when modest hazards are present if the number of water users is high or if those water users are particularly vulnerable to the hazards due to low water competency or low hazard awareness. Conversely, if only a few people of average vulnerability enter the water on a given day but each one of those people gets caught in a current and needs to be rescued, the number of incidents would be relatively low, but the hazard can be considered high as the probability of each water user being in an incident approaches unity. Assuming it is informed by a suitably large number of observations, this relationship between past incidents and hazard level can be simplified to

$$\begin{array}{}\text{(5)}& \text{hazard }=\mathrm{incidents}/\mathrm{exposure}.\end{array}$$

This parameterisation of hazard represents the probability of an individual water user of “average” vulnerability (i.e. average swimming ability and surfzone competency) being involved in a flow-related incident over a given time frame, and it has been applied in previous studies to define hazard at the coast (Stokes et al., 2017; Castelle et al., 2019; Scott et al., 2014).

The thresholds in Table 2 were optimised by analysing past bathing incidents at Crantock Beach over the years 2016–2021. Only flow-related incidents (n = 648) were considered where a lifeguard was required to rescue or assist a water user back to shore (Fig. 13). The lifeguard data were discretised into 2 h time bins, and the number of incidents were divided by the bather head count made by the lifeguards during each 2 h period (representing an estimate of the average exposure over that period), resulting in an “observed” hazard level from Eq. (5) for each time step. The hazard time series was then used to compute bin-averaged hazard values across a number of discrete U_off and E bins. The distribution of hazard over these bins suggests that sharp increases in hazard occur when U_off reaches 0.2 and 0.4 m s⁻¹. The lower threshold is corroborated by Moulton et al. (2017a), who identified that rip current speeds greater than 0.2 m s⁻¹ may be hazardous to swimmers. For E we find a single threshold of 0.2 (20 % likelihood of a drifter exiting the surfzone), which distinguishes between lower and higher levels of hazard. An obvious second increase in hazard with E was not visible from the distribution. Using these thresholds, two scores are obtained from Table 2 which are added together and rounded to achieve a final hazard score, following the approach of Austin et al. (2013).

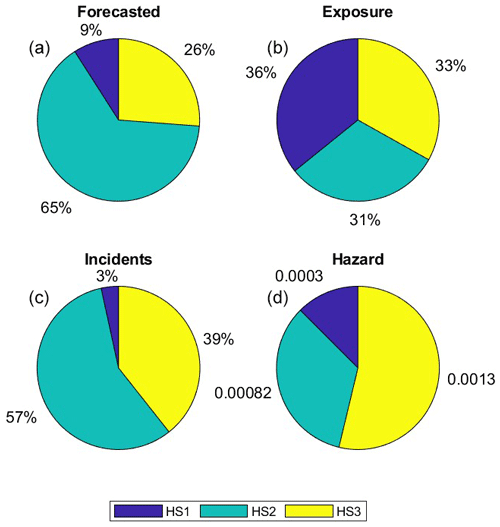
Figure 13 Performance summary of the developed bathing hazard forecast over the hindcast period (2016–2022). Proportion of forecasted hazard scores (HS1, HS2, HS3; a), relative average water-user exposure (b), proportion of total incidents (c), and probability of an individual water user being in a flow-related incident (hazard, d).

To assess the skill of the developed forecast system we consider how often the upper hazard scores (HS2 and HS3) were hindcasted when an incident was recorded by the lifeguards. This is termed the probability of detection (Panofsky and Brier, 1953), also known as the recall or sensitivity, of the predictive system and represents the rate of true positives achieved. We also examine how often the hindcast missed an incident (i.e. HS1 was predicted when an incident occurred), which represents the rate of false negatives. It is not possible to examine the rate of false alarms (“false positives”) because bathing hazard can be high without an incident occurring, for example if no one enters the water or due to lifeguard preventative actions.

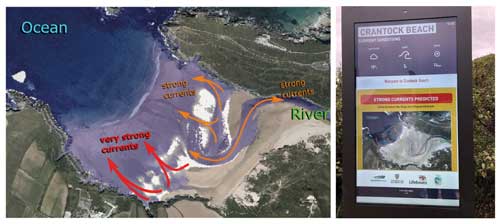
Figure 14 In the left panel is an example of simplified beach hazard information derived from simulated drifter patterns. In the right panel is an operational digital bathing hazard sign at Crantock Beach next to a key beach access point showing dynamic hazard predictions for the next hour. Aerial imagery courtesy of National Network of Regional Coastal Monitoring Programmes of England, © 2024 NNRCMP.

The highest hazard scores (HS2 and HS3) were forecasted most often (65 % and 26 % of the time, respectively) but also captured most of the observed incidents and hazard. True positives (false negatives) were achieved 98 % (2 %) of the time. HS1 was forecasted least often (8 %) but satisfactorily captured only 2 % of the observed incidents, with an average hazard probability of 1 incident per 3303 bathers (Fig. 13), and therefore represents a low incident, low hazard scenario. HS2 represents a high incident, medium hazard scenario, capturing 57 % of past incidents with an average hazard probability of 1 in 1227. HS3 represents a high incident, high hazard scenario, capturing 39 % of past incidents with an average hazard probability of 1 in 770. The likelihood of an individual bather being involved in an incident therefore increases by 2.7 times between HS1 and HS2 and by 5.7 times between HS1 and HS3. Interestingly, exposure is almost equal at each hazard level, indicating that water users either are knowingly entering the water during hazardous conditions or, more likely, are unaware of the higher hazard occurring at certain times. The developed predictive system appears to be able to differentiate periods of low and high bathing hazard with a high probability of detection of recorded incidents and is therefore deemed suitable for use in the predictive forecast system at Crantock Beach to forewarn bathers of hazardous conditions (Fig. 14).

6 Discussion

6.1 Comparison to rip current hazards

It is well known that strong flows can occur in estuaries, and they have previously been identified as hazardous locations for bathing, for example in Goa, India, by Chandramohan et al. (1997). In this study it has been shown that the presence of a large ebb delta on a macro-tidal beach can lead to powerful and spatially complex surfzone flows. At Crantock the estuary is inactive below mid-tide, at which point surfzone currents consist of onshore and alongshore wave-driven flows and seaward-flowing boundary rip currents (for example, Fig. 8a), which exhibit velocities that are typical of rips observed globally in other studies. For example, under a range of different wave conditions we predict wave-driven rip velocities of U_off = 0.5–1 m s⁻¹ (Fig. 10) during the lower half of the tide, which is in line with Lagrangian velocities of 0.4–1 m s⁻¹ measured at micro-tidal, meso-tidal, and macro-tidal bar–rip beaches around the world (Scott et al., 2014; Austin et al., 2010; MacMahan et al., 2010; McCarroll et al., 2017; McCarroll et al., 2018; Moulton et al., 2017a). Similarly, the proportion of surfzone exits per hour that we predict when the estuary is inactive is on average E = 15 % (range E = 0 %–42 %), in line with global field and modelling studies of morphologically controlled rip currents that find average exits of E = 14 %–19 % (range E = 0 %–34 %) (MacMahan et al., 2010). Therefore, when the estuary is inactive, the bulk characteristics of the rip currents at this beach are no different from those observed at other beaches globally.

When the estuary is ebbing, however, the time-averaged surfzone velocities we measured and modelled reached U_off = 1.5 m s⁻¹, which is ≥ 50 % faster than velocities typically measured in channel rips (Austin et al., 2010; Scott et al., 2014; MacMahan et al., 2010; McCarroll et al., 2017; McCarroll et al., 2018). Even boundary rip currents typically exhibit Lagrangian velocities below 1 m s⁻¹ (Castelle and Coco, 2013; McCarroll et al., 2014a), even under high-energy waves (Mouragues et al., 2020, 2021).

6.2 Embayment, estuary, and wave controls on surfzone exits

The exit potential during the ebbing phase of the tide (E≤ 62 %) is high but is in line with observed and modelled wave-driven boundary rips from embayed beaches of a similar size (McCarroll et al., 2014a; Castelle and Coco, 2013). The predominant oblique wave approach results in varying alongshore wave exposure, driving an alongshore current towards the south headland where it deflects offshore. We find that considerably more surfzone exits occur either at the southern “downstream” headland of Crantock (max E = 90 %) or at the northern “upstream” headland (max E = 72 %) depending on the angle of wave approach, in line with previous findings for embayed beaches (Castelle and Coco, 2013; McCarroll et al., 2014a).

During the upper half of the tide, surfzone exits are maximised when wave power is below average, allowing the estuary to ebb unhindered by waves, and exits decrease when wave conditions are more energetic than average (W_f > 1). When the estuary is flooding, surfzone exits cease completely, regardless of the level of wave energy. Surfzone exits at an estuary mouth beach are therefore strongly controlled by both wave and estuary processes. While landward flows on the flood tide intuitively reduce the likelihood of material exiting the surfzone, waves breaking seaward of the ebb shoal delta under neap high tides or high wave energy (W_f > 1) can also reduce surfzone exits by increasing shoreward Stokes drift and broken wave bores (Castelle et al., 2016) within the river channels. In the context of river and estuary discharges, this surfzone retention has been shown to be controlled by the ratio of river momentum flux to wave momentum flux (Rodriguez et al., 2018; Olabarrieta et al., 2014) or similarly of river plume length to surfzone width (Kastner et al., 2019). In the context of bathing hazard, this is akin to breaker saturation reducing rip current exits through an inner bar–rip channel under larger waves (MacMahan et al., 2010) or above average wave power (Scott et al., 2014). At Crantock, this effect does not seem to occur during the lower tidal stages, however, with exits remaining at 15 %–20 % for 1 < W_f < 4 due to the well-defined boundary rip channels extending beyond the surfzone.

We present U_off and E in terms of relative wave power, as Scott et al. (2014) and Castelle et al. (2019) found this to be an important parameter in controlling the occurrence of rip-related bathing incidents in southwest England and southwest France, respectively. Although they studied only a limited range of wave periods, Moulton et al. (2017a) and Moulton et al. (2017b) did not observe a dependence of rip current velocity on wave period and concluded that only wave height and direction (as well as water depth) were important for offshore-directed flow velocity due to their control on breaker-induced set-up and alongshore current speed. Here we find that surfzone exits are slightly more sensitive to relative wave power (incorporating wave period) than wave height alone. Below mid-tide, when the estuary is inactive, U_off and E varied by up to 0.16 m s⁻¹ and 51 %, respectively, when averaged at each simulated wave height, while changing the level of wave power varied U_off and E by up to 0.17 m s⁻¹ and 63 %, on average. The simulations therefore indicate that seaward wave-driven velocity at an embayed beach is influenced to a similar degree by either wave height or power but that wave power exerts a greater influence on surfzone exits than wave height alone.

6.3 River channel bathymetric rips

During both the ebbing and flooding high tide, the estuary dictates the flow velocity in the river channels (Fig. 10). Switching estuary discharge off in the model indicates that wave-driven rip currents in the deep river channels flow at a similar velocity to typical channel rips (∼ 0.6 m s⁻¹) under average wave conditions (Sect. 4.3.2). These “river channel bathymetric rips” fit with the concept (McCarroll et al., 2018) that intense rip flows occur in shore-normal channels with high alongshore non-uniformity (i.e., deep and narrow), regardless of whether the channels were formed by estuarine or wave processes. This also demonstrates that river channel morphology on a beach can facilitate both strong estuary flows and strong rip current flows, regardless of the level of estuarine discharge. Furthermore, the channels efficiently convey water towards wave-driven rip currents further down the beach, linking flows across the surfzone and providing a conveyor belt to transport bathers from the shore to deeper water offshore.

It is also noteworthy that the main river channel tends to exit seaward in approximately the middle of the embayment, albeit with some variation in its position (Sect. 4.3.3). Narrow embayments with curvature at the shoreline such as Crantock can promote cellular rip circulation (Castelle and Coco, 2012), where seaward flows form in the centre of the bay, especially during energetic conditions (Castelle et al., 2016). This wave-driven process may, therefore, influence the position of the river channel at Crantock by enhancing seaward flows and promoting channelisation in the middle of the beach.

6.4 Importance of tidal level and phase

Channel rips have been observed globally to increase in intensity at low tide as a result of flow constriction through low-tide bar–rip channels or increased intensity of wave breaking over sandbars (Castelle et al., 2016; Aagaard et al., 1997; Brander and Short, 2001; MacMahan et al., 2006, 2005). As a result, low-tide levels have been linked with a higher occurrence of bathing incidents (Koon et al., 2023; Scott et al., 2014; Castelle et al., 2019) and drowning risk (Koon et al., 2023). In contrast, here we find a mechanism for dangerous seaward flows to occur during the high-tide phase, either from estuary discharge or as river channel bathymetric rips. While the efficacy of these high-tide rips was sensitive to the estuary discharge, they were present whether the estuary was ebbing or flooding (for example, Fig. 9). Koon et al. (2023) found that on Australian beaches, there was no link between tidal phase or tide range and coastal drownings. However, here we demonstrate a clear difference in bathing hazard during rising and falling stages of the tide when an estuary mouth is involved, albeit in a location with a much larger tidal excursion. During the upper half of the tidal cycle, hazard is strongly controlled by tidal phase, range, water level, and wave conditions, while during the lower half of the tidal cycle only water level and wave conditions appear to be important.

6.5 Bathing hazard forecasts

Rip current forecasts have been developed in several previous studies. Some of these systems operate at a regional/national scale using data-driven empirical relationships that link forecasted wave, tide, and weather conditions to lifeguard rescue statistics (Scott et al., 2022; Lushine, 1991; Lascody, 1998; Engle et al., 2002; Dusek and Seim, 2013a, b; Gibbs et al., 2015). Other studies have developed site-specific calibrated process-based models to predict where and when rip current activity will occur on a beach (Austin et al., 2013; Kim et al., 2013; McCarroll et al., 2018, 2015), but these have rarely been applied operationally and none have yet included dynamics from channel rips, boundary rips, and estuary flow. The forecast system developed for Crantock (Sect. 5) has been implemented operationally at the beach since 2022 and provides real-time warnings about where and when peak bathing hazards will occur, in addition to simplified flow visualisations, via novel digital display screens located at the two main beach access points (Fig. 14). To the best of our knowledge, this represents the first process-based forecast system used to provide bathing warnings directly to the public. Work is now underway to better understand whether such warning systems are effective at influencing and informing beach-user decision-making and therefore contribute to a reduction in life risk.

7 Limitations

The developed XBeach model and the forecast system derived from it show skill in capturing the circulation patterns and associated bathing hazards at this embayed, estuary mouth beach. However, there are several limitations to acknowledge that could be tackled in future research at similar sites:

• The simplified estuary discharges applied at the boundary ignore any potential gradients in water level over the length of the estuary and ignore some fluvial–estuarine interaction. However, the enhancement of the estuary flow due to high fluvial flow was included by adding a conservative 5 % exceedance river flow.

• While the observed circulation behaviour was overall reproduced by the XBeach model and the NRMSE in flow velocity was comparable to other similar studies (for example, Mouragues et al., 2021), the modelled velocities were at times underestimated by the developed model (Sect. 4.2). Model bias was −0.07 m s⁻¹ for flow magnitude, compared to the acoustic Doppler current profiler (ADCP) measurements. Therefore, the modelled flows do not always represent a conservative estimate of the real flow speeds.

• The surfbeat mode of XBeach was employed in this study, which captures the wave variations and associated wave-driven flows at the wave group (infragravity) timescale (Roelvink et al., 2010) expected to drive the bathymetric and topographically controlled rips at Crantock (Scott et al., 2014; Austin et al., 2010, 2014). However, transient flows driven at the incident wave timescale such as flash rips (Castelle et al., 2016) are not captured by the model, which may occur over the planar lower-beach morphology (Castelle et al., 2014) away from the headlands.

• The influences of wave directional spreading and bimodality in the wave spectra have not been explored in this paper.

• The model is depth averaged, meaning that vertical stratification in flow is not considered. However, this is not considered to be important for studying hazard characteristics, as only surface flows are of interest.

• The results of the present study are highly tuned to this specific estuary. For example, the flow velocities and exit rates are likely to be a product of local factors such as geomorphic setting, estuarine tidal prism, and wave exposure, while the variation in circulation between low and high tide may be a direct result of the large tidal range. The ebb dominance of the estuary and required discharge tuning coefficient α are also likely to be site-specific and driven by geomorphological factors. The embaymentisation and oblique angle of the beach to the prevailing wave approach is also expected to elicit specific flow behaviours (shadow rips, for example) that will not necessarily occur in the same way at other estuary mouth beaches.

• The high variability in the river channel morphology appears to not fundamentally vary the bathing hazard in terms of U_off and E, based on the four bathymetric datasets that were collected (Sect. 4.3.3). However, a more dramatic change in the river channel morphology could feasibly occur (for example, if the river channel were to be naturally or artificially relocated once again against the north headland), and this has not been simulated in the present study.

• Several other relatively predictable factors cause a bathing hazard at this and other similar beaches which are not considered by the developed forewarning system but could feasibly be included in future developments. For example, beach users frequently get cut off from the shore on the ebb-tide sandbars during the rising tide and are forced to enter the water unprepared. Plunging breakers at the shore (“shorebreak” conditions) can occur during low- and high-tide periods at Crantock when waves break on the steepest parts of the shoreface, and these can lead to surfzone injuries (Castelle et al., 2019).

8 Conclusions

Surfzone currents at an embayed, estuary mouth beach were both measured and modelled, revealing complex surfzone circulation patterns, including circulating, alongshore, and exiting flow regimes. The river channel morphology is a key driver of the circulation above mid-tide. The river channels act to constrain both estuarine and wave-driven currents, directing the flows alongshore and offshore, often connecting with boundary and channel rip currents lower on the beach face. Flow velocities through the river channels were enhanced by increasing estuary discharge, increasing wave power, and decreasing water depth. Wave direction was also found to alter bathing hazards, hindering seaward estuary flows during shore-normal waves and exacerbating shadow boundary rips during obliquely arriving waves. Overall, tidal stage exerted the greatest control on surfzone exits and seaward flows at this embayed, estuary mouth beach.

The most hazardous flows are predicted to occur during ebbing high spring tides with wave power at or below average when estuary discharge and wave-driven return flows can flow seaward through the river channels unhindered by the surfzone. Under such conditions, the highest seaward velocities (up to 1.5 m s⁻¹) and maximum potential for surfzone exits (> 60 %) occurred. While wave-driven channel rips have been widely observed to occur preferentially over low-tide bar–rip morphology, we demonstrate a novel mechanism for “river channel bathymetric rips” to occur near high tide due to wave breaking over an ebb shoal delta, which can drive strong seaward return flows in the adjacent river channels even in the absence of estuary discharge.

The combined action of estuarine and wave-driven flows on this beach generates seaward currents that are up to 50 % faster than peak rip current velocities observed in the literature and are combined with very high surfzone exit rates. This indicates that the presence of an estuary mouth within an energetic surfzone poses a highly hazardous situation for bathers which was previously unstudied in the literature, despite potentially exceeding the hazard that would be expected from rip currents alone. Surprisingly, despite significant spatio-temporal variability in the position of the river channels on the beach face, it was found to be possible to predict the timing and severity of past bathing incidents from model simulations, providing a means to simulate and forecast bathing hazards to forewarn bathers about times of peak bathing hazard.