Modelling hazards impacting the flow regime in the Hranice Karst due to the proposed Skalička Dam

This study examines the hydrogeological hazard associated with the construction of the proposed Skalička Dam in the vicinity of the Hranice Karst. Prompted by the catastrophic regional floods in 1997 and 2010, the design of the dam aims to mitigate floods along the Bečva River downstream of the reservoir. However, concerns have been raised regarding the potential disturbance of the natural groundwater regime in the Hranice Karst and the source of mineral waters for the Teplice spa. This is due in particular to the dam's location in an area with limestone outcrops potentially susceptible to surface-water infiltration. Previous studies have also highlighted the strong correlation between the water level in the Bečva River and the water level in karst formations such as the Hranice Abyss, Zbrašov Aragonite Caves, and other caves in the locality. To address these concerns, a nonlinear reservoir-pipe groundwater flow model was employed to simulate the behaviour of the Hranice Karst aquifer and specifically the effects of the dam reservoir's impoundment. The study concluded that the lateral variant of the dam would have a practically negligible impact on the karst water system, with the rise in water level being only a few centimetres. The through-flow variant was found to have a more significant potential impact on water levels and the outflow of mineral water to the spa, with a piezometric rise of about 1 m and an increase in the karst water discharge to the Bečva River of more than 50 %. Based on these results, recommendations for further investigations concerning the design of the dam and its eventual construction have been formulated to reduce geological uncertainties and to minimize the potential impact of the hydraulic scheme on the hydrogeology of the karstic system.

1 Introduction

In the Bečva river catchment (Fig. 1) in the eastern part of the Czech Republic, extreme regional floods occurred in 1997 and 2010 (CHMI, 1997, 2010). The Skalička Dam is planned in two variants (through-flow and lateral) as a part of a flood protection system being constructed on the Bečva River as a response to the catastrophic floods mentioned above. A more detailed description of the locality and scheme can be found in Sect. 2. Potential environmental and geological hazards associated with the construction and operation of the Skalička Dam have been described by Geršl and Konečný (2018). They point out the possible unfavourable impact of the dam on the natural groundwater regime in the Hranice Karst and the potential for degradation of the abundant sources of mineral water used by the Teplice spa. Aside from the pumping wells that supply the Teplice spa, mineral water containing high concentrations of dissolved carbon dioxide rises into the Bečva River, the Zbrašov Aragonite Caves (ZAC), and the Hranice Abyss (HA). Gaseous carbon dioxide may also be found at observation wells and “breathing spots” (Faimon et al., 2020) occurring in the area. However, the infiltration zone of the karstic system is still unclear; some authors (Vysoká et al., 2019; Bruthans et al., 2021) point out the significant role that may be played by surface water in the Bečva River, whose water stages probably govern water pressure in the karst formations. The older estimates of total spring discharge ranged from 12 to 17 L s⁻¹ (Bruthans et al., 2021), while new research using hydrometric measurements combined with a conductivity assessment shows an amount of about 100 L s⁻¹ (Il Faut, 2022). This supports the hypothesis that the Bečva River is an abundant water source for the Hranice Karst at a location lying a few kilometres upstream of the Teplice spa. At this point, limestone outcrops rise to the level of the local terrain and interfere with the Bečva River channel (Vysoká et al., 2019; Bruthans et al., 2021; Il Faut, 2022).

Figure 1 Locality of interest – current state (the base map is from CUZK, 2024).

Parise et al. (2018) generally summarize current knowledge about karst areas, including karst geology, geomorphology and speleogenesis, karst hydrogeology, karst modelling, and karst hazards and management. Numerous authors deal with the karst environment, which is characterized by distinctive landforms related to dissolution and a dominant subsurface drainage that brings risks for the planning, construction, and operation of engineering works (Gutierrez et al., 2014; Parise et al., 2015). Klimchouk (2007) provides an overview of the principal environments, main processes, and manifestations of hypogenic speleogenesis. He states that elementary patterns typical of hypogenic caves are network mazes, sponge-work mazes, irregular chambers, and passage clusters. Palmer (1991) presents various types of cave systems that can gradually form in the karst area under the action of water. The process of the formation and expansion of cave systems usually takes more than 10 000 years, which significantly exceeds the live cycle of dams.

The Skalička Dam will be located about 5 km upstream of the Teplice spa in the vicinity of the aforementioned limestone outcrops, which also occur within the dam reservoir. Therefore, the question arises as to whether the construction of such a dam would have an impact on the karstic waters in the area and thus significantly affect hydrogeological conditions. Building dams in karst areas is always a technical challenge. It involves a number of risks connected to unintended water losses and dam stability issues (Milanović, 2005, 2018). Based on experience with dam construction and operation in karstic regions, Milanović (2018) recommends that the karst in the vicinity and wider region of the proposed dam be carefully explored and understood. The groundwater regime in karstified rocks can be extremely complex and often is not readily predictable (Yevjevich, 1976), rendering it a far-from-friendly environment for constructing dams and reservoirs (Milanović, 2021). The latter author emphasizes that the amount of certainty or uncertainty in the crucial parameters (geological structure, groundwater regime, and intensity and depth of karstification) should be recognized.

One of the first dams successfully constructed on limestone bedrock was El Kansera, where grouting was used to seal the bedrock (Caille, 1955). In the case of the Genissiat Dam, the grouting was reduced to a minimum, as the karstic channels were filled naturally with impervious clays (Delattre, 1955). Cutoffs have been also used to seal porous carbonate rocks in the subbase of dams in karst (Breznik, 1985). At the El Cajón Dam in Honduras, a massive quantity of grout was applied in order to connect moderately karstified limestone with upstream impervious vulcanite (Flores et al., 1985). Large dams on karst have also been built in Türkiye, such as the Keban Dam, where massive grouting, backfilling, and cut-offs were performed in order to reduce water loss from the reservoir to an acceptable level (Gilmore et al., 1991). If the foundation of the dam is soluble, detailed monitoring at the dam site and karst formations with additional grouting of permeable zones in dam foundations must be adopted (Guzina et al., 1991). Further, a warning system should be implemented (Heitfeld and Krapp, 1991). The issue of locating dams in karst areas and the use of water resources in karst is addressed by numerous authors, who regularly share their knowledge at thematic workshops and seminars, and many problems have been described during the construction and after the completion of such engineering works (Palma et al., 2012; Stevanovic, 2015; Milanovic and Stevanovic, 2018; Golian et al., 2021).

Due to the significantly varying geological conditions at different locations, the dam-related problems mentioned above are complex and site specific, which makes each dam a unique case requiring specific solutions (Talebbeydokhti et al., 2006). Many authors from different parts of the world have addressed the problems of dams in karst in case studies, e.g. de Waele (2008), Mozafari and Raeisi (2015), and others. Mohammadi et al. (2007) proposed a methodology including three steps that should be applied before the construction of a dam: (a) recognition of geological and hydrogeological settings, (b) delineation of the system related to the future reservoir and its function, and (c) assessment of the leakage potentials. Following the application of this methodology, the most probable leakage zone(s) and path(s) at the dam site should be highlighted.

Modelling the groundwater regime in karst is a complex engineering problem (Mikszewski and Kresic, 2015). Malenica et al. (2018) presented a novel numerical model for groundwater flow in karst aquifers. They used a discrete-continuum (hybrid) approach in which a three-dimensional matrix flow is coupled with a one-dimensional conduit flow. They also conducted laboratory testing on the model. This model is applicable to well-explored karstic systems. Chang et al. (2015) applied a nonlinear reservoir-pipe model to simulate a karst spring near Guilin, China, with satisfactory results, especially with respect to the discharge peaks and recession curves of the spring under storm conditions. Jeannin et al. (2021) compared 13 models using a single data set. Neural networks, reservoir models, and semi-distributed and fully distributed models were directly compared within their study, which drew the conclusion that most models fit the field data reasonably well, although they predicted low water flow rates poorly. Petrović and Marinović (2023) used stochastic modelling for the characterization of the Mokra Karst aquifer. They also used a time series analysis.

Even though numerous attempts have been made to predict the impact of anthropogenic changes on karst groundwater, there is a lack of experience with groundwater flow modelling in poorly explored deep karstic formations. The current study aims to simulate behaviour of the Hranice Karst using a numerical model based on the hydraulics of conduit flow in underground channels of unknown shape, dimensions, and hydraulic characteristics (e.g. roughness) coupled with reservoir model simulating filling the Hranice Abyss and caves in the area. The unknown characteristics of the network of “pipes” interconnecting reservoirs in the studied locality (the Hranice Abyss – the deepest continental abyss in the world, as well as the Zbrašov Aragonite Caves and the Kuče Caves, KC) are calibrated using data from hydrological observations. The final objective was to assess the impact of the proposed Skalička Dam on the Hranice Karst and the source of mineral waters for the Teplice spa.

In the text, the locality of interest is delineated first, then the methods used are explained, and finally the results of the numerical analysis are presented and discussed. In this way, this study improves the existing body of knowledge about the Hranice Karst and the mechanics of groundwater flow in deep karstic formations.

2 Description of the locality

2.1 Overview

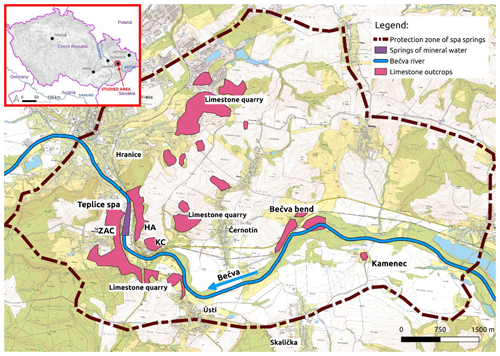
The locality of interest is located on the border of the Olomouc and Zlín regions in the Czech Republic and belongs to the administrative district of the Hranice regional municipality. The area of the proposed dam and reservoir is located to the north-east of the village of Skalička (Fig. 1).

2.2 Geological and hydrogeological conditions

In the locality, the most prominent types of Devonian limestone are those that rise to the surface in the western part of the area between the Teplice spa and the railway cut to the east from the village of Černotín. Their very easternmost outcrop is found in the locality of Kamenec in the area of the proposed reservoir (Fig. 2). Concern exists about the seepage of the water from the reservoir to the karstic system. In some places, the outcrops are tectonically broken and scarred.

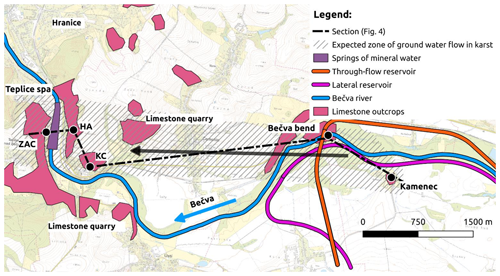
Figure 2 Details of the Hranice Karst with the locations of the two variants (through-flow, lateral) of the dam (CUZK, 2024).

The Hranice Karst is a hypogenic karst at which the confined karst water flow is upward (Klimchouk, 2009). The Hranice Karst in the area of Devonian limestone is a distinctive geological feature that has a significant influence on the implementation of the dam and its technical arrangement. These rocks are about 350 to 380 million years old and are overlain by flysch, chalk, and Palaeogene sediments. For the protection of the Teplice spa and valuable mineral springs, the protection zone was declared (Fig. 1) based on the observed limestone outcrops and the results of historical drilling. The total thickness of the limestone forming the Hranice Karst has not yet been determined because its bedrock has not been reached by the drilling work; however, it is assumed to be on the order of thousands of metres thick (Geršl and Konečný, 2018). The main karst phenomena of the Hranice Karst are the Hranice Abyss, the Zbrašov Aragonite Caves, and the Kuče Caves. Until now, over 31 local caves and other karst phenomena, such as sinkholes and breathing spots (the sites on a karst landscape surface across which air is exchanged between the external atmosphere and underground cavities), have been registered (Faimon et al., 2020). Furthermore, Hranice Karst contains the following features.

• Kamenec is the easternmost outcrop situated in the area to be covered by the proposed reservoir. It is a separate outcrop that rises to the surface to a limited extent and descends steeply.

• Outcrops at the Bečva River bend are close to the village of Černotín – the limestone outcrops reach the surface and are also found below the Bečva riverbed.

• Limestone layers in the quarry close to the village of Ústí on the left bank are about 3 km downstream of the reservoir.

• Limestone is intensively mined in the Černotín quarry.

• The Teplice spa – mineral water used for therapeutic purposes is taken from deep wells drilled into the aforementioned Devonian structures.

The details of the Hranice Karst and the location of the proposed Skalička Dam are shown in Fig. 2.

The Devonian limestones are tectonically divided into several “blocks”. The main fault lines proceed in an east–west direction and are followed by springs of carbonated mineral waters rising at the Teplice spa and into the Bečva River and the Hranice Abyss (Fig. 2). According to Geršl and Konečný (2018), the Devonian limestone outcrops east of the Teplice spa probably form the main infiltration zone of the springs of mineral water. The outcrop in the Bečva River bend east of the village of Černotín has been identified as the place with the best conditions for surface waters to sink into the karst formations. It is supposed that a certain amount of the surface water from the Bečva River sinks along the faults and then flows further on to a significant depth (estimated at about 1 km), where it becomes saturated with juvenile carbon dioxide (Sracek et al., 2019). After mineralization, the water proceeds upward and emerges into the Bečva River, the pumping wells at the Teplice spa, and the Hranice Abyss.

The easternmost limestone outcrop, located in the Kamenec region, is also characterized by high local permeability, although a direct connection to the lower karst system has not been confirmed. Even if no interconnection between the shallow groundwater and deeper karst waters was observed during the recent survey (Il Faut, 2022) in the Kamenec area, there is still a certain degree of concern among hydrogeologists about the possibility of mutual interference in the case of dam impoundment. The main doubts are related to the permanent water storage in the reservoir, which might cause unfavourable changes to the groundwater regime in the karst.

The observations of water stages in these surface and subsurface water bodies and in the system of observation wells have provided valuable time series used for the calibration and verification of the hydraulic model (see Sect. 3).

2.3 Karst landforms

For the assessment of the groundwater regime in the karst system (Fig. 3), observations of water levels in both surface and underground landforms were carried out. For the hydrological modelling and water balance calculations, basic dimensions of the significant local landforms such as the Hranice Abyss, Zbrašov Aragonite Caves, and caves at Kuče were determined, namely the area of the water surface. The observations indicated that the water level in the landforms mentioned changes according to the water stages in the Bečva River with a certain time lag due to the filling and/or emptying of the water storage in water bodies. The surface areas (Table 1) were calculated using geodetic measurements performed during the no-flood period, i.e. for a steady state corresponding approximately to the mean annual discharge in the Bečva River.

Table 1 Overview of water surface areas.

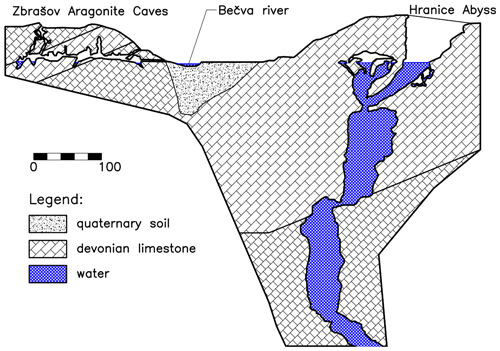
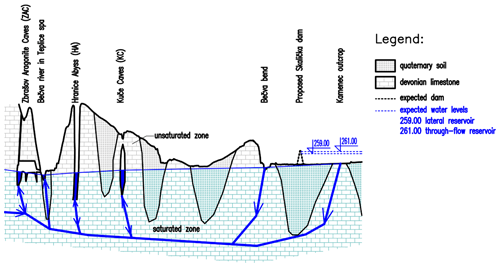
Figure 3 A detailed interpretation of the ZAC and HA at the Teplice spa, cross-section from the ZAC to HA in Fig. 2 (Sracek et al., 2019). Vertical and horizontal scales are the same.

The Hranice Abyss (Fig. 3), which is located on the right bank of the Bečva River, is the deepest abyss and the deepest lake in the Czech Republic, with a validated total depth of 473.5 m (Vysoká et al., 2019). The HA was formed by a hydrothermal hypogenic “bottom-up” karstification process. The abyss is filled with water mineralized by CO₂ (carbon dioxide) with a concentration of about 2.5 g L⁻¹ (acid) at a temperature between 22 and 24 °C. The theoretical base of the Devonian limestone probably also indicates the total depth of the Hranice Abyss, even though the total thickness of the limestone has never been verified in the Hranice Karst.

The HA consists of an open abyss and caves called the Rotunda (Fig. 3). The lake in the abyss has an area of approximately 511 m², while the area of the Rotunda is 272 m².

The Zbrašov Aragonite Caves are located at the massif on the left bank of the Bečva River at the Teplice spa. With a length of 1435 m, they are the largest cave system in the Hranice Karst. They were formed by hydrothermal karst processes and include a system of passages and domes, including six lakes that also contain warm acid water. Similarly, as in the HA, the water in the ZAC is mineralized by carbon dioxide with a concentration of about 2.5 g L⁻¹.

The caves at Kuče are a system of smaller domes and passages with a total length of 130 m. The caves have been gradually explored since 1950, when an exploratory audit was first performed in the Kuče quarry by the Czech Geological Survey, and they still have not been completely explored. There are several small karst lakes with a total area of about 220 m².

An important piece of information that came from the geological survey (Il Faut, 2022) is that mineral water rises into the lakes of the Zbrašov Aragonite Caves and the Hranice Abyss and emerges into the Teplice spa and the Bečva River at the spa, while the water in the Kuče Caves, the observation wells close to Černotín, and the limestone quarry (Fig. 2) has no mineralization.

2.4 Description of the dam concept

The idea of placing a dam on the Bečva River is quite old. The proposed location of the dam has changed several times due to the results of new surveys. In the latest version, the dam is planned to be built near the village of Skalička. The reservoir will be multipurpose: the water storage in the reservoir will be divided into permanent and flood control storage. Two basic concepts of the reservoir and dam layout have been studied (Fig. 2).

• First, a lateral reservoir situated on the left bank of the Bečva River was proposed. The main possible connection to the waters of the Hranice Karst is via the limestone outcrop in Kamenec.

• Second, a through-flow reservoir situated in the floodplain on both banks of the Bečva River was proposed. The main connections to the waters of the Hranice Karst are via the Kamenec outcrops and the Bečva River bend.

In case of the lateral reservoir, the lowest bottom of the reservoir would be at a level of 251.0 m a.s.l. (above sea level), and the storage water level would be at H_z=259.0 m a.s.l. As regards the through-flow reservoir, the reservoir bottom would be at 253.0 m a.s.l. and the storage water level at H_z=261.0 m a.s.l.

The design concept for the reservoir has been optimized for the attenuation of extreme floods exceeding the return period N=500 years to the level of a harmless flood in the Bečva River, which can hold Q=660 m³ s⁻¹ (20-year flood). The aim of the study is to evaluate the impact of the reservoir's operation on the water regime in the Hranice karst when the permanent effect of the reservoir can be expected. For this reason, a flow of 25 m³ s⁻¹ was chosen as the medium flow, along with a 20-year flood with a peak discharge of Q=660 m³ s⁻¹.

2.5 Available data

At the locality, the monitoring of water stages and discharges into the Bečva River has been carried out since 1960 in the gauging stations at the Teplice spa and at the Bečva River bend. Occasional monitoring of water levels was carried out in the lakes of the HA, ZAC, and KC during some months in the years 2005, 2020, and 2021. Unfortunately, the series are not complete and continuous, and some data are missing in some formations due to various reasons. The measurements from the Bečva River are complete and continuous. In the HA and ZAC, obtaining the measurements was quite difficult as the entrances to the caves and abyss are not public due to the high carbon dioxide concentration. Personnel must enter wearing a mask, and at least two people are required. Therefore, it was complicated to check the measuring device and data logger and to perform remedial works in case of permanent outage. The KC are private, and entry is possible only when accompanied by an owner.

The outflow discharge from the karst into the Bečva River at the Teplice spa was determined using a current meter, hydrometric propeller, an acoustic Doppler current profiler, and measurements of electric conductivity of water in the Bečva River at the spa (Il Faut, 2022).

The surface areas of the lakes in the caves are specified in Sect. 2.3.

3 Methods

3.1 Rationale

Various types of mathematical models can be applied to groundwater flow modelling in a karst system (Stevanovic, 2015; Hartmann et al., 2015; Kuniansky, 2016; Leins et al., 2023).

Due to the deep formation of the Hranice Karst being only poorly explored and the fact that there is practically no information about the configuration of karst channels, a modelling approach using a hypothetical pipe network that connects the caves, domes, and lakes via a system of channels was applied in this study.

The pipes represent a system of karst channels with “unknown” configurations, dimensions, and hydraulic characteristics, while the reservoirs represent karst landforms with a known free surface area (HA, ZAC, KC). A confined (pressure) flow regime was expected in the channels in the deep karst formations. To describe hydraulic behaviour of the deep karst formations, an aggregated flow resistance factor was introduced and calibrated for each channel of the pipe network using the monitoring data (see following sections).

Preliminary calculations have shown that due to temperature differences, the density of water in the Bečva River and in the boreholes of the Teplice spa may differ by up to about 0.08 %, and the effect of mineralization on the water density is about 0.05 %. Therefore, a constant water density of ρ=1000 kg m⁻³ was assumed during the modelling.

With water flow rates ranging from tens to single hundreds of litres per second, a turbulent flow regime with a Reynolds criterion exceeding Re>5000 can be expected in most karst channels. The flow will then proceed in a quadratic resistance region.

3.2 Topology of the Hranice Karst model

The network of karst channels was replaced by a system of interconnected pressure pipes and open “reservoirs”. The system of hypothetical pipes was developed based on the layout shown in Fig. 2 and on the schematic sketch of the functioning of the karst system (Fig. 4). The network diagram with the proposed interconnections of karst landforms is in Fig. 5. The water inlets to the system were localized at the limestone outcrops at Kamenec (node 1) and at the Bečva River bend (node 7), and the water outlet is represented by the Bečva River at the Teplice spa (node 6), where the springs of mineral water can be observed in the river.

Figure 4 The sketch with the conceptual model of a karst system.

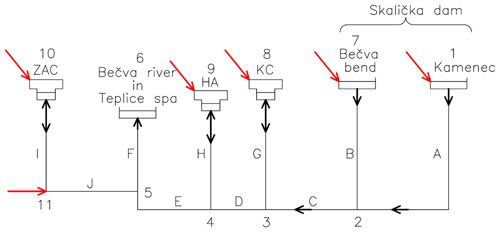
Figure 5 Diagram of the conceptual model: red arrows represent water inflows to the karst aquifer; black arrows represent flow directions in karst conduits.

Conduits A and B interconnect the sources of water (nodes 1 and 7) with the network of the deep karst channels (conduits C, D, E, F). The conduits connecting the Hranice Abyss (H) and caves at Kuče (G) are linked to these hypothetical deep channels. The most remote landform, the Zbrašov Aragonite Caves on the left bank of the Bečva River (node 10), is connected to the main branch adjacent to the Bečva River (conduits I and J).

During rainfall periods, the caves and abyss are supplied (next to the Bečva River) by surface runoff and subsurface sources. Node 11 represents water inflow coming from Malenik Hill. The runoff and surface inflow are also directed to nodes 8 (KC), 9 (HA), and 10 (ZAC). Their discharge was modelled using simple rainfall–runoff relations and was calibrated using the measurements taken in the HA, KC, and ZAC caves.

3.3 Mathematical model

The topological diagram in Fig. 5 is the basis for the hydraulic conceptual model of water flow in the network of karst channels and subsurface systems. While the reservoirs are relatively well-described, the deeper karst system is practically unrecognizable, as it probably reaches a depth of up to 1000 m b.g.l. (below ground level) or even more (Klanica et al., 2020). Therefore, its hydraulic function and characteristics are derived via backward analysis using the monitoring data.

The hydraulic state variables describing the problem are

• the piezometric (hydraulic) head h, representing the approximate energy level at relatively low flow velocities in karst channels, and

• water flow Q through the pipe system.

The relation between hydraulic head loss Δh_i and the discharge Q_i along conduit i comes from the Darcy–Weisbach equation (Streeter and Wylie, 1979; Munson et al., 1994):

$$\begin{array}{}\text{(1)}& \begin{array}{rl}\mathrm{\Delta }{h}_i& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}g}}\left[{\mathit{\alpha }}_{i\mathrm{1}}{\displaystyle \frac{\mathrm{1}}{S_{i\mathrm{1}}^{\mathrm{2}}}}-\mathit{\alpha }{\displaystyle \frac{\mathrm{1}}{S^{\mathrm{2}}}}-\sum {\mathit{\xi }}_{ik}{\displaystyle \frac{\mathrm{1}}{S_{ik}^{\mathrm{2}}}}-\sum {\mathit{\lambda }}_{ij}{\displaystyle \frac{L_{ij}}{D_{ij}}}{\displaystyle \frac{\mathrm{1}}{S_{ij}^{\mathrm{2}}}}\right]\\ & \cdot Q_i\cdot \left|Q_i\right|,\end{array}\end{array}$$

where Δh_i is the head loss along conduit i (between two adjacent nodes) of the “pipe network”, g is the acceleration due to gravity, α_i is the kinetic energy coefficient, ξ_ik is the coefficient of the kth form (local) loss along conduit i, λ_ij is the friction loss coefficient related to the jth sub-length L_ij of the conduit, D_ij is the corresponding diameter of the jth conduit fragment, and S_ij is the corresponding local cross-sectional area of the conduit fragment. Subscripts 1 and n refer to the first and last node in the system.

All loss characteristics in the brackets in Eq. (1) are unknown, therefore the coefficient κ_i aggregating all losses was introduced:

$$\begin{array}{}\text{(2)}& {\mathit{\kappa }}_i={\displaystyle \frac{\mathrm{1}}{\mathrm{2}g}}\left[{\mathit{\alpha }}_{i\mathrm{1}}{\displaystyle \frac{\mathrm{1}}{S_{i\mathrm{1}}^{\mathrm{2}}}}-\mathit{\alpha }{\displaystyle \frac{\mathrm{1}}{S^{\mathrm{2}}}}-\sum {\mathit{\xi }}_{ik}{\displaystyle \frac{\mathrm{1}}{S_{ik}^{\mathrm{2}}}}-\sum {\mathit{\lambda }}_{ij}{\displaystyle \frac{L_{ij}}{D_{ij}}}{\displaystyle \frac{\mathrm{1}}{S_{ij}^{\mathrm{2}}}}\right].\end{array}$$

κ_i expresses the aggregated flow resistance factor along conduit i and is a function of the length of the conduit, its tortuosity and roughness, and the size and shape of the flow cross-section.

When introducing Eq. (2) into Eq. (1), one obtains

$$\begin{array}{}\text{(3)}& \mathrm{\Delta }{h}_i={\mathit{\kappa }}_i\cdot Q_i\left|Q_i\right|.\end{array}$$

Equation (3) is the principal governing equation used in the numerical modelling of the flow regime in the system of conduits. The coefficients κ_i related to individual conduits were subject to calibration by the model.

Due to the relatively small velocity head (on the order of single decimetres), hydraulic loss Δh_i can be considered both pressure and energy head loss. Therefore, the piezometric head measured in boreholes and other features such as caves and abysses may be considered energy head expressed in metres above sea level (m a.s.l).

Free surface changes in the karst water bodies studied (HA, ZAC, KC) were determined from the relation

$$\begin{array}{}\text{(4)}& A\cdot {\displaystyle \frac{\mathrm{d}h}{\mathrm{d}t}}=\sum _{l=\mathrm{1}}^m{Q}_l,\end{array}$$

where A is the area of the water surface, Q_l is the inflow to (outflow from) the lake, m is the number of inflows and outflows (via karst conduit, surface runoff, etc.), and h is the water level (piezometric head).

The Dirichlet boundary condition (BC) at the boundary nodes of the flow domain holds that

$$\begin{array}{}\text{(5)}& h(f,t)=h_f\left(t\right),\end{array}$$

where h_f is the known time course of the piezometric (energy) head in the fth boundary node of the domain (the Bečva River, Skalička Dam reservoir). It was derived from the known time course of the level in the Bečva River in nodes 6 and 7 and in the Kamenec outcrop in the Skalička Reservoir according to the corresponding water level in the reservoir.

The Neumann boundary prescribes the outflow discharge in node 6 taken from the hydrometric measurements (Il Faut, 2022):

$$\begin{array}{}\text{(6)}& Q(\mathrm{6},t)=Q_{\mathrm{6}}\left(h\right(t\left)\right).\end{array}$$

The initial condition is represented by the known piezometric head at the beginning of the unsteady solution at time t=0 for individual scenarios (see Sect. 3.4). The values were taken from the steady-state solution for the selected period before the flood's arrival or before the eventual filling of the Skalička Reservoir:

$$\begin{array}{}\text{(7)}& h(i,t=\mathrm{0})=h_i.\end{array}$$

The numerical solution of Eq. (4) was performed using the finite difference scheme:

$$\begin{array}{}\text{(8)}& \mathrm{\Delta }h={\displaystyle \frac{\mathrm{\Delta }t}{A}}\sum _{j=\mathrm{1}}^m{Q}_j.\end{array}$$

The procedure was set up in an MS EXCEL spreadsheet. The built-in iterative procedure for finding the resistance coefficients in Eq. (3) was used to calibrate the steady-state model for the no-flood period. A trial-and-error approximation procedure was used to calibrate the model for selected flood scenarios. During the simulations of each variant, the solution of Eq. (8) was performed with the time step Δt=1 h.

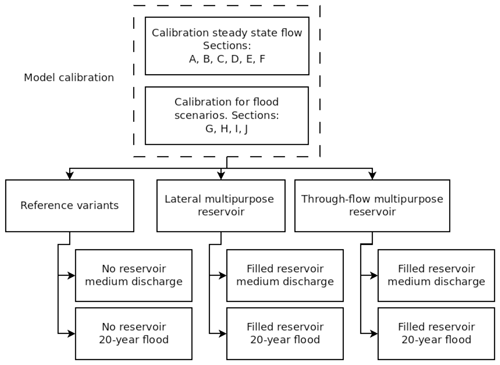
3.4 Scenarios and numerical analysis

The aim of the analysis was to evaluate the effect of the implementation of the two aforementioned variants of the Skalička Dam Reservoir on the regime of karstic waters, namely on the mineral water springs at the Teplice spa and water levels in the lakes in the ZAC. The water levels and discharges into the individual karst phenomena were analysed by comparing the present state represented by reference variants to selected scenarios of reservoir operation. Prior to the simulations, the model was calibrated using the measured water levels in the Bečva River and lakes in the HA, ZAC, and KC.

Present hydrological extreme floods in the Bečva River temporarily influence the groundwater regime in the area including the karst system. However, experience shows that a few weeks after the flood, the groundwater system returns to the pre-flood conditions. Therefore, the main concern is associated with a permanent increase in the water level in planned reservoir that is represented by the levels 259 m a.s.l. in the case of a lateral reservoir (variant III) and 261 m a.s.l. in the case of a through-flow variant (variant IV). For each reservoir variant two scenarios were investigated, namely the average discharge into the Bečva River, about 25 m³ s⁻¹ (III A, IV A), and during the theoretical flood with a return period of 20 years, with the discharge of about 660 m³ s⁻¹ (III B, IV B). For these scenarios the results were compared with corresponding reference variants (II A, II B).

The study consists of the following scenarios (see also Fig. 6).

Figure 6 The calculation flowchart.

I. Model calibration

Model calibration was carried out in order to derive resistance coefficients characterizing hydraulic losses along the individual conduits (Fig. 5). The calibration procedure consisted in the approximation of measured piezometric levels by the calculated values. The calibration was carried out in two steps.

• A.

  Long-term monitoring of the observation wells; in the Bečva River at the Teplice spa and in its bend; and in the HA, ZAC, and KC indicated steady water levels with no change over time during long dry spells. Therefore, during these periods, no water flow is expected in conduits G, H, I, and J. The calibration of the conduit consisting of conduits A, B, C, D, E, and F between nodes 1 and 6 was carried out under the assumption of steady-state flow during relatively small discharges into the Bečva River and a discharge of 118 L s⁻¹ of the mineral water into conduit F and into the Bečva River at the spa. It was found in practice (Il Faut, 2022) that this discharge does not change for various small water stages in the Bečva River, as the difference in water levels in the Bečva between the bend and spa does not change. At the same time no external inflows to the caves were observed during dry spells.

• B.

  The calibration was based on the monitoring of steady water stages at all monitoring points in the locality, i.e. the Bečva River and in the HA, ZAC and KC. The steady-state conditions correspond to the time period.

• C.

  To calibrate remaining conduits (G, H, I, and J interconnecting the lakes in the HA, ZAC, and KC), the results of the previous calibration step (steady state for dry spells) were used. The hydraulic characteristics of calibrated conduits G, H, I, and J were derived from the changes in water levels in the HA, ZAC, and KC during flood events in the Bečva River using Eqs. (3) and (4).

II. Reference variants

These variants represent the current state of the groundwater regime in the karst not affected by the planned Skalička Dam. These variants have been used as a reference to assess the potential impact of the Skalička Reservoir.

• A.

  A steady-state scenario representing a discharge of Q=25 m³ s⁻¹ into the Bečva River corresponding to its average discharge.

• B.

  An unsteady regime with a 20-year flood in the Bečva River with a peak discharge of 660 m³ s⁻¹. This scenario corresponds to a “harmless” discharge into the Bečva River. After this discharge is exceeded, the flood routing by the Skalička Reservoir starts, which is not the aim of the assessment (see explanation above).

III. Lateral multipurpose reservoir

The main concern relates to routine reservoir operation corresponding to the maintenance of permanent storage capacity at an elevation of 259 m a.s.l. The two scenarios for the operation of the reservoir correspond to the reference variants (II A, II B).

• A.

  The reservoir water level is 259 m a.s.l.; discharge is Q=25 m³ s⁻¹ into the Bečva River.

• B.

  The reservoir water level is 259 m a.s.l.; there is a 20-year flood with the peak discharge of Q₂₀=660 m³ s⁻¹ into the Bečva River.

IV. Through-flow multipurpose reservoir

The operational regime is the same as in scenario III. Permanent storage capacity is maintained at an elevation of 261 m a.s.l. Two scenarios corresponding to the reference variants were dealt with.

• A.

  The reservoir water level is 261 m a.s.l.; discharge is Q=25 m³ s⁻¹ into the Bečva River.

• B.

  The reservoir water level is 261 m a.s.l.; there is a 20-year flood with the peak discharge of Q₂₀=660 m³ s⁻¹ into the Bečva River.

4 Results and discussion

4.1 Calibration and verification

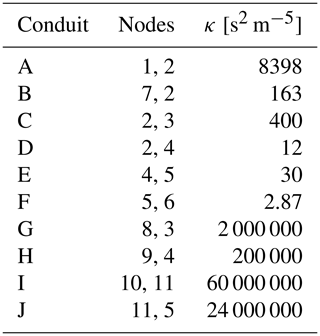
During the calibration, the resistance coefficients κ corresponding to all conduits of the topological scheme (Fig. 5) were derived.

First, the calibration of the proposed model was performed for the steady state (scenario I A) during the dry season in June and July 2019 when the discharge into the Bečva River was 4.5 m³ s⁻¹; the water levels in the Hranice Abyss and the Kuče Caves remained constant with zero inflow or outflow; and only the karst channels A, B, C, D, E, F, and J were functional. Here, based on the field tests made by Il Faut (2022), the flow through branch A was estimated at 20 L s⁻¹. Measured water stages in nodes and discharges along individual conduits according to Fig. 5 for the steady-state scenario of the model calibration are shown in Table 2.

Table 2 Discharges along individual conduits and water stages at nodes for the steady-state scenario for the model calibration.

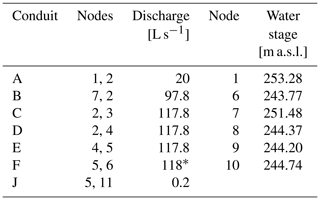
^* Measured value.

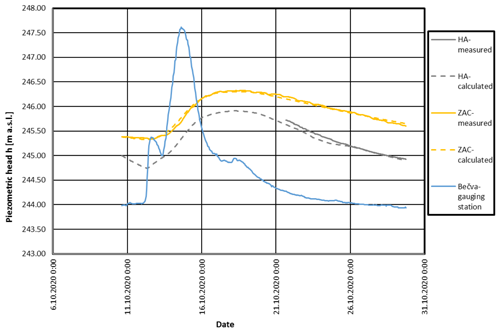
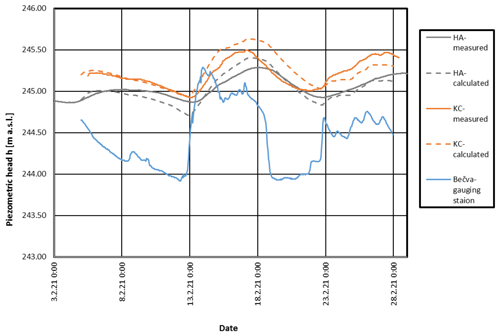
Secondly, the coefficients for side branches G, H, I, and J supplying water to the storage areas of the HA, ZAC, and KC were derived. At the same time, the amount of external water flowing during and after some rainfall episodes into the HA, ZAC, and KC was calculated using a simplified rainfall–runoff model. For the calibration, the observed unsteady rise and drawdown of water levels in the Bečva River were used as a boundary condition in Eq. (5). These resulted in changes in the water level in the reservoirs of the HA, ZAC, and KC, which were also subject to monitoring. Unfortunately, for available flood scenarios in the years 2005, 2020, and 2021, the data were not complete for the lakes monitored in the HA, ZAC, and KC. Therefore, one calibration and two verification scenarios were used to determine the aggregated roughness coefficients in conduits G, H, and I.

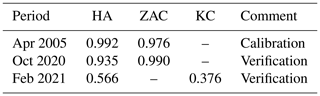
The verification of the calibrated hydraulic model was performed using two other flood scenarios in the Bečva River. The results of the calibration and verification of the unsteady model are shown in Figs. 7–9. The resulting calibrated values of coefficient κ_i are in Table 3.

Table 3 The resistance coefficients for the individual parts of the network.

Figure 7 Calibration for March–April 2005.

Figure 8 Verification for October 2020.

Figure 9 Verification for February 2021.

To quantify the efficiency of the model, the Nash–Sutcliffe efficiency was calculated (Nash and Sutcliffe, 1970):

$$\begin{array}{}\text{(9)}& \mathrm{NSE}=\mathrm{1}-{\displaystyle \frac{\sum _{t=\mathrm{1}}^T\left(H_{\mathrm{o}}^t-H_{\mathrm{m}}^t\right)}{\sum _{t=\mathrm{1}}^T\left(H_{\mathrm{o}}^t-{\stackrel{\mathrm{‾}}{H}}_{\mathrm{o}}\right)}},\end{array}$$

where NSE is the Nash–Sutcliffe efficiency coefficient, $H_{\mathrm{o}}^t$ is the observed water level, $H_{\mathrm{m}}^t$ is the modelled water level, and ${\stackrel{\mathrm{‾}}{H}}_{\mathrm{o}}$ is the mean of the observed water levels. The results are shown in Table 4.

Table 4 The Nash–Sutcliffe efficiency coefficients for the calibration and verification data.

From Table 3 it can be seen that individual karst conduits have significantly different resistance characteristics expressed by the coefficient κ. These differences can be attributed to the significantly and randomly different geometries of the karst channels (length, flow profile). In general, the branch channels G, H, I, and J supplying the caves and the abyss have significantly higher resistance, probably due to the overall smaller size of their cross-section (see discussion in the Sect. 4.4).

Table 4 and Figs. 7 and 8 show good agreement between the measured and modelled data for the HA and ZAC. For the KC, the agreement is rather worse (Fig. 9), which is mainly due to the caves being less well-explored, the extent of the lakes, and the lack of calibration data, as the measurements at the KC had only recently been carried out (in 2021), and the response at higher discharges was not measured for the purpose of this study due to complications with access to the caves, which are private. Therefore, despite the lower Nash–Sutcliffe coefficient at the KC, the model calibration can be considered to have been successful. Moreover, the impact of the Skalička Reservoir on the Kuče Caves is of less importance as there are no environmental conflicts and requirements related to the Kuče Caves.

4.2 Reference scenarios

For the reference scenarios the calibrated model was used.

Scenario II A corresponds to the no-flood period with a constant average discharge of 25 m³ s⁻¹ into the Bečva River.

The boundary conditions were as follows.

• The Bečva River gauging station at the spa – 244.24 m a.s.l.

• The Bečva River bend – 251.55 m a.s.l.

• Kamenec outcrop – 253.92 m a.s.l.

The resulting calculated water levels in the monitored objects are as follows.

• Hranice Abyss – 244.68 m a.s.l.

• Zbrašov Aragonite Caves – 245.24 m a.s.l.

• Kuče Caves – 244.84 m a.s.l.

The flow rate through outlet conduit F is Q=0.118 m³ s⁻¹.

Compared to the calibration scenario I A, the water level in the Bečva River in the reference scenario II A is rather higher due to higher discharge into the Bečva River. This results in a higher water level in monitored lakes, while the outflow discharge via conduit F practically does not change.

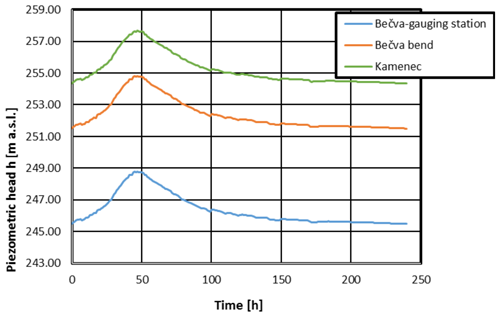
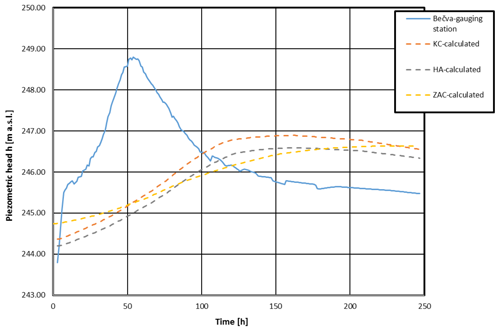
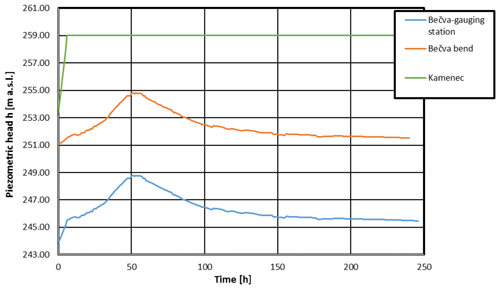
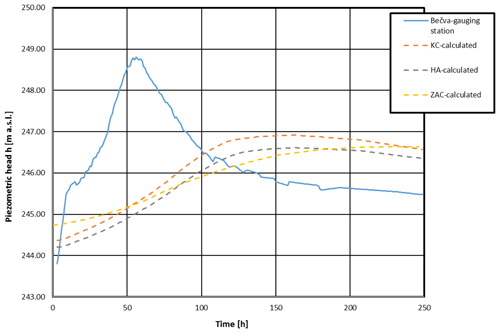
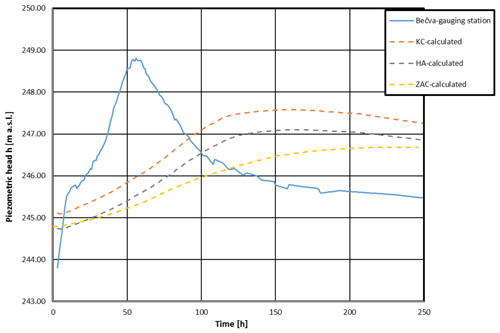
Scenario II B corresponds to a 20-year flood wave in the Bečva River unaffected by the Skalička Dam with a peak discharge of Q₂₀=660 m³ s⁻¹. The boundary conditions for this variant are in Fig. 10. The resulting maximum water levels in individual lakes are as follows (Fig. 11).

• Hranice Abyss – 246.59 m a.s.l.

• Zbrašov Aragonite Caves – 246.63 m a.s.l.

• Kuče Caves – 246.89 m a.s.l.

The flow rate through the principal conduit (emerging into the Bečva River at the Teplice spa) is between Q=0.099 m³ s⁻¹ and Q=0.107 m³ s⁻¹.

Figure 10 Boundary conditions for scenario II B.

Figure 11 Water levels in locations monitored for scenario II B.

4.3 Reservoir operation

In the case of a lateral multipurpose reservoir with the no-flood scenario (III A), the following boundary conditions were applied.

• The Bečva River gauging station at the spa – 244.24 m a.s.l.

• The Bečva River bend – 251.55 m a.s.l.

• Kamenec outcrop – 259.00 m a.s.l.

This scenario represents a steady-state situation with the discharge of 25 m³ s⁻¹ into the Bečva River and with a permanent reservoir water level (259.00 m a.s.l.), so only the Kamenec infiltration zone may be affected by the reservoir.

When the results of the steady-state simulation are compared with reference scenario II A (Table 5), it can be seen that only an insignificant permanent increase in the water level in the lakes of the HA, ZAC, and KC occurs. This is due to the drainage effect of the Bečva, both at the spa and partly in the river bend downstream of the dam. The flow in conduit F is Q=0.117 m³ s⁻¹ and represents only a minor increase of 1.7 % compared to the reference variant.

Table 5 Results for scenario III A.

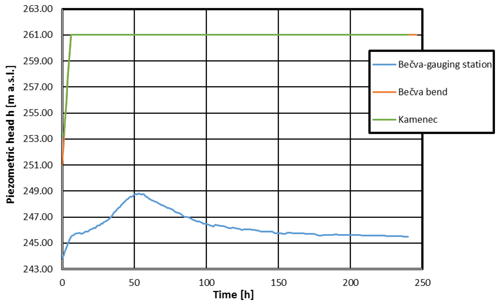
Scenario III B concerns a lateral multipurpose reservoir with a permanent reservoir water level of 259 m a.s.l. and a 20-year flood wave in the Bečva River passing along the dam outside the Skalička Reservoir. The boundary conditions applied to the Bečva River and the Kamenec outcrop inside the reservoir are shown in Fig. 12, and the resulting water levels in the HA, ZAC, and KC during the flood are shown in Fig. 13. The comparison with reference variant II B indicates that there is only a minor increase in the water level in the Hranice Karst and spa, amounting to a mere few centimetres. Similar to in scenario III A, this can be attributed to the drainage effect of the Bečva, both at the spa and partly in the river bend downstream of the dam. The results can be seen in Table 6: the discharge into conduit F is Q=0.100 to 0.109 m³ s⁻¹ and represents an increase of about 2 % when compared to the reference variant.

Figure 12 Boundary conditions for scenario III B.

Figure 13 Results for scenario III B.

Table 6 Results for scenario III B.

Scenario IV A concerns a through-flow multipurpose reservoir with a discharge of Q=25 m³ s⁻¹ into the Bečva River passing through the reservoir. The boundary conditions are as follows.

• The Bečva River gauging station at the spa – 244.24 m a.s.l.

• The Bečva River bend – 261.00 m a.s.l.

• Kamenec outcrop – 261.00 m a.s.l.

This scenario represents the steady-state situation with a discharge of 25 m³ s⁻¹ into the Bečva River and with a permanent reservoir water level (261.00 m a.s.l.) that affects both the Kamenec and Bečva River bend infiltration zones.

Comparison with reference variant II A shows a more significant increase in the water level in the HA and KC (Table 7), which is mainly due to the interconnection of the through-flow reservoir with the massive outcrops at the Bečva River bend at the lowest part of the reservoir, supported by the effect of the Kamenec outcrops also located inside the Skalička Reservoir. Only minor changes in the water level are expected in the ZAC due to the significant drainage effect of the Bečva River at the Teplice spa, whose water level strongly correlates with the water level in the lakes of the Zbrašov Aragonite Caves. The rise in the discharge into outflow conduit F is Q=0.172 m³ s⁻¹, which represents an increase of about 50 % when compared to reference variant II A. This increase in the outflow discharge may cause a certain degree of dilution of the mineral waters rising into the Bečva River and also into the wells withdrawing mineral water for the spa.

Table 7 Results for variant IV A.

In scenario IV B, when a 20-year flood wave in the Bečva passes through the reservoir, the inflow water will pass through a completely open outlet structure into the Bečva downstream of the reservoir. The boundary conditions are shown in Fig. 14.

Figure 14 Boundary conditions for variant IV B.

The simulation results can be seen in Fig. 15 and Table 8. The results show a higher increase in the water levels in the observed lakes in the HA and KC, on the order of decimetres (not exceeding 1 m) when compared to reference variant II B. Similarly to the previous scenario (IV A), negligible changes in the level are expected in the ZAC due to the significant drainage effect of the Bečva River at the Teplice spa. The flow rate in conduit F is Q=0.114 to 0.167 m³ s⁻¹, which is a rise of 15 % to 56 % compared with reference variant II B.

Table 8 Results for scenario IV B.

Figure 15 Results for scenario IV B.

4.3.1 Discussion

The model presented was used for the assessment of the effect of the permanent increase in water level in the Skalička reservoir in two variants. The model calibration was carried out using rather-incomplete monitoring data, namely due to complicated access into the HA, ZAC, and KC. Moreover, for the complete model calibration, monitoring during a flood situation in the Bečva River is necessary. Therefore, the model calibration and verification were carried out for three periods when a temporary increase in the Bečva River was identified, namely during March and April 2005, October 2020, and February 2021.

During the model calibration and verification, fairly good agreement of measured and calculated water levels in the HA and ZAC were obtained. In the case of the less-explored KC, the verification provided rather worse agreement, as in the KC only one data series measured in 2021 was available.

As can be seen from Table 3, the calibrated values of the coefficient of aggregated resistance vary over several orders of magnitude. Equation (2) indicates that the aggregated flow resistance factor depends on local (form) losses (i.e. changes in shape and direction of the flow); the length of canals and their tortuosity; diameters; micro and macro roughness; and the existence of subsurface caves, sediments, etc. Significant variability in the resistance coefficient indicates considerable changes in the shape, length, and other abovementioned factors. From Eq. (2) it can be seen that, for example, doubling the pipe diameter may result in increasing the coefficient by about 30 times, while a 5-fold increase in pipe diameter (which is not uncommon in karst channels) results in a coefficient increase by more than 3 orders of magnitude.

Time-dependent reference and simulation scenarios were solved with a time step of 1 h; the simulation period was 246 h. During this time, the maximum water level was reached at all landforms, namely the HA, ZAC, and KC.

5 Conclusion

In this paper, the nonlinear reservoir-pipe model was successfully applied to simulate conditions in the Hranice Karst with the aim of assessing the impact of the proposed Skalička Dam on the groundwater regime in local karstic formations, namely in the Zbrašov Aragonite Caves, in the Hranice Abyss, and on the mineral waters at the Teplice spa. The main concern is that the dam with permanent storage would have an impact on the natural conditions in the karst. Two variants of the reservoir layout were considered, namely a lateral and a through-flow reservoir.

Based on calibration and verification results, the applicability of the simplified hydraulic model is justified, especially if the knowledge about the deep karst formation is very poor. In contrary to pure regression models (Vysoká et al., 2019) the model proposed is physically based; pipe and reservoir hydraulics are incorporated into the solution.

The study indicated that the through-flow scheme would result in a permanent rise in the water levels in karst landforms such as the Hranice Abyss and Kuče Caves of about 0.7 to 1 m, and the discharge of rising mineral water would increase by more than 50 %. The lateral reservoir was found to have only a minor effect, with a rise in water levels of a few centimetres. With this proposal, the outflow discharge to the mineral springs would increase by only 2 %, which is considered to be negligible.

The results of the study provide valuable information for decision-makers and stakeholders involved in flood protection and water resource management in the Hranice Karst region. The conclusions given above result in the recommendation that the lateral reservoir be chosen for more-detailed future investigation and studies.

For further refinement of the model, an extensive hydrogeological survey is needed, and more extensive long-term parallel monitoring data should be provided for all karst phenomena in the area. The model indicated that additional places of surface water inflows to the karst system exist and should be systematically measured. These are inflows to the caves and the abyss.