Shallow-landslide stability evaluation in loess areas according to the Revised Infinite Slope Model: a case study of the 7.25 Tianshui sliding-flow landslide events of 2013 in the southwest of the Loess Plateau, China

The occurrence of shallow loess landslides induced by prolonged heavy rainfall is prevalent in loess-dominated regions, often leading to property damage, human casualties, and sediment pollution. Developing an accurate prediction model for shallow landslides in loess areas is crucial for effective landslide mitigation. In 2013, prolonged heavy rains from 19–25 July triggered mass sliding-flow loess landslides in Tianshui, China. Landslide data, along with the characteristics of the sliding-flow loess landslides, were obtained through extensive field investigations and remote sensing interpretations. The sliding-flow loess landslide event demonstrated clustering, high density, small areas, and long travel distance. The depth of the sliding surface is correlated with the saturated layer resulting from rainfall infiltration; it is typically less than 2 m deep and negatively correlated with slope steepness. Based on the common characteristics of shallow loess landslides, the mechanisms involved in the sliding-flow landslide are proposed. The Revised Infinite Slope Model (RISM) was introduced using an equal differential unit method to address deficiencies when the safety factor remains constant or increases with increasing slope greater than 40°, as calculated using the Taylor slope infinite model. The relationship between the critical depth and the slope of the shallow loess landslide was determined. The intensity–duration (I–D) prediction curve of the rainfall-induced shallow loess landslides for different slopes was constructed and combined with the characteristics of rainfall infiltration for use in forecasting regional shallow loess landslides. Additionally, the influence of loess strength on the shallow loess landslide stability was analyzed. The shallow loess landslide stability responds to slope and cohesion but is not sensitive to the internal friction angle.

1 Introduction

Loess is a porous and loose eolian deposit of silt-sized particles mainly formed during the Quaternary period, and it is widely distributed in Asia, Europe, North America, and South America (Li et al., 2019). In China, loess is widely distributed, with an area of 630 000 km², accounting for 6.63 % of the total land area in northwest, north, and northeast China. The loess deposit reaches a depth of up to 300 m, and the integrity and continuity of the loess layers are unparalleled globally (Liu, 1985). However, environments dominated by loess are exceptionally fragile, experiencing significant soil erosion, topographical variation, and concentrated rainfall, and they have now emerged as some of the most developed geohazard areas in China (Derbyshire, 2001; Zhang and Liu, 2010; Zhuang et al., 2018). Loess is a distinctive soil characterized by its large pores, high compressibility, strong collapsibility, and high-water sensitivity, making it prone to surface failure (Xu et al., 2014; Li et al., 2007; Peng et al., 2015; Juang et al., 2019; Zhuang et al., 2022). The primary factor contributing to loess failure is the interaction between water and loess, which can disrupt the loess structure and diminish its mechanical strength. In over 85 % of loess landslides, water plays a crucial role, exhibiting characteristics such as early small-scale deformation, long runout distance, unpredictable location distribution, rapid occurrence, and liquefaction. These factors lead to severe property damage and human casualties (Dijkstra et al., 1995; Wang et al., 2014; Zhuang et al., 2018; Zhu et al., 2022).

Rainfall-induced slope failures are a common form of shallow landslides in the Chinese Loess Plateau (CLP). Field investigations have revealed that more than 50 000 landslides have occurred in the CLP in recent decades (Zhuang et al., 2018; Zhuang et al., 2022). Most of those landslides were triggered by prolonged heavy rainfall and had a slip surface depth of no more than 2 m (Zhuang et al., 2017, 2018, 2022). Precipitation infiltrates into the soil and percolates through the loess to a depth of approximately 2 m, attributed to the decreased infiltration rate with increasing depth (Tu et al., 2009; Xu et al., 2011; Zhuang et al., 2018). Shallow loess landslide events, due to prolonged heavy rainfall, mostly occur as sliding-flow landslides, occurring in the north of Shaanxi Province in 2013 and 2017 and in Tianshui, Gansu Province, in 2013 and 2015 (Peng et al., 2015; Wang et al., 2015; Zhuang et al., 2017; Zhang et al., 2020). Another impact of these landslides is the significant transportation of sediment into local rivers, resulting in river pollution, elevated riverbeds, and heightened flood risks.

Numerous researchers have investigated rainfall infiltration, landslide mechanisms, and the prediction of rainfall-induced shallow landslides. Among these studies, the most prevalent focus is on forecasting shallow loess sliding-flow landslides caused by rainfall, as this knowledge can be utilized for geohazard mitigation (Brenning, 2005; Bordoni et al., 2015, 2020; Ahmadi-adli et al., 2017; Reichenbach et al., 2018; Thomas et al., 2018; Cogan and Gratchev, 2019; Berti et al., 2020). Shallow-landslide forecasting can be divided into four categories based on the prediction method. (1) The first category is early warning of landslides through monitoring time-based deformation data (von Ruette et al., 2011; Galve et al., 2015; Roccati et al., 2018; Segoni et al., 2018; Lombardo et al., 2020; Marino et al., 2020). The failure processes of most landslides advance through stages of deformation that gradually culminate in catastrophic failure. Throughout this progression, deformation is readily observable and can be monitored, making it the most critical factor for landslide prediction. This approach is particularly pertinent for large-scale landslides with evident early deformation trends. (2) The second category is forecasting landslides through temporal and spatial rainfall monitoring (Giannecchini, 2006; Salciarini et al., 2006; De Vita et al., 2012; Giannecchini et al., 2012; Cevasco et al., 2013; Stähli et al., 2015). Rainfall is a key inducing factor of geohazards, and researchers have studied the critical rainfall values for intensity, duration, and total rainfall within specific areas for predicting landslides. (3) The third category is the utilization of statistical and qualitative methods to assess landslide susceptibility; this, in connection with the occurrence of landslides, can enable the generation of maps delineating hazard zones. These maps are valuable for land use planning and long-term forecasting (Jia et al., 2008; Zizioli et al., 2013; Cevasco et al., 2014; Goetz et al., 2015; Guzzetti et al., 2006; Di Napoli et al., 2020, 2021; Keles and Nefeslioglu, 2021). However, it is important to note that statistical method results are largely dependent on the quality of data and the specific method employed. (4) The fourth category is landslide early warning and forecasting based on physical modeling (Montgomery and Dietrich, 1994; Montrasio and Valentino, 2007; Formetta et al., 2016; Schilirò et al., 2016; Lizarraga et al., 2017; Wang et al., 2020; Leonarduzzi et al., 2021). Researchers have concentrated their efforts on elucidating the mechanisms and conditions that contribute to soil failure. The data for analysis are derived from soil tests, providing evidence of the decay of cohesiveness and angles with precipitation infiltration (Skempton, 1985; Iverson, 2000; Baum et al., 2008; Baum and Godt, 2010; Medina et al., 2021), as well as quantitative landslide assessment. Several physically based models have been proposed, including steady-state hydrology (SHALSTAB and SINMAP) (Montgomery and Dietrich, 1994; Pack et al., 1999), quasi-steady hydrology (dSLAM, IDSSM) (Dhakal and Sidle, 2003), and transient hydrology (TRIGRS) (Iverson, 2000; Baum et al., 2008).

However, due to the occurrence of shallow loess landslides on saturated or nearly saturated steep slopes that transition into loess flow, models such as TRIGRS, which is based on an infinite slope model and is primarily designed for predicting shallow landslides in areas with gentle slopes, are challenging to apply in the CLP (Wang et al., 2015; Zhuang et al., 2017). The SINMAP and SHALAD prediction models are also based on infinite slope models, with the sliding or soil depths being fixed parameters associated with landforms (Montgomery and Dietrich, 1994; Pack et al., 1999; Michel et al., 2020). According to previous studies, shallow loess landslides with sliding-flow landslide characteristics are mainly induced by prolonged heavy rainfall and the sliding surface is the saturated or nearly saturated layer (Wang and Sassa, 2001; Zhang et al., 2013; Peng et al., 2015; Wang et al., 2015; Zhuang et al., 2017; Guo et al., 2019). Due to their small scale and difficult identification, shallow landslides on the CLP are a significant safety threat to local residential areas (Peng et al., 2015; Wang et al., 2015; Guo et al., 2019; Zhang et al., 2020). Given that the majority of shallow loess landslides occur within the upper 2 m and transition into high-speed, long-runout loess flows, the depth of the saturated layer plays a critical role in the study of loess sliding-flow landslides induced by prolonged heavy rainfall. However, there is currently no quantitative assessment for the critical slip depth, making it impossible to develop a rainfall criticality model based on physical processes.

The current study provides a comprehensive evaluation of the distinct characteristics of shallow loess sliding-flow landslides induced by prolonged precipitation. After adjusting for the constant or increasing safety factor with slopes greater than 40°, calculated using the Taylor slope infinite model through the equal differential unit method, we propose the Revised Infinite Slope Model (RISM). The objectives of this study were to determine the sliding depths of the saturated layer at different slopes and to consider rainfall intensity and duration for developing a shallow loess landslide prediction model using loess infiltration characteristics. The model was verified using the 7.25 Tianshui sliding-flow landslide events of 2013 in Tianshui, Gansu Province, a sliding-flow loess landslide triggered by prolonged precipitation.

2 Study area

2.1 Geological and geomorphological characteristics

The study area is a hilly loess region located southwest of the CLP and is part of the transition zone between the Qinling and the Longshan (Peng et al., 2015; Zhang et al., 2020). The loess is deeply and widely distributed with vertical joints and fissures, creating a fragile geological environment where geohazards such as landslides and debris flows frequently occur (Peng et al., 2015; Zhang et al., 2020; Qi et al., 2021). The terrain of the study area is generally high in the southeast and low in the northwest, with altitudes ranging from 748 to 2120 m and a relative height difference of 100 to 1430 m. This geomorphic unit includes the loess hill area comprised of platforms (Yuan in Chinese), ridges (Liang in Chinese), domes (Mao in Chinese), and valleys. The loess hill area is dissected by the Wei River and western Han River along with their tributaries and features numerous ravines (Fig. 1). The hilltops of the loess hills form nearly horizontal surfaces at an elevation ranging from 1900 to 2000 m, with a relative height difference between the ridges of approximately 500 m. The Wei River traverses the loess hilly area from west to east.

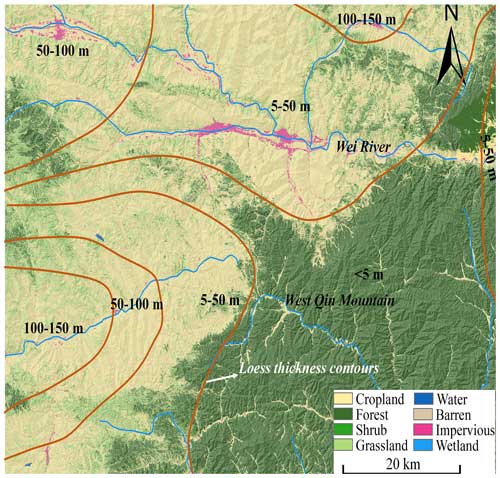
Figure 1 The geological and land use of the study area. Base DEM data are from https://geocloud.cgs.gov.cn/#/home (last access: 25 July 2024); land use data are from http://www.geodata.cn (last access: 25 July 2024).

The Tianshui region is located in the western part of the Qilyu–Helan mountain zigzag structural system and the Qinling zonal structural belt. The sub-northeast-trending structural belts and Longxi structural insertions, folds, and compressive faults are highly developed in this area. The neotectonic movement is strong, and the average annual elevation of the mountains is 0.6–8 mm. Additionally, the study area is located within the north–south and Tianshui–Lanzhou seismic belts, with frequent seismic activity (Sun et al., 2017).

2.2 Climate characteristics

The study area is located in a mid-latitude inland region and experiences a cold, temperate, semi-arid, continental monsoon climate with four distinct seasons, characterized by dry winters and springs (low precipitation) and hot and humid summers (high precipitation). The annual average temperature is 10.6 °C, while the annual precipitation ranges from 400 to 700 mm.

Elevation is the primary factor affecting the precipitation amount, with high precipitation in the high-altitude area and low precipitation in the low-altitude area. According to the precipitation data in recent decades (Peng et al., 2015; Zhang et al., 2020), the greatest precipitation occurred in 1967 with 772.2 mm and the least precipitation occurred in 1939 with 316.6 mm. There are also fluctuations in the annual rainfall distribution. Most rainfall is observed from June to September, representing 70 % of the annual precipitation (Peng et al., 2015; Zhang et al., 2020). In July 2013, long-duration and large-scale heavy rainfall resulted in severe flooding and geological disasters.

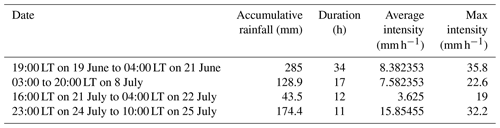
Beginning on 19 June 2013, prolonged heavy precipitation occurred in the Tianshui region. The total cumulative precipitation and the maximum rainfall intensity of this event represent a 100-year return period (Peng et al., 2015; Qi et al., 2021). This heavy-rainfall event lasted for 37 d and induced a mass sliding-flow landslide disaster. During this extreme-rainfall event, there were four heavy-rainfall stages, with different rainfall periods. The first heavy-rainfall period began on 19 June at 19:00 LT and ended on 21 June at 04:00 LT, with a cumulative rainfall of 285 mm. The second period was from 03:00 to 20:00 LT on 8 July (128.9 mm), and this was followed by the third period from 16:00 LT on 21 July to 04:00 LT on 22 July (43.5 mm). The last period was from 23:00 LT on 24 July to 10:00 LT on 25 July (174.4 mm) (Table 1). Over 45 000 shallow sliding-flow landslides were triggered, characterized by shallow and small scar areas and resulted in the deaths of 25 people.

Table 1 The precipitation data from the 7.25 Tianshui sliding-flow landslide events.

3 The 7.25 Tianshui sliding-flow landslide event characteristics

3.1 Landslide data

High-precision remote sensing imaging data (∼2 m resolution from Google Earth images) from October 2012 (before the sliding-flow landslide event) and December 2013 (after the sliding-flow landslide event), along with field observations, were used to determine that a total of 47 005 sliding-flow landslides occurred in the study area. It can be seen from Fig. 2 that the sliding-flow landslide distribution is primarily concentrated in the middle of the study area along the NNE direction and decreased gradually to the southeast and northwest.

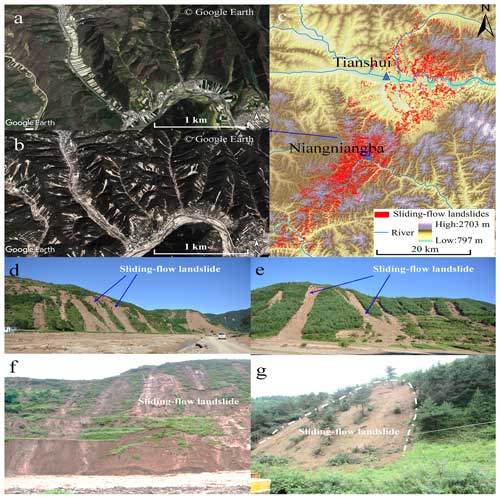
Figure 2 The landslides triggered by the 7.25 Tianshui sliding-flow landslide events (a: before the 7.25 Tianshui sliding-flow landslide events in October 2012 of Niangniangba, Tianshui; b: after the 7.25 Tianshui sliding-flow landslide events in December 2013 of Niangniangba, Tianshui; c: the landslide distribution triggered by the 7.25 Tianshui sliding-flow landslide events; d–g: typical sliding-flow landslides of the 7.25 Tianshui sliding-flow landslide events). Base DEM data from https://geocloud.cgs.gov.cn/#/home (last access: 25 July 2024).

The landslides occurred in the shallow loess layer at a depth of no more than 2 m and exhibited sliding-flow landslide characteristics as observed through extensive field investigations. Shallow landslides are typically triggered by prolonged heavy-rainfall events, leading to a rapid increase in pore pressure or loss of cohesion (Iverson, 2000; Wang and Sassa, 2001; Sassa and Wang, 2005; Tu et al., 2009; Zhang et al., 2013). Consequently, a failure surface develops within the soil profile or at the depth of precipitation infiltration. This indicates that the sliding soil layer is close to its liquid-limit water content when the landslide occurs, resulting in flowing characteristics after slope failure.

3.2 Size characteristics

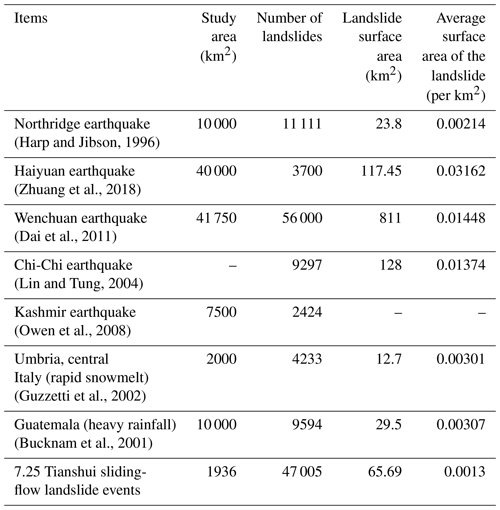
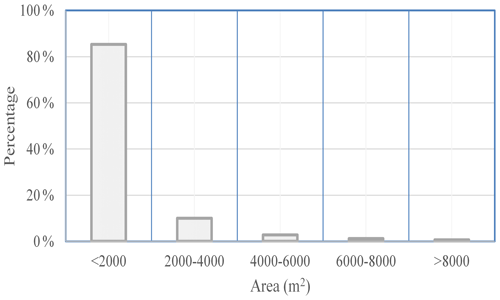
The sliding-flow landslide impacted area is 65.69 km², and the density is greater than 25 sliding-flow landslides per square kilometer. As shown in Fig. 2, the area of sliding-flow landslides in the town of Niangniangba of the Tianshui region accounts for more than 35 % of the total area, and shallow-flow slips occurred on most of the slopes. The mean sliding-flow landslide area was 0.0013 km², which is smaller than what is typical of landslides triggered by rainfall or earthquakes (Table 2). Figure 3 shows the proportion of landslides in different areas. It can be seen that most of the sliding-flow landslides were smaller than 2000 m² and accounted for more than 80 % of the total landslides. Landslides larger than 5000 m² accounted for only 3 % (Fig. 3), indicating that the 7.25 Tianshui sliding-flow landslide events were primarily small sliding-flow landslides occurring in groups.

Table 2 Landslide size and numbers triggered by earthquakes or rainfall in recent years.

Figure 3 The proportion of 7.25 Tianshui sliding-flow landslides in different areas.

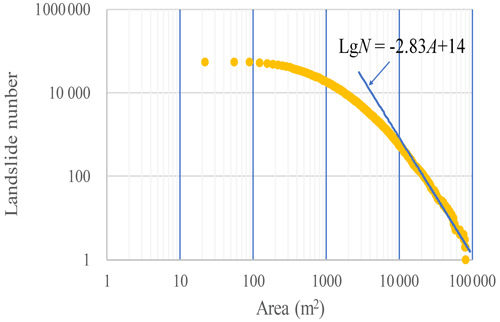
Figure 4 depicts the 7.25 Tianshui sliding-flow landslide area, cumulative frequency distribution, and statistical significance of sliding-flow landslides with an area of failure ≥ 5000 m², accounting for 90 % of the total landslides, and the largest landslide was only 0.099 km². We examined the area–frequency distribution of the 7.25 Tianshui sliding-flow landslide events via log-binning a normalized non-cumulative size–frequency distribution to plot frequency–density ($\log N=aA+b$, where N refers to the number of landslides in each bin) as a function of binned landslide area (A) (Fig. 4) (Stark and Hovius, 2001; Malamud et al., 2004). The higher value a may reflect a greater ability to identify smaller landslides via high-quality imagery. The value for the 7.25 Tianshui sliding-flow landslide events ($a=-\mathrm{2.83}$) is higher than the exponents reported for other coseismic inventories. For example, $a=-\mathrm{2.39}$ for Northridge, California; $a=-\mathrm{2.30}$ for Chi-Chi (alternately Jiji), Taiwan; $a=-\mathrm{2.19}$ for Wenchuan, China; and $a=-\mathrm{2.3}$ for the average of event-based and historical inventories reported by Van den Eeckhaut et al. (2007) (Roback et al., 2018), also showing that landslides triggered by the 7.25 Tianshui sliding-flow landslide events were primarily small landslides occurring in groups.

Figure 4 The cumulative frequency distribution of the 7.25 Tianshui sliding-flow landslide area.

3.3 Mobility characteristics

We examined the probability densities of equivalent friction coefficients (landslide vertical height (H) $/$ landslide travel distance (L)) for the 7.25 Tianshui sliding-flow landslide events using MATLAB (Fig. 5). The landslide vertical height (H) was based on the altitudes of the highest and the lowest points, and the movement distance was the distance between the highest point and the lowest point. The above two parameters were obtained and calculated using ArcGIS spatial analysis.

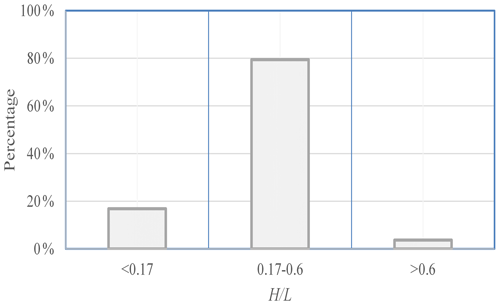
Figure 5 The probability densities of equivalent coefficients of friction of the 7.25 Tianshui sliding-flow landslides.

The $H/L$ ratio frequency ratio of the 7.25 Tianshui sliding-flow landslide events ranged from 0.01 to 0.88 with a mean of 0.32. According to a study by Wang (2000), landslide fluidization occurs when the equivalent friction coefficient is below 0.17. In our study, 16.85 % of the loess sliding-flow landslides had equivalent friction coefficients below 0.17, indicating that the loess sliding-flow landslides moved with flow motion and resulted in longer sliding distances. For more than 96.27 % of landslides, $H/L$ was less than 0.6 ($H/L<\mathrm{0.6}$ indicates a long-runout landslide).

To model the empirical relationship between sliding-flow landslide height and travel length, which was later verified using images and field investigations, the aforementioned datasets were utilized to generate a plot of H and L on a single graph (Fig. 6), where L (x axis) is the landslide travel distance and H (y axis) is the landslide height.

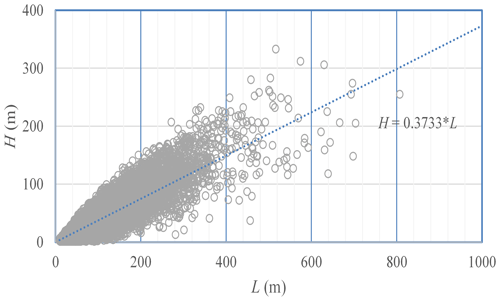
Figure 6 The relationship between the height differential and travel distance of the 7.25 Tianshui sliding-flow landslides.

The relationship between height difference and travel distance is positively correlated. With an increase in the height differential, the travel distance increases and the slope of the fitting trend line between the height difference and travel distance is 0.37, indicating that the travel distance is greater than the height difference and showing evident characteristics of a long runout travel distance.

3.4 Sliding depth characteristics

To obtain sliding-flow landslide depths, we conducted a detailed investigation of sites throughout the study area, such as the town of Niangniangba of the Tianshui region, and obtained depth data for 83 landslides based on the characteristics of the sliding-flow landslide and the thickness of the loess scar at the edge of the landslide. Figure 7 displays the distribution of sliding-flow landslide depths and area; no landslide had a depth greater than 2.0 m, and over 70 % ranged from 0 to 1 m (Fig. 7). Additionally, we found that the depth of the sliding-flow landslide had no correlation with the landslide area and had a negative correlation with the slope. With increasing slope, the depth of the landslide decreases; that is, the greater the slope, the shallower the sliding surface, and the smaller the slope, the greater the depth of the sliding surface.

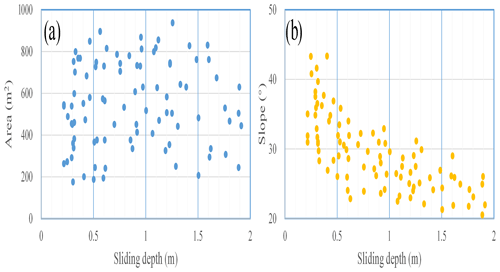
Figure 7 The distribution of sliding-flow landslide depths and the area of the 7.25 Tianshui sliding-flow landslides: (a) landslide surface area vs. sliding surface depth and (b) slope vs. sliding surface depth.

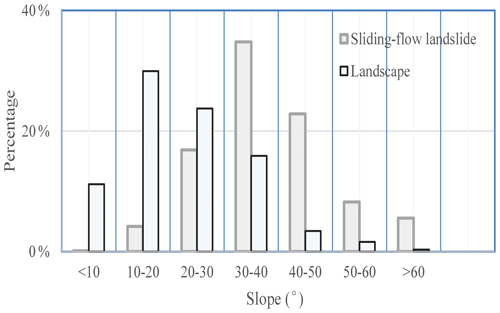
Meanwhile, the distribution of the slope and sliding-flow landslides in the study area was analyzed statistically. It was observed that the majority of sliding-flow landslides had a gradient value within the range of 30–50°, while landscape areas were concentrated in the range of 10–30°. Furthermore, sliding-flow landslides with slopes greater than 50° accounted for 13.81 % in the study area. Consequently, there is a higher probability of failure for sliding-flow landslides on steep slopes (50°) in the CLP (Fig. 8).

Figure 8 Map showing the relationship between the sliding-flow landslide, landscape, and slope.

3.5 The shallow sliding-flow landslide formation process

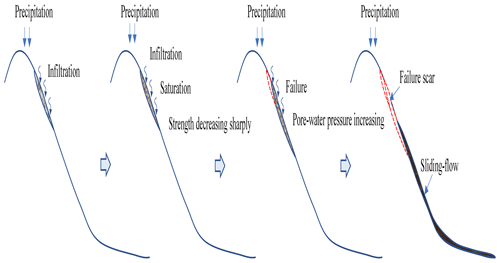
Force analysis shows that a slope will fail when the gravity component along the slope direction is greater than the shear strength of the soil (Sassa, 2000; Ochiai et al., 2004; Gabet and Mudd, 2006). If the stability coefficient of the slope is high and the soil reaches its liquid-limit water content before the failure, the slope will spontaneously liquefy and flow during the sliding process (Wang and Sassa, 2001; Wang et al., 2015). Usually, the ratio of pore-water pressure to the total normal stress of the soil is used to express the soil liquefaction ratio. When the liquefaction rate is 1, the pore-water pressure equals the normal stress of the soil and the failing slope is in a state of complete liquefaction (Hungr et al., 2001; Wang and Sassa, 2001; Sassa and Wang, 2005; Wang et al., 2015). Typically, the normal stress of shallow landslides is low and the slope deformation is attributed to decreased strength. The soil has an obvious volume reduction due to the large pore structure of the collapsing soil structure and is followed by a sharp increase in the pore-water pressure (Wang and Sassa, 2001; Sassa and Wang, 2005; Peng et al., 2018). Shallow sliding-flow landslides are triggered by prolonged heavy precipitation and rainfall infiltration to a certain loess depth (mostly 1–2 m) close to the liquid-limit water content, which is followed by a decrease in the soil strength (Tu et al., 2009; Xu et al., 2011; Zhuang et al., 2018). When the anti-slip force of the saturated soil is less than the sliding force, the saturated soil layer will fail. Due to the large pore structure of the soil, once soil deformation occurs, the water in the pores cannot be released, resulting in the pore-water pressure increasing sharply and causing liquefaction of the saturated soil to form a mudflow (Fig. 9).

Figure 9 The shallow sliding-flow landslide formation process.

4 Forecast model of shallow loess landslide development

4.1 Infinite slope model

According to field investigations and other research results, the shallow sliding-flow landslides are concentrated within 2 m of the surface and are negatively correlated with slope (Tu et al., 2009; Xu et al., 2011; Zhuang et al., 2017, 2018, 2022). Therefore, infinite slope models that take into account the soil layer thickness and maximum infiltration depth cannot be directly applied in shallow-landslide assessments. Previous studies have indicated that short-duration heavy precipitation has a lower impact on the stability of loess slopes, while prolonged heavy precipitation significantly increases water content and reduces slope stability (Wang and Sassa, 2001; Wang et al., 2015; Peng et al., 2018). Shallow-landslide transformation into mudflows occurs most often on slopes of 25 to 45°, and the sliding body is close to the liquid-limit water content before slope instability. Pore-water pressure is a key factor for soil slope failure (Iverson, 2000). Previous studies have demonstrated that pore-water pressure is the primary cause of soil landslides, and excess pore-water pressure serves as the triggering factor for fluidization (Iverson et al., 1997; Sassa and Wang, 2005; Gabet and Mudd, 2006). The failure of the sliding body is mainly attributed to a reduction in soil strength, leading to an increase in the sliding force exceeding cohesive forces following rainfall infiltration that saturates the soil (Wang et al., 2015; Peng et al., 2018).

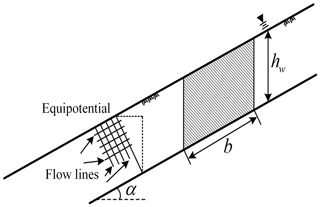
According to the infinite slope model (Fig. 10), Taylor proposed the following safety factor equation (Taylor, 1948):

$$\begin{array}{}\text{(1)}& K={\displaystyle \frac{\left({\mathit{\gamma }}_{\mathrm{sat}}-{\mathit{\gamma }}_{\mathrm{w}}\right)h_{\mathrm{w}}{\cos }^{\mathrm{2}}\mathit{\alpha }\tan {\mathit{\varphi }}^{\prime }+c^{\prime }}{{\mathit{\gamma }}_{\mathrm{sat}}{h}_{\mathrm{w}}\sin \mathit{\alpha }\cos \mathit{\alpha }}},\end{array}$$

where α is the slope angle, γ_w is the soil floating weight, γ_sat is the saturation weight of the soil, h_w is the depth of the sliding surface, c^′ (cohesive) is the approximate depth of loess at the liquid-limit water content due to infiltration, and ϕ^′ (internal friction angle) is the effective strength index of the soil at the sliding surface.

Figure 10 The cross-section of an infinite slope (modified from Taylor, 1948).

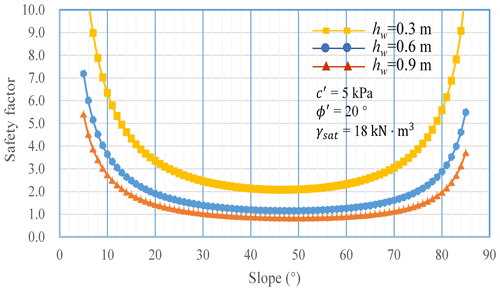
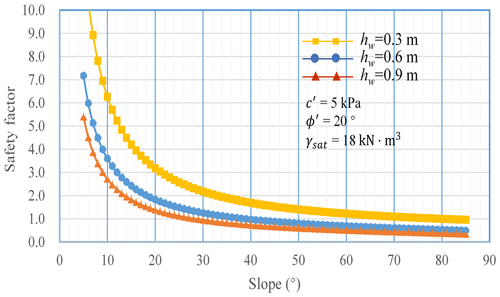
Using the mean strength of the saturated loess, the stability factor is calculated according to the infinite slope model proposed by Taylor (1948). The results are shown in Fig. 11.

Figure 11 The safety factor according to the infinite slope model proposed by Taylor (1948).

Figure 11 shows that for a cohesive soil slope, the safety factor decreases with increasing slope when the slope is less than 40°. There is little difference for slopes from 40 to 50°; however, the safety factor increases when the slope is greater than 50°. The calculated results exhibit discrepancies with the actual conditions, particularly regarding the aspect of the model indicating an increase in the safety factor with increasing slope. However, most shallow-landslide physical prediction models (e.g., TRIGRS, SINMAP, SHALAD) are based on Taylor's infinite slope model. As a result, these models cannot be effectively applied to areas with high slopes (>40°), limiting their widespread applicability (Montgomery and Dietrich, 1994; Baum et al., 2008; Zhuang et al., 2017).

4.2 The Revised Infinite Slope Model

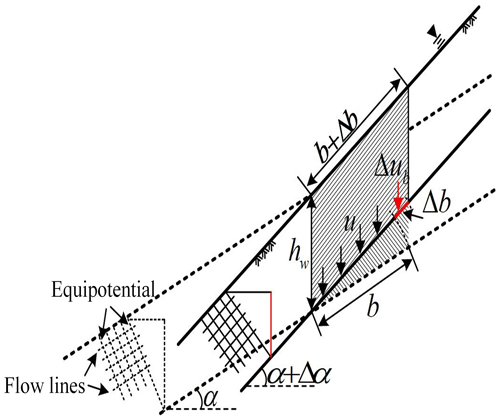
To ensure the consistency of Taylor's infinite slope model calculation results with actual conditions, this study has made modifications to the model using an equal differential unit method. As depicted in Fig. 12, by maintaining a constant depth of the saturation zone as the slope increases, the formula for calculating the self-weight of the soil strip unit has been revised as follows:

$$\begin{array}{}\text{(2)}& W={\mathit{\gamma }}_{\mathrm{sat}}{h}_{\mathrm{w}}(b+\mathrm{\Delta }b)\cos (\mathit{\alpha }+\mathrm{\Delta }\mathit{\alpha }),\end{array}$$

where b is the length of the sliding body and Δα is the value of the increasing slope.

Figure 12 An infinite slope model with variation in the slope.

In Eq. (2), the self-weight of the soil strip unit and the control condition of the soil strip area are unchanged:

$$\begin{array}{}\text{(3)}& h_{\mathrm{w}}(b+\mathrm{\Delta }b)\cos (\mathit{\alpha }+\mathrm{\Delta }\mathit{\alpha })=h_{\mathrm{w}}b\cos \mathit{\alpha }.\end{array}$$

Equation (2) shows that, although the change in slope does not affect the self-weight of the differential element, it leads to a change in the bottom area of the element, which causes the cohesion strength and pore-water pressure of the bottom surface of the soil strip element to change. The change in slope only influences the component values of forces in normal and tangential directions on the sliding surface. Therefore, when evaluating slope stability with different slopes, it is essential to account for changes in cohesion strength and pore-water pressure caused by an increase in slope Δα.

The change in cohesive strength (ΔC) and pore-water pressure (Δu_b) resulting from increasing the slope of Δα are described as

$$\begin{array}{}\text{(4)}& {\displaystyle }& {\displaystyle }\mathrm{\Delta }C=c^{\prime }\mathrm{\Delta }b,\text{(5)}& {\displaystyle }& {\displaystyle }\mathrm{\Delta }{u}_b={\mathit{\gamma }}_{\mathrm{w}}{h}_{\mathrm{w}}\mathrm{\Delta }b{\cos }^{\mathrm{2}}(\mathit{\alpha }+\mathrm{\Delta }\mathit{\alpha }).\end{array}$$

The effective normal stress (N^′) and effective anti-sliding force (T_f) at the bottom of the soil strip element due to the slope increasing from α to α+Δα are expressed as

$$\begin{array}{}\text{(6)}& {\displaystyle }\begin{array}{rl}{N}^{\prime }& ={\mathit{\gamma }}_{\mathrm{sat}}{h}_{\mathrm{w}}(b+\mathrm{\Delta }b){\cos }^{\mathrm{2}}(\mathit{\alpha }+\mathrm{\Delta }\mathit{\alpha })\\ & -{\mathit{\gamma }}_{\mathrm{w}}{h}_{\mathrm{w}}(b+\mathrm{\Delta }b){\cos }^{\mathrm{2}}(\mathit{\alpha }+\mathrm{\Delta }\mathit{\alpha }),\end{array}\text{(7)}& {\displaystyle }\begin{array}{rl}{T}_{\mathrm{f}}& =\left[{\mathit{\gamma }}_{\mathrm{sat}}{h}_{\mathrm{w}}(b+\mathrm{\Delta }b){\cos }^{\mathrm{2}}(\mathit{\alpha }+\mathrm{\Delta }\mathit{\alpha })\right.\\ & \left.-{\mathit{\gamma }}_{\mathrm{w}}{h}_{\mathrm{w}}(b+\mathrm{\Delta }b){\cos }^{\mathrm{2}}(\mathit{\alpha }+\mathrm{\Delta }\mathit{\alpha })\right]\tan {\mathit{\varphi }}^{\prime }+c^{\prime }(b+\mathrm{\Delta }b).\end{array}\end{array}$$

The sliding force of the soil strip unit is changed to

$$\begin{array}{}\text{(8)}& S={\mathit{\gamma }}_{\mathrm{sat}}{h}_{\mathrm{w}}(b+\mathrm{\Delta }b)\cos (\mathit{\alpha }+\mathrm{\Delta }\mathit{\alpha })\sin (\mathit{\alpha }+\mathrm{\Delta }\mathit{\alpha }).\end{array}$$

The revised effective anti-slip force according to Eqs. (4), (5), and (7) is

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{T}_{\mathrm{f}}& =\left[{\mathit{\gamma }}_{\mathrm{sat}}{h}_{\mathrm{w}}(b+\mathrm{\Delta }b){\cos }^{\mathrm{2}}(\mathit{\alpha }+\mathrm{\Delta }\mathit{\alpha })\right.\\ & \left.-{\mathit{\gamma }}_{\mathrm{w}}{h}_{\mathrm{w}}b{\cos }^{\mathrm{2}}(\mathit{\alpha }+\mathrm{\Delta }\mathit{\alpha })\right]\tan {\mathit{\varphi }}^{\prime }+c^{\prime }b.\end{array}\end{array}$$

Combining Eqs. (8) and (9), the safety factor can be obtained:

$$\begin{array}{}\text{(10)}& \begin{array}{rl}& K=\\ & {\displaystyle \frac{\left[{\mathit{\gamma }}_{\mathrm{sat}}\cos \mathit{\alpha }-{\mathit{\gamma }}_{\mathrm{w}}\cos (\mathit{\alpha }+\mathrm{\Delta }\mathit{\alpha })\right]h_{\mathrm{w}}\cos (\mathit{\alpha }+\mathrm{\Delta }\mathit{\alpha })\tan {\mathit{\varphi }}^{\prime }+c^{\prime }}{{\mathit{\gamma }}_{\mathrm{sat}}{h}_{\mathrm{w}}\cos \mathit{\alpha }\sin (\mathit{\alpha }+\mathrm{\Delta }\mathit{\alpha })}}.\end{array}\end{array}$$

Making α=α₁, $\mathit{\alpha }+\mathrm{\Delta }\mathit{\alpha }={\mathit{\alpha }}_{\mathrm{2}}$, and $({\mathit{\alpha }}_{\mathrm{1}},{\mathit{\alpha }}_{\mathrm{2}})\in \mathit{\alpha }$, Eq. (10) can be expressed as

$$\begin{array}{}\text{(11)}& K={\displaystyle \frac{\left({\mathit{\gamma }}_{\mathrm{sat}}-{\mathit{\gamma }}_{\mathrm{w}}{m}_{\mathit{\alpha }}\right)h_{\mathrm{w}}\cos {\mathit{\alpha }}_{\mathrm{2}}\tan {\mathit{\varphi }}^{\prime }+c^{\prime }\sec {\mathit{\alpha }}_{\mathrm{1}}}{{\mathit{\gamma }}_{\mathrm{sat}}{h}_{\mathrm{w}}\sin {\mathit{\alpha }}_{\mathrm{2}}}}.\end{array}$$

Making $m_{\mathit{\alpha }}=\frac{\cos {\mathit{\alpha }}_{\mathrm{2}}}{\cos {\mathit{\alpha }}_{\mathrm{1}}}$, for a simple equation, the term c^′secα₁ in Eq. (11) can be defined as the reference cohesion strength. Since the value of c^′secα₁ varies monotonically with α₁ changing, to make the reference cohesion strength corresponding to any slope angle equal, it only needs to satisfy the condition that α₁ is less than or equal to α₂:

$$\begin{array}{}\text{(12)}& {\mathit{\alpha }}_{\mathrm{1}}=\min \left\{{\mathit{\alpha }}_{\mathrm{2}}\right\}{\mathit{\alpha }}_{\mathrm{2}}\in \mathit{\alpha }.\end{array}$$

Therefore, the safety factor of the RISM can be expressed as

$$\begin{array}{}\text{(13)}& K={\displaystyle \frac{\left({\mathit{\gamma }}_{\mathrm{sat}}-{\mathit{\gamma }}_{\mathrm{w}}\cos \mathit{\alpha }\right)h_{\mathrm{w}}\cos \mathit{\alpha }\tan {\mathit{\varphi }}^{\prime }+c^{\prime }}{{\mathit{\gamma }}_{\mathrm{sat}}{h}_{\mathrm{w}}\sin \mathit{\alpha }}}.\end{array}$$

Using the mean strength of saturated loess in the loess area, the stability is calculated according to the RISM proposed by this study, and the results are shown in Fig. 13. According to the equal differential unit method, the RISM corrects the safety factor, which increases with the slope increasing when the slope is larger than 50° (calculated using the Taylor slope infinite model). The results obtained by the RISM maintain consistency with the calculation results of the Taylor method at low angles, and the calculated results decrease with an increased slope when the slope is larger than 40°.

Figure 13 The safety factor according to the RISM.

4.3 Critical depth of shallow loess landslides

When the stability coefficient K is 1 in Eq. (13), the critical depth of loess close to liquid-limit water content or the sliding surface of the shallow loess landslide can be obtained:

$$\begin{array}{}\text{(14)}& h_{\mathrm{cr}}={\displaystyle \frac{c^{\prime }}{{\mathit{\gamma }}_{\mathrm{sat}}\sin \mathit{\alpha }-\left({\mathit{\gamma }}_{\mathrm{sat}}-{\mathit{\gamma }}_{\mathrm{w}}\cos \mathit{\alpha }\right)\cos \mathit{\alpha }\tan {\mathit{\varphi }}^{\prime }}}.\end{array}$$

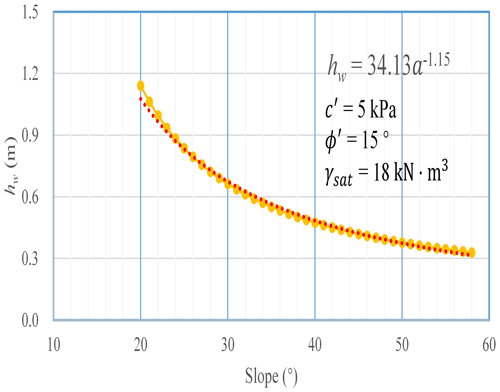
The critical depth of the liquid-limit water content or the sliding surface of the shallow loess landslide for different slopes can be determined by obtaining the soil strength of the nearly saturated state. Upon reaching the critical depth of the liquid-limit water content, the layer will experience failure. The cohesion and angle of internal friction were tested using the triaxial test method at saturation following the soil test standard GBT50123-1999. According to the loess test results, the cohesive forces of undisturbed loess at the liquid-limit water content (0–2 m) range from 3 to 9 kPa with an average of 5 kPa, and the internal friction angle ranges from 11 to 21° with an average of 15° (Fig. 14). Therefore, the relationship between the critical approximate depth of the liquid-limit water content and the slope can be calculated. With increasing slope, the critical approximate liquid-limit water content layer gradually decreases, but the rate of decrease slows, from 1.14 m at 20° to 0.47 m at 40° (Fig. 14). This relationship can be expressed via the power law as

$$\begin{array}{}\text{(15)}& h_{\mathrm{w}}=\mathrm{34.13}{a}^{-\mathrm{1.15}}.\end{array}$$

Figure 14 The relationship between the critical depth and the slope.

4.4 The I–D curve of the loess shallow landslide

The critical rainfall intensity–duration (I–D) method is often used in forecasting rainfall-induced shallow landslides (Guzzetti et al., 2007, 2008; Baum and Godt, 2010; Zhuang et al., 2015). Thresholds empirically derived from rainfall intensity–duration have been widely used to identify rainfall conditions that result in the occurrence of landslides (Guzzetti et al., 2007, 2008; Baum and Godt, 2010). Inspection of the I–D thresholds reveals the following general form:

$$\begin{array}{}\text{(16)}& I=\mathit{\beta }{D}^b+c,\end{array}$$

where I is the mean rainfall intensity; D is rainfall duration; and c, β, and b are other parameters. For the majority of I–D thresholds, c=0, and Eq. (16) takes the form of a simple power law.

$$\begin{array}{}\text{(17)}& I=\mathit{\beta }{D}^b\end{array}$$

Previous studies have created statistical I–D curves based on landslide data and rainfall data. However, these empirical models require many years of precipitation data and calibration parameters. Even so, the determination of the landslide threshold I–D curve is inaccurate due to the uncertainty in rainfall monitoring, such as the location and quantity of monitoring sites and the definition of the start and end time of rainfall events (Zhuang et al., 2015; Guo et al., 2016).

The critical I–D curve for slope instability for different slopes can be constructed using the model of the critical approximate depth of the liquid-limit water content combined with the saturated infiltration characteristics of loess in the study area. Six infiltration tests were carried out in the study area using the single-ring infiltration test to determine the infiltration coefficient (i) of loess under rainfall. The constant infiltration rates were 38.6, 33.1, 39.1, 32.2, 36.2, and 31.6 mm h⁻¹. Additionally, it was observed that the time between initial infiltration and stable infiltration is less than 10 min. Therefore, in this study, the average stable infiltration rate of 36.0 mm h⁻¹ was selected as the infiltration coefficient.

$$\begin{array}{}\text{(18)}& {\displaystyle }\begin{array}{rl}D=& h_{\mathrm{w}}/i\mathrm{for}\mathrm{when}\mathrm{the}\mathrm{precipitation}\mathrm{intensity}\mathrm{is}\\ & \mathrm{higher}\mathrm{than}\mathrm{the}\mathrm{infiltration}\mathrm{coefficient}(\mathrm{Eq}.\mathrm{7}).\end{array}\text{(19)}& {\displaystyle }\begin{array}{rl}D=& h_{\mathrm{w}}/I\mathrm{for}\mathrm{when}\mathrm{the}\mathrm{precipitation}\mathrm{intensity}\mathrm{is}\\ & \mathrm{lower}\mathrm{than}\mathrm{the}\mathrm{infiltration}\mathrm{coefficient}(\mathrm{Eq}.\mathrm{8}).\end{array}\end{array}$$

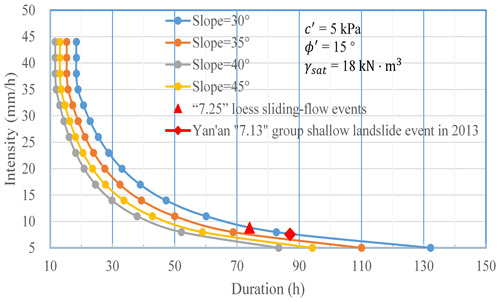
To model the relationship between I and D, the two variables were plotted on a single graph, where D (x axis) is the rainfall duration and I (y axis) is the rainfall intensity. According to the critical sliding surface depth with different slopes (Eq. 14), curves I and D with different slopes can be calculated using Eqs. (7)–(9). The I–D curve of the different slopes in the area can be obtained based on the infiltration coefficient and the sliding depth (Fig. 15).

Figure 15 The I–D curve of the different slopes in the loess area.

5 Discussion

5.1 Model comparison

Upon comparing the I–D curves for different slopes with existing models, it was observed that the I–D curves derived from the physical model in this study exhibit higher values compared to other statistical and probabilistic models. Additionally, while the I–D curves for other regions are obtained through statistical methods, any individual landslide occurrence within this area is considered a separate event. Meanwhile, many researchers have pointed out that antecedent rainfall plays a significant role in triggering landslides in loess areas, which is different for other regions, such as Hong Kong SAR, fire-impacted areas in the USA, and the southwest mountains in China (Cui et al., 2008; Zhuang et al., 2015). Therefore, the I–D curves of other areas will be lower than the I–D curve constructed based on physical models (Fig. 16).

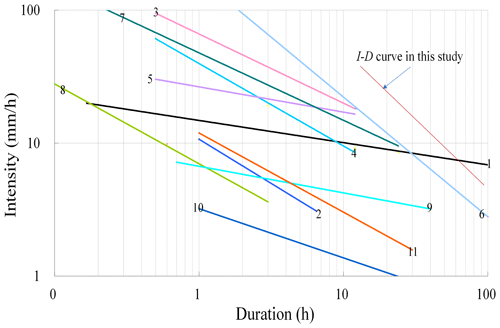
Figure 16 Comparison of I–D curves from the current study and prior studies (no. 1: Caine, 1980; no. 2: Wieczorek, 1987; nos. 3, 4, 5: Jibson, 1989; no. 6: Guadagno, 1991; no. 7: Paronuzzi et al., 1998; no. 8: Crosta and Frattini, 2001; no. 9: Shieh et al., 2009; no. 10: Guo et al., 2013; no. 11: Zhuang et al., 2015).

From the distribution of shallow landslides in this area, it can be seen that these landslides mainly occur on slopes of 35 to 50°. Marking the rainfall duration and intensity of the 7.25 Tianshui sliding-flow landslide events and the “7.13”-group shallow landslide in Yan'an in 2013 (Wang et al., 2015; Zhuang et al., 2017) on the I–D line, it can be seen that the rainfall duration and intensity of both events are above the I–D curve of 35° (Fig. 15), indicating that the constructed curve is reliable and can be used to forecast shallow landslides in this area.

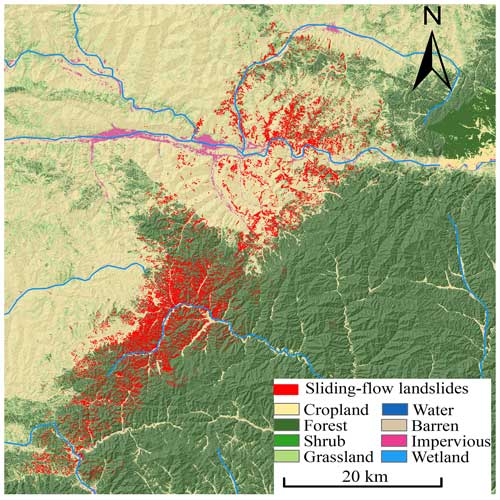
Figure 17 The 7.25 Tianshui sliding-flow landslides and land use in the study area (base DEM data from https://geocloud.cgs.gov.cn/#/home, last access: 25 July 2024; land use data from http://www.geodata.cn, last access: 25 July 2024).

Figure 18 The safety factor varies with the internal friction angle, cohesion change, and slope.

5.2 Model limitations

Previous studies have assumed that restoration of vegetation is beneficial for preventing landslides, mainly because of the reinforcement effect of roots on soil (Waldron, 1977; Roering et al., 2003). However, the inhibitory effect of vegetation on landslides is gradually being questioned due to research on the negative relationship between vegetation and landslides in recent mass landslides in loess and other well-vegetated areas. For example, the “9.16” mass shallow landslides in Changning, Yunnan, in 2014; the Yan'an “7.13” mass shallow-landslide event; the 2015 Tianshui mass shallow-landslide event; and the 2010 Nanping mass shallow-landslide event in Fujian Province all had mass shallow landslides induced by prolonged heavy precipitation, often occurring in well-vegetated areas (Fig. 17; Wang et al., 2015; Peng et al., 2015; Zhuang et al., 2017, 2020). Due to the complexity of the influence of vegetation on slope stability, most studies have not clarified whether the vegetation induces or inhibits landslides (Rickli and Graf, 2009; Preti, 2013; Zhuang et al., 2022). In general, plant roots can reinforce the slope soil and improve the shear strength of the soil (Waldron, 1977; Roering et al., 2003). However, the increase in vegetation can also result in greater stored precipitation and infiltration into the soil (Wang et al., 2015; Zhuang et al., 2017, 2022). Plant root systems also provide channels for preferential flow, resulting in higher soil water content, which promotes the occurrence of shallow landslides (Zhuang et al., 2017, 2022). The vegetation on the CLP is often shrubs with shallow root systems that do not exceed the sliding surface. Since most shallow landslides slide along the bottom of the root system, according to field investigations, they do not prevent these landslides (Wang et al., 2015). Slopes with good vegetation coverage increase the weight of the sliding body during precipitation. The prediction model proposed in this study does not consider the impact of vegetation on shallow landslides. According to data from monitoring numerous loess areas, increased restoration of vegetation results in more rainwater infiltrating into the loess, increasing the water content of the shallow loess, and results in an increased possibility of shallow landslides (Xu et al., 2024). There is not only downward vertical infiltration but also horizontal infiltration along the slope direction in the process of rainfall infiltration on the slope surface, resulting in the confluence of water in the slope body (Wang et al., 2015; Zhuang et al., 2022).

At the same time, according to the assumption of the infinite slope model, the model is mainly applicable to when the slope extent is much larger than the depth of potential slip surface, the slope angle is not too large, and soil characteristics are homogeneous along the slope direction, which means that the infinite slope model is only suitable for the prediction of homogeneous soil slope instability due to rainfall (Taylor, 1948). For slopes constituted of binary structures, analysis of slope failure controlled by the strength of the structure of the rock–soil mass is often not able to produce a correct factor of safety for the slope. Therefore, the RISM is also suitable for homogeneous soil slopes, and slope extent is undefined or much larger than the depth of the potential slip surface but can be applied to steeper slopes in the CLP.

5.3 Sensitivity analysis

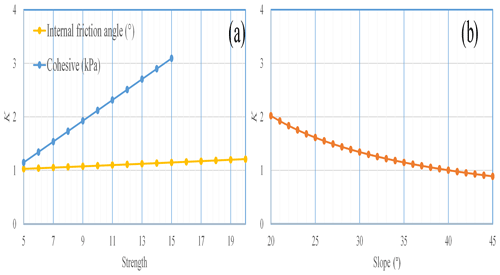
Dry loess has high cohesive strength but loses strength significantly when wetted (Derbyshire et al., 2001; Zhuang et al., 2018), and it has water-sensitive characteristics, with the strength parameters changing rapidly with the water content increasing. According to existing research, the cohesion of loess can be reduced from greater than 50 kPa at low water content to less than 10 kPa at high water content (Zhuang et al., 2018). The internal friction angle of loess varies slightly, generally from about 25° in low water content to about 16° in a saturated state. To assess the loess strength influence on shallow loess landslides caused by prolonged heavy precipitation, the response of the slope stability to the strength change in saturated loess was calculated. Our results demonstrate that slope stability is greatly affected by cohesion, while the stability of the slope is less responsive to changes in the internal friction angle. Meanwhile, by changing the slope and fixing loess strength, the relationship between the safety factor and slope was obtained. The safety factor varies obviously with slope change, indicating that the cohesion and slope are key factors affecting soil stability and shallow landslides, whereas the internal friction angle has a minimal effect on shallow landslides in loess areas (Fig. 18).

6 Conclusions

A rainfall-induced slope failure is a common cause of shallow landslides in the CLP. This study examines the shallow loess landslide triggered by prolonged heavy rainfall on 25 July 2013, in Tianshui, China, as a case study. The following results were obtained:

1. The 7.25 Tianshui sliding-flow landslide event triggered 47 005 landslides with a total area of 65.69 km², and the mean landslide area was 0.0013 km², which is smaller than most landslides triggered by other rainfall or earthquakes. Most of the landslides evaluated (80 %) are smaller than 2000 m², and landslides larger than 5000 m² accounted for only 3 %, indicating that the 7.25 Tianshui sliding-flow landslide events are primarily small landslides with group occurrence characteristics.

2. The $H/L$ ratio frequency ratio of the 7.25 Tianshui sliding-flow landslide event ranged from 0.01 to 0.88 with a mean of 0.32. The equivalent coefficient of friction was below 0.17 for 16.85 % of the loess landslides, indicating that loess landslides travel via flow motion and resulting in longer sliding distances.

3. The Revised Infinite Slope Model (RISM) was proposed using an equal differential unit method that corrects for any deficiencies associated with increased safety factors on slopes that are invariable or increasing when the slope is greater than 40° according to the Taylor slope infinite model.

4. The depth of the critical approximate liquid-limit water content (also the sliding surface depth) of the shallow loess landslides with different slopes can be described as $h_{\mathrm{w}}=\mathrm{34.13}{a}^{-\mathrm{1.15}}$. The critical I–D curve for slope instability for different slopes was constructed using the infiltration characteristics of loess in the study area.