the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The 2021 La Palma volcanic eruption and its impact on ionospheric scintillation as measured from GNSS reference stations, GNSS-R and GNSS-RO
Badr-Eddine Boudriki Semlali
Guillermo González-Casado
Hyuk Park
Adriano Camps
Ionospheric disturbances induced by seismic activity have been studied in recent years by many authors, showing an impact both before and after the occurrence of earthquakes. In this study, the ionospheric scintillation produced by the 2021 La Palma volcano eruption is analyzed. The Cumbre Vieja volcano was active from 19 September to 13 December 2021, and many earthquakes of magnitude 3–4 were recorded, with some of them reaching magnitude 5. Three methods, GNSS reference monitoring, GNSS reflectometry (GNSS-R) from NASA CYGNSS, and GNSS radio occultation (GNSS-RO) from COSMIC and Spire constellations, are used to compare and evaluate their sensitivity as proxies of earthquakes associated with the volcanic eruption. To compare the seismic activity with ionospheric scintillation, seismic energy release, and 95th percentile of the intensity scintillation parameter (S4), measurements have been computed at 6 h intervals for the whole duration of the volcanic eruption. GNSS-RO has shown the best correlation between earthquake energy and S4, with values up to 0.09 when the perturbations occur around 18 h after the seismic activity. GNSS reference monitoring station data also show some correlation 18 h and 7–8 d after. As expected, GNSS-R is the one that shows the smallest correlation, as the ionospheric signatures get masked by the signature of the surface where the reflection is taking place. Additionally, the three methods show a smaller correlation during the week before earthquakes. Given the small magnitude of the seismic activity, the correlation is barely detectable in this situation, and thus would be difficult to use in any application to find earthquake proxies.
- Article
(10546 KB) - Full-text XML
- BibTeX
- EndNote
Ionospheric disturbances such as scintillation constitute a notable problem for satellite communications, global navigation satellite systems (GNSS), and Earth observation systems, notably at the P- and L-bands. They can disturb the signals, making it difficult or even impossible to transmit the correct information through the ionosphere. Nevertheless, they can also be seen as an opportunity to detect, measure, or infer other physical phenomena, not necessarily related to the ionosphere itself. For example, in the last decades, several studies have shown that ionospheric disturbances can occur during solar eclipses (Das et al., 2022) and geomagnetic storms (Ding et al., 2007; Li et al., 2008), which are due to causes external to the Earth, coming from the Sun or space weather.
Recent evidence shows that the ionosphere may also be impacted by other “internal” geophysical events. There are studies relating severe atmospheric phenomena such as cyclones or hurricanes to ionospheric anomalies (Kamogawa, 2006; Camps et al., 2018; Xu et al., 2019). Anomalous variations in the total electron content (TEC) and peaks in the ionospheric scintillation have been detected during the passage of a large cyclone or hurricane, generating gravity waves that are coupled with the lower ionosphere, leading to ionospheric disturbances.
Another source of perturbations in the ionosphere is related to the seismic activity within the lithosphere, as supported by many recently published studies (Liu et al., 2004; Pulinets, 2004; Kamogawa, 2006; Pulinets and Davidenko, 2014; Pulinets et al., 2021; Molina et al., 2021, 2022). The physical mechanisms behind this interaction are still not very clear but there are several research paths open. Some of them explain this interaction by the generation of low-frequency electromagnetic signals from underground rock under massive pressure during the earthquake preparation period. Other authors explain the interaction by changes in the surface electric potential due to the piezoelectric effect in the underlying rocks, which can induce changes in the ionosphere's TEC.
This study looks for ionospheric anomalies related to the seismic activity generated by a recent volcano eruption on La Palma (Canary Islands, Spain). Past studies have analyzed the impact of volcanic eruptions on the ionosphere (De Ragone et al., 2004; Shults et al., 2016; Astafyeva, 2019; Yong-Qiang et al., 2006). For example, the submarine eruption in Tonga on 12 January 2022 created traveling ionospheric disturbances (TIDs) from the eruption site (Themens et al., 2022). The Tonga eruption was so strong that the gravity waves generated within the atmosphere traveled to the ionosphere and then propagated concentrically all around the globe producing these perturbations. While the 2021 La Palma eruption was less explosive than the Tonga eruption, it occurred over a longer period and had significant seismic activity leading up to and over the duration of the event.
The September 2021 Cumbre Vieja volcanic eruption on La Palma (Spain)
La Palma is a volcanic island located in the northwest of the Canary Islands (Spain) in the Atlantic Ocean, ∼ 500 km from the coast of Africa. The island has relatively low volcanic activity, with only three eruptions in the last century and seven in the last 500 years. Even with infrequent eruptions, La Palma is one of the archipelago islands facing the highest potential risks (Fernández et al., 2021).
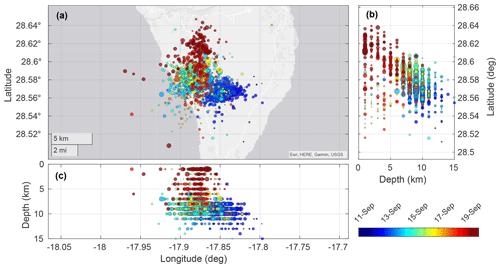
Figure 1Series of earthquakes from 11 to 19 September preceding the volcanic eruption, with position (a), depth (b, c), and date (in the color bar) indicated.
The most recent eruption started at 13:43 UTC on 19 September 2021, near the former Cumbre Vieja volcano, and it lasted for 85 d until 13 December 2021, when it was declared finished. Starting on 11 September, for 8 d preceding the eruption, a series of earthquakes were registered in the region where the eruption took place. Around 6000 earthquakes occurred during this time frame, with magnitudes ranging from 1 to 3.8 mbLg (mbLg is the magnitude unit used by the Instituto Geográfico Nacional (IGN) to characterize earthquakes on the island, and it is equivalent to the local Richter magnitude at a distance of 100 km). In this period, the epicenters migrated north, approaching the eruptive cone location, at the same time as the hypocenter depths rose starting from 15 km below the surface to near-surface depths. The evolution of the locations and depths of this precursory earthquake swarm is shown in Fig. 1.
For 10 d following the start of the eruption, while lava, gases, and ashes were being expelled from the volcano, seismic activity was relatively low. At the beginning of October, around 15 d after the start of the eruption, seismic activity increased again and remained stable until the end of the eruption, which was declared on 13 December.
This study is focused on the simultaneous analysis of several sources of data measuring the ionospheric scintillation with GNSS signals and correlating them with the seismic activity related to the eruptive event on La Palma in 2021.
Global navigation satellite systems (GNSS) are systems that can provide precise geolocation on the Earth by using the electromagnetic signal received from several satellites at a point. Current GNSS networks are the US GPS, Russian GLONASS, European Galileo, and Chinese BeiDou. To ensure global coverage, they are composed of a satellite constellation of 18 to 30 medium Earth orbit (MEO) satellites, with orbital periods of about 12 h. In recent decades, the signal from these satellites has proved to be very useful in remote sensing of the Earth and in studying properties such as soil moisture (Rodriguez-Alvarez et al., 2009), sea ice thickness (Munoz-Martin et al., 2020), and wave height and roughness (Wang et al., 2022).
GNSS signals are also handy for studying the ionosphere. As these signals pass through the ionosphere, they undergo effects like bending, delay, and absorption. These effects help us learn about ionospheric properties, such as TEC and ionospheric scintillation (Shanmugam et al., 2012; Camps et al., 2018; Angling et al., 2021). In this study, we have used three methods to measure ionospheric scintillation using GNSS signals. All these methods rely on the fact that disturbances in the ionosphere's electron density affect how GNSS signals propagate, especially in their frequency bands.
Ionospheric scintillation refers to the rapid fluctuations in the phase and/or intensity of the electromagnetic signal received after crossing the ionosphere. The study will be centered only on the intensity, also called “amplitude scintillation”. It is usually measured as the normalized standard deviation of the intensity of a radio electromagnetic signal after crossing the ionosphere, and it is computed with Eq. 1:
where I is the signal intensity and 〈⋯〉 represents the average of a certain period, usually on the order of tens of seconds.
The three GNSS-related techniques used to measure ionospheric amplitude scintillation are (1) static ground-based GNSS reference monitoring, (2) GNSS-R (GNSS reflectometry), and (3) GNSS-RO (GNSS radio occultation). The novelty and interest of this work come from the analysis of the effects that the same physical phenomenon, a volcanic eruption, produces in the ionosphere, as observed by three different techniques measuring the same magnitude at the same frequency.
2.1 Ground station data
Ground-based GNSS stations continuously monitor the signals emitted by GNSS satellites, providing valuable TEC and scintillation data used to make ionospheric corrections for navigation and to assess the quality of the service.
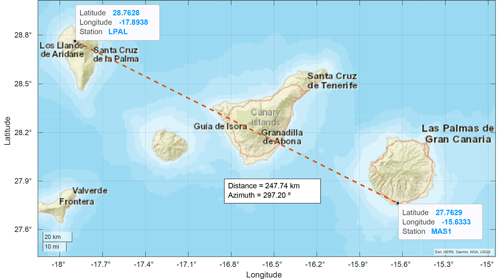
Figure 2Relative position of LPAL (on La Palma, top left) and MAS1 (Maspalomas, bottom right) ground stations. Map source: Esri, HERE, Garmin, NGA, USGS.
One disadvantage of this technique is the sparse spatial coverage compared to other satellite-based techniques. GNSS stations are typically sparsely installed at fixed ground locations, only providing data for the local region. Fortunately for this study, there are two ground stations close to the volcano. One station (LPAL) is located on the same island as the volcano (La Palma) and the second one is in Maspalomas (MAS1), a town in the south of Gran Canaria Island, which is around 250 km southeast of the volcano. Figure 2 shows a map displaying the two ground stations.
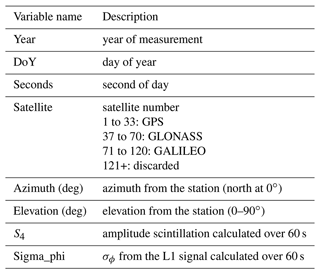
The GNSS monitoring ground station data contain the measurements for every minute of all the GNSS satellites in view for each station (Juan et al., 2018; Rovira-Garcia et al., 2020). The database has been pre-processed using the algorithms described in Juan et al. (2017), which includes the variables listed in Table 1, as follows.
The S4 data here are obtained by using Eq. 1, averaging over a period of 1 min, and using the direct intensity received in ground stations from the GNSS satellites in view. A clear trend between the elevation angle and the measured scintillation has been observed. The smaller the elevation angle, the larger the S4, which can be attributed to the longer path within the ionosphere of the lower-elevation rays, which may suffer from stronger scintillation and multipath propagation. This behavior is displayed in Fig. 3. Therefore, data with an elevation lower than 30∘ have been discarded.
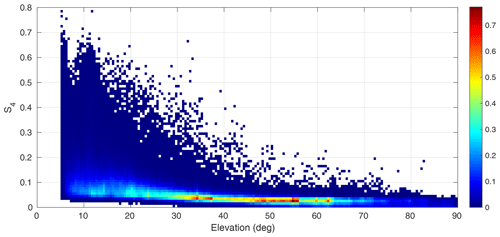
Figure 3Histogram of S4 values with respect to the elevation angle for La Palma ground station data.
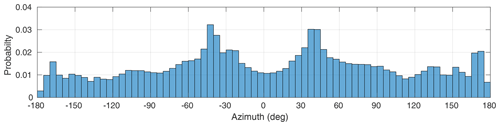
Also, the dependence on azimuth has been studied. A certain dependence of the number of measurements vs. the azimuth has also been found. As shown in Fig. 4, the most probable azimuths for receiving GNSS signals at the LPAL station are +45 and −45∘.
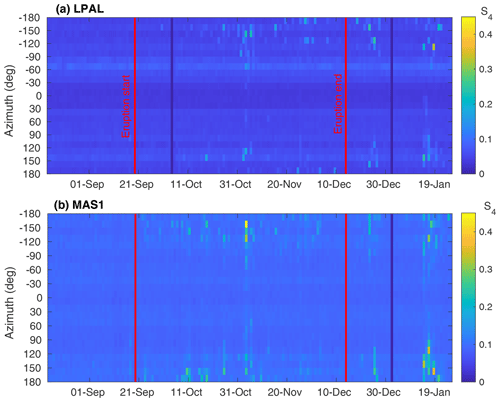
Figure 5 shows the 95th percentile of S4 values as a function of time and azimuth, and it can be seen that the largest values are obtained, for both stations, mostly when the GNSS satellites are located southwards, near 180∘ azimuth.
2.2 GNSS-R data
GNSS reflectometry has also proven to be a good way to detect ionospheric scintillation over calm oceanic regions (Molina and Camps, 2020). The open-access NASA CYGNSS GNSS-R constellation, which started providing science data in March 2017, was utilized for this study. The CYGNSS orbit inclination is around 35∘, so the coverage is from 40∘ S to 40∘ N, which includes the latitude of the islands (28.5∘ N).
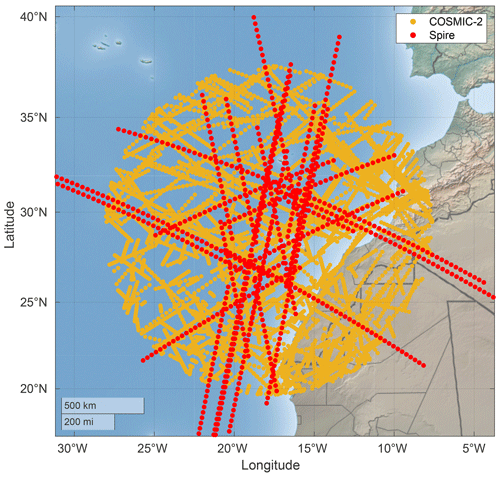
The eight satellites comprising the CYGNSS constellation are continuously tracking with up to four GPS satellites in view and taking measurements at a sample rate of 2 Hz, providing good data availability for the region close to La Palma. Over the full 139 d eruptive period, about 65 000 points were recorded within a radius of 50 km around the island.
The location of each point corresponds to the specular reflection point of each trajectory between the GPS satellite and the CYGNSS receiver, as shown in Fig. 6. The signals' path crosses the ionosphere twice because the height of the CYGNSS satellites is around 520 km, which is above the typical height of the ionosphere's maximum density (∼ 350 km). The receiver GNSS-R instrument cannot determine if the scintillation was generated in the ascending or descending paths or a combination of both; therefore, we have used the specular reflection point to tag the scintillation measurements.
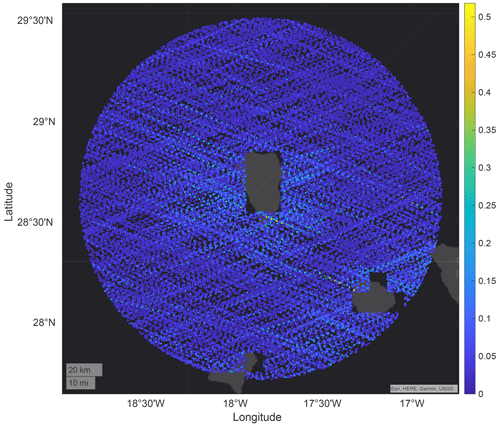
Figure 6Position of CYGNSS GNSS-R specular reflection points inside a circle of 100 km around La Palma Island for the whole period studied, indicating the S4 in colors. Map source: Esri, HERE, Garmin, USGS.
GNSS-R data have been processed following the methodology detailed in Molina and Camps (2020), taking the moving average and standard deviation of the signal-to-noise ratio (SNR) for a 10 s window and computing the S4 index with Eq. 1, in which I has been computed from the SNR of the Delay Doppler Map (DDM) of the CYGNSS product.
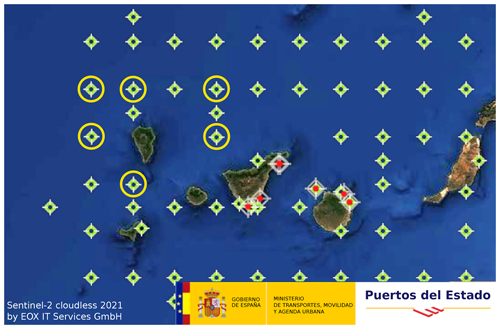
Figure 7Set of SIMAR model points around the island, indicating the ones selected to extract the SWH around La Palma. Dataset downloaded from Puertos del Estado (2022) website. Map source: Sentinel-2 cloudless 2021 by EOX IT Services GmbH.
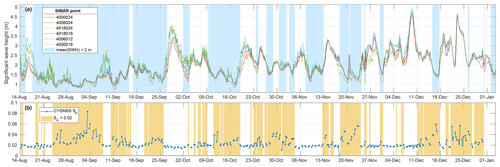
Figure 8The SWH from six SIMAR model points every hour around La Palma (a) compared to the estimated S4 from CYGNSS GNSS-R data (b). Light blue shaded areas mark the periods with an average SWH less than 2 m and the yellow areas mark the intervals in which the S4 is larger than 0.02, showing that most of the S4 peaks typically appear when the SWH is low.
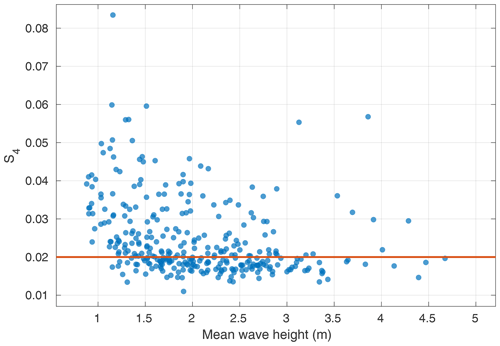
As the performance of the GNSS-R technique to estimate the scintillation is affected by the sea surface roughness, another filter has been applied. A wavy water surface destroys the signal coherence, making it impossible to infer the scintillation suffered along the path. Using data from maritime buoys around the islands, the model SIMAR detailed in Puertos del Estado (2020) documentation extrapolates the wave height in a grid of points along the ocean. Figure 7 shows the position of these points around La Palma Island and the ones selected to estimate the wave height during the eruptive period. The wave height extracted from them is compared to the detected scintillation from CYGNSS in Fig. 8. It can be observed that the high values of scintillation can appear only when sea roughness is small, as indicated by the color-shaded areas. For example, the peaks around 4 September appear during a period of waves lower than 1.5 m. Similar behavior is observed around 25 September, 16 October, and 2 November.
Figure 9 shows the comparison between the significant wave height (SWH) in the horizontal axis vs. the detected value of S4, confirming what was observed in the timeline in Fig. 8. In this correlation, we can define a noise floor at 0.02 to remove all the values that are prone to be affected by the sea surface roughness. In the study, we compare the results of the two cases: when using all data without filtering and when using only S4 values above 0.02.
2.3 GNSS-RO data
The GNSS radio occultation method is another way to retrieve information about the ionosphere using GNSS signals. In this case, the signal emitted by the GNSS satellites is received by the receiver onboard a LEO satellite when they are setting under or rising above the horizon. The use of this technique has the advantage of not being affected by ground reflection disturbances as in GNSS-R. For the same reason, land and oceanic regions can be studied indistinctly.
For this study, Spire and open-access data from COSMIC-2 (UCAR/NCAR, 2019) have been used. Spire Global (Jales et al., 2020; Irisov et al., 2018) operates a constellation of more than 80 3U CubeSats that can perform GNSS-RO, and more recently GNSS-R. From Spire, measurements from around 58 000 GNSS-RO occultations in the region around La Palma Island from 15 August to 31 October 2019 have been used.
Cosmic data include all the occultations of GPS satellites as seen from the constellation of COSMIC-2 LEO satellites. COSMIC-2, also known as FORMOSAT-7, is a constellation of six LEO mini-satellites (300 kg) that were launched on 25 June 2019 into a 24∘ inclination orbit. The Level 1b podTc2 dataset contains the information used in this study, which is detailed in Table 2.
With these data, the tangent point (i.e., the point in the trajectory which is closer to the Earth) can be computed from the GPS and LEO satellite positions. For each of these points, the corresponding S4 value has been computed, and their coordinates will be used later to filter according to the distance from the volcano. Given that the occultations have been recorded over long periods, including high elevation angles (almost 90∘ in some cases), a method is proposed to filter the data points that correspond to the rays traversing the ionosphere.
Using the slant TEC (STEC) value during the occultation, we can assume that the maximum value coincides with the path in which the ray crosses its longest path in the ionosphere, as shown in Fig. 10. Selecting the points that have a STEC larger than 80 % of the maximum TEC in each occultation leaves the points that are inside the ionosphere, which are more likely to suffer from scintillation, as shown in Fig. 11.
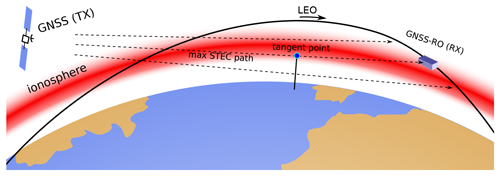
Figure 10Schematic of the GNSS-RO technique used to measure the ionosphere, indicating the location of the tangent point in the path with maximum STEC value.
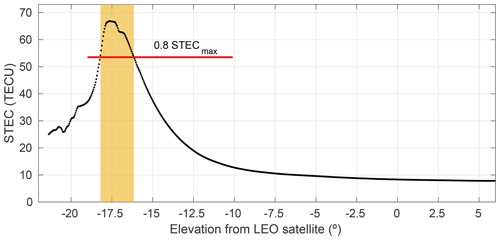
Figure 11STEC variation during a GNSS occultation as a function of the elevation angles seen from a COSMIC-2 satellite on 19 September 2021.
Figure 12 shows the location of the points with STEC larger than 80 % of the maximum one and within a circle of 1000 km radius around the eruption coordinates.
2.4 Seismic activity data
The database of earthquakes has been retrieved from the Spanish Instituto Geográfico Nacional (IGN) (2022). For the whole duration of the eruption, around 9200 earthquakes were recorded in the database, which includes information about their time, magnitude, location, and depth.
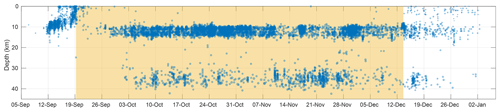
Figure 13Series of earthquakes associated with the volcanic eruption on La Palma Island, indicating their depth in the vertical axis, and their magnitude proportional to the point size. The active volcanic eruption period is shown in yellow shading.
Earthquakes are presented in Fig. 13, indicating their depth in the vertical axis over the whole eruption period (yellow shading). As observed in the figure, there is a precursor seismic activity close to the surface with decreasing depths, then a relatively calm period of 8 d preceding roughly stable activity with earthquakes at two differentiated depths but with homogeneous magnitudes in each group. When the eruption ended, the seismic activity lasted for approximately 15 more days with decreasing magnitude and frequency.
To allow for comparison between the seismic activity and the corresponding ionospheric scintillation indicator, it is proposed to use the seismic energy released per earthquake and then integrate the energy from all earthquakes over a time interval. The rationale behind the selection of these metrics is that, regardless of the mechanism involved in the perturbation of the ionosphere, the larger the energy dissipated into the environment, the larger the induced perturbations should be. The formula used to compute the energy per earthquake is taken from the work of (Gutenberg and Richter, 1955):
where m is the magnitude of the earthquake, and E is the dissipated energy in units of erg.
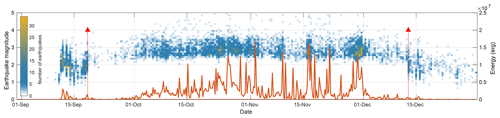
Figure 14Seismic activity associated with the La Palma volcano eruption for the whole period, showing in colors the histogram of magnitudes and the integrated seismic energy with an orange line. The red arrows mark the start and end of the volcanic eruption.
Figure 14 shows a temporal histogram of the magnitude of earthquakes over the eruption period, indicating the magnitude in the vertical axis and the number of earthquakes per bin in colors. Red arrows mark the beginning and end of the eruption. The orange line represents the integrated energy every 6 h intervals, computed for each earthquake using Eq. (2).
2.5 Geomagnetic and solar activity data
Other important factors that impact the ionosphere and can produce ionospheric scintillation are geomagnetic perturbations and solar weather. The geomagnetic data used in this study are that of the planetary index, Kp, which is an internationally recognized index usually used in aerospace technologies and physical models of the geomagnetic environment. It is obtained from geomagnetic perturbations produced by the solar wind and is measured from the K indices of 13 observatories around the world located outside the auroral zone.
The data are gathered by the GFZ German Research Centre for Geosciences (Matzka et al., 2021), from where the period corresponding to the La Palma volcanic eruption has been downloaded. The Kp is presented in 3 h intervals.
The solar activity data have been taken into account by studying the solar flux at the radiofrequency range 10.7 cm (F10.7). The solar flux is one of the main sources of geomagnetic and ionospheric perturbations. Its value is expressed in solar flux units (SFUs), and it is recorded with a periodicity of 1 d from 1947.
The dataset used is the Penticton solar radio flux at 10.7 cm (National Research Council Canada (NRC), 2023), which contains two variables: the observed solar flux at Earth and the adjusted solar flux, which compensates for the varying distance from the Sun to the Earth. In our case, the actual flux arriving at the Earth is that which is impacting the ionosphere; therefore, the observed flux has been used. Both geomagnetic disturbances and solar activity data are analyzed in this work in relation to the scintillation index to complete the study and explain, or discard, some signatures found in the ionospheric perturbations.
The three GNSS techniques studied to measure the ionospheric scintillation are correlated to the seismic activity induced by the volcanic eruption. In each of the cases, instantaneous measurements of the S4 index at every geographic coordinate have been recorded. To integrate this information into something comparable to the integrated energy dissipated by earthquakes, measurements were averaged and integrated into 6 h segments, corresponding to the same discretization of the earthquake energy dataset. This 6 h period is long enough to include many measurements and reduce noise but short enough to allow for tracking possible variations within the day.
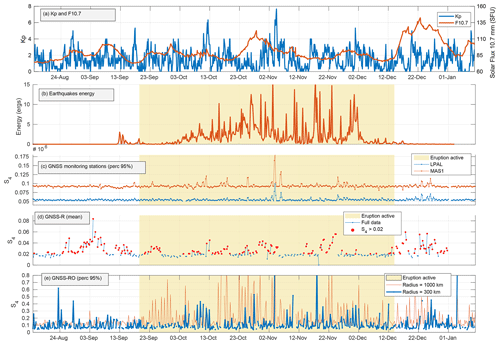
Figure 15Comparison of (a) geomagnetic planetary index and solar flux with (b) integrated earthquake energy every 6 h interval vs. estimated S4 from the three sources: (c) 95th percentile of S4 obtained from ground stations on La Palma and in Maspalomas, (d) mean S4 obtained from CYGNSS GNSS-R, and (e) 95th percentile of S4 obtained from GNSS-RO with two different filtering distances.
Figure 15 shows the comparison between the integrated seismic energy by the earthquakes and the different methods used to estimate the S4 ionospheric scintillation index used around La Palma Island. Figure 15a shows the geomagnetic perturbations measured by the planetary index (Kp) and the solar activity represented by the solar flux F10.7. Figure 15b shows the integrated earthquake energy every 6 h interval over a yellow background indicating the time when the eruption was active. Figure 15c shows the ground station data obtained from LPAL and MAS1 stations and then the 95th percentile computed every 6 h intervals. Figure 15d shows the GNSS-R data from CYGNSS, at the same 6 h intervals. Finally, Fig. 15e shows the GNSS-RO data. The 95th percentile of the S4 values is shown in these plots after filtering them by distance to the eruption: 300 km in blue and 1000 km in red.
A first visual inspection of these data shows a high correlation between the seismic energy and the estimated scintillation. For example, the largest peak in the seismic activity on 3 November at 09:00 UTC almost matches with the peaks in the GNSS monitoring ground stations and GNSS-RO measurements, both at the 6 h interval at 00:00 UTC on 4 November. Similarly, the second largest peak in the seismic activity on 17 November at 15:00 UTC has a corresponding replica in the 300 km radius GNSS-RO measurements on 18 November at 00:00 UTC.
It can be observed that the GNSS monitoring ground station data present an offset between LPAL and MAS1 stations, but they are highly correlated most of the time as both stations can sense the region of the ionosphere likely to be perturbed by the eruptive activity. Figure 15d shows the CYGNSS GNSS-R data, which represent the least correlated measurement. As mentioned previously, this can be explained by sea surface conditions affecting GNSS-R in correctly estimating the ionospheric scintillation index. The red points in Fig. 15d represent the S4 values larger than 0.02; lower values were filtered out as they are more prone to be affected by sea roughness, as explained in Sect. 2.2.
Figure 15e shows the GNSS-RO data after being filtered by their distance to the eruption site: 1000 km in the red line and 300 km in the blue line. The 1000 km line shows a greater number of peaks and higher peaks for almost the whole period, which may indicate that it is being affected by other sources of perturbations than the volcanic eruption.
To undertake quantitative analysis of the different GNSS data sources, and to allow for a better comparison of them, a linear correlation between each pair of data (earthquake energy vs. each of the GNSS measurement methods) has been performed. Before correlating each signal, they have been shifted by a certain amount of time from −10 d to +10 d, in steps of 6 h, equal to the sampling rate for all signals. This way we can also see if the impact of earthquakes in the ionosphere is a precursor or a consequence of it.
After the temporal shift, using the corresponding pair of points (S4 vs. integrated earthquake energy), a least-squares linear correlation is computed, obtaining for each case its Pearson correlation coefficient, R. Then, for each shifted time, the values of R over time are plotted in Fig. 16. In all cases, the x axis indicates the amount of time shifted, being negative when the scintillation is a precursor of the earthquakes, and the y axis is the correlation coefficient R.
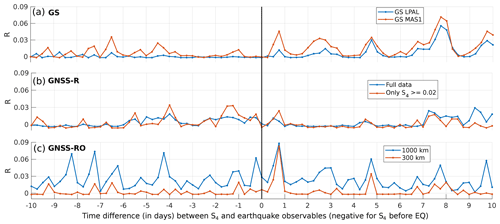
Figure 16Results of the correlation analysis for each GNSS method and each shifted period in the x axis: (a) GNSS monitoring ground stations, (b) GNSS-R data, and (c) GNSS-RO data. EQ stands for earthquakes.
Figure 16b proves that the GNSS-R method presents the smallest correlation for all shifting times. Even though it presents a weak correlation in several points, it tends to be larger when using only the S4 values larger than 0.02. GNSS-R data present peaks of correlation from 7 to 4 d before the earthquake energy peaks, from 2 d before to 1 d after, and from 7 to 10 d after.
For GNSS monitoring ground station data in Fig. 16a, the largest peaks of correlation occur when the scintillation is produced around 8 d later, and also 3 and 5 d later with smaller intensities. Additionally, there is a peak that is higher at Maspalomas than at the La Palma monitoring station 18 h after the eruption, which supports observations from Fig. 15 that the highest peak in the time series occurs 18 h after the energy peak of the largest earthquake.
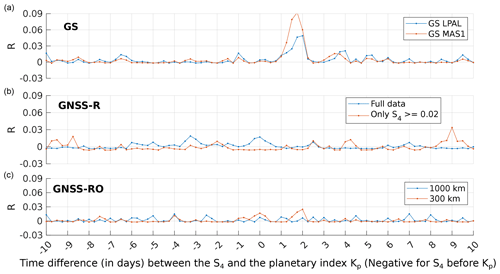
Figure 17Correlation analysis between the planetary index (Kp) and S4 from all GNSS methods: (a) GNSS monitoring ground stations, (b) GNSS-R data, and (c) GNSS-RO data.
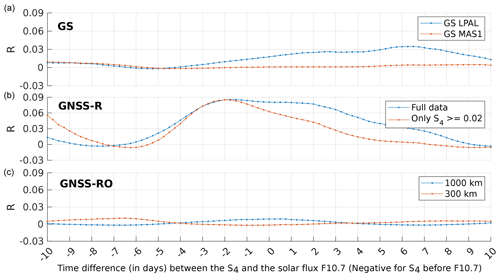
Figure 18Correlation analysis between the solar flux (F10.7) and S4 from all GNSS methods: (a) GNSS monitoring ground stations, (b) GNSS-R data, and (c) GNSS-RO data.
Figure 16a also shows that the Maspalomas (MAS1) station always has a higher correlation than the La Palma station. A possible explanation for this is that the lower the elevation angle, the larger the detected scintillation, increasing the possibility of detection of small ionospheric signatures. This is why larger correlations are found in the GNSS-RO measurements.
In the results for GNSS-RO in Fig. 16c it can be seen the largest correlation peak occurs 18 h after the seismic activity, as for the GNSS monitoring ground station data. It can also be seen that the data filtered with a 1000 km radius are noisier than those filtered with a 300 km radius because the latter are more related to the eruptive activity than to other external causes. This is despite that, for the 1000 km radius curve, there are some correlation peaks when the seismic activity precedes the ionospheric perturbations by approximately 4, 7, and 8 d. Also, another peak is found 4.75 d after the seismic activity, with a smaller replica in the 300 km radius, being the second larger peak for this case.
The same technique has been also applied to correlate the ionospheric scintillation with geomagnetic and space weather indicators: planetary index (Kp) and solar flux (F10.7), respectively. Figure. 17 shows the correlation analysis for the planetary index and the three methods used to estimate the S4: GNSS monitoring ground stations, GNSS-R, and GNSS-RO.
A peak of correlation can be observed when the Kp peaks appear from 1 to 2 d before the S4 perturbations when using the ground station method. These peaks reach a value of 0.09 for the MAS1 station and 0.05 for the LPAL station. For the rest of the time windows, the correlation is almost null. The same happens for the GNSS-R and GNSS-RO results, where the correlation is always less than 0.03, which it can be considered negligible.
In Fig. 16, a cross-correlation between two or more techniques is observed sometimes. There are several points that present correlation peaks approximately at the same time interval, reinforcing the results presented and confirming that the different methods can actually detect the same signatures related to seismic activity.
Fig. 18 shows the results of the correlation between the solar weather variable, F10.7, and the S4 value from each method used. In this case, the solar flux is more correlated with the scintillation when using the GNSS-R method from CYGNSS data, with values up to 0.09. It is less correlated for the ground stations and the GNSS-RO method, being almost zero all the time for the latter.
These last two results indicate that there is a stronger correlation between the ionospheric scintillation and the earthquakes than with solar weather or geomagnetic perturbations. Only in the cases for the GNSS-R compared with the solar flux, and the ground stations with the planetary index, does the influence of earthquakes sometimes appear to be smaller than that of space weather variables. This means that the impact of earthquakes is locally a stronger factor perturbing the ionosphere. These results support the hypothesis that the local perturbations generated by an impending earthquake can be larger than the ones originating from solar weather and are, therefore, detectable with instruments.
An analysis of the impacts of the La Palma eruption on ionospheric scintillation has been made by correlating three different GNSS datasets (GNSS monitoring ground stations, GNSS-R, and GNSS-RO) and relating seismic activity from the eruption to anomalies in the signal.
This allows for comparing the performance of the three methods in detecting tiny signals in the ionosphere produced by seismic activity. A detectable correlation for the GNSS monitoring ground stations and the GNSS-RO methods is present. The GNSS-R technique resulted in the least favorable technique for this methodology, which may be explained by the rough sea state (SWH > 2 m) for the majority of the observed eruption period. The correlation peaks found in the other two methods are obtained after computing the data for the complete duration of the eruption, from 19 September to 13 December 2021. They show the largest peaks 18 h after the seismic activity, with a correlation coefficient R of around 0.09 and 0.05 for GNSS-RO and GNSS monitoring ground stations, respectively. These detectable correlation signals can be related to the direct energy transfer from the earthquakes to the ionosphere by mechanical gravity waves (pressure waves coupling the atmosphere and the ionosphere), as other studies have reported in other eruptions.
Some correlation has also been found when the earthquakes occur some days before ionospheric scintillation, mainly in the GNSS-R method, as well as in the GNSS-RO method. In GNSS-RO, peaks occur 4, 7, and 8 d before the earthquakes.
In the case of the La Palma volcanic eruption, the pre-earthquake ionospheric perturbations may be produced through a piezoelectric effect caused by the severe seismic activity under La Palma over the whole duration of the eruption. As some studies affirm (Qian et al., 2001), the piezoelectric effect induced by the pressure of the large underground rocks can induce electric charges in the surface, generating perturbations in the ionosphere's electron density for some days before the earthquakes.
The general conclusion of this study is that the small correlation found between earthquakes and ionospheric scintillation using the Pearson coefficient makes it very difficult to use these proxies, at present, in practical applications. This can be due to the small magnitude of the earthquakes associated with this volcanic eruption. When studying earthquakes with higher magnitudes, the results may show clearer correlations. The importance of this study is that – to authors' knowledge – this is the first time that ionospheric scintillation derived from three different GNSS-based methods, namely ground-based monitoring stations, GNSS-RO, and GNSS-R, have been used to analyze ionospheric scintillation and their potential correlation with seismic activity, discarding other sources of geomagnetic activity and space weather events.
Data analysis code is not available as the analysis followed standard statistical practices that can be reproduced by following the explanations given in the text.
Some of the data used in this study are already publicly available, as is the case of the USGS earthquake database (USGS, 2023), COSMIC (UCAR/NCAR, 2019) and CYGNSS data (CYGNSS, 2023), SIMAR wave height (SIMAR, 2023), and geomagnetic activity/solar flux (Matzka et al., 2021). Other data are property of a third-party organization, such as the Spire scintillation data and monitoring ground stations' scintillation data. However, the data derived from this study can be reproduced by following the explanations given in the article.
All authors contributed to conceptualization, data curation, formal analysis, visualization, and article revision. Additionally, CM performed software implementation and original draft writing, GGC contributed to software implementation, and AC was in charge of project administration, funding acquisition, and resource provision.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
The authors sincerely express their thanks to Spire for their support in pre-processing and interpreting their GNSS-RO data, as well as to the gAGE UPC team for pre-processing and providing the GNSS monitoring ground station data.
This research was supported in part by grant PID2021-126436OB-C21 from the Programa Estatal para Impulsar la Investigación Científico-Técnica y su Transferencia, del Plan Estatal de Investigación Científica, Técnica y de Innovación 2021–2023 (Spain) and in part by the European Social Fund (ESF). GNSS-RO Spire data have been provided by the European Space Agency through the ESA TPM SPIRE project ID 67176.
This paper was edited by Rachid Omira and reviewed by Brianna Corsa and one anonymous referee.
Angling, M. J., Nogués-Correig, O., Nguyen, V., Vetra-Carvalho, S., Bocquet, F.-X., Nordstrom, K., Melville, S. E., Savastano, G., Mohanty, S., and Masters, D.: Sensing the ionosphere with the Spire radio occultation constellation, J. Space Weather Spac., 11, 56, https://doi.org/10.1051/swsc/2021040, 2021. a
Astafyeva, E.: Ionospheric Detection of Natural Hazards, Rev. Geophys., 57, 1265–1288, https://doi.org/10.1029/2019rg000668, 2019. a
Camps, A., Park, H., Juan, J. M., Sanz, J., González-Casado, G., Barbosa, J., Fabbro, V., Lemorton, J., and Orús, R.: Ionospheric Scintillation Monitoring Using GNSS-R?, in: IGARSS 2018 – 2018 IEEE International Geoscience and Remote Sensing Symposium, 3339–3342, Valencia, Spain, https://doi.org/10.1109/IGARSS.2018.8519088, 2018. a, b
CYGNSS: https://podaac.jpl.nasa.gov/dataset/CYGNSS_L1_V3.1, last access: 27 November 2023. a
Das, B., Barman, K., Pal, S., and Haldar, P. K.: Impact of Three Solar Eclipses of 2019–2020 on the D-Region Ionosphere Observed From a Subtropical Low-Latitude VLF Radio Station, J. Geophys. Res.-Space, 127, e2022JA030353, https://doi.org/10.1029/2022JA030353, 2022. a
De Ragone, A. H., De Manzano, A. N., Elias, A. G., and De Artigas, M. Z.: Ionospheric effects of volcanic eruptions, Geofis. Ints, 43, 187–192, 2004. a
Ding, F., Wan, W., Ning, B., and Wang, M.: Large-scale traveling ionospheric disturbances observed by GPS total electron content during the magnetic storm of 29–30 October 2003, J. Geophys. Res.-Space, 112, A06309, https://doi.org/10.1029/2006JA012013, 2007. a
Fernández, J., Escayo, J., Hu, Z., Camacho, A. G., Samsonov, S. V., Prieto, J. F., Tiampo, K. F., Palano, M., Mallorquí, J. J., and Ancochea, E.: Detection of volcanic unrest onset in La Palma, Canary Islands, evolution and implications, Sci. Rep.-UK, 11, 1–15, 2021. a
Gutenberg, B. and Richter, C.: Magnitude and energy of earthquakes, Nature, 176, 795–795, 1955. a
Instituto Geografico Nacional (IGN): Catalogo de terremotos, https://doi.org/10.7419/162.03.2022, 2022. a
Irisov, V., Nguyen, V., Duly, T., Masters, D. S., Nogues-Correig, O., Tan, L., Yuasa, T., and Ector, D. R.: Recent Ionosphere Collection Results From Spire's 3U CubeSat GNSS-RO Constellation, in: AGU Fall Meeting Abstracts, Washington DC, US, vol. 2018, PA24B–05, 2018. a
Jales, P., Esterhuizen, S., Masters, D., Nguyen, V., Correig, O. N., Yuasa, T., and Cartwright, J.: The new Spire GNSS-R satellite missions and products, in: Image and Signal Processing for Remote Sensing XXVI, edited by Bruzzone, L., Bovolo, F., and Santi, E., vol. 11533, p. 1153316, International Society for Optics and Photonics, SPIE, https://doi.org/10.1117/12.2574127, 2020. a
Juan, J. M., Aragon-Angel, A., Sanz, J., González-Casado, G., and Rovira-Garcia, A.: A method for scintillation characterization using geodetic receivers operating at 1 Hz, J. Geodesy, 91, 1383–1397, https://doi.org/10.1007/s00190-017-1031-0, 2017. a
Juan, J. M., Sanz, J., González-Casado, G., Rovira-Garcia, A., Camps, A., Riba, J., Barbosa, J., Blanch, E., Altadill, D., and Orus, R.: Feasibility of precise navigation in high and low latitude regions under scintillation conditions, J. Space Weather Spac., 8, A05, https://doi.org/10.1051/swsc/2017047, 2018. a
Kamogawa, M.: Preseismic lithosphere-atmosphere-ionosphere coupling, Eos T. Am. Geophys. Un., 87, 417–424, https://doi.org/10.1029/2006EO400002, 2006. a, b
Li, G., Ning, B., Zhao, B., Liu, L., Liu, J., and Yumoto, K.: Effects of geomagnetic storm on GPS ionospheric scintillations at Sanya, J. Atmos. Sol.-Terr. Phy., 70, 1034–1045, https://doi.org/10.1016/j.jastp.2008.01.003, 2008. a
Liu, J. Y., Chuo, Y. J., Shan, S. J., Tsai, Y. B., Chen, Y. I., Pulinets, S. A., and Yu, S. B.: Pre-earthquake ionospheric anomalies registered by continuous GPS TEC measurements, Ann. Geophys., 22, 1585–1593, https://doi.org/10.5194/angeo-22-1585-2004, 2004. a
Matzka, J., Bronkalla, O., Tornow, K., Elger, K., and Stolle, C.: Geomagnetic Kp index V. 1.0, GFZ Data Services, Potsdam, Germany, https://doi.org/10.5880/KP.0001, 2021. a, b
Molina, C. and Camps, A.: First evidences of ionospheric plasma depletions observations using GNSS-R data from CYGNSS, Remote Sens.-Basel, 12, 3782, https://doi.org/10.3390/rs12223782, 2020. a, b
Molina, C., Semlali, B. B., Park, H., and Camps, A.: Possible Evidence of Earthquake Precursors Observed in Ionospheric Scintillation Events Observed from Spaceborne GNSS-R Data, in: 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 8680–8683, IEEE, 2021. a
Molina, C., Boudriki Semlali, B.-E., Park, H., and Camps, A.: A Preliminary Study on Ionospheric Scintillation Anomalies Detected Using GNSS-R Data from NASA CYGNSS Mission as Possible Earthquake Precursors, Remote Sens.-Basel, 14, 2555–2577, 2022. a
Munoz-Martin, J. F., Perez Portero, A., Camps, A., Ribo, S., Cardellach, E., Stroeve, J., Nandan, V., Itkin, P., Tonboe, R., Hendricks, S., Huntemann, M., Spreen, G., and Pastena, M.: Snow and ice thickness retrievals using GNSS-R: Preliminary results of the MOSAiC experiment, Remote Sens.-Basel, 12, 4038, https://doi.org/10.3390/rs12244038, 2020. a
National Research Council Canada (NRC): Solar radio flux – archive of measurements – spaceweather.gc.ca, https://www.spaceweather.gc.ca/forecast-prevision/solar-solaire/solarflux/sx-5-en.php (last access: 3 May 2023), These data were accessed via the LASP Interactive Solar Irradiance Datacenter (LISIRD), (https://lasp.colorado.edu/lisird/, last access: 3 May 2023), 2023. a
Puertos del Estado: Conjunto de datos SIMAR, https://bancodatos.puertos.es/BD/informes/INT_8.pdf (last access: 23 September 2022), Puertos del Estado, Madrid, Spain, 2020. a
Puertos del Estado: Predicción de oleaje, nivel del mar. Boyas y mareografos, https://www.puertos.es/en-us/oceanografia/Pages/portus.aspx (last access: 23 Setember 2022), Puertos del Estado, Madrid, Spain, 2022. a
Pulinets, S.: Ionospheric Precursors of Earthquakes: Recent Advances in Theory and Practical Applications, Terr. Atmos. Ocean. Sci., 15, 413–435, https://doi.org/10.3319/TAO.2004.15.3.413(EP), 2004. a
Pulinets, S. and Davidenko, D.: Ionospheric precursors of earthquakes and global electric circuit, Adv. Space Res., 53, 709–723, 2014. a
Pulinets, S., Krankowski, A., Hernandez-Pajares, M., Marra, S., Cherniak, I., Zakharenkova, I., Rothkaehl, H., Kotulak, K., Davidenko, D., Błaszkiewicz, L., Fron, A., Flisek, P., Rigo, A., and Budnikov, P.: Ionosphere Sounding for Pre-seismic anomalies identification (INSPIRE): Results of the project and Perspectives for the short-term earthquake forecast, Frontiers in Earth Science, 9, 131–147, https://doi.org/10.3389/feart.2021.610193, 2021. a
Qian, S.-Q., qi Hao, J., guo Zhou, J., tian Gao, J., ling Wang, M., and Liang, J.: ULF electromagnetic precursors before the 1999 Jiji, Taiwan, earthquake and the comparison with results of simulating experiments, Acta Seismologica Sinica, 14, 342–348, https://doi.org/10.1007/s11589-001-0012-8, 2001. a
Rodriguez-Alvarez, N., Bosch-Lluis, X., Camps, A., Vall-Llossera, M., Valencia, E., Marchan-Hernandez, J. F., and Ramos-Perez, I.: Soil moisture retrieval using GNSS-R techniques: Experimental results over a bare soil field, IEEE T. Geosci. Remote, 47, 3616–3624, 2009. a
Rovira-Garcia, A., González-Casado, G., Juan, J. M., Sanz, J., and Pérez, R. O.: Climatology of High and Low Latitude Scintillation in the Last Solar Cycle by Means of the Geodetic Detrending Technique, in: Proceedings of the 2020 International Technical Meeting of The Institute of Navigation, Institute of Navigation, San Diego, CA, USA, https://doi.org/10.33012/2020.17187, 2020. a
Shanmugam, S., Jones, J., MacAulay, A., and Van Dierendonck, A.: Evolution to modernized GNSS ionoshperic scintillation and TEC monitoring, in: Proceedings of the 2012 IEEE/ION Position, Location and Navigation Symposium, IEEE, 265–273, Myrtle Beach, SC, USA, https://doi.org/10.1109/PLANS.2012.6236891, 2012. a
Shults, K., Astafyeva, E., and Adourian, S.: Ionospheric detection and localization of volcano eruptions on the example of the April 2015 Calbuco events, J. Geophys. Res.-Space, 121, 10–303, https://doi.org/10.1002/2016ja023382, 2016. a
SIMAR: https://www.puertos.es/es-es/oceanografia/Paginas/portus.aspx, last access: 27 November 2023. a
Themens, D. R., Watson, C., Žagar, N., Vasylkevych, S., Elvidge, S., McCaffrey, A., Prikryl, P., Reid, B., Wood, A., and Jayachandran, P.: Global propagation of ionospheric disturbances associated with the 2022 Tonga Volcanic Eruption, Geophys. Res. Lett., 49, e2022GL098158, https://doi.org/10.1029/2022GL098158, 2022. a
UCAR/NCAR: UCAR COSMIC Program, 2019: COSMIC-2 Data Products, https://doi.org/10.5065/T353-C093, 2019. a, b
USGS: https://earthquake.usgs.gov/earthquakes/search/, last access: 27 November 2023. a
Wang, F., Yang, D., and Yang, L.: Retrieval and assessment of significant wave height from CYGNSS mission using neural network, Remote Sens.-Basel, 14, 3666, https://doi.org/10.3390/rs14153666, 2022. a
Yong-Qiang, H., Zuo, X., and Dong-He, Z.: Responses of the ionosphere to the Great Sumatra earthquake and volcanic eruption of Pinatubo, Chinese Phys. Lett., 23, 1955, https://doi.org/10.1088/0256-307X/23/7/082, 2006. a
Xu, J., Ke, F., Zhao, X., and Qi, X.: Characteristics of the Ionospheric Disturbances Caused by Typhoon Using GPS and Ionospheric Sounding, 509–517, https://doi.org/10.1007/978-981-15-6113-9_57, 2019. a