Dynamic response and breakage of trees subject to a landslide-induced air blast

Landslides have been known to generate powerful air blasts capable of causing destruction and casualties far beyond the runout of sliding mass. The extent of tree damage provides valuable information on air blast intensity and impact region. However, little attention has been paid to the air blast–tree interaction. In this study, we proposed a framework to assess the tree destruction caused by powerful air blasts, including the eigenfrequency prediction method, tree motion equations and the breakage conditions. The tree is modeled as a flexible beam with variable cross-sections, and the anchorage stiffness is introduced to describe the tilt of the tree base. Large tree deflection is regarded when calculating the air blast loading, and two failure modes (bending and overturning) and the associated failure criteria are defined. Modeling results indicate that although the anchorage properties are of importance to the tree eigenfrequency, tree eigenfrequency is always close to the air blast frequency, causing a dynamic magnification effect for the tree deformation. This magnification effect is significant in cases with a low air blast velocity, while the large tree deflection caused by strong air blast loading would weaken this effect. Furthermore, failure modes of a specific forest subject to a powerful air blast depend heavily on the trunk bending strength and anchorage characteristics. The large variation in biometric and mechanical properties of trees necessitates the establishment of a regional database of tree parameters. Our work and the proposed method are expected to provide a better understanding of air blast power and to be of great use for air blast risk assessment in mountainous regions worldwide.

1 Introduction

Long runout landslides involve massive amounts of energy and can be extremely hazardous owing to their long movement distance, high mobility and potential chain disasters (Nicoletti and Sorriso-Valvo, 1991; Nicoletti et al., 1993; Johnson and Campbell, 2017; Shugar et al., 2021; Zhang et al., 2022). A moving landslide with high velocity can generate a powerful air blast capable of uprooting trees, lifting people into the air and even flattening buildings (Adams, 1881; Penna et al., 2021). In recent decades, destructive air blasts frequently occurred in mountainous regions worldwide and caused casualties and economic loss far beyond the landslide runout (e.g., Yin, 2014; Bartelt et al., 2016; Kargel et al., 2016). Understanding their force of destruction is of great use for landslide risk assessment and disaster mitigation, especially in high-altitude regions.

Monitoring equipment has been confirmed to provide great performance in determining the dynamic characteristics of landslide-induced air blasts (Grigoryan et al., 1982; Sukhanov, 1982; Caviezel et al., 2021). However, most case histories occurred in high-altitude mountainous regions without witnesses (Yin and Xing, 2012), and the in situ equipment also got damaged because of the near-field destruction of landslides and associated air blasts. Therefore, very few air blast cases have been measured in history. Geologists can only evaluate the air blast hazard for most recorded events using historical evidence after the landslide occurred. In situ information about forest destruction and tree breakage is often used for the air blast risk assessment (Feistl et al., 2015; Fujita et al., 2017; Zhuang et al., 2019, 2022b) (Fig. 1). Uprooted trees and snapped stems delineate the impact region of air blasts and create a natural vector field, indicating the primary movement direction of the landslide, greatly helping to analyze the disaster-causing process of the event. In many cases, observations of forest destruction are the only data to quantify air blast danger.

Figure 1 Tree breakage caused by a large landslide-induced air blast in Sichuan, China, 2008.

The question that remains for air blast mitigation planning using the information of tree damage is how to establish a simple relationship between air blast impact pressure and tree failure. Bending and overturning are two common tree failure modes caused by strong winds. Trees snap when the bending stress exerted by the air blast exceeds the wood strength (Peltola et al., 1999; Gardiner et al., 2000), while overturning will occur if the applied moment overcomes the anchorage resistance of root systems (Jonsson et al., 2006; Nicoll et al., 2006). The occurrence of these two failure modes depends heavily on both the air blast loading and the tree properties. Considering the minor destruction of air blasts relative to the landslide, although it has long been recognized that sliding mass can easily break or uproot trees (Bartelt and Stöckli, 2001; Šilhán, 2020), little attention has been paid to the tree destruction resulting from air blasts. Furthermore, existing models describing the tree–air blast interaction are mostly static (Feistl et al., 2015) or established based on the small-deflection theory (Bartelt et al., 2018a). These methods could aid in a rapid assessment of air blast power, but further research is needed to establish a dynamic model to represent the dynamic response of trees in strong wind. A mechanical understanding of how trees are damaged by air blasts is therefore essential for quantifying the air blast power and for providing valuable data to verify the possible numerical results.

In this study, we established a simple dynamic model capable of calculating the natural frequency of trees and simulating their dynamic response subject to a powerful air blast. The proposed model regards the tree as a multi-degree-of-freedom beam with variable diameters and accounts for large tree deflections and impacts of root anchorage. Both bending and overturning failure modes are involved in the model. The work conducted in this study is expected to make people better understand the power of landslide-induced air blasts and to provide an applicable method to assess the air blast hazard.

2 Model description

Measurements of historical events indicated that the landslide-induced air blast is intermittent and of short duration, lasting only a few seconds, and could reach a high velocity (Grigoryan et al., 1982; Sukhanov, 1982; Caviezel et al., 2021). This impulse wave has a propagation distance of hundreds of meters in both horizontal and vertical directions and acts over the entire tree. Thus, the impact of air blasts on trees is similar to extreme wind gusts, producing large bending moments in the stem- and root-based system, forcing trees to deform or get damaged. Furthermore, fallen trees often point to the movement direction of the landslide, illustrating that there is little time for trees to sway and react to air blasts and the inertial effects are greatly important.

To characterize the dynamic response of trees under the impact load of air blasts, we established a mechanical model to predict the eigenfrequency of trees subject to air blasts and developed a dynamic tree-swaying model that accounts for the large tree deflection. In what follows, we present the eigenfrequency prediction method, tree motion equations and the breakage conditions.

2.1 Eigenfrequency prediction

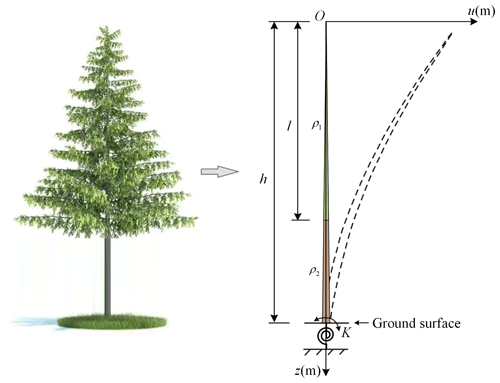
The tree is modeled as a flexible cantilever beam with variable diameters that are hinged at ground level using elastic support. The beam diameter is assumed to continuously linearly decrease with height regarding the decreasing diameters of the trunk and crown from the bottom to the top, while the anchorage stiffness of the root system (K) helps to describe the tilt of the tree base in response to the moment (Neild and Wood, 1999). In the eigenfrequency prediction mode, the tree beam is divided into two segments with a splitting point located at the starting point of the tree crown (Fig. 2). We assume that the tree crown shows minor impacts of elastic modulus. The tree crown is accounted for through the crown mass, and thus the natural difference between the two segments is the material density.

Figure 2 Schematic representation of the eigenfrequency prediction model.

The governing differential equation for the dynamic bending of a nonuniform Euler–Bernoulli beam is (Keshmiri et al., 2018)

$$\begin{array}{}\text{(1)}& \mathit{\rho }A\left(z\right){\displaystyle \frac{{\partial }^{\mathrm{2}}u}{\partial t^{\mathrm{2}}}}+{\displaystyle \frac{{\partial }^{\mathrm{2}}u}{\partial z^{\mathrm{2}}}}\left[EI\left(z\right){\displaystyle \frac{{\partial }^{\mathrm{2}}u}{\partial z^{\mathrm{2}}}}\right]=\mathrm{0},\end{array}$$

where z is the position variable along the beam length. For ease of calculation, the original point (z=0) is set at the treetop, and the maximum value of z is at the tree base so that the beam diameter d(z) corresponding to the position z can be described using a gradient coefficient (μ): d(z)=μz. u is the beam displacement; E is the elastic modulus; and $A\left(z\right)=\frac{\mathit{\pi }}{\mathrm{4}}{\left(dz\right)}^{\mathrm{2}}$ and $I\left(z\right)=\frac{\mathit{\pi }}{\mathrm{64}}{\left(dz\right)}^{\mathrm{4}}$ are the cross-sectional area and moment of inertia, respectively.

Plugging the expression of A(z) and I(z) into Eq. (1) gives

$$\begin{array}{}\text{(2)}& z^{\mathrm{2}}{\displaystyle \frac{{\partial }^{\mathrm{4}}u}{\partial z^{\mathrm{4}}}}+\mathrm{8}z{\displaystyle \frac{{\partial }^{\mathrm{3}}u}{\partial z^{\mathrm{3}}}}+\mathrm{12}{\displaystyle \frac{{\partial }^{\mathrm{2}}u}{\partial z^{\mathrm{2}}}}-{\displaystyle \frac{\mathrm{16}\mathit{\rho }{\mathit{\omega }}^{\mathrm{2}}u}{E{\mathit{\mu }}^{\mathrm{2}}}}=\mathrm{0},\end{array}$$

where ω is known as the eigenfrequency of the beam. The general solution of Eq. (2) can be expressed as

$$\begin{array}{}\text{(3)}& \begin{array}{rl}u\left(z\right)& ={\displaystyle \frac{\mathrm{1}}{z}}[A_{\mathrm{1}}{J}_{\mathrm{2}}\left(\mathrm{2}\sqrt{\mathit{\lambda }z}\right)+A_{\mathrm{2}}{Y}_{\mathrm{2}}\left(\mathrm{2}\sqrt{\mathit{\lambda }z}\right)\\ & +A_{\mathrm{3}}{J}_{\mathrm{2}}\left(\mathrm{2}i\sqrt{\mathit{\lambda }z}\right)+A_{\mathrm{4}}{Y}_{\mathrm{2}}\left(\mathrm{2}i\sqrt{\mathit{\lambda }z}\right)],\end{array}\end{array}$$

where $\mathit{\lambda }=\sqrt{\frac{\mathrm{16}\mathit{\rho }{\mathit{\omega }}^{\mathrm{2}}}{E{\mathit{\mu }}^{\mathrm{2}}}}$; J₂ and Y₂ are the Bessel functions of the first and second kind (Mocica, 1988), respectively; and A₁–A₄ are coefficients that need to be determined based on the boundary conditions.

The deflection of the upper segment (crown) and the lower segment (trunk) can be generated in a similar manner:

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{u}_{\mathrm{1}}\left(z\right)& ={\displaystyle \frac{\mathrm{1}}{z}}[A_{\mathrm{1}}{J}_{\mathrm{2}}\left(\mathrm{2}\sqrt{{\mathit{\lambda }}_{\mathrm{1}}z}\right)+A_{\mathrm{2}}{Y}_{\mathrm{2}}\left(\mathrm{2}\sqrt{{\mathit{\lambda }}_{\mathrm{1}}z}\right)\\ & +A_{\mathrm{3}}{J}_{\mathrm{2}}\left(\mathrm{2}i\sqrt{{\mathit{\lambda }}_{\mathrm{1}}z}\right)+A_{\mathrm{4}}{Y}_{\mathrm{2}}\left(\mathrm{2}i\sqrt{{\mathit{\lambda }}_{\mathrm{1}}z}\right)]\mathrm{0}⩽z<l,\end{array}\end{array}$$

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{u}_{\mathrm{2}}\left(z\right)& ={\displaystyle \frac{\mathrm{1}}{z}}[B_{\mathrm{1}}{J}_{\mathrm{2}}\left(\mathrm{2}\sqrt{{\mathit{\lambda }}_{\mathrm{2}}z}\right)+B_{\mathrm{2}}{Y}_{\mathrm{2}}\left(\mathrm{2}\sqrt{{\mathit{\lambda }}_{\mathrm{2}}z}\right)\\ & +B_{\mathrm{3}}{J}_{\mathrm{2}}\left(\mathrm{2}i\sqrt{{\mathit{\lambda }}_{\mathrm{2}}z}\right)+B_{\mathrm{4}}{Y}_{\mathrm{2}}\left(\mathrm{2}i\sqrt{{\mathit{\lambda }}_{\mathrm{2}}z}\right)]l⩽z⩽h,\end{array}\end{array}$$

where l is the length of the crown, h is the tree height, and ${\mathit{\lambda }}_{\mathrm{1}}=\sqrt{\frac{\mathrm{16}{\mathit{\rho }}_{\mathrm{1}}{\mathit{\omega }}^{\mathrm{2}}}{E{\mathit{\mu }}^{\mathrm{2}}}}$ and ${\mathit{\lambda }}_{\mathrm{2}}=\sqrt{\frac{\mathrm{16}{\mathit{\rho }}_{\mathrm{2}}{\mathit{\omega }}^{\mathrm{2}}}{E{\mathit{\mu }}^{\mathrm{2}}}}$ are the single-valued functions of eigenfrequency. ρ₂ is the wood density, and ρ₁ is the equivalent density regarding the contribution of both the tree trunk and the crown. The same as A₁–A₄, B₁–B₄ are also coefficients of the tree deflection equation that need to be determined based on the boundary and continuity conditions.

The boundary condition at the origin (z=0) is the free end, and thus Eq. (4) can be simplified as

$$\begin{array}{}\text{(6)}& u_{\mathrm{1}}\left(z\right)={\displaystyle \frac{\mathrm{1}}{z}}\left[A_{\mathrm{1}}{J}_{\mathrm{2}}\left(\mathrm{2}\sqrt{{\mathit{\lambda }}_{\mathrm{1}}z}\right)+A_{\mathrm{3}}{J}_{\mathrm{2}}\left(\mathrm{2}i\sqrt{{\mathit{\lambda }}_{\mathrm{1}}z}\right)\right]\mathrm{0}\le z<l.\end{array}$$

According to continuity conditions of two segments at the splitting point and the boundary condition at the tree base, the following constraints are determined: u₁(l)=u₂(l), $u_{\mathrm{1}}^{\prime }\left(l\right)=u_{\mathrm{2}}^{\prime }\left(l\right)$, $u_{\mathrm{1}}^{\prime \prime }\left(l\right)=u_{\mathrm{2}}^{\prime \prime }\left(l\right)$, $u_{\mathrm{1}}^{\prime \prime \prime }\left(l\right)=u_{\mathrm{2}}^{\prime \prime \prime }\left(l\right)$, u₂(h)=0 and $K{u}_{\mathrm{2}}^{\prime }\left(h\right)+EI\left(h\right)u_{\mathrm{2}}^{\prime \prime }\left(h\right)=\mathrm{0}$. Introducing the constraints into Eqs. (5)–(6), a total of six equations are determined here. These six equations can be written in a matrix format:

$$\begin{array}{}\text{(7)}& {\left[F\left({\mathit{\lambda }}_{\mathrm{1}},{\mathit{\lambda }}_{\mathrm{2}}\right)\right]}_{\mathrm{6}\times \mathrm{6}}\cdot {\left[\begin{array}{cccccc}{A}_{\mathrm{1}}& A_{\mathrm{3}}& B_{\mathrm{1}}& B_{\mathrm{2}}& B_{\mathrm{3}}& B_{\mathrm{4}}\end{array}\right]}^T=\mathrm{0},\end{array}$$

where ${\left[F\left({\mathit{\lambda }}_{\mathrm{1}},{\mathit{\lambda }}_{\mathrm{2}}\right)\right]}_{\mathrm{6}\times \mathrm{6}}$ is a matrix that is composed of λ₁ and λ₂. The orders of eigenfrequency and the corresponding vibration mode can be obtained by solving the equation: the determinant of matric $\left|F({\mathit{\lambda }}_{\mathrm{1}},{\mathit{\lambda }}_{\mathrm{2}})\right|=\mathrm{0}$. Notably, the derivatives of u₁(z) and u₂(z) have very complicated expressions but could easily be calculated using MATLAB. Therefore, we did not provide the complete expression here.

2.2 Tree motion

The mechanical response of trees subject to an air blast is modeled using a modified multi-degree-of-freedom tree-swaying model with variable cross-sections (Zhuang et al., 2022a). Different from the simplification in the eigenfrequency prediction method, the size of the tree crown here is determined based on real tree data, corresponding to the frontal-area distribution of the tree crown (Fig. 3a). The model divides the tree beam into a set of segments and calculates the tree motion using linear modal analysis. Specifically, the tree deformation is decomposed into a set of vibration modes so that the total displacement is the combined contribution of each mode. According to preliminary research performed by Sellier et al. (2008) and Pivato et al. (2014), the contribution of the first vibration model is far ahead of the other modes for trees with a slender shape. Thus, only the first vibration mode and the corresponding eigenfrequency are utilized in this study. The modeling of air blast pressure accounts for the wind–tree relative motion and large tree deflection by regarding the beam velocity and geometric nonlinearities resulting from the inclination of beam segments relative to the wind direction (θ_i) (Fig. 3b). With respect to the large tree deflection, we also introduce the impact of eccentric gravity into the model, which significantly contributes during the interaction with a powerful air blast. The gravity and wind load acting on each segment can be easily calculated based on the predetermined diameter and frontal-area distribution (Fig. 3a). Considering that trees often fall in the direction of landslide motion and have little time to sway, the maximum response of the tree is assumed to be reached before the damping forces act (Bartelt et al., 2018a). Only the undamped response to a short-duration blast is considered. The tree motion equations and the expression of air blast force are as follows:

$$\begin{array}{}\text{(8)}& m{\displaystyle \frac{{\partial }^{\mathrm{2}}y}{\partial t^{\mathrm{2}}}}+ky={\int }_{\mathrm{0}}^h{F}_i\mathit{\varphi }\mathrm{d}s+{\int }_{\mathrm{0}}^h{G}_i\mathit{\varphi }\mathrm{d}s,\end{array}$$

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{F}_i& =\mathrm{0.5}\mathit{\rho }{C}_{\mathrm{d}}{A}_{\mathrm{f}}\left|v\cos {\mathit{\theta }}_i-{\displaystyle \frac{\partial y}{\partial t}}\cos {\mathit{\theta }}_i\right|\\ & \cdot \left(v\cos {\mathit{\theta }}_i-{\displaystyle \frac{\partial y}{\partial t}}\cos {\mathit{\theta }}_i\right)\cos {\mathit{\theta }}_i,\end{array}\end{array}$$

$$\begin{array}{}\text{(10)}& G_i=m_{i}g\cdot \sin {\mathit{\theta }}_i\cdot \cos {\mathit{\theta }}_i,\end{array}$$

where ϕ, w, $m={\int }_{\mathrm{0}}^h\stackrel{\mathrm{‾}}{m}{\mathit{\varphi }}^{\mathrm{2}}\mathrm{d}s$ and k=4π²mω² are the first mode shape, eigenfrequency, modal mass and stiffness, respectively; $\stackrel{\mathrm{‾}}{m}$ is the mass distribution; y is the associated generalized displacement; F_i and G_i are the air blast loading and eccentric beam gravity act on the ith segment; h is the tree height; C_d is the drag efficient; A_f is the frontal area; and ρ and v are the density and velocity of the air blast, respectively. Our model is able to calculate the scenarios for both full-height and part-height air blasts.

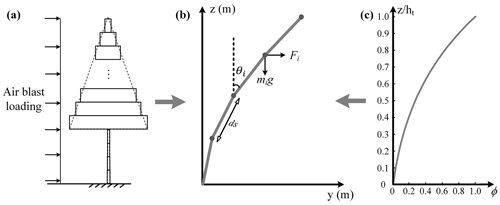
Figure 3 (a–b) Modeling the tree as a multi-degree-of-freedom flexible beam to calculate the dynamic response of trees subjected to a powerful air blast. (c) The first mode shape of the beam helps to model the tree deformation.

In this study, the air blast velocity is expressed as a sine wave impulse with a short duration time t₀:

$$\begin{array}{}\text{(11)}& v=v_{max}\sqrt{\sin \mathit{\varpi }t},\end{array}$$

where v_max is the maximum velocity of the landslide-induced air blast, and ϖ can be regarded as the circular frequency of the wind force $\mathit{\varpi }=\mathit{\pi }/t_{\mathrm{0}}$ (wind force is related to the square of its velocity).

The mechanical response of trees subject to an air blast is deduced by introducing the calculated wind velocity from Eq. (11) into the tree-motion model (Eqs. 8–9) and subsequently solving the equations using the central finite-difference scheme. The validity of this tree-motion model has been checked by Pivato et al. (2014) and Zhuang et al. (2022a), and thus the validation process is not involved here.

2.3 Tree breakage

Two failure modes commonly caused by air blasts are involved in this work: bending and overturning (Gardiner et al., 2000).

In the case of tree bending, trees are expected to break when the maximum bending stress σ_max exceeds a critical value σ_crit:

$$\begin{array}{}\text{(12)}& {\mathit{\sigma }}_{max}={\left[{\displaystyle \frac{M(t,z)\cdot d\left(z\right)/\mathrm{2}}{I\left(z\right)}}\right]}_{max}\ge {\mathit{\sigma }}_{\mathrm{crit}},\end{array}$$

where σ_crit is the bending strength of the tree, which depends highly on the material property. M(t,z) is the bending moment, and its value is calculated at each time step all along the beam:

$$\begin{array}{}\text{(13)}& M(t,z)=EI\left(z\right){\displaystyle \frac{\mathrm{d}\mathit{\theta }}{\mathrm{d}s}},\end{array}$$

where $\frac{\mathrm{d}\mathit{\theta }}{\mathrm{d}s}$ represents the local beam curvature, and θ is the angle between the beam segment with the vertical direction.

For the tree-overturning case, trees are expected to break at the base when the air-blast-induced moment reaches the anchorage resistance (M_crit):

$$\begin{array}{}\text{(14)}& M_{\mathrm{base}}\left(t\right)\ge M_{\mathrm{crit}},\end{array}$$

where M_base(t) is the moment at the tree base calculated at each time step, and the anchorage resistance M_crit is often determined based on in situ tests (e.g., tree-pulling tests).

3 Application

To demonstrate the power of air blasts and how they damage trees, we consider the problem proposed by Bartelt et al. (2018a): a landslide-induced air blast enters a spruce forest at high speed (maximum velocity of 20 m s⁻¹). The short-duration air blast lasts a few seconds with a frequency ϖ. Trees in the forest have a height between 25 and 30 m, which is also the height of the air blast. The sliding mass has stopped before reaching the forest, and only the air blast loads on the trees.

Table 1 Model parameters used in the numerical simulations of the tree response. Parameters are derived from data contained in Kantola and Mäkelä (2004) and Bartelt et al. (2018a).

Using the measured biomass parameters presented in Table 1, we set the total crown mass of a single tree to be 540 kg. The tree crown is assumed to be a cone with a length of 18 m $\left(\frac{\mathrm{2}}{\mathrm{3}}h\right)$ and a width of 5 m. The wood density is 480 kg m⁻³, and the elastic modulus is 10 GPa. Measurements of root-anchorage stiffness (K) are very rare, and in situ tests on spruce performed by Neild and Wood (1999) show a value variation of 80–1200 kN m. This value range indicates a large variation in K depending on the growth conditions, and the values of 100–1200 kN m are applied in the prediction of eigenfrequency and vibration mode in this study.

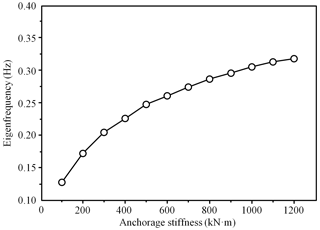
The eigenfrequency ranging from 0.13 Hz (K=100 kN m) to 0.32 Hz (K=1200 kN m) is calculated based on the above parameters (Fig. 4). The modeled results are in a good agreement with measurements performed by Jonsson et al. (2006) (0.16–0.30 Hz), indicating the validity of our proposed eigenfrequency-prediction method. Although the tree eigenfrequency varies significantly with the anchorage stiffness, all the calculated values are less than 0.5 Hz. The same order of magnitude between tree eigenfrequency and air blast frequency necessitates a further investigation into the possible impact of resonance. The dynamic magnification effect caused by impulse loading can greatly amplify the static stress state, making the trees easier to damage.

Figure 4 Eigenfrequency of trees corresponding to different anchorage stiffnesses.

To investigate the impact of dynamic magnification, we performed simulations for all the scenarios using the tree eigenfrequency of 0.26 Hz (K=600 kN m) and the associated vibration mode. A magnification factor D is defined to describe this effect:

$$\begin{array}{}\text{(15)}& \begin{array}{rl}D& ={\displaystyle \frac{u_{\mathrm{d},max}\left(\mathit{\beta }\right)}{u_{\mathrm{sta}}}}={\displaystyle \frac{u_{\mathrm{d},\max }\left(\mathit{\beta }\right)}{{\int }_{\mathrm{0}}^h{F}_{\mathrm{s},max}\mathit{\varphi }\mathrm{d}s/k}}\\ & ={\displaystyle \frac{u_{\mathrm{d},max}\left(\mathit{\beta }\right)}{{\int }_{\mathrm{0}}^h\mathit{\rho }{C}_{\mathrm{d}}{A}_{\mathrm{f}}{v}_{max}^{\mathrm{2}}\mathit{\varphi }\mathrm{d}s/k}},\end{array}\end{array}$$

where $u_{\mathrm{d},max}$ and u_sta are the maximum displacements subject to dynamic load and static load, respectively; $F_{\mathrm{s},max}$ is the static wind force corresponding to the maximum air blast velocity; and $\mathit{\beta }=\frac{\mathit{\varpi }}{\mathit{\omega }}$ is the ratio between the air blast frequency (ϖ) and the eigenfrequency of the tree (ω). Notably, the air blast is a multi-medium fluid that contains numerous dusts, showing a higher density than air. Measurements and numerical modeling performed by Swiss researchers (Feistl et al., 2015) suggest ρ=5 kg m⁻³. In this scenario u_sta is calculated to be 9.8 m.

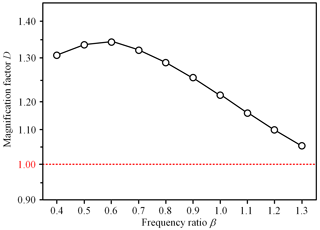
Figure 5 shows the impact of air blast frequency on the dynamic magnification effect. A parabola relationship is identified between the magnification factor and the frequency ratio. Consider first an impulse air blast lasting 1.6 s (β=1.2). The air blast frequency is higher than that of the tree, implying the maximum displacement reaches after the loading time. The modeled maximum dynamic deformation $u_{\mathrm{d},max}$ reaches 10.7 m, and the magnification factor is 1.09. In this case, the magnification effect of tree deformation seems not significant because of the large tree deflection and short-duration loading, and the modeled result is similar to the static stress state. For a longer air blast duration of 3.2 s (β=0.6), we find D=1.34, a high value. The maximum tree deformation reaches during the air blast loading. In such a scenario, an air blast traveling at 20 m s⁻¹ can exert similar destruction as a long-duration wind that moves at 25 m s⁻¹. The dynamic magnification effect significantly increases the tree displacement and thus causes such a phenomenon. Measurements of air blast duration reported by Russian and Swiss researchers (Grigoryan et al., 1982; Sukhanov, 1982) are within this range, lasting only a few seconds. Although the large tree deflection decreases the wind loading, the impulse air blast load is prone to damaging the trees because of the dynamic magnification effect.

Figure 5 Magnification factor with various frequency ratios.

Additional simulations were performed on the air-blast-induced tree breakage. The impulse air blast is assumed to have a maximum velocity of 20 m s⁻¹ and a duration of 3.2 s. For this case, numerical results demonstrate the maximum bending stress and moment of 35 MPa and 192 kN m, respectively. The maximum bending stress reaches at 9 m height ($\mathrm{1}/\mathrm{3}h$), and the maximum bending moment is identified at the tree base. In natural forest areas, the bending strength σ_crit and anchorage resistance M_crit are highly variable, depending on tree species, soil characteristics and temperatures, etc. Measurements conducted by Peltola et al. (2000) and Lundström et al. (2007) indicate that the bending stress to destroy mature trees needs to exceed a value of 30 MPa, while mature spruces with a height of 20–40 m have an anchorage resistance reach up to 100–400 kN m. For the case performed in this study, the forest is likely to be damaged in both bending and overturning failure modes. Reliable values of critical parameters are needed during the assessment of tree destruction, and this will improve the prediction accuracy of the likely failure mode.

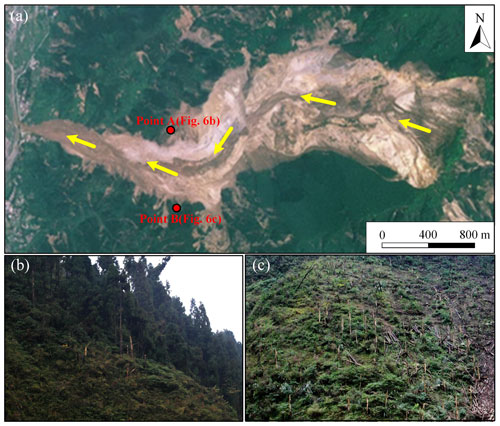
A further application was performed on the 2008 Wenjia Valley avalanche-induced air blast in Sichuan, China (Fig. 6a). This large avalanche had a volume of over 40×10⁶ m³ and generated a powerful air blast. According to our previous investigations and numerical modeling (Zhuang et al., 2019), the air-blast-damaged trees are mostly tall spruce concentrated near the turning points of the valley (Fig. 6b–c). The simulated air blast velocity at turning points reaches 30 m s⁻¹ (point A) and 35 m s⁻¹ (point B). Using the spruce-related parameters indicated in Table 1 and an assumed air blast duration of 3.2 s (a long duration for large avalanches), the maximum displacement of spruces is calculated to be 18.5 and 22.2 m at points A and B, respectively. In this case, the maximum bending stress of trees at two turning points could reach 51 and 57 MPa, significantly larger than the bending strength suggested by Peltola et al. (2000) (36 MPa). Therefore, bending failure of tall spruces was widely identified in situ.

Figure 6 Wenjia Valley avalanche-induced air blast (according to Zhuang et al., 2019). (a) Overview of the Wenjia Valley avalanche. (b–c) Trees damaged by the generated air blast.

4 Discussion

Risk assessment and disaster mitigation of landslide-induced air blasts are hot issues in mountainous regions. Developing a simple but applicable relationship between air blast pressure and tree failure is of great use to scientists to quantify the air blast power. Compared with existing models, one significant improvement of our model is to model the tree as a flexible beam with a variable cross-section and to involve the impact of anchorage. This improvement allows the tree to move as its natural vibration mode rather than a hypothetical trajectory (e.g., rotate around the tree base as a rigid body; Bartelt et al., 2018a). Moreover, the variable cross-section makes the modeling of tree-bending failures more realistic. We can simulate the failure position of trees subjected to a powerful air blast. For the existing model with a constant diameter (Feistl et al., 2015), the rigidity EI is constant along the beam, and the maximum bending stress is always identified at the tree base. This failure characteristic cannot match the actual situation well.

Our proposed model accounts for the factors of large tree deflection: eccentric gravity and modeling of air blast force regarding the wind–tree relative motion and geometric nonlinearities. To investigate the impact of these factors and to confirm the necessity of considering large deflection, a comparative analysis is needed to make readers have a better understanding. Therefore, we designed a comparative analysis by simplifying the tree-motion model of Eq. (8) without involving the impact of large tree deflection. The simplified model is similar to that proposed by Bartelt et al. (2018a):

$$\begin{array}{}\text{(16)}& \begin{array}{rl}m{\displaystyle \frac{{\partial }^{\mathrm{2}}y}{\partial t^{\mathrm{2}}}}+ky& ={\int }_{\mathrm{0}}^h\mathrm{0.5}\mathit{\rho }{C}_{\mathrm{d}}{A}_{\mathrm{f}}{v}_{max}^{\mathrm{2}}\mathit{\varphi }\mathrm{d}s\cdot \sin \mathit{\varpi }t\\ & ={\int }_{\mathrm{0}}^h{F}_{\mathrm{s},max}\mathit{\varphi }\mathrm{d}s\cdot \sin \mathit{\varpi }t.\end{array}\end{array}$$

The displacement at the tree top can be written as

$$\begin{array}{}\text{(17)}& \left\{\begin{array}{l}\begin{array}{rl}& u\left(t\right)={\displaystyle \frac{{\int }_{\mathrm{0}}^h{F}_{\mathrm{s},max}\mathit{\varphi }\mathrm{d}s}{k}}{\displaystyle \frac{\mathrm{1}}{\mathrm{1}-{\mathit{\beta }}^{\mathrm{2}}}}\left(\sin \mathit{\varpi }t-\mathit{\beta }\sin \mathit{\omega }t\right)\\ & \mathrm{0}\le t\le t_{\mathrm{0}}\end{array}\\ \begin{array}{rl}& u\left(t\right)={\displaystyle \frac{u^{\prime }\left(t_{\mathrm{0}}\right)}{\mathit{\omega }}}\sin \mathit{\omega }(t-t_{\mathrm{0}})+u\left(t_{\mathrm{0}}\right)\cos \mathit{\omega }(t-t_{\mathrm{0}})\\ & t>t_{\mathrm{0}}.\end{array}\end{array}\right.\end{array}$$

The maximum deformation occurs during the loading time when β≤1 and after the loading time when β>1. The magnification factor D for both scenarios can be expressed as

$$\begin{array}{}\text{(18)}& \left\{\begin{array}{ll}D=\frac{\mathrm{1}}{\mathrm{1}-{\mathit{\beta }}^{\mathrm{2}}}\left[\sin \left(\frac{\mathrm{2}\mathit{\pi }\mathit{\beta }}{\mathit{\beta }+\mathrm{1}}\right)-\mathit{\beta }\sin \frac{\mathrm{2}\mathit{\pi }}{\mathit{\beta }+\mathrm{1}}\right]& \mathit{\beta }\le \mathrm{1}\\ D={\displaystyle \frac{\mathrm{2}\mathit{\beta }}{{\mathit{\beta }}^{\mathrm{2}}-\mathrm{1}}}\cos {\displaystyle \frac{\mathit{\pi }}{\mathrm{2}\mathit{\beta }}}& \mathit{\beta }>\mathrm{1}.\end{array}\right.\end{array}$$

Figure 7 presents the impact of large tree deflection on the magnification effect. We first perform the simulation using the proposed model without regarding the impact of large tree deflection. A very low air blast velocity (maximum velocity of 0.1 m s⁻¹) is performed, and the eccentric gravity is not considered. The D_max value of 1.77 is identified in the scenario, which is consistent with the analytical solution from Eq. (18). The tree deformation is small with such a weak air blast loading, and the comparison result verifies the validity of our proposed model. Further calculations with higher air blast velocities show different results. In the case of a low air blast velocity, the eccentric gravity contributes a lot to the tree deformation, causing a rather large magnification factor (>2). However, D_max greatly decreases with an increase in wind velocity. For a high air blast velocity, the dynamic response and eccentric gravity amplify the tree deflection, but the inclination of the trees to the wind direction significantly reduces the air blast loading. This special mechanism was rarely considered during the previous assessment of landslide-induced air blasts. We suggest that the modeled tree deformation subjected to a powerful air blast might be overestimated without considering large tree deflection, although this simplified model of Eq. (18) has the advantage of rapid assessment of air blast pressure. The impact of large tree deflection should be accounted for when using forest destruction to quantify the air blast danger.

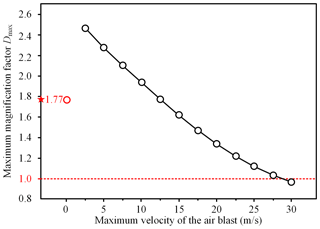
Figure 7 Impact of large tree deflection on the maximum magnification factor D_max. The red star represents the D_max calculated from Eq. (18). The red circle represents the D_max corresponding to the scenario with a very low air blast velocity (maximum velocity of 0.1 m s⁻¹), and the eccentric gravity is not considered.

The dynamic response of trees subject to a landslide-induced air blast is a complex problem, depending heavily on the biometric characteristics of trees. Some biomass variations can be represented by the parameters in the proposed model. For example, for the leafless trees, air blasts pass through the tree crown and only act on the branches, causing a smaller wind load. A reduction of drag efficient C_d is needed in such a condition. Single trees in the impact region of air blasts are subject to a larger loading than trees in dense forest stands, where tree crowns tend to be narrower and form a shielding effect. We can make a reduction in the frontal area A_f to simulate this mechanism. Furthermore, although much effort has been paid to the biometric and mechanical characteristics of tree crowns and trunks, less information is available on the anchorage stiffness and resistance. The root anchorage properties significantly influence the tree eigenfrequency and the likely failure mode. A reliable measurement value of tree-bending strength and anchorage resistance is of use to improve the accuracy of tree failure prediction and to clarify which failure mode is prone to occur. Overall, biomass-related parameters selected to estimate the air blast pressure are recommended to be determined based on in situ investigations. In the future, more measurements need to be conducted on the anchorage properties of trees. Regional databases for biometric and mechanical properties of trees are worthwhile to establish. This would help to provide reliable parameters for the air blast risk assessment.

In this study, the tree is modeled as a variable cross-section that is hinged at ground level using elastic support. Root anchorage is complex and sensitive to many factors such as soil mechanical properties, soil water content and root morphology, and we acknowledge that it is difficult to establish a model that accounts for all the factors that affect the anchorage. Most importantly, we developed a simple but practical model that can simulate the dynamic response of trees subject to a powerful air blast and their two possible failure modes. Bartelt and his colleagues (Bartetl et al., 2018b) have developed a dynamic model named RAMMS, which can efficiently model the entire movement process of ice, rock and snow avalanches and the associated air blasts. It is anticipated that the combination of our proposed tree model and the RAMMS dynamic model could help in the risk assessment of potential air blasts through modeling the air blast impact region and forest destruction.

5 Conclusions

Air blasts are short-duration impulses and can cause fatalities and destruction far beyond the sliding mass. Tree destruction in situ can provide valuable data to quantify the air blast danger and to make us better understand its force of destruction. In this study, we developed a framework for forest destruction assessment subject to a powerful air blast, including the eigenfrequency prediction method, tree motion equations and breakage conditions. The tree is modeled as a flexible variable cross-section beam hinged at ground level using elastic support. The impacts of root anchorage and large tree deflection are regarded during the dynamic response analysis. The framework also involved two failure modes (bending and overturning) and their corresponding failure criteria so that the risk of forest damage could be assessed.

Using the proposed framework, we assumed conditions to investigate the air blast power. Modeling results demonstrate that although the anchorage properties significantly influence the tree eigenfrequency, the latter is always on the same order as air blast frequency. The associated dynamic magnification effect amplifies the tree deformation and thus makes the tree damage easier. In the scenario with a similar frequency between air blasts and trees, an air blast traveling at 20 m s⁻¹ causes a similar force of destruction as a long-duration wind load that moves at 25 m s⁻¹. Notably, this magnification effect caused by the dynamic response and eccentric gravity is significant in the case of a low wind velocity, while the large tree deflection caused by strong air blast loading would weaken this effect. Furthermore, bending and overturning are two likely failure modes for trees subject to a powerful air blast, but exactly what kind of failure will occur for a specific forest depends heavily on the properties of both trees and soils. A case application was further performed on the 2008 Wenjia Valley avalanche-induced air blast in China, testing the validity of our proposed model. In the future, more measurements should be conducted on biometric and mechanical properties of trees, and a regional parameter database is worthwhile to establish. This would greatly improve the prediction accuracy of tree damage and air blast pressure.