Multiscale effects caused by the fracturing and fragmentation of rock blocks during rock mass movement: implications for rock avalanche propagation

The fracturing and fragmentation of rock blocks are important phenomena that occur ubiquitously during the propagation of rock avalanches. Here, the movement of a rectangular rock block characterized by different joint sets along an upper sloped and lower horizontal plane is simulated using discrete element method (DEM) models. The pattern of the joint set allows the block to break along weak joint planes at the onset of fragmentation. With this design, the fracturing and fragmentation of the sliding rock block and their influences on the conversion and transmission of energy within the system are investigated. The results show that rock fragmentation can significantly alter the horizontal velocities and kinetic energies of fragments in the block system, accelerating the front sub-block while decelerating the rear sub-block. Such energy conversion and transmission between the front and rear sub-blocks are attributed to the accumulation and release of elastic strain energy caused by fragmentation. The energy transfer induced by fragmentation is more efficient than that induced by collision. Furthermore, positive relationships between the kinetic energy increase in the front sub-block induced by joint fracturing and the joint strength can be reliably fitted with linear functions, indicating that a rock mass with a higher joint strength experiences more-energetic fragmentation effects.

1 Introduction

Rock avalanches are characterized by extremely rapid, massive, flow-like motions of fragmented rock pieces originating from large rockslides or rockfalls that intensely experience disintegration and fragmentation during propagation (McSaveney and Davies, 2006; Hungr et al., 2014; Knapp and Krautblater, 2020). Due to their extremely high mobility and destructiveness, these events, which are powerful enough to effectively shape mountainous landscapes (Lucas et al., 2014; Crosta et al., 2018; Francioni et al., 2019; von Wartburg et al., 2020), have caused severe casualties and economic losses in recent decades (Evans et al., 2007, 2009; Fan et al., 2017; Zhang et al., 2021; Shugar et al., 2021). For example, the 2006 Leyte Island rock avalanche in the Philippines caused the death of over 1100 people and completely overwhelmed the village of Guinsaugon downstream (Evans et al., 2007). The 2019 Shuicheng rock avalanche that struck Guizhou, China, affected over 1600 people, leaving 43 people dead and 9 people missing (Fan et al., 2020). The hypermobility of rock avalanches, i.e. their exceptionally long run-out distance, is usually quantified by the apparent friction coefficient ($H/L$, where H and L represent the vertical and horizontal distances, respectively, between the crest of the failure mass and the distal point of deposition) (Heim, 1932). When the volume of the failure mass is > 10⁶ m³, $H/L$ shows a decrease with volume, leading to hypermobility in mega rock avalanches (Scheidegger, 1973; Nicoletti and Sorriso-Valvo, 1991; Strom et al., 2019). At present, the hypermobility of rock avalanches continues to draw substantial scientific interest because it cannot be solved simply by a Coulomb frictional model of a sliding rock block (Legros, 2002).

Many dynamic mechanisms have been proposed to explain the hypermobility of rock avalanches. Some mechanisms involve fluid media, such as air (Kent, 1966), water (Wang et al., 2002; Hungr and Evans, 2004), a fluid-like fine grain matrix (Hsü, 1975), melted rock or vapour (Habib, 1975; Goguel, 1978; Hu et al., 2018), and thermal pressurization and thermal moisture fluidization (Wang et al., 2017, 2018a). Others invoke the interactions of materials in rock avalanche systems, such as shearing and impacting between a sliding mass and undulate path-generated acoustic fluidization (Melosh, 1979; Collins and Melosh, 2003), shearing between a rock mass and the ground (Foda, 1994; Wang et al., 2015), shearing between particles in the basal layer (Preuth et al., 2010), momentum transfer caused by the collisions of particles or different parts of the rock mass (Heim, 1932; Van Gassen et al., 1989; Miao et al., 2001), and dispersive pressure caused by dynamic fragmentation (Davies et al., 1999; Davies and McSaveney, 2009). Nevertheless, a universal consensus is still far out of reach (Weidinger et al., 2014). For a rigorous mechanism apt to explain the hypermobility, geological evidences coming from their depositions must be considered, with many field observations suggesting that the following phenomena commonly occur in large rock avalanches (Nicoletti et al., 1993; Weidinger et al., 2014; Dufresne et al., 2016):

1. “volume effect”, where the apparent friction coefficient ($H/L$) decreases as the volume of the rock mass increases (Scheidegger, 1973);

2. intense fragmentation in the deposit (McSaveney and Davies, 2006);

3. close packing of grains during movement (dense grain flows) (Pudasaini and Hutter, 2007);

4. “inverse grading” at depth in the deposit (Heim, 1932; Cruden and Hungr, 1986);

5. shear stress concentrated in basal facies (Dufresne et al., 2016);

6. “jigsaw puzzle” structures and local shear bands in the deposit (Shreve, 1968);

7. preservation of the host rock massif structure in the rock avalanche deposit (Heim, 1932; Strom, 2006).

Unfortunately, few mechanisms can account for the hypermobility of rock avalanches and explain the formation of the main features listed above. Some mechanisms even contradict geological evidence (McSaveney and Davies, 2006). Among these mechanisms, dynamic fragmentation, first proposed by Davies et al. (1999), has been extensively investigated and augmented (McSaveney and Davies, 2006; Davies and McSaveney, 2009; Zhao et al., 2017). This run-out-enhanced mechanism is based on solid geological evidence that intense fragmentation occurs universally in the deposits of rock avalanches; additionally, this mechanism does not conflict with the main structural features in the deposits of rock avalanches. Moreover, special deposit structures, including inverse grading, jigsaw structures and local shear bands, are closely related to the fragmentation process of avalanches (McSavaney and Davies, 2006; Dufresne et al., 2016; Wang et al., 2018b).

Recently, fragmentation and its effects on the emplacement of rock avalanches have been widely investigated by means of field evidence (Pollet and Schneider, 2004; Locat et al., 2006; Crosta et al., 2007; Perinotto et al., 2015; Wang et al., 2019, 2020), laboratory experiments (Imre et al., 2010; Bowman et al., 2012; Haug et al., 2016) and numerical simulations (Rait et al., 2012; De Blasio and Crosta, 2015; Langlois et al., 2015; Zhao et al., 2017, 2018). On the one hand, fragmentation is considered to consume some proportion of kinetic energy. Specifically, according to many scholars, the fragmentation process is estimated to dissipate 1 %–30 % of the total potential energy in a rock avalanche (Locat et al., 2006; Crosta et al., 2007; De Blasio et al., 2018), although some studies unrealistically truncated their rock avalanche particle-size distributions (as stated by Davies et al., 2019). Upon incorporating the existence of submicron particles in this estimate, the amount of energy supposedly dissipated by fragmentation rises to substantially exceed 100 % of the initially available energy (Davies et al., 2020). On the other hand, some studies have shown that fragmentation may enhance the distal travel distance of the sliding mass (Bowman et al., 2012; De Blasio and Crosta, 2015; Haug et al., 2016). The flow structure of fine particles created by intense fragmentation also facilitates the flow mobility of the fragmented mass (Langlois et al., 2015; Lai et al., 2017).

For those who support the mobility-enhanced effects of dynamic fragmentation, the release of elastic strain energy caused by fragmentation is considered to be a key dynamic process accounting for hypermobility (Davies and McSaveney, 2009; De Blasio and Crosta, 2015; Zhao et al., 2017). Based on the theories of rock dynamics and fracture mechanics, rocks fragment when the peak of the stress wave exceeds the strength of the rock itself; then, while part of the strain energy is consumed by cracking or the so-called generation of new surfaces, the remaining elastic strain energy may be released outward as elastic stress waves or may be transferred to the kinetic energy of the fragments (Grady and Kipp, 1987; Zhang et al., 2000; Ghaffari et al., 2019). McSaveney and Davies (2006) proposed that the release of elastic energy induced by dynamic fragmentation may generate the universal outward dispersion of stress, which can offset part of the overburden pressure and reduce shear resistance. Perinotto et al. (2015) examined the fractal dimension and circularity variation with the deposit distance travelled of the La Reunion volcanic debris avalanche and indicated that the exceptional mobility of the debris avalanche was caused by the comprehensive effect of the dynamic disintegration-induced release of elastic energy of larger clasts and the reduction in friction due to the interactions between fragmentation-formed fine particles. Davies et al. (2019) stated that the main fraction of the energy acting on fragmented rock radiates to the surrounding material as elastic body waves when a rock is fragmented, while only a small fraction of the energy is dissipated by newly created fragment surfaces. Haug et al. (2021) indicated that the run-out of a rock avalanche is largely dependent on fragmentation, controlled by the competition between mobility-enhancing spreading and energy-consuming internal friction. Pervasive grain fragmentation was observed in the high-speed rotary shear tests conducted by Hu et al. (2020), who hypothesized the occurrence of shear-thinning thixotropy due to grain fragmentation and a special grain-crushing-induced grain structure primarily to explain the great reduction in shear resistance; however, the underlying mechanism for this hypothesis remains unknown.

As mentioned above, many core issues of fragmentation dynamics and related fragmentation effects are still controversial (Davies and McSaveney, 2009; Haug et al., 2016, 2021). For example, how does the elastic strain energy related to fragmentation transform during the propagation of a rock mass, and what are the effects on the surrounding rock mass? Do the run-out-enhancing effects of elastic strain energy release via fragmentation offset and even surpass the run-out-hindering effects of energy consumption caused by fragmentation? To further understand these questions, studies on the energy conversion processes of rock avalanches caused by rock fragmentation and their effects on the fragmenting block system are conducted herein. In this study, we reproduce the fragmentation process of a sliding rock mass with different joint sets using a discrete element method (DEM) model, aiming to investigate the microscopic energy conversion processes caused by dynamic fragmentation. Then, the dynamic fragmentation effects in real rock avalanches are discussed based on the numerical simulation results. Section 2 provides details about the DEM set-up. In Sect. 3, the results derived from numerical simulations are presented. Section 4 focuses mainly on discussing the implications of the results regarding the fragmentation effects in natural rock avalanches.

2 DEM model set-up

Previous studies have proven that DEM models can successfully simulate the dynamic behaviour of dry granular flows (Silbert et al., 2001; Bi et al., 2005; Morgan and McGovern, 2005; Utili et al., 2015; Kermani et al., 2015; Lai et al., 2017), the crack nucleation and propagation of rock blocks under different loading rates (Yoon, 2007; Wang and Tonon, 2011; Shen et al., 2017; Ma et al., 2018), and the fragmentation processes of rock avalanches (Thompson et al., 2010; Lo et al., 2011; Li et al., 2012; Deng et al., 2016; Zhao and Crosta, 2018). Therefore, commercial Particle Flow Code in Two Dimensions (PFC2D) DEM software is employed here to run all of the simulations (Cundall, 1971; Cundall and Strack, 1979).

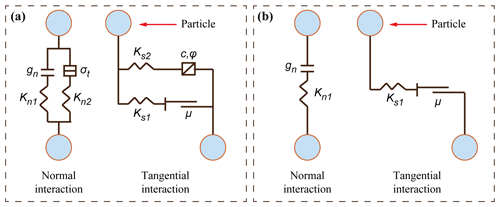
In PFC2D, the basic element is a disc, and granular material is simulated as an assembly of discs. By using the force-displacement law to update the position and force of each particle (disc) and using Newton's second law to determine the motion of each particle, the behaviour of a granular flow can be simulated according to the motion and interaction of particle aggregates. The code employs a time-step algorithm to update the position and force of each particle, and the macroscopic kinetics of particle aggregates are determined based on the continuous accumulation of force and displacement at each time step (Lin et al., 2021). In general, a rock block is modelled as numerous tightly packed discs (particles) cemented together through a linear parallel bond model (i.e. consisting of a linear model and a parallel bond model, as shown in Fig. 1a), which presents brittle fracture characteristics as bonds instantly break and disappear when the force acting on those bonds reaches the failure criterion (Potyondy and Cundall, 2004). After a bond breaks, the interaction between dispersed particles is replaced by a linear model (i.e. the parallel bond model vanishes, while the linear model is sustained; Fig. 1b), in which the motions of particles and blocks are controlled by Newton's second law of motion. Using this model, the dynamic fragmentation of blocks can be accurately simulated (Zhao et al., 2017, 2018). With the generation of macrocracks during fragmentation, the elastic strain energy carried by bonds vanishes; meanwhile, the elastic strain energy stored in unbroken bonds and the overleap deformation of particles will continue to transform, accumulate and release. This process provides exceptional opportunities to observe and analyse the conversion of elastic strain energy for the movement of breakable blocks during the fragmentation process (Potyondy and Cundall, 2004; Timar et al., 2012; Shen et al., 2017; Gao et al., 2020, 2021). In the linear parallel bond model, the interaction of two discs can be described as follows (Potyondy and Cundall, 2004):

$$\begin{array}{}\text{(1)}& {\displaystyle }{F}_{\mathrm{c}}=F_{\mathrm{l}}+F_{\mathrm{b}}\text{(2)}& {\displaystyle }{M}_{\mathrm{c}}=M_{\mathrm{b}}\text{(3)}& {\displaystyle }{F}_{\mathrm{l}}=K_{\mathrm{n}\mathrm{1}}{g}_{\mathrm{n}}+F_{\mathrm{s}}^{i-\mathrm{1}}+K_{\mathrm{s}\mathrm{1}}\mathrm{\Delta }{g}_{\mathrm{s}}\text{(4)}& {\displaystyle }{F}_{\mathrm{b}}=K_{\mathrm{n}\mathrm{2}}\left(d-d_{\mathrm{0}}\right)+K_{\mathrm{s}\mathrm{2}}\mathrm{\Delta }{g}_{\mathrm{s}}\text{(5)}& {\displaystyle }{M}_{\mathrm{b}}=K_{\mathrm{n}\mathrm{3}}\mathrm{\Delta }{g}_{\mathrm{b}},\end{array}$$

where F_c is the contact force, F_l is the linear force in the linear model, and F_b is the parallel bond force. M_c and M_b are the contact moment and parallel bond moment, respectively. As the linear model does not resist relative rotation, M_c is always equal to the moment carried by the parallel bond model (M_b). F_l consists of the normal force and the shear force in the linear model, where the normal force is calculated as the normal stiffness of contact in the linear model (K_n1) times the overlapping distance between two contacting discs (g_n), and the shear force is calculated as the shear stiffness of contact in the linear model (K_s1) times the incremental shear displacement (Δg_s) added to the shear force calculated at the previous time step ($F_{\mathrm{s}}^{i-\mathrm{1}}$). Likewise, F_b consists of the normal force and the shear force in the parallel bond model. K_n2 and K_s2 are the corresponding bond stiffnesses in the normal and shear directions, respectively, and d and d₀ are the current and initial distances, respectively, between the two discs. M_b is resolved into a twisting moment and a bending moment, while the former is equal to 0 in the linear model. Thus, M_c is always equal to the bending moment carried by the parallel bond model, expressed as the bond stiffness in the bending direction (K_n3) times the relative displacement between bonded discs in the bending direction (Δg_b). More details related to these contact models and the basic theories of the DEM model can be found in Itasca Consulting Group (2014).

Figure 1 Schematic diagrams of the linear parallel bond model (a) and the linear model (b).

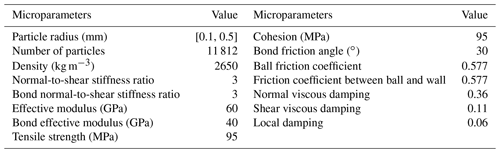
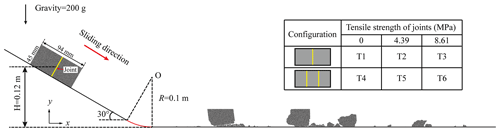
Based on the linear parallel bond model and related theories, a schematic view of the simulated model configuration used herein to analyse the fragmentation of a propagating rock mass is shown in Fig. 2. The travel path is composed mainly of an inclined slope and a horizontal plane connected by an arc with a radius of curvature of 0.1 m. The inclined plane is a frictionless rigid plane with a slope angle of 30^∘, while the friction angle of both the arc and the horizontal plane is 30^∘ to dissipate kinetic energy. Referring to Zhao et al. (2017, 2018) and Bowman et al. (2012), the size of each rock block used here is 94 mm × 45 mm, which consists of 11 812 particle aggregates cemented by the parallel bond model. The microparameters of each rock block in the DEM model are based on the numerical procedure applied in Potyondy and Cundall (2004), in which the macroproperties of Lac Du Bonnet granite (Martin, 1993) are used. Uniaxial compressive tests and uniaxial tensile tests are employed to calibrate the microparameters of the rock blocks in the simulation. The input values of the microscopic parameters in the DEM model are selected by trial and error to ensure that the mechanical characteristics of the rock block in the simulation match those of real Lac Du Bonnet granite. Table 1 lists the input microparameter values of the DEM model. The uniaxial compressive strength, Young's modulus, Poisson's ratio and tensile strength of the rock block in the simulation are 200.4 MPa, 67.6 GPa, 0.259 and 40.97 MPa, respectively. The drop height of the rock block (H) in this simulation is 0.12 m. The gravitational constant of acceleration (g^′) is enhanced to 1962 m s⁻² (200g) to approximate the real stress field of a rock avalanche (Zhao et al., 2017, 2018).

Table 1 Input microparameters of the DEM model.

Different from the traditional plane strain or plane stress situation, no results of laboratory experiments can be directly used to calibrate the damping values in 2D DEM simulations (i.e. the energy dissipation caused by particle–particle and particle–boundary interactions). Based on our previous 3D DEM simulation and other similar simulations (Giani et al., 2004; Lo et al., 2014; Murugaratnam et al., 2015; Lin et al., 2020), the local, normal and shear viscous damping terms are set to 0.06, 0.36 and 0.11, respectively. Note that viscous damping affects only the efficiency of energy dissipation and the eventual run-out distance of sliding blocks (Johnson et al., 2016), whereas the dynamics of the block system and the fragmentation mechanism of the rock blocks do not change. Each simulation shows the typical processes of rock fracturing and emplacement, which validates the applicability of these microparameters for the DEM model.

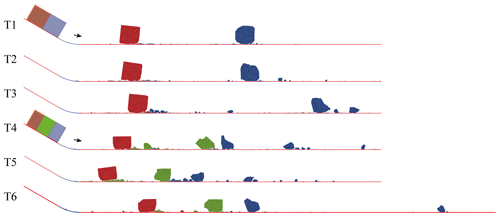
As the inset table in Fig. 2 shows, joints with different strengths and numbers that equally divide each block are predesigned in the rock blocks, yielding a total of six testing conditions. T1, T2 and T3 represent simulated rock blocks with one joint featuring different tensile strengths, while T4, T5 and T6 represent rock blocks with two joints featuring the same varying tensile strengths. The tensile strengths of the joints (σ) are 0 MPa (T1 and T4), 4.39 MPa (T2 and T5) and 8.61 MPa (T3 and T6). The joints with different tensile strengths are defined by reducing the bond cohesion within the joint planes. The joint planes have a width of 1.5 mm (3 times the mean particle size) and a length of 45 mm (the height of the rock block). The joints with no tensile strength are defined simply by debonding the particles within the joint plane. Furthermore, the block strength remains unchanged (200.4 MPa) under all simulated conditions. With the design of pre-existing planes of weakness (joints), the rock blocks break mainly along these weak joint planes at the initial stage of fragmentation during motion. Then, the energy conversion processes within the block system and the variation in the motion of sub-blocks can be clearly recorded and analysed (here, a sub-block represents an intact block cut by a pre-existing joint). The blocks with a joint tensile strength of 0 (T1 and T4) aim to represent the separation of blocks that have been fractured, while the blocks containing joints with nonzero tensile strengths are intended to represent the effects of joint fracturing on blocks. Note that the cracking of a rock block along a specific direction or plane of weakness does not change the nature of rock fragmentation (Ghaffari et al., 2019). Instead of trying to replicate the complicated fragmentation processes that occur in real rock avalanches, this simplified configuration is intended only to provide an opportunity to investigate the detailed microprocesses of fragmentation and the effects of fragmentation on a sliding and fragmenting rock mass system. Table A1 in the Appendix shows the main variables used in this study.

Figure 2 Schematic view of the model configuration. The detailed configurations of jointed rock blocks are shown in the inset table, where the yellow lines in the grey blocks represent the positions of joints. The joints, which are 3 mm wide and 45 mm long, equally divide each block.

3 Results

3.1 Fragmentation of rock blocks

In this section, the cracking along pre-existing joints and the fragmentation of sliding masses are examined. Considering that all of the tests experience a similar process, only the evolutions of T1 and T3 are presented in Fig. 3; these evolutions are described in detail to illustrate the fragmentation processes of rock blocks. For T1, local fragmentation (S_1T1) first occurred at the frontal bottom as it reached the arcuate segment of the travel path (Fig. 3a). Next, further local fragmentation occurred in the same part of the block due to the impact, and fracturing began along the pre-existing joint; this is called the separation stage (S_2T1). In this stage, the joint fractured completely from the bottom surface to the top surface of the block within a short time. In the following stage (S_3T1), the front sub-block was pushed forwards by the rear sub-block, and local fragmentation occurred at the middle top surface. Finally, both of the sub-blocks were deposited along the horizontal plane with different degrees of further fragmentation. For T3, characterized by a higher tensile strength, similar processes of fragmentation and separation were observed (Fig. 3b). Similar to T1, T3 also showed local fragmentation at the frontal bottom of the block as it slid onto the arcuate path (S_1T3). Subsequently, more intense local fragmentation occurred (S_2T3). Due to the high tensile strength, however, no fracture occurred along the predesigned joint at this stage. Rather, fracturing along the pre-existing joint occurred in a later stage, called the cracking stage (S_3T3).

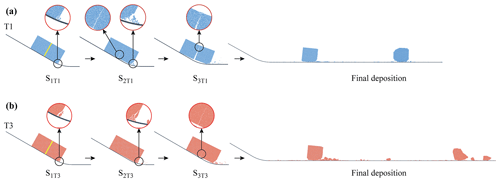
Figure 3 (a) Evolution of T1 in the initial stage of fragmentation and its depositional characteristics and (b) evolution of T3 in the initial stage of fragmentation and its depositional characteristics (S_1T1, S_2T1, S_3T1, S_1T3, S_2T3 and S_3T3 represent three specific stages and times for T1 and T3 that are described and analysed later). The light-blue sub-block in the final deposition stage represents the rear sub-block, while the dark-blue sub-block represents the front sub-block.

The separation stage for T1 (S_2T1) is represented by two tightly packed rock blocks disintegrating and separating along a specific orientation, which may be any type of discontinuity (rock blocks do not fragment but separate). In contrast, the cracking stage for T3 (S_3T3) is represented by the rock block experiencing dynamic cracking and “fragmentation” along a specific orientation (rock blocks separate due to fragmentation). Accordingly, we directly compare these two stages to examine the dynamic mesoscale fragmentation of rock blocks and the rock fragment system dynamics. Note that the travel distance of the centre of mass for T1 is slightly shorter than that for T3.

To determine the exact times when these fragmentation processes occurred, especially the times when the blocks separated along the joints, six monitoring particles near the joint are selected to record their velocity variations. The monitoring particles are symmetrically distributed along both sides of the joint and are equally spaced in the vertical direction, as shown in the inset diagram in Fig. 4a. The distance between the joint and monitoring particles is approximately twice the mean particle size. Following Zhao et al. (2017), nondimensional parameters are employed. The sliding time (t) is normalized by $(\mathrm{2}H/g^{\prime }{)}^{\mathrm{1}/\mathrm{2}}$, and the normalized particle velocity ($V_{\mathrm{p}}^{\prime }$) is defined as $V_{\mathrm{p}}^{\prime }=V_{\mathrm{p}}/(\mathrm{2}{g}^{\prime }H{)}^{\mathrm{1}/\mathrm{2}}$. The variations in the velocities of the monitoring particles in T1 and T3 are plotted in Fig. 4a and b, respectively. To highlight the fracturing effects along the joints, only the stage when the block reached and travelled along the arcuate path was plotted ($t^{\prime }=\mathrm{1.443}$–1.808 s). In general, the velocity curves continuously fluctuate due to the interaction between the rock block and sliding path, which leads to the propagation of stress waves and a minuscule velocity difference inside the block (Zhao et al., 2017), as shown in Fig. 4a. At the very beginning, the velocity of each monitoring particle was the same. When the rock block reached the arcuate section of the path, the velocities of the monitored particles at different positions began to diverge. The first local fragmentation time (S_1T1) corresponds to the time when the velocities of all monitoring particles began to exhibit vigorous fluctuations, i.e. $t^{\prime }=\mathrm{1.527}$ s. S_2T1 is the time when the velocities of particles P₃ and P₆ bifurcated, i.e. $t^{\prime }=$ 1.585 s. Then, the joint entered the transient cracking stage (with a duration time of 0.00257 s) and completely fractured at $t^{\prime }=$ 1.587 s. After $t^{\prime }=$ 1.617 s, the three monitored particles in the front sub-block maintained their velocity differences and continued to move, while the velocities of the three particles in the rear sub-block gradually converged. As time passed, further fragmentation, i.e. S_3T1, occurred at $t^{\prime }=$ 1.750 s, when the velocities of the monitored particles abruptly fluctuated once again. Figure 4b shows the variations in the velocities of the monitored particles of T3. Two velocity variations were recorded at $t^{\prime }=$ 1.519 and 1.589 s, corresponding to the local fragmentation stages S_1T3 and S_2T3. After that, the velocities of particles P₃ and P₆ separated at $t^{\prime }=$ 1.627 s, i.e. the S_3T3 stage, which is similar to S_2T1. The duration time of cracking stage S_3T3 (0.00154 s) is significantly shorter than that of the separation stage of T1 (S_2T1).

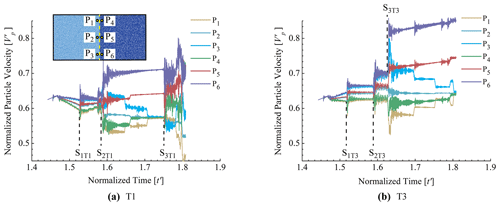
Figure 4 (a) Normalized particle velocities of monitoring particles in T1 versus time (the inset diagram shows the relative positions of the six monitoring particles, where $t^{\prime }=t/(\mathrm{2}H/g^{\prime }{)}^{\mathrm{1}/\mathrm{2}}$ and $V_{\mathrm{p}}^{\prime }=V/(\mathrm{2}{g}^{\prime }H{)}^{\mathrm{1}/\mathrm{2}}$). (b) Normalized particle velocities of monitoring particles in T3 versus time.

The velocity increases in P₅ and P₆ at S_3T3 were larger and more transient than those at S_2T1 during the separation stage. In addition, the velocities of P₁ and P₃ at S_3T3 experienced energetic increases and decreases at the very beginning of the cracking stage, which did not occur during S_2T1. As revealed by Fig. 4, the variations in the velocities between the block separation stage (S_2T1) and block cracking stage (S_3T3) display different characteristics, which may indicate different kinetics and energy conversion styles between block interactions and collisions and the dynamic fragmentation of the rock mass (which is discussed in the following section).

The variations in the velocities of the monitoring particles show a certain difference between the separation (S_2T1) and cracking (S_3T3) stages of the blocks. To quantify the influences of microscopic differences in the separation and cracking processes on the movement of the block system, the mean horizontal velocities (V_b) of the entire block and the rear and front sub-blocks are calculated. V_b is defined as

$$\begin{array}{}\text{(6)}& V_{\mathrm{b}}={\displaystyle \frac{{\sum }_i^n{v}_{x,i}{m}_i}{{\sum }_i^n{m}_i}},\end{array}$$

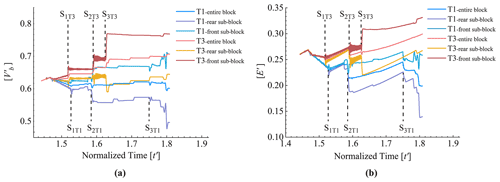
where n is the total number of particles in the calculated region, and v_x,i and m_i are the horizontal velocity and mass of particle i, respectively. Here, V_b is normalized as $V_{\mathrm{b}}^{\prime }=V_{\mathrm{b}}/(\mathrm{2}{g}^{\prime }H{)}^{\mathrm{1}/\mathrm{2}}$ for analysis. Figure 5a plots the normalized mean horizontal velocities ($V_{\mathrm{b}}^{\prime }$) of T1 and T3 versus time. Corresponding to Fig. 4, the different times when the blocks locally fragmented and separated along joints, i.e. S_1T1, S_2T1, S_3T1, S_1T3, S_2T3 and S_3T3, are also marked in Fig. 5a. $V_{\mathrm{b}}^{\prime }$ obviously fluctuates at the marked times, effectively matching the times when the velocities of the monitored particles abruptly changed (Fig. 4). At the local fragmentation stages (S_1T1, S_1T3 and S_2T3), $V_{\mathrm{b}}^{\prime }$ of the front sub-block increased rapidly when a collision occurred, while $V_{\mathrm{b}}^{\prime }$ of the rear sub-block first presented a rapid decrease and then recovered in a short time. Additionally, $V_{\mathrm{b}}^{\prime }$ of the T3 rear sub-block recovered to higher levels than before after rapid decreases at S_1T3 and S_2T3. $V_{\mathrm{b}}^{\prime }$ of the T1 rear sub-block recovered to its precollision value only after a rapid decrease at S_1T1. Moreover, $V_{\mathrm{b}}^{\prime }$ of the entire T3 block increased significantly at the local fragmentation stages (i.e. S_1T3 and S_2T3), while that of T1 presented only a minor increase at its local fragmentation stage (S_1T1). This contrast may be due to the local fragmentation at the frontal bottom of the front sub-block causing the horizontal ejection of some fragments that achieved a high velocity from the release of strain energy (Fig. 3).

At the separation stage (S_2T1), $V_{\mathrm{b}}^{\prime }$ of the T1 front sub-block rapidly increased, while $V_{\mathrm{b}}^{\prime }$ of the T1 rear sub-block inversely decreased. $V_{\mathrm{b}}^{\prime }$ of the entire T1 block first experienced a slight decrease, and then part of the lost velocity recovered in a short time. Similar to S_2T1, $V_{\mathrm{b}}^{\prime }$ of the T3 front sub-block and rear sub-block experienced the same increasing and decreasing phases at the cracking stage (S_3T3), respectively. However, the increase in $V_{\mathrm{b}}^{\prime }$ of the T3 front sub-block was more energetic than that of the T1 front sub-block at this stage. Moreover, as illustrated in Fig. 5a, the $V_{\mathrm{b}}^{\prime }$ of the entire T3 block shows a slight increase at S_3T3, which is different from that of the entire T1 block at S_2T1. Particularly, in S_3T1, $V_{\mathrm{b}}^{\prime }$ of the entire T1 block and the T1 rear and front sub-blocks all decreased when both sub-blocks collided at the middle top point, and then, $V_{\mathrm{b}}^{\prime }$ of the entire T1 block recovered to its value before collision or was slightly higher than before. Notably, the $V_{\mathrm{b}}^{\prime }$ values of T3 are generally higher than those of T1 after the blocks slid onto the arcuate path (1.48–1.78 s).

To analyse the energy variations in the fragmentation process, the kinetic energy of the entire block, the rear sub-block and the front sub-block is calculated for both T1 and T3. Here, the kinetic energy of the block is calculated as

$$\begin{array}{}\text{(7)}& E={\sum }_i^n{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{m}_i(v_{x,i}^{\mathrm{2}}+v_{y,i}^{\mathrm{2}}),\end{array}$$

where n is the total number of particles in the calculated region; v_x,i and v_y,_i are the horizontal and vertical velocities of particle i, respectively; and m_i is the mass of particle i. Figure 5b shows the variations in the normalized kinetic energies ($E^{\prime }=E/m{g}^{\prime }H$) of T1 and T3 versus the travel time. It should be noted that only $E^{\prime }/\mathrm{2}$ of the entire block (half of the normalized kinetic energy of the entire block) is plotted in Fig. 5b for clarity.

Similar to the variation in the mean horizontal velocity of the rock block (Fig. 5a), in the local fragmentation stages of T1 and T3 (S_1T1, S_1T3 and S_2T3), the kinetic energy of the rear sub-block significantly decreased, while that of the front sub-block obviously increased. Corresponding to such variations, small fragments were ejected from the frontal bottom part of the block after impact, as shown in Fig. 3. This local impact-generated fragmentation was accompanied by a sudden decrease in the total kinetic energy of the entire block, which indicates that the impact–fragmentation process consumes energy. However, although E^′ of the entire T3 block shows a decreasing trend at the local fragmentation stage, the mean horizontal velocity ($V_{\mathrm{b}}^{\prime }$) of the entire T3 block presents an increasing trend at this stage, as described above (Fig. 5a). Thus, this increase in the mean velocity of the entire T3 block may be derived from the conversion of energy due to an increase in the vertical velocity loss.

At the separation stage, S_2T1, the kinetic energies of the entire T1 block, rear sub-block and front sub-block all suddenly decreased, while E^′ of the front sub-block rapidly recovered and increased after the sudden decrease. The characteristics of the variation in the E^′ of T3 are different from those at S_3T3, with E^′ of the T3 front sub-block increasing more than that of T1. More interestingly, E^′ of the entire block for T3 quickly rebounded after a transient slight decrease. The magnitudes of the variations in E^′ for the rear and front sub-blocks of T3 at S_3T3 are much larger than those at S_2T1.

Moreover, after the separation of sub-blocks for T1, the rear sub-block impacted and pushed the front sub-block at the middle top part (S_3T1). At S_3T1, E^′ of the entire T1 block and the rear and front sub-blocks all decreased. After this point, E^′ of the T1 front sub-block gradually recovered, but E^′ of the entire T1 block and rear sub-block continuously decreased. This phenomenon illustrates a typical collision-induced momentum transfer process (Heim, 1932; Van Gassen & Cruden, 1990; Miao et al., 2001).

Figure 5 (a) Normalized horizontal velocities of the blocks in T1 and T3 versus time ($V_{\mathrm{b}}^{\prime }=V_{\mathrm{b}}/(\mathrm{2}{g}^{\prime }H{)}^{\mathrm{1}/\mathrm{2}}$). (b) Normalized kinetic energy evolutions of the blocks in T1 and T3 versus time ($E^{\prime }=E/m{g}^{\prime }H$). Note that $E^{\prime }/\mathrm{2}$ of the entire block is plotted.

3.2 Energy variation

At the local fragmentation stage (S_1T1, S_1T3 and S_2T3), the velocity and kinetic energy for the front part of the block exhibit a clearly increasing trend, while the opposite trend can be observed for the rear part of the block. More importantly, the variations in the block velocities and the kinetic energies of the entire blocks are very different between S_2T1 and S_3T3. In this section, the effects of joint fracturing and block fragmenting on the redistribution of energy are quantified. For this analysis, the mean horizontal velocity before and after sub-block separation in each test (v_be and v_af) is calculated; then, the incremental ratio in the separation stage of each test is calculated (${\mathit{\phi }}_{\mathrm{v}}=(v_{\mathrm{af}}-v_{\mathrm{be}})/v_{\mathrm{be}}$); φ_v of the entire block and of the rear and front sub-blocks is obtained in the tests. For the two-joint conditions (T4, T5 and T6) (Fig. 2), sub-blocks usually separated along the frontal joint first. Then, separation occurred along the other joint, accompanied by the concomitant impacting, fragmenting, rolling (usually at the surface of the rock avalanche but not inside the rock mass in real events) and sliding of fragments, resulting in very complicated monitoring curves. Thus, only the incremental velocity ratio of the front joint separation under such conditions is presented and analysed here. The same method is used to calculate the incremental kinetic energy ratios of the blocks (${\mathit{\phi }}_{\mathrm{e}}=(E_{\mathrm{af}}-E_{\mathrm{be}})/E_{\mathrm{be}}$, where E_be and E_af are the kinetic energies of the rock block before and after joint separation). Figure 6 depicts the calculated values of φ_v and φ_e.

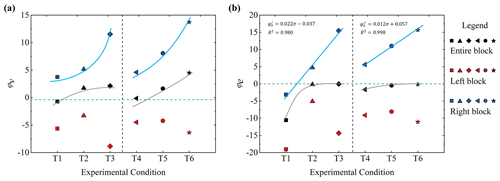
Figure 6 (a) Mean horizontal velocity increment expressed as a percentage (φ_v) and (b) kinetic energy increment expressed as a percentage (φ_e) in the block separation stage for all tests.

As shown in Fig. 6, the φ_v and φ_e values of the rear sub-block in each test are all less than 0, indicating that the rear sub-block lost its horizontal velocity and kinetic energy in the joint cracking stage. In the tests with the same joint set, φ_v and φ_e of the entire blocks show increasing trends versus the joint strength. For φ_v under different joint sets, the values for both blocks increase from nearly 0 to higher values, and the rates of increase in the tests with both joint sets are higher than those characterized by one joint set. Different from φ_v, the φ_e values of the entire blocks under both joint set conditions are entirely negative, and both display increasing trends versus the joint strength, with their values tending to 0. The φ_v values of the front sub-blocks in both joint sets present increasing trends versus increasing joint strength, with all values positive. The highest incremental ratio of φ_v reaches 15 %. The φ_e values of the front sub-blocks also show increasing trends versus joint strength, with the highest incremental percentage exceeding 15 %. Different from the regular increasing variations in φ_v and φ_e of the entire block and front sub-block, those of the rear sub-blocks present a different feature versus joint strength, namely, an increasing part and a following decreasing trend.

According to the curves shown in Fig. 6b, the relationship between the kinetic energy incremental ratio (φ_e) of the front sub-block and the tensile strength of the joints (σ, which represents the general strength of the rock mass) can be described by a linear fitting function:

$$\begin{array}{}\text{(8)}& \left\{\begin{array}{l}{\mathit{\phi }}_{\mathrm{e}}^{\prime }=\mathrm{0.022}\mathit{\sigma }-\mathrm{0.037}\left(\mathrm{T}\mathrm{1},\mathrm{T}\mathrm{2},\mathrm{T}\mathrm{3}\right)R^{\mathrm{2}}=\mathrm{0.980}\\ {\mathit{\phi }}_{\mathrm{e}}^{\prime \prime }=\mathrm{0.012}\mathit{\sigma }+\mathrm{0.057}\left(\mathrm{T}\mathrm{4},\mathrm{T}\mathrm{5},\mathrm{T}\mathrm{6}\right)R^{\mathrm{2}}=\mathrm{0.998}.\end{array}\right.\end{array}$$

The linear fitting function (Eq. 8) shows that the energy of the front sub-block is greatly enhanced after joint fracturing (which represents the cracking process or the simplest fragmentation process) as the rock mass strength increases. Note that the linear fitting function (Eq. 8) is presented here to describe only the increasing trend of φ_e with rock strength but is not enough to be considered the real relationship between φ_e and σ because of insufficient data.

3.3 Deposition characteristics

Figure 7 presents the final deposit features of the rock blocks under all simulated conditions. All of the rock masses cracked mainly along joints. Furthermore, intense fragmentation occurred within the sub-blocks and contributed to the generation of fine particles in the deposits. The frontal sub-blocks clearly present higher degrees of fragmentation than the middle and rear sub-blocks, and the rock masses with two joint sets show higher degrees of fragmentation in the deposits than the rock masses with one joint. Moreover, the deposits of all tests show good preservation of the initial rock mass sequences, which has also been reported in many natural rock avalanches (Heim, 1932; Strom, 2006; Hewitt et al., 2008; Dufresne et al., 2009).

Figure 7 Deposit profiles of all simulations.

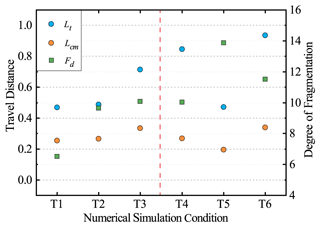
Figure 8 plots the travel distances and degrees of fragmentation of the rock masses. Here, the run-out of the distal edge (L_t) and the run-out of the centre of mass (L_cm) are used to describe the travel distances of the rock masses (Lin et al., 2020). The relative breakage ratio (F_d) is used to describe the degree of fragmentation (Hardin, 1985; Bowman et al., 2012). For the rock masses with one joint (T1, T2 and T3), both L_t and L_cm increase with increasing joint strength, as does the degree of fragmentation (F_d). For the rock masses with two joints (T4, T5 and T6), both L_t and L_cm first display a decreasing trend and then increase versus the joint strength, and the variation in L_t is obviously greater than that in L_cm. Correspondingly, the degree of fragmentation of the deposits first displays an increasing trend and then decreases with the joint strength, indicating the highest degree of fragmentation for T5. Furthermore, the degree of fragmentation of the rock masses with two joints is obviously higher than that of the corresponding rock masses with one joint, although the run-outs of their centres of mass are similar. As shown, T5 has a shorter travel distance (for both the distal edge and the centre of mass) and achieved a higher degree of fragmentation. This difference may be due to the different interactions of the fragments after the initial fragmentation of T5.

Figure 8 Travel distance and degree of fragmentation of all simulations (L_t represents the travel distance of the distal edge, L_cm represents the travel distance of the centre of mass, and F_d represents the degree of fragmentation).

4 Discussion

4.1 Variations in energy accumulation and dissipation

Here, the conversion and transformation of energy within the sliding mass during joint fracturing and fragmentation are discussed. McSaveney and Davies (2006) indicated that the remaining strain energy stored in fragmented rock pieces after cracking may be converted into kinetic energy, allowing fragments to be ejected during dynamic fragmentation in an avalanche. However, few direct experiments or numerical simulations have illustrated the energy variation related to the fragmentation of a rock mass during movement (Haug et al., 2016; Zhao et al., 2017). Hence, in this study, the conversion of elastic strain energy during rock mass fragmentation and sliding is analysed.

In the linear parallel bond model, both linear and bond springs can bear stress and generate elastic strain when loaded by a force, although part of the energy may be consumed by dashpots (Potyondy and Cundall, 2004). Thus, the strain energies carried by both linear (E_s) and bond (E_bs) springs are calculated, where the total strain energy ($E_{\mathrm{ts}}=E_{\mathrm{s}}+E_{\mathrm{bs}}$) is obtained by PFC2D. The elastic strain energy variations in T1 and T3 over time are shown in Fig. 9a, in which the normalized elastic strain energy is normalized by the maximum total strain energy (E_ts-max) for better comparison. As shown in Fig. 9a, E_bs is larger than E_s most of the time, indicating that parallel bonds carry more strain energy than linear springs between discs when pressurized. The variations in these two strain energy components are synchronized. Furthermore, compared with Figs. 4 and 5, the time when the total strain energy peaks is consistent with the time when the particle velocity, block velocity and kinetic energy abruptly fluctuate. In addition, the value of the elastic strain energy in the cracking stage of T3 (S_3T3) is much larger than that in the separation stage of T1 (S_2T1), indicating that a rock block with a higher joint strength accumulates more strain energy before fracturing.

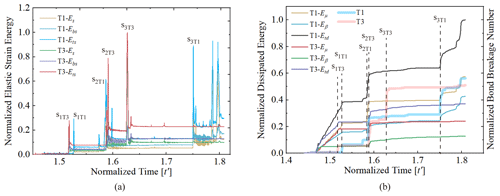
Figure 9 (a)  Normalized elastic strain energy variation in the sliding blocks in T1 and T3 (normalized by the maximum total strain energy, E_ts-max) versus time. (b) Normalized dissipated energy variation in the sliding blocks in T1 and T3 (normalized by the maximum total dissipated energy, E_td-max) versus time. The two bold curves represent the variations in the number of broken bonds (also normalized by the maximum number of broken bonds) in T1 and T3 versus time.

Figure 9b shows the variation in energy dissipation during the rock mass movements of T1 and T3. The energy dissipation is composed of energy dissipated by frictional slip (E_μ, slip energy) and by dashpots (E_β; dashpot energy represents the energy loss by the collision of clasts). The total dissipated energy ($E_{\mathrm{td}}=E_{\mathit{\mu }}+E_{\mathit{\beta }}$) is also calculated. The total dissipated energy is simply normalized by the maximum value of the total dissipated energy (E_td-max) during the recorded stage. Figure 9b also shows the variations in the numbers of broken bonds in T1 and T3 over time, where the value is normalized by the total number of broken bonds during the recorded stage. The evolution of the number of bonds broken and the trend of dissipated energy are synchronized, which is consistent with the variations in the strain energy shown in Fig. 9a. In general, the dashpot energy is lower than the slip energy, but both increase with time. The total energy dissipation of T1 is always larger than that of T3, and their difference increases over time. Correspondingly, the slip energy and dashpot energy of T1 are also larger than those of T3; in particular, the slip energy of T1 greatly increases at S_2T1 due to frictional slip along the joint. The fragmentation energy caused by joint fracturing and sub-block breaking can also be reached, albeit with values obviously lower than E_μ and E_β. In addition, the fragmentation energy of T3 is higher than that of T1, which is consistent with the variations in their numbers of broken bonds. Combined with the variations in the kinetic energy shown in Fig. 5b, the energy conversion of the sliding mass in the recorded time can be deduced. First, when the rock block slides along the arcuate path and interacts with the path surface, part of the kinetic energy is transformed into elastic strain energy stored in bonds and linear springs. Second, bonds break once the impact force is locally greater than the bond strength, and the elastic strain energy stored in those broken bonds vanishes. As the number of broken bonds increases, a crack forms; during this period, the number of broken bonds increases. Third, as the crack continues to develop and the block rebounds, the impact force gradually decreases. At the same time, the remainder of the strain energy stored in the entire block is released, which is eventually converted into the kinetic energy of fragments. The high consistency between the variations in the dissipated energies and the block propagation stages indicates that the energy dissipation due to joint fracturing and sub-block fragmentation is minimal, whereas most energy dissipates due to friction. The existence of joint planes with no initial tensile strength greatly contributes to the dissipation of energy due to the high-frequency interaction between the front and rear sub-blocks along the joint, for example, during the S_2T1 stage.

4.2 Energy transfer induced by rock fragmentation

As described above, in T1, we set a joint without tensile strength. With this design, the motion and separation of two closely packed blocks are simulated and reproduced. During the separation stage (i.e. S_2T1), the horizontal velocity of the T1 front sub-block increases (↑ 3.72 %), with the rear sub-block losing part of its horizontal velocity (↓ 5.30 %) (Fig. 6a). Moreover, the kinetic energy of the front sub-block increases slightly after a sharp decrease during separation (↓ 2.90 % in total), while that of the rear sub-block shows a continuous decrease (↓ 16.45 %) (Fig. 6b). This process constitutes a typical momentum transfer phenomenon caused by unrelenting collisions between the rear and front sub-blocks, which is very common in granular flows (Heim, 1932; Manzella and Labiouse, 2009; Lai et al., 2017). Considering that the tensile strength of the joint in T1 is 0, collisions are how the front and rear sub-blocks interact during the joint separation process. Hence, we describe this phenomenon as collision-induced energy transfer.

Different from T1, a joint with tensile strength is designed in T3, and the fracturing process of a rock block along a weak joint is simulated. As revealed in Fig. 6, the horizontal velocity and kinetic energy of the T3 front sub-block also increase (↑ 12.56 % and ↑ 15.23 %, respectively), with those of the rear sub-block decreasing (↓ 5.30 % and ↓ 8.89 %, respectively). Considering that the tensile strength of the joint in T3 is not 0, we describe this phenomenon (S_3T3) as fragmentation-induced energy transfer. According to Figs. 5, 6 and 8, the fragmentation-induced energy transfer from the rear sub-block to the front sub-block in T3 is due to the release of elastic strain energy and its conversion into kinetic energy, which is also inferred in the literature (Zhang et al., 2000; Li et al., 2005; Davies and McSaveney, 2009; De Blasio and Crosta, 2015). Through a comparison of the kinetic energy evolutions of the entire T1 and T3 blocks (Figs. 5b and 6b), it is concluded that fragmentation-induced energy transfer can clearly lead to a greater increase in kinetic energy (E^′) of the frontal sub-block and less energy lost for the entire block (↓ 0.07 %) than can collision-induced energy transfer (resulting in an overall energy loss of 10.76 % for the entire block). Since the efficiency of fragmentation-induced energy transfer is higher than that of collision-induced energy transfer and because fragmentation is a ubiquitous phenomenon in natural rock avalanches, we suggest that dynamic fragmentation may play a more efficient run-out-enhanced role in the spreading of rock masses than particle interactions within unbreakable granular flows during the emplacement of rock avalanches. Indeed, field investigations show that many rock avalanches with high degrees of fragmentation have unpredicted thin deposits (Crosta et al., 2017; Wang et al., 2018b, 2018c), which may be related to fragmentation-induced energy transfer, as indicated by our results.

4.3 Multiscale effects caused by rock fragmentation in rock avalanches

With the design of joints characterized by different strengths and numbers, this study simulates a simplified fragmentation process of rock masses, thereby providing insights into the contribution of fragmentation to rock mass propagation. Although this simplified simulation cannot reproduce the real fragmentation processes of natural rock avalanches, some of the results can still shed light on the details of rock avalanche propagation. Therefore, the following discussion focuses primarily on the multiscale effects of rock fragmentation based on the simulated results and natural rock avalanches to better understand the fragmentation and emplacement of natural rock avalanches.

This study indicates that the release of elastic strain energy is caused predominantly by fragmentation. Energy is transferred between the front and rear sub-blocks due to fragmentation, which promotes the forward movement of the front sub-block and hinders the movement of the rear sub-block (Figs. 5 and 6). Such energy conversion and transfer processes as a result of fragmentation have also been discussed in previous studies (Zhang et al., 2000; Lin et al., 2021; Haug et al., 2016; Bowman et al., 2012). As shown in Fig. 10a and b, the rock blocks along the surface of a sliding rock mass (carapace facies) may experience this kind of dynamic fragmentation (thus, fragments after block fragmentation carry a considerable amount of kinetic energy).

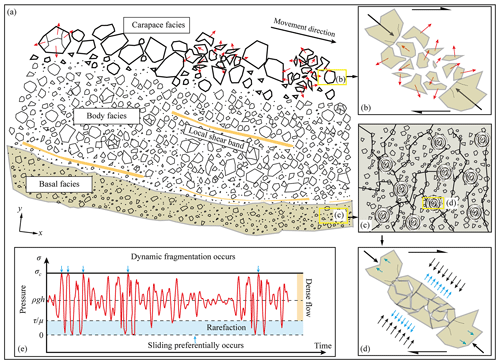
Figure 10 (a) Schematic illustration of the fragmentation of countless grains during the propagation of a rock avalanche. (b) Dynamic fragmentation of a rock block without confining pressure (in the carapace facies). (c) Force chain in the shear layer (basal facies) and local fragmentation points (grey–white rings represent the fragmentation points and related radiating stress waves). (d) Schematic illustration of the dynamic fragmentation of a rock block in a force chain with confining pressure (small black arrows represent the confining pressure, and small blue arrows represent the outward stress caused by fragmentation that develops into a stress wave propagating through the entire sliding rock mass) (modified from Melosh, 1979). (e) Pressure variation (red curve) at a point inside a rock mass caused by rock fragmentation during an avalanche (modified from Melosh, 1979). Blue arrows represent the times at which dynamic fragmentation occurs; σ_c is the critical stress for the rock to fracture.

Generally, normal-stress- and shear-stress-induced fragmentation processes are concentrated under the carapace facies in natural rock avalanches (Estep and Dufek, 2013; De Blasio and Crosta, 2015; Zhang and McSaveney, 2017). For dense granular flows (e.g. rock avalanches), force chains commonly occur. Grains in the force chain experience a higher stress than the surrounding grains (Fig. 10c); thus, they break first when the stress in the force chain is equal to the failure strength of the grains. The entire conversion and transfer process of one rock block observed in our simulation may also reproduce one episode of dynamic rock fragmentation in this force chain for real rock avalanches (Fig. 10c). Note that within a force chain, the strain rate, confining pressure and fracture form do not change the nature of energy conversion during the fragmentation of the rock block (Ghaffari et al., 2019). However, the occurrence of confining pressure in a force chain may alter the mechanism by which elastic strain energy is released. Based on our simulation results, rock fragments spread out with some kinetic energy when there is no confining pressure, as mentioned above (Fig. 10b) (Zhang et al., 2000; Davies and McSaveney, 2009), causing part of the elastic strain energy to transform into the kinetic energy of fragments (fragmentation-induced energy transfer). However, since the grains in the force chains of natural rock avalanches are closely packed under high confining pressure, there is not enough space for the elastic strain energy stored inside the broken grains to be released in the form of the kinetic energy of fragments. For this reason, elastic strain energy is released in the form of outward elastic stress (pressure), also called an elastic body wave by Davies et al. (2019) (Fig. 10d). Thus, as indicated by our simulations, the energy transfer caused by dynamic rock fragmentation in a natural rock avalanche still occurs by means of outward elastic body waves, which eventually affects the movement of the avalanche. Based on the physics of elastic stress wave propagation, the release of elastic stress waves from rock fragmentation during an entire rock avalanche has three effects:

1. Sliding preferentially occurs in the local grain region of dynamic fragmentation in a force chain. As shown in Figs. 3 and 4, fragmented clasts separate because elastic strain energy is released outward. In a natural rock avalanche, these outward elastic stress waves introduced by dynamic rock fragmentation eventually cause the release of pressure carried by other grains within the force chain and their surrounding grains (stress drop after dynamic fragmentation; Fig. 10e). Then, sliding may occur as the shear stress remains unaltered, and the normal stress carried by the force chain suddenly decreases (de Arcangelis et al., 2018).

2. The propagation of elastic stress rarefaction waves superimposed on the stress field of the sliding mass causes the local normal stress to decrease and allows sliding to preferentially occur at locations where fragmentation does not occur (Fig. 10e) (Melosh, 1979; Johnson et al., 2016; Davies and McSaveney, 2016).

3. The elastic stress wave superimposed on the stress field of the sliding mass strengthens the local normal stress and allows fragmentation to subsequently occur at another location.

Note that all three of these effects are based on elastic stress wave fluctuations caused by fragmentation. For the entire basal layer or the main body in a rock avalanche, each fragmentation event may cause an elastic stress wave to be released according to our simulation results. Additionally, rarefaction-stress-wave-induced local sliding (Johnson et al., 2016) can occur within the entire sliding mass and become more concentrated near the bottom of the sliding mass (Fig. 10e). Rarefaction-stress-induced local sliding is controlled by the propagation and interaction of stress waves, the rock strength in the force chain, the overburden pressure, the local shear rate and so on. Therefore, the shear layer in the rock avalanche may thicken due to the random occurrence of local sliding. Moreover, the concentration of rarefaction-stress-induced local sliding in the body facies may lead to the formation of local shear bands despite the low shear rate in the main sliding mass. In contrast, rock breaks when the local superimposed stress exceeds the grain strength in the body facies (Fig. 9e); then, a jigsaw structure forms, and the main part of the strain energy is released as an elastic stress wave once again (Davies and McSaveney, 2009). Such a jigsaw structure may remain in the deposit due to the tight consolidation of the rock mass during the propagation of the rock avalanche and the persistence of grain fragmentation until the rock avalanche stops.

5 Conclusions

The fracturing and fragmentation processes of a sliding rock block and their influences on the conversion and transmission of energy within the rock mass system are investigated using 2D DEM simulations. Accordingly, the temporal evolutions of the particle velocities and of the velocities and kinetic energies of sub-blocks and the variations in the energy and degree of fragmentation of the entire rock mass system are examined in detail. With these observations, we present the multiscale effects of rock fragmentation on rock mass movement, which should shed light on the dynamics of fragmenting rock masses, such as rock avalanches.

The results show that rock fragmentation can greatly affect the energy variations in different parts of the rock mass. When a rock block cracks, the front sub-block gains additional kinetic energy, while the rear sub-block loses part of its kinetic energy, enabling the front sub-block to travel long distances. These kinetic energy variations are closely related to the release of elastic strain energy during the process of rock fragmentation, which has the same effect as the momentum transfer caused by collisions in a multiblock system. In particular, the energy transfer induced by rock fragmentation more efficiently induces energy transmission in a rock mass system than that induced by collision. Moreover, the increase in kinetic energy of the front sub-block is enhanced with increasing rock strength. This variation in kinetic energy indicates that a rock mass with a higher strength experiences a more energetic fragmentation effect.

Furthermore, the effects of dynamic rock fragmentation on the propagation of rock avalanches and the formation of some deposit structures are qualitatively examined based on our simulation results. Three possible effects of rock fragmentation on an entire rock avalanche are addressed: (1) sliding preferentially occurs at the points of fragmentation, and (2) sliding and (3) fragmentation both preferentially occur at locations that have not yet been fragmented as a result of the superposition of stress waves.

Appendix A

Table A1 List of variables considered in this study.