the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Exploring the partial use of the Mo.S.E. system as effective adaptation to rising flood frequency of Venice
Riccardo A. Mel
The Venice lagoon (Italy) is particularly vulnerable to the impact of subsidence and sea level rise driven by climate change. Some structural measures have been adopted over time to protect Venice from flooding, among which a system of flap gates (Experimental Electromechanical Module, Mo.S.E., system) has been operational in the testing phase since October 2020. However, relative sea level rise and wind set-up pose relevant management challenges, as a frequent closing of the lagoon would have negative impacts on flushing capacity, the fishing industry, and port activities. Here, the focus is on the hydrodynamic effects of a partial closure of the Mo.S.E. barriers that, compared to closing all the three inlets of the lagoon, could play a role in reducing the economic and environmental impacts of the Mo.S.E. system. The main goal is to identify the flooding events that can be counteracted by closing only the Lido inlet, which is the closest to the city of Venice. Based on the tidal and meteorological dataset collected in the period 2000–2019, a robust modelling exercise identifies a linear relationship between tidal range and reduction of the sea level peaks, which results in the protection of all urban settlements within the lagoon from two-thirds of the flooding events up to a relative sea level rise of +0.4 m.
- Article
(7913 KB) - Full-text XML
- BibTeX
- EndNote
Floods are a significant long-term risk to society (Wadey et al., 2012). While the population generally adapts to them (Van Koningsveld et al., 2008; Jongman, 2018), this is mostly accomplished as a consequence of real events (Mel et al., 2021b), which can involve significant economic losses and deaths (Hinkel et al., 2014; Jongman et al., 2014). In Europe coastal flooding is one of the most threatening natural hazards (e.g. Capobianco et al., 1999), and flood risk is expected to further increase in the near future in all the acting components, like sea level (SL) rise, tides, waves, and storm surges (Semedo et al., 2013; Wang et al., 2014; Androulidakis et al., 2015; Marcos et al., 2012; Jongman, 2018), with particular reference to extreme events (e.g. Menéndez and Woodworth, 2010; Wahl et al., 2011; MedECC, 2020). Coastal flood hazard is exacerbated by climate change, anthropogenic modifications of the land and environment, and by socio-economic factors (Pycroft et al., 2016), driving morphological changes and erosion processes (Ciavola et al., 2011), as well as coastal protection failures (Oumeraci, 1994; Matias et al., 2008), reducing the effectiveness of the traditional defence strategies (Few et al., 2007; OECD, 2016). As the flooding risk can never be entirely prevented, effective adaptation strategies are needed (Klein et al., 2001; Hinkel et al., 2014; Cutter and Gall, 2015), based on a diversified approach of interventions, which may include structural and non-structural measures aimed at preserving the social, economic, and environmental functions of coastal areas (Jongman, 2018; Tiggeloven et al., 2020). Structural measures (i.e. hard and soft flood defence works designed for long-term operating; see Maiolo et al., 2020) should be supported by non-structural measures, comprising laws, policies, regulations, planning instruments, optimal management protocols, risk assessment, and informational systems for coastal ecosystems and resource management (Smith and Lenhart, 1996; Kundzewicz, 2002; Elko and Briggs, 2020; Mel et al., 2020). Although several approaches and models have been proposed to optimize planning and management actions, implementing effective strategies requires complex decision-making processes and an innovative approach to flood defence (Few et al., 2007; Tobey et al., 2010), addressing the major institutional, economic, and environmental barriers (EC, 2009; Molinaroli et al., 2018).
Floods are a recurrent hazard for the iconic city of Venice (Mel and Lionello, 2014), a clear example of a huge historical, cultural, and environmental heritage at risk. Flood frequency has significantly worsened since the 1950s (Lionello et al., 2012; Mel et al., 2019a; Lionello et al., 2021) due to relative sea level rise (RSLR) which is caused by local subsidence and decadal-scale acceleration in the rate of global sea level rise driven by climate changes (Carbognin et al., 2004; Ferla et al., 2007; Lionello, 2012; Zanchettin et al., 2021). The detrimental effect produced by storm surges in the Adriatic Sea has been shown by the events of 4 November 1966 (De Zolt et al., 2006; Lionello et al., 2021) and 12 November 2019 (Cavaleri et al., 2020) which produced severe loss and damage to the historical buildings, economic activities in the coastal settlements located within the Venice lagoon, and even deaths.
The resilience of the Venice lagoon has been permanently linked to the human presence since remote times. The Venetians altered the environment by building several hard structures, with the aim of preserving economic interests and of maintaining the very existence of the lagoon, as well as for defence purposes (Molinaroli et al., 2009; Sarretta et al., 2010; Ferrarin et al., 2013). As non-structural measures adopted for prevention, preparedness, and response to floods, the Venetians raised the ground floors, placed steel barriers at the entrance to buildings, and adapted the existing electrical systems (Indirli, 2014; Molinaroli et al., 2018). Extreme storms were catalysts to the rising awareness that the lagoon had lost much of its natural resilience to floods (Samiolo, 2012), highlighting the need to build new flood defence structures and to invest more in adaptation strategies (Munaretto et al., 2012). After the 1966 flood, the Italian government supported by the scientific community and supranational organizations like UNESCO (UNESCO, 1969) promoted several structural measures to reduce the impact of flooding, erosion processes, and water pollution (e.g. Italian Law n. 171 of April 16, 1973; Italian Law n. 798 of 29 November 1984), like the Experimental Electromechanical Module (Mo.S.E.), a system of mobile barriers aimed at closing the inlets temporarily to protect the Venice lagoon through a set of 78 independent flap gates (Eprim, 2005).
In response to the devastating flood event which occurred in 2019, the safeguarding of the Venice lagoon became a pressing priority. Works to build the Mo.S.E. system began in 2003. Since 3 October 2020, the Mo.S.E. system has been operating in the testing phase (see Mel et al., 2021b). Within the first 3 months, the Mo.S.E. system was operated 20 times during high tide conditions (see Appendix A for the details of each operation). However, poor meteorological forecast, novel management options, and the economic and environmental impact of the closures raised a wide-ranging debate about the optimal use of the system. According to recent studies, the use of the Mo.S.E. system on the one hand contributes to lowering the short-term monetary costs induced by the periodical flooding (Nunes et al., 2005); on the other hand, if implemented too frequently or for too long a time, it could affect the water quality of the lagoon (Melaku et al., 2001; Viero and Defina, 2016) and induce additional direct and indirect costs to fishing and port activities (Costa, 1993; Vergano et al., 2010). As the need to close the barriers becomes more frequent in view of the ongoing processes of land subsidence and RSLR, the optimal management of the Mo.S.E. system will play a crucial role in balancing the needs of flood protection with the issues related to port activities and ecosystem preservation. According to Umgiesser (2020) and Mel et al. (2021a), only +0.3 m of RSLR would generate almost 100 closures per year, often involving multiple tidal cycles and disrupting a significant portion of vessel traffic (Brotto and Gentilomo, 1998; Umgiesser and Matticchio, 2006). In addition, the flushing of the lagoon would be greatly reduced, building up toxic substances and damaging its delicate ecosystem (AGU, 2002; UNESCO, 2011). In this context, a possible adaptation strategy consists of limiting the extent of the closure of the inlets through a partial use of the Mo.S.E. system (i.e. the closure of one or two inlets at a time or a partial closure of each inlet). In particular, the closure of the Lido inlet only can mitigate the flood hazard without significantly affecting the water quality and the economy of the lagoon since it is scarcely used for commercial traffic, like the Malamocco inlet, or fisheries, like the Chioggia inlet. Hereinafter, such partial operation of the Mo.S.E. system is named as partial closure of the lagoon involving the Lido inlet only (PCL).
Some recent studies that attempted to quantify the effects of the partial operation of the Mo.S.E. system (Cavallaro et al., 2017; Umgiesser et al., 2020) are affected by important limitations: the sea level thresholds associated with the partial closure of the barriers were kept fixed and equal to the thresholds associated with the full Mo.S.E. closure (Eprim, 2005), and the role of tidal range, wind set-up, and intra-gate infiltration was neglected. The present contribution aims to fill this knowledge gap by a systematic numerical investigation of the effects of the PCL on the hydrodynamics of the lagoon. Specifically, the main goals are (a) identifying a relationship between tidal range and reduction of the SL peak at the main settlements of the Venice lagoon, namely Venice, Burano, and Chioggia; (b) investigating the effects of wind set-up and intra-gate infiltration on such relationship; and (c) addressing the potential benefit of the PCL in reducing the frequency of full Mo.S.E. closures in the present and future scenarios. The results of the study can be beneficial for research and decision-making efforts toward an optimal management of the Mo.S.E. system.
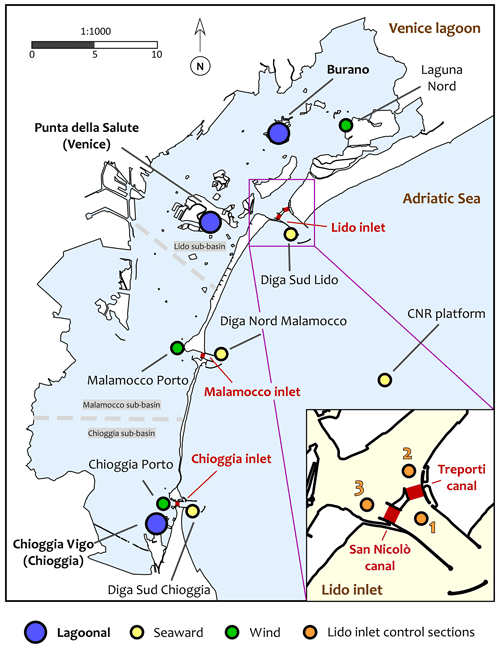
Figure 1The Venice lagoon with the location of the watersheds (dashed grey lines) and the Mo.S.E. barriers (thick red lines). The bullets show the location of wind (green) and tide stations (blue, lagoonal gauges; yellow, seaward gauges) used in the present work, coming from the database of the Tidal Forecast Centre of the Venice Municipality (Centro Previsioni e Segnalazioni Maree, CPSM).
2.1 Venice lagoon and Mo.S.E. system
The Venice lagoon, stretching for more than 60 km from north to south and about 12–16 km from west to east, is the largest Mediterranean brackish water body. It is connected to the Adriatic Sea through three inlets, namely, from north to south, Lido, Malamocco, and Chioggia, whose widths range from 400 to 800 m and depths between 6 and 14 m. Note that the Lido inlet is divided in two parts by the Mo.S.E. infrastructure, named “Treporti canal” and “San Nicolò canal”; see Fig. 1. The lagoon, characterized by an average water depth of about 3 m, consists of a complex system of channels, tidal flats, salt marshes, and small islands, as well as a high heterogeneity in physical and biogeochemical conditions of mutually interacting habitats (Carniello et al., 2009; Finotello et al., 2018; Molinaroli et al., 2018). The most prominent urban settlements are Burano, in the northern lagoon, Venice in the central lagoon, and Chioggia, located in the southern lagoon (Fig. 1). The main circulation forcing factors are a semi-diurnal tidal regime and the wind. The average residence time ranges from 1 d for the areas located close to the inlets to 30 d for the inner areas (Viero and Defina, 2016). Nutrient and pollutants mostly originate from urban areas and from the drainage basin (Melaku et al., 2001). For each tidal cycle, the water exchanged through the inlets is about a third of the total volume of the lagoon (Gacic and Solidoro, 2004). In calm atmospheric conditions, when circulation is influenced by the tide only, the Venice lagoon is subdivided into three sub-basins, one for each inlet, separated by two watersheds through which the residual flow is minimum (Fig.1, see also Solidoro et al., 2004). The propagation of the tide is affected by the shape of the inlets and the morphology of the lagoon. The tidal range reduces by proceeding from the inlets towards the lagoon interior, showing a progressive propagation lag. These alterations in tidal signal produce significant lagoonal currents, triggered by the prevailing SL differences between different regions of the same sub-basin. Prevalent winds are north-easterly (Bora wind) and south-easterly (Sirocco) at speeds of up to 20–25 m s−1 (Mel et al., 2021a).
For more than a millennium, Venice has endured by altering the environment of the lagoon (Brambati et al., 2003). Several hydraulic works, such as river diversion, the building of a large sea wall, and digging new navigation canals, enabled the historical heritage of Venice and the related industrial and economic activities to survive, producing a significant impact on the morphology of the lagoon and on the local tidal regimes (Carniello et al., 2009; Sarretta et al., 2010; Silvestri et al., 2018). By the 1970s, more than half of the lagoonal surface had been reclaimed or cordoned off for business-related purposes, altering the natural morphological features and amplifying the tidal range (Molinaroli et al., 2018). As from the very beginning Venice has co-existed with the sea by adopting several measures to adapt to the flood hazard, at present the Mo.S.E. system is conceived to protect the lagoon by temporarily separating it from the sea during the flood events. The Mo.S.E. system consists of four separate storm surge barriers (Fig. 1) formed by some independent flap gates 20 m wide, 5 m thick, and between 18 and 28 m high, hinged on the bottom of the inlets. The Lido inlet has two barriers with 21 (Treporti canal) and 20 (San Nicolò canal) elements, and Malamocco and Chioggia have a single barrier of 19 and 18 elements, respectively (see https://www.mosevenezia.eu/progetto/ (last access: 14 May 2021) for more technical details). In normal tidal conditions, the flap gates rest full of water on the bottom of the inlets. When a tide is expected to exceed the safeguard threshold, compressed air is pumped into the gates, allowing the barriers to rotate upwards interrupting the tidal flow (Gentilomo and Cecconi, 1997). The safeguard threshold, defined as the SL that should not be exceeded during high tides (Umgiesser, 2020), is set to 1.10 m above the local datum at Venice and Burano and 1.30 m at Chioggia, which has been protected since 2012 by a local defensive work installed at both ends of the main canal crossing the historical centre. As an important note, during the present testing phase of the Mo.S.E. system no specific management protocols have been adopted. The barriers have been operated partially and/or asynchronously in order to estimate the time needed to raise and drop the gates, monitor the hydrodynamics of a regulated lagoon, and highlight possible shortcomings (see Appendix A for the details).
In this work, SL elevations refer to the official local datum of the Punta della Salute (PS) SL gauging station, located in Venice city centre, whose zero is located 0.23 m below the national vertical level datum (IGM 1942) and 0.34 m below the present mean SL (Cavaleri et al., 2020).
2.2 Data and tidal characteristics
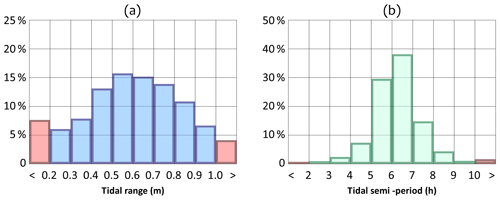
The SL, wind speed, and wind direction data used in the present work come from the database of the Tidal Forecast Centre of the Venice Municipality (i.e. Centro Previsioni e Segnalazioni Maree, CPSM). A first dataset consists of 2-year-long (2019–2020) records of SL, wind speed, and direction collected every 10 min, which are used to reproduce some recent flood events (all the gauges used in this work are reported in Fig. 1). From the same institution, SL peaks and troughs gauged within the period 2000–2019 (including a Metonic cycle) define the scope of the present work in terms of tidal range during the flood tide (i.e. the SL difference between the peak and the previous trough, hereinafter named as tidal range) and of tidal semi-period during the flood tide (hereinafter named as tidal period). Mean tidal range at PS is 0.60 m, with more than 20 % of the data greater than 0.80 m (i.e. spring tide; see Fig. 2a). Tidal period shows a lower variability in the distribution, with a mean value at PS of about 6 h 20 min and almost 90 % of the data located between 4 and 8 h (Fig. 2b).
2.3 Hydrodynamic model
Numerical simulations were carried out using the WWTM (Defina, 2000; Carniello et al., 2011), a two-dimensional mathematical model developed at the Department of Civil, Environmental and Architectural Engineering, University of Padua, and successfully applied in the Venice lagoon and in other tidal environments (Carniello et al., 2005; Mariotti et al., 2010; Zarzuelo et al., 2018; Mel et al., 2019b; Pivato et al., 2020). WWTM is a coupled wind–wave tide model that solves the full shallow water equations using a semi-implicit staggered numerical scheme based on Galerkin's approach (D'Alpaos and Defina, 2007). The finite element method allows us to employ elements with different shapes and sizes, providing high flexibility in the spatial discretization of complex geometries, typical of shallow water basins. WWTM describes the hydrodynamic flow field including the flooding and drying processes using a statistical, physics-based approach (Defina, 2000). The wind–wave generation and propagation are computed by solving the equation of wave action conservation, parameterized using the zero-order moment of the wave action spectrum in the frequency domain. The spatial variability in the wind field is accounted for by adopting the interpolation technique proposed by Brocchini et al. (1995). WWTM has been used to reproduce tide propagation, wind set-up, and the effect of the closure of the Lido inlet (i.e. the Treporti and San Nicolò canals; see Fig. 1) by reproducing the raising of the flap gates of the Mo.S.E. system. The computational mesh used in this study reproduces the Venice lagoon and a portion of the Adriatic Sea in front of the three inlets for a total area of about 600 km2. It consists of about 51 000 nodes and 97 000 triangular elements with side lengths of about 100 m for tidal flats and 10 m at the three inlets, where the spatial gradients of the velocity are significant even for small tidal ranges. The elevation of the computational elements is assigned on the basis of the most recent bathymetry of the Venice lagoon provided by the Venice Water Authority. The Strickler bed roughness coefficient (Ks) has been calibrated (Carniello et al., 2005, 2011) to represent the energy dissipation over the different, morphologically representative portions of the lagoon. It is worthwhile pointing out that the capability of the model to reproduce the tide propagation within the lagoon and the flow rates across the three inlets has been widely tested by comparing WWTM results to data records (e.g. Carniello et al., 2011; Mel et al., 2019b), showing absolute errors generally comparable to measurement precision (i.e. lower than 0.02–0.03 m; see Appendix A for the simulation of all the events that involved the raising of the Mo.S.E. barriers which occurred from 3 October 2020 to 11 February 2021).
In the present work WWTM is forced by imposing the tidal signal at the three inlets (i.e. Diga Sud Lido, Diga Nord Malamocco, and Diga Sud Chioggia). The spatial and temporal distribution of the wind field is reconstructed following the approach described in Carniello et al. (2012) and considering the wind climate gauged at Laguna Nord, Malamocco Porto, and Chioggia Porto (see Fig. 1). The wind shear stress at the water surface has been widely calibrated and tested against data collected during the most prominent storms, including three recent events that occurred when the Mo.S.E. system was operational (Mel et al., 2021b).
2.4 Simulation set-up
The effect of the PCL has been addressed on three different scenarios, namely scenario (I), (II), and (III). In scenario (I), the simulations were designed to reproduce tidal circulation with no wind, and the only forcing was a synthetic sinusoidal tide imposed at the three inlets. Different tidal ranges (from 0.1 to 1.4 m) and different periods (from 4 to 8 h) were investigated. All the forcing tides are characterized by an SL peak of 1.20 m, given that the PCL would be effective for peaks from 1.10 m (the safeguard threshold of PS and Burano) to 1.30 m (the safeguard threshold of Chioggia, which would marginally benefit from the closure of the Lido inlet). In scenario (II), constant velocities (from 5 to 20 m s−1) of north-easterly wind (i.e. Bora, incoming direction of 45∘ N) and south-easterly wind (i.e. Sirocco, incoming direction of 165∘ N) have been superimposed on the same tidal forcings as scenario (I). Scenario (III) comprises all the 42 events occurring in the period 2019–2020 with gauged SL peak ≥ 1.10 m at PS, including some events when the Mo.S.E. system was operational (in such cases the safeguard threshold has been referred to as the SL gauged at the CNR platform). In this scenario, the model has been forced with the SLs gauged at the three inlets and the wind measured at Laguna Nord, Malamocco Porto, and Chioggia Porto (Fig. 1). These events are characterized by different tidal ranges (from 0.3 to 1.5 m), different periods (from 3 to 8.5 h, plus two events that involved two tidal cycles), different meteorological conditions (i.e. wind speed and direction), and different initial conditions (i.e. SL at the troughs and tidal range of the previous tidal cycle).
For all the three scenarios and for each event, the tidal dynamics have been reproduced through four different runs, namely the following:
-
run (a), without any operation at the Mo.S.E. barriers (unregulated lagoon);
-
run (b), by closing the Treporti and San Nicolò canals at the beginning of the flood tide, i.e. when the flow rate through the Lido inlet computed in run (a) is null;
-
run (c), like run (b), but including the intra-gate infiltration through the Treporti and San Nicolò barriers estimated by using a classical formulation for orifice flows as proposed by Mel et al. (2021b) on the basis of the SL difference computed in run (b) between control section 1 and 2 (Treporti) and between control section 1 and 3 (San Nicolò) (Fig. 1);
-
run (d), like run (c), but opening the Treporti and San Nicolò canals when the SL difference computed in run (c) between control section 1 and 2 (Treporti) and between control section 1 and 3 (San Nicolò) is null.
The effect of the PCL has been addressed by comparing the SL peaks computed at PS, Burano, and Chioggia between run (d) and (a).
3.1 Scenario (I): reduction of the sea level peak
Figure 3 shows the reduction of the SL peak (i.e. the SL peak difference between run (a) and (d), hereinafter named as ΔH) due to the PCL under scenario (I), i.e. a sinusoidal tide with no wind. Figure 3a–c show the ΔH at PS, Burano, and Chioggia for a forcing tide characterized by a period of 6 h and different tidal ranges. A first, important, result is the linearity of the relationship between tidal range and ΔH at the three gauges. Notably, a linear relationship is achieved only if the tidal range refers to the tide signal imposed at the inlets (solid bullets, hereinafter named as seaward tidal range, HSW) and not at the specific lagoonal gauge (opaque bullets). This can be explained by the effect of tide propagation on the lagoonal tidal range, which can be significantly altered far from the inlets. The benefit of the PCL in terms on ΔH is significant.
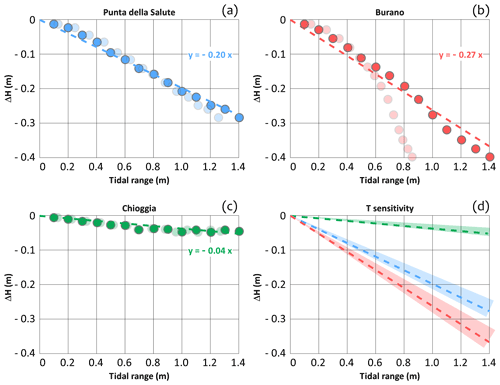
Figure 3Synthetic sinusoidal tide; no wind condition (scenario I). Reduction of the sea level peak (ΔH) due to a partial use of the Mo.S.E. system (Lido inlet closed, PCL). (a–c) Tidal period of 6 h. (a) Punta della Salute; (b) Burano; (c) Chioggia. Solid bullets refer to the seaward tidal range and opaque bullets to the tidal range computed at the specific lagoonal gauge. (d) Effect of the tide period on the slope of the linear regression (range 4–8 h). Dashed lines refer to the relationships computed for a tidal period of 6 h at PS (blue, panel a), Burano (red, panel b), and Chioggia (green, panel c).
For a tidal range (i.e. seaward tidal range, to which this study hereinafter refers) of 0.6 m, the PCL would reduce the SL peak by about 0.12 m at PS, 0.16 m at Burano, and 0.02 m at Chioggia. For tidal periods between 4 and 8 h, results are not significantly affected by the tidal period, as shown in Fig. 3d. Drawing a linear relationship is fundamental for investigating the effectiveness of the PCL on a large dataset as the ΔH can be estimated through the SL difference gauged between the SL peak and the previous trough. As a note, the contribution of the flow rate discharged into the lagoon due to leakage (run c) through the gates is between 5 % and 10 % of the total ΔH, independently of the tidal range (not shown).
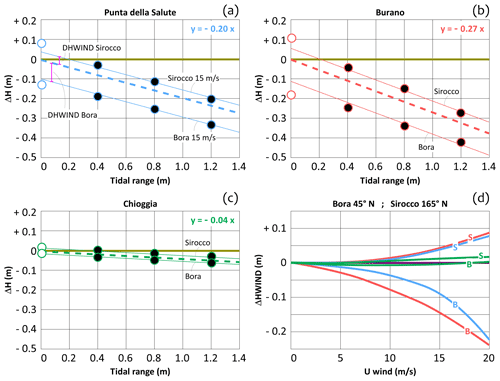
Figure 4Synthetic sinusoidal tide, tidal period of 6 h, PCL. ΔH variation in the case of wind (ΔHWIND). (a) Punta della Salute; (b) Burano; (c) Chioggia. Dashed lines refer to the relationship obtained with no wind (scenario I, Fig. 3) and solid thin lines to scenario (II), with Sirocco and Bora winds of 15 m s−1. White bullets refer to the simulations performed with no tide. (d) ΔH variation with respect to the no wind condition (ΔHWIND) computed at PS (blue lines), Burano (red), and Chioggia (green), ranging the speeds of Bora and Sirocco from 0 to 20 m s−1.
3.2 Scenario (II): the wind set-up constraint
Mel et al. (2019a) showed that the wind set-up during the closure of the lagoon is significantly larger if compared to the unregulated condition. As the full use of the Mo.S.E. system could flood Chioggia during intense north-easterly winds (Mel et al., 2019a, 2021a), it is crucial to investigate the specific effect of the PCL on wind set-up. Figure 4 compares the relationship between tidal range and ΔH if Bora (45∘ N) and Sirocco (165∘ N) winds are superimposed on a tide of 6 h period. Figure 4a–c illustrate the results at PS, Burano, and Chioggia for a wind speed of 15 m s−1. The relationship is still linear (black bullets and solid lines). If compared to scenario (I) (dashed lines), the slope of the regression does not change, but the intercept is not null. In the case of wind, the PCL would produce an additional variation in the SL peak with respect to scenario (I) (namely, ΔHWIND, i.e. the distance between solid and dashed lines). ΔHWIND can be positive or negative and depends only on the characteristics of the wind (speed and direction) and not on the tidal range. Specifically, in the case of Sirocco the PCL could be detrimental, producing SL peaks even higher with respect to the unregulated condition (up to 0.1 m; Fig. 4a and b). Conversely, Bora, which is the prevailing wind in the Venice lagoon, would reduce the SL peak at all the three gauges if the PCL is implemented. This result is very important as the PCL does not enhance the wind set-up at Chioggia, as occurs when all the three inlets are closed. Notably, in the case of Bora, the PCL enhances the SL gradient between PS at Chioggia but only by reducing the SL at PS and not by increasing the SL at Chioggia. Panel (d) shows the relationship between wind speed and ΔHWIND for Bora and Sirocco, confirming an additional reduction of the SL in the whole lagoon in the case of north-easterly winds and an SL increase in the case of south-easterly winds. This result can be explained by the hydrodynamic effect of a wind blowing over Venice lagoon on the flow rate across the three inlets (see Zecchetto et al., 1997; Mel et al., 2019a). In an unregulated lagoon, when Bora wind is blowing, SL increases in the southern part of the lagoon and decreases in its northern part. Therefore, an additional water volume flows into the lagoon through the northern Lido inlet and out of the lagoon through the southern Chioggia inlet. Conversely, Sirocco wind produces an additional volume entering the lagoon through the Chioggia inlet and an additional volume discharged toward the sea through the Lido inlet. In both the cases, the additional water volume flowing through the Lido inlet will disappear during the PCL. Therefore, in the case of Sirocco, the net volume entering the lagoon will increase, raising the SL in the whole lagoon. Conversely, Bora wind reduces the total water volume entering the lagoon, decreasing the SL accordingly (Fig. 4d).
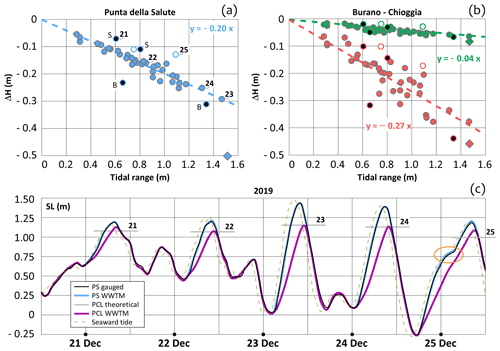
Figure 5Dataset 2019–2020. SL peaks ≥ 1.10 m at PS (or at the CNR platform during the tests performed at the Mo.S.E. barriers since October 2020). Relationship between tidal range and ΔH at (a) Punta della Salute (blue), (b) Burano (red), and Chioggia (green). Black bullets indicate the events characterized by strong Bora (B) or Sirocco (S), white bullets are the events when two tidal cycles were merged due to a prominent seiche wave in the Adriatic Sea, and rhombus is the event of 12 November 2019. (c) Time series 21–25 December 2019 at PS. SL observed (black line) and computed by means of the hydrodynamical model (PCL, purple; unregulated condition, blue). SLs computed at the peak by Eq. (1) are represented by the horizontal grey lines and mean gauged seaward SL by the grey dashed line.
3.3 Scenario (III): 2019–2020 dataset
The three linear relationships (Eqs. 1–3) provided in Sect. 3.1 for estimating the ΔH referring to the seaward tidal range were verified considering data from the 42 storm events which occurred in the years 2019 and 2020 (Fig. 5). Results refer to the gauges of PS (blue), Burano (red), and Chioggia (green). Figure 5a and b compare the ΔH computed by the hydrodynamic model forced by the observed tidal and meteorological data (bullets) to the ΔH estimated by using Eqs. (1)–(3) (dashed lines, scenario I). The bullets nicely match the dashed lines, confirming the robustness of the linear regression. The mean error considering all the events is 2 cm for PS, 4 cm for Burano, and 1 cm for Chioggia. The reliability of the linear regression can be improved if some events are excluded from the comparison. Specifically, the most important discrepancies affect (i) events when a significant Bora (B) or Sirocco (S) wind blew over the lagoon (U wind > 10 m s−1) at the SL peak (black bullets); (ii) events that involved two tidal cycles due to a prominent seiche wave in the Adriatic Sea, failing the hypothesis of sinusoidal tide (white bullets, see the example of 25 December 2019 in Fig. 5c); (iii) the exceptional storm that occurred on 12 November 2019 (rhombus; see Cavaleri et al., 2020, for more details about the singularity of such an event). Remarkably, Bora and Sirocco respectively enhance and reduce the ΔH, as demonstrated in Sect. 3.2 (Fig. 4d). Figure 5c illustrates an example of the effect of the PCL on the SL peak at PS within the period 21–25 December 2019 (these events are labelled in Fig. 5a as 21–25). The five events falling within that period are characterized by different tidal and meteorological forcings. Specifically, on 21 December Sirocco reduces the ΔH by introducing a positive ΔHWIND, i.e. the discrepancy between the purple line, which represents the SL computed by the model, and the grey horizontal line, which is the SL computed at the peak by using Eq. (1). On 25 December, the tide signal was significantly altered by a longitudinal seiche affecting the Adriatic Sea, showing an inflection (highlighted by the orange circle in Fig. 5c) which reduces the benefit of the PCL. Notably, the events which occurred on 23 and 24 December, characterized by the highest tidal ranges (≥ 1.30 m), nicely fit the linear regression (Fig. 5a).
Results confirm the reliability of Eqs. (1)–(3), with particular reference to events not involving more than one tide cycle (which are very rare) and not affected by strong winds. Such equations can be conveniently applied to any surge based on the tidal and wind dataset (see Sect. 3.5).
3.4 Flow rate through the inlets
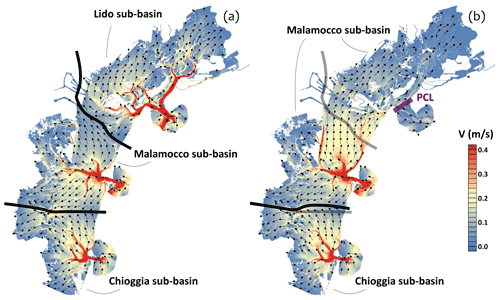
The impact of the PCL on the lagoon hydrodynamics is significant (Fig. 6). The PCL affects the velocity field during the flood tide and depletes the Lido sub-basin, causing an enlargement of the Malamocco sub-basin and a slightly different position of the Chioggia sub-basin (Fig. 6, solid black lines).
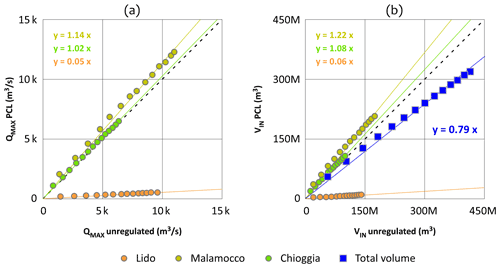
Figure 7Sinusoidal tide, no wind (scenario I). Tidal range from 0.1 to 1.4 m and period of 6 h. Comparison of maximum flow rate (a) and water volume entering the lagoon (b) at the three inlets during the flood tide (x axes unregulated lagoon; y axes PCL).
The effects of the PCL on the Venice lagoon hydrodynamics have been addressed in terms of alteration of flow rates through the three inlets. For each inlet and tidal range belonging to scenario (I), the incoming fluxes during the flood tide have been compared to the conditions of an unregulated lagoon, in accordance with the method described in Sect. 2.4. Figure 7 shows the results for a tidal period of 6 h. The comparison of the average and maximum flux is evidence that the PCL enhances the flow rate through the Malamocco and Chioggia inlets for all the tidal ranges (Fig. 7a). The relationship is linear, with regression slopes of 1.14 (Malamocco inlet, yellow) and 1.02 (Chioggia inlet, green), for the maximum flow rate. Similar values (not shown) are obtained for the average flow rate. A wider difference is observed in the water volumes flowing into the lagoon (Fig. 7b) as the PCL increases the duration of the flood tide due to lower internal SL. Specifically, there is evidence of a volume increase of 22 % through the Malamocco inlet and 8 % through the Chioggia inlet. Conversely, the total volume flowing into the lagoon through the three inlets is reduced by 21 % (blue squares).
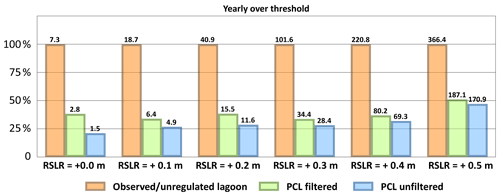
Figure 82000–2019 dataset with a RSLR ranging from +0.0 m (present condition) to +0.5 m. Comparison of the annual number of closures to the increasing RSLR. Orange bars illustrate the total number of SL peaks over threshold, green bars the residual events over threshold by implementing the PCL under the filtered scenario, and blue bars the residual events if the PCL will be implemented during all the SL peaks.
3.5 Operating the Lido inlet under climate change
The linear relationship described in Sect. 3.1 allows us to estimate the number of PCL closures capable of limiting the SL below the threshold at PS, Burano, and Chioggia. The hindcast dataset of tidal and meteorological observations of the period 2000–2019 has been analysed. For investigating possible future scenarios, SLs were increased by adding different values of RSLR up to +0.5 m (i.e. slightly exceeding the projected RSLR in the northern Adriatic Sea for the year 2100 under the IPCC RCP 2.6 scenario; see Zanchettin et al., 2021) at steps of +0.1 m, assuming that the mean SL does not significantly affect tidal range and surge characteristics, as shown by several studies (Bondesan et al., 1995; Umgiesser and Matticchio, 2006; Mel et al., 2013). Figure 8 shows the annual number of events over threshold. Specifically, orange bars represent the unregulated condition and blue bars the residual events over threshold by implementing the PCL to all the events (unfiltered analysis). Nevertheless, strong winds and events that involve multiple tidal cycles can reduce the benefit of the PCL, as shown in Sects. 3.2 and 3.3. Accordingly, in a second analysis some events have been excluded from the potential to implement the PCL (filtered analysis, green bars). Specifically, the filtered analysis omitted the following: (i) the events with a period greater than 8 h, filtering possible flood tides that involve two or more tidal cycles (see Sect. 3.3); (ii) the events showing significant southern winds at the SL peak (i.e. wind speed ≥ 10 m s−1 and wind direction in the range 150–210∘ N at the Laguna Nord gauge), filtering possible lower ΔHs due to the wind set-up (i.e. positive ΔHWIND; see Sect. 3.2); (iii) the events showing SL peaks ≥ 1.30 m at Diga Sud Chioggia, filtering possible water levels over threshold at Chioggia as the small benefit of the PCL on Chioggia SL had been neglected. Green bars represent the residual annual number of events over threshold if the PCL is implemented only in the events which do not show the above-mentioned characteristics (i)–(iii) (filtered analysis). The filtered analysis provides a residual number of events over threshold ranging from 33 % to 38 % of the total events for a RSLR up to +0.40 m and of 50 % for a RSLR of +0.50 m. These residual events should be faced by closing all the three inlets (i.e. a full use of the Mo.S.E. system). Though the filters (i)–(iii) are very precautionary, a modest discrepancy between filtered and unfiltered analysis is evidenced.
Although the uncertainties regarding climate change are still large, this study confirms the efficiency of the PCL as an adaption strategy to extend the lifetime of the Mo.S.E. system. Results (Fig. 8) show that the PCL would keep the frequency of the full use of the Mo.S.E. to an acceptable level for a few decades, gaining precious time to verify the ongoing evolution of the climatic scenarios, narrowing the actual large uncertainty ranges.
This analysis focuses only on flood protection. As the PCL would significantly modify the lagoon hydrodynamics (Fig. 6), the long-term morphological and ecological consequences of such an operation strategy, which are beyond the scope of this work, surely deserve further investigations. The optimal adaption and management strategy need to be carefully investigated and identified with the aim of balancing flood protection with economic issues and the safeguarding of the lagoon ecosystem.
Structural measures, as well as a high level of technical knowledge, are not necessarily the panacea for the long-term safety of the coast. Adaptation to climate change requires an effective and integrated management of coastal areas, with particular reference to the Venice lagoon, a World Heritage site increasingly threatened by flooding and erosion processes. Though the Mo.S.E. system has the potential to reduce the vulnerability of the Venice lagoon, serious questions arise of whether it is beneficial to the morphology, the ecosystem, and to the wide range of uses of the lagoon. It is of paramount importance to integrate the management of the barriers into a strategic context that addresses the social, economic, and environmental issues raised in any coastal area. Accordingly, some measures should be undertaken to minimize the impacts of the operation of the Mo.S.E. system on water renewal, port activities, and the fishing industry. In order to reduce the number of simultaneous closures of the three inlets during flood events characterized by non-extreme SL, the Malamocco and Chioggia inlets can be left open ensuring the flow of part of the water and the transit of vessels. Such a solution requires the current management criteria of the barriers to be adapted. Toward this goal, the present study shows the results of a hydrodynamic investigation in which the partial use of the Mo.S.E. has been simulated by closing only the Lido inlet (PCL). Simulations were carried out considering both synthetic and realistic tide and wind scenarios. Results show the following:
-
A linear relationship was obtained between the tidal range of the seaward tide signal and the reduction of the sea level (SL) peak in the lagoon (ΔH). Specifically, the reduction has been estimated at 20 % at Punta della Salute (Venice), 27 % at Burano, and 4 % at Chioggia; the linear contribution (5 %–10 %) of intra-gate infiltration has been accounted for. Tidal semi-period does not significantly affect the results.
-
North-easterly winds would produce beneficial effects within all the lagoon, reducing the SL peaks. Conversely, in the case of south-easterly winds, the partial closure of the lagoon involving the Lido inlet only (PCL) could increase the SL.
-
Events that involve multiple tidal cycles often show inflections of the tide signal, reducing the effectiveness of the PCL.
-
Two-thirds of the flood events can be effectively faced by the PCL under relative sea level rise scenarios up to +0.4 m.
Besides this attempt to study some major hydrodynamic aspects related to the partial use of the Mo.S.E. barriers, many open issues remain to be analysed, like the possible long-term effects of such an operation strategy on the bio-morphodynamic evolution of the Venice lagoon. A thorough cost-benefit analysis should be pursued to identify the optimal Mo.S.E. management strategy supporting the resilience of Venice and its lagoon to high tides. The Venice lagoon test case points out the importance of combining non-structural and structural measures to counteract flood risk in coastal areas, bearing in mind the need of investigating the long-term effects related to the strategies adopted to face present priorities.
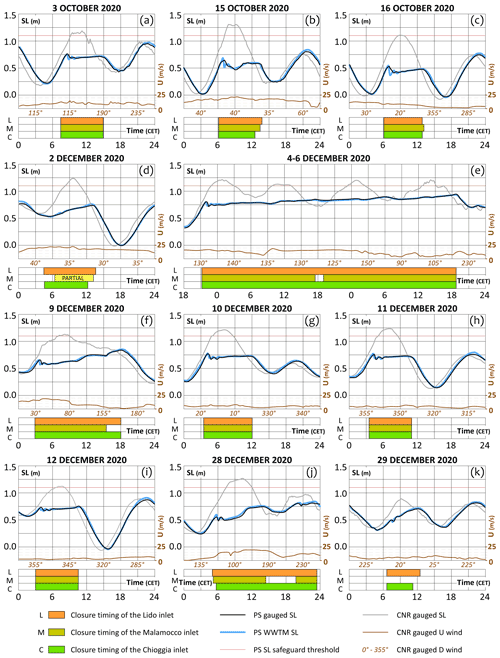
Figure A1Events when the Mo.S.E. barriers have been raised in testing phase. Comparison between SLs observed at the CPSM gauge of PS (black lines) and computed by the WWTM model forcing the closure of the Mo.S.E. barriers (blue lines). Grey and brown lines represent, respectively, the SLs and the wind speeds observed at the CPSM gauge of the CNR platform. The red line represents the safeguard threshold at PS (1.10 m). Bars indicate the periods when the barriers of Lido (orange), Malamocco (yellow), and Chioggia (green) were temporarily closed in the respective inlets.
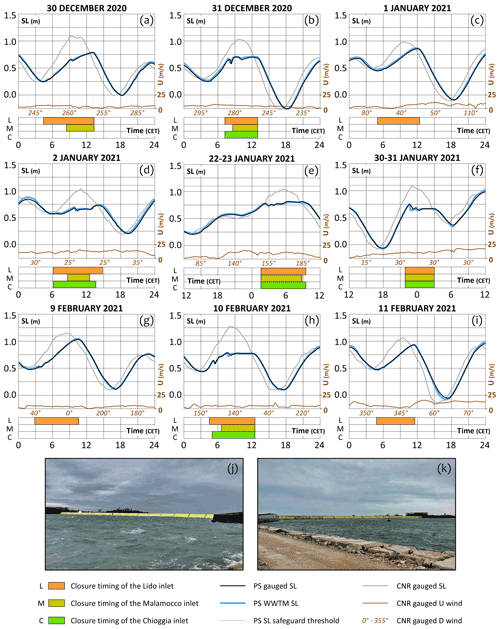
Figure A2Events when the Mo.S.E. barriers were raised in the testing phase. (a–i) Comparison between SLs observed at the CPSM gauge of PS (black lines) and computed by the WWTM model forcing the closure of the Mo.S.E. barriers (blue lines). Grey and brown lines represent, respectively, the SLs and the wind speeds observed at the CPSM gauge of the CNR platform. The red line represents the safeguard threshold at PS (1.10 m). Bars indicate the periods when the barriers of Lido (orange), Malamocco (yellow), and Chioggia (green) were temporarily closed in the respective inlets. (j) and (k) Seaward and lagoonal view of the flap gates raised in the test of 28 December 2020 (photos by R. A. Mel).
The use of the hydrodynamic model WWTM shall be subject to specific authorization. More information is available by contacting the corresponding author. All the data used in the paper are available by contacting the corresponding author.
The contact author has declared that there are no competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the special issue “Future risk and adaptation in coastal cities”. It is not associated with a conference.
Luca Carniello and Daniele Pietro Viero are gratefully thanked for fruitful discussions.
This paper was edited by Javier Revilla Diez and reviewed by two anonymous referees.
American Geophysical Union (AGU): Scientists Debate Wisdom of Plan To Save Venice From Flooding, ScienceDaily, 9 May 2002, available at: http://www.sciencedaily.com/releases/2002/05/020509072937.htm (last access: 22 April 2021), 2020.
Androulidakis, Y. S., Kombiadou, K. D., Makris, C. V., Baltikas, V. N., and Krestenitis, Y. N.: Storm surges in the Mediterranean Sea: Variability and trends under future climatic conditions, Dynam. Atmos. Oceans, 71, 56–82, https://doi.org/10.1016/j.dynatmoce.2015.06.001, 2015.
Bondesan, M., Castiglioni, G., Elmi, C., Gabbianelli, G., Marocco, R., Pirazzoli, P. A., and Tomasin, A.: Coastal areas at risk from storm surges and sea-level rise in northeastern Italy, J. Coastal Res., 11, 1354–1379, 1995.
Brambati, A., Carbognin, L., Quaia, T., Teatini, P., and Tosi, L.: The Lagoon of Venice: Geological setting, evolution and land subsidence, Episodes, 26, 264–268, https://doi.org/10.18814/epiiugs/2003/v26i3/020, 2003.
Brocchini, M., Wurtele, M., Umgiesser, G., and Zecchetto, S.: Calculation of a mass consistent two-dimensional wind-field with divergence control, J. Appl. Meteorol., 34, 2543–2555, 1995.
Brotto, M. T. and Gentilomo, M.: The Venice Lagoon Project. The Barriers at the Lagoon Inlets for Controlling High Tides, Bulletin AIPCN-PIANC, 98, 17–26, 1998.
Capobianco, M., De Vriend, H. J., Nicholls, R. J., and Stive, M. J. F.: Coastal Area Impact and Vulnerability Assessment: The Point of View of a Morphodynamic Modeller, J. Coastal Res., 15, 701–716, 1999.
Carbognin, L., Teatini, P., and Tosi, L.: Eustacy and land subsidence in the Venice Lagoon at the beginning of the new millennium, J. Marine Syst., 51, 345–35, 2004.
Carniello, L., Defina, A., Fagherazzi, S., and D'Alpaos, L.: A combined Wind Wave-Tidal Model for the Venice lagoon, Italy, J. Geophys. Res., 110, F04007, https://doi.org/10.1029/2004JF000232, 2005.
Carniello, L., Defina, A., and D'Alpaos, L.: Morphological evolution of the Venice lagoon: Evidence from the past and trend for the future, J. Geophys. Res., 114, F04002, https://doi.org/10.1029/2008JF001157, 2009.
Carniello, L., D'Alpaos, A., and Defina, A.: Modeling wind-waves and tidal flows in shallow microtidal basins, Estuar. Coast. Shelf S., 92, 263–276, https://doi.org/10.1016/j.ecss.2011.01.001, 2011.
Carniello, L., Defina, A., and D'Alpaos, L.: Modeling sand-mud transport induced by tidal currents and wind waves in shallow microtidal basins: Application to the Venice Lagoon (Italy), Estuar. Coast. Shelf S., 102–103, 105–115, https://doi.org/10.1016/j.ecss.2012.03.016, 2012.
Cavaleri, L., Bajo, M., Barbariol, F., Bastianini, M., Benetazzo, A., Bertotti, L., Chiggiato, J., Ferrarin, C., Trincardi, F., and Umgiesser, G.: The 2019 Flooding of Venice and its implications for future predictions, Oceanography, 33, 42–49, 2020.
Cavallaro, L., Iuppa, C., and Foti, E.: Effect of Partial Use of Venice Flood Barriers, J. Mar. Sci. Eng., 5, 58, https://doi.org/10.3390/jmse5040058, 2017.
Ciavola, P., Ferreira, O., Haerens, P., Van Koningsveld, M., and Armaroli, C.: Storm impacts along European coastlines, Part 2: lessons learned from the MICORE project, Environ. Sci. Policy, 14, 924–933, https://doi.org/10.1016/j.envsci.2011.05.009, 2011.
Costa, P.: Venezia. Economia e analisi urbana, Etaslibri, Milano, 1993.
Cutter, S. L. and Gall, M.: Sendai targets at risk, Nat. Clim. Change, 5, 707–709, https://doi.org/10.1038/nclimate2718, 2015.
D'Alpaos, L. and Defina, A.: Mathematical modeling of tidal hydrodynamics in shallow lagoons: A review of open issues and applications to the Venice lagoon, Comput. Geosci., 33, 476–496, https://doi.org/10.1016/j.cageo.2006.07.009, 2007.
Defina, A.: Two dimensional shallow flow equations for partially dry areas, Water Resour. Res., 36, 3251–3264, 2000.
De Zolt, S., Lionello, P., Nuhu, A., and Tomasin, A.: The disastrous storm of 4 November 1966 on Italy, Nat. Hazards Earth Syst. Sci., 6, 861–879, https://doi.org/10.5194/nhess-6-861-2006, 2006.
EC: White paper – Adapting to climate change: towards a European framework for action, available at: http://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=CELEX:52009DC0147:EN:NOT (last access: 27 April 2021), 2009.
Elko, N. and Briggs T. R.: National coastal management challenges and needs, Shore & Beach, 88, 34–43, 2020.
Eprim, Y.: Venice mobile barriers project: barrier caissons construction details, in: Flooding and environmental challenges for Venice and its lagoon: state of knowledge, edited by: Fletcher, C. A. and Spencer, T., Cambridge University Press, Cambridge, 257–265, 2005.
Ferrarin, C., Ghezzo, M., Umgiesser, G., Tagliapietra, D., Camatti, E., Zaggia, L., and Sarretta, A.: Assessing hydrological effects of human interventions on coastal systems: numerical applications to the Venice Lagoon, Hydrol. Earth Syst. Sci., 17, 1733–1748, https://doi.org/10.5194/hess-17-1733-2013, 2013.
Ferla, M., Cordella, M., Michielli, L., and Rusconi, A.: Long term variations on sea level and tidal regime in the lagoon of Venice, Estuar. Coast. Shelf S., 75, 214–222, 2007.
Few, R., Brown, K., and Tompkins, E.: Climate change and coastal management decisions: Insights from Christchurch Bay, UK, Coast. Manage., 35, 255–270, 2007.
Finotello, A., Lanzoni, S., Ghinassi, M., Marani, M., Rinaldo, A., and D'Alpaos, A.: Migration rates of tidal meanders, P. Natl. Acad. Sci. USA, 115, 1463–1468, https://doi.org/10.1073/pnas.1711330115, 2018.
Gacic, M. and Solidoro, C.: Lagoon of Venice – circulation, water exchange and ecosystem functioning – Introduction, J. Marine Syst., 51, 1–3, 2004.
Gentilomo, M. and Cecconi, G.: Flood protection system designed for Venice, Hydropower & Dams, 2, 46–52, 1997.
Hinkel, J., Lincke, D., Vafeidis, A. T., Perrette, M., Nicholls, R. J., Tol, R. S. J., Marzeion, B., Fettweis, X., Ionescu, C., and Levermann, A.: Coastal flood damage and adaptation costs under 21st century sea-level rise, P. Natl. Acad. Sci. USA, 111, 3292–3297, https://doi.org/10.1073/pnas.1222469111, 2014.
Indirli, M., Knezic, S., Borg, R., Kaluarachchi, Y., Ranguelov, B., Romagnoli, F., and Rochas, C.: The ANDROID Case Study, Venice and Its Territory: a General Overview, Proc. Econ. Financ., 18, 837–848, https://doi.org/10.1016/S2212-5671(14)01009-0, 2014.
Jongman, B.: Effective adaptation to rising flood risk, Nat. Commun., 9, 1986, https://doi.org/10.1038/s41467-018-04396-1, 2018.
Jongman, B., Hochrainer-Stigler, S., Feyen, L., Aerts, J. C. J. H., Mechler, R., Botzen, W. J. W., Bouwer, L. M., Pflug, G., Rojas, R., and Ward, P. J.: Increasing stress on disaster-risk finance due to large floods, Nat. Clim. Change, 4, 264–268, 2014.
Klein, R., Nicholls, R., Ragoonaden, S., Capobianco, M., Aston, J., and Buckley, E.: Technological options for adaptation to climate change in coastal zones, J. Coastal Res., 17, 531–543, 2001.
Kundzewicz, Z. W.: Non-structural flood protection and sustainability, Water Int., 27, 3–13, 2002.
Lionello, P.: The climate of the Venetian and North Adriatic region: variability, trends and future change, Phys. Chem. Earth, 40–41, 1–8, 2012.
Lionello, P., Cavaleri, L., Nissen, K. M., Pino, C., Raicich, F., and Ulbrich, U.: Severe marine storms in the Northern Adriatic: characteristics and trends, Phys. Chem. Earth, 40–41, 93–105, https://doi.org/10.1016/j.pce.2010.10.002, 2012.
Lionello, P., Barriopedro, D., Ferrarin, C., Nicholls, R. J., Orlić, M., Raicich, F., Reale, M., Umgiesser, G., Vousdoukas, M., and Zanchettin, D.: Extreme floods of Venice: characteristics, dynamics, past and future evolution (review article), Nat. Hazards Earth Syst. Sci., 21, 2705–2731, https://doi.org/10.5194/nhess-21-2705-2021, 2021.
Maiolo, M., Mel, R. A., and Sinopoli, S.: A Stepwise Approach to Beach Restoration at Calabaia Beach, Water, 12, 2677, https://doi.org/10.3390/w12102677, 2020.
Marcos, M., Chust, G., Jorda, G., and Caballero, A.: Effect of sea level extremes on the western Basque coast during the 21st century, Clim. Res., 51, 237–248, https://doi.org/10.3354/cr01069, 2012.
Mariotti, G., Fagherazzi, S., Wiberg, P., McGlathery, K., Carniello, L., and Defina, A.: Influence of storm surges and sea level on shallow tidal basin erosive processes, J. Geophys. Res.-Oceans, 115, C11012, https://doi.org/10.1029/2009JC005892, 2010.
Matias, A., Ferreira, O., Vila-Concejo, A., Garcia, T., and Dias J. A.: Classification of washover dynamics in barrier islands, Geomorphology, 97, 655–674, https://doi.org/10.1016/j.geomorph.2007.09.010, 2008.
MedECC: Summary for Policymakers, in: Climate and Environmental Change in the Mediterranean Basin – Current Situation and Risks for the Future. First Mediterranean Assessment Report, edited by: Cramer, W., Guiot, and J., Marini, K., Union for the Mediterranean, Plan Bleu, UNEP/MAP, Marseille, France, 34 pp., 2020.
Mel, R. and Lionello, P.: Verification of an ensemble prediction system for storm surge forecast in the Adriatic Sea, Ocean Dynam., 64, 1803–1814, 2014.
Mel, R., Sterl, A., and Lionello, P.: High resolution climate projection of storm surge at the Venetian coast, Nat. Hazards Earth Syst. Sci., 13, 1135–1142, https://doi.org/10.5194/nhess-13-1135-2013, 2013.
Mel, R., Carniello, L., and D'Alpaos, L.: Addressing the effect of the Mo.S. E. barriers closure on wind setup within the Venice lagoon, Estuar. Coast. Shelf S., 225, 106249, https://doi.org/10.1016/j.ecss.2019.106249, 2019a.
Mel, R., Carniello, L., and D'Alpaos, L.: Dataset of wind setup in a regulated Venice lagoon, Data in Brief, 26, 104386, https://doi.org/10.1016/j.dib.2019.104386, 2019b.
Mel, R., Carniello, L., Viero, D. P., and D'Alpaos, L.: Optimal floodgate operation for river flood management: The case study of Padova (Italy), J. Hydrol. Reg., 30, 100702, https://doi.org/10.1016/j.ejrh.2020.100702, 2020.
Mel, R., Carniello, L., and D'Alpaos, L.: How long the Mo.S. E. barriers will be effective in protecting all urban settlements within the Venice Lagoon? The wind setup constraint, Coast. Eng., 168, 103923, https://doi.org/10.1016/j.coastaleng.2021.103923, 2021a.
Mel, R., Carniello, L., Viero, D. P., Defina, A., and D'Alpaos, L.: The first operations of Mo.S. E. system to prevent the flooding of Venice: Insights on the hydrodynamics of a regulated lagoon, Estuar. Coast. Shelf S., 261, 107547, https://doi.org/10.1016/j.ecss.2021.107547, 2021b.
Melaku-Canu, D., Umgiesser, G., and Solidoro, C.: Short-term simulations under winter conditions in the lagoon of Venice: a contribution to the environmental impact assessment of temporary closure of the inlets, Ecol. Model., 138, 215–230, https://doi.org/10.1016/S0304-3800(00)00403-8, 2001.
Menéndez, M. and Woodworth, P. L.: Changes in extreme high-water levels based on a quasi-global tide-gauge data set, J. Geophys. Res., 115, C10011, https://doi.org/10.1029/2009JC005997, 2010.
Molinaroli, E., Guerzoni, S., Sarretta, A., Masiol, M., and Pistolato, M.: Thirty-year changes (1970–2000) in bathymetry and sediment texture recorded in the lagoon of Venice sub-basins, Italy, Mar. Geol., 258, 115–125, 2009.
Molinaroli, E., Guerzoni, S., and Suman, D.: Adaptations to Sea Level Rise: A Tale of Two Cities – Venice and Miami, arXiv, https://doi.org/10.31230/osf.io/73a25, 2018.
Munaretto, S., Vellinga, P., and Tobi, H.: Flood Protection in Venice under Conditions of Sea-Level Rise: An Analysis of Institutional and Technical Measures, Coast. Manage., 40, 355–380, 2012.
Nunes P. A. L. D., Breil M., and Gambarelli G.: Economic Valuation of On Site Material Damages of High Water on Economic Activities based in the City of Venice: Results from a Dose-Response-Expert-Based Valuation Approach, Feem WP, Nota di Lavoro 53.05, Fondazione Eni Enrico Mattei, 2005.
OECD: The Ocean Economy in 2030, OECD Publishing, Paris, France, 2016.
Oumeraci, H.: Review and analysis of vertical breakwater failures – Lessons learned, Coast. Eng., 22, 3–29, 1994.
Pivato, M., Carniello, L., Viero, D. P., Soranzo, C., Defina, A., and Silvestri, S.: Remote Sensing for Optimal Estimation of Water Temperature Dynamics in Shallow Tidal Environments, Remote Sens.-Basel, 12, 51, https://doi.org/10.3390/rs12010051, 2020.
Pycroft, J., Abrell, J., and Ciscar, J. C.: The Global Impacts of Extreme Sea-Level Rise: A Comprehensive Economic Assessment, Environ. Resour. Econ., 64, 225–253, https://doi.org/10.1007/s10640-014-9866-9, 2016.
Samiolo, R.: Commensuration and styles of reasoning: Venice, cost–benefit, and the defence of place, Account. Org. Soc., 37, 382–402, https://doi.org/10.1016/j.aos.2012.04.001, 2012.
Sarretta A., Pillon, S., Molinaroli, E., Guerzoni, S., and Fontolan, G.: Sediment budget in the Lagoon of Venice, Italy, Cont. Shelf Res., 30, 934–949, https://doi.org/10.1016/j.csr.2009.07.002, 2010.
Semedo, A., Weisse, R., Behrens, A., Sterl, A., Bengtsson, L., and Günther, H.: Projection of global wave climate change toward the end of the twenty-first century, J. Climate, 26, 8269–8288, https://doi.org/10.1175/jcli-d-12-00658.1, 2013.
Silvestri S., D'Alpaos, A., Nordio, G., and Carniello, L.: Anthropogenic modifications can significantly influence the local mean sea level and affect the survival of salt marshes in shallow tidal systems, J. Geophys. Res.-Earth, 123, 996–1012 https://doi.org/10.1029/2017JF004503, 2018.
Smith, J. B. and Lenhart, S. S.: Climate change adaptation policy options, Clim. Res., 6, 193–201, 1996.
Solidoro, C., Melaku Canu, D., Cucco, A., and Umgiesser, G.: A partition of the Venice Lagoon based on physical properties and analysis of general circulation, J. Marine Syst., 51, 147–160, https://doi.org/10.1016/j.jmarsys.2004.05.010, 2004.
Tiggeloven, T., de Moel, H., Winsemius, H. C., Eilander, D., Erkens, G., Gebremedhin, E., Diaz Loaiza, A., Kuzma, S., Luo, T., Iceland, C., Bouwman, A., van Huijstee, J., Ligtvoet, W., and Ward, P. J.: Global-scale benefit–cost analysis of coastal flood adaptation to different flood risk drivers using structural measures, Nat. Hazards Earth Syst. Sci., 20, 1025–1044, https://doi.org/10.5194/nhess-20-1025-2020, 2020.
Tobey, J., Rubinoff, P., Robadue, D., Ricci, G., Volk, R., Furlow, J., and Anderson, G.: Practicing coastal adaptation to climate change: Lessons from integrated coastal management, Coast. Manage., 38, 317–335, 2010.
Umgiesser, G.: The impact of operating the mobile barriers in Venice (MOSE) under climate change, J. Nat. Conserv., 54, 125783, https://doi.org/10.1016/j.jnc.2019.125783, 2020.
Umgiesser, G. and Matticchio, B.: Simulating the mobile barrier (MOSE) operation in the Venice Lagoon, Italy: Global sea level rise and its implication for navigation, Ocean Dyn., 56, 320–332, https://doi.org/10.1007/s10236-006-0071-4, 2006.
UNESCO: Rapporto Su Venezia, Mondadori, Milan, 1969.
UNESCO: From Global to Regional: Local Sea Level Rise Scenarios Focus on the Mediterranean Sea and the Adriatic Sea, Workshop “The future of Venice and its lagoon”, Report 1, 15 pp., available at: http://www.unesco.org/venice/thefutureofvenice (last access: 22 April 2021), 2011.
Van Koningsveld, M., Mulder, J. P. M., Stive, M. J. F., van der Valk, L., and van der Weck, A. W.: Living with sea-level rise and climate change: A case study of the Netherlands, J. Coastal Res., 24, 367–379, 2008.
Vergano, L., Umgiesser, G., and Nunes, P. A. L. D.: An economic assessment of the impacts of the MOSE barriers on Venice port activities, Transport. Res. D-Tr. E., 15, 343–349, 2010.
Viero, D. P. and Defina, A.: Water age, exposure time, and local flushing time in semi-enclosed, tidal basins with negligible freshwater inflow, J. Mar. Syst., 156, 16–29, https://doi.org/10.1016/j.jmarsys.2015.11.006, 2016.
Wadey, M. P., Nicholls, R. J., and Hutton, C.: Coastal Flooding in the Solent: An Integrated Analysis of Defences and Inundation, Water, 4, 430–459, https://doi.org/10.3390/w4020430, 2012.
Wahl, T., Jensen, J. Frank, T., and Haigh, I.: Improved estimates of mean sea level changes in the german bight over the last 166 years, Ocean Dyn., 61, 701–715, 2011.
Wang, X. L., Feng, Y., and Swail, V. R.: Changes in global ocean wave heights as projected using multimodel CMIP5 simulations, Geophys. Res. Lett., 41, 1026–1034, https://doi.org/10.1002/2013GL058650, 2014.
Zanchettin, D., Bruni, S., Raicich, F., Lionello, P., Adloff, F., Androsov, A., Antonioli, F., Artale, V., Carminati, E., Ferrarin, C., Fofonova, V., Nicholls, R. J., Rubinetti, S., Rubino, A., Sannino, G., Spada, G., Thiéblemont, R., Tsimplis, M., Umgiesser, G., Vignudelli, S., Wöppelmann, G., and Zerbini, S.: Sea-level rise in Venice: historic and future trends (review article), Nat. Hazards Earth Syst. Sci., 21, 2643–2678, https://doi.org/10.5194/nhess-21-2643-2021, 2021.
Zarzuelo C., López-Ruiz, A., D'Alpaos, A., Carniello, L., and Ortega-Sánchez, M.: Assessing the morphodynamic response of human-altered tidal embayments, Geomorphology, 320, 127–141, https://doi.org/10.1016/j.geomorph.2018.08.014, 2018.
Zecchetto, S., Umgiesser, G., and Brocchini, M.: Hindcast of a storm surge induced by local real wind fields in the Venice lagoon, Cont. Shelf Res., 17, 1513–1538, 1997.